A feasibility study of the therapeutic application of a mixture of ^67/64Cu radioisotopes produced by cyclotrons with proton irradiation

Abstract

Purpose

⁶⁴Cu and ⁶⁷Cu radioisotopes have nuclear characteristics suitable for nuclear medicine applications. The production of ⁶⁴Cu is already well established. However, the production of ⁶⁷Cu in quantities suitable to conduct clinical trials is more challenging as it leads to the coproduction of other Cu isotopes, in particular ⁶⁴Cu. The aim of this study is to investigate the possibility of using a CuCl₂ solution with a mixture of ^67/64Cu radioisotopes for therapeutic purposes, providing an alternative solution for the cyclotron production problem.

Methods

Copper radioisotopes activities were calculated by considering proton beam irradiation of the following targets: (i) ⁷⁰Zn in the energy range 70–45 MeV; (ii) ⁶⁸Zn in the energy range 70–35 MeV; (iii) a combination of ⁷⁰Zn (70–55 MeV) and ⁶⁸Zn (55–35 MeV). The contribution of each copper radioisotope to the human‐absorbed dose was estimated with OLINDA/EXM software using the biokinetic model for CuCl₂ published by ICRP 53. The total absorbed dose generated by the ^67/64CuCl₂ mixture, obtained through different production routes, was calculated at different times after the end of the bombardment (EOB). A simple spherical model was used to simulate tumors of different sizes containing uniformly distributed ^67/64Cu mixture and to calculate the absorbed dose of self‐irradiation. The biological damage produced by ⁶⁷Cu and ⁶⁴Cu was also evaluated through cellular dosimetry and cell surviving fraction assessment using the MIRDcell code, considering two prostate cancer cell lines with different radiosensitivity.

Results

The absorbed dose to healthy organs and the effective dose (ED) per unit of administered activity of ⁶⁷CuCl₂ are higher than those of ⁶⁴CuCl₂. Absorbed dose values per unit of administered activity of ^67/64CuCl₂ mixture increase with time after the EOB because the amount of ⁶⁷Cu in the mixture increases. Survival data showed that the biological damage caused per each decay of ⁶⁷Cu is greater than that of ⁶⁴Cu, assuming that radionuclides remain accumulated in the cell cytoplasm. Sphere model calculations demonstrated that ⁶⁴Cu administered activity must be about five times higher than that of ⁶⁷Cu to obtain the same absorbed dose for tumor mass between 0.01 and 10 g and about 10 times higher for very small spheres. Consequently, the ⁶⁴CuCl₂‐absorbed dose to healthy organs will reach higher values than those of ⁶⁷CuCl₂. The supplemental activity of the ^67/64CuCl₂ mixture, required to get the same tumor‐absorbed dose produced by ⁶⁷CuCl₂, triggers a dose increment (DI) in healthy organs. The waiting time post‐EOB necessary to keep this DI below 10% (t _10%) depends on the irradiation methods employed for the production of the ^67/64CuCl₂ mixture.

Conclusions

A mixture of cyclotron produced ^67/64Cu radioisotopes proved to be an alternative solution for the therapeutic use of CuCl₂ with minimal DI to healthy organs compared with pure ⁶⁷Cu. Irradiation of a ⁷⁰Zn+⁶⁸Zn target in the 70–35 MeV proton energy range for 185 h appears to be the best option from among all the production routes investigated, as it gives the maximum amount of activity, the shortest t _10% (10 h), and less than 1% of ⁶¹Cu and ⁶⁰Cu impurities.

1. INTRODUCTION

Copper is an essential element for a multitude of biological processes, being a catalytic cofactor of many enzymes and a key structural component of functional proteins with fundamental roles in cellular biology. ¹ Copper also plays a key role in cell replication and growth, and it has been found to be deeply involved in cancer development and progression. The potential role of Cu²⁺ ions and their ability to selectively target cancerous cells was recently assessed. ² Preliminary results showed a high uptake of ⁶⁴Cu²⁺ in prostate cancer cells, demonstrating the great diagnostic potential of ⁶⁴CuCl₂ for cancer. ³ The therapeutic potential of ⁶⁴CuCl₂ was also assessed in malignant melanoma ⁴ and glioblastoma tumor‐bearing mice ⁵ and a high tumor uptake of ⁶⁷CuCl₂ was observed in colorectal tumor‐bearing mice. ⁶ Despite only two preliminary reports have demonstrated a therapeutic effect of ⁶⁴CuCl₂ in patients affected by relapsing malignancies (i.e. glioblastoma, prostate and uterine cancer), ⁷ , ⁸ these findings suggest that both ⁶⁴CuCl₂ and ⁶⁷CuCl₂ could be used to further treat these types of tumors in future.

The five copper radioisotopes with the nuclear characteristics most suitable for nuclear medicine applications are ⁶⁰Cu, ⁶¹Cu, ⁶²Cu, ⁶⁴Cu, and ⁶⁷Cu. ⁹ Among them, ⁶⁰Cu (t _1/2 = 23.7 m), ⁶¹Cu (t _1/2 = 3.333 h), and ⁶²Cu (t _1/2 = 9.673 m) are pure positron emitters; ⁶⁷Cu (t _1/2 = 61.83 h) decays emitting a combination of β^– particles with E _max = 0.56 MeV (100%) and γ‐rays at 92 keV (23%) and 185 keV (48%), suitable for SPECT imaging, and could thus be used as a theranostic agent; ⁶⁴Cu (t _1/2 = 12.7 h) decays mostly through the emission of β^– (38%), β⁺ (18%) particles and Auger electrons, so it can find both diagnostic and therapeutic applications. ⁶⁴Cu‐based therapy can be advantageous if the radionuclide is incorporated into the cell nucleus as its Auger electron emission could deliver a very high dose to the DNA, killing the cells.

While ⁶⁴Cu radiopharmaceuticals are employed in the clinical diagnosis of some types of tumors, ¹⁰ the limited availability of ⁶⁷Cu ¹¹ has to date severely restricted its use, despite its promising results in radioimmunotherapy, ¹² , ¹³ , ¹⁴ peptide receptor radionuclide therapy, ¹⁵ , ¹⁶ and PSMA targeting therapy. ¹⁷ , ¹⁸

The production of ⁶⁴Cu is well‐established, and it is mainly based on the use of ⁶⁴Ni or ⁶⁸Zn targets, irradiated by proton or deuteron beams. ¹⁹

The production of ⁶⁷Cu is instead more challenging and still under investigation, ²⁰ as emerged from the dedicated Coordinated Research Project (CRP) promoted by the International Atomic Energy Agency (IAEA). ²¹ It emerges from recent publications on ⁶⁷Cu production ²² , ²³ , ²⁴ , ²⁵ that the use of highly enriched target materials results in a pure final product at the end of irradiation with the ⁶⁸Zn(γ,p)⁶⁷Cu, ⁷⁰Zn(p,α)⁶⁷Cu, and ⁷⁰Zn(d,x)⁶⁷Cu reactions at low energy (E _p < 35 MeV, E _d < 27 MeV). All nuclear reactions concerned have low cross‐section values (below 30 mb), leading to a rather low ⁶⁷Cu yield. In order to increase the proton‐based production of ⁶⁷Cu, it is necessary to use ⁶⁸Zn‐ or ⁷⁰Zn‐enriched targets and irradiations at intermediate beam energies (i.e., larger than 30 MeV). However, this approach leads to the coproduction of Cu isotopic impurities, in particular ⁶⁴Cu. As Cu isotopes cannot be separated by standard (i.e., radiochemical) methods, this is a concern from a pharmaceutical point of view. According to the European Pharmacopeia, the radionuclidic purity of a radiopharmaceutical must indeed be greater than 99%. In general, this limit guarantees that the dose increase due to the impurities remains below 10%. ²⁶ , ²⁷ If ⁶⁴Cu is considered an impurity, it will be then necessary a long waiting time after the irradiation of targets to achieve the required radionuclidic purity, losing most of the ⁶⁷Cu produced activity. However, as both ⁶⁷Cu and ⁶⁴Cu have promising therapeutic characteristics, ⁶⁴Cu could not be considered as an impurity, but, on the contrary, as a therapeutic coadjuvant of ⁶⁷Cu, with also the possibility of exploiting its β⁺ emission for the monitoring of the radiopharmaceutical uptake and the biodistribution in the body by PET imaging, with higher accuracy compared to the SPECT imaging allowed by the γ‐emissions of ⁶⁷Cu. Therefore, a combination of the two radionuclides is worthwhile to be investigated.

The energy of released particles is an important parameter to be evaluated for cancer therapy with β emitters because therapeutic effectiveness can be low if electron penetration ranges are greater than the tumor dimensions. Generally, tumors come in a variety of sizes, ranging from a single or a few cells to large tumors with radii of several centimeters. A radionuclide that releases a high absorbed dose to large tumors may be nonoptimal for small ones because a substantial fraction of the β‐particle energy will be delivered to healthy tissues adjacent to the tumors. Therefore, an optimal tumor diameter range for each radionuclide has been identified in order to produce an effective treatment. ²⁸ , ²⁹ Wheldon et al. ²⁸ were the first to propose the use of a panel of β^–‐emitting radionuclides for clinical scenarios involving a vast number of tumors and metastases of different sizes. The authors reported that the overall level of variation in the probability of cure of tumors with extensive differences in radii could be reduced when using β^– emitters with different β end‐point energies. ²⁸ A clinical study, using a combined ⁹⁰Y/¹⁷⁷Lu‐DOTATATE therapy, demonstrated that the combination of the two radionuclides with differing β^– energy and, therefore, a different maximum range in tissues (2.27 MeV and 10 mm for ⁹⁰Y, and 0.497 MeV and 2–4 mm for ¹⁷⁷Lu, respectively), produced longer overall patient survival than a single radioisotope treatment. ³⁰ Nevertheless, it is important to underline that the chemical properties of the same molecule, labeled with different radionuclides, are not identical. The radiolabeled molecules seem to be similar, but can present different stability and biodistribution, because each element has a specific chemical demand arising from its fundamental characteristics such as the atomic number, charge, and radius, which result in a distinct coordination number and geometry. ³¹ The advantage of using a radionuclide cocktail with isotopes of the same element is that their labeled conjugates will have the same stability and biodistribution due to identical chemical properties. In case of ⁶⁴Cu and ⁶⁷Cu, despite their different decay schemes, the β^– end‐point energies are quite similar (0.65310 and 0.56170 MeV for ⁶⁴Cu and ⁶⁷Cu, respectively). Therefore, a mixture of the two radionuclides is not expected to provide a therapeutic benefit for treating tumors of different sizes, as demonstrated by the similar therapeutic potential of ⁶⁴Cu and ⁶⁷Cu on a per‐decay basis by both in vitro and in vivo studies. ³² , ³³ However, supposing that the presence of ⁶⁴Cu will not adversely affect the absorbed dose to healthy organs compared with the administration of pure ⁶⁷Cu, the possibility of using a mixture of ⁶⁷Cu and ⁶⁴Cu for therapeutic purposes will provide an alternative solution to the ⁶⁷Cu supply.

This work investigated the production of ⁶⁷Cu/⁶⁴Cu using proton beams up to 70 MeV in three scenarios: (i) the use of ⁷⁰Zn targets in the energy range 70–45 MeV; (ii) the use of ⁶⁸Zn targets in the energy range 70–35 MeV; (iii) the use of a combination of ⁷⁰Zn (70–55 MeV) and ⁶⁸Zn (55–35 MeV) targets, as presented in the INFN patent. ³⁴

To assess the possibility of using a mixture of ^67/64Cu radioisotopes for therapeutic purposes, the contribution of each radioisotope to the human‐absorbed dose after the administration of the CuCl₂ solution was estimated using the biokinetic model published by ICRP 53 ³⁵ with the OLINDA/EXM software's adult male/female reference phantoms. ³⁶ The total absorbed dose from a CuCl₂ solution containing a mixture of both radioisotopes was then calculated considering different production methods at different times after the end of bombardment (EOB). Furthermore, a simple model was used to simulate tumors as isolated unit density spheres immersed in an infinite unit density medium and to calculate the absorbed dose attributable to self‐irradiation for the activity uniformly distributed into the spheres. Cellular dosimetry and cell surviving fraction were also evaluated assuming the administration of ⁶⁷CuCl₂ or ⁶⁴CuCl₂ to two prostate cancer cell lines with different radiosensitivity to determine the biological damage produced by each radioisotope.

2. MATERIALS AND METHODS

2.1. Copper‐67 and Copper‐64 production yields

The production of ⁶⁷Cu, ⁶⁴Cu, ⁶¹Cu, and ⁶⁰Cu radionuclides was calculated with the IAEA tool ISOTOPIA, ³⁷ taking into account the following priority list for the selection of nuclear cross sections (xs):

1. the IAEA recommended values ³⁸ ;

2. the experimental values available in the literature and the EXFOR database ³⁹ ;

3. the TALYS estimated trend available in the TENDL library. ⁴⁰

These criteria led to the following configuration for the different scenarios: (A) a ⁶⁸Zn target with a proton beam energy in the range 70–35 MeV (the exit energy for a 6.2 mm thick ⁶⁸Zn target): ⁶⁷Cu and ⁶⁴Cu activities were calculated by taking the IAEA xs recommended data into account, ^{38 61}Cu activity by considering experimental xs values, ³⁹ , ⁴¹ and ⁶⁰Cu activity considering TENDL nuclear model predictions ⁴⁰ ; (B) a ⁷⁰Zn target with a proton beam in the energy range 70–45 MeV (the exit energy for a 5.08 mm thick ⁷⁰Zn target): ⁶⁷Cu and ⁶⁴Cu activities were calculated by considering experimental xs data, ²⁵ , ^{39 61}Cu activity was estimated based on the use of the TENDL library, ⁴⁰ and ⁶⁰Cu production was not foreseen; (C) the combined ⁷⁰Zn+⁶⁸Zn target: in the energy range 70–55 MeV (⁷⁰Zn target), ⁶⁷Cu and ⁶⁴Cu activities were calculated by considering experimental data, ²⁵ , ^{39 61}Cu activity was based on the use of TENDL‐predicted cross sections, ⁴⁰ while ⁶⁰Cu production was not foreseen; in the energy range 35–55 MeV (⁶⁸Zn target), ⁶⁷Cu and ⁶⁴Cu activities were calculated by taking IAEA data into account, ^{38 61}Cu activity was based on the use of experimental values, ⁴¹ and ⁶⁰Cu activity by considering the TENDL library. ⁴⁰

The yield for all the different nuclear reaction routes concerned was estimated by considering a proton beam current of 1 µA and irradiation times of 62 h (corresponding to a saturation factor [SF] of about 50% of ⁶⁷Cu), 124 h (⁶⁷Cu SF ≈ 75%) and 185 h (⁶⁷Cu SF ≈ 88%) as irradiation parameters.

2.2. Biokinetic model of CuCl₂

The biokinetic model published by ICRP 53 ³⁵ was used to estimate the total number of disintegrations in the main human source organs after administration of ^xx CuCl₂.

According to a general first‐order kinetic model, and assuming an immediate uptake into the organs, the fractional activity in a source organ S at time t, A _s(t), after administration of the activity A ₀ is given by the relationship:

$$\frac{A_{\mathrm{S}}\left(t\right)}{A_0}=F_{\mathrm{S}}\sum _{i=1}^m{a}_i{e}^{\left(-\frac{\ln \left(2\right)}{T_{i,\mathrm{eff}}}t\right)}$$ (1)

where F _s is the fractional distribution to organ or tissue S, m is the number of elimination components, and a_i is the fraction of F _S eliminated with effective half‐life T_{i ,eff}, which can be calculated from the corresponding biological half‐life T_i and the physical half‐life T _p of the radioisotope:

$$\frac{1}{T_{i,\mathrm{eff}}}=\frac{1}{T_{\mathrm{p}}}+\frac{1}{T_i}$$ (2)

The model parameters to calculate copper uptake in the main human source organs such as the liver, brain, kidneys, pancreas, and in the entire body are reported in Table S1. ³⁵ The normalized cumulated activity is then calculated according to the formula:

$$\frac{{\stackrel{\sim }{A}}_{\mathrm{S}}}{A_0}=F_{\mathrm{S}}\sum _{i=1}^m{a}_i\frac{T_{i,\mathrm{eff}}}{\ln \left(2\right)}$$ (3)

2.3. Dosimetric calculations applied to human phantoms

Dosimetric calculations for ^xx CuCl₂ were performed with the Organ Level Internal Dose Assessment (OLINDA) software code version 2.2.0, ³⁶ , ⁴² based upon the RADAR method for internal dose estimation, ⁴³ aiming at obtaining both the absorbed doses per unit of administered activity in each organ and the effective dose (ED). The normalized cumulated activity in the source organs obtained with the ICRP 53 biokinetic model ³⁵ and both female and male NURBS‐type phantoms, ⁴⁴ based on the standardized masses defined by ICRP 89, ⁴⁵ were used as input for the calculations with the OLINDA software. Effective dose equivalent (EDE) and ED values were calculated by using the three different tissue‐weighting factors sets, recommended by ICRP 26, ⁴⁶ ICRP 60, ⁴⁷ and ICRP 103. ⁴⁸

Finally, the absorbed doses to different healthy organs (D _organ,_t) and the total ED (ED_t) per unit administered activity caused by the mixture of copper radioisotopes obtained from different production methods were calculated at different times after EOB, using the following equations:

$$D_{\mathrm{organ},t}\left(t\right)=\sum _{xx}{f}_{x{x}_{\mathrm{Cu}}}\left(t\right)·D_{\mathrm{organ},x{x}_{\mathrm{Cu}}}$$ (4)

$$\mathrm{E}{\mathrm{D}}_t\left(t\right)=\sum _{xx}{f}_{x{x}_{\mathrm{Cu}}}\left(t\right)·\mathrm{E}{\mathrm{D}}_{x{x}_{\mathrm{Cu}}}$$ (5)

where f_{xx Cu} (t) is the fraction of total activity corresponding to ^xx Cu radioisotope at the time t after EOB and D _organ, _{xx Cu} and ED _{xx Cu} are the absorbed dose to an organ and the ED due to unit administered activity of ^XX CuCl₂.

2.4. Dosimetric calculations applied to a macroscopic tumor (sphere model)

The OLINDA software's sphere model module was used to simulate tumors as isolated unit density spheres immersed in an infinite unit density medium. This module allows for the evaluation of the absorbed dose solely from self‐irradiation for activity uniformly distributed throughout the spheres. Data are available for discrete sphere masses ranging from 0.01 to 6000 g. Calculations for smaller spheres were performed using the MIRDcell programme, ⁴⁹ evaluating self‐doses to spheres ranging from 10 µm of diameter (mass: 5 × 10^–10 g) up to 2.5 mm (mass: 8 × 10^–3 g). Both programmes were used to calculate the absorbed doses for ⁶⁷Cu and ⁶⁴Cu radionuclides, which were then compared with the data for ¹⁷⁷Lu.

The tumor‐absorbed dose generated by the mixture of copper radioisotopes obtained from different irradiations was also calculated at different times after EOB. Calculations were performed assuming an immediate uptake of the ^67/64CuCl₂ mixture in the tumor and disregarding biological elimination. The percentage of the number of nuclear transformations (%nt) occurring within the tumor due to each ^xx Cu radioisotope in the mixture was evaluated on the basis of the total activity fraction corresponding to each ^xx Cu radioisotope at the time of injection and the physical half‐life of the radioisotope:

$$\%\mathrm{n}{\mathrm{t}}_{{}^{xx}\mathrm{Cu}}\left(t\right)=100·\frac{\%A{}^{xx}\mathrm{Cu}\left(t\right)·T_{\mathrm{p}}\left({}^{xx}\mathrm{Cu}\right)}{{\sum }_{xx}\%A{}^{xx}\mathrm{Cu}\left(t\right)·T_{\mathrm{p}}\left({}^{xx}\mathrm{Cu}\right)}$$ (6)

The tumor‐absorbed dose for the ^67/64CuCl₂ mixture was then obtained by weighting the absorbed dose of each ^xx Cu radioisotope according to the fraction of decays inside the sphere.

2.5. Cellular dosimetry and survival

MIRDcell software ⁴⁹ was used to compare the biological damage caused by ⁶⁷Cu or ⁶⁴Cu radionuclides. This programme makes it possible to determine the cellular radiation absorbed doses as well as the surviving fraction of cells in a 3D multicellular cluster after radionuclide treatment. Calculations were performed considering all β and conversion electron emissions with a contribution to the total energy emitted per nuclear transformation greater than 0.1%. Calculations considered the full energy spectrum for β particles. Cellular S values (mean absorbed dose per unit cumulated activity in the source region) were obtained using a model that considers the cell as two concentric spheres with a 10 and 4 µm radius, representing the whole cell (c) and its nucleus (n), respectively. The cell size was selected based upon the mean size of some of the most studied cancer cell lines, ⁵⁰ whereas the cell nucleus size was calculated by using the assumption that the nucleus volume is approximately 8% of the whole cell volume. ⁵¹ The region between both spheres represents the cytoplasm (cy), whereas the surface of the outer larger sphere represents the cell surface.

The cellular S value is a dose factor that is determined by the radioisotope used and the spatial relationship between the target and the source region. In this work, cellular S values were obtained assuming that radioactivity was uniformly distributed inside one of the cell regions (source region) and taking into account different distances between the target and the source cells (from 20 to 124 µm). Two types of treatment were studied: the first one assuming that the entire cell was both the source and target region, whereas the second one assuming that the cell nucleus was the target region and the cytoplasm the source region. Finally, calculated S values were used to obtain the absorbed dose (D) to the target region using the following equation:

$$D_{\mathrm{target}\leftarrow \mathrm{source}}=N_{\mathrm{source}}\times S_{\mathrm{target}\leftarrow \mathrm{source}}$$ (7)

where N _source is the number of disintegrations in the source region per unit of administered activity (Bq‐h/Bq).

The MIRDcell programme was used to estimate survival for each treatment, assuming a cluster of cells with a spherical shape and a radius of 124 µm, containing 1021 cells with a distance of 20 µm between centers of neighboring cells, and considering that only 50% of the cells were labeled with radioactivity. The programme randomly selects labeled cells in the cluster. Cell activity can vary from zero up to a maximum activity, which in this study was set at 0.02 Bq per cell. The time‐integrated activity coefficient, also known as residence time, representing the cumulative number of nuclear transformations (Bq‐h) occurring in the source region per unit administered activity A ₀ (Bq), was set at 100 h for both ⁶⁷Cu and ⁶⁴Cu radionuclides.

The surviving fraction was obtained by using the linear quadratic model, which assumes that each cell is killed due to the inactivation of two or more targets and considers two possibilities: lethal damage when the cell injury is irreparable, and sublethal damage when the injury is reparable by the cell itself. Then cell survival curve can be determined through two components, αD, which accounts for the linear behavior (proportional to the radiation dose, related to the irreparable injury), and βD, ² which is proportional to the square of the radiation dose (related to the repairable damage). Survival curves were obtained taking into account the absorbed dose generated by both the radiation emitted within the same cell (self‐dose [D _self]) and the radiation emitted by neighboring cells (cross dose [D _cross]), using the next equation:

$$P=e^{-{\alpha }_{\mathrm{self}}{D}_{\mathrm{self}}-{\beta }_{\mathrm{self}}{D^2}_{\mathrm{self}}}\times e^{-{\alpha }_{\mathrm{cross}}{D}_{\mathrm{cross}}-{\beta }_{\mathrm{cross}}{D^2}_{\mathrm{cross}}}$$ (8)

where α _self and β _self and α _cross and β _cross are the linear quadratic parameters that characterize the cellular response to D _self and to D _cross, respectively. Calculations were carried out using α _self = α _cross = α and β _self = β _cross = β and choosing α and β values reported for two types of prostate cancer cell lines with different radiosensitivity, LNCaP (α = 1.081 and β = 0) and PC3 (α = 0.551 and β = 0.021). ⁵²

The biological damage caused by Cu‐radionuclides was also compared with that obtained with ¹⁷⁷Lu, currently the most used radionuclide in theranostics. Therefore, the MIRDcell programme was also run under the same conditions by considering the radionuclide ¹⁷⁷Lu.

3. RESULTS

3.1. ⁶⁷Cu and ⁶⁴Cu production yields

The production yields of ⁶⁷Cu, ⁶⁴Cu and the radioisotopic impurities ⁶¹Cu and ⁶⁰Cu are reported in Table 1. Production yields were estimated considering the proton irradiation of both ⁶⁸Zn and ⁷⁰Zn targets for the different scenarios and irradiation times described.

TABLE 1.

Calculated yields (MBq/µA) of ⁶⁷Cu,⁶⁴Cu,⁶¹Cu, and ⁶⁰Cu radionuclides obtained at the EOB through the proton irradiation of ⁶⁸Zn and ⁷⁰Zn targets for the different scenarios and irradiation times, the waiting time necessary to achieve a ⁶⁷Cu radionuclidic purity of 99% and the amount of ⁶⁷Cu activity at this time

	Irr. time (h)	67Cu at EOB (MBq/µA)	64Cu at EOB (MBq/µA)	61Cu at EOB (MBq/µA)	60Cu at EOB (MBq/µA)	t 99% (h)	67Cu at t99% (MBq/µA)
68Zn: 70–35 MeV	62	1240.1	6512.0	1140.1	26.5	145	244.1
	124	1859.4	6732.9	1140.1	26.5	136	404.8
	185	2165.2	6740.4	1140.1	26.5	133	487.5
70 Zn: 70–45 MeV	62	1751.7	7506.7	11.7	–	139	368.7
	124	2626.5	7761.4	11.7	–	131	604.8
	185	3058.5	7770.0	11.7	–	128	728.3
70 Zn: 70–55 MeV + 68 Zn: 55–35 MeV	62	1881.3	5825.0	40.0	0.0012	132	428.3
	124	2820.9	6022.6	40.0	0.0012	123	710.5
	185	3284.9	6029.3	40.0	0.0012	120	855.6

Table 1 demonstrates that both ⁶⁷Cu and ⁶⁴Cu are produced in all the scenarios investigated and their amount increases with the irradiation time. The activity of ⁶⁴Cu is always greater than that of ⁶⁷Cu at the EOB. However, due to the different half‐lives of the two radioisotopes, the percentage amount of ⁶⁴Cu activity in the total decreases with time after irradiation, whereas the percentage amount of ⁶⁷Cu activity increases (see Figure 1). However, as also reported in Table 1, considering ⁶⁴Cu as an impurity (besides ⁶¹Cu and ⁶⁰Cu) with respect to the ⁶⁷Cu production process, the waiting time necessary to achieve a radionuclidic purity higher than 99% (t _99%) would be quite long (between 120 and 145 h, depending upon the irradiation conditions), causing a decay of about 75–80% of the ⁶⁷Cu produced activity. Both ⁶¹Cu and ⁶⁰Cu radioisotopic impurities are produced by the irradiation of the ⁶⁸Zn target (for both the 70–35 and 55–35 MeV energy ranges), whereas only ⁶¹Cu is generated by the irradiation of the ⁷⁰Zn target for both 70–45 and 70–55 MeV. The fraction of total activity due to both ⁶¹Cu and ⁶⁰Cu radionuclides is, however, lower than 1% at EOB for the irradiation of the ⁷⁰Zn target alone or in combination with the ⁶⁸Zn target. The fraction of total activity due to ⁶¹Cu plus ⁶⁰Cu radionuclides for the irradiation of the ⁶⁸Zn target at 70–35 MeV is about 12–13%. However, this percentage decreases with time, achieving 1% of total activity from 16 to 17 h after the EOB due to the short half‐lives of both ⁶¹Cu and ⁶⁰Cu radionuclides.

FIGURE 1.

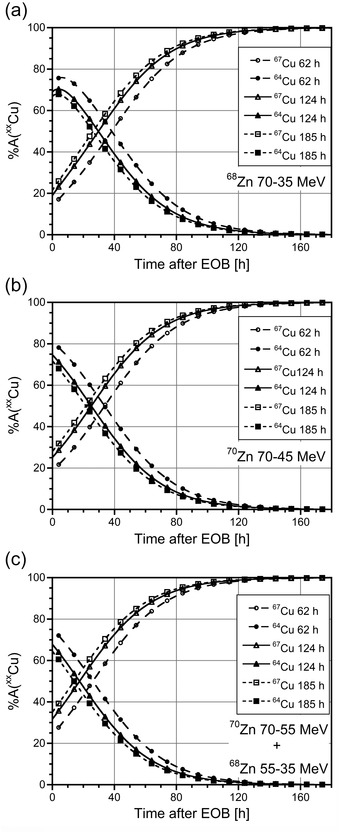
Percentage of activity due to ⁶⁷Cu and ⁶⁴Cu radionuclides as a function of time postirradiation, obtained with a 1 µA proton beam and different irradiation times (circles: 62 h; triangles: 124 h; squares: 185 h) of (a) a ⁶⁸Zn target in the energy range 70–35 MeV; (b) a ⁷⁰Zn target in the energy range 70–45 MeV; (c) a composite ⁷⁰Zn–⁶⁸Zn target in the energy range 70–55 and 55–35 MeV, respectively.

It should be recalled that the irradiation of ⁷⁰Zn targets at low energy (30–10 MeV range) only produces ⁶⁷Cu, yet the amount of activity obtained is rather low: 258.5 MBq/µA for 62 h of irradiation, 387.6 MBq/µA for 124 h, and 451.4 MBq/µA for 185 h, corresponding to about 15% or 65% of the ⁶⁷Cu activity obtained at EOB or at t _99%, respectively, irradiating ⁷⁰Zn at higher energy (70–45 MeV). For this reason, this scenario was not included in the current work.

3.2. Dosimetry of ^XX CuCl₂

Table 2 illustrates the normalized cumulated activity in the main source organs, calculated for the copper radioisotopes ⁶⁷Cu, ⁶⁴Cu, ⁶¹Cu, and ⁶⁰Cu according to the formula (3). The normalized cumulated activity in the rest of the body corresponds to the difference between the cumulated activity evaluated in the total body and the sum of the cumulated activity recorded in the main source organs.

TABLE 2.

Normalized cumulated activity calculated for ⁶⁷Cu, ⁶⁴Cu, ⁶¹Cu, and ⁶⁰Cu according to the ICRP 53 biokinetic model

	$\frac{{\stackrel{\sim }{A}}_{\mathrm{S}}}{A_0}$ (MBq‐h/MBq)
Organ	67Cu	64Cu	61Cu	60Cu
Brain	7.10	1.74	0.47	0.06
Liver	32.4	9.65	2.91	0.37
Kidneys	0.71	0.17	0.05	<0.01
Pancreas	0.14	0.03	0.01	<0.01
Rest of the body	30.60	5.80	1.30	0.14

These results show that the predominant uptake of CuCl₂ is in the liver, since this organ is involved in the storage and subsequent redistribution of copper ions to other tissues. Consequently, the hepatobiliary system is the most relevant elimination pathway of excess copper ions from the organism.

Table 3 shows the results of dosimetric calculations performed using both the ICRP 89 male and female phantoms ⁴⁵ for ⁶⁷Cu–, ⁶⁴Cu–, ⁶¹Cu–, and ⁶⁰Cu–Cl_2, respectively. ED values were obtained with the more recent tissue‐weighting factors given by ICRP 103. ⁴⁸ In addition, EDE and ED values were obtained using the given ICRP 26 ⁴⁶ and ICRP 60 ⁴⁷ tissue‐weighting factors in order to compare them to EDE results published by ICRP 53 ³⁵ for a hermaphroditic phantom and to other published data.

TABLE 3.

Organ doses (mGy/MBq), effective dose equivalent (EDE), and effective doses (ED) due to ⁶⁷Cu–, ⁶⁴Cu–, ⁶¹Cu–, and ⁶⁰Cu–Cl₂ for the ICRP 89 male and female phantoms calculated with OLINDA 2.2.0 software

Radioisotope	67Cu		64Cu		61Cu		60Cu
Half‐life	61.83 h		12.72 h		3.333 h		23.7 min
Target organ	Male	Female	Male	Female	Male	Female	Male	Female
Adrenals	0.148	0.171	0.0522	0.0581	0.0665	0.0729	0.0355	0.0394
Brain	0.483	0.537	0.108	0.12	0.0840	0.0931	0.0327	0.0362
Breasts	–	0.065	–	0.0155	–	0.0143	–	0.00686
Esophagus	0.086	0.107	0.0232	0.0321	0.0258	0.0364	0.0126	0.0178
Eyes	0.059	0.072	0.0133	0.0169	0.0119	0.0154	0.00548	0.00704
Gallbladder wall	0.195	0.157	0.0731	0.0514	0.0949	0.0620	0.0499	0.0309
LLI wall/left colon	0.066	0.077	0.0164	0.0187	0.0161	0.0179	0.00769	0.00835
Small intestine	0.066	0.080	0.0164	0.02	0.0160	0.0198	0.00759	0.00936
stomach wall	0.081	0.091	0.0227	0.0244	0.0247	0.0258	0.0122	0.0125
ULI wall/right colon	0.088	0.095	0.0256	0.0262	0.0286	0.0280	0.0141	0.0139
Rectum	0.053	0.064	0.0111	0.0133	0.00891	0.0106	0.00387	0.00454
Heart wall	0.089	0.089	0.0266	0.0234	0.0300	0.0243	0.0148	0.0116
Kidneys	0.263	0.301	0.0659	0.077	0.0598	0.0714	0.0261	0.0316
Liver	1.780	2.270	0.482	0.612	0.415	0.523	0.168	0.211
Lungs	0.078	0.094	0.0217	0.0261	0.0241	0.0290	0.012	0.0144
Ovaries	–	0.067	–	0.0143	–	0.0119	–	0.00525
Pancreas	0.149	0.206	0.0413	0.0624	0.0420	0.0689	0.0194	0.0332
Prostate	0.054	–	0.0116	–	0.00965	–	0.00427	‐
Salivary glands	0.061	0.070	0.0141	0.0162	0.0128	0.01450	0.00585	0.00662
Red marrow	0.053	0.062	0.0143	0.0166	0.0145	0.0168	0.00701	0.00805
Osteogenic cells	0.080	0.084	0.0137	0.015	0.0125	0.0145	0.00549	0.00648
Spleen	0.062	0.077	0.0152	0.0195	0.0146	0.0191	0.00694	0.00877
Testes	0.047	–	0.00902	–	0.00653	–	0.00265	–
Thymus	0.063	0.076	0.015	0.0177	0.0146	0.0170	0.00694	0.00807
Thyroid	0.055	0.064	0.0121	0.0142	0.0106	0.0122	0.00478	0.00542
Urinary bladder wall	0.052	0.063	0.0107	0.0118	0.00850	0.00911	0.00364	0.00382
Uterus	–	0.066	–	0.0139	–	0.0114	–	0.00499
Total Body	0.101	0.134	0.0231	0.0327	0.0185	0.0286	0.00757	0.0124
EDE (ICRP26) (mSv/MBq)	0.204	0.258	0.0542	0.0677	0.0502	0.0612	0.0220	0.0265
ED (ICRP60) (mSv/MBq)	0.149	0.189	0.0391	0.0497	0.0356	0.0450	0.0155	0.0195
ED (ICRP103) (mSv/MBq)	0.131	0.168	0.0351	0.0444	0.0329	0.0410	0.0146	0.0180

The absorbed doses calculated for ⁶⁷Cu and ⁶⁴Cu radioisotopes with OLINDA 2.2.0 using the male phantom are generally in agreement with values reported by ICRP 53 for the hermaphroditic phantom. The most significant divergences were found for absorbed dose values in the adrenals and in the total body. Higher differences were found for absorbed doses calculated with the female phantom compared with the hermaphroditic one. Consequently, the EDE values calculated for the male phantom (0.204 mSv/MBq for ⁶⁷Cu and 0.0542 mSv/MBq for ⁶⁴Cu) are quite similar to the values published by ICRP 53 (0.22 mSv/MBq for ⁶⁷Cu and 0.053 mSv/MBq for ⁶⁴Cu), whereas EDE values calculated for the female phantom are higher (0.258 mSv/MBq for ⁶⁷Cu and 0.0677 mSv/MBq for ⁶⁴Cu). Comparing the results calculated with OLINDA for both phantoms, it can be observed that the absorbed doses are higher for female than for male phantoms, as already reported for other radiopharmaceuticals. ²⁶ , ⁵³ , ⁵⁴ In this case, the difference is also due to the fact that the same organ cumulated activities were used for the male and female phantoms. The dosimetric estimation in humans proved that, with both radioisotopes, the liver received the highest dose, followed by the brain and the kidneys. Due to its longer half‐life, the absorbed doses due to ⁶⁷Cu are higher than those due to ⁶⁴Cu by a factor of between 3 and 6, depending upon the organ. This resulted in a 3.8‐fold increased value of ED or EDE, for both female and male phantoms.

As regards the ⁶¹Cu impurity, it can be observed that despite the almost fourfold shorter half‐life, the absorbed doses and the ED or EDE values due to this radioisotope are quite similar to those due to ⁶⁴Cu. This is a result of the higher total energy emitted by ⁶¹Cu for nuclear transformation (1.1327 MeV/nt for ⁶¹Cu and 0.3102 MeV/nt for ⁶⁴Cu ⁵⁵ ). Due to the high energy emitted for nt (4.8087 MeV/nt ⁵⁵), the absorbed doses of ⁶⁰Cu are not negligible, despite its very short half‐life.

3.3. Tumor dosimetry (sphere model)

Dose factors obtained with the OLINDA and MIRDcell codes for spheres of mass larger and smaller than 0.01 g, respectively, were used to calculate the absorbed dose to the spheres, considering 1 nt/µm³ (that is 10¹² nt per g of tissue). The results obtained for ⁶⁷Cu, ⁶⁴Cu, and ¹⁷⁷Lu radionuclides are plotted in Figure 2. It can be noted that the absorbed doses due to ⁶⁷Cu and ¹⁷⁷Lu are almost identical for small spheres up to 10 g of mass. This is due to the emitted energy per decay in the form of electrons, which is quite similar for the two radionuclides (0.1504 MeV/nt for ⁶⁷Cu and 0.1479 MeV/nt for ¹⁷⁷Lu). The same holds true for their mean β^– energy (0.1359 MeV for ⁶⁷Cu and 0.1333 MeV for ¹⁷⁷Lu) as reported in Table S2, which describes the main decay characteristics of the ⁶⁴Cu, ⁶⁷Cu, and ¹⁷⁷Lu radionuclides. ⁵⁵ Since a 10 g sphere ⁵⁶ absorbs almost all of the energy released by both radionuclides’ electron emission, the absorbed dose for ⁶⁷Cu becomes larger than that for ¹⁷⁷Lu beyond this size. This is due to the contribution of photons whose emission is higher for ⁶⁷Cu than for ¹⁷⁷Lu (see Table S2). The lower value of emitted energy per decay in the form of electrons in the case of ⁶⁴Cu (0.1248 MeV/nt) explains the lower absorbed dose values of this radionuclide for the smaller spheres. The ratio of the absorbed dose due to the two copper radionuclides D _67Cu/D _64Cu is about 1.1 for the 10 g sphere, increasing to 1.2 for the 0.01 g sphere. This value rises strongly as the mass of the spheres decreases, reaching a maximum of about 2.3 for a sphere of 4 × 10^–6 g (200 µm diameter) as a result of the higher mean energy of electron emission by ⁶⁴Cu compared to that of ⁶⁷Cu (see Table S2). Because of the rather similar total emitted energy per decay (0.2657 MeV/nt for ⁶⁷Cu and 0.3102 MeV/nt for ⁶⁴Cu), the absorbed dose for the two copper radioisotopes only converges for spheres larger than 10³ g.

FIGURE 2.

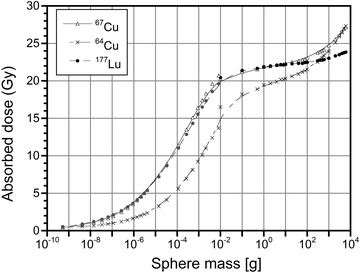
Absorbed dose (Gy) to spheres resulting from a uniform concentration of events (1 decay for µm³) due to ⁶⁷Cu, ⁶⁴Cu, and ¹⁷⁷Lu radioisotopes.

3.4. Cellular dosimetry and survival

Cellular S values calculated for ⁶⁷Cu, ⁶⁴Cu, and ¹⁷⁷Lu for each target region, nucleus (n), and the whole cell, assuming that the radionuclide was uniformly distributed in one of the source regions, the cytoplasm (cy) or the entire cell (c), demonstrated that in all cases, the self S values are the highest. These values decrease as the distance between the source and target cells increases (see Table S3). In general, the calculated ¹⁷⁷Lu and ⁶⁷Cu S values are similar because, as previously discussed, the emitted energy per decay in the form of both radionuclides’ electrons is comparable. Consequently, the mean absorbed doses to cells obtained after treatments with ¹⁷⁷Lu and ⁶⁷Cu at parity of number of disintegrations were also relatively similar (see Figure 3(a)). As expected, higher differences were found between the mean absorbed doses produced by ⁶⁷Cu and ⁶⁴Cu treatments (see Figure 3(a)).

FIGURE 3.

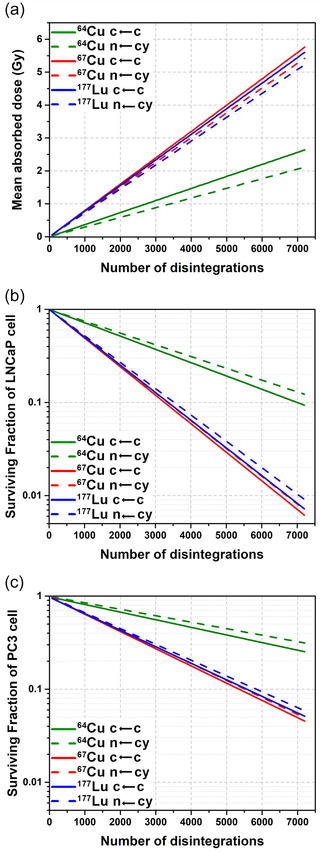
(a) Mean absorbed doses to cells obtained after treatment with ⁶⁷Cu, ⁶⁴Cu, and ¹⁷⁷Lu and the surviving fractions of (b) LNCaP cells and (c) PC3 cells.

Mean cell absorbed doses obtained for both LNCaP and PC3 cell lines were the same since only one cell model was used for both of them, however, some differences were found between their surviving fractions (Figures 3(b) and 3(c)). The surviving fraction of LNCaP cells after treatment with ¹⁷⁷Lu or ⁶⁷Cu was less than 10% and 1% considering 3500 and 7000 disintegrations per cell, respectively. Nevertheless, more than 6000 disintegrations are required to reduce the surviving fraction of the more radioresistant PC3 cells to 10% (see Figure 3(c)). A much larger number of disintegrations is required to achieve the same level of cell survival in the case of ⁶⁴Cu treatments.

3.5. Dosimetry of the ^67/64CuCl₂ mixture

The absorbed doses to healthy organs generated by the ^67/64CuCl₂ mixture per unit of administered activity were calculated for the male adult ICRP 89 phantom for different production conditions at different times after the EOB. As can be observed in Figure 4, in all cases the absorbed dose to the liver (the most irradiated organ) increases with time. This is due to the increasing contribution of ⁶⁷Cu (see Figure 1) and to its higher value of absorbed dose compared to that of ⁶⁴Cu (see Table 3), approaching the value of 1.78 mGy/MBq, corresponding to 100% ⁶⁷Cu in the mixture.

FIGURE 4.

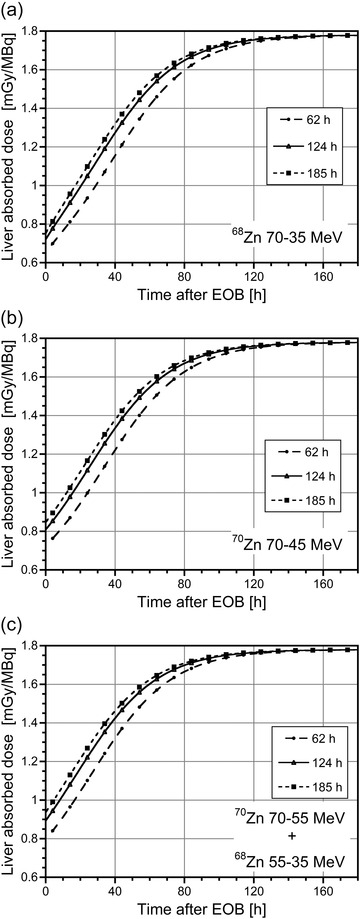
Absorbed dose to the liver per unit of administered activity for the male adult ICRP 89 phantom as a function of time postirradiation due to injection of the ^67/64CuCl₂ mixture obtained with 1 µA proton beam and different irradiation times (circles: 62 h; triangles: 124 h; squares: 185 h) of (a) a ⁶⁸Zn target in the energy range 70–35 MeV; (b) a ⁷⁰Zn target in the energy range 70–45 MeV; (c) a composite ⁷⁰Zn–⁶⁸Zn target in the energy range 70–55 and 55–35 MeV, respectively.

The same time dependent behavior was found for the absorbed dose to other healthy organs and also for total ED (ED_t), as can be observed in Figure 5 for the case of a mixture obtained from ⁷⁰Zn target irradiation in the energy range 70–45 MeV. Similar results were obtained for the irradiation of the ⁶⁸Zn target in the energy range 70–35 MeV and for the composite target ⁷⁰Zn–⁶⁸Zn in the energy range 70–35 MeV. The contribution of the ⁶¹Cu and ⁶⁰Cu impurities to the liver‐absorbed dose and to the ED_t was always less than 10% at the EOB, rapidly decreasing over time.

FIGURE 5.

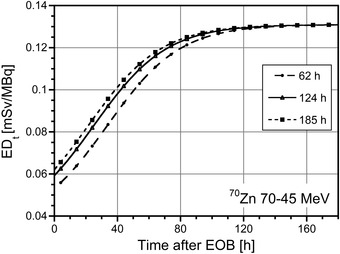
Total ED (ED _t ) per unit of administered activity for the male adult ICRP 89 phantom as a function of time postirradiation due to injection of the ^67/64CuCl₂ mixture obtained with 1 µA proton beam and different irradiation times (circles: 62 h; triangles: 124 h; squares: 185 h) of a ⁷⁰Zn target in the energy range 70–45 MeV.

The tumor‐absorbed dose attributable to the ^67/64CuCl₂ mixture, evaluated with the sphere model, was also calculated for different production conditions at different postirradiation times. The results obtained are plotted in Figure 6 for spheres of different mass and a uniform concentration of events (1 decay per µm³). The tumor‐absorbed dose increases with time when the ⁷⁰Zn target is irradiated in the energy range 70–45 MeV for each tumor size, reaching a plateau value corresponding to 100% ⁶⁷Cu in the mixture (Figure 6(b)). The absorbed doses are higher for the larger spheres: the absorbed dose for the 10 g sphere is about 15% higher at EOB and 10% higher at the plateau when compared to the 0.01 g sphere (see Figure S1(b)).

FIGURE 6.

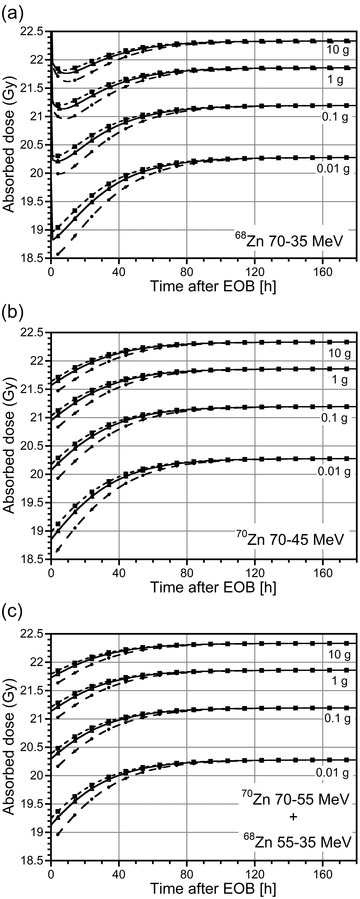
Absorbed doses (Gy) to spheres of different mass (0.01, 0.1, 1, and 10 g) resulting from a uniform concentration of events (1 decay per µm³) due to injection of the ^67/64CuCl₂ mixture obtained with 1 µA proton beam and different irradiation times (circles: 62 h; triangles: 124 h; squares: 185 h) of (a) a ⁶⁸Zn target in the energy range 70–35 MeV; (b) a ⁷⁰Zn target in the energy range 70–45 MeV; (c) a composite ⁷⁰Zn–⁶⁸Zn target in the energy range 70–55 and 55–35 MeV, respectively.

The relative increment in the absorbed dose at the plateau with respect to the EOB for 62 h of irradiation (situation corresponding to the largest variation) is less than 10% for the smaller spheres (0.01 and 0.1 g), and about 5% for the larger ones (1 and 10 g) (see Figure S2(b)). Similar results were obtained for the irradiation of the combined ⁷⁰Zn–⁶⁸Zn target (see Figure 6(c), S1(c), and S2(c)). Due to the decay of the ⁶¹Cu and ⁶⁰Cu impurities, the tumor‐absorbed doses initially decrease with time when a ⁶⁸Zn target is irradiated in the energy range 70–35 MeV; this behavior is more evident in the larger spheres (see Figure 6(a)). After a few hours, the absorbed doses increase again with time until they reach a plateau value, similar to the other irradiation conditions.

4. DISCUSSION

The ⁶⁴CuCl₂ dosimetric evaluation conducted in this study revealed that the liver was the organ that received the highest dose, as already reported in ICRP 53 and validated by other authors in human healthy volunteers, ⁵⁷ prostate cancer patients, ³ , ⁵⁸ and glioblastoma multiforme patients. ⁵⁹ Table 4 depicts the comparison of our dosimetric data with those previously reported. The liver‐absorbed dose values calculated in this study are higher than those published in the literature, possibly due to the limited number of time points used to estimate radionuclide accumulation in preceding studies. Nevertheless, ED values are in line with those previously published.

TABLE 4.

Comparison of the liver‐absorbed dose and the effective dose calculated per unit of ⁶⁴CuCl₂ administered activity in human models

	Human model
	Capasso et al. 2015	Righi et al. 2018	Panichelli et al. 2016	Avila‐Rodriguez et al. 2017			ICRP 53	This study (ICRP 89 phantom)
	Male	Male	Male	Male	Female	Mean	Hermaphroditic	Male	Female
Liver (μGy/MBq)	294	271	321	310	421	366	480	482	612
EDE ICRP26 (μSv/MBq)	–	–	40 a	–	–	–	53	54.2	67.7
ED ICRP60 (μSv/MBq)	33.8	31	40 a	51.2	61.8	56.5	–	39.1	49.7
ED ICRP103 (μSv/MBq)	–	29.1	–	–	–	–	–	35.1	44.4

^a Calculated on the basis of the published organ dose.

Our ⁶⁷CuCl₂ dosimetric data are also comparable to those reported by ICRP 53, even if higher absorbed doses were calculated for the female phantom compared to the hermaphroditic one used by ICRP 53. It should also be noted that the adoption of the most recent ICRP 103 tissue weighting factors determines a substantial decrease of the ED values, for both male and female phantoms and for both ⁶⁴CuCl₂ and ⁶⁷CuCl₂, compared with the EDE values based on the ICRP 26 data set used in ICRP 53 evaluation (see Table 3). The overall consistency of our dosimetric evaluation with published data is encouraging for the application of the same model to the ^67/64CuCl₂ mixture.

Absorbed doses to healthy organs per unit of administered activity of ⁶⁷CuCl₂ are higher by a factor of between 3 and 6 (3.7 for the liver) compared with those attributable to ⁶⁴CuCl₂, resulting in an ED coefficient that is 3.8 times higher (see Table 3). Nevertheless, given that for most organs the maximum tolerated dose (MTD) to radiation is in the order of some tens of Gy, and the MTD for the gonads and red bone marrow are as low as 1–2 Gy, ⁶⁰ , ⁶¹ our dosimetric estimations suggest that it is feasible to administer ⁶⁷CuCl₂ therapeutic activities in the order of several GBq without jeopardizing the function of these organs. In the case of ^67/64CuCl₂, the amount of ⁶⁷Cu in the mixture increases with time after the EOB and, therefore, the absorbed dose to healthy organs and ED values per unit of administered activity increase as well.

Absorbed dose calculations using the sphere model demonstrated that approximately the same total number of ⁶⁷Cu and ¹⁷⁷Lu radioactive decays are required for the same absorbed dose to a tumor of up to 10 g of mass (see Figure 2). In general, the biodistribution of ⁶⁷Cu‐ and ¹⁷⁷Lu‐radiopharmaceuticals will be different. However, assuming that the same fraction of administered activities (A ₀) accumulates in the tumor for both radionuclides, and considering an immediate uptake without biological elimination, it follows that the same absorbed doses can be attained with ⁶⁷Cu and ¹⁷⁷Lu by scaling A ₀ according to the radioisotope half‐lives (A ₀ = nt ln2/T _1/2). Therefore, the required activity of ⁶⁷Cu will be about 2.6 times higher than the activity of ¹⁷⁷Lu. Given that a 10–20% higher value of radioactive decays is necessary in the case of ⁶⁴Cu compared with ¹⁷⁷Lu to produce the same absorbed doses for tumor masses ranging between 0.01 and 10 g, the required activity of ⁶⁴Cu will be about 14–15 times higher than that of ¹⁷⁷Lu. Consequently, when comparing the two copper radioisotopes, the ⁶⁴Cu administered activity must be about 5.5 higher than that of ⁶⁷Cu to get the same tumor‐absorbed dose in this range of sizes, causing the absorbed dose to healthy organs and ED to be higher with respect to ⁶⁷CuCl₂. The number of ⁶⁴Cu disintegrations necessary to release the same absorbed dose attributed to ⁶⁷Cu becomes about two times higher for very small spheres, necessitating up to 10 times higher ⁶⁴Cu activity in these cases.

However, the biological effect of ⁶⁴Cu would be much higher than that of ¹⁷⁷Lu or ⁶⁷Cu if this radionuclide were incorporated into the cell nucleus, close to the DNA, because the ⁶⁴Cu Auger electrons would produce high‐density ionizations and high‐energy deposition in a few nanometers. Consequently, the biological effectiveness of Auger electrons emitted inside the cell nucleus could be similar to that of α particles, but it would be minimal if the particles were emitted outside the nucleus. Therefore, to calculate the survival fraction of cells after treatment with an Auger‐electron‐emitting radionuclide localized inside the nucleus cell, it is generally necessary to make a distinction between self‐dose and cross‐dose parameters (see Equation 8). ⁶² It was discovered that a protein called Atox1 could transport copper into the cell's nucleus, ⁶³ but it was recently reported that CuCl₂ could be accumulated inside the nucleus only if it is present in cytotoxic concentrations. ⁶⁴ Given that the concentrations of administered radiopharmaceuticals are several orders of magnitude below cytotoxic concentrations, the amount of Cu in the cell's nucleus would be minimal. Consequently, we used the same α and β values for self‐doses and cross doses to calculate the surviving fraction for all the radionuclides studied.

The evaluation of mean cell absorbed doses and cell survival after both treatments with all radionuclides studied revealed that, when it was assumed that radioactivity was distributed evenly throughout the cell, higher values of absorbed doses were obtained compared to the more realistic approach which considered the cytoplasm as the source region (see Figure 3(a)). The small differences between the mean absorbed doses obtained with both kinds of treatments for ¹⁷⁷Lu or ⁶⁷Cu do not change the biological effects, since the cell surviving fractions of both treatments are almost identical (see Figures 3(b) and 3(c)). Treatment with ⁶⁴Cu, however, cause lower values of absorbed doses to the cells, producing less biological damage because it was considered that, in these treatment conditions, CuCl₂ is not concentrated inside the cell's nucleus (see Figures 3(b) and 3(c)). Therefore, in these hypotheses, not only a greater amount of ⁶⁴Cu activity must be injected to obtain the same number of ⁶⁷Cu decays, due to the different radioisotopes half‐lives, but also an additional activity must be administered to obtain the same absorbed dose levels, and consequently the same cell survival. When considering the ^67/64CuCl₂ mixture, the supplemental activity necessary to get the same tumor‐absorbed dose produced by ⁶⁷CuCl₂ depends on the time of administration, since the ⁶⁷Cu concentration in the mixture increases with time after EOB (see Figure 1), as does the relative absorbed dose resulting from a uniform concentration of events, D _mix(t)/D _67Cu (see Figure S2). For example, with D _mix(t = 0)/D _67Cu ≈ 0.9 for the 0.01 g sphere and an irradiation time of 62 h, approximately 10% more decays of the mixture are required at EOB when compared with those of ⁶⁷CuCl₂ in order to produce the same absorbed dose. The number of decays occurring in the sphere per unit of administered activity of the mixture, nt_mix/A _0, are given by the equation:

$$\begin{array}{ccc}\hfill \frac{\mathrm{n}{\mathrm{t}}_{\mathrm{mix}}\left(t\right)}{A_0}& =& k\frac{1}{100}\left[\%A^{67}\mathrm{Cu}\left(t\right)·T_{\mathrm{p}}\left({}^{67}\mathrm{Cu}\right)\right.\hfill \\ & & +\left.\%A{}^{64}\mathrm{Cu}\left(t\right)·T_{\mathrm{p}}\left({}^{64}\mathrm{Cu}\right)\right]\hfill \end{array}$$ (9)

where k is a proportionality constant, representing the fraction of Cu radioisotopes accumulating inside the tumor.

The percentage of ⁶⁴Cu activity in the mixture obtained by the irradiation of the ⁷⁰Zn target in the energy range 70–45 MeV is about 80% at EOB, giving the coefficient nt_67Cu/nt_mix(t = 0) = 2.78, which decreases with time after EOB. By considering this coefficient's ratio and the relative absorbed dose attributed to the mixture D _mix(t)/D _67Cu, it is possible to calculate the increase in the activity of the ^67/64CuCl₂ mixture necessary to obtain the same absorbed dose in the sphere as when using ⁶⁷CuCl₂:

$$\frac{A_{\mathrm{mix}}\left(t\right)}{A_{67\mathrm{Cu}}}=\left(\frac{\mathrm{n}{\mathrm{t}}_{67\mathrm{Cu}}}{\mathrm{n}{\mathrm{t}}_{\mathrm{mix}}\left(t\right)}\right)/\left(\frac{D_{\mathrm{mix}}\left(t\right)}{D_{67\mathrm{Cu}}}\right)$$ (10)

This suggests that the administered activity of the ^67/64CuCl₂ mixture must be almost three times higher than that of ⁶⁷CuCl₂ at EOB in order to obtain an equivalent absorbed dose to the 0.01 g sphere.

The dose increment (DI) caused by the use of the ^67/64CuCl₂ mixture rather than ⁶⁷CuCl₂ can be estimated by multiplying the A _mix/A _67Cu coefficient for the liver‐absorbed dose per unit of administered activity or the ED_t value per unit of administered activity (see Figures 4 and 5). For the considered scenario, the increase in the liver‐absorbed dose and in the ED is about 25% at EOB, decreasing to almost 10% approximately 30 h after EOB. Setting the maximum DI limit to 10% after administering the ^67/64CuCl₂ mixture, the waiting time required to reach this limit (t _10%) after the EOB can be used to compare the quality of the different ^67/64CuCl₂ mixtures_. Table 5 shows the values of t _10% and the total activity available at that time, evaluated for the different scenarios and taking the sphere of 0.01 g of mass as a reference. For all the different scenarios, the percentage of ⁶⁷Cu activity at t _10% is about 45% and the A _mix/A _67Cu coefficient at this time is about 1.8. As irradiation time rises, the amount of available total activity increases and the t _10% decreases in all cases (see Table 5). A comparison of the amount of activity of ^67/64CuCl₂ available at t _10% with that of ⁶⁷CuCl₂ at t _99%, reported in Table 1, clearly indicates the advantage of administering the radionuclidic mix instead of the pure ⁶⁷Cu radioisotope, even taking into account that a greater amount of mixing activity is required. It should be noted that the estimated production yields of all the radionuclides of interest are based on the hypothesis of 100% isotopically enriched target material. However, the material available on the international market for use as a target may have a lower enrichment level (materials with enrichment levels higher than 98.7% for ⁷⁰ZnO and 99% for ⁶⁸ZnO are currently available) and different amounts of Cu isotopes will be produced based on the specific target composition. Given that the natural abundance of ⁷⁰Zn is only 0.61% and that of ⁶⁸Zn is 18.45%, ⁶⁵ the price of these enriched materials varies, with the price of ⁷⁰Zn approximately four times more expensive than that of ⁶⁸Zn. From a technical point of view, it is customary to recover and reuse costly enriched materials in the routine production of radionuclides. ¹⁹

TABLE 5.

Minimum waiting time necessary after EOB to keep the dose increment lower than 10% (t _10%) and the activity (MBq/µA) of the ⁶⁷Cu and ⁶⁷Cu + ⁶⁴Cu mixture at that time obtained through the proton irradiation of ⁶⁸Zn and ⁷⁰Zn targets for different scenarios and irradiation times

	Irr. time (h)	t 10%(h)	67Cu + 64Cu(MBq/µA)	67Cu(MBq/µA)
68Zn 70–35 MeV	62	35	1801.8	837.6
	124	26	3018.5	1389.3
	185	23	3594.2	1673.1
70Zn 70–45 MeV	62	30	2711.6	1251.4
	124	21	4542.8	2075.6
	185	18	5409.0	2499.6
70Zn 70–55 MeV + 68Zn 55–35 MeV	62	22	3223.4	1470.1
	124	13	5400.9	2438.3
	185	10	6430.0	2936.5

5. CONCLUSIONS

This study assessed the feasibility of using a ^67/64Cu radioisotope mixture for therapeutic purposes by calculating the total absorbed dose into unit density spheres through the simulation of small‐sized tumors after administration of a ^67/64CuCl₂ solution. Owing to the increased contribution of ⁶⁷Cu in the mixture, it was found that the DI resulting from the administration of the ^67/64CuCl₂ mixture rather than ⁶⁷CuCl₂ decreases with time after EOB. The post‐EOB waiting time required to reduce this increment to below 10% (t _10%) depends upon the choice of target and irradiation conditions. The irradiation of a multilayer target composed of ⁷⁰Zn+⁶⁸Zn for 185 h appears to be the best option for CuCl₂ administration from among all the production parameters studied, since maximum activity was obtained under this condition with the shortest t _10% (10 h) and less than 1% calculated percentages of ⁶¹Cu and ⁶⁰Cu impurities. Based on these results, we can conclude that the use of a ^67/64Cu mixture for therapy could be an advantage because the larger amount of available activity will allow to treat more patients and to reduce the cost of the treatment.

FUNDING

This work was supported by the COME experiment (funded by INFN) as part of the activities of the LARAMED project of the INFN‐LNL and it was also included in the framework of the IAEA Coordinated Research Project (CRP) on “Therapeutic Radiopharmaceuticals Labelled with New Emerging Radionuclides (67Cu, 186Re, 47Sc)” (IAEA CRP No. F22053).

CONFLICT OF INTEREST

The authors have no conflicts of interest to disclose.

Supporting information

Supporting information

De Nardo L, Pupillo G, Mou L, Esposito J, Rosato A, Meléndez‐Alafort L. A feasibility study of the therapeutic application of a mixture of ^67/64Cu radioisotopes produced by cyclotrons with proton irradiation. Med Phys. 2022;49:2709–2724. 10.1002/mp.15524