A single-index model with a surface-link for optimizing individualized dose rules

Abstract

This paper focuses on the problem of modeling and estimating interaction effects between covariates and a continuous treatment variable on an outcome, using a single-index regression. The primary motivation is to estimate an optimal individualized dose rule and individualized treatment effects. To model possibly nonlinear interaction effects between patients’ covariates and a continuous treatment variable, we employ a two-dimensional penalized spline regression on an index-treatment domain, where the index is defined as a linear projection of the covariates. The method is illustrated using two applications as well as simulation experiments. A unique contribution of this work is in the parsimonious (single-index) parametrization specifically defined for the interaction effect term.

1. Introduction

In precision medicine, a primary goal is to characterize individuals’ heterogeneity in treatment responses so that individual-specific treatment decisions can be made (Murphy, 2003; Robins, 2004). Most work on developing methods for individualized treatment decisions has focused on a finite number of treatment options. The focus of this paper is to develop individualized treatment decision methodology in the realm of a continuous treatment. Specifically, we consider a semiparametric regression approach for developing optimal individualized dosing rules based on baseline patient characteristics. Often in clinical practice, the maximum dose that a patient can tolerate is the most effective one, however, there are situations where this is not the case. In the example section, we present a study of warfarin (an anticoagulant), where too high doses lead to severe bleeding and thus the highest dose is not the the optimal dose. In finding the optimal dose, there is an essential non-monotone and nonlinear relationship that needs to be accounted for. A similar case is with insulin for controlling blood glucose levels.

To establish notation, let $X={\left(X_1,\dots ,X_p\right)}^{\top }\in \mathcal{X}$ be the set of baseline covariates, $Y\in ℝ$ be the outcome variable, and $A\in \mathcal{A}$ denote the dose. Let Y*(a) be the potential outcome when a dose level $a\in \mathcal{A}$ is given. Throughout, we assume: 1) consistency, i.e., $Y={\int }_{\mathcal{A}}\delta (A=a)Y*(a)da$, where δ(·) is the Dirac delta function; 2) no unmeasured confoundedness, i.e., $\left\{Y^{*}(a),a\in \mathcal{A}\right\}$ is conditionally independent of A given X; 3) positivity, i.e., $p(A=a\mid X=x)\ge c$, for all $a\in \mathcal{A}$, $x\in \mathcal{X}$, for some c > 0 (where p(a|x) is the conditional density of A = a given X = x), which are standard assumptions adopted in the causal inference literature (Gill and Robins, 2001). Without loss of generality, we assume that a larger value of the outcome Y is better. The goal is then to find an optimal individualized dose rule $f:\mathcal{X}\mapsto \mathcal{A}$ such that for a patient with covariate X, the dose assignment A = f(X) maximizes the expected response, the so-called value function, $\mathcal{V}(f)=\mathbb{E}\left[Y^{*}(f(X))\right]$, that is,

$$\mathcal{V}(f)=\mathbb{E}[\mathbb{E}[Y\mid A=f(X),X]]$$ (1)

which holds and can be empirically approximated under the above three assumptions. In settings in which the treatment can be administered at continuous doses (i.e., when $\mathcal{A}$ is an interval), Chen et al. (2016) proposed to optimize the individualized dosing rule f by maximizing a local approximation of the value function (1), optimized under the framework of outcome weighted learning (Zhao et al., 2012). Laber and Zhao (2015) proposed a tree-based decision rule for treatment assignment with minimal impurity dividing patients into subgroups with different discretized doses. Kallus and Zhou (2018) developed an inverse propensity weighted estimator of (1) for continuous treatments with the doubly robust property (Dudík et al., 2014), and recently, kernel assisted learning with linear dimension reduction (Zhou et al., 2020; Zhu et al., 2020) for direct optimization of (1) have been developed. However, implementation of these approaches for general exponential family distributions is not straightforward and has not been accomplished. In this paper, we consider a regression-based approach to optimizing f that uses a semiparametric regression model for $\mathbb{E}[Y\mid A,X]$. There is also extensive literature on multi-armed bandit (e.g., Lattimore and Szepesvari, 2019) problems in the context of reinforcement learning (e.g., Kaelbling et al., 1996), incorporating context (i.e., feature $X\in \mathcal{X}$) (see, e.g., Lu et al. (2010); Perchet and Rigollet (2013); Slivkins (2014); Jun et al. (2017); Li et al. (2017); Kveton et al. (2020); Chen et al. (2020)) for making a sequential decision that minimizes the notion of cumulative regret, with relatively fewer works on contextual bandits with continuous actions (see, e.g., Krishnamurthy et al., 2020; Kleinberg et al., 2019; Majzoubi et al., 2020). However, these works are focused on optimizing online performance (addressing the exploration issue) and are considerably different from personalized dose-finding focused on a single stage with feature X. Kennedy et al. (2017) considered a method for estimating the average dose effect allowing for flexible doubly robust covariate adjustment, but the method is not intended for optimal dose finding for individual patients. For multi-stage personalized dose-finding, Rich et al. (2014) proposed adaptive strategies, and more recently Schulz and Moodie (2020) developed a doubly robust estimation approach based on a linear model. All these approaches are limited by the stringent linear model assumptions for the heterogeneous dose effects.

While the methods of directly optimizing the value function (1), including the outcome weighted learning of Chen et al. (2016) and the tree-based method of Laber and Zhao (2015), are highly appealing, the proposed semi-parametric regression modeling has the advantage of being easy to implement and readily generalizable to an exponential family response.

It is straightforward to see that, given X, the optimal dose f_opt (X) (i.e., that which maximizes the value function (1)) is

$$f_{\text{opt}}(X)=\underset{a\in \mathcal{A}}{\mathrm{argmax}}m(a,X),$$ (2)

where $m(a,X)=\mathbb{E}[Y\mid A=a,X]$. If we estimate m(a, X) with $\widehat{m}(a,X)$, then the optimal rule f_opt in (2) can be approximated as

$$\widehat{f}(X)=\underset{a\in A}{\mathrm{argmax}}\widehat{m}(a,X).$$ (3)

Methodologies for optimizing individualized treatment rules f in the precision medicine literature are developed predominantly for the cases in which the treatment variable A is binary or discrete-valued. Regression-based methodologies first estimate the treatment a-specific mean response functions m(a, X) and then obtain a treatment decision rule, i.e., the left-hand side of (3) (e.g., see Qian and Murphy, 2011; Zhang et al., 2012; Gunter et al., 2011; Lu et al., 2013; Park et al., 2020) given X. In particular, Qian and Murphy (2011) show that the optimal individualized treatment rule (2) depends only on the interaction between treatment A and covariates X, and not on the main effects of X in the mean models m(a, X). For regression-based methodologies, a successful estimation of the function f_opt in (2) boils down to efficiently estimating the A-by-X interaction effects on the treatment response. In this paper, we consider a semi-parametric model that is useful for estimating such interactions in the case where A is a continuous dose variable.

2. Models

Our goal is to provide an interpretable and flexible approach to modeling the A-by-X interaction effects on Y. To achieve this goal, we consider the following additive single-index model:

$$\mathbb{E}[Y\mid X,A]=\mu (X)+g\left({\beta }^{\top }X,A\right)$$ (4)

where μ(X) represents an unspecified main effect of X, and g(β^⊤X, A) models the A-by-X interaction effects. Here, g(·,·) is an unspecified smooth two-dimensional surface link function of the variable A and a single index β^⊤X. We shall call model (4) a single-index model with a surface-link (SIMSL). We restrict $\beta \in \mathrm{\Theta }:=\{\beta ={\left({\beta }_1,\dots ,{\beta }_p\right)}^{\top }\in {ℝ}^p:\Vert \beta {\Vert }_2=1,{\beta }_1>0\}$, as β in (4) is only identifiable up to a scale constant without further constraint, due to the unspecified nature of g.

Without loss of generality, we assume $\mathbb{E}[\mu (X)]=0$ and $\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\right]=0$ (where the expectation is with respect to X and A), i.e., each of the additive components in model (4) has mean 0, and that these components have finite variances, as are typically assumed in generalized additive models (GAM; Hastie and Tibshirani, 1999). That is, let ${\mathcal{H}}_1$ and ${\mathcal{H}}_2^{(\beta )}$ (for a fixed β∈Θ) denote the L² spaces of measurable functions μ(X) on X and measurable functions g(β^⊤X, A) on (β^⊤X, A), respectively, and we assume $\mu \in {\mathcal{H}}_1$ and $g\in {\mathcal{H}}_2^{(\beta )}$.

Due to the unspecified nature of μ and g (and that X is involved in both μ and g), model (4) is not identifiable without further constraints. We will constrain the smooth function $g\in {\mathcal{H}}_2^{(\beta )}$ to satisfy:

$$\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]=0,a.s\text{.}(X)X\in \mathcal{X},\beta \in {ℝ}^p,$$ (5)

which acts as an identifiability condition of model (4).

Applying the constraint (5) to the function g in (4) essentially reparametrizes the model (4), by replacing g(β^⊤X, A) with $g_0\left({\beta }^{\top }X,A\right)=g\left({\beta }^{\top }X,A\right)-\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]$, and μ(X) with ${\mu }_0(X)=\mu (X)+\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]$. This yields an equivalent model of (4), $\mathbb{E}[Y\mid X,A]={\mu }_0(X)+g_0\left({\beta }^{\top }X,A\right)$, where the term g₀(β^⊤X, A) satisfies the identifiability condition (5). Since any arbitrary (μ, g) in (4) can be rearranged to give such reparametrized components (μ₀, g₀), without loss of generality, we will represent (μ₀, g₀) as (μ, g) subject to (5).

Under the SIMSL (4) (subject to constraint (5)), the optimal individualized dose rule, f_opt, is specified as: $f_{\text{opt}}(X)=\underset{a\in \mathcal{A}}{\mathrm{argmax}}g\left({\beta }^{\top }X,a\right)$, which does not involve the component μ. Therefore, in terms of estimating f_opt in (2), our modeling focus is on estimating (g,β) in (4).

Using the constrained least squares framework, the right-hand side of (4), subject to constraint (5), can be optimized by solving:

$$\begin{array}{l}\left({\mu }^{*},g^{*},{\beta }^{*}\right)=\underset{\mu \in {\mathcal{H}}_1,g\in H_2^{(\beta )},\beta \in \mathrm{\Theta }}{\mathrm{argmin}}\mathbb{E}\left[{\left(Y-\mu (X)-g\left({\beta }^{\top }X,A\right)\right)}^2\right]\\ \text{subject}\text{to}\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]=0.\end{array}$$ (6)

Constraint (5) ensures that $\mathbb{E}\left[\mu (X)g\left({\beta }^{\top }X,A\right)\right]=\mathbb{E}\left[\mu (X)\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]\right]=0$ (in which we apply the iterated expectation rule to condition on X), which implies the orthogonality,

$$\mu (X)\perp g\left({\beta }^{\top }X,A\right),$$ (7)

in L². The orthogonality (7) implies that the optimization for μ* and that for (g*, β*) on the left-hand side of (6) can be performed separately, without iterating between the two optimizations. Specifically, we can solve for the X main effect component:

$${\mu }^{*}=\underset{\mu \in {\mathcal{H}}_1}{\mathrm{argmin}}\mathbb{E}\left[{(Y-\mu (X))}^2\right],$$ (8)

and separately solve for the A-by-X interaction effect component:

$$\begin{array}{l}\left(g^{*},{\beta }^{*}\right)=\underset{g\in {\mathcal{H}}_2^{(\sigma )},\beta \in \mathrm{\Theta }}{\mathrm{argmin}}\mathbb{E}\left[{\left(Y-g\left({\beta }^{\top }X,A\right)\right)}^2\right]\\ \text{subject}\text{to}\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]=0,\end{array}$$ (9)

without alternating between the two optimization procedures. We can fit f_opt by: $\widehat{f}(X)=\underset{a\in \mathcal{A}}{\mathrm{argmax}}{\widehat{g}}^{*}({\widehat{\beta }}^{*\top }X,a)$, where $({\widehat{g}}^{*},{\widehat{\beta }}^{*})$ denotes an estimate of (g*, β*) in (9). This approach using optimization (9) is appealing, because, due to orthogonality (7), misspecification of the functional form for μ in (6) does not affect specification of (g*, β*) on the left-hand side of (9). If primary interest is in estimating f_opt in (2), then utilizing f^ˆ based on optimization (9) circumvents the need to estimate the term μ in (4), obviating the need to specify its form and thus avoiding the issue of model misspecification on the X main effect. The equivalence between (g*, β*) on the left-hand side of (9) and (g, β) in (4) is given in Proposition 1 in Section 4 (in the context where Y follows an exponential family response).

Since our primary focus is on estimating f_opt, we focus on solving (9). However, we also note that modeling the μ term in (4) can generally improve the performance of the estimator of (g, β), as discussed in Supplementary Materials Section C.1. For each fixed β, the term g(β^⊤X, A) depends the covariates $X\in \mathcal{X}$ only through the 1-dimensional projection β^⊤X. Therefore, for each fixed β, the distribution of g(β^⊤X, A)| X is equal to that for g(β^⊤X, A)|β^⊤X, which implies $\mathbb{E}[g(\beta X,A)\mid X]=\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid {\beta }^{\top }X\right]$, for each fixed β. Then, for each fixed β∈Θ, the following constraint on $g\in {\mathcal{H}}_2^{(\beta )}$,

$$\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid {\beta }^{\top }X\right]=0,X\in \mathcal{X},$$ (10)

is a sufficient condition for the orthogonality constraint (5). Thus, for each fixed β, the constraint (5) can be simplified to (10). The following iterative procedure will be used to solve (9):

1. For fixed β, optimize the smooth g(·,·) by solving:

   $$\underset{g\in H_2^{(\theta )}}{\mathrm{argmin}}\mathbb{E}\left[{\left(Y-g\left({\beta }^{\top }X,A\right)\right)}^2\right],$$ (11)

   subject to the constraint (10).

2. For fixed g, optimize the coefficient β∈Θ by minimizing the squared error criterion of (11).

3. Iterate steps (1) and (2) until convergence with β∈Θ.

The data version of optimizing (g,β) can be derived as an empirical counterpart of the iterative procedure given above. Details on implementing this algorithm are given below.

3. Estimation

3.1. Representation of link surface

Suppose we have observed data $\left(Y_i,A_i,X_i\right)(i=1,\dots ,n)$. For each candidate vector β∈Θ, let

$$u_i=u_i^{(\beta )}={\beta }^{\top }{X}_i(i=1,\dots ,n),$$

where (on the left-hand side), for the notational simplicity, we suppress the dependence of the linear predictor $u^{(\beta )}\in ℝ$ on the candidate vector β.

Eilers and Marx (2003) have used tensor products of B-splines (de Boor, 2001) to represent two-dimensional surfaces, which they termed tensor product P-splines, with separate difference penalties applied to the coefficients of the B-splines along the covariate axes. Although alternative nonparametric methods could also be used to estimate the smooth function $g\in {\mathcal{H}}_2^{(\beta )}$ given each coefficient vector β in model (4), in this paper we focus on one smoother, the tensor-product P-splines, for the ease of presentation.

Specifically, for each u = β^⊤X, to represent the 2-dimensional function g(u, A) in (11), we consider the tensor product of the two sets of univariate cubic B-spline basis functions, say B and $\check{B}$, with N (and $\check{N}$) B-spline knots for the basis functions that are placed along the u (and A) axis. The number of knots N (and $\check{N}$) is chosen to be large, i.e., to allow the surface much flexibility. Associated with the basis representation defined by the marginal basis function B (resp., $\check{B}$) is an N × N (resp., $\check{N}\times \check{N}$) roughness penalty matrix, which we denote by $\mathbb{P}$ (and $\check{\mathbb{P}}$). The penalty matrix $\mathbb{P}$ (and $\check{\mathbb{P}}$) can be easily constructed, for example, based on a second-order difference matrix (e.g, see Eilers and Marx (2003)).

For each fixed $u_i={\beta }^{\top }{X}_i(i=1,\dots ,n)$, let us write the n × N (and n× N ) B-spline evaluation matrix B (and B), in which its ith row is B_i = B(u_i)^⊤ (and B_i =B(A_i)^⊤). Given a knot grid, a flexible surface can be approximated (Marx, 2015) at n points (u_i, A_i) (i = 1,…,n):

$$g\left(u_i,A_i\right)=\sum _{r=1}^N\sum _{s=1}^{\check{N}}{B}_r\left(u_i\right){\check{B}}_s\left(A_i\right){\gamma }_{rs}=\left({\mathit{B}}_i\otimes {\check{\mathit{B}}}_i\right)\mathit{\theta }(i=1,\dots ,n),$$ (12)

where the vector $\theta ={({\gamma }_{11},\dots ,{\gamma }_{1\check{N}};\dots ;{\gamma }_{N1},\dots ,{\gamma }_{N\check{N}})}^{\top }\in {ℝ}^{N\check{N}}$ corresponds to an unknown (vectorized) coefficient vector of the tensor product representation of g, and ⨂ represents the usual Kronecker product. Equation (12) can be compactly written as:

$$\mathrm{vec}\left\{g\left(u_i,A_i\right)\right\}=g\left(u_{n\times 1},A_{n\times 1}\right)=\mathit{D}\mathit{\theta },$$ (13)

where

$$\mathit{D}=\mathit{B}\square \mathit{B}=\left(\mathit{B}\otimes {\mathit{1}}_N^{\top }\right)\odot \left({\mathit{1}}_N^{\top }\otimes \mathit{B}\right),$$ (14)

in which the symbol ⊙ denotes element-wise multiplication of matrices. In Wood (2017), the symbol □ in (14) is called the row-wise Kronecker product, which results in a n× N $\check{N}$ tensor product design matrix D from the two marginal design matrices B and $\check{\mathit{B}}$.

Similarly, the roughness penalty matrices associated with the tensor product representation (12) can be constructed from the roughness penalty matrices $\mathbb{P}$ and $\mathbb{P}$ associated with the univariate (marginal) basis matrices B and $\check{\mathit{B}}$, and are given by $\mathit{P}=\mathbb{P}\otimes {\mathit{I}}_{\check{N}}$ and $\check{\mathit{P}}={\mathit{I}}_N\otimes \check{\mathbb{P}}$, for the axis directions u and A, respectively. Here, I denotes the identity matrix, and both P and $\check{\mathit{P}}$ are square matrices with dimension N $\check{N}$.

We now need to impose the constraint (10) on the 2-dimensional smooth function g under the tensor product representation (13). For each fixed β, the constraint (10) on g amounts to excluding the main effect of u = β^⊤X from the function g. We deal with this by a reparametrization of the representation (13) for g. Consider the following sum-to-zero (over the n observed values) constraint for the marginal function of A:

$${\mathit{1}}^{\top }\check{\mathit{B}}\check{\mathit{\gamma }}=0,$$ (15)

for any arbitrary $\check{\mathit{\gamma }}\in {ℝ}^{\check{N}}$, where 1 is a length n vector of 1’s. With constraint (15), the linear smoother associated with the basis matrix $\check{\mathit{B}}$ cannot reproduce constant functions (Hastie and Tibshirani, 1999). That is, the linear constraint (15) removes the span of constant functions from the span of the marginal basis matrix $\check{\mathit{B}}$ associated with A. Constraint (15) results in a tensor product basis matrix, D = B□$\check{\mathit{B}}$ in (13), that will not include the main effect of u that results from the product of the marginal basis matrix B with the constant function in the span of the other marginal basis matrix $\check{\mathit{B}}$. Therefore, the resultant fit, under representation (13) (subject to (15)) of the smooth function g, excludes the main effect of u. See Section 5.6 of Wood (2017) for some more details.

We impose the linear constraint (15) on the matrix $\check{\mathit{B}}$, and consequently, the resulting basis matrix D of representation of g in (13) becomes independent of the basis associated with the main effect of u. Imposition of such a linear constraint (15) on a basis matrix is routine. The key is to find an (orthogonal) basis for the null space of the constraint (15), and then absorb the constraint into the basis construction (14). To be specific, we can create a $\check{N}\times (\check{N}-1)$ matrix, which we denote as Z, such that, given any arbitrary coefficient vector ${\check{\mathit{\gamma }}}_0\in {ℝ}^{\check{N}-1}$, if we set $\check{\mathit{\gamma }}=\mathit{Z}{\check{\mathit{\gamma }}}_0$, then we have 1^⊤ $\check{\mathit{B}}\check{\mathit{\gamma }}$ = 0, automatically satisfying the constraint (15). Such a matrix Z is constructed using a QR decomposition of ${\check{\mathit{B}}}^{\top }$ 1. Then we can reparametrize the marginal function of A by setting its model matrix to $\check{\mathit{B}}\leftarrow \check{\mathit{B}}\mathit{Z}$ (and its penalty matrix ton $\check{\mathbb{P}}\leftarrow {\mathit{Z}}^{\top }\check{\mathbb{P}}\mathit{Z}$). From this point forward, for notational simplicity, we redefine the matrix $\check{\mathit{B}}$ (and $\check{\mathbb{P}}$) to be this reparameterized, constrained marginal basis matrix (and the reparameterized constrained penalty matrix).

This sum-to-zero reparametrization of the marginal basis matrix $\check{\mathit{B}}$ of A to satisfy (15) creates a term $\mathrm{vec}\left\{g\left(u_i,A_i\right)\right\}\in {ℝ}^n$ in (13) that specifies such a pure A-by-X interaction (plus the A main effect) component, that is also orthogonal to the X main effect. In Wood (2006), this reparameterization approach is used to create an analysis of variance (ANOVA) decomposition of a smooth function of several variables. In this paper we use this same reparameterization to orthogonalize the interaction effect component g(β^⊤X, A) from the main effect, and to allow an unspecified/misspecified main effect for X in the estimation of the SIMSL (4). Provided that the orthogonality constraint (i.e., (15)) issue is addressed, the interaction effect term g(β^⊤X, A) of model (4), for each fixed β, can be represented using penalized regression splines and estimated based on penalized least squares, which we describe next.

3.2. Estimation algorithm

We define the criterion function for estimating (g,β) in the SIMSL (4):

$$\begin{gathered} Q(\mathit{\theta },\beta )={\Vert Y_{n\times 1}-g\left(\mathit{X}\beta ,A_{n\times 1}\right)\Vert }^2+\lambda \Vert \mathit{P}\mathit{\theta }{\Vert }^2+\check{\lambda }\Vert \check{\mathit{P}}\mathit{\theta }{\Vert }^2 \\ ={\Vert Y_{n\times 1}-\mathit{D}\mathit{\theta }\Vert }^2+\lambda \Vert \mathit{P}\mathit{\theta }{\Vert }^2+\check{\lambda }\Vert \check{\mathit{P}}\mathit{\theta }{\Vert }^2 \end{gathered}$$ (16)

subject to the constraint that the function g(·,·) empirically satisfies (5). In (16), X is a n × p matrix whose ith row is $X_i^{\top }$. Since both θ and β are unknown in (16), estimation of θ and β is conducted iteratively. We describe below the estimation procedure.

1. For a fixed estimate of β (that defines the linear predictor u), minimize the following criterion function over $\mathit{\theta }\in {ℝ}^{N\check{N}}$,

   $${\Vert Y_{n\times 1}-\mathit{D}\mathit{\theta }\Vert }^2+\lambda {\Vert \mathit{P}\mathit{\theta }\Vert }^2+\check{\lambda }{\Vert \check{\mathit{P}}\theta \Vert }^2,$$ (17)

   where D is given by (14). Given tuning parameters $(\lambda ,\check{\lambda })$, the minimizer θ of (17) is:

   $$\widehat{\mathit{\theta }}={\left({\mathit{D}}^{\top }\mathit{D}+\lambda {\mathbf{P}}^{\top }\mathbf{P}+\check{\lambda }{\check{\mathit{P}}}^{\top }\check{\mathit{P}}\right)}^{-1}{\mathit{D}}^{\top }{Y}_{n\times 1}.$$
2. For a fixed estimate of the surface g (i.e., given θ), perform a first-order Taylor approximation of g(Xβ, A_n×1) in (16) with respect to β, around the current estimate, say, $\tilde{\beta }\in \mathrm{\Theta }$,

   $$g\left(\mathit{X}\beta ,A_{n\times 1}\right)\approx g\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)+\mathrm{diag}\left\{{\dot{g}}_{{\partial }_1}\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)\right\}\mathit{X}(\beta -\tilde{\beta }),$$ (18)

   where ${\dot{g}}_{{\partial }_1}(u,a)$ denotes the partial first derivative of g(u, a) with respect to u, i.e., $\frac{\partial g(u,a)}{\partial u}$. Utilizing (18), we approximate the quadratic loss in (16) by (as a function of β given θ):

   $$\begin{array}{l}{\Vert Y_{n\times 1}-g\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)-\mathrm{diag}\left\{{\dot{g}}_{{\partial }_1}\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)\right\}\mathit{X}(\beta -\tilde{\beta })\Vert }^2\\ ={\Vert Y_{n\times 1}-g\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)+\mathrm{diag}\left\{{\dot{g}}_{{\partial }_1}\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)\right\}\mathit{X}\tilde{\beta }-\mathrm{diag}\left\{{\dot{g}}_{{\partial }_1}\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)\right\}\mathit{X}\beta \Vert }^2\\ ={\Vert Y_{n\times 1}^{*}-{\mathit{X}}^{*}\beta \Vert }^2,\end{array}$$ (19)

   where $Y_{n\times 1}^{*}=Y_{n\times 1}-g\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)+\mathrm{diag}\left\{{\dot{g}}_{{\partial }_1}\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)\right\}\mathit{X}\tilde{\beta }$, and ${\mathit{X}}^{*}=\mathrm{diag}\left\{{\dot{g}}_{{\partial }_1}\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)\right\}\mathit{X}$. The minimizer $\widehat{\beta }$ of (19) is:

   $$\widehat{\beta }={\left({\mathit{X}}^{*\top }{\mathit{X}}^{*}\right)}^{-1}{\mathit{X}}^{*\top }{Y}_{n\times 1}^{*}.$$ (20)

   Then we scale $\widehat{\beta }$ to have unit L² norm, i.e, $\widehat{\beta }/\Vert \widehat{\beta }\Vert$, and enforce a positive first element to restrict the estimate of β to be in Θ.

These two steps can be iterated until convergence to obtain an estimate of (g*,β*) in (9), which we denote as $\left({\widehat{g}}^{*},{\widehat{\beta }}^{*}\right)$. For Step 1, the tuning parameters $(\lambda ,\check{\lambda })$ can be automatically selected, for example, by the generalized cross-validation (GCV) or the restricted maximum likelihood (REML) methods. In this paper, we use REML for the simulation examples and the applications.

Lastly, for model hierarchy, it is common practice to include all lower order effects of variables if there are higher-order interaction terms including that set of variables. Once convergence of the estimate $\widehat{\beta }$ is reached in the above algorithm and the single-index β^⊤X in the term g(β^⊤X, A) of model (4) is estimated, we recommend fitting one final (unconstrained) smooth function g of A and ${\widehat{\beta }}^{\top }X$, without enforcing the constraint (15) on g. Given the final estimate of β, the unconstrained final surface-link g(·,·) retains the main effect of β^⊤X and preserves model hierarchy.

4. Generalized single-index models for optimizing dose rules

The proposed approach to optimizing the heterogeneous dose effect (i.e., the X-by-A interaction effect) term of model (4) can be extended to a more general setting in which the response Y follows an exponential family distribution. Given (X, A), we assume an additive single-index model (4):

$$m(X,A)=\mathbb{E}[Y\mid X,A]={\mu }_0(X)+g_0\left({\beta }_0^{\top }X,A\right),$$ (21)

(in which subscript (0) is used to indicate the “true” value), and the variance of Y is determined based on the exponential family density of the form:

$$\exp \{[Yh(m(X,A))-b(h(m(X,A)))]/a(\varphi )+c(Y,\varphi )\},$$ (22)

where h is the canonical link function associated with the assumed distribution of Y, and the functions a, b and c are distribution-specific known functions. For model identifiability, we assume β₀∈Θ, and $g_0\in {\mathcal{H}}_2^{\left({\beta }_0\right)}$ to satisfy $\mathbb{E}\left[g_0\left({\beta }_0^{\top }X,A\right)\mid X\right]=0$. The dispersion parameter ϕ> 0 in (22) takes on a fixed, known value in some families (e.g., ϕ = 1, in Bernoulli and Poisson), while in other families, it is an unknown parameter (e.g., in Gaussian).

We estimate (g₀,β₀) in model (21) by utilizing the following working mean model:

$$m(X,A)=h^{-1}\left(g\left({\beta }^{\top }X,A\right)\right)\left(g\in {\mathcal{H}}_2^{(\beta )};\beta \in \mathrm{\Theta }\right),$$ (23)

subject to the constraint $\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]=0$ on g, and the distribution of Y is described by the exponential family chosen in (22). We optimize the population logarithmic version of (22) over the unknowns (g,β) of (23):

$$\begin{array}{l}\left(g^{*},{\beta }^{*}\right)=\underset{g\in H_2^{(\beta )},\beta \in \mathrm{\Theta }}{\mathrm{argmax}}\mathbb{E}\left[Yg\left({\beta }^{\top }X,A\right)-b\left(g\left({\beta }^{\top }X,A\right)\right)\right]\\ \text{subject}\text{to}\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]=0,\end{array}$$ (24)

where (we use the convention that the terms (i.e., a(ϕ) and c(Y,ϕ) ) that do not contain the parameter of interest can be dropped from the expression of a log likelihood) the expectation in the criterion function is with respect to the joint distribution of (Y, A, X). Thus, the solution (g*,β*) on the left-hand side of (24) corresponds to the minimizer of the Kullback-Leibler (KL) divergence between the distributions with the working mean model (23) and the true mean model (21). In (24), b(s) = s²/2 for a Gaussian Y (for which the optimization (9) is a special case of (24)), b(s) = log{1+ exp(s)} for a Bernoulli Y, and b(s) = exp(s) for a Poisson Y.

The constraint $\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid X\right]=0$ in optimization (24) implies:

$$\begin{gathered} \mathbb{E}\left[Yg\left({\beta }^{\top }X,A\right)-b\left(g\left({\beta }^{\top }X,A\right)\right)\right]=\mathbb{E}\left[\left\{{\mu }_0(X)+g_0\left({\beta }_0^{\top }X,A\right)\right\}g\left({\beta }^{\top }X,A\right)-b(g({\beta }^{\top }X,A))\right] \\ =\mathbb{E}\left[\mathbb{E}\left[{\mu }_0(X)g\left({\beta }^{\top }X,A\right)\mid X\right]\right]+\mathbb{E}[g_0({\beta }_0^{\top }X,A)(g\left({\beta }^{\top }X,A\right)-b(g\left({\beta }^{\top }X,A\right)] \\ =\mathbb{E}[g_0\left({\beta }_0^{\top }X,A\right)\left(g\left({\beta }^{\top }X,A\right)-b\left(g\left({\beta }^{\top }X,A\right)\right)\right], \end{gathered}$$ (25)

which is free of μ₀ in model (21). Therefore, the left-hand side, (g*,β*), of (24) does not depend on the unspecified X “main” effect function μ₀.

Proposition 1.

The solution (g*,β*) of the constrained optimization problem (24) satisfies:

$$g_0=h^{-1}\text{o}{g}^{*}\text{and}{\beta }_0={\beta }^{*}$$ (26)

(a.s.), where $g_0\in {\mathcal{H}}_2^{\left({\beta }_0\right)}$ and β₀∈Θ are given from the true mean model (21), and the function h⁻¹ is the inverse of the canonical link function associated with the assumed exponential family distribution and the operator ° represents the composition of two functions.

The proof of Proposition 1 is in Supplemental Materials Section A.1. In (26), h⁻¹(s)=s (the identity function) for a Gaussian Y, h⁻¹(s)=exp(s)/{1+exp(s)} for a Bernoulli Y, and h⁻¹(s)=exp(s) for a Poisson Y.

To solve (24) based on observed data $\left(Y_i,A_i,X_i\right)(i=1,\dots ,n)$, we replace the quadratic loss term in (16) by the negative of the log likelihood of the data. For a fixed β∈Θ, given the representation of g with Dθ in (13), the basis coefficient θ is estimated by the inner iteratively re-weighted least squares (IRLS) and the associated smoothing parameters (λ and λ in (16)) are estimated by the outer optimization of, e.g., REML or GCV, as part of Step 1 (of Section 3.2) of the model fitting. The only adjustment to be made to the conventional GAM estimation is to enforce the constraint $\mathbb{E}\left[g\left({\beta }^{\top }X,A\right)\mid {\beta }^{\top }X\right]=0$ on g. As in Section 3.1, this constraint can be absorbed into the tensor product basis representation (13). For Step 2 (of Section 3.2), once g is profiled out (by Step 1), we replace the normal residual vector in (19), i.e., $Y_{n\times 1}-g\left(\mathit{X}\tilde{\beta },A_{n\times 1}\right)$, by the working residual from the final IRLS fit of Step 1. Then we perform a weighted least squares (instead of the least squares (20)) for β, where the weights are given from the final IRLS fit of Step 1. We alternate between the Steps 1 and 2 until convergence of $\widehat{\beta }$, as in Section 3.2. The resulting estimate for (g*,β*) in (24) is then used to estimate (g₀,β₀) in (21), based on the relationship (26). We also note that the framework (24) can be extended to incorporate a multinomial response, an instance of which we discuss in the following remark.

Remark 1.

The approach (24) to optimizing the component (g,β) of SIMSL can be generalized to the context of a proportional odds single-index model, where we have an ordinal response Y, in which its value exists on an arbitrary scale (in K categories), with only the relative ordering between different values being important. To deal with such a case, we introduce a length-K response vector Y = (Y₁,Y₂,…,Y_K)^⊤ where its component Y_j denotes the indicator for category j, with associated vector of probabilities (p₁,p₂,…,p_K)^⊤, in which $p_K=1-\sum _{j=1}^{K-1}{p}_j$ (and p_j>0), together with their cumulative probabilities: $P(Y\le j)=q_j=\sum _{s=1}^j{p}_s(j=1,2,\dots ,K-1)$. We can model these cumulative probabilities ${\left(q_1,q_2,\dots ,q_{K-1},1\right)}^{\top }$ a by cumulative logit SIMSL:

$$h(P(Y\le j\mid X,A))=h\left(q_j(X,A)\right)={\alpha }_j+\mu (X)+g\left({\beta }^{\top }X,A\right)(j=1,2,\dots ,K-1)$$ (27)

where ${\alpha }_j\in ℝ\left({\alpha }_1<{\alpha }_2<\dots <{\alpha }_{K-1}\right)$ are unknown cut-point parameters associated with the ordered response categories j =1,2,…,K −1, and h(s) = log(s/(1−s)) is the logit link. For the (K-category) multinomial exponential family response Y, let us consider its canonical parameter $\mathit{\eta }:={\left({\eta }_1,{\eta }_2,\dots ,{\eta }_{K-1},0\right)}^{\top }\in {ℝ}^K$, where its nonzero components are specified by: ${\eta }_j=\log \left(p_j/p_K\right)=\log \left(\left(q_j-q_{j-1}\right)/\left(1-q_{K-1}\right)\right)(j=1,\dots ,K-1)$(with q₀ = 0), in which the cumulative probabilities (q₁,q₂,…,q_K−1,1)^⊤ are specified by model (27). This multinomial exponential family representation for the distribution of Y allows us to use the optimization framework (24), with its criterion function extended to incorporate the multivariate response: $\mathbb{E}\left[{\mathit{Y}}^{\top }\mathit{\eta }-b(\mathit{\eta })\right]$, where $b(\mathit{\eta })=\log \left\{1+\sum _{j=1}^{K-1}\exp \left({\eta }_j\right)\right\}$, for optimization of the cumulative logit SIMSL (27). The threshold-point parameters ${\alpha }_j\in ℝ\left({\alpha }_1<{\alpha }_2<\dots <{\alpha }_{K-1}\right)$ in model (27) are estimated as part of Step 1 of model fitting in Section 3.2 (alongside the model smoothing parameters), in which the model (27), for each fixed β which is estimated as part of Step 2, is optimized via the penalized IRLS with an empirical version of $-\mathbb{E}\left[{\mathit{Y}}^{\top }\mathit{\eta }-b(\mathit{\eta })\right]$; the Steps 1 and 2 are iterated until convergence. The heterogeneous treatment effect g(β^⊤X, A) in model (27) does not depend on j nor μ(X); this allows us to develop an individualized dose rule independently of the arbitrary categorization of Y, and of the unspecified X main effect μ(X) that does not influence the treatment effect. Given X, the cumulative logit SIMSL-based individualized dose rule is $f(X)=\underset{a\in A}{\mathrm{argmax}}g\left({\beta }^{\top }X,a\right)$.

In Supplemental Materials Section C, we provide a real data example illustrating the approach (24) to modeling interaction effects between X and A on a count response variable Y, and a simulation illustration for the utility of the proportional odds SIMSL (27) when the treatment response Y is ordinal, which is common in biomedical and epidemiological studies.

5. Simulation example

In this section, we consider a set of simulation studies with data generated from the four scenarios described in Chen et al. (2016). We generate p-dimensional covariates X = (X₁,…, X_p)^⊤, where each entry is generated independently from Uniform[−1,1]. In Scenarios 1 and 2, the treatment A is generated from Uniform[0,2] independently of X, mimicking a randomized trial. In Scenarios 3 and 4, the distribution of A (described below) depends on X, mimicking an observational study setting. In each scenario, the outcome Y given (X, A) is generated from the standard normal distribution, with the following four different mean function scenarios:

1. Scenario 1: $\mathbb{E}[Y\mid X,A]=8+4X_1-2X_2-2X_3-25{\left(f_{\text{opt}}(X)-A\right)}^2$, where $f_{\text{opt}}(X)=1+0.5X_1+0.5X_2$. Here, the optimal individualized dose rule is a linear function of X.

2. Scenario 2: $\mathbb{E}[Y\mid X,A]=8+4\cos \left(2\pi X_2\right)-2X_4-8X_5^3-15\left|f_{\text{opt}}(X)-A\right|$, where

   $$f_{\text{opt}}(X)=0.6\left(-0.5<X_1<0.5\right)+1.2\left(X_1>0.5\right)+1.2\left(X_1<-0.5\right)+X_4^2+0.5\log \left(\left|X_7\right|+1\right)-\mathrm{0.6.}$$

   Here, the optimal individualized dose rule is a nonlinear function of X.
3. Scenario 3 is the same as in Scenario 2, except that A depends on X as follows:

   $$A~\{\begin{array}{ll}\mathrm{Trunc}\text{N}\left(-0.5+0.5X_1+0.5X_2,0,2,0.5\right),\hfill & \text{when}{X}_3<0\hfill \\ \text{TruncN}\left(\left|0.5+1.5X_2\right|,0,2,1\right),\hfill & \text{when}{X}_3>0\hfill \end{array}$$

   where TruncN(μ,a,b,σ) denotes the truncated normal distribution with mean μ, lower bound a and upper bound b, and standard deviation σ.
4. Scenario 4 is the same as in Scenario 2, except that A depends on X as follows:

   $$A~\mathrm{TruncN}\left(f_{\text{opt}}(X),0,2,0.5\right).$$

Following Chen et al. (2016), we set p = 30 in Scenario 1, and p = 10 for Scenarios 2, 3 and 4. (In Section A.2 of Supplementary Materials, we describe how these scenarios’ mean models can be reparametrized to fit in the framework (4).) For each simulated dataset, we apply the proposed method of estimating the A-by-X interaction term in the SIMSL (4) based on (9), and the optimal dose rule f_opt by $\widehat{f}(X)=\underset{a\in A}{\mathrm{argmax}}{\widehat{g}}^{*}\left({\widehat{\beta }}^{*\top }X,a\right)$. We simulated 200 data sets for each scenario. For comparison, we report results of the estimation approaches considered in Chen et al. (2016), including their Gaussian kernel-based outcome-weighted learning (K-O-learning) and linear kernel-based outcome-weighted learning (L-O-learning). We also report a support vector regression (SVR; Vapnik, 1995; Smola and Scholopf, 2004) with a Gaussian kernel to estimate the nonlinear relationship between Y and (X, A) (Zhao et al., 2009) that was used for comparison. In Scenario 1, we used (X, A) as the predictors for the outcome in the SIMSL. In Scenarios 2, 3 and 4, we used (X, X², A) (i.e., including a quadratic term in X) as the predictors for the SIMSL.

Since we are simulating data from known models in which the true relationship $\mathbb{E}[Y\mid X,A]$ is known, we can compare the estimated dose rules $\widehat{f}$ derived from each method in terms of the value (1). Specifically, an independent test set of size was $\tilde{n}=5000$ generated and the value (1) of $\widehat{f}$ was approximated using $\mathcal{V}(\widehat{f})={\tilde{n}}^{-1}\sum _{i=1}^{\tilde{n}}\mathbb{E}\left[Y_i\mid X_i,A_i=\widehat{f}\left(X_i\right)\right]$, for each simulation run. Given each scenario and a training sample size n, we replicate the simulation experiment 200 times, each time estimating the value. Again, following Chen et al. (2016), we report the averaged estimated values (and standard deviations) for the cases where $\widehat{f}$ is estimated from a training set of size n = 50,100,200,400 and 800 for Scenario 1 and 2, and the cases with n = 200 and 800 for Scenario 3 and 4. The simulation results are given in Tables 1 and 2.

Table 1.

Average (sd) value $\mathcal{V}(f)$ from 200 replicates from randomized trials. In both settings, the oracle f_opt attains a value $\mathcal{V}\left(f_{\text{opt}}\right)=8$ (boldface denotes the largest in each row).

	n	SIMSL	K-O-learning	L-O-learning	SVR
Scenario 1	50	1.04 (4.06)	4.78 (0.48)	4.83 (1.40)	−12.21 (7.53)
	100	6.63 (0.63)	5.69 (0.40)	5.39 (0.93)	−2.57 (6.34)
	200	7.45 (0.20)	6.68 (0.26)	6.85 (0.34)	3.46 (1,97)
	400	7.77 (0.08)	7.28 (0.15)	7.41 (0.14)	6.13 (0.47)
	800	7.88 (0.04)	7.54 (0.08)	7.67 (0.08)	7.36 (0.12)
Scenario 2	50	0.90 (2.04)	2.00 (0.29)	1.16 (0.71)	−1.96 (1.70)
	100	3.65 (0.76)	2.19 (0.43)	1.57 (0.52)	0.24 (1.42)
	200	4.71 (0.41)	2.84 (0.37)	2.02 (0.30)	2.01 (0.84)
	400	5.25 (0.20)	3.69 (0.27)	2.30 (0.18)	3.47 (0.37)
	800	5.59 (0.12)	4.41 (0.19)	2.49 (0.10)	4.35 (0.19)

Table 2.

Average (sd) value $\mathcal{V}(f)$ from 200 replicates from observational studies. In both settings, the oracle f_opt attains a value $\mathcal{V}\left(f_{\text{opt}}\right)=8$ (boldface denotes the largest in each row).

	n	SIMSL	K-O-learning	K-O-learning(Prp)	SVR
Scenario 3	200	4.03 (0.97)	2.68 (0.30)	2.74 (0.29)	1.99 (0.83)
	800	5.46 (0.20)	4.06 (0.30)	4.19 (0.20)	4.09 (0.28)
Scenario 4	200	4.07 (0.72)	3.29 (0.28)	3.23 (0.28)	−0.95 (1.57)
	800	5.51 (0.19)	4.91 (0.14)	4.73 (0.17)	3.04 (0.52)

The results in Tables 1 and 2 indicate that the proposed regression method for optimizing dose rules outperforms the alternative approaches presented in Chen et al. (2016) in all cases except when the training sample size is very small (n = 50). In Table 2, K-O-learning(Prp) refers to the propensity score-adjusted K-O-learning of Chen et al. (2016). When n = 50, the outcome-weighted learning methods outperform the regression-based approaches (i.e., SIMSL and SVR), especially for Scenario 1 (with p = 30) where the regression approaches exhibit large variances. However, when n = 100, the performance of SIMSL improves dramatically in terms of both value and small variance. We also note that using (A, X, X²) instead of (A, X) as predictors of SIMSL in Scenario 2 lead to a substantial improvement in performance. If (X, A) is used for SIMSL in Scenario 2, the estimated values (and sd) are: −0.98(2.15),0.56(1.54),1.91(0.89),2.70(0.64) and 3.23(0.41), for n = 50,100,200,400 and 800, respectively.

6. Application to optimization of the warfarin dose with clinical and pharmacogenetic data

In this section, the utility of the SIMSL approach to personalized dose finding is illustrated from an anticoagulant study. Warfarin is a widely used anticoagulant to treat and prevent blood clots. The therapeutic dosage of warfarin varies widely across patients. Our analysis of the data will broadly follow that of Chen et al. (2016). After removing patients with missing data, the dataset provided by International Warfarin Pharmacogenetics Consortium et al. (2009) (publicly available to download from https://www.pharmgkb.org/downloads/) consists of 1780 subjects, including information on patient covariates (X), final therapeutic dosages (A), and patient outcomes (INR, International Normalized Ratio). INR is a measure of how rapidly the blood can clot. For patients prescribed warfarin, the target INR is around 2.5. To convert the INR to a measurement responding to the warfarin dose level, we construct an outcome Y =−| 2.5− INR |, and a larger value of Y is considered desirable.

There were 13 covariates $X={\left(X_1,\dots ,X_{13}\right)}^{\top }$ in the dataset (both clinical and pharmacogenetic variables): weight (X₁), height (X₂), age (X₃), use of the cytochrome P450 enzyme inducers (X₄; the enzyme inducers considered in this analysis includes phenytoin, carbamazepine, and rifampin), use of amiodarone (X₅), gender (X₆; 1 for male, 0 for female), African or black race (X₇), Asian race (X₈), the VKORC1 A/G genotype (X₉), the VKORC1 A/A genotype (X₁₀), the CYP2C9 *1/*2 genotype (X₁₁), the CYP2C9 *1/*3 genotype (X₁₂), and the other CYP2C9 genotypes (excluding the CYP2C9 *1/*1 genotype which is taken as the baseline genotype) (X₁₃). Further details on these covariates are given in International Warfarin Pharmacogenetics Consortium et al. (2009). The first 3 covariates (weight, height, age) were treated as continuous variables, standardized to have mean zero and unit variance; the other 10 covariates are indicator variables.

In estimating the optimal individualized dose rule f_opt, modeling the drug (dose level A) interactions with the patient covariates X is essential. Under the proposed SIMSL approach (4), $f_{\text{opt}}(X)=\underset{a\in \mathcal{A}}{\mathrm{argmax}}g\left({\beta }^{\top }X,a\right)$ and thus the A-by-X interaction effect term g(β^⊤X, A) is the target component of interest. In SIMSL, due to orthogonality (7), we can solve (9) for (g,β), without having to model the μ term in (4). However, modeling the μ term, even with a misspecified working model, can generally improve the efficiency of the estimator of (g,β) (i.e., yielding smaller variances for estimators; see Park et al. (2020) for a theoretical justification in the case where treatment A is a discrete or binary variable), which leads to improve the efficiency of the estimator of f_opt (see Supplementary Materials Section C.1 for a simulation illustration in which an enhanced estimation performance is illustrated when the X main effect is incorporated to the estimation of f_opt).

Thus, in this application, we model the μ term of (4) with a possibly misspecified working model, which consists of a set of linear terms for the indicators X₄,…, X₁₃ and a set of cubic P-spline smooth terms for the continuous covariates X₁, X₂ and X₃. These terms are estimated alongside the heterogeneous treatment effect term g(β^⊤X, A) by the procedure described in Supplementary Materials Section C.1, which is a slight modification to that described in Section 3.2. (The estimated coefficient β, with or without incorporating the μ term in the estimation, along with their bootstrap confidence intervals, are provided in Section D of Supplementary Materials.) The third panel in Figure 1 displays a surface plot of the estimated 2-dimensional link function g(β^⊤X, A), showing an interactive relationship on the index-treatment domain. The first two panels in Figure 1 display the estimated marginal effect function for the dose A and that for the estimated index β^⊤X.

Fig. 1.

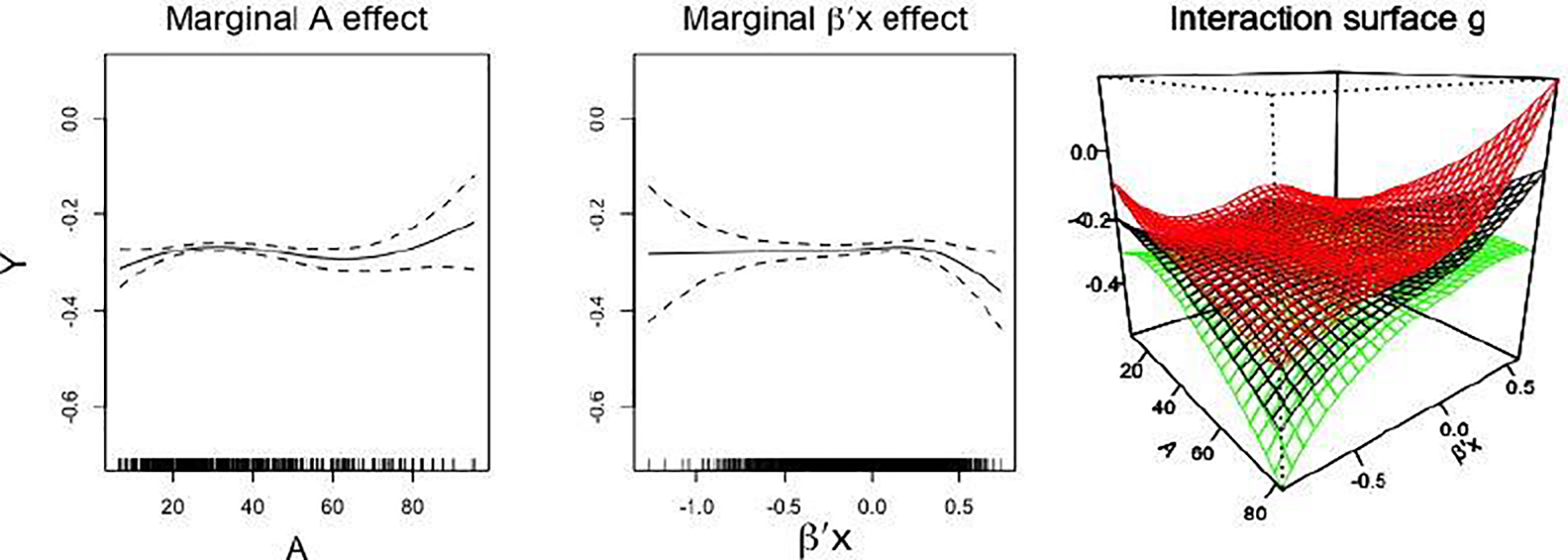
The first two panels: the marginal effect of dose A (left panel) and that of the estimated single-index (middle panel) with 95% confidence bands (dashed curves) given the estimated β^⊤X. The third panel: the estimated link surface (g) for the dose (A) and index (β^⊤X) interaction; the red and green surfaces are at ±2 standard error from the estimated surface (the black) in the middle, conditioning on the estimated single-index.

We construct a 95% normal approximation bootstrap confidence interval for β, based on 500 bootstrap replications (see Supplementary Materials Section C.3 for the confidence interval construction and for a coverage probability simulation). The confidence intervals for the β_j’s associated with the covariates weight (X₁), height (X₂), the use of the cytochrome P450 enzyme inducers (X₄), Asian race (X₈), the VKORC1 A/G genotype (X₉), and the CYP2C9 *1/*2 genotypes (X₁₁) do not include 0. We infer that these covariates are potentially clinically important drug effect modifiers, interacting with warfarin in their effects on INR.

Chen et al. (2016) noted that the analysis results from International Warfarin Pharmacogenetics Consortium et al. (2009), as well as their linear kernel-based outcome-weighted learning results, suggest increasing the dose if patients are taking Cytochrome P450 enzyme (X₄). Roughly speaking, the interaction surface g (the right-most panel) in Figure 1 indicates that for a smaller value of β^⊤X (e.g., β^⊤X < −0.3), a moderate or a relatively low dose A (e.g., A < 50) may be preferred, whereas for a larger value of β^⊤X (e.g., β^⊤X > 0), a relatively high dose A (e.g., A > 50) may be preferred. Considering the sign of the estimated coefficient $\left({\widehat{\beta }}_4=-0.60\right)$ associated with X₄, this is roughly consistent with International Warfarin Pharmacogenetics Consortium et al. (2009) and Chen et al. (2016).

To evaluate the performance of the individualized dose rules estimated from the 6 methods, including the propensity score-adjusted outcome-weighted learning with a linear/Gaussian kernel, denoted as L-O-learning(Prp) and K-O-learning(Prp), respectively) considered in Section 5, we randomly split the dataset at a ratio of 1-to-1 into a training set and a testing set, replicated 100 times, each time estimating f_opt using the 6 methods based on the training set, and estimating the value (1) of each estimated f_opt based on the testing set. Unlike the simulated data in Section 5, the true relationship between the covariate-specific dose and the response is unknown. Therefore, for each dose rule f, we need to estimate the value (1) from the testing data. Given a dose rule f, only a very small proportion (or none) of the observations will satisfy A_i = f(X_i), and thus only a very small proportion (or none) of the observations in the testing data will contribute information to estimate the value (1). However, Cai and Tian (2016) noted that the value (1) for each f can also be written as $\mathcal{V}(f)=\mathbb{E}[\mathbb{E}[Y\mid A=f(X),f(X)]]$. Therefore, using a 2-dimensional smoother of A and f(X) for Y, one may first obtain a nonparametric estimate of $\mathbb{E}[Y\mid A,f(X)]$, denoted as $\widehat{m}(A,f(X))$, and then $\mathcal{V}(f)$ may be estimated as $\mathcal{V}(f)=n^{-1}\sum _{i=1}^n\widehat{m}\left(f\left(X_i\right),f\left(X_i\right)\right)$. Specifically, given a dose rule f estimated from a training set, we can estimate $\mathbb{E}[Y\mid A,f(X)]$ based on $\left(Y_i,A_i,f\left(X_i\right)\right)$ from a test set, using a set of thin plate regression spline bases obtained from a rank-100 eigen-approximation to a thin plate spline, with the smoothness parameter selected by REML, implemented via the R (R Core Team, 2019) function mgcv::gam (Wood, 2019). A thin plate spline is an isotropic smooth; isotropy is often appropriate for two variables observed on the same scale, which is the case here.

Figure 2 displays boxplots describing the distributions for the estimated values (1) of the approaches “SIMSL(w. X main)” (SIMSL with the μ term in the estimation) and “SIMSL(w.o. X main)” (SIMSL without the μ term in the estimation), and the other five estimation methods described in Section 5, obtained from the aforementioned 100 random training/testing splits. The boxplots indicate that the proposed SIMSL methods (note that “SIMSL(w. X main)” slightly outperforms “SIMSL(w.o. X main)”) and the propensity-score adjusted K-O-learning of Chen et al. (2016) perform at a similar level, while outperforming all other approaches, illustrating the potential utility of the proposed method. In comparison to the outcome-weighted learning approach of Chen et al. (2016), one advantage of the proposed approach is that it allows visualization of the estimated interactive structure on the dose-index domain, as illustrated in the right panel of Figure 1. Additionally, if each of the covariates is standardized to have, say, unit variance, then the relative importance of each covariate in characterizing the heterogeneous dose response can be determined by the magnitude of the estimated coefficients in β, rendering a potentially useful interpretation when examining the drug-covariates interactions.

Fig. 2.

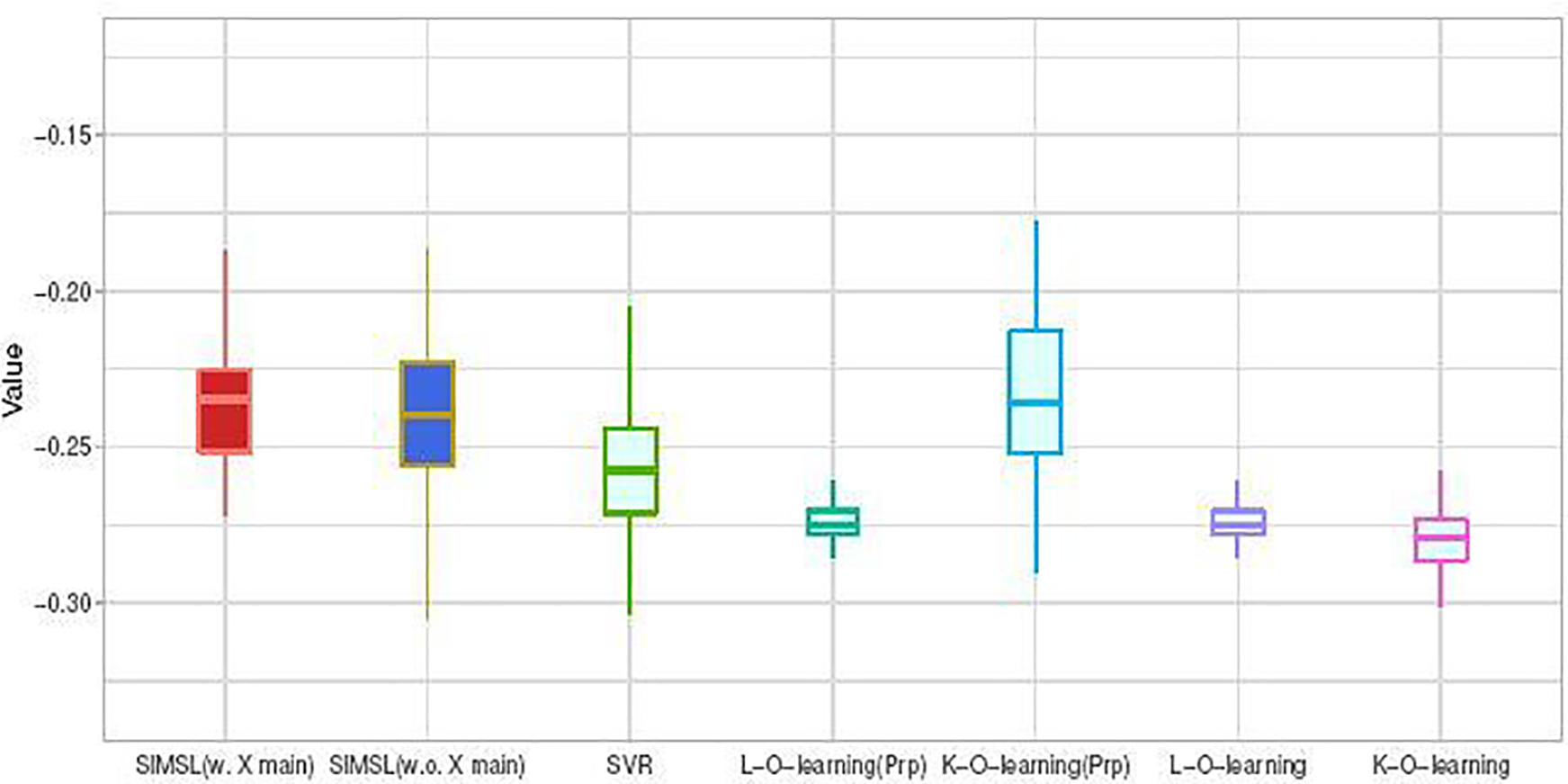
Boxplots of the estimated values of the individualized dose rules using 7 approaches, obtained from 100 randomly split testing sets. Mean (and standard deviation) of the value estimates: SIMSL(w. X main): −0.231 (0.03); SIMSL(w.o. X main): −0.237 (0.03); SVR: −0.254 (0.02); L-O-learning(Prp): −0.274 (0.01); K-O-learning(Prp): −0.234 (0.03); L-O-learning: −0.274 (0.01); K-O-learning: −0.279 (0.01).

7. Discussion

In this paper, we proposed a single-index model that utilizes a surface link-function as a function of a linear projection of covariates and a continuous “treatment” variable, which parsimoniously represents the interaction effect between covariates and a treatment defined on a continuum. The model provides an intuitive tool for investigating personalized dose finding in precision medicine, without the need for a significant change in the established generalized additive regression modeling framework.

One important limitation is that the confidence band associated with the estimated surface g is computed conditional on the estimated β^⊤X, and the uncertainty in β is not accounted for. The fact that the domain of g varies depending on the estimate of β complicates the confidence band construction for g. One potential approach is to consider a Bayesian framework and a posterior distribution of g(β^⊤X, A), and make probabilistic statements about the prediction of the component g(β^⊤X, A) given (X, A). Furthermore, depending on context, for scientific interpretability of the model, it may be sometimes desirable to consider shape constraints such as monotonicity or convexity/concavity (see Supplementary Materials Section C.4 for discussion on shape constraints), as well as optimization under safety constraints (Laber et al., 2018). The development of a Bayesian model estimation and inference, with potential monotonicity or convexity/concavity constraints on the link surface is currently under investigation. In many applications, only a subset of variables may be useful in determining an optimal individualized dose rule. Also, high-dimensional settings can lead to instabilities and issues of overfitting. Forthcoming work will introduce a regularization method that can both avoid overfitting and choose among multiple potential covariates by obtaining a sparse estimate of the single-index coefficient β. Future extensions of this work could also include an extension to incorporate a functional covariate.

Supplementary Material

Supp 1

Supplementary Materials:

a pdf file containing supporting information for the main manuscript, including the proof of Proposition 1, a real data analysis and additional simulations illustrating an application of the generalized single-index regression approach in Section 4, and construction of bootstrap confidence intervals and supplementary information for Section 6.

R-package for SIMSL routine:

R-package simsl (Park et al., 2021) available on CRAN containing code to perform the proposed single-index regression method, and the datasets and the simulation examples illustrated in this article.