Bright Luminescence by Combining Chiral [2.2]Paracyclophane with a Boron–Nitrogen‐Doped Polyaromatic Hydrocarbon Building Block

Abstract

Novel BN‐doped compounds based on chiral, tetrasubstituted [2.2]paracyclophane and NBN‐benzo[f,g]tetracene were synthesized by Sonogashira–Hagihara coupling. Conjugated ethynyl linkers allow electronic communication between the π‐electron systems through‐bond, whereas through‐space interactions are provided by strong π–π overlap between the pairs of NBN‐building blocks. Excellent optical and chiroptical properties in racemic and enantiopure conditions were measured, with molar absorption coefficients up to ϵ=2.04×10⁵ M⁻¹ cm⁻¹, fluorescence quantum yields up to Φ _PL=0.70, and intense, mirror‐image electronic circular dichroism and circularly polarized luminescence signals of the magnitude of 10⁻³ for the absorption and luminescence dissymmetry factors. Computed g _lum,calcd. values match the experimental ones. Electroanalytical data show both oxidation and reduction of the ethynyl‐linked tetra‐NBN‐substituted paracyclophane, with an overlap of two redox processes for oxidation leading to a diradical dication.

Coupling through‐bond and through‐space by a chiral building block results in excellent optical and chiroptical properties: ϵ up to 2.04×10⁵ M⁻¹ cm⁻¹, Φ _PL up to 0.70, and intense, mirror‐image electronic circular dichroism and circularly polarized luminescence (CPL) signals of a magnitude of 10⁻³ for the absorption and luminescence dissymmetry factors.

Introduction

Conjugated organic compounds are of ever‐growing importance for modern technology.[ ¹ , ² , ³ , ⁴ , ⁵ , ⁶ , ⁷ ] They can provide superior characteristics over inorganic alternatives, such as flexibility in the solid state, enhanced charge transfer capabilities, and favorable optical properties,[ ⁸ , ⁹ , ¹⁰ ] while also offering the opportunity for easy modification. In the case of emitting compounds, due to the quantum mechanical property of being a massless boson with spin ±1 ħ, each generated photon can be in one of two circularly polarized states: either left or right handed circularly polarized. ^[11] For achiral emitting samples both states become equally populated, therefore the net polarization of the emitted light beam is zero. This changes for chiral luminescent systems in enantiopure or enantioenriched samples. ^[12] The absence of improper rotation symmetry elements allows for the favored emission of photons with one of the two possible polarizations, effectively transmitting molecular chirality to the light beam. ^[13] The differential emission of left‐ and right‐handed circularly polarized light can be measured through circularly polarized luminescence (CPL) spectroscopy and is quantified by the luminescence dissymmetry factor g _lum, calculated as g _lum=2 ΔI(λ)/I(λ), where ΔI(λ)=I _L(λ)−I _R(λ) and I(λ)=I _L(λ)+I _R(λ). ^[14] The value of g _lum is therefore ranging from −2 to +2. For chiroptical applications, a high value of |g _lum| is desirable; however, isolated chiral organic molecules usually exhibit relatively small dissymmetry factors of about 10⁻⁴–10⁻², ^[12] but offer several other advantages as discussed above. In addition to a high |g _lum|, for many applications a high photoluminescence (PL) quantum yield and extinction coefficient are necessary. ^[15] Potential applications for organic chromophores capable of circularly polarized emission are in the fields of &bk(bio‐)assay probing, sensing, asymmetric synthesis, and display and optical storage devices.[ ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ ]

One class of planar chiral organic compounds are monosubstituted or appropriately multisubstituted regioisomers of [n.n]paracyclophanes (PCP). Short aliphatic bridges between the phenylene rings hinder free rotation, thus making the compounds conformationally stable. ^[19] Especially the [2.2]PCP with two short ethylene bridges offers not only a planar chiral scaffold, but also a heavily strained structure with cofacial phenylene rings in close vicinity. ^[20] Their distance of around 3 Å ^[21] is substantially shorter than the van der Waals distance found in arene crystals, making them prone to transannular interactions. ^[19] By extension of the π‐system of the [2.2]PCP and introduction of chromophore substituents their absorption and emission properties should be significantly altered and potentially improved for (chir‐)optical applications. This approach has been used by Morisaki and Chujo et al., who have been very active in the field of optically active chiral [2.2]paracyclophanes in recent years, successfully designing conjugated microporous polymers, dendrimers and 3D propeller‐like structures with exceptionally high |g _lum|=1.1×10⁻².[ ²² , ²³ , ²⁴ , ²⁵ , ²⁶ ] Others have developed PCP‐based compounds capable of thermally activated delayed fluorescence or solvent‐induced switching of the CPL sign.[ ²⁷ , ²⁸ ]

Formal substitution of polycyclic aromatic hydrocarbons (PAHs) with boron–nitrogen (BN) units that are isoelectronic to a CC pair is a common way in organic materials science to modify the electronic properties of a compound without altering its structure.[ ²⁹ , ³⁰ , ³¹ ] This technique is used for the design of compounds for applications as semiconducting and optoelectronic materials.[ ³² , ³³ , ³⁴ , ³⁵ , ³⁶ , ³⁷ ] However, there are very few examples of the investigation of BN‐doped chiral PAHs towards their CPL activity. One of the exceptions are several NBN‐heterohelicenes featuring NBN‐heteroacene subunits with high fluorescence quantum yields up to Φ _PL=0.83 associated to CPL signals with |g _lum|=7.5×10⁻⁴ reported by Sun et al., certifying that such structures can have desirable chiroptical properties. ^[38] To our knowledge, BN‐doped PAHs have not been attached as substituents to [2.2]PCP scaffolds, such as the chiral 4,7,12,15‐tetrasubstituted [2.2]PCP, yet. Close proximity of the BN‐PAH pendants and bonding to the [2.2]PCP core aromatic system through ethynyl linkers potentially allows for electronic communication of the π‐systems through‐space and through‐bond. Paired with the induced chirality by the conformationally stable [2.2]PCP building block this could prove to be a successful approach towards new chiroptically active materials.

Here we have combined the [2.2]PCP core with four photoluminescent NBN‐benzo[f,g]tetracene (1) subunits (Φ _PL=0.24; ^[39] Scheme 1) and report racemic rac‐6, as well as enantiopure forms (R)‐6, (S)‐6, and the characterization of (chir‐)optical and electrochemical properties.

Scheme 1.

Synthesis sequences toward 6, 7  m and 7  p . a) 1 (1.0 equiv), NBS (0.8 equiv), MeCN/CH₂Cl₂/CHCl₃ 1 : 4 : 4 v/v, 0 °C to RT, 12 h, 52 %; b) 2 (1.0 equiv), hydroxyphenylboronic acid pinacol ester (1.4 equiv), Pd(PPh₃)₄ (10 mol %), 2 M K₂CO₃ (4.0 equiv), THF, reflux, 40 h, 86–99 %; c) 3 (1.0 equiv), Tf₂O (2.4 equiv), pyridine (10.3 equiv), CH₂Cl₂, 0 °C to RT, 2 h, 89 %; d) 5 (1.0 equiv), 2 (4.4 equiv), CuI (22 mol %), Pd₂(dba)₃ (11 mol %), (t‐Bu)₃PH ⋅ BF₄ (44 mol %), THF/Et₃N (1 : 1 v/v), 50 °C, 18 h, 79–82 %. e) 5 (1.0 equiv), 4 (4.4 equiv), CuI (20 mol %), PdCl₂(dppf) (20 mol %), THF/Et₃N (1 : 1 v/v), 50 °C, 18 h, 61–64 %.

Results and Discussion

Synthesis

We started the synthesis of the target molecules with the bromination of commercially available [2.2]paracyclophane to 4,7,12,15‐tetrabromo[2.2]PCP, ^[40] followed by a modification of the procedure of Hopf et al. ^[41] to obtain 4,7,12,15‐tetra(trimethylsilylethynyl)[2.2]PCP by Sonogashira coupling with trimethylsilylacetylene. Deviating from the literature procedure of Hopf et al., ^[41] we used CuI/Pd₂(dba)₃ as catalysts with (tBu)₃PH ⋅ BF₄ as co‐ligand instead of CuI/Pd(PPh₃)₄, resulting in higher yield (86 % compared to 45 %) and the formation of fewer side‐products. In the next synthesis step, the TMS groups are quantitatively cleaved off with K₂CO₃ to give rac‐5. For enantiopure (R)‐5 and (S)‐5, we followed Morisaki et al. who developed a six‐step synthesis starting from 4,7,12,15‐tetrabromo[2.2]PCP to obtain the enantiomers in 14 % yield with ee>99.5 %. ^[42] We obtained (R)‐5 and (S)‐5 with yields of 17 and 20 %, respectively, and an ee≥99.9 % as estimated through HPLC‐MS experiments of the diastereomeric camphanic ester intermediates. For the final step, the terminal ethynyl groups of rac‐5, (R)‐5, or (S)‐5 are coupled with 1‐bromo‐NBN‐benzo[f,g]tetracene 2 reported recently by our group ^[43] in a fourfold palladium‐catalyzed cross‐coupling reaction, again using CuI/Pd₂(dba)₃/(tBu)₃PH ⋅ BF₄, to afford the desired products rac‐6 (82 %), (R)‐6 (79 %), and (S)‐6 (80 %).

For comparison, the structure of compound 6 was extended by meta‐ and para‐phenylene linkers between the PCP core and NBN pendants to give new materials m‐Ph‐NBN‐PCP 7  m and p‐Ph‐NBN‐PCP 7  p (Scheme 1). Synthesis attempts of the ortho‐phenylene linked derivative were unsuccessful, presumably due to steric constraints. For the synthesis of phenylene‐linked derivatives 7  m and 7  p , compound 2 was treated with commercially available 2‐ or 3‐hydroxyphenylboronic acid pinacol ester in a Suzuki coupling reaction to obtain 3  m in 99 % and 3  p in 86 % yield. Triflation of 3  m and 3  p yielded the desired precursors 4  m and 4  p (89 % each). The final steps were performed in a fashion similar to compound 6 by Sonogashira coupling with tetraethynyl[2.2]PCPs rac‐5, (R)‐5, and (S)‐5, to afford the desired products rac‐7  m (63 %), (R)‐7  m (64 %), (S)‐7  m (61 %), rac‐7  p (61 %), (R)‐7  p (62 %), and (S)‐7  p (61 %).

The synthesis routes presented herein provide access to 6 from 2 and 4,7,12,15‐tetrabromo[2.2]PCP with overall yields of 70 % over three steps for the racemic compound rac‐6 and 14 and 16 % over seven steps for (R)‐6 and (S)‐6, respectively. Phenylene‐linked derivatives 7  m and 7  p can be obtained from 2 and 4,7,12,15‐tetrabromo[2.2]PCP in six steps for rac‐7  m (46 % overall yield) and rac‐7  p (40 %) and in nine steps for (R)‐7  m (9 %), (S)‐7  m (11 %), (R)‐7  m (8 %), and (S)‐7  p (9 %), respectively. The novel compounds 6, 7  m , and 7  p were fully characterized by multinuclear (¹H, ¹³C, ¹¹B) and correlated NMR spectroscopy (H,H COSY, HSQC, HMBC), as well as by high‐resolution mass spectrometry.

Optical properties

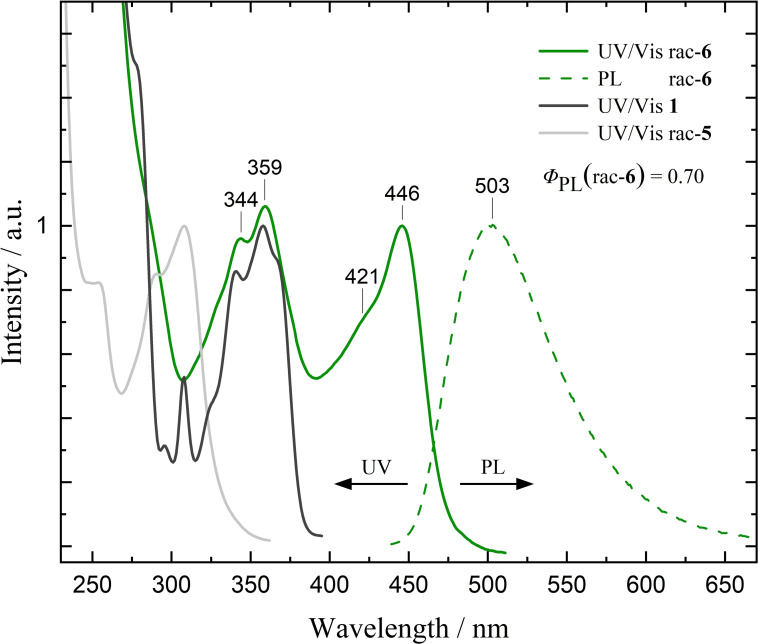
The UV/Vis spectrum of 6 in CH₂Cl₂ shows three main absorption features in the regions of 230–290, 310–380, and 400–475 nm (Figure 1). Comparison with absorption spectra of the subunits 1 and rac‐5 indicates considerable changes due to coupling of the building blocks, most notably the rise of the most longwave absorption bands around 400–475 nm with maximum at 446 nm. Note that the related molar extinction coefficients of 6 are particularly large with ϵ _251 nm=204 000 M⁻¹ cm⁻¹, ϵ _359 nm=86 300 M⁻¹ cm⁻¹, and ϵ _446 nm=81 700 M⁻¹ cm⁻¹. For all three samples of 6 – racemic and enantiopure – identical spectra were recorded, thus hinting towards no significant aggregation in solution. This is in agreement with additional aggregation experiments of solutions of rac‐6 ranging from c=2.0×10⁻⁶ M up to c=1.0×10⁻³ M, which show that the UV/Vis spectra are unchanged in the concentration range investigated (Figure S50 in the Supporting Information).

Figure 1.

Normalized UV/Vis absorption spectra of rac‐6, rac‐5 and 1 (2×10⁻⁶ M in CH₂Cl₂, 293 K) and emission spectrum of rac‐6 (λ _ex=345 nm, 2×10⁻⁶ M in CH₂Cl₂, 293 K) with PL quantum yield Φ _PL of 6. All spectra are normalized to the respective lowest energy transition.

The emission spectrum of compound 6 (Figure 1) in CH₂Cl₂, recorded with an excitation wavelength of 345 nm, consists of one broad emission band with maximum at 503 nm without any resolved vibrational fine structure. The unstructured PL spectrum is indicative of an excited state with strong intramolecular charge transfer character. A rather large Stokes shift of 2460 cm⁻¹ in CH₂Cl₂ was observed. Emission spectra recorded in THF show an identical emission band with λ _max=498 nm, but for a sample in toluene a far narrower and more hypsochromically shifted band with λ _max=474 nm is observed with a Stokes shift of 1530 cm⁻¹ (Figure S49). As charge‐separated excited states are less stabilized in nonpolar solvents, the higher energy of the emission band observed in toluene compared to more polar solvents indicates that the emitting electronic state of compound 6 is (at least partially) charge separated. Following Kasha's rule, the position of the observed structureless emission band in either CH₂Cl₂, THF, or toluene is independent of excitation wavelength. The PL quantum yield of 6 was measured to be Φ _PL=0.70 for both racemic and enantiopure samples, greatly outperforming pristine NBN‐benzo[f,g]tetracene (Φ _PL=0.24). ^[39] Combined with the high extinction coefficients, this certifies excellent optical properties of the compound, considering possible applications in optoelectronics. A commonly employed metric to assess the performance of fluorophores is the PL brightness B, ^[44] defined as the product of the molar extinction coefficient at the excitation wavelength and the PL quantum yield. ^[15] Applied to rac‐6, a brightness of 5.5×10⁴ M⁻¹ cm⁻¹ (λ _ex=345 nm) is determined (Table 1), placing it close to very bright fluorophores such as fluorescein (6.3×10⁴ M⁻¹ cm⁻¹ in 0.1 M NaOH, λ _ex=491 nm). ^[44]

Table 1.

Optical properties of rac‐6, rac‐7  m and rac‐7  p .

	UV/Vis[a]	PL[b]
	λ max [nm] (ϵ [105 M−1 cm−1])	λ max [nm]	τ[c] [ns] (rel. ampl. [%])	χ2[d]	Φ PL [e]	B [f] [103 M−1 cm−1]
rac‐6	251 (2.04), 359 (0.86), 446 (0.82)	503	3.34 (24), 5.01 (76)	1.07	0.70	55
rac‐7  m	252 (2.91), 360 (1.24), 375 (1.21)	515	3.03 (36), 11.3 (64)	1.11	0.014	1.4
rac‐7  p	252 (2.67), 360 (1.23), 379 (1.23)	499	2.94 (29), 6.32 (71)	1.10	0.45	48

[a] In CH₂Cl₂ (2×10⁻⁶ M, 293 K). [b] In CH₂Cl₂ (2×10⁻⁶ M, 293 K), excited at λ _ex=345 nm. [c] Luminescence lifetimes. [d] PL decay curves were best fitted to bi‐exponential equations. [e] PL quantum yield. [f] Brightness ^[44] B=ϵ _λ ×Φ _PL at the excitation wavelength λ _ex=345 nm.

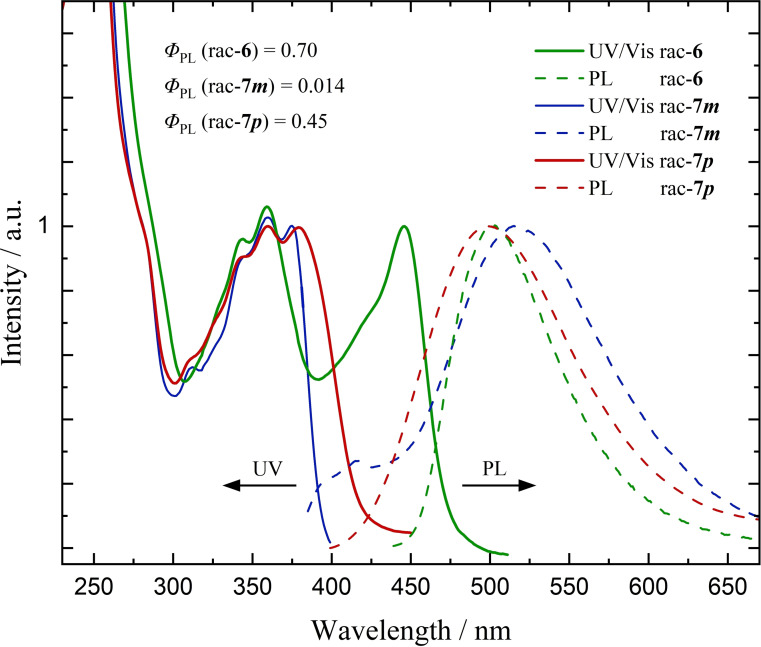
Compounds rac‐7  m and rac‐7  p were investigated in a similar fashion (Figure 2). Most noticeably, both phenylene linked derivatives are lacking the most longwave absorption features around 400–475 nm observed in rac‐6. This suggests a lack of conjugation between the PCP and the NBN aromatic system in the ground state. However, the detected emission bands in CH₂Cl₂ are very much comparable within all three derivatives with λ _max (rac‐6)=503 nm, λ _max (rac‐7  m )=515 nm, and λ _max (rac‐7  p )=499 nm, although the quantum yields are considerably lower at Φ _PL=0.014 and 0.45 for rac‐7  m and rac‐7  p , respectively. One reason for the differing quantum yields might be the higher structural flexibility of the phenylene linked compounds as compared to the acetylene linked compound, thereby opening up nonradiative relaxation pathways of the excited states. The ability for large amplitude motions can facilitate access to a conical intersection, ^[45] effectively lowering the PL quantum yields. ^[46] Especially the meta phenylene linker leads to rather effective quenching of the emission. The observed Stokes shifts for the compounds with phenylene linkers are considerably higher (rac‐7  m 7250 cm⁻¹, rac‐7  p 6350 cm⁻¹) than the Stokes shift of 2460 cm⁻¹ determined for rac‐6.

Figure 2.

Normalized UV/Vis absorption and emission spectra (λ _ex=345 nm) of freshly prepared solutions of rac‐6, rac‐ 7   m, rac‐7  p (2×10⁻⁶ M in CH₂Cl₂, 293 K) with PL quantum yields Φ _PL. All spectra are normalized to the respective lowest energy transition.

Much to our regret, both rac‐7  m and rac‐7  p undergo rapid photoinduced decomposition in oxygen‐free solutions, hampering not only easy handling but also accurate optical measurements of the pure compounds. Within the timespan of recording photoluminescence spectra, rac‐7  m forms unstable luminescent photoproducts (λ _max,em=417 nm), whereas rac‐7  p quickly loses emission intensity without the rise of new bands. Neither of these findings were observed for compound 6. Further investigations by irradiation of deoxygenated samples with a laboratory grade UV lamp (λ=366 nm, 2×6 W) confirmed a much higher stability of rac‐6 (4 % loss of integrated intensity after 45 min) compared to rac‐7  m (loss of 54 %) and rac‐7  p (complete vanishing of initial emission band) (Figure S53). Considering photolability, further chiroptical and computational studies were pursued only for the most promising compound 6.

Computation

To further investigate the optical properties, computational studies were performed for 6′ (R isomer, replacing the n‐butyl groups by hydrogen atoms for simplicity) at the TPSS‐D3(BJ)/def2‐QZVP level of theory (see the Supporting Information for details). Rotation about the C−C single bonds that link the NBN units to the PCP core provides in principle access to a number of conformers of 6′. We found that the rotamer of D ₂ point group symmetry is lowest in energy. Within this isomer the π–π overlap between the pairs of NBN building blocks, and consequently London dispersion interaction, is maximized. The distance between the boron atoms is 3.228 Å in this isomer (Figure 3b). The importance of the latter attraction is vividly seen in the relative energies of the rotamers: while all are within 1 kcal mol⁻¹ in energy without the dispersion correction (D3(BJ)), the D ₂ isomer turns more stable in energy by 18, 13, and 7 kcal mol⁻¹ than C ₁ and C ₂ symmetry isomers with a reduced degree of π–π overlap (see Figure S62 for structures of the higher lying rotamers). As the energy differences are so large, the energetically higher lying isomers will not be populated significantly at room temperature. This is confirmed by variable temperature NMR experiments of rac‐6 (Figure S33) that present only one set of resonances in the temperature range monitored (218–318 K). Although the chemical shifts of some signals change greatly with temperature, no splitting of signals could be observed that would hint towards a dynamic equilibrium of multiple conformers. Hence, only the D ₂ rotamer was investigated further.

Figure 3.

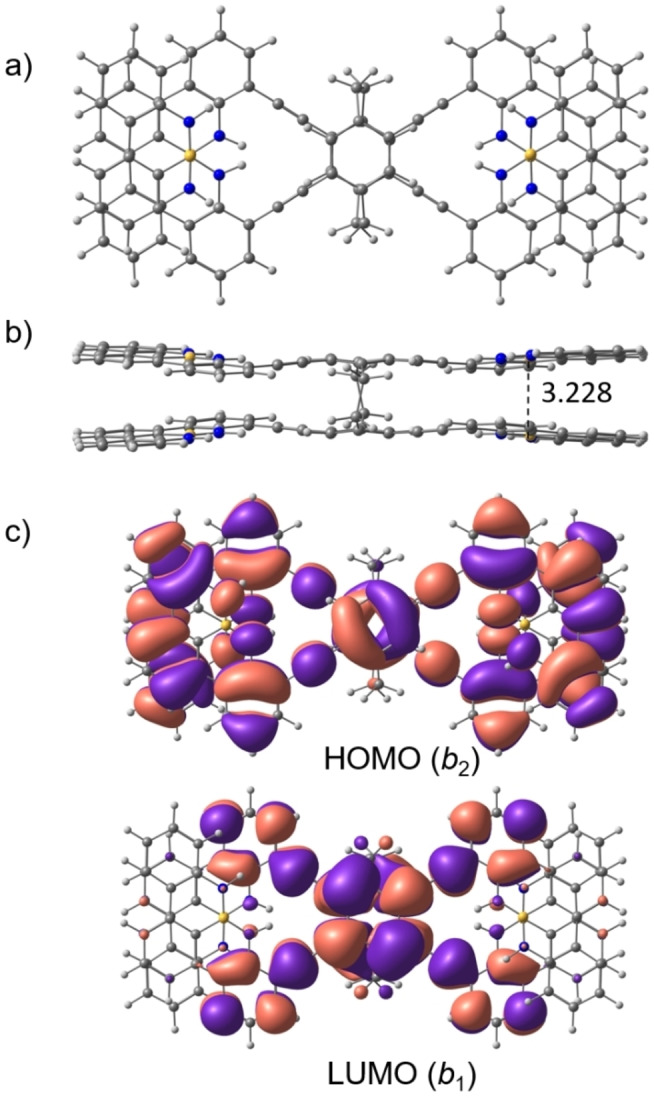
a) Top and b) side views of the structure of the D ₂ isomer of 6′ (n‐butyl groups replaced by H) computed at the TPSS‐D3(BJ)/def2‐QZVP level of theory. The boron–boron distance is given in Å. c) HOMO and LUMO (contour value 0.01) computed at the RHF/def2‐TZVP//TPSS‐D3(BJ)/def2‐QZVP level of theory. The irreducible representations of the orbitals in the D ₂ point group are given in parentheses.

The energy of excited states was computed using the wavefunction based ADC(2) level of theory with the def2‐TZVP basis set for four states each of B₁, B₂, and B₃ symmetry. We chose this computationally demanding method as it was found to perform very well for π→π* excitations and charge‐transfer states.[ ⁴⁷ , ⁴⁸ ] The lowest energy transition (1¹A→1¹B₃) to S₁ is computed to be at 426 nm with a very large oscillator strength (f=1.373). The 1¹B₂ (415 nm) and 1¹B₁ (393 nm) states correspond to S₂ and S₃, respectively, and transitions to these states have very small oscillator strengths (f=0.026 and 0.002, respectively). Hence, the absorption band observed at λ _max=446 nm is assigned to arise from the S₀→S₁ transition that is dominated (80 %) by an electronic excitation of one electron from HOMO to LUMO (Figure 3c). The HOMO is distributed over the entire molecule with large coefficients on the NBN subunits, while the LUMO is primarily located on the central [2.2]PCP core. This suggests that the electronic transition has some charge transfer character and shows that the electronic interaction of NBN and PCP subunits results in a strong broad band observed in the absorption spectrum that is absent for either building block.

As an alternative to the ADC(2) method, we employed time‐dependent density functional theory (TD‐DFT) for analysis of the optical spectrum using the def2‐TZVP basis set. In view of the charge transfer character, the long‐range corrected functionals CAM‐B3LYP‐D3(BJ) ^[49] and ωB97XD ^[50] as well as the multi‐parameter hybrid meta‐GGA functional M06‐2X ^[51] were chosen. While the latter considers dispersion interactions to some degree by construction, the other two functionals use Grimme's[ ⁵² , ⁵³ , ⁵⁴ ] dispersion corrections. Note that the description of dispersion interaction between the NBN subunits of 6′ in the excited states is problematic for TD‐DFT as the dispersion corrections were derived for electronic ground states. ^[55] All functionals place the 1¹B₂ state slightly below (0.01–0.05 eV) the 1¹B₃ state. As the oscillator strength of the 1¹B₂ transition is very small, the computed absorption spectrum is unaffected by this change of the order of excited states. Indeed, the spectrum obtained at the M06‐2X level is in good agreement with experiment (Figure S64).

Chiroptical properties

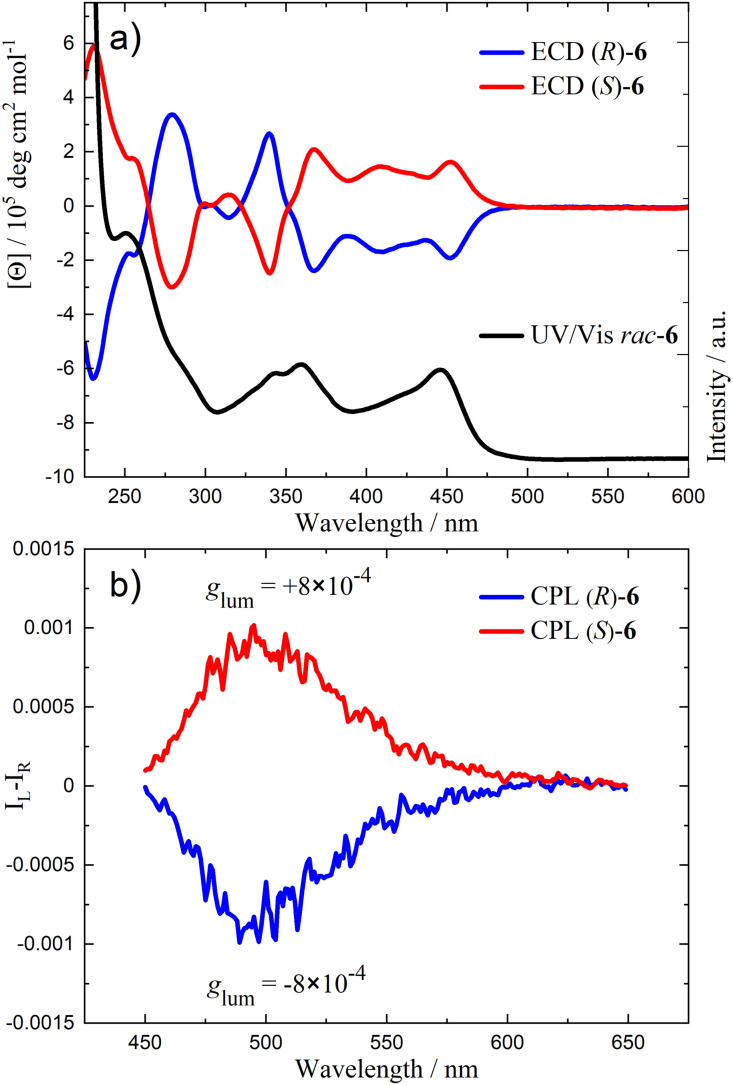
To gain an insight into the chiroptical properties in the ground and excited states of 6, enantiopure samples were investigated by ECD and CPL spectroscopy. Intense and mirror image Cotton effects were observed in the ECD spectra of (R)‐6 and (S)‐6 (Figure 4a). The computed spectrum (M06‐2X/def2‐TZVP, Figure S65) is in good agreement with the experimental one in terms of sign, sequence, and magnitude of bands, which is in support of considering only the D ₂ conformer of 6′. A value of [θ]=±6.1×10⁵ deg cm² dmol⁻¹ was obtained for the molar ellipticity at λ=232 nm. The absorption dissymmetry factors (g _abs) calculated for the most red‐shifted Cotton effect in the ECD spectrum at 451 nm are +8×10⁻⁴ and −8×10⁻⁴ for (S)‐6 and (R)‐6, respectively. The specific rotation ${\left[\alpha \right]}_{589}^{20}$ (c=0.50, CHCl₃) was determined to be +1192° for (R)‐6 and −1189° for (S)‐6.

Figure 4.

Chiroptical data of (R)‐6 and (S)‐6: a) ECD spectra (6.5×10⁻⁵ M, CH₂Cl₂, 293 K) with UV/Vis absorption spectrum. b) CPL spectra (λ _ex=365 nm, 2.0×10⁻⁴ M, CH₂Cl₂, 293 K).

The samples display clear mirror image CPL bands (Figure 4b) centered around 500 nm (positive for (S)‐6 and negative for (R)‐6), closely retracing the luminescence spectrum. The g _lum values calculated for (S)‐6 and (R)‐6 are +8×10⁻⁴ and −8×10⁻⁴, respectively (Table 2). With the molar extinction coefficient at excitation wavelength ϵ _λ , the PL quantum yield Φ _PL, and the dissymmetry factor g _lum, a circular polarized brightness B _CPL of 21.9 M⁻¹ cm⁻¹ can be determined for compound 6 via B _CPL=ϵ _λ ×Φ _PL×|g_lum|/2. ^[56] Typical B _CPL obtained for CPL‐active [2.2]PCPs are in the range of 5.2–333 M⁻¹ cm⁻¹ with a median of 31.9 M⁻¹ cm⁻¹. ^[15] The g _lum versus wavelength plot (Figure S54) shows that the dissymmetry factor g _lum is constant throughout the emission band, which is compatible with a single transition responsible for the emission spectrum. It is worth noting that these values agree in sign and magnitude with the absorption dissymmetry factors (g _abs) calculated for the most red‐shifted Cotton effect in the ECD spectrum (451 nm). This usually indicates that the geometries of the ground and the emitting excited states are relatively similar. The nearby NBN‐benzo[f,g]tetracene units seen in Figure 3 may suggest that emission originates from a diffuse state adjoining two closely stacked chromophores, that is, a sort of intramolecular excimer. This event can be ruled out by the constant g _lum observed above and by the similarity of g _abs and g _lum.

Table 2.

Chiroptical properties of (R)‐6 and (S)‐6

	g abs [a]	g lum [b]	B CPL [c] [M−1 cm−1]	${\left[\alpha \right]}_{589}^{20}$ [d] [°]
(R)‐6	−8×10−4	−8×10−4	21.9	+1192
(S)‐6	+8×10−4	+8×10−4	21.9	−1189

[a] g _abs=Δϵ/ϵ, in CH₂Cl₂ (2×10⁻⁴ M, 293 K) calculated at 451 nm. [b] g _lum=2(I _L−I _R)/(I _L+I _R), in CH₂Cl₂ (4.5×10⁻⁵ M, 293 K), excited at λ _ex=365 nm. [c] Brightness for CPL ^[15] B _CPL=ϵ _λ ×Φ _PL×|g _lum|/2 at λ _ex=365 nm. [d] ${\left[\alpha \right]}_{589}^{20}$ =α _obs/(cl), in CHCl₃ (0.500 g mL⁻¹, 293 K).

Although rare, TD‐DFT computations of CPL dissymmetry factors have been reported several times, most recently by Kubo et al.[ ⁵⁷ , ⁵⁸ , ⁵⁹ , ⁶⁰ , ⁶¹ , ⁶² ] Using the values for the transition electronic dipole moment (TEDM) μ, the transition magnetic dipole moment (TMDM) m, and the angle θ _μ,m between TEDM and TMDM computed at the optimized structure of the emitting S₁ state, a theoretical value of g _lum,calcd. can be obtained with Equation (1), where R is the rotatory strength of the emitting transition. ^[57]

$${\displaystyle g_{\mathrm{l}\mathrm{u}\mathrm{m},\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{c}\mathrm{d}.}=\frac{I_{\mathrm{L}}-I_{\mathrm{R}}}{\frac{1}{2}\left(I_{\mathrm{L}}+I_{\mathrm{R}}\right)}=\frac{4\left|\mu \right|\left|m\right|\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_{\mu ,m}}{|\mu {|}^2+\left|m\right|{}^2}=\frac{4R}{|\mu {|}^2+\left|m\right|{}^2}}$$ (1)

We applied this approach to compute g _lum,calcd. of (R)‐6′ using a number of functionals (Table 3). As stated above, the description of London dispersion interactions in the excited state is problematic for these functionals. However, the good agreement between experiment and theory for the absorption spectrum obtained with M06‐2X encouraged us to also compute g _lum,calcd. using this and other functionals. Note that during geometry optimization the order of the energy of electronic states 1¹B₃ and 1¹B₂ switches. Hence, the geometry optimized S₁ state corresponds for all functionals to 1¹B₃ with large oscillator strength, in agreement with the observation of bright luminescence. We used CAM‐B3LYP to take advantage of the improved charge transfer excitation representation of the Coulomb‐attenuating method. ^[49] A very low g _lum,calcd. of +2.48×10⁻⁵ was obtained, mainly because the angle θ _μ,m between TEDM and TMDM is close to 90°. With D3(BJ) correction, θ _μ,m is increased to 93.73° and consequently the absolute value of g _lum,calcd. becomes larger. Also, the sign switches from positive to negative (−4.16×10⁻⁴), agreeing with the experimental value of (R)‐6. The ωB97XD functional arrives at a similar value (−3.50×10⁻⁴). The result that is closest to the experimentally measured g _lum=−8×10⁻⁴ was obtained with M06‐2X (−7.13×10⁻⁴).

Table 3.

TD‐DFT computations of g _lum,calcd. for compound (R)‐6′, compared with the experimental value. All computations utilize the def2‐SV(P) basis set.

Method	|μ| [10−20 esu cm]	|m| [10−20 erg G−1]	θ μ,m	g lum,calcd [10−4]
CAM‐B3LYP	1125	1.697	89.76	+0.248
CAM‐B3LYP‐D3(BJ)	1109	1.773	93.73	−4.16
ωB97XD	1096	1.862	92.95	−3.50
M06‐2X	1106	1.771	96.39	−7.13
experimental for (R)‐6				−8

To test the performance of M06‐2X for the g _lum computation of similar systems, the R isomers of the known compounds (R)‐tetra(phenylethynyl)[2.2]PCP ((R)‐Ph‐PCP), (R)‐tetra(naphthylethynyl)[2.2]PCP ((R)‐Naph‐PCP), and (R)‐tetra(anthracenylethynyl)[2.2]PCP ((R)‐Anth‐PCP) were computed and the theoretical values were compared with the reported ^[63] experimental ones (Table 4).

Table 4.

Comparison of experimental and computed (M06‐2X/def2‐SV(P)) g _lum values.

Compound	g lum,calcd. [10−4]	g lum [10−4]
(R)‐6	−7.13[a]	−8
(R)‐Ph‐PCP	−20.1	−12 [63]
(R)‐Naph‐PCP	−17.7	−17 [63]
(R)‐Anth‐PCP	−13.6[a]	−4 [63]

[a] The values computed for (R)‐6 and (R)‐Anth‐PCP were obtained with the respective model compounds (R)‐6′ and (R)‐Anth‐PCP′ that had the n‐butyl groups replaced by hydrogen atoms.

Given that these computations are performed for isolated molecules without consideration of solvation effects and that a correct representation of the dispersion interactions in the excited state is not guaranteed in M06‐2X (in fact in none of the currently available functionals), the calculated g _lum,calcd. are surprisingly close to the experimental values, most certainly in the right magnitude. These results demonstrate the potential of g _lum calculations for material design of CPL emitters, and we encourage further research.

Electrochemical studies

In contrast to optical methods, which deal with ground and excited states of the molecules, electrochemical techniques probe the electron transfer properties, that is, processes that involve different redox states remaining in the electronic ground state. Thus, rac‐6 and its subunits 1 and rac‐5 were investigated by cyclic voltammetry (CV) using a Pt or a glassy carbon (GC) working electrode in a CH₂Cl₂/0.1 M NBu₄PF₆ electrolyte at various scan rates (0.02≤v≤10 V s⁻¹) and bulk concentrations c ⁰ in the mM range.

The paracyclophane unit rac‐5 does not show any CV signal in the potential range between +1.093 and −2.607 V (all potentials are reported vs. the ferrocene/ferricinium standard redox couple). ^[64] This covers potentials down to the negative potential limit of the electrochemical window and extends even more positive than the positive potentials used for oxidation of 1 and rac‐6 (see below). The absence of redox processes is in accordance with the relatively high potentials reported for reduction[ ⁶⁵ , ⁶⁶ ] or oxidation ^[67] of cyclophane‐type hydrocarbons without electronically active substituents.

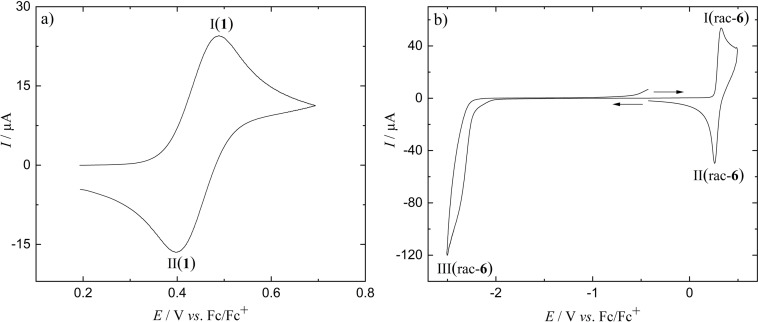
On the other hand, bis‐n‐butyl substituted NBN‐benzo[f,g]tetracene 1 is oxidized in a chemically reversible one‐electron transfer reaction featuring peaks I(1) and II(1) at E ⁰=+0.444±0.002 V with a peak current ratio $I\genfrac{}{}{0pt}{}{\mathrm{red}}{\mathrm{p}}$ /$I\genfrac{}{}{0pt}{}{\mathrm{ox}}{\mathrm{p}}$ =0.98±0.01 (see Figure 5a for the voltammogram at v=0.2 V s⁻¹ and the Supporting Information for current‐potential curves at other scan rates). The process is diffusion controlled and electrochemically reversible (peak current proportional to the square root of the scan rate; ΔE _p=83±8 mV, somewhat increased above the ideal value of 58 mV) up to v=0.5 V s⁻¹ with a transition to quasireversibility (increasing ΔE _p with increasing v) at higher scan rates. A combination of steady‐state microelectrode and chronoamperometric data ^[68] allows the determination of the diffusion coefficient (D=1.38±0.02×10⁻⁵ cm² s⁻¹) and the number of transferred electrons per molecule n=0.89±0.01, consistent with the one‐electron oxidation of 1 to its radical cation. Voltammograms extending to more positive potentials show a second, chemically irreversible oxidation peak, which was, however, not analyzed in detail. No reduction signal of 1 could be observed at potentials extending down to the negative limit of the electrochemical window.

Figure 5.

Cyclic voltammograms in CH₂Cl₂/0.1 M NBu₄PF₆ at v=0.2 V/s of a) 1, Pt electrode, c ⁰=1.2 mM. b) rac‐6, GC electrode, c ⁰=1.12 mM.

The cyclic voltammogram of rac‐6, which combines both subunits, in the positive potential range shows two peaks I(rac‐6) and II(rac‐6) for oxidation and an associated reduction (Figure 5b). The voltammetric signal is slightly distorted by adsorption of the oxidation product, as indicated by the pointed shape of the reduction peak and an increased peak current ratio $I\genfrac{}{}{0pt}{}{\mathrm{red}}{\mathrm{p}}$ /$I\genfrac{}{}{0pt}{}{\mathrm{ox}}{\mathrm{p}}$ >1, in particular at low scan rates, where also ΔE _p decreases significantly below 58 mV. At larger v, the value of ΔE _p increases, again indicating the transition to a quasi‐reversible electron transfer. Scans to more positive potentials reveal two additional oxidation signals. However, under these conditions the adsorption phenomena become prohibitive for further analysis of the voltammograms, and these data are not considered further. The number of electrons transferred in peak I(rac‐6) is determined as n=2.3±0.2 (D=5.8±0.4×10⁻⁶ cm² s⁻¹). The two electron transfer steps are not resolved in the voltammograms, and individual E ⁰ cannot be estimated. The signal is characterized by a midpoint potential Ē=+0.309±0.02 V close to the oxidation formal potential of subunit 1, where Ē is the mean value of E _p(I(rac‐6)) and E _p(II(rac‐6)). The shift to less positive potentials as compared to 1 is explained by the inductive effect of the ethynyl linkers and possibly by the larger extension of the π‐system, stabilizing the product.

The nature of the two‐electron oxidation in peaks I/II of rac‐6 was investigated computationally. Vertical (diabatic) ionization is not sufficient to describe electron transfers between a molecule in solution and an electrode owing to the comparably slow time scale of charge transfer. ^[69] Instead, adiabatic ionization energies have to be determined that are defined as the difference between the zero‐point energy corrected total energies of the two respective redox species. Extended research by Isegawa et al. proved that the hybrid meta‐GGA DFT functional M06‐2X is well suited for calculations of ionization energies with a mean unsigned error of around 0.1 eV. ^[70] We assume that the neutral compound is oxidized first to a radical cation and then to a diradical dication. For the latter, we consider the triplet state for computational simplicity. The geometries of neutral 6′, radical cation 6′⁺ , and diradical dication 6′²⁺ were optimized at the TPSS‐D3(BJ)/def2‐TZVP level followed by single‐point energy computation at the M06‐2X/def2‐TZVP level of theory. The solvation model based on density (SMD) ^[71] was used to simulate the solvation energies in CH₂Cl₂. From the computed harmonic vibrational frequencies, the zero‐point energy corrected energy difference ΔE _ZPE, the enthalpy ΔH ⁰ (at 298 K) and the Gibbs free energy ΔG ⁰ (at 298 K) can be calculated (TPSS‐D3(BJ)/def2‐TZVP) for each ionization state (Table 5). As a result, a small energy difference ΔΔG ⁰ of +0.12 eV between the first and second oxidation step of 6′ is obtained. The spin density distribution (Figure S66) strongly differs between the redox states: while it is mainly located on the central cyclophane unit and the directly surrounding atoms in the radical cation, it is mostly shifted to the NBN substituents in the diradical dication.

Table 5.

Zero‐point energy corrected electronic energy ΔE _ZPE, enthalpy ΔH ⁰ (at 298 K) and Gibbs free energy ΔG ⁰ (at 298 K) in solution (SMD method in CH₂Cl₂, M06‐2X/def2‐TZVP//TPSS‐D3(BJ)/def2‐TZVP) for the adiabatic oxidation steps of 6′ to the radical cation 6′⁺ and the diradical dication 6′²⁺ .

Oxidation step	ΔE ZPE [eV]	ΔH 0 [eV]	ΔG 0 [eV]
6′→6′+	5.76	5.74	5.75
6′+→6′2+	5.89	5.89	5.87

Some necessary simplifications have to be considered when attempting to relate the calculated energy difference to the corresponding difference between two redox potentials associated with the oxidation steps of rac‐6: the replacement of butyl groups with hydrogen atoms to reduce convergence and conformational issues and the neglect of supporting electrolyte in the solvation model. The electrolyte is expected to increase the polarity, which in turn should preferentially stabilize the dication and result in a decreased ionization potential associated with its formation. Still the computed small value of ΔΔG ⁰ is in agreement with the absence of a noticeable peak splitting in the voltammograms. For paracyclophanes with multiple redox centers attached by both ethynyl and vinyl linkers only small effects of interaction between the redox active groups have been reported,[ ⁷² , ⁷³ , ⁷⁴ ] resulting in overlapping peaks for the two subsequent electron transfers. An analogous situation must apply here.

The reduction of rac‐6 is chemically irreversible (III(rac‐6), Figure 5b) without a reverse peak and superimposed on the current resulting from decomposition of the supporting electrolyte at the negative limit of the electrochemical window.

A HOMO‐LUMO gap of ≈2.3 eV for rac‐6 is estimated as the difference between the onset potentials for the reduction in wave III(rac‐6) and oxidation in peak I(rac‐6). ^[75] This is lower than the optical and computational HOMO–LUMO gap of ΔE≈2.8 eV. It should be noted, however, that although such estimations from CV data are common in the literature, the onset potential is only loosely defined as compared to, for example, a formal potential. There are also fundamental and practical differences between electrochemical potentials and orbital energies, which inevitably limits the reliability of such values.[ ⁶⁹ , ⁷⁶ , ⁷⁷ ]

Conclusion

We have extended the class of multisubstituted [2.2]paracyclophanes for the first time by a BN‐doped polycyclic aromatic hydrocarbon. Within the novel structures, four NBN‐benzo[f,g]tetracenes are either directly coupled to the chiral PCP core via ethynyl linkers (compound 6) or have an additional m‐ or p‐phenylene spacer in between the PCP and the NBN building blocks (7  m and 7  p ). Density functional computations indicate large London dispersion between the NBN units in a graphite‐like layering with short distances between these moieties. Electrochemical studies of 6 and its subunits indicate a two‐electron process for the first oxidation of 6. Quantum‐mechanical calculations of the first and second adiabatic ionization energies are in accordance with the assumption of two consecutive one‐electron transfers leading to a radical cation and then a diradical dication. The small difference in the ionization energies is consistent with a small difference in formal potentials for the two steps that leads to a single voltammetric peak. While 6 proved to have high chemical stability in the presence of water, oxygen, and light, 7  m and 7  p undergo rapid photodegradation in solution. Formation of these large structures has an exceptional impact on the optical and chiroptical properties compared with either building block, mainly contributed to a significant charge transfer character of the transitions and intense chromophore coupling. ECD and CPL spectroscopy of 6 revealed a strong chiral environment in the ground and excited states with values of g _abs and g _lum of ±8×10⁻⁴. Quantum‐mechanical computations were performed to obtain theoretical values of g _lum,calcd. that match the experimental values. Combined with an excellent PL quantum yield Φ _PL of 0.70 and very high absorption coefficients ϵ of up to 2.04×10⁵ M⁻¹ cm⁻¹, the novel compound 6 is a proficient chiral emitter. ^[15] These results suggest that the 3D arrangement evoked by the PCP scaffold, a combination of strong chromophore coupling through‐space and through‐bond, and a resulting CT character might lead to drastically improved (chir‐)optical characteristics, even with chromophores that are lowly to moderately emissive as monomers. With this work, we could demonstrate that the combination of nonclassical chromophores like BN‐doped polyaromatic hydrocarbons and a [2.2]PCP scaffold can be a promising approach for emergent highly luminescent CPL materials.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

M. R. Rapp, W. Leis, F. Zinna, L. Di Bari, T. Arnold, B. Speiser, M. Seitz, H. F. Bettinger, Chem. Eur. J. 2022, 28, e202104161.

Data Availability Statement

The data that support the findings of this study are available in the supplementary material of this article.