Frequency‐Selective Manipulations of Spins allow Effective and Robust Transfer of Spin Order from Parahydrogen to Heteronuclei in Weakly‐Coupled Spin Systems

Abstract

We present a selectively pulsed (SP) generation of sequences to transfer the spin order of parahydrogen (pH₂) to heteronuclei in weakly coupled spin systems. We analyze and discuss the mechanism and efficiency of SP spin order transfer (SOT) and derive sequence parameters. These new sequences are most promising for the hyperpolarization of molecules at high magnetic fields. SP‐SOT is effective and robust despite the symmetry of the ¹H‐¹³C J‐couplings even when precursor molecules are not completely labeled with deuterium. As only one broadband ¹H pulse is needed per sequence, which can be replaced for instance by a frequency‐modulated pulse, lower radiofrequency (RF) power is required. This development will be useful to hyperpolarize (new) agents and to perform the hyperpolarization within the bore of an MRI system, where the limited RF power has been a persistent problem.

More spin order: We propose a new generation of frequency‐selective methods for parahydrogen spin order transfer to heteronuclei magnetization. The novel sequences require less RF power and hence are well‐suited for implementations on MRI systems. Moreover, they are most effective and robust as undesired J‐couplings are suppressed during the polarization transfer and the symmetry of the ¹H‐¹³C coupling pattern plays no role anymore.

NMR and MRI exploit the interaction of nuclear spins with magnetic field to analyze chemical structures, reaction kinetics, and biological tissue. Given the rich portfolio of magnetic resonance (MR) methods to interrogate these properties, MR has become indispensable in chemistry,[ ¹ , ² ] medical diagnostics,[ ³ , ⁴ , ⁵ , ⁶ ] and related fields.[ ⁷ , ⁸ ] However, most of these methods effectively use only a small fraction of all available spins: the equilibrium thermal polarization of ¹H is about 3 ppm per Tesla at room temperature. The hyperpolarization (HP) of nuclear spins allows to increase this fraction and to enhance the MR signal by 10⁴–10⁵‐fold.[ ⁹ , ¹⁰ , ¹¹ ] HP techniques have enabled entirely new applications of MR, such as real‐time monitoring of metabolism in vivo, pH mapping, ^[12] or coronary angiography. ^[10] Among current techniques, parahydrogen (pH₂)‐based methods offer a cost‐ and time‐efficient way to hyperpolarize molecules in solution.[ ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ] Thanks to parahydrogen‐induced polarization (PHIP) by sidearm hydrogenation (PHIP‐SAH),[ ¹⁷ , ¹⁸ ] the number of biologically relevant molecules amenable to this technique has been rapidly expanding. pH₂ polarizers operate at zero‐fields,[ ¹⁹ , ²⁰ ] in the millitesla‐,[ ²¹ , ²² ] or tesla‐regime,[ ²³ , ²⁴ ] or integrated to the bore of the MRI system. ^[25] Rapid purification of the polarized solution has brought in vivo applications much closer.[ ²⁶ , ²⁷ , ²⁸ ] With this in mind, PHIP has unambiguously become one of the most flexible and promising polarization methods, despite its lack of clinical application (yet).

As a source of spin order, pH₂ is virtually unlimited for most practical matters. pH₂ is easily produced in large amounts and can be stored for days.[ ²⁹ , ³⁰ , ³¹ ] At the same time, however, it is an MR invisible singlet state, ^[32] which needs to be transformed before it can be used to increase the MR signal.

If pH₂ is added to chemically nonequivalent sites of a molecule at a high magnetic field (by hydrogenation), these protons, referred to as I and S, become weakly coupled (the difference in Larmor frequencies is much larger than their indirect spin‐spin interaction, $\delta \nu \gg J$ ). ^[33] The singlet state of pH₂ is projected on the eigenstates of the newborn system so that $I_{\mathrm{Z}}{S}_{\mathrm{Z}}$ two‐spin order results (Figure 1a). ^[34] This pH₂ effect is also known as parahydrogen and synthesis allow dramatically enhanced nuclear alignment (PASADENA). ^[35]

Figure 1.

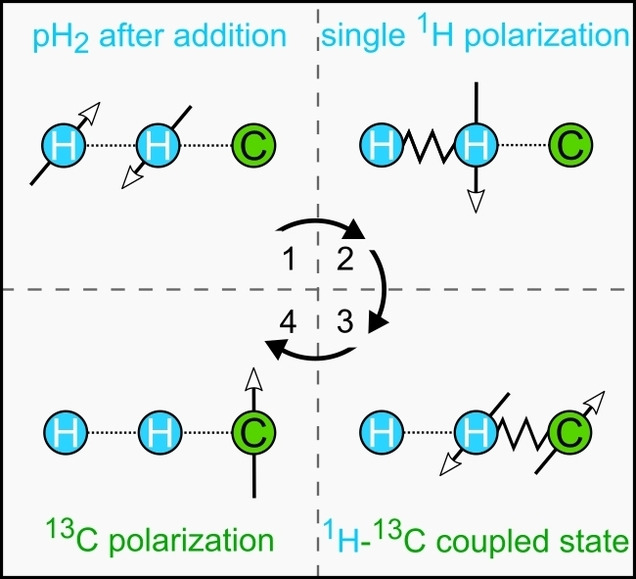
¹H‐PHIP: hydrogenation reaction (a), ¹H‐SOT sequences OPE (b) and SEPP (c). The spin order of pH₂ is added to an unsaturated precursor by catalytic hydrogenation, often in the liquid homogeneous phase (a). Some of the spin order of the nonequivalent protons is preserved and results in an ${\mathbf{I}}_{\mathbf{Z}}{\mathbf{S}}_{\mathbf{Z}}$ state in the newly formed AB‐type system (i. e. weakly‐coupled spin system). OPE or SEPP sequences convert this spin order into net magnetization of two (OPE) or one spin (SEPP), the latter with double intensity.

The PASADENA spin order can be directly observed by ¹H NMR after a 45° broadband excitation[ ³⁵ , ³⁶ ] or after a more complex spin‐order transfer sequence (¹H‐SOT) like out‐of‐phase echo (OPE)[ ³⁷ , ³⁸ ] or selective excitation of polarization using PASADENA (SEPP, Figure 1b, c). ^[39] OPE polarizes both protons (to the same amount), while SEPP provides transversal magnetization of one proton at double intensity; both sequences are also referred to as OPE‐45 and OPE‐s90. ^[40] This observation gave us two first hints, (a) that selective excitation can increase the polarization yield and (b) that both protons have to be excited to exploit the PASADENA spin order arising from both nuclei and to convert it into net magnetization.

For metabolic MR imaging or spectroscopy, usually, X‐nuclear polarization is advantageous, because of longer relaxation times, a wider range of chemical shifts, and no background signal in vivo.[ ¹⁸ , ²⁶ , ⁴¹ ] To transfer the pH₂ order into X‐nuclei polarization, several approaches have been presented.[ ⁴² , ⁴³ , ⁴⁴ , ⁴⁵ , ⁴⁶ , ⁴⁷ , ⁴⁸ ] Pulse sequences are very promising, having demonstrated ¹³C‐polarizations of ≈50 %, ^[23] which is close to their theoretical maximum of 100 % (neglecting relaxation). Two challenges persist for radiofrequency (RF) pulsed polarization transfer at high fields:

1. The polarization maximum of P=1 is theoretically only achievable in molecules that contain only the two pH₂‐nascent protons. This requires typically fully perdeuterated precursors. If additional protons are present, their J‐couplings interfere with the polarization transfer. ^[49]

2. While pulse sequences have enabled the hyperpolarization of molecules inside the MRI system, where they are to be applied as imaging contrast agents, the RF power typically limits the pulse length and frequency bandwidth. ^[50] This effect is already relevant in preclinical systems and likely more important in clinical setups if no dedicated hardware is developed and used.

Therefore, we explored the application of weak, frequency‐selective RF pulses during SOT in molecules with weakly‐coupled pH₂‐nascent protons. These conditions are given e. g. in PHIP‐SAH molecules at fields above 1 T. ^[23]

Selectively‐pulsed (SP) SOT sequences require little RF power. As an important advantage, undesired J‐coupling interactions are suppressed as the states evolve only under couplings between spins which are both refocused during the intervals of free‐evolution (see SI).[ ⁵¹ , ⁵² ]

Here, we extended the concept further and considered SP‐modifications of existing SOT sequences (analyzed sequences include: pH₂ insensitive nuclei enhanced by polarization transfer (phINEPT+), ^[53] the selective‐90‐ (s90‐) phINEPT+, ^[54] the selective excitation of polarization using PASADENA (SEPP)‐INEPT+, ^[55] and the efficient spin order transfer to heteronuclei via relayed INEPT chains (ESOTHERIC)).[ ²³ , ⁵⁶ ] To distinguish the new variants from their non‐selective ancestors, we refer to the versions with selective pulses (SP) as phSPINEPT+, ^[57] SEPP‐SPINEPT+, and SP‐ESOTHERIC throughout this manuscript (Figure 2). Note that phSPINEPT+ was already proposed by us only recently ^[57] and we include it in our more detailed analysis presented here for completeness.

Figure 2.

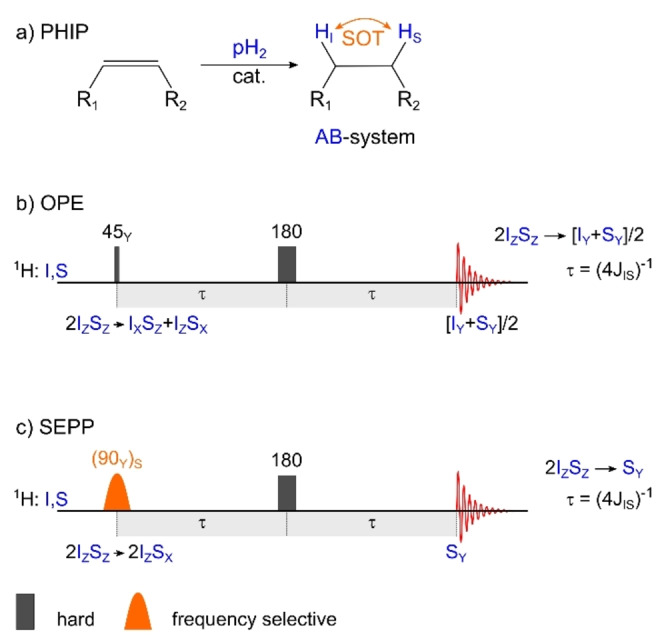
¹³C‐PHIP: hydrogenation reaction with subsequent polarization transfer to ¹³C in an ABX‐system (a) and three variants of SP‐SOT sequences (b, c, d). After hydrogenation with pH₂, the resulting two‐spin order ${\mathbf{I}}_{\mathbf{Z}}{\mathbf{S}}_{\mathbf{Z}}$ is transferred into the net magnetization of ¹³C (here ${\mathbf{F}}_{\mathbf{X}}$ that can be flipped to ${\mathbf{F}}_{\mathbf{Z}}$ at the end of the sequence). SEPP‐INEPT+ and SP‐ESOTHERIC convert ${\mathbf{I}}_{\mathbf{Z}}{\mathbf{S}}_{\mathbf{Z}}$ to ${\mathbf{F}}_{\mathbf{X}}$ in three steps while phSPINEPT+ requires only two steps. When the time interval $\tau =$ (4 J)⁻¹, SEPP‐SPINEPT+ and SP‐ESOTHERIC provide 100 % conversion. However, as phSPINEPT+ squeezes two transformations into the ${\tau }_1$ ‐intervals, the efficiency of polarization transfer is equal to $\mathbf{k}=\mathbf{s}\mathbf{i}\mathbf{n}\left(2\pi {\mathbf{J}}_{\mathbf{I}\mathbf{S}}{\tau }_1\right)\mathbf{s}\mathbf{i}\mathbf{n}\left(2\pi {\mathbf{J}}_{\mathbf{S}\mathbf{F}}{\tau }_1\right)$ , which should be maximized for the given coupling constants. Note that the hollow (90_‐Y)_S pulse from the original ESOTHERIC sequence in (d) is not necessary for SP‐ESOTHERIC. 180° pulses that act on both $\mathbf{I}$ and $\mathbf{S}$ protons are represented by a blue trapezoid with an arrow indicating a chirp pulse, but other excitation schemes are possible (see text).

We found that for all sequences, only one ¹H refocusing pulse has to flip both protons stemming from pH₂ at the same time, which is necessary to convert the two‐spin order of two protons into magnetization of one of them, like in the SEPP sequence ^[39] (Figure 1c). All other ¹H RF pulses can act selectively on one ¹H nucleus, which naturally should be the same one throughout the sequence. For the sake of a short SOT, we suggest to play it out on the ¹H that features a larger J‐coupling to the target ¹³C nucleus.

We did not consider using adiabatic ramp pulses for adiabatic‐passage spin order conversion (APSOC).[ ⁵⁸ , ⁵⁹ , ⁶⁰ ] APSOC can convert PASADENA spin order into magnetization of one spin; the spin state after APSOC can be similar to the one after the SEPP sequence. ^[58] When APSOC was played out, a SPINEPT+ sequence can transfer the obtained ¹H magnetization to ¹³C magnetization (APSOC‐SPINEPT). However, APSOC is more complex in application than SEPP, and to keep it consistent we discuss here only selective or broadband RF excitation.

In some cases, a limited RF bandwidth and power may hinder the on‐resonant and homogeneous excitation of both protons. On such occasions, we suggest using dual resonant pulses, chirp pulses (in the context of MRI sometimes referred to as adiabatic pulses),[ ⁶¹ , ⁶² ] bimodal pulses, or other suitably modulated shaped pulses. ^[63] Naturally, one may apply two selective pulses sequentially, each operating at a different frequency; however, this may lead to losses in polarization transfer. The optimal approach will ultimately be dictated by the hardware capabilities and the spin system of interest.

SEPP‐SPINEPT+, SP‐ESOTHERIC, and phSPINEPT+ have a very similar logic of polarization transfer, based on three different “modules” or functions applied in different orders. We will analyze these transfer schemes in the following, useing $I$ and $S$ spin symbols to refer to ¹H coming from pH₂, and $F$ and $G$ for ¹³C nuclear spins of interest.

SEPP‐SPINEPT+ (Figure 2b) first converts the ¹H‐¹H two spin order $I_Z{S}_Z$ into net magnetization of one of them (e. g., $S_X$ ) using a SEPP block and a period of free evolution of length $2{\tau }_1$ . Then, using SP‐INEPT+, magnetization is transferred to ¹H‐¹³C two‐spin order $S_Y{F}_Z$ via $J_{SF}$ ‐couplings in $2{\tau }_2$ , which then is converted into magnetization of a target ¹³C nucleus $F_X$ in $2{\tau }_3$ (and to longitudinal magnetization $F_Z$ after an additional ¹³C RF‐pulse, if desired). Note that only two spins are refocused per time interval, hence the mutual J‐coupling drives their evolution. The couplings to the other nuclei are “suspended” (SI and Ref. [51, 52]).

This results in straightforward rules to determine the optimal free‐evolution intervals for three‐spin systems: ${\tau }_1={\left(4J_{IS}\right)}^{-1}$ , ${\tau }_2={\tau }_3={\left(4J_{\mathrm{S}\mathrm{F}}\right)}^{-1}$ . Strictly speaking, these rules apply for a molecule consisting of three interacting spins $I$ , $S$ , and $F$ . These conditions are also fulfilled when other ¹H sites are deuterated or when only the $I$ or $S$ proton is excited by SP ¹H RF pulses. The same holds for ¹³C: if more than one ¹³C nucleus is present, the ¹³C RF pulses should excite only the $F$ spin.

SP‐ESOTHERIC (Figure 2c) is relatively similar to SEPP‐SPINEPT+, but the order of the first two conversion steps is reversed. Hence, the spin‐order $I_Z{S}_Z$ is first transformed into three‐spin order $I_Z{S}_Y{F}_Z$ (¹H‐¹H‐¹³C three‐spin order). Next, evolution under the ¹H‐¹H J‐couplings converts $I_Z{S}_Y{F}_Z$ into $S_X{F}_Z$ (¹H‐¹³C two‐spin order). The last step is identical to SEPP‐SPINEPT+ and results in net magnetization $F_X$ of ¹³C. Again, in each $\tau$ ‐period, only two nuclei are refocused and, consequently, interact. Hence, in a three‐spin system, polarization transfer is optimal for ${\tau }_2={\left(4J_{\mathrm{I}\mathrm{S}}\right)}^{-1}$ , ${\tau }_1={\tau }_3={\left(4J_{\mathrm{S}\mathrm{F}}\right)}^{-1}$ .

The relaxation of different multispin states was studied before[ ⁶⁴ , ⁶⁵ , ⁶⁶ , ⁶⁷ ] and is not the subject of this work. However, we think that a detailed experimental analysis could help assess the differences in relaxation of the multispin orders. Ultimately, their effect on SOT efficiency using SP‐ESOTHERIC or SEPP‐SPINEPT+ could be analyzed. Often, the relaxation of three‐spin orders is faster than for one‐ or two‐spin orders. Therefore, SEPP‐SPINEPT+ may be the preferred choice between the SP‐SOTs. Also, note that the second 90° ¹H pulse of ESOTHERIC is not needed for SP‐ESOTHERIC and should not be played out to limit errors from experimental imperfections.

phSPINEPT+ (Figure 2d) is very similar to SEPP‐SPINEPT+. However, following the selective 90° ¹H excitation, a ¹³C excitation is applied in parallel with a non‐selective ¹H refocusing pulse. Hence, instead of transferring polarization sequentially in three steps, the first two steps of the SEPP‐SPINEPT+ take place simultaneously. Hence, the polarization transfer during ${\tau }_1$ is modulated by two J‐couplings, and polarization of the third nucleus scales with $\sin \left(2\pi J_{IS}{\tau }_1\right)\sin \left(2\pi J_{SF}{\tau }_1\right)$ . Consequently, in contrast to the other SP‐SOTs considered above, for phSPINEPT+ there are combinations of J _IS and J _SF where the sequence does not provide a maximum theoretical polarization of 100 % within a reasonable time (SI, Figures S1–2). In these cases, SEPP‐SPINEPT+ seems to be the most robust and versatile sequence of choice.

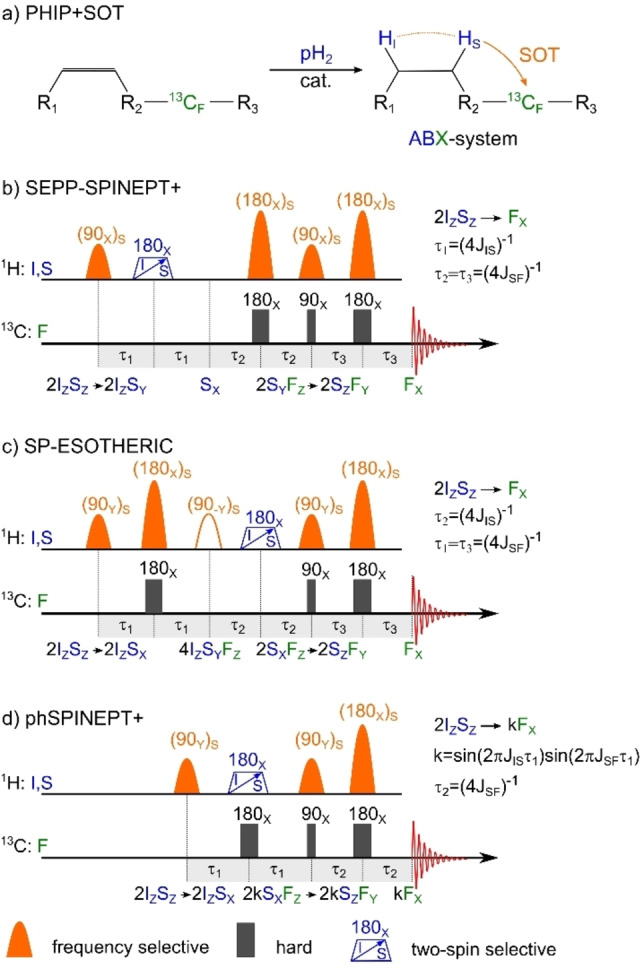
Korchak, Glöggler, and coworkers recently reported impressively high ¹³C‐polarizations of pyruvate and acetate esters using a relayed ¹³C‐¹³C polarization transfer. ^[56] Here, polarization was transferred from the pH₂ protons to the target ¹³C (G‐spin) via an intermediate ¹³C nucleus (F‐spin; Figure 3a). The same concept can be applied to perdeuterated 1‐¹³C‐allyl‐1‐¹³C‐pyruvate or any other double‐¹³C‐labeled compound. Allyl pyruvate is a popular PHIP‐SAH precursor of pyruvate with demonstrated imaging applications. ^[68]

Figure 3.

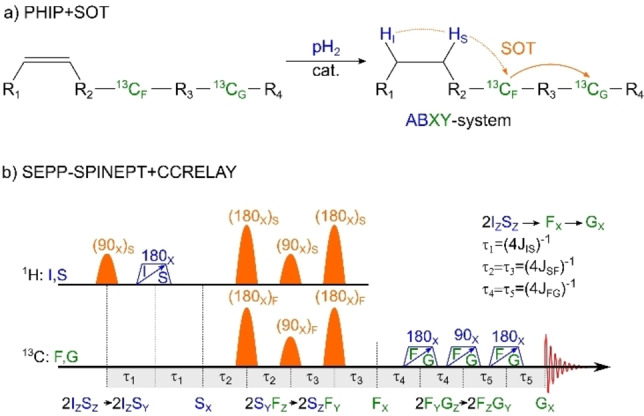
¹³C‐PHIP via an intermediate ¹³C‐nucleus: hydrogenation reaction with a successive transfer of polarization to a first ¹³C ($F$ ), followed by a transfer to a second ¹³C ($G$ ) in an ABXY‐system (a) and a proposed SEPP‐SPINEPT+ SP‐SOT with CCRELAY (b). If the target ¹³C nucleus (G) is located far from the pH₂‐nascent ¹H, the ¹³C‐¹³C‐relayed polarization pathway ^[56] may turn out to be more effective than direct polarization transfer. This is achieved with an adaption of the SP‐SOTs (here SEPP‐SPINEPT+). In the presence of more than one ¹³C nucleus, the first three ¹³C‐pulses should act selectively on the ¹³C spin $\mathbf{F}$ . The other ¹³C pulses must excite $F$ and $G$ . Again, 100 % polarization transfer is expected with the ¹³C‐relayed SP‐SOT. Note that the CCRELAY block is an INEPT+ block applied to transfer polarization between the same type of nuclei.

The sequences considered above transfer pH₂ spin order to net magnetization on $F_X$ , the first ¹³C nucleus. To facilitate the transfer to the second ¹³C, $G$ , an INEPT‐type block acting only on the two carbon nuclei is sufficient (Figure 3b).

As before, $F_X$ evolves into $F_Y{G}_Z$ by the mutual J‐coupling, before evolving into net magnetization $G_X$ of the target ¹³C nucleus at the end. This polarization scheme will be most effective if the ¹³C RF pulses during the ¹H‐¹³C transfer are selective on the F‐spin only. However, during the ¹³C‐¹³C transfer, the RF pulses need to act on both ¹³C nuclei. As the chemical shift between ¹³C nuclei can be significant, frequency‐modulated pulses or two subsequent pulses may be exploited here, too. At the same time, the chemical shift separation makes selective excitation simpler, suppressing any interferences with undesired J‐couplings during the polarization transfer. The $\tau$ ‐parameters immediately follow from the J‐coupling constant between the F‐ and G‐spins (i. e. ${\tau }_4={\tau }_5={\left(4J_{\mathrm{F}\mathrm{G}}\right)}^{-1}$ ; Figure 3b). The transfer efficiency for the last C‐C step is 100 % (theoretically). Note, that Glöggler and coworkers also suggested a transfer scheme that includes a relayed ¹H‐¹H transfer to avoid double ¹³C labeling. ^[69] While a corresponding SP variant of this scheme could be derived analogously, it was not further investigated here.

In the end, we found that the selective variants of the sequences discussed are effective independent from the symmetry of the ¹H‐¹³C J‐couplings: high polarization is reached when J _IF is ‘«’, ‘≈’, or ‘»’ than J _SF. As discussed above, phSPINEPT+ may be a suboptimal choice in some cases when ${\tau }_1$ becomes long. Then, the SEPP‐SPINEPT+ and SP‐ESOTHERIC sequences represent the most efficient polarization pathways.

We analyzed the ideal cases where the hyperpolarized molecule consists only of the spins exchanging polarization. Nonetheless, this consideration is valid for fully perdeuterated reagents or molecules in which a selective excitation of the pH₂ protons (without exciting other protons) is possible. The protonated and partially protonated precursor will be favorable to save costs when new compounds are synthesized for testing or when a kinetic isotope effect is to be avoided.[ ⁷⁰ , ⁷¹ ] In such cases, the presented SOT schemes will be particularly advantageous, as undesired ¹H‐¹H J‐couplings are refocused. The SP‐SOT for protonated compounds can be optimized numerically ^[72] (SP‐SOT for 1‐¹³C‐ethyl pyruvate is exemplified in SI, Figure S3).

The SP‐SOT sequences require precise positioning of excitation frequencies and may potentially suffer from the drifts of the static magnetic field or erroneous flip‐angle calibration. However, modern NMR spectrometers and MRI systems feature a stable and well‐controlled B ₀ field and frequency lock. Narrow and broadband shape pulses are routinely used in both NMR and MRI applications. For instance, they have enabled fascinating applications such as ultra‐fast 2D spectroscopy ^[73] that are compatible with PHIP, ^[74] or J‐edited MR spectroscopy in humans. ^[63] Hence, while a proper calibration of the resonance frequency of the MR system is necessary, the sequences are suitable, likely without significant restrictions.

In summary, we have extended the concept of SP‐SOT to some of the most promising SOT sequences for weakly coupled systems. As only one RF pulse per sequence needs to be broadband, a low RF power is sufficient, which makes these sequences best suited for the polarization in MRI setups in SAMBADENA ^[75] ‐like experiments where non‐selective pulses are often difficult. These circumstances and recent advances in PHIP research make SP‐SOT most promising, and we anticipate further experimental investigation of the concept, including in situ polarization in the MRI.

Methods

Spin Dynamics and Liouville von Neuman Equation

The spin state of the nuclei system in NMR is convenient to represent using density matrices instead of wave functions because the state of the system is not always pure: the wave function of the system is not always defined. The Liouville von Neuman equation (LvN) describes the evolution of the density matrix $\widehat{\rho }$ of the system with the Hamiltonian $\widehat{\mathrm{H}}$ :

$${\displaystyle \frac{\delta \widehat{\rho }}{\delta t}=-i\left[\widehat{\mathrm{H}},\widehat{\rho }\right]}$$ (1)

The liquid‐state NMR Hamiltonian of N‐spins consists of nuclei spin ${\widehat{\mathrm{I}}}_{}^{\mathrm{k}}$ with magnetic field interaction (Zeeman effect) and scalar spin‐spin interaction (J‐coupling):

$${\displaystyle \widehat{\mathrm{H}}={\widehat{\mathrm{H}}}_{\mathrm{Z}}+{\widehat{\mathrm{H}}}_{\mathrm{J}}=-2\pi \sum _{\mathrm{k}=1}^{\mathrm{N}}{\nu }_{\mathrm{k}}{\widehat{\mathrm{I}}}_{\mathrm{Z}}^{\mathrm{k}}+2\pi \sum _{\mathrm{k}<l}^{\mathrm{N}-1,\mathrm{N}}{\mathrm{J}}_{\mathrm{k},\mathrm{l}}\left({\widehat{\mathrm{I}}}_{}^{\mathrm{k}}·{\widehat{\mathrm{I}}}_{}^{\mathrm{l}}\right)}$$ (2)

Conventionally, the Hamiltonian is given in units of rad/s, the magnetic field ${\mathrm{B}}_0$ is along the Z‐axis,${\nu }_{\mathrm{k}}={\gamma }_{\mathrm{k}}{\mathrm{B}}_0\left(1+{\delta }_{\mathrm{k}}\right)/2\pi$ is the Larmor precession frequency (in Hz) of the spin k with a magnetogyric ratio ${\gamma }_{\mathrm{k}}$ , and chemical shift ${\delta }_{\mathrm{k}}$ . ${\mathrm{J}}_{\mathrm{k},\mathrm{l}}$ is the J‐coupling constant between spins k and l.

The LvN equation [Eq. (1)] with Hamiltonian $\widehat{\mathrm{H}}$ was used to simulate spin order transfer sequences when analytical calculations are too complex: for example, SOT in 9 spin system of ethyl pyruvate (Figure S3, SI).

Product Operator Formalism

When all spins are weakly coupled $\left|{\nu }_{\mathrm{k}}-{\nu }_{\mathrm{l}}\right|\gg \left|{\mathrm{J}}_{\mathrm{k},\mathrm{l}}\right|$ the secular approximation can be applied to Hamiltonian [Eq. 2]:

$${\displaystyle {\widehat{\mathrm{H}}}_0={\widehat{\mathrm{H}}}_{\mathrm{Z}}+{\widehat{\mathrm{H}}}_{\mathrm{J}\mathrm{Z}\mathrm{Z}}=-2\pi \sum _{\mathrm{k}=1}^{\mathrm{N}}{\nu }_{\mathrm{k}}{\widehat{\mathrm{I}}}_{\mathrm{Z}}^{\mathrm{k}}+2\pi \sum _{\mathrm{k}<l}^{\mathrm{N}-1,\mathrm{N}}{\mathrm{J}}_{\mathrm{k},\mathrm{l}}\left({\widehat{\mathrm{I}}}_{\mathrm{Z}}^{\mathrm{k}}·{\widehat{\mathrm{I}}}_{\mathrm{Z}}^{\mathrm{l}}\right)}$$ (3)

For this Hamiltonian [Eq. (3)], LvN equation [Eq. (1)] can be solved approximately, and the solution is a superposition of different rotations of the spins. This approach is called product operator formalism. ^[51] This method is well described in the textbooks. ^[52] Here we will only illustrate transformations of nuclei spins under the action of Zeeman interaction (rotation around Z axis on angle $\phi =2\pi vt$ ): ^[76]

$${\displaystyle \begin{array}{c}{\widehat{\mathrm{I}}}_{\mathrm{X}}\underset{}{\overset{\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}}{\to }}+{\widehat{\mathrm{I}}}_{\mathrm{X}}\cos \phi +{\widehat{\mathrm{I}}}_{\mathrm{Y}}\sin \phi \\ {\widehat{\mathrm{I}}}_{\mathrm{Y}}\underset{}{\overset{\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}}{\to }}-{\widehat{\mathrm{I}}}_{\mathrm{X}}\sin \phi +{\widehat{\mathrm{I}}}_{\mathrm{Y}}\cos \phi \\ {\widehat{\mathrm{I}}}_{\mathrm{Z}}\underset{}{\overset{\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}}{\to }}{\widehat{\mathrm{I}}}_{\mathrm{Z}}\end{array},}$$ (4)

and J‐coupling interaction (rotation around “ZZ axis” by the angle $\phi =\pi Jt$ ) [Eq. 5]:

$${\displaystyle \begin{array}{c}\begin{array}{c}{\widehat{\mathrm{I}}}_{\mathrm{X}}^1\underset{}{\overset{2\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2}{\to }}+{\widehat{\mathrm{I}}}_{\mathrm{X}}^1\cos \phi +2{\widehat{\mathrm{I}}}_{\mathrm{Y}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\sin \phi \\ {2\widehat{\mathrm{I}}}_{\mathrm{Y}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\underset{}{\overset{2\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2}{\to }}-{\widehat{\mathrm{I}}}_{\mathrm{X}}^1\sin \phi +2{\widehat{\mathrm{I}}}_{\mathrm{Y}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\cos \phi \end{array}\\ \begin{array}{c}{\widehat{\mathrm{I}}}_{\mathrm{Y}}^1\underset{}{\overset{2\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2}{\to }}+{\widehat{\mathrm{I}}}_{\mathrm{Y}}^1\cos \phi -2{\widehat{\mathrm{I}}}_{\mathrm{X}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\sin \phi \\ {2\widehat{\mathrm{I}}}_{\mathrm{X}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\underset{}{\overset{2\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2}{\to }}+{\widehat{\mathrm{I}}}_{\mathrm{Y}}^1\sin \phi +2{\widehat{\mathrm{I}}}_{\mathrm{X}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\cos \phi \end{array}\\ \begin{array}{c}{\widehat{\mathrm{I}}}_{\mathrm{Z}}^1\underset{}{\overset{2\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2}{\to }}{\widehat{\mathrm{I}}}_{\mathrm{Z}}^1\\ {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\underset{}{\overset{2\phi {\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2}{\to }}{\widehat{\mathrm{I}}}_{\mathrm{Z}}^1{\widehat{\mathrm{I}}}_{\mathrm{Z}}^2\end{array}\end{array}}$$ (5)

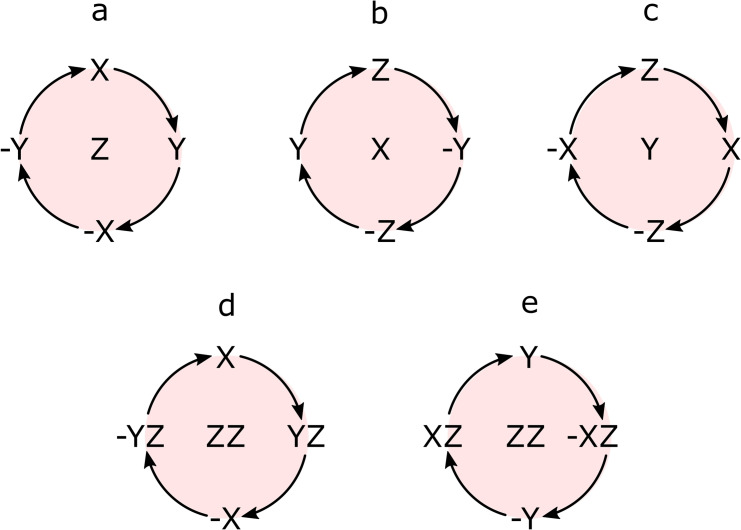
Note that if the rotation axis coincides with the operator, no rotation happens. RF pulses used for SOT are also represented with corresponding spin rotations analogous to Equation (4). ^[76] For the simplicity of the analysis and description of the mechanism of polarization transfer discussed above, the rotations around X, Y, Z and “ZZ” axis are illustrated in Figure 4. We used the rotation diagram (Figure 4) together with equations 4 and 5 and their analogs for corresponding axises to calculate SOT performance and to find optimal parameters.

Figure 4.

Schematic diagram of spin rotations around X, Y, Z, and “ZZ” axis. Rotation around the Z‐axis results from the Zeeman interaction of spins with an external field (a). RF pulses along the corresponding axis induce rotations around the X or Y‐axis (b, c). Rotations around effective “ZZ”‐axis are the result of scalar spin‐spin coupling (d, e). See Equations (4) and (5) for details.

Spin echo elements of SOT and selective pulses are discussed in more detail in SI.

Supporting information

Comparison of the total SP‐SOT time for different J‐coupling constants and application of SP‐SOT sequences to ethyl pyruvate and 1‐¹³C‐ethyl pyruvate(‐d6) and analysis of J‐coupling evolution and suppression during spin‐echo (PDF). The MOIN spin library ^[77] and scripts to simulate SP‐SOT performance (.zip).

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

Supporting Information

A. N. Pravdivtsev, J.-B. Hövener, A. B. Schmidt, ChemPhysChem 2022, 23, e202100721.