Strain-Dependent Diffusivity of Small and Large Molecules in Meniscus

Abstract

Due to lack of full vascularization, the meniscus relies on diffusion through the extracellular matrix to deliver small (e.g., nutrients) and large (e.g., proteins) to resident cells. Under normal physiological conditions, the meniscus undergoes up to 20% compressive strains. While previous studies characterized solute diffusivity in the uncompressed meniscus, to date, little is known about the diffusive transport under physiological strain levels. This information is crucial to fully understand the pathophysiology of the meniscus. The objective of this study was to investigate strain-dependent diffusive properties of the meniscus fibrocartilage. Tissue samples were harvested from the central portion of porcine medial menisci and tested via fluorescence recovery after photobleaching to measure diffusivity of fluorescein (332 Da) and 40 K Da dextran (D40K) under 0%, 10%, and 20% compressive strain. Specifically, average diffusion coefficient and anisotropic ratio, defined as the ratio of the diffusion coefficient in the direction of the tissue collagen fibers to that orthogonal, were determined. For all the experimental conditions investigated, fluorescein diffusivity was statistically faster than that of D40K. Also, for both molecules, diffusion coefficients significantly decreased, up to ∼45%, as the strain increased. In contrast, the anisotropic ratios of both molecules were similar and not affected by the strain applied to the tissue. This suggests that compressive strains used in this study did not alter the diffusive pathways in the meniscus. Our findings provide new knowledge on the transport properties of the meniscus fibrocartilage that can be leveraged to further understand tissue pathophysiology and approaches to tissue restoration.

Introduction

Meniscus fibrocartilage is a key component in the function of the knee, protecting the joint from acute injury as well as chronic conditions such as osteoarthritis (OA): this tissue bears 45–75% of the total load on the knee and provides lubrication and congruency to the joint during motion [1–3]. Meniscus damage is the second most prevalent sports-related injury and often leads to OA [4–6]. Current treatment options for this ailment ideally include meniscal repair; however, partial or total meniscectomy is often the case following meniscal damage or degeneration [7]. It is known that health and function of the knee are directly related to the amount of remaining meniscal tissue [8]. Therefore, significant research effort is being conducted to develop repairing strategies based on drug delivery or bio-engineered surrogates for partial or total meniscal replacement [9,10]. To develop successful drug delivery protocols, as well as surrogates recapitulating the properties of the native tissue, it is crucial to understand transport phenomena within the meniscus. The specific mechanisms and relations for transport in the meniscus fibrocartilage have not yet been fully characterized.

The meniscus lacks full vascularization: blood vessels are only found in the outer 10–30% of the tissue (red zone) at maturity [11–13]. Therefore, the delivery of nutrients and larger proteins to the cells of the inner avascular region (white zone) relies on diffusion from the porous extracellular matrix of the red zone and the synovial fluid surrounding the tissue [14,15]. Previous studies have characterized molecular diffusivity in meniscal tissues explants: it has been shown that diffusivity is anisotropic, being faster along the direction parallel to the circumferential collagen fibers, and slower in the orthogonal direction [16–18]. In addition, the magnitude of the diffusion coefficient is inversely related to the hydrodynamic radius of the diffusing molecule [16]. While highly informative on meniscal diffusivity in general, these studies only investigated the case of noncompressed tissue. In normal physiological conditions, the meniscus is subjected to mechanical loads. Average compressive strains of the meniscus are between 10 and 20% during normal daily activities [19–21]. A previous study from Kleinhans et al. showed that glucose diffusivity in the porcine meniscus decreased by about 50% when the tissue was compressed by up to 20% of its initial height [18].

The objective of this study was to conduct a preliminary investigation on the strain-dependent diffusive properties of a protein-sized molecule in the meniscus to determine the effect of compression on the magnitude of the diffusion coefficient and on the anisotropic ratio (defined as the ratio of diffusivity in the direction parallel to the collagen fibers to the direction orthogonal to fibers). Based on previous studies on both porcine meniscus and other fibrocartilaginous tissues [18,22–28], we hypothesized that increased compressive strain would decrease solute diffusivity but not alter the anisotropic ratio. To our knowledge, this is the first study to investigate the combined effects of compression and solute size on the diffusion coefficient and its anisotropic ratio in meniscus fibrocartilage.

Solute diffusivity was measured via fluorescence recovery after photobleaching (FRAP). This experimental technique has already been successfully used in multiple studies investigating solute diffusivity in cartilaginous tissues [16,29–35]. A 40 K Da dextran (D40K) was selected as a molecular probe since its steric magnitude is comparable to that of a medium-sized protein, and relatively large (∼100×) compared to small, nutrient-sized molecules. In addition, the strain-dependent diffusion of fluorescein (332 Da) was also determined. This was done to obtain a baseline measurement for comparison with the results obtained from the larger D40K. Also, fluorescein is comparable in size to glucose thereby permitting comparison of our results to previous studies [18,22].

Materials and Methods

Specimen Preparation.

Meniscal tissue samples were cut from the core of the central portion of medial menisci obtained from fourteen 2+-year-old pigs. A corneal trephine was used to punch 6 mm diameter cylindrical specimens in the axial orientation; a microtome (SM2010R, Leica Biosystems, Wetzlar, Germany) was used to cut the specimens to a height of 2 mm. Immediately after harvesting, specimens were confined in a custom-made compressing chamber which allowed for equilibration in a protease inhibited 1X phosphate buffer solution (PBS) solution (Sigma-Aldrich Co., St. Louis, MO) containing the molecular probe of interest. Equilibration occurred overnight at 4 °C. Initially, the compressive plunger of the chamber was set to the sample height of 2 mm, thus providing a 0% compressive strain. Compressive strains of 10% and 20% were attained by displacing the compressive plunger to compress the sample to heights of 1.8 mm and 1.6 mm, respectively. Our measurements indicate that the errors in applying such compressive strains were ∼1%, <1%, and ∼3% for 0%, 10%, and 20% strain, respectively. A total of two molecules were investigated. Specifically, fluorescein (MW 332 Da, hydrodynamic radius 5.02 Å, Sigma-Aldrich [16]) and dextran (D40K) conjugated with fluorescein (MW 40,000 Da, hydrodynamic radius 48 Å, Molecular Probes, Thermo Fisher Scientific, Waltham, MA [36]).

For each molecule investigated, a total of 7 (n = 7) meniscal samples were tested (one per meniscus), and a minimum of three FRAP tests were performed on each sample for each compression level. Specimens remained embedded in the PBS solution during the entire duration of the imaging. A schematic of specimen harvesting and preparation, together with a graphical description of the compressing chamber is reported in Fig. 1.

Fig. 1.

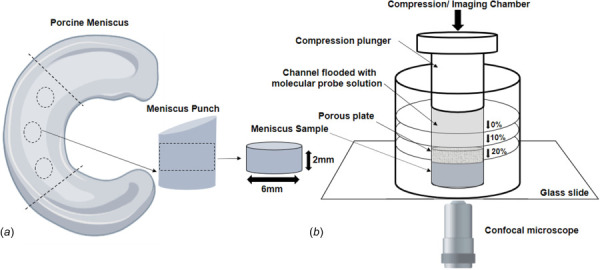
Schematic of specimen preparation. Location and size of the specimens are shown: (a) for FRAP tests, cylindrical specimens with a height of 2 mm and diameter of 6 mm were prepared from the central region of the meniscus along the axial direction and (b) the discs were then placed into the custom-made compression chamber, submerged in 1X PBS solution containing the molecular probe of interest. To apply compressive strains of 0%, 10%, or 20%, the plunger is pushed and locked into predefined positions of the flooded channel.

Measurement of Diffusivity.

A custom FRAP technique, developed in our lab [17], was used to simultaneously measure the diffusion coefficient of solute in the direction parallel to and orthogonal to the tissue fibers. Experiments were carried out at room temperature (22 °C) using a confocal laser scanning microscope (A1R-SI, Nikon, Japan). The specimens were photobleached by an argon laser (488 nm wavelength) using a Plan Apo 20x/0.75 DIC N2 WD 1.0 objective (Nikon, Japan). A multi-layer bleaching protocol was used to minimize the error due to the out-of-plane diffusivity contribution [35,37,38]. For each test, a time series of 300 video images of 128 × 128 pixels (460.7 × 460.7 μm²) were collected, including five images prior to bleaching. To minimize the contribution of the fluorescence emission of the background, prebleach images were averaged and then subtracted from the postbleach image series. Images were analyzed using a custom matlab-based algorithm [37] performing fast Fourier transform combined with Karhunen–Loeve transform [39] to determine the components of the diffusion tensor (D)

$$\left[\begin{array}{cc}{D}_{xx}& D_{xy}\\ D_{xy}& D_{yy}\end{array}\right]=\left[\begin{array}{cc}\mathrm{c}\mathrm{os}\mathrm{ɵ}& -\text{sin}\mathrm{ɵ}\\ \mathrm{s}\mathrm{in}\mathrm{ɵ}& \mathrm{c}\mathrm{os}\mathrm{ɵ}\end{array}\right]\left[\begin{array}{cc}{D}_{xx}^{\prime }& 0\\ 0& D_{xx}^{\prime }\end{array}\right]\left[\begin{array}{cc}\mathrm{c}\mathrm{os}\mathrm{ɵ}& \mathrm{s}\mathrm{in}\mathrm{ɵ}\\ -\text{sin}\mathrm{ɵ}& \mathrm{c}\mathrm{os}\mathrm{ɵ}\end{array}\right]$$ (1)

where D_xx, D_xy, and D_yy are the components of the D in the coordinate system of the microscope focal plane. Instead, D $\prime$_xx and D $\prime$_yy are components of D along the principal components of the tissue, whose orientation with respect to the coordinate system of the microscope is q. It can be shown that fast Fourier transform analysis of the FRAP image sequence allows for determining D_xy and the trace of D [17], which is defined as

$$\text{tr}(\mathit{D})\hspace{0.17em}=D_{xx}+D_{yy}=D_{xx}^{\mathrm{\prime }}+D_{yy}^{\mathrm{\prime }}$$ (2)

It can also be shown that [17]

$$D_{xx}^{\prime }-D_{yy}^{\prime }=\frac{D_{xy}}{\text{sin}\mathrm{ɵ}\text{cos}\mathrm{ɵ}}$$ (3)

The orientation θ is related to the elliptical shape that the bleached spot assumes during recovery. This can be measured via Karhunen–Loeve transform. It should be noted that the major axis of the ellipse corresponds to the direction in which diffusion is the slowest, and the minor axis represents the direction of fastest diffusion [17]. Once tr(D), D_xy, and θ are determined, the principal components of D (D′_xx and D′_yy) can be calculated via Eqs. (2) and (3). It has been shown that measurements of anisotropic diffusivity using this technique are affected by a relative error below 10% [17].

For each specimen, an initial set of diffusivity measurements were carried out at 0% strain. After measurement, specimens were compressed to 10% and allowed to equilibrate for a minimum of 30 min before conducting a new set of FRAP tests. Previous studies indicate that a time frame of 30 min is sufficient to relax the stress in the tissue caused by the compression [40]. A similar protocol was used to attain measurements at 20% strain. During the entire duration of the experiments, the samples were kept in the custom-made chambers in order to prevent dehydration.

Statistical Analysis.

A two-way analysis of variance with replication with factors being molecular type (fluorescein and D40K) and strain level (0%, 10%, and 20%) was used to investigate possible significant interactions and main effects on the magnitude of diffusivity. Post hoc analysis via Tukey's test was used to investigate significant differences among the levels of the factors. A similar statistical approach was followed to detect the effects of strain level and molecular type on the anisotropic ratio of diffusivity (i.e., ratio between diffusion coefficients parallel to and orthogonal to the direction of the collagen fibers in the tissue). All the statistical analyses were conducted using minitab^®20.3 statistical software (Minitab, LLC, State College, PA). For each test conducted, a level of significance of (α = 0.05) was used. All the data are reported in terms of mean ± standard deviation.

Results

Fluorescein diffusivity varied from 84.4 ± 33.9 μm²/s to 58.5  ±  24.3 μm²/s, with the highest values attained at 0% strain. The average values of diffusivity for D40K varied from 21.3 ± 10.1 μm²/s to 11.9 ± 5.2 μm²/s. Also, for this molecule, the largest average diffusivity values were attained at 0% compression, see Fig. 2. Results from two-way analysis of variance indicated that the interaction between the effects of strain level and molecular type was not statistically significant (p = 0.29). In contrast, a significant main effect was found for the molecular type (p < 0.01), with fluorescein diffusing significantly faster than D40K. The strain level did not have a significant effect on the diffusivity of the solutes (p = 0.05). However, fluorescein diffusivity at 0% was significantly larger than the corresponding values found at 10% or 20% strain (p < 0.01). Also, the diffusivity of D40K at 0% was significantly faster than that at 20% strain (p = 0.03).

Fig. 2.

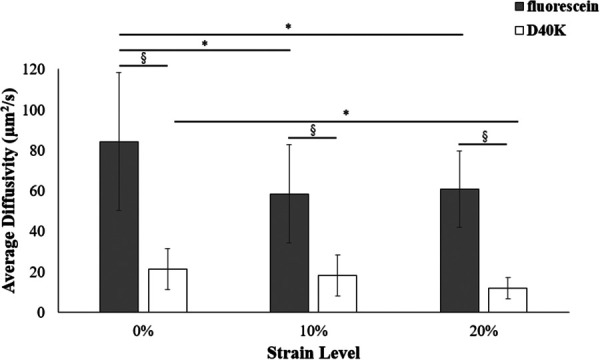
Strain-dependent diffusivity of fluorescein (gray) and D40K (white). For all the data reported, (*) indicates statistical significance (p < 0.05) across compression levels and (§) indicates statistical significance (p < 0.05) between molecules.

Fluorescein anisotropic ratio varied from 1.8 ± 0.3 to 2.2 ± 0.5, while that of D40K from 1.69 ± 0.5 to 2.32 ± 0.4, see Fig. 3. A significant interaction between molecular type and strain level was found (p = 0.03). For each molecule investigated, no significant differences were found between anisotropic ratios across compression levels. Also, no significant differences were observed when comparing the anisotropic ratios of the two solutes at both 0% and 10% compression. However, at 20% strain, the anisotropic ratio of fluorescein was significantly smaller than that of D40K (p = 0.01).

Fig. 3.

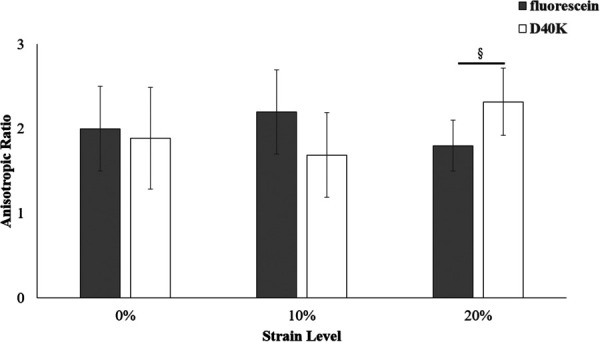
Strain-dependent anisotropic ratio of fluorescein (gray) and D40K (white). The anisotropic ratio was defined as the ratio between diffusion coefficient parallel to and orthogonal to the direction of the collagen fibers in the tissue. For all the data reported, (§) indicates statistical significance (p-value < 0.05) between molecules.

Discussion

This study investigated the strain-dependent diffusivity of small and large molecular solutes in the meniscus. Specifically, the diffusion coefficients of fluorescein (332 Da) and D40K (40,000 Da) were measured. Previous studies have documented diffusive properties of probes of a wide range of hydrodynamic radii in human and animal menisci [16,17]. Also, the effect of static compression on glucose diffusion in the porcine meniscus has been reported [18]. To the authors' best knowledge, this is the first study reporting the effect of compressive strain on the diffusive transport of a large molecule in meniscus tissue.

Measurements of the diffusion coefficients of fluorescein at 0%, 10%, and 20% compressive strain were conducted with the dual purpose of a direct comparison with experimental results reported for a similar-sized molecule (glucose [18]) and to obtain a baseline for comparing the observations conducted on the larger D40K probe. The average diffusion coefficient of fluorescein at 0% strain was 84.4 ± 33.9 μm²/s, which is similar to earlier measurements conducted on both human (110.00 ± 29.35 μm²/s) and bovine meniscus (101.50 ± 57.50 μm²/s) [16,17], and slightly smaller than that of glucose (168.00 ± 69.00 μm²/s) [18], whose molecular weight is 180 Da. In comparison, the diffusivity of D40K was significantly smaller (21.3 ± 10.1 μm²/s) and similar to that reported for BSA (66,000 Da) in human tissue (27.3 ± 18 μm²/s) [16]. The general trend observed in both investigated molecules indicates that diffusivity reduces as the magnitude of applied compressive strain increases (see Fig. 2). Such behavior is likely due to the changes in water content occurring in the tissue because of the application of a compressive strain. It has been estimated that meniscal water content decreases from ∼3% to 4% for every 10% of compression applied [18]. Several theoretical models of transport in hydrated porous media [38] and experimental evidence in numerous cartilaginous tissues, including the meniscus [17,18,22,29,30,35,41–45], suggest that the diffusion coefficient is directly correlated to the water content of the tissue. The strain-dependent behavior of both fluorescein and D40K diffusion coefficients reported here, which are reduced up to ∼45% when 20% compressive strain is applied, are similar to those reported for glucose for similar compressive magnitude (∼50%) [18]. Previous studies suggest that under the experimental conditions adopted in this contribution, effects of electrostatic interactions between fluorescein and tissue extracellular matrix are negligible [37]. Since the dextran probe used in this study was conjugated with fluorescein, we expect a similar behavior.

Our results also indicate that diffusion of both fluorescein and D40K are anisotropic (i.e., direction dependent). This is a confirmation of similar findings previously reported for meniscus and similar other fibrocartilaginous tissues [16,22,33,35,45–50]. The anisotropic ratios associated with fluorescein and D40K ranged from 1.8 ± 0.3 to 2.2 ± 0.5, and 1.7 ± 0.5 to 2.3 ± 0.4, respectively (see Fig. 3). These magnitudes are similar to those reported in previous diffusivity studies in meniscus [16,18]. It was observed that anisotropy was not affected by the magnitude of compressive strain, suggesting that compression does not alter the mechanisms (pathways) of diffusion in the tissue of an individual molecule. Also, for lower levels of strain (0% and 10%), no differences were found in the anisotropic ratios of fluorescein and D40K. This was consistent with a previous study on human meniscus showing that the anisotropic ratio does not change with the size of the diffusing molecule [16]. However, it was observed that at 20% compressive strain, the anisotropic ratio of D40K was significantly larger than that of fluorescein. This would suggest that, at this strain level, it becomes more difficult for a large molecule to move orthogonally to the fibers when compared to a small, nutrient-sized solute. Based on our findings, a further investigation including a wider range of molecules and strain levels may be needed to validate this trend.

Some limitations to this study should be noted. This study used animal tissue in lieu of human samples. It would have been desirable to conduct experiments on human meniscus for its translational implications. However, potential differences in donor demographics and levels of degeneration of the tissue would cause human menisci to present a larger variability in structure, composition, and properties when compared to tissue obtained from animals of the same geographic location and age group. Accordingly, aimed at obtaining baseline measurements for future comparison with human tissue samples, we preferred to use porcine menisci. Besides, porcine meniscus tissues have similar properties to the human ones [51–53] and have been successfully used as animal models for human meniscus [54]. Moreover, all samples used in this study were extracted from the core of the central region of medial menisci. In future studies, to gain a more comprehensive picture of the diffusive properties of meniscus, we will investigate potential regional variations (i.e., medial versus lateral, central versus horns, and core versus superficial layers) given the reported in homogeneity of mechanical and transport properties of meniscus tissues [40,53,55–60].

In conclusion, the strain-dependent anisotropic diffusivity of a small and a large molecule in the porcine meniscus were investigated. It was found that, for both molecules, solute diffusivity significantly decreases as the strain is increased. In contrast, the anisotropic ratio was not affected by the strain applied to the tissue, suggesting that compression does not alter the diffusive pathways in the meniscus. However, for larger strain levels, our results indicate that large molecules may find greater hindrance in diffusing orthogonally to the tissue fibers when compared to nutrient-sized solutes. A healthy meniscus is paramount for the proper functioning of the knee and for its potential implications in the onset and progression of OA this tissue may have, if compromised. Therefore, expanding knowledge on the mechanisms of transport of small (e.g., nutrients) and large (e.g., proteins, cellular signals, and therapeutics) molecules in relation to the mechanical environment characterizing the meniscus is fundamental for a better understanding of meniscal pathophysiology as well as for developing new strategies to treat and/or prevent tissue degeneration and related OA. Furthermore, this study helps to illustrate the limitations of the delivery of larger molecules to the meniscus, which has important implications for the development of new therapies for treating meniscus pathology. Such therapies must be designed such that delivery to the intended target is efficient and optimized. The findings of this study indicate that the focus should be on reducing the size of molecules for delivery to increase the rate of transport through the tissue extracellular matrix. In this context, this contribution provides a steppingstone for future studies further elucidating the mechanisms of solutes transport in meniscus fibrocartilage.

Funding Data

• NIH (NIAMS) (Grant No. 1R01AR073222; Funder ID 10.13039/100000069).