Reproducibility and Replicability in Neuroimaging Data Analysis

Abstract

Purpose of review:

Machine learning solutions are being increasingly used in the analysis of neuroimaging (NI) data, and as a result, there is an increase in the emphasis of the reproducibility and replicability of these data-driven solutions. While this is a very positive trend, related terminology is often properly defined, and more importantly, (computational) reproducibility that refers to obtaining consistent results using the same data and the same code is often disregarded.

Recent Findings:

We review the findings of a recent paper on the topic along with other relevant literature, and present two examples that demonstrate the importance of accounting for reproducibility in widely used software for NI data.

Summary:

We note that reproducibility should be a first step in all NI data analyses including those focusing on replicability, and introduce available solutions for assessing reproducibility. We add the cautionary remark that when not taken into account, lack of reproducibility can significantly bias all subsequent analysis stages.

1. Introduction

As in multiple fields, in neuroscience as well, data-driven solutions are playing an increasingly important role. With this shift away from the traditional model-driven approaches, there is also an increased emphasis on the interpretability of solutions. This is due to the fact that, with data-driven solutions, we often do not have a clear connection to a physical model, however, it is through interpretation that we can gain insights about the problem and generalize it to other scenarios. Finally, reproducibility and replicability are intimately related to interpretability, as without these two basic requirements, interpretations are hardly useful. As a result, there is an increasing emphasis in the emphasis of these important properties, particularly in the analysis of neuroimaging (NI) data. However, most often, it is difficult to compare the results across publications and to put them into proper context. One reason is that these terms, reproducibility and replicability, are not defined properly. They are used interchangeably, along with other properties such as robustness, consistency, and stability. Even more importantly, (computational) reproducibility, defined as obtaining consistent results using the same data and the same code [1] is most often, not even taken into account [2]. Our goal in this article is to emphasize the importance of reproducibility by reviewing the relevant work, as when not taken into account, it is likely to introduce significant bias into all subsequent stages of the analyses. This is an important concern for many of the widely used NI toolboxes. Here we provide examples using the Group ICA of fMRI Toolbox (GIFT) [3] for assessing data-driven functional network and the FreeSurfer software package [4] for the analysis and visualization of structural and functional neuroimaging data, though the issues we highlight are pervasive in the field, including many other iterative approaches, such as inverse modeling for magnetoencephalography and electroencephalography (M/EEG).

In addition, reproducibility is an important prerequisite for replicability. In literature, references to reproducibility often actually consider replicability, which is defined as consistency of results using the same code but with different data. Again, we follow the definitions given by the US National Academies of Sciences, Engineering, and Medicine [1], also promoted by [5]. Many studies including hyperparameter choice, effect sizes, or different generalization properties (of site, population, and so on) all rely on replicability studies. Hence, leaving out the critical reproducibility step in these evaluation poses a problem.

A recent overview, [2], starts with these definitions and underlines the importance of reproducibility as the starting point for all studies, including those on replicability. The focus in [2] is on unsupervised machine learning methods based on matrix and tensor decompositions (MTDs), which have found fruitful application in NI data analysis. In this review, we revisit the conclusions of [2] with an emphasis on applications in neuroscience, especially of independent component analysis (ICA) and review (the limited) work that addresses reproducibility in other machine learning solutions such as iterative optimization approaches including computational morphometry implemented in FreeSurfer.

2. Definitions: Reproducibility and Replicability

In the definition of reproducibility, obtaining consistent results using the same data and the same code, “same code” implies that a given algorithm is used with the same set of hyperparameters. Thus, the only source of variability is due to random initializations. Given that the cost functions for most data-driven methods are non-convex, one can only guarantee convergence to a local optimum. Since in most cases, closed form solutions do not exist, iterative techniques are employed, and most commonly, using random initializations, see e.g., [6–8]. Even when all algorithmic quantities are fixed, and the only variability is due to random initializations, the resulting decompositions can be quite different as demonstrated in [2]. Hence, for reproducibility, we should select an appropriate metric such as correlation to measure the consistency (repeatability, stability) of the final results.

For replicability, consistency of the solutions with the same algorithm are studied using different data. Here, there are two ways the data can be different. In the first case, this can be due to sampling from the same dataset (e.g., different folds) with a goal such as selecting hyperparameters to be used for the final analysis, or studying properties such as effect sizes. Alternatively, different data might mean the use of a completely different dataset which is data collected with the same general goal but where the site, scanner, population is different. We identify the first case as partially different data and the second one as completely different data. In the first case, we could use a similarity metric as in the evaluation for reproducibility since the goal is obtaining essentially similar solutions, and in the second case, one would expect to replicate the general conclusions of the study, rather than obtaining estimates that are very close to each other. The terminology used for replicability and reproducibility varies in the literature, the two terms often being used interchangeably [9], with reproducibility used for referring to what we call replicability [10, 11]. Other terms used include stability [12, 13], repeatability [14], similarity [15], and (algorithmic) reliability [16]. Thus, while consulting other references, it is important to remember the definitions we make here, in this section, and when we talk about replicability, we do consider partially different data.

3. Two case studies for reproducibility: ICA of fMRI Data and FreeSurfer

Almost all of current work in NI data analysis concentrates on replicability—even though it might be called reproducibility. One notable exception has been in the application of ICA to fMRI analysis where the practice has been using multiple runs with different initializations, and then selecting one run as the one for further study. in the following, we review metrics used for reproducibility in ICA, which are also used in other matrix and tensor decompositions, and then present two examples that demonstrate the importance of assessing reproducibility in ICA as implemented in GIFT, and for another widely used NI toolbox, FreeSurfer.

3.1. Reproducibility in ICA of fMRI

Characterizing reproducibility in ICA of fMRI data requires use of a well-defined best run selection mechanism. Three solutions proposed for this task are ICASSO [16], minimum spanning tree (MST) [17], and Cross ISI [6]. ICASSO is the first systematic approach introduced for ICA, specifically for the FastICA algorithm, where a highly repeatable solution is selected by performing multiple runs followed by a clustering step of the estimated components to select a set of estimates. In [18], the approach is modified such that a single run (and the estimates from that run) can be selected rather than a set of estimates that might come from different runs as reconstructing the original fMRI observation set is important. In [8], another modification of ICASSO is proposed where the number of clusters is determined using a lowrank graph approximation whereas in ICASSO, this is a user-defined parameter. In MST, components across multiple ICA runs are aligned and a one sample t-test is used to evaluate the reproducibility of estimated components, and the best run is selected using the run most highly correlated to this given tmap. For ICA, inter-symbol interference (ISI) is a frequently used global distance metric for performance evaluation when the ground truth is available. It is a normalized quantity, with zero indicating perfect separation and takes the inherent permutation and scaling ambiguities in ICA into account. Cross ISI is defined by replacing the true mixing matrix—which is unavailable in practical implementations—with the demixing matrix estimates from other runs, such that the average distance of each run to all the others are calculated. The run with the smallest distance to all others yield the most reproducible run. All three metrics are included in GIFT and have been used for best run selection [6, 17–19].

Reproducible solutions are also more interpretable

Model-based solutions are usually fully interpretable through their connection to the physical model. Matrix and tensor decompositions, while allowing the discovery of structure in the data in an unsupervised manner, can also result in fully interpretable solutions, by which we mean we can associate the rows/columns of the final factor matrices with (physical) quantities of interest. In other data-driven solutions like multilayered neural networks, interpretability generally requires a subsequent analysis stage, e.g., generation of heat maps [20].

Linear mixing model of independent component analysis (ICA) provides a good match to fMRI data where the observations are modeled through the linear mixing of intrinsic functional networks (FN) with their temporal modulations [21]. This is a key reason for the success of ICA in application to fMRI analysis [22, 23]. In addition, the ICA model is unique under very general conditions [24], which is an essential property when interpretability is the goal. Interpretation of estimated components without guarantees on their uniqueness would make little sense.

A functional network connectivity (FNC) map is a measure of the covariance or cross-correlation of the timecourses of the components estimated by ICA. As such, it provides an effective summary of interactions between functional networks. In [2], the desirable match of the ICA model for fMRI analysis is demonstrated with an example using FNC maps, which we reproduce in Figure 1. GIFT is used to perform ICA analysis using the entropy bound minimization (EBM) algorithm with 176 subjects (88 healthy controls (HCs) and 88 patients with schizophrenia) from https://coins.trendscenter.org/, and 28 components were selected as functionally relevant (see [2] for experimental details). The FNC maps corresponding to the run with the lowest Cross-ISI (best run) and the one to lowest Cross-ISI among 100 runs with random initializations are shown in the figure. We observe higher connectivity within functional domains, and the expected anti-correlations with DMN to other networks for the best run, while these aspects are weaker for the run with the highest Cross-ISI. These results provide examples where the selection of most reproducible run also results in better interpretability.

Figure 1:

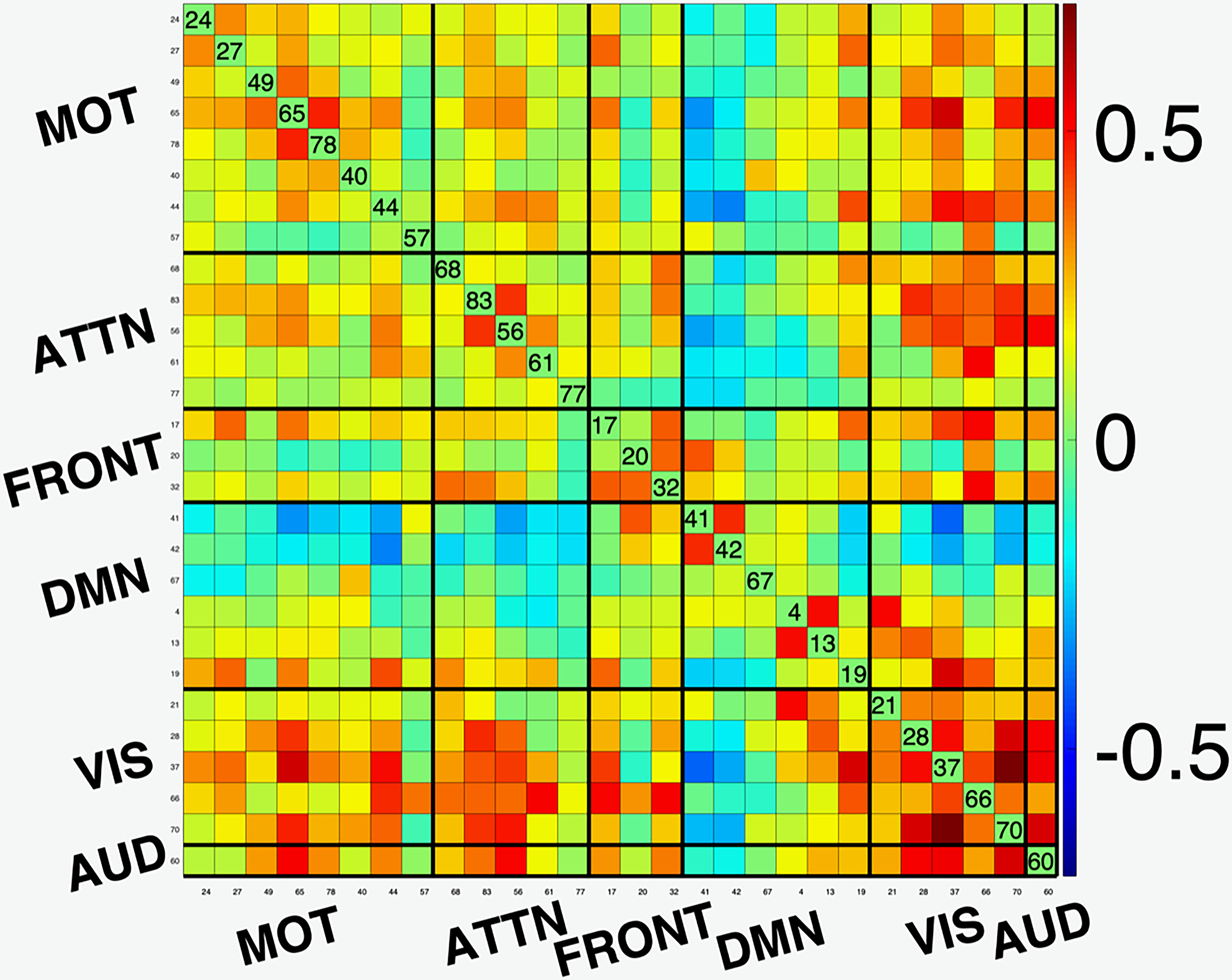
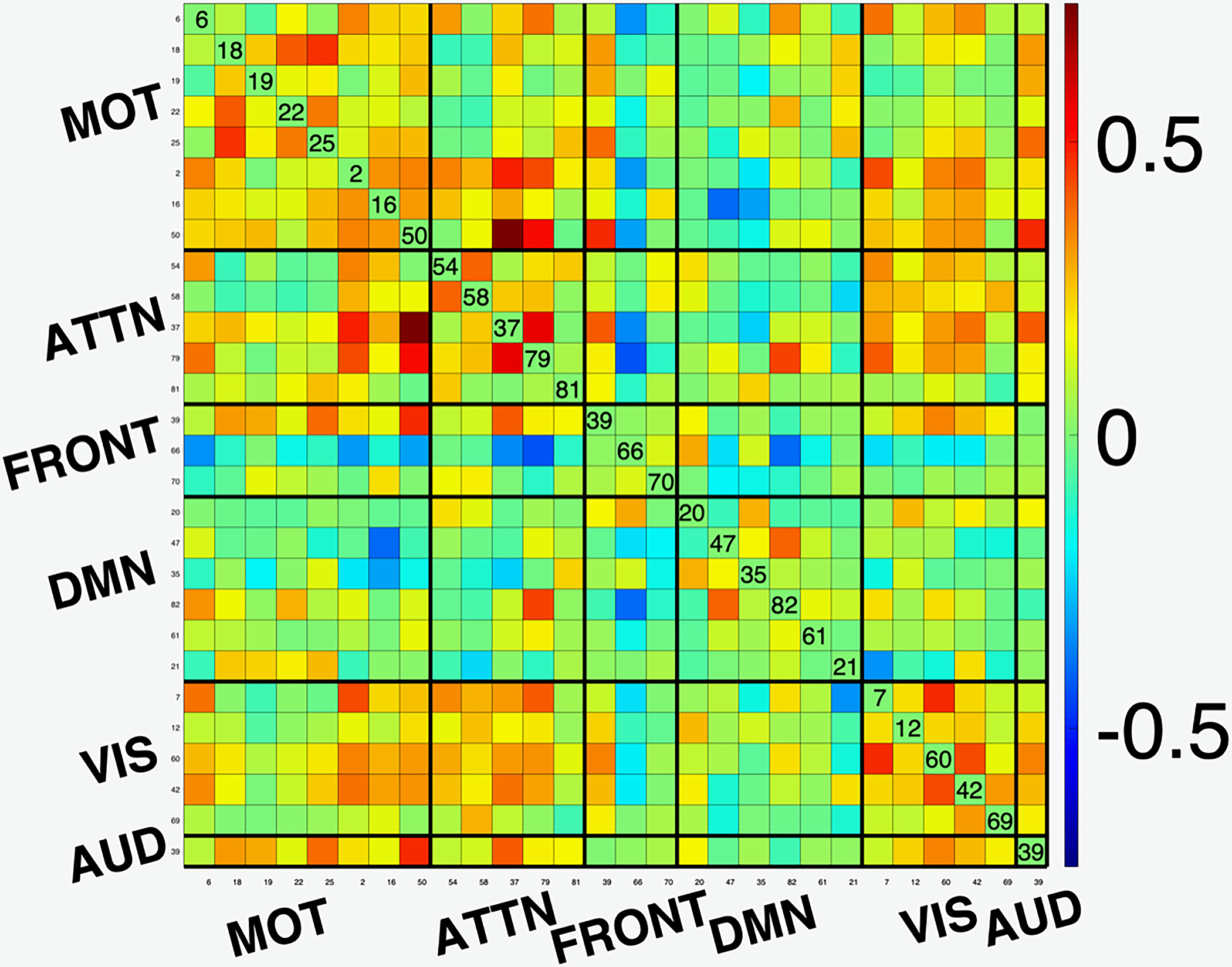
Functional network connectivity (FNC) maps for (a) run with the lowest Cross-ISI (best run); and (b) run with the highest Cross-ISI (low reproducibility). Note that the best run result has better interpretability. (AUD: Auditory; MOT: Sensorimotor; VIS: Visual; ATTN: Attentional, and FRONT: Frontal networks; DMN Default mode network.)

Bias and variance dilemma: Algorithmic variability might be desirable

It is also worth noting that a highly reproducible solution is not always attractive. This is due to the bias variance dilemma in estimation theory, where a solution lacking flexibility might not be able to capture the informative characteristics of the data and might yield a high bias, difference from the “truth”. In ICA, the most frequently used algorithm Infomax [25] which is also the first algorithm applied to fMRI analysis [22] is rather stable as it uses a fixed nonlinearity. While this nonlinearity provides a good match to most of the sources in fMRI, which tend to be super-Gaussian in nature, it cannot as reliably capture certain networks like the default mode network (DMN) [6] and certain noise and interference components, whose estimation help improve estimation of the components of interest. In these cases algorithms with flexible density models such as the EBM might provide a better overall decomposition. In addition, an algorithm taking properties such as smoothness of the voxels in fMRI data, entropy rate bound minimization (ERBM) might be even more attractive by providing a better match to the properties of fMRI data [6]. This bias variance dilemma for the two algorithms is demonstrated with a simulated example in [2] where another important point is made: if only Cross-ISI is used in the evaluation of reproducibility, one might end up with a highly sub-optimal solution with high bias.

Similarly, in [15], evaluation of accuracy versus reproducibility is proposed for a canonical-polyadic decomposition model to determine the order. The argument is similar, the true order for the model (number of components in the decomposition) provides a better model match, and hence will be more reproducible and will achieve the desirable bias and variance tradeoff.

3.2. Computational morphometry estimated via FreeSurfer

FreeSurfer [4, 26] is arguably one of the most widely used tools for computational morphometry, and offers the ability to compute metrics estimated along a surface including cortical thickness. Freesurfer constructs a cortical surface model by aligning the data to a spherical atlas. The result then allows a number of anatomical measures including cortical thickness, surface area, curvature, and more, defined at each point on the cortex. The optimization approach in FreeSurfer is iterative and thus depends on initial conditions. The default option in FreeSurfer is to use a nonrandom, single estimation. While there is an option to vary the random seed, this only applied to the cortical estimation, not the subcortical, and it is not widely used. This has important implications in studies that use FreeSurfer, as seen in Figure 2, the percent change in volume and the change in volume (max-min) across regions within a single run goes up to almost 20% and over 650mm3 with an average change of about 5% and 230mm3. This level of variability can easily impact individual classification performance and even group level differences. In addition, FreeSurfer results are often used as head models in M/EEG studies, and as such can also impact the solutions in those cases.

Figure 2:

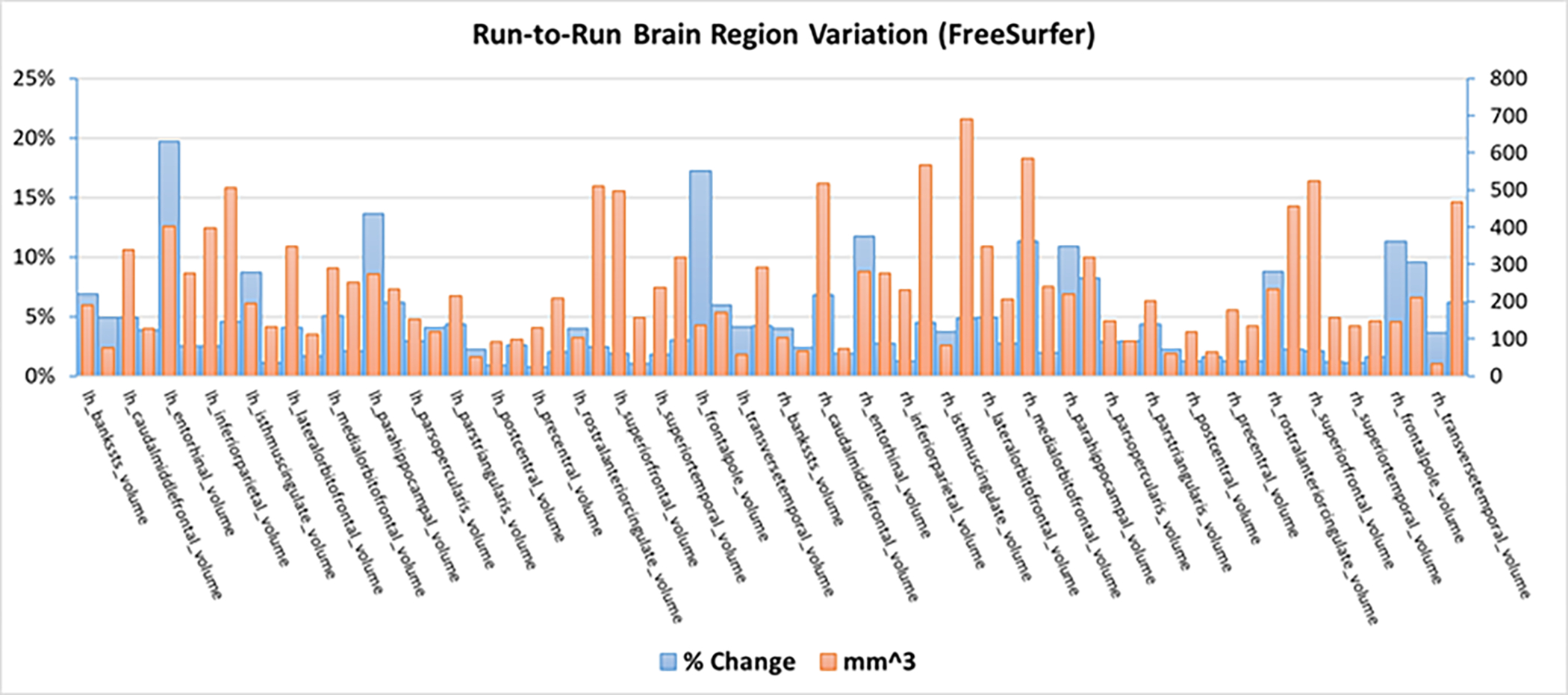
Variability in volume (max-min) and percent signal change in various brain regions produced by FreeSurfer while using different random seeds.

3.3. Summary and other machine learning solutions

As our two examples demonstrate, without guarantees on reproducibility, use of toolboxes such as the GIFT, FreeSurfer, and inverse approaches such as dipole modeling might yield suboptimal solutions, potentially introducing undesirable bias to following post-processing steps. While tools like GIFT [6, 17–19] and certain dipole modeling approaches [27] have included approaches to account for computational variability for over 15 years, other tools such as FreeSurfer have implemented partial solutions such as an option to vary the random seed for cortical (but not subcortical) estimates, and yet, this is missing in many other widely used tools in NI analysis. In addition, variability due to initialization also plays an important role in the training of deep nets, another important class of machine learning solutions, since again, we have a nonconvex optimization problem.

A closely related concept to reproducibility is that of interpretability. In solutions like ICA, interpretability is direct due to their intimate connection to the linear blind source separation problem, where the assumption is that there are a number of linearly mixed latent variables of interest. This allows direct investigation of the output for reproducibility as in the example in Figure 1, and also suggests that with a good model match, the most reproducible solution is also the most interpretable. In other data-driven solutions like deep nets, interpretability takes an indirect form and generally requires a second-level analysis, e.g., generation of heat maps in multilayered neural networks [20]. In this case, incorporation of available prior information about the data and/or the problem is likely to improve interpretability and provide some model match. Examples include reliable modeling assumptions, e.g., for task NI data, or priors such as sparsity and smoothness. MTD allow one to take such information into account naturally through their connection with simple modeling assumptions, and this can be an option for deep nets as well, and indeed this is a very recent trend, see [28] for a recent overview. With better model match and interpretability, we can gain insights about a disorder, help explain the associated mechanisms, so that one can come up with preventive measures and devise new treatment strategies.

We remind the reader that our definition of reproducibility and replicability follows previous definitions [1,2] and refers to use of the same data and the same algorithm. As we noted, terminology widely varies in literature, with reproducibility often used to actually refer to replicability (with our definition) where the datasets differ, e.g., one might study variability due to use of multi site data [29], or use of different scanners, pulse sequences, and/or scanning sessions [30–32]. While outside the scope of our current review, these are very important considerations as well, and replicability should be always considered along with (computational) reproducibility, which we address.

Our guidance on reproducibility related to machine learning applications to NI data can have im- portant implications in many areas relevant to neurology. For example, the use of NI data, whether it be at the level of networks, regions, or voxels, to provide individual level predictions, will be heavily dependent on the input features computed from that subject. This concern is applicable to any type of NI data, including volumetric studies, brain function, structural/function connectivity, and more. Without accounting for stochastic variation in the input features, one can easily obtain opposite answers along a given decision boundary (e.g., patient versus control, or typical vs atypical). Secondly, as more large-scale open datasets are available, given the scale of computation, preprocessed features (e.g., brain volumes, functional networks) are often downloaded and used by the community. The stochastic variability in the estimation of these features is rarely, if ever, assessed, leading to a potential for large-scale bias across the community as these data are used to train models. And finally, the variation can also impact the brain regions which are highlighted as predictive or relevant for a given test, potentially leading to incorrect pointers towards underlying brain mechanisms. This can be further complicated by the fact that variability can change across the brain, and potential interact with the variable being studied (e.g., the developing or ageing brain), resulting in incomplete or misleading conclusions. On a more optimistic note, there are existing ways to address the above concerns as we have discussed in this review. However, it is important that the community is made aware of, and adopts, solutions that can facilitate replicability and reproducibility in the use of machine learning approaches applied to neuroimaging data.

4. Conclusion

We introduced the important concept of reproducibility in NI data analysis, and noted that it should be the initial step in all analyses, including studies for replicability. We provided examples from widely used toolboxes for neuroimaging, and noted that without guarantees on reproducibility, their use might yield suboptimal solutions, potentially introducing undesirable bias to following post-processing steps. Today, this component is missing from many of these tools, and as more large-scale studies share preprocessed features (such as cortical volumes and connectomes), it is critical to accurately capture the variability related to the generation of these features.

Bullet points.

• (Computational) reproducibility should be a first step in all neuroimaging data analyses including those focusing on replicability.

• As more large-scale open datasets are available, given the scale of computation, preprocessed features are often downloaded and used by the community, most often without assessing their reliability.

• Most of the widely used toolboxes for neuroimaging today do not provide a tool to assess the reproducibility of features obtained through their use.

• Without guarantees on reproducibility of features used in subsequent analyses, their use might yield suboptimal solutions, potentially introducing undesirable bias to following post-processing steps.

• It is important that the community is made aware of, and adopts, solutions that can facilitate replicability and reproducibility in the use of machine learning approaches applied to neuroimaging data.