A Combined Spectroscopic and Theoretical Study on a Ruthenium Complex Featuring a π‐Extended dppz Ligand for Light‐Driven Accumulation of Multiple Reducing Equivalents

Abstract

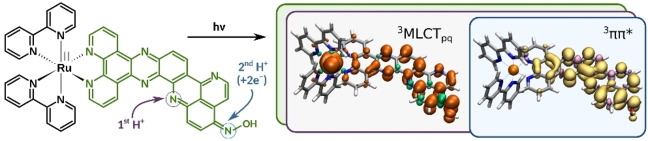
The design of photoactive systems capable of storing and relaying multiple electrons is highly demanded in the field of artificial photosynthesis, where transformations of interest rely on multielectronic redox processes. The photophysical properties of the ruthenium photosensitizer [(bpy)₂Ru(oxim‐dppqp)]²⁺ (Ru), storing two electrons coupled to two protons on the π‐extended oxim‐dppqp ligand under light‐driven conditions, are investigated by means of excitation wavelength‐dependent resonance Raman and transient absorption spectroscopies, in combination with time‐dependent density functional theory; the results are discussed in comparison to the parent [(bpy)₂Ru(dppz)]²⁺ and [(bpy)₂Ru(oxo‐dppqp)]²⁺ complexes. In addition, this study provides in‐depth insights on the impact of protonation or of accumulation of multiple reducing equivalents on the reactive excited states.

The photophysical properties of a charge‐photoaccumulating ruthenium complex are deciphered by mean of excitation wavelength‐dependent resonance Raman, steady‐state and time‐resolved absorption and emission spectroscopies, in combination with time‐dependent density functional theory. This study sheds light on the decisive role played by the pyridoquinolinone subunit of the π‐extended dppz ligand in the photoinduced processes.

Introduction

Multielectron/multiproton transfer reactions are at the core of important biological and chemical processes, such as small molecule activation and energy conversion.[ ¹ , ² ] Optimization of these kinetically arduous reactions, that intrinsically require accumulation of electrons and protons, is a critical challenge for energy‐related applications, typically for the conversion and storage of solar energy under a chemical form such as hydrogen or carbon‐based fuels.[ ³ , ⁴ ] Three fundamental issues arise specifically when driving multielectronic catalytic processes with light: First, the absorption of one photon by a photosensitizer intrinsically yields a monoelectronic charge‐separated state, which means that several successive cycles at the photosensitizer are needed in order to produce the required amount of photogenerated electrons. Second, multielectron/multiproton catalytic processes proceed – the fastest – on the microsecond to millisecond timescale, whereas light‐driven processes are at least three orders of magnitude faster. Therefore, charge recombination is likely to compete with catalysis. A third issue is related to the redox properties of the photoreduced catalytic center that can act as a quencher for the excited photosensitizer, therefore short‐circuiting the process and regenerating the initial state of the system. ^[5]

Nature elegantly circumvents this by decoupling the light‐induced charge separation steps from catalysis thanks to specific cofactors acting as reversible multielectron relays. A typical example is the quinone/hydroquinone couple, such as found in plastoquinone QB, transporting electrons two‐by‐two via proton‐coupled electron transfer (PCET) processes, after two consecutive photon absorption – charge separation events at Photosystem II (PSII). These PCETs are essential to avoid excessive charge build‐up, to stabilize the reduced species (no formation of highly reactive radical species) and so, to prevent charge recombination. Inspired by these naturally occurring processes, various examples of molecular systems performing light‐driven accumulation of multiple reducing equivalents were reported over the last decades.[ ³ , ⁴ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ , ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ] In particular, quinone‐containing units were exploited to perform 2e⁻/2H⁺ storage via sequential electron and proton transfer steps.[ ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ ] Unfortunately, the reducing power of the corresponding hydroquinone derivatives is very low and typically not suitable to activate proton or CO₂ reduction catalysis. We recently contributed to the field with the design of a mononuclear ruthenium tris‐diimine photosensitizer able to reversibly store two electrons coupled to two protons on a pyridoquinolinone (pq) based π‐extended ligand, namely oxo‐dppqp (dipyrido[3,2‐a:2’,3’‐c]pyrido[2’’,3’’‐4,5]quinolino[2,3‐h]phenazin‐15‐one; Figure 1). Thus, we were able to reproduce the mechanism at work with the PSII – plastoquinone couple in the photosynthetic chain.[ ²¹ , ²² ] Furthermore, we have demonstrated that it is possible to use a DFT‐guided approach to design better performing systems, with the oxime derivative, namely [(bpy)₂Ru(oxim‐dppqp)]²⁺ (Ru, bpy=2,2’‐bipyridine), storing electrons at a potential 200 to 300 mV more negative. ^[23] In this contribution, we study key intermediates involved in the 2e⁻/2H⁺ storage in this oxime complex Ru. To this end, the photophysical properties and photoinduced dynamics, supported by quantum chemical simulations, of Ru, together with its singly protonated (RuH⁺ ) and photogenerated doubly reduced, doubly protonated derivatives (RuH₂ ) are thoroughly investigated.

Figure 1.

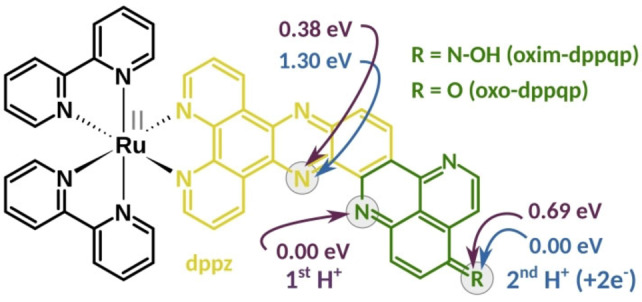
Structure of [(bpy)₂Ru(L)]²⁺ bearing an oxim‐dppqp (R=N−OH, Ru) or oxo‐dppqp (R=O) ligand as L. The dipyridophenazine (dppz) and pyridoquinolinone (pq) moieties are highlighted in yellow and green, respectively. Violet arrows indicate considered protonation sites (grey circles, see also Figure S1) and their thermodynamical preference for Ru as predicted at the B3LYP/def2SVP level of theory. Blue arrows indicate positions of the second protonation site (first protonation occurs at the pq‐moiety) upon two‐electron reduction, relative energies are given accordingly.

Results and Discussion

The ground state absorption spectra of Ru, RuH⁺ and RuH₂ were studied by UV‐vis absorption and time‐dependent density functional theory (TD‐DFT). Computationally, the thermodynamic and photophysical properties of three different protonation isomers of both, RuH⁺ and RuH₂ , were screened using DFT and TD‐DFT, ultimately allowing insights into the most stable redox and protonation isomers in the singlet and triplet manifold (see Supporting Information for Computational Details). To understand the changes in the Franck‐Condon region after protonation or proton‐coupled reduction of Ru, resonance Raman (rR) spectra were also explored. Finally, the sub‐ns photoinduced dynamics were investigated by means of ultrafast transient absorption (fs‐TA) spectroscopy, and their assignment was supported by TD‐DFT.

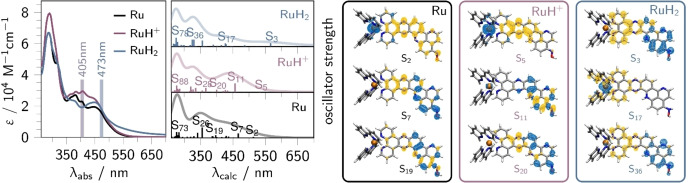
Ground state absorption. The UV‐vis absorption spectrum of Ru (Figure 2) features three major bands, which are unambiguously assigned by quantum chemical simulations. The intense absorption centered at 280 nm and the weaker features with maxima at 370 and 405 nm are associated with ligand‐centered transitions on the terminal bpy ligands, such as to an excitation into S₇₃ at 284 nm (f=0.399), as well as on the dppz (S₂₆, 355 nm, f=0.725) and the pq‐moiety (S₁₉, 397 nm, f=0.194) of the π‐extended dppz ligand (see black lines in Figures 2 and S2; Tables S1 and S2). With respect to the parent complex [(bpy)₂Ru(dppz)]²⁺, the latter transitions involve the pq‐moiety mainly as π‐electron donor. In the visible region, the broad, featureless band from 405 nm to 600 nm stems from metal‐to‐ligand charge‐transfer (MLCT) transitions. According to TD‐DFT, this absorption band is composed of MLCT transitions where electron density is shifted from ruthenium to either the bpy (MLCT_bpy, S₁₃, 429 nm, f=0.137), dppz (MLCT_dppz, S₁₄, 428 nm, f=0.074) or the pq (MLCT_pq, S₂, 513 nm, f=0.069) sphere (Tables S1 and S2).

Figure 2.

Left: UV‐vis absorption spectra of Ru (black), its singly‐protonated (RuH⁺ , violet) and doubly‐reduced doubly‐protonated (RuH₂ , blue) derivatives and their respective TD‐DFT simulated vertical transitions. Right: Selected charge density differences of Ru, RuH⁺ and RuH₂ (most stable isomers for RuH⁺ and RuH₂ , see Table S3 and S10); charge transfer takes place from blue to yellow.

The stepwise addition of trifluoroacetic acid (TFA; 1 to 1000 molar equivalents) to Ru in acetonitrile (20 μM) yields the singly protonated species, RuH⁺ . This is revealed by the presence of an isosbestic point at 340 nm (Figure S3, top). The spectra of Ru and RuH⁺ are obtained from the spectrophotometric absorption data by multivariate curve resolution based on the least squares optimization procedure (MCR‐LS, see Figure S3).[ ²⁴ , ²⁵ ] Thereby, an equilibrium point (inflection point) at a proton concentration (c_eq) of 60 μM is estimated, ultimately allowing insights into the base and acid strength of Ru/RuH⁺ , respectively (pK=−log(c_eq)=4.22).[ ²⁶ , ²⁷ , ²⁸ ] The protonation of Ru was spectroscopically monitored and causes a rise of absorptivity between 400 and 470 nm, while the fine structures of the absorption bands, i.e., the band maxima (positions), are maintained. Furthermore, the equilibrium structure of RuH⁺ was explored by means of DFT, while protonation at three different positions of the oxim‐dppqp ligand, namely at the pyrazine (pz) (0.38 eV), pq (0.00 eV), and N‐oxime moiety (0.69 eV) were considered (see gray circles and violet arrows in Figure 1). To this end, the pq‐protonated species turned out as the most stable protonation isomer (Table S3). The respective electronic transitions – underlying the UV‐vis absorption spectrum of RuH⁺ – were analyzed at the TD‐DFT level of theory (Tables S4–S9) for all three protonation isomers considered: The electronic transitions in RuH⁺ (pq‐protonated, see Tables S6 and S7) can be divided into ¹MLCT transitions (into S₅, S₁₅ and S₁₆) similar to [(bpy)₂Ru(dppz)]²⁺ as well as ¹ILCT transitions (into S₁₁, S₂₀, S₂₆ and S₂₈) and a local ππ* excitation (into S₂₈) on the oxim‐dppqp ligand (Figure 2 and Table S7). As observed UV‐vis experiments, the mean molar absorptivity of the pq to phz ¹ILCT transition, centered at 405 nm, increases upon protonation. This is supported by TD‐DFT, predicting a circa two‐fold higher molar absorptivity of S₁₁ (2.71 eV, f=0.615) in RuH⁺ compared to S₇ (2.66 eV, f=0.317) in Ru (Figure 2, Tables S1 and S6). Contrary, the oscillator strength of the dppz to pq ILCT transitions is higher in Ru (S₂₉, 3.64 eV, f=0.360) compared to RuH⁺ (S₂₆, 3.38 eV, f=0.295). This is further reflected in the absence of the high‐energy pq to dppz ILCT absorption shoulder at 340 nm as predicted by TD‐DFT when comparing RuH⁺ and Ru (S₂₆, 3.49 eV, f=0.725). This can be related to the weakening of the π‐donor strength of the pq‐moiety in RuH⁺ compared to the non‐protonated parent species.

The doubly‐reduced doubly‐protonated derivative RuH₂ was prepared by photolysis of Ru, i.e. continuous illumination in the presence of triethylamine (TEA) as sacrificial agent (photoreaction yield of circa 24 %), according to our previous studies (cf. Figure S5).[ ²¹ , ²² , ²³ ] Likewise, as performed for Ru⁺ and based on the most stable singly‐protonated species (pq), the equilibrium structure of RuH₂ was investigated by means of DFT. Therefore, three doubly‐protonated species were considering a doubly‐protonated and doubly‐reduced species at the i) pq and pz (1.30 eV), ii) pq and N‐oxime (0.00 eV), and iii) pz and N‐oxime moiety (0.90 eV). As initially proposed, ^[23] the most stable doubly‐reduced and doubly‐protonated structure, i.e., a formal hydrogenated species, is the aminophenylhydroxylamine derivative (Figure 1 and Table S10). A similar structure, namely an aminophenol species, was previously experimentally supported for the photogenerated doubly‐reduced doubly‐protonated derivative of [(bpy)₂Ru(oxo‐dppqp)]²⁺. ^[22]

Upon light‐driven reduction and subsequent protonation (protons are released upon degradation of TEA ^.+ ) of the π‐extended ligand in Ru, four major absorption changes occur (Figure 2), the final spectrum being very similar to the one obtained for the structurally closely related [(bpy)₂Ru(oxo‐dppqp)]²⁺ (Figure S6): a) the dppz‐centered ππ* absorption (between 350 and 400 nm) decreases, b) the MLCT_pq band at 405 nm vanishes, c) a structured MLCT band with maximum at 458 nm is formed, and d) new absorption features beyond 500 nm appear.

In RuH₂ , the pq‐moiety acts as a stronger π‐electron donor than in Ru. This is in agreement with TD‐DFT simulations and reflected in the absence of the pq‐centered MLCT absorption band at 405 nm and a red‐shift of the pq‐to‐phz ILCT transitions (e.g., S₃ at 2.19 eV vs. S₇ at 2.66 eV in Ru, see CDDs in Figure 2), causing the appearance of new absorption features between 500 and 700 nm. Those features are blue‐shifted (by 0.23 eV) compared to the low‐lying absorption maximum of the doubly‐reduced form of Ru (655 nm). ^[23] As the excess charge of the reduced complex is localized on the pq‐moiety[ ²¹ , ²³ ] this blue‐shift indicates a charge‐compensation upon addition of protons, causing a stabilization of the pq‐centered molecular orbitals. This additionally supports the two‐fold reduction and protonation on the pq‐moiety.

The decrease of the dppz‐associated ππ* features can be explained by a red‐shift of the underlying transitions (from 383 to 387 nm, see Figure S6). The presence of a similar peak observed in the difference spectrum taken between [(bpy)₂Ru(LH₂)]²⁺‐ and [(bpy)₂Ru(L)]²⁺‐type complexes bearing a dppz‐derived ligand as L,[ ¹⁰ , ¹⁷ , ²⁹ , ³⁰ ] hints towards intramolecular hydrogen bonding between the protonated pq and the neighbouring nitrogen atom of the pyrazine ring.

Upon two‐fold reduction and protonation a MLCT band with maximum at circa 458 nm (see difference spectrum in Figure S6) – similar to the absorption features of for example [Ru(bpy)₃]²⁺ or [(bpy)₂Ru(phen)]²⁺ – is formed.[ ³¹ , ³² ] This indicates, that additional features, i.e., that stem from ³MLCT_pq states, vanish. This is supported by TD‐DFT allowing an unambiguous assignment of the 458 nm absorption band to ¹MLCT_bpy transitions (e.g., S₁₆, see Table S11).[ ¹⁰ , ²² , ²³ , ²⁹ , ³⁰ , ³³ ] The higher molar absorptivity of RuH₂ (and [(bpy)₂Ru(oxo‐dppqpH₂ )]²⁺) compared to [(bpy)₂Ru(dppzH₂)]^2+[29] presumably stems from additional MLCT_phen and ILCT transitions (S₁₇ and S₂₂, see Table S12) on the π‐extended dppz‐ligand as predicted by TD‐DFT.

Resonance Raman. To further explore the character of the Franck‐Condon point of absorption, resonance Raman (rR) spectra were recorded upon excitation at 405 and 473 nm. To identify signatures of the pq‐moiety, the rR spectra are compared to the parent complex [(bpy)₂Ru(dppz)]²⁺ (Figure S7).

Light absorption of Ru at both 405 and 473 nm promotes the complex into a mixture of MLCT_bpy, MLCT_phen and MLCT_pq as well as ILCT and pq‐centered ππ* states. The dominant vibrational modes in the rR spectrum of Ru collected at both excitation wavelengths (see black curves in Figure 3) are associated with the terminal bpy ligands (1031, 1134, 1284, 1320, 1484, 1540 and 1605 cm⁻¹), the dppz (1184, 1410, 1445, 1470, 1570, 1596 and 1625 cm^‐1) and the pq‐moiety (1410, 1560 and 1582 cm⁻¹), on the basis of the comparison with the parent complexes [(bpy)₂Ru(dppz)]^2+[34–36] and [(bpy)₂Ru(oxo‐dppqp)]^2+[21] (see Figure S7). Noteworthy, photoexcitation in all three complexes yields the population of similar excited states, namely ¹MLCT_bpy and ¹MLCT_dppz states. The appearance of additional pq‐type modes at 1410 and 1560 cm⁻¹ shows that ¹ILCT and ¹MLCT_pq states also contribute to the Franck‐Condon region of Ru. At 403 nm excitation, the vibrations of the pq moiety at 1410, 1560 and 1585 cm⁻¹ and dppz‐type modes at 1445, 1447, 1570, 1596 and 1625 cm⁻¹ dominate the rR spectrum. This supports the oxim‐dppqp centered nature of the electronic transitions arising from the ILCT (S₇) and ππ* (S₁₉ and S₂₂) transitions (see Table S2). Overall, the weight of pq‐type modes increases upon shifting the excitation wavelength from 473 to 405 nm, indicating that the ¹ILCT and ¹ππ* states are blue‐shifted with respect to the ¹MLCT_bpy and ¹MLCT_dppz states – as supported by TD‐DFT (see Table S1). This agrees with previous findings on [(bpy)₂Ru(oxo‐dppqp)]²⁺, ^[21] underlining that replacing the carbonyl unit by the stronger electron‐donating oxime group does not alter the composition of the initially excited states upon 405 and 473 nm excitation, although the respective ground state absorption spectra differ significantly from each other (Figure S6).

Figure 3.

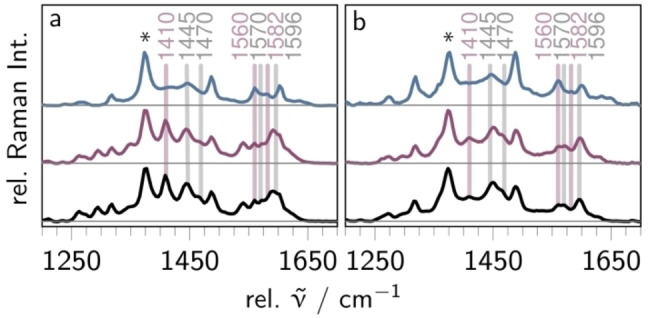
Resonance Raman spectra of Ru (bottom, black), RuH⁺ (middle, violet), and RuH₂ (top, blue) in acetonitrile upon 405 nm (a, 4 mW) and 473 nm (b, 5 mW) excitation. The spectra are normalized to the solvent band at 1373 cm⁻¹ (asterisk).

The rR spectra of RuH⁺ excited at 405 and 473 nm (violet spectra in Figure 3a and b, respectively) closely resemble the respective spectra of Ru, indicating no significant alterations in the nature and composition of the initially excited states upon single‐protonation. This is further supporting that protonation only affects the oscillator strength of the ¹ILCT transitions, while the relative positions of the absorption features are maintained.

The rR spectrum of RuH₂ collected at 473 nm excitation (blue line in Figure 3b) resembles the respective spectrum of Ru. However, differences are apparent when comparing the rR spectra of RuH₂ and Ru upon excitation at 405 nm (see Figure 3a): Upon two‐fold reduction and protonation of Ru (forming RuH₂ ), the dppz modes at 1445, 1470, 1570 and 1596 cm⁻¹ as well as the pq mode at 1410 cm⁻¹ decrease. Instead, the pq associated modes at 1560, 1582 cm⁻¹ remain basically unaffected. Additionally, new signals between 1605 and 1650 cm⁻¹ arise, which cannot be assigned to either dppz or bpy. Thus, those modes are ascribed to the hydrogenated pq‐moiety. Noteworthy, the intensity of the bpy‐centered mode at 1540 cm⁻¹ vanishes upon two‐fold proton‐coupled reduction, while the bands at 1484 and 1605 cm⁻¹ are maintained, indicating lower contribution of ¹MLCT_bpy states to the formation of the initially excited states at 405 nm excitation. In direct comparison to Ru, the weakening primarily of the dppz‐type modes can be explained by predominant ¹ILCT (S₂₂) as well as ¹MLCT_bpy and ¹MLCT_phen (S₁₇ and S₂₂) absorption at this wavelength. This further supports two‐fold reduction and protonation at the pq‐moiety since a doubly‐reduced and doubly‐protonated dppz unit is assumed to cause a Franck‐Condon region similar to [(bpy)₂Ru(phen)]²⁺.[ ²⁹ , ³¹ , ³² , ³³ , ³⁷ ]

Emission properties. The emission of Ru, RuH⁺ , and RuH₂ was studied by means of steady‐state (see Figure S8) and time‐resolved emission spectroscopy (ns‐Em, see Figure 4f and S9) upon excitation at 420 nm in acetonitrile. The steady‐state emission spectra of Ru and RuH⁺ show an emission band maximum at around 650 nm (see black and violet lines in Figure S8) and closely resemble the spectrum of the parent complex [(bpy)₂Ru(dppz)]²⁺ (see black/violet vs. green line in Figure S8 and S9). This indicates, that the emission of both complexes stems from a proximal ³MLCT state (³MLCT_prox: excess electron density on the terminal bpy‐ligands and the phen moiety of the oxim‐dppqp/oxim‐dppqpH⁺ ligand) as observed also for [(bpy)₂Ru(dppz)]²⁺.[ ³⁸ , ³⁹ , ⁴⁰ ] In RuH₂ the emission maximum is blue‐shifted (by 0.07 eV) and appears at 625 nm (see blue lines in Figure S8). We associate this blue shift with an increased electron density on the oxim‐dppqpH₂ compared to the oxim‐dppqp/oxim‐dppqpH⁺ ligand, which leads to a destabilization of the emissive ³MLCT_prox state. The emission quantum yields (ϕ_em) of the three complexes follows the order Ru (1.8 %)>RuH⁺ ≈RuH₂ (0.1 %), indicating the existence of rapid deactivation channels in the MLCT excited state manifold of RuH⁺ and RuH₂ . This is reflected in the emission lifetime (τ_em) of the complexes, which is 180 ns for Ru but lower than 10 ns for RuH⁺ and RuH₂ (see symbols in Figure 9).

Figure 4.

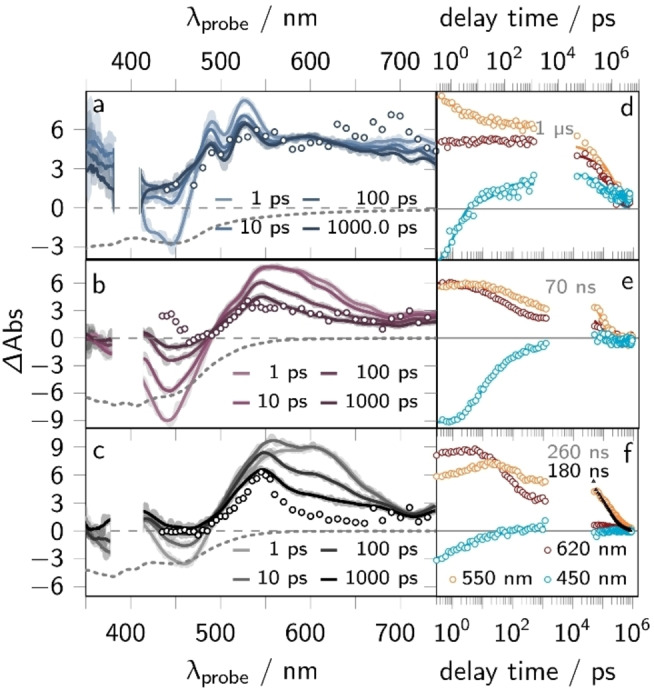
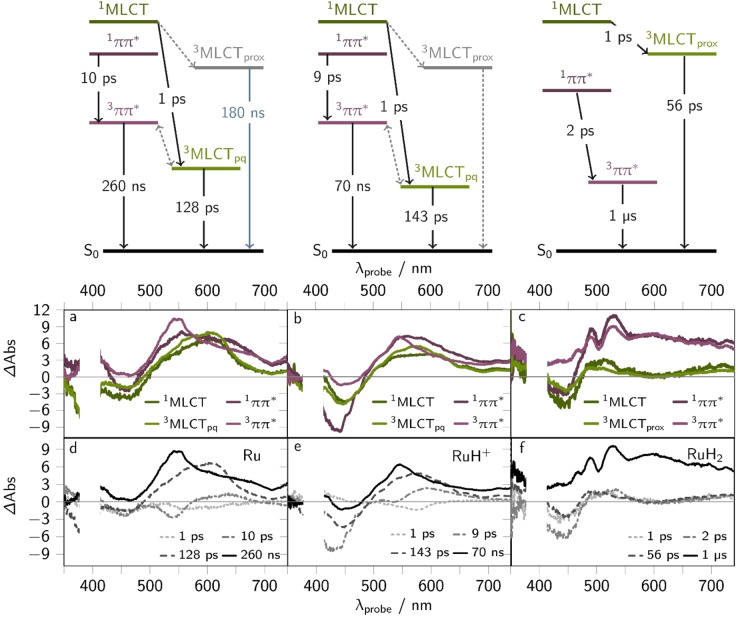
fs‐ and ns‐transient absorption (TA) data, i.e., transient spectra at selected delay times and kinetic traces at certain probe wavelengths (450, 500 and 620 nm), of Ru (a and d), RuH⁺ (b and e) and RuH₂ (c and f) in acetonitrile. The fs‐TA spectra are shown as solid lines at selected delay times (a–c) and the spectrum of the long‐lived state (see gray numbers in panel d–f, i.e., the lifetime of the ³ππ* states) is represented by symbols. The black symbols in panel f show the emission kinetics (ns‐Em) of Ru (summed kinetics between 500 and 800 nm). The respective emission lifetime is given in black. The fs‐ and ns‐TA (and ns‐Em) data was collected upon 400 nm (0.4 mW) or 420 nm (0.5 mW) excitation, respectively (excitation density of 5 %).

τ_em and ϕ_em of Ru coincide with the respective observables of the parent complex [(bpy)₂Ru(dppz)]²⁺ (τ_em=180 ns, ϕ_em=1.2 %) when measured in acetonitrile (cf. dashed, green line in Figure S9).[ ³⁵ , ³⁸ , ³⁹ , ⁴⁰ ] This further supports the notion that the emission stems from the ³MLCT_prox sphere. The lower τ_em and ϕ_em‐values of RuH⁺ and RuH₂ can likely be related to the occurrence of high‐frequency N‐H stretching vibrations, which provide efficient and fast non‐radiative decay channels (that do not exist for Ru).

Character of the long‐lived excited state. To complement the ns‐Em findings, the long‐lived excited state nature of Ru, RuH⁺ , and RuH₂ was investigated by means of ns‐transient absorption (ns‐TA, see Figure 4) spectroscopy upon excitation at 420 nm (cf. symbols in Figure 4a ‐ c). The ns‐TA spectra of Ru show comparably strong excited state absorption (ESA) between 490 and 600 nm that mono‐exponentially decays with 260 ns (see Figure S4f). That the signals are zero in the range of the ground state absorption, i.e., between 400 and 470 nm, can be attributed to relatively strong ESA features, which cancel the ground state bleaching (GSB) contributions. This is typically associated with the population of ³ππ* states for Ru(II) complexes bearing linear expanded dppz ligands.[ ²¹ , ⁴¹ , ⁴² , ⁴³ , ⁴⁴ ] In those states, the excess electron density is localized on the π‐extended chromophore, i.e., the pq‐moiety in case of Ru. Consequently, this ³ππ* shows MLCT absorption features (ESA between 400 and 470 nm) energetically close to them of the ground state and additional ππ* absorption (ESA at 550 nm). In connection with the emission results, we assume that the non‐emissive ³ππ* excited states ^[21] dominate the ns‐TA spectra[ ²¹ , ⁴³ , ⁴⁵ ] and have a longer lifetime than the emissive ³MLCT_prox states. Therefore, the typical ³MLCT_prox absorption features, i.e., GSB between 400 and 500 nm accompanied by weak and broad ESA between 500 and 650 nm, are absent in the ns‐TA spectra. This is reflected in the mono‐exponential decay of the TA signals, which can be associated with the non‐radiative deactivation of the ³ππ* excited states. Noteworthy, the ³ππ* lifetime of Ru is circa 30 times higher compared to the structurally related complex [(bpy)₂Ru(oxo‐dppqp)]²⁺ (9 ns). ^[21] This can be tentatively assigned to a lower energy difference of the ³MLCT_pq and ³ππ* states in Ru. Consequently, the deactivation of ³ππ* via ³MLCT_pq states is less exergonic in Ru compared to [(bpy)₂Ru(oxo‐dppqp)]²⁺, ^[21] ultimately yielding the longer ³ππ* excited state lifetime according to Marcus theory. The ns‐TA spectra of RuH⁺ and RuH₂ also indicate the population of a long‐lived, non‐emissive ³ππ* state, which is manifested in the comparably strong ESA between 490 and 750 nm, as observed for Ru (see symbols in Figure 4b and c). The ns‐TA signals mono‐exponentially decay with a characteristic rate of 70 ns (RuH⁺ ) and 1 μs (RuH₂ ), respectively (see Figure S4e and f).

The nature of the long‐lived ³ππ* state for RuH₂ is supported by TD‐DFT (Table S10). The simulated TA spectrum of that long‐lived state obtained from the difference between the absorption spectra of the equilibrated, lowest lying ³ππ* excited state and the singlet ground state resembles the essential features of the long‐lived spectrum (see Figure S10). According to those TD‐DFT results, the structured ESA with maxima at 480, 525 and 610 nm can be ascribed to ππ* (e.g., T₈ and T₁₉) transitions and MLCT states, where electron density is shifted from the central Ru(II) ion towards the proximal phen‐moiety (e.g., T₂₆ and T₄₁, see Table S11). This further supports that the ³ππ* absorption features dominate the TA signals, like in RuH⁺ and Ru, which agrees with previous findings on the structurally closely related complex [(bpy)₂Ru(oxo‐dppqp)]²⁺. ^[21] We conclude that the ³ππ* states are non‐emissive regardless of the oxidation and protonation state, i.e., for Ru, RuH⁺ , and RuH₂ . In agreement with studies on the structurally closely related complex [(bpy)₂Ru(oxo‐dppqp)]²⁺, we suggest this to be an inherent feature of the π‐extended ligand oxim‐dppqp.[ ²¹ , ²³ ]

Photoinduced excited state dynamics. The photoinduced processes in Ru, RuH⁺ and RuH₂ were investigated by means of ultrafast transient absorption (fs‐TA) spectroscopy. The experiments were conducted upon 400 nm excitation of the complexes in acetonitrile.

Photoinduced dynamics of Ru . The spectral changes observed for Ru resemble the ones previously reported for [(bpy)₂Ru(oxo‐dppqp)]²⁺. ^[21] The initial TA spectrum of Ru, collected at a delay time of 0.3 ps, shows a ground state bleach (GSB) between 400 and 500 nm and a broad excited state absorption (ESA) band with a maximum at 610 nm and a well‐resolved shoulder at around 550 nm (see Figure 4c). Within the first 10 ps the ESA increases and sharpens forming a band maximum at 550 nm and a shoulder at 600 nm (Figures 4c). The latter feature vanishes within the first 200 ps, yielding a long‐lived, broad ESA band with a distinct maximum at 550 nm. These TA signals decay on a timescale beyond the experimentally accessible window of 2 ns, i.e., 260 ns (as obtained from ns‐TA experiments, cf. Figure 4f). Global (see Figure S11) and target analysis (cf. Jablonski diagrams in Figure 5 and Supporting Information section 4.2) of the sub‐ns TA data reveals three characteristic rate constants, namely k₁=(1 ps)⁻¹, k₂=(10 ps)⁻¹ and k₃=(128 ps)⁻¹. The spectral changes are associated with the population of two excited state branches in the ππ* and MLCT manifold, i.e., ¹ππ*, ³ππ*, ¹MLCT, and ³MLCT_pq states (see Figure 5). The respective species associated spectra (SAS) and derived decay associated spectra (DAS) are shown in Figure 5a and d.

Figure 5.

Species associated spectra (SAS, a–c) and their corresponding reconstructed decay associated spectra (DAS, d–f) of the fs‐TA data of Ru (left), RuH⁺ (middle), and RuH₂ upon 400 nm excitation (0.4 mW) in acetonitrile. The employed target models are shown on top. States (solid lines) and processes (dotted lines) that are not included in the target model are shown in grey in the Jablonski diagrams: Since the ππ* excited states dominate the TA signals the proximal MLCT states (MLCT_prox: MLCT_bpy and MLCT_phen), which typically show strong GSB between 400 and 450 nm and weak ESA ranging from 500 to 750 nm, were not included in the target models (cf. grey states and dashed lines in the Jablonski schemes). The DAS were qualitatively constructed from the SAS by: DAS(k₁)=SAS(¹MLCT) – SAS(³MLCT), DAS(k₂)=¹ππ*– ³ππ*, DAS(k₃)=SAS(³MLCT), DAS(k₄)=SAS(³ππ). The DAS obtained by fitting the data within a parallel model are shown in Figure S11.

The characteristic rate constants k₁ and k₃ correspond to processes in the MLCT manifold: The first rate constant, k₁, describes inter‐system crossing (ISC) and vibrational cooling[ ⁴⁶ , ⁴⁷ , ⁴⁸ , ⁴⁹ , ⁵⁰ , ⁵¹ ] within the MLCT sphere, populating thermally equilibrated ³MLCT states. This is reflected in the build‐up of signals between 400 and 500 nm as well as ranging from 520 to 650 nm (cf. SAS(¹MLCT) and SAS(³MLCT), i.e., the green lines in Figure 5a). In comparison with the TA data of [(bpy)₂Ru(dppz)]²⁺, the feature at 620 nm can be associated with excess electron density on the pq‐moiety, as previously observed in spectroelectrochemical experiments.[ ²¹ , ²³ ] This hints towards the population of pq‐centered states, namely ³MLCT_pq states. The ESA maximum of Ru is blue shifted (by 0.15 eV) with respect to [(bpy)₂Ru(oxo‐dppqp)]²⁺ (660 nm). However, such a blue shift (by 0.05 eV) is also apparent in the steady state absorption spectra of the singly‐reduced species of Ru (635 nm), [(bpy)₂Ru(oxo‐dppqp)]^2+[21,22] (653 nm), supporting that the 620 nm feature can be associated with MLCT_pq states. The build‐up of signals between 400 and 500 nm, i.e., cancellation of GSB can be associated with the formation of ³ππ* excited states. Since the ππ* excited states absorbs in the same energy range as Ru in the ground state, the population of those states causes an apparent reduction of GSB contributions to the TA spectra.[ ²¹ , ⁴¹ , ⁴² , ⁴³ , ⁵² , ⁵³ , ⁵⁴ , ⁵⁵ ] These contributions are observed even when the kinetics in the MLCT and ππ* branches are considered independently. We attribute this to the fact that the ππ* excited states dominate the TA signals at each measurement time (0.3 ‐ 2000 ps).

With the characteristic time constant, k₃, the ³MLCT_pq states non‐radiatively decay back to the ground state, ^[21] which is manifested in the decay of signals between 500 and 650 nm, centered at 620 nm (cf. bright green line in Figure 5a). ^[23] This is further supported by TD‐DFT simulations on the thermally equilibrated lowest‐lying ³MLCT_pq state (see spin density in Table S2). This state absorbs between 450 and 750 nm mainly due to ³ππ* and ligand‐to‐metal charge‐transfer (³LMCT) states (e.g., T₁₄ and T₃₄, see Figure S10 and Table S2). The respective TA spectrum of that ³MLCT_pq state, constructed from the absorption features of the ³MLCT_pq and the ground state (S₀) resembles the ³MLCT_pq species associated spectrum (see Figure S10), i.e., shows the spectral shape as typically observed for ³MLCT states of Ru‐polypyridyl type complexes.[ ²¹ , ³¹ , ⁴⁶ , ⁴⁹ , ⁵⁰ ]

The sub‐ns spectral changes in the ππ* excited state branch are described by the characteristic time‐constant k₂. We associate this time‐constant with ISC, vibrational cooling and intra‐ligand charge transfer in the ¹ππ* manifold, populating ³ππ* states, with excess electron density delocalized on the pq‐moiety (cf. gray dashdotted line in Figure 5d). This is reflected in DAS(k₂), which describes the build‐up of signals between 400 and 570 nm and the decay of signals ranging from 570 to 650 nm (see dash dotted line in Figure 5d and Figure S11d). The remaining signals stem from long‐lived ³ππ* (τ_TA=260 ns) and ³MLCT_prox states (τ_em=180 ns), whereas the signals are dominated by the ³ππ* states (cf. bright violet line in Figure 5a).

Photoinduced dynamics of RuH ⁺ . As described above for Ru, the sub‐ns processes of RuH⁺ reflect the formation of a long‐lived ³ππ* state. The transient absorption spectra of RuH⁺ resemble those of Ru (cf. Figure 4b vs. 4c). In contrast to Ru, the fs‐TA spectra of RuH⁺ do not reveal a pronounced shoulder at 620 nm at any delay time. Instead, the initial TA spectrum at 0.3 ps shows comparably strong GSB contributions between 400 and 500 nm. Within the first 100 ps this GSB contributions vanish, and the ESA sharpens at around 545 nm, ultimately forming the long‐lived species, with a TA spectrum that resembles the one of Ru.

The spectral changes can be quantitatively (see target model in Supporting Information section 4.2 and Jablonski diagram in Figure 5) described by two characteristic rate constants in the MLCT excited state branch, namely k₁=(1 ps)⁻¹ and k₃=(143 ps)⁻¹ as well as by a characteristic rate constant in the ππ* excited state branch, namely k₂=(9 ps)⁻¹.

In the MLCT manifold, the first process, k₁, describes the build‐up of an ESA between 500 and 600 nm. As the SAS of the ¹MLCT and ³MLCT state (cf. green lines in Figure 5b) overlap between 400 and 500 nm (DAS(k₁) is zero in that region), i.e., the ground state MLCT absorption region, k₁ can be assigned to relaxation of the photoexcited ¹MLCT to energetically lower triplet states via ISC, vibrational cooling and inter‐ligand hopping.[ ⁴⁶ , ⁴⁷ , ⁴⁸ , ⁴⁹ ] With k₃ the ³MLCT_pq states non‐radiatively decay back to the ground state, which is consistent with the findings for Ru. This is manifested in the decay of signals centered at around 600 nm and partial GSB recovery. This is supported by TD‐DFT calculations, predicting that the ³MLCT_pq state of RuH⁺ (see spin density of the pq‐protonated form in Table S3) mainly absorbs due to ³LMCT (e.g., T₃₁, T₃₄, and T₄₆) and ³ππ* transitions (e.g., T₁₆, T₂₆, and T₃₀) between 400 and 800 nm (see Tables S6 and S7). Noteworthy, the ESA of the ³MLCT_pq state in RuH⁺ (circa 590 nm) is blue shifted compared to that of Ru (620 nm). This can be explained by the stabilization of the pq‐centered states upon protonation at that moiety. That the GSB features are more pronounced in RuH⁺ compared to Ru, is presumably due to the higher oscillator strength of the respective ground state absorption features centered at around 450 nm (see Figure 2), i.e., S₁₁ (f=0.615, 457 nm) in RuH⁺ compared to S₇ (f=0.317, 467 nm) in Ru (see Tables S1 and S6). Since the ππ* excited states dominate the TA signals (ESA maximum at 546 nm and the comparably weak GSB features) the population and radiative decay of ³MLCT_prox states (see emission properties) cannot be modelled reasonably (see dashed lines in the Jablonski diagrams in Figure S11).

Consistent with [(bpy)₂Ru(oxo‐dppqp)]²⁺, the ³MLCT_pq excited state lifetime of Ru and RuH⁺ is significantly shorter compared to commonly studied Ru‐trisbipyridyl complexes like [Ru(bpy)₃]²⁺ or [(bpy)₂Ru(dppz)]²⁺.[ ³⁸ , ³⁹ , ⁴⁰ , ⁴⁹ , ⁵⁶ ] This can be explained by the energy gap between the ground and excited ³MLCT_pq state.[ ²¹ , ⁵⁷ , ⁵⁸ ] These (optical) gaps were determined by (TD)‐DFT simulations, i.e., the minimum energy of the ³MLCT_pq state and the respective energy in the singlet manifold, which is 1.27 eV (Ru) and 1.06 eV (RuH⁺ , see Table S3), respectively. Those gaps are smaller with respect to [(bpy)₂Ru(dppz)]²⁺ (1.59 eV). This is consistent with the gap between the highest‐occupied and lowest‐unoccupied molecular orbital (HOMO‐LUMO gap) obtained from electrochemical measurements, where ΔE_1/2 is 2.00 V for Ru (E_ox=0.86 V vs. Fc^0/+ and E_red=−1.11 V vs. Fc^0/+) and 1.47 V for RuH⁺ (E_red=−0.61 V vs. Fc^0/+), whereas the half‐wave potential of [Ru(bpy)₃]²⁺ is 2.55 V in dry acetonitrile.[ ²¹ , ²² , ²³ ]

The sub‐ns process observed in the ππ* excited state branch, i.e., k₂, is associated with ISC, vibrational cooling and intra‐ligand charge‐transfer in the ¹ππ* manifold, forming the long‐lived ³ππ* state. This is reflected in the build‐up of signals between 400 and 500 nm, i.e., the cancellation of GSB accompanied by the decay of signals at around 600 nm (associated with the ¹ππ* state, see violet lines in Figure 5b).

Photoinduced dynamics of RuH ₂ . Like for Ru and RuH⁺ , the fs‐TA spectra of RuH₂ are dominated by the absorption of a long‐lived (1 μs) oxim‐dppqp centered ³ππ* state. The initial TA spectrum (0.3 ps) reveals GSB contributions between 400 and 460 nm that are overlayed by a broad, structured ESA band at probe wavelengths >460 nm with distinct maxima at 480 and 525 nm (see Figure 4a). The ESA maxima are blue‐shifted compared to Ru and RuH⁺ due to two‐fold reduction and two‐fold protonation of the pq‐moiety, causing a loss of electron delocalization on that unit. Within the first 100 ps, the ESA in the region of the ground state absorption, i.e., between 400 and 500 nm, increases. This is associated with the population of excited ³ππ* states (see Figure 5).[ ²¹ , ⁴² , ⁴³ ] Global analysis of the sub‐ns TA data within the same model as proposed for Ru and RuH⁺ (see Jablonski diagram in Figure 5), reveals the following characteristic rate constants in the MLCT excited state branch: k₁=(1 ps)⁻¹ and k₃=(56 ps)⁻¹, as well as k₂=(2 ps)⁻¹ in the ππ* excited state branch.

We associate the first process in the MLCT manifold, i.e., k₁, with ISC, vibrational cooling and inter‐ligand hopping populating a ³MLCT state with excess electron density on the proximal ligand sphere (³MLCT_prox). This is manifested in the build‐up of signals between 400 and 480 nm (cancellation of GSB) and the decay of signals centered at 520 nm. The latter ESA feature is typically associated with ³MLCT states with excess electron density on the phenanthroline sphere of the dppz ligand.[ ³⁵ , ⁴³ , ⁴⁴ , ⁴⁸ , ⁵⁰ ] The second process in the MLCT excited state branch (associated with k₃) is ascribed to the non‐radiative decay of the ³MLCT_prox states back to the ground state. This is reflected in the SAS of the ³MLCT state (cf. bright green line in Figure 5c), which exhibits the typical MLCT‐like properties, namely comparably strong GSB contributions between 400 and 500 nm accompanied by comparably weak ESA between 500 and 550 nm.[ ⁴⁹ , ⁵⁰ ]

We attribute k₂ with ISC, vibrational cooling, and intra‐ligand charge transfer in the ππ* excited state branch, populating the long‐lived ³ππ* state (see bright violet line in Figure 5c). This is reflected in the rise of ESA at around 490 and 520 nm, which we associate with ππ* ESA features, where electron density is shifted form the phz‐ to the pq‐moiety of the oxim‐dppqp ligand (T₈, see Table S12).

Conclusion

In this work, the photophysical properties of the charge‐photoaccumulating complex [(bpy)₂Ru(oxim‐dppqp)]²⁺ (Ru) were investigated in relation to those of its singly protonated (RuH⁺ ) and doubly reduced doubly protonated (RuH₂ ) derivatives, as well as the parent [(bpy)₂Ru(dppz)]²⁺ and [(bpy)₂Ru(oxo‐dppqp)]²⁺ complexes. In the ground state, the electronic properties of the pyridoquinolinone (pq) unit of the π‐extended dppz ligand is altered either by the protonation or the redox state of the oxim‐dppqp ligand: while protonation weakens its π‐electron donor character, proton‐coupled reduction strengthens it. Moreover, this study highlights the decisive role played by the pq‐moiety in the photochemistry of the three investigated complexes, controlling not only the composition of the initially excited states but also the photoinduced dynamics. Transient absorption as well as time‐resolved and steady‐state emission studies reveal that the photoinduced dynamics of Ru, RuH⁺ , and RuH₂ occurs in two excited state branches, namely in the ππ* and MLCT manifold. While emission stems from ³MLCT states, the pq‐moiety of Ru gives rise to low‐lying, long‐lived (260 ns) and non‐emissive ³ππ* states. The latter states dominate the signals on the sub‐ns up to sub‐μs timescale. The availability of such low‐lying, long‐lived states is maintained upon protonation at the pq‐moiety (RuH⁺ , 70 ns) or proton‐coupled reduction (two‐fold) forming the aminophenylhydroxylamine derivative (RuH₂ , 1 μs). Hence, it is assumed that these ³ππ* states are reductively quenched by sacrificial electron donors such as TEA during the charge photoaccumulation process. Future work will focus on the implementation of pump‐pump‐probe spectroscopic experiments ^[15] performed in the presence of the sacrificial electron donor and at different timescales to address the two successive photon absorption steps that are required. This will provide a comprehensive mechanistic picture of the light‐driven charge accumulation process towards future photocatalytic applications.

Experimental Section

Complex [(bpy)₂Ru(oxim‐dppqp)](PF₆)₂ was prepared according to our previously reported procedure. ^[23] UV‐vis absorption spectra were recorded on a Jasco V780 UV‐vis spectrophotometer. The ground state protonation of Ru (forming RuH⁺ ) was monitored by UV‐vis spectroscopy upon stepwise addition of trifluoroacetic acid (20 mM stock solution) to a solution of Ru in acetonitrile (200 μM). Similarly, the proton coupled photoreduction of Ru (forming RuH₂ ) upon LED‐illumination at 455 nm in the presence of triethylamine (TEA, 1 M) was monitored by the UV‐vis‐spectroscopic changes. The steady‐state emission properties were studied in acetonitrile (1 cm cuvettes) using a FLS980 (edinburgh instruments) emission spectrometer. The emission quantum yields were determined with respect to the homoleptic reference complex [Ru(bpy)₃]²⁺ (ϕ_em=9.5 %). ^[59]

The resonance Raman (rR) spectra were collected in a 180°‐scattering arrangement, using a 1 mm quartz cuvette. As excitation light sources a 405 nm diode laser (TopMode‐405‐HP, Toptica) and a 473 nm diode pumped solid‐state laser (HB‐Laser) were used. After passing through a clean‐up filter (Semrock) the laser beam is focussed by an objective onto the sample. To prevent the detection of Rayleigh‐scattered light in transmission mode a long‐pass filter (>405 and >473 nm, Semrock) is installed before the detector, which is a spectrometer (entrance slit 0.05 mm, focal length of 7.5 cm, grating with 1200 liner per 1 mm, IsoPlane 160, Princeton Instruments) connected with a thermoelectrically cooled camera (Pixis eXcelon, Princeton Instruments).

The ultrafast transient absorption (fs‐TA) spectra were collected upon 400 nm excitation. The setup is based on a titanium‐doped sapphire laser (Legend Elite, Coherent Inc.) yielding pulses centered at 795 nm (pulse‐duration: 100 fs, repetition rate: 1 kHz). The 400 nm pump pulses were generated by second harmonic generation (BBO crystal). Those pulses were focused on the sample (1 mm cuvette) with an average intensity of 0.4 mW (gaussian beam profile of 400×400 μm). At the sample position the pump‐ and probe pulses are temporally and spatially overlapped (relative magic angle polarization). As probe pulses white‐light was used, which was generated from the 795 nm fundamental laser pulses by focussing it on a rotating CaF₂ plate. Those probe pulses were temporally delayed with respect to the pump pulses by means of an optical delay stage (maximum delay of 2 ns). The probe pulses are split into two trains, namely a reference and probe path. Both pulses are focused on a diode array, directly (reference) or after the pulses were focused on the sample (probe). The probe pulses are recollimated and spectrally dispersed by a prism and detected by a diode array (Pascher Instruments AB, readout frequency of 1 kHz). The spectra were analysed by employing a parallel model (yielding decay associated spectra, DAS) and target model (see Supporting Information section 3.2 and Figure S11, yielding species associated spectra SAS) using the kimopack software.

The sub‐μs time‐resolved emission (ns‐Em) and transient absorption (ns‐TA) spectra were collected at a pump wavelength of 420 nm, The excitation light was provided by a Nd:YAG Laser (Continuum Surelite, 5 ns pulses with a repetition rate of 10 Hz) using an optic parametric oscillator (Continuum Surelite). The kinetics were studied using probe‐light provided by a 75 W xenon arc lamp, which was focused on the sample by a concave mirror. After passing through the sample the probe‐pulses were spectrally dispersed (Acton Princeton Instrument 2300), detected on a photomultiplier (Hamamatsu R928) and processed (Pascher Instruments AB). The ns‐TA kinetics were detected as single‐wavelength kinetic between 440 and 750 nm in steps of 5 (440–560 nm) or 10 nm (560–750 nm), respectively. The emission kinetics were recorded using the ns‐TA system without probe‐light between 500 and 800 nm in 10 nm (Ru) or 25 nm (RuH⁺ , RuH₂ ) steps. For Ru, both the ns‐TA signals I_TA(t) (pump‐on, probe‐on) and the emission signals I_em(t) (pump‐on, probe‐off) were recorded at each examined probe wavelength to correct for the contribution of emission to the TA signals (consisting of GSB, ESA, and emission signals). For this purpose, the emission signals were subtracted from the TA signals (I_GSB,ESA(t)=I_TA(t) – I_em(t)).

All quantum chemical calculations determining structural and electronic properties of the present ruthenium‐based photosensitizer were the Gaussian 16 program. ^[60] Initially, the fully relaxed equilibrium geometry of Ru was obtained within its singlet and triplet ground state at the density functional level of theory (DFT) by means of the B3LYP XC functional.[ ⁶¹ , ⁶² ] The def2‐SVP basis[ ⁶³ , ⁶⁴ ] as well as the respective core potentials were applied for all atoms. Subsequently, three singly‐protonated species, whereas protonation was considered at the dipyridophenazine (dppz), pyrido‐quinolinone (pq) and N‐oxime‐moiety, respectively, were optimized within their singlet and their triplet ground states (see Figure S1). Finally, the doubly‐reduced and doubly‐protonated, i.e., hydrogenated, species were equilibrated (see Figure S1), while both singlet and triplet multiplicity was assumed. A vibrational analysis was carried out for each species to verify that a minimum on the potential energy (hyper‐)surface (PES) was obtained.

Subsequently, excited state properties such as excitation energies, oscillator strengths and electronic characters were calculated within the Frack‐Condon structure at the time‐dependent DFT (TD‐DFT) level of theory for the non‐reduced and non‐protonated species as well as for all three non‐reduced and singly‐protonated species illustrated in Figures S1. Therefore, the 200 lowest excited states were calculated within the respective multiplicity of the electronic ground state, i.e., singlet and triplet multiplicity. Thereby, the same XC functional, basis set and core potentials were applied as for the preceding ground state calculations. Effects of interaction with a solvent (acetonitrile, ϵ=35.688, n=1.344) were taken into account on the ground and excited states properties by the solute electron density variant of the integral equation formalism of the polarizable continuum model.[ ⁶⁵ , ⁶⁶ ] The non‐equilibrium procedure of solvation was used for the calculation of the excitation energies within the Franck‐Condon point, which is well adapted for processes, where only the fast reorganization of the electronic distribution of the solvent is important. All calculations were performed including D3 dispersion correction with Becke‐Johnson damping. ^[67]

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

C. Müller, A. Schwab, N. M. Randell, S. Kupfer, B. Dietzek-Ivanšić, M. Chavarot-Kerlidou, Chem. Eur. J. 2022, 28, e202103882.