Impact of selection for birth weight variability on reproductive longevity: A mice model

Abstract

Uniformity, understood as a similar performance in relevant livestock traits, such as birth weight within the litter, is being included as one of the selection objectives in breeding programmes, especially for polytocous livestock species. A divergent selection experiment for birth weight within‐litter variability in mice during 23 generations showed that homogeneous animals were better for litter size, survival and feed efficiency but less heavy than heterogeneous animals. The aim of this study was to compare the reproductive longevity in both divergent lines as time to the end of the reproductive period. Two generations from both lines with an initial number of 43 females and 43 males were mated one to one and stayed together to have consecutive parturitions until the end of the reproductive life. Females were discarded when the time elapsed from the last parturition was longer than 63 days. The time to the end of the reproductive period between both lines was compared by fitting a Cox proportional hazard regression model adjusting for line, generation and its interaction. The rate of parturitions in both lines was also compared using a Prentice–Williams–Peterson model adjusted for the same effects. The low variability line was associated with a higher parturition rate, e.g., adjusted hazard ratio was 2.93 (95% CI 2.17–3.94). The Cox model showed that the low variability females also presented benefits of time to the end of the reproductive period, with an adjusted hazard ratio of 0.26 (95% CI 0.16–0.41). The median of reproductive days was 55.50 in the high variability line whilst the median was 252.50 days for the low variability females. The homogeneous line presented important reproductive advantages suggesting higher robustness and animal welfare. Further research should confirm whether the findings presented here of a better performance in the low variability line could be properly applied to some livestock species.

1. INTRODUCTION

Improving productivity is the main objective of animal breeding programmes. However, the focus is now evolving to include uniformity by reducing the variability performance of some traits. Homogeneity, also called uniformity, has been associated with a reduction in handling and production costs for the animal production industry, leading to homogeneous batches of animals, diminishing mortality in prolific species, and greater economic benefits (Bolet et al., 2007). Homogeneity of relevant traits in livestock has also been related to robustness, which improves functional traits, whilst maintaining high production potential as much as possible (Mormede & Terenina, 2012). In fact, selection for uniformity has resulted in more robust animals that were resilient to environmental challenges (Broom, 2008).

Longevity is an economically important trait directly related to productivity efficiency, particularly for meat yield, in production systems (Van Melis et al., 2010). Animal breeding programmes are also focussed on increasing body weight or short‐term weight gain to produce more kilograms of meat per individual (Morales et al., 2017). Nevertheless, this is also important in dairy cattle breeding programmes that include longevity because this implies the improvement of several functional trait categories and, thus, the farm economy (Knaus, 2009; Sewalem et al., 2008; Shabalina et al., 2020). Longevity is becoming very common in breeding programmes of all production species, including prolific species like rabbits and pigs. Therefore, it is important to assess properly the genetic determinism in the different populations of these programmes and to know the role that systematic factors associated with management and animal‐dependent factors have on longevity (EL Nagar et al., 2020).

Survival and longevity are two closely related concepts. Survival is a compound trait affected by many effects such as weather conditions, management, behaviour and other environmental factors (Hossein‐Zadeh et al., 2018). Survival and longevity would improve by implementing genetic selection programmes in addition to better farm management. In this regard, understanding the genetic parameters of longevity and survival is necessary to evaluate the possibility of including these traits in the selective breeding programmes. Specific models of survival analysis are required to distinguish between these models and traditional linear models used for conventional evaluation of survival, so that time‐dependent factors and censored records may be included in the models of survival analysis (Borg, 2007). Survival analysis models were applied to appraise the survival of many farm animal species: dairy cattle (Caraviello et al., 2004; Sewalem et al., 2005; Vukasinovic et al., 2001), beef cattle (Rogers et al., 2004), pigs (Serenius & Stalder, 2004), sheep (Barazandeh et al., 2012; Sawalha et al., 2007) and rabbits (EL Nagar et al., 2020; Piles et al., 2006) and are also useful to deal with longevity.

Longevity is then a production objective, being as important as not only high individual birth and weaning weights, but also weights with intralitter homogeneity weight at birth. Thus, mortality would be reduced, and consequently, the productivity potential of the farm would improve (Gyovai et al., 2003; Pollesel et al., 2020). The reduction in the residual variance in the models is usually the selection criterion to increase uniformity, which is denoted as environmental variability. Bolet et al. (2007) investigated the effectiveness of genetic selection for higher uniformity of within‐litter birth weight in rabbits. They concluded that breeding strategies aiming at decreasing the within‐litter standard deviation of birth weight have positive implications on the reproductive performance does. Formoso‐Rafferty et al. (2016a) developed a divergent selection experiment for birth weight environmental variability (BW variability across this text) in mice, and they concluded that the genetic control of the birth weight environmental variability was possible by selection. They also showed that this selection criterion directly affected other interesting traits in livestock such as litter size, weaning weight and pup survival (Formoso‐Rafferty et al., 2016b). The experiment led to two divergent lines with the low line presenting benefits in production (Formoso‐Rafferty et al., 2016b), animal welfare (Formoso‐Rafferty et al., 2016a), the increase in heritability due to reduced residual variance (Formoso‐Rafferty et al., 2017) and traits usually considered robustness indicators such as feed efficiency (Formoso‐Rafferty et al., 2018, 2019). However, the implications of uniformity on reproductive longevity are still unknown.

Therefore, the objective of this study was to compare the reproductive longevity of two divergent mice selected lines for BW variability by analyzing their differences in time until the end of the reproductive period and their differences in the rate of parturitions, to infer a new possible relationship between homogeneity and robustness.

2. MATERIAL AND METHODS

2.1. Data

The dataset was obtained from two mice lines divergently selected for BW variability. These selected divergent lines for low and high BW variability will be referred to, respectively, as “low” and “high” across the rest of the present paper. The animals were housed at the experimental facility of the Department of Animal Production of the Veterinary Faculty of the Complutense University of Madrid. The housing and management conditions of the animals were in accordance with Spanish legislation RD 53/2013, on the basic rules for the protection of animals used in experiments and other scientific purposes (BOE, 2013).

Data were then taken from a previous experiment that showed a divergent response for BW residual variance, with mean ± standard error BW within‐litter standard deviations of 0.2131 ± 0.0147 g and 0.0891 ± 0.0066 g, respectively, for high and low lines in the 28th generation. For the selection process, animals were mated following a weighted selection design determined by simulated annealing (Fernéndez & Toro, 1999). This selection process optimizes the mean genetic breeding values of the progeny without exceeding the coancestry level determined by a standard balanced selection design. Also, a restriction of not sharing grandparents was imposed on the animals to be mated. More details of the selection process are described in Formoso‐Rafferty et al. (2016a).

From each line, 43 females from the 20th generation and 43 females from the 21st generation of the selection experiment were used leading to a total of reproductive performances of 172 females for this study. The females were those available in each generation, and they were sampled to be of similar age at mating (AM) within a generation, as this can influence the female reproductive performance. Here, AM was not necessarily the start of a new gestation but was defined as the difference between the date when the animals were lodged together and their birth date. There were significant differences in animal AM between generations and between lines: 174 days for the high line and 179 days for the low line at 20th generation, and 86 days for the high line and 99 days for the low line at 21st generation. These values were the least square means from a linear model including both line and generation as effects. AM differences between generations averaged 84 days. This important AM difference between generations was due to labour development at the facility where the mice were being held. However, it was the unique most important parameter that differed between these two generations, and that was useful to explore the influence of age on reproductive longevity. Instead, the possible impact of selection due to only one generation on the differences observed for reproduction can be expected to be comparatively limited as shown for other traits such as litter size, weaning weight and pup survival (Formoso‐Rafferty et al., 2016b). AM differences between lines were not external consequences of the experiment management but due to natural reasons. They averaged 9 days, with those of the high line being younger probably due to difficulties of this line performing parturitions in the precedent generation. The females in the high line were, therefore, mostly born later than those of the low line.

Animals were mated one male to one female from the same line and stayed permanently together to have consecutive parturitions until the end of their reproductive life. Note that due to the design, it is not possible to elucidate if the birth weight variability is on the male or female side, but it becomes irrelevant to achieve an outstanding successful response in the selection experiment. The females were checked daily during the parturition period, and all the newborns from the females having litters were registered with the litter size at birth (LSB) of the female and the parturition number (PN). At 21 days old, the pups were weaned, sexed, and the litter size at weaning (LSW) was also registered. The interval between consecutive parturitions in days (IBP) was also registered for those females performing at least two parturitions. Females were discarded when the time elapsed from the last parturition was longer than 63 days, a period equivalent to three gestation lengths. Longevity was evaluated using the length of reproductive life (LRL) as the days elapsed between first mating and the last litter on record, or zero for those females who had no parturition.

Records from a total of 1107 parturition attempts involving 172 females were analyzed, which were also considered the referred events in this study. The distribution of the records was 798 records from the low line and 309 from the high line. The total number of parturitions (TNP) was also registered for each female. Out of the total, 137 females had at least one parturition, and for those females who had no parturition, their time to end of reproductive life was fixed at 0. Figure 1 shows the number of females having parturitions per line and per parturition number. The low variability line had 49% more first births than the high variability line, twice second births, threefold more fourth births, fourfold more sixth births and sevenfold more eight births. As a summary of the available information, Table 1 shows descriptive statistics for the variables: AM, TNP, IBP, LSB, LSW and LRL.

FIGURE 1.

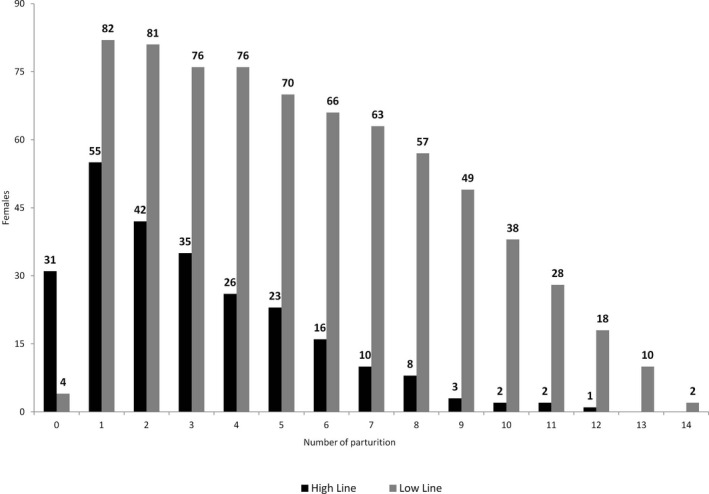
Frequency of females by parturition number and birth weight variability line

TABLE 1.

Mean/median, standard deviation (SD) or interquartile range (IQR) and number of records (n), for analyzed traits for birth weight variability line and generation

	Generation 20		Generation 21
	High line	Low line	High line	Low line
AM
Mean	173.91	179.28	86.21	98.53
SD	11.41	11.00	18.54	16.95
n	43	43	43	43
Minimum	157	164	56	59
Maximum	189	190	111	113
TNP
Mean	1.95	6.84	3.23	9.81
SD	2.41	3.72	3.34	3.06
n	43	43	43	43
Minimum	0	0	0	1
Maximum	8	13	12	14
IBP
Mean	36.13	28.93	32.73	28.06
SD	13.33	9.00	12.14	9.00
n	60	255	108	379
Minimum	19	17	16	17
Maximum	63	63	60	62
LSB
Mean	4.58	5.68	4.61	6.55
SD	1.80	2.65	1.84	2.67
n	84	294	138	422
Minimum	1	1	1	1
Maximum	14	15	13	16
LSW
Mean	4.03	5.20	3.99	6.13
SD	1.79	2.70	1.99	2.75
n	84	294	138	422
Minimum	0	0	0	0
Maximum	13	15	13	15
LRL
Median	29	207	77	267
IQR	140	161	209	128
n	43	43	43	43
Minimum	0	0	0	25
Maximum	259	340	303	429

Abbreviations: AM, age at mating (days); IBP, interval between consecutive parturitions (days); LRL, length of reproductive life (days); LSB, litter size at birth (newborns); LSW, litter size at weaning (pups); TNP, total number of parturitions.

2.2. Statistical analyses

IBP, LSB and LSW were compared between lines using linear mixed models where generation, line, the interaction between line and generation, and PN were included as fixed effects, and the female as a random effect. The expression of the mixed model was:

$$y_{\mathit{ijkl}}=\mu +l_i+g_j+{lg}_{\mathit{ij}}+p_k+f_l+{\epsilon }_{\mathit{ijkl}}$$

where y_ijkl is either IBP, LSB or LSW of the female l of the line i, in the generation j, l_i the effect of the line i with two levels (high and low), g_j the effect of the generation j with two levels (20 and 21), lg_ij the interaction between them, p_k the effect of the parturition number k with 14 levels, f_l the random effect of the female l with 172 levels and ε _ijkl the residual. The least squared means were computed to show the observed differences between levels of relevant effects and were compared under different significance levels: p < .05, p < .01 and p < .001. The Statistical Analysis System software (SAS, 1990) was used to perform this statistical analysis of the data.

LRL was analyzed under a survival model, and all females were uncensored for this analysis. The standard Cox proportional hazard model for LRL of female i was:

$$\begin{array}{c}{h}_i(t)=h_0(t)\exp (\beta X_i)\\ i=1,2,\dots ,n\\ \end{array}$$

where h_i (t) is the hazard of female i (for i = 1, 2, …, n) to experience an event at the time t (i.e. end of reproductive life), h ₀(t) refers to a common baseline hazard function,β = (β ₁, β ₂, β ₃) are the corresponding parameters for line, generation and interaction effects, and X_i  = (X_{i 1}, X_{i 2}, X_{i 3}) is the corresponding incidence vector. The results of the Cox model are shown graphically by Kaplan–Meier curves.

The rate of parturitions in both lines was compared using an extension of the standard Cox model, the model from Prentice et al. (1981). In this analysis, females who did not deliver parturition within 63 days after mating were right censored at that time, whilst all the others were censored after the last recurrence.

$$\begin{array}{c}{h}_{\mathit{ij}}(t)=h_{0j}(t)Y_{\mathit{ij}}(t)\exp \left({\beta }_j{X}_i(t)\right)\\ i=1,\dots ,n;j=1,2,\dots ,\text{number}\text{of}\text{recurrences}\\ Y_{\mathit{ij}}(t)=\left\{\begin{array}{cc}1& \text{if}\text{animal}i\text{is}\text{not}\text{at}\text{risk}\text{on}\text{time}t\\ 0& \text{if}\text{animal}i\text{is}\text{at}\text{risk}\text{on}\text{time}t\end{array}\right.\end{array}$$

where h_ij (t) is the hazard function of the individual female i having a new parturition j at time t,h _{0 j} (t) is the baseline hazard of having a new parturition j, β = (β_{j 1}, β_{j 2}, β_{j 3}) are the parameters for line, generation and interaction, corresponding to parturition j, and X_i (t) = (X_{i 1}(t), X_{i 2}(t), X_{i 3}(t)) is the covariate vector for female i at time t. With this model, β_j may take different values for each recurrence, but a common value across all the strata was considered because a large number of recurrences did not occur very often (Collet, 2014). In practice, the data may need to be limited to a specific number of recurrent events if the risk set becomes very small for later strata, and event‐specific estimates become too unreliable (Prentice et al., 1981), but all the parturitions were used to clearly establish the differences between groups. A stratum variable was included to accommodate the number of previous parturitions, allowing the hazard for a new parturition to change after a previous event. The female was thus incorporated as a cluster and the Huber–White Sandwich robust variance estimator (Huber, 1967) was used to account for female heterogeneity. Survival package in R was used (Therneau & Lumley, 2015).

3. RESULTS

Table 2 shows the least square means and the standard error of LSB, LSW and IBP traits in both lines and generations. There were significant differences between lines in LSB, LSW and IBP (p < .001). Both, the LSB and LSW were higher in the low line than in the high line, whilst IBP was longer in the high line, regardless of the generation. The low line presented 2.75 pups more for LSB and 2.90 for LSW than the high line, and their IBP was 30.79 and 37.23 days respectively (Table 2).

TABLE 2.

Least square means and standard error (in brackets) for litter size at birth, weaning and interval between consecutive parturitions in both birth weight variability lines and generation, and significance of line, generation and parturition number effects

		LSB	LSW	IBP
Line	Low	6.01 (0.17)	5.55 (0.19)	30.79 (0.70)
	High	3.26 (0.25)	2.65 (0.27)	37.23 (1.05)
	p	***	***	***
Generation	20	4.18 (0.23)	3.60 (0.25)	35.22 (0.96)
	21	5.09 (0.19)	4.60 (0.21)	32.80 (0.80)
	p	***	***	**
Line × Generation	p	ns	ns	ns
Parturition number	p	***	***	***

Abbreviations: IBP, interval between consecutive parturitions (days); LSB, litter size at birth (pups); LSW, litter size at weaning (pups); ns, non‐significant.

*p < .05; **p < .01; ***p < .001

The least square means for LSB, LSW and IBP by PN are given in Figure 2. The results show that PN was inversely correlated with both LSB and LSW (p < .001), and a regular and steady decrease of LSB and LSW was observed as the PN increased. The parallel evolution of LSB and LSW revealed a constant survival ratio at weaning across the number of parturitions. In addition, Figure 2 also includes the significant (p < .001) evolution of IBP as PN increases. This shows an important impact from the 10th parturition onwards, revealing the difficulties females have at becoming pregnant when reaching this number of parturition. However, in this study, there was no evidence of any difference in the traits as a consequence of the interaction between line and generation (Table 2).

FIGURE 2.

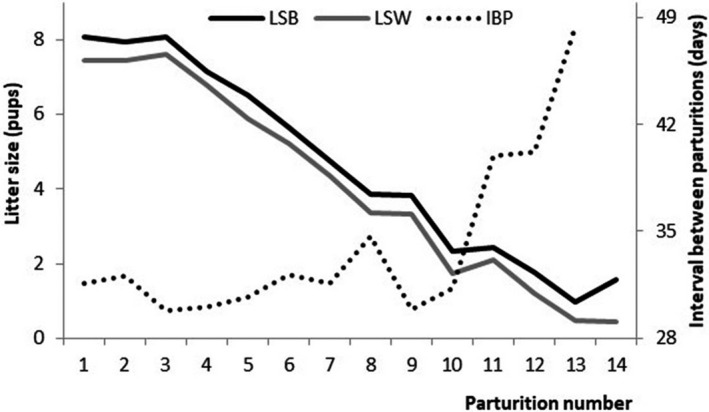
Least square means obtained from the corresponding linear model considering litter size at birth (LSB), weaning (LSW), and interval between parturitions (IBP) as traits by parturition number (PN)

Kaplan–Meier curves for the length of reproductive life for females are shown in Figure 3 stratified by the combination of line and generation. According to the LRL medians, a female in high variability would reach the end of the experiment at 29 (95% CI 0 to 226) days (generation 20) and at 77 (95% CI 0 to 266) days (generation 21), whilst low variability females would arrive at 207 (95% CI 0 to 327) days (generation 20) and 267 (95% CI 88 to 397) days (generation 21). The global median of reproductive days was 55.50 in the high variability line whilst the median was 252.50 days for the low variability. Table 3 shows the hazard ratio (HR) and confidence interval (CI) for LRL regarding line, generation and its interaction. The hazard of ending the reproductive life was much lower in the low variability line: HR 0.26 (95% CI 0.16 to 0.41). In addition to the differences caused by the selection process and other minor environmental reasons, the generations, basically differing in AM, also became significant. The risk of stopping parturitions was twothirds, HR 0.63 (95% CI 0.41 to 0.96) in generation 21. Interaction between line and generation provided a non‐significant HR 0.65 (95% CI 0.34 to 1.22).

FIGURE 3.

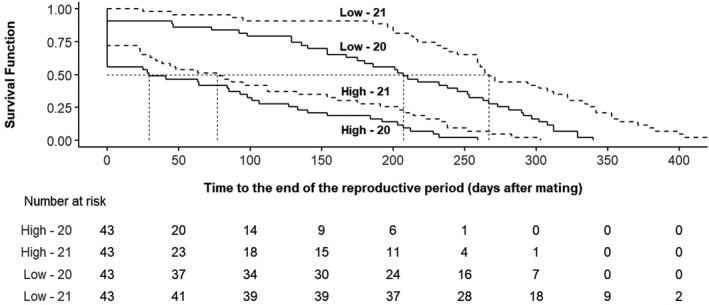
Kaplan–Meier plot for length of reproductive life (LRL) stratified by birth weight variability line and generation

TABLE 3.

Hazard ratios (HR) for length of reproductive life obtained in analyses by line generation and interaction

	HR (95% CI)	Pr(>|z|)
Low line / High line	0.26 (0.16; 0.41)	<.001
Generation 21 / Generation 20	0.63 (0.41; 0.96)	<.05
Line × Generation interaction a	0.65 (0.34; 1.22)	ns

Data presented as hazard ratios (95% confidence interval). ns, non‐significant.

Ratio (Low line × Generation 21) / (High line × Generation 20).

Figure 4 shows the HR for having a new parturition (PNP) under the Prentice–Williams–Peterson model for recurrent events adjusted by line and generation effects and its interaction. Again the low line was superior in reproductive ability by an HR of 2.93; CI 95% (HR) = (2.17:3.94), showing that the probability of having a new parturition was almost triple in this line than in the high line. The influence of the generation was also significant as shown in the HR of 1.60; CI 95% (HR) = (1.17:2.19). This means that the probability of having a new parturition increased by 60% when the females started their reproductive performance younger. The line*generation interaction was insignificant.

FIGURE 4.

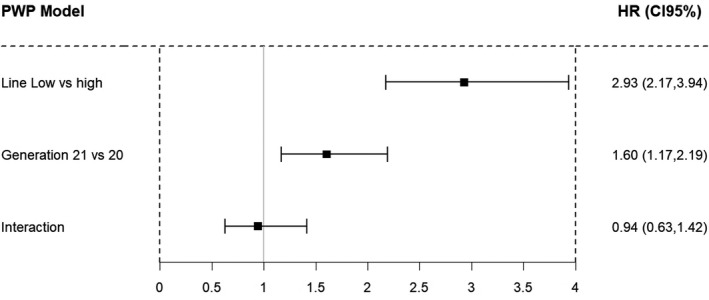
Estimated hazard ratios (HR) for the rate of a new parturition (PNP). Reference groups were high birth weight variability line and generation 20. PWP Model: Prentice–Williams–Peterson model

4. DISCUSSION

The goal of this study was to take a further step in the research area regarding the relationship between homogeneity and robustness by determining the differences in reproductive longevity between two divergent mice lines selected for BW variability. To achieve this objective, the females belonging to both lines were allowed to mate indefinitely until the animals stopped giving birth.

Important reproductive advantages were evident in the line selected for low variability in this study. A higher reproductive longevity was found in homogeneous animals. After 20 generations of divergent selection, the superiority of the low line over the high line was overwhelming with approximately triple higher performance when analyzing the probability for a new parturition (Figure 4), and about fourfold higher longevity when compared to the LRL (Table 3). The first result related to the ability to perform a new parturition, and the second reflected the ability of the female to still have parturitions at an older age. They would both be understood as two different measures of the same reproductive longevity concept under a common IBP, therefore, not being exactly the same, as the low line had in addition a significant 21% lower IBP (Table 2). Both show interesting findings for animal production: in pigs, a sow's production persistency and fertility in successive parities should be analyzed separately but both improved since the key to increase the overall herd efficiency is to increase both the length of the sow's herd productive life and the number of piglets reared per litter (Warda et al., 2021). This was reinforced by the significantly higher probability of the low line to experiment a new parturition according to the longevity analysis (Figure 4). In addition, this higher probability to have a new parturition was accompanied by a higher litter size at birth of almost three more pups with a still higher superiority also in litter size at weaning (Table 2). This confirms for all the parturitions that had already been reported in the first two parturitions in rabbits (EL Nagar et al., 2020). Moreover, when difficulties in having new births from the tenth parturition (Figure 2) substantially increased, only a relevant number of low line females remained reproductively active (Figure 1). Another interesting result is the reproductive behaviour when females became older, which is shown by comparing the reproductive performance between generations. Younger females significantly increased their probability to have parturitions by a 60% whatever the trait was analyzed as LRL or as PNP. This difference did not affect the females differently from different lines since the interaction was found insignificant.

Reproductive longevity has been studied here by means of survival analysis models. These have been applied to appraise the survival of many farm animal species. Lamb survival and ewe longevity would be improved by implementing genetic selection programmes in addition to the improvement of management practices (Hossein‐Zadeh et al., 2018). Fertility and longevity are traits of economic and welfare importance in livestock species (Martínez‐Paredes et al., 2018) and particularly for prolific animals like rabbits (Penadés et al., 2020) and pigs (Warda et al., 2021). Factors that affect the survival and fitness of females are of great interest to develop strategies (for breeding, nutrition, genetics, etc) that ensure compliance with the specific values of these traits and reduce the risk of females being eliminated from the herd. If these objectives are met, the longevity of the females would increase, with a low replacement rate that allows a higher selection intensity, and improved robustness and resilience in all farms (Penadés et al., 2020). Nowadays, searching for a resilience indicator in farms is important; resilience indicators have been explored from bodyweight deviations in layer chickens (Berghof et al., 2019), feed intake in pigs (Putz et al., 2019) and daily milk yield in cows (Poppe et al., 2020). These studies showed that these traits were useful as resilience indicators for breeding because of their favourable genetic correlations with health and survival traits. Low variability in daily milk yield and quick recovery was expected to indicate good resilience in terms of health, longevity, fertility and metabolic traits (Poppe et al., 2021). Moreover, studies in dairy cattle suggested that the variance of daily milk yield records as a resilience indicator, where low variance was expected to indicate good resilience (Elgersma et al., 2018; Poppe et al., 2021).

These new findings concerning reproductive longevity are framed as a new robustness indicator within the mice selection experiment for BW variability, and as such, benefits of birth weight uniformity in a more global context seem to be relevant. Improving the productivity of livestock is a lifelong objective in animal science. However, the relative importance of productivity is decreasing these past few years and being replaced by a search for the sustainability of the production system (Neeteson‐van Nieuwenhoven et al., 2013; Penadés et al., 2020). Having the divergent lines selected for BW variability has improved our understanding of the beneficial relationship between homogeneity and animal productivity and welfare and robustness. Furthermore, we were also able to better understand the relationship between robustness and traits such as reproductive longevity, and the ability of female mice to cope with energy requirements that gestation requires. Low line animals performed better in reproductive indicators but marked lower BW. This reduction in the individual weight was accompanied by an increase in litter size and survival at weaning (Formoso‐Rafferty et al., 2018) without negative impact in the weaning weight nor in the weight at the beginning of the reproductive age in this mice population (Formoso‐Rafferty et al., 2019). This impact of the selection on body weight seemed to be a consequence of a statistical scale effect, since a lower variability results in a lower mean (Tatliyer et al., 2019), but this did not negatively affect the total litter weight (Formoso‐Rafferty et al., 2016b). Moreover, low line animals clearly survive more at weaning, at least in this mice experiment, suggesting that the concerns of mortality are not due to low BW but to high variability in which smaller animals are compromised. In the same way, higher uniformity would ensure a greater number of females reaching a minimum adult weight to present a good reproductive performance. It does not have to be the same in livestock animals, but it is still worth studying.

Mice are considered to be a convenient model for other prolific species, such as rabbits or pigs. The findings presented here of a better performance in the low variability line could be applied to livestock if applied properly. Litter size is traditionally considered amongst the most important selection criteria and objectives for pigs. Litter size has been greatly increased without changes in standard deviation, and this has led to a higher coefficient of variation of piglet weight within the litter, thus creating a competitive environment where the smallest lose out and die (Damgaard et al., 2003). As a consequence of genetic selection for increased litter size, the pig industry has seen an associated increase in birth weight variability within the litter and an increase in the proportion of piglets with low birth weight (Yuan et al., 2015). The low birth weight in young sows has increased preweaning mortality. Whilst the selection criteria in pigs take into account body weight, survival, and litter size, the mice experiment only focussed on BW variability. Even though homogeneous litters could lead to heterogeneous batches across litters and dams, this uniformity has a positive impact on preweaning survival, the point at which survival difficulties are always reported (Yuan et al., 2015). However, there are no reports in the literature on the relevant mortality rates after weaning, and in addition, weaning weight variability within line across litters might also be favourably affected (Formoso‐Rafferty et al., 2016b).

A dramatic difference in reproductive longevity has been shown in this study as a new advantage of the mice selected for low birth weight variability. Animals in the low line were homogeneous, and they were smaller due to the genetic correlation between the trait and its variability. However, the selected homogeneity was also accompanied by signs of higher robustness, with higher litter size, improved survival and better reproductive performance without losses in the total weaned weight (Formoso‐Rafferty et al., 2016b). This was contrary to that observed in pigs with an increase in the mortality related to the selection by litter size. Selecting to reduce environmental variability seems to be then advisable. Rönnegard et al. (2012) reported that selecting on breeding values for microenvironmental sensitivity was convenient when it was economically important to have low variation amongst animals, or for a trait with an intermediate optimum value, or individual trait values run the risk of transgressing a certain threshold (Mulder et al., 2008). Moreover, a substantial level of genetic variation for residual variance was detected from a range of animal species, which implies a standard deviation change in the breeding values for microenvironmental for t he trait. This suggests that the residual variance could be changed by selection (Hill & Mulder, 2010). The selection to reduce the variability of weight seems to be worthwhile to be assayed more in livestock.

We observed in mice a superior reproductive longevity of females when selected for birth weight uniformity who are more persistent in reproduction despite being older when compared to heterogeneous females. These results, linked to previous studies of the same mice selection experiment, showed higher robustness indicators of the homogeneity line suggesting advantages of such selection objective even when animals become smaller. This idea could be transferred to prolific livestock species, but this study has not yet been performed.

CONFLICT OF INTEREST

The authors declare that they have no competing interests.

ETHICS APPROVAL

All experimental procedures were carried out at the animal facilities of the Complutense University of Madrid (UCM, Spain), which meet the requirements of the European Union for scientific procedure establishments, under the project licence of the UCM Scientific Ethics Committee. Animal manipulation was performed in accordance with the Spanish Guidelines for Care and Use of Animals in Research (RD53/ 2013).

Formoso‐Rafferty, N. , Gutiérrez, J. P. , García‐Álvarez, A. , Pérez, T. , & Cervantes, I. (2022). Impact of selection for birth weight variability on reproductive longevity: A mice model. Journal of Animal Breeding and Genetics, 139, 370–379. 10.1111/jbg.12676

DATA AVAILABILITY STATEMENT

The datasets generated and/or analyzed during the current study are available from the corresponding author upon reasonable request.