Theoretical Optimization of Compositions of High‐Entropy Oxides for the Oxygen Evolution Reaction

Abstract

High‐entropy oxides are oxides consisting of five or more metals incorporated in a single lattice, and the large composition space suggests that properties of interest can be readily optimised. For applications within catalysis, the different local atomic environments result in a distribution of binding energies for the catalytic intermediates. Using the oxygen evolution reaction on the rutile (110) surface as example, here we outline a strategy for the theoretical optimization of the composition. Density functional theory calculations performed for a limited number of sites are used to fit a model that predicts the reaction energies for all possible local atomic environments. Two reaction pathways are considered; the conventional pathway on the coordinatively unsaturated sites and an alternative pathway involving transfer of protons to a bridging oxygen. An explicit model of the surface is constructed to describe the interdependency of the two pathways and identify the composition that maximizes catalytic activity.

High‐entropy oxides are investigated theoretically as catalysts for the oxygen evolution reaction. The energetics of the reaction is calculated on individual active sites following two different pathways, and it is shown that the overpotential and preferred pathway depend on the local atomic environment. A surface model is constructed in order to identify the composition that maximises the catalytic activity.

Introduction

The transition to a society based on renewable energy requires new ways to store electricity from intermittent energy sources, e.g. in the form of chemical fuels. H₂ is a convenient fuel in this respect, as it can be produced by the electrolysis of water. ^[1] The efficiency of this process is however limited by the poor kinetics of the oxygen evolution reaction (OER) at the anode. The origin of this problem is that the adsorption energies of the catalytic intermediates in this four‐step reaction are related by the scaling relations, prohibiting the independent tuning necessary to make the reaction run at the thermodynamic potential. ^[2] For applications in proton exchange membrane fuel cells, IrO₂ and RuO₂ are currently some of the best candidates for the anode catalyst material, exhibiting reasonably high activity and stability. ^[3] However, due to the cost and scarcity of Ir and Ru, efforts to increase the activity relative to the amount of precious metal employed are continuing alongside efforts to replace these materials with cheaper and more abundant alternatives. ^[4]

High‐entropy oxides (HEOs) consist of five or more metals in equimolar or near‐equimolar ratios, incorporated in a single‐phase solid solution with oxygen. ^[5] Since the first characterisation of a HEO in 2015, ^[6] these materials have been investigated for their distinct thermal, magnetic and electrochemical properties, ^[7] and furthermore inspired the development of other multi‐component ceramic materials. ^[8] Thermodynamically, HEOs are analogous to high‐entropy alloys (HEAs) in that the configurational entropy, arising from the many possible arrangements of the different elements, plays an important role in the thermodynamic stability of the materials. ^[9] The large combinatorial space of a multinary phase diagram also suggests that properties of interest can be precisely tuned. Within catalysis, this has been demonstrated for HEAs, where the large number of different atomic environments results in a distribution of binding energies of the catalytic intermediates, with some sites thereby reaching the maximum activity according to the Sabatier principle. ^[10] The catalytic properties of HEOs are less studied. ^[11] The transferability of this principle is therefore yet to be explored, however recent studies suggest that they are promising candidate materials for electrocatalysis. ^[12]

Here we outline a strategy for the theoretical investigation of HEOs as catalysts for the oxygen evolution reaction. Inspired by the high catalytic activity of IrO₂ and RuO₂, the (110) surface of a rutile oxide based on Ir, Ru, Ti, Os and Rh is chosen as example. The procedure follows four steps: Firstly, a set of elements is chosen, and the stability of mixtures of these elements is considered. Secondly, a limited number of adsorption energies are calculated by density functional theory (DFT) for relevant catalytic intermediates. In the third step, a linear model is then fitted in order to predict the adsorption energies for all possible local atomic environments and based on these adsorption energies, the catalytic activity of individual sites is predicted. In a final step, the composition is optimised such that the catalytic activity is maximised. This procedure is similar to the one previously described for HEAs for the oxygen reduction reaction (ORR),[ ¹⁰ , ¹³ ] however extensions have been made to suit the new problem. Most importantly, two different reaction mechanisms are considered, and our results show that the preferred pathway depends on the local atomic environment. The co‐existence of two reaction pathways furthermore results in an interdependency of neighbouring active sites, implying that the composition cannot be optimised directly. Instead, an explicit surface model is constructed and the catalytic activity is evaluated at regular intervals throughout the four‐dimensional composition space in order to identify the optimum composition. Our calculations identify mixtures consisting primarily of IrO₂ and RuO₂ as having higher catalytic activity than any of the pure oxides, and highlight the importance of a detailed mechanistic understanding of the reaction in obtaining this result.

Results and Discussion

For the present study we consider an oxide in the rutile structure based on Ru, Ti, Ir, Os and Rh. These elements are chosen for several reasons. Firstly, IrO₂ and RuO₂ are both known to have a high catalytic activity for OER.[ ^3a , ^3b ] Furthermore, the mixing of different oxides might be beneficial for their stability under acidic OER conditions. A prominent example of this is the dimensionally stable anodes, composed of a mixture of TiO₂, RuO₂ and other platinum group metal oxides, which are used for industrial chlorine production due to their high corrosion resistance, but mixing of RuO₂ and IrO₂ have also been shown to increase the stability of RuO₂ for OER.[ ^3c , ¹⁴ ] In addition, with the exception of TiO₂, the chosen oxides are conductive, resulting in a conductive HEO. Thus, charge is readily provided for the reaction and computational challenges in describing the adsorption energies on doped semiconducting oxides are avoided. ^[15] Finally, the oxides have similar lattice constants in the rutile structure (cf. Section S1 of the Supporting Information), minimising the possibility that strain will prevent the formation of the mixed oxide.

Since Ru_0.2Ti_0.2Ir_0.2Os_0.2Rh_0.2O₂ has not yet been synthesised, to give a further indication of the ability of these five metals to mix, the enthalpy of inserting one atom of each element in the oxides of all the other elements is calculated by DFT (see Section S1 of the Supporting Information for computational details). The results (c.f. Section S2 of the Supporting Information) show that it is generally favourable to mix Ru, Ir, Os and Rh with each other. For Ti the calculated enthalpy of mixing is positive, but since the entropy contribution to the free energy will be negative, mixing might still be possible.

The conventional pathway for the OER consists of four proton‐coupled electron transfers:

$${\displaystyle {}^{*}+\mathrm{H}{}_2\mathrm{O}\left(\mathrm{l}\right)\to {}^{*}\mathrm{OH}+\mathrm{H}{}^{+}+\mathrm{e}{}^{-}\left(\Delta G{}_1\right)}$$

$${\displaystyle {}^{*}\mathrm{OH}\to {}^{*}\mathrm{O}+\mathrm{H}{}^{+}+\mathrm{e}{}^{-}\left(\Delta G{}_2\right)}$$

$${\displaystyle {}^{*}\mathrm{O}+\mathrm{H}{}_2\mathrm{O}\left(\mathrm{l}\right)\to {}^{*}\mathrm{OOH}+\mathrm{H}{}^{+}+\mathrm{e}{}^{-}\left(\Delta G{}_3\right)}$$

$${\displaystyle {}^{*}\mathrm{OOH}\to \mathrm{O}{}_2\left(\mathrm{g}\right)+\mathrm{H}{}^{+}+\mathrm{e}{}^{-}+{}^{*}\left(\Delta G{}_4\right)}$$ (1)

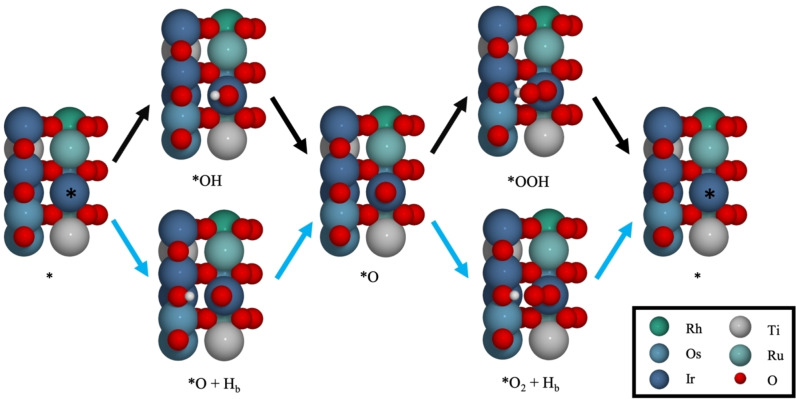
where, * denotes the active site on the surface. On the rutile (110) surface this is the coordinatively unsaturated (cus) site as shown in Figure 1, which also illustrates the reaction intermediates. Assuming this pathway, the OER is limited by the scaling relation between the binding energy of the *OH and *OOH intermediates (G _ads(OOH)≈G _ads(OH)+3.2 eV), which has been found for a number of oxide surfaces including rutile oxides. ^[2a] This relation implies that a minimum potential of 1.6 V is required to run the reaction even though the thermodynamic potential is only 1.23 V. An alternative catalytic pathway involving transfer of the proton from *OH and *OOH to a neighbouring bridging oxygen to form *O+H_b and *O₂+H_b is also illustrated in Figure 1. This pathway gives a favourable comparison between experimental and theoretical results for (doped) RuO₂, and theoretical calculations on RuO₂ and IrO₂ suggest that it results in a better scaling relation (G _ads(*O₂+H_b)≈G _ads(*O+H_b)+2.7 eV). ^[16]

Figure 1.

Reaction pathways for the OER: conventional pathway (black arrows) and pathway involving the bridge site (blue arrows). A combination of the two pathways is also possible. The cus adsorption site is marked by a *, and the surface is shown without pre‐adsorbed *O for clarity.

A large number of possible local environments exist for a cus site on a high‐entropy oxide. Considering only the nearest neighbour (NN) metal sites, there are four bridge atoms, two cus atoms and two sub‐surface atoms (see Figure 2a). This results in a total of 5⁹=1.95⋅10⁶ different adsorption sites, however some of these will be equivalent by symmetry. Likewise, the bridge site (Figure 2b) consists of two metal atoms having six cus NN, two bridge NN and three subsurface NN, resulting in an even larger number of possible sites. This number of structures is clearly too large to be calculated by DFT. However, some information may still be extracted from a limited number of DFT calculations, and in the following the calculated energies will be used to fit a model that predicts the adsorption energies of all possible adsorption sites. Therefore, oxide slabs with the average composition of Ru_0.2Ti_0.2Ir_0.2Os_0.2Rh_0.2O₂ are randomly generated and a total of 450 adsorption energies of *O, *OH and *O+H_b are calculated.

Figure 2.

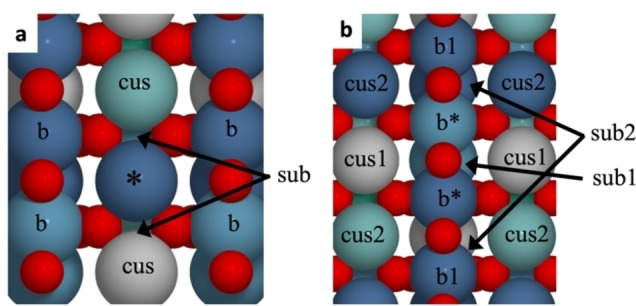
a) Cus adsorption site (*) on the rutile (110) surface. The three different types of nearest neighbour metal sites are marked; cus, bridge (b) and subsurface (sub). b) Bridge adsorption site (b*) with different types of NN atoms marked.

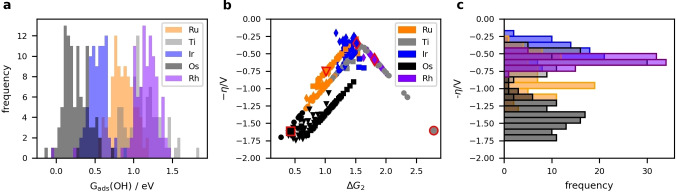
The distribution of *OH adsorption energies on the cus site is shown in Figure 3a (c.f. Section S3 of the Supporting Information for a similar plot for *O). For each element, the different local environments around the adsorption site leads to a spread in the adsorption energies of approximately 0.5 eV. This effect is also observed for high entropy alloys, and is of a similar magnitude. ^[10]

Figure 3.

Histogram of the *OH adsorption energies a) for 450 cus sites calculated by DFT. b) Calculated overpotential for these sites, assuming individual scaling relations for the bridge pathway, with colours indicating the element on the (*) cus site. Circles and triangles indicate sites that follow the conventional and bridge pathway, respectively, while squares represent sites where the *O+H_b and *OOH intermediates are preferred and diamonds represent sites where the *OH and *O₂+H_b intermediates are preferred. Large markers with red edges are the calculated values for the pure oxides at high coverage. c) Histogram of the overpotentials calculated in b).

The reason for the improved performance following the bridge pathway is that the scaling relation between *O+H_b and *O₂+H_b differs from that of *OH and *OOH. In Ref. [16c] the scaling was found to be G _ads(*O₂+H_b)≈G _ads(*O+H_b)+2.7 eV for RuO₂. To investigate if this relationship holds on our HEO, the energies of *O+H_b and *O₂+H_b are calculated for 75 different adsorption sites. Fitting to straight lines with a slope of 1 shows that the points follow different scalings, depending on the identity of the cus adsorption site of *O/*O₂, with an energy difference of 2.6 eV for Ir, 3.0 eV for Ru, 1.9 eV for Rh, 3.3 eV for Ti and 3.6 eV for Os. The different values correlate with the different binding strengths of *O, since the binding of *O₂ is expected to be close to 0 eV (c.f. Section S4 of the Supporting Information). For comparison, the energies of *OOH vs. *OH can be fitted to a single line with an energy difference of 3.2 eV, consistent with previous results for oxide surfaces. ^[2a] It should be noted that O₂(g) in the ground (triplet) state is poorly described by DFT. Some of this error may still be present in adsorbed O₂, giving some uncertainty to the exact value for the scaling relations. The values obtained from the fit have been used in the following but a further discussion is provided in Section S4 of the Supporting Information.

From the calculated adsorption energies for *O and *OH/(*O+H_b) and the scaling relations derived above, the free energy of the four reaction steps can be calculated. It is assumed that the reaction follows the minimum energy path, i.e. the bridge site is used when the energy of *O+H_b is lower than the energy of *OH on the neighbouring cus site and similarly *O₂+H_b is favoured when it is lower in energy than *OOH. From the free energies, the overpotential (η) can be calculated:

$${\displaystyle \eta =\frac{\max \left\{\Delta G_1,\Delta G_2,\Delta G_3,\Delta G_4\right\}}{e}-1.23V}$$

The overpotential as a function of ΔG ₂ is plotted for each site in the volcano plot in Figure 3b. The points fall on several different lines on the left side of the volcano, due to the multiple scaling relations for cus and bridge sites. The shape of each marker shows the favoured pathway for that site; circles indicate that the conventional pathway is followed, triangles indicate that the bridge pathway is followed and sites that mixes the two pathways are represented by squares when *O+H_b and *OOH are the favoured intermediates and diamonds when *OH and *O₂+H_b are the favoured intermediates.

The plot demonstrates that *O+H_b is more stable than *OH on many Ru and Os sites. This is rarely the case on Rh and Ir, however the *O₂+H_b intermediate is favoured over *OOH on many of these sites. Ti mostly follows the conventional pathway.

Using the bridge site for one or both intermediates does not necessarily result in an improved overpotential, even if the value of ΔG ₂ is improved, because points are no longer confined to follow the conventional volcano. For the strong binding Os, the scaling relation becomes less favourable when the bridge site is used, while for the weak binding Rh, the formation of *O₂+H_b instead of *OOH does not change the energy of the rate‐limiting step, which remains the conversion of *OH to *O. For Ir, the formation of *O₂+H_b can lead to a change in the rate limiting step such that it becomes the final step (*O₂+H_b→O₂(g)+H⁺+e⁻+*), but due to the better scaling, which is close to the optimum value of 2.46 eV, this can still result in an improved overpotential. Ru can also improve the overpotential by following the bridge pathway, while Ti rarely uses the bridge pathway which also has a scaling relation very similar to that of the conventional pathway.

Overall, the histogram of overpotentials for the calculated bridge sites in Figure 3c shows that Ir sites have the lowest overpotentials followed by Ru and Ti. Furthermore, the improved scaling relations allow overpotentials lower than the 0.37 V defined by the scaling relation for the conventional pathway. For the sites calculated here, 25 % of the Ir sites and 3 % of the Ru sites have overpotentials lower than this value.

The DFT calculated energies are not necessarily representative of all the possible local environments around the adsorption sites of a HEO, and it may be difficult to determine how the different elements influence the activity of a given site. Therefore, the calculated energies are used to make a linear fit. Considering the cus site first, it is assumed that the adsorption energy on site i (E ⁱ _ads), depends on the number of atoms of each element (k) that are present in each of the three types of NN sites shown in Figure 2a (N ⁱ _cus,k , N ⁱ _b,k , N ⁱ _sub,k ), but not on their relative locations:

$${\displaystyle E_{\mathrm{a}\mathrm{d}\mathrm{s}}^i=C_0+\sum _k^{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{s}}{C}_{\mathrm{c}\mathrm{u}\mathrm{s},k}{N}_{\mathrm{c}\mathrm{u}\mathrm{s},k}^i+\sum _k^{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{s}}{C}_{b,k}{N}_{b,k}^i+\sum _k^{\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{s}}{C}_{\mathrm{s}\mathrm{u}\mathrm{b},k}{N}_{\mathrm{s}\mathrm{u}\mathrm{b},k}^i}$$ (2)

Five independent fits are made according to the identity of atom i. The coefficients of the fit (C_xx ) are found by ridge regression and the resulting model is used to calculate the adsorption energies for all possible sites. The histogram of adsorption energies for *OH is shown in Figure 4a and compares well with the DFT calculated histogram in Figure 3a. Further details of the fit and a corresponding plot of the *O adsorption energies are given in the Section S5 and S3 of the Supporting Information.

Figure 4.

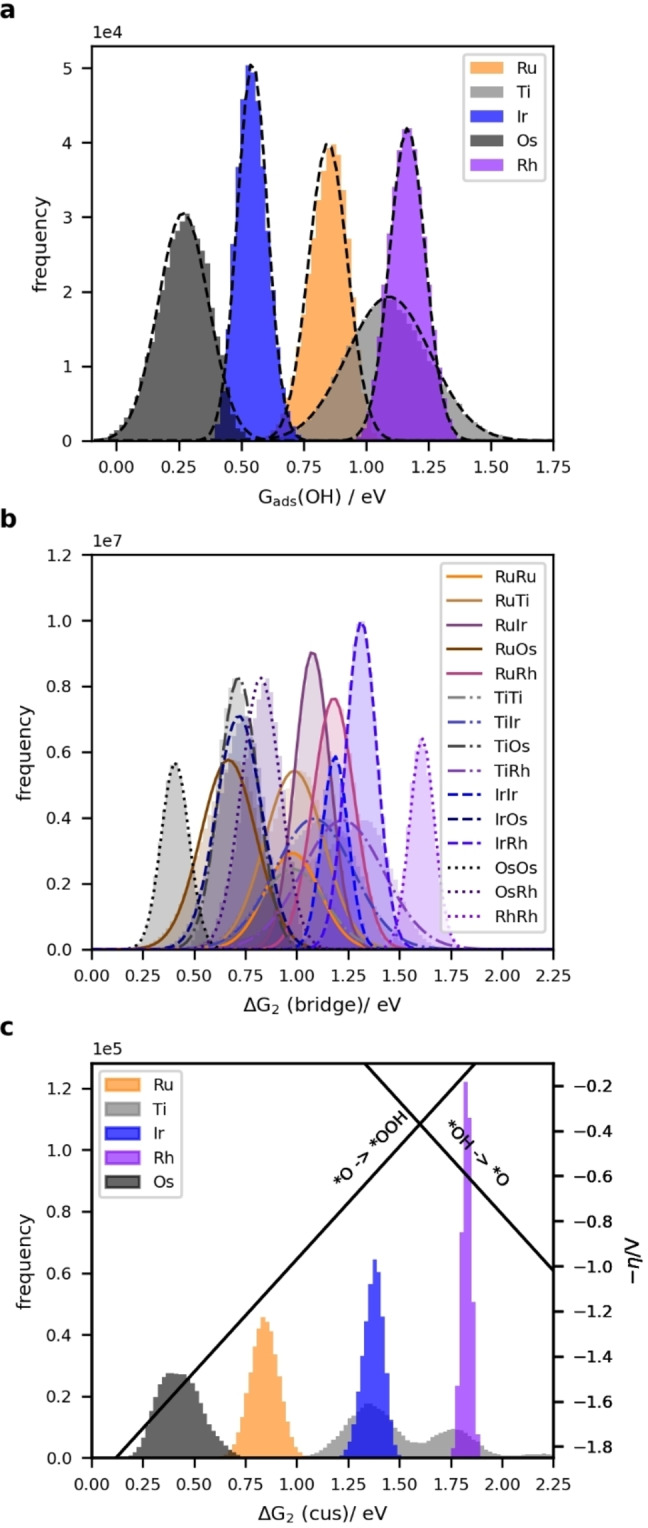
Distribution of energies for a) adsorption of *OH on all possible cus sites, b) ΔG ₂ on all possible bridge sites and c) ΔG ₂ on all possible cus sites as calculated with the fitted model. Gaussian fits to each distribution are drawn in a, b, as guide to the eye. Black lines in c) indicate the volcano defined by the conventional scaling relation.

To make a fit for *O+H_b, an additional 150 adsorption energies are calculated. This is because an individual fit is made for each of the 15 different combinations of two metal atoms in the bridge adsorption site, thus more data is required than for the cus adsorption energies. Slabs with *O are used as reference such that the calculated energy is the adsorption energy of H_b on a bridging oxygen with a hydrogen bond to *O, corresponding to −ΔG ₂. In this way the fingerprint of the adsorption site is that of the bridge site only, as shown in Figure 2a. The expression for E ⁱ _ads is of a similar form to Equation (2), but with additional coefficients to reflect that the bridge site has five different types of NN sites. The linear fits result in 15 distributions of adsorption energies (plotted as ΔG ₂ in Figure 4b) that together span an energy range of 1.5 eV. Figure 4c shows a corresponding plot of ΔG ₂ using the predicted energies of *OH. A lowering of the *OH energy corresponds to moving along the x‐axis, thus it can be seen that for an Os cus site there are many bridge adsorption sites that result in a lower energy, consistent with the plot in Figure 3b showing that most Os sites will follow the bridge pathway. Conversely, for most Rh cus sites it is impossible to find a bridge site with a lower adsorption energy. The volcano representing the conventional pathway is also plotted in Figure 4c, showing that, if the bridge pathway is not active, Ti sites have the lowest possible overpotential within the scaling relation, while Rh and Ir sites have overpotentials slightly higher than the optimum value.

The final goal of our study is to optimise the composition of the HEO to increase the likelihood of finding one of the highly active sites. However, it is not possible to create a histogram of overpotentials that include both the conventional and the bridge pathway. This is because each bridge site has two neighbouring cus sites, but it can only accept a proton from one of them, and each cus site can use at most one of the two neighbouring bridge sites, resulting in a coupling between all sites on the surface. To identify the optimum composition a brute‐force search is therefore performed. For all possible compositions in 10 % intervals, a 100×100 surface is randomly generated and the total current arising from that surface (j _tot) is calculated as a sum of the currents from the N(=10 000) individual sites (j_i ) (c.f. Section S6 of the Supporting Information for details):

$${\displaystyle j_{\mathrm{t}\mathrm{o}\mathrm{t}}=\sum _i^N{j}_i}$$ (3)

The current arising from an individual site, i, is calculated as:

$${\displaystyle \frac{1}{j_i}=\frac{1}{j_k}+\frac{1}{j_d}}$$ (4)

where j _d is the diffusion current and j _k is the kinetic current at the given potential (U) arising from the electrochemical reaction:

$${\displaystyle j_{\mathrm{k}}=\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{-\left|{\Delta G}_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\Delta G}_{\mathrm{o}\mathrm{p}\mathrm{t}}\right|+\Delta G_{\mathrm{o}\mathrm{p}\mathrm{t}}-eU}{k_{\mathrm{b}}T}\right)}$$ (5)

where k _b is the Boltzmann constant and T is the temperature, here taken to be 298 K, ΔG _max is the largest of the reaction free energies ΔG ₁–ΔG ₄, and ΔG _opt is the optimal value, which is 1.3 eV within the scaling relations of the Ir bridge site.

The value of j _d in Equation (4) deserves some consideration. In the case of ORR, the reactant is O₂ which is only present at a low concentration and diffusion is thus a limitation except at low overpotentials, giving rise to the typical sigmoid shape of the polarisation curves. In the case of OER the reactant is water, which is always present at the active site and the polarisation curves have the shape of an exponential, indicating that they are dominated by the kinetic current. Based on this observation, one could consider setting j _d=$\infty$ . This would be possible for a homogeneous surface since all sites become active at the same time, but for a heterogeneous surface it would imply that the current produced by the surface is dominated by the site with the lowest overpotential, even if this is the only active site on a macroscopic surface. Thus, j _d describes the balance between having a few sites that are very active (high j _d) or having a larger number of sites that are less active (low j _d) and it is necessary to choose a finite value for our HEO. Tafel plots for RuO₂ and IrO₂, ^[17] show that the current increases exponentially over at least two orders of magnitude, and a value of j _d=100 is therefore chosen. It should be noted that, plotting j _tot/j _max against potential, where j _max is the maximum possible current assuming all sites on the surface are fully active, produces curves with identical shapes for any choice of j _d, which are shifted along the potential axis by 58 mV when j _d is increased by a factor of 10 (See Section S6 of the Supporting Information). Thus, varying the value of j _d is equivalent to evaluating the optimum composition at different potentials.

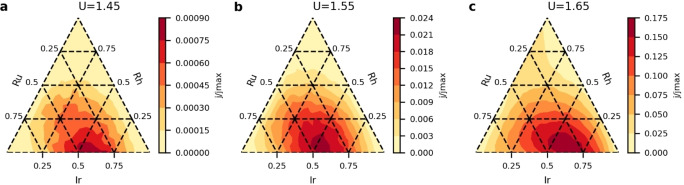
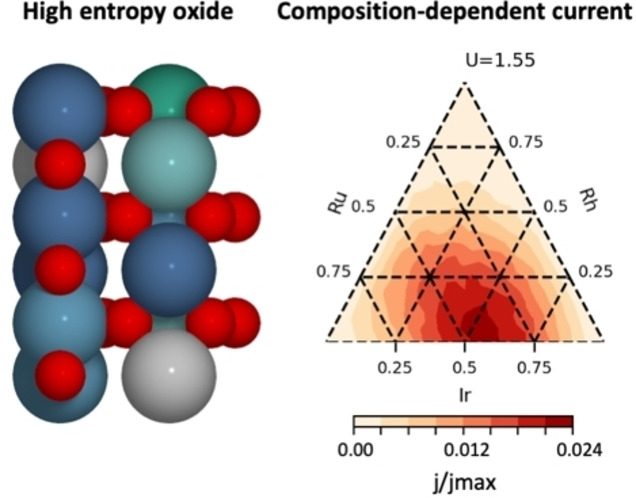
Considering only the low overpotential region, our surface model shows that the most active compositions are combinations of Ir, Ru and in some cases a small amount of Rh. This region of composition space is therefore investigated further with a 5 % resolution, and the resulting most active compositions at different potentials are listed in Table 1. Figure 5 shows the current as a function of potential for combinations of these three elements.

Table 1.

Optimum composition at different potentials, current relative to the equimolar composition (j _tot/j _eq) and current as a fraction of the maximum possible current within the model (j _tot/j _max).

U/V	Opt. Comp.	j tot/j eq	j tot/j max
1.45	Ru45Ir55O2	12.9	0.0009
1.55	Ru40Ir55Rh0.05O2	9.0	0.02
1.65	Ru35Ir60Rh0.05O2	6.2	0.17
1.75	Ru30Ir70O2	5.1	0.45

Figure 5.

Current as a function of composition for combinations of Ru, Ir and Rh at a potential of a) 1.45 V, b) 1.55 V and c) 1.65 V.

The current relative to the maximum current when all sites are fully active is also given in Table 1, giving an indication of the fraction of surface sites that are active at a given potential. In all cases, most of the highly active sites are Ir‐sites but a larger fraction of Ru results in a lower overpotential for these sites, while a higher fraction of Ir leads to a larger number of active sites with slightly higher overpotentials. The results are consistent with experimental observations that a combination of Ru and Ir can result in a higher catalytic performance than any of the two pure oxides.[ ^14c , ¹⁸ ] We note that this result would not have been obtained if only the conventional pathway had been considered. As can be seen from the histogram of ΔG ₂ values and the relative position of the conventional volcano in Figure 4c, Ti sites have the highest activity for this pathway, and the optimised compositions thus primarily consists of Ti, Rh and Os (c.f. Section S6 of the Supporting Information).

Conclusion

The catalytic properties of a high entropy oxide for the oxygen evolution reaction have been investigated. The different local environments around the catalytically active sites result in a distribution of adsorption energies for the catalytic intermediates and therefore also in a range of overpotentials, with some sites having lower overpotentials than any of the pure oxides. The composition with the highest catalytic activity depends on the assumed reaction path; considering only the conventional pathway the optimised composition is heavy in Ti, while the inclusion of the bridge pathway reveals a mixture of Ru, Ir and possibly a small amount of Rh as the optimum. Our work describes a route to identify the optimum composition of a catalyst within a complex composition space and furthermore highlights the importance of a detailed understanding of the catalytic processes in order to perform such optimisations.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

K. L. Svane, J. Rossmeisl, Angew. Chem. Int. Ed. 2022, 61, e202201146; Angew. Chem. 2022, 134, e202201146.

Data Availability Statement

DFT optimised structures and scripts used to analyse the data and generate the figures are available from https://nano.ku.dk/english/research/theoretical‐electrocatalysis/katladb/high‐entropy‐oxides‐oer/.