A Poisson-multinomial spatial model for simultaneous outbreaks with application to arboviral diseases

Abstract

Dengue, Zika, and chikungunya are arboviral diseases (AVD) transmitted mainly by Aedes aegypti. Rio de Janeiro city, Brazil, has been endemic for dengue for over 30 years, and experienced the first joint epidemic of the three diseases between 2015-2016. They present similar symptoms and only a small proportion of cases are laboratory-confirmed. These facts lead to potential misdiagnosis and, consequently, uncertainty in the registration of the cases. We have available the number of cases of each disease for the $n=160$ neighborhoods of Rio de Janeiro. We propose a Poisson model for the total number of cases of Aedes-borne diseases and, conditioned on the total, we assume a multinomial model for the allocation of the number of cases of each of the diseases across the neighborhoods. This provides simultaneously the estimation of the associations of the relative risk of the total cases of AVD with environmental and socioeconomic variables; and the estimation of the probability of presence of each disease as a function of available covariates. Our findings suggest that a one standard deviation increase in the social development index decreases the relative risk of the total cases of AVD by 28%. Neighborhoods with smaller proportion of green area had greater odds of having chikungunya in comparison to dengue and Zika. A one standard deviation increase in population density decreases the odds of a neighborhood having Zika instead of dengue by 18% but increases the odds of chikungunya in comparison to dengue by 18% and by 43% in comparison to Zika.

1. Motivation

In the last decade, the abundant presence of Aedes mosquitoes and the high human mobility allowed the rapid establishment and spread of emerging arboviruses in several tropical countries. In Brazil, for more than 30 years the public actions were insufficient to control dengue, an arboviral disease that caused over 1.5 million probable cases and 782 confirmed deaths in 2019 (Ministério da Saúde and Secretaria de Vigilância em Saúde, 2020). Between 2015 and 2016, Zika and chikungunya viruses, also transmitted by Aedes mosquitoes, caused epidemics in the country, alongside with a dengue one, in a phenomenon that has been called “triple epidemic”. ¹ Any suspected case of dengue, Zika or chikungunya, assisted in health care facilities, has to be reported to the Brazilian Notifiable Diseases Information System (SINAN – Sistema de Informação de Agravos de Notificação), with a specification of the probable diagnosis. However, because the three diseases share similar symptoms, the correct diagnosis is hindered without laboratory exams, while only a small proportion of the cases are actually tested (418,572 in 1,543,665, or 27.1%, dengue cases were laboratory-confirmed in 2019). Therefore, for most cases the diagnosis is based solely on clinical-epidemiological criteria. Because misdiagnosis is common, especially in a scenario of co-circulation such as the triple epidemic, there is an uncertainty associated with the registered cases.^2,3 Taking this into account, we propose a Poisson model for the total number of cases of arboviral diseases and, conditioned on the total number of cases, we assume a multinomial model for the number of cases of the three diseases. The model is motivated by data from the city of Rio de Janeiro, Brazil, which experienced a triple epidemic between 2015 and 2016.

Rio is the main tourist destination in Brazil and has a long history of fighting dengue. With nearly 6.3 million inhabitants, Rio’s territory presents different environmental and socioeconomic characteristics that are involved in the spatial distribution of Aedes-borne diseases. ⁴ Aedes aegypti - dengue, Zika and chikungunya main vector in Brazil - is highly adapted to urban settings. In fact, more urbanized locations favors the ecology of the mosquito.^5,6 Additionally, poorer sanitary conditions are associated with the presence of potential breeding sites for the mosquito, such as containers filled with rain water that can be found in inadequate garbage disposal.^7,8 For this analysis, we have available the proportion of green area (which is inversely associated with the level of urbanization in Rio), the social development index (an index that includes different socioeconomic indicators, including some related with sanitary conditions and level of income) and the population density. The population density is associated with the number of arboviral diseases cases, with higher density favouring the contact between the mosquito and the human host. ⁷ Our goal is to investigate how these covariates are associated with the spatial distribution of cases of dengue, Zika and chikungunya during the triple epidemic. Figure 1 shows the distribution of the available covariates across the $n=160$ neighborhoods of Rio.

Figure 1.

Spatial distribution of the (a) levels of the social development index (SDI) in 2010, (b) observed percentage of green area in 2015, and (c) the population density (inhab/ $m^2$ ) in 2010, across the neighborhoods of the city of Rio de Janeiro, Brazil.

1.1. Literature review

The modelling of observed counts of multiple diseases across a spatial region has experienced an enormous growth in the last three decades. Assume that the number of registered cases of each of the diseases is available for each of the neighborhoods of Rio. A typical approach is to assume that each of the disease counts follow conditionally independent Poisson distributions whose mean is described by the product of an offset and the relative risk associated with each disease. In the case of multiple diseases, it is common practice to decompose the log-relative risk as the sum of fixed effects and some latent, multivariate, spatially structured random effect. Commonly, this latent component follows a multivariate conditional autoregressive model (MCAR). ⁹ There are different proposals in the literature on how to parametrize the MCAR component. See Banerjee ¹⁰ for a review of multivariate spatial models for areal data.

In Section 2 we propose an alternative approach to the one described above for modelling counts related to multiple diseases observed across the neighborhoods of a city. We have available observations associated with diseases transmitted by the same vectors that share some similar symptoms. It is of interest to health authorities to model the number of cases of each of the diseases, together with the total number of cases of the three diseases across the neighborhoods of Rio de Janeiro. Understanding how the total number of cases was distributed across the city during this first joint epidemic is important as it allows the identification of areas that were hit hardest and may also be at-risk for future emerging Aedes-borne diseases outbreaks. In particular, we propose a Poisson model for the total number of cases of urban Aedes-borne diseases for each neighborhood of the city, and conditional on the total number of cases, we model the probability of presence of cases of dengue, Zika and chikungunya for each neighborhood.

The idea of combining a model for the total cases and, conditioned on the total, model the components of the sum that make up the total is not new. Terza and Wilson ¹¹ propose a mixed Poisson-multinomial approach to jointly predict households’ choices among types of trips and frequency of trips. In particular, they propose a multinomial Poisson-hurdle model (MPH). As they point out, the advantage of the MPH model over the multinomial Poisson model is that if the multinomial probabilities are modelled as multinomial logit, the latter reduces to the product of conditionally independent Poisson distributions. We discuss the parametrization issue of the unknowns in the Poisson and multinomial distributions in detail in Sections 2.1 and 2.2. Baker ¹² discusses advantages of the multinomial-Poisson transformation to simplify maximum likelihood estimation. Illian et al. ¹³ approximate a Poisson point process model through the number of occurrences of plants on a grid cell, and conditioned on this observed number of occurrences, they let the number of plants categorized as being healthy, or not, in a given grid cell, follow a binomial distribution. In a sense, our proposed approach to model the cases of the three Aedes-borne diseases extends the model of Illian et al. ¹³ by considering three possible categories (the different diseases) for the allocation of the total cases.

Using a multinomial distribution to model multivariate counts of diseases has been proposed before. Knorr-Held et al. ¹⁴ model cumulative probabilities of disease risk; in particular they model the probability that a person is diagnosed with the disease in a specific stage given that they are diagnosed in this or in a higher stage. Dreassi ¹⁵ proposes a polytomous logit model, wherein the counts of oral cavity, larynx and lung cancers observed across municipalities of the Region of Tuscany are modelled as following a multinomial distribution. Different from our proposed approach, the resultant covariance structure imposed by this assumption is not discussed, and the total number of cases of the three diseases at each municipality is assumed known.

This paper is organized as follows. Section 2 discusses the proposed model for the total of cases, and the distribution of the total across the different Aedes-borne diseases: dengue, Zika and chikungunya. We discuss different parametrizations for the probability of each of the diseases within a neighborhood in the city. Then Section 3 starts by briefly describing the results of a simulation study (see Section D of the Supplementary Material) performed to make sure that we are able to estimate the parameters of the proposed model; then it focuses on the analysis of cases related to the first joint epidemic of dengue, Zika and chikungunya in Rio de Janeiro. Section 4 concludes by discussing our findings and pointing out future avenues of research.

2. Proposed Model

Let $D_i$ , $Z_i$ and $C_i$ denote, respectively, the number of registered cases of dengue, Zika and chikungunya in neighborhood $i$ of the city of Rio de Janeiro, Brazil during the period of the joint epidemic, from August, 2 2015 until December, 31 2016. And let $tota{l}_i=(D_i+Z_i+C_i)$ be the total number of cases of Aedes-borne diseases, and ${\mathbf{y}}_i=(y_1,y_2,y_3{)}_i=(D,Z,C{)}_i^{\prime }$ be a 3-dimensional vector, with components containing the number of registered cases of each of the three diseases in neighborhood $i$ , $i=1,2,\dots ,n=160$ . We propose a joint model for $(total,\mathbf{y}{)}_i$ such that

$$\begin{array}{r}p(tota{l}_i,{\mathbf{y}}_i\mid \mathbf{\Theta })=\{\begin{array}{cc}p(tota{l}_i\mid \mathbf{\Theta })p({\mathbf{y}}_i\mid tota{l}_i,\mathbf{\Theta }),& tota{l}_i>0\\ p(tota{l}_i=0\mid \mathbf{\Theta }),& tota{l}_i=0,\end{array}\end{array}$$ (1)

where $\mathbf{\Theta }$ represents the parameter vector involved in the probability density functions (pdf’s) of the $tota{l}_i$ and the vector ${\mathbf{y}}_i$ . The $tota{l}_i$ , $i=1,\dots ,n$ is modelled as conditionally independent realizations from a Poisson distribution, such that

$$(tota{l}_i\mid {\lambda }_i,E_i)\sim Poisson(E_i{\lambda }_i),$$ (2)

where $E_i=(\frac{\sum _{i=1}^n(total{)}_i}{\sum _{i=1}^{n}populatio{n}_i}\times populatio{n}_i)$ is the offset term and it is based on the total number of arboviral disease cases in neighborhood $i$ ; and ${\lambda }_i$ is the relative risk associated with the total number of cases of Aedes-borne diseases. And when $tota{l}_i>0$ , the conditional distribution of $({\mathbf{y}}_i\mid tota{l}_i,\mathbf{\Theta })$ follows a multinomial distribution with parameters $tota{l}_i$ and ${\pi }_i=({\pi }_{i1},{\pi }_{i2},{\pi }_{i3},{)}^{\prime }$ , that is,

$$({\mathbf{y}}_i\mid tota{l}_i,{\pi }_i)\sim Multinomial(tota{l}_i,{\pi }_i),$$ (3)

where ${\pi }_i$ is the vector of probabilities of occurrence of dengue, Zika or chikungunya in neighborhood $i$ , with $\sum _{k=1}^3{\pi }_{ik}=1$ . The co-circulation of dengue, Zika and chikungunya makes the correct diagnosis without laboratory confirmation difficult, as the diseases share very similar symptoms. In the context of the first joint epidemic, this issue was probably aggravated by the lack of experience with Zika and chikungunya by healthcare workers, and possibly because they were not initially aware of the circulation of these diseases. As a consequence, many Zika and chikungunya cases may have been notified as dengue, which has been endemic in the city for decades.

Note that the assumption of a multinomial distribution for ${\mathbf{y}}_i$ implicitly assumes that the outcomes are mutually exclusive with corresponding probabilities ${\pi }_{ik}$ . We believe this is a reasonable assumption as recent studies have suggested that co-infection of the different arboviruses rarely happens.^16,17

2.1. Modelling ${\lambda }_i\mathbf{a}\mathbf{n}\mathbf{d}{\pi }_i$

For the relative risk ( ${\lambda }_i$ ) of the total of vector borne diseases in neighborhood $i$ , we assume

$$\log {\lambda }_i={\mathbf{X}}_i^{\prime }\beta +{\theta }_{i1},$$ (4)

where ${\mathbf{X}}_i$ is a $p$ -dimensional vector of covariates observed in neighborhood $i$ , including an intercept, $\beta =({\beta }_1,\dots ,{\beta }_p{)}^{\prime }$ is a $p$ -dimensional vector of coefficients and ${\theta }_{i1}$ is a random effect for neighborhood $i$ which captures whatever structure is left after adjusting for the covariates. The prior specification of ${\theta }_{i1}$ is described below. Note that as is usual in Poisson regression, $\exp ({\beta }_j)$ represents the relative risk of an one unit increase in $X_{ij}$ , for $j=1,\dots ,p$ keeping the other $X_{il}$ ’s, for $l\ne j$ , and ${\theta }_{i1}$ fixed.

For ${\pi }_{ik}$ we assume a baseline-category logit model, ¹⁸ such that

$$\begin{array}{rl}\log \left(\frac{{\pi }_{ik}}{{\pi }_{i1}}\right)& =\log \left(\frac{P({\mathbf{y}}_i=k\mid {\mathbf{y}}_i=1\text{ or }{\mathbf{y}}_i=k)}{1-P({\mathbf{y}}_i=k\mid {\mathbf{y}}_i=1\text{ or }{\mathbf{y}}_i=k)}\right)\\ & ={\mathbf{X}}_i^{\prime }{\alpha }_{\mathbf{k}}+{\theta }_{ik},k=2,3,\end{array}$$ (5)

where the coefficients of the covariates vary with $k$ and $\exp ({\alpha }_{kj})$ represents the odds ratio between Zika ( $k=2$ ) or chikungunya ( $k=3$ ) and dengue ( $k=1$ ) of an one unit increase in $X_{ij}$ , $j=1,\dots ,p$ . In other words, dengue is chosen as the baseline category; this is because it is endemic in Rio de Janeiro for more than 30 years. Following equation (5), we model the conditional probability of presence of Zika ( $k=2$ ) given that it is Zika or dengue, and the conditional probability that it is chikungunya ( $k=3$ ) given that it is chikungunya or dengue. Note that the model in (5) also determines the equation for $\log (\frac{{\pi }_{i3}}{{\pi }_{i2}})$ as $\log (\frac{{\pi }_{i3}}{{\pi }_{i2}})=\log (\frac{{\pi }_{i3}}{{\pi }_{i1}})-\log (\frac{{\pi }_{i2}}{{\pi }_{i1}})$ ¹⁸ which according to equation (5) is given by

$$\log \left(\frac{{\pi }_{i3}}{{\pi }_{i2}}\right)={\mathbf{X}}_i^{\prime }({\alpha }_3-{\alpha }_2)+({\theta }_{i3}-{\theta }_{i2}).$$ (6)

We follow the Bayesian paradigm to obtain samples from the resultant posterior distribution of the parameter vector. Once a sample is available, it is straightforward to obtain samples from ${\alpha }^{*}=({\alpha }_3-{\alpha }_2)$ and ${\theta }_i^{*}=({\theta }_{i3}-{\theta }_{i2})$ , for $i=1,2,\dots ,n$ . As $\sum _{k=1}^3{\pi }_{ik}=1$ , it follows from (5) that

$${\pi }_{ik}=\frac{\exp ({\mathbf{X}}_i^{\prime }{\alpha }_{\mathbf{k}}+{\theta }_{ik})}{1+\sum _{k=2}^3\exp ({\mathbf{X}}_i^{\prime }{\alpha }_{\mathbf{k}}+{\theta }_{ik})}\text{ for }k=2,3,\text{ and }{\pi }_{i1}=\frac{1}{1+\sum _{k=2}^3\exp ({\mathbf{X}}_i^{\prime }{\alpha }_{\mathbf{k}}+{\theta }_{ik})}.$$

Following equations (1), (4), and (5), it results that the joint distribution of $tota{l}_i$ and ${\mathbf{y}}_i$ for each neighborhood $i$ is given by

$$\begin{array}{rl}& p(tota{l}_i,{\mathbf{y}}_i\mid \mathbf{\Theta })=\left(\frac{\exp (-{\lambda }_i){{\lambda }_i}^{tota{l}_i}}{tota{l}_i!}\right)\frac{tota{l}_i!}{y_{i1}!y_{i2}!y_{i3}!}\prod _{k=1}^3{\left({\pi }_{ik}\right)}^{y_{ik}}\\ & =\left(\frac{\exp (-{\lambda }_i)\exp \left[y_{i1}({\mathbf{X}}_i^{\prime }\beta +{\theta }_{i1})\right]}{y_{i1}!y_{i2}!y_{i3}!}\right){\left(\frac{1}{1+\sum _{k=2}^3\exp ({\mathbf{X}}_i^{\prime }{\alpha }_{\mathbf{k}}+{\theta }_{ik})}\right)}^{tota{l}_i}\\ & \prod _{k=2}^3\left\{\exp \left[y_{ik}({\mathbf{X}}_i^{\prime }({\alpha }_{\mathbf{k}}+\beta )+{\theta }_{ik}+{\theta }_{i1})\right]\right\},\end{array}$$ (7)

with the total number of cases and the vector ${\mathbf{y}}_i$ clearly involved in the joint distribution of $(tota{l}_i,{\mathbf{y}}_i)$ . We denote the model defined by equations (4) and (5) as the Poisson-Multinomial model.

Modelling ${\theta }_{ik}$

The components ${\theta }_{ik}$ , $k=1,2,3$ , are present in the model to capture whatever is left after adjusting for the available covariates. As the three diseases are transmitted by the same vectors we assume that, conditional on a local effect ${\varphi }_i$ , ${\theta }_{i.}=({\theta }_{i1},{\theta }_{i2},{\theta }_{i3}{)}^T$ follows conditional independent multivariate normal distributions with covariance $\mathbf{\Sigma }$ , that is,

$${\theta }_{i.}\sim N_3[{\mathbf{1}}_3{\varphi }_i,\mathbf{\Sigma }],\text{ for }i=1,2,\dots ,n,$$

where ${\mathbf{1}}_3$ is a 3-dimensional column-vector with all elements equals $1$ . This prior specification induces a correlation among the latent components in the different stages of the model, as within neighborhood $i$ the ${\theta }_{ik}$ ’s share a common effect ${\varphi }_i$ . This is an important assumption as ${\varphi }_i$ captures unobserved effects that are common to the spread of the three diseases. The covariance matrix $\mathbf{\Sigma }$ captures possible covariance structure among the diseases that is left after accounting for the common effect ${\varphi }_i$ .

To understand the correlation structure induced by this prior specification of the ${\varphi }_i$ ’s, assume that $\varphi =({\varphi }_1,\dots ,{\varphi }_n{)}^{\prime }$ follows a proper conditional autoregressive prior distribution (see e.g., Banerjee et al. ¹⁹ ) such that $\varphi \sim N_n(\mathbf{0},\mathrm{\Sigma })$ , where $\mathrm{\Sigma }=[{\sigma }^2({\mathbf{D}}_w-\rho \mathbf{W}){]}^{-1}$ , where the parameter $\rho$ controls spatial dependence and ensures propriety of the prior distribution as long as $\rho \in (1/{\rho }_{min};1/{\rho }_{max})$ where ${\rho }_{min}$ and ${\rho }_{max}$ are, respectively, the minimum and maximum eigenvalues of ${\mathbf{D}}^{-1/2}\mathbf{W}{\mathbf{D}}_w^{-1/2}$ ; $\mathbf{W}$ is a $n$ -dimensional neighborhood matrix and ${\mathbf{D}}_w$ is a diagonal matrix with elements $w_{i+}=\sum _j{w}_{ij}$ . If a 0-1 neighborhood structure is assumed, then the conditional distribution of each ${\varphi }_i$ given its neighbors is

$${\varphi }_i\mid {\varphi }_{j\in {\delta }_i}\sim N(\frac{\rho \sum _{j\in {\delta }_i}{\varphi }_j}{n_i},\frac{{\sigma }^2}{n_i}),$$

where ${\delta }_i$ is an index set of the neighboring neighborhoods of $i$ , $i=1,2,\dots ,n$ . When $\rho =1$ the prior distribution of $\varphi$ is the well known intrinsic conditional autoregressive (CAR) ²⁰ distribution which is an improper distribution. In case the prior distribution for $\varphi$ is proper then $Cov({\varphi }_i,{\varphi }_j\mid \rho ,{\sigma }^2,{\varphi }_l,l\ne i,j)=\frac{{\sigma }^2\rho w_{ij}}{w_{i+}{w}_{j+}\rho w_{ij}^2}$ and $Var({\varphi }_i)=\frac{{\sigma }^2}{w_{i+}}$ . ²¹ Using the law of total covariance it can be shown that the marginal covariance between the latent components ${\theta }_{ik}$ and ${\theta }_{jl}$ for $i,j=1,2,\dots ,n$ and $k,l=1,2,3$ is given by

$$\begin{array}{r}Cov({\theta }_{ik},{\theta }_{jl})=\{\begin{array}{cc}\frac{{\sigma }^2\rho w_{ij}}{w_{i+}{w}_{j+}\rho w_{ij}^2},& \text{if }i\ne j\text{ and }k\ne l,\\ \frac{{\sigma }^2}{w_{i+}}+{\mathrm{\Sigma }}_{kl},& \text{if }i=j\text{ and }k\ne l,\\ {\mathrm{\Sigma }}_{kk}+\frac{{\sigma }^2}{w_{i+}},& \text{if }i=j\text{ and }k=l.\end{array}\end{array}$$ (8)

Clearly there is a covariance structure being imposed among the latent effects that go in the equations for ${\lambda }_{ik}$ and $\log \frac{{\pi }_{ik}}{{\pi }_{i1}}$ . We believe this is a reasonable assumption as the diseases are transmitted by the same vectors and their spatial distribution is highly influenced by the vectors’ ecology.

As suggested by a reviewer, we compare the proposed parametrization of ${\theta }_{i.}$ above with a separable multivariate conditional autoregressive (MCAR) model. ²² This is described in detail in Section 3.

2.2. Comparison of the proposed approach with a standard one

When cases of different diseases are available across the neighborhoods of a city, a straightforward way to proceed is to assume that each of the counts are conditionally independent realizations from a Poisson distribution (see e.g., Jin et al. ²² ), that is,

$$y_{ik}\mid E_i,{\delta }_{ik}\sim Poisson(E_i{\delta }_{ik}).$$ (9)

To complete model specification, one can assume

$$\log {\delta }_{ik}={\mathbf{X}}_i^{\prime }{\gamma }_k+{\theta }_{ik},$$ (10)

where ${\theta }_{ik}$ are latent components that capture whatever is left after adjusting for the covariates considered in the $p$ -dimensional vector of covariates ${\mathbf{X}}_i$ , and ${\gamma }_k$ is a $p$ -dimensional vector of coefficients, allowing the relative risk of each disease to have its own set of coefficients. For example, Xin et al. ²² discuss different multivariate structures of the latent effect ${\theta }_{ik}$ to capture possible correlations among the counts ${\mathbf{y}}_i$ .

Next we show that this approach is equivalent to a particular parametrization of the proposed model for the total cases of Aedes-borne diseases and the distribution of counts of cases, ${\mathbf{y}}_i$ , described, respectively, in equations (2) and (3). In equations (2) and (3), let

$${\lambda }_i=\sum _{k=1}^3{\delta }_{ik}\text{ and }{\pi }_{ik}=\frac{{\delta }_{ik}}{{\lambda }_i},\text{ for }i=1,2,\dots ,n\text{ and }k=1,2,3,$$ (11)

then, from equation (1) and when $tota{l}_i>0$ , it follows that

$$\begin{array}{rl}p(tota{l}_i,{\mathbf{y}}_i\mid \mathbf{\Theta })& =\left(\frac{\exp (-{\lambda }_i){{\lambda }_i}^{tota{l}_i}}{tota{l}_i!}\right)\frac{tota{l}_i!}{y_{i1}!y_{i2}!y_{i3}!}\prod _{k=1}^3{\left(\frac{{\delta }_{ik}}{{\lambda }_i}\right)}^{y_{ik}}\\ & =\prod _{k=1}^3\frac{\exp (-{\delta }_{ik}){{\delta }_{ik}}^{y_{ik}}}{y_{ik}!},\end{array}$$ (12)

which results from the relationship between the Poisson and multinomial distributions. Note that the distribution in (12) does not depend on $tota{l}_i$ . Assuming ${\lambda }_i$ and ${\pi }_i$ as in equation (11) is equivalent to assume that each $y_{ik}$ follows independent Poisson distributions. We denote the model in (9) as the multivariate Poisson model.

2.3. Inference procedure and model comparison

Let $\mathbf{t}\mathbf{o}\mathbf{t}=(tota{l}_1,\dots ,tota{l}_n{)}^{\prime }$ and $\mathbf{y}=({\mathbf{y}}_1,\dots ,{\mathbf{y}}_n{)}^{\prime }$ be, respectively, the vectors containing the observations associated with the total number of Aedes-borne diseases and the observed allocation of these number of cases among dengue, Zika and chikungunya for each neighborhood $i$ in Rio de Janeiro. Inference procedure is performed under the Bayesian framework. Model specification is complete after assigning a prior distribution for the parameter vector of the model, $\mathbf{\Theta }=(\beta ,{\alpha }_2,{\alpha }_3,\theta ,{\sigma }^2,{\tau }^2{)}^{\prime }$ , where ${\alpha }_k=({\alpha }_{k1},\dots ,{\alpha }_{kp}{)}^{\prime }$ , $\theta =({\theta }_{11},\dots ,{\theta }_{n1},{\theta }_{12},\dots ,{\theta }_{n2},\dots ,{\theta }_{n3}{)}^{\prime }$ , and ${\tau }^2=({\tau }_1^2,{\tau }_2^2,{\tau }_3^2{)}^{\prime }$ . The prior specification for the elements of $\theta$ have already been discussed above. For the other parameters in the model we assign independent prior distributions. For the coefficients of the covariates we assign a zero mean prior normal distribution with reasonably large variances, and we assign independent half-Cauchy ²³ prior distributions to the standard deviations, ${\tau }_k$ and $\sigma$ . Following Bayes’ theorem, the posterior distribution is proportional to the likelihood function times the prior distribution, that is

$$\begin{array}{rl}& p(\mathbf{\Theta }\mid \mathbf{t}\mathbf{o}\mathbf{t},\mathbf{y})\propto [\prod _{i=1}^{n}p(tota{l}_i,{\mathbf{y}}_i\mid \mathbf{\Theta })][\prod _{i=1}^n\prod _{k=1}^{3}p({\theta }_{ik}\mid {\varphi }_i,{\tau }_k^2)]\\ & [\prod _{i=1}^{n}p({\varphi }_i\mid {\sigma }^2)]\prod _{j=1}^{p}p({\beta }_j)\prod _{k=2}^3\prod _{j=1}^{p}p({\alpha }_{kj})\prod _{k=1}^{3}p({\tau }_k)p({\sigma }^2),\end{array}$$ (13)

which does not have a closed form. Posterior samples from $\mathbf{\Theta }$ are obtained through Markov chain Monte Carlo (MCMC) methods. Section A of the Supplementary Material shows the posterior full conditional distributions of the parameters. Here, in particular, we use the software Stan ²⁴ within the package RStan in R ²⁵ to obtain posterior samples of interest. Note that Stan makes use of Hamiltonian Monte Carlo to sample from the target distribution of interest. For each of the models, we run three chains, each for $10,000$ iterations and considered the first $3,000$ as burn-in and stored every 7-th sampled value. Convergence of the chains was checked following the tools proposed in Vehtari et al. ²⁶ . Section C of the Supplementary Material provides trace plots of the fixed effects and summaries of a couple of statistics suggested by Vehtari et al. ²⁶ .

In the following Section we fit different models to the data and we use three model comparison criteria to compare the fitted models: the widely available information criterion (WAIC), ²⁷ the logarithm Score (logS) ²⁸ and the energy score (es). ²⁹ Section B of the Supplementary Material describes in more detail these three criteria.

3. Data Analysis

Before fitting the proposed model to the dataset described in Section 1 we performed a simulation study to check if we were able to recover the true values of the parameters that are used to generate the data. The results of the simulation study are shown in Section D of the Supplementary Material. They suggest that we recover both the coefficients of the covariates in equations (4) and (5) as well as the random effects ${\theta }_{ik}$ .

We now proceed with the analysis of the data for the number of cases of dengue, Zika, and chikungunya for each neighborhood of the city of Rio de Janeiro. As described in Section 1, the available covariates are the social development index, the proportion of green area of each neighborhood, and the population density, such that in the fitted models we consider ${\mathbf{X}}_i=(1,\text{SDI},\text{green area},\text{,pop. dens.}{)}_i^T$ . For each of the parameterizations in equations (4)–(5) and (10), we fit four different models considering different structures for ${\theta }_{ik}$ . These different structures are particular cases of the general model proposed in Section 2. We also fit a separable MCAR model. The fitted models are the following:

• M0: ${\theta }_{ik}={\varphi }_i$ , for $k=1,2,3\text{ and }i=1,2,\dots ,n$ ;
• M1: ${\theta }_{i1}={\varphi }_i$ , ${\theta }_{i2}={\gamma }_1{\varphi }_i$ and ${\theta }_{i3}={\gamma }_2{\varphi }_i$ , for $i=1,2,\dots ,n$ ;
• M2: $({\theta }_{ik}\mid {\varphi }_i,{\tau }^2)\stackrel{\text{indep.}}{\sim }N({\varphi }_i,{\tau }^2)$ , a priori, for $k=1,2,3\text{ and }i=1,2,\dots ,n$ ;
• M3: $({\theta }_{ik}\mid {\varphi }_i,{\tau }_k^2)\stackrel{\text{indep.}}{\sim }N({\varphi }_i,{\tau }_k^2)$ , for $k=1,2,3$ , and $i=1,2,\dots ,n$ ;
• M4: ${\theta }_{i.}=({\theta }_{i1},{\theta }_{i2},{\theta }_{i3}{)}^T\stackrel{\text{indep.}}{\sim }{N}_3[({\mathbf{1}}_3{)}^T{\varphi }_i,\mathbf{\Sigma }]$ , for $i=1,2,\dots ,n$ .
• M5: ${\theta }_i\sim MCAR(1,\mathbf{\Sigma })$ , that is, we follow the multivariate, separable, CAR model as described in Jin et al. ²² with ${\theta }_i=A{\varphi }_i$ , where $A$ is the Cholesky decomposition of a covariance matrix $\mathbf{\Sigma }$ , that captures the covariance among diseases, and ${\varphi }_i=({\varphi }_{i1},{\varphi }_{i2},{\varphi }_{i3}{)}^{\prime }$ with each ${\varphi }_{ik}$ following an independent CAR model with variance 1.

Note that the parameters ${\theta }_{ik}$ will have different interpretations under the parameterizations in equations (4)–(5) and (10). In what follows we focus on the interpretation based on equations (4)–(5). We also fit models M0–M5 under parameterization (10) (denoted as the multivariate Poisson model) in order to investigate the gain in fitting the Poisson-Multinomial model under parametrization (4)–(5).

Model M0 assumes that after adjusting for the covariates, whatever is left in equations (4) and (5) is the same and varies only per neighborhood. Model M1, on the other hand, assumes that ${\varphi }_i$ captures the residual structure after adjusting for the covariates in the model for the log relative risk of the total cases in (4), whereas the baseline-category logit models assume that this residual adjustment is proportional to ${\varphi }_i$ , such that ${\gamma }_j\in \mathbb{R}$ ( $j=1,2$ ) are parameters to be estimated; M2 assumes that the ${\theta }_{ik}$ ’s are independent realizations from the same normal distribution with mean ${\varphi }_i$ and same variance ${\tau }^2$ . Different from M2, model M3 allows the variances of the ${\theta }_{ik}$ ’s to change with the equations they are related with, such that each ${\theta }_{ik}$ has its own variance ${\tau }_k^2$ . Among these models, M4 is the more general proposed model, which allows the elements of ${\theta }_{i.}$ to be correlated within neighborhood $i$ even after accounting for the common mean ${\varphi }_i$ . Finally, model M5 does not include an independent effect, this is because we believe it would be challenging to identify spatial and independent components for each of the equations, (4)–(5), if some sort of prior correlation among them was not imposed. Models M2-M4 assume a single spatial structure for all diseases, which we find it reasonable because they are all caused by the same vector, so it is expected, a priori, that there is some common component they share.

Table 1 shows the values of WAIC and its components together with the logarithm Score (logS) and the energy score (es) under each of the fitted models. Regarding WAIC, the smallest value is attained by model M5 under the multivariate Poisson parametrization followed very closely by M5 under the Poisson-Multinomial parametrization, suggesting that, according to WAIC, there is not much evidence of one parametrization in favor of the other. When the logS is used for comparison, models M3, M4, and M5 also result in very similar values under both parametrizations. The energy score, however, suggests some difference between the parametrizations and results in smaller values under the Poisson-Multinomial parametrization when compared to the multivariate Poisson one. As the energy score better differentiates both parametrizations when compared to WAIC and the log Score, we now focus on the discussion of the results provided by models M4 under the Poisson-Multinomial parametrization and M3 under the multivariate Poisson parametrization, as these models resulted in the smallest values of the energy score.

Table 1.

Model comparison based on the Widely Applicable Information Criterion (WAIC), the logarithm Score (logS) and the energy score (es). For all three criteria, smaller values indicate better fitting models.

Model	Poisson-Multinomial model equations (4) and (5)					Poisson model equation (10)
	$elp{d}_{WAIC}$	$p_{WAIC}$	$WAIC$	logS	es	$elp{d}_{WAIC}$	$p_{WAIC}$	$WAIC$	logS	es
M0	$-8879.4$	788.2	17758.7	8351.22	84.08	$-7210.3$	658.9	14420.7	6783.48	76.67
M1	$-6653.5$	725.4	13307.0	6184.50	67.00	$-6639.9$	686.9	13279.8	6191.50	74.34
M2	$-3640.5$	369.8	7281.0	3409.22	30.41	$-3271.3$	342.1	6542.7	3055.96	29.59
M3	$-1876.2$	235.8	3752.3	1713.37	5.44	$-1875.3$	235.0	3750.6	1713.22	7.36
M4	$-1875.7$	236.2	3751.4	1712.53	5.43	$-1872.9$	233.5	3745.8	1711.76	7.38
M5	$-1869.9$	231.1	3739.7	1710.67	5.55	$-1869.2$	230.3	3738.5	1710.63	7.50

Columns of Table 2 show the posterior summary (mean and limits of the 95% credible interval) of the relative risk (column for the total) and odds ratio (columns “Zika-dengue”, “chik.-dengue” and “chik.-Zika”) of the Poisson-Multinomial model under model M4. Focusing on the column for the total, the overall relative risk for the total of cases of Aedes-borne diseases in the city of Rio de Janeiro during this period is 0.928. Clearly the relative risk of the total of Aedes-borne diseases decreases by, approximately, 28% with a standard deviation increase of SDI when the other covariates are held fixed. On the other hand, percentage of green area and population density do not seem to influence the relative risk of the total number of cases as $1$ is included in the respective 95% posterior credible intervals of the relative risks. Now, care must be taken when interpreting the posterior summaries in the remaining columns of Table 2. For the columns “Zika-dengue” and “chik.-dengue” the odds ratios are compared to dengue (see equation (5)), as dengue is the baseline category; and the odds ratio on the column “chik.-Zika” is the odds of a neighborhood having chikungunya when compared to Zika (see equation (6)).

Table 2.

Posterior summary (mean and 95% credible intervals in brackets) of the relative risks associated with each of the covariates in equation (4) for the relative risk of the total number of cases, and for the odds ratio of a neighborhood having Zika or chikungunya in comparison to dengue, and chikungunya in comparison to Zika (see equations (5)–(6)) under model M4.

	Equations associated with each of the coefficients Poisson-Multinomial model
Covariate	Total	Zika-dengue	chik.-dengue	chik.-Zika
	( ${\lambda }_i$ )	( ${\pi }_{i2}/{\pi }_{i1}$ )	( ${\pi }_{i3}/{\pi }_{i1}$ )	( ${\pi }_{i3}/{\pi }_{i2}$ )
Intercept	0.928	1.641	0.533	0.325
	(0.862 ; 0.997)	(1.490 ; 1.797)	(0.487 ; 0.583)	(0.284 ; 0.373)
SDI	0.725	1.071	0.962	0.899
	(0.662 ; 0.795)	(0.955 ; 1.194)	(0.850 ; 1.086)	(0.773 ; 1.043)
Pct green area	0.963	1.020	0.816	0.803
	(0.868 ; 1.060)	(0.903 ; 1.146)	(0.722 ; 0.923)	(0.685 ; 0.930)
Pop. density	0.964	0.825	1.175	1.430
	(0.860 ; 1.071)	(0.717 ; 0.954)	(1.006 ; 1.358)	(1.179 ; 1.713)

Clearly all the coefficients for SDI include $1$ in the respective 95% posterior credible intervals of the odds ratios, suggesting that a one standard deviation increase in SDI does not change the odds of a neighborhood having cases of Zika (column “Zika-dengue”) or chikungunya (column “chik.-dengue”) when compared to dengue, or even the odds of a neighborhood having chikungunya when compared to Zika (column “chik.-Zika”). However, the posterior summaries of the odds ratios associated with the percentage of green area and population density have different behavior across the different equations. A one standard deviation increase in the percentage of green area increases by 2% the odds ratio of a neighborhood having Zika when compared to dengue, however $1$ falls within the 95% posterior credible interval of this odds ratio. The odds ratio of a neighborhood having cases of chikungunya in comparison to dengue are decreased by 18%; and the odds of a neighborhood having chikungunya in comparison to Zika is decreased by 20%, with a one unit standard deviation increase in the percentage of green area. For population density, a one standard deviation increase in population density reduces the odds of a neighborhood having Zika when compared to dengue by 18%. The odds of a neighborhood having chikungunya is increased by 18% when compared to having dengue, and increased by 43% when compared to Zika, with a one standard deviation increase in population density.

For comparison, Table 3 shows the posterior summaries of the relative risks ( $\exp ({\gamma }_k)$ , $k=1,2,3$ ) associated with a one standard deviation increase of the covariates based on model M3 under the multivariate Poisson model (see equation (10)) for each of the diseases. The relative risk of all three diseases decreases with a one standard deviation unit increase of SDI when the other covariates are held fixed. A one standard deviation unit increase in the percentage of green area decreases the relative risk of chikungunya by 15%. There is no association between population density and the relative risks of dengue and chikungunya as $1$ is within its 95% posterior credible interval. On the other hand, the relative risk of Zika decreases by 15% with a one standard deviation increase of population density when the other covariates are held fixed.

Table 3.

Posterior summary (mean and 95% credible intervals in brackets) of the relative risks ( $\exp ({\gamma }_k)$ , k=1,2,3,4) of each of the diseases (columns) associated with each of the covariates (rows) in equation (10) under model M3.

	Equations associated with each of the coefficients Poisson model in equation (10)
Covariate	dengue	Zika	chik.
	( ${\delta }_{i1}$ )	( ${\delta }_{i2}$ )	( ${\delta }_{i3}$ )
Intercept	0.271	0.439	0.146
	(0.254 ; 0.291)	(0.409 ; 0.471)	(0.132 ; 0.159)
SDI	0.761	0.851	0.757
	(0.677 ; 0.856)	(0.758 ; 0.960)	(0.649 ; 0.873)
Pct green area	1.047	1.062	0.848
	(0.926 ; 1.183)	(0.932 ; 1.202)	(0.735 ; 0.973)
Pop. density	0.981	0.836	1.169
	(0.853 ; 1.121)	(0.728 ; 0.947)	(0.991; 1.377)

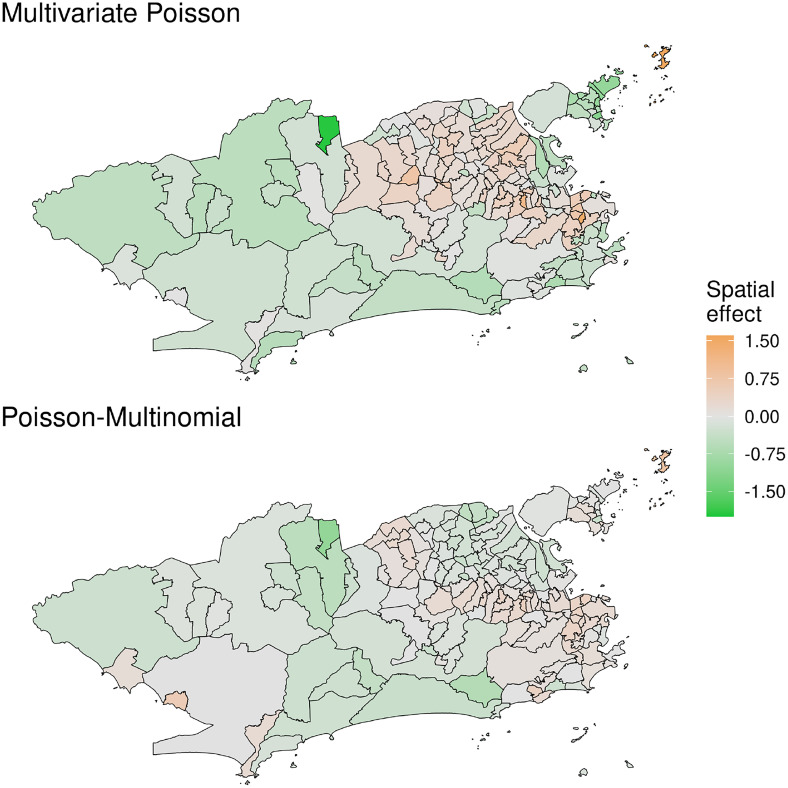
Panels of Figure 2 show the posterior mean of the spatial effects ${\varphi }_i$ , $i=1,2,\dots ,n$ under the Poisson-Multinomial (M4) and multivariate Poisson (M3) models, respectively. This component captures latent spatial structures that the diseases share among them. While these estimates are not directly comparable, they suggest that the North-Eastern part of the city has higher values of this local effect.

Figure 2.

Posterior mean of the common latent spatial effect ${\varphi }_i$ , $i=1,2,\dots ,n$ from model M3 under the multivariate Poisson (top) and model M4 under the Poisson-Multinomial parametrizations (bottom).

Figure 3 shows the posterior mean of the relative risk of the total (based on equation (4)) cases of Aedes-borne diseases across the city. It is clear that during this joint epidemic, the three diseases were spread all over the city, with some neighborhoods resulting in quite high values of the estimated relative risk.

Figure 3.

Posterior mean of the relative risk (RR) for the total cases of Aedes-borne (dengue, Zika and chikungunya) diseases across the neighborhoods of Rio de Janeiro under model M4.

Panels of Figure 4 show the posterior mean of the probability of presence of each disease estimated from the Poisson-Multinomial parametrization (top row) and the log of the posterior mean of the relative risk of each disease estimated under the multivariate Poisson parametrization (bottom row). The maps on the top row show that the probability of presence of Zika was around 50% for the majority of neighborhoods, whereas the probability of presence of chikungunya was higher in the eastern portion of the city. Because Zika resulted in quite high relative risks for some of the neighborhoods we show the log of the posterior mean of the relative risks. Clearly, among the three vector borne diseases considered, chikungunya resulted in the smallest values of the relative risk across the city, with the Eastern portion of the city resulting in higher risks associated with chikungunya.

Figure 4.

Posterior mean of the probabilities of presence of each disease ${\pi }_{ik}$ , $i=1,2,\dots ,n$ and $k=1,2,3$ under model M4 for the Poisson-multinomial parametrization (top row) and log of the posterior mean of the relative risks (RR) of each of the diseases under model M3 for the multivariate Poisson model (bottom row).

4. Discussion

Dengue, Zika and chikungunya are vector borne diseases transmitted by the same species of Aedes mosquitoes. Between 2015 and 2016 the city of Rio de Janeiro experienced a joint epidemic of the three diseases for the first time, leading to what is known as a triple epidemic. We had available the number of cases of each disease across the neighborhoods of Rio de Janeiro. We proposed a model for the total cases of vector borne diseases and, conditional on the total number of cases, we proposed to model the probability of presence of each of the three diseases across the neighborhoods of the city. This was done by assuming a Poisson model for the total number of cases and, conditional on the total, we assumed a multinomial distribution for the vector of observed cases in each neighborhood.

In Section 2 we discussed different parametrizations for the probabilities of presence of each disease. Because of the relationship between the Poisson and multinomial distributions, depending on the proposed parametrization, the total number of cases does not bring information to the likelihood function (see equations (11) and (12)). To allow the total number of cases to bring information to the likelihood function we proposed to model the probabilities in the multinomial component of the model through the baseline category logit model. ¹⁸ As dengue is endemic in the city for more than 30 years, it was considered as the baseline category. This implies that we are modelling the probability of a neighborhood having cases of Zika given it is either cases of dengue or Zika, and the probability of having chikungunya given it is either cases of dengue or chikungunya. A simulation study (Section D of the Supllementary Material) showed that we are able to recover the true values of the parameters when the data are generated from the Poisson-multinomial model (equations (4) and (5)).

We fitted particular cases of the proposed model to the data available from Rio de Janeiro; we considered both parametrizations, the Poisson-Multinomial model as in equations (4) and (5) and the multivariate Poisson model as in equation (10). And for each parametrization, we explored different prior specifications for the latent effects ${\theta }_{ik},i=1,\dots ,n;k=1,2,3$ . Note that the ${\theta }_{ik}$ ’s are not comparable between parametrizations (4)–(5) and (10). Three model comparison criteria were used to compare the different models: the WAIC, the log-score and the energy score. We believe it is reasonable to compare the models through WAIC as the multivariate Poisson model results from a particular parametrization of the Poisson-multinomial model. The WAIC and the log score resulted in similar values when the Poisson-multinomial and the multivariate Poisson are compared under the same fitted model; this suggests that these criteria do not prefer one parametrization over the other. The energy score, on the other hand, suggested differences between the two parametrizations, preferring the Poisson-multinomial model over the multivariate Poisson. Regardless of the results based on the model comparison criteria we believe our proposed approach provides an alternative and interesting way to look at the available data.

As dengue is endemic in the city of Rio de Janeiro, we believe the parametrization in equations (4) and (5) provide multiple advantages in comparison to the one in equation (10). First it allows to account for the uncertainty in the total notified number of cases of Aedes-borne diseases. In particular, the multinomial component allows for uncertainty in the allocation of the total number of cases across the different diseases (categories). This is an interesting feature of the model as most of the notified cases are based on clinical-epidemiological criteria, without laboratory confirmation. As the three Aedes-borne diseases have similar symptoms, cases are often mistakenly classified when there is co-circulation,^3,2 which is aggravated by the fact that it was the first time the city experienced epidemics of Zika and chikungunya. At the beginning of the triple epidemic, health workers were not aware that Zika and chikungunya were circulating in the city, and had little experience in clinically distinguishing the three diseases. Second, it provides a tool to understand how the number of cases of Zika and chikungunya are spread over the city in comparison to dengue, which has been present for more than 30 years in the city. The SDI of a neighborhood does not seem to affect differently the odds ratio of Zika or chikungunya in comparison to dengue as 1 is included in the respective 95% posterior credible interval of the odds ratios (see 2nd row of Table 2). We learned that the odds of a neighborhood having Zika instead of dengue increases by 2% with a one standard deviation increase of percentage of green area, but $1$ is within the 95% posterior credible interval of the odds ratio, suggesting that there is no difference in the percentage of green area profile of neighborhoods affected by dengue and Zika. However, the odds of a neighborhood having chikungunya instead of dengue decreases by nearly 18% with a one standard deviation increase of percentage of green area, suggesting that chikungunya affected more urban neighborhoods when compared to dengue. The odds of a neighborhood having chikungunya instead of Zika is also reduced by approximately 20% with a one standard deviation increase of percentage of green area. This suggests that chikungunya affected more urban areas of the city. If population density is considered, a one standard deviation increase, decreases the odds of a neighborhood having Zika instead of dengue by 18%, and increases the odds of chikungunya instead of Zika by 43%. And the odds of a neighborhood having chikungunya instead of dengue is increased by 18% with a one standard deviation increase in population density.

The multivariate Poisson model can be seen as a particular case of the Poisson-Multinomial model. It provides estimates of the relative risks of the different diseases without providing a clear comparison among them. For the considered period, the multivariate Poisson model suggests that for all three diseases, the relative risk of neighborhoods decreases as the value of SDI increases. And as population density increases the relative risk of Zika decreases by approximately 16%; and as the percentage of green area increases the relative risk of chikungunya decreases by 15%.

The assumption of a multinomial distribution for the number of cases of each of the diseases implies on a negative conditional covariance structure. This is because in the multinomial distribution the events are assumed mutually exclusive. We do not believe this is an issue in the case of the Aedes-borne diseases because previous studies have suggested that co-infection of the different vector borne diseases rarely happens. However, we suggest to think carefully about this assumption before fitting the proposed model to the joint counts of other diseases.

A natural extension of the proposed model is to assume a negative binomial distribution for the total number of Aedes-vector borne diseases in each neighborhood. We fitted the negative binomial model to the total number of cases in our dataset, but it did not improve model fitting, and for this reason we only show the results based on the Poisson distribution for the total cases. See Section E of the Supplementary Material for more details.