Bacteriophage Latent-Period Evolution as a Response to Resource Availability

Abstract

Bacteriophages (phages) modify microbial communities by lysing hosts, transferring genetic material, and effecting lysogenic conversion. To understand how natural communities are affected it is important to develop predictive models. Here we consider how variation between models—in eclipse period, latent period, adsorption constant, burst size, the handling of differences in host quantity and host quality, and in modeling strategy—can affect predictions. First we compare two published models of phage growth, which differ primarily in terms of how they model the kinetics of phage adsorption; one is a computer simulation and the other is an explicit calculation. At higher host quantities (∼10⁸ cells/ml), both models closely predict experimentally determined phage population growth rates. At lower host quantities (10⁷ cells/ml), the computer simulation continues to closely predict phage growth rates, but the explicit model does not. Next we concentrate on predictions of latent-period optima. A latent-period optimum is the latent period that maximizes the population growth of a specific phage growing in the presence of a specific quantity and quality of host cells. Both models predict similar latent-period optima at higher host densities (e.g., 17 min at 10⁸ cells/ml). At lower host densities, however, the computer simulation predicts latent-period optima that are much shorter than those suggested by explicit calculations (e.g., 90 versus 1,250 min at 10⁵ cells/ml). Finally, we consider the impact of host quality on phage latent-period evolution. By taking care to differentiate latent-period phenotypic plasticity from latent-period evolution, we argue that the impact of host quality on phage latent-period evolution may be relatively small.

Bacteriophages (phages) are important ecological components because of their impact on bacteria. By lysing the prokaryotes found at the base of aquatic food webs, phages can disrupt the flow of energy and carbon within ecosystems (15, 30, 32). Phages are also employed as models for predator-prey interactions (8, 26) and are of increasing interest as mediators of the phage therapeutic treatment of bacterial disease (11, 24). Increasing rates of phage exponential growth—larger burst sizes, shorter generation times, or, for well-mixed cultures (33), faster phage adsorption—should lead to faster phage-mediated exploitation of host populations. Both burst size and the phage generation time, however, are controlled by the phage latent period, with greater burst sizes associated with longer latent periods but shorter generation times associated with shorter latent periods. This conflict between burst size enlargement and generation time reduction complicates phage latent-period optimization.

The phage latent period is defined by the timing of phage-induced host cell lysis, which typically is under the control of a phage protein complex known as a holin. Holins restrain the activity of cell-wall-digesting endolysins, and mutations in holin genes can significantly modify the timing of host cell lysis (34). The timing of phage-induced host cell lysis—as well as the eclipse period, the burst size, and the rate of phage adsorption—is also influenced by host physiology (i.e., host quality), as Hadas et al. (16), for example, have quantitatively demonstrated. Binder (7), using mathematical models, argues that the timing of phage-induced host cell lysis is of primary importance when considering the relationship in aquatic environments between rates of phage infection and rates of phage-induced bacteria mortality. Abedon (1) and Wang et al. (29) in turn suggest that the timing of phage-induced host cell lysis may be subject to a host quantity- and host quality-dependent selection. The latter study concludes that a phage will evolve a shorter latent period when either host density is high or host quality is good.

Here we explore to what extent quantitative predictions of how the phage latent period may evolve can be affected by differences in modeling strategies. We develop and then compare two relatively simple predictive models of phage population growth, one a computer simulation that is similar in principle to that employed by Abedon (1) and the second an explicit calculation that is similar to that employed by Wang et al. (29). We find that the computer simulation is a reliable predictor of phage population growth at both high and low host densities (e.g., 10⁸ and 10⁶ cells/ml, respectively), while the explicit calculation is reliable only at higher host densities (∼10⁸ cells/ml). Based on our observation of differences in model predictions and reliability, we suggest that the impact of lower host quantities on phage latent-period evolution may be a great deal smaller than what Wang et al. (29) concluded. We then employ our computer simulation to explore how phage latent periods may evolve in response to changes in host quality. As a consequence of our inclusion of considerations of latent-period phenotypic plasticity, we suggest that the impact of host quality on phage latent-period evolution can also be a great deal smaller than what Wang et al. (29) concluded.

PHAGE GROWTH MODELS

Simulating phage growth.

Our purpose in employing simulations is to obtain predictions of phage population growth rates under conditions of low phage multiplicity, constant host quantity, and constant host quality. The lytic phage life cycle involves free-phage diffusion, host cell adsorption, an eclipse period, a period of progeny maturation, and host cell lysis. Lysis ends the phage latent period but initiates the extracellular diffusion of phage progeny to new host cells. Here we consider the impact of the phage eclipse period (E), the rate of intracellular phage progeny maturation (R), the phage adsorption constant (k), the phage latent period (L), and the density of uninfected host cells (N) on phage population growth rates.

In our simulations of phage growth we make all of the usual simplifying assumptions: (i) thorough environmental mixing is done such that phages encounter bacteria only at random, (ii) infected hosts do not divide, and (iii) phage adsorption to already infected cells does not occur. The latter assumption is common among simulations of phage growth (1, 21, 29) and may be justified as a reasonable approximation when phage multiplicities—the ratio of free phages to host cells—are low. See reference 2 for consideration of the modeling of phage biology at higher phage multiplicities. During our simulations we keep phage growth rates uniform by holding host quantity and quality constant over both time and space. We also prevent phages from reaching any environmental carrying capacity by employing in our models the equivalent of very large (essentially infinite) culture volumes. Our approach is equivalent to that of Abedon (1) and also is similar to the phage growth portion of the model presented by Levin et al. (21).

We increment computer simulations in discrete steps of t₁ min (which equals 0.5 or 1 min). Because there is a delay between phage adsorption and host lysis (i.e., the phage latent period, L) and because different numbers of host cells are phage adsorbed over different simulation intervals, we model populations of infected cells as one-dimensional arrays containing 1 + (L/t_I) members. In each simulation step the last array member, L/t_I, instantaneously releases a burst size (B) of free phages for each infected cell found in that L-minutes-of-infection cohort. All other array members are then incremented forward in the array by one step. The first array member, designated zero, is defined as the number of host cells that adsorb free phages over the course of a single simulation step (ignoring those free phages just released during the same step from the L/t_I member of the array). In this way, and similar to the strategy employed by Levin et al. (21), each array member defines the number of cells that became infected over specific intervals of ≤L min in the past. Unless otherwise indicated, at the beginning of simulations a single phage is not discretely adsorbed but instead is distributed evenly over all of the latent-period array members plus the free-phage adsorption pool. This strategy is employed to model phage population growth with a minimum of infection synchronization.

Using simulations to calculate latent-period optima.

To calculate latent-period optima we determined the total number of phages produced by individual simulations as the sum of free phages, eclipse period infected cells, and progeny phages found within post-eclipse infected cells. We ran multiple simulations, varying only latent period—in 1-min intervals—between computer simulations. For a given phage, host quantity, and host quality, it is the latent period used in the simulation producing the most phage progeny that we call the latent-period optimum. Thus, the latent-period optimum is the latent period that produces the most phage progeny during phage growth within an infinitely large vessel in the presence of a constant density of uninfected host cells (N) and in the presence of a constant quality of host cells (such that E, R, and k are also held constant). In all cases, predicted latent-period optima therefore are conditional for specific values of E, R, k, and N.

Calculating optimal latent period explicitly.

When the ratio of uninfected hosts to phages is large, phage populations are expected to grow exponentially (3, 12, 19). This growth occurs at a rate that we assume is a function of both the phage generation time (t_G) and burst size (B). The phage generation may be divided into (i) a period of extracellular diffusion of phage progeny to new host cells; (ii) the phage eclipse period (E), during which infection is occurring but no mature phage progeny are found within an infected cell; and (iii) a period of progeny maturation that begins at the end of the phage eclipse period and is terminated, along with the overall latent period, at the time of host cell lysis (i.e., period of progeny maturation equals latent period [L] minus eclipse period [E]). The intracellular rate of phage progeny maturation (R) helps define the phage burst size and is equal to the per-unit-of-time rate of increase of mature phage progeny within an infected cell. R may be measured directly via Doermann-style (13) intracellular single-step growth experiments or may be approximated as the ratio of the phage burst size to the duration of the phage period of progeny maturation [R = B/(L − E)]. Burst size, therefore, may be defined as the product of the period of progeny maturation (L − E) and the intracellular rate of phage progeny maturation (R) (1, 25):

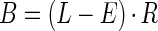1

Possible values of E, L, R, and B, compiled from the literature, are listed in Table 1. Note that Table 1 additionally presents a range of simulation-determined latent-period optima (L_opt, far-right column) associated with the presented values of E, R, and k for N = 10⁹ cells/ml down to N = 10⁵cells/ml.

TABLE 1.

Effect of host quality on latent-period optima^a

Growth mediumb	Host doubling time (min)	E	R	kc	B	L	Lopt
LBG	23	14	13.7	3.35	110	18–36	19–46
GC	28	20	30.4	ND	152	21–33	ND
CASA	33	22	10.5	ND	63	24–36	ND
GLU	50	26	6.0	2.09	60	36–56	35–87
GLY	68	32	3.9	1.25	27	35–54	43–127
SUC	96	35	3.5	ND	14	37–58	ND
ACET	136	27	1.3	0.72	12	35–53	43–231
WDS	56	10	5	1.04	98	30–46	15–90

^aGrowth parameter values were obtained from Hadas et al. (16), except for the bottom row, which is from Wang et al. (29), and the far-right column (L_opt), which was calculated here. E, eclipse period (min); R, rate of progeny maturation (phages/min); k, adsorption constant (ml/min); B, burst size (phages/cell); L, beginning to end of rise period (min); L_opt, estimated latent-period optimum using simulations (based on equations 1 and 3) ranging from 10⁹ down to 10⁵ cells/ml. ND, not determined. 

^bGrowth media (broth) are LBG (containing 0.4% glucose) (16), M9 minimal medium supplemented with 1% (wt/vol) casein hydrolysate and 50 μg of tryptophan per ml (CASA), CASA with 0.4% glucose (GC), 0.4% glucose (GLU), 0.4% glycerol (GLY), 0.4% succinate (SUC), and 0.4% acetate (ACET). 

^ck values (shown times 10⁹) were determined via analysis of the adsorption curves (presented in Fig. 1) from Hadas et al. (16) or are from Wang et al. (29). By way of comparison, the adsorption constant from Stent (28) is 2.5 × 10⁻⁹ ml/min, which is the odds of 1 free phage colliding with and then adsorbing to 1 cell found alone in 1 ml of culture over a period of 1 min. 

^dB, k, and L values used by Wang et al. (29) for their virtual medium (WDS) were experimentally determined for phage T2 by Levin et al. (21). E was chosen by Wang et al., perhaps based on the results of Doermann (13). R was calculated by Wang et al. as a function of B, E, and L (equation 1). 

We define phage generation time (t_G) as a sum of the phage latent period (L) and some expression of the duration of the diffusion-limited phage progeny extracellular search for new host cells, which we will call time adsorption, or t_A. Typically, t_A is defined as some function that is inversely related to host density, N, and the phage adsorption constant, k. Following the lead of Wang et al. (29), in these explicit calculations we define t_A as the mean free time (MFT): t_A = (kN)⁻¹. The MFT represents the average length of time a cohort of free phages requires to adsorb to host cells.

Phage populations increase by one burst size (B) per generation. Consequently, the phage population size after t min of growth, P_t, may be given simply as the product of exponential growth occurring over the number of generations (of length t_G) that t represents, i.e., t/t_G generations (22, 23, 29):

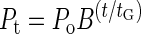2

where P₀ is the phage population size at t = 0 and the phage generation time is equal to the sum of the phage latent period and the MFT: t_G = L + (kN)⁻¹. P_t is a function of latent period, i.e., P_t = f(L), since both the phage generation time and the phage burst size (see equation 1) are functions of L. Latent-period optima (L_opt) therefore may be determined graphically by plotting the number of phages produced over some interval, P_t, against the phage latent period. To calculate latent-period optima explicitly, we employed the computer program Maple (release 5.1) to determine the derivative of f(L) with respect to L, set this derivative equal to zero, and then solved for L_opt.

MFT-based phage growth simulation.

In some phage growth simulations we employed a MFT-based adsorption algorithm. To keep phage adsorption constant per free-phage cohort, MFT-based adsorption is modeled in a manner that is similar to the modeling of the phage latent period described above. A one-dimensional array is defined as length (MFT / t₁) rounded to the nearest integer plus one. Per simulation increment the phage cohort found in the last array member instantaneously adsorbs to a like number of uninfected host cells, converting with replacement those cells to infected cells. The array is then incremented forward one step. The now-empty zero member is filled with the free-phage cohort released from lysing hosts.

Estimating latent-period optima without MFT simplification.

To incorporate greater realism into our computer simulations, we replaced the MFT calculation of t_A with a more complex exponential free-phage decay. Virtual phages were thus adsorbed to host cells using the following equation (28):

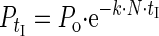3

where P₀ is the free-phage concentration at t = 0, P_tI is the free-phage concentration at time t_I, and t_I is the simulation step length over which phage adsorption occurs. Though differing slightly in detail, this approach to modeling phage adsorption is equivalent to that employed by Levin et al. (21) [i.e., P_tI = P₀ · e^−k·N·t_I ≈ P₀ · (1 − k · N · t_I)].

Estimating optimal latent period without burst-size simplification.

Wang et al. (29) estimate burst size assuming that the rate of progeny maturation within an infected cell decreases over the time of an infection:

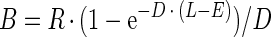4

where D represents a decline with time in the output of a host's phage-synthesizing machinery (D = 0.001 was used by Wang et al. [29]). Though existing data on declines in phage progeny maturation over time are at best sparse, for comparison purposes we employ some simulations where we substitute equation 4 for equation 1 as a calculator of burst size.

MATERIALS AND METHODS

Measuring phage growth.

The T-even-like phage RB69 (4, 27) and its Escherichia coli CR63 host (6) were both obtained from the laboratory of John W. Drake of the National Institute of Environmental Health Sciences, Research Triangle Park, N.C. Latent period and burst size were determined by employing the single-step growth method (9), and the phage adsorption constant was calculated based on adsorption experiments employing the chloroform-lysis approach (5). Otherwise phage preparation and handling were as previously described (3), except that the medium employed here is a hybrid of premixed tryptic soy broth (Difco) and Hershey broth (10) that consists, per liter, of 30 g of dehydrated tryptic soy broth and 2.9 g of NaCl. To initiate and propagate phage batch growth experiments, E. coli CR63 was first grown to 10⁸ cells/ml, pelletted, washed, and then resuspended in prewarmed (37°C), aerated broth containing approximately 400 wild-type RB69 phages per ml. Starting at 27 min, and every 27 min from then on for the duration of experiments, cultures were split 1:1 with prewarmed fresh broth. Following these splits phage titers and viable cell counts were determined.

Simulating phage growth as a function of host quantity.

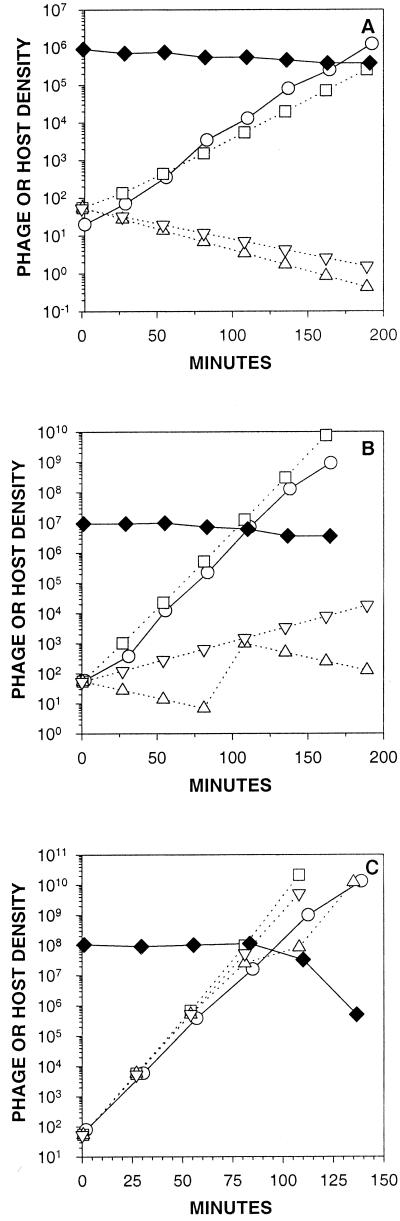
For experiments depicted in Fig. 2, phage growth was simulated starting with unadsorbed free phages and growing phage populations were virtually diluted 1:1 (as above) every 27 min but with the host densities held constant at 1.26 × 10⁶ (10^6.1; panel A of Fig. 2), 1.26 × 10⁷ (panel B), or 1.26 × 10⁸ (panel C) cells/ml (L = 21, B = 290 phages, k = 10⁻⁹ ml/min, t₁ = 0.5 min).

FIG. 2.

Phage growth, theoretical versus experimental. Results from experiments are shown as solid lines (circles represent phage titers, diamonds represent cell viable counts). Initial host densities for panels A, B, and C are approximately 10⁶, 10⁷, and 10⁸ cells/ml, respectively. Simulations (dotted lines) were done with phage adsorption modeled by using the equation 3 exponential decay function (squares) or by employing the MFT phage adsorption algorithm (triangles). A MFT-based calculation employing equation 2 is also presented (inverted triangles). The last cell count point shown in panel C was arbitrarily given a value of 5 × 10⁵ cells/ml to substitute for the otherwise not graphable 0 × 10⁶ cells/ml actually observed.

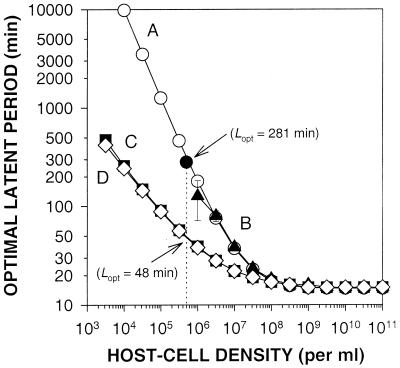
For experiments depicted in Fig. 3, simulations and calculations were made to estimate the phage latent-period optima at various host densities ranging, in half-log intervals, from 10³ to 10¹¹ host cells/ml. A total of 21 individual simulations, 5,000, 5,100, 5,200, …6,800, 6,900, and 7,000 virtual minutes in duration, were employed at each host density determination to generate the curves B, C, and D depicted in Fig. 3. Error bars are estimated standard deviations associated with the results of these individual simulations and are present, though not necessarily visible, in all three curves. Growth parameters E, R, and k are those employed by Wang et al. (29 and Table 1), and t₁ was 1.0 min.

FIG. 3.

Impact of host density on phage latent-period optima. For curve A, latent-period optima were explicitly calculated (open circles). Computer simulations were used to generate all other curves, including curve B, which employs the MFT and equation 1 (triangles), curve C, which employs equations 3 and 1 (squares), and curve D, which employs equations 3 and 4 (diamonds). The solid circle is a single datum from Wang et al. (29).

Simulating phage growth as a function of host quality.

Hadas et al. (16) experimentally determined phage T4's eclipse period (E), rate of progeny maturation (R), adsorption constant (k), and latent period (L) as observed during growth in various media. In these experiments Luria-Bertani broth medium with added glucose (LBG) supported a higher quality host, while various less-rich defined synthetic media supported lower host quality (Table 1). Here we employ phage growth simulations, based on these Hadas et al. phage growth values, to determine latent-period optima while (i) holding R and k as observed during growth in LBG medium, with E defined as measured during growth on lower quality hosts; (ii) holding E and k as observed in LBG medium while defining R as it was on lower quality hosts; and (iii) holding E and R as observed in LBG medium while defining k as it was on lower quality hosts. We additionally determined latent-period optima with E, R, and k defined in terms of growth in the same less-rich medium. Recall that in all cases a latent-period optimum is defined over the course of a series of simulations, during which host quantity (N) and host quality (E, R, and k) are held constant, and as the latent period that gives rise to the most phage growth. These simulations employ equations 1 and 3, t_I = 0.5 min, and were 3,000 virtual minutes in duration.

We also estimate the effect of latent-period phenotypic plasticity on latent-period optimization. To do this we calculate a scaling-up factor that is the ratio of the experimentally determined timing of lysis for wild-type T4 phages in a less-rich medium to the experimentally determined timing of lysis in LBG medium. Latent period (i.e., the constant period [12]) technically can refer only up to the beginning of what is known as the rise period (the time over which an otherwise simultaneously infected population of cells lyse [12]). Consequently, the experimentally determined overall timing of lysis and the experimentally determined latent period may not be synonymous. To convert this overall timing of lysis into a single, latent-period-comparable number—while avoiding making an arbitrary decree—here we employ three definitions of lysis timing that we use to define similar (though not identical) scaling-up factors: the latent period (i.e., the start of the rise period), the geometric mean of the beginning and the end of the rise period, and the arithmetic mean of the beginning and the end of the rise period. In all cases experimentally determined lysis timing data are from Hadas et al. (16 and see Table 1). For example, with wild-type phage T4, lysis timing in LBG medium is 25.5 min (geometric mean), while the lysis timing with a glucose medium (GLU) is 44.9 min. If, by simulation, we determine an optimal latent period for a given cell density in LBG medium of 20 min, then we expect that the same phage's latent period in GLU medium would be 20 min × 44.9 min/25.5 min = 35.2 min. Keep in mind that the latter number, 35.2 min, represents an estimated degree of latent-period phenotypic plasticity (i.e., versus 20 min in LBG medium) rather than a calculated latent-period optimum.

RESULTS

Modeling lytic phage growth.

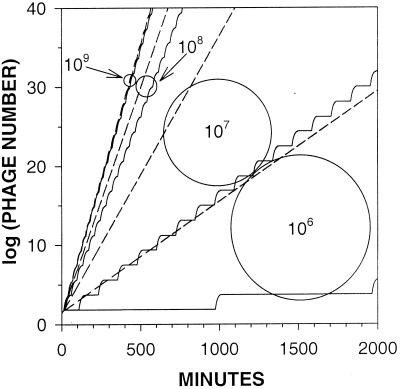
To model the growth of phages in liquid culture one typically employs some measure of phage infection productivity (burst size), a delay between phage adsorption and phage-induced lysis of infected cells (latent period), and some algorithm describing phage adsorption. Two schools of thought exist for how to model phage adsorption. On the one hand are the efforts of Levin et al. (21) as well as of Abedon (1), where phage adsorption is modeled as an exponential decay in free-phage concentrations. On the other hand, Wang et al. (29) treat adsorption as a more convenient single variable (= 1/kN), which is equivalent to the MFT associated with the exponential decline of a free-phage cohort (i.e., average unadsorbed time). Our initial efforts were to compare computer simulations of phage growth using Wang et al. (29) versus Abedon (1) adsorption algorithms. The results of such a comparison are presented in Fig. 1. Note that the two methods are very similar at higher host densities (10⁹ cells/ml) but are quite distinct at lower host densities (10⁶ cells/ml), with a significant growth advantage going to the Abedon method at the lower host densities (dashed lines). Given that an exponential decline better describes the adsorption of a free-phage cohort than does MFT (28), we interpret the discrepancy between the phage growth predicted using the two methods as an indication that MFT may not be adequate in describing phage adsorption, particularly at lower host densities.

FIG. 1.

Phage production with and without MFT simplification. Computer simulations were run for 2,000 min, starting with 1 phage per environment. Shown is the number of phages produced by simulations using equation 3 (dashed lines) or MFT (solid lines) to define phage adsorption. E, R, and k are defined according to Wang et al. (29 and see Table 1), and L was set equal to 25 min. The shown simulations were incremented in 1-min intervals. Curves differ in terms of the density of host cells (per milliliter) as indicated. The 10⁹-cells/ml curves from both methods nearly overlap.

Testing models.

The adsorption algorithms used by Abedon (1) and Wang et al. (29) make different predictions of phage growth kinetics (Fig. 1). To further distinguish these methods we compare model predictions to experimental measurements of phage growth in environments where E. coli densities are held somewhat constant by repeated dilution (1:1) of cultures to fresh media (approximately once per E. coli doubling time). Note in Fig. 2 how the equation 3-based simulations (squares) approximate actual phage growth (circles) fairly well at host densities in the range of 10⁶, 10⁷, or 10⁸ cells/ml, while the MFT-based predictions (triangles) dramatically under-estimate rates of phage growth except, as expected (Fig. 1), at higher host densities (∼10⁸ cells/ml; Fig. 2C).

Phage growth rates are a function of both the length of phage generations and the phage burst size (equation 2). Generation time is a function of both phage latent period and the rate of phage adsorption. Consequently, the preponderance of phage population growth is made by those phages that, by chance, adsorb their hosts sooner. Using MFT as an adsorption algorithm ignores this earlier adsorption, instead treating all adsorptions as delayed to some average (mean free) value. At lower host densities this average value becomes increasingly long relative to the timing of the adsorption of those phages that contribute, by virtue of their earlier adsorption, the most to phage population growth. In addition, due to the nature of exponential decay, a larger fraction of a given free-phage cohort adsorbs during any earlier interval of a phage adsorption curve than during any later interval of the same duration. Consequently we observe, in Fig. 1 and 2, that MFT-based simulations become increasingly flawed predictors of phage growth kinetics as host densities decline.

Predicting latent-period optima as a function of host quantity.

We define latent-period optima as that phage latent period providing the greatest phage population growth, with host quantity and host quality held constant. Furthermore, holding the eclipse period, the rate of progeny maturation, and rates of phage adsorption all constant, burst size will vary monotonously with phage latent period such that a longer latent period results in a proportionately larger burst size. For a given host density there will exist some phage latent period that bestows an optimal (most rapid) rate of phage population growth. Such a latent period most effectively balances the conflicting demands of rapid infection turnover—to allow for the more rapid acquisition of uninfected host cells by phage progeny—and the requirement for the production of an adequate number of phage progeny (burst size) to acquire those cells. Given that the MFT-based simulations can poorly predict phage growth kinetics, especially at lower host densities (Fig. 1 and 2), can the employment of MFT as an adsorption algorithm affect the determination of latent-period optima?

In Fig. 3 we present latent-period optima calculated by various methods. In curve A (open circles) latent-period optima are calculated explicitly using a MFT-based phage adsorption algorithm [i.e., by employing the derivative of equation 2, where t_G = L + (kN)⁻¹]. The single solid circle is from the data of Wang et al. (29) and corresponds to an optimal latent period of 281 min at a host density of 5 × 10⁵ cells/ml. We believe that Wang et al.'s burst size calculation using equation 4—which posits a decline in the rate of progeny maturation with time during the infection of a cell—versus our employment of the simpler equation 1 explains the slight discrepancy between their data and curve A.

Curve B (Fig. 3, triangles) was generated using a computer simulation employing MFT-based phage adsorption. As indicated by the associated error bars, the resulting latent-period optima become increasingly dependent (at lower host densities) on the precise duration of simulations. This corresponds to the increasing synchronization of the lower-host-density MFT-based growth curves presented in Fig. 1 (solid lines). By the point a density of 10⁶ cells/ml is reached, this imprecision is large. On the other hand, error bars, though present, are not visible in curves C and D, even with host densities as low as 3.2 × 10³ cells/ml. This latter observation implies a relative lack of dependence in these curves on the precise duration of simulations, which is consistent with the smoothness of corresponding growth curves in Fig. 1 (dashed lines).

Curve C (Fig. 3, squares) presents latent-period optima determined via the computer simulation method employed for Fig. 1 and 2. Phage adsorption is based on equation 3 (not on MFT), with burst size estimated using the relatively simple equation 1. Note that the employment of the non-MFT adsorption algorithm results in predictions of phage latent-period optima that are somewhat shorter than those predicted by employing the MFT adsorption algorithm (compare curves C and D with curves A and B in Fig. 3). The explanation for this discrepancy is that using the MFT increasingly delays phage adsorption at lower host densities relative to modeling phage adsorption by exponential decay. This overestimation of delays in phage adsorption is equivalent to an overestimation of the rarity of the host cell resource and consequently results in an overestimation of the latent-period duration necessary to maximize phage growth.

Curve D (Fig. 3, diamonds) is identical to curve C, except that burst size is determined using equation 4. Note that the equation 4 method of burst size determination results in an increasing decline in the optimal phage latent period as host densities decline (the difference between curves C and D) but that this decline is small. All subsequent simulations were done using the method of curve C.

Predicting latent-period optima as a function of host quality.

Phages infecting hosts whose doubling times have been lengthened due to growth on less-suitable carbon sources tend to display longer eclipse periods, longer latent periods, and slower rates of phage maturation (16 and Table 1): in short, slower, less productive infections. The rate of phage adsorption also declines, because phage adsorption rates are proportional to host cell surface area and the size of host cells tends to decline with declining host quality (16). From our perspective, changes in host quality result in changes in the phage growth parameters that underlie our simulations. Furthermore, there is a predicted tendency for changes in host quality to result in changes in the latent period optimum at a given host density, particularly for that optimal latent period to be longer when host quality is lower (29).

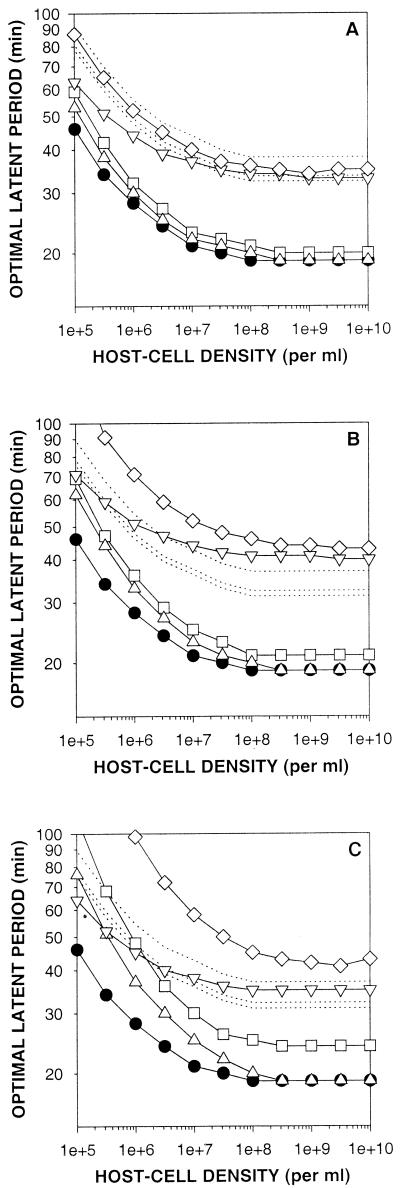
With the Hadas et al. (16) data set we can make more quantitative predictions. To make these predictions we vary the eclipse period, rate of progeny maturation, or the adsorption constant from those employed to generate Fig. 3 (curve C) to coincide with the media and phage growth parameters presented in Table 1. Here we consider LBG medium a rich medium in which host quality is high, while GLU (glucose-based; Fig. 4A), GLY (glycerol-based; Fig. 4B), and ACET (acetate-based; Fig. 4C) media each show increasing declines in host quality. Latent-period optima associated entirely with LBG medium and various host densities are presented in all three panels as circles. Latent-period optima for each of the less-rich media are indicated as diamonds. Note that in all panels and at all host densities, the circles are associated with the shortest latent-period optima while the diamonds are associated with the longest latent-period optima. Together these observations are consistent with the above-noted prediction that for a given host density a declining host quality tends to be associated with longer latent-period optima.

FIG. 4.

Impact of host quality on latent-period optima. Solid-line curves represent latent-period optima and were found as described for Fig. 3 (curve C). Dotted-line curves indicate latent-period phenotypic plasticity and were generated as described in the text. Solid circles represent latent-period optima determined by employing E, R, and k values found using the richer LBG medium. Phage growth was also simulated with E, R, and k (as presented in Table 1) obtained from host growth on GLU (A), GLY (B), and ACET (C). Curves represented by open symbols define E, R, or k in terms of growth with either only E varied from LBG values (inverted triangles), only R varied (squares), only k varied (upright triangles), or E, R, and k simultaneously varied (diamonds).

Wang et al. (29) considered only changes in the rate of phage maturation in hosts whose eclipse period and adsorption constants remained otherwise unchanged. Note that with all three lower quality hosts (Fig. 4A, B, and C) the impact of changing only the rate of progeny maturation (squares) is greater at lower host densities than it is at higher host densities. Similarly, we predict that reducing instead only the phage adsorption constant—while holding the phage eclipse period and rate of progeny maturation constant at LBG-associated values—will also have an increasing impact on latent-period optimization as host densities decline (Fig. 4, upright triangles).

Eclipse period and phage adsorption both contribute to the phage generation time (t_G = t_A + E + L − E) and serve as intervals during which mature progeny are not yet accumulating intracellularly. The impact of the eclipse period and the phage adsorption constant on latent-period optimization can differ, however, because while absolute rates of phage adsorption increase with higher host densities, the phage eclipse period remains constant. Consequently, the relative contribution of the eclipse period to a delay in progeny maturation, and therefore to latent-period optimization, is greater at higher host densities than it is at lower host densities (Fig. 4, inverted triangles).

Our results are consistent with a general conclusion that latent-period optima will tend to increase as host quality declines. In addition, we predict that the impact of changes in host quality on latent-period optimization depends on which aspect of phage growth is varied and at what host quantity. In the following section, which further complicates considerations of the impact of host quality on latent-period optimization, we will propose that even though decreases in host quality should result in longer latent-period optima, selection will not necessarily favor a latent-period increase.

Selection in response to changes in host quality.

An argument that latent period will evolve as a function of host quality requires not only that latent periods will change but also that changes in phage genotype underlie at least some of these latent-period changes. However, it is well known that a decline in host quality can result in an increase in phage latent period, even if one holds phage genotype constant (for example, see reference 16 and Table 1). To what extent, then, are changes in phage genotype necessary to explain the host-quality-dependent changes in phage latent-period optima postulated by Wang et al. (29) and here in Fig. 4?

Addressing this question requires a means of comparing changes in phage latent-period optima (as host quality varies) to the changes in phage latent period that result solely from the immediate physiological impact of changes in host quality. This latter impact is a consequence of a phenotypic plasticity observed in the latent period of phages during their growth in different environments. One observes that poorer growth environments result in lower quality hosts which, in turn, negatively affect phage growth by reducing the phage burst size, lengthening the phage latent period, or reducing the phage adsorption constant (for examples see Table 1). A reduction in the phage burst size can be a reflection, for example, of a reduced synthetic capacity within host cells growing in poorer environments (16). Latent period, too, is affected by the host synthetic capacity, since the synthesis of phage proteins, particularly phage holins, is involved both in effecting host cell lysis and in controlling its timing (34). The phage adsorption constant may also be affected by the host size, the chemical makeup of the phage adsorption environment, and characteristics of the host surface, all of which can vary with environmental conditions. Thus, in general poorer environmental conditions along with the resulting lower host quality can result in phage infections displaying reduced burst sizes, delaying their lysis, and adsorbing host cells at different, often lower, rates.

Predicted new latent-period optima that follow changes in host quality are presented in Fig. 4 by using open symbols. To isolate the physiological impact of changes in host quality on latent-period length from the impact of latent-period optimization, we employed latent periods experimentally determined during phage growth in GLU, GLY, and ACET media as well as in the richer LBG medium (16 and Table 1). The ratio of phage latent period with GLU, GLY, or ACET medium to that found with LBG medium serves as a measure of phage latent-period phenotypic plasticity, which is an increase in phage latent period following a decline in host quality that does not involve any change in phage genotype. We then multiplied these ratios by our simulation-determined LBG medium latent-period optima (Fig. 4, circles). The resulting curves, presented as dotted lines in Fig. 4, are not necessarily graphs of latent-period optima but instead are estimations of the isolated physiological impact of declines in host quality on the length of the phage latent period.

We find that some of our phage latent-period optima (open symbols) fall below the dotted-line curves, implying that selection, given growth on a lower quality host, would favor phages with shorter rather than longer latent periods. Other latent-period optima are approximately even with these curves (implying that evolution would favor no change in the genotype underlying lysis timing), and still other latent-period optima may be found above the dotted-line curves. Only in this last case would we predict that selection would favor phages displaying genotypes that code for longer latent periods.

Plasticity in the phage latent period in response to changes in host quality may therefore impact on both the direction and the magnitude of selection for latent-period optima. First, whether changes in host quality result in selection for phage alleles that increase, decrease, or provide no change in phage latent period appears to be a function of specific details of how phage growth accommodates changes in host quality. Second, the absolute strength of selection for optimizing alleles coding for longer latent periods presumably is a great deal smaller than what would be the case were a phage unable to physiologically delay its lysis in response to reductions in host quality.

DISCUSSION

Elaborating on comments made by Levin and Lenski (20), Abedon (1) suggested that rapid bacteria acquisition and killing by lytic phages should be favored by natural selection, particularly when bacteria are common but not when bacteria are scarce. By reducing the period of progeny maturation, a phage will release, upon lysis, a smaller number of phage progeny (smaller burst size). The rapidity of phage exponential growth is dependent on more than just the phage burst size, however, and of particular additional relevance is the delay between lysis and progeny acquisition of new host cells (a function of host cell density and the phage adsorption constant) and the delay between adsorption and the maturation of the first phage progeny within a cell (the eclipse period). When these two intervals are short, then phages with shorter periods of progeny maturation may display greater rates of exponential growth than do otherwise identical phages displaying larger burst sizes but longer periods of progeny maturation.

For a given host density (and host quality) there should exist an optimal latent period that represents a balance between the constraints on phage exponential growth that come from too-small burst sizes and the constraints on phage exponential growth that come from too-long latent periods. In homogeneous environments of large volume of those phages that have minimized their likelihood of inactivation, time until adsorption, eclipse period, and the time it takes to lyse their host cell (once lysis has been initiated), and have maximized their rate of intracellular progeny maturation, only those lytic phages that additionally display an optimal latent period will also display maximal rates of host cell acquisition, bacteria lysis, and phage population growth. Here we have refined models of phage growth to make quantitative predictions of phage latent-period optima as a function of both host quantity and host quality. These efforts strongly parallel earlier efforts by Wang et al. (29). However, by employing a more complex, more realistic, and more standard (21) method of modeling phage adsorption, we predict that latent-period optima can be substantially shorter at lower host densities (Fig. 3 and 4) than those suggested by Wang et al. And, as suggested by Kokjohn et al. (18), it is likely that there exists no fundamental reason for why phage replication could not occur at even very low host or nutrient densities.

The study of phages in the laboratory typically involves the productive infection of hosts grown on relatively rich media. Latent periods may be determined experimentally and may be modified through either changes in phage genes or via the manipulation of host physiology. Individuals with an interest in the control of lysis timing ultimately should ask why a given phage isolate employs a certain latent period under a given set of conditions rather than one that is longer or one that is shorter. A reasonable assumption is that a phage's latent-period genotype underlies an in situ latent-period phenotype that has evolved to maximize a phage's Darwinian fitness. Interpreting measurements of latent period in terms of phage in situ evolution, however, is complicated by differences in host quality between the laboratory and a phage's growth environment outside of the laboratory. We find here, though, that the physiological component of differences in the latent-period optima with one host quality versus another may be sufficiently large (dotted lines versus diamonds and circles in Fig. 4) that, in fact, laboratory determinations of latent period and latent-period optimization may be more applicable to phage in situ growth than we could previously have appreciated. We predict, therefore, that it may be difficult to confirm the predictions of our models in terms of the evolution of phage latent period in response to changes in host quality.

By contrast, though we expect smaller differences with changes in host density than those predicted by Wang et al. (29), we still expect host density to be a reasonably strong determinant of phage latent-period optimization (Fig. 3), and we find that experimental evidence is consistent with a conclusion that lower host densities select for longer phage latent periods, while higher host densities select for shorter phage latent periods. Hershey (17), for example, competed T-even phages possessing short latent periods (rapid lysis mutants) with wild-type T-even phages displaying conditionally longer latent periods (lysis inhibition). Wild-type phages out-competed rapid lysis mutants during growth in broth culture. Presumably this occurs, at least in part, because the longer latent periods displayed upon lysis inhibition are an adaptation by T-even phages to environments in which uninfected host densities are declining (2).

As with lysis inhibition, we can also consider phage reduction to lysogeny as an example of an inducible extension of the phage latent period, though one in which the eclipse period is extended rather than the period of progeny maturation. Just as with lysis inhibition, reduction to lysogeny is thought to occur with greater likelihood when phage multiplicities are greater than 1 (14, 31). This is a circumstance during which uninfected host densities should be in decline.

We additionally have initiated a more direct approach to testing the predictions made by our models. In these experiments we compete various phages that differ in terms of latent period and burst size. Because of a slightly faster rate of exponential growth in the presence of relatively high densities of host cells (∼10⁷ to ∼10⁸ cells/ml), we find relatively strong selection, versus that of the wild-type parent, for a phage mutant that displays a latent period that is ∼25% shorter than that of the wild type. This mutant's growth advantage occurs despite its displaying a burst size that is only about one third that of the wild type (S. T. Abedon, unpublished data).

The impact of lytic phage latent-period optimization should be to make bacteria more rapidly acquired by phages and thereby less available to nonphage consumers of bacteria. Optimization as we are defining it, however, demands a constant host density and a constant host quality. We might suppose that variation in host density or quality over time or space would serve to reduce the optimality of phage growth and therefore reduce the relative rapidity with which a given phage population can exploit a given host population. Consequently, we envisage a constant selection for increasingly optimized phage latent periods, but ultimately we expect ecosystems to vary sufficiently in both space and time that the end point of successful latent-period optimization is effectively never attained.