Abstract
To determine the significance of differences between clonal libraries of environmental rRNA gene sequences, differences between homologous coverage curves, CX(D), and heterologous coverage curves, CXY(D), were calculated by a Cramér-von Mises-type statistic and compared by a Monte Carlo test procedure. This method successfully distinguished rRNA gene sequence libraries from soil and bioreactors and correctly failed to find differences between libraries of the same composition.
The sequencing of 16S rRNA genes from clone libraries of DNAs from environmental samples has led to a wealth of information concerning prokaryotic diversity. However, in addition to methodological problems in producing libraries representative of the environmental sample (for a review, see reference 8), this approach is also limited by the difficulty in comparing libraries and determining if they are significantly different.
This problem can be addressed quantitatively by application of the formula for coverage as described by Good (4). Let X be a collection of sequences, such as a library of 16S rRNA genes. Define the “homologous” coverage of X (or CX) by a sample from X to be CX = 1 − (NX/n), where NX is the number of unique sequences in the sample (i.e., sequences without a replicate) and n is the total number of sequences. In practice, the definition of NX depends upon the criteria used to define uniqueness. For instance, McCaig et al. (6) considered sequences without a homolog of ≥97% similarity to be unique. Other authors have used ≥99% sequence similarity as the criterion. In principle, uniqueness can be defined at any level of sequence similarity or evolutionary distance (D) and a “homologous coverage curve,” or CX(D), can be generated by plotting CX versus D (Fig. 1). The coverage curve then describes how well the sample represents the entire library X at various levels of relatedness. Typically, coverage might be low at high levels of relatedness (low values of D), indicating that only a small fraction of the sequences representing unique species are, in fact, sampled. In contrast, coverage might be much higher at low levels of relatedness, indicating that representatives of most of the deep phylogenetic groups present in X are found in the sample.
FIG. 1.
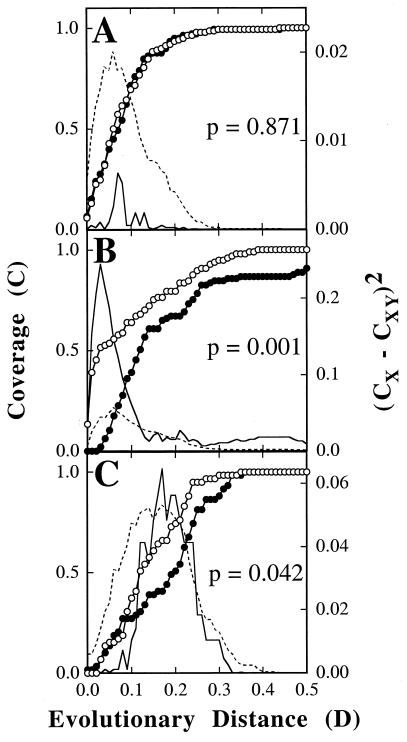
Results of selected LIBSHUFF comparisons. Homologous (○) and heterologous (●) coverage curves for 16S rRNA gene sequence libraries from environmental samples are shown. Solid lines indicate the value of (CX − CXY)2 for the original samples at each value of D. D is equal the Jukes-Cantor evolutionary distance determined by the DNADIST program of PHYLIP (3). Broken lines indicate the 950th value (or P = 0.05) of (CX − CXY)2 for the randomized samples. (A) Comparison of clones from grassland soils with odd (X) and even (Y) accession numbers. (B) Comparison of bioreactor clones SBR1 (X) and grassland soil SL clones (Y). (C) Comparison of C0 (X) and S0 (Y) clones from arid soils.
While CX is the “homologous coverage” of X by a sample of X, it is also possible to calculate a “heterologous coverage” of X (or CXY) by a sample Y from another collection of sequences by the following formula: CXY = 1 − (NXY/n), where NXY is the number of sequences in a sample of X that are not found in a sample of Y and n is the number of sequences in the sample of X. Similarly to NX, NXY can also be defined at different levels of D to generate a coverage curve, CXY(D). Moreover, if X = Y, one might expect the coverage curves CX(D) and CXY(D) [as well as CY(D) and CYX(D)] to be similar. Thus, a test for differences between these coverage curves is also a test for differences between X and Y. To determine if the coverage curves CX(D) and CXY(D) are significantly different, the distance between the two curves are first calculated by using the Cramér-von Mises test statistic (7):
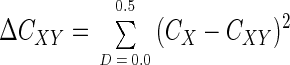 |
where D increases in increments of 0.01. If X = Y, then ΔCXY should not be significantly different than a ΔC calculated after randomly shuffling sequences between the two samples, X and Y. Typically, the sequences are randomly shuffled a large number (N) of times (e.g., N = 999) and ΔCXY is calculated after each shuffling. The randomized values plus the empirical value of ΔCXY are ranked from largest to smallest, and then the P value is estimated to be r/(N + 1), where r denotes the rank of the empirical value of ΔCXY (5). The two libraries are considered significantly different when P < 0.05. We have created a computer program (LIBSHUFF) that uses a sorted distance matrix containing both X and Y as input and returns the coverage curves CX(D), CY(D), CXY(D), and CYX(D), as well as the P values for both ΔCXY and ΔCYX, from the distribution of ΔC. In addition, the distribution of (CX − CXY)2 with D appears to be informative and is given as well (see below). The computer program LIBSHUFF was written in Perl and can be downloaded along with more detailed instructions on its use at http://www.arches.uga.edu/∼whitman/libshuff.html.
A first test of this method was done to ensure that samples from the same library were not shown to be different. Thus, a collection of clonal sequences (n = 275) from a soil community study (6) was divided into two samples based upon accession numbers (138 odds and 137 evens). Although the study contained sequences from two sample sites (SL and SAF clones), sequences from both sites were placed in each data set to form nearly equivalent samples. A comparison of ΔCodds/evens to ΔC values resulted in P = 0.871, which indicated that the two samples were not significantly different (Fig. 1A). Similar results were obtained for ΔCevens/odds and other arbitrarily divided sequence libraries (Table 1). Thus, as expected, samples taken from the same library were not found to be different.
TABLE 1.
Comparisons of environmental clone libraries
| Site (reference) | Homologous (X)
|
Heterologous (Y)
|
Pb | |
|---|---|---|---|---|
| Clones | n | Clones | ||
| Grassland soils (6) | Oddsa | 138 | Evensa | 0.871 |
| Evensa | 137 | Oddsa | 0.933 | |
| SAF | 138 | SL | 0.120 | |
| SL | 137 | SAF | 0.135 | |
| Bioreactors (1) | Oddsa | 95 | Evensa | 0.853 |
| Evensa | 94 | Oddsa | 0.623 | |
| SBR1 | 97 | SBR2 | 0.308 | |
| SBR2 | 92 | SBR1 | 0.824 | |
| Arid soils (2) | Oddsac | 56 | Evensa | 0.251 |
| Evensa | 56 | Oddsac | 0.516 | |
| C0 | 59 | S0 | 0.042 | |
| S0 | 53 | C0 | 0.398 | |
| Grassland soil/bioreactor | SAF | 138 | SBR1 | 0.001 |
| SBR1 | 97 | SAF | 0.002 | |
| SL | 137 | SBR1 | 0.001 | |
| SBR1 | 97 | SL | 0.001 | |
Sequences with odd or even accession numbers. Contains mixtures of both libraries described in the reference, and they are not expected to be different.
Value of r/(N + 1) as described in the text.
Accession number AF128647 could not be found and was not included.
To demonstrate that this procedure could correctly differentiate samples from different libraries, sequences of clones obtained from an activated sludge (SBR1; n = 97; reference 1) were compared to grassland soil SL clones. The SBR1 clones were found to be significantly different from the SL clones (P = 0.001; Fig. 1B). More information on the nature of this difference was obtained by examination of the distribution of (CX − CXY)2 with D (Fig. 1B). At low D, the actual (CX − CXY)2 exceeded the comparable values at P = 0.05 obtained during the calculation of ΔC. This result suggested that the libraries differed greatly at D < 0.10 but shared many deep taxa. However, smaller differences at D > 0.3 suggested that not all deep phylogenetic groups were found in both libraries. Similar results were also obtained for comparisons of other soil and bioreactor libraries (Table 1 and data not shown).
Three sequence collections consisting of multiple samples were analyzed to determine if differences between the samples could be detected (Table 1). Clonal libraries derived from the microbial populations of phosphate-removing (SBR1) and non-phosphate-removing (SBR2) bioreactors differed in the abundance of certain taxa (1). However, these differences were not shown to be significant by our method (Table 1). The compositions of libraries from the microbial communities of improved (SL) and unimproved (SAF) upland grass pasture soils were not found to be significantly different (6). We also obtained the same conclusion by our method (Table 1). Finally, comparisons of restriction fragment length types from C0 and S0, two clonal libraries derived from arid soils, suggested that C0 was more diverse than S0 (2). Our analysis of the sequences obtained from this study was consistent with this conclusion and further suggested that S0 was a subset of C0. ΔCS0/C0 was not significant, which suggested that all of the taxa present in S0 were also present in C0 (Table 1). However, the reciprocal value ΔCC0/S0 was significant; therefore, C0 also contained sequences of one or more taxa not found in S0. The distribution of (CX − CXY)2 with D further indicated that the additional taxa in C0 represented moderately deep phylogenetic groups, 0.15 < D < 0.25 (Fig. 1C).
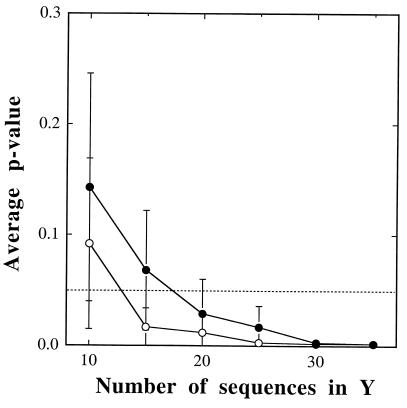
Sample size should have a major effect on comparisons of libraries. The minimum number of sequences necessary to distinguish two dissimilar libraries was expected to increase with the complexity of the libraries and decrease with the magnitude of the dissimilarity. This point was examined in detail by using two libraries of high diversity and dissimilarity. Variable numbers of clonal sequences were randomly selected from either library SBR1 or SL (Y) and compared to the opposite library (X), and P values were determined for 10 replicates. Approximately 20 and 25 sequences from SBR1 and SL, respectively, were required to differentiate the two libraries (P < 0.05) when X was represented by 97 and 137 sequences, respectively (Fig. 2). Tests were also performed to investigate the required sample size of X (SBR1) when the size of Y (SL) was small. It was found that nearly all (≥90) of the sequences from the SBR1 library were required to distinguish these libraries when the SL library (Y) was represented by 20 sequences (data not shown). When the sizes of both libraries were varied, they were consistently detected as different when the SBR1 (X) and SL (Y) libraries were represented by ≥40 and ≥30 sequences, respectively (data not shown). While these results may not generalize to all environmental samples, they should be representative of comparisons of libraries from diverse communities, such as those found in soil and bioreactors. Importantly, these results suggest than modestly sized libraries from microbial communities similar in complexity to those used in this study will be distinguished by this method.
FIG. 2.
Effect of sample size on the discrimination of libraries. A comparison of the SL library from grassland soil (Y; n = variable) to the bioreactor library SBR1 (X; n = 97) (●) and a comparison of the SBR1 (Y; n = variable) library to the SL (X; n = 137) library (○) shown. Each point represents an average of 10 replicates, and the error bars are 1 standard deviation. The broken line indicates P = 0.05.
Acknowledgments
We thank Kamyar Farahi and Rob Waldo for help with programming in Perl. We also thank Lihua Wang of the Statistical Consulting Office at the University of Georgia for help.
This work was supported in part by an award from the Division of Molecular and Cellular Biosciences at NSF (MCB-0084164).
REFERENCES
- 1.Bond P L, Hugenholtz P, Keller J, Blackall L L. Bacterial community structures of phosphate-removing and non-phosphate-removing activated sludges from sequencing batch reactors. Appl Environ Microbiol. 1995;61:1910–1916. doi: 10.1128/aem.61.5.1910-1916.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dunbar J, Takala S, Barns S M, Davis J A, Kuske C R. Levels of bacterial community diversity in four arid soils compared by cultivation and 16S rRNA gene cloning. Appl Environ Microbiol. 1999;65:1662–1669. doi: 10.1128/aem.65.4.1662-1669.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Felsenstein J. PHYLIP (phylogenetic inference package) version 3.5c. Seattle: University of Washington; 1993. [Google Scholar]
- 4.Good I J. The population frequencies of species and the estimation of population parameters. Biometrika. 1953;40:237–264. [Google Scholar]
- 5.Hope A C A. A simplified Monte Carlo significance test procedure. J Royal Statist Soc B. 1968;30:582–598. [Google Scholar]
- 6.McCaig A E, Glover L A, Prosser J I. Molecular analysis of bacterial community structure and diversity in unimproved and improved upland grass pastures. Appl Environ Microbiol. 1999;65:1721–1730. doi: 10.1128/aem.65.4.1721-1730.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Pettitt A N. Cramer-von Mises statistic. In: Kotz S, Johnson N L, editors. Encyclopedia of statistical sciences. New York, N.Y: Wiley-Interscience; 1982. pp. 220–221. [Google Scholar]
- 8.von Wintzingerode F, Göbel U B, Stackebrandt E. Determination of microbial diversity in environmental samples: pitfalls of PCR-based rRNA analysis. FEMS Microbiol Rev. 1997;21:213–229. doi: 10.1111/j.1574-6976.1997.tb00351.x. [DOI] [PubMed] [Google Scholar]