Dissipative Control over the Toehold‐Mediated DNA Strand Displacement Reaction

Abstract

Here we show a general approach to achieve dissipative control over toehold‐mediated strand‐displacement, the most widely employed reaction in the field of DNA nanotechnology. The approach relies on rationally re‐engineering the classic strand displacement reaction such that the high‐energy invader strand (fuel) is converted into a low‐energy waste product through an energy‐dissipating reaction allowing the spontaneous return to the original state over time. We show that such dissipative control over the toehold‐mediated strand displacement process is reversible (up to 10 cycles), highly controllable and enables unique temporal activation of DNA systems. We show here two possible applications of this strategy: the transient labelling of DNA structures and the additional temporal control of cascade reactions.

How to rationally re‐engineer the classic strand displacement reaction is reported such that the high‐energy fuel strand is converted into a low‐energy waste product through an energy‐dissipating reaction, allowing the spontaneous return to the original state. Two possible applications are also demonstrated: the transient labelling of DNA structures and the additional temporal control of cascade reactions.

Introduction

Cellular growth, division and reproduction are only few of the phenomena that illustrate the non‐equilibrium nature of living systems.[ ¹ , ² , ³ ] At the molecular level, chemical fuels drive dissipative reaction cycles of the biomolecular machinery, such as pumps and motors, as well as the self‐assembly of non‐equilibrium structures, such as microtubule filaments.[ ⁴ , ⁵ , ⁶ , ⁷ , ⁸ , ⁹ , ¹⁰ ] There is a strong current interest to develop chemically‐fueled synthetic materials and devices to harness the emerging properties associated to life.[ ¹¹ , ¹² , ¹³ , ¹⁴ , ¹⁵ , ¹⁶ ]

Within the context of creating artificial dissipative nanodevices[ ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² ] and structures,[ ²³ , ²⁴ , ²⁵ , ²⁶ ] synthetic DNA has been rapidly emerging as a powerful material. The programmability and predictability of DNA hybridization, together with the possibility to use nucleic acids as fuels that can be enzymatically or chemically fragmented into waste, have been providing a strong momentum for the establishment of the field of dissipative DNA nanotechnology.[ ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ ] Contrary to classical dynamic DNA nanotechnology, ^[27] which relies on the chemically‐triggered activation of complex kinetic pathways that transit into new thermodynamic final states, dissipative DNA technology is based on reactions which enable a transient and repetitive activation of the system through the batch‐wise addition of fuel (Figure 1). Advancement of the field of dissipative DNA nanotechnology will crucially rely on the toolbox of available reactions to permit a rational design of dissipative processes in the system. Toehold‐mediated (or toehold‐exchange) DNA strand displacement is the most frequently used reaction in dynamic DNA nanotechnology. In this reaction, pioneered by Yurke, ^[28] and later expanded by Winfree, Zhang and Yurke himself,[ ²⁹ , ³⁰ , ³¹ ] an added DNA invader strand (further called fuel) displaces an incumbent strand (further called output) that had been pre‐hybridized to a complementary target. The toehold‐mediated strand displacement reaction has been employed to operate functional DNA nanodevices and to assemble DNA‐based nanostructures[ ³² , ³³ , ³⁴ , ³⁵ ] under strict thermodynamic control. The possibility to reset such strand displacement reactions has been demonstrated through different strategies that rely on the presence of secondary reactions or logic circuits to reinstall the original state of the system.[ ³⁶ , ³⁷ , ³⁸ ] Transcriptional circuits and oscillators have also employed dissipative resettable strand displacement reactions as composable units for more complex dynamical system behaviours.[ ³⁹ , ⁴⁰ , ⁴¹ , ⁴² ] Recently, two transcription‐free strategies have been demonstrated to control strand displacement processes in a dissipative way based on an ATP‐controlled fully self‐resettable strand‐displacement system ^[43] or on dissipative cascaded DNA networks. ^[44] Motivated and inspired by these examples we report here the implementation and detailed characterization of two simple general strategies free of sequence constraints to achieve dissipative toehold‐mediated strand displacement reactions that could enable the operation of the abovementioned DNA systems in closer analogy to the biological machinery.

Figure 1.

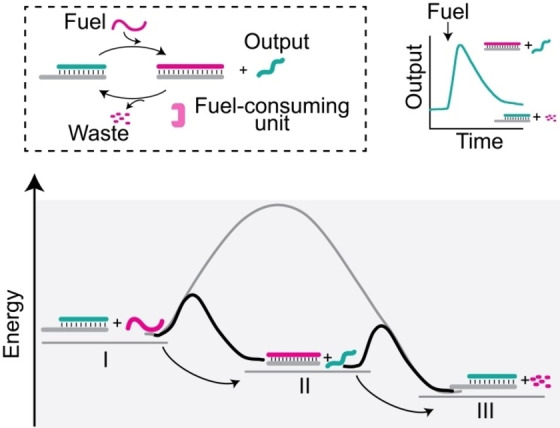
General strategy to achieve dissipative DNA strand displacement reactions. A dissipative mechanism can be established by performing the experiment in the presence of a selective fuel‐consuming unit. Progressive fuel degradation provides only transient displacement followed by reloading of the output stand. The energy diagram depicts the three relevant energy states of the system: I) target/output duplex+fuel; II) target/fuel duplex+output; III) target/output duplex+fuel waste. Indicated are also the free energy barriers for all the possible pathways. The grey line indicates the unfavored pathway from I to III.

The dissipative toehold‐mediated strand displacement reactions we report here are based on an energy‐dissipating step to convert the fuel strand into low‐affinity waste fragments. In this way, fuel addition transiently alters the free energy landscape of the system, and after fuel‐to‐waste conversion the system restores its original composition (Figure 1).

Results and Discussion

To establish sequence‐independent dissipative strand displacement reactions, we rationally designed an enzyme‐mediated as well as an enzyme‐free mechanism for fuel consumption. For enzyme‐mediated fuel consumption we took inspiration from the composable units of transcriptional circuits reported by Winfree and others ^[36] and used an RNA strand as fuel and RNase H endoribonuclease (RNase H), which hydrolyzes RNA only within an RNA/DNA heteroduplex, as fuel‐consuming unit. Upon binding to the toehold portion, the fuel activates the strand displacement process, leading to the release of the output and the formation of an RNA/DNA heteroduplex. Then, RNase H recognizes this heteroduplex followed by the degradation and the dissociation of the RNA fuel allowing for the reloading of the output strand over time (Figure 2a). The strand displacement reaction is followed in real‐time with a fluorimeter by labeling the initial output‐target duplex with a fluorophore/quencher pair.

Figure 2.

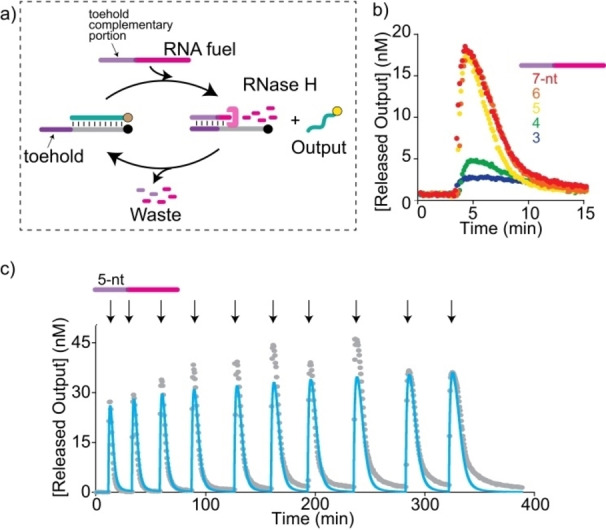
a) Enzymatically‐driven dissipative strand displacement reaction. b) Time trajectories of the dissipative strand displacement reaction after the addition of 100 nM fuel with different toeholds lengths (3–7 nts). c) Time trajectory showing multiple transient strand‐displacement cycles following repeated addition of the same amount of the RNA fuel strand (100 nM) to a solution containing the preformed duplex (50 nM) and RNase H (15 U mL⁻¹). The fluorescence signal here is reported as [Released Output] (nM), indicating the concentration of the output strand transiently released at each cycle. Experimental values (grey) are shown together with a prediction from a parameterized kinetic model (blue).

We first tested a series of RNA fuel strands sharing the same 20‐nt invading domain but differing in the length of the toehold‐complementary portion. More specifically we tested toeholds ranging from 3 to 7 nucleotides (Figure 2b). In the absence of the enzyme, a monotonous signal increase was observed upon the addition of the RNA fuel, indicating the stable release of the output strand (Figure S1) with second order kinetics (see Supporting Information for details). In contrast, in the presence of the RNase H, the signal increase was followed by a signal decrease to the base level indicating the reloading of the output strand (Figure 2b). Of note, the amplitude of the transient signal was strongly dependent on the toehold length of the fuel strands. We selected 5‐nt toeholds as the optimal system for further experiments, since longer toeholds did not significantly increase the transient amplitude nor the rate constant of the initial displacement (Figure S1) but may increase inhibition effects of the waste products (see below).

Our dissipative strand displacement reaction was highly efficient and practically free of leak reactions. Therefore, multiple repeats of transient displacements could be obtained through repeated addition of the same amount of RNA fuel strand to a solution containing the preformed duplex complex and the fuel‐consuming unit (RNase H) (Figure 2c). Of note, after each cycle we observed a slight slow‐down of the reloading process likely due to a minimal inhibition effect of the waste products or the limited stability of the enzyme over time.

To test whether our dissipative reactions can be precisely modulated, we performed experiments in which we varied fuel and enzyme concentrations. We first measured the time‐course of the reaction for different concentrations of the RNA fuel strand at a fixed concentration of RNase H (15 U mL⁻¹) (Figure 3a). Notably, the half‐life for the transient amplitude increased from 3 to 17 minutes upon increasing the RNA fuel concentration from 30 to 500 nM (Figure 3b). Secondly, it was also possible to regulate the process by using different concentrations of the RNase H but a fixed concentration of the RNA fuel strand (100 nM) (Figure 3c). In this case the half‐life for the strand displacement reaction could be increased from 4 to 15 minutes when decreasing the RNase H concentration from 30 to 3 U mL⁻¹ (Figure 3d). Similarly, the maximum amplitudes of the transient reaction were strongly dependent on the fuel and the enzyme concentrations (Figure 3e, f).

Figure 3.

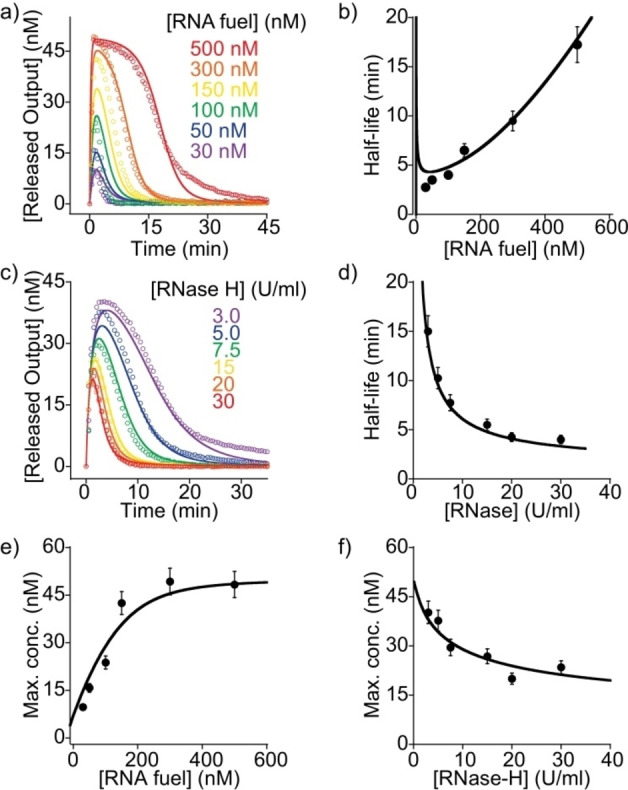
Transient behaviour and half‐lives of the strand displacement at different concentrations of a), b) RNA fuel and c), d) the fuel‐consuming unit (RNase H). Solid lines represent the best fits to the kinetic model (see text and Supporting Information). e), f) Maximum concentrations for each transient cycle are shown as function of RNA fuel and RNase H concentration. In panel a, a fixed concentration of RNase H was used (15 U mL⁻¹), while in panel b a fixed concentration of RNA fuel strand was applied (100 nM). Experiments shown in this figure are conducted at a fixed concentration of the preformed duplex (50 nM). Error bars represent the standard deviations from triplicate measurements.

To gain further insight into the kinetic processes involved and to better understand the dynamics of the transient signal, we developed a minimalistic kinetic model based on a simple reaction pathway (Figure S2) (see Supporting Information section for more details on the model). Modelling the experimental data provided a very good agreement with our kinetic model over the entire range of fuel and enzyme concentrations (Figure 3, solid lines) as well as toehold lengths (Figure S3). A slow phase for elevated times and large maximum amplitudes that is not described by the model (see 500 nM trajectory in Figure 3a) is attributed to inhibitory effects from accumulating waste. Importantly, the modelling provided also estimates for the rate constants of strand displacement (k _displ.=(1.5±0.3) ×10⁵ M⁻¹ s⁻¹), fuel cleavage (k _cleave=(1.2±0.1)x10⁻³ M⁻¹ s⁻¹) as well as the dissociation constant of RNase H inhibition by RNA waste fragments (K _frag=(0.3±0.1) μM). Using these parameters, the modelling was able to predict the repetitive strand displacement reactions including the modulation of the pulse shape over time (Figure 2c).

To generalize the concept of our approach, we developed a second non‐enzymatic strategy, based on disulfide‐thiol redox reactions, to transiently control the strand displacement process. To set up a transient redox‐control of our fuel strands, we split a 25‐nt DNA fuel into two parts (of different lengths) that were linked to each other through a disulfide bond. In the absence of any reducing agent the disulfide containing fuel strand could activate the strand displacement reaction and release the output (Figure S4). In contrast, a reducing agent, by breaking the disulfide bond in ssDNA or dsDNA disulfide strands, can act as the fuel‐consuming unit. The resulting fuel fragments should then spontaneously dissociate from the target, allowing for reloading of the output strand and the formation of the original duplex (Figure 4a, S5).

Figure 4.

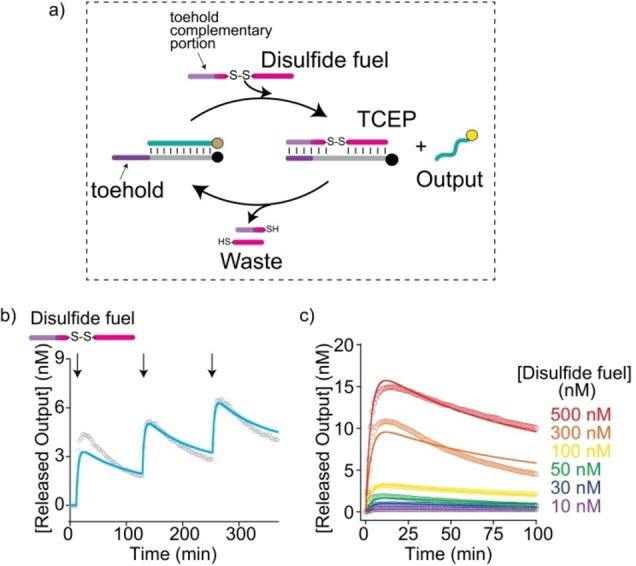
a) Redox‐driven dissipative strand displacement reaction. b) Time trajectory of the displacement reaction showing repetitive strand‐displacement cycles of the output strand after sequential addition of a fixed concentration of the disulfide fuel (100 nM) to a solution containing the preformed duplex and the fuel consuming agent (TCEP, 1 mM). Experimental values (grey) are shown together with the data from the kinetic model (blue). c) Transient strand displacement measured at different concentrations of the disulfide fuel. Solid lines represent the best fits to the data using the kinetic model (see text and Supporting Information).

We first tried to find an optimal thermodynamic trade‐off in which the disulfide fuel could efficiently displace the output strand while simultaneously supporting an efficient dissociation of the fuel fragments upon reduction of the disulfide bond using TCEP (tris(2‐carboxyethyl)phosphine). To achieve this, we rationally designed three disulfide fuels with the same total length, but with a different position of the disulfide bond (5–7 nt from the toehold end). Experiments carried out at different concentrations of these disulfide fuels successfully demonstrated a transient response for all three fuel strands (Figure 4b, S6). Applying the reversibility of this new system, we furthermore demonstrated that one can achieve multiple repeats through the repetitive addition of disulfide fuel DNA‐strands (100 nM) in the presence of a fixed concentration of 1 mM TCEP as the fuel‐consuming unit (Figure 4b, S6). As for the RNA‐based system, the half‐life of the transient strand displacement could be controlled by the concentration of the disulfide fuel strand as corresponding measurements at a fixed concentration of reducing agent but varying concentration of fuel revealed (Figure 4c, S7). We note that the disulfide‐based systems exhibited a slightly lower efficiency as well as reversibility compared to the enzymatic degradation of the fuel. This is likely due to the following reasons. First, the presence of the disulfide bond in the fuel reduces the strand displacement efficiency (see Figure S1, S4). Second, the fuel reduction also occurs in the unbound fuel (contrary to the RNA fuel which is cleaved by RNase H only in the heteroduplex). Third, the waste fragments produced by the fuel reduction are larger than those produced by enzymatic degradation accounting for a more significant waste inhibition.

To substantiate the observed transient behaviour, we developed again a minimalistic kinetic model to fit the experimental data (Figure S5, Supporting Information section for more details). The model could well describe the measured transient kinetics for different fuel concentrations as well as different positions of the disulfide bond (Figure 4c, S6). Additionally, it was able to describe repetitive transient strand displacement following successive additions of fuel strand (Figure 4b, S7).

We next set up two applications of the dissipative strand displacement in order to demonstrate a successful integration within more complex reaction schemes. As a first approach, we employed our dissipative reaction for the transient labelling of DNA nanostructures. To do this, we assembled tubular DNA structures of micrometer lengths using a DNA tile‐based approach.[ ⁴⁵ , ⁴⁶ ] Each of the tiles forming the tube is composed of five DNA strands and contains four sticky ends (5‐nt each) that enable their self‐assembly into tubular structures. To an additional ssDNA overhang on each tile, a target‐output duplex is attached (Figure 5b, S8). The output strand is conjugated with a Quasar‐570 fluorophore (Q570), such that the tubes can be imaged in a fluorescent microscope (Figures 5a, c). Upon addition of a Cy5‐conjugated RNA fuel strand (green, Figure 5a) the output strand is replaced by strand displacement (Figure 5b), such that the structures emit at a different wavelength (Figure 5c). In the presence of RNase H such re‐labeling is transient since the Cy5‐labelled RNA fuel strand is degraded over time allowing the Q570‐conjugated output strand to rebind (Figure 5c). The transient labelling is reversible and efficient over multiple reaction cycles (Figure 5c, d). Control experiments in the absence of RNase H or with a Cy5‐labeled DNA fuel strand show, as expected, a permanent substitution of the labeling (Figure S9).

Figure 5.

Transient labelling of DNA‐based nanostructures. a) Cartoon showing the transient labelling of a tubular DNA tile structure when adding an RNA fuel strand. b) Scheme of the transient relabeling reaction. Initially each DNA tile carries a target strand hybridized to a Quasar‐570 fluorophore‐conjugated DNA output strand (red). Addition of a Cy‐5 conjugated‐RNA fuel strand displaces the output strand resulting in a different labeling of the nanotubes. In the presence of RNase H the re‐labeling is transient and reversible due to fuel degradation and output rebinding. c) Fluorescence microscopy images of aliquots of the sample solution taken at different times (indicated). The sample contains DNA tubular structures labelled with a Quasar‐570‐conjugated DNA strand (both at 250 nM) and RNase H (30 U mL⁻¹). RNA fuel conjugated to Cy5 was added at 500 nM concentration. Scale bar corresponds to 2.5 μm. Shown are the merged images obtained from both fluorescent channels (Q570 and Cy5). d) Average length ($<\mathrm{L}>$ , μM) of the structures obtained from the analysis of the merged channel (left, $<\mathrm{L}>$ _merged, grey) and the Cy5 channel (right, $<\mathrm{L}>$ _Cy5, green) showing that the structures remained intact during relabeling and imaging. Light green bars correspond to $<\mathrm{L}>$ _Cy5=0 when no Cy5‐fluorescence could be detected. Error bars represent standard deviations of the mean based on triplicate measurements.

In a second application we demonstrated how the dissipative strand displacement can be integrated into a small reaction network to allow its temporal control. To do this, we re‐engineered a simple two‐step self‐amplification circuit. ^[47] Here, a target strand species carries an incumbent and an output strand (Figure 6a). Upon addition of a sub‐stoichiometric amount of RNA fuel, part of the incumbent strands become displaced. This liberates a toehold (cyan region in Figure 6a) for the binding of a long capture strand, which can then displace the fuel strand and the output strand. Fuel strand liberation allows further displacement of incumbent strands such that an RNA‐driven multi‐turnover self‐amplification reaction is obtained (Figure 6a, left). Setting up this reaction provided that the self‐amplification ran until completion at which the target as well as capture strands were consumed (Figure 6b, grey curve). Under dissipative conditions, i.e. in the presence of the RNase H, the addition of RNA‐fuel resulted in a limited signal increase (Figure 6b, black curve), such that it could be reinitiated multiple times by step‐wise fuel addition. Thus, the self‐amplification was only temporarily turned on and the turnover was mainly limited to just a single cycle. The turnover of the temporary amplification could however be modulated using different concentrations of the capture strand (see Figure S10). This temporal control was achieved by the degradation of the target‐bound RNA fuel strand, such that no further displacement cycles could be initiated. In first approximation, the output signal can be seen as the integral in time over the transient displaced incumbent concentration such that the reaction can be considered as an integration unit. Furthermore, we note that the sequence of the produced DNA output can be freely chosen and used in further downstream reactions, such that our system represents a minimal cascade.

Figure 6.

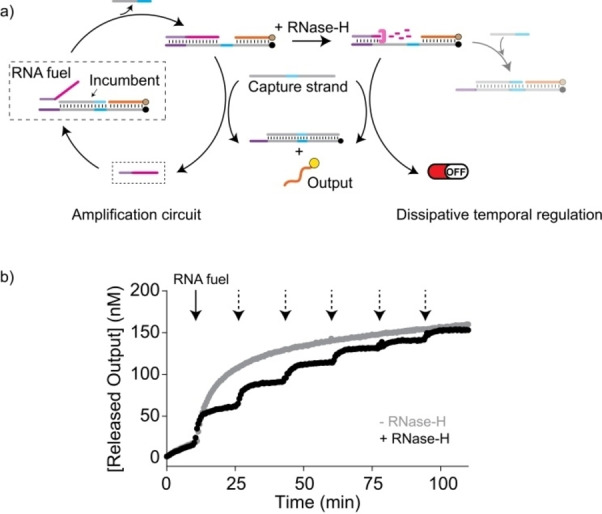
a) Temporal control of a self‐amplification circuit using dissipative strand displacement. A separate output and an additional capture strand drive a self‐amplification reaction upon fuel strand addition (left). Under dissipative conditions, the fuel is degraded and the self‐amplification is stopped (right). b) Time trajectory of the output strand release upon addition of RNA fuel strand (50 nM, indicated by black arrows) in the absence (grey curve) or presence (black curve) of RNase H (15 U mL⁻¹). Due to the transient amplification in presence of RNase H, the amplification could be initiated multiple times by repeated addition of RNA (indicated by dashed arrows). The amplification system in the solution contained 300 nM of target, incumbent, output and capture strands.

Conclusion

In summary, we have described here two versatile strategies to gain dissipative control over the basic strand displacement reaction scheme. So far, the majority of dynamic DNA systems has been controlled by classical DNA‐exchange reactions, like the toehold‐mediated strand displacement that over sufficient time adopt a new and stable equilibrium state.[ ²⁹ , ³⁰ , ³¹ , ³² , ³³ , ⁴⁴ ] To better mimic reaction networks of living systems, the functional operation of DNA systems should however rely on energy dissipation allowing for the formation of transient states. The examples reported here demonstrate that the classical strand displacement reaction can be easily altered to allow a transient activation with excellent efficiency and reversibility. This supported also multiple displacement‐release cycles. We note that the established systems do not require specific sequences. Additionally, one can easily control the half‐life and the amplitude of the reactions by the concentrations of fuel or the fuel‐consuming unit. Furthermore, an enzyme‐based and an enzyme‐free version of the reaction is provided.

To demonstrate the utility of our strategy we set up two applications. In the first, we employed our dissipative strand displacement reaction for the transient fluorescent‐encoding of DNA nanostructures. This approach can be useful to overcome signal problems due to fluorophore bleaching and to allow labelling of different structures in the same sample at different time points. In the second application we integrated our dissipative strand‐displacement reaction in a small reaction network, representing an integration unit and providing the basis for downstream cascaded reactions. In its current design, the transient strand displacement by the RNA fuel liberated a toehold to initiate a downstream reaction. The latter would barely interfere with the RNA degradation and thus only little affect the duration of the transient reaction. This may be different in network designs in which transiently displaced DNA strands would be directly used in downstream reactions.

Given the described versatility of our reaction scheme for dissipative reversible strand displacement, we expect that it can become a highly useful tool to set up active fine‐tuned cascaded reaction networks with temporal control as well as to transiently control other DNA‐based processes.

Conflict of interest

The authors declare no conflict of interest.

Supporting information

As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer reviewed and may be re‐organized for online delivery, but are not copy‐edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.

Supporting Information

E. Del Grosso, P. Irmisch, S. Gentile, L. J. Prins, R. Seidel, F. Ricci, Angew. Chem. Int. Ed. 2022, 61, e202201929; Angew. Chem. 2022, 134, e202201929.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.