Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jul 14;7(29):25353–25365. doi: 10.1021/acsomega.2c02329

Dynamic Effect of Shaped Charge Blasting and Its Application in Coal Seam Permeability Enhancement

Xiangshang Li †,*, Kai Si ‡, Tuan He †, Chunyuan Li †,*
PMCID: PMC9330100  PMID: 35910146

Abstract

graphic file with name ao2c02329_0022.jpg

The dynamic effect of shaped charge blasting and its application in coal seam permeability enhancement have been investigated. Comparative experiments of shaped charge blasting and conventional blasting to fracture the concrete are carried out. Then, the propagation characteristics of explosion stress waves under shaped charge blasting and conventional blasting are analyzed by ANSYS/LS-DYNA. Finally, the fracture mechanical model of shaped charge blasting is established. The experimental results show that the width of the four main cracks formed after conventional blasting is 0.3 cm, while the width of the cracks in the energy accumulation direction after shaped charge blasting is 1.1 cm and the width of that in the vertical energy accumulation direction is 0.4 cm. The numerical simulation results show that the crushing area after shaped charge blasting is “dumbbell type”, and the area is smaller than that of conventional blasting. However, the cracking area is “spindle type”, and the development of the fracture degree is better than that of conventional blasting. In addition, shaped charge blasting is used to improve the permeability of coal seams. The results show that shaped charge blasting effectively improves the permeability and gas extraction rate of coal seams.

1. Introduction

Coal, as the primary energy source in China, has played a leading role in meeting the energy demand of the nation.1−3 However, the geological structure of China’s coal fields is complex, and most of them are high coal-mine gas and low-permeability coal seams.4−6 With the increase of mining depth, coal and gas outburst disasters have become more serious.7−11 Field practice shows that gas extraction can effectively control coal and gas outburst disasters.12−14 The permeability of coal seams is very low, which seriously restricts the gas extraction efficiency. Improving the permeability of coal seam has become an urgent problem to be solved.

In view of how to improve the permeability of high-gas and low-permeability coal seams, scholars have proposed measures such as hydraulic fracturing15,16 and liquid CO2 phase transformation fracturing,17,18 which have achieved certain results. The principle of hydraulic fracturing technology involves injecting a liquid with chemicals into the coal seam to improve the permeability of the coal seam. For example, Lu et al. used hydraulic fracturing to increase the permeability of coal seams for the improvement of methane drainage in underground coal mines.19 To address the problem of extension direction of coal seam hydraulic fracturing, Zhai et al. analyzed the course of fracture variation around the boreholes in the process of hydraulic fracturing.20 The above studies indicate that hydraulic fracturing proved successful in improving the permeability of coal seams. However, it also causes a series of problems. For instance, the hydraulic fracturing technology not only wastes water resources but also the chemical reagents in hydraulic fluids are likely to pollute the groundwater. The principle of liquid CO2 phase-change fracturing technology is that liquid CO2 changes phase in a very short time21 (CO2 changes from liquid to gas); the resulting stress wave and high-energy gas effect on coal produced cracks, thereby increasing the permeability of the coal seam. However, the technology is still immature and has not been widely used.

With the development of blasting technology, loose blasting technology provides a new way to solve the problem of high-gas and low-permeability coal seam gas disaster.22−24 Compared with rocks, the internal cracks in a coal body are more developed and the mechanical strength is lower. When conventional blasting is used, the coal seam crushing area is often larger and the cracking area is smaller, resulting in the poor performance of enhanced-permeability coal seams. The plane structure of conventional blasting is shown in Figure 1a. Therefore, scholars propose to apply the shaped charge blasting technology to increase the permeability of coal seams, and the plane structure of shaped charge blasting is shown in Figure 1b. Shaped charge blasting is mainly used in military weapons in the early stage. After the end of World War II, shaped charge became gradually popular in the industrial field. Since then, important progress in shaped charge blasting has been made in mining, oil and gas exploitation, and tunnel excavation.25−27 Yang et al. used the dynamic caustics experimental method to study the crack propagation behavior related to slit charge blasting under such high static stress conditions.28,29 Meng et al. applied shaped charge blasting to directionally fracture the hard roof and release the mining pressure, and they identified the failure type of the rock mass and the fracture development area.30 Yin found that the optimal blasting effect, which has the longest directional cracks, few nondirectional cracks, and light damage to the surrounding rock, can be achieved by decoupling shaped charge blasting.31 He proposed the shaped hydraulic smooth blasting technology based on the form of bilateral-groove tube charge, but only the empirical methods were discussed, without providing a theoretical analysis.32 Guo improved the shaped charge blasting technology and successfully carried out the penetration enhancement test of coal seam deep-hole shaped charge blasting in Zhengzhou, Pingdingshan, and Jiaozuo mining areas.33 Luo qualitatively described the mechanical behavior of cumulative blasting and numerically evaluated the stress condition around the blasting borehole required as well as the formation of various fractures.34

Figure 1.

Figure 1

Open in a new tab

(a) Plane structure of a conventional roll; (b) plane structure of a shaped charge roll.

Previous investigations have indicated that there is a relative lack of research on the application of shaped charge blasting in coal seams. The dynamic effect of shaped charge blasting and the mechanism of deep-hole shaped charge blasting in coal seams are not thoroughly understood, and further investigation is necessary. The present work addresses this gap in this literature by exploring the aforementioned topic. A comparative experiment of concrete cracking by shaped energy blasting and conventional blasting is carried out. The forming mechanism of the shaped charge jet, the propagation characteristics of the stress wave, and crack propagation during shaped charge blasting are studied using the finite element program LS-DYNA. Meanwhile, the shaped charge blasting technology is applied to the Pingmei 10 mine to further explore the mechanism of shaped charge blasting. The research results can provide guidance for the engineering application of coal seam shaped charge blasting to increase permeability in theory, which is of great significance to improving the gas drainage efficiency and preventing coal and gas outburst disasters.

2. Blasting Experiment

2.1. Experimental Design

To analyze the different characteristics of crack evolution after cumulative blasting and conventional blasting, six concrete model specimens of the same size were poured, among which three groups of specimens were subjected to shaped charge blasting and the other three groups were subjected to conventional blasting. The size of the specimen was 80 cm × 80 cm × 60 cm. The blasthole was 20 cm deep with a 2.6 cm diameter, which was located in the center of the specimen. Six strain bricks, nos. 1–6, were buried in the horizontal plane 17 cm from the upper surface of the specimen. Strain brick nos. 1, 3, and 5 were 10 cm away from the center of the blasthole, and strain brick nos. 2, 4, and 6 were 20 cm away from the center of the blasthole, as shown in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Layout of the strain brick in the blasting model.

2.2. Specimen-Making Process

The detachable steel plate was used to assemble the test box with an external size of 84 cm × 84 cm × 84 cm, and the internal cavity size of the box was 80 cm × 80 cm × 60 cm. To prevent leakage of cement mortar during specimen pouring, before pouring the specimen, first yellow sand was laid on the ground followed by a plastic film. Oil was applied around the mold so that the specimen could fall off smoothly, as shown in Figure 3a. After the preparation work was complete, the mixing and pouring were carried out in strict accordance with the mass ratio of cement/sand/gypsum/water of 1.7:4.1:0.2:0.8, as shown in Figure 3b,c. During the pouring process, a vibrator was used to eliminate the air inside the specimen and ensure the overall homogeneity of the specimen, as shown in Figure 3d. Finally, the strain brick was positioned and embedded, as shown in Figure 3e. The size of the strain brick was 2 cm × 2 cm × 1 cm. To prevent reflection when the stress wave propagates to the strain brick after blasting, the ratio of the strain brick and concrete made was kept exactly the same. After the specimen was allowed to solidify for one day, the mold was disassembled, as shown in Figure 3f. The next concrete specimen was poured according to the above steps. After the fabrication of all specimens, they were cured for 28 days. The cured specimens are shown in Figure 4.

Figure 3.

Figure 3

Open in a new tab

Concrete block pouring process: (a) applying oil inside the mold, (b) weighing the material, (c) mixing the material, (d) eliminating the air inside the specimen, (e) positioning and embedding the strain brick, and (f) disassembling the mold.

Figure 4.

Figure 4

Open in a new tab

Cured test block.

2.3. Process of Making Medicine Rolls

A poly(vinyl chloride) (PVC) tube was used as a shaped charge tube and a conventional charge tube. The length of the tube was 8 cm, the outer diameter was 1.5 cm, and the wall thickness was 0.1 cm. The shaped charge metal liner was made of a copper sheet with a thickness of 0.1 mm. First, the copper sheet was cut into long strips with the size of 0.8 cm × 0.42 cm. Then, both sides of the copper sheet were folded into 90°, and the axis of the metal liner was 0.2 cm high. Finally, the copper sheet was stuck to the inner side of the PVC tube with 502 glue to ensure that the distance between both sides of the shaped energy cover was 1 cm. Before the test, 3.5 g of 2,4,6-trinitrotoluene (TNT) equivalent RDX (hexogen) was placed into the tube; then, a detonator was inserted in the center of the tube. Finally, 502 glue was dropped while injecting fine sand into the tube, which not only plays a certain role in sealing the hole but also ensures that the detonator is in the center of the tube. The specific manufacturing process of a shaped charge tube is shown in Figure 5. There is no metal liner on the inner side of the conventional charge tube, and the other operations are the same as the manufacturing process of the shaped charge tube.

Figure 5.

Figure 5

Open in a new tab

Manufacturing process of the shaped charge tube.

3. Experimental Results and Discussion

3.1. Comparative Analysis of Macroscopic Fractures

TST5912 ultradynamic strain instrument is selected for the experiment. The tube was placed into the blasthole with a diameter of 2.5 cm, and 502 glue was dropped while injecting fine sand to seal the hole. To prevent the concrete test block from splashing during blasting, a thick wooden board was placed on the top of the specimens, and then, the blasting experiment was carried out.

After conventional blasting, specimen failure is shown in Figure 6a. It can be seen that the crushing area of the specimen was distributed in a circular shape, with a diameter of about 4 cm, and the diameter of the crushing ring was 1.5 times the diameter of the blasthole. Four main cracks extending from the blasthole to the boundary of the specimen were formed on the surface of the test piece, accompanied by several disordered microcracks. The width of the four main cracks was basically the same, about 0.3 cm, and the width of the main crack was small. This is because after conventional blasting, the detonation wave propagates evenly around, and a large part of the explosive energy is wasted on the crushing of the specimen. However, the explosive energy is certain, resulting in a large crushing area and a small crack area of the specimen.

Figure 6.

Figure 6

Open in a new tab

(a) Specimen failure diagram of conventional blasting, and (b) specimen failure diagram of shaped charge blasting.

After shaped charge blasting, specimen failure is shown in Figure 6b. The measurement found that the crushing area is distributed in an elliptical shape after the shaped charge blasting. The crushing area length in the horizontal direction was about 3.2 cm, and the crushing area length in the vertical direction was about 3.8 cm. It was smaller than the crushing area of the specimen after conventional blasting. After blasting, the specimen also formed four main cracks, which extended from the blasthole to the boundary of the specimen. The width of the main crack in the horizontal direction was 1.1 cm, and the width of the main crack in the vertical direction was 0.4 cm. The widths of the four main cracks were all larger than those formed after conventional blasting, and the width of the horizontal cracks was obviously larger than that of the vertical cracks. This was because after shaped charge blasting, the detonation wave compresses the copper shaped charge liner, forming the metal jet in the horizontal direction. The metal jet penetrates into the specimen to form the guided crack, which is beneficial to the stress wave and explosion gas to further crack the specimen. The width of the crack formed in the vertical gathering direction was also slightly larger than that of conventional blasting because when the detonation wave compresses the metal liner, some reflected detonation waves collide with each other, which strengthens the energy in the vertical gathering direction and promotes crack propagation in this direction.

3.2. Comparative Analysis of Strain Evolution

The blasting process is inevitably interfered with by external signals. Waveform screening was carried out in the data processing, and the waveform with good repeatability and stability was selected for analysis. The strain time curves of each strain brick in conventional blasting are shown in Figure 7.

Figure 7.

Figure 7

Open in a new tab

(a) Strain of the strain gauge 10 cm from the blasthole varying with time, and (b) strain of the strain gauge 30 cm from the blasthole varying with time.

According to Figure 7a, the strain gauges P1, P3, and P5 all reach the compressive strain peak for the first time within 0–100 μs, and the compressive strain peak values are −7210, −6960, and −6840 με, respectively. The strain gauges P2, P4, and P6 all reach the compressive strain peak for the first time within 100–150 μs, and the compressive strain peak values are −6205, −5990, and −6086 με, respectively. The strain peak values of strain gauge at the same position from the center of the hole are basically the same. The results show that the detonation wave propagates in a circular manner after conventional blasting, and the compressive stress of the strain gauge at the same distance with the explosive is basically the same.

Figure 8 shows the strain time curves of each strain brick in shaped charge blasting. The strain gauges J1, J3, and J5 all reached the compressive strain peak for the first time within 0–160 μs, and the compressive strain peak values are −9156, −7927, and −5645 με, respectively. In other words, the compressive strain of the strain gauge in the horizontal direction is the maximum, followed by the compressive strain of the strain gauge in the vertical direction, and the compressive strain of the strain gauge in the diagonal is the minimum. Because the copper metal liner is installed on both sides of the tube, after the explosive is detonated, the two wings of the copper liner are severely compressed and deformed by the huge pressure of the detonation wave and finally collide at a high speed in the axial direction. Since the copper metal liner has the characteristics of low compressibility and high density, the copper sheets finally form a high-speed, high-energy, and high-pressure metal jet in the axial direction. The metal jet penetrates the concrete and strengthens the compressive stress of the concrete in the horizontal direction. The process achieves energy convergence in the horizontal direction, so the strain of the strain gauge in the horizontal direction is the maximum. When the detonation wave compresses the metal liner, the detonation waves reflect and collide with each other to enhance the detonation energy of the vertical direction, so the strain of the strain gauge in the vertical direction is the second. Part of the detonation energy in the diagonal direction is transformed into a shaped charge jet, so the strain of the strain gauge in the diagonal direction is the minimum.

Figure 8.

Figure 8

Open in a new tab

(a) Strain of the strain gauge 10 cm from the blasthole varying with time, and (b) strain of the strain gauge 30 cm from the blasthole varying with time.

At the same time, it is found that the J1 strain gauge produces compressive strain at 25 μs, while the vertical and diagonal strain gauges produce compressive strain at 0 μs. It is because the formation of a metal jet requires the detonation wave to compress the metal liner first, and then, the metal liner collides. That is, the formation of a metal jet takes a certain time, while the detonation waves in other directions directly act on the concrete. Therefore, the time of horizontal compression strain is slightly behind the other two directions.

Comparing the strains of strain gauges J1, J2 and P1, P2, it is found that the compressive strain peaks of strain gauges J1 and J2 are greater than those at the same position of conventional blasting. Taking strain gauge 1 as an example, the peak strain of strain gauge J1 in cumulative blasting is −9156 με, and the peak strain of strain gauge P1 in conventional blasting is −7410 με. The peak strain of strain gauge in cumulative blasting is 1.24 times that of the peak strain gauge in conventional blasting. By comparing the strains of strain gauges 1 and 2 within 150–400 μs, it is found that the strain in the horizontal direction of shaped charge blasting is larger than that of the conventional blasting, that is, the effective strain produced by shaped charge blasting is larger than that of the conventional blasting. It shows that the detonation energy in the horizontal direction is strengthened, and the ability to crack concrete in the horizontal direction is promoted by the addition of a copper metal liner in shaped charge blasting.

Comparing the strains of strain gauges J3, J4 and P3, P4, it is found that the compressive strain peaks of J3, J4 are basically equal to the compressive strain of strain gauge at the same position of conventional blasting. Taking strain gauge 3 as an example, the strain peak value of strain gauge J3 in cumulative blasting is −6680 με and that of strain gauge P3 in conventional blasting is −6960 με. The strain gauge peak value in cumulative blasting is 0.96 times that in conventional blasting, indicating that the cracking capacity of the two blasting methods is similar in this direction.

Comparing the strains of strain gauge J5, J6 and P5, P6, it is found that the compressive strain peaks of J5, J6 are much lower than the compressive strain of strain gauge at the same position of conventional blasting. Taking strain gauge 5 as an example, the compressive strain peak value of strain gauge 5 in cumulative blasting is −5542 με, while that of conventional blasting is −6752 με. The compressive strain peak value of strain gauge in cumulative blasting is 0.82 times that in conventional blasting. The result shows that shaped charge blasting reduces the cracking capacity near the diagonal in a certain range due to the addition of the copper metal liner.

In conclusion, compared with conventional blasting, the addition of the copper metal liner changes the charge structure, greatly strengthens the detonation energy in the horizontal direction, has little influence on the cracking ability of concrete in the vertical direction, and weakens the fracture ability of concrete near the diagonal in a certain range.

4. Numerical Simulation

4.1. Finite Element Model

Finite element (FE) simulations were performed to further elucidate the dynamic effect of shaped charge blasting and the response of structures that could hardly be observed during the experiment. Numerical simulations were performed with ANSYS/LS-DYNA software using the arbitrary Lagrange–Euler (ALE) method. The models were composed of concrete, explosive, copper metal hood, and air. The diameter of the explosive was 1.5 cm, the thickness of the copper metal hood was 0.07 cm, and the size of the concrete was 80 cm × 80 cm × 0.5 cm. The hole was located in the center of the concrete specimen with a diameter of 2.5 cm. Due to the symmetry of the model, only 1/4 of the model needed to be established, and it is shown in Figure 9. The ALE algorithm can not only overcome the mesh distortion problem induced by large deformation that may happen in the Lagrangian method but also solve the problem that the erosion algorithm cannot make the remaining elements continue to be subjected to quasi-static detonation gas pressure due to element deletion. In the blasting calculation model, the ALE and Lagrange coupling calculation method is adopted, which has been successfully applied in many studies.35−37 The fluid structure coupling method is used to calculate the energy exchange between a solid and fluid by setting the keyword constrained_solid_in_ale. The copper metal liner, explosive, and air are simulated by the ALE algorithm. The rock material is simulated by the Lagrange method, and the element type is solid 164.

Figure 9.

Figure 9

Open in a new tab

Model of shaped charge blasting.

In the blasting process, considering that the concrete exhibits a high strain, large deformation, and even damages under strong impact, the H–J–C constitutive model proposed by Holqmuist is selected for the concrete material model. The mechanical parameters of concrete are shown in Table 1.

Table 1. Parameters of Concrete.

ρ (g·cm–3) E (GPa) μ tensile strength (MPa) compressive strength (MPa)
2.35 31.9 0.15 2.74 35.2
Open in a new tab

The explosive in this experiment is RDX, and the explosive constitutive model is *MAT_HIGH_EXPLOSIVE_BURN. The Jones–Wilkins–Lee (JWL) equation is adopted to describe the relationship between the pressure applied to the borehole wall by a unit detonation and the volume of the detonation products, which can be expressed as follows38,39

4.1. 1

where P is the detonation pressure; V is the relative volume; E0 is the initial internal energy density; and A, B, R1, R2, and ω are the constants of the explosive. The related parameters of the explosive are shown in Table 2.

Table 2. Parameters of the RDX Explosive.

ρ (g·cm–3) P (GPa) A B R1 R2 ω E0 (GPa)
1.2 6.125 52.4 0.768 4.2 1.1 0.34 8.5
Open in a new tab

The air constitutive model is *MAT_NULL, and the air material is defined by the following equation

4.1. 2

Air parameters and state equation parameters are shown in Table 3, where E is the air internal energy.

Table 3. Parameters of Air.

ρ (g·cm–3) C0 C1 C2 C3 C4 C5 C6 E (GPa)
1.29 × 10–5 0 6.125 52.4 0.768 4.2 1.1 0.34 8.5
Open in a new tab

The JOHNSON_COOK model and the GRUNEISEN equation are used to predict the dynamic behavior of the metal liner.39,40 The yield stress of the metal liner is shown below

4.1. 3

where ε and Inline graphic represent the equivalent strain and plastic strain rate of the copper metal liner, respectively; A, B, C, n, and r are all fixed constants; and T is the material temperature ratio, which can be determined by the following formula

4.1. 4

where Tm represents the melting temperature of the shaped energy hood, Tr represents the environment temperature, and Ts represents the real-time temperature of the metal liner.

When the metal liner is damaged, the material damage factor D can be determined by eq 5. When the material damage factor D is equal to 1, the metal liner is damaged and then melted.

4.1. 5

where εf is the strain value when the metal cover is damaged, which can be calculated by eq 6

4.1. 6

where D1, D2, D3, D4, and D5 are the parameters when the metal liner is damaged; P is the pressure borne by the metal liner; εf is the strain value when the metal liner is damaged; and σe is the effective stress of the metal liner.

4.2. Formation and Migration of the Shaped Charge Jet

The formation and migration process of the shaped charge jet is shown in Figure 10. After explosive initiation, a detonation wave propagates outward from the detonation point, as shown in Figure 10a. The detonation wave propagates to the copper metal cap, and the copper metal liner compresses violently under the intense pressure of the detonation wave, as shown in Figure 10b. Due to the low compressibility of the metal cap, only a small part of the energy is converted into internal energy in the fusion process, while most of the energy is converted into kinetic energy, and the energy is concentrated, as shown in Figure 10c. Due to the different velocities at the front and back ends of the fusion body, the fusion body has a high velocity at the front to form the shaped charge jet tip, while the fusion body has a low velocity at the tail end to form the clubbing body. The shaped charge jet continuously migrates forward and penetrates the concrete, eventually forming guide cracks, as shown in Figure 10d.

Figure 10.

Figure 10

Open in a new tab

Formation and migration process of the shaped charge jet: (a)1.99 μs, (b)1.99 μs, (c) 15.99 μs, and (d) 43.99 μs.

4.3. Cracking Process of Concrete by Shaped Charge Blasting

After detonation, high-heat and high-temperature explosive gas is generated, which rapidly fills the entire hole and then impacts the hole wall to compress concrete in the form of an explosive shock wave. The explosive shock wave carries high energy and produces compressive stress far greater than the compressive strength of concrete and finally forms the crushing area of concrete, as shown in Figure 11b. The concrete in the vertical direction is first crushed, and the concrete in the horizontal direction is then crushed. The measurement shows that the length of the crushing area in the horizontal direction is 3 cm, while the length of the crushing area in the vertical direction is 3.9 cm. The crush area formed in the horizontal direction is smaller than that in the vertical direction, and a “dumbbell-shaped” crush area is finally formed, as shown in Figure 11c.

Figure 11.

Figure 11

Open in a new tab

Crack propagation process under the shaped charge blasting: (a) 0 μs, (b) 1.99 μs, (c) 9.99 μs, (d) 25.99 μs, (e) 53.99 μs, (f) 65.99 μs, (g) 89.99 μs, (h) 116.99 μs, and (i) 133.99 μs.

With the propagation of the detonation wave in concrete, its energy decreases rapidly. When the detonation wave decays into a stress wave, it no longer produces a crushing effect on concrete. Concrete produces radial displacement under the action of the compressive stress wave, accompanied by tangential tensile stress. When the tangential tensile stress is greater than the tensile strength of concrete, radial cracks occur in concrete, and radial cracks continue to expand and extend under the action of a compressive stress wave, as shown in Figure 11f. With the attenuation of the stress wave, the failure velocity (crack formation velocity) of the concrete element in the vertical direction becomes slower and slower. In the horizontal direction, due to the effect of the metal liner, the energy in the horizontal direction is promoted to gather, and more energy is used for the crack expansion of concrete. Finally, a “spindle-shaped” crack area is formed, as shown in Figure 11i.

4.4. Numerical Simulation Analysis of Conventional Blasting

Conventional blasting only includes concrete, explosive, and air, and the parameters and constitutive equations of the three parts are exactly the same as those of shaped charge blasting. The crack propagation process under conventional blasting is shown in Figure 12.

Figure 12.

Figure 12

Open in a new tab

Crack propagation process under the conventional blasting: (a) 0 μs, (b) 3.99 μs, (c) 31.99 μs, (d) 47.97 μs, (e) 115.97 μs, and (f)133.97 μs.

It can be seen from Figure 12b that after detonation, the detonation wave collides violently with the borehole wall and compresses the borehole wall until it is crushed. The radius of the crushing area is the same everywhere, and the crushing area is circular. This is because after conventional blasting, the detonation wave spreads outward from the center of the hole in a circular shape, and the compression stress generated is the same everywhere, so the crushing area is circular, and a lot of explosive energy is wasted in the process of concrete crushing. Subsequently, the detonation wave attenuates to a stress wave. When the stress wave propagates in concrete, cracks are preferentially generated in the horizontal and vertical directions of concrete, as shown in Figure 12c. In addition, the final crack area is circular, as shown in Figure 12f.

To further study the difference in concrete crack under shaped charge blasting and conventional blasting loads, the crack diagram of the moment before the stress wave propagates to the free concrete is compared and analyzed, as shown in Figure 13.

Figure 13.

Figure 13

Open in a new tab

Propagation characteristics of cracks around the blasting borehole of (a) the shaped charge blasting and (b) the conventional blasting.

According to Figure 13a, the concrete cracking diagram under shaped charge blasting includes three parts: the crushing area, the shaped charge jet penetration area, and the others are concrete crack areas. The crushing area formed under the shaped charge blasting is dumbbell-shaped. The measurement shows that the length of the crushing area in the horizontal direction is 3 cm and the length in the vertical direction is 3.7 cm. The crack length in the horizontal direction is 52 cm and that in the vertical direction is 44 cm.

According to Figure 13b, the cracking diagram under conventional blasting includes a concrete crushing area and a crack area. The crushing area under a conventional blasting load is circular, with a radius of 4.3 cm, which is 1.43 times the length of the crushing area in the horizontal direction of shaped charge blasting and 1.16 times the length of the crushing area in the vertical direction of shaped charge blasting. It can be seen that the scope of the crushing area of conventional blasting is much larger than that of shaped charge blasting. It shows that a large amount of energy of conventional blasting is wasted in the concrete crushing area, resulting in poor subsequent crack development. It is found that the development length of the concrete crack is 42 cm, which is 0.80 times the horizontal crack length of shaped charge blasting and 0.95 times the vertical crack length of shaped charge blasting.

To sum up, after shaped charged blasting, the concrete finally forms a dumbbell-shaped crushing area. On the contrary, the shape of the crack area is “spindle”-shaped. The crushing area after shaped charge blasting is smaller than that of conventional blasting, while the crack area is much larger than that of conventional blasting. It shows that shaped charge blasting changes the propagation mechanism of the stress wave and achieves the purpose of “reducing the crushing area and increasing the crack area”.

4.5. Establishing the Mechanical Model of Shaped Charge Blasting and Discussion

According to the experiment and numerical simulation results, the energy accumulation in the opening direction of the shaped charge liner is the maximum, followed by the energy in the opening direction of the vertical-shaped charge liner, and the energy in the diagonal direction is the minimum. This is because when the detonation wave propagates to the shaped charge liner, the detonation energy accumulated in the opening direction (direction I) of the shaped charge liner keeps increasing, and the shaped charge jet is formed by compressing the metal liner to realize the directional accumulation of energy. After the shaped charge jet is formed, the action surface of penetration into coal decreases significantly, and the coal breaks rapidly under high-intensity impact load and forms initial guided cracks. With the propagation of the detonation wave, the intensity of detonation energy gathering perpendicular to the opening direction of the shaped charge blasting is enhanced to a certain extent when the detonation wave reflected by the two symmetric-shaped charge covers collides with each other. However, the energy impacting the coal surface in this direction is larger, resulting in a larger crushing area in the opening direction of the vertical-shaped charge liner. Part of the detonation energy in the diagonal direction is transformed into a shaped charge jet, and the energy in this direction is the minimum.

In summary, according to the difference of the detonation energy concentration degree under the shaped blasting, the area around the blasthole can be divided into three types: energy-gathering directions, secondary energy-gathering directions, and nonenergy-gathering directions, as shown in Figure 14.

Figure 14.

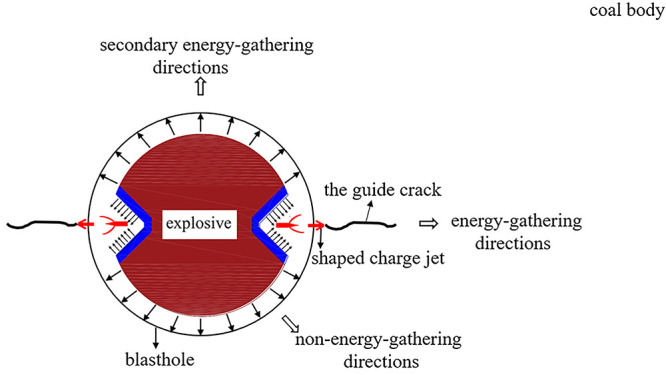
Figure 14

Open in a new tab

Cracking mechanical model of shaped charge blasting.

To analyze the universality of the mechanical model of shaped charge blasting, the results of shaped charge blasting cracking obtained by Xiao and Zhu are quoted.42,41 Xiao carried out an experiment of shaped charge blasting penetrating the steel plate. It can be seen that after the shaped charge blasting, obvious deformation occurred in all directions of the steel plate, in which the penetration marks in the opening direction of the shaped charge liner and perpendicular to the opening direction of the shaped charge liner are obvious. However, the other directions are mainly compression deformation. The experimental results are consistent with the mechanical model of shaped charge blasting, as shown in Figure 15.

Figure 15.

Figure 15

Open in a new tab

Penetration of the steel plate by shaped charge blasting.

Zhu et al. carried out a rock tunneling test of shaped charge blasting and used the digital camera of drilling to peep into the blasting holes. The condition of the blasting hole wall before and after cumulative blasting is shown in Figure 16. The experimental results are consistent with the mechanical model of shaped charge blasting.

Figure 16.

Figure 16

Open in a new tab

Observation of the hole before and after blasting.

Therefore, after shaped charge blasting, energy-gathering directions, secondary energy-gathering directions, and nonenergy-gathering directions will form around the blasting hole, which means that the shaped charge blasting cracking coal model in this paper is reliable.

5. Field Experiment

5.1. Engineering Background

To further explore the influence of shaped charge blasting on coal seam permeability improvement, we considered the 15, 16-24130 working face of Pingmei No. 10 Coal Mine as the test area. The average thickness of the coal seam in this working face is 3.2 m, and the dip angle of the coal seam is 6–12°. The strike length, dipping length, and elevation of the working face are 954, −540, and 850 m, respectively. The fault drop of the coal seam is small, the geological structure is relatively simple, and the overall stability of the coal seam is good. The maximum gas pressure of the coal seam is 1 MPa, and the maximum gas content is 12.5 m3·t–1. The gas permeability coefficient of the working face is 0.052–0.076 m2 (MPa2·days)−1, which belongs to a low-permeability coal seam.

5.2. Field Test Scheme

According to the geological conditions, to reduce the experimental error, six groups of bedding blasting holes are arranged along the dip of the coal seam: three groups are shaped charged blasting, and the other groups comprise conventional blasting. The diameter of the borehole was 75 mm, and the diameter of the cartridge was 45 mm. The explosive was a tertiary emulsion explosive, as shown in Figure 17a, the density of the cartridge was 1.14 g·cm–3, and the quantity of charged powder per hole was 16 kg. To facilitate the filling of explosives, a guide shuttle was bound at the front end of the explosives during the charging process. The shaped charge tube was made of aluminum alloy, as shown in Figure 17b.

Figure 17.

Figure 17

Open in a new tab

(a) Diagram of the tertiary emulsion explosive, and (b) the shaped charge tube.

The borehole and sealing of the hole are, respectively, 45 and 10 m deep. The explosives were connected in series, and finally, the hole was sealed by a combination of yellow mud and yellow sand. To ensure the hole sealing effect, the hole sealing length of yellow mud was not less than 3 m. The charging process is shown in Figure 18.

Figure 18.

Figure 18

Open in a new tab

Structure of shaped charge blasting in the hole.

The crack length cannot be measured directly in blasting engineering. The permeability improvement effect of coal can be quantitatively reflected by comparing the gas volume fraction of each extraction hole. The depth of the extraction hole was 90 m, and the distances between the gas extraction hole and the blasting hole were 3, 5, and 7 m. The specific blasting drilling scheme is shown in Figure 19.

Figure 19.

Figure 19

Open in a new tab

Specific blasting drilling scheme.

After blasting, the gas content of each extraction hole was monitored for 10 consecutive days, in which the first 3 days were the gas content before blasting and the last 7 days were the gas content after blasting. After the experiment, the gas volume fraction in the corresponding holes of the six groups of tests was calculated, and its average value was calculated. After shaped charge blasting, the gas volume fraction of each extraction hole is shown in Figure 20a. However, after conventional blasting, the gas volume fraction of each extraction hole is shown in Figure 20b.

Figure 20.

Figure 20

Open in a new tab

(a) Average volume fraction of gas before and after shaped charge blasting, and (b) average volume fraction of gas before and after conventional blasting.

As shown in Figure 20a, the average volume fraction of gas in each extraction hole is about 8.5% before cumulative blasting. It is proved that the degree of fracture development of a coal body near each extraction hole is basically the same before cumulative blasting. After blasting, it is found that the gas volume fraction of each extraction hole is strengthened to different degrees. The average gas volume fractions of extraction holes A, B, and C are, respectively, 80.47, 70.62, and 49.67%. It shows that shaped charge blasting can effectively improve the permeability of the coal seam. At the same time, it is found that the permeability of the coal seam gradually weakens with the increase in distance between the extraction hole and the blasthole.

Figure 20b shows the variation curve of gas volume in each extraction hole with time before and after conventional blasting. Compared with Figure 20a, it is found that the development degree of coal fractures near each extraction hole before conventional blasting and shaped charge blasting is basically the same. After conventional blasting, the average gas volume fractions of extraction holes A′, B′, and C′ are 61.3, 40.01, and 26.07%, respectively. The results show that the conventional blasting can also improve the permeability of the coal seam, but the gas volume fraction of each extraction hole is less than that of shaped charge blasting, in which the gas volume fraction of A′ extraction hole is 0.76 times that of A extraction hole, the gas volume integral of B′ extraction hole is 0.57 times that of B extraction hole, and the gas volume fraction of C′ extraction hole is 0.52 times that of C extraction hole. To sum up, deep-hole shaped charge blasting can effectively promote the permeability in high-gas and low-permeability coal seams, so as to improve the gas extraction rate. At the same time, it is found that the ability of shaped charge blasting to increase the permeability of the coal seam is much stronger than that of conventional blasting, finally achieving the purpose of controlling coal and gas outburst.

6. Field Experiment

The dynamic effects and the mechanism of deep-hole shaped charge blasting in coal seams are studied by an experiment, numerical simulation, and field test. It is found that shaped charge blasting can effectively reduce the crushing area of the coal seam, increasing the cracking area. It shows that shaped charge blasting is more conducive to coal seam permeability enhancement.

  • (1)

    The experiment of shaped charge blasting and conventional blasting to fracture concrete is carried out. It was found that the crushing area of conventional blasting is circular, while the crushing area of shaped charge blasting is dumbbell-shaped. The crushing area of conventional blasting is larger than that of shaped charge blasting. The width of the four main cracks formed after conventional blasting is 0.3 cm, the width of the crack in the energy-gathering directions is 1.1 cm, and the width of the crack perpendicular to the energy-gathering directions is 0.4 cm. The cracking area is larger than that with conventional blasting.

  • (2)

    Comparing the peak value of the strain gauge under shaped charge blasting, it is found that the strain of the strain gauge in the energy-gathering directions is the maximum, followed by the vertical energy-gathering directions, and the strain at the diagonal is the minimum. In addition, the strain peak value in the direction of energy accumulation is much larger than that of conventional blasting, and the strain peak value in the direction perpendicular to energy gathering is basically equal to that of conventional blasting. The strain peak value of the diagonal strain gauge is smaller than that of the conventional blasting strain gauge.

  • (3)

    ANSYS/LS-DYNA is used to reproduce the whole process of shaped energy jet formation, migration, and penetration into concrete. After shaped charge blasting, the concrete forms a dumbbell-shaped crushing area, and the crushing area is smaller than that of conventional blasting. The cracking area is spindle-shaped, and the cracking area is larger than that of conventional blasting.

  • (4)

    The coal seam antireflection model of shaped charge blasting is constructed; according to the difference in the detonation energy concentration degree under shaped blasting, the area around the blasthole can be divided into three types: energy-gathering directions, secondary energy-gathering directions, and nonenergy-gathering directions.

  • (5)

    The field practice once again shows that shaped charge blasting can effectively improve the gas extraction rate of coal seams, and its antireflection effect is better than that of conventional blasting.

Acknowledgments

This research was supported by the fellowship of China Postdoctoral Science Foundation (Grant No. 2021M701540), the Key Research Program of China Coal Science and Industry Group (Grant No. 2020-2-ZD001), and the Natural Science Foundation of Hebei Province (E2021402061).

The authors declare no competing financial interest.

References

  1. Ding L.; Zhao Z.; Han M. Probability density forecasts for steam coal prices in China: The role of high-frequency factors. Energy 2012, 220, 119758. [Google Scholar]
  2. Ma L. W.; Allwood J. M.; Cullen J. M.; Li Z. The use of energy in China: Tracing the flow of energy from primary source to demand drivers. Energy 2012, 40, 174–188. 10.1016/j.energy.2012.02.013. [DOI] [Google Scholar]
  3. Zhang L.; Zhou H. W.; Wang X. Y.; Zhao J. W.; Ju Y.; Deng T. F. On permeability evolution of coal induced by temperature, creep, and matrix–fracture interaction. Energy Fuels 2022, 36, 1470–1481. 10.1021/acs.energyfuels.1c03917. [DOI] [Google Scholar]
  4. Cao Y. X.; Zhang J. S.; Zhai H.; Fu G. T.; Tian L.; Liu S. M. CO2 gas fracturing: A novel reservoir stimulation technology in low permeability gassy coal seams. Fuel 2017, 203, 197–207. 10.1016/j.fuel.2017.04.053. [DOI] [Google Scholar]
  5. Liang M. Z.; Li X. Y.; Lin Y. L.; Zhang K. F.; Lu F. Y. Influence of multi-layer core on the blast response of composite sandwich cylinders. Int. J. Appl. Mechan. 2020, 12, 2050018 10.1142/S1758825120500180. [DOI] [Google Scholar]
  6. Zhou L. J.; Zhou X. H.; Fan C. J.; Bai G. Coal permeability evolution triggered by variable injection parameters during gas mixture enhanced methane recovery. Energy 2022, 252, 124065 10.1016/j.energy.2022.124065. [DOI] [Google Scholar]
  7. Zhou B.; Xu J.; Peng S. J.; Yan F. Z.; Yang W.; Cheng L.; Ni G. H. Experimental Analysis of the Dynamic Effects of Coal–Gas Outburst and a Protean Contraction and Expansion Flow Model. Nat. Resour. Res. 2020, 29, 1617–1637. 10.1007/s11053-019-09552-y. [DOI] [Google Scholar]
  8. Zhou B.; Xu J.; Peng S.; Yan F.; et al. Influence of Geo-stress on Dynamic Response Characteristics of Coal and Gas Outburst. Rock Mechan. Rock Eng. 2020, 53, 4819–4837. 10.1007/s00603-020-02154-8. [DOI] [Google Scholar]
  9. Zhou B.; Xu J.; Peng S. J.; Yan F. Z.; Gao Y. B.; Li Q. X.; Cheng L. Effects of geo-stress on the dynamic response of multi-physical field parameters during coal and gas outbursts under true triaxial stress. Int. J. Rock Mechan. Min. Sci. 2021, 142, 104759 10.1016/j.ijrmms.2021.104759. [DOI] [Google Scholar]
  10. Li X. L.; Cao Z. Y.; Xu Y. L. Characteristics and trends of coal mine safety development. Energy Sources, Part A 2020, 12, 1–19. 10.1080/15567036.2020.1852339. [DOI] [Google Scholar]
  11. Li X. L.; Chen S. J.; Zhang Q. M.; Cao X.; Feng F. Research on theory, simulation and measurement of stress behavior under regenerated roof condition. Geomechan. Eng. 2021, 26, 49–61. [Google Scholar]
  12. Wang L.; Lu Z.; Chen D. P.; Liu Q. Q.; Chu P.; Shu L. Y.; Ullah B.; Wen Z. J. Safe strategy for coal and gas outburst prevention in deep-and-thick coal seams using a soft rock protective layer mining. Safety Sci. 2020, 129, 104800 10.1016/j.ssci.2020.104800. [DOI] [Google Scholar]
  13. Liu S. M.; Li X. L.; Wang D. K.; Zhang D. M. Investigations on the mechanism of the microstructural evolution of different coal ranks under liquid nitrogen cold soaking. Energy Sources, Part A 2020, 7, 1–17. 10.1080/15567036.2020.1841856. [DOI] [Google Scholar]
  14. Li X. L.; Chen S. J.; Liu S. M.; Li Z. H. AE waveform characteristics of rock mass under uniaxial loading based on Hilbert-Huang transform. J. Cent. South Univ. 2021, 28, 1843–1856. 10.1007/s11771-021-4734-6. [DOI] [Google Scholar]
  15. Zhou L.; Zheng X. L.; Lu Y. Y.; Li H. L.; Feng M. J. Fracture pattern and caprock integrity analyses via hydraulic fracturing for CO2 enhanced coal bed methane. Eng. Fract. Mechan. 2020, 228, 106894 10.1016/j.engfracmech.2020.106894. [DOI] [Google Scholar]
  16. Fan C. J.; Wen H. O.; Sun H.; Zhou L. J.; Zhang X. P.; Zhu C.; Su W. W. Experimental Investigation on the Effect of Loading and Unloading on Coal Permeability with Different Sediment Beddings. Lithosphere 2022, 2022, 9949201 10.2113/2022/9949201. [DOI] [Google Scholar]
  17. Wang H. D.; Cheng Z. H.; Zou Q. L.; Li Z. H.; Sun F. L.; Yang H. W.; Lei Y. Elimination of coal and gas outburst risk of an outburst-prone coal seam using controllable liquid CO2 phase transition fracturing. Fuel 2021, 284, 119091 10.1016/j.fuel.2020.119091. [DOI] [Google Scholar]
  18. Yi M. H.; Wang L.; Hao C. M.; Liu Q. Q.; Wang Z. Y. Method for designing the optimal sealing depth in methane drainage boreholes to realize efficient drainage. Int. J. Coal Sci. Technol. 2021, 8, 1–11. 10.1007/s40789-021-00448-y. [DOI] [Google Scholar]
  19. Lu Y. Y.; Tian R. R.; Liu W. C.; Tang J. R.; Li H. L.; Chen X. Y.; Sun X. Mechanisms of shale water wettability alteration with chemical groups after CO2 injection: Implication for shale gas recovery and CO2 geo-storage. J. Nat. Gas Sci. Eng. 2021, 90, 103922 10.1016/j.jngse.2021.103922. [DOI] [Google Scholar]
  20. Zhai C.; Li M.; Sun C.; et al. Guiding-controlling technology of coal seam hydraulic fracturing fractures extension. Int. J. Min. Sci. Technol. 2012, 22, 831–836. 10.1016/j.ijmst.2012.12.013. [DOI] [Google Scholar]
  21. Liao Z. W.; Liu X. F.; Song D. Z.; He X. Q.; Nie B. S.; Yang T.; Wang L. K. Micro-structural Damage to Coal Induced by Liquid CO2 Phase Change Fracturing. Nat. Resour. Res. 2021, 30, 1613–1627. 10.1007/s11053-020-09782-5. [DOI] [Google Scholar]
  22. Guo D. Y.; Lv P. F.; Zhao J. C.; Zhang Chao. Research progress on permeability improvement mechanisms and technologies of coalbed deep-hole cumulative blasting. Int. J. Coal Sci. Technol. 2020, 7, 329–336. 10.1007/s40789-020-00320-5. [DOI] [Google Scholar]
  23. Li X. L.; Chen S. J.; Wang S.; Zhao M.; Liu H. Study on in situ stress distribution law of the deep mine taking Linyi Mining area as an example. Adv. Mater. Sci. Eng. 2021, 2021, 5594181 10.1155/2021/5594181. [DOI] [Google Scholar]
  24. Leng Z. D.; Fan Y.; Gao Q. D.; Hu Y. G. Evaluation and optimization of blasting approaches to reducing oversize boulders and toes in open-pit mine. Int. J. Min. Sci. Technol. 2020, 30, 373–380. 10.1016/j.ijmst.2020.03.010. [DOI] [Google Scholar]
  25. Baykara T.; Günay; Demirural A. Structural Evolution and Microstructural Features of the Hydrodynamically Penetrating Copper Jet of a Shaped Charge. J. Mater. Eng. Perform. 2021, 30, 1862–1871. 10.1007/s11665-021-05514-9. [DOI] [Google Scholar]
  26. Yue Z. W.; Qiu P.; Yang R. S.; Zhang S. C.; Yuan K.; Li Z. F. Stress analysis of the interaction of a running crack and blasting waves by caustics method. Eng. Fract. Mechan. 2017, 184, 339–351. 10.1016/j.engfracmech.2017.08.037. [DOI] [Google Scholar]
  27. Mandal S. K.; Singh M. M.; Dasgupta S. Theoretical Concept to Understand Plan and Design Smooth Blasting Pattern. Geotech. Geol. Eng. 2008, 26, 399–416. 10.1007/s10706-008-9177-4. [DOI] [Google Scholar]
  28. Yang R. S.; Ding C. X.; Li Y. L.; Yang L.; Zhao Y. Crack propagation behavior in slit charge blasting under high static stress conditions. Int. J. Rock Mechan. Min. Sci. 2019, 119, 117–123. 10.1016/j.ijrmms.2019.05.002. [DOI] [Google Scholar]
  29. Ding C.; Yang R.; Lei Z.; Wang M.; Zhao Y.; Lin H. Fractal damage and crack propagation in decoupled charge blasting. Soil Dyn. Earthquake Eng. 2020, 141, 106503 10.1016/j.soildyn.2020.106503. [DOI] [Google Scholar]
  30. Meng N.; Chen Y.; Bai J.; Wang X.; Wu W.; Wu B. Numerical simulation of directional fracturing by cumulative blasting. Energy Sci. Eng. 2020, 8, 1824–1839. 10.1002/ese3.635. [DOI] [Google Scholar]
  31. Yin Y.; Sun Q.; Zou B. P.; Mu Q. Y. Numerical Study on an Innovative Shaped Charge Approach of Rock Blasting and the Timing Sequence Effect in Microsecond Magnitude. Rock Mechan. Rock Eng. 2021, 54, 4523–4542. 10.1007/s00603-021-02516-w. [DOI] [Google Scholar]
  32. He C. L.; Yang J. Experimental and numerical investigations of dynamic failure process in rock under blast loading. Tunnelling Underground Space Technol. 2019, 83, 552–564. 10.1016/j.tust.2018.08.047. [DOI] [Google Scholar]
  33. Guo D. Y.; Zhao J. C.; Lv P. F. Discussion on effective splitting range of deep hole cumulative blasting in coal seam. Chin. J. Eng. 2019, 41, 582–590. [Google Scholar]
  34. Luo Y.; Shen Z. W. Study on orientation fracture blasting with shaped charge in rock. J. Univ. Sci. Technol., Miner., Metall., Mater. 2006, 13, 193–198. 10.1016/S1005-8850(06)60042-X. [DOI] [Google Scholar]
  35. Song Y. Q.; Li X. S.; Zhou T.; Li M. Experimental and finite element analysis of marble with double pre-existing flaws under loading-unloading conditions. Arabian J. Geosci. 2020, 13, 392 10.1007/s12517-020-05368-w. [DOI] [Google Scholar]
  36. Song Y. Q.; Li X. S.; Guo D. Y.; Shi B. K. Study on the Decoupled Charge Effect in Deep-Hole Cumulative Blasting of Coal Seam. Adv. Civil Eng. 2019, 2019, 8486198 10.1155/2019/8486198. [DOI] [Google Scholar]
  37. Liang M. Z.; Li X. Y.; Lin Y. L.; Lu F. Y. Compaction wave propagation in layered cellular materials under air-blast. Int. J. Appl. Mechan. 2019, 11, 1950003 10.1142/S1758825119500030. [DOI] [Google Scholar]
  38. Qiu P.; Yue Z. W.; Yang R. S.; Li J. C. Effects of vertical and horizontal reflected blast stress waves on running cracks by caustics method. Eng. Fract. Mechan. 2019, 212, 164–179. 10.1016/j.engfracmech.2019.03.018. [DOI] [Google Scholar]
  39. Kim K. H.; Yoh J. J. A particle level-set based Eulerian method for multi-material detonation simulation of high explosive and metal confinements. Proc. Combust. Inst. 2013, 34, 2025–2033. 10.1016/j.proci.2012.07.010. [DOI] [Google Scholar]
  40. Xu P.; Yang R. S.; Zuo J. J.; Ding C. X.; Chen C.; Guo Y.; Fang S. Z.; Zhang Y. Research progress of the fundamental theory and technology of rock blasting. Int. J. Miner., Metall. Mater. 2022, 29, 705–716. 10.1007/s12613-022-2464-x. [DOI] [Google Scholar]
  41. Xiao S.-Y.; Su L.-J.; Jiang Y.-J.; Liu Z.-X. Numerical analysis of hard rock blasting unloading effects in high in situ stress fields. Bull. Eng. Geol. Environ. 2019, 78, 867–875. 10.1007/s10064-017-1067-7. [DOI] [Google Scholar]
  42. Zhu F. H.; Liu Z. G.; Gao K.; Liu J. Experimental study on rock damage of roadway excavation by cumulative blasting in structural coal. Chin. J. Rock Mechan. Eng. 2018, 37, 2037–2047. [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES