Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jul 13;7(29):25278–25290. doi: 10.1021/acsomega.2c02200

Experimental and Numerical Study of Natural Gas Leakage and Explosion Characteristics

Peng Cai †, Mingzhi Li †,*, Zhenyi Liu †, Pengliang Li †, Yao Zhao †, Yi Zhou ‡
PMCID: PMC9330169  PMID: 35910168

Abstract

graphic file with name ao2c02200_0011.jpg

Frequent occurrence of indoor natural gas explosion accidents seriously threatens the safety of people and property. To determine the law of indoor natural gas leakage and explosion hazards, based on experiment and simulation, the nature of natural gas explosion, the distribution law of natural gas volume fraction, flame propagation, temperature, and shock wave overpressure were studied. The results show that the flame structure can be divided into three zones, i.e., preheat zone, reaction zone, and product zone. OH + CO ⇔ H + CO2 is the main exothermic reaction in the combustion process. The overall distribution law of natural gas volume fraction shows that the higher the position, the greater the volume fraction, and the closer the distance to the leak source at the same height, the greater the volume fraction, and the natural gas volume fraction of the hose falling off is the largest under different leakage conditions. The difference in the wrapping structure of the kitchen package has a significant impact on the diffusion distribution of natural gas. The flame development goes through five stages of ignition, slow burning, detonation, slow burning, and extinguishing. The indoor temperature reaches about 1400 °C. Although the simulated value of shock wave overpressure is larger than the experimental value, the relationship between overpressure and distance is expressed by Y = A + B * ln(X + C). This study can provide certain technical support for natural gas accident rescue. The research can provide certain technical support for natural gas accident rescue and can also be used for accident investigation to form the determination procedure and method of leakage location and leakage amount.

1. Introduction

With the rapid advancement of urbanization, natural gas consumption has developed rapidly. Due to the continuous reconstruction and expansion of natural gas pipelines, the increase in the number of people who use gas, and the aging of equipment, natural gas explosion accidents have occurred from time to time.1−4 According to relevant statistics, in 2021, there were 401 natural gas explosion accidents in China, resulting in 76 deaths and ∼507 injuries. Among them, there were 205 indoor natural gas explosions, mainly concentrated in residential users, accounting for 51%. It can be seen that the safety of natural gas use by residents in China cannot be ignored. Therefore, revealing the reaction mechanism of natural gas combustion, determining the law of natural gas leakage and diffusion, and mastering explosion hazards contribute to safe use of gas.5−7

Essentially, gas explosion is a fierce redox reaction accompanied by light and heat, and the explosion process is a typical combustion process with pressure waves.8−10 At present, there are many studies on the mechanism of methane combustion, including the GRI 3.0 mechanism,11 the Berkeley mechanism,12 the Leeds 1.5 mechanism,13 the USC 2.0 mechanism,14 etc. Among them, the rationality and reliability of the GRI 3.0 mechanism have been verified by a large number of experiments. It is the most widely used mechanism and is suitable for the combustion reaction of CH4 and CH4-based natural gas.15−17 Nie18 used a closed homogeneous 0-D reactor to obtain the profiles of four reactants, toxic gases, and free radicals in the process of gas explosion. The results showed that the O2 concentration decreases from 19 to 2% at a stoichiometric ratio, which could not support normal respiration after explosion. Wang et al.19 studied the explosion characteristics of methane near the explosion limit based on GRI-mech3.0 and found that with the increase in the volume fraction of the mixed gas, the peak flame temperature and the flammability exponent gradually increased when approaching the lower flammability limit. Experiments can clarify the law of accidents objectively and accurately.20−22 Li et al.23 conducted a small-scale gas cloud explosion experiment through a balloon and determined that the overpressure and maximum flame velocity increase with the size of the gas cloud, and the relationship is not linear and cannot be used to predict large-scale gas explosions. Zhou et al.24 investigated the effect of built-in obstacles on unconfined methane explosion in a 1 m3 cubic frame. The results showed that the overpressure wave traveled slower and the maximum overpressure could almost keep constant in the near field. Akram et al.25 used meso-scale diverging channels to study the flame propagation velocity of methane–air premixed gas and observed planar flames near the flash back limit. Yang et al.26 carried out a large-scale urban shallow buried pipe trench methane gas explosion experiment. The results show that the overpressure is the largest when the methane concentration is 9.5%, and adding vents to the top of the pipe trench significantly reduced the upstream overpressure and overall impulse. Gu et al.27 studied the propagation law of methane explosion characteristics in the non-premixed region. The experimental research results indicated that an obvious secondary explosion pressure occurs at L/D = 3.5. The experiment is often restricted by factors such as personnel safety and high cost; numerical simulation has unique advantages in visualization and reducing research costs, especially in destructive experiments.28−30 CFD is widely used in gas explosion experiments, especially the LES simulation method, which has a high degree of matching with the experimental results.31−33 Ivings et al.34 determined that the volume fraction of flammable gas largely depends on the release rate of flammable gas and ventilation rate. Wang et al.35 simulated the leakage and diffusion law of natural gas in the tunnel based on FLUENT and proposed the emergency accident ventilation for different pipeline pressures and leak sizes. Fu et al.36 studied the relationship between the distribution law of gas concentration and leakage diameter, internal pressure, and wind speed. Wang et al.37 used CFD to simulate the hazards of a natural gas leak and explosion of the East Harlem gas explosion in Manhattan, New York, and the simulation results are consistent with the actual accident results. Li et al.38 used FLACS to simulate the characteristics of gas explosion in a natural gas compartment of the urban utility tunnel. Song et al.39 studied the consequences of gas explosion accidents in residential buildings, and the effects of vent area ratio and broken pressure of glasses were investigated to propose the effective risk reduction measures.

From the current research, it can be clearly found that there are many achievements in natural gas leakage and explosion, but most of the research only adopts one of the methods of experiment or numerical simulation, which cannot fully determine the hazards of natural gas leakage and explosion. In addition, the current experiments are often small-scale experiments or open spaces. There are almost no natural gas diffusion and explosion experiments for full-scale closed indoor scenarios, and the two scenarios are quite different. According to Li’s23 conclusion, there is a nonlinear relationship between overpressure and gas cloud size. Therefore, the obtained rules cannot accurately describe the natural gas leakage and explosion process in a full-scale closed indoor room. Moreover, most of the full-scale explosion research only adopts numerical simulation.

Therefore, the paper adopts two methods of experiment and simulation to study the hazard of natural gas leakage and explosion. The research established a full-size model of 2 m × 4 m × 2.6 m, revealed the reaction mechanism of natural gas combustion, analyzed the evolution law of the natural gas volume fraction under different leakage conditions, and studied the flame propagation process and shock wave overpressure (P); the relationship between the maximum explosion shock wave overpressure (Pmax) and the distance under different volume fractions was determined. The research can provide a basis for the calculation of key parameters of natural gas explosion accidents and safety measures and can also be applied to accident investigations to determine the location of natural gas leakage points, ignition sources, leakage time, and leakage amount.

2. Settings of Experimental Conditions and Simulation Boundary Conditions

2.1. Experimental Conditions

The layout of the experimental platform is shown in Figure 1. The platform consists of the following systems: natural gas volume fraction real-time monitoring system, explosive shock wave pressure experiment system, explosion field temperature experiment system, an ignition synchronization trigger, etc. The synchronous trigger detonator provides 10 J of energy for electric fire and synchronously triggers the data acquisition system. The length, width, and height of the houses are 4, 2, and 2.6 m, respectively. The main component of natural gas is methane, and other components are relatively small. Without affecting the experimental results, this study uses methane instead of natural gas to improve efficiency. The intake pressure was set to 2.5 kPa according to the natural gas user terminal pressure. At the same time, through the analysis of natural gas leakage accidents, four main types of leakage were set up for research, i.e., the hose falls off, the switch is not closed tightly, corrosion cracks, and the hard object penetrates the natural gas pipeline. To ensure the safety of the experiment, all experiments are carried out in the outdoor experimental base.

Figure 1.

Figure 1

Open in a new tab

Layout of the experimental platform.

2.2. Simulation Boundary Condition

2.2.1. CHEMKIN

The laminar flame velocity of a methane/air mixture with an equivalence ratio of 1 is about 0.4 m/s. The laminar flame velocity is much lower than the speed of sound, and the Mach number is much less than 1. Therefore, a one-dimensional laminar premixed flame model is chosen to solve. The one-dimensional laminar premixed flame model can display the flame structure and calculate the flame velocity.40,41 Therefore, the diffusion transport of components plays an important role in this process.42

The continuity equation is shown in eq 1

2.2.1. 1

The composition equation is shown in eq 2(18)

2.2.1. 2

The component transport equation is shown in eq 3

2.2.1. 3

The gas state equation is shown in eq 4

2.2.1. 4

where Ṁ is the mass flow rate, kg·s–1; ρ is the density, kg·m–3; u is the flow rate of the mixture, m·s–1; A is the cross-sectional area of flame propagation, m2; Yn is the mass fraction of the component n; c is the heat capacity of mixture, J·kg–1·K–1; ω̇n is the net formation rate of the component n, kg·m–3·s–1; Wn is the molecular weight of the component n, kg·mol–1; kg is the total number of species; x is the spatial coordinate, m; Vn is the diffusion velocity of the component n, m·s–1; p is the pressure, Pa; W̅ is the average molecular weight of the mixture, kg·mol–1; and R is the universal gas constant, J·mol–1·K–1.

2.2.2. FLUENT

Natural gas diffusion is a two-phase flow problem. FLUENT is widely used in the flow field.43,44 Natural gas leakage and diffusion are simulated by FLUENT.

The mass conservation equation is shown in eq 5

2.2.2. 5

In the inertial coordinate system, the momentum conservation equation in the i direction is shown in eq 6

2.2.2. 6

The energy equation is shown in eq 7

2.2.2. 7

where ρ is the density, kg·m–3; u is the fluid velocity in the direction of the coordinate axis, m·s–1; Sm is the mass that the sparse phase adds to the continuous phase—it is 0 in single-phase flow; P is the static pressure; ρgi and Fi are the gravitational body force and other body forces (such as from the interaction between two phases), respectively, and Fi can also include other model source terms or custom source terms; τij is stress tensor, 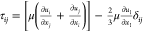Inline graphic; keff is the effective thermal conductivity (turbulent thermal conductivity is defined according to the turbulent flow model). hj′ is the enthalpy of component j′; Jj′ is the diffusive flux of component j′;Sh is the source term that includes the heat of chemical reaction and other volumetric heat sources. The first three terms on the right side of the energy equation are the thermal conductivity phase, the component diffusion phase, and the viscous dissipation term, respectively

2.2.2. 8

where, for the ideal gas, 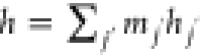Inline graphic; for incompressible gases, 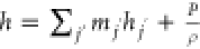Inline graphic; mj′ is the mass fraction of component j′; 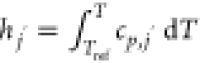Inline graphic, Tref = 298.15 K.

To close the basic governing equations of fluid dynamics and solve them, a turbulence model is used in conjunction with the above equations. In this paper, the standard k – ε model is selected for calculation.

The k equation is shown in eq 9

2.2.2. 9

The ε equation is shown in eq 10

2.2.2. 10

where k is the turbulent kinetic energy, J; ε is the dissipation rate of the turbulent kinetic energy; μt is the turbulent viscosity coefficient, m2·s–1; Gk is the turbulent kinetic energy due to the mean velocity gradient, Gb is the turbulent kinetic energy due to buoyancy effects, YM is the effect of the compressible turbulent pulsation expansion on the overall dissipation rate; and C1ε, C2ε, and C3ε are constants.

According to the experimental layout and the current kitchen decoration trend, a full-scale kitchen model with a length of 4 m, a width of 2 m, and a height of 2.6 m was constructed, and two kitchen structures were set up, including no kitchen wrapping structure and kitchen wrapping structure. The specific settings are shown in Table 1. The boundary type of the inlet is set to pressure inlet, and the inlet pressure of CH4 is 2.5 kPa.

Table 1. Settings of Simulation Conditions.
kitchen structure leak form and location
without kitchen wrapping structure the hose falls off/in kitchen cabinet
the switch is not closed tightly/in kitchen cabinet
cracks in the natural gas pipeline due to corrosion/indoor
with kitchen wrapping structure the hose falls off/in kitchen cabinet
the switch is not closed tightly/in kitchen cabinet
cracks in the natural gas pipeline due to corrosion/in kitchen wrapping structure
the valve body assembly is not tightly matched/indoor
Open in a new tab

2.2.3. FLACS

FLACS is the industry standard for CFD explosion simulation, which can accurately predict the consequences of accidents.45,46 During the FLACS solution process, the gas deflagration is set as the heating and expansion of an ideal gas, and the gas dynamics can be represented by a series of equations such as the continuity equation, the momentum equation, and the energy equation. The basic equations included in the mathematical model are: continuity equation, momentum equation, energy equation, turbulent kinetic energy equation, turbulent kinetic energy dissipation rate equation, fuel composition equation, and mixture composition equation, and the unified form of the mathematical model is as shown in eq (11)(47,48)

2.2.3. 11

where φ is a general variable representing the velocity components u, v, and w, turbulent kinetic energy k, the rate of turbulent kinetic energy ε, enthalpy h, flammable gas mass fraction Yn, etc.; Γφ is the exchange coefficient of flux φ and Sφ is the energy source term.

In the process of establishing the numerical model, the turbulent combustion time-averaged equations are used to describe the flow field, the k – ε turbulence model is used to describe the turbulent flow changes in the combustion process, and the β-flame model is used to describe the combustion reaction rate changes during the combustion process which can improve the three-dimensional numerical model of the flammable gas explosion in the confined space.

The reaction rates of the fuel of the β-flame model are shown in eqs (12) and (13)(49,50)

2.2.3. 12
2.2.3. 13

where Rfuel is the reaction rate of fuel; CβR is the dimensionless constant of the β-flame model; S is the burning flame speed, m·s–1; Δ is the side length of the control body, m; c is the dimensionless process variable; and Yf0 is the initial fuel mass fraction present in the current control volume, dimensionless.

FLACS is used to simulate the explosion of premixed gas clouds with different natural gas volume fractions, which are 5, 7.5, 9.5, 12, and 13.5%, respectively. Three measuring points are set at 0.5, 1, 1.5, 2, and 2.5 m from the door. The specific boundary conditions are set as shown in Table 2.

Table 2. Boundary Condition Settings for FLACS.
boundary condition settings boundary condition settings
TMAX –1 HEAT_SWITCH 1
LAST –1 temperature/°C 25
CFLC 2.5 ambient pressure/Pa 101 325
CFLV 0.5 time of ignition/s 0.05
Open in a new tab

3. Results and Discussion

3.1. Results of the Chemical Reaction Mechanism

The research used GRI 3.0 and USC 2.0 to study the reaction mechanism of methane combustion; the one-dimensional laminar premixed flame model was used for calculation. The initial pressure was 0.1 MPa, the ambient temperature was 298 K, and the reaction zone was 0.3 cm.

Figure 2 shows the spatial distribution of mole fractions of main components and flame temperature in the methane combustion process at a concentration of 9.5%. The combustion reaction processes obtained by GRI 3.0 and USC 2.0 are almost identical, which proves the accuracy of obtaining the methane combustion mechanism. The abscissa flame height represents different positions of the entire flame structure. It can be clearly seen that the entire flame structure is divided into three areas: from left to right are the preheat area, the reaction area, and the product area. In the preheating zone, the temperature will not rise basically, the consumption of reactants is very small, and a certain concentration of free radicals will accumulate in this area at the beginning of the reaction. After entering the reaction zone, the temperature gradually increases. The initial temperature increase is caused by the reaction to generate H2O. At this time, no CO2 is generated. As the reaction progresses, CO is gradually generated and reacts with OH to generate CO2 by OH + CO ⇔ H + CO2. This reaction is also the main exothermic reaction in the methane combustion process, and it can be seen that the temperature starts to rise rapidly at this time. In the product zone, the concentration of each component reaches an equilibrium state. It should be noted that even at the stoichiometric concentration, the oxygen is not completely consumed, this is because the CO is not completely oxidized, and there is a small amount of CO in the equilibrium state. Carbon monoxide can cause poisoning in humans, and the degree of poisoning depends on the inhaled dose, which is determined by the concentration and exposure time. The final CO value is about 2.1%, and people exposed to this environment will die quickly. And, as can be seen from the CO history during the natural gas explosion, the CO concentration experienced a sudden increase and then decreased to a stable value, which can be attributed to the pyrolysis of CH4, and the generated CO was then partially oxidized.

Figure 2.

Figure 2

Open in a new tab

Mole fraction of main components and the spatial distribution of flame temperature in the combustion process of methane with the concentration of 9.5%.

3.2. Results of the Experiment

3.2.1. Distribution Law of Natural Gas Concentration

As shown in Figure 3, in the form of natural gas hose falling off, natural gas is first detected at about 200 s. The natural gas concentration reaches the lower explosion limit after 1096 s of leakage, and the natural gas volume fraction is stable at about 2300 s, up to 7.1%. When the switch is not closed tightly, natural gas is detected at around 550 s at the earliest. The earliest time to reach the lower limit of explosion is 4670 s, and the volume fraction is stable at around 9000 s, reaching 5.8%. In the form of corrosion crack leakage, natural gas is first detected at about 400 s, the concentration of natural gas at the roof above the gas stove reaches the lower explosion limit for the first time at 3018 s, and the volume fraction is stable at about 6000 s, reaching 6%. In the form of small hole leakage, natural gas is first detected at about 450 s, the concentration of natural gas reaches the lower explosion limit at 5131 s, and the volume fraction is stable at about 8300 s, reaching 5.7%. It can be seen that the amount of natural gas leakage per unit time is the largest in the form of natural gas hose falling off and the natural gas volume fraction increases the fastest, the value is the highest, and the damage is the most serious. When the gas hose falls off and leaks, it takes the shortest leakage time to cause an explosion, and when a hard object breaks through the natural gas pipeline to form a small hole leak, the leakage time required to cause an explosion is the longest, which is about 4.7 times that of the former.

Figure 3.

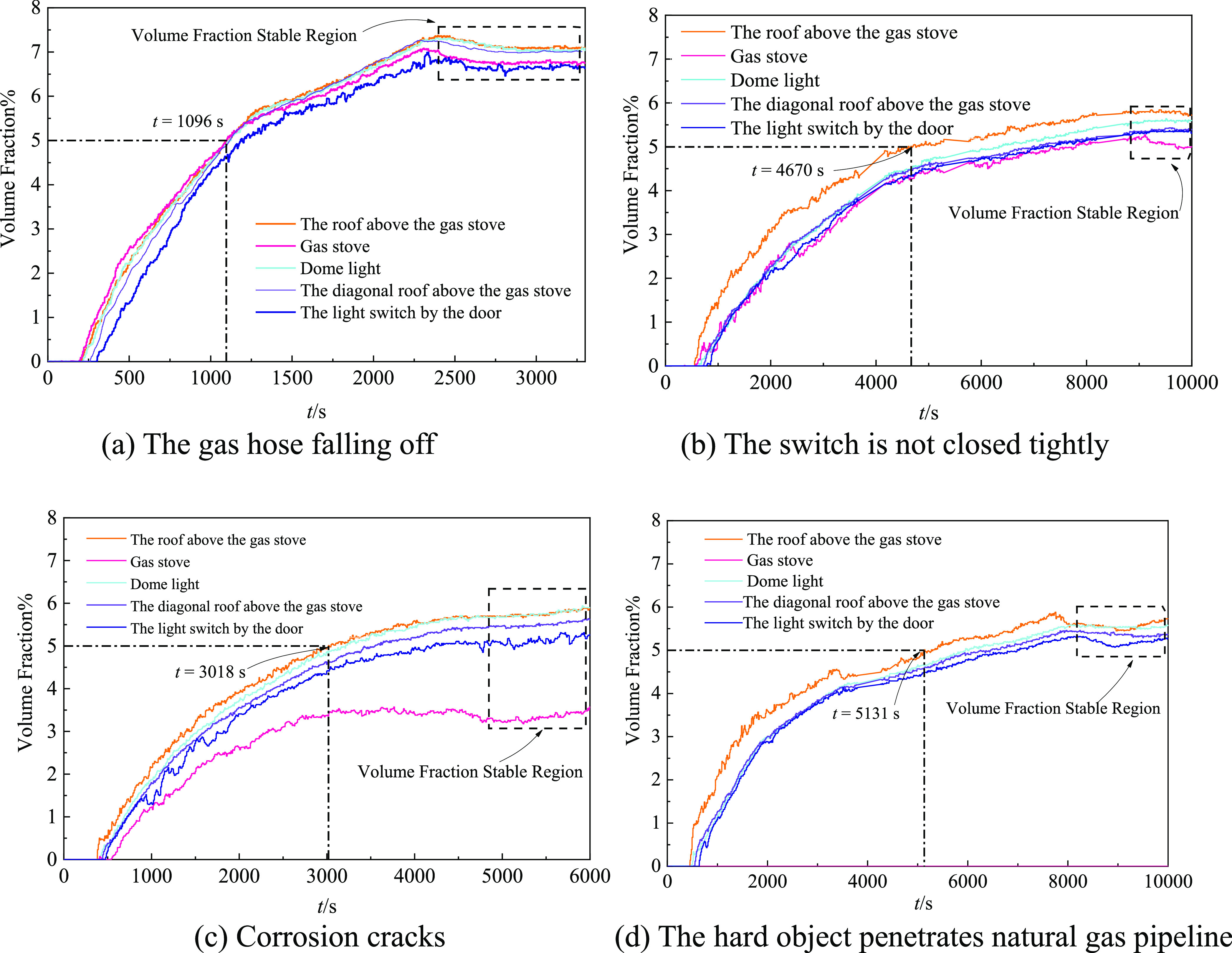
Figure 3

Open in a new tab

Evolution law of natural gas volume fraction.

By analyzing the law of natural gas leakage and diffusion, it can be seen that the natural gas volume fraction of the leakage increases faster in the initial stage, and the volume fraction increases slowly until stable due to the gaps between doors and windows. In a stable state, the gas volume fraction of each measuring point exceeds the lower explosive limit (5%) when the leakage source is inside the kitchen cabinet. When the leak source is indoors, the volume fraction of other measuring points except natural gas kitchen cabinets exceeds the lower explosive limit. The reason for the lower volume fraction of the natural gas kitchen cabinet is the height of the leakage source; especially, the location of the small hole leakage source is higher than the natural gas kitchen cabinet surface, so that no natural gas is detected at the natural gas kitchen cabinet. On the whole, the distribution law of natural gas volume fraction shows that the higher the measuring point, the larger the volume fraction, and the closer the measuring point of the same height is to the leakage source, the larger the volume fraction, which is consistent with Chen’s51 conclusion. Analyzing the evolution law of natural gas concentration distribution at different leakage locations is helpful to determine the location of leakage and accidents.

3.2.2. Process of Natural Gas Explosion

Figure 4 shows the explosion process with the natural gas concentration of 9.5%. Since the ignition head releases about 10 J of energy, which is relatively small, natural gas has experienced three stages of slow combustion, deflagration, and slow combustion within 6 s from the ignition. It can be seen that after ignition, a fireball is formed with the ignition source as the center. Except for the ignition source, due to the drop of the ignition head, fire sources appear in many areas at 0.2 s, and the fireball formed by the fire source continuously ignites the surrounding natural gas and forms a light blue spherical flame. The flame burning releases a lot of energy, the internal pressure of the unburned area affected by high temperature increases, generating a pressure gradient and forming a precursor shock wave, which widens the width of the door gap, and the flame is ejected from the door gap at 0.4 s. The shock wave and flame surface generated by multiple light blue spherical flames constantly superimpose and disturb the unburned area, speeding up the combustion chemical reaction rate. The increase in the chemical reaction rate not only promotes the generation of shock waves but also releases a lot of energy, both of which are positive feedback mechanism, resulting in the 0.8 s flame being ejected from the window. At this time, the gas cloud is disturbed by external factors, and the combustion chemical reaction is intensified. The flame develops from slow combustion to deflagration, and the color changes from light blue to bright white. The maximum distance of flame injection exceeds 2.5 m. After ignition for 2.8 s, the flame no longer sprays from the window on the door frame, and the spray time lasts ∼2.4 s. As the fuel is exhausted, the combustion state develops into slow combustion, and the flame gradually dissipates until it is completely extinguished at 8 s.

Figure 4.

Figure 4

Open in a new tab

Flame propagation process.

Temperature sensors were arranged at the center of the indoor space and at the middle position of the windowed wall 1 m above the ground. Figure 5 shows the temperature changes at two measuring points. Through the analysis of the temperature–time curve and the flame diffusion process, an open flame is quickly generated in the room after ignition. Since the center of the room is close to the ignition source, the temperature of the center of the room reaches its peak at 0.0812 s, and the peak temperature reaches 1440 °C. The temperature of the measuring point on the wall reaches its peak value of 1386 °C at 0.5778 s. The peak time of the measuring point on the wall is delayed by 0.4966 s from the peak time of the indoor central measuring point, and the peak temperature is reduced by about 54 °C. Based on the simulation, Cen et al.52 obtained the indoor temperature of the natural gas explosion. The temperature is about 1900 °C, which is higher than the temperature data obtained by the experiment. This is because the simulation is an ideal condition, but in reality, the gas cannot react completely, and the sensor has a certain delay, the explosion process is very short, and it is difficult to achieve real-time measurement. The temperature data obtained from the experiment is enough to prove that the explosion can cause a secondary fire. A temperature of 700 °C is enough to ignite most plastic products, with a duration of 4.58 s for the center of the room above 700 °C, and 2.75 s for the wall measuring point. Comparing the temperature curves of the two measuring points, it can be found that the temperature of the measuring point at the wall shows a downward trend after reaching the peak value, while the indoor center position fluctuates repeatedly above 1000 °C. This phenomenon is because the unburned gas cloud and high-temperature combustion products are ejected from the room and pass through the indoor center during the movement. The repeated passing of the flame surface and the superposition of high-temperature products cause the indoor center to maintain a high temperature for a long time. Long-term high temperature can cause the burning of indoor fabrics, plastics, and other materials, leading to secondary fires and further increasing the risk of natural gas leakage and the probability of death. Relatively speaking, the central location of the room is more dangerous.

Figure 5.

Figure 5

Open in a new tab

Evolution of indoor temperature.

As we all know, the shock wave overpressure of 50 kPa can cause serious damage to internal organs or even death and large cracks in the wall. As shown in Figure 6(a), the overpressure reaches peak at 1.44 s at 1.5 m from the door, which is 34.13 kPa, and the overpressure peak is 8.36 kPa at 1.65 s at 2.5 m from the door. Because the sensor at 1 m away from the door was disturbed by the flame sprayed from the door glass, no valid data was measured, and the flame acceleration process could not be judged. Pressure sensors located in the room also failed to detect data due to the flame. Based on the bending degree of the structural steel beam shown in Figure 6b, it can be explained that the shock wave overpressure in the room is greater than 50 kPa. The shock wave causes a high probability of death and huge damage to the house structure.

Figure 6.

Figure 6

Open in a new tab

Hazards of explosive shock wave.

3.3. Results of Numerical Simulation

3.3.1. Distribution Law of Natural Gas Concentration

The lower limit of the explosion of natural gas at normal temperature and pressure is 5%, so the maximum value of rainbow live is set to 5%, indicating that the areas where the concentration of natural gas exceeds 5% are displayed in red.

It can be seen from Figure 7 that the evolution law of the natural gas volume fraction of different leakage forms is different. The volume fraction of natural gas in the form of hose shedding and leakage has increased the fastest. The volume fraction of natural gas in the kitchen cabinet exceeds 5% at 300 s, and the volume fraction of natural gas above 1.3 m above the ground exceeds 5% at 3000 s. In the steady state, the volume fraction of the leaking form of the corrosive cracks is similar to the leaking form of the unclosed switch, and the volume fraction of the natural gas above 1.6 m above the ground is more than 5%. Although the distribution of natural gas volume fractions of different leakage forms is different, they have some commonalities: natural gas in the indoor headspace accumulates to form a natural gas–air premixed layer. As the leakage time increases, the area of the premixed layer, the thickness, and the volume fraction increase. The gas volume fraction does not increase all the time due to gaps in the house, and it will form an equilibrium state in the room.

Figure 7.

Figure 7

Open in a new tab

Evolution of volume fraction of natural gas without the kitchen wrapping structure. (1) Natural gas volume fraction without kitchen wrapping structure.

The simulation shows the evolution law of the indoor natural gas volume fraction. It can be seen from Figure 7c that, under the influence of gravity, the natural gas mainly diffuses to the upper space after being ejected from the leak under the condition of corrosion crack leakage. Under the action of the initial velocity, the natural gas diffuses laterally, but the diffusion distance is short, which leads to a low volume fraction of natural gas at the gas stove, which explains and verifies the reason why the volume fraction at the gas stove does not exceed the lower explosion limit under the experimental conditions. In the case that the switch is not tightly closed and the corrosion cracks, the horizontal height of 1.6 m from the ground is the boundary layer, the volume fraction of the upper space exceeds the lower explosion limit, and the volume fraction of the lower space does not reach the lower explosion limit. It can be seen from Figure 3b,c that the volume fraction of the light switch vibrates slightly around 5%, and the light switch is 1.5 m away from the ground, which is close to the height of the boundary line of the simulation results, and the simulation results can objectively reflect the experimental process. And the indoor natural gas volume fraction is the highest when the hose falls off, which is consistent with the experimental results. Therefore, the study of natural gas diffusion under other conditions can be carried out based on the simulation method.

From Figure 8a,d, it can be seen that the kitchen wrapping structure limits the diffusion of natural gas. In the steady state, the volume fraction of natural gas in the space enclosed by the kitchen wrapping structure exceeds the lower explosive limit, while the volume fraction of indoor space areas is less than 3%. Due to the kitchen wrapping structure constraint, natural gas does not pass through the indoor space when it diffuses to the top, but directly diffuses to the top through the kitchen wrapping structure, which reduces the lateral diffusion in the room, resulting in the volume fraction of indoor natural gas being smaller than that of no kitchen wrapping structure. The valve body assembly of gas stoves is not tightly matched, the leakage source is located indoors, and the volume fraction of natural gas in the space enclosed by the kitchen wrapping structure is much smaller than indoor natural gas volume fraction. Therefore, kitchen wrapping structure and leak location have decisive influence on indoor space natural gas concentration. The evolution law of natural gas volume fraction under the condition of unclosed switch and corrosion cracks is similar to the evolution law of natural gas volume fraction under the condition of the hose falling off, and the main difference is the time to reach the steady state and the volume fraction of the steady state. The indoor natural gas volume fraction is the highest under the condition of the hose falling off, followed by corrosion crack leakage, and the indoor natural gas volume fraction is less than 1% when the switch is not tightly closed. However, the volume fraction of natural gas in the space enclosed by the kitchen wrapping structure exceeded the lower explosion limit under the three leakage conditions.

Figure 8.

Figure 8

Open in a new tab

Evolution of volume fraction of natural gas with the kitchen wrapping structure. (2) Natural gas volume fraction with kitchen wrapping structure.

3.3.2. Simulation of Natural Gas Explosion Shock Wave

Figure 9 shows the values of different concentrations of natural gas explosions at different locations. Yang53 studied the explosion overpressure when the natural gas volume fraction was 9.5, and the indoor overpressure exceeded 100 kPa, which is close to the overpressure value in Figure 9. The results were different due to the inconsistency of the room size, pressure relief pressure, and pressure relief port surface size. When the natural gas volume fraction is 9.5%, the shock wave overpressure is 41.7 and 12.3 kPa at 1.5 and 2.5 m away from the door, respectively. Compared with the experimental values, the simulated values are larger. This is because the experiment was carried out in the field, and environmental factors interfered more. The simulation is based on theoretical calculations and does not fully consider external interference factors, but the simulation results can still reflect the development law of shock wave overpressure. The relationship between shock wave overpressure and distance for different concentrations of natural gas explosions is fitted, and there is a logarithmic relationship between shock wave overpressure and distance, which can be expressed by Y = A + B * ln(X + C), and the correlation coefficients are all above 0.99, as shown in Figure 9. The equation based on the fitting can predict the explosion risk more clearly and provide certain technical guidance for accident rescue.

Figure 9.

Figure 9

Open in a new tab

Relationship between shock wave overpressure and distance under different natural gas concentrations.

The paper studies the distribution law of natural gas concentration under different leakage conditions through experiments and simulations and finally guides the safe use of natural gas. For example, 304 stainless steel gas bellows are used instead of hoses and timely replacement of gas stoves that have exceeded their service life. In particular, engineers of natural gas companies can optimize the location of natural gas alarms according to the research, quickly and accurately find the location of leaks, and prevent explosions. At the same time, it is not recommended to wrap the natural gas pipeline. The kitchen wrapping hinders the ventilation and causes the accumulation of natural gas. In addition, people cannot directly contact the high-concentration natural gas, which is easy to produce paralysis and carelessness. If the pipeline is in a harsh environment, the pipeline must be sealed to avoid being hit; the installation and layout of the alarm can be planned and designed according to the research. Moreover, according to the traces of fire and the degree of damage to buildings caused by shock waves, the research can provide a basis for the calculation of key parameters of natural gas explosion accidents and can also be applied to accident investigations to determine the location of natural gas leakage points, ignition sources, leakage time, and leakage amount.

4. Conclusions

In the present study, the chemical reaction mechanism of natural gas combustion, the law of leakage and diffusion, and the law of flame propagation and shock wave propagation in the explosion process were studied through experiments and simulations. The main conclusions are as follows.

  • (1)

    The flame structure can be divided into three zones, i.e., the preheat zone, the reaction zone, and the product zone. OH + CO ⇔ H + CO2 is the main exothermic reaction in the methane combustion process, and oxygen is not completely consumed even at stoichiometric concentrations.

  • (2)

    The distribution law of natural gas volume fraction as a whole shows the characteristics that the higher the position, the larger the volume fraction, and the closer the point of the same height is to the leakage source, the greater the volume fraction, and the natural gas volume fraction of the hose shedding leakage is the highest. With the kitchen wrapping structure, the volume fraction of natural gas in the ceiling space exceeds the lower explosive limit when the leakage source is in the wrapping structure,and the volume fraction of natural gas in the room directly in contact is small. And the wrapping structure obstructs ventilation, so it is not recommended to wrap the natural gas pipeline. If the pipeline is in a harsh environment, the pipeline must be sealed to avoid being hit; the installation and layout of the alarm can be planned and designed according to the research.

  • (3)

    The flame development has gone through five stages of ignition, slow burning, detonation, slow burning and extinction. During deflagration, the color of the flame changes from light blue to bright white. The indoor temperature reaches about 1400 °C. The simulated value of shock wave overpressure is slightly larger than the experimental value. However, the simulation results can still reflect the evolution law of shock waves, and the relationship between overpressure and distance can be expressed by Y = A + B * ln(X + C). According to the traces of fire and the degree of damage to buildings caused by shock waves, the research can provide a basis for the calculation of key parameters of natural gas explosion accidents.

  • (4)

    In the study, the natural gas leakage and explosion scene is set as a full-size single enclosed kitchen. In the future, research on the natural gas leakage and explosion mechanism, process, and effect of the whole indoor structure scene of civil buildings can be carried out. The shock wave can be derived from the explosion effect, and then the natural gas volume fraction can be determined to obtain the leakage amount. The location of the leak is determined through the explosion site inspection, and the amount of leakage is determined based on the evolution law of the natural gas volume fraction under different leakage conditions studied in this paper and the data recorded by the natural gas alarm. Mutual verification of the two forms the research results of the indoor natural gas leakage and explosion accident.

Acknowledgments

The authors are grateful for the financial support provided by the National Natural Science Foundation of China (12172053), and the independent research project of the State Key Laboratory of Explosion Science and Technology (Beijing Institute of Technology) (YBKT22-01).

The authors declare no competing financial interest.

References

  1. Qiao A.; Zhang S. Advanced CFD modeling on vapor dispersion and vapor cloud explosion. J. Loss Prev. Process Ind. 2010, 23, 843–848. 10.1016/j.jlp.2010.06.006. [DOI] [Google Scholar]
  2. Wang C.; Han W. H.; Ning J. G.; Yang Y. Y. High resolution numerical simulation of methane explosion in bend ducts. Safety Sci. 2012, 50, 709–717. 10.1016/j.ssci.2011.08.047. [DOI] [Google Scholar]
  3. Chi M. H.; Jiang H. Y.; Lan X. B.; Xu T. L.; Jiang Y. Study on overpressure propagation law of vapor cloud explosion under different building layouts. ACS Omega 2021, 6, 34003–34020. 10.1021/acsomega.1c05332. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Li A.; Si J. H.; Zhou X. H. Experimental research on rapid fire zone sealing and explosion venting characteristics of an explosion venting door using a large-diameter explosion pipeline. ACS Omega 2021, 6, 27536–27545. 10.1021/acsomega.1c04561. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Li S. N.; Gao K.; Liu Y. J.; Ma M. R.; Huo C. Y.; Cong M. Z.; Li Y. X. Influence of the cavity structure in the excavation roadway on the gas explosion characteristics. ACS Omega 2022, 7, 7240–7250. 10.1021/acsomega.1c07027. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Li P. L.; Huang P.; Liu Z. Y.; Du B. X.; Li M. Z. Experimental study on vented explosion overpressure of methane/air mixtures in manhole. J. Hazard. Mater. 2019, 374, 349–355. 10.1016/j.jhazmat.2019.04.046. [DOI] [PubMed] [Google Scholar]
  7. Li C. W.; Qiao Z.; Hao M.; Zhang H.; Li G. Effect of ignition energy on environmental parameters of gas explosion in semiclosed pipeline. ACS Omega 2022, 7, 10394–10405. 10.1021/acsomega.1c07097. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gavelli F.; Scott G. D.; Olav R. H. Evaluating the potential for overpressures from the ignition of an LNG vapor cloud during offloading. J. Loss Prev. Process Ind. 2011, 24, 908–915. 10.1016/j.jlp.2011.07.002. [DOI] [Google Scholar]
  9. Qian X. M.; Zhang R. H.; Zhang Q.; Yuan M. Q.; Zhao Y. Cause analysis of the large-scale LPG explosion accident based on key investigation technology: A Case Study. ACS Omega 2021, 6, 20644–20656. 10.1021/acsomega.1c02837. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cai P.; Liu Z. Y.; Li M. Z.; Zhao Y.; Li P. L.; Li S. H.; Li Y. K. Experimental study of effect of equivalence ratio and initial turbulence on the explosion characteristics of LPG/DME clean blended fuel. Energy 2022, 250, 123858 10.1016/j.energy.2022.123858. [DOI] [Google Scholar]
  11. Gregory P.; Smith D. M. G.; Frenklaeh M.. http://www.me.berkeley.edu/gri_mech/.
  12. Appel J.; Bockhorn H.; Frenklach M. Kinetic modeling of soot formation with detailed chemistry and physics: laminar premixed flames of C2 hydrocarbons. Combust. Flame 2000, 121, 122–136. 10.1016/S0010-2180(99)00135-2. [DOI] [Google Scholar]
  13. Hughes K. J.; Turányi T.; Clague A. R.; Pilling M. J. Development and testing of a comprehensive chemical mechanism for the oxidation of methane. Int. J. Chem. Kinet. 2001, 33, 513–538. 10.1002/kin.1048. [DOI] [Google Scholar]
  14. Wang H.; You X.; Joshi A. V.; Davis S. G.; Laskin A.; Egolfopoulos F.; Law C. K.. High-Temperature Combustion Reaction Model of H2/CO/C1-C4 Compounds. http://ignis.usc.edu/USC_Mech_II.htm, May, 2007.
  15. Su B.; Luo Z. M.; Wang T.; Xie C.; Cheng F. M. Chemical kinetic behaviors at the chain initiation stage of CH4/H2/air mixture. J. Hazard. Mater. 2021, 403, 123680 10.1016/j.jhazmat.2020.123680. [DOI] [PubMed] [Google Scholar]
  16. Li Y. C.; Bi M. S.; Li B.; Zhou Y. H.; Gao W. Effects of hydrogen and initial pressure on flame characteristics and explosion pressure of methane/hydrogen fuels. Fuel 2018, 233, 269–282. 10.1016/j.fuel.2018.06.042. [DOI] [Google Scholar]
  17. Wang X.; Fan X.; Yang K.; Wang J.; Jiao X.; Guo Z. Laminar flame characteristics and chemical kinetics of 2-methyltetrahydrofuran and the effect of blending with isooctane. Combust. Flame 2018, 191, 213–225. 10.1016/j.combustflame.2017.12.028. [DOI] [Google Scholar]
  18. Nie B. S.; Yang L. L.; Ge B. Q.; Wang J. W.; Li X. C. Chemical kinetic characteristics of methane/air mixture explosion and its affecting factors. J. Loss Prev. Process Ind. 2017, 49, 675–682. 10.1016/j.jlp.2017.02.021. [DOI] [Google Scholar]
  19. Wang T.; Liang H.; Luo Z. M.; Su B.; Liu L. T.; Su Y.; Wang X. Q.; Cheng F. M.; Deng J. Near flammability limits behavior of methane-air mixtures with influence of flammable gases and nitrogen: An experimental and numerical research. Fuel 2021, 294, 120550 10.1016/j.fuel.2021.120550. [DOI] [Google Scholar]
  20. Garcia-Soriano G.; Margenat S.; Higuera F. J.; Castillo J. L.; Garcia-Ybarra P. L. Non-linear response of the flame velocity to moderately large curvatures in laminar jet flames of methane-air mixtures. Combust. Flame 2019, 205, 123–132. 10.1016/j.combustflame.2019.03.035. [DOI] [Google Scholar]
  21. Song X. Z.; Su H.; Xie L. F.; Li B.; Cao Y.; Wang Y. X. Experimental investigations of the ignition delay time, initial ignition energy and lower explosion limit of zirconium powder clouds in a 20 L cylindrical vessel. Process Saf. Environ. Prot. 2020, 134, 429–439. 10.1016/j.psep.2019.10.032. [DOI] [Google Scholar]
  22. Sma A.; Von Rotz B.; Herrmann K.; Boulouchos K.; Bruneaux G. Experimental investigation of pilot-fuel combustion in dual-fuel engines, Part 1: Thermodynamic analysis of combustion phenomena. Fuel 2019, 255, 115642 10.1016/j.fuel.2019.115642. [DOI] [Google Scholar]
  23. Li M. Z.; Liu Z. Y.; Chen L.; Zhao Y.; Li P. L.; Wang K. Flame propagation characteristics and overpressure prediction of unconfined gas deflagration. Fuel 2021, 284, 119022 10.1016/j.fuel.2020.119022. [DOI] [Google Scholar]
  24. Zhou Y. H.; Li Y. C.; Jiang H. P.; Huang L.; Zhang K.; Gao W. Experimental study on unconfined methane explosion: Explosion characteristics and overpressure prediction method. J. Loss Prev. Process Ind. 2021, 69, 104377 10.1016/j.jlp.2020.104377. [DOI] [Google Scholar]
  25. Akram M.; Kumar S. Experimental studies on dynamics of methane–air premixed flame in meso-scale diverging channels. Combust. Flame 2011, 158, 915–924. 10.1016/j.combustflame.2011.02.011. [DOI] [Google Scholar]
  26. Yang Y.; Yang S. G.; Fang Q.; Xiang H. B.; Sun W. S.; Liu X. Large-scale experimental and simulation study on gas explosion venting load characteristics of urban shallow buried pipe trenches. Tunn. Undergr. Space Technol. 2022, 123, 104409 10.1016/j.tust.2022.104409. [DOI] [Google Scholar]
  27. Gu Z. J.; Liu Z. T.; Wang Z. R.; Shen R. X.; Qian J. F.; Lin S. Study on characteristics of methane explosion flame and pressure wave propagation to the non-methane area in a connected chamber. Fire Mater. 2021, 46, 639–650. 10.1002/fam.3012. [DOI] [Google Scholar]
  28. Di Sarli V.; Benedetto A. D.; Russo G. Sub-grid scale combustion models for large eddy simulation of unsteady premixed flame propagation around obstacles. J. Hazard. Mater. 2010, 180, 71–78. 10.1016/j.jhazmat.2010.03.006. [DOI] [PubMed] [Google Scholar]
  29. Magdalena T.; Brodhy J.; John A. The application of model-based tests for analysing the consequences of methane combustion in a mine heading ventilated through a forcing air duct. Mechanika 2019, 25, 204–209. 10.5755/j01.mech.25.3.23739. [DOI] [Google Scholar]
  30. He G. X.; Liang Y. T.; Li Y. S.; Wu M. Y.; Sun L. Y.; Xie C.; Li F. A method for simulating the entire leaking process and calculating the liquid leakage volume of a damaged pressurized pipeline. J. Hazard. Mater. 2017, 332, 19–32. 10.1016/j.jhazmat.2017.02.039. [DOI] [PubMed] [Google Scholar]
  31. Di Sarli V.; Benedetto A. D. Sensitivity to the presence of the combustion submodel for large eddy simulation of transient premixed flame vortex interactions. Ind. Eng. Chem. Res. 2012, 51, 7704–7712. 10.1021/ie202061u. [DOI] [Google Scholar]
  32. Di Sarli V.; Benedetto A. D.; Russo G. Large eddy simulation of transient premixed flame–vortex interactions in gas explosions. Chem. Eng. Sci. 2012, 71, 539–551. 10.1016/j.ces.2011.11.034. [DOI] [Google Scholar]
  33. Di Sarli V.; Benedetto A. D.; Russo G. Using large eddy simulation for understanding vented gas explosions in the presence of obstacles. J. Hazard. Mater. 2009, 169, 435–442. 10.1016/j.jhazmat.2009.03.115. [DOI] [PubMed] [Google Scholar]
  34. Ivings M. J.; Gant S. E.; Saunders C. J.; Pocock D. J. Flammable gas cloud build up in a ventilated enclosure. J. Hazard. Mater. 2010, 184, 170–176. 10.1016/j.jhazmat.2010.08.020. [DOI] [PubMed] [Google Scholar]
  35. Wang X. M.; Tan Y. F.; Zhang T. T.; Zhang J. D.; Yu K. C. Diffusion process simulation and ventilation strategy for small-hole natural gas leakage in utility tunnels. Tunn. Undergr. Space Technol. 2020, 97, 103276 10.1016/j.tust.2019.103276. [DOI] [Google Scholar]
  36. Fu L. Z.; Li Y. F.; Li G. Numerical simulation of gas leakage and diffusion based on FLUENT. Adv. Mater. 2013, 726–731, 888–891. 10.4028/www.scientific.net/AMR.726-731.888. [DOI] [Google Scholar]
  37. Wang K.; Shi T. T.; He Y. R.; Li M. Z.; Qian X. M. Case analysis and CFD numerical study on gas explosion and damage processing caused by aging urban subsurface pipeline failures. Eng. Failure Anal. 2019, 97, 201–219. 10.1016/j.engfailanal.2019.01.052. [DOI] [Google Scholar]
  38. Li Z. X.; Wu J. S.; Liu M. Y.; Li Y. T.; Ma Q. J. Numerical analysis of the characteristics of gas explosion process in natural gas compartment of utility tunnel using FLACS. Sustainability 2020, 12, 153. 10.3390/su12010153. [DOI] [Google Scholar]
  39. Song B.; Jiao W. L.; Cen K.; Tian X. H.; Zhang H. Y.; Lu W. Quantitative risk assessment of gas leakage and explosion accident consequences inside residential buildings. Eng. Failure Anal. 2021, 122, 105257 10.1016/j.engfailanal.2021.105257. [DOI] [Google Scholar]
  40. Li X. M.; Zhang H.; Yang C. L.; Zhao J. F.; Bai S.; Long Y. Z. Effect of water on the chain reaction characteristics of gas explosion. ACS Omega 2021, 6, 12513–12521. 10.1021/acsomega.1c00153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Luo Z. M. Applications of chain reaction for gas explosion suppression. Saf. Coal Mines 2009, 40, 67–69. [Google Scholar]
  42. Harstad K.; Bellan J. Prediction of premixed, n-heptane and iso-octane unopposed jet flames using a reduced kinetic model based on constituents and light species. Combust. Flame 2013, 160, 2404–2421. 10.1016/j.combustflame.2013.06.005. [DOI] [Google Scholar]
  43. Wen Z.Fluid Calculation Application Tutorial; Tsinghua University Press: Beijing, 2013; pp P77–78. [Google Scholar]
  44. Lee C. C.; Tran M.; Scribano G.; Chong C. T.; Ooi J. B.; Cong H. T. Numerical study of NOx and soot formations in hydrocarbon diffusion flames. Energy Fuel 2019, 33, 12839–12851. 10.1021/acs.energyfuels.9b03282. [DOI] [Google Scholar]
  45. Li P. J.; Chen C. S.; Chang H. P.; Ho H. H.; Xie B. Explosion mechanism analysis during tunnel construction in the Zengwen Reservoir. Tunn. Undergr. Space Technol. 2020, 97, 103279 10.1016/j.tust.2019.103279. [DOI] [Google Scholar]
  46. Zhang S. H.; Ma H. T.; Huang X. M.; Peng S. N. Numerical simulation on methane-hydrogen explosion in gas compartment in utility tunnel. Process Saf. Environ. Prot. 2020, 140, 100–110. 10.1016/j.psep.2020.04.025. [DOI] [Google Scholar]
  47. Luo Z. M.; Zhang Q.; Wang H.; Cheng F. M.; Wang T.; Deng J. Numerical simulation of gas explosion in confined space with FLACS. J. China Coal Soc. 2013, 38, 1381–1387. [Google Scholar]
  48. Gao E. X.; Bai C. H.; Xue Y.; Cheng Z. H.; Wang L. Computer simulation of gas explosion in tunnel. Blasting 2003, 20, 29. [Google Scholar]
  49. Arntzen B. J.Modelling of Turbulence and Combustion for Simulation of Gas Explosions in Complex Geometries; Norwegian University of Science and Technology: Trondheim, 1998. [Google Scholar]
  50. Zhu Y. F.Propagation of Gas Explosion Fire and Pressure Waves in Coalmine Tunnels; China University of Mining and Technology: Xuzhou, 2021. [Google Scholar]
  51. Chen Q.; Chen C. X.; Wu T. T.; Wang T.; Fang R. On the lateral stability control of a blownout vehicle based on the fractional calculus. J. Safety Environ. 2018, 18, 2224–2229. [Google Scholar]
  52. Cen K.; Song B.; Shen R. Q.; Zhang Y. D.; Yu W. G.; Wang Q. S. Dynamic characteristics of gas explosion and its mitigation measures inside residential buildings. Math. Probl. Eng. 2019, 2019, 2068958 10.1155/2019/2068958. [DOI] [Google Scholar]
  53. Yang K.; Lv P. F.; Hu Q. R.; Pang L. Research on synergetic effect of large-scale obstacles and explosion vents on indoor explosion of natural gas. China Safety Sci. J. 2018, 14, 21–27. [Google Scholar]

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES