Abstract
This paper develops an approach to optimize a vaccine distribution network design through a mixed-integer nonlinear programming model with two objectives: minimizing the total expected number of deaths among the population and minimizing the total distribution cost of the vaccination campaign. Additionally, we assume that a set of input parameters (e.g., death rate, social contacts, vaccine supply, etc.) is uncertain, and the distribution network is exposed to disruptions. We then investigate the resilience of the distribution network through a scenario-based robust-stochastic optimization approach. The proposed model is linearized and finally validated through a real case study of the COVID-19 vaccination campaign in France. We show that the current vaccination strategies are not optimal, and vaccination prioritization among the population and the equity of vaccine distribution depend on other factors than those conceived by health policymakers. Furthermore, we demonstrate that a vaccination strategy mixing the population prioritization and the quarantine restrictions leads to an 8.5% decrease in the total number of deaths.
Keywords: Vaccine distribution network, Bi-objective mathematical optimization model, Disruption, Uncertainty, Robust-stochastic optimization, COVID-19
1. Introduction
As of 10th May 2022, more than 6.3M people have died because of the ongoing severe respiratory syndrome coronavirus 2 (SARS-CoV-2) pandemic [1]. Despite imposing different sanitary restrictions and employing various mitigation strategies, vaccination became the ultimate way to cope with the COVID-19 pandemic. From the very beginning of the pandemic, more than 100 vaccines were under development [2]. By the beginning of 2021, several efficient vaccines were approved for injection, and a remarkable decrease was reported in the number of infections and deaths. However, allocating and distributing a limited vaccine stockpile to the whole population has been challenging [3], [4], [5]. Due to a limited supply of vaccines, different countries adopted different vaccination strategies by targeting/prioritizing the population for vaccination, including vulnerable populations (elderly populations), frontline healthcare workers, people with high social interaction (teachers and home carers), pregnant women, etc. [6], [7], [8].
For instance, the US National Academies of Science, Engineering, and Medicine (NASEM) [9], [10] put frontline healthcare workers and individuals with comorbidities at top priority for vaccination [11]. At the same time, EU countries consider the top priority for individuals of all ages with comorbidities and individuals working in critical infrastructures (e.g., teachers and school staff, public transportation, and food sectors) [12]. Putting frontline healthcare workers and vulnerable individuals at top priority has been a similarity between the vaccination strategies of different communities. The reason of this similarity is that almost all communities have followed a similar objective as reducing the total number of deaths among the population [13]. Surprisingly, it was scientifically reported that prioritizing vulnerable populations for vaccination might not be necessarily an optimal policy for controlling the pandemic [14], [15]. In fact, vaccination strategies are influenced by other factors such as the population density, the type/effectiveness of available vaccines, the emergence of new variants of the virus, and even the quarantine (lockdown) restrictions [14], [15]. This is why EU countries were evolving their vaccination strategies over time [6], [14].
Along with figuring out efficient vaccination strategies in prioritizing the population, establishing these strategies requires taking detailed operational actions (i.e., shipping, storing, delivering, allocating, etc.) to distribute the vaccines effectively among the population based on demographic, clinical, and geographic factors [15]. In addition to operational decisions, determining the number and the location of vaccination centers are also essential to ensure that vaccines are reliably available for the whole population. Regarding the number of the vaccination centers, a health policymaker may locate a lower number of (geographically dispersed) centers with a high capacity or a higher number of centers with less vaccination capacity. A low-number-high-capacity policy may lead to a lower cost for the vaccination campaign. However, it increases the congestion of the population in vaccination centers, which possibly exposes the population to a higher risk of infection. On the other hand, a high-number-low-capacity policy reduces the congestion and accelerates the vaccination rate, but it is costly. Therefore, the number, location, and capacity of vaccination centers play critical roles in the effectiveness of a vaccination campaign [15]. In this study, the capacity of the vaccination centers is determined using an advanced queuing system explained in Section 3.4.
Two significant challenges in front of designing any distribution network are the uncertainty of the input parameters [16], [17] and the disruption of different network components [18], [19], [20], [21], [22], [23], [24], [25]. Accordingly, in finding optimal vaccination strategies and designing an optimal distribution network, the uncertainty of input parameters (e.g., the effectiveness of different vaccines, the progress of the pandemic, the emergence of new variants of the virus, etc.) and the disruption of different network components (e.g., capacity degradation in vaccine storage, unexpected delays in delivering the vaccines, etc.) [26], [27], [28] are important factors that need to be taken into account.
Finally, this paper studies the design of a vaccine distribution network (VDN) to locate a set of vaccination centers with particular capacities and distribute different types of vaccines with limited supplies among various warehouses at different hierarchical levels. In this network, the parameters are uncertain, and the network is exposed to disruptions. For this aim, we develop a bi-objective stochastic mixed-integer nonlinear programming model with two objectives as 1) minimizing the expected total number of deaths among the population and 2) minimizing the total distribution cost.
The rest of this paper is organized as follows. Section 2 reviews the most relevant papers in the literature and theoretically positions our study compared to existing works. Section 3 describes the problem and proposes a bi-objective mixed-integer nonlinear programming model. To cope with the uncertainty of the input parameters, Section 4 develops a scenario-based robust optimization model. Section 5 explains the real case study and designs the set of scenarios. The proposed model and solution approach are validated through the real case study, and the results and a set of sensitivity analyses are provided in Section 6. Furthermore, the results are discussed in Section 7, and a set of managerial insights are provided. Finally, the paper is concluded, and the future research directions are presented in Section 8.
2. Literature review
This section reviews the most relevant papers in the literature studying the design of VDNs through developing (mixed-) integer (non-) linear programming models. In the following, we first classify the papers, then provide a critical analysis on theoretical positioning of our study compared to the literature.
2.1. Classification of the literature
Table 1 classifies the papers based on different characteristics as 1) “Objectives”: whether developing single- (S) or multi-objective (M) models, 2) “Vaccines”: whether studying a VDN with single (S) or multiple (M) types of vaccines and if considering single- (S) or multiple-dose (M) injections (e.g., SS and SM stand for a single type of vaccine with single-dose and multiple-dose vaccination, respectively), 3) “Priority”: whether prioritizing the population for the vaccination (e.g., age groups, risk classes, etc.), 4) “Disruption”: whether occurring disruption at different elements of the network, including facilities (Fac.), inventories (Inv.), and vaccination services (Ser.), 5) “Congestion” (Cong.): whether studying the congestion of the population in the vaccination center to avoid the additional risk of infection, 6) “Periodic” (Prdc.): whether developing a mathematical model with multiple periods, 7) “Uncertainty” (Uncrt.): whether considering the parameters under the uncertainty, and the type of approaches to coping with the uncertainty, including scenario-based stochastic optimization (Sc-SO) or robust optimization (RO), and finally 8) “Case study” to know which type of disease or pandemic has been dealt with. We have provided this classification to better position our work compared to the literature.
Table 1.
Classification of the papers studying the VDN problem.
| Ref. | Objectives |
Vaccines | Priority | Disruption |
Cong. | Prdc. | Uncrt. | Case study | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | Type | Fac. | Inv. | Ser. | ||||||||
| [29] | S | Min total cost | SS | ✓ | ✓ | Sc-SO | General | |||||
| [30] | S | Min total death | SS | ✓ | Sc-SO | Smallpox | ||||||
| [31] | S | Max vaccine availability | MS | ✓ | ✓ | Multiple | ||||||
| [32] | M | Min total cost (2-phase) | SS | Sc-SO | Influenza | |||||||
| [33] | S | Min total cost | SS | ✓ | ✓ | Sc-SO | Influenza | |||||
| [34] | M | Min total cost | MS | Non-flu | ||||||||
| Min global warming | ||||||||||||
| [35] | S | Min unsatisfied demand | MS | ✓ | Sc-SO | Smallpox | ||||||
| [36] | S | Max herd effect | SS | Influenza | ||||||||
| [37] | M | Max economic factor | MS | ✓ | Sc-SO | MMR* | ||||||
| Min environmental factor | ||||||||||||
| Max social factor | ||||||||||||
| [38] | S | Min total cost | SS | ✓ | RO | General | ||||||
| [39] | S | Min unsatisfied demand | SS | ✓ | H1N1 | |||||||
| [4] | S | Min total infections | SS | ✓ | ✓ | COVID-19 | ||||||
| [40] | S | Max vaccine usage | SS | ✓ | Sc-SO | Influenza | ||||||
| [3] | S | Min total risk | SS | ✓ | Sc-SO | COVID-19 | ||||||
| [41] | S | Max-min delivery-to-demand | SS | ✓ | ✓ | Sc-SO | Influenza | |||||
| [42] | M | Min travel distance | SS | ✓ | Sc-SO | General | ||||||
| Max vaccination stations | ||||||||||||
| Min total cost | ||||||||||||
| [43] | S | Min total cost | SS | ✓ | ✓ | Sc-SO | Encephalitis | |||||
| [44] | S | Min total cost | SS | General | ||||||||
| [15] | S | Min total cost | SS | ✓ | COVID-19 | |||||||
| [45] | M | Min total cost | SS | ✓ | COVID-19 | |||||||
| M | Min total distance | ✓ | ||||||||||
| This study | M | Min total death | MM | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | Sc-SO/RO | COVID-19 | |
| Min total cost | ||||||||||||
*MMR: Measles, Mumps, Rubella.
Regarding the number and the type of objectives, most of the studies have considered a single objective of minimizing the total cost of the network. Minimizing the cost of a VDN is an essential concern in low and middle-income countries [44]; however, in developed countries, cost minimization might not be the primary concern but rather minimizing the number of fatalities during the pandemic [4], [30], [36]. Accordingly, incorporating multiple objectives in the design of a VDN could be a possible way to design a network that minimizes the total number of deaths and is also cost-efficient. In this regard, few papers [32], [34], [37], [42] have incorporated multiple objectives to be optimized, e.g., minimizing the total cost or maximizing the vaccine usage, and only a single paper [30] has directly dealt with minimizing the total number of deaths.
Other important factors when designing a VDN are the type of vaccines and the number of recommended doses to be injected for each vaccine. To the best of our knowledge, almost all the studies, except a few papers [31], [34], [35], [37], have considered a single type of vaccines, and no study deals with the multiple-dose injection of the vaccines. Since different vaccines may require different modes of transportation (e.g., refrigerated trucks, airplanes, etc.), the VDN of different types of vaccines requires different modeling compared to the existing literature [31], [34], [35], [37].
Prioritizing the population to receive vaccines is a crucial decision when the supply of vaccines is limited. As also elaborated in Section 1, no optimal vaccination strategy exists to prioritize the population. In a recent work regarding the COVID-19 pandemic [3], the authors prioritize the population based on their risk of infection or their number of social contacts. The goal has been to vaccinate the individuals who are more exposed to the risk of death. In another study [46], the authors argue that, in pandemics, the priority for vaccination should be given to the groups of individuals who are at a higher risk of death and who would experience difficulty reaching healthcare centers (e.g., homeless people and other disadvantaged groups). As Table 1 also reports, a considerable number of studies have considered the population prioritization for vaccination.
An important issue when designing a VDN under a pandemic situation is the robustness of the network against any out-of-control disruptions. In fact, even minor disruptions in any network components may have considerable negative impacts on the network’s performance in delivering the vaccines to the right persons at the right time. These disruptions may either lead to a delay in the vaccination of high-risk/high-contact individuals, that itself (the delay) leads to a higher number of deaths, or postpone the end of the pandemic. These disruptions may also jeopardize the infrastructure facilities (e.g., storage warehouses), the inventory of vaccines, or even the vaccination services. In the case of any disruptions in facilities, the capacity of those facilities might probabilistically degrade to a lower level, and consequently, they store fewer vaccines. In the case of disruption in inventories as a potential disruption in VDNs, a part of the vaccine stockpile becomes unusable (e.g., expired or destroyed) in particular periods. Finally, in case of disruption in vaccination services, the vaccination process stochastically degrades (e.g., decelerated vaccination rate).
In case of an ongoing pandemic with an unknown disease, the ultimate way to control the pandemic is a mass vaccination of the population. In this situation, depending on the availability of vaccines and the number and capacity of the vaccination centers, the individuals refer to vaccination centers to be vaccinated. In an appropriate vaccination planning, the individuals refer to vaccination centers based on scheduled appointments or their proximity. In both cases, an important issue that needs to be avoided is the congestion of the people in these centers, which disrupts the vaccination process, if not increasing the probability of possible infections. In this situation, the vaccination centers should be established with an appropriate vaccination capacity [47].
It can be observed from Table 1 that the majority of the papers in the literature have designed a VDN with a periodic decision-making process. Intrinsically, vaccine distribution is not a single-period decision-making process, but a periodic one. In fact, the pandemic situation evolves over time, and the most appropriate vaccination strategy should be adopted in each period.
In addition to disruptions, any source of uncertainty (e.g., supply, demand, the effectiveness of the vaccines, infection rates, new variants of the disease, etc.) also significantly affects the network’s performance and, consequently, the success of vaccination campaigns. In fact, in new pandemics, the lack of information on the progress of the pandemic imposes a high level of uncertainty and causes critical challenges to piloting the vaccination campaign. The considerable number of studies in Table 1 taking into account the uncertainty demonstrates the importance of this issue when designing a VDN. To cope with the uncertainty of the input parameters, the literature has either used scenario-based stochastic programming models or robust optimization models. The former models have gained more popularity because estimating the behavior of uncertain parameters can be modeled more appropriately through stochastic scenarios.
2.2. Theoretical positioning of the study
In this section, we aim to position our study in the literature and elaborate on its contributions. In this paper, we seek to fill essential gaps in the literature by designing a VDN through a mixed-integer nonlinear programming model. The contribution of our study lies in several axes.
The first contribution of our study to the literature is designing a VDN to distribute multiple types of vaccines with multiple-dose injections. In real settings, particularly in emerging pandemics (e.g., the recent coronavirus pandemic), multiple vaccines are identified with different properties. On the other hand, in such pandemics, the supply of vaccines is very limited, and no unique vaccine (e.g., the one with the highest effectiveness) can be produced and distributed to the whole population. The monopolies in the distribution and consumption of superior vaccines by developed countries could be another reason that the governments should order a portfolio of different types of vaccines. In addition, multiple-dose injection of vaccines is another emerging issue in long-lasting pandemics. Designing a VDN with these properties is closer to reality and is more practical for real settings. However, it becomes a challenging task since different types of vaccines may require different modes of transportation (e.g., refrigerator or freezer trucks) and storage (e.g., ultra-cold freezer or refrigerator), and the distribution network should guarantee the delivery of the second dose of the same or compatible vaccines for the previously delivered first doses. Almost all the studies in the literature have ignored these issues, and this paper addresses them for the first time.
The second contribution of this study relates to the fact that the primary goal of a vaccination campaign in pandemics should not only be decreasing the number of deaths by vaccinating the individuals exposed to a higher risk of death, but also decreasing the number of infections by vaccinating the individuals who have more social contacts. The former decreases the saturation of the critical care capacities and the pressure on the healthcare workers. However, vaccinating the individuals with a higher number of contacts is as essential as the high-risk individuals, since decreasing the number of infections is vital to control/stop the pandemic. Accordingly, this paper does not pre-prioritize the population for vaccination and only categorizes the population into age-based classes. Hence, we let the model determine which population class should receive vaccines first in each period. This leads to a dynamic vaccination strategy that allows us to account for the evolution of the pandemic over time.
Furthermore, our study contributes to the literature by investigating the impact of three types of disruptions (i.e., facilities, inventories, and services) in designing a VDN. Few papers have considered disruptions in the design of a VDN by considering the effect of disruption either on facilities [29] or inventories [31], [43]. No paper has studied the impact of disruption on vaccination services.
Another central contributing axis of our paper is the determination of the capacity of the vaccination centers through the control of the congestion in these centers. To the best of our knowledge, no paper in the literature has studied the capacity determination and the impact of congestion in the vaccination centers when designing a VDN. The main reason can be that most of the papers only decide how to distribute the vaccines, and they do not deal with the vaccination process itself. However, the distribution of vaccines without estimating the appropriate capacity of the vaccination centers, particularly nonmedical centers (e.g., social centers), may lead to an inefficient distribution process that unintentionally results in congested vaccination centers.
The above-mentioned contributions of our study to the literature make the designed VDN closer to reality and provide results that serve health policymakers as practical insights. In this regard, a comprehensive discussion of the results will be provided in Section 7, where we discuss those that confirm the existing knowledge and those that are counter-intuitive. This discussion also figures among the contributions of our study.
3. Problem statement and formulation
In many countries, the vaccines are usually distributed through a hierarchical logistic network consisting of a central inventory warehouse at a national level and a set of downstream (low-level) warehouses (e.g., regional, departmental/district, clinical, etc.) [31], [35], [38], [41], [43], [44], [48], [49]. This hierarchy becomes even more crucial in low and middle-income countries [44]. Such a hierarchical structure helps to decentralize the control/monitoring of the vaccination campaign from a single national level into downstream regional/departmental/clinical levels. This hierarchy also allows the logistics network to react rapidly to any alteration in demand for vaccines [38], [44], [48]. This multi-level structure also provides horizontal transshipment between warehouses of the same level. Such transshipment allows to quickly share extra vaccines from specific warehouses to fulfill the shortage of others. However, such a hierarchical structure is more sensitive to disruption at higher levels than a more flat structure [35], [43]. This paper, therefore, investigates the impact of disruption in such a hierarchical network.
Fig. 1 illustrates the hierarchical VDN of this study. The first three levels include vaccine warehouses at national, regional, and departmental levels. Instead of regional and departmental levels, one may consider state and urban levels [31], [35], [43], [48], respectively. The fourth level consists of vaccination centers, and the last level represents the demand points (i.e., the population to be vaccinated). At the national level, the government places orders to purchase different vaccines. A delivery delay is required once an order is placed until the command arrives. Next, on arrival, vaccines are stored in the national warehouse to be transported to downstream regional warehouses. Due to the lack of vaccines for a mass vaccination, the government purchase different available vaccines. The vaccines may differ in price, effectiveness to protect the population from the disease, and the number of doses to be injected (i.e., single or multiple doses). A timing gap should be respected for the vaccines requiring multiple doses between the two injections.
Fig. 1.
Vaccine distribution network (VDN).
At the regional level, there is also the possibility of vaccine transshipment between different regions to balance the number of vaccinated people among different regions or even accelerate the vaccination in the regions with a higher number of infections. Next, the vaccines are transferred to smaller warehouses at the level of departments. Similar to the regional level, the transshipment is also allowed between the departments of a region. This transshipment is not allowed between two departments from two different regions.
Finally, vaccines are distributed to vaccination centers, where the individuals are vaccinated. Transshipment is not allowed among the vaccination centers. We decide which vaccination centers need to be opened/equipped at this level. These centers could be medical centers or even other social buildings suitable for vaccination. Considering only a limited number of healthcare centers for vaccination leads to a considerable delay in vaccination; hence, it is essential to consider other appropriate centers parallel to healthcare centers for a massive vaccination. Each vaccination center should be equipped with proper refrigerators/freezers, depending on the type of the stored vaccines. At the last level of the network, we have demand points consisting of individuals belonging to different risk classes (i.e., age groups, disabled individuals, etc.). In addition, each vaccination center only serves specific demand points based on their proximity. In other words, each vaccination center has a coverage distance, and that center only serves the demand points under its coverage.
Furthermore, the individuals from different demand points and belonging to different risk classes refer to their corresponding vaccination centers to be vaccinated. Such assignment may lead to congestion in the vaccination centers; consequently, a limited number of individuals can be vaccinated in each period at each center. To determine the capacity of each vaccination center (i.e., the maximum number of individuals that can be vaccinated at each period), the congestion of the population from different risk classes in vaccination centers is modeled as a queuing system (see Section 3.4 for more details). In addition, we consider that the capacity of the warehouses is limited, and the remaining vaccines at the end of each period are stored to be injected in further periods.
Accordingly, in the design of a VDN, a set of essential questions should be answered as: 1) where to locate the vaccination centers with what capacity? 2) how many of each type of vaccine to allocate to each warehouse in the network? and, 3) whom to vaccinate first with which vaccine? In order to cope with the daunting task of a mass vaccination under strict operating constraints, these questions should be solved optimally. To answer the first question, it should be decided where to locate the vaccination centers among different potential centers and determine how many individuals each center should vaccinate (at maximum) in each period. The second question determines the flow of different vaccines across the network, from upstream warehouses (national warehouses) to downstream ones (vaccination centers). Finally, answering the third question necessitates determining the priority of vaccination among different risk classes of the population.
It is worth mentioning that each period in our study represents one week. In fact, in emerging pandemics, the health policymakers in almost all countries monitor the pandemic’s progress and make/change decisions week by week. Actually, managing a vaccination campaign in an emerging pandemic is neither a real-time (daily) nor a long-term (monthly) decision-making process. For instance, the vaccines are ordered in advance, but their delivery to the national warehouse is weekly. Therefore, all the decisions mentioned above are made over periods of one week.
We also consider that the designed VDN is exposed to three sorts of disruptions; i.e., capacity degradation, inventory destruction, and vaccination service failures. In addition, a set of input parameters are considered uncertain (e.g., transmission rate, death rate, number of contacts, etc.). A scenario-based robust optimization approach is employed to cope with disruption and uncertainty issues (see Section 4). Therefore, when we solve the model, we design a VDN that performs the best under any probable scenario. Accordingly, the government does not need to revise the VDN and its vaccination strategy if any considered scenarios happen. In other words, the designed VDN is robust under the considered probable uncertainty/distribution scenarios. Finally, the described VDN of Fig. 1 with disruption and uncertainty concerns is formulated through a bi-objective mixed-integer nonlinear programming model with two objectives: 1) minimizing the expected total number of deaths during the vaccination campaign, and 2) minimizing the total cost of the vaccination campaign.
3.1. Notations
Before presenting the proposed model, the mathematical notations are provided in Table 2 .
Table 2.
Notations.
| Notation | Description |
|---|---|
| Sets and Indices | |
| Set of regions () / departments () / vaccination centers () / demand points () | |
| Set of departments in region / vaccination centers in department / demand points in department | |
| Set of risk classes (i.e., age groups; ) / available and approved vaccines () | |
| Set of approved vaccines for risk class / risk classes demanding vaccine | |
| Set of capacity levels () / planning periods () / scenarios () | |
| Parameters | |
| Network design parameters: | |
| Fixed cost of equipping a warehouse at national level / region / department for vaccine with capacity level | |
| Fixed cost of opening/equipping vaccination center for vaccine with capacity level | |
| Fixed cost of placing an order for vaccine at period | |
| Unit purchase cost of vaccine at period | |
| Unit holding cost of vaccine in region / department / vaccination center at period | |
| Unit transportation cost of transferring vaccine to region / department / vaccination center from their upstream at period | |
| Unit cost of vaccinating individuals in risk class using vaccine | |
| Distance of demand point from vaccination center | |
| Coverage radius of vaccination center | |
| 1 if demand point is under the coverage of vaccination center (i.e., ); 0 otherwise | |
| Unit transshipment cost of vaccine from region to region / department to department at period | |
| Delivery lead-time of vaccine (# of period) to the national warehouse under scenario | |
| Trust rate on the quantity of vaccine to be delivered on time under scenario | |
| Initial inventory of vaccine at national warehouse / region / department / vaccination center | |
| Maximum capacity of the national warehouse / region / department / vaccination center for vaccine at level | |
| Maximum supply capacity for vaccine at period under scenario | |
| Destruction rate of vaccine due to transporting the vaccines to region / department / vaccination center | |
| Vaccination parameters: | |
| Ineffectiveness of vaccine after the first dose injection under scenario ; : effectiveness of the first injection of vaccine under scenario | |
| Ineffectiveness of vaccine after the second dose injection under scenario ; : effectiveness of the second injection of vaccine under scenario | |
| 1 if vaccine needs to be injected in two doses; 0 otherwise | |
| Time lag (# of periods) between the first and the second dose of vaccine ; if it needs two injections (i.e., ) | |
| Population of risk class at demand point | |
| Rate of population of risk class at demand point , | |
| Death rate of population of risk class under scenario | |
| Infection rate among population of risk class under scenario | |
| Mean hospitalization cost for a member of risk class in case of severe infection | |
| Number of possible social contacts of a member of population of risk class at demand point under scenario | |
| Disruption parameters: | |
| Inventory disruption probability at the national warehouse / region / department / vaccination center in period under scenario | |
| Inventory degradation factor at the national warehouse / region / department / vaccination center under scenario | |
| Capacity disruption probability at the national warehouse / region / department / vaccination center in period under scenario | |
| Capacity degradation factor at the national warehouse / region / department / vaccination center under scenario | |
| Decision variables | |
| Quantity of national order of vaccine at period under scenario | |
| Quantity of vaccine transferred to region / department / vaccination center at period under scenario | |
| Quantity of vaccine transshipped from region to region / department to department at period under scenario | |
| Inventory of vaccine at national warehouse / region / department / vaccination center at the end of period under scenario ; , , , | |
| Number of individuals of risk class from demand point that receive their first/second dose of vaccine at vaccination center at period under scenario | |
| Cumulative number of unvaccinated individuals of risk class from demand point at the end of period under scenario ; | |
| Cumulative number of first/second-dose vaccinated individuals of risk class from demand point at the end of period under scenario ; , (first-dose vaccinated individuals still wait to receive the second dose of the same vaccine) | |
| 1 if a national order is placed for vaccine at period | |
| 1 if capacity level is considered at national warehouse / region / department / vaccination center for vaccine | |
3.2. Objective functions
The objectives of the proposed model are minimizing the total distribution cost and minimizing the expected total number of deaths during the vaccination campaign. In the following, these objectives are explained in detail.
3.2.1. Minimizing the total distribution cost
The cost objective function of the proposed model under scenario , , is formulated as (1). Different terms of are, respectively, the fixed and variable costs of ordering vaccines, fixed cost of equipping the national warehouse, fixed cost of equipping regional and departmental warehouses, fixed cost of opening vaccination centers, variable cost of transferring vaccines to regional and departmental warehouses as well as vaccination centers, variable cost of transshipping vaccines between regions and between departments, inventory holding cost of vaccines at different storage points (i.e., regions, departments, and vaccination centers), the vaccination cost of the individuals, and finally the mean hospitalization cost of unprotected (unvaccinated) or semi-protected (single-dose vaccinated) individuals in case of infection. We consider that completely protected individuals (double-dose vaccinated) will not need to be hospitalized in case of any symptomatic/asymptomatic infection.
| (1) |
3.2.2. Minimizing the expected total number of deaths
The total number of deaths is approximated as a percentage (i.e., death rate) of the total number of infected individuals. To calculate the total number of infections, we first categorize the population into unvaccinated, single-dose, and double-dose vaccinated groups. The death rate differs among these three groups due to the level of immunization that different doses of vaccines provide. We approximate the total number of infections through a mutual interaction among the three groups as depicted in Fig. 2 , where the arrows represent mutual infections. These three groups are mutually interacting, and they are all potential virus carriers. However, each group has a different contamination potential (transmission probability) depending on the number of doses they have received (i.e., double-dose vaccinated are less contaminating than single-dose and unvaccinated ones).
Fig. 2.
Mutual infection among three categories of individuals.
The objective function (2) estimates the expected total number of deaths under each scenario due to nine mutual infections in Fig. 2. This objective function includes three main parts representing three sources of infection (i.e., unvaccinated, single-dose vaccinated, and double-dose vaccinated groups). Each part consists of three components representing the three groups exposed to infection (unvaccinated, single-does vaccinated, and double-dose vaccinated). For instance, the first part of approximates the total number of deaths that unvaccinated individuals impose on society. Inside this part, the first to the third components represent the expected total number of deaths among unvaccinated, single-dose, and double-dose vaccinated individuals. The total number of deaths among single-dose and double-dose vaccinated individuals, respectively, decreases with rates and (i.e., ) compared to the unvaccinated individuals.
| (2) |
3.3. Constraints
The constraint body of the proposed model consists of four main types of constraints: 1) constraints to monitor the level of inventory in warehouses at each period at different points of the network, 2) constraints to monitor the number of unvaccinated, single-dose, and double-dose vaccinated individuals at each period, 3) capacity constraints on the number of affected vaccines, and 4) constraints to control the congestion of individuals in vaccination centers.
In this paper, we assume that the inventory and the capacity of warehouses in the network are subject to partial disruptions, and their levels stochastically degrade to a lower level. Some vaccines at the end of each period are destroyed in inventories due to unexpected events (e.g., the temperature variation of refrigerators/freezers, human errors when storing the vaccines, etc.), and only a part of the inventory is transferred to the next period. In another situation, the nominal capacity of the warehouses might be disrupted in particular periods, and the capacity of warehouses for those periods becomes partially unavailable (degraded to a lower level). In case of capacity degradation, the vaccines’ entering flow will exceed the warehouses’ nominal capacity by specific probabilities. It is desirable to guarantee that the probability of such a violation be lower than a given level. Considering disruption parameters in Table 2, the inventory and the capacity of warehouses are degraded to a lower level with corresponding coefficients and , respectively. The inventories and the capacities of warehouses are then variables and follow a uniform distribution. Depending on the value of disruption parameters, they vary between a degraded level up to their nominal values.
In the following, Constraints (3)–(6) represent the inventory level at the end of each period at national, regional, and departmental warehouses and vaccination centers, respectively. As it can be seen, the inventory of each warehouse at the end of period is degraded by a coefficient for period .
| (3) |
| (4) |
| (5) |
| (6) |
Constraints (7)–(14) are the capacity constraints, where Constraints (7) and (8) restrict the number of ordered vaccines that the national warehouse can receive to the minimum value between the available inventory capacity and the maximum supply capacity of vaccines’ manufacturers. Constraints (9)–(12) limit the level of inventories to a maximum capacity level at national, regional, and departmental warehouses as well as the vaccination centers. Constraint (13) ensures that vaccines should be delivered only to open/equipped vaccination centers. As it can be seen in Constraints (7)–(13), the nominal capacity of each warehouse probabilistically degrades to a lower level by coefficient for period . Finally, Constraints (14)–(17) represent how a single capacity level can be established at different network points. More precisely, Constraint (17) ensures that, at most, a single level of capacity can be established at each vaccination center for a particular vaccine.
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
Constraints (18)–(20) not only calculate the number of unvaccinated, single-dose vaccinated, and double-dose vaccinated individuals at the end of each period, respectively, but also they guarantee that the individuals of each demand point can get vaccinated in a vaccination center if they are under the coverage of that center. Moreover, Constraint (21) ensures that the single-dose vaccinated individuals should receive their second dose after periods. Constraint (22) guarantees that the sum of the unvaccinated, single-dose vaccinated, and double-dose vaccinated individuals at each period should be less than the corresponding population.
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
Constraint (23) controls the congestion of individuals at vaccination centers. It ensures that the mean waiting time of individuals at vaccination centers (see Section 3.4) must be less than a given threshold, where is the maximum allowable waiting time at vaccination center to avoid the spread of the disease, and the variable represents the mean waiting time of individuals to get vaccinated at vaccination center in period under scenario . Finally, Constraints (24) and (25) are the integrity constraints of the decision variables.
| (23) |
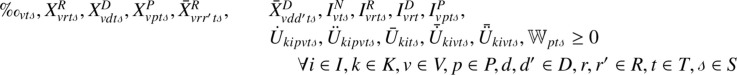 |
(24) |
| (25) |
3.4. Capacity determination & service disruption at vaccination centers
Sanitary rules highly recommend social distancing and not staying long in crowded areas since any congestion may disrupt the vaccination process, if not increasing the probability of possible infections. In this situation, the vaccination centers should be established with an appropriate vaccination capacity [47]. This paper considers that individuals from different demand points refer to vaccination centers, and they have to wait in a queue if the center is busy, as illustrated in Fig. 3 .
Fig. 3.
Congestion of individuals with different classes of risk at vaccination centers.
This waiting mainly depends on the arrival rate of each risk class of individuals at the vaccination centers and the rate at which these individuals are vaccinated. Since the inter-arrival time between the two arrivals and the vaccination time of different individuals are not deterministic and are distributed around a mean value, it is essential to include the variability in time and its distribution while evaluating the performance indicators that account for the congestion in the vaccination centers (e.g., waiting time). The vaccination time varies depending on each person’s health status since an initial analysis should be done to check each individual’s eligibility for vaccination, and this analysis may differ from one person to another. Most of the studies in the literature model the congested centers as a queuing system with arrival and/or service rates with Poisson distributions (i.e., M/D/c and M/M/c queuing systems) [50], [51], [52]; however, the stochastic demand for vaccination may impose a high degree of uncertainty on the arrival rate of the individuals. This phenomenon becomes very evident in a mass vaccination.
Therefore, we model each vaccination center as a multiserver GI/G/c queue [53]. The inter-arrival times between the individuals of each risk class at period , , are given by a random variable with general distribution and a mean of . The service times are random variables with general distribution and a mean of . There is a queue of infinite size at each vaccination center, wherein the individuals are served in a first-come-first-served (FCFS) rule. At a vaccination center , parallel vaccination lines vaccinate the individuals, and each line vaccinates only one person of each risk class at a time and devotes all of its resources to complete the vaccination.
We also consider that vaccination lines are subject to random disruptions (e.g., emergencies, unexpected reactions of individuals due to vaccination, vaccine destruction, etc.), which affect the vaccination rate at vaccination centers. Accordingly, the vaccination lines at vaccination center stochastically fail with rate . Consequently, the inter-arrival time of failures in vaccination center is exponentially distributed with a mean of . Once a failure occurs, the vaccination process is completely interrupted, and the process is stochastically retrieved with rate . Hence, the mean availability of vaccination center is [54]. After incorporating the congestion of vaccination centers, Constraint (23) can be re-written as Inequality (26) that limits the waiting time of individuals (i.e., the left-hand side of the inequality) to the maximum threshold . The details of calculating the waiting time have been provided in Appendix A.
| (26) |
Inequality (26) is nonlinear, and it is impossible to import it to the proposed model directly. To cope with this non-linearity, an enumeration technique is used [55] to replace this inequality with the linear Constraint (27), where is a parameter. The procedure of the enumeration approach to obtain Constraint (27) has been provided in Appendix B.
| (27) |
4. Robust counterpart model
In this section, two robust optimization approaches are used not only to cope with the uncertainty of the input parameters but also to convert the proposed bi-objective model into a single-objective model by representing the objective function (1) as a set of constraints and keeping the objective function (2) as the main objective of the model. The reason is that a VDN is not a business network with a cost minimization objective. Hence, minimizing the total number of deaths is more important than cost issues; however, the cost of the network is controlled through constraints.
A classical way of handling uncertainty is to estimate the probability distribution of uncertain parameters. However, different factors may affect the parameters’ uncertainty, and thus collecting historical data and estimating the probabilities become difficult (if not impossible) tasks. This paper employs robust optimization methods that do not need to estimate probabilistic information. Furthermore, the uncertainties are defined in scenarios with a particular occurrence probability. To cope with the uncertainty in the proposed model, we adopt two robust optimization approaches: 1) the -robustness concept [51], [56], wherein the relative regret in each scenario should be less than a constant , and 2) the loss-function based robust optimization approach proposed by [57], [58], where the sum of the mean and the variability of the objective values are optimized. These approaches are used to handle the uncertainty of the first and the second objective functions, respectively.
Applying the -robustness approach converts the objective function (1) to the following set of constraints (28). Accordingly, the proposed bi-objective model of Section 3 is converted to a single-objective model. However, changing the value of obtains the frontier of the Pareto solutions.
| (28) |
where is the desired robustness level in scenario and is the optimal value of the objective function (1) under scenario , which can be obtained by solving the proposed model of Section 3 with only the first objective function and the whole body of the constraints. Constraint (28) actually ensures that the cost of any scenario should not exceed of the optimal cost of the corresponding scenario, .
To handle the uncertainty in the second objective function based on [57], the robust counterpart objective function is developed as a minimization objective with multiple scenarios. In this regard, first, consider the following linear optimization model (29).
| (29) |
Considering the parameters , , and as well as decision variable to be related to the scenarios, the robust model can be expressed as model (30)
| (30) |
Functions and account for the expected value and the violation of the objective function under different scenarios, respectively. The latter is also called the feasibility penalty function, which is used to penalize violations of the constraints under some scenarios. These functions can be formulated as Eqs. (31) and (32).
| (31) |
| (32) |
where is the probability of scenario and is the variable objective function under scenario (i.e., ), and is the degree of importance of variability compared to the mean value. In fact, the higher the value of , the lower the variability among the objective function values in different scenarios. Eq. (32) is a quadratic penalty function that addresses both positive and negative violations. Finally, the robust counterpart of the second objective function (2) can be presented as (33).
| (33) |
4.1. Linearization
The objective function (33) is nonlinear due to two terms: the product of variables in the objective function (2) (), and the absolute term in the robust counterpart of represented as the objective function (33). The linearization of objective function (33) has been provided in Appendix C. After linearization, the robust counterpart optimization model of the proposed robust model is, finally, provided as follows:
| (34) |
s.t.: Constraints (3)–(22), (24), (25), (27), (28), (50), and (51); where is calculated through Eq. (35)
| (35) |
5. Experimental design
To assess the effectiveness of the proposed model and the robust solution approach, we applied them to a real case study in metropolitan France to distribute the COVID-19 vaccines under disruptions and uncertainty. In the following, the case study is first described, then, the disruption/uncertainty scenarios are designed and explained.
5.1. Case study description
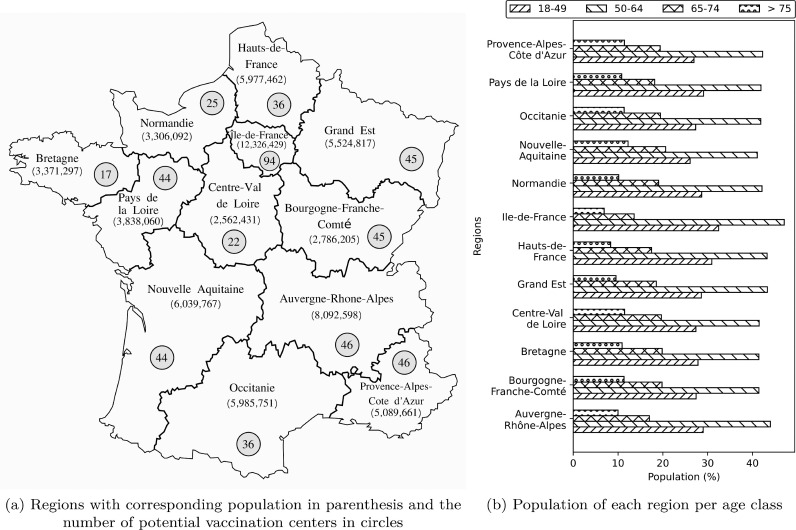
The case study represents the VDN in metropolitan France for distributing the COVID-19 vaccines and planning the vaccination of the individuals living in France. The total population of metropolitan France (not including oversea regions) is about 65,249,843 in 2021 [59], which is spread over regions and departments. The country includes 34,967 cities, among which the 300 most populous cities are selected to represent the demand points (i.e., ). These selected 300 cities possess the minimum requirements for establishing vaccination centers. The population of other cities has been merged into the population of the selected cities based on their proximity. More than 2400 potential centers have been identified for vaccination, among which we have selected centers that can be equipped to store different types of vaccines. The selected centers include both medical and even a set of social centers. The fixed cost of opening/equipping vaccination centers depends on their inherent tasks. This fixed cost is normally higher for equipping social centers than medical centers.
Fig. 4 a depicts different regions of France metropolitan, with their corresponding populations in parentheses and the number of potential points in each region to establish the vaccination centers. In addition, Fig. 4b provides the detail of the population in each region by different age groups. The total population is classified into risk classes based on their age. As can be seen, in all the regions, the majority and the minority of the population belong to the second () and the fourth () age groups, respectively. In this case study, approved and available vaccines have been considered, including “Pfizer-BioNTech” (Pfizer), “Moderna”, “AstraZeneca/Oxford” (AstraZeneca), and “Johnson&Johnson” (J&J).
Fig. 4.
The case study information on each province.
Table 3 provides the information regarding each age group, including the age interval (), the death rate (), infection rate (), the number of possible contact cases (), eligible vaccines (), hospitalization cost (), and vaccination cost (). It is worth mentioning that differs from one demand point to another, and people are likely to have a higher number of contacts in the populated areas. Table 4 shows the information related to each vaccine, including the type of vaccine (), whether each vaccine requires single or multiple doses (), first- () and second-dose () effectiveness against the original variant of the COVID-19 (D614G [60], [61], [62]), time lag between two injections (), purchase cost (), unit holding cost (), unit transportation cost (), delivery lead-time (), delivery trust rate (), and supply capacity ()). Furthermore, different vaccines require specific modes of storage. For instance, Pfizer and Moderna should be stored in ultra-cold freezers between [80 C, 60 C] and [50 C, 15 C], respectively. On the other hand, AstraZeneca and J&J should be stored in refrigerators between [2 C, 8 C]. The price of refrigerators and ultra-cold freezers also varies from 5k€ to 15k€. In addition, depending on the size of refrigerators/freezers and the package size of the vaccines, they can store 2000 to 300,000 doses of different vaccines.
Table 3.
Information on each risk class of population.
| (€) | (€) | |||||
|---|---|---|---|---|---|---|
| 18–49 | X | 4X | [15,50] | Pfizer-BioNTech, Moderna | 1500 | 2 |
| 50–64 | 3X | 6X | [10,35] | All | 3000 | 3 |
| 65–74 | 7X | 5X | [5,25] | All | 6000 | 5 |
| 13X | 8X | [2,10] | All | 7000 | 5 |
Table 4.
Information on vaccines.
| (%) | (%) | (week) | (€) | (€ / km) | (week) | (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Pfizer-BioNTech | 1 | 85 | 92 | 4 | 20 | 8 | 5 | 4 | 80 | 4 M |
| Moderna | 1 | 80 | 95 | 4 | 35 | 13 | 5 | 4 | 75 | 1.5 M |
| AstraZeneca | 1 | 64 | 74 | 4 | 4 | 1 | 2 | 2 | 90 | 3 M |
| J&J | 0 | 72 | – | – | 10 | 2 | 2 | 4 | 70 | 1 M |
Two capacity levels () are considered for all storage capacities throughout the network. At the national level, the storage capacity for each vaccine is considered to be 5 M and 10 M doses at the first and second levels of capacity, respectively. These capacity levels (min-max) for regional and departmental warehouses are 200k–400k and 50k–100k, respectively. We have also considered two capacity levels (i.e., 2000, 4000) for both refrigerators and freezers in the vaccination centers. The fixed cost of establishing a particular capacity level at national, regional, and departmental warehouses and the fixed cost of opening/equipping the vaccination centers relate directly to their capacity levels (i.e., the number of refrigerators/freezers that should be utilized). Furthermore, the destruction rates of vaccines (i.e., , , and ) are generated randomly from the interval .
In terms of congestion parameters, we consider that the nominal vaccination rate follows a general distribution with a mean of 20 () per period (i.e., 8 h), and each individual should not spend more than 30 min in the vaccination center (i.e., ). In addition, each vaccination center includes 8 to 10 vaccination lines that vaccinate the individuals in parallel (i.e., ). On the other hand, each vaccination center stochastically fails with rate uniformly distributed in per period. Once failed, they retrieve their normal activity with rate uniformly distributed in per period. It is worth mentioning that the proposed queuing-based method in Section 3.4 is not integrated into the mathematical model. However, it performs as a pre-processing step and only approximates the values of of the vaccination centers a priori.
5.2. Uncertainty/disruption scenarios
This section defines different scenarios to consider the uncertainty of input parameters and the disruption at different network components. Based on the government’s report, three main aspects that affect the progress of the pandemic and the performance of the VDN are quarantine restrictions, the emergence of new variants of the disease with higher transmission and mortality rates, and any disruption in the network especially delays in the delivery of the vaccines. Any structural disruption in the network, including inventory/capacity/vaccination service degradation, must also be considered. We consider two levels (i.e., 0 and 1) for each of these aspects as follows:
-
•
Quarantine: is 1 if the government has imposed a quarantine restriction; 0 otherwise. In case of a quarantine restriction, the affected parameters are the possible number of contacts (), the death rate (), and the infection rate (). In fact, when a person is in contact with fewer people under a quarantine restriction, the infection rate and consequently the death rate decrease.
-
•
Variants: is 1 if a new higher-transmissible variant of the virus emerges; 0 otherwise. In this case, the infection rate and consequently the death rate increase. More importantly, the effectiveness of the vaccines (i.e., first and second doses) decreases, which leads to a higher propagation of the virus among the population compared to the original variant of the virus.
-
•
Disruption: is 1 if any disruption occurs in the network; 0 otherwise. In case of disruption, we assume that a set of parameters are degraded to a lower level, and this degradation directly affects the availability of the vaccines in the network. These parameters include trust rate on the quantity of the vaccines (), delivery lead-time of vaccines (), maximum supply capacity of vaccines from vaccine manufacturers (), amount of inventory, and the storage capacity at different points of the network (i.e., national/regional/departmental warehouses and vaccination centers), and vaccination rate ().
To account for the above-mentioned uncertainty/disruption aspects, a set of (i.e., ) scenarios are defined (i.e., we have three aspects and two levels for each). Each scenario is presented in the form of a tuple as , where , , and stand for Quarantine, Variants, and Disruption aspects, respectively. Table 5 represents the set of all scenarios and the proportional level of corresponding parameters at each scenario compared to the basic scenario Sc1 (first row of Table 5): .
Table 5.
Uncertainty/disruption scenarios and the proportional level of parameters based on the basis scenario.
| Sc. |
Aspects levels |
Parameters level |
||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # | ||||||||||||||||||
| 1 | 0.10 | 0 | 0 | 0 | X | X | X | X | X | X | X | X | X | X | X | X | X | X |
| 2 | 0.15 | 0 | 0 | 1 | X | X | X | 0.6X | 0.8X | 2X | 0.7X | 3X | 0.8X | 1.5X | 2X | 0.8X | 2X | 0.6X |
| 3 | 0.10 | 0 | 1 | 0 | 2X | X | 4X | X | X | X | X | X | X | X | X | X | X | X |
| 4 | 0.15 | 0 | 1 | 1 | 2X | X | 4X | 0.6X | 0.8X | 2X | 0.7X | 3X | 0.8X | 1.5X | 2X | 0.8X | 2X | 0.6X |
| 5 | 0.10 | 1 | 0 | 0 | 0.5X | 0.1X | 0.5X | X | X | X | X | X | X | X | X | X | X | X |
| 6 | 0.15 | 1 | 0 | 1 | 0.5X | 0.1X | 0.5X | 0.6X | 0.8X | 2X | 0.7X | 3X | 0.8X | 1.5X | 2X | 0.8X | 2X | 0.6X |
| 7 | 0.10 | 1 | 1 | 0 | 0.8X | 0.1X | X | X | X | X | X | X | X | X | X | X | X | X |
| 8 | 0.15 | 1 | 1 | 1 | 0.8X | 0.1X | X | 0.6X | 0.8X | 2X | 0.7X | 3X | 0.8X | 1.5X | 2X | 0.8X | 2X | 0.6X |
The value of the affected parameters has been presented throughout this section, except for disruption parameters in Table 2. In this regard, the value of disruption parameters , , , and for the basis scenario belong to the intervals [0.05,0.10], [0.90,1.00], [0.10,0.20], and [0.80,1.00], respectively. Based on the identified value of disruption and congestion parameters, the values of are calculated based on the queuing system developed in Section 3.4.
6. Numerical results and discussions
This section presents the numerical results of applying the proposed robust model (i.e., objective function (34) and its corresponding constraints) to the real case study of Section 5.1. In this regard, the desired robustness levels in Constraint (28) are considered to be [0.4,0.4,0.2,0.2,0.4,0.4,0.3,0.3] and the value of in objective function (34) is considered to be 0.5. Regarding the robustness levels, a higher value of is considered for the scenarios that seem less expensive in terms of cost. The proposed robust model has been implemented in Python 3.7 and solved using Gurobi 9.1, with 8 Intel processors and 32G of RAM running at 2.3 GHz. We use a barrier method to solve each linear program, with a barrier convergence tolerance of . Solving the proposed model took around 20 h to find the optimal solution.
In the following, the results are provided in Sections 6.1–6.5, and all the results are presented in %. The real values will not be reported, since the main goal throughout this section is to compare different scenarios and extract managerial insights from the results.
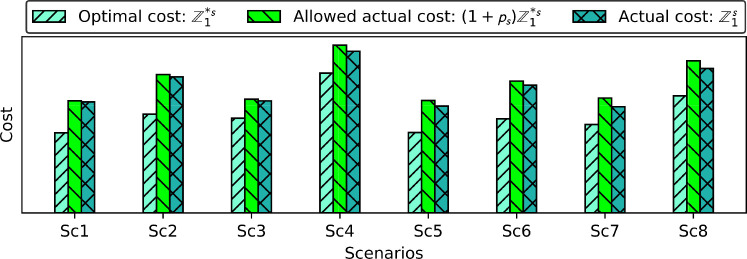
6.1. Optimal cost vs. actual cost
The first result of this paper deals with comparing the optimal cost of each scenario () with its actual cost (). The actual cost is the total cost of each scenario when the objective function (34) is optimized. The difference between the actual cost and the optimal cost () is typically called the robustness cost; the extra cost spent to make a solution robust. In this paper, the extra robustness cost is charged to the network to go from a cost-oriented VDN to a resilient vaccination-oriented VDN to probable uncertainty and disruption.
By making pair comparisons between scenarios (Sc1, Sc5), (Sc2, Sc6), (Sc3, Sc7), and (Sc4, Sc8) in Fig. 5 , it can be seen that the optimal and the actual costs of scenarios Sc1, Sc2, Sc3, and Sc4 are correspondingly higher than the actual cost of scenarios Sc5, Sc6, Sc7, and Sc8. This reveals that in a situation without quarantine restriction (i.e., scenarios Sc1, Sc2, Sc3, and Sc4) – where the individuals will have higher contact with each other and the virus is transmitted rapidly – a higher cost is charged to the network to either accelerate the vaccination or increase the capacity of the vaccination campaign by opening/equipping more vaccination centers or even establishing national, regional, and departmental warehouses and the vaccination centers with a higher capacity level. In this regard, the extra cost of hospitalization in case of more infections should also be considered. The cost savings thanks to imposing quarantine restrictions are 4%, 5%, 6.5%, and 12% for the pair comparisons (Sc1, Sc5), (Sc2, Sc6), (Sc3, Sc7), and (Sc4, Sc8), respectively. It can then be postulated that imposing quarantine restrictions will be more efficient in case of new disease variants.
Fig. 5.
Optimal cost of each scenario vs. Actual cost.
Furthermore, by making pair comparisons between scenarios (Sc1, Sc2), (Sc3, Sc4), (Sc5, Sc6), and (Sc7, Sc8), it is observed that the cost of scenarios Sc2, Sc4, Sc6, and Sc8 is significantly higher than the cost of scenarios Sc1, Sc3, Sc5, and Sc7, respectively. The cost differences (i.e., robustness costs) are 22.5%, 44.5%, 19.5%, and 36% for the corresponding comparisons. These differences reveal the impact of disruption in terms of costs on the VDN. As it can be seen, the paired comparison (Sc3, Sc4) represents the highest difference since both scenarios belong to a situation when new variants of the virus have appeared with higher transmissibility, while Sc4 is the scenario under disruption. Therefore, it can be deduced that, in the case of new variants of the virus with a higher transmission rate, any disruption in the network causes a high extra cost to the network. Similar to scenarios Sc3 and Sc4, both Sc7 and Sc8 represents a situation with new variants of the virus but under a quarantine restriction with a cost difference of 36%.
Therefore, by comparing the pair scenarios (Sc3, Sc4) with (Sc7, Sc8), it can be concluded that establishing a quarantine restriction can decrease the actual cost of the network by limiting the social contacts. Consequently, the virus spread among the population. In our case study, the quarantine restriction decreases the actual cost up to 8.5% (44.5% - 36%).
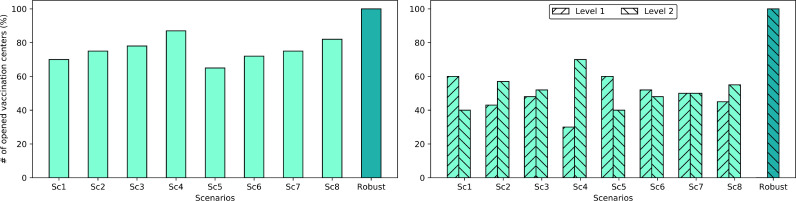
6.2. Number of opened/equipped vaccination centers
Fig. 6 illustrates the number of opened/equipped vaccination centers (% per total number of potential centers) in different scenarios of Table 5 and the number of opened/equipped vaccination centers of the robust model. In Fig. 6, scenarios {Sc1, Sc2, ..., Sc8} represent the results with the optimal value of the cost objective function (1) (, {Sc1, Sc2, ..., Sc8}), and the “Robust” scenario represents the result of the robust model with the optimal value of the robust objective function (34) (). Fig. 6a and b depict the total number of opened/equipped vaccination centers and the number of opened/equipped vaccination centers with different capacity levels, respectively.
Fig. 6.
Number of vaccination centers opened in different scenarios ().
As can be seen in Fig. 6a, depending on the scenario, different numbers of vaccination centers have been opened/equipped in each of the scenarios {Sc1, Sc2, ..., Sc8}, where the minimum and the maximum numbers belong to scenarios Sc5 and Sc4 with 65% and 87%, respectively. As an initial insight, there is no need to open/equip all the (100%) vaccination centers since the objective function (1) is a cost-oriented objective with a focus more on the fixed and variable costs of designing the VDN and a lesser focus on a mass vaccination that may require the highest number of vaccination centers.
Under scenario Sc5 with , the minimum number of vaccination centers need to be opened/equipped. The reason goes back to the fact that scenario Sc5 is the safest scenario in case of the total number of deaths since the individuals have the least contact with each other due to the quarantine restriction, a virus with a lower transmission rate circulates, and the vaccination campaign operates at its maximum capacity without any disruption. Therefore, there would be no need to open/equip more centers to accelerate the vaccination or compensate for the disruptions. On the other hand, the maximum number of opened/equipped centers belongs to scenario Sc4 with , which represents the worst situation of the pandemic without quarantine restrictions, with new variants of the virus with a higher transmission rate, and disruptions in the network. In this situation, more vaccination centers must be opened/equipped to vaccinate more individuals to avoid hospitalization costs (the last two parts of the objective function (1) and the increasing total number of deaths.
Despite scenarios {Sc1, Sc2, ..., Sc8}, 100% of the potential vaccination centers have been opened/equipped in the “Robust” scenario. This is logical since, in the “Robust” scenario, the goal is a mass vaccination of the population. Consequently, the maximum possible number of potential vaccination centers tends to be opened/equipped for this aim. It is worth mentioning that opening/equipping a higher number of vaccination centers in the “Robust” scenario depends on the desired robustness levels that allow for expending more funds to open/equip more vaccination centers. With the considered values in our case study, the proposed model is allowed to open/equip the entire number of vaccination centers if necessary.
Finally, Fig. 6b distinguishes the capacity levels of the opened/equipped vaccination centers. For instance, in scenario Sc1, among the 70% of the opened/equipped vaccination centers, 60% and 40% of the centers have been opened/equipped with capacity levels 1 and 2, respectively. These values are 30% and 70% for Sc4. On the other hand, in the “Robust” scenario, 100% of the opened/equipped vaccination centers have been established with capacity level 2 to utilize the maximum possible capacity for mass vaccination.
By making a comparison among scenarios in both Fig. 6a and b, an overall insight is that whenever new variants of the virus with higher transmission rates emerge or the VDN is exposed to disruptions, the proposed model tends not only to open/equip a higher number of vaccination centers, but it also opens/equips the centers with a higher capacity level. This phenomenon happens for two reasons; first, fighting against new variants of the virus with a higher transmission rate requires accelerating the vaccination and, consequently, a higher number of vaccination centers; and second, absorbing the degradation impact of the disruption in the network requires establishing the vaccination centers with higher capacity levels. Moreover, among disruptions and the emergence of new variants of the virus, the latter shows a higher impact on the number of opened/equipped vaccination centers with an 11% of increase compared to a 7% of increase due to disruptions.
6.3. Quantity of vaccines ordered
This section aims to discuss how the orders of different vaccines should be placed in different scenarios when solving the proposed robust model. Fig. 7 shows the total order (Fig. 7a) and the exact order of each vaccine (Fig. 7b) placed in each scenario. As shown in Fig. 7a, there is a meaningful difference between the order of vaccines under scenarios Sc2, Sc4, Sc6, and Sc8, respectively, compared with scenarios Sc1, Sc3, Sc5, and Sc7. The main reason is the disruption in scenarios Sc2, Sc4, Sc6, and Sc8. Obviously, in case of disruption, the network encounters a set of challenges as 1) the storage capacity throughout the network is degraded to a lower level, 2) a higher percentage of the vaccines might be destroyed/lost both through transportation or storage operations, and 3) vaccine suppliers may exceed their commitments in three ways: they may supply fewer vaccines than ordered, but on time; they may deliver the same number of vaccines as ordered, but with a delay, or they may deliver fewer vaccines even with a delay. The last challenge has happened several times to the vaccination campaign in France and has had a negative impact on its performance.
Fig. 7.
Total proportional order of vaccines at different scenarios.
Accordingly, under scenarios Sc2, Sc4, Sc6, and Sc8, a threefold decision is made by the proposed model: 1) the storage centers (i.e., national/regional/departmental warehouses and vaccination centers) are set up with a higher capacity level to cancel out the impact of capacity degradation as well as vaccine destruction, 2) a higher quantity of vaccines is ordered from suppliers in earlier periods to avoid the impact of the suppliers’ inability, or simple failure, to deliver the ordered quantity on time, and 3) the orders are given to those suppliers presenting a higher trust rate. The third decision can be observed in Fig. 7b, where in scenarios Sc2, Sc4, Sc6, and Sc8, the contribution of Moderna and Pfizer to the total order is significantly higher compared to other vaccines. In addition, the J&J vaccine has not been ordered in these scenarios. Indeed, in our case study, we have assumed that the suppliers of Moderna, Pfizer, and AstraZeneca vaccines have a higher trust rate with fewer delivery times than J&J.
Another insight can be extracted from Fig. 7b by comparing the contribution of different vaccines to the total order from scenarios Sc1 and Sc5 to scenarios Sc3 and Sc7, respectively. These scenarios are disruption-free scenarios, and from scenarios Sc1 to Sc3 and from Sc5 to Sc7, only the impact of new variants of the virus can be investigated on the contributions of different vaccines to the total order. In scenarios Sc1 and Sc5, where no new variants of the virus have emerged, the contribution of all the vaccines are almost identical since all the vaccines have high effectiveness against the original variant of the virus with a lower transmission rate. However, in scenarios Sc3 and Sc5, where new variants of the virus with higher transmission rates emerge, the contribution of the Moderna and Pfizer vaccines increase significantly since they are more effective and provide higher protection against most of the variants of the virus compared with other vaccines.
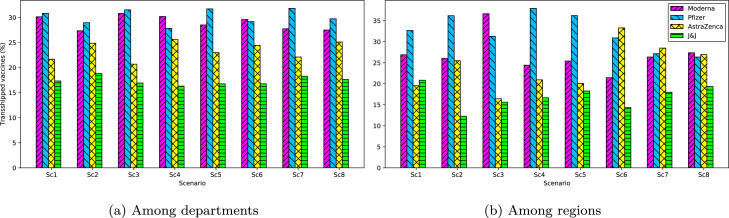
6.4. Transferred and transshipped quantities of vaccines
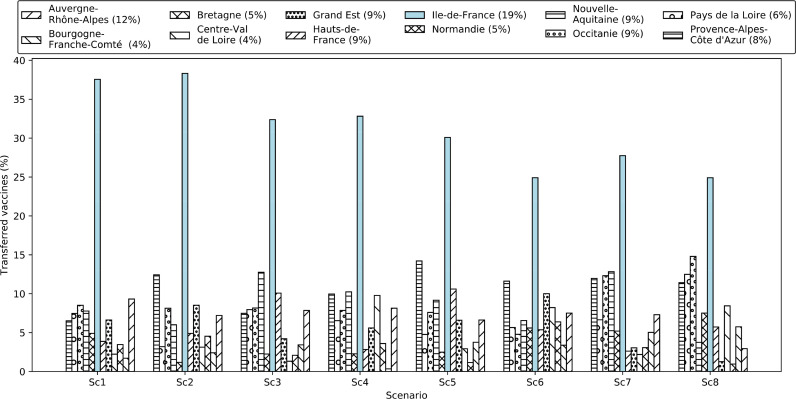
This section aims at studying the total quantity of vaccines transferred (%) to different regions (Fig. 8 ) as well as the transshipped quantity (%) of different vaccines among departments (Fig. 9 a) and regions (Fig. 9b). As shown in Fig. 8, the number of vaccines transferred to different regions is significantly different. We realized that this quantity depends on several factors, including the total population of the region, the population of different risk classes in each region, the number of possible contacts for each member of the population in each region, the emergence of the new variants of the virus with a higher transmission rate, and the quarantine restrictions in place. The following set of rules was obtained from the results: 1) the higher the total population (of high-risk classes) of a region, the higher the number of vaccines transferred to that region, 2) the higher the number of possible contacts of individuals in a region, the higher the number of vaccines transferred to that region, 3) the higher the transmission rate of the virus in a region, the higher the number of vaccines with higher effectiveness transferred to that region, and 4) the tighter the quarantine restrictions in a region, the lower the number of vaccines transferred to that region.
Fig. 8.
Quantity of vaccines (%) transferred to each region in each scenario (see scenarios separately). The percentage of the population in each region to the total national population has been provided in parentheses in the legends.
Fig. 9.
Quantity of vaccines (%) transshipped in each scenario.
It can be observed from Fig. 8 that the total quantity of vaccines transferred to the “Île-de-France” region is the highest compared to other regions, since the “Île-de-France” region alone possesses 19% of the total population. The population-to-surface ratio in this region is also high, which leads to an increased number of contacts among all risk classes. The “Provence-Alpes-Côte d’Azur” is another region that received a high quantity of vaccines compared to other regions (except “Île-de-France”). It only represents 8% of the total population, but it has other conditions, as mentioned above, to receive a higher quantity of vaccines. Accordingly, the quantity of vaccines allocated to each region does not depend only on the region’s potential demand (population). This relationship will be discussed further in Section 7.
Finally, Fig. 9a and b illustrate the quantity (%) of vaccines transshipped among departments and regions, respectively. At the level of departments, Moderna and Pfizer vaccines make a higher contribution to the total transshipment compared to AstraZeneca and J&J. We observed that some departments with higher storage capacities also played the role of intermediate warehouses for other departments. In fact, the transportation cost of transferring the vaccines with higher transportation costs (e.g., Moderna and Pfizer) from a regional warehouse to two different but close (in terms of distance) departmental warehouses become more expensive than transferring a higher volume of vaccines from the regional warehouse to the closest departmental warehouse then transshipping the vaccines from this department to the second department. The same behavior was also observed at the level of regional warehouses. This phenomenon allows the transportation cost of vaccines through the network to be reduced.
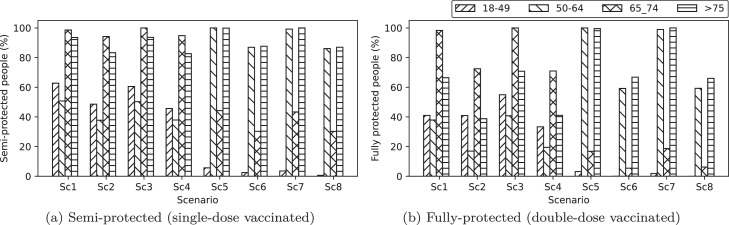
6.5. Single‐dose and double‐dose vaccinated individuals
Fig. 10 shows the number of individuals (%, proportional to the population of each class) from different risk classes that have received their first and second doses of vaccination. Interestingly, it can be observed from both Fig. 10a and b that the priority of vaccination is not simply based on the age of the individuals (i.e., risk classes) but also on other factors, including the total population, death rate, number of contacts, the effectiveness of the available vaccines, new variants of the virus, and the quarantine restrictions. For instance, as the number of possible contact cases increases for a particular risk class, the population of that risk class gets a higher vaccination priority. Another set of rules also relates vaccination priority to the model’s parameters. With this aim in mind, in Section 7, we will discuss how these factors affect the prioritization of vaccination among different risk classes of the population.
Fig. 10.
Vaccinated individuals (%) with different risk classes (proportional to their population) in each scenario.
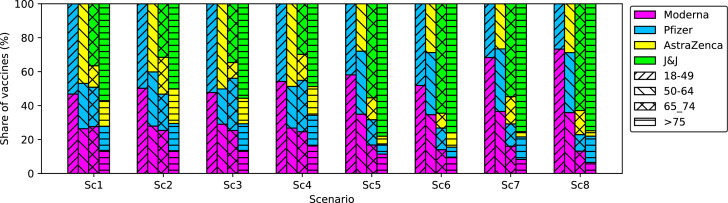
It would also be interesting to see how different vaccines contribute to the vaccination program. In this regard, Fig. 11 illustrates the contribution of each vaccine to the first-dose vaccination of the population in different risk classes and under different scenarios. It is observed that in a situation without any quarantine restrictions (i.e., scenarios Sc1 to Sc4), the contribution of vaccines with higher effectiveness (i.e., Moderna and Pfizer) is higher compared to other vaccines with lower effectiveness (i.e., AstraZeneca and J&J). The reason is linked to the fact that without quarantine restrictions, the effort is to use the vaccines that decrease the total number of deaths and effectively restrict the circulation of the virus. Accordingly, highly effective vaccines are recommended for use if the government does not tend to establish quarantine restrictions. On the other hand, in the case of quarantine restrictions, the contribution of vaccines with lower effectiveness becomes higher. The main effort will then be vaccinating the individuals with a probable higher death rate to decrease the number of hospitalizations.
Fig. 11.
Share of different vaccines (%) at the first-dose vaccination of each risk class of individuals.
6.6. Sensitivity analyses
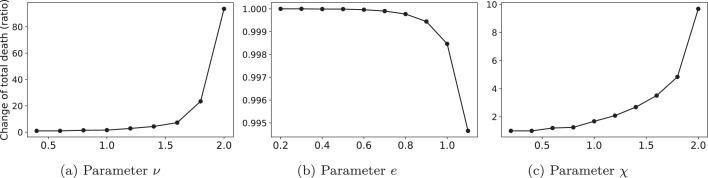
In this section, we conducted two sets of experiments. First, we investigate the sensitivity of the total number of deaths and the number of first-dose vaccinated individuals of different risk classes to specific parameters of the VDN, including the maximum capacity of the warehouses (i.e., ), delivery lead-time of vaccines (i.e., ), time lag between the first- and the second-dose vaccination (i.e., ), and trust rate on the quantity of vaccines delivered by the manufacturers (i.e., ). Second, we show the sensitivity of the total number of deaths to pandemic parameters, including death rate (i.e., ), vaccination effectiveness (i.e., ), and the number of possible social contacts (i.e., ). The results of the first sensitivity analyses have been depicted in Fig. 12 a–d, respectively. In addition, Figs. 13 a–c show the results of the second sensitivity analysis. In all figures, the -axis shows the change (ratio) of parameters compared to their actual value (i.e., label “1.0” of the -axis) in the case study. Furthermore, depending on the figures, the -axis shows either the changes (ratio) in the total number of deaths or the number of first-dose vaccinated individuals of different risk classes.
Fig. 12.
Sensitivity of the total number of deaths to the vaccination campaign’s parameters.
Fig. 13.
Sensitivity of the total number of deaths to pandemic parameters.
As a first observation, it can be seen that by increasing the maximum capacity of warehouses, the timing lag between vaccinations, and the trust rate parameters, the total number of deaths decreases. This decrease is more significant when increasing the maximum capacity and the trust rate parameters. Indeed, increasing these two parameters directly affects the availability of vaccines and consequently increases the number of vaccinated individuals in the campaign and lowers the total number of deaths. An interesting result from Fig. 12a is that the priority of vaccination among risk classes “”, “18–49”, and “50–64” changes when the vaccines become more available. When the availability of vaccines increases to 70%, the highest priority belongs to the population of the “” risk class; however, when 70% is passed, priority is given to risk classes “18–49” and “50–64”. Accordingly, the vaccination priority depends also on the availability of the vaccines. Based on Fig. 12b, it is observed that increasing the delivery lead-time of vaccines increases the total number of deaths since the vaccines are not available as rapidly as possible, and as long as the pandemic lasts, the total number of deaths will consequently increase.
A significant result from Fig. 12c is that increasing the timing lag between two vaccination doses (i.e., , where and are the actual and the postponed time lags) decreases the total number of deaths. In contrast, this decrease becomes zero when the postponement becomes excessive (i.e., ). As a matter of fact, by increasing the timing lag between two injections, more individuals can receive their first dose. Since the vaccines in this study possess a high level of effectiveness, even their first dose can considerably decrease the total number of deaths. Interestingly, the postponement of the second-dose injection affects the vaccination prioritization among different risk classes, discussed further in Section 7.
Fig. 13 reveals that any increase in death rates (Fig. 13a) and the number of contacts (Fig. 13c) considerably increase the total number of deaths. This increase is more noticeable concerning the death rate. The increase in death rate can be inferred as the emergence of new variants of the virus with higher transmission and death rates, and the increase in contacts can represent a situation without quarantine restrictions. Accordingly, it can be concluded that the emergence of new variants could be the most critical challenge in jeopardizing the success of a vaccination campaign. Furthermore, Fig. 13b illustrates that increasing the effectiveness of vaccines decreases the total number of deaths, but this decrease is less significant compared to two other parameters. It can also be seen that once the vaccine possesses an effectiveness higher than 80% of its total effectiveness, the total number of deaths decreases considerably. Therefore, it can be understood that massively vaccinating the population with different types of vaccines with different effectiveness is more effective than vaccinating a limited amount of the population with a single highly effective vaccine.
7. Discussion and managerial insights
This section aims at discussing the results from a more general viewpoint to provide a set of managerial insights. Accordingly, different results are discussed separately, and the corresponding insights are elaborated.
The first challenge facing health policymakers when establishing an efficient vaccination campaign is how to allocate a limited stockpile of vaccines to different risk classes. In other words, how to prioritize the population for vaccination. In this study, we discover that this prioritization depends on several factors. Based on a comprehensive study of the results, a set of insights were obtained regarding this prioritization as 1) the larger the population/the higher the death rate/the higher the number of contacts, the higher the priority of vaccination; 2) the higher the transmission rate of the virus, the higher the priority of vaccination toward risk classes with the higher number of contacts, and 3) the tighter the quarantine restriction, the higher the priority of vaccination toward risk classes with higher death rates. Based on the latest insights on the existence of quarantine restrictions, it was observed that when no quarantine restriction is established, almost all the population of risk class “65–74” are vaccinated (). Next, the population of risk classes “”, “18–49”, and “50–64” are further priorities for vaccination. Moreover, the risk class “18–49” has even a higher priority compared to the risk class “50–64”. The reason is the higher number of contacts that the risk class “18–49” has when no quarantine restriction is established by the government. Accordingly, we learned (from an optimization viewpoint) that controlling the pandemic not only involves vaccinating the high-risk classes of the population, but also vaccinating the population with higher social contacts. Although the former may directly decrease the number of deaths among the population, the latter directly brakes/decreases the circulation of the virus in society and indirectly reduces the number of deaths among the population. In addition, we also learned that when a quarantine restriction is established, vaccination priority should be given to the risk class with the highest death rate. The reason is that, in the case of quarantine, the number of contacts severely decreases, and the risk classes with higher possible contacts (e.g., “18–49”) are no longer prioritized for vaccination. Therefore, the health policymakers are recommended to adopt the most appropriate vaccination strategy if they mix the vaccination campaign with lockdown decisions.
In addition to the prioritization issue, the availability of vaccines also plays an important role in piloting a vaccination campaign. It was observed that the availability of the vaccines alternates vaccination priority between the risk classes with higher death rates but a lower number of contacts (e.g., risk class “”) and the risk classes with lower death rates but a higher number of contacts (e.g., risk classes “18–49” and “50–64”). Indeed, depending on the availability of the vaccines, the vaccination campaign alternates between two main strategies: a high-risk strategy when the availability of vaccines is low or a high-contact strategy when the availability of vaccines is high. If the availability of vaccines is low, the pandemic should be controlled by prioritizing the high-risk individuals to decrease the total number of deaths (i.e., high-risk strategy). If the availability of vaccines is high, the pandemic should be controlled by prioritizing high-contact individuals to decrease the circulation of the virus (i.e., high-contact strategy). Another factor that affects the availability of the vaccines, and consequently the vaccination prioritization, is the timing lag between two injections. More interestingly, it became apparent that the vaccination prioritization changes among the risk classes when extending the timing lag between two injections (see Fig. 12c). In reality, several countries have adopted this extension [12]. For instance, by June 2021, 16 EU countries had extended the timing lag between the injections to provide as many of the first doses as possible to individuals of the high-risk classes. Romania applied such extension only in particular circumstances [63], and seven other EU countries (Iceland, Latvia, Lithuania, Malta, Slovakia, Slovenia, and Spain) did not apply such extension. Seven countries removed this extension in September 2021 (Austria, Belgium, Czechia, Finland, Ireland, Portugal, and Spain).
The main reason for this removal was the emergence of new virus variants with higher transmission and death rates, particularly the Delta variant, and the necessity to provide complete vaccination of the high-risk individuals [12]. The possibility of such an extension, and its impact on the pandemic, introduces the new concept of fractional dosing. Actually, due to the limited availability of vaccines (at least at the beginning of the pandemic), fractional-dosing could be an important decision to make a trade-off between reducing the number of deaths (by vaccinating high-risk individuals with complete doses) or decelerating the pandemic’s progression (by vaccinating a higher number of individuals with a single dose). In fact, the second-dose injection is delayed when the timing lag between two injections is extended, and the vaccination strategy goes from a complete-dosing strategy toward a fractional-dosing. Consequently, more vaccines become available for first-dose injection. However, it should be noticed that since a single-dose injection will not solely lead to the highest immunity of individuals, this increase in the availability of vaccines should not allow the vaccination campaign to adopt a high-contact vaccination strategy. In such situations, the vaccination campaign should adopt a mixed high-risk-high-contact strategy, where vaccination priority is given to two extreme risk classes: the risk class with the highest death rate but the lowest number of contacts (i.e., “”) and the risk class with the lowest death rate but the highest number of contacts (i.e., “18–49”).
We also discuss how the emergence of new variants of the virus affects the vaccination campaign and which vaccination strategies the health policymakers are recommended to adopt when confronting this emergence. In terms of the design of the VDN, reacting to new variants of the virus with higher transmission and death rates requires an increased vaccination capacity to accelerate the vaccination program. Accordingly, health policymakers should be prepared for such an increase by either opening/equipping a higher number of vaccination centers or establishing a higher capacity level. In addition, it was also observed that whenever new variants of the virus emerge, the differences between the quantity of the transferred vaccines to different regions become more unbalanced. Accordingly, the allocation of vaccines to a region does not depend only on demand for vaccines in that region. This is in conflict with the notion of equity in vaccine allocation in pandemic situations [40], [64]. Indeed, the optimal vaccination campaign focuses on regions where the pandemic is growing fast (e.g., in case of new variants of the virus) or can grow fast (e.g., in case of higher contacts between individuals). From another viewpoint, it can be interpreted that the equity of the vaccination among different regions should not be only based on the total demand (population) in each region but also based on the population of different risk classes, the possible number of contacts, the emergence of new variants of the virus as well as the quarantine restrictions. Therefore, equity is better addressed when focusing on the potential deaths among the regions and not simply on demand.
Another important insight can be provided concerning transshipment between departmental warehouses. It was observed that some departments with a higher storage capacity also play the role of an intermediate distribution center for other departments. Realistically, the transportation of vaccines should not be only direct region-department transportation. However, department-department transshipment can also help to accelerate the vaccine distribution and decrease the distribution cost. This phenomenon highlights the importance of resource sharing between warehouses. Therefore, it is recommended that health policymakers assign an extra inventory holding capacity at vaccination centers. Indeed, holding inventory in departmental warehouses provides the distribution network with an agile reaction in case of an augmented demand for vaccines in particular regions. Accordingly, the departmental warehouses with an extra inventory of vaccines can, if necessary, share a part of their inventory, at least, with their neighboring departments. Such resource sharing among warehouses provides the highest utilization of the limited vaccine resources and helps combat the pandemic in a more optimal way.
Last but not least, it was figured out that in a situation without any quarantine restriction, the contribution to the vaccination program of the vaccines with higher effectiveness is significant compared to other vaccines with lower effectiveness. Suppose policymakers do not plan to establish quarantine restrictions. In this case, their effort should be given to procuring the vaccines with the highest effectiveness, effectively decreasing the number of deaths and braking the virus’s circulation. On the contrary, if a part of the budget is spent on establishing quarantine restrictions, the contribution of the vaccines with lower effectiveness (and with a lower price) could be higher, and the vaccination campaign should adopt a high-risk vaccination strategy to decrease the total number of deaths as well as the hospitalization costs.
8. Conclusion and perspectives
This paper studied the design of a robust vaccine distribution network under uncertainty and disruption through a bi-objective stochastic mixed-integer nonlinear programming model. The proposed model incorporated two objectives, including minimizing the total distribution cost of the network and minimizing the expected total number of deaths among the population. Furthermore, the vaccination centers were modeled as queuing systems. Their capacities were determined based on the risk classes and the vaccination rates to avoid the congestion of individuals in these centers. Furthermore, vaccine storage and vaccination centers are exposed to disruption, and their capacity level is stochastically degraded to a lower level, either temporarily or permanently. Next, the proposed model was linearized, and a scenario-based robust optimization technique was employed to cope with the uncertainty of the input parameters. Finally, the proposed model and the solution approach were validated through a real case study, the COVID-19 vaccination campaign in France.
Through this study, important results were observed, and several managerial insights were provided. More importantly, it was observed that the priority of different risk classes of individuals for vaccination positively correlates with the population, death rate, and the number of possible contacts. In fact, a higher priority should be given to a risk class that collectively has a higher population, death rate, and possible contacts. On the other hand, the priority of a risk class for vaccination might be impacted by the effectiveness of the available vaccines, the emergence of new variants of the virus, and the quarantine restrictions.
The proposed optimization model in this paper is not without limitations. For instance, our case study forms the risk classes by partitioning the population according to age groups. However, other risk classes can be considered, including healthcare workers, other essential workers, or patients with comorbidities. Moreover, epidemiological models in the literature [15], [65], [66] and machine learning techniques [67], [68] can be employed to predict the spread of the disease. In this regard, a simple mathematical description of the spread of a disease in a population is the so-called susceptible-infectious-recovered (SIR) model. The SIR model divides the population of individuals into three compartments: susceptible, infectious, and recovered, which interact and vary as a function of time according to two parameters: effective transmission rate for the contact between susceptible and infectious individuals and the recovery rate of the infectious individuals. A variant of the SIR model is the SVIR model that incorporates the vaccination at a fixed rate into the SIR model. Although the vaccination rate is variable in our proposed model, one of the main decisions is to determine the optimal vaccination rate over time. Accordingly, a promising research direction could be investigating how the SIR model can be integrated into our proposed mathematical model to find the optimal vaccine allocation among different risk classes of the population.
Apart from developing a robust network for vaccine distribution, digitalization and the collaboration between different actors of the network can improve resilience of the network [69], [70]. In fact, providing end-to-end visibility through Blockchain technology to facilitate transparency, traceability, and trust in data and information use is a critical capability toward a resilient distribution network [71], [72]. As a future research direction, we recommend investigating the role of digitalization and digital technologies in improving resilience of vaccine distribution network and helping to implement the proposed bi-objective mathematical model of this paper in practice.
CRediT authorship contribution statement
Mehrdad Mohammadi: Software, Methodology, Validation, Formal analysis, Writing – review & editing, Supervision, Project administration. Milad Dehghan: Software, Methodology, Writing – original draft. Amir Pirayesh: Methodology, Validation, Formal analysis, Writing – review & editing. Alexandre Dolgui: Validation, Formal analysis, Writing – review & editing, Supervision, Project administration.
Footnotes
This manuscript was processed by Associate Editor Prof. Benjamin Lev.
Appendix A. Waiting time of individuals at vaccination centers
Table 6 lists the congestion-related parameters and decision variables. In the proposed GI/G/c queue system of Fig. 3, the vaccination rate, , and the SCV of vaccination time, , for risk class at vaccination center in period are updated as Eqs. (36) and (37), respectively.
| (36) |
| (37) |
Table 6.
Notations.
| Notation | Description |
|---|---|
| Congestion parameters | |
| Nominal vaccination rate for risk class at vaccination center in period under scenario | |
| Real vaccination rate for risk class at vaccination center in period in case of disruption under scenario | |
| Nominal vaccination time for risk class at vaccination center in period () under scenario | |
| Real vaccination time for risk class at vaccination center in period () in case of disruption under scenario | |
| Squared coefficient of variation (SCV) of the inter-arrival time of individuals of risk class at vaccination center in period under scenario | |
| Nominal SCV of the vaccination time of individuals of risk class at vaccination center in period under scenario | |
| Real SCV of the vaccination time of individuals of risk class at vaccination center in period in case of disruption under scenario | |
| Number of vaccination lines at vaccination center in period | |
| Disruption rate of the vaccination process at vaccination center | |
| Retrieve rate of the vaccination process at vaccination center | |
| Maximum allowable waiting time at vaccination center to avoid the circulation of the disease | |
| Decision variables | |
| Mean waiting time of individuals to get vaccinated at vaccination center at period under scenario | |
The throughput rate of vaccination of people from risk class at vaccination center in period is then calculated as (i.e., , ). Other parameters of the aggregated queue are approximated as follows:
| (38) |
| (39) |
| (40) |
| (41) |
| (42) |
where , , (i.e., ), and . Finally, the mean waiting time of people to get vaccinated at vaccination center at period , , is approximated in Eq. (43).
| (43) |
where and are calculated as Eqs. (44) and (45), respectively.
| (44) |
| (45) |
Appendix B. An enumeration approach to linearize constraint (27)
We first need to prove that the left-hand-side of Eq. (43) is convex.
Lemma B.1
Eq.(43)is convex.
Proof
We must show that the nonlinear Eq. (43) is convex w.r.t variable throughput , and consequently, w.r.t variable arrival rate since is a linear function of (i.e., , considering as a parameter).
By considering that the exponential function is strictly increasing and convex [73], we transform Eq. (43) to a simpler equation in the form of by considering a single risk class (), a single vaccination center (), and a single period (). Furthermore, we ignore all other parameters in Eq. (43) since they are all positive parameters. Finally, the first and the second-order derivatives of can be obtained as and , respectively. These derivatives are strictly positive, then, Eq. (43) is convex. □
Considering Lemma B.1 and according to Mohammadi et al. [55], we can numerically solve Inequality (26) for the variable and find its maximum value, . Once this value is found, any smaller value of will satisfy Inequality (26). This means that Inequality (26) is equivalent to:
| (46) |
Consequently, the nonlinear Constraint (23) can be replaced by the linear Constraint (27). Accordingly, by having a priori values of , the corresponding can be obtained by numerically solving Inequality (26).
Appendix C. Linearization of objective function (33)
To linearize objective function (33), first, let’s re-write objective function (2) as (47):
| (47) |
The objective function (47) is a positive-definite quadratic function of the form of (48).
| (48) |
The minimum value of this function is achieved where its first derivative is equal to zero. Accordingly, instead of minimizing the nonlinear objective function (48), the objective function (35) can be minimized in the model.
In order to linearize the absolute term of the objective function (33), we employ the linearization technique proposed by Yu and Li [74]. Accordingly, the objective function (33) can be re-written as follow:
| (49) |
s.t.:
| (50) |
| (51) |
where is an auxiliary variable as conditional expression (52):
| (52) |
Finally, the robust counterpart optimization model of the proposed robust model is provided as follows:
s.t.: Constraints (3)–(22), (24), (25), (27), (28), (50), and (51).
References
- 1.Johns Hopkins University and Medicine. Coronavirus COVID-19 global cases by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (JHU). https://coronavirus.jhu.edu/map.html; 2021.
- 2.Mullard A. COVID-19 vaccine development pipeline gears up. Lancet. 2020;395(10239):1751–1752. doi: 10.1016/S0140-6736(20)31252-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Abbasi B., Fadaki M., Kokshagina O., Saeed N., Chhetri P.. Modeling vaccine allocations in the COVID-19 pandemic: a case study in Australia. Available at SSRN 37445202020;.
- 4.Chen X., Li M., Simchi-Levi D., Zhao T.. Allocation of COVID-19 vaccines under limited supply. Available at SSRN 36789862020;.
- 5.Ivanov D. Predicting the impacts of epidemic outbreaks on global supply chains: a simulation-based analysis on the coronavirus outbreak (COVID-19/SARS-CoV-2) case. Transp Rese Part E. 2020;136:101922. doi: 10.1016/j.tre.2020.101922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Curiel R.P., Ramírez H.G. Vaccination strategies against COVID-19 and the diffusion of anti-vaccination views. Sci Rep. 2021;11(6629):1–13. doi: 10.1038/s41598-021-85555-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cuschieri S., Agius S., Souness J., Brincat A., Grech V. The fastest national COVID vaccination in Europe-Malta’s strategies. Health Sci Rev. 2021;1:100001. doi: 10.1016/j.hsr.2021.100001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Badoual M., Grammaticos B., Nakamura G. Vaccination strategies for a seasonal epidemic: a simple SIR model. Open Commun Nonlinear Math Phys. 2021;1:20–40. [Google Scholar]
- 9.Schmidt H., Pathak P., Sönmez T., Ünver M.U. COVID-19: how to prioritize worse-off populations in allocating safe and effective vaccines. BMJ. 2020;371:1–4. doi: 10.1136/bmj.m3795. [DOI] [PubMed] [Google Scholar]
- 10.Centers for Disease Control and Prevention. COVID-19 vaccination program interim playbook for jurisdiction operations. Version 1.0.https://www.cdc.gov/vaccines/imz-man-agers/downloads/COVID-19-Vaccination-Program-Interim_Playbook.pdf; 2021.
- 11.Kahn B., Brown L., Foege W., Gayle H., NASEM . The National Academies Press (US); 2020. A framework for equitable allocation of COVID-19 vaccine. [PubMed] [Google Scholar]
- 12.Overview of the implementation of COVID-19 vaccination strategies and deployment plans in the EU/EEA. https://www.ecdc.europa.eu/en/publications-data/overview-implementation-covid-19-vaccination-strategies-and-deployment-plans/; 2021.
- 13.Harnden A., Earnshaw A. Lessons from the United Kingdom’s COVID-19 vaccination strategy. Med J Aust. 2021;214(9):417. doi: 10.5694/mja2.51042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Matrajt L., Eaton J., Leung T., Brown E.R. Vaccine optimization for COVID-19: who to vaccinate first? Sci Adv. 2021;7(6):eabf1374. doi: 10.1126/sciadv.abf1374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bertsimas D., Digalakis Jr V., Jacquillat A., Li M.L., Previero A. Where to locate COVID-19 mass vaccination facilities? Naval Res Logist (NRL) 2022;69(2):179–200. doi: 10.1002/nav.22007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ivanov D., Dolgui A. OR-methods for coping with the ripple effect in supply chains during COVID-19 pandemic: managerial insights and research implications. Int J Prod Econ. 2021;232:107921. doi: 10.1016/j.ijpe.2020.107921. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ardolino M., Bacchetti A., Ivanov D. Analysis of the COVID-19 pandemic’s impacts on manufacturing: a systematic literature review and future research agenda. Oper Manag Res. 2022:1–16. doi: 10.1007/s12063-021-00225-9. In press. [DOI] [Google Scholar]
- 18.Simchi-Levi D., Schmidt W., Wei Y., Zhang P.Y., Combs K., Ge Y., et al. Identifying risks and mitigating disruptions in the automotive supply chain. Interfaces. 2015;45(5):375–390. [Google Scholar]
- 19.Gao S.Y., Simchi-Levi D., Teo C.-P., Yan Z. Disruption risk mitigation in supply chains: the risk exposure index revisited. Oper Res. 2019;67(3):831–852. [Google Scholar]
- 20.Burgos D., Ivanov D. Food retail supply chain resilience and the COVID-19 pandemic: a digital twin-based impact analysis and improvement directions. Transp Res Part E. 2021;152:102412. doi: 10.1016/j.tre.2021.102412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Dehghan M., Hejazi S.R., Karimi-Mamaghan M., Mohammadi M., Pirayesh A. Capacitated location routing problem with simultaneous pickup and delivery under the risk of disruption. RAIRO–Oper Res. 2021;55(3):1371–1399. [Google Scholar]
- 22.Dolgui A., Ivanov D., Sokolov B. Reconfigurable supply chain: the X-network. Int J Prod Res. 2020;58(13):4138–4163. [Google Scholar]
- 23.Paul S.K., Chowdhury P. Strategies for managing the impacts of disruptions during COVID-19: an example of toilet paper. Global J Flex Syst Manag. 2020;21(3):283–293. doi: 10.1007/s40171-020-00248-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Cheramin M., Saha A.K., Cheng J., Paul S.K., Jin H. Resilient NdFeB magnet recycling under the impacts of COVID-19 pandemic: stochastic programming and Benders decomposition. Transp Res Part E. 2021;155:102505. [Google Scholar]
- 25.Rahman T., Taghikhah F., Paul S.K., Shukla N., Agarwal R. An agent-based model for supply chain recovery in the wake of the COVID-19 pandemic. Comput Ind Eng. 2021;158:107401. doi: 10.1016/j.cie.2021.107401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ivanov D., Dolgui A. Viability of intertwined supply networks: extending the supply chain resilience angles towards survivability. a position paper motivated by COVID-19 outbreak. Int J Prod Res. 2020;58(10):2904–2915. [Google Scholar]
- 27.Ivanov D. Exiting the COVID-19 pandemic: after-shock risks and avoidance of disruption tails in supply chains. Ann Oper Res. 2021:1–18. doi: 10.1007/s10479-021-04047-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ivanov D. Supply chain viability and the COVID-19 pandemic: a conceptual and formal generalisation of four major adaptation strategies. Int J Prod Res. 2021;59(12):3535–3552. [Google Scholar]
- 29.Rottkemper B., Fischer K., Blecken A., Danne C. Inventory relocation for overlapping disaster settings in humanitarian operations. OR Spectrum. 2011;33(3):721–749. [Google Scholar]
- 30.Ren Y., Ordóñez F., Wu S. Optimal resource allocation response to a smallpox outbreak. Comput Ind Eng. 2013;66(2):325–337. [Google Scholar]
- 31.Chen S.-I., Norman B.A., Rajgopal J., Assi T.M., Lee B.Y., Brown S.T. A planning model for the WHO-EPI vaccine distribution network in developing countries. IIE Trans. 2014;46(8):853–865. [Google Scholar]
- 32.Yarmand H., Ivy J.S., Denton B., Lloyd A.L. Optimal two-phase vaccine allocation to geographically different regions under uncertainty. Eur J Oper Res. 2014;233(1):208–219. [Google Scholar]
- 33.Hovav S., Tsadikovich D. A network flow model for inventory management and distribution of influenza vaccines through a healthcare supply chain. Oper Res Health Care. 2015;5:49–62. [Google Scholar]
- 34.Saif A., Elhedhli S. Cold supply chain design with environmental considerations: a simulation-optimization approach. Eur J Oper Res. 2016;251(1):274–287. [Google Scholar]
- 35.Dasaklis T.K., Rachaniotis N., Pappis C. Emergency supply chain management for controlling a smallpox outbreak: the case for regional mass vaccination. Int J Syst Sci. 2017;4(1):27–40. [Google Scholar]
- 36.Duijzer L.E., van Jaarsveld W.L., Wallinga J., Dekker R. Dose-optimal vaccine allocation over multiple populations. Prod Oper Manag. 2018;27(1):143–159. doi: 10.1111/poms.12788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.de Carvalho M.I., Ribeiro D., Barbosa-Povoa A.P. Pharmaceutical supply chains-medicines shortages. Springer; 2019. Design and planning of sustainable vaccine supply chain; pp. 23–55. [Google Scholar]
- 38.Sadjadi S.J., Ziaei Z., Pishvaee M.S. The design of the vaccine supply network under uncertain condition. J Model Manag. 2019;14(4):841–871. [Google Scholar]
- 39.Liu M., Xu X., Cao J., Zhang D. Integrated planning for public health emergencies: amodified model for controlling H1N1 pandemic. J Oper Res Soc. 2020;71(5):748–761. [Google Scholar]
- 40.Enayati S., Özaltın O.Y. Optimal influenza vaccine distribution with equity. Eur J Oper Res. 2020;283(2):714–725. [Google Scholar]
- 41.Rastegar M., Tavana M., Meraj A., Mina H. An inventory-location optimization model for equitable influenza vaccine distribution in developing countries during the COVID-19 pandemic. Vaccine. 2021;39(3):495–504. doi: 10.1016/j.vaccine.2020.12.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Li X., Pan Y., Jiang S., Huang Q., Chen Z., Zhang M., Zhang Z. Locate vaccination stations considering travel distance, operational cost, and work schedule. Omega. 2021;101:102236. [Google Scholar]
- 43.Sinha P., Kumar S., Chandra C. Strategies for ensuring required service level for COVID-19 herd immunity in Indian vaccine supply chain. Eur J Oper Res. 2021 doi: 10.1016/j.ejor.2021.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yang Y., Bidkhori H., Rajgopal J. Optimizing vaccine distribution networks in low and middle-income countries. Omega. 2021;99:102197. [Google Scholar]
- 45.Tang L., Li Y., Bai D., Liu T., Coelho L.C. Bi-objective optimization for a multi-period COVID-19 vaccination planning problem. Omega. 2022;110:102617. doi: 10.1016/j.omega.2022.102617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Buccieri K., Gaetz S. Ethical vaccine distribution planning for pandemic influenza: prioritizing homeless and hard-to-reach populations. Public Health Ethics. 2013;6(2):185–196. [Google Scholar]
- 47.Markhorst B., Zver T., Malbasic N., Dijkstra R., Otto D., van der Mei R., et al. A data-driven digital application to enhance the capacity planning of the COVID-19 vaccination process. Vaccines. 2021;9(10):1181. doi: 10.3390/vaccines9101181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Anparasan A., Lejeune M. Resource deployment and donation allocation for epidemic outbreaks. Ann Oper Res. 2019;283(1):9–32. [Google Scholar]
- 49.Kis Z., Papathanasiou M., Calvo-Serrano R., Kontoravdi C., Shah N. A model-based quantification of the impact of new manufacturing technologies on developing country vaccine supply chain performance: a Kenyan case study. J Adv Manuf Process. 2019;1(3):e10025. [Google Scholar]
- 50.Vahdani B., Mohammadi M. A bi-objective interval-stochastic robust optimization model for designing closed loop supply chain network with multi-priority queuing system. Int J Prod Econ. 2015;170:67–87. [Google Scholar]
- 51.Mohammadi M., Tavakkoli-Moghaddam R., Siadat A., Dantan J.-Y. Design of a reliable logistics network with hub disruption under uncertainty. Appl Math Model. 2016;40(9–10):5621–5642. [Google Scholar]
- 52.Karimi-Mamaghan M., Mohammadi M., Jula P., Pirayesh A., Ahmadi H. A learning-based metaheuristic for a multi-objective agile inspection planning model under uncertainty. Eur J Oper Res. 2020;285(2):513–537. [Google Scholar]
- 53.Karimi-Mamaghan M., Mohammadi M., Pirayesh A., Karimi-Mamaghan A.M., Irani H. Hub-and-spoke network design under congestion: alearning based metaheuristic. Transp Res Part E. 2020;142:102069. [Google Scholar]
- 54.Mohammadi M., Dauzère-Pérès S., Yugma C., Karimi-Mamaghan M. A queue-based aggregation approach for performance evaluation of a production system with an AMHS. Comput Oper Res. 2020;115:104838. [Google Scholar]
- 55.Mohammadi M., Jolai F., Rostami H. An M/M/c queue model for hub covering location problem. Math Comput Model. 2011;54(11–12):2623–2638. [Google Scholar]
- 56.Snyder L.V., Daskin M.S. Stochastic p-robust location problems. IIE Trans. 2006;38(11):971–985. [Google Scholar]
- 57.Mulvey J.M., Vanderbei R.J., Zenios S.A. Robust optimization of large-scale systems. Oper Res. 1995;43(2):264–281. [Google Scholar]
- 58.Homayouni Z., Pishvaee M.S., Jahani H., Ivanov D. A robust-heuristic optimization approach to a green supply chain design with consideration of assorted vehicle types and carbon policies under uncertainty. Ann Oper Res. 2021:1–41. doi: 10.1007/s10479-021-03985-6. [DOI] [Google Scholar]
- 59.I. national de la statistique et des études économiques. Population totale par sexe et âge au 1er janvier 2021, France. https://www.insee.fr/fr/statistiques/1892086?sommaire=1912926; 2021.
- 60.Moghadas S.M., Vilches T.N., Zhang K., Nourbakhsh S., Sah P., Fitzpatrick M.C., et al. Evaluation of COVID-19 vaccination strategies with a delayed second dose. PLoS Biol. 2021;19(4):e3001211. doi: 10.1371/journal.pbio.3001211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Salje H., Kiem C.T., Lefrancq N., Courtejoie N., Bosetti P., Paireau J., Andronico A., Hozé N., Richet J., Dubost C.-L., et al. Estimating the burden of SARS-CoV-2 in France. Science. 2020;369(6500):208–211. doi: 10.1126/science.abc3517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Stéphane K.-N.. Variants de SARS-CoV-2 : quelle efficacité pour les vaccins en vie réelle ?https://www.vidal.fr/actualites/27475-variants-de-sars-cov-2-quelle-efficacite-pour-les-vaccins-en-vie-reelle.html; 2021.
- 63.Dascalu S., Geambasu O., Covaciu O., Chereches R.M., Diaconu G., Dumitra G.G., et al. Prospects of COVID-19 vaccination in Romania: challenges and potential solutions. Front Public Health. 2021;9:1–5. doi: 10.3389/fpubh.2021.644538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.C. of Disease Control, P. (CDC). COVID-19 Vaccine Equity for Racial and Ethnic Minority Groups. https://www.cdc.gov/coronavirus/2019-ncov/community/health-equity/vaccine-equity.html; 2021.
- 65.Saha S., Samanta G., Nieto J.J. Epidemic model of COVID-19 outbreak by inducing behavioural response in population. Nonlinear Dyn. 2020;102(1):455–487. doi: 10.1007/s11071-020-05896-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Gamchi N.S., Torabi S.A., Jolai F. A novel vehicle routing problem for vaccine distribution using SIR epidemic model. OR Spectrum. 2021;43(1):155–188. [Google Scholar]
- 67.Karimi-Mamaghan M., Mohammadi M., Meyer P., Karimi-Mamaghan A.M., Talbi E.-G. Machine learning at the service of meta-heuristics for solving combinatorial optimization problems: a state-of-the-art. Eur J Oper Res. 2022;296(2):393–422. [Google Scholar]
- 68.Karimi-Mamaghan M., Mohammadi M., Pasdeloup B., Meyer P. Learning to select operators in meta-heuristics: an integration of Q-learning into the iterated greedy algorithm for the permutation flowshop scheduling problem. Eur J Oper Res. 2022 doi: 10.1016/j.ejor.2022.03.054. [DOI] [Google Scholar]
- 69.Choi T.-M., Dolgui A., Ivanov D., Pesch E. OR and analytics for digital, resilient, and sustainable manufacturing 4.0. Ann Oper Res. 2022;310(1):1–6. [Google Scholar]
- 70.Ivanov D., Dolgui A., Sokolov B. Cloud supply chain: integrating industry 4.0 and digital platforms in the “supply chain-as-a-service”. Transp Res Part E. 2022;160:102676. [Google Scholar]
- 71.Li G., Xue J., Li N., Ivanov D. Blockchain-supported business model design, supply chain resilience, and firm performance. Transp Res Part E. 2022;163:102773. [Google Scholar]
- 72.Dolgui A., Ivanov D. 5G in digital supply chain and operations management: fostering flexibility, end-to-end connectivity and real-time visibility through internet-of-everything. Int J Prod Res. 2022;60(2):442–451. [Google Scholar]
- 73.Abou-Tair I., Sulaiman W. Inequalities via convex functions. Int J Math Math Sci. 1999;22(3):543–546. [Google Scholar]
- 74.Yu C.-S., Li H.-L. A robust optimization model for stochastic logistic problems. Int J Prod Econ. 2000;64(1–3):385–397. [Google Scholar]