Abstract
This study demonstrates the major role played by the healthcare and pharmaceutical industries during the COVID-19 pandemic. For this purpose, it provides evidence of a better risk–return relationship in these sectors through a multivariate study of monthly frequency. A global and dynamic ratio is developed to summarize different investor profiles according to their attitude toward risk and to consider the dynamic and changing nature of the economy and financial markets. This global ratio synthesizes the information from different orders of Kappa indices and Farinelli–Tibiletti ratios into a single measure. Additionally, we verify that Principal Component Analysis allows summarizing the information contained in the initial variables from the first new component. Our findings confirm that a filtering asset screening rule strategy is relevant and necessary. In this respect, passive management of midterm equal-weighted pharmaceutical portfolios outperforms both the pure financial and the healthcare investment strategies used during the pandemic.
Keywords: Screening rules, Risk aversion, Principal Component Analysis, Downside risk, Upside risk
1. Introduction
The current global pandemic caused by COVID-19 has drastically changed society, modifying the economy and people’s preferences, ways of relating to others, and customs. Moreover, the financial markets have changed, adapting the investment strategies of both large funds and individual investors. The onset of the pandemic caused a sharp increase in stock market volatility, drastically reducing liquidity. The collapse of the S&P 500 stock market index, which went from a record high on February 19, 2020, to a 34 % drop in just one month [1], exemplifies the instability experienced by the stock market during the first wave of the pandemic.
Despite these difficulties worldwide, certain niche sectors have been on the rise during this pandemic, and the pharmaceutical sector is undoubtedly-one such niche. According to [2], this sector already had significant growth potential before the onset of the virus, mainly supported by the positive evaluations that it received, an increase in demand for its products, and an increase in the rate of drug approvals by the Food and Drug Administration (FDA) in recent years. COVID-19 is giving an additional boost to this industry, providing it with access to a source of revenue that it did not have in previous years, as empirical evidence shows that vaccine administration is the only way to control virus transmission.1 Thus, the laboratories that had their vaccines approved by the various health control bodies signed substantial sales agreements for the entirety of 2021.2
However, the question arises whether the boom in the pharmaceutical sector is simply due to the high valuation resulting from investors’ immunological expectations. On the one hand, pharmaceutical companies, in addition to obtaining liquidity from the capital market, are financed in part by public entities. A case in point is the vaccine developed by Moderna, a pharmaceutical company that had no approved product prior to its COVID-19 antidote, which received funding from the U.S. government. On the other hand, Novavax received funding only from the U.S. Operation Warp Speed (OWS) vaccine program; the World Health Organization (WHO) COVAX program ordered more than one billion doses from the company. Therefore, it seems clear that the rise in the values of pharmaceutical companies is not only due to their high expectations of placing vaccines on the market but also because they are backed by entities with little or no probability of insolvency, which makes them very attractive to investors and portfolio managers due to the considerable reduction in their exposure to risk [3].
Not only have pharmaceutical and healthcare stocks risen during some of the most severe waves of the pandemic,3 but large funds that allocate most of their portfolios to these sectors also showed good financial performance.4 According to Trackinsight, the platform specializing in Exchange-Traded Funds (ETFs), the iShares S&P 500 Health Care Sector UCITS ETF, which measures the performance of companies in the U.S. healthcare sector, described a clear uptick in its market price value between the end of March 2020 and April 2021, rising from $5.84 to $9.36. Further evidence confirming that the pharmaceutical sector beat the market during the pandemic is that the Health Care Select Sector SPDR Fund, which tracks the U.S. healthcare sector, barely suffered a 4.4 % decline in its market price value during March 2020, while concurrently, the Vanguard Total Stock Market ETF, an ETF representing the overall U.S. stock market, plunged by 15 % [4]. Thus, in this study, we analyze the evolution of 21 international ETFs belonging to the financial, healthcare, and pharmaceutical sectors with the aim of demonstrating the significant role played by healthcare-related sectors during the COVID-19 pandemic.
Within the literature related to the risk and volatility inherent in financial markets, a line of research has emerged that focuses solely on the loss moments or left tail of the return distribution, i.e., the downside risk, which seems particularly relevant in a context of high uncertainty, such as the current pandemic [5], [6]. In this context, this study proposes a new asset selection method of special interest to institutional investors and portfolio managers based on screening rules, downside risk, upside risk, and dimensionality reduction econometric techniques, such as Principal Component Analysis (PCA). The new methodology attempts to synthesize the different attitudes toward risk, denoted by the different orders of Kappa measures and Farinelli–Tibiletti (FT) ratios, into a single overall measure or ratio. Specifically, the first principal component of the PCA method, which accounts for most of the variability in the initial rankings, will facilitate summarizing the different preliminary classifications into a single or overall ranking.
Our study makes fundamental contributions to the literature. Specifically, we closely follow the approach of [7] but expands on both the methodological terms and the economic and financial implications as follows: (i) Our overall filtering measure is constructed by considering different sets of performance measures, not merely-one. Specifically, our study synthesizes performance measures from two very different families, Kappa and FT, one based primarily on the expected return/downside risk ratio and the other on the upside risk/downside risk ratio; (ii) Unlike [7], who construct synthesized rankings by performance measure and then select the best performing assets in an in-sample static period, we conduct a time-varying asset allocation from a PCA-dynamic approach based on a rolling window re-estimation procedure. Accordingly, we have developed a new dynamic screening rule; (iii) While the former authors use the majority of S&P 500 stock components, we focus our study on ETFs that belong to the financial, healthcare and pharmaceutical sectors; (iv) Rather than considering a boom economic period such as the in-sample year 2005 used by [7], we study a short timeframe that considers only the first waves of the COVID-19 outbreak. This sample length choice comes from the evidence that downside risk-based performance measures do particularly well at capturing the information contained in asset returns in turbulent and bear market scenarios. In addition, it is well-timed to introduce an aggregate asset selection measure based on different and highly diverse risk-aversion profiles at a very unstable stage in terms of investors' attitude toward risk. As is well documented in the financial literature, risk aversion is countercyclical [8], increasing just before or at the onset of negative events and decreasing in boom or bull market periods.
Both the preliminary and final results of the study demonstrate the major role played by the healthcare and pharmaceutical sectors compared with a purely pecuniary sector, such as finance, during the pandemic. On a preliminary level using disaggregated measures, the Kappa indices and FT ratios show that the pharmaceutical portfolio significantly outperforms the financial portfolio in terms of the mean and median. However, we find that the pharmaceutical portfolio outperforms the healthcare portfolio in terms of the mean only in the moderate profile of the FT ratios, while it outperforms the healthcare portfolio in terms of the median for the moderate and aggressive profiles of the same ratio. After constructing the generalized ratio and obtaining the final results of the study, we find that the gap between the pharmaceutical and financial sectors is larger than that determined with the disaggregated measures, which may be because the generalized ratio captures the different aversion profiles in a single ratio. Importantly, the final results indicate the better performance of the pharmaceutical sector over the healthcare sector in terms of deviation, which underlines the stability of the pharmaceutical sector and makes it a more attractive investment niche. Finally, we prove that our main findings based on the global performance measure derived from PCA are robust to the consideration of additional control sectors.
The remainder of this study is organized as follows. Section 2 details the literature review. Section 3 describes both the methodology that we use to calculate the generalized ratio to select the best ETF based on its performance and the data analysis, presenting the data source and the summary statistics of the financial series. Section 4 presents the empirical results. Finally, Section 5 concludes the study.
2. Literature review
Asset selection is a key element in the investment decision process, wherein the so-called screening rules are useful. These rules aim to restrict potential assets to a reasonably limited set of investment opportunities formed by securities that exhibit the best risk–return characteristics [7]. Performance measures are a clear example of screening rules. Numerous studies throughout the financial literature evaluate the performance of different types of assets, portfolios, or investment funds using a wide variety of risk–return measures. Among these are classic measures, which attempt to measure the profitability obtained, conveniently adjusted for the overall risk of the strategy. Along these lines, indices such as Jensen’s index [9], Treynor’s index [10] and Sharpe’s ratio [11] are widely known and recurrently implemented. Different authors analyze the performance of large mutual funds during periods of relative calm in the markets using Jensen’s index [12], while others examine the performance of various equity markets in crisis periods using the Treynor index [13]. Another strand of literature investigates the trend in the performance of a portfolio by introducing commodity indices based on the Sharpe ratio [14]. Using the same ratio, topical studies analyze the risk–return trade-off of cryptocurrencies [15].
In contrast to traditional measures based on risk, understood as volatility (considering both upside and downside risk), within the financial literature, there is a need to interpret risk simply based on losses, or what is known as downside risk [16]. The expected return of an investment is directly related to the downside risk; that is, if investors want to reduce the risk related to the left tail of the distribution, the expected return of an investment will decrease as well [17]. Therefore, there is a positive and significant relationship between downside risk and return on investment [18]. According to [19], investors with low risk aversion will demand a premium to hold investments susceptible to downside risk; thus, stocks with high downside risk exposure have a higher average return. An alternative to reduce downside risk is diversified portfolios, as they maximize downside risk reduction [20]. The financial literature highlights the investment horizon as one of the factors that has the most influence on downside risk [21]. Throughout the financial literature, we find wide variability regarding the assets and markets evaluated based on this type of risk–return measure. Some studies have focused on measuring downside risk across equity markets using measures such as Value at Risk (VaR) [22]. Others use ratios such as the Omega index [23] or Kappa indices [24] to assess downside risk in equity investments.
The applicability of downside risk measures only increased with the arrival of the pandemic. In this context of uncertainty, much of the financial literature is eagerly searching for so-called safe havens and hedging assets to mitigate the large losses caused by the global economic instability resulting from the pandemic. Many of these studies suggest the use of left-tailed performance measures to make refined and accurate choices of these safe haven securities [24], [25]. Most studies conducted after the COVID-19 outbreak provide significant evidence that commodities, such as gold, have good hedging and safe haven properties [25]. Other commodities, such as oil, which had shown diversifying and safe haven properties in previous crises, have plummeted during the current pandemic in the wake of partial lockdowns and severe mobility restrictions [26]. Another strand of literature yields mixed evidence regarding the safe haven role of cryptocurrencies, showing that cryptocurrencies can generally be considered a great diversifying asset but never a safe haven security due to their own intrinsic risk hampering their ability to reduce the downside risk of a portfolio [27]. In the wake of the pandemic, another diversifying or even speculative asset that is attracting particular interest is the healthcare market, particularly the pharmaceutical submarket. In this regard, some recent studies analyze the downside risk of equity portfolios of pharmaceutical companies globally, concluding that emerging markets generally have higher tail risk exposure than developed markets [28].
Finally, the PCA method arises from the increasing trend of datasets to be larger in size, with more variables involved [29]. Several papers prove that the use of the PCA method allows for improving the predictive performance of econometric models [29], [30], [31]. Throughout the financial literature, authors study the correlations between the commodity market and stock indices, such as the S&P 500 [32] and the CSI 300 [33], by using the PCA method. Other authors conduct PCA to detail common factors in fixed income [34]. Furthermore, some financial papers design a cryptocurrency index, using PCA, to study changes in the market for this type of asset [35]. One line of research focuses on applying the PCA method to extract the principal components to predict the stock prices of companies in the pharmaceutical sector [36]. Currently and closer to our study, [7] implement the PCA technique to analyze the use of the alternative performance measures suggested by [37] in asset allocation procedures.5 These authors select the assets recommended by each performance measure (ranking) and analyze the out-of-sample performance of the portfolio composed of the best 20 stocks. They compare the different portfolios constructed by examining the percentages of individual stocks that are simultaneously selected by each pair and show that the composition of the portfolios is remarkably similar between strategies of the same family (downside risk or upside risk, among others). This allows them to reduce the number of portfolios and the size of the results by applying the PCA technique to all portfolios in each family and projecting the out-of-sample returns.
Our study is based on the findings by [7], who assert that the composition of portfolios must be practically identical when they are formed based on the screening rules of the same performance family, and goes further by designing a global performance ranking or screening rule to properly select assets considering not only the spectrum of attitudes toward risk concerning the same performance family, but also the risk investment profiles related to other very distant performance families. It is intended to present a global selection measure that is the synthesis of performance relationships that measure very diverse aspects of financial returns, as opposed to the synthesis of very similar ratios proposed by [7].
3. Materials and methods
3.1. Methodology
This subsection is divided into two clearly defined parts: downside risk and upside risk measures and PCA. While the former is focused on the different numerical calculus and analytical specifications proposed in the financial literature of performance measures, the latter shows how to reduce dimensionality given a set of initial variables.
3.1.1. Upper and lower partial moments
The present research is placed in the framework of Lower Partial Moments (LPM) and Upper Partial Moments (UPM). In the first case, LPM, risk is considered a negative deviation of stock returns, , taking as a reference the minimum acceptable return or threshold . According to [16], the LPM of order is expressed as:
| (1) |
where denotes expectation and is the probability density function. Instead of considering standard deviations (i.e., both positive and negative deviations from the mean return), the LPM considers only negative deviations of returns (i.e., the left tail of the return distribution), so the only concern of investors is losses. Therefore, the LPM can be considered investors’ attitude toward risk. Conversely, the UPM of order , which considers only the right tail of the return distribution or profit zone, is defined as:
| (2) |
3.1.2. Downside and upside risk
The first downside risk measures with proven and effective empirical applicability, the so-called Kappa indices, were introduced by [38]; they are estimated using the LPM. The Kappa index of order is defined as:
| (3) |
More recently, [39] proposed FT ratios that consider not only the LPM but also the UPM, thus providing a quotient between:
| (4) |
3.1.3. Principal component analysis (PCA)
PCA is a statistical method that aims to reduce the dimensionality of a dataset in a reduced number of factors or variables, which are known as principal components. Such a process is performed to minimize the loss of information, creating new variables that are not correlated and obtaining the latter to explain most of the variance of the original series [40], [41]. However, when the original time series are influenced by external trends (high correlation in mean and variance variations), this method may present unreliable principal components [42].
3.1.3.1. Principal components computation
Given a set of standardized initial variables, , the goal of this method is to replace them with new variables or components that are not correlated with each other, , and whose variances will be progressively reduced.6, 7 In other words, the aim is to explain the initial P variables with n elements arranged in an X matrix with a new random set of H-components Z with n elements per component so that in the new H-dimensional space, they preserve most of the variance in the original P-dimensional space. Each of the initial variable vectors, , can be defined as , with to realizations.
The PCA is conducted assuming that . Thus, we use the same counter, , for the number of initial variables and new components . However, in the subsequent empirical Section 4, we will exclude some of the new components and reduce the dimensionality of the problem with minimal information loss.
Thus, the first new component can be defined as a linear combination of the initial variables, , that has maximum variance. The values of this first new component in the realizations will be represented by a vector , given by:
| (5) |
where is the eigenvector of the covariance matrix, , which is associated with the largest eigenvalue, . Each of the vector elements, , represents the weights allocated to each initial variable realization . Note that corresponds to the number of initial variables, while counts the realizations. is a dimensional matrix composed of the variances and covariances between the set of initial variables, .
The original variables, , have a zero mean, so will also exhibit a zero mean. Then, the variance of can be defined as:
| (6) |
where is the variance of the first new component and is the initial covariance matrix.
By increasing the modulus of the vector , we can maximize the variance of the first new component, without limit. For the maximization of to have a solution, we should impose an additional constraint on the module of the vector . Accordingly, we will specify that . By applying this constraint via the Lagrange multiplier method, the PCA allows us to demonstrate that the variance of the first new component, , corresponds to the largest eigenvalue of the matrix , :
| (7) |
Then, the second new component, , is defined by a new linear combination of the initial :
| (8) |
where is the eigenvector of the covariance matrix, , which is associated with the second-largest eigenvalue, .
Then, the variance of the second new component, , can be expressed as:
| (9) |
When maximizing in the PCA, the aim is to find a vector, , such that . Additionally, we impose an orthogonality constraint between the first two eigenvectors, , to ensure that is uncorrelated with Then, as in Equation (7), it can be demonstrated by the Lagrange multiplier method that the variance of the second new component, , is equal to the second-largest eigenvalue of the matrix , .
Remembering that , it is possible to calculate the new component as:
| (10) |
where is the eigenvector of the matrix associated with the smallest eigenvalue, .
Then, it can be demonstrated using PCA that the variance of the new component, , is equal to the eigenvalue, :
| (11) |
As in previous new components, for the new component, the orthogonality constraints are also imposed regarding the remaining eigenvectors to ensure the uncorrelation between the different new components. Additionally, .
3.1.3.2. Explained variability
One of the main properties of PCA is that the new components preserve the initial variability; i.e., the sum of the variances of the new components is equal to the sum of the variances of the initial variables, and the generalized variance of the components is equal to the original generalized variance. This issue can be assessed in two steps. On the one hand, we know that and that the sum of is equal to the trace of , so:
| (12) |
The new variables exhibit the same joint variability as the original variables, . The sum of variances is the same, but the distribution is very different in the two sets. Additionally, since is a dimensional matrix, there are eigenvalues; i.e., the discussion continues with the assumption made in Subsection 3.1.3.1., .
On the other hand, we check whether the principal new components also keep the generalized variance or value of the determinant of . As the determinant is the product of the different , we have that, calling the covariance matrix of the new components, which is diagonal with terms :
| (13) |
Furthermore, we can assess the proportion of variability explained by each new component, , as the quotient between its variance or eigenvalue associated with the eigenvector that defines it, , and the sum of the eigenvalues of the matrix :
| (14) |
Additionally, we can show that the part of variability explained by the first new components can be calculated as follows:
| (15) |
where represents the component number up to which the new components’ variance is accumulated, thus allowing the expression of the percentage of explained cumulative variance of the original series, , when an additional new component is added.
3.2. Data analysis
Table 1 shows a comparison of the ETFs with the highest market cap in the financial, healthcare, and pharmaceutical sectors during the study period.8 Information about the market cap of the different sectors is extracted from the ETF database ( https://etfdb.com/) as of the end of April 2021. The data are selected for the period from the beginning of January 2019 to the end of April 2021 to capture both periods of relatively calm markets or the prepandemic period (January 2019 to March 2020) and intervals of instability, such as that marked by the onset of the COVID-19 pandemic and the effects of global vaccination (March 2020 to April 2021). The pharmaceutical sector is undoubtedly the main focus of this study; it ostensibly conditions the data sample considered, as only seven ETFs’ data could be obtained for the sample period. Thus, to carry out a coherent and balanced study, we choose the seven largest ETFs in each sector by market cap. Of the 21 ETFs considered, the ETF with the highest market cap, the Financial Select Sector SPDR Fund, is in the financial sector. The next three funds are in the healthcare sector. Although the financial sector has the ETF with the highest market cap, the overall market cap of the selected healthcare market is higher. However, the pharmaceutical sector can be considered a subsector within the healthcare sector, so it is not surprising that its ETFs have the lowest market cap.
Table 1.
Set of investment opportunities. This table reports the assets considered as a potential pool of investment opportunities. This spectrum of assets is broken down into three panels differentiating between the financial sector, the healthcare sector and the pharmaceutical sector (Panels A, B and C, respectively). By columns, the ticker or identifier of each ETF, the denomination, and the market cap of the ETFs as of the date of the study (April 2021) are shown.
| Ticker | Exchange Traded Fund (ETF) | Market cap ($MM) |
|---|---|---|
| Panel A: financial sector | ||
| XLF | Financial Select Sector SPDR Fund | 44,500.20 |
| VFH | Vanguard Financials | 10,955.10 |
| KRE | SPDR S&P Regional Banking | 5,276.72 |
| KBE | SPDR S&P Bank | 3,545,74 |
| FAS | Direxion Daily Financial Bull 3X Shares | 3,404.33 |
| KBWB | Invesco KBW Bank | 2,656.13 |
| IYF | iShares U.S. Financials | 2,456.56 |
| Panel B: healthcare sector | ||
| XLV | Health Care Select Sector SPDR Fund | 27,840.90 |
| VHT | Vanguard Health Care | 14,860.20 |
| IBB | iShares Nasdaq Biotechnology | 10,956.50 |
| ARKG | ARK Genomic Revolution | 8,910.70 |
| XBI | SPDR S&P Biotech | 7,485.38 |
| IHI | iShares U.S. Medical Devices | 7,446.87 |
| IXJ | iShares Global Healthcare | 3,103.29 |
| Panel C: pharmaceutical sector | ||
| PJP | Invesco Dynamic Pharmaceuticals | 372.37 |
| IHE | iShares U.S. Pharmaceuticals | 375.76 |
| XPH | SPDR S&P Pharmaceuticals | 272.56 |
| PPH | VanEck Vectors Pharmaceutical | 241.03 |
| KURE | KraneShares MSCI All China Health Care Index | 250.58 |
| CHIH | Global X MSCI China Health Care | 21.66 |
| FTXH | First Trust Nasdaq Pharmaceuticals | 22.40 |
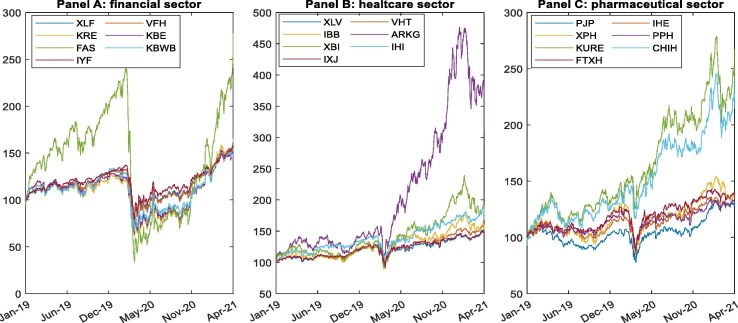
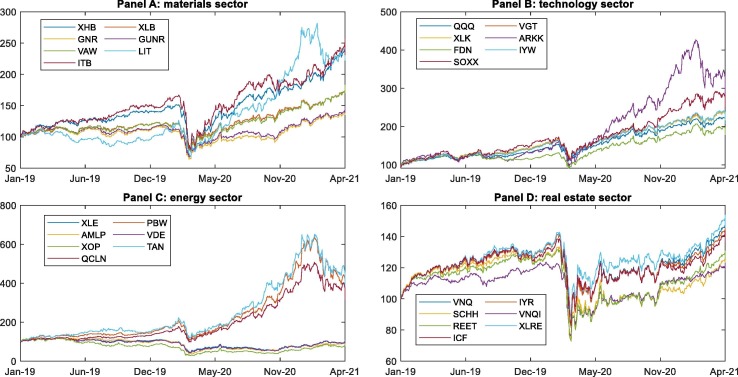
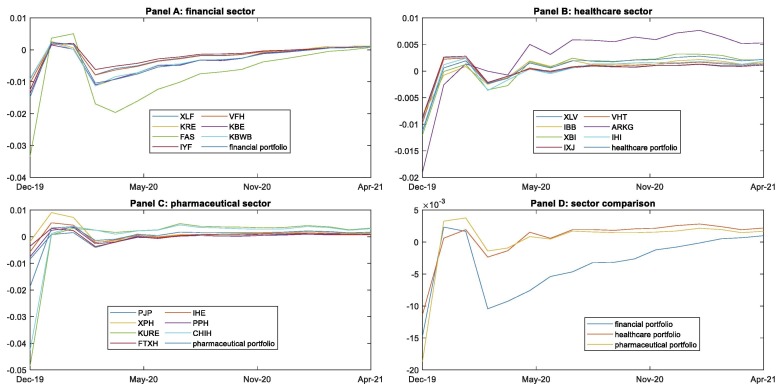
Fig. 1 shows the evolution of the quoted prices of financial, healthcare, and pharmaceutical sector ETFs from January 2019 to April 2021. We analyze the trends and patterns of the quoted prices of the different ETFs of the three sectors in a prepandemic situation (January 2019 to February 2020) and during the pandemic period (March 2020 to April 2021). During the prepandemic period, we observe that most of the funds considered followed an upward trend, while in March 2020, with the onset of the pandemic, they suffered a collapse and hit lows in many cases. This was mainly due to the increase in confirmed cases of COVID-19, which increased price volatility and had a clear contagion effect among markets [43]. After this significant decline in ETF prices, prices recovered to and even surpassed prepandemic levels; however, there are certain differences and particularities depending on the sector. In the financial sector, it is evident that the listed price of the FAS fund has followed an upward rally since April 2020, practically increasing its value tenfold by the end of April 2021 and placing it well above the rest of the increases recorded in this sector. Regarding the healthcare sector, its most representative ETFs suffered a less abrupt decline than that of the financial sector during the month of March 2020, but subsequently, these ETFs recorded less substantial increases in their listed values (multiplying by a maximum of five, in the case of ARKG). Notably, in the pharmaceutical sector, similar to the previous sectors, among the seven ETFs analyzed, the KURE and CHIH fund trends differ greatly from those of the rest, with both funds doubling their values in April 2021 compared to their values in mid-March 2020.
Fig. 1.
Sector overview. The figure shows the trading prices of the different ETFs representing the financial, healthcare and pharmaceutical sectors (Panels A, B and C, respectively). All traded prices are expressed on a 100 basis to ensure proper comparability. The trend of all ETFs shown can be evaluated with respect to the left-hand ordinate axis, with the exception of the ARKG healthcare ETF (brown solid line) which is interpreted according to the right-hand ordinate axis.
Table 2 presents the summary statistics of the log returns calculated for the financial, healthcare, and pharmaceutical sectors. For the average annualized returns, the average returns of the seven ETFs analyzed are observably higher in the healthcare sector, followed by the financial and pharmaceutical sectors. The ETF with the highest average return is ARKG, which is in the healthcare sector. However, the same is not true in terms of volatility, as the financial sector has the highest average volatility, followed by the healthcare and pharmaceutical sectors. Therefore, the pharmaceutical sector is the least exposed to risk and not too far from the average profitability of the other two sectors. This facilitates analyzing the behavior of this sector in a time of recession such as the current pandemic. The three sectors present negative asymmetry, that is, a greater concentration of values in the left part of the mean or loss zone, which is notably higher in the financial sector. For the kurtosis coefficient, the three sectors have positive values, which indicates that the distributions are leptokurtic, with heavier tails than the standard normal. The above evidence of nonnormality in asset returns is endorsed econometrically with the Jarque–Bera (JB) test, which rejects the null hypothesis at the 1 % significance level for all the assets analyzed. These results suggest that a study based on downside risk measures, especially-one concerned with the left tail of the distribution and the asymmetric nature of the time series, is relevant and necessary.
Table 2.
Descriptive statistics of logarithmic yields during the period December 2019 - April 2021). This table provides information on the continuous log returns of the different ETFs for the financial, healthcare and pharmaceutical sectors (Panels A, B and C, respectively). By rows we find the different ETFs, while each column reports the different statistics. The average return and standard deviation () are shown in annualized terms, while skewness and kurtosis () are reported in daily format. Additionally, non-normality is assessed by the JB test. Note that the p-values relative to that test are presented in parentheses. *, ** and ***reveal statistical significance at the 10%, 5% and 1% levels, respectively.
| Panel A: financial sector | ||||||
| XLF | 0.2116 | 0.3204 | −0.7142 | 16.1380 | 4282.5565 | (0.0000)*** |
| VFH | 0.2084 | 0.3272 | −0.8280 | 15.4513 | 3868.5776 | (0.0000)*** |
| KRE | 0.1920 | 0.4346 | −0.2975 | 9.5022 | 1042.1344 | (0.0000)*** |
| KBE | 0.1805 | 0.4142 | −0.3937 | 9.6785 | 1105.7042 | (0.0000)*** |
| FAS | 0.4232 | 0.8896 | −1.8073 | 20.9072 | 8193.5096 | (0.0000)*** |
| KBWB | 0.2055 | 0.4075 | −0.4129 | 12.1395 | 2062.1253 | (0.0000)*** |
| IYF | 0.1995 | 0.2940 | −0.9441 | 17.8198 | 5475.0967 | (0.0000)*** |
| Panel B: healthcare sector | ||||||
| XLV | 0.1727 | 0.2204 | −0.4903 | 14.5669 | 3302.7152 | (0.0000)*** |
| VHT | 0.1880 | 0.2275 | −0.7691 | 16.2887 | 4388.4467 | (0.0000)*** |
| IBB | 0.1867 | 0.2686 | −0.3372 | 7.2623 | 453.9101 | (0.0000)*** |
| ARKG | 0.5163 | 0.4273 | −0.5802 | 6.7142 | 369.1508 | (0.0000)*** |
| XBI | 0.2357 | 0.3500 | −0.5070 | 6.6045 | 341.5890 | (0.0000)*** |
| IHI | 0.2423 | 0.2480 | −0.5274 | 12.6950 | 2329.5764 | (0.0000)*** |
| IXJ | 0.1688 | 0.2072 | −0.7153 | 15.6699 | 3986.0810 | (0.0000)*** |
| Panel C: pharmaceutical sector | ||||||
| PJP | 0.1037 | 0.2305 | −0.4796 | 11.9160 | 1969.0223 | (0.0000)*** |
| IHE | 0.1250 | 0.2183 | −0.4532 | 10.5369 | 1409.9512 | (0.0000)*** |
| XPH | 0.1364 | 0.2625 | −0.9814 | 11.0483 | 1680.9745 | (0.0000)*** |
| PPH | 0.1301 | 0.2178 | −0.6838 | 13.2580 | 2624.1588 | (0.0000)*** |
| KURE | 0.3976 | 0.3345 | −1.0493 | 9.4461 | 1125.2334 | (0.0000)*** |
| CHIH | 0.3586 | 0.3069 | −0.6470 | 6.5079 | 340.8799 | (0.0000)*** |
| FTXH | 0.1310 | 0.2280 | −0.3202 | 9.2021 | 950.0583 | (0.0000)*** |
4. Results and discussion
This section is divided into three subsections. The first presents the estimation of the different measures of downside risk and upside risk and the calibration of the generalized ratios using PCA. The second focuses on the preliminary analysis of the Kappa and FT measures. The last subsection evaluates the main findings regarding the evolution of the generalized ratio.
4.1. Risk aversion and dynamic estimation
The aim of this study is to test whether health-related sectors (i.e., the healthcare and pharmaceutical sectors) are chosen over a traditional sector based on the risk–return ratio in its strictest sense (i.e., the financial sector). To examine the supremacy of the health-related sectors in average terms, three equal-weighted portfolios are constructed with the seven ETFs corresponding to each sector.
Within the context of asset selection, this study attempts to rank the 21 ETFs analyzed to report an optimal investment decision for each month of the pandemic period (December 2019 to April 2021). To this end, two performance measures (Kappa indices and FT ratios) are used and evaluated according to three risk-attitude profiles: defensive, moderate, and aggressive. Specifically, this study follows the ranges suggested by [7], establishing the following values to characterize the order of the LPM and thus considering the different risk attitudes of investors: (defensive investors), (moderate investors), and (aggressive investors). As with the Kappa ratio, values are established for the parameters detailing risk aversion for the FT ratios. For the parameters , the values are set as follows: for defensive investors, the Omega ratio for moderate investors, and the upside potential ratio for aggressive profiles. In addition, to calculate the risk-free interest rate, which serves as a threshold or minimum acceptable return (), three-month U.S. Treasury bills are used.9
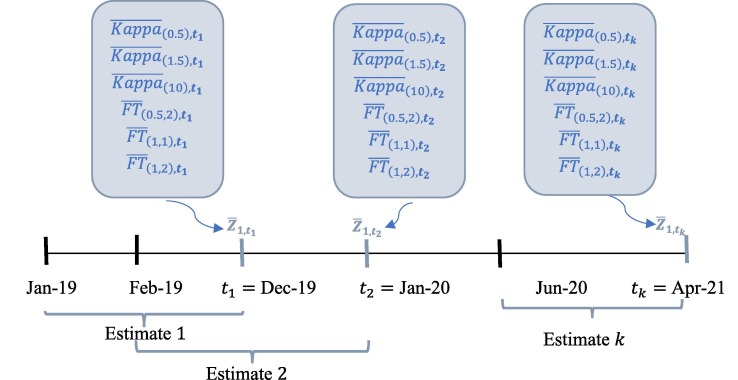
Following Fig. 2 , to carry out the empirical analysis, the statistical technique of the rolling window is used so that both the beginning and the end of each assessment period are moved one month forward. This method, although simple to apply, usually produces better results compared with other more complex and current statistical approaches [44].10 The asset allocation is performed at the end of each month (every 22 trading days) based on the information gathered by the returns in the previous 252 trading days, thus reporting 17 monthly assessments (k) throughout the aforementioned interval, with the first and last assessments corresponding to December 2019 and April 2021, respectively (see Fig. 2). Specifically, the screening asset process consists of two stages that are carried out in each month of revaluation: (1) calculation of six rankings of the considered ETFs based on the different downside and upside risk measures and the different risk-aversion profiles (i.e., selected Kappa and FT ratio orders); and (2) application of the PCA method to summarize the information of the six rankings in a single global ranking associated with the first new component (which explains most of the variability of the initial Kappa and FT classifications) from which the best-performing ETF for each window is extracted. Thus, this global classification allows us to assess which ETF has shown the best performance over time and in aggregate for different downside and upside risk profiles.
Fig. 2.
The rolling window estimation procedure. The figure represents the rolling window method, whereby every 22 trading days a new ranking is carried out, considering the information contained in the previous 252 trading days. At the end of each rolling re-estimation, the Kappa indices and FT ratios are shown, and the subsequent first new component, , after applying the PCA method. refers to the 17 monthly performance assessments conducted throughout the studied period via the rolling window approach and goes from to , thus indicating the dates of rolling re-estimation.
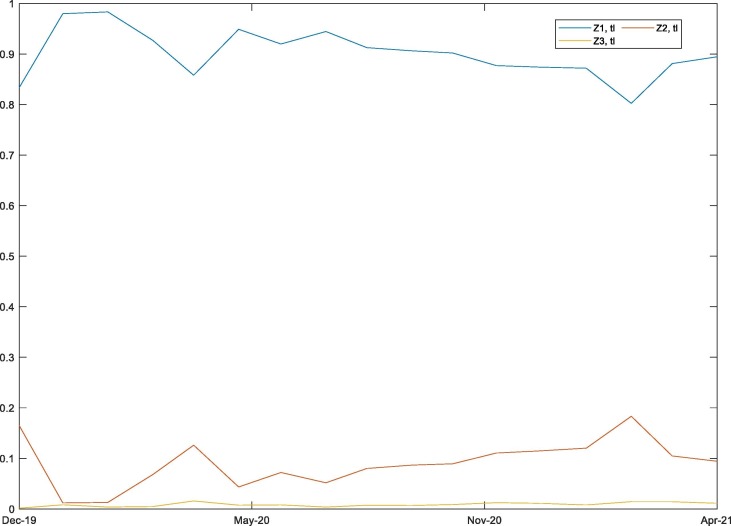
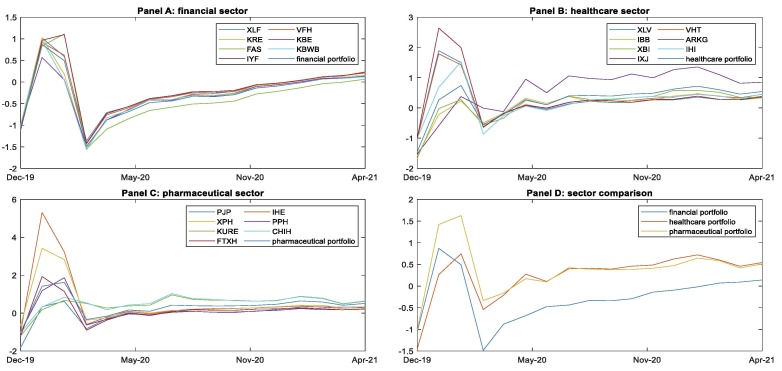
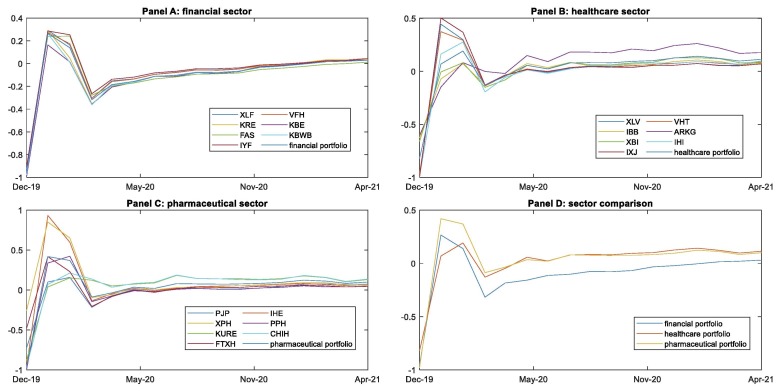
After the rolling window PCA estimation is performed as described in Fig. 2, we obtain as many time-varying principal new components, , as initial variables or time-varying rankings, . Specifically, since we consider six initial rankings at each rebalancing time of the rolling window, , , we obtain a total of six uncorrelated and time-varying new components, . Following the notions of Equation (14), Fig. 3 shows the evolution of the percentage of variance in the initial Kappa and FT rankings () that is explained by each of the first three PCA components and for the 17 months of asset evaluation (). This variance corresponds to the deviation of the ratings given by each initial performance measure to the assets or ETFs from the average ratings given by them. There is no need to represent components from four to six since 100 % of the variance is explained from the third component onward, so they are of no significance in the analysis. In addition, the graph highlights that the second and third components have residual importance in explaining the variance in the initial rankings across time. Therefore, they should not be included in the screening rule development. In turn, the first component explains approximately 90 % of the variance of the initial asset rankings. In addition, it is reported that this component reaches explanatory maximums of approximately 100 % at some points (e.g., January 2020). Therefore, there is clear evidence that the first component can be used as a global measure to filter asset sets in evaluation contexts by considering both downside risk and upside risk under different investment profiles.
Fig. 3.
Proportion of variance explained by new components. The figure shows the evolution of the proportion of variance explained by each of the first three principal new components resulting from the PCA method at each rebalancing time in the rolling window, . The evolution is presented over the 17 months that make up the asset allocation time space.
4.2. Preliminary evidence
This subsection presents the preliminary analysis of the evolution of the different ETF rankings based on Kappa and FT measures for the different risk profiles (defensive, moderate and aggressive). For concision, the figures plotting the monthly ETF classifications for the considered investor risk attitudes can be consulted in the Appendix, while the tables reporting the summary statistics are placed above the text.
Panels A to C of Table 3 summarize the main statistics relating to the Kappa measures for the three sectors and investors’ attitude toward risk over the study period. Overall, it is notable that both the means and medians of the Kappa indices are negative across all the financial sector ETFs and investor profiles, while they are mostly positive for the pharmaceutical and healthcare sector funds. Regarding deviation and except for the aggressive profile, pharmaceutical funds exhibit the greatest instability in the evolution of the index, mainly associated with the market turmoil of prepandemic months (January to February 2020).11 Despite this initial variability, the ETFs with the highest average Kappa indices and, therefore, the alternatives that are selected on more occasions throughout the evaluation period are those related to the health industry. Specifically, the ARKG ETF—a fund in the healthcare sector—is the best-performing strategy for the defensive and aggressive investment profiles, whereas the supremacy of the pharmaceutical sector can be assessed from the moderate profile, where the XPH ETF reports the best results on average.
Table 3.
Descriptive statistics of the Kappa index during the period December 2019 - April 2021. This table provides information on the descriptive statistics of the Kappa index of the different ETFs for the Financial, Healthcare and Pharmaceutical Sectors (Panels A, B and C, respectively). Panel D reports on the test for equality of means (t-Test), test for equality of variances (F-test) and test for equality of medians (W-test) between the Pharmaceutical portfolio and the Healthcare and Financial portfolios. Note that the p-values relative to such test are presented in parentheses. *, ** and *** reveal statistical significance at the 10%, 5% and 1% levels, respectively. The Student's t-test is a parametric approach that analyzes the mean of related samples and determines whether there is a difference between them, while the non-parametric Wilcoxon test (W-test) does the same for medians. The F-test for equality of variances is a parametric test for the null hypothesis that two normal series exhibit the same variance.
| Defensive profile |
Moderate profile |
Aggressive profile |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. dev. | Median | Mean | Std. dev. | Median | Mean | Std. dev. | Median | |
| Panel A: financial sector | |||||||||
| XLF | −0.1825 | 0.5706 | −0.2117 | −0.0763 | 0.2536 | −0.0473 | −0.0019 | 0.0033 | −0.0014 |
| VFH | −0.2021 | 0.5706 | −0.2166 | −0.0776 | 0.2501 | −0.0485 | −0.0021 | 0.0036 | −0.0015 |
| KRE | −0.2445 | 0.5707 | −0.2533 | −0.1033 | 0.2679 | −0.0694 | −0.0031 | 0.0046 | −0.0027 |
| KBE | −0.2923 | 0.496 | −0.2707 | −0.1166 | 0.2552 | −0.0718 | −0.0034 | 0.0046 | −0.0027 |
| FAS | −0.3499 | 0.6634 | −0.4406 | −0.1004 | 0.2468 | −0.0829 | −0.0076 | 0.0098 | −0.0061 |
| KBWB | −0.2804 | 0.5521 | −0.2731 | −0.1098 | 0.2576 | −0.0701 | −0.0031 | 0.004 | −0.0026 |
| IYF | −0.1568 | 0.628 | −0.1927 | −0.0641 | 0.2538 | −0.0386 | −0.0018 | 0.0036 | −0.0011 |
| Panel B: healthcare sector | |||||||||
| XLV | 0.246 | 0.6587 | 0.2166 | 0.0071 | 0.2883 | 0.0438 | 0.0002 | 0.0026 | 0.0009 |
| VHT | 0.275 | 0.6416 | 0.2551 | 0.0114 | 0.2764 | 0.0525 | 0.0003 | 0.0028 | 0.0011 |
| IBB | 0.0821 | 0.4973 | 0.2452 | 0.0034 | 0.1747 | 0.0616 | 0.0004 | 0.0026 | 0.0013 |
| ARKG | 0.5925 | 0.7603 | 0.9339 | 0.0922 | 0.2084 | 0.175 | 0.0029 | 0.0064 | 0.0053 |
| XBI | 0.1223 | 0.5507 | 0.2831 | 0.0107 | 0.1879 | 0.0793 | 0.0006 | 0.0038 | 0.0018 |
| IHI | 0.2017 | 0.5689 | 0.3065 | −0.006 | 0.2712 | 0.0672 | 0.0001 | 0.0033 | 0.0013 |
| IXJ | 0.3317 | 0.8416 | 0.2574 | 0.0148 | 0.299 | 0.0476 | 0.0002 | 0.0026 | 0.0009 |
| Panel C: pharmaceutical sector | |||||||||
| PJP | −0.0096 | 0.5656 | 0.0975 | −0.0198 | 0.1991 | 0.0222 | −0.0002 | 0.0025 | 0.0005 |
| IHE | 0.5351 | 1.4926 | 0.2525 | 0.0567 | 0.3681 | 0.0537 | 0.0007 | 0.0024 | 0.001 |
| XPH | 0.4603 | 1.0468 | 0.2399 | 0.1019 | 0.2615 | 0.0534 | 0.0015 | 0.0028 | 0.0012 |
| PPH | 0.1326 | 0.6283 | 0.0951 | −0.0122 | 0.288 | 0.0202 | −0.0001 | 0.0024 | 0.0004 |
| KURE | 0.4895 | 0.4808 | 0.6278 | 0.0646 | 0.246 | 0.1325 | 0.0000 | 0.0126 | 0.0032 |
| CHIH | 0.5338 | 0.4562 | 0.6457 | 0.0658 | 0.2696 | 0.1341 | 0.0002 | 0.0111 | 0.0029 |
| FTXH | 0.1379 | 0.6863 | 0.1712 | 0.0154 | 0.1812 | 0.0371 | 0.0002 | 0.0018 | 0.0007 |
| Panel D: portfolio comparison | |||||||||
| Financial portfolio | −0.2689 | 0.5656 | −0.2937 | −0.0963 | 0.2555 | −0.0675 | −0.0034 | 0.0048 | −0.0026 |
| t, F, W tests | −3.2437 | 0.9031 | 55.00 | −1.4308 | 0.7769 | 62.00 | −2.1323 | 0.9071 | 55.00 |
| (0.0028)*** | (0.841) | (0.0015)*** | (0.1623) | (0.6196) | (0.0038)*** | (0.0408)** | (0.8478) | (0.0015)*** | |
| Healthcare portfolio | 0.2514 | 0.5463 | 0.4116 | 0.0226 | 0.2292 | 0.0833 | 0.0007 | 0.0034 | 0.0019 |
| t, F, W tests | −0.6416 | 0.8425 | 147.00 | −0.1702 | 0.6253 | 154.00 | 0.2909 | 0.4541 | 174.00 |
| (0.5257) | (0.736) | (0.9458) | (0.866) | (0.3574) | (0.7596) | (0.7732) | (0.1247) | (0.3223) | |
| Pharmaceutical portfolio | 0.3771 | 0.5952 | 0.4115 | 0.0378 | 0.2898 | 0.0800 | 0.0002 | 0.0050 | 0.0016 |
Additionally, Panel D of Table 3 presents a descriptive summary of the Kappa indices for the sector portfolios, as well as the tests for equality of means (t test), variances (F test), and medians (Wilcoxon–Mann–Whitney, or W-M−W, test) among the reference sector portfolio (i.e., pharmaceutical portfolio) and the other two equally-weighted strategies under study (healthcare and financial portfolios). Based on the results, the pharmaceutical portfolio outperforms the financial portfolio in terms of the mean and median in a highly significant way for the defensive profile, also keeping this supremacy for the aggressive profile, albeit with lower significance. Furthermore, although the pharmaceutical portfolio seems to sufficiently outperform the healthcare portfolio (in terms of the mean, median, and deviation), we find no evidence to demonstrate the superiority of one portfolio over the other in statistical terms. Therefore, based on the results of the Kappa index, it seems clear that the pharmaceutical investment niche beats the purely pecuniary investment of the traditional financial markets and the overall healthcare industry during the COVID-19 pandemic, although it significantly outperforms only the financial portfolio.
Panels A to C of Table 4 display the descriptive statistics for the FT ratios. In contrast to the results reported in Table 3, the means and medians are positive for the FT ratios and the different attitudes toward risk, but those of the healthcare and pharmaceutical funds remain vastly superior. In general, pharmaceutical and healthcare ETFs are the most stable. As with the results for the Kappa index, the ETFs selected on average as potential investment assets are those related to the health industry. Thus, the first two funds selected for each risk-attitude profile correspond to the healthcare and pharmaceutical sectors (IXJ and IHE for the defensive profile, ARKG and XPH for the moderate profile, and XLV and IHE for the aggressive profile). Regarding sector portfolio analysis (Panel D of Table 4), for the defensive profile, both the mean and median of the pharmaceutical portfolio are significantly higher than those of the financial portfolio. Comparing the pharmaceutical and healthcare portfolios, the former significantly outperforms the latter in terms of the median for the moderate and aggressive profiles.12 As with the Kappa indices, the results indicate the supremacy of the health-related sectors during the study period. Specifically, the pharmaceutical portfolio continues to be evidently selected by the FT ratios as an investment alternative to the financial portfolio, while the evidence in terms of medians confirms the somewhat higher eligibility of pharmaceutical investment compared to healthcare investment in LPM-UPM evaluation contexts.
Table 4.
Descriptive statistics of the FT ratio during the period December 2019 - April 20,214 This table provides information on the descriptive statistics of the FT ratio of the different ETFs for the Financial, Healthcare and Pharmaceutical Sectors (Panels A, B and C, respectively). Panel D reports on the test for equality of means (t-Test), test for equality of variances (F-test) and test for equality of medians (W-test) between the Pharmaceutical portfolio and the Healthcare and Financial portfolios. Note that the p-values relative to such test are presented in parentheses. *, ** and *** reveal statistical significance at the 10%, 5% and 1% levels, respectively. The Student's t-test is a parametric approach that analyzes the mean of related samples and determines whether there is a difference between them, while the non-parametric Wilcoxon test (W-test) does the same for medians. The F-test for equality of variances is a parametric test for the null hypothesis that two normal series exhibit the same variance.
| Defensive profile |
Moderate Profile |
Aggressive Profile |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. dev. | Median | Mean | Std. dev. | Median | Mean | Std. dev. | Median | |
| Panel A: financial sector | |||||||||
| XLF | 5.0763 | 1.5421 | 5.3241 | 0.9012 | 0.3077 | 0.9228 | 1.8779 | 0.5727 | 1.9642 |
| VFH | 5.0387 | 4.5143 | 5.2558 | 0.897 | 0.3062 | 0.9209 | 1.8555 | 0.5705 | 1.9395 |
| KRE | 4.3793 | 1.4937 | 4.3439 | 0.868 | 0.3071 | 0.8949 | 1.7583 | 0.6005 | 1.8028 |
| KBE | 4.3226 | 1.4015 | 4.4375 | 0.8487 | 0.2847 | 0.8904 | 1.7196 | 0.5549 | 1.7967 |
| FAS | 5.1697 | 1.5157 | 5.5755 | 0.8558 | 0.3087 | 0.8579 | 1.71 | 0.5145 | 1.7837 |
| KBWB | 4.5335 | 1.4812 | 4.6413 | 0.8567 | 0.2984 | 0.8918 | 1.7755 | 0.5861 | 1.8357 |
| IYF | 5.5802 | 1.6231 | 5.9687 | 0.918 | 0.3136 | 0.9352 | 1.9017 | 0.5549 | 2.0103 |
| Panel B: healthcare sector | |||||||||
| XLV | 6.3428 | 1.7155 | 6.6511 | 1.047 | 0.3348 | 1.0738 | 2.2013 | 0.5962 | 2.3127 |
| VHT | 6.3438 | 1.7539 | 6.7078 | 1.0528 | 0.3259 | 1.0884 | 2.169 | 0.5843 | 2.2942 |
| IBB | 5.0237 | 1.4044 | 5.4483 | 1.0171 | 0.2299 | 1.0954 | 1.9127 | 0.4744 | 2.0796 |
| ARKG | 6.2957 | 1.8254 | 6.9239 | 1.1674 | 0.294 | 1.2837 | 1.9746 | 0.5204 | 2.1912 |
| XBI | 4.9542 | 1.3628 | 5.451 | 1.0291 | 0.2493 | 1.1141 | 1.8224 | 0.4579 | 1.9816 |
| IHI | 5.8392 | 1.6759 | 6.5172 | 1.0276 | 0.3079 | 1.1101 | 2.0187 | 0.5613 | 2.2197 |
| IXJ | 6.7613 | 1.9563 | 7.0094 | 1.0615 | 0.3581 | 1.0817 | 2.195 | 0.603 | 2.3082 |
| Panel C: pharmaceutical sector | |||||||||
| PJP | 5.3246 | 1.4484 | 5.7688 | 0.9816 | 0.2629 | 1.0366 | 2.0221 | 0.5239 | 2.1719 |
| IHE | 6.4512 | 2.5789 | 6.3226 | 1.1296 | 0.5151 | 1.0879 | 2.1957 | 0.7419 | 2.2156 |
| XPH | 5.6176 | 1.614 | 5.5682 | 1.1608 | 0.3862 | 1.0877 | 2.0679 | 0.5391 | 2.0539 |
| PPH | 5.6824 | 1.6076 | 5.9897 | 1.0121 | 0.3314 | 1.0336 | 2.0589 | 0.5761 | 2.1683 |
| KURE | 5.5631 | 1.5064 | 5.9315 | 1.1303 | 0.2987 | 1.2152 | 1.8812 | 0.4988 | 2.0307 |
| CHIH | 5.8257 | 1.5632 | 6.1375 | 1.14 | 0.302 | 1.2154 | 1.946 | 0.5275 | 2.0514 |
| FTXH | 5.7673 | 1.4844 | 6.016 | 1.034 | 0.2607 | 1.061 | 2.0274 | 0.4636 | 2.1309 |
| Panel D: portfolio comparison | |||||||||
| Financial portfolio | 4.7436 | 1.4333 | 4.9512 | 0.8706 | 0.3018 | 0.891 | 1.7702 | 0.5537 | 1.8427 |
| t, F, W tests | −2.0333 | 0.7421 | 46.5 | −2.0379 | 0.8102 | 59.5 | −1.1965 | 1.0014 | 65.5 |
| (0.05057)* | (0.5577) | (0.0008)*** | (0.04999)** | (0.6788) | (0.0036)*** | (0.2403)** | (0.9978) | (0.0069)*** | |
| Healthcare portfolio | 5.7154 | 1.6384 | 6.297 | 1.0564 | 0.2963 | 1.1386 | 1.9873 | 0.5405 | 2.1518 |
| t, F, W tests | −0.1963 | 0.9696 | 133.5 | −0.3429 | 0.781 | 148.5 | −0.0535 | 0.9541 | 162.5 |
| (0.8456) | (0.9515) | (0.7176) | (0.7339) | (0.6209) | (0.904) | (0.9577) | (0.9263) | (0.5466) | |
| Pharmaceutical portfolio | 5.8266 | 1.6639 | 6.3748 | 1.0936 | 0.3353 | 1.1366 | 1.9973 | 0.5534 | 2.1158 |
4.3. Global ranking assessment for asset allocation
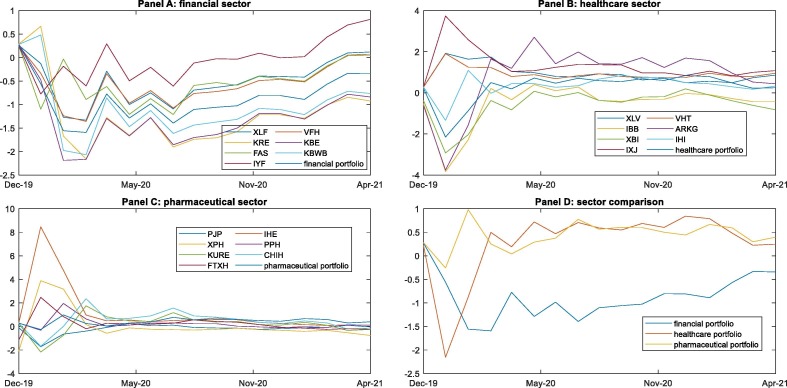
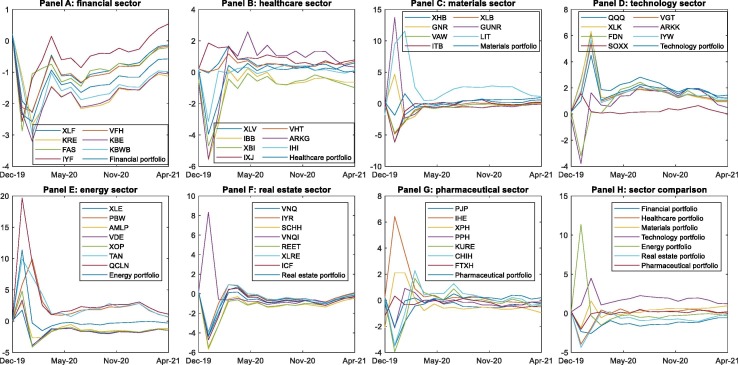
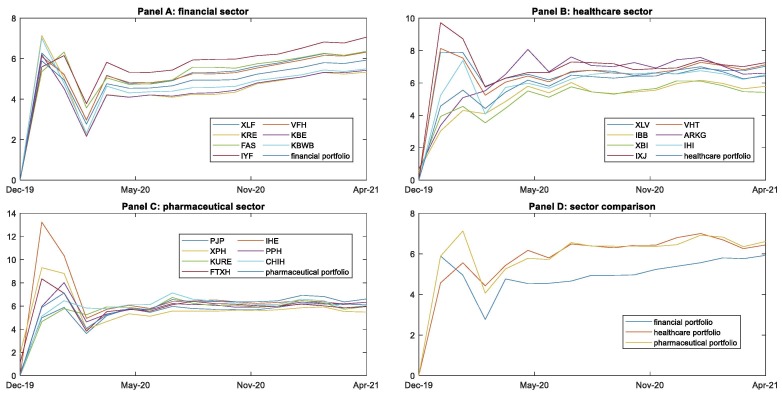
Fig. 4 describes the performance of the ETFs based on the global measure associated with the first new component obtained from the PCA over the investigated period. We find that most ETFs suffered significant declines in their global rankings during the prepandemic period. On the one hand, the financial sector (Panel A) experienced a large drop in March 2020 due to increased volatility stemming from the onset of the pandemic and the first global travel restrictions, social distancing, and stay-at-home orders. In the following months, the financial sector continued exhibiting poor performance, with some ETFs reporting negative values for the global measure until April 2021. On the other hand, the healthcare sector (Panel B) exhibited disparate trends during the prepandemic period, with some healthcare ETFs experiencing more abrupt declines than those of the financial sector, probably due to the collapse of the healthcare system globally and the lack of means to curb the spread of the virus [45]. However, the behavior of healthcare ETFs has tended to homogenize since the outbreak of the pandemic. The pharmaceutical sector (Panel C) follows a very similar pattern to that of the healthcare sector over the entire period but performs better overall. Our results generally indicate homogeneity in ETFs’ performance for the three considered sectors since the onset of the COVID-19 pandemic, which is consistent with the contagion effect across international stock markets reported in the literature [43].
Fig. 4.
Time-varying global ratio assessment. The figure shows the evolution of the global ratio for the ETFs of the three sectors (Panel A to C), while Panel D does the same for sector portfolios. The y-axis shows the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
In terms of comparison and investment selection, Panel D presents the global classification for the three weighted sector portfolios. Overall, the health-related portfolios (healthcare and pharmaceutical) sufficiently outperform the financial portfolio in most of the evaluation period, thus underlining the supremacy of this sector and its status as an attractive investment niche. Specifically, in the prepandemic period, the three portfolios underwent a period of decline, with the pharmaceutical portfolio showing a considerably less severe drop, barely reaching negative values. From the onset of the pandemic, the health-related portfolios experienced a clear recovery, resulting from the good performance of these sectors in mitigating the virus, while the financial portfolio reported negative values for the rest of the evaluation period.
Table 5 (Panels A to C) presents the descriptive statistics of the performance of the sector ETFs based on the global measure derived from the PCA over the period under study. Our results demonstrate that the global measure of the performance of financial ETFs is negative on average, while the mean of the health-related ETFs is predominantly positive. The same holds for the three quartiles, except for the first quartile corresponding to the pharmaceutical sector, where the proportion of negative and positive values is roughly the same. Moreover, it is observed that the maximum value in the global performance measure is recorded by an ETF in the pharmaceutical sector (IHE), while the global minimum is recorded by a healthcare fund (IBB).
Table 5.
Descriptive statistics of the global ratio during the period December 2019 - April 2021. This table provides information on the descriptive statistics of the global ratio of the different ETFs for the Financial, Healthcare and Pharmaceutical Sectors (Panels A, B and C, respectively). Panel D reports on the test for equality of means (t-Test), test for equality of variances (F-test) and test for equality of medians (W-test) between the Pharmaceutical portfolio and the Healthcare and Financial portfolios. Note that the p-values relative to such test are presented in parentheses. *, ** and *** reveal statistical significance at the 10%, 5% and 1% levels, respectively. The Student's t-test is a parametric approach that analyzes the mean of related samples and determines whether there is a difference between them, while the non-parametric Wilcoxon test (W-test) does the same for medians. The F-test for equality of variances is a parametric test for the null hypothesis that two normal series exhibit the same variance.
| Mean | Std. dev. | Max. | Min. | Q1 | Q2 | Q3 | |
|---|---|---|---|---|---|---|---|
| Panel A: financial sector | |||||||
| XLF | −0.506 | 0.4808 | 0.2602 | −1.3329 | −0.7509 | −0.4158 | −0.1265 |
| VFH | −0.5563 | 0.4553 | 0.2559 | −1.3582 | −0.7642 | −0.5172 | −0.3345 |
| KRE | −1.2071 | 0.7281 | 0.6655 | −2.1586 | −1.6694 | −1.2803 | −1.0077 |
| KBE | −1.2825 | 0.6169 | 0.2867 | −2.1879 | −1.6667 | −1.2957 | −1.0139 |
| FAS | −0.5196 | 0.4456 | 0.2542 | −1.2123 | −0.8733 | −0.5315 | −0.1774 |
| KBWB | −1.0743 | 0.6663 | 0.4814 | −2.0671 | −1.4371 | −1.1267 | −0.8574 |
| IYF | −0.0261 | 0.444 | 0.814 | −0.7756 | −0.2068 | −0.0248 | 0.2554 |
| Panel B: healthcare sector | |||||||
| XLV | 0.9095 | 0.4549 | 1.9214 | 0.2863 | 0.6252 | 0.7988 | 0.98 |
| VHT | 0.9016 | 0.3359 | 1.9067 | 0.2746 | 0.7525 | 0.8058 | 0.95 |
| IBB | −0.5094 | 1.0358 | 0.4013 | −3.8373 | −0.4296 | −0.3153 | −0.0313 |
| ARKG | 0.8201 | 1.542 | 2.7052 | −3.7608 | 0.5256 | 1.3911 | 1.6457 |
| XBI | −0.565 | 0.7895 | 0.1925 | −2.927 | −0.6082 | −0.3728 | −0.1867 |
| IHI | 0.3676 | 0.518 | 1.092 | −1.3398 | 0.2832 | 0.44 | 0.6707 |
| IXJ | 1.3239 | 0.7804 | 3.7368 | 0.287 | 0.9746 | 1.0764 | 1.367 |
| Panel C: pharmaceutical sector | |||||||
| PJP | −0.2028 | 0.4399 | 0.2415 | −1.7182 | −0.1807 | −0.1098 | −0.0375 |
| IHE | 1.1395 | 2.1752 | 8.4658 | 0.0887 | 0.2656 | 0.4789 | 0.5712 |
| XPH | 0.0348 | 1.4044 | 3.8856 | −2.095 | −0.4164 | −0.2711 | −0.1519 |
| PPH | 0.221 | 0.4957 | 1.9576 | −0.3215 | −0.0176 | 0.1117 | 0.2733 |
| KURE | 0.202 | 0.835 | 1.7529 | −2.1723 | 0.102 | 0.3512 | 0.4707 |
| CHIH | 0.473 | 0.8357 | 2.3564 | −1.6826 | 0.2279 | 0.4728 | 0.7832 |
| FTXH | 0.2103 | 0.7295 | 2.4713 | −1.1558 | −0.1895 | 0.1889 | 0.3613 |
| Panel D: portfolio comparison | |||||||
| Financial portfolio | −0.871 | 0.4772 | 0.2703 | −1.593 | −1.1039 | −0.8902 | −0.5658 |
| t, F, W tests | −9.6752 | 2.8269 | 3.0000 | ||||
| (0.0000)*** | (0.0451)** | (0.0000)*** | |||||
| Healthcare portfolio | 0.2818 | 0.7411 | 0.8417 | −2.1542 | 0.2237 | 0.4974 | 0.6869 |
| t, F, W tests | −0.8339 | 6.8107 | 145 | ||||
| (0.4139) | (0.0004)*** | (1.0000) | |||||
| Pharmaceutical portfolio | 0.4351 | 0.2857 | 0.9799 | −0.2588 | 0.291 | 0.4417 | 0.5993 |
Panel D in Table 5 reports the descriptive statistics associated with the aggregate performance measure for sector portfolios. Additionally, we also provide t test, F test and W-M−W test results for the null hypothesis that the mean, the variance and the median of the pharmaceutical portfolio and either the financial or the healthcare portfolio are equal. Comparing the portfolio selection results from the Kappa and FT measures for the different risk-attitude profiles versus the global measure derived from the former, it seems evident that the aggregate measure allows for a clearer snapshot of the existing differences among the pharmaceutical, healthcare, and financial sectors. Thus, some noteworthy findings arise from this analysis. First, the pharmaceutical portfolio yields better performance results than the financial portfolio, both in average and median terms and in variance. Moreover, the null hypothesis of equality of means and medians between the pharmaceutical and the financial portfolios is rejected at the 1 % significance level, while the W-M−W statistic results allow for the rejection of the null hypothesis that the variances of the two sector portfolios are equal at the 5 % significance level. Second, the reports of successful vaccinations regarding mitigating the virus are likely to be the main reason why the average performance results corresponding to the pharmaceutical portfolio are better than those corresponding to the healthcare portfolio. Interestingly, although the pharmaceutical portfolio does not significantly outperform the healthcare portfolio in terms of either mean or median, it does so in terms of variance. Third, overall, there is consistent evidence that the performance of the pharmaceutical portfolio over the investigated period is significantly more stable than those of the two competing portfolios, which is an appealing finding for academics and practitioners and very different from the results obtained from the Kappa and FT measures at the disaggregated level.
4.4. Robustness check for global ranking
Although the aim of this paper is to investigate the performance of the pharmaceutical sector against the purely pecuniary financial sector during the COVID-19 pandemic, in this subsection, we check whether our major findings on the outperformance of the pharmaceutical portfolio remain robust once we include other control sectors in the construction of our global measure through PCA. For the choice of extra sectors that act as control variables in the main analysis of health-related and financial investment niches, we apply a filtering process based on two factors to ensure the active market status of the selected categories. First, similar to the ETF selection strategy employed for the three sectors investigated in this paper, we select seven of the largest ETFs by market cap for each of the nine additional sectors (beyond healthcare and financial) provided by the ETF database as of the end of April 2021. Second, our choice of the control sectors considered for the robustness test is motivated by a liquidity factor. Thus, we download from the Yahoo Finance database the average daily trading volume for every selected ETF comprising each of the nine sectors over the sample period (January 2019 to April 2021). Then, we calculate the mean of the average daily trading volume for every ETF and for every sector and select as controls the four sectors with the highest mean trading volume, as reported in Table 6 . Accordingly, the four control sectors that we consider in this robustness subsection are materials, technology, energy and real estate. Fig. 5 offers an overview of the evolution of trading prices for the seven ETFs comprising each of the four control sectors. Overall, we find that, comparatively, the most severe drops following the outbreak of the pandemic in March 2020 were experienced by ETFs in the materials and energy sectors. Thereafter, a recovery is observed, and all the ETFs in the materials and technology sectors and some ETFs in the energy sector exceed their highest prepandemic recorded values by the end of the sample. This is especially evident for the energy sector, where QCLN, PBW and TAN consistently more than double their prepandemic prices.
Table 6.
Additional ETF sectors and trading volume. This table provides the names of additional ETF sectors and their respective selected ETFs and the mean of the average daily trading volume for each sector based on data for each comprising ETF over the period from January 2019 to April 2021.
| Sectors | ETFs | Mean of average daily trading volume (number of contracts) |
|---|---|---|
| Materials | XHB, XLB, GNR, GUNR, VAW, LIT, ITB | 9,308,751.99 |
| Technology | QQQ, VGT, XLK, ARKK, FDN, IYW, SOXX | 8,174,493.34 |
| Energy | XLE, PBW, AMLP, VDE, XOP, TAN, QCLN | 5,720,908.59 |
| Real estate | VNQ, IYR, SCHH, VNQI, REET, XLRE, ICF | 2,984,909.34 |
| Industrials | XLI, VIS, JETS, ITA, IYT, FXR, IYJ | 2,320,151.57 |
| Consumer staples | XLP, VDC, IEV, FSTA, IYK, KXI, RHS | 1,885,582.70 |
| Consumer discretionary | XLY, XLC, VCR, PEJ, FXD, FDIS, IYC | 1,258,574.54 |
| Utilities | VPU, IGF, PAVE, NFRA, FUTY, IDU, IFRA | 217,869.52 |
| Telecommunications | VOX, NXTG, FCOM, IYZ, IXP, XTL, WBIF | 114,628.48 |
Fig. 5.
Control sectors overview. The figure shows the trading prices of the different ETFs representing the materials, technology, energy and real estate sectors (Panels A, B, C and D, respectively). All traded prices are expressed on a 100 basis to ensure proper comparability.
Based on the global measure associated with the first new component derived from the PCA, Fig. 6 presents the evolution of the performance scoring assigned to the ETFs for the financial, healthcare and pharmaceutical sectors and the four control sectors (Panels A to G) and a sector portfolio comparison (Panel H). Overall, the dynamic scores for the seven ETFs and portfolios for the three sectors investigated in this study (i.e., financial, healthcare and pharmaceutical) continue to display the same trend as depicted in Fig. 4, albeit with a change of scale due to the increased number of observations (new ETFs and sector portfolios) for the initial variables or rankings included in the subsequent PCA. The global measure for the financial sector (Panel A), for example, keeps showing a very similar trend, that is, a large drop between the end of February and early March 2020 and a subsequent poor performance in the following months, with a positive performance only at the end of the evaluation period for IYF. In addition, by including the new sectors as control variables, we observe a general pattern that is common to all of them, namely, the high initial variability in their global rankings between the end of December 2019 and March 2020. This pattern undoubtedly confers robustness to our empirical analysis and affirms that the worldwide spread of COVID-19 is a common risk factor affecting the performance of ETFs across sectors of very different natures. Regarding the new sectors, technology (Panel D) and energy (Panel E) seem to stand out, achieving very high scores in the rankings for various ETFs and keeping predominantly positive scores throughout the evaluation period (this is especially evident for the technology sector).
Fig. 6.
Time-varying global ratio assessment including control sectors. From Panel A to Panel G this figure shows the evolution of the global ratio for the ETFs of the different sectors. Panel H reports on the evolution of the global ratio for the portfolios of the seven sectors. The y-axis shows the values recorded by the ETFs and portfolios, while the x-axis shows the time evolution in months.
Table 7 reports the descriptive statistics for the performance of the ETFs comprising the three sectors under study (financial, healthcare and pharmaceutical) and the four control sectors, based on the global measure derived from the PCA. By adding new sectors as control variables, our results suggest that the dominant position of the pharmaceutical sector described in Subsection 4.3 has been nuanced and depends, of course, on the width of the set to be contrasted. However, the global measure of performance yields positive values for two (three) ETFs in the pharmaceutical sector in terms of mean (median), which still sharply contrasts with the negative mean and median values that are obtained for all the ETFs in the financial sector. Moreover, we find that the control sectors show poor performance on average, as, except for technology, the majority of sector ETFs report predominantly negative rankings. The materials sector becomes the new sector to record the lowest scores, with an overall minimum ranking of −6.15 for the XHB ETF.
Table 7.
Descriptive statistics of the global ratio for sector ETFs including control sectors during the period December 2019 - April 2021. This table provides information on the descriptive statistics of the global ratio of the different ETFs for the three sectors under study (financial, healthcare and pharmaceutical) and four control sectors (materials, technology, energy and real estate).
| Mean | Std. Dev. | Max. | Min. | Q1 | Q2 | Q3 | |
|---|---|---|---|---|---|---|---|
| Panel A: financial sector | |||||||
| XLF | −0.9000 | 0.6300 | 0.1844 | −2.2861 | −1.1175 | −0.9564 | −0.4548 |
| VFH | −0.9447 | 0.6332 | 0.1792 | −2.2528 | −1.1348 | −1.0348 | −0.5024 |
| KRE | −1.5878 | 0.6419 | 0.2152 | −2.6796 | −2.0605 | −1.5733 | −1.2383 |
| KBE | −1.6653 | 0.7127 | 0.2152 | −3.2005 | −2.0667 | −1.6296 | −1.4680 |
| FAS | −0.9021 | 0.6512 | 0.1772 | −2.8709 | −1.0526 | −0.8752 | −0.7165 |
| KBWB | −1.4587 | 0.6466 | 0.2069 | −2.9793 | −1.7330 | −1.4767 | −1.1509 |
| IYF | −0.4208 | 0.7133 | 0.5394 | −2.5714 | −0.6055 | −0.3943 | 0.1349 |
| Panel B: healthcare sector | |||||||
| XLV | 0.4794 | 0.3872 | 1.6781 | −0.0545 | 0.2245 | 0.4373 | 0.5503 |
| VHT | 0.4840 | 0.2577 | 1.1719 | 0.0301 | 0.3403 | 0.5023 | 0.5857 |
| IBB | −0.9028 | 1.4267 | 0.2408 | −5.5896 | −0.6977 | −0.5957 | −0.3599 |
| ARKG | 0.4548 | 1.9006 | 2.5747 | −5.5270 | 0.4148 | 1.0408 | 1.3313 |
| XBI | −0.9489 | 1.1693 | −0.0778 | −4.6946 | −0.8145 | −0.5822 | −0.4240 |
| IHI | −0.0274 | 0.8203 | 0.4590 | −3.1437 | 0.0290 | 0.1313 | 0.2884 |
| IXJ | 0.8918 | 0.4362 | 1.8604 | 0.2147 | 0.6158 | 0.8226 | 0.9584 |
| Panel C: materials sector | |||||||
| XHB | −0.3508 | 1.6117 | 0.7392 | −6.1494 | −0.3987 | 0.1803 | 0.3870 |
| XLB | −0.6414 | 1.3172 | 0.1952 | −4.8598 | −0.5162 | −0.1780 | 0.0851 |
| GDR | −0.3314 | 1.4672 | 4.6629 | −2.7723 | −0.6134 | −0.3939 | −0.2392 |
| GUNR | 0.1872 | 3.5281 | 13.7110 | −2.3323 | −0.6471 | −0.4838 | −0.3886 |
| VAW | −0.7332 | 1.2236 | 0.2151 | −4.6663 | −0.6053 | −0.2946 | −0.0990 |
| LIT | 2.7667 | 3.1721 | 11.5370 | −1.8076 | 1.2563 | 2.5773 | 2.6787 |
| ITB | −0.3324 | 1.5501 | 0.6003 | −6.1448 | −0.1289 | 0.0094 | 0.2034 |
| Panel D: technology sector | |||||||
| QQQ | 2.1767 | 1.1878 | 6.1345 | 0.2015 | 1.6822 | 1.9725 | 2.4187 |
| VGT | 1.5887 | 1.0605 | 5.3764 | 0.1877 | 1.2204 | 1.4941 | 1.7813 |
| XLK | 1.7253 | 1.2877 | 6.3053 | 0.1748 | 1.2604 | 1.4753 | 1.8564 |
| ARKK | 0.9953 | 1.4000 | 2.1223 | −3.7966 | 0.6868 | 1.4075 | 1.8332 |
| FDN | 1.0450 | 1.3045 | 2.4363 | −3.2074 | 0.8813 | 1.3345 | 1.7885 |
| IYW | 1.6642 | 1.1185 | 5.6419 | 0.1924 | 1.1450 | 1.5400 | 1.7712 |
| SOXX | 0.3058 | 0.3631 | 1.5567 | 0.0086 | 0.1415 | 0.1870 | 0.3659 |
| Panel E: energy sector | |||||||
| XLE | −1.4513 | 1.1447 | 1.7456 | −3.9597 | −1.8061 | −1.6371 | −1.1962 |
| PBW | 2.4007 | 2.3194 | 9.9394 | 0.2137 | 1.0984 | 1.8203 | 2.4320 |
| AMLP | −1.1726 | 1.2601 | 2.9706 | −2.6808 | −1.6238 | −1.4678 | −1.1522 |
| VDE | −1.4129 | 1.4429 | 3.3744 | −3.8754 | −1.8571 | −1.6637 | −1.2973 |
| XOP | −1.2754 | 1.7751 | 4.7820 | −4.1550 | −1.7609 | −1.5783 | −1.2406 |
| TAN | 2.5991 | 2.4894 | 9.9534 | 0.1956 | 1.1847 | 1.9896 | 2.8123 |
| QCLN | 3.4278 | 4.6116 | 19.6869 | 0.1987 | 1.4909 | 2.2211 | 2.6649 |
| Panel F: real estate sector | |||||||
| VNQ | −0.6021 | 1.0867 | 0.6851 | −4.2831 | −0.6899 | −0.4769 | −0.1700 |
| IYR | −0.4723 | 1.0312 | 0.9354 | −3.9111 | −0.6500 | −0.4473 | −0.1295 |
| SCHH | −1.3090 | 1.3277 | 0.1951 | −5.6703 | −1.3312 | −1.0910 | −0.6675 |
| VNQI | −0.1386 | 2.2064 | 8.3459 | −1.0960 | −0.8656 | −0.6407 | −0.4856 |
| REET | −1.2723 | 1.2922 | 0.2014 | −5.4913 | −1.2018 | −1.0598 | −0.7743 |
| XLRE | −0.5044 | 1.0715 | 0.9360 | −3.9454 | −0.5939 | −0.4780 | −0.0080 |
| ICF | −0.8258 | 1.2012 | 0.5537 | −4.7103 | −0.8739 | −0.6687 | −0.3469 |
| Panel G: pharmaceutical sector | |||||||
| PJP | −0.6020 | 0.8317 | 0.0955 | −3.5045 | −0.5343 | −0.3922 | −0.2678 |
| IHE | 0.7092 | 1.7222 | 6.4303 | −0.1880 | −0.1107 | 0.1736 | 0.3264 |
| XPH | −0.3571 | 1.0216 | 2.1062 | −2.1061 | −0.6915 | −0.6070 | −0.5331 |
| PPH | −0.1869 | 0.6111 | 0.9094 | −2.1196 | −0.3609 | −0.1595 | −0.0334 |
| KURE | −0.1832 | 1.1929 | 1.6790 | −3.9501 | −0.2590 | 0.0427 | 0.1724 |
| CHIH | 0.0829 | 1.1528 | 2.2793 | −3.4656 | −0.1437 | 0.2054 | 0.5122 |
| FTXH | −0.2608 | 0.3485 | 0.3280 | −1.1924 | −0.4657 | −0.2315 | −0.0068 |
Table 8 displays the main performance statistics and tests for the sector portfolios based on the global performance measure. Overall, we find that our main results on the outperformance of the pharmaceutical sector against the financial sector remain robust. Thus, the current analysis reinforces the dominance of the pharmaceutical portfolio over the financial portfolio by showing that the mean and the median of the scores given by the global screening measure for these two sector portfolios significantly differ from each other even after accounting for additional control sectors. The statistically significant outperformance of the pharmaceutical portfolio over the healthcare portfolio in terms of variance is also consistent with the result documented in Subsection 4.3. Moreover, the inclusion of new sectors in the empirical analysis yields several relevant findings. First, it is noteworthy that in addition to the financial portfolio, the pharmaceutical portfolio significantly outperforms the real estate portfolio in terms of the mean and the real estate and energy portfolios in terms of the median. Second, we find that the pharmaceutical portfolio consistently exhibits less variability than all the other sector portfolios and that differences in variance are statistically significant with respect to four of the six competing portfolios, namely, healthcare, real estate, energy and technology. Third, our results emphasize the ability of the pharmaceutical portfolio to surpass not only portfolios consisting of ETFs in purely pecuniary sectors, such as financial or real estate, but also portfolios from sectors such as energy, which includes ETFs that are predominantly linked to sustainable energy and, hence, attract investors concerned not only with risk–return performance but also with environmental issues. Moreover, our results highlight that although clean energy ETFs (e.g., TAN, PBW and QCLN) are a clearly booming niche in the evaluation period, as shown in Fig. 5, the pharmaceutical sector outperforms the energy sector in both median and variance values associated with the global performance measure.13 Overall, the empirical evidence in this subsection reinforces the importance that we placed on the pharmaceutical sector in our previous analysis by showing that our performance results are robust not only to downside risk and upside risk performance measures and diverse investor risk profiles but also to the consideration of control sectors that have seen a boost during the pandemic.
Table 8.
Descriptive statistics of the global ratio for sector portfolios including control sectors during the period December 2019 - April 2021. This table offers information on the descriptive statistics of the global ratio of the three sector portfolios under study (financial, healthcare and pharmaceutical) and four control sectors (materials, technology, energy and real estate). Tests for the equality of means (t-Test), variances (F-test) and medians (W-test) between the Pharmaceutical portfolio and the rest of the sector portfolios are also provided. Note that the p-values relative to such test are presented in parentheses. *, ** and *** reveal statistical significance at the 10%, 5% and 1% levels, respectively. The Student's T-test is a parametric approach that analyzes the mean of related samples and determines whether there is a difference between them, while the non-parametric Wilcoxon test (W-test) does the same for medians. The F-test for equality of variances is a parametric test for the null hypothesis that two normal series exhibit the same variance.
| Mean | Std. Dev. | Max. | Min. | Q1 | Q2 | Q3 | |
|---|---|---|---|---|---|---|---|
| Financial portfolio | −1.2547 | 0.6450 | 0.1967 | −2.5757 | −1.4693 | −1.3250 | −0.9325 |
| t, F, W tests | −6.2447 | 1.3319 | 24 | ||||
| (0.0000)*** | (0.5732) | (0.0000)*** | |||||
| Healthcare portfolio | −0.1187 | 1.1316 | 0.5621 | −3.9511 | 0.0606 | 0.2032 | 0.4237 |
| t, F, W tests | −0.5120 | 4.0995 | 165 | ||||
| (0.6135) | (0.0075)*** | (0.4958) | |||||
| Materials portfolio | 0.3072 | 0.7398 | 1.5772 | −1.8679 | 0.0957 | 0.4571 | 0.6318 |
| t, F, W tests | 1.1970 | 1.752 | 200 | ||||
| (0.2407) | (0.2726) | (0.0575)*** | |||||
| Technology portfolio | 1.7406 | 0.8756 | 4.4877 | 0.1793 | 1.2676 | 1.6857 | 1.9634 |
| t, F, W tests | 6.7582 | 2.4542 | 280 | ||||
| (0.0000)*** | (0.0819)* | (0.0000)*** | |||||
| Energy portfolio | 0.3161 | 2.8707 | 11.3633 | −1.5268 | −0.4277 | −0.3043 | −0.1428 |
| t, F, W tests | 0.3921 | 26.381 | 45 | ||||
| (0.00001)*** | (0.0000)** | (0.0003)*** | |||||
| Real estate portfolio | −0.8389 | 1.0616 | 0.1925 | −4.3643 | −0.8891 | −0.7081 | −0.3438 |
| t, F, W tests | −3.0136 | 3.608 | 36 | ||||
| (0.006)*** | (0.01435)** | (0.0001)*** | |||||
| Pharmaceutical portfolio | 0.0380 | 0.5589 | 0.4954 | −2.0410 | 0.0741 | 0.1805 | 0.2146 |
5. Conclusions and remarks
This study aims to shed some light on the attractiveness of the pharmaceutical sector as an investment niche compared with a purely pecuniary sector, such as finance, during the pandemic period. In addition, the performance of the pharmaceutical industry is compared with the overall sector to which it belongs, the healthcare sector. Specifically, to conduct the empirical analysis, a global performance measure is created to synthesize different investors’ attitudes toward risk (i.e., defensive, moderate and aggressive) based on measures of both downside risk and upside risk, such as Kappa indices and FT ratios. This global performance measure is calibrated using the PCA method, which facilitates summarizing the different ETF performance rankings derived from the Kappa and FT measures into a single performance classification, or first new component, which explains most of the variability of the original series (initial Kappa and FT ETF rankings). Our results reveal that the ETFs with the highest averages and medians in the global ranking are in health-related sectors, which demonstrates their supremacy over financial sector ETFs. In fact, all the ETFs in the financial sector yield negative mean and median overall performance values over the investigated period.
To provide relevant insights regarding the performance comparison among sectors and whether the differences are statistically significant, equally weighted portfolios are constructed. Interestingly, the estimation of the global performance ranking allows us to find substantial differences from those reported by the various disaggregated classifications, Kappa and FT. First, although the pharmaceutical portfolio outperforms the financial portfolio in terms of mean and median for most of the disaggregated ratios (different Kappa and FT) and the global measure (in this case, also in terms of variance), these differences are greater and more statistically significant in the latter case. Thus, the supremacy of the pharmaceutical sector over the financial sector during the pandemic is evident when the global measure is applied, which reinforces the utility of synthetizing different investment profiles across various risk–return ratios into a single measure. Second, the pharmaceutical portfolio performance exceeds the healthcare portfolio in terms of the mean at the aggregated level (global measure) and for most cases at the disaggregated level (Kappa and FT ratios) but does not do so in a statistically significant way. However, in terms of variance, the global measure shows that the pharmaceutical portfolio significantly outperforms the healthcare portfolio, which does not occur at the disaggregated level. This second piece of evidence suggests the superiority of the pharmaceutical subsector and places it at the top of the overall healthcare industry to which it belongs in terms of temporal stability.
Moreover, based on our PCA-based global measure, we show that our major findings regarding the outperformance of the pharmaceutical portfolio over the financial portfolio remain robust to the inclusion of other control industries that have seen a boost during the pandemic. Our results further reveal that in addition to the financial portfolio, the pharmaceutical portfolio outperforms the real estate portfolio in terms of the mean and the real estate and energy portfolios in terms of the median. In addition, we report that the pharmaceutical portfolio is consistently more stable than all the other sector portfolios and that the variance differences are statistically significant between the former and the healthcare, real estate, energy, and technology portfolios. Finally, the results of our study highlight the potential of pharmaceutical portfolios to outperform not only portfolios made of ETFs from purely pecuniary sectors such as finance or real estate but also portfolios from booming investment niches such as clean energy, which are based on ETFs that appeal predominantly to investors with concerns beyond the risk–return ratio.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Healthy Alternative | Financial Times, 2021. Retrieved June 20, 2021, from https://www.ft.com/content/b99bb9f1-bc58-4df5-ae4b-f8e586d20f7f.
One of the first vaccines to receive the green light for commercialization was that of the biotech company Moderna, which reported revenues of $18.5 billion in 2021, compared to $803 million in 2020. In collaboration with BioNTech, the U.S. pharmaceutical giant Pfizer presented revenues of $81,288 million in 2021, thus almost doubling previous year’s records of $41,651 million. Another remarkable example of boost in total revenue attributed chiefly to commercial sales of its Covid-19 vaccine is Novavax, which reported revenues of $1.1 billion for 2021 against $476 million for 2020.
Recent relevant studies focus on identifying the multiple waves of pandemic progression accounting for very different factors and variables of interest [46].
These funds are large institutional portfolios that invest in companies that manufacture medical equipment, health services and insurance and develop new drugs and treatments (Esposito, A. How Healthcare Funds Performed in the Covid-19 Crisis | Morningstar, 2020. Retrieved May 15, 2021, from https://www.morningstar.co.uk/uk/news/200961/how-healthcare-funds-performed-in-the-covid-19-crisis.aspx).
[37] relate the different orders of downside risk, upside risk, and Omega ratios’ measures to investors' risk aversion. They further encourage the construction of alternative performance measures that could be plotted similarly while respecting the risk aversion for all assets with positive excess returns. The basic idea of this construction of measures is to separate the threshold or minimum return that defines excess return from the threshold that characterizes undesirable outcomes.
Standardizing involves expressing different variables on the same scale. From the initial variables, it is conducted by subtracting the mean and dividing by the standard deviation.
In this research, the matrix corresponds to six standardized rankings established according to different orders of and , as detailed in Section 4 of the empirical analysis. Thus, in each element of the matrix , represents the number of initial variables or rankings, while counts the realizations or assets ranked.
Market cap is calculated by multiplying the outstanding shares by their market price on each date.
Specifically, when quoting in yields to maturity in the Federal Reserve's data provider (fred.stlouisfed.org), we must calculate daily logarithmic yields from zero coupon bond prices at each maturity.
Both the size and the frequency with which we recalculate the window remain fixed throughout the evaluation period.
Although the first COVID-19 cases were detected in Wuhan (China) in December 2019, the virus did not severely affect global financial markets until March 2020 [48].
As evidenced in Section 3, considering the median instead of the mean to evaluate models in nonparametric contexts such as financial series seems a suitable alternative to support our empirical evidence.
Clean energy funds have become a fundamental investment vehicle in recent years for investors motivated not only by pecuniary issues but also by environmental awareness (https://www.morningstar.co.uk/uk/news/209411/sustainable-funds-record-breaking-year.aspx). Most are baskets of company stocks that exhibit a certain environmental relation. We find them in ETFs with very little diversification, such as TAN, which invests only in 35 international companies related to solar energy, as well as others with high diversification, such as PBW or QCLN, which include many companies focused not only on solar power but also on biofuels, advanced batteries and technology, among others.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ins.2022.07.146.
Appendix A.
Fig. A1. Fig. A2. Fig. A3. Fig. A4. Fig. A5. Fig. A6.
Fig. A1.
Time-varying defensive Kappa index assessment. Panels A to C show the evolution of the Kappa index, from the perspective of defensive investors, for the ETFs of the three sectors, while Panel D does the same for sector portfolios. The y-axis reports on the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
Fig. A2.
Time-varying moderate Kappa index assessment. Panels A to C show the evolution of the Kappa index, from the perspective of moderate investors, for the ETFs of the three sectors, while Panel D does the same for sector portfolios. The y-axis shows the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
Fig. A3.
Time-varying aggressive Kappa index assessment. Panels A to C show the evolution of the Kappa index, from the perspective of aggressive investors, for the ETFs of the three sectors, while Panel D does the same for sector portfolios. The y-axis shows the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
Fig. A4.
Time-varying defensive FT ratio assessment. Panels A to C show the evolution of the FT ratio, from the perspective of defensive investors, for the ETFs of the three sectors, while Panel D does the same for sector portfolios. The y-axis shows the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
Fig. A5.
Time-varying moderate FT ratio assessment. Panels A to C show the evolution of the FT ratio, from the perspective of moderate investors, for the ETFs of the three sectors, while Panel D does the same for sector portfolios. The y-axis shows the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
Fig. A6.
Time-varying aggressive FT ratio assessment. Panels A to C show the evolution of the FT ratio, from the perspective of aggressive investors, for the ETFs of the three sectors, while Panel D does the same for sector portfolios. The y-axis shows the values recorded by the different ETFs and portfolios, while the x-axis shows the time evolution in months.
Appendix B. Supplementary data
The following are the Supplementary data to this article:
Data availability
Data will be made available on request.
References
- 1.B. Anciano. Markets Now - Martes 24 de marzo de 2020 | Tiempos financieros https://www.ft.com/content/b5c640c3-e431-48ca-8b0d-688e2371d761 (accessed May 8, 2021).
- 2.L. Fletcher. Hedge fund veteran looks to cash in on biotech boom | Financial Times, 2020. https://www.ft.com/content/c2788e4e-35df-11ea-a6d3-9a26f8c3cba4 (accessed May 14, 2021).
- 3.H. Kuchler. Novavax closes in on Covid triumph after 33 years of failure | Financial Times, 2021. https://www.ft.com/content/22d3805e-c304-4d95-ae32-f559ff34886a (accessed May 15, 2021).
- 4.B. O’Connor. Health Care Funds Held Their Own. But They May Not Be Bargains. - The New York Times, 2020. https://www.nytimes.com/2020/04/17/business/mutfund/health-care-invest-not-bargains.html?searchResultPosition=9 (accessed May 15, 2021).
- 5.Dai X., Wang Q., Zha D., Zhou D. Multi-scale dependence structure and risk contagion between oil, gold, and US exchange rate: a wavelet-based vine-copula approach. Energy Econ. 2020;88 doi: 10.1016/j.eneco.2020.104774. [DOI] [Google Scholar]
- 6.Qiao X., Zhu H., Hau L. Time-frequency co-movement of cryptocurrency return and volatility: evidence from wavelet coherence analysis. Int. Rev. Financ. Anal. 2020;71 doi: 10.1016/j.irfa.2020.101541. [DOI] [Google Scholar]
- 7.León A., Navarro L., Nieto B. Screening rules and portfolio performance. North Am. J. Econ. Financ. 2018;2019(48):642–662. doi: 10.1016/j.najef.2018.08.001. [DOI] [Google Scholar]
- 8.Nieto B., Rubio G. The risk aversion and uncertainty channels between finance and macroeconomics. Financ. Res. Lett. 2022;45 doi: 10.1016/J.FRL.2021.102188. [DOI] [Google Scholar]
- 9.Jensen M.C. The performance of mutual funds in the period 1945–1964. J. Finance. 1968;23(2):389–416. [Google Scholar]
- 10.Treynor J.L. How to rate management investment funds. Harv. Bus. Rev. 1965;18:63–79. [Google Scholar]
- 11.Sharpe W.F. Mutual fund performance. J. Bus. 1966;39(1):119–138. [Google Scholar]
- 12.Graham J.E., Lassala C., Ribeiro-Navarrete B. A fuzzy-set analysis of conditions influencing mutual fund performance. Int. Rev. Econ. Financ. 2019;61:324–336. doi: 10.1016/j.iref.2018.01.017. [DOI] [Google Scholar]
- 13.Al-Yahyaee K.H., Mensi W., Rehman M.U., Vo X.V., Kang S.H. Do islamic stocks outperform conventional stock sectors during normal and crisis periods? extreme co-movements and portfolio management analysis. Pacific Basin Financ. J. 2020;62 doi: 10.1016/j.pacfin.2020.101385. [DOI] [Google Scholar]
- 14.Boako G., Alagidede I.P., Sjo B., Uddin G.S. Commodities price cycles and their interdependence with equity markets. Energy Econ. 2020;91 doi: 10.1016/j.eneco.2020.104884. [DOI] [Google Scholar]
- 15.Nagy B.Z., Benedek B. Higher co-moments and adjusted sharpe ratios for cryptocurrencies. Financ. Res. Lett. 2021;39 doi: 10.1016/j.frl.2020.101543. [DOI] [Google Scholar]
- 16.Fishburn P. Mean-risk analysis with risk associated with below-target returns. Am. Econ. Rev. 1977;67(2):116–126. doi: 10.2307/1807225. [DOI] [Google Scholar]
- 17.Bai J., Bali T.G., Wen Q. Common risk factors in the cross-section of corporate bond returns. J. financ. econ. 2019;131(3):619–642. doi: 10.1016/j.jfineco.2018.08.002. [DOI] [Google Scholar]
- 18.Bali T.G., Demirtas K.O., Levy H. Is there an intertemporal relation between downside risk and expected returns? J. Financ. Quant. Anal. 2009;44(4):883–909. doi: 10.1017/S0022109009990159. [DOI] [Google Scholar]
- 19.A. Ang, J. Chen, Y. Xing. Downside Risk. Review of Financial Studies. Oxford Academic December 1, 2006, pp 1191–1239. https://doi.org/10.1093/rfs/hhj035.
- 20.Mensi W., Rehman M.U., Al-Yahyaee K.H., Al-Jarrah I.M.W., Kang S.H. Time frequency analysis of the commonalities between bitcoin and major cryptocurrencies: portfolio risk management implications. North Am. J. Econ. Financ. 2018;2019(48):283–294. doi: 10.1016/j.najef.2019.02.013. [DOI] [Google Scholar]
- 21.Chen W., Zhang H., Mehlawat M.K., Jia L. Mean-variance portfolio optimization using machine learning-based stock price prediction. Appl. Soft Comput. 2021;100 doi: 10.1016/j.asoc.2020.106943. [DOI] [Google Scholar]
- 22.Abuzayed B., Bouri E., Al-Fayoumi N., Jalkh N. Systemic risk Spillover across global and country stock markets during the COVID-19 pandemic. Econ. Anal. Policy. 2021;71:180–197. doi: 10.1016/J.EAP.2021.04.010. [DOI] [Google Scholar]
- 23.Bessler W., Taushanov G., Wolff D. Optimal asset allocation strategies for international equity portfolios: a comparison of country versus industry optimization. J. Int. Financ. Mark. Institutions Money. 2021;72 doi: 10.1016/j.intfin.2021.101343. [DOI] [Google Scholar]
- 24.Díaz A., Esparcia C., López R. The diversifying role of socially responsible investments during the COVID-19 crisis: a risk management and portfolio performance analysis. Econ. Anal. Policy. 2022;75:39–60. doi: 10.1016/J.EAP.2022.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Esparcia C., Jareño F., Umar Z. Revisiting the Safe Haven Role of Gold across Time and Frequencies during the COVID-19 Pandemic. North Am. J. Econ. Financ. 2022;61 doi: 10.1016/J.NAJEF.2022.101677. [DOI] [Google Scholar]
- 26.Salisu A.A., Vo X.V., Lawal A. Hedging oil price risk with gold during COVID-19 pandemic. Resour. Policy. 2021;70(August) doi: 10.1016/j.resourpol.2020.101897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mensi W., Al-Yahyaee K.H., Wanas Al-Jarrah I.M., Vo X.V., Kang S.H. Does volatility connectedness across major cryptocurrencies behave the same at different frequencies? A portfolio risk analysis. Int. Rev. Econ. Financ. 2021;76:96–113. doi: 10.1016/j.iref.2021.05.009. [DOI] [Google Scholar]
- 28.Zhou X., Qian H., Pérez-Rodríguez J.V., González López-Valcárcel B. Risk dependence and cointegration between pharmaceutical stock markets: the case of China and the USA. North Am. J. Econ. Financ. 2020;52 doi: 10.1016/j.najef.2020.101175. [DOI] [Google Scholar]
- 29.Sun L., Wang K., Xu L., Zhang C., Balezentis T. A time-varying distance based interval-valued functional principal component analysis method – A case study of consumer price index. Inf. Sci. (Ny) 2022;589:94–116. doi: 10.1016/J.INS.2021.12.113. [DOI] [Google Scholar]
- 30.Zheng H., Fu L., Ye Q. Flexible capped principal component analysis with applications in image recognition. Inf. Sci. (Ny) 2022 doi: 10.1016/J.INS.2022.06.038. [DOI] [Google Scholar]
- 31.Chu Z., Yu J., Hamdulla A. LPG-Model: a novel model for throughput prediction in stream processing, using a light gradient boosting machine, incremental principal component analysis, and deep gated recurrent unit network. Inf. Sci. (Ny) 2020;535:107–129. doi: 10.1016/J.INS.2020.05.042. [DOI] [Google Scholar]
- 32.Liang C., Tang L., Li Y., Wei Y. Which sentiment index is more informative to forecast stock market volatility? Evidence from China. Int. Rev. Financ. Anal. 2020;71 doi: 10.1016/j.irfa.2020.101552. [DOI] [Google Scholar]
- 33.Xiong L., Zhu F. Robust quasi-likelihood estimation for the negative binomial integer-valued GARCH(1,1) model with an application to transaction counts. J. Stat. Plan. Inference. 2019;203:178–198. doi: 10.1016/j.jspi.2019.03.010. [DOI] [Google Scholar]
- 34.Wan R., Fulop A., Li J. Real-time Bayesian learning and bond return predictability. J. Econom. 2022;230(1):114–130. doi: 10.1016/J.JECONOM.2020.04.052. [DOI] [Google Scholar]
- 35.Shah A., Chauhan Y., Chaudhury B. Principal component analysis based construction and evaluation of cryptocurrency index. Expert Syst. Appl. 2021;163 doi: 10.1016/j.eswa.2020.113796. [DOI] [Google Scholar]
- 36.Kamphuis B.W., Kanavos P. Assessing pricing and reimbursement policies for generic pharmaceuticals in the MENA region for improved efficiency, affordability and generic penetration. Heal. Policy OPEN. 2021;100045 doi: 10.1016/j.hpopen.2021.100045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Balder S., Schweizer N. Risk aversion vs. the omega ratio: consistency results. Financ. Res. Lett. 2017;21:78–84. doi: 10.1016/j.frl.2016.12.012. [DOI] [Google Scholar]
- 38.Kaplan P.D., Knowles J.A. Kappa: a generalized downside risk-adjusted performance measure. J. Perform. Meas. 2004;8:42–54. [Google Scholar]
- 39.Farinelli S., Tibiletti L. Sharpe thinking in asset ranking with one-sided measures. Eur. J. Oper. Res. 2008;185(3):1542–1547. doi: 10.1016/J.EJOR.2006.08.020. [DOI] [Google Scholar]
- 40.I.T. Jollife, J. Cadima. Principal component analysis: a review and recent developments. Philos. Trans. Royal Soc. A: Math., Phys. Eng. Sci.. Royal Society of London April 13, 2016. https://doi.org/10.1098/rsta.2015.0202. [DOI] [PMC free article] [PubMed]
- 41.Wellmann D., Trück S. Factors of the term structure of sovereign yield spreads. J. Int. Money Financ. 2018;81:56–75. doi: 10.1016/j.jimonfin.2017.10.006. [DOI] [Google Scholar]
- 42.Zhu X. Cross-correlations between the CSI300 index and commodity markets: non-stationary principal component analysis (NSPCA) Phys. A Stat. Mech. its Appl. 2019;529 doi: 10.1016/j.physa.2019.121534. [DOI] [Google Scholar]
- 43.Foroni C., Marcellino M., Stevanovic D. Forecasting the Covid-19 recession and recovery: lessons from the financial crisis. Int. J. Forecast. 2021 doi: 10.1016/j.ijforecast.2020.12.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Adams Z., Füss R., Glück T. Are correlations constant? Empirical and theoretical results on popular correlation models in finance. J. Bank. Financ. 2017;84:9–24. doi: 10.1016/j.jbankfin.2017.07.003. [DOI] [Google Scholar]
- 45.Kondilis E., Tarantilis F., Benos A. Essential public healthcare services utilization and excess non-COVID-19 mortality in Greece. Public Health. 2021;198:85–88. doi: 10.1016/J.PUHE.2021.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sohrabi C., Alsafi Z., O’Neill N., Khan M., Kerwan A., Al-Jabir A., Iosifidis C., Agha R. World health organization declares global emergency: a review of the 2019 novel coronavirus (COVID-19) Int. J. Surg. 2020;76:71–76. doi: 10.1016/J.IJSU.2020.02.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Data will be made available on request.