Abstract
Convection-enhanced delivery of rhenium-186 (186Re)-nanoliposomes is a promising approach to provide precise delivery of large localized doses of radiation for patients with recurrent glioblastoma multiforme. Current approaches for treatment planning utilizing convection-enhanced delivery are designed for small molecule drugs and not for larger particles such as 186Re-nanoliposomes. To enable the treatment planning for 186Re-nanoliposomes delivery, we have developed a computational fluid dynamics approach to predict the distribution of nanoliposomes for individual patients. In this work, we construct, calibrate, and validate a family of computational fluid dynamics models to predict the spatio-temporal distribution of 186Re-nanoliposomes within the brain, utilizing patient-specific pre-operative magnetic resonance imaging (MRI) to assign material properties for an advection-diffusion transport model. The model family is calibrated to single photon emission computed tomography (SPECT) images acquired during and after the infusion of 186Re-nanoliposomes for five patients enrolled in a Phase I/II trial (NCT Number NCT01906385), and is validated using a leave-one-out bootstrapping methodology for predicting the final distribution of the particles. After calibration, our models are capable of predicting the mid-delivery and final spatial distribution of 186Re-nanoliposomes with a Dice value of 0.69 ± 0.18 and a concordance correlation coefficient of 0.88 ± 0.12 (mean ± 95% confidence interval), using only the patient-specific, pre-operative MRI data, and calibrated model parameters from prior patients. These results demonstrate a proof-of-concept for a patient-specific modeling framework, which predicts the spatial distribution of nanoparticles. Further development of this approach could enable optimizing catheter placement for future studies employing convection-enhanced delivery.
Keywords: radiation therapy, glioblastoma multiforme, convection-enhanced delivery, mathematical oncology, computational oncology, computational fluid dynamics
1. Introduction
Glioblastoma multiforme (GBM) is the most common and deadliest of all primary brain cancers [1,2]. Shortly after diagnosis, patients typically receive maximal allowable resection (to remove the bulk tumor and reduce intracranial pressure), followed by fractionated radiotherapy concurrent with temozolomide to target any residual disease [3]. The extraordinary difficulty of resecting the entire tumor, combined with its infiltrative nature all but guarantees disease recurrence resulting in a median overall survival of 15 months [4]—a time period that has only improved marginally over the last decade despite great effort and numerous clinical trials [1,2]. Given the current limitations a number of therapeutic strategies are under investigation with the goal of extending overall survival and improving quality of life [5]. An increasing number of these therapies take advantage of convection-enhanced delivery (CED) to overcome the inherent limitations of the blood brain barrier.
Due to the short pathlength (2-4 mm) of beta particles, beta-emitting radionuclides are capable of delivery a locally high dose of radiation to diseased tissue, while simultaneously limiting exposure to healthy brain tissue [6]. One such radiotherapeutic in development is 186Re-nanoliposomes (RNL) which is delivered via CED directly to the site of the glioblastoma recurrence. A promising pre-clinical study, has shown that RNL effectively halts disease progression in GBM xenografts, and that radio-nanoliposome retention in the tumor region is much higher than that of molecular radiotherapeutics [7,8]. Given that one of every ten emissions is associated with a non-therapeutic gamma photon, RNL can be localized via standard clinical single-photon emission computed tomography (SPECT). This approach is now being investigated in an on-going phase I/II clinical trial (NCT Number NCT01906385) to deliver high doses of radiation. The immediate goal of this trial is to treat recurrent tumors and their associated margins with high dose radiation to slow and potentially prevent subsequent recurrent disease, with the ultimate goal of significantly extending patient survival without further surgical resections [7–9].
Many therapeutics delivered via CED have had limited success in clinical trials [5,10]. While the direct delivery of a concentrated drug or radioactive agent to the tumor avoids systemic toxicity and bypasses challenges associated with passing the blood-brain barrier, successful delivery and treatment is highly dependent on the individual patient and the therapeutic being administered [5]. Jahangiri et. al stated that accurate prediction of the spatio-temporal distribution of therapeutic delivered via CED is necessary to maximize the chance of success for any given experimental therapy [5]. In particular, a lack of systematic investigation into the positioning of the cannula and delivery of the agent was noted. For example, 68% of the patients entered into the PRECISE trial ([11]; convection-enhanced delivery of IL13-PE38QQR) had catheter placements that did not follow the trial protocol, potentially adversely impacting the efficacy of the therapy. Computational modeling of the distribution of the therapeutic is one approach that may improve catheter placement, potentially resulting in improved treatment efficacy [5,11].
With the above concerns, and, given the high doses of beta radiation delivered by RNL, it is of great importance to ensure a catheter placement that minimizes the leakage into the cerebrospinal fluid (CSF) while minimizing healthy tissue exposure and simultaneously maximizing tumor coverage. While surgical planning software exists for the delivery of molecular therapeutics [12–14], there is no such software tool or model (to our knowledge) specifically designed to predict the spatiotemporal distribution of nanoparticles delivered via CED. As nanoparticles can be an order of magnitude larger in size than molecular agents (~100 nm versus 10-15 nm for antibodies and <3 nm for most small molecular drugs), therapeutic particles will have more frequent interaction with boundaries within the brain and undergo more drag, therefore travelling slower and require more pressure to distribute than a fully dissolved therapeutic. Further, current state-of-the-art computational models of CED rely on particle-based discretization, which is computationally expensive to run, slow to converge, and are highly sensitive to initial conditions and random seeds [12].
The goal of this study is to define, calibrate, and validate a computational fluid dynamics model of CED delivery of RNL to recurrent GBM. This approach is designed to account for decreased nanoparticle mobility associated with their larger size in comparison to molecular agents, and utilizes patient-specific pre-operative imaging to assign patient-specific material properties. To achieve this goal, a family of twelve models are designed to represent different approaches for the characterizing the relevant material properties of the system. The models are calibrated to the observed distribution of RNL measured via SPECT during and immediately following the infusion of RNL as part of an ongoing clinical trial. To assess the validity of each model, a leave-one-out framework is utilized, such that only the imaging data obtained prior to a patient’s RNL infusion is utilized for predicting the final spatial distribution of RNL within the patient. Finally, we employ model selection to identify the most parsimonious means to accurately assign patient-specific material properties and predict the delivery of RNL on a patient-specific basis.
2. Methods
2.1. Clinical protocol and delivery of rhenium-186 nanoliposomes
Five patients from the Phase I/II clinical trial of RNL performed at The University of Texas Health Science Center at San Antonio [9] were included in the study. The population consists of adult patients suffering from recurrent GBM after an initial tumor resection. While a complete description of the study (patient population, entry criteria, and full details on image acquisition, etc.) can be found in the public clinical trial documentation (NCT Number NCT01906385), here we summarize the salient details relevant to our modeling efforts.
After initial screening and baseline imaging were performed (see Imaging details, below), a single catheter was surgically inserted intracranially to the site of infusion, and the patient was allowed to rest for approximately 8 hours. We note that this catheter is not an intra-vascular catheter (i.e., a catheter positioned within a blood vessel); rather it is an intra-cranial catheter that is surgically placed within the tumor. RNL was then delivered via an automated syringe pump, initially at a rate of 1 microliters (μl) per minute to ensure minimal leakage into the cerebral spinal fluid (CSF) and nearby vasculature. After 20 minutes, the distribution of RNL was verified to be within the tumor using a planar gamma camera image, and the infusion rate was increased to 2 μl/min. After an additional 20 minutes, the distribution of RNL was again verified to be within the tumor using a dynamic planar gamma camera image, and the infusion rate was increased to 5 μl/min. The infusion rate remained at 5 μl/min for the remainder of the infusion. For the purposes of this study, and due to the minimal amount of RNL delivered during the initial ramping of the rate, we assumed that the rate of delivery was a constant 5 μl per minute. The total volume of RNL infused and time of infusion for each patient are listed in Table 1.
Table 1.
Clinical patient details
| Patient | Infused volume (mL) | Infusion time (min) | Dose (mCi) | CSF leak? |
|---|---|---|---|---|
| 1 | 0.66 | 132 | 1 | yes |
| 2 | 1.32 | 264 | 2 | no |
| 3 | 2.64 | 528 | 4 | no |
| 4 | 2.64 | 528 | 4 | yes |
| 5 | 2.64 | 528 | 4 | yes |
2.2. Imaging details
Each patient first underwent an initial imaging protocol consisting of multimodal magnetic resonance imaging (MRI) for surgical planning on a Philips Acheiva 3T (Best, Netherlands) scanner using an 8-channel coil. The MR measurements consisted of T1- and T2- weighted images, T2-fluid attenuated inversion recovery (FLAIR) images, post-contrast T1-weighted (after intravenous injection of Gadovist (Bayer, Whippany, NJ), and diffusion weighted images. Additionally, apparent diffusion coefficient (ADC) maps were derived from the diffusion weighted imaging data and are reconstructed on the Philips console. All images considered in the present study were acquired in the axial plane, and collected with no overlap between adjacent slices. Additional details on the MRI acquisition parameters are provided in Tables 2 and 3.
Table 2.
Clinical MR image acquisition parameters
| Image | Sequence | TR (ms) | TE (ms) | TI (ms) | Flip angle | b-values |
|---|---|---|---|---|---|---|
| T1 | Fast field echo | 25 | 2.1 | - | 30° | - |
| T1+contrast | Fast field echo | 25 | 2.1 | - | 30° | - |
| T2 | Turbo spin echo | 8,052 | 100 | - | 90° | - |
| T2-FLAIR | Turbo spin echo | 11000 | 125 | 2800 | 90° | - |
| ADC | Single Shot SENSE | 4,390 | 56 | - | 90° | 0, 1000 |
Table 3.
Clinical imaging details
| Modality | In-plane Resolution (mm) | Slice Resolution (mm) | FOV (voxels) |
|---|---|---|---|
| T1 | 1.0 | 1.0 | 256 × 256 × 165 |
| T1+Contrast | 1.0 | 1.0 | 256 × 256 × 165 |
| ADC | 0.98 | 5.0 | 256 × 256 × 30 |
| SPECT | 4.42 | 4.42 | 128 × 128 × 128 |
| CT | 1.10 | 4.42 | 512 × 512 × 90 |
On the day of the RNL infusion, SPECT images were acquired using a GE Healthcare Infinia SPECT / computed tomography (CT) (Milwaukee, WI) scanner. Within the SPECT field of view, an imaging standard containing one fifth of the total amount of RNL delivered to the patient was included to facilitate decay correction and consistency between imaging time points. X-ray CT data acquired simultaneously with the SPECT images provided anatomical landmarks for interpretation of the SPECT images and enabled registration to the MRI data. Additionally, the x-ray CT data was used to identify the location of the catheter tip. SPECT/CT images were collected after half of the RNL volume was infused, and at the end-of-infusion (EOI) of the RNL. The field of view and resolution of each imaging modality used in this study are listed in Table 3. (We note that an additional set of SPECT/CT images are acquired one week after infusion, to track RNL retention over a longer time period, but those images are not considered in the present study.)
2.3. Image processing
All image processing was performed in MATLAB 2019a using the Image Processing Toolbox (Mathworks, Natick, MA). The reader is encouraged to refer to Figure 1 which provides a schematic of our image processing and modeling framework, and Figure 2 which shows representative tissue segmentations. For each imaging modality, voxels which presented non-physical values (e.g., ADC < 0 mm2/s, or SPECT signal intensity < 0) were replaced with the mean of the eight nearest non-zero neighboring voxels in the same axial slice. A Gaussian filter with a 3 × 3 voxel kernel was applied to each MR image on each axial slice to reduce the effect of noise on individual voxels and reduce large gradients in the images. We then performed manual image segmentations of the gross tumor volume and the brain-skull boundary. Both regions were segmented on the imaging slice that corresponded to the maximal SPECT intensity at the end of injection. The gross tumor volume defined as the enhancing volume on the post-contrast T1-weighted image was segmented by hand (arrow a in Figure 2). The skull-brain boundary was manually segmented using the T1-weighted image (arrow b in Figure 2). For both manual segmentations, we first visualized the T1-weighted post-contrast (for the tumor segmentation) or the pre-contrast (for skull-brain boundary) image using imagesc in MATLAB 2019a. We then used roipoly in MATLAB 2019a to manually segment the region of interest which returns a binary mask equal to 1 within the ROI and zero outside the ROI. Using the brain segmentation mask, we then applied a k-means clustering to the T1-weighted image using three clusters (white matter, gray matter, other) [15] (arrow c in Figure 2). CSF was segmented using a threshold of ADC values greater than 3 × 10−3 mm2/sec, and validated by comparison to T2 and FLAIR images [16].
Figure 1. Schematic of the patient-specific modeling framework.
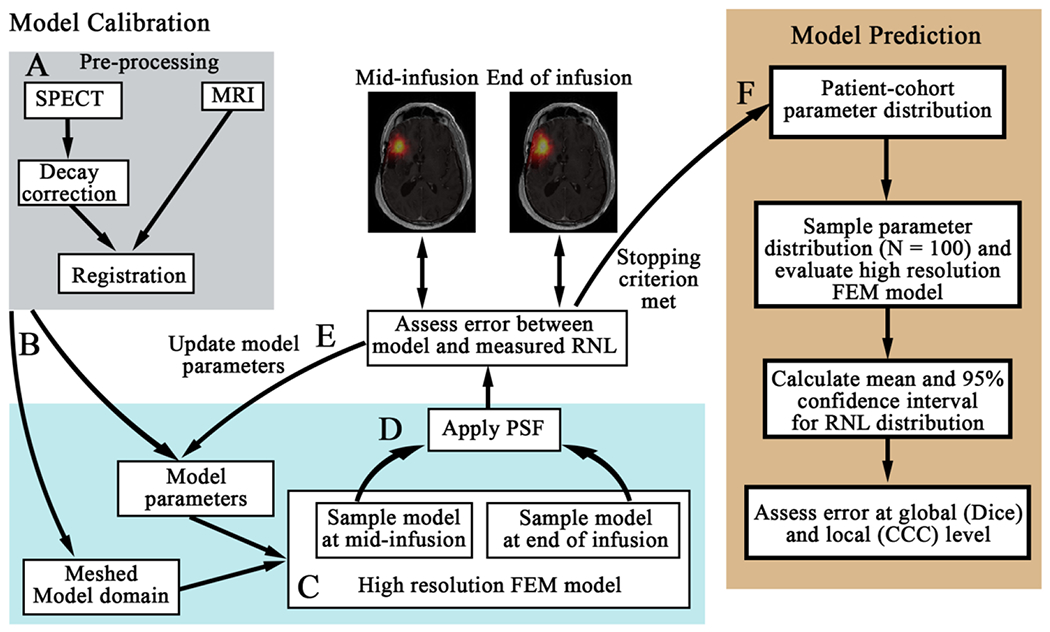
First, the SPECT data is decay corrected and co-registered to the MRI data (panel A). The registered domains are used to generate the FEM mesh (arrow B) and assign spatially-varying model parameters. Each model within the model family is then run forward using an initial guess of model parameters on the high-resolution mesh (panel C). The model estimated distribution of RNL is sampled at the mid-infusion and end of infusion time points. We apply our estimated point spread function (PSF) of the SPECT data and resample the image to the lower-resolution of the SPECT data (arrow D). The error between the model estimated distribution of RNL and the measured distribution are compared. Model parameters are updated (arrow E) until stopping criterion are met (arrow F). The optimized model parameters are saved for the patient-cohort parameter distribution (arrow F). Once all of the models are calibrated for each patient, we then performed our prediction scenario using a leave-one-out approach (right panel). We first determine the cohort parameter distribution using data from all but the patient whose RNL distribution we will predict. We sample this distribution 100 times and evaluate the high-resolution FEM model. The mean and 95% confidence interval are calculated from the 100 simulations, and the mean predicted RNL distribution is compared to the measured RNL distribution at the global and local levels.
Figure 2. Representative tissue segmentation for a representative patient.
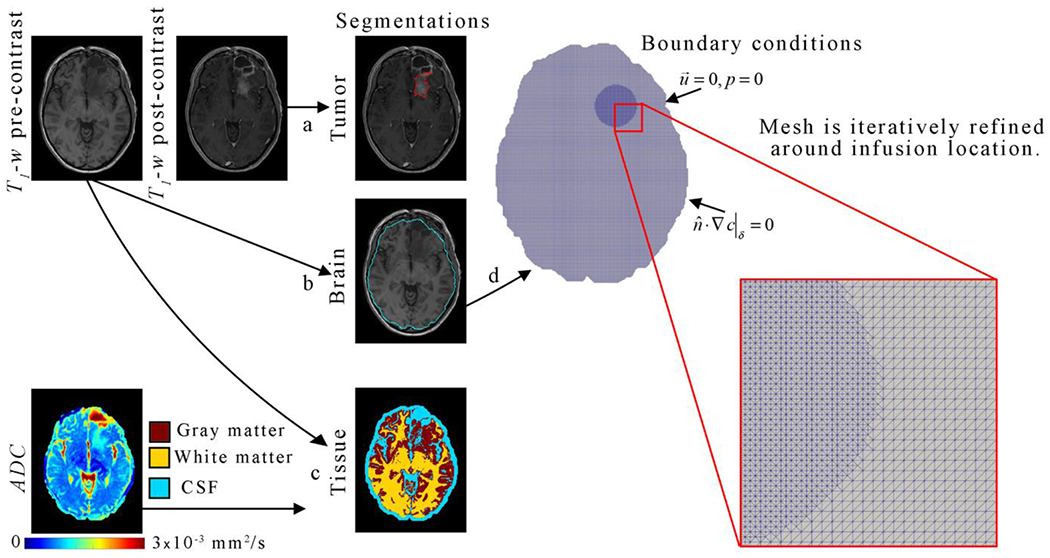
The gross tumor volume was manually segmented (arrow a) using the post-contrast T1-weighted image. Similarly, the skull-brain boundary (or brain segmentation) was manually segmented (arrow b) on the pre-contrast T1-weighted image. Using the brain segmentation mask, a k-means clustering algorithm was applied to the pre-contrast T1-weighted image to segmented (arrow c) gray matter (red), white matter (yellow), and other (including CSF, cyan). Diffusion weighted estimates of the ADC were also used to identify CSF as areas with an ADC greater than or equal to 3 x 10−3 mm2/s (arrow c). The brain segmentation was used to define the computational domain and mesh boundary. Mesh elements within a 30 mm diameter circle surrounding the infusion location was refined (red inset).
SPECT images were first normalized to the total intensity of the SPECT standard within the image, to correct for decay in radioactivity and to obtain a map of relative RNL concentration. Prior to normalization to the standard, the SPECT images provide a map of radioactive activity as the signal is directly proportional to concentration in any given voxel. After normalization, the signal intensity estimates the actual concentration of RNL, which serves as our (internal) gold standard for quantifying the spatial distribution of RNL concentration across time [7,8].
All images were aligned via rigid registration using the ‘imregtform’ and ‘imwarp’ functions in MATLAB using the ‘multimodal’ option. The MR images were first registered to the T1-weighted image. Then the co-registered CT and SPECT images at the EOI were cropped to include only the skull within the FOV. The T1-weighted image was then registered to the cropped CT image acquired at EOI, and the resulting transformation was applied to the remaining MR image sets. SPECT and CT images collected midway through injection were also cropped to include only the skull within the FOV and were registered to the CT image collected at the EOI. For our analysis, we isolated the axial slice containing the maximal SPECT intensity at the EOI.
To directly compare the experimentally measured SPECT image to our model derived SPECT image, we developed an empirical SPECT point-spread function (PSF) to facilitate transforming a predicted RNL distribution into the corresponding predicted SPECT image. The SPECT PSF was approximated using a Jaszczak Deluxe SPECT Phantom (Biodex, Shirley, NY). The phantom was imaged while submerged in water, and in air, according to the same imaging conditions as an individual patient. A digital representation of the phantom (identical in dimensions to the Jaszczak phantom) was approximated by a 3D sphere, with uniform intensity, and a resolution 10× higher than the SPECT image (0.442 mm), positioned to match the center of mass between the phantom image and the simulated phantom. The simulated phantom image was then convolved with Gaussian point-spread functions of varying standard deviations, and down-sampled to match the SPECT resolution (4.42 mm). The summed square-error (SSE) between the actual SPECT phantom image and the simulated phantom image was minimized. Using this method, it was empirically determined that the standard deviation of the Gaussian PSF was 5.23 mm which agrees with values previously reported for clinical SPECT scanners [17,18]. This PSF was then applied to all simulated RNL fields to simulate a SPECT acquisition, thereby enabling direct comparison of the predicted RNL distribution to that measured from the SPECT data.
2.4. Fluid dynamics model
To determine the distribution of RNL at EOI we solve a system of fluid dynamic equations describing the delivery and interstitial transport of RNL in two dimensions within the brain domain. (We recognize that 2D represents a simplification and we return to this important point in the Discussion section.) Interstitial pressure and fluid velocity are modeled using the laws of Darcy and Starling, respectively. There are three main phenomena that we are considering in our framework: 1) the flow of fluid through the brain, (2) pressure loss into capillaries, and 3) the transport of RNL within the brain. Darcy’s law describes the flow of fluid through porous media (e.g., biological tissue, sand, or granular material) and is given by:
| (1) |
where is the interstitial fluid velocity at the 2D position x, p(x) is the interstitial fluid pressure, and K(x) is the hydraulic conductivity of the tissue. Darcy’s law states that fluid velocity is proportional to the gradient of pressure, with a proportionality constant K in the direction opposite of the fastest decreasing pressure. Starling’s law describes the pressure loss into capillaries within the tissue:
| (2) |
where Lp(x) is the capillary hydraulic conductivity, S/V(x) is the ratio of the capillary surface area to the volume (Lp and S/V are not separable in the current formulation and are therefore combined into a single term), and f(x) is the source term used to introduce the fluid flow from the catheter. While Starling’s Law is typically used to describe the influx of velocity through capillaries, here the capillaries act as a fluid sink rather than a source because the fluid infusion pumped through the catheter causes a higher pressure in the interstitial space than the capillaries. However, in this formulation the pressure p represents the pressure differential between capillary and interstitial compartments (pcap - pint, pcap << pint) due to the high pressures required for CED; hence, the negative sign in Eq. (2). The catheter fluid flux source term, f, is implemented as a 2D Gaussian with a total volumetric flux of 5 μL/min, with the mean located at the catheter tip, and a standard deviation of 0.25 mm. (Thus, 95.4% of the RNL volume is distributed within the 1 mm diameter of the catheter tip). A Gaussian source term was selected as it is smooth and more numerically stable to implement compared to a point source. It provides a simplified, but rational, representation of fluid infusion in a 2D situation (limitation and potential refinements are addressed in the Discussion section). The precise catheter tip location was obtained from the x-ray CT data. Interstitial velocity and pressure are assumed to rapidly equilibrate within the tissue, thereby leading to a steady state flow field [12]. In this initial formulation, mechanical deformation and stiffening of the brain tissue, along with formation of an annular void at the catheter tip are not considered [12]. Pressure is assumed to have equilibrated at the domain boundary, and a zero-slip boundary condition for velocity result in the following Dirichlet boundary conditions:
| (3) |
| (4) |
where ∂Ω denotes the domain boundary. Both Starling’s and Darcy’s laws have been used extensively in the modeling of fluid flow and interstitial pressure in (for example) the brain [12], breast [21], cancer [19,20], and biological tissues in general [22].
Transport of RNL is modeled as an advection-diffusion system within the skull, using the modified advection-diffusion equation from Jain et. al [23,24]:
| (5) |
where c(x,t) is the concentration of RNL at 2D position x and time t, D(x) is the diffusion of RNL within the domain due to random thermal motion, R is a restriction factor which accounts for decreased liposome velocity with respect to interstitial fluid velocity (R ϵ [0,1]), and g(x) is a 2D Gaussian source term identical in shape to f, with a total mass determined by the total normalized RNL intensity divided by the duration of the RNL infusion for each patient. RNL is not permitted to cross the skull boundary, resulting in a Neumann boundary condition for the transport equation:
| (6) |
where denotes the normal vector at the domain boundary. The initial RNL concentration c(x, t = 0) is assumed to be 0. (The supplemental material further discusses assumptions behind this formulation).
2.5. Numerical implementation and analysis
Eqs. (1) – (6) are solved numerically using the finite element method in two-dimensions, on the central axial tumor slice. The region within the skull-boundary identified on the T1-weighted image is first meshed by converting each voxel within the skull boundary into two isosceles right triangle elements as shown in Figure 3. The two short sides of each triangular element are 1 mm on a side, corresponding to the size of the T1-weighted image voxels. A second, lower resolution, mesh for comparing results at the resolution of the SPECT data was generated using the SPECT image dimensions to produce to two isosceles right triangular elements, with short side lengths equal to the SPECT voxel resolution of 4.42 mm. Simulations are performed on the high resolution mesh, but all comparisons between the predicted and measured SPECT data are performed after projecting the results onto the lower resolution mesh which corresponds to a simulated SPECT measurement.
Figure 3. Representative FEM mesh for a given patient.
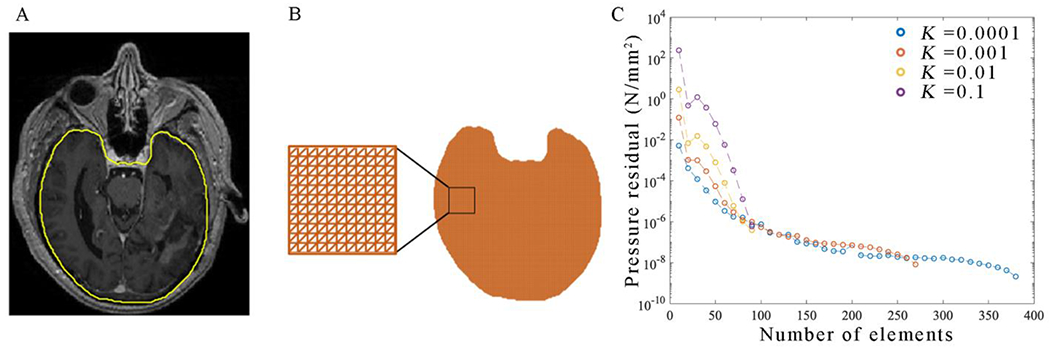
The brain-skull interface is segmented on post-contrast an T1-weighted MRI (panel A). Each voxel within the mask in panel A is meshed into two isosceles right-triangular elements as shown in panel B. This mesh is then refined until the pressure residuals in each element are below 10−6 N/mm2 (panel C). Panel C reports the total residuals (defined as the L-2 norm) of the steady-state pressure field. For all values of K, Pressure residuals decrease with increasing mesh refinement. An initial mesh resolution of 1 element per 1 mm (corresponding to N = 100 elements per dimension) is selected, as residuals for each value of K are below a tolerance of 10−6 N/mm2. Further local refinement is iteratively performed on the patient-specific imaging-derived mesh, until the pressure residual everywhere is less than 10−6 N/mm2.
The steady-state pressure and interstitial fluid velocity are simultaneously determined by solving a mixed element system of Eqs. (1) and Eq. (2). The continuous variational problem is:
| (7) |
| (8) |
where and are second-order Brezzi-Douglas-Marini test and trial functions [25], respectively, and q and p are first-order discontinuous Galerkin test and trial functions, respectively. (The <•,•>Ω notation denotes the inner product operator on the domain Ω.) Note that the boundary term from integration by parts in Eq. (7) has vanished due to application of the Dirichlet boundary conditions summarized by Eqs. (3) and (4). The boundary conditions and functional spaces are chosen for the consideration of the stability and well-posing the weak form problem (see Supplemental Material for the associated justification). The above system is solved on a non-homogeneous mesh with local refinements surrounding the catheter tip. Briefly, the system is iteratively solved initially on the high-resolution mesh, and the mesh is then locally refined within a circular area centered on the infusion location and with a radius of 30 mm. The refinement is performed by splitting the elements from the previous mesh in half, and continues until the residuals in p are reduced below 1×10−6 N/mm2. (See arrow d in Figure 2 for a representative non-homogeneous mesh.) The resulting refined mesh and steady state velocity field is used in implementing the transient transport model (i.e., Eqs. (5) and (6)), with implicit forward time-stepping,
| (9) |
where Δt = 1 min is the simulation timestep, w and c are first-order Lagrange test and trial functions, respectively. However, it is known that this formulation is unstable, and requires stabilization [26]. We can redefine Eq. (9) in terms of the residual resulting from using finite test and trial functions as:
| (10) |
which indicates that Eq. (9) is a minimization of residuals with respect to a set of test functions w. Stabilization of Eq. (10) is performed by adding diffusion in the direction of the velocity streamlines, using the streamline upwind Petrov-Galerkin method [27],
| (11) |
where
| (12) |
and
| (13) |
with Peclet number (i.e., the ratio of advective to diffusive flux in an element)
| (14) |
where τ is a scaling factor determined by both the local element size, h, and Pe, such that more diffusive stabilization is applied in regions of high Pe. Again, note that the boundary term introduced by integration by parts in Eq. (9) vanishes, this time due to the implementation of the zero-flux conditions of Eq. (6). All finite element modeling is done in Python 2.7 , using the Fenics 2017.2 library [28], and the SuperLu distributed solver method [29].
2.6. In silico assessment of model fidelity
To ensure the model converges to a single solution, and becomes more accurate with refinement, we perform a refinement-based convergence analysis [30]. The model is first run on a 100 mm × 100 mm domain, with a source term located at the center, and boundary conditions described above. The mesh is initially subdivided by 10 triangular elements in each of the two dimensions (10 mm on a short side), the model (i.e., Eqs. (7) – (14)) is run forward in time, and the spatial distribution of RNL is recorded at mid- and final timepoints. The mesh is then progressively refined, and the model run again, adding 10 to the total number of elements per dimension, until the mesh is subdivided into 400 elements per dimension (0.25 mm on a short side). The L2-norm of each progressive model run is calculated between the current iteration and the highest resolution iteration at the final time point. This process is performed for four values of hydraulic conductivity of varying orders of magnitude (K = [1.0×10−1, 1.0×10−2, 1.0×10−3, 1.0×10−4] mm/min). The results of this analysis are demonstrated in Figure 3.
2.7. Model family
Table 4 contains a full mathematical description of each of the models in the family. Each model represents a different approach for assigning material properties (i.e., K, D, R, and LpS/V) for individual patients. In particular, Models 1 and 2 utilize spatially homogenous material properties, while Models 3 and 4 utilized material properties which are linearly weighted by the ADC map [12]. Models 5 and 6 weight material properties by exponential weighting of the ADC map, such that parameter value for the field asymptotically approaches the calibrated maximum [31]. Models 7-9 utilize bulk material properties for CSF and brain tissue, while Models 10-12 further categorize brain tissue into white matter and grey matter. Models 1, 3, 5, 7, and 10 assume a fixed value of LpS/V, while Models 2, 4, 6, 8 and 11 consider LpS/V as a parameter to be calibrated globally. Finally, Models 9 and 12 assume LpS/V is 0 in CSF (consistent with the assumption of an incompressible fluid), but allows for it to be a calibrated material property within the segmented brain region.
Table 4:
List of each member of the model family and their associated and unknown parameters
| Model | Apparent Tissue Hydraulic Conductivity (K, mm2) | Apparent Liposome Diffusivity (D, mm2 s−1) | Restriction Factor (R, unitless) | Hydraulic conductivity and capillary area to volume ratio (LpS/V, mm2 N−1 s−1) | Total Parameters |
|---|---|---|---|---|---|
| 1 | K = θ1 | D = θ2 | R = θ3 | LpS/V = 0.01 | 3 |
| 2 | K = θ1 | D = θ2 | R = θ3 | 4 | |
| 3 | K = θ1 × ADC | D = θ2 × ADC | R = θ3 | 3 | |
| 4 | K = θ1 × ADC | D = θ2 × ADC | R = θ3 | 4 | |
| 5 | K = θ1exp (−θ2/ADC) | D = θ3exp (−θ4/ADC) | R = θ5 | 5 | |
| 6 | K = θ1exp (−θ2/ADC) | D = θ3exp (−θ4/ADC) | R = θ5 | 6 | |
| 7 | R = θ5 | 5 | |||
| 8 | R = θ5 | 6 | |||
| 9 | R = θ5 | 6 | |||
| 10 | R = θ7 | 7 | |||
| 11 | R = θ7 | 8 | |||
| 12 | R = θ7 | 8 |
2.8. Model calibration, statistical analysis, and model selection
The parameters in each model are calibrated to minimize the SSE between the model predicted and SPECT gold standard at times t = 0, t = ½, and t = 1 (times which correspond to the total fraction of RNL delivered, respectively). Note, the RNL concentration at t = 0 is assumed to be identically zero everywhere. Parameters are calibrated via the SciPy (Python 2.7) least squares minimization (‘scipy.optimize.least_squares’) [32] using a multi-start framework to avoid local minima in the objective function (left panel in Figure 1). To estimate the gradient of the objective function, each parameter is perturbed by a factor of 1×10−4 to approximate an element-wise objective function gradient. These perturbations require a forward solve for each parameter, and are therefore run in parallel. The least-squares algorithm is then run until the change in parameters is less than a tolerance of 1×10−4, the change in SSE (Eq. (15)) is less than 1×10−4, or the gradient of the objective function is less than 1×10-6. All model evaluations and calibrations were performed on a system consisting of 4 × Intel Xeon E5-4627 v4 2.6Ghz, 25 M Cache, 8.0 GT/s, and 256 GB of Memory= 256 GB.
We compare the results of calibrating each model to data from the five representative patients at the global and local level. At the global level we consider the overall quality of the fit and the level of agreement between predicted and observed RNL distribution. The quality of the model fit to the data is calculated as:
| (15) |
where j denotes the spatial index of each voxel in the measured or simulated images, and t denotes the temporal index of the measured or simulated images. 2D masks describing the extent of RNL distribution are defined as voxels that have a signal intensity exceeding 5% of the maximum-intensity threshold; voxels below this threshold are considered as noise. The resulting masks for both the measured and predicted RNL distributions are then compared using the Dice correlation coefficient, where a Dice value of 1 corresponds to a perfect spatial overlap, while a Dice value of 0 corresponds to no spatial overlap [33]. By utilizing masks for the predicted and measured RNL distribution, the Dice value is insensitive to variations in the underlying concentration field. At the local level, we use the concordance correlation coefficient (CCC) to quantify the degree of agreement between the predicted and measured RNL distribution at each spatial location within the SPECT image [34]. A CCC of 1 indicates perfect agreement between the predicted and measured RNL distributions.
We use two model selection criteria to determine the optimal member of the model family. The first is the Akaike Information Criteria (AIC) [35] which balances goodness of fitness with the number of free parameters, k, as follows:
| (16) |
where n is the number of samples (in this case, the number of non-zero voxels). The model with the smallest AIC is selected as the most parsimonious model. Second, we consider which model maximizes the overlap of the simulated and measured RNL distributions (i.e., maximizes the Dice value). This second model selection criteria identifies the model that most accurately matches the spatial distribution of RNL immediately following the infusion.
2.9. Validation
To determine the ability of each model to predict the final spatial distribution of RNL in each patient, we employed a leave-one-out method (right-most panel in Figure 1). That is, we would calibrate four of the five patients to a specific model to yield a distribution of parameter values. These distributions would then be used to assign the model parameters for the fifth patient, thereby enabling the model to be run forward to predict the final spatial distribution of RNL which could then be directly compared to the experimentally measured value for that patient. More specifically, with one patient held back, the mean, μ, and standard deviation, σ, of the model parameters for the remaining four calibrated parameter sets are used to determine a beta-distribution [36]:
| (17) |
| (18) |
| (19) |
where a and b are the beta distribution shape parameters, in terms of the sample mean and variance. The beta-distribution is a generalized monomodal distribution, defined on the interval [0,1], and is used in place of the normal distribution which is defined on the interval (−∞,∞). This distribution allows for appropriate sampling of the prior distribution for model parameters which exist between some pre-specified lower and upper bounds. If σ2 < μ(1- μ), the beta distribution is replaced with a uniform distribution. Sample parameters are selected from 100 randomly generated parameter distributions defined by Eq. (17). The forward model is then run using the geometry and imaging data corresponding to the fifth patient that was held back. This approach simulates the results of the model prediction as if the fifth patient were newly entered into the clinical trial. From these 100 independent simulations, a mean and 95% confidence interval are determined on a voxel-wise basis, at the times corresponding to the SPECT acquisitions. These means and 95% confidence intervals are compared to the measured SPECT data using the CCC, Dice, and SSE.
3. Results
3.1. Convergence analysis
The results of our convergence analysis as a function of the number of model elements are reported in Figure 3. Panel C in Figure 3 demonstrates that the global L2-norm continues to slowly decrease upon further refinement of the mesh. At a resolution of one element per 1 mm in each direction (corresponding to 100 elements), a global L2-norm of less than 10−6 is achieved for all values of K.
3.2. Calibration and model selection
Table 5 reports the results of the model calibration and selection for all twelve models and five patients. Model 12 (where model parameters are tissue specific) minimized the AIC for each patient except for patient 4. Model 12 also yielded the highest mean CCC and Dice ranging from 0.71 to 0.95 and 0.84 to 0.97, respectively. Note that the model with the fewest parameters, Model 1, performed similarly, with only fitting three global parameters, with CCC and Dice values ranging from 0.70 to 0.92 and 0.76 to 0.97, respectively. However, the AIC for Model 1 yielded one of the highest values. The models which performed most poorly were Models 5 and 6 (exponentially weighted).
Table 5.
Error analysis and model selection for the model calibration scenario
| Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Patient 1 | AIC | −188 | −186 | −187 | −185 | −186 | −183 | −241 | −292 | −292 | −305 | −333 | −338 |
| CCC | 0.85 | 0.85 | 0.88 | 0.88 | 0.87 | 0.87 | 0.87 | 0.89 | 0.89 | 0.89 | 0.91 | 0.90 | |
| Dice | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.93 | 0.94 | 0.94 | 0.94 | 0.95 | 0.95 | |
|
| |||||||||||||
| Patient 2 | AIC | 725 | 727 | 780 | 782 | 886 | 889 | 711 | 713 | 713 | 695 | 693 | 691 |
| CCC | 0.92 | 0.92 | 0.91 | 0.91 | 0.89 | 0.89 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | 0.95 | |
| Dice | 0.97 | 0.97 | 0.96 | 0.96 | 0.93 | 0.93 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | |
|
| |||||||||||||
| Patient 3 | AIC | 1,187 | 1,190 | 1,173 | 1,175 | 1,308 | 1,310 | 1,181 | 1,169 | 1,169 | 1,180 | 1,185 | 1,162 |
| CCC | 0.87 | 0.87 | 0.88 | 0.88 | 0.88 | 0.88 | 0.87 | 0.88 | 0.88 | 0.87 | 0.87 | 0.88 | |
| Dice | 0.96 | 0.96 | 0.96 | 0.96 | 0.92 | 0.92 | 0.96 | 0.96 | 0.96 | 0.96 | 0.96 | 0.97 | |
|
| |||||||||||||
| Patient 4 | AIC | 433. | 492 | 494 | 459 | 461 | 335 | 337 | 333 | 278 | 280 | 262 | 278 |
| CCC | 0.70 | 0.70 | 0.71 | 0.71 | 0.70 | 0.70 | 0.70 | 0.70 | 0.70 | 0.71 | 0.71 | 0.71 | |
| Dice | 0.76 | 0.76 | 0.74 | 0.74 | 0.74 | 0.74 | 0.81 | 0.81 | 0.81 | 0.83 | 0.83 | 0.84 | |
|
| |||||||||||||
| Patient 5 | AIC | 276 | 278 | 298 | 300 | 282 | 269 | 218 | 220 | 218 | 132 | 131 | 128 |
| CCC | 0.81 | 0.81 | 0.80 | 0.80 | 0.81 | 0.80 | 0.82 | 0.82 | 0.82 | 0.82 | 0.82 | 0.83 | |
| Dice | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 | 0.95 | 0.95 | 0.95 | |
|
| |||||||||||||
| Mean | AIC | 487 | 500 | 512 | 507 | 550 | 524 | 441 | 429 | 417 | 396 | 388 | 384 |
| CCC | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.83 | 0.84 | 0.85 | 0.85 | 0.85 | 0.85 | 0.85 | |
| Dice | 0.91 | 0.91 | 0.90 | 0.90 | 0.89 | 0.89 | 0.92 | 0.92 | 0.92 | 0.93 | 0.93 | 0.93 | |
3.3. Model prediction
For clarity we present prediction results for only two of the models: Model 1, which has the fewest parameters, and Model 12, which minimizes the mean AIC across 4 of 5 patients, and maximizes the mean Dice across all patients. Figures 4 and 5 show representative results for the model prediction scenario for an individual patient normalized to the maximum SPECT measure observed post-infusion, while Table 6 reports the results for the patient cohort. Figure 4 presents the Model 1 prediction results for patient 5. As Model 1 does not take into account spatially varying material properties, the predicted distribution of RNL is radially symmetric (Figure 4a). Model 1 underestimates the peak intensity at the center of the distribution at both mid- and post- infusion time points by greater than 10% (Figure 4a), and the model prediction confidence interval is widest at the center of the RNL distribution (greater than 0.65 on the normalized SPECT measurement), near the location where the catheter is placed (Figure 4a). The 95% confidence interval show in Figure 4a can be interpreted as a spatial map of the uncertainty in model predictions at the voxel level. The model has regions of high error (underestimating the SPECT data by a factor greater than 90% relative error) near the edge of the brain, where it fails to predict a small leak into the CSF (Figure 4a). A high degree of correlation and agreement was observed in Panel 4b with a CCC of 0.94 between the predicted and normalized SPECT measurement
Figure 4. Visualization of the Model 1 prediction for a representative patient.
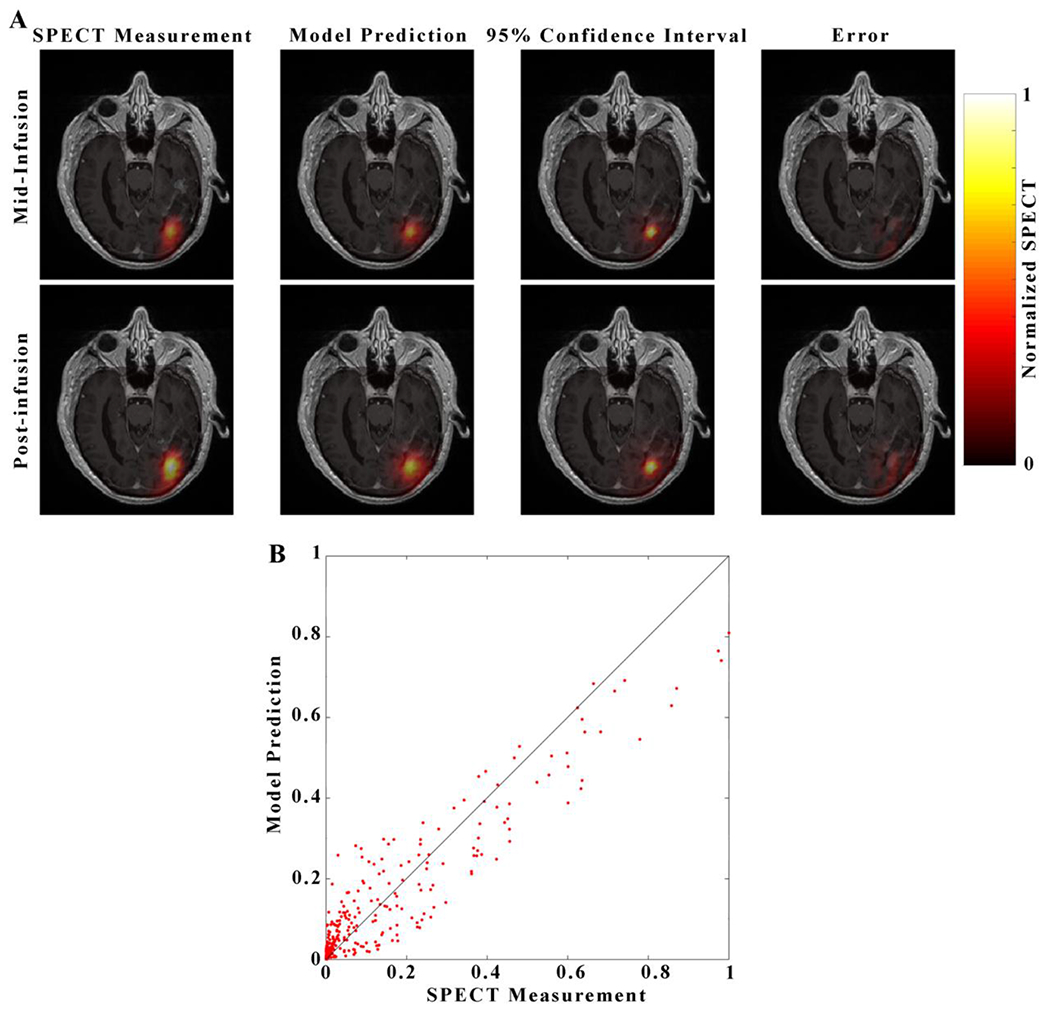
Each image in panel A consists of a heatmap of the model prediction overlaid over on a grayscale, post-contrast, T1-weighted image through the central axial tumor slice for Patient 5. Images in the top row of panel A correspond to the mid-infusion time point, and images in the bottom row correspond to the post-infusion time point. The left-most column depicts the true distribution of RNL within the central tumor slice, the second column the mean of 100 simulations from Model 1, the third column 95% confidence interval of the model prediction, and right-most column the absolute value of prediction error. A strong degree of overlap between the predicted and measured RNL distribution resulted in a Dice value of 0.82. The predicted voxel-wise values of RNL are plotted against the measured values in Panel B with the line of unity shown in black. A high level of agreement at the voxel level resulted in a CCC of 0.94.
Figure 5. Visualization of the Model 12 prediction for a representative patient.
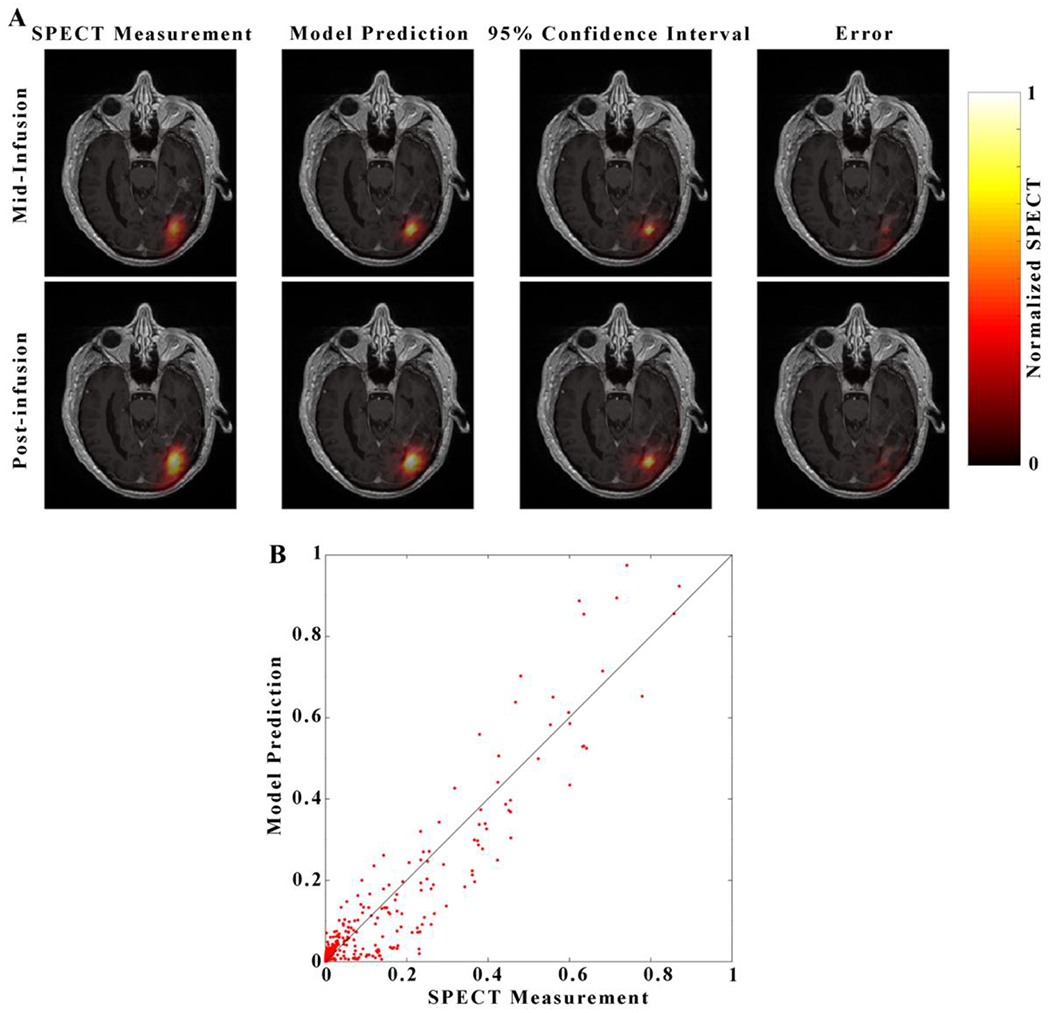
Visualization For each image in panel A, each image consists of a heatmap of the model prediction is overlaid over of a grayscale post-contrast T1-weighted image through the central axial tumor slice for patient 5. Images in the top row correspond to the mid-infusion time point, and images in the bottom row correspond to the post-infusion time point. The left-most column depicts the true distribution of RNL within the central tumor slice, the second column the mean of 100 model predictions, the third column 95% confidence interval, and right-most column the absolute value of prediction error. A strong degree of overlap between the predicted and measured RNL distribution resulted in a Dice value of 0.84. The predicted voxel-wise values of RNL are plotted against the measured values in Panel B with the line of unity shown in black. A high level of agreement at the voxel level resulted in a CCC of 0.96.
Table 6:
Error analysis for the prediction scenario
| Patient 1 | Patient 2 | Patient 3 | Patient 4 | Patient 5 | Mean | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||||
| Model | CCC | Dice | CCC | Dice | CCC | Dice | CCC | Dice | CCC | Dice | CCC | Dice |
| 1 | 0.80 | 0.60 | 0.91 | 0.65 | 0.70 | 0.49 | 0.80 | 0.46 | 0.94 | 0.82 | 0.83 | 0.60 |
| 12 | 0.84 | 0.74 | 0.98 | 0.79 | 0.81 | 0.48 | 0.83 | 0.58 | 0.96 | 0.84 | 0.88 | 0.69 |
Figure 5 presents the prediction results from patient 5 for Model 12 which assigns separate material properties to white matter, gray matter, and CSF. The predicted maximum values for Model 12 overestimates (Figures 5a, 5b) the RNL concentration by over 20% within the central region of the distribution, in contrast to Model 1 which underestimates the concentration by 12% at the final time point. The region of highest uncertainty in the model prediction for Model 12 is located (greater than 0.70 on the normalized SPECT measurement) at the center of the distribution (near the catheter placement site, similar to Model 1), and in CSF within and surrounding the brain (Figure 5a). Compared to Model 1, Model 12 captures the leak into the CSF surrounding the brain (Figure 5a). A high degree of correlation and agreement was observed in Panel 5b with a CCC of 0.96 between the predicted and normalized SPECT measurement
Table 6 summarizes the Dice and CCC values observed from the patient cohort following the leave-one-out approach described above in section 2.9. Model 1 predicts the distribution of RNL with a CCC ranging from 0.70 to 0.94, and Dice ranging from 0.46 to 0.82. A low level of spatial agreement was observed for Model 1 (Dice values less than 0.50) for patients 3 and 4. Model 12 increased the CCC values for all patients, while the Dice value was decreased for only patient 3. Model 12 resulted in a strong voxel-wise agreement between the predicted and measured RNL distribution with CCCs ranging from 0.81 to 0.98. Dice values ranged from 0.58 to 0.84 indicating a strong spatial agreement in the extent of RNL distribution.
4. Discussion
We have presented a family of twelve models designed to characterize the distribution of RNL delivered to a patient’s tumor via CED as constrained by their pre-injection MRI data. Through calibration, we demonstrated that we can recapitulate the shape and voxel-wise concentration of RNL to a high degree (mean Dice = 0.91 ± 0.10, CCC = 0.83 ± 0.10, Table 5) using spatially invariant material properties (Model 1). Upon addition of spatial information, implemented through calibration of material properties determined through pre-operative MRI (Model 12), these metrics improve (mean Dice = 0.93 ± 0.07, mean CCC = 0.83 ± 0.11, Table 5). Utilizing prior-knowledge from other patients in a leave-one-out method, Model 12 is highly predictive of the distribution of RNL (Dice = 0.69 ± 0.18, CCC = 0.88 ± 0.12), indicating that this model has potential for predicting the distribution of RNL for future patients within this clinical trial. In addition to predicting the spatio-temporal distribution of RNL, this framework provides a map of model uncertainty that indicates the statistical level of confidence in the model prediction at a local voxel level.
While several models of CED have been presented previously [12,14,37–39], they have focused on the distribution of molecular agents, and may therefore systematically overestimate the distribution of nanoliposomes (e.g., RNL). Additionally, existing models utilize literature values for material properties (e.g., K and D) which apply only in situations with identical conditions to which the measurement are taken—and may not apply in the case of larger molecules [13,38]. We hypothesize that modeling approaches that ignore patient-specific geometry and assume parameter values from small molecular agents may result in substantial inaccuracies in treatment planning for RNL delivery. Thus, in this work we leverage both a patient’s unique geometry and cohort calibrated material properties to characterize the interstitial distribution of RNL for individual patients.
Other modeling approaches (e.g., iPlanFlow; BrainLab, Munich, Germany) have used patient imaging data (such as diffusion tensor imaging, DTI) to inform models of CED. For example, Rosenbluth et al. utilize a linear scaling of the DTI maps to inform K as a tensor [12,14,39]. While our model does not utilize the DTI tensor field, Kim et. al. hypothesize that fully informing K with DTI imaging may not be necessary, and that large changes in K, such as those found between boundaries between differing tissue types, are the most important feature to capture in modeling CED [39]. We believe this hypothesis is supported by the fact that Model 12, which uses only segmented tissue types instead of a scaling of the ADC map, was the most accurate at predicting the distribution of RNL on both voxel-wise and volumetric basis. Some models of CED couple tissue deformation at the catheter tip with changes to the hydraulic conductivity [12,14]. While we do not take this phenomenon into account explicitly, it is possible that the empirical nature utilized to determine material properties (i.e., calibration versus direct measurement) may implicitly capture this phenomenon.
Further development of this modeling framework may improve current approaches to identifying appropriate catheter positioning. We note that this 2D framework is a simplification of the patient’s disease and the physical domain. However, before extending this effort to 3D and translating into clinical use, the 2D domain is suitable for developing and testing approaches for modeling the spatio-temporal distribution of RNL via the integration of patient-specific imaging data and treatment protocol with mathematical models of CED. Once further developed and validated, precision catheter positioning can be obtained using standard neurosurgery techniques including an image-guided stereotactic system such as the Varioguide (BrainLAB, AG, Feldkirchen Germany) used in this study. A study on the accuracy of the Varioguide system demonstrated a mean point deviation 0.9 mm [40] in target accuracy. This mean point deviation is roughly the size of the MRI voxel dimensions for the T1 sequences used for treatment planning, and is therefore practical for controlling the catheter placement within the tumor. The accuracy of catheter positioning, however, may be influenced by the type of fiducials (e.g., extracranial vs. intracranial) used to align the stereotactic frame itself. While the catheter may be placed accurately within the brain, there are also a number of practical factors that may limit where the catheter can be placed including (for example): location of the tumor within the brain, critical fiber tracts, and blood vessels. These practical factors can limit the accuracy of catheter placement, and need to be considered when translating a 3D model to clinical application.
There are a number of opportunities for improving this modeling framework. First, the model was implemented in 2D and future work should extend it to 3D. In spite of this, the predictive ability of the model in this preliminary data set is high, which we attribute largely to the differences between the in-plane and through-plane spatial resolution in the imaging data: 0.98 mm versus 5 mm. Second, the spatial resolution of the SPECT data (4.42 mm on each side) also fundamentally limits the accuracy of the predictions. The limited spatial resolution afforded by SPECT is, of course, well-known and there is little that can be done at this time. It is possible that calibrating to MR-labeled nanoparticles [41], may be a way to improve the spatial resolution of the input data and this would, in turn, potentially improve the predictive ability of our modeling scheme. Third, our model also assumes that resting-state interstitial velocity is dominated by the flow due to CED, and resting-state interstitial fluid velocity is therefore ignored. This simplifying assumption may not be valid, particularly in the case of slow, multi-day infusions. The effects of CED on interstitial flow, and its effects on tumor growth is a growing field, and is currently under investigation [42,43]. Fourth, patient-specific boundary conditions (as done in [12]) should be considered in future iterations. While the current formulation does include patient-specific information including the RNL infusion location and volume, tissue geometry, and properties (i.e., tissue hydraulic conductivity K, RNL diffusivity D and convective restriction factor R within tissue, capillary hydraulic conductivity Lp and surface area S/V), it does not account for all patient-specific boundary conditions. In particular, a more realistic representation (recognized by Rosenbluth et al. [12]) is to consider the backflow of infused fluid from the catheter tip to the reflux-preventing step (15 mm in length with our catheter design), so that the pressure and RNL concentration along the catheter can be calculated as patient-specific boundary values. In a 2D representation the catheter trajectory is not always aligned with the modeled planes which limits the applicablity of this backflow calculation. However, extending this approach to 3D would enable this refinement. Given the modest sample size (N = 5), the results above should be interpreted as an initial contribution that must be validated in a large patient set that includes patients of heterogeneous physiologies and outcomes, including those with and without significant CSF leaks. It is our opinion that these positive results in the current dataset warrants further investigation.
5. Conclusion
We have presented a family of twelve models calibrated by patient-specific, multi-modality imaging data, of which the most parsimonious is capable of predicting the final spatial distribution of RNL with a DICE value of 0.69 ± 0.18 and a CCC of 0.88 ± 0.12. With further development and expansion to 3D, we aim to utilize this modeling methodology for the optimization of CED catheter placement, such that tumor coverage is maximized while healthy tissue exposure is minimized, for treatment of recurrent glioblastoma in ongoing clinical studies of RNL for the treatment of recurrent glioblastoma multiforme. Further, while this specific model is developed for the prediction of RNL delivery within the context of a specific clinical trial, we propose that this framework is extendable to simulate the distribution of any therapeutic delivered by CED, given the proper data to calibrate and constrain model parameters.
Supplementary Material
Acknowledgments
We thank the National Institutes of Health for funding through R01 CA235800, T32 EB007507, NCI 1R01 CA186193 and NCI 1U01CA253540, and 1U01 CA174706. We thank CPRIT for funding through RR160005. T.E.Y. is a CPRIT Scholar of Cancer Research. We thank the American Association of Physicists in Medicine for Research Seed Funding. We offer a sincere thank you to all the patients who volunteer to participate in our studies; your strength and courage are examples for all of us.
Footnotes
Ethical Statement
All clinical data presented in the present study is used by permission of Clinical Trial NCT Number NCT01906385, which is approved and compliant to the ethical standards of IRB, HIPPA, and the FDA.
References
- [1].Cowling BJ, Aiello A, Kong H, Hill C. 2020; Glioblastoma in Adults: A Society for Neuro-Oncology (SNO) and European Society of Neuro-Oncology (EANO) Consensus Review on Current Management and Future Directions. 1–10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Tabatabai G, Wakimoto H. 2019; Glioblastoma: State of the art and future perspectives. Cancers (Basel). 11 8 10–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Stupp R, Warren, Masonvan den Bent MJ, Weller M, Fisher B, Taphoorn MJB, Belanger K, Brandes AA, Marosi C, Bogdahn U, Curschmann J, et al. 2005; Radiotherapy plus Concomitant and Adjuvant Temozolomide for Glioblastoma. N Engl J Med. Boston: Massachusetts Medical Society; 352 10 987–96. [DOI] [PubMed] [Google Scholar]
- [4].Oberheim Bush NA, Hervey-Jumper SL, Berger MS. 2019; Management of Glioblastoma, Present and Future. World Neurosurg. Elsevier Inc; 131 328–38. [DOI] [PubMed] [Google Scholar]
- [5].Jahangiri A, Chin AT, Flanigan PM, Chen R, Bankiewicz K, Aghi MK. 2017; Convection-enhanced delivery in glioblastoma: a review of preclinical and clinical studies. J Neurosurg. 126 1 191–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Shieh LT, Guo HR, Chang YK, Lu NM, Ho SY. 2020; Clinical implications of multiple glioblastomas: An analysis of prognostic factors and survival to distinguish from their single counterparts. J Formos Med Assoc. 119 3 728–34. [DOI] [PubMed] [Google Scholar]
- [7].Phillips WT, Goins B, Bao A, Vargas D, Guttierez JE, Trevino A, Miller JR, Henry J, Zuniga R, Vecil G, et al. 2012; Rhenium-186 liposomes as convection-enhanced nanoparticle brachytherapy for treatment of glioblastoma. Neuro Oncol. England; 14 4 416–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Bao A, Goins B, Klipper R, Negrete G, Phillips WT. 2003; 186Re-liposome labeling using 186Re-SNS/S complexes: In vitro stability, imaging, and biodistribution in rats. J Nucl Med. 44 12 1992–9. [PubMed] [Google Scholar]
- [9].Floyd J, Phillips W, Goins B, Bao A, Brenner A. 2015; ATNT-03FIRST IN HUMAN STUDY OF RHENIUM NANOLIPOSOMES FOR INTRATUMORAL THERAPY OF GLIOMA. Neuro Oncol. 17 suppl 5 v10.3–v10. [Google Scholar]
- [10].Shi M, Sanche L. 2019; Convection-Enhanced Delivery in Malignant Gliomas: A Review of Toxicity and Efficacy. J Oncol. 2019 9342796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Kunwar S, Chang S, Westphal M, Vogelbaum M, Sampson J, Barnett G, Shaffrey M, Ram Z, Piepmeier J, Prados M, et al. 2010; Phase III randomized trial of CED of IL13-PE38QQR vs Gliadel wafers for recurrent glioblastoma. Neuro Oncol. 12 8 871–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Rosenbluth KH, Eschermann JF, Mittermeyer G, Thomson R, Mittermeyer S, Bankiewicz KS. 2012; Analysis of a simulation algorithm for direct brain drug delivery. Neuroimage. United States; 59 3 2423–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Linninger AA, Somayaji MR, Erickson T, Guo X, Penn RD. 2008; Computational methods for predicting drug transport in anisotropic and heterogeneous brain tissue. 41 2176–87. [DOI] [PubMed] [Google Scholar]
- [14].Støverud KH, Darcis M, Helmig R, Hassanizadeh SM. 2012; Modeling Concentration Distribution and Deformation During Convection-Enhanced Drug Delivery into Brain Tissue. Transp Porous Media. 92 1 119–43. [Google Scholar]
- [15].Ashburner J, Friston KJ. 2004. Human Brain Function. Elsevier; Ch 5 p. [Google Scholar]
- [16].ELLINGSON BM, KIM E, WOODWORTH DC, MARQUES H, BOXERMAN JL, SAFRIEL Y, McKINSTRY RC, Bokstein F, JAIN R, Chi TL, et al. 2015; Diffusion MRI quality control and functional diffusion map results in ACRIN 6677/RTOG 0625: A multicenter, randomized, phase II trial of bevacizumab and chemotherapy in recurrent glioblastoma. Int J Oncol. 46 5 1883–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Chun SY, Fessler JA, Dewaraja YK. 2013; Correction for Collimator-Detector Response in SPECT Using Point Spread Function Template. IEEE Trans Med Imaging. 32 2 295–305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Zeeberg BR, Bice AN, Loncaric S, Wagner HN. 1988. A Theoretically-Correct Algorithm to Compensate for a Three-Dimensional Spatially-Variant Point Spread Function in Spect Imaging. Information Processing in Medical Imaging. Boston, MA: Springer US; p. 245–54. [Google Scholar]
- [19].Phipps C, Kohandel M. 2011. [cited 2012 Nov 30]; Mathematical model of the effect of interstitial fluid pressure on angiogenic behavior in solid tumors. Comput Math Methods Med [Internet]. 2011 843765. Available from: http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3168276&tool=pmcentrez&rendertype=abstract [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Liu Y, Sadowski SM, Weisbrod AB, Kebebew E, Summers RM, Yao J. 2013. Multimodal Image Driven Patient Specific Tumor Growth Modeling BT - Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013: 16th International Conference, Nagoya, Japan, September 22–26, 2013, Proceedings, Part III. In: Mori K, Sakuma I, Sato Y, Barillot C, Navab N, editors. Berlin, Heidelberg, Heidelberg: Springer Berlin Heidelberg; p. 283–90. Available from: 10.1007/978-3-642-40760-4_36 [DOI] [PubMed] [Google Scholar]
- [21].Wu C, Hormuth DA, Oliver TA, Pineda F, Lorenzo G, Karczmar GS, Moser RD, Yankeelov TE. 2020; Patient-Specific Characterization of Breast Cancer Hemodynamics Using Image-Guided Computational Fluid Dynamics. IEEE Trans Med Imaging. 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].D’Angelo C, Quarteroni A. 2008; On the coupling of 1D and 3D diffusion-reaction equations. Application to tissue perfusion problems. Math Model Methods Appl Sci. 18 8. [Google Scholar]
- [23].Baxter LT, Jain RK. 1989; Transport of fluid and macromolecules in tumors. I. Role of interstitial pressure and convection. Microvasc Res. 37 1 77–104. [DOI] [PubMed] [Google Scholar]
- [24].Jain RK. 1987; Transport of Molecules in the Tumor Interstitium : A Review1. 500 17 3039–52. [PubMed] [Google Scholar]
- [25].2-Arnold, Brezzi F, and Fortin M. A stable finite element for the Stokes problem.pdf. [Google Scholar]
- [26].Harari I, Hughes TJR. 1994; Stabilized finite element methods for steady advection-diffusion with production. Comput Methods Appl Mech Eng. 115 C 165–91. [Google Scholar]
- [27].Hughes TJR, Franca LP, Mallet M. 1987; A new finite element formulation for computational fluid dynamics: VI. Convergence analysis of the generalized SUPG formulation for linear time-dependent multidimensional advective-diffusive systems. Comput Methods Appl Mech Eng. 63 1 97–112. [Google Scholar]
- [28].Logg A., Mardal GNW K-A et al. 2012. Automated Solution of Differential Equations by the Finite Element Method. Logg A, Mardal K-A, Wells G, editors. Berlin, Heidelberg: Springer Berlin Heidelberg; [Google Scholar]
- [29].Dongarra J, Luszczek P, Wolf F, Träff JL, Quinton P, Hellwagner H, Fränzle M, Lengauer C, Ceze LH, Hiraki K, et al. 2011. SuperLU. Encyclopedia of Parallel Computing. Boston, MA: Springer US; p. 1955–62. [Google Scholar]
- [30].Ansari SU, Hussain M, Ahmad SM, Rashid A, Mazhar S. 2017; Stabilized mixed finite element method for transient darcy flow. Trans Can Soc Mech Eng. 41 1 85–97. [Google Scholar]
- [31].Hormuth II DA, Weis JA, Barnes SL, Miga MI, Rericha EC, Quaranta V, Yankeelov TE. 2015; Predicting in vivo glioma growth with the reaction diffusion equation constrained by quantitative magnetic resonance imaging data. Phys Biol. 12 4 46006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, Burovski E, Peterson P, Weckesser W, Bright J, et al. 2020; SciPy 1.0: fundamental algorithms for scientific computing in Python. Nat Methods. 17 3 261–72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Dice LR. 1945; Measures of the Amount of Ecologic Association Between Species. Ecology. 26 3 297–302. [Google Scholar]
- [34].Akoglu H. 2018; User’s guide to correlation coefficients. Turkish J Emerg Med. 18 3 91–3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Yamaoka K, Nakagawa T, Uno T. 1978; Application of Akaike’s information criterion (AIC) in the evaluation of linear pharmacokinetic equations. J Pharmacokinet Biopharm. Kluwer Academic Publishers-Plenum Publishers; 6 2 165–75. [DOI] [PubMed] [Google Scholar]
- [36].Balding DJ, Nichols RA. 1995; A method for quantifying differentiation between populations at multi-allelic loci and its implications for investigating identity and paternity. Genetica. 96 1–2 3–12. [DOI] [PubMed] [Google Scholar]
- [37].Linninger AA, Somayaji MR, Mekarski M, Zhang L. 2008; Prediction of convection-enhanced drug delivery to the human brain. J Theor Biol. 250 1 125–38. [DOI] [PubMed] [Google Scholar]
- [38].Zhan W, Arifin DY, Lee TK, Wang CH. 2017; Mathematical Modelling of Convection Enhanced Delivery of Carmustine and Paclitaxel for Brain Tumour Therapy. Pharm Res. Pharmaceutical Research; 34 4 860–73. [DOI] [PubMed] [Google Scholar]
- [39].Kim JH, Astary GW, Kantorovich S, Mareci TH, Carney PR, Sarntinoranont M. 2012; Voxelized computational model for convection-enhanced delivery in the rat ventral hippocampus: Comparison with in vivo MR experimental studies. Ann Biomed Eng. 40 9 2043–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Ringel F, Ingerl D, Ott S, Meyer B. 2009; VarioGuide: A new frameless image-guided stereotactic system - Accuracy study and clinical assessment. Neurosurgery. 64 SUPPL. 5 365–73. [DOI] [PubMed] [Google Scholar]
- [41].Krauze MT, Forsayeth J, Yin D, Bankiewicz KS. 2009. Chapter 18 Convection-Enhanced Delivery of Liposomes to Primate Brain. p. 349–62. [DOI] [PubMed] [Google Scholar]
- [42].Kingsmore KM, Vaccari A, Abler D, Cui SX, Epstein FH, Rockne RC, Acton ST, Munson JM. 2018; MRI analysis to map interstitial flow in the brain tumor microenvironment. APL Bioeng. 2 3 031905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Stine CA, Munson JM. 2019; Convection-Enhanced Delivery: Connection to and Impact of Interstitial Fluid Flow. Front Oncol. 9 October. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


