Phase II Trial Design with Growth Modulation Index as the Primary Endpoint

Abstract

Recently molecularly targeted, genomic-driven and immunotherapy clinical trials continue to be advanced for the treatment of relapse or refractory cancer patients, where growth modulation index (GMI) is often considered as a primary endpoint of the treatment efficacy. However, there are few literature available for consideration of trial design with GMI as the primary endpoint. In this article, we derived a sample size formula for the score test under a log-linear model of the GMI. The study designs using the derived sample size formula are illustrated under a bivariate exponential model, Weibull frailty model and generalized treatment effect size. The proposed designs provide sound statistical methods for single-arm phase II trial with GMI as the primary endpoint.

1. Introduction

Advances in the understanding of tumor biology, success in sequencing of cancer genomes and increasing knowledge of the molecular basis of antitumor immune response have led to an increase in molecularly targeted, genomic-driven and immunotherapy clinical trials.^1,2 For phase II trials of largely cytostatic therapies where antitumor activity based on tumor shrinkage cannot be directly hypothesized, more appropriate endpoints are recommended.³ Specifically, progression-free survival (PFS) or time to disease progression (TTP) have been proposed,^3,4 where PFS is defined as TTP or death and TTP is defined time to disease progression. Patients who die without disease progression is censored in the TTP analysis. Furthermore, randomized trials are recommended for these trials due to lack of appropriate historical data and the subjective nature of assessing disease progression. However, a randomized trial needs a lot more patients which is often not achievable for numerous reasons, including logistic feasibility, funding, and time limitations, etc. Therefore, a single-arm phase II trial that utilizes an intra-patient comparison is attractive.

Von Hoff⁵ recommended the use an intra-patient TTP ratio (PFS ratio), or growth modulation index (GMI) as the primary endpoint for such trial design. Here the GMI is defined for individual patients as the ratio of their TTP on the current therapy to their TTP on the most recent previous therapy. Thus, patients served as their own control. The TTP on the most recent previous therapy, T₁ is uncensored. The TTP on the current therapy, T₂ can be right censored. The TTP pair of (T₁, T₂) is from the same patient, thus, T₁ and T₂ are correlated. To design the study, Von Hoff et al.⁶ used a simple percentage of GMI > 1.3 as a criteria for the assessment of treatment activity. There are several drawbacks for this approach. First, it ignores the censoring of T₂, which results in a conservative estimate of the probability of GMI > 1.3. Second, the threshold value of 1.3 categorizes the GMI as a binary endpoint and results in an inefficient study design by using the exact binomial test. Third, a study design based on an arbitrary percentage of GMI > 1.3 as a criteria for treatment activity is difficult to justify. Even with these drawbacks, this trial endpoint is utilized due to convenience despite the lack of sound statistical method to design the trial.

There are few literature available for the consideration of trial designs with GMI as the primary endpoint. Mick et al.⁷ discussed a hypothesis testing approach for the trial design and did simulation for the study power under an exponential model. They demonstrated that the correlation between paired TTP times is the key for the efficiency of the trial design. Kovalchik and Mietlowski⁸ proposed an estimation approach. They provided nonparametric and parametric methods to estimate the probability of GMI survival beyond the threshold value. However, their recommendation for the trial design is also based on the simulation results under the Weibull-Gamma frailty model. Similar arguments are recently discussed by Texier et al.⁹ Both the hypothesis testing and estimation approach have not been used in practice because the simulations are limited to the exponential or Weibull model, hence the results are model specific and directly using their simulation results could be misleading to a specific trial design.

Several published trials used a GMI-based approach to assess the activity of second-line treatments. For example, Bonetti et al.¹⁰ conducted a trial using GMI as the primary endpoint and has pointed out that further research is needed in order to define the appropriate sample size and the amount of benefit required to conclude that a new regimen used in second-, third-, or fourth-line treatment is effective in a given type of malignancy. With the advances in cancer drug development described above, our institution has been pursuing precision medicine trials on patients with targetable molecular alterations and combination targeted and immunotherapy trials for the treatment of relapse or refractory cancer patients whereby the GMI is the primary endpoint in single-arm phase II trial design settings. Thus, an appropriate statistical method for such trial design is urgently needed.

Motivated by the institutional studies, we derived a sample size formula which provides a sound statistical method for the trial design with GMI as the primary endpoint. The rest of the article is organized as follows. In section 2, the test statistics are introduced. In section 3, a sample size formula is derived and trial designs are illustrated under various models. Simulations are conducted in section 4. Study designs using real trial data are illustrated in section 5. Discussions and concluding remarks are given in section 6.

2. Test Statistics

To assess the treatment effect of the trial with correlated paired survival data {(T_1i, T_2i), i = 1, … , n}, a log-linear model for paired difference is considered

$$\log (T_{2i})-\log (T_{1i})=\gamma +w_i,$$ (1)

where γ = log(Δ) and Δ(≥ 1) is an acceleration factor for the accelerated failure time (AFT) model (or a hazard ratio of T₁ vs. T₂ for the special case of exponential model) and $w_i^{\prime }s$ are independent random errors with a common symmetric distribution. In order to test the hypothesis for the acceleration factor γ, a score is defined for each data pair i as follows:

$$r_i=\{\begin{array}{cc}1\hfill & \text{if}{T}_{2i}>T_{1i}\hfill \\ -1\hfill & \text{if}{T}_{2i}\le T_{1i}\text{and}{T}_{2i}\text{is uncensored}\hfill \end{array}\phantom{\}}$$

For the pair i in which T_2i ≤ T_1i and T_2i is censored, the pair i does not contribute to the test statistic defined by following equation (2). Excluding the pairs from the test statistic (2) for which r_i can’t be specified does not bias the test since r_i takes value −1 and +1 with probability 0.5. Let ñ be the total number of pairs that contribute to the test statistic, we refer to it as the number of paired events. In fact if T_2i > T_1i, whether T_2i is uncensored or censored, makes the same contribution to the test statistics. Therefore, it can be treated as an uncensored observation. To test the null hypothesis H₀ : γ = 0 (or Δ = 1), a score test statistic^7,11 is defined as follows:

$$Q=\frac{({\sum }_{i=1}^{\tilde{n}}{r}_i{)}^2}{{\sum }_{i=1}^{\tilde{n}}{r}_i^2},$$ (2)

which is approximately a central chi-square distribution with degree freedom of 1 (see Appendix 1). Thus, we reject the null hypothesis if $Q>{\chi }_{1,\alpha }^2$, where ${\chi }_{1,\alpha }^2$ is the α% upper quantile of the central chi-square distribution with degree freedom of 1.

3. Sample Size and Study Design

To calculate the sample size, we need to derive the asymptotic distribution of the test statistic Q under the alternative H_a : Δ > 1. As shown in Appendix 1, the test statistic Q follows a non-central chi-square distribution with degree freedom of 1, where the non-central parameter is given as follows:

$$\delta =4\tilde{n}(p-0.5{)}^2,$$

in which p = P(T₂ > T₁∣H_a). Thus, given type I error of α, the study power 1 − β satisfies

$$1-\beta =P(Q>{\chi }_{1,\alpha }^2\mid H_a)=1-F_{1,\delta }({\chi }_{1,\alpha }^2),$$

where F_1,δ(·) is the non-central chi-square distribution with degree freedom of 1 and non-central parameter δ. Hence, the non-central parameter can be solved from above equation and defined as δ_α,β. Therefore, the number of paired events can be calculated by

$$\tilde{n}=\frac{{\delta }_{\alpha ,\beta }}{4(p-0.5{)}^2},$$ (3)

where p = P(T₂ > T₁∣H_a). We will discuss the study designs under various models in the next three subsections.

3.1. Study Design Under GBVE Model

We consider a bivariate exponential model which is a transformed Gumbel’s type B bivariate extreme-value distribution with a joint bivariate survival distribution function as follows:

$$S(t_1,t_2)=\text{exp}[-\{(t_1∕{\theta }_1{)}^{1∕\nu }+(t_2∕{\theta }_2{)}^{1∕\nu }{\}}^{\nu }],$$

where 0 < t₁, t₂ < ∞, 0 < θ₁, θ₂ <, ∞, 0 < ν ≤ 1. Here θ₁ and θ₂ are the scale parameters and ν is the dependence parameter, and ν = 1 corresponding to the case of independence. This distribution is referred to as GBVE(θ₁, θ₂, ν). It is obvious that the marginal distributions of T₁ and T₂ are exponential with scale parameters θ₁ and θ₂, respectively.

Lu and Bhattacharyya¹² have shown that log(T₂/T₁) follows a logistic distribution of Logistic(γ, ν) with location parameter γ = log(Δ) (Δ = θ₂/θ₁) and scale parameter ν, and the survival function of log(T₂/T₁) is given by

$$S(t;\gamma ,\nu )=P(\log (T_2∕T_1)>t)=(1+e^{\frac{t-\gamma }{\nu }}{)}^{-1},-\infty <t<\infty .$$

Thus, the pair (T₁, T₂) satisfies the AFT model (1), where the random error w follows a symmetric distribution of Logistic(0, ν). They have also shown that the Pearson correlation coefficient between T₁ and T₂ is given by

$$\rho =2{\Gamma }^2(\nu +1)∕\Gamma (2\nu +1)-1,$$

where Γ(·) is a gamma-function, and the probability of the growth modulation index GMI > 1 is given by

$$p=P(\text{GMI}>1)=\frac{1}{1+{\Delta }^{-1∕\nu }},$$ (4)

where Δ = θ₂/θ₁ is the hazard ratio of control versus treatment. Thus, the study effect size is determined by the correlation ρ and hazard ratio Δ. A higher correlation and larger hazard ratio, indicate a larger effect size and higher study power. A graphic presentation of the relationship between the generalized effect size p = P(GMI > 1) with correlation ρ and hazard ratio Δ is given in Figure 1.

Figure 1:

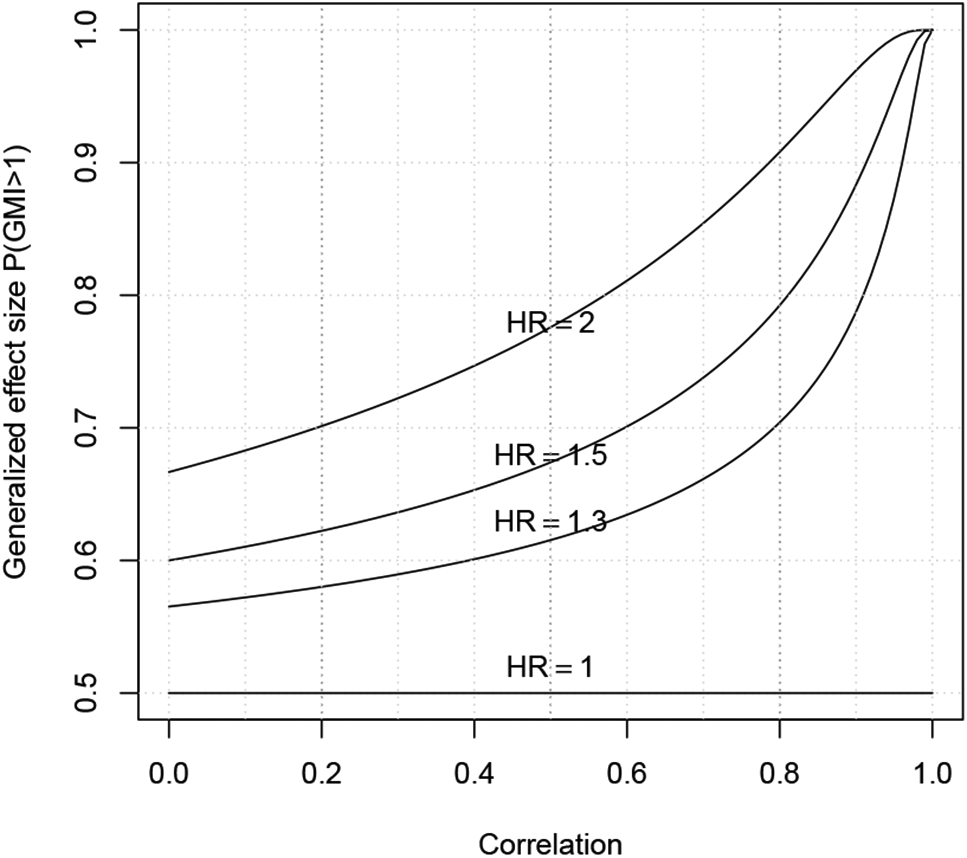
Graphic representation of the relationship between correlation ρ, hazard ratio Δ and generalized effect size p = P(T₂ > T₁).

Given ρ = 0.1 to 0.8, and hazard ratio Δ = 1.2 to 2.5, the required number of events calculated for a one-sided type I error of 5% and power of 80% are given in Table 1. From the sample size calculation, it is again demonstrated that the correlation between paired TTP times is the key for the efficiency of the trial design. Furthermore, the sample size calculation also shows that it is unrealistic to design a phase II trial when the correlation is small (ρ = 0.1 − 0.3) and hazard ratio is also small (Δ = 1.2 − 1.3). However, for a moderate correlation (ρ = 0.4 − 0.6) and moderate hazard ratio (Δ = 1.4 − 1.6), less than 100 patients can provide 80% power to detect the significant treatment effect. When hazard ratio is large (Δ ≥ 1.7), then even a small correlation, with less than 100 patients still provides 80% of power for the study design.

Table 1:

The number of paired events ñ required of the trial under the GBVE model for various correlations and hazard ratios for a one-sided hypothesis with type I error of 5% and power of 80%. Based on 100,000 simulation runs, the empirical type I errors ($\widehat{\alpha }$) and empirical powers (EP) corresponding to the calculated number of paired events are also recorded in the table.

Number of paired events ñ ($\widehat{\alpha }∕\text{EP}$)
Correlation ρ
Δ	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
1.2	776(.048/.80)	628(.050/.80)	502(.054/.81)	393(.055/.81)	300(0.056/.82)	219(.042/.79)	150(.041/.78)	92(.047/.81)
1.3	377(.051/.80)	306(.045/.79)	245(.055/.82)	193(.044/.79)	147(.048/.80)	109(.056/.82)	75(.065/.84)	47(.040/.80)
1.4	232(.056/.82)	188(.049/.80)	151(.050/.81)	119(.043/.79)	92(.047/.81)	68(.038/.78)	48(.060/.84)	31(.070/.88)
1.5	161(.059/.82)	131(.053/.82)	106(.041/.79)	84(.063/.84)	65(.046/.81)	49(.043/.81)	35(.041/.81)	23(.035/.82)
1.6	121(.045/.79)	99(.043/.79)	80(.057/.83)	64(.060/.84)	50(.065/.86)	38(.035/.79)	27(.051/.85)	19(.064/.90)
1.7	96(.054/.82)	79(.041/.80)	64(.060/.84)	51(.048/.82)	40(.038/.80)	31(.070/.88)	23(.035/.82)	16(.076/.92)
1.8	79(.041/.80)	65(.046/.81)	53(.053/.83)	43(.067/.86)	34(.057/.85)	26(.075/.89)	19(.064/.88)	14(.057/.91)
1.9	67(.050/.81)	56(.044/.81)	45(.035/.78)	37(.046/.83)	29(.061/.86)	23(.035/.82)	17(.049/.87)	13(.022/.84)
2.0	59(.036/.78)	48(.060/.84)	40(.038/.80)	32(.050/.84)	26(.075/.89)	20(.041/.84)	16(.076/.93)	12(.039/.91)
2.1	52(.036/.79)	43(.067/.86)	35(.041/.80)	29(.061/.87)	23(.035/.81)	18(.031/.81)	14(.057/.90)	11(.064/.95)
2.2	47(.040/.80)	39(.054/.84)	32(.050/.84)	26(.046/.89)	21(.079/.90)	17(.049/.88)	13(.022/.81)	11(.064/.96)
2.3	42(.044/.81)	35(.041/.81)	29(.061/.86)	24(.050/.88)	20(.041/.85)	16(.076/.92)	13(.022/.84)	10(.022/.88)
2.4	39(.054/.84)	32(.050/.83)	27(.051/.85)	22(.061/.86)	18(.031/.81)	15(.035/.86)	12(.039/.90)	10(.022/.91)
2.5	36(.065/.86)	30(.044/.82)	25(.044/.83)	21(.075/.91)	17(.049/.87)	14(.057/.91)	12(.039/.92)	10(.022/.93)

3.2. Study Design Under Weibull Frailty Model

An alternative model for the trial design with GMI endpoint is the Weibull frailty model^8,9. In this approach, we assume that conditional on a frailty term u, T₁ and T₂ have distributions of Weibull(uθ₁, κ) and Weibull(uθ₂, κ) with a common shape parameter κ, and survival distribution function is given by

$$S(t;{\theta }_j,\kappa \mid u)=e^{-(\frac{t}{u{\theta }_j}{)}^{\kappa }},j=1,2$$

where frailty u has density function h(u), u > 0. Owen¹⁵ have shown that log(T₂/T₁) follows a logistic distribution of Logistic(γ, κ⁻¹) which does not depend on the shared frailty u, where γ = log(R) and R = θ₂/θ₁ is an acceleration factor. Thus, the generalized effect size p = P(T₂ > T₁) is given by

$$p=\frac{1}{1+R^{-\kappa }}=\frac{1}{1+{\Delta }^{-1}},$$ (5)

where Δ = R^κ = (θ₂/θ₁)^κ is the hazard ratio of T₁ versus T₂. Given R = 1.5 to 2.5 and κ=0.5, 1 and 2 to reflect cases of decreasing, constant, and increasing hazard functions, respectively, the required number of events calculated for a one-sided type I error of 5% and power of 80% are given in Table 2. The distribution of log(T₂/T₁) does not depend on the correlation between the pair of TTPs, it depends on the shape parameter κ which plays a similar role as the correlation parameter ν for the GBVE model. The shape parameter κ = 1 and 2 in the Weibull frailty model correspond to the cases of independent (ν = 1 or ρ = 0) and moderate correlation (p ≃ 0.57) for the GBVE model, respectively. Thus, study design is not very efficient under the Weibull frailty model when κ ≤ 1 and more efficient when κ > 1 by using the score test Q (see Table 2).

Table 2:

The number of paired events ñ required of the trial under the Weibull frailty model for one-sided hypothesis with type I error of 5% and power of 80%. Based on 100,000 simulation runs, the empirical type I errors ($\widehat{\alpha }$) and empirical powers (EP) corresponding to the calculated number of paired events are also recorded in the table.

Number of paired events ñ ($\widehat{\alpha }∕\text{EP}$)
R	Δ	κ = 0.5	Δ	κ = 1	Δ	κ = 2
1.5	1.2247	769(.051/.80)	1.5	196(.053/.81)	2.25	53(.053/.83)
1.6	1.2649	574(.049/.80)	1.6	147(.048/.80)	2.56	41(.059/.85)
1.7	1.3038	451(.048/.80)	1.7	117(.041/.79)	2.89	33(.035/.79)
1.8	1.3416	369(.048/.80)	1.8	96 (.051/.81)	3.24	28(.036/.80)
1.9	1.3784	310(.048/.80)	1.9	81 (.045/.80)	3.61	24(.064/.87)
2.0	1.4142	267(.051/.81)	2.0	71 (.058/.83)	4.00	22(.051/.87)
2.1	1.4491	233(.049/.80)	2.1	62 (.057/.83)	4.41	20(.042/.85)
2.2	1.4832	207(.053/.81)	2.2	56 (.045/.81)	4.84	18(.030/.82)
2.3	1.5166	186(.047/.80)	2.3	51 (.049/.82)	5.29	17(.049/.88)
2.4	1.5492	169(.046/.79)	2.4	46 (.054/.83)	5.76	16(.077/.92)
2.5	1.5811	155(.054/.82)	2.5	43 (.065/.86)	6.25	15(.036/.86)

3.3. Study Design Using Generalized Effect Size

In a real trial design, because the relapsed patients are identified and enrolled on the study at a closer time period, there is no historical data available to estimate the correlation ρ between the pair of (T₁, T₂) and to validate the underlying bivariate survival model. Therefore, an alternative way to design the study is using a generalized treatment effect size p = S_GMI(1) = P(T₂ > T₁), which has been considered for assessing treatment effects by O’Brien¹³ and Hauck et al.¹⁴ The generalized treatment effect size is intuitive to clinicians. It is the probability of T₂ greater than T₁. Under the null hypothesis (no treatment effect) S_GMI(1) = 50%, and one can set an alternative hypothesis of S_GMI(1) = 65%, 70%, or 75% that is a 15%, 20% and 25% increase in the probability of TTP for the current therapy greater than that of TTP for the previous therapy. The required number of paired events calculated using formula (3) are 88, 50 or 32, respectively for a one-sided type I error of 5% and power of 80%. This design makes no assumption for the correlation and bivariate survival distribution. Of course, whether a 15% to 25% increase of the generalized effect size is achievable depends on how high the paired TTP are correlated and the structure of the bivariate distribution to connect the correlation and hazard ratio into the generalized effect size S_GMI(1). The relationship between an amount of increasing the probability S_GMI(1) and an amount of increasing the hazard ratio Δ is illustrated in Figure 2 under the GBVE model with a moderate correlation ρ = 0.5.

Figure 2:

Graphic representation of the relationship between the survival distribution of GMI and generalized effect size p = P(T₂ > T₁).

Remark: under the GBVE model with a moderate correlation ρ = 0.5, the alternative hypotheses of the generalized effect size S_GMI(1) = 65%, 70%, and 75% correspond to the hazard ratio of 1.413, 1.605 and 1.846, respectively, however under the Weibull frailty model, they correspond to the hazard ratio of 1.857, 2.333 and 3.0, respectively.

Finally, if T_2i ≤ T_1i and T_2i is censored, the pair does not contribute to the test statistics and makes no contribution to the study power. Thus, to calculate the sample size (total number of pair), we need to adjust the required number of paired events ñ by a percentage of the cases in which T_2i ≤ T_1i and T_2i is censored, which is often a small percentage. Based on our simulations, we recommend a 5% up to 10% increase to the number of events for the total sample size, that is the sample size can be calculated by

$$n=\frac{\tilde{n}}{1-5\%}=1.05\tilde{n}\text{or}\frac{\tilde{n}}{1-10\%}=1.11\tilde{n}.$$

If we assume the annual accrual rate is a patients, then accrual period of the trial is n/a. The follow-up time should be longer than the median of TTP of T₂. For relapse or refractory cancer patients, the median TTP is often within one-year. Thus, a two-year follow-up could be sufficient for the trial to observe the planned number of events.

4. Simulation

To study the performance of the test statistic Q and accuracy of the formula (3) in finite sample cases, we conducted simulation studies under the GBVE model and Weibull-Gamma frailty model. Random bivariate paired samples of (T_1i,T_2i) are generated from GBVE(θ₁, θ₂, ν) according to the method given in Appendix 2, and the Gamma frailty is generated from gamma distribution of Gamma(2, 2). Without loss of generality, the parameter θ₁ is set to 1, hazard ratio Δ set from 1.2 to 2.5 by 0.1, and correlation ρ set from 0.1 to 0.8 by 0.1 for the GBVE model, and R set from 1.5 to 2.5 by 0.1 and κ = 0.5, 1, and 2 for the Weibull-Gamma frailty model. The corresponding number of events are calculated by formula (3) with a type I error of 5% (one-sided) and power of 80%. Because the simulations are done for the number of events, thus, no censoring is assumed. The empirical type I error and empirical power are simulated based on 100,000 simulated trials (Table 1-2). When the number of events is between 30 and 100 which is the size for majority of phase II trials, the simulation results show that the test statistic Q preserves the type I error well and formula (3) provides correct power for the study design. When the number of events is small, the empirical type I error could be slightly inflated. This is because of the discreteness of the test statistic Q. If we want better control of the type I error, we can either set a small type I error, e.g. α = 4.5% for the trial design or apply a continuity correction to the Q which will preserve the type I error but it will slightly reduce the power. For example, for the case of correlation ρ = 0.6 and hazard ratio Δ = 1.7 in Table 1 (where ñ = 31), the empirical type I error and power reduce to 2.9% and 78%, respectively, by using the Q with a continuity correction.

5. Example

The data from a trial reported by Bonetti et al.¹⁰ is used to illustrate study design using proposed methods. In the trial, treatment efficacy was assessed by GMI for a second-line therapy (combination of LV-modulated 5-FU and oxaliplatin) in patients with advanced colon carcinoma after failure of a first-line chemotherapy (LV-modulated 5-FU or raltitrexed). A scatter plot of 34 observed pairs of TTPs (reconstructed data from Figure 1 of Kovalchik and Mietlowski.⁸) is given in Figure 3, which shows a significant correlation between the pairs (correlation ρ = 0.514.¹⁰). Sixteen patients (47%) had a GMI > 1.3, twenty-two patients (64.7%) had a GMI > 1 and three patients (9%) had censored T₂ less than T₁. The marginal distributions of T₁ and T₂ are estimated by Kaplan-Meier curves and fitted by the Weibull models with a common shape parameter κ (Figure 4). The estimated scale parameters are ${\widehat{\theta }}_1$ = 21.06 and ${\widehat{\theta }}_2$ = 31.89 and shape parameter is $\widehat{\kappa }$ = 1.91. Figure 4 shows that the Weibull models fit the data well. An estimate of the generalized effect size p = S_GMI(1) from the Kaplan-Meier curve is 72% (95% confidence interval: 53%-84%). Suppose we design a new trial for the same group of patients to detect an R = 1.5 with shape parameter κ = 1.9 or a hazard ratio Δ = R^κ = 1.5^1.9 = 2.16, then, the generalized effect size p = S_GMI(1) is 68%. Thus, with one-sided type I error of 5% and power of 80%, the required number of events calculated by formula (3) is ñ = 61. In case of the Weibull frailty model can’t be justified, then the trial can be designed by using the generalized effect size p = S_GMI(1). For example, the generalized effect size at alternative hypothesis is set to 70%, the required number of events is ñ = 50. By adjusting 10% censored observations which do not contribute to the test statistic, a total of n = 68 and n = 56 patients are needed for the trial corresponding to the above two design scenarios, respectively.

Figure 3:

Scatter plot of T₂ against T₁ for the data from a trial reported by Bonetti et al.¹⁰ and reconstructed from Figure 1 of Kovalchik and Mietlowski.⁸ Dotted line represents line of T₂ = T₁.

Figure 4:

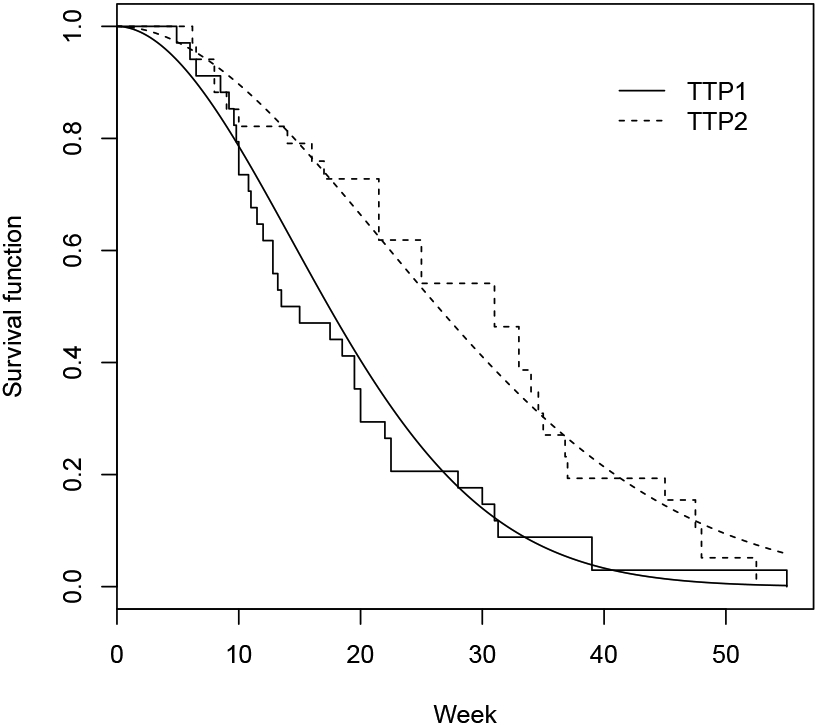
Kaplan-Meier curves (step functions) and fitted Weibull distributions (smooth curves) for first-line therapy arm and second-line therapy arm, respectively.

6. Discussion

The GMI as a primary endpoint for single-arm phase II trials with cytostatic cancer treatment was first proposed by Von Hoff.⁵ The GMI has advantages of being a more suitable indicator of delayed growth than traditional response measures. Furthermore with the GMI endpoint, patients served as their own controls, which makes the outcome less heterogeneous and more personalized, thus more feasible to establish benchmarks for evidence of treatment efficacy.⁸ However, it has not been put into practice because of lack sound statistical method for the trial design. Even though, Mick et al.⁹ have discussed a hypothesis testing approach and Kovalchik and Mietlowski⁸ recommended an estimation approach under the Weibull frailty model, their results are limited to the simulations under the restricted model assumption. Directly using their simulation results could be misleading to the trial design.

Von Hoff considered GMI > 1.3 as a criterion for treatment activity. Under the GBVE(θ₁, θ₂, ν) model, the survival function of GMI can be calculated as

$$S_{\text{GMI}}(s)=P(\text{GMI}>s)=\frac{1}{1+(\Delta ∕s{)}^{-1∕\nu }}.$$

Thus, S_GMI(1.3) = 1/{1+(Δ/1.3)^−1/ν}. Von Hoff et al.⁶ set the null hypothesis S_GMI(1.3) = 15% versus the alternative hypothesis S_GMI(1.3) = 30% for the study design. However, the choice of S_GMI(1.3) = 15% as an inactive criteria and S_GMI(1.3) = 30% as an active criteria are arbitrary and difficult to justify. For example, under the GBVE model with a moderate correlation ρ = 0.5, S_GMI(1.3) = 15% versus 30% correspond to the hazard ratio 0.49 versus 0.81, respectively, which obviously were both set too low for the hypothesis of treatment efficacy.

Remark: The above study design proposed by Von Hoff et al. set the null hypothesis of hazard ratio 0.49 (not commonly used hazard ratio=1) and alternative hypothesis of hazard ratio 0.81 under the GBVE model with a moderate correlation ρ = 0.5, which means that the second line therapy is only approximately 50% effective as the first line therapy, the study will conclude that the second line treatment is ineffective, and if the second line therapy is approximately 80% effective as the first line therapy, the study will conclude that the second line therapy is effective.

To overcome those drawbacks, a sample size formula is derived under an AFT model for the paired TTP data. Trial design with GMI endpoint was discussed under a bivariate exponential model, Weibull frailty model and generalized treatment effect size. The advantage of using bivariate exponential model or Weibull frailty model is that the sample size can be calculated in a traditional way through specifying the hazard ratio of the paired TTPs. However, because the relapsed patients are identified and enrolled on the study at a closer time period, there is no historical data available to estimate the correlation ρ between the paired TTPs and to validate the underlying bivariate survival model. Thus, an alternative design using the generalized effect size is attractive which does not rely on specifying the correlation and bivariate survival distribution. The number of events or sample size calculation is extremely simple by using formula (3).

Finally, since in relapse and refractory cancer patients, successive TTPs tend to be shorter and shorter, Kovalchik and Mietlowski⁸ discussed a trial design under the null hypothesis of median GMI = 0.7 versus alternative hypothesis median GMI = 1 as the treatment equivalence or Von Hoff’s median GMI = 1.3 as the treatment efficacy. In this case, the generalized effect size can be defined by p = S_GMI(0.7) and the null hypothesis will be S_GMI(0.7) = 50% versus alternative, of say S_GMI(0.7) = 70%. The sample size formula (3) can still be used for such trial design.

Overall, the derived formula gives accurate estimation of the number of events and the trial design using the generalized effect size is simple and intuitive to clinicians. The proposed study designs provide sound statistical methods for single-arm phase II trial to test more appropriate endpoints such as paired TTPs for new cancer treatment paradigms being advanced to clinical trials for relapse or refractory cancer patients.

Appendix 1: Derivation asymptotic distribution of Q

By the definition of the test statistic (2), we have

$$Q=\frac{({\sum }_{i=1}^{\tilde{n}}{r}_i{)}^2}{{\sum }_{i=1}^{\tilde{n}}{r}_i^2}=\frac{({\tilde{n}}_2-{\tilde{n}}_1{)}^2}{\tilde{n}},$$

where ñ₁ and ñ₂ are #{i; r_i = −1} and #{i; r_i = 1}, respectively, and ñ = ñ₁+ñ₂. By some calculations, we can show an alternative representation of Q as follows:

$$Q=\sum _{k=1}^2\frac{\tilde{n}({\widehat{p}}_k-p_k^0{)}^2}{p_k^0},$$

where ${\widehat{p}}_k={\tilde{n}}_k∕\tilde{n}$ and $p_k^0=P(T_2>T_1\mid H_0)=0.5$, k = 1, 2. The null hypothesis H₀ : γ = 0 is equivalent to H₀ : $p_k=p_k^0$, k = 1, 2, where p₂ = p = P(T₂ > T₁) and p₁ = 1 − p. Thus, Q is a goodness fit test statistic. By Pearson’s theorem,¹⁶ Q converges in distribution to a central chi-square distribution with degree freedom of 1, that is $Q\sim {\chi }_1^2$.

To calculate sample size, we have to derive the distribution of Q under the alternative. By assuming local alternatives,¹⁷ that is $p_k=p_k^0+c_k∕\sqrt{\tilde{n}}$, k = 1, 2, where c_k is fixed constant as ñ increases, thus, we have

$$\frac{\sqrt{\tilde{n}}({\widehat{p}}_k-p_k^0)}{\sqrt{p_k^0}}=\frac{\sqrt{\tilde{n}}({\widehat{p}}_k-p_k)}{\sqrt{p_k}}\sqrt{\frac{p_k}{p_k^0}}+\frac{\tilde{n}(p_k-p_k^0)}{\sqrt{p_k^0}}.$$

From the definition of local alternatives, it is easy to see,

$$\sqrt{\frac{p_k}{p_k^0}}=\sqrt{1+\frac{p_k-p_k^0}{p_k^0}}=\sqrt{1+\frac{c_k}{p_k^0\sqrt{\tilde{n}}}}\to 1,\tilde{n}\to \infty$$

and

$$\frac{\sqrt{\tilde{n}}(p_k-p_k^0)}{\sqrt{p_k^0}}=\frac{c_k}{\sqrt{p_k^0}}.$$

Thus, under local alternatives, by the central limit theorem,

$$Z_k=\frac{\sqrt{\tilde{n}}({\widehat{p}}_k-p_k)}{\sqrt{p_k}}\sqrt{\frac{p_k}{p_k^0}}\sim N(0,1),$$

where the Z_k are subject to the linear constrain ${\sum }_{k=1}^2{Z}_k\sqrt{p_k^0}=0$. Now, we have

$$Q=\sum _{i=1}^k(Z_k+\frac{c_k}{\sqrt{p_k^0}}{)}^2.$$

Thus, Q follows a non-central chi-square distribution with degree freedom of 1 and non-central parameter

$$\delta =\sum _{k=1}^2\frac{c_k^2}{p_k^0}=\tilde{n}\sum _{k=1}^2\frac{(p_k+p_k^0{)}^2}{p_k^0}=4\tilde{n}(p-0.5{)}^2,$$

where p = P(T₂ > T₁∣H_a).

Appendix 2: Generate random variables from GBVE model

Let U, V₁₁, V₁₂ and M_ν are independent random variables such that U ~ uniform(0, 1), V_1i ~ exp(1), i = 1, 2, and M_ν = 0 or 1 with probability 1 − ν and ν, respectively, where 0 < ν ≤ 1. Let θ_i, i = 1, 2 be positive constants. Define V = V₁₁ + M_νV₁₂, T₁ = θ₁U^νV and T₂ = θ₂(1 − U)^νV, then, as shown by Lee,¹⁸ (T₁ T₂) ~ GBVE(θ₁, θ₂, ν).