Competition between growth and shear stress drives intermittency in preferential flow paths in porous medium biofilms

Significance

Biofilms are ubiquitous in porous media, including soils and technical applications such as bioremediation and wastewater treatment systems. Biofilms can drastically alter the transport of nutrients and contaminants through porous media by forming preferential flow paths, which are subject to strong intermittency in fluid flow. This intermittency manifests through the opening and closing and spatiotemporal rearrangement of flow paths, and its mechanism has to date remained unresolved. Here, we show that intermittency is driven by the competition between microbial growth that governs the closing of preferential flow paths and biofilm compression and rupture that control their opening.

Abstract

Bacteria in porous media, such as soils, aquifers, and filters, often form surface-attached communities known as biofilms. Biofilms are affected by fluid flow through the porous medium, for example, for nutrient supply, and they, in turn, affect the flow. A striking example of this interplay is the strong intermittency in flow that can occur when biofilms nearly clog the porous medium. Intermittency manifests itself as the rapid opening and slow closing of individual preferential flow paths (PFPs) through the biofilm–porous medium structure, leading to continual spatiotemporal rearrangement. The drastic changes to the flow and mass transport induced by intermittency can affect the functioning and efficiency of natural and industrial systems. Yet, the mechanistic origin of intermittency remains unexplained. Here, we show that the mechanism driving PFP intermittency is the competition between microbial growth and shear stress. We combined microfluidic experiments quantifying Bacillus subtilis biofilm formation and behavior in synthetic porous media for different pore sizes and flow rates with a mathematical model accounting for flow through the biofilm and biofilm poroelasticity to reveal the underlying mechanisms. We show that the closing of PFPs is driven by microbial growth, controlled by nutrient mass flow. Opposing this, we find that the opening of PFPs is driven by flow-induced shear stress, which increases as a PFP becomes narrower due to microbial growth, causing biofilm compression and rupture. Our results demonstrate that microbial growth and its competition with shear stresses can lead to strong temporal variability in flow and transport conditions in bioclogged porous media.

Porous media often constitute an ideal habitat for the formation of bacterial biofilms, both in the environment and in technological and medical settings. Biofilms in porous media contribute to enhancing reaction rates in biomineralization, bioremediation, enhanced oil recovery, water treatment, and biochemical production (1–4), but they also have major negative impacts in medical and filtration applications, where they cause clogging. Within biofilms, bacteria embed themselves in a secreted matrix of extracellular polymeric substances mainly consisting of lipids, exopolysaccharides, proteins, and extracellular DNA (5–7). This gel-like matrix protects the bacteria from nutrient fluctuations, dehydration, and mechanical and chemical insults (7, 8). The matrix also has a structural role, as its composition determines the biofilm’s rheological properties (6, 7, 9), which are crucial in controlling the detachment and spatial rearrangement of biomass when exposed to shear stresses (10). Biofilms have a complex rheology, which has been described as viscoelastic (9, 11) or viscoplastic behavior (12), and confers on them the ability to retain their structure while undergoing shear-induced deformation. Biofilm morphology depends on flow conditions; in the absence of flow (e.g., on agar plates), bacteria form compact biofilm colonies, sometimes crossed by channels (13), whereas under flow, bacteria form dense, layered biofilms (14) or suspended filaments known as streamers (15).

Within porous media, biofilms are exposed to a wide range of fluid flow velocities (16). They form through several characteristic stages, as follows: initial attachment of cells to the solid surfaces of the porous medium, the formation of clusters and streamers, and finally, the clogging of pore spaces (17). Biofilm development is driven by the balance of attachment (18), growth, and detachment (19). While bacterial transport through porous media is mainly controlled by the flow field (20–22), the spatial distribution of biofilm is additionally governed by shear forces, which influence bacterial transport and thereby determine initial bacterial attachment (23). The production of extracellular polymeric substances by biofilms, their matrix structure, and thereby their macroscopic appearance is a function of the interplay between hydrodynamics and nutrient availability (24, 25). As they grow, biofilms cause bioclogging, reducing the porosity (26) and the hydraulic conductivity (27) of the porous medium. Experimental studies and numerical models have shown that under conditions in which a given flow rate is imposed, biofilms can lead to the formation of preferential flow paths (PFPs) through the composite structure made by the porous medium and the biofilm. They also reveal the emergence of recurrent opening and closing behavior of the PFPs, resulting in intermittency (2, 28, 29). Studies to date have been limited to a single porous geometry (2, 28, 30) and have relied on the simplified assumption of a constant cell decay (29). Therefore, a mechanistic understanding of the intermittent opening and closing of PFPs and their spatiotemporal rearrangement in biofilms has been missing.

Here, we report experiments and mathematical simulations of fluid flow through a biofilm–porous medium structure and show that the mechanism for intermittency is the competition between microbial growth that closes flow paths and flow-induced stress that opens them abruptly through compression and rupture of the biofilm. Using microfluidic experiments that combine imaging at high temporal and spatial resolution and direct pressure measurements, together with mathematical simulations based on the Darcy–Brinkman–Biot model, we systematically studied biofilms in porous media for a range of flow rates and pore sizes. Our results reveal that the coupling between fluid flow and microbial growth can drastically alter transport properties in bioclogged porous media, with far-reaching implications for the distribution of nutrients and contaminants.

Results

PFP Intermittency in Bioclogged Porous Media.

While studying biofilm development by the wild-type bacterium Bacillus subtilis within model porous media, we observed a reproducible formation of PFPs and strong intermittency in their opening and closing. Porous media were formed by a microfluidic device containing an array of pillars with diameter and spacing between pillars (the pore size, d) of 300 µm for the initial experiments, in an array measuring 22 mm × 4.05 mm with a height 100 µm (Fig. 1A and Materials and Methods). The initial porosity of this model medium was 0.77. The flow of a nutrient solution (for details of composition, see Materials and Methods) was imposed with a flow rate, Q, of 1 mL/h. Within such a system, the vertical velocity profile at a given position is controlled by the distance between the two nearest pillars (31). In our device, this distance was of the same order as the height; this results in a quasi-two-dimensional (2D) flow, where the vertical profile of the horizontal velocity, v_x(z), is intermediate between the parabolic profile expected for a lower model height and the plug-flow profile with narrow limit boundaries at the top and bottom boundaries expected for a higher model height (32). After the bacterial culture was loaded into the microfluidic device and initial attachment of individual bacteria took place (Fig. 1B), biofilms formed on the pillars as clusters (surface-attached chunks of biofilm; white outline, Fig. 1C) and streamers (biofilm suspended in the flow; orange outline, Fig. 1C). Further growth resulted in complete clogging of most pores after 20 h (Fig. 1D and E). In the bioclogged porous medium, we observed PFPs. PFPs consisted of biofilm-free channels forming an often-tortuous path through the biofilm–porous medium structure, spanning the length of the system (highlighted in yellow in Fig. 1F–H). PFPs were seen to branch (blue circle, Fig. 1F) and coalesce (green circle, Fig. 1F). The position of PFPs changed over time until a steady geometrical configuration was reached after about 35 h (SI Appendix, Fig. S1).

Fig. 1.

PFP formation and intermittency in a model porous medium. Fluid flow rate, Q = 1 mL/h. (A) Schematic of the microfluidic device showing the porous domain (height, h = 100 µm; pore size, d = 300 µm) and locations of the pressure measurements (P). (B–E) Bright-field time-lapse images of biofilm formation, from initial attachment (B), through the formation of streamers (orange outline) and clusters (white outline) (C), to near clogging (D and E). (F–H) Segmented images of the porous medium at three points in time, showing the pillars (white), biofilm (black), and PFPs (yellow). The images were taken at times t = 33.7 h (F), t = 33.8 h (G), and t = 35.2 h (H), with the recorded pressure difference Δp = 185 mbar (F), Δp = 50 mbar (G), and Δp = 160 mbar (H). Closing PFPs have a narrow width (F and H), while open PFPs have a larger width (G). PFPs can branch (blue circle) and coalesce (green circle). (I) Mean PFP width, w, (yellow curve) and pressure difference, Δp, (red curve) across the entire porous domain as a function of time. Gray bars indicate every second cycle of rapid PFP opening and gradual PFP closing. An opening event was defined to occur at a PFP width change of 5 µm. Biofilm behavior causes a decrease in pressure difference across the porous domain when PFPs open and an increase in pressure difference when PFPs close. For example, narrowing of the PFPs by 27 µm over a period of 1.4 h (G, H) increases the pressure difference by 110 mbar, and very rapid widening of the PFPs by 54 µm decreases the pressure difference by 135 mbar (F, G). Letters correspond to the experimental images in F–H. Note that the pressure difference for the initial biofilm-free porous domain at the imposed fluid flow rate was subtracted, in order to isolate the impact of the biofilm on the pressure difference.

The bioclogged porous medium exhibited strong intermittency in the opening and closing of PFPs. To quantify changes in PFP width over time, we used high-resolution bright-field imaging (13,500 × 2,500 pixels acquired at 4× magnification) from 16 locations spanning the entire porous domain. We calculated the mean PFP width, w, by measuring width along the PFP and averaging over 6-min time windows, between 24 h and 45 h (Materials and Methods). We found that PFP width varied over time, between 50 µm and 110 µm (Fig. 1I). This intermittent opening and closing behavior occurred while the PFPs were still varying in position as well as when the PFPs were in a steady position.

To characterize PFP intermittency, we measured the pressure difference, $\mathrm{\Delta }p$, between the inlet and the outlet of the microfluidic device using pressure sensors (Materials and Methods). A comparison of the temporal changes in the pressure difference, $\mathrm{\Delta }p$, and in the PFP width, w, revealed that opening and closing events correlated with changes in pressure difference (Fig. 1I, e.g., at t = 33.8 h, t = 35.2 h). Narrowing of the mean PFP width resulted in an increase in the pressure difference (Fig. 1I). The increased pressure difference was due to a reduction in the hydraulic conductivity of the system (according to Darcy’s law). Similarly, the opening of the PFPs resulted in an increase in w and a decrease in the pressure difference (Fig. 1I). Furthermore, a gradual increase of the pressure difference was observed over time. The timescales of opening and closing were very different; closing of the PFPs was a gradual process that took 2 to 5 h, whereas the opening of the PFPs was extremely rapid, completed below the temporal resolution of the image acquisition, on a timescale of 0.2 to 2 s (Movie S1).

Microbial Growth Drives Flow Path Closing, and Hydromechanical Processes Drive Their Opening.

A systematic analysis of PFP formation and quantitative investigation of PFP opening and closing enabled us to determine the biological and hydromechanical mechanisms controlling PFP intermittency.

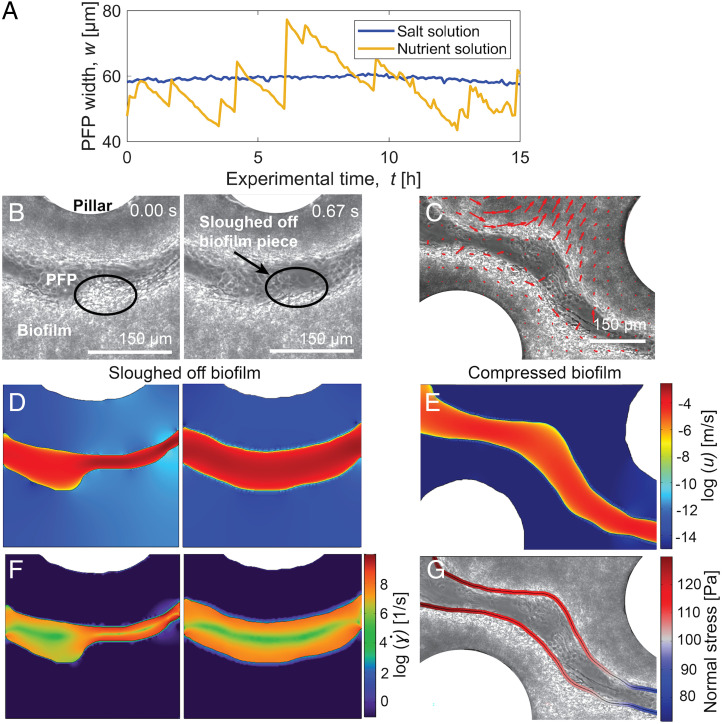
The long timescale of PFP closing (2 to 5 h) suggested that the process was driven by microbial growth. To test this hypothesis, we switched the flow of the medium provided to a mature biofilm from the nutrient solution to an isotonic salt solution. This switch deprived the cells of nutrients and thus suppressed growth without altering the osmotic pressure to avoid any change in shape or stiffness of the biofilm. A halt in previously observed intermittency was observed in the porous medium exposed to the flow of isotonic salt solution (Fig. 2A), confirming that microbial growth is necessary for intermittency. We infer from this that growth is responsible for the closing of PFPs, which is confirmed by the fact that no closing of PFPs was observed during the flow of the isotonic salt solution (Fig. 2A). We further note that no detachment was observed in this experiment, suggesting that starvation associated with the lack of nutrients does not cause an increase in biomass decay on the timescale of these observations (24 h).

Fig. 2.

In the intermittency observed in PFPs, PFP closing is driven by microbial growth, while PFP opening is driven by hydrodynamically induced stresses on the biofilm. (A) For a mature biofilm, replacing the flowing nutrient solution with a nutrient-free salt solution causes the intermittency in the PFP width to cease (blue curve), in comparison with continued intermittency under constant nutrient flow (yellow curve). This demonstrates that PFP closing is driven by microbial growth. Before data collection, biofilms were allowed to develop for 24 h, and the solution within the porous medium was allowed to equilibrate for 2 h after the change to a salt solution, before flow was resumed. Bright-field image sequences of the biofilms corresponding to this data are shown in SI Appendix, Fig. S4. (B) Images acquired in rapid sequence during PFP opening, showing the detachment of a portion of the biofilm (area ∼3,600 µm²) adjacent to the PFP. The black ellipse indicates the location of the sloughed-off biofilm. (C) DIC analysis of high-speed videos showing biofilm movement during PFP opening through compression of the biofilm structure. Red arrows indicate local movement within the biofilm mostly normal to the PFP, with larger arrows signifying a larger local biofilm movement. (D, E) Numerically computed fluid velocity u (note logarithmic color scale) for the geometries corresponding to the images in B and C, showing higher velocities in the narrower PFP regions. (F) Shear rate (note logarithmic color scale) computed from the numerical velocity field. Shear rates next to the PFP boundaries are much higher in a narrow path compared to an open path. (G) The stress normal to the PFP boundaries, obtained from the numerical simulations.

The rapidity of PFP opening, in contrast, in the order of 0.2 to 2 s (Movie S1), led us to hypothesize that opening was driven by a physical process and specifically by the shear forces associated with flow through the biofilm. As PFPs become narrower due to microbial growth, the same flow rate passing through the PFPs induces a stronger shear force. In order to test the hypothesis that this shear controls PFP opening, we recorded 1-h-long phase-contrast microscopy videos (10× objective) at high speed (20 frames/s) to capture the details of the very rapid opening events. From the videos, we tracked biofilm movement using digital image correlation (DIC) (33). DIC is an optical method that employs a tracking technique and cross-correlation to measure changes in the pixels of images. This analysis allowed us to identify the direction of movement of microscale regions of the biofilm adjacent to PFPs and thus quantify structural changes associated with PFP opening.

Based on this analysis, we identified two processes driving PFP opening (Movie S1 and Fig. 2B and C). The first process was sloughing off of biofilm, in which large parts of the biofilm directly bordering a PFP detached and were flushed out through the PFP. A sloughing-off event was identified from the videos as a portion of biofilm suddenly disappearing from the image sequence (Fig. 2B). The area of the biofilm bordering the PFP mainly affected by the sloughing off displayed a lighter gray color compared to the layers of the biofilm further away from the PFP, the denser layer (Fig. 2B). The second process was the compression of regions of the biofilm directly adjacent to a PFP and the associated movement of the biofilm structure perpendicular to the PFP, resulting in the widening of the flow path. Compression was detected from the DIC analysis of the videos as the local movement of the biofilm moving away perpendicularly from the PFP (Fig. 2C). During compression, the biofilm structure moved at speeds in the order of 10⁻² mm/s, which is one order of magnitude lower than the initial mean flow velocity.

PFP closing causes an increase in the shear rate within the PFP, which is released upon a PFP opening event. To analyze the evolution of shear rate in the PFPs, we performed numerical simulations of the fluid flow velocity based on the experimental images of Figs. 1 F–H and 2 B and C using COMSOL Multiphysics (SI Appendix). We validated these flow simulations using experimental particle image velocimetry (PIV) data (SI Appendix, Fig. S3). From the numerical simulations, we quantified both the shear rates and the normal forces acting on the boundaries of the PFP. The shear rate distribution in the PFPs for the entire biofilm–porous medium domain depends on the state of the PFPs (SI Appendix, Fig. S2); in an open PFP, the probability density function of the shear rate peaks at lower values compared to those in a narrow PFP. This result confirms that PFP opening events cause the shear rate to decrease, which conversely increases in the PFP during their narrowing. From a pore-scale perspective, we numerically computed the velocity field and shear rates based on the images in Fig. 2B (Fig. 2D and F). Before the sloughing of the biofilm fragment responsible for narrowing the PFP in Fig. 2B (circled in black), the shear rates at the biofilm interface were two orders of magnitude higher compared to those in the open PFP (Fig. 2F). Additionally, we computed the force acting perpendicular to the biofilm walls at the boundary of the PFP, finding that the biofilm deformation occurs perpendicular to the mean flow direction and that the normal force decreases downstream (Fig. 2G), thus confirming the role of compression in the opening of PFPs.

A Mathematical Model Supports the Dependence of PFP Intermittency on Biofilm Growth and Hydrodynamic Stress.

To further investigate the physical and biological mechanisms of PFP intermittency, we developed a mathematical model of biofilm formation in porous media based on a Darcy–Brinkman–Biot formulation used to model flow within and around deformable porous media (34, 35), yet never applied to biofilms. The model resolved flow through the biofilm and represented the biofilm as a viscoplastic continuum (12). The model included both flow in the PFPs and through the biofilm matrix, with the former described by Stokes flow (the inertial terms of the Navier–Stokes equation are negligible) and the latter represented using Darcy’s law and Biot poromechanics. The following assumptions were made in the model: 1) biofilm growth can be approximated as a first-order reaction obeying the mass conservation law (36); 2) the biofilm behaves as a viscoplastic material, meaning that it deforms viscously only after the shear stress on the biofilm exceeds the critical yield stress (12); and 3) all biofilm properties are independent of porosity, except for permeability, viscosity, and yield stress. These assumptions are used to solve the hydrodynamics within the biofilm and capture the biofilm growth process without fitting parameters. Technical details of the model and the assumptions can be found in SI Appendix.

No fitting parameters were used for the model. The model reproduces PFP formation and the intermittency phenomenon. For a model porous domain similar to the experimental system (5 mm × 4 mm, containing pillars of diameter 300 µm in an array with spacing 300 µm), the model yielded a very similar opening and closing behavior (Fig. 3A–C), replicating the spatiotemporal dynamics of biofilm behavior within the microfluidic model system. We compared model and experimental results quantitatively by investigating the evolution over time of the mean PFP width, w (Fig. 3D). The mean PFP width predicted by the model fluctuated around 100 µm and varied between 65 and 130 µm, in a manner comparable to the experimental data (Figs. 3D and 1I). As in the experiments, the model results showed that the increase in PFP width was very rapid, whereas the closing was slow (Fig. 3D).

Fig. 3.

A model of biofilm formation and behavior in flow predicts that PFP intermittency is dependent on microbial growth and fluid flow velocity. (A–C) Simulated biofilm growth and PFP intermittency, similar to experimental images in Fig. 1 F–H. The segmented images represent the simulation of a porous domain of 5 × 2 mm at time points t = 77.4 h (A), t = 77.6 h (B), and t = 79.2 h (C). PFPs are highlighted in yellow, biofilm is shown in black, and pillars are shown in white. The mathematical model was implemented using the same parameters and boundary conditions as the experimental setup (Fig. 1A), with d = 300 µm, h = 100 µm, porosity = 0.77, and fluid flow rate = 1 mL/h. Biofilm-related parameters such as kinematic viscosity = 6.67 × 10⁻⁶ m²/s, yield stress = 0.4 Pa, and permeability = 2.2 × 10⁻¹⁴ m² were taken from experimental measurements following existing protocols (SI Appendix). Biofilm density = 1,200 kg/m³ was obtained from the literature (37). A detailed description of the derivation of these parameters can be found in SI Appendix. (D) Predicted PFP width showed intermittency when microbial growth was included (yellow curve) but not when growth was excluded from the model (blue curve). A lower fluid flow rate of 0.05 mL/h (green line) induced a decrease in mean PFP width and subsequent disappearance of the PFPs. Letters correspond to the images in A–C. Shading indicates the error bars showing the SD of PFP width.

The model results confirm that intermittency is controlled by the interplay between microbial growth and shear stresses (SI Appendix, Fig. S5). Eliminating microbial growth during a model run resulted in the intermittency disappearing, as evidenced by the near constancy of the mean PFP width (Fig. 3D, blue curve). The small residual fluctuations in PFP width were considered noise, as their magnitude was considerably lower than the changes in w caused by intermittency. Therefore, the halt in PFP intermittency without microbial growth in the model confirmed the experimental result in which the suppression of growth eliminated intermittency (Fig. 2A). Additionally, decreasing the fluid flow rate (and thus the fluid flow velocity and shear rate) in the model led to a fully bioclogged system; PFPs entirely disappeared (note that fluid flow can still occur through the biofilm due to its porosity). This modeling result shows that removing the shear stresses exerted by the fluid flowing in the PFPs resulted in the disappearance of intermittency, confirming the experimental observations on the role of flow in causing the opening of PFPs (Fig. 2B and C).

Intermittency Occurs for High Fluid Flow Velocities and Large Pore Sizes.

To investigate the influence of pore size and fluid flow velocity on the emergence of PFP intermittency, we repeated experiments in microfluidic devices with three different values of pore size, namely, d = 75, 150, and 300 µm (Fig. 4A), all with the same porosity (0.77). For each pore size, experiments were performed at four different flow rates, Q, as follows: 0.2, 0.5, 1, and 2 mL/h. The corresponding mean fluid flow velocities can be found in SI Appendix, Table S5. For a given fluid flow rate, the mean fluid velocity was the same in the three devices with different pore sizes because their porosity was the same. In contrast, the local shear force within the porous medium increases with decreasing pore size (Fig. 4A).

Fig. 4.

PFP intermittency occurs at high flow velocities and large pore sizes. (A) Schematics of part of the porous domain showing the three pore sizes, d, considered in experiments (300 µm, yellow; 150 µm, purple; 75 µm, blue) and magnified views of the initial velocity field and shear rate field before biofilm growth obtained from a mathematical model at fluid flow rate, Q = 1 mL/h. The porosity of all models is 0.77. (B) Time course of mean PFP width, w, for different pore sizes, d (color-coding as in A), for a fluid flow rate of Q = 1 mL/h. Shading indicates the SD of w computed over the length of the PFPs. (C) Phase diagram for PFP intermittency in experiments as a function of pore size and fluid flow rate.

In mature biofilms that developed within these porous media, we found that a larger pore size led to larger mean PFP width, w (Fig. 4B and SI Appendix, Fig. S6). This, in turn, resulted in a lower pressure difference across the microfluidic device (SI Appendix, Fig. S7A). In general, for the conditions investigated, the mean PFP width at the maximal opening was approximately half of the pore size (Fig. 4B); for example, at the pore size of 300 µm, PFPs had a maximal mean width of about 150 µm. The fact that the maximal mean PFP width was about half the pore size indicates that some stable biofilm structure remained in the pores while the PFPs were open. Therefore, we conclude that for the range of experimental conditions investigated, parts of the biofilm were sufficiently stable to withstand the shear forces causing PFP opening. As described above for the largest pore size of 300 µm, in the other conditions studied, the PFP width, w, and the pressure difference, $\mathrm{\Delta }p$, also varied through time and were interdependent (Fig. 1F–I and SI Appendix, Fig. S7). We found that the relationship between $\mathrm{\Delta }p$ and w can be described by a power law, $\mathrm{\Delta }p=a\cdot w^{-b}$, with a and b depending on the flow velocity and the pore size (SI Appendix, Fig. S7). In order to place our results in a hydrodynamic context, we compared the experimentally obtained PFP width, w, and corresponding pressure difference, $\mathrm{\Delta }p$, with the analytical solutions for fluid flow through an equivalent rectangular pipe with a width equal to the average width of the PFPs (Hagen–Poiseuille law, $\mathrm{\Delta }p\sim w^{-2.4}$ [38]) and through a porous domain of the size of the microfluidic device (Darcy’s law, $\mathrm{\Delta }p\sim w_{\text{pd}}{}^{-1}$, where w_pd is the width of the porous domain [39]) (SI Appendix, Table S2). We found that our experimental data lie between the two analytical solutions, i.e., with 1 < b < 2.4 (SI Appendix, Fig. S7), meaning that the flow through a bioclogged porous medium containing PFPs can be described as the combination of the flow through a pipe and the flow through a continuum domain described by Darcy’s law. The bioclogged system thus consists of a dual-porosity domain having macropores (PFPs) and a porous matrix (biofilm).

Experiments revealed that the occurrence of intermittency depended on both the pore size and the fluid flow rate. Based on the experimental results for different pore sizes and fluid flow rates, we constructed a phase diagram representing the regimes in which intermittency occurs (Fig. 4C). For this, we define intermittency as the presence of PFPs that show repeated changes in the width of 5 µm between narrow and opened paths. The phase diagram displays two regions. Flow path intermittency was observed in the upper-right region, for high fluid flow rates and large pore sizes (Fig. 4C, green region), while it was absent (Fig. 4C, red region) at the lowest fluid flow rate tested (0.2 mL/h) for all pore sizes, and also for a flow rate of 0.5 mL/h at the smallest pore size (75 µm).

Characterizing PFP Closing Speed and Opening Frequency.

For PFP intermittency to occur, the biofilm must first clog the individual pores. Once the PFPs are formed, the biofilm must experience sufficient shear to open the PFPs by sloughing and compression while continuing to grow. In order to quantify the timescale of clogging of individual pores, we computed the pore-clogging speed, v_c, for the range of flow rates and pore sizes studied using the Gompertz growth model (Materials and Methods and SI Appendix, Figs. S8 and S9). We found that the mean pore-clogging speed (v_mc), increases with increasing fluid flow rate, Q, and pore size, d (Fig. 5A). We observed PFP intermittency (stars in Fig. 5A) under conditions that supported high pore-clogging speed. We further explored the link between pore-clogging speed and the following two parameters related to fluid flow velocity and pore size: 1) the shear rate and 2) the nutrient mass flow per pore. In our experiments, the pore-clogging speed correlated with the relative nutrient mass flow per pore, calculated by dividing the imposed flow rate by the number of pore throats orthogonal to the flow direction for each microfluidic device and normalizing by the maximal nutrient mass flow rate (Fig. 5B). Pore clogging speed during the early stages of biofilm growth can be described by Monod kinetics adapted to our parameters as

$$v_{\text{mc}}=v_{\text{max}}\frac{S}{S+K_{\text{N}}}\approx v_{\text{mc},\text{max}}\left(\frac{M}{M+K_{\text{N}}\cdot Q}\right),$$ [1]

with v_max as the maximum growth rate, S as the nutrient concentration, K_N as the half-saturation constant, $M$ as the relative nutrient mass flow per pore, Q as the imposed fluid flow rate, and v_mc,max as the maximal pore-clogging speed of all experimental conditions. The Monod kinetic model describes the dependence of cellular growth on the availability of nutrients (40). Similarly, as the closing of the PFPs depends on biofilm growth, we found that the mean PFP closing speed, M_PFP, also follows Monod kinetics as a function of the relative nutrient mass flow rate (Eq. 1) (Fig. 5C). However, the curve for PFP closing speed reaches a lower plateau for the maximum closing speed compared with the behavior of individual pores. In contrast to the PFP closing speed, the pore-clogging speed was measured in the early stages of the porous medium clogging and prior to PFP formation, so the lower maximal value for the PFP closing speed is likely explained by a higher shear stress in the PFP compared to that in the individual pores during the initial stages of clogging. These correlations of PFP closing speed and individual pore-clogging speed with the relative nutrient mass flow are in accordance with our conclusion from the nutrient removal experiment (Fig. 2A) that the mechanism for PFP closing is biofilm growth. The mean pore-clogging speed and the mean PFP closing speed both reach a plateau at a high relative nutrient mass flow rate (Fig. 5B and C), suggesting that the growth at different stages of the clogging process is limited by some environmental factor. However, massive biofilm dispersal was never observed in the experiment, confirming that the supplied nutrients are sufficient to sustain biofilm survival.

Fig. 5.

Bioclogging of porous media and PFP closing speeds depend on the nutrient mass flow, while the frequency of PFP opening depends on the average shear rate within PFPs. (A) Mean pore-clogging speed, v_mc, depends on the pore size, d, and the fluid flow rate, Q. Data points (black) represent the mean of experimental replicates (SI Appendix, Table S1), and error bars represent the SD. The plane was fitted by linear interpolation and colored according to values of v_mc. Stars indicate conditions in which PFP intermittency was observed. (B) The relationship between nutrient mass flow per pore, M, and the mean pore-clogging speed, v_mc, follows a Monod kinetic (dashed line). Mean values of v_mc for each nutrient mass flow rate are shown as black circles with their corresponding SD. Values of v_mc are also shown for each experimental combination of fluid flow rate (symbols: circle, 0.2 mL/h; square, 0.5 mL/h; upward-pointing triangle, 1 mL/h; downward-pointing triangle, 2 mL/h) and pore size (colors: yellow, 300 µm; purple, 150 µm; blue, 75 µm). The fitted parameters for the Monod kinetic equation (Eq. 1) are v_mc,max = 84.13 µm/h and $K_{\text{N}}\cdot Q$= 0.086. (C) The relationship between the relative nutrient mass flow rate, M_PFP, and the mean PFP closing speed, v_pcs, follows a Monod kinetic (solid line) with fitted parameters of the Monod equation v_pcs,max = 7.75 µm/h and $K_{\text{N}}\cdot Q$ = 0.178. For this analysis, the nutrient mass flow rate in the PFPs, M_PFP, was assumed proportional to the imposed fluid flow rate. Circles represent the mean for each nutrient mass flow rate, and bars represent the SD. Other symbols show the values for individual experimental combinations of fluid flow rate and pore size, with symbols and colors as in B. (D) The frequency of opening, F, of the PFPs increases with the shear rate,${\dot{\gamma }}_w.$ Shear rate within the PFPs was estimated from the flow rate and mean PFP dimensions (Results). Data are shown for each combination of fluid flow rate and pore size (symbols and colors as in B). Only data from experiments with more than one opening event were used to determine the frequencies.

As PFP opening was driven by a hydromechanical mechanism related to shear forces, we hypothesized that the frequency of PFP opening, F, would correlate with the shear rate. In our experiments, we indeed observed a positive correlation between the average shear rate in the PFP and F (Fig. 5D). The shear rate,${\dot{\gamma }}_w$, acting on the PFP walls was computed as

$${\dot{\gamma }}_w=8\cdot Q/D_h\cdot h\cdot \overline{w},$$ [2]

with Q the imposed flow rate, D_h the hydraulic diameter of the PFP, h the height of the microfluidic device, and $\overline{w}$ the mean width of the PFP during each experiment (41), obtained by averaging the PFP width over the entire duration of one experiment (24 h). This estimate of the shear rate relies on the assumption that all of the fluid flow passes through the PFP (as demonstrated by numerical simulations, SI Appendix, Fig. S2B), and we have a no-slip condition at the PFP walls, owing to the low permeability of the biofilm a no-slip condition at the PFP wall, owing to the low permeability of the biofilm (10⁻¹⁴ m², SI Appendix). The analysis of opening frequency showed that F increased with the shear rate up to a value of the shear rate of 1.2 × 10⁴ s⁻¹, at which point F stabilized around 0.7 h⁻¹ (Fig. 5D). This result indicates that larger fluid flow rates and smaller mean PFP widths maximize and stabilize the opening frequency.

Discussion

Our work has elucidated the mechanism underlying PFP intermittency in biofilm-bearing porous media and has shown that intermittency is due to the competition between microbial growth and fluid shear stress. Closing of the PFPs is controlled by the nutrient mass flow; in an experiment in which flow contained no nutrients, intermittency ceased completely. The opening of the PFPs, due to detachment of the biofilm and its compression normal to the flow direction, results from the viscoelastic mechanical behavior of the biofilm under shear stress (42). Using a mathematical model based on the Darcy–Brinkman–Biot formulation, we confirmed that suppressing biofilm growth or decreasing the shear stress exerted by the fluid flow halted PFP intermittency.

To compare the dynamics of PFP closing to that of the clogging of individual pores, we characterized individual pore clogging by using the extended Gompertz growth model, which is extensively used to describe both bacterial growth in bulk (43) and biofilm growth under flow (44). We found that biofilm growth dynamics appear to be maintained in porous media both at the pore scale and during clogging of the entire system, despite the shear forces to which the biofilm is exposed. When comparing the plateaus of the Monod fits for the clogging of individual pores and for the closing of PFPs, we found that the maximal PFP closing speeds were an order of magnitude smaller than the maximal individual pore-clogging speeds. This is likely explained by differences in the shear rate, which is much higher in PFPs as the porous medium approaches full clogging than in individual pores in the early stages of clogging. The shear rates in a microfluidic device of pore size d = 300 µm at a flow rate Q = 1 mL/h range from 10¹ to 10³ 1/s in the early stage (Fig. 4A), whereas in a PFP, shear rates are estimated to range from 10⁴ to 10⁶ 1/s (Fig. 2F). Once PFPs have formed, most of the fluid flow is channeled through the open paths since very little flow can be accommodated by the biofilm due to its very low permeability (13).

Biofilm sloughing off within porous media leading to the rapid opening of PFPs will affect downstream clogging, as the flow transports chunks of biofilm and individual bacterial cells. Mass transport and the regaining of cell motility can lead to the subsequent spreading of bacteria within a pore network (45, 46). The occurrence of detachment is determined by fluid flow, nutrient supply, and the geometry of the habitat but also by the mechanical properties of the biofilm (42, 47). The mechanical properties of the biofilm can vary in space and time depending on the depth (normal to the direction of the PFP) into the biofilm. In space, we observed a gradual increase in density (i.e., a decrease of light intensity) deeper into the biofilm. In time, we observed a gradual pressure increase in the successive closing–opening cycles of the PFP. Furthermore, the elastic properties allow the biofilm to withstand disturbances shorter than the elastic relaxation time, while longer stress will lead to nonreversible viscoplastic deformation, sloughing, and detachment (48). In our experiments, we observed that the biofilm was sloughed off intermittently. This hints at a non-Newtonian behavior: a critical shear stress is required to overcome the yield stress of the biofilm in order to trigger PFP intermittency. These results have an abiotic analogy in cohesive sediment transport, where a critical shear stress is required to induce sloughing (49). In natural settings, biofilms in sediments can prevent sediment erosion, thanks to the yield stress of the biofilm (50, 51). In order to capture biofilm behavior in models of porous media, it is crucial to take the mechanical properties of the biofilm into account. In our study, we modeled the biofilm as a viscoplastic material with a yield stress, which allowed us to reproduce the intermittent PFP behavior. The viscoplastic behavior captures the observed, intermittent sloughing off better than a viscoelastic behavior, which would imply greater flowing of the biofilm rather than detachment.

The rheological properties of the biofilm depend on the composition of the extracellular polymeric substances, which, in turn, can vary greatly depending on the microorganisms present, the nutrient availability, and the environmental conditions (52). The interplay between biofilm rheology and local flow conditions determines biofilm morphology, as recently demonstrated (53). In particular, our results show that the biofilm’s viscoplastic behavior drives its capability of clogging and forming PFPs in a porous medium, as the rheological descriptors of the biofilm were critical parameters of the mathematical model we developed. We hypothesize that a change in biofilm rheology, for example, due to the presence of a different bacterial species or a drastic shift in environmental conditions, may affect the occurrence of PFP intermittency and the frequency of opening and closing events. Furthermore, fast-growing bacterial communities are more efficient in clogging porous structures and will consequently reduce their access to flowing nutrients so that slow-growing competitors may be favored (54). Similarly, the occasional sloughing will increase access to nutrients by preventing flow paths from being choked off, thus promoting bacterial growth locally. This implication is counter to the implied consensus in the literature that more robust biofilms or stronger biofilm growth are always beneficial to bacteria growing on surfaces under shear stress and may imply that biofilms can tune their physical properties depending on cell density and access to nutrient supply in order to promote survival.

The intermittent opening and closing of the PFPs were reflected in the pressure difference through the system: the closing of the PFPs resulted in an increase in the pressure difference due to a reduction in the bulk hydraulic conductivity of the system, whereas the opening of the PFPs reduced the pressure difference. We observed this behavior for completely clogged porous media; this stands in contrast to bioinduced partial clogging of a porous medium, where the continuous reduction in pressure difference results mainly from biofilm formation in the upstream part of the porous medium (2). From this, it can be concluded that the observation of a recurring pressure increase and decrease within a porous medium cannot solely be attributed to the breakthrough of a bioinduced plug but can also be due to intermittent PFPs. We demonstrated that a power law with a negative exponent that falls between the Hagen–Poiseuille and Darcy solutions best describes the relation between pressure difference and PFP width.

Our systematic study of the dependency of PFP intermittency on fluid flow rate and pore size expands and generalizes the conditions under which PFP intermittency is known to occur (28, 29). We showed that intermittency occurs only under certain conditions, at fluid flow rates larger than 0.5 mL/h and pore sizes larger than 75 µm. Whether PFP intermittency occurs can be explained by the impact of fluid shear stresses in combination with the material properties of the biofilm. We observed an increased frequency of opening of PFPs with increasing shear forces, which caused more biofilm detachment (19, 29). We observed a stabilization in the frequency of PFP opening over time. We attribute this to a more stable biofilm structure over time because of densification deeper into the biofilm due to compression and the regular removal by shear of the newly formed biofilm closest to the PFP (Movie S1). The PFP closing speed correlated with the nutrient mass flow rate and followed a Monod kinetic, as we also observed for the clogging speed of individual pores. Weak or no PFP intermittency was observed at low flow rates because no PFPs were formed. Instead, complete bioclogging was observed. For the smallest pore size, in contrast, a PFP was formed due to a catastrophic rupturing, but without subsequent intermittent opening and closing (SI Appendix, Fig. S10). This is likely explained by the larger surface for biofilm attachment with a smaller pore size, which allows the biofilm to form a denser and more rigid network. The biofilm can thus withstand higher pressures until it abruptly ruptures and forms a large flow path without intermittency (SI Appendix, Fig. S10).

By combining microfluidic experiments and mathematical modeling, we were able to unravel the competing mechanisms driving PFP intermittency and fully characterize PFP behavior under a range of geometric and hydraulic conditions relevant in environmental sciences and industrial technologies such as filters and bioreactors. In our microfluidic devices, the grains are regularly arranged and all pores have the same initial fluid flow conditions. Despite this scenario being a simplification of the irregular nature of soils, it allowed a systemic study of pore-clogging and an unprecedented comparison of different hydrodynamic conditions. In our experiments, the fluid flow rates ranged from 0.2 to 2 mL/h (corresponding to velocities of 16 to 160 m/d), which are comparable to transport velocities of microorganisms in soils (55) and in bioremediation applications (56). In addition to determining the effect of irregular grain arrangements on intermittency, it will be interesting to study how intermittency changes when one considers pressure-driven flow, which is common in natural environments, rather than an imposed flow rate as done here. Additionally, we highlight that imposed flow is found in certain technical applications, including biomineralization (57) and biochemical reactors (58) and that our experimental fluid flow velocities are of the same order of magnitude as in those applications. The formation and dynamics of PFPs in porous media strongly impact mass transport by creating spontaneous chemical inundations during PFP opening. Each opening results in a rapid change of the velocity distribution in the biofilm–porous medium system, leading to a transient flow system with high variance in residence time and strong mixing of chemicals with resident solutions and hence increasing the efficiency of reactions (59). PFP intermittency, a phenomenon based on the interplay between hydromechanical and biological processes, can be relevant in natural and industrial systems, with applications ranging from soil and aquifer bioremediation, bioreactors, filtration (design of membranes), and enhanced oil recovery. Our findings can contribute to improving the understanding of natural systems and assist in the design of applications that harness the properties of biofilms.

Materials and Methods

Microfluidic Device Design.

Microfluidic devices were used to enable imaging of biofilm formation in a controlled environment at very high spatial and temporal resolution (60). Cylindrical polydimethylsiloxane (PDMS) pillars in the microfluidic device represent the grains. Pore and grain sizes were designed to be 75, 150, and 300 µm, corresponding to the range found in natural soil environments (55). In order to obtain comparable flow velocity conditions, the geometries were designed to have equal overall porosity (0.77). The initial fluid flow field in each porous geometry was computed using a 2D mathematical model that included an additional term to take drag forces in the third dimension into account (61). The model provided the velocities, and the shear rates were computed from the spatial derivative of the simulated fluid velocity field. The combination of 3 different pore sizes and 4 fluid flow rates (0.2, 0.5, 1, and 2 mL/h) allowed us to study 12 geometric and hydrodynamic experimental conditions.

Microfluidic Device Fabrication.

The microfluidic devices were fabricated using standard soft lithography techniques. Microchannel molds were prepared by depositing SU-8 photoresist (MicroChem Corp.) on a silicon wafer via photolithography. The mold was silanized with trichloromethylsilane (Sigma Aldrich) prior to use. Microfluidic devices were prepared with a 10% wt/wt cross-linking agent in the PDMS solution (Sylgard 184 Silicone Elastomer Kit, Dow Corning). Devices were cured at 80 °C for 2 h and plasma-bonded to a clean glass slide.

Bacterial Cultures.

Experiments were performed using wild-type B. subtilis NCIB 3610 as model organism. B. subtilis is a ubiquitous soil microbe, found predominantly on plant roots, where it provides protection against plant pathogens. It is a well-studied biofilm former (11, 36, 62). The biofilm grown under flow presents a porous internal structure (14).

B. subtilis solutions were prepared by inoculating 3 mL nutrient solution no. 3 (Sigma Aldrich; 1 g/L meat extract, 5g/L peptone, 5 g/L NaCl, 2 g/L yeast extract) from a frozen bacterial stock and incubating overnight at 30 °C, while shaking at 200 rpm. Before experiments, the solution was diluted 1:1,000 into fresh nutrient solution and incubated under the same conditions for 4 h to early exponential phase (optical density at 600 nm= 0.1), ensuring motile cells and minimizing cluster formation.

Microfluidic Assays.

The flow of the nutrient solution (the same as that used for bacterial culture) was driven by a Harvard syringe pump at fluid flow rates 0.2, 0.5, 1, and 2 mL/h. Prior to use, all microfluidic devices were washed with 2 mL nutrient solution, and then 150 µL (approximately the volume of the connecting tubes and the microfluidic device) of a bacterial suspension was loaded into the microfluidic device by reversing the flow. A sterile filter (pore size, 1.2 µm) separated the microfluidic device from the syringe to avoid bacterial contamination of the nutrient solution. After 3 h of incubation to allow the surface attachment of the cells, the flow was started. Biofilm growth and behavior were imaged for a period of 48 h at 25 °C. Imaging was performed on an inverted microscope (Ti-Eclipse 2, Nikon) using a digital camera (Orca). Time-lapse images were acquired using bright-field microscopy (13,500 × 2,500 pixels at 4× magnification, 1 frame per 6 min) in an array of 16 positions spanning the entire porous domain of the microfluidic device. A pressure sensor (Elveflow) recorded the pressure drop caused by the biofilm. The initial pressure was measured upstream of the porous medium prior to biofilm growth and manually set to zero in the recording software.

To study PFP behavior in the absence of cell growth, an experiment was performed in which the nutrient solution was replaced by an isotonic NaCl (Sigma Aldrich) solution. After 48 h of biofilm growth during which PFP intermittency was observed, the nutrient flow was exchanged for salt flow (5 g/L NaCl) by switching through a Y-connector. All other parameters were kept constant. The porous domain was imaged for a further 24 h, together with a second domain exposed to the continued flow of nutrient solution over the same period.

To capture the opening behavior of an individual PFP at high temporal resolution, a region was imaged at 10× magnification in phase contrast at 20 frames per s for 1 h during an ongoing experiment (with a flow rate, Q, of 1 mL/h and pore size of 300 µm).

Image Analysis, Statistics, and Derivations.

To obtain an image of the entire porous domain, images of the array of positions were stitched using Fiji ImageJ (63). All further image analysis was performed in MATLAB (MathWorks) using an in-house algorithm.

Experimental replicates (1 to 4) were carried out for each combination of pore size and flow rate, with a greater number for the scenarios in which PFP formation and intermittency were observed (numbers of replicates are provided in SI Appendix, Table S1). All images were normalized by the mean intensity of the pillars and were binarized with a threshold of 0.3 in order to segment the image and differentiate biofilm from void space. The individual pore clogging speed was quantified by evaluating the change over time in the number of pixels allocated to the biofilm, measured along the shortest line transect between two pillars. As pore-clogging is a bacterial growth process, the Gompertz model, typically used to model bacterial growth, can be fitted to the “clogging curve” (43), Eq. 3, and the maximal pore-clogging speed extracted from the model (corresponding to the maximal growth rate of bacterial cultures). The corresponding Gompertz model is

$$y=A\cdot \text{exp}\left\{-\exp \left[v_c\cdot \frac{\exp \left(1\right)}{A}\left(\lambda -t\right)+1\right]\right\},$$ [3]

with $\lambda$ the lag time, v_c the maximum individual pore clogging speed, and A the maximum value of the asymptote. The fitted clogging curves and the distribution of individual pore-clogging speeds are shown in the supplementary material (SI Appendix, Figs. S8 and S9). The goodness of fit and the obtention of physically realistic values were confirmed prior to computing the mean pore-clogging speed. Only data from growth curves with a coefficient of determination of R² > 0.98 were retained in our calculation of the corresponding individual pore-clogging speed, v_c. The number of pores evaluated for each experiment is given in the supplementary material (SI Appendix, Table S4).

The mean PFP width was obtained by computing the Euclidean distance in the PFP and calculating the mean PFP width per image (the number of measures depends on the length of the PFP expressed in pixels). The average PFP closing speed was quantified based on linear interpolation from the open state (maximal PFP width) to the closed state (minimal PFP width) in the PFP width data (SI Appendix, Fig. S11). Opening frequency was estimated based on the timescale of opening events, calculated as the inverse of the time between two opening events. The Monod kinetics were fitted to the individual pore-clogging speeds and PFP closing speeds using least squares regression. To track biofilm movement during PFP opening (SI Appendix, Movie S1), DIC, adapted from ref. 33, was computed using the PIVlab tool in MATLAB (MathWorks). DIC provided information about the direction of movement and detachment of the biofilm during PFP opening by tracking and cross-correlating changes in the image and therefore allowed the identification of the physical processes involved.

Data Availability

Images, pressure data, and scripts have been deposited in a publicly accessible database https://doi.org/10.3929/ethz-b-000552719.