ADOpy: A Python Package for Adaptive Design Optimization

Abstract

Experimental design is fundamental to research, but formal methods to identify good designs are lacking. Advances in Bayesian statistics and machine learning offer algorithm-based ways to identify good experimental designs. Adaptive design optimization (ADO; Cavagnaro, Myung, Pitt, & Kujala, 2010; Myung, Cavagnaro, & Pitt, 2013) is one such method. It works by maximizing the informativeness and efficiency of data collection, thereby improving inference. ADO is a general-purpose method for conducting adaptive experiments on the fly and can lead to rapid accumulation of information about the phenomenon of interest with the fewest number of trials. The nontrivial technical skills required to use ADO have been a barrier to its wider adoption. To increase its accessibility to experimentalists at large, we introduce an open-source Python package, ADOpy, that implements ADO for optimizing experimental design. The package, available on GitHub, is written using high-level modular-based commands such that users do not have to understand the computational details of the ADO algorithm. In this paper, we first provide a tutorial introduction to ADOpy and ADO itself, and then illustrate its use in three walk-through examples: psychometric function estimation, delay discounting, and risky choice. Simulation data are also provided to demonstrate how ADO designs compare with other designs (random, staircase).

1. Introduction

A main goal of psychological research is to gain knowledge about brain and behavior. Scientific discovery is guided in part by statistical inference, and the strength of any inference depends on the quality of the data collected. Because human data always contain various types of noise, researchers need to design experiments so that the signal of interest (experimental manipulations) is amplified while unintended influences from uncontrolled variables (noise) are still present. The design space, the stimulus set that arises from decisions about the independent variable (number of variables, number of levels of each variable) is critically important for creating a high-signal experiment.

A similarly important consideration is the stimulus presentation schedule during the experiment. This issue is often guided by two competing goals: efficiency and precision. How much data must be collected to be confident that differences between conditions could be found? This question is similar to that asked when performing a power analysis, but is focused on the performance of the participant during the experiment itself. Too few trials yield poor precision (low signal-to-noise ratio); there are simply not enough data to make an inference, for or against a prediction, with confidence. Adding more trials can increase precision along with practice effects. However, it may not be efficient to add too many trials, especially with a clinical population where time is really of the essence and when participants can easily get fatigued or bored. What then is the optimal number of trials that will provide the most precise performance estimates? A partial answer lies in recognizing that not all stimuli are equally informative. By optimizing stimulus selection in the design space, efficiency and precision can be balanced.

Methods of optimizing efficiency and precision have been developed for some experimental paradigms. The most widely used one is the staircase procedure for estimating a threshold (Cornsweet, 1962; Feeny et al., 1966; Rose et al., 1970), such as when measuring hearing or visual acuity. Stimuli differ along a one-dimensional continuum (intensity). The procedure operates by a simple heuristic rule, of which there are a handful of variants: The stimulus to present on one trial is determined by the response on the previous trial. Intensity is increased if the stimulus was not detected, decreased if it was. The experiment is stopped after a given number of reversals in direction has been observed. The staircase method is efficient because the general region of the threshold is identified after a relatively small number of trials, after which the remaining trials concentrate on obtaining a precise threshold estimate. Its ease of implementation and generally good results have made it a popular method across many fields in psychology.

Formal approaches to achieving these same ends (good efficiency and precision) have also been developed. They originated in the fields of optimal experimental design in statistics (Lindley, 1956; Atkinson and Donev, 1992) and active learning in machine learning (Cohn et al., 1994; Settles, 2009). In psychology, the application of these methods began in visual psychophysics (e.g., Kontsevich and Tyler, 1999), but has since expanded into other content areas (neuroscience, memory, decision making) and beyond. Common among them is the use of a Bayesian decision theoretic framework. The approach is intended to improve upon the staircase method by using not only the participant’s responses to guide the choice of the stimulus on the next trial, but also a mathematical model that is assumed to describe the psychological process of interest (discussed more fully below). The model-based algorithm integrates information from both sources (model predictions and participants’ responses) to present what it identifies as the stimulus that should be most informative on the next trial.

The method developed in our lab, adaptive design optimization (ADO), has been shown to be efficient and precise. For example, in visual psychophysics, contrast sensitivity functions (i.e., thresholds) can be estimated so precisely in 50 trials that small changes in luminance (brightness) can be differentiated (Gu et al., 2016; Hou et al., 2016). In delayed discounting, precise estimation of the k parameter of the hyperbolic model (a measure of impulsivity) can be obtained in fewer than 20 trials, and the estimate is 3-5 times more precise than the staircase method (Ahn et al., 2019). Other applications of ADO can be found in several areas of psychology such as retention memory (Cavagnaro et al., 2010, 2011), risky choice decision (Cavagnaro et al., 2013a,b; Aranovich et al., 2017), and in neuroscience (Lewi et al., 2009; DiMattina and Zhang, 2008, 2011; Lorenz et al., 2016).

The technical expertise required to implement the ADO algorithm is nontrivial, posing a hurdle to its wider use. In this paper, we introduce an open-source Python package, dubbed ADOpy, that is intended to make the technology available to researchers who have limited background in Bayesian statistics or cognitive modeling (e.g., the hBayesDM package, Ahn et al., 2017). Only a working knowledge of Python programming is assumed.¹ For an in-depth, comprehensive treatment of Bayesian cognitive modeling, the reader is directed to the following excellent sources written for psychologists (Lee and Wagenmakers, 2014; Farrell and Lewandowsky, 2018; Vandekerckhove et al., 2018). ADO is implemented in three two-choice tasks: psychometric function estimation, the delay discounting task (Green and Myerson, 2004) and the choice under risk and ambiguity (CRA) task (Levy et al., 2010). ADOpy easily interfaces with Python code running one of these tasks, requiring only a few definitions and one function call. Most model parameters have default values, but a simulation mode is provided for users to assess the consequences of changing parameter values. As we discuss below, this is a useful step that we encourage researchers to use to ensure the algorithm is optimized for their test situation.

The algorithm underlying ADO is illustrated in Figure 1. It consists of three steps that are executed on each trial of an experiment: (1) design optimization; (2) experimentation; and (3) Bayesian updating. In the first step, we identify the optimal design (e.g., stimulus) of all possible designs, the choice of which is intended to provide the most information about the quantity to be inferred (e.g., model parameters). In Step 2, an experiment is carried out with the chosen experimental design. In Step 3, the participant’s response is used to update the belief about the informativeness of all designs. This revised (updated) knowledge is used to repeat the ADO cycle on the next trial of the experiment.

Fig. 1:

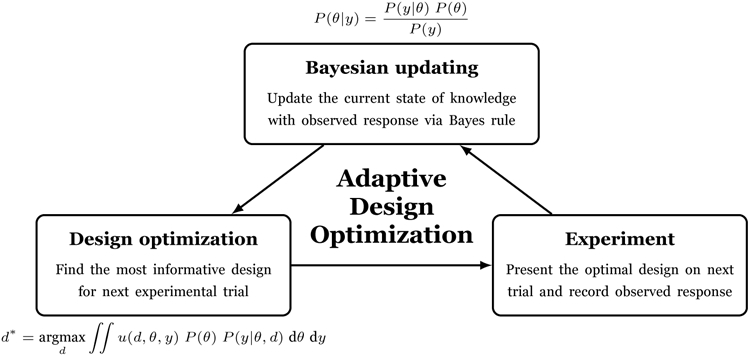
Schematic diagram illustrating the three iterative steps of adaptive design optimization (ADO).

The following section provides a short technical introduction to the ADO algorithm. Subsequent sections introduce the package and demonstrate how to use ADOpy for optimizing experimental design with walk-through examples from three domains: psychometric function estimation, delay discounting, and risky choice. Readers who prefer to concentrate on the practical application of the algorithm rather than its technicalities should skip Section 2 and jump directly to Section 3.

2. Adaptive Design Optimization (ADO)

ADO follows in the tradition of optimal experimental design in statistics (Lindley, 1956; Atkinson and Donev, 1992) and active learning in machine learning (Cohn et al., 1994; Settles, 2009). ADO is a model-based approach to optimization in the sense that it requires a quantitative (statistical, cognitive) model that predicts experimental outcomes based on the model’s parameters and design variables (e.g., experimentally controllable independent variables). Statistically speaking, a model is defined in terms of the probability density function (PDF)², a parametric family of probability distributions indexed by its parameters, denoted by p(y∣θ,d), where y represents a vector of experimental outcomes, θ is the parameter vector, and finally, d is the vector of design variables.

ADO is formulated in a Bayesian framework of optimal experimental design (Chaloner and Verdinelli, 1995; Müller, 1999; Müller et al., 2004; Amzal et al., 2006). On each ADO trial, we seek to identify the optimal design d* that maximizes some real-valued function U (d) that represents the utility or usefulness of design d. Formally, the “global” utility function U (d) (Chaloner and Verdinelli, 1995) is defined as:

$$U(d)=\iint u(d,\theta ,y)p(y\mid \theta ,d)p(\theta )dyd\theta ,$$ (1)

where p(θ) is the prior distribution. In the above equation, u(d, θ, y), called the “local” utility function, measures the utility of a hypothetical experiment carried out with design d when the model outputs an outcome y given the parameter value θ. Note that the global utility U (d), which is a function of design d, represents the mean of the local utility u(d, θ, y) calculated across all possible outcomes and parameter values, weighted by the likelihood function³ p(y∣θ, d) and the prior p(θ).

As is typically done in ADO, the ADOpy package adopts an information theoretic framework in which the optimal design is defined as the one that is maximally informative about the unknown quantity of interest, i.e., the values of the parameter θ in our case. Specifically, by using Shannon’s entropy, a particular local utility function is defined as $u(d,\theta ,y)=\log \frac{p(\theta \mid y,d)}{p(\theta )}$. The global utility function in Equation (1) becomes the mutual information between the outcome random variable Y (d) and the parameter random variable Θ conditional on design d (Cover and Thomas, 1991):

$$U(d)=H(Y(d))-H(Y(d)\mid \Theta ),$$ (2)

where H(Y(d)) is the marginal entropy (i.e., overall uncertainty) of the outcome event and H(Y(d)∣Θ) is the conditional entropy of the outcome event given the knowledge of the parameter θ.⁴ Accordingly, the optimal design d* that maximizes the mutual information in Equation (2) is the one that maximally reduces the uncertainty about the parameters of interest.

Once the optimal design d* is identified, we then conduct an actual experiment on the current trial with the optimal design and observe an experimental outcome y_obs. The prior distribution p(θ) is updated via Bayes rule with this new observation to obtain the posterior distribution p(θ∣y_obs), which in turn becomes the new prior on the next trial, i.e., by replacing p(θ) with p(θ∣y_obs) in Equation (1). This “trilogy scheme” of design optimization, experimentation, and Bayesian updating, depicted in Figure 1, is applied successively on each ADO trial until the end of the experiment.

Finding the optimal design d* that maximizes U (d) in Equation (1) is computationally non-trivial as it involves solving a high dimensional maximization and integration problem. As such, obtaining an analytic form solution for the problem is generally not possible; instead, approximate solutions must be sought numerically. For this purpose, the ADOpy package implements a grid-based algorithm for both the design optimization and Bayesian updating steps in Figure 1. Implementation of the algorithm requires the discretization of both the continuous parameter and design spaces. That is, each element of the parameter vector θ and the design vector d is represented as a one-dimensional discretized line with a finite number of grid points. Further, the local utility function u(d, θ, y), the likelihood function p(y∣θ,d), and the prior p(θ) are all represented numerically as vectors defined on the grid points.

Figure 2 describes the grid-based ADO algorithm implemented in the ADOpy package in four steps, which is adapted from Bayesian adaptive estimation algorithms in psychophysics (Kontsevich and Tyler, 1999; Kujala and Lukka, 2006; Lesmes et al., 2006). In Step 0, which is performed once at the start of the experiment, the algorithm first creates and stores in memory a look-up table of various functions over all possible (discretized) outcomes and parameter values. This involves pre-computation of the likelihood function p(y∣θ,d) and the entropy H(Y(d)∣θ) for all possible values for response y, parameter θ, and design d. Also, the prior knowledge for model parameter p₀(θ) is initialized based on researchers’ beliefs, typically from a uniform distribution. The use of pre-computed look-up tables makes it possible to run ADO-based experiments on the fly without additional computational time on each trial. The three steps of the ADO trilogy scheme illustrated in Figure 1 are then executed.

Fig. 2:

Three steps of a grid-based ADO algorithm with an initial step for pre-computation.

In brief, users can find an optimal experimental design with ADO that maximizes information gain. To use it efficiently in an experiment, grid-based ADO discretizes the possible design and parameter spaces and generates pre-computed look-up tables. For a more thorough description of the algorithm, see Cavagnaro et al. (2010) and Myung et al. (2013).

3. ADOpy

In this section, we provide a step-by-step guide on how to use the ADOpy package to compute optimal designs adaptively with walk-through examples. It is assumed that readers are familiar with Python programming and have written experiment scripts using Python or some other language. For further information, the detailed guide on how to use the ADOpy package is also provided on the official documentation (https://docs.adopy.org).

3.1. Overview

ADOpy is designed in a modular fashion to ensure functional flexibility and code readability. At the core of the package are three classes: Task, Model, and Engine. The Task class is used to define design variables of a task. The Model class is used to define model parameters and the probability density (or mass) function that specifies the probability of responses given parameters and designs (e.g., Myung, 2003; Farrell and Lewandowsky, 2018). The Engine class is used for implementing design optimization and Bayesian updating.

The general workflow of these classes is illustrated in Figure 3. After loading the three classes, users should initialize each object, with the engine requiring the most parameters. The for-loop is an experiment itself divided into three parts: 1) obtain the design (stimulus) for the next trials and present the stimulus to the participant; 2) obtain a response from the participant, which would come from a keyboard or mouse, as defined by the experimenter; 3) update the ADO engine using the participant response together with the design.

Fig. 3:

ADOpy workflow. Each function call above is described in greater detail in Section 3.5. Note that ADOpy itself is soley the engine for stimulus selection and does not include code to conduct an experiment (e.g., present the stimuli or collect responses, save the data); the user must program these steps.

ADOpy implements a grid-search algorithm in which the design space and parameter space are discretized as sets of grid points. How to set grid points and the range of each grid dimension is described in detail in Section 3.5.

Owing to the modular structure of ADOpy, users do not have to concern themselves with how the Engine works, other than defining the Task and the Model classes. Consequently, ADOpy dramatically reduces the amount of coding, and the likelihood of coding errors, when implementing ADO.

3.2. Prerequisites

Before installing ADOpy, users should install Python (version 3.5 or higher). Using the Anaconda distribution (https://www.anaconda.com) is recommended because it ensures compatibility among dependencies.

ADOpy depends on several core packages for scientific computing: NumPy, SciPy, and Pandas. Since ADOpy uses high dimensional matrices to compute optimal designs, it is strongly recommended to install linear algebra libraries (e.g., Intel Math Kernel Library, LAPACK, BLAS) to make the operations fast. If the Anaconda distribution is used, the Intel Math Kernel Library will be used as the default.

3.3. Installation

The ADOpy package is available from the Python Package Index (PyPI) and GitHub. The easiest way to install ADOpy is from PyPI using pip as follows:

  pip install adopy

To install the developmental version, users can install it from GitHub. However, it can be unstable, so use it with caution.

  git clone https://github.com/adopy/adopy.git

cd adopy
git checkout develop
pip install.

To check that ADOpy was installed successfully, run the following code at the Python prompt. As of now, the latest version is 0.3.1.

import adopy
adopy.__version__ # ‘0.3.1’

3.4. Module structure

Inside the ADOpy package, the two most important modules are adopy.base and adopy.tasks. The module adopy.base contains three basic classes: Task, Model, and Engine (see more details in Section 3.5). Using these classes, users can apply the ADO procedure into their tasks and models. For convenience, users can load these classes directly from adopy itself as follows:

# Load three classes from ADOpy
from adopy import Task, Model, Engine

The other module, adopy.tasks, contains three pre-implemented tasks and models (see Section 4 and Table 1). The three tasks are psychometric function estimation (adopy.tasks.psi), the delay discounting task (adopy.tasks.ddt), and the choice under risk and ambiguity task (adopy.tasks.cra).

Table 1:

Tasks and models implemented in the ADOpy package (alphabetized order). For detailed information, see the documentation website for ADOpy (https://github.com/adopy/adopy).

Module	Task		Model			Engine
	Class	Designs	Class	Model name	Parameters
Choice under risk & ambiguity (adopy.tasks.cra)	TaskCRA	p_var, a_var, r_var, r_fix	ModelLinear	Linear	alpha, beta, gamma	EngineCRA
			ModelExp	Exponential
Delay discounting (adopy.tasks.dd)	TaskDD	t_ss, t_ll, r_ss, r_ll	ModelExp	Exponential	tau, r	EngineDD
			ModelHyp	Hyperbolic	tau, k
			ModelHPB	Hyperboloid	tau, k, s
			ModelCOS	Constant Sensitivity	tau, r, s
			ModelQH	Quasi-Hyperbolic	tau, beta, delta
			ModelDE	Double Exponential	tau, omega, r, s
Psychometric function estimation (adopy.tasks.psi)	Task2AFC	stimulus	ModelLogistic	Logistic function	guess rate, lapse_rate, threshold, slope	EnginePsi
			ModelWeibull	Log-Weibull CDF
			ModelProbit	Normal CDF

3.5. Basic usage

Implementation of ADOpy requires execution of the four steps shown in Figure 3, the most important and complex of which is the Initialization step, in which ADOpy objects to be used in the subsequent steps are defined. The Initialization step itself comprises four sub-steps: defining a task, defining a model, defining grids, and initializing an ADO engine. In this section, we explain the coding involved in each of these sub-steps using the delay discounting task as an example.

Defining a task

The Task class is for defining the experimental task. Using the Task class, a task object is initialized by specifying three types of information: the name of the task (name), the design variables (designs), and the response variable (responses).

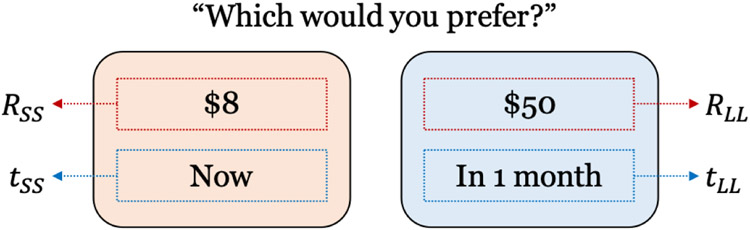
Delay discounting (DD; the task is depicted in Figure 4), refers to the well-established finding that animals, including humans, tend to discount the value of a delayed reward such that the discount progressively increases as a function of the receipt delay (e.g., Green and Myerson, 2004; Vincent, 2016). The delay discounting task has been widely used to assess individual differences in temporal impulsivity and is a strong candidate endophenotype for addiction (Green and Myerson, 2004; Bickel, 2015). In a typical DD task, a participant is asked to indicate his/her preference between two options, a smaller-sooner (SS) option (e.g., 8 dollars now) and a larger-later (LL) option (e.g., 50 dollars in a month). Let us use a formal expression (R_SS,t_SS) to denote the SS option where R_SS represents the reward amount, and t_SS represents the receipt delay. Similarly, (R_LL,t_LL) denotes the LL option. By definition, the following constraints are imposed on the reward amounts and the delay times: R_SS < R_LL and t_SS < t_LL for a given pair of options. The choice response is recorded as either y = 1 (LL option) or y = 0 (SS option).

Fig. 4:

Illustrated scheme of the delay discounting (DD) task. On each trial, a participant is asked to choose between two options, a smaller-sooner (SS) option on the left and a larger-later (LL) option on the right. The dotted lines and arrows indicate the design variables of the task to be optimized.

The DD task therefore has four design variables, i.e., d = (t_SS,t_LL,R_SS,R_LL), with a binary response on each trial (i.e., 0 or 1). As such, we define a Task object for the DD task as follows:

from adopy import Task

task = Task(name=‘Delay discounting task’,
            designs=[‘t_ss’, ‘t_ll’, ‘r_ss’, ‘r_ll’],
            responses=[0, 1])

where the four symbols (t_ss, t_ll, r_ss, r_ll) denote short notations for the respective design variables (t_SS,t_LLR_SS,R_LL). Note that designs argument should be specified as labels for design variables, while responses argument should be given as possible values of responses.

With the task object defined, the information passed into the object can be accessed by task.name, task.designs, and task.responses, respectively:

task.name # ‘Delay discounting task’
task.designs # [‘t_ss’, ‘t_ll’, ‘r_ss’, ‘r_ll’]
task.responses # [0, 1]

Defining a model

Before making a model object, users should define a function that describes how to compute the response probability given design variables and model parameters. For example, the hyperbolic model for the delay discounting task is defined with the following set of equations:

$$\begin{gathered} D(t)=\frac{1}{1+kt} \\ {V}_{LL}=R_{LL}\cdot D(t_{LL}) \\ {V}_{SS}=R_{SS}\cdot D(t_{SS}) \\ P(LLoverSS)=\frac{1}{1+\text{exp}[-\tau (V_{LL}-V_{SS})]} \end{gathered}$$ (3)

where P(LL over SS) denotes the probability of choosing the LL option over the SS option, and V_LL and V_SS denote subjective value estimates for the LL and SS options respectively. There are two model parameters: k represents the discounting rate and τ represents the inverse temperature that measures the consistency or stability in choice responses. For further details about the above model, the reader is referred to Section 4.2.

Based on the above model, the following Python snippet computes the response probability:

import numpy as np

def compute_likelihood(t_ss, t_ll, r_ss, r_ll, k, tau):
    v_ss = r_ss * np.divide(1, 1 + t_ss * k)
    v_ll = r_ll * np.divide(1, 1 + t_ll * k)
    p_obs = np.divide(1, np.exp(−tau * (v_ll – v_ss)))
    return p_obs

The argument names for design variables in the above function definition must be the same as those used in the task definition (i.e., t_ss, r_ss, t_ll, r_ll). We also recommend using NumPy functions for the definition, given that it can vectorize basic mathematical operations.

Specification of a mathematical model is performed by the Model class. Four arguments are required: the name of the model (name), a task object related to the model (task), labels of model parameters (params), and the response probability of the model (func), which in the current case is defined by the function compute_likelihood(). In terms of these arguments, a model object is defined as below:

from adopy import Model

model = Model(name=‘Hyperbolic model’,
              task=task,
              params=[‘k’, ‘tau’],
              func=compute_likelihood)

As in the task object, the information passed into the model object can be accessed by model.name, model.task, and model.params:

model.name # ‘Hyperbolic model’
model.task # Task(‘Delay discounting task’, …)
model.params # [‘k’, ‘tau’]

Further, users can run the response probability passed into the model object by model.compute(), which uses the same arguments that are used for the compute_likelihood() function, as follows:

model.compute(t_ss, t_ll, r_ss, r_ll, k, tau)

Defining grids

As mentioned earlier, ADOpy implements a grid-based algorithm that requires the discretization of both parameter and design spaces. As such, before running ADO using model and task objects, users must specify the grid resolution to be used for the design optimization and Bayesian updating steps in Figure 1. This amounts to defining the number and spacing of grid points on each dimension of the design and parameter variables. The grid passed to the ADO engine determines (1) the range of values in design variables that the ADO engine can suggest and (2) the range of the model parameters over which the computations will be carried out.

It is important to note that the number of grid points affects the efficiency and reliability of parameter estimation. The more sparse the grid, the more efficient but less precise parameter estimation will be; the denser the grid, the more precise but less efficient parameter estimation will be. Specifically, sparse grids can lead to poorly estimated model parameters whereas dense grids can require large amounts of memory and long computing times. Thus, before conducting an ADO-based experiment with participants, it is worth identifying the optimal grid resolution for each parameter/design variable. A simulation mode provided with ADOpy can help facilitate this process.

A grid object for ADOpy can be defined as a Python dictionary object by using the name of a variable as its key and a list of the grid points as its values. If a design variable or model parameter needs to be fixed to a single value, users would simply assign a single grid point for the variable. Also, to restrict the values of a variable, users can manually make a matrix in which each column vector indicates possible values for the variable, then pass it as a value with a key of the column labels. Example codes below illustrate various ways of defining the grids for two design variables, t_ss and t_ll:

# A grid object for two design variables, t_ss and t_ll.
grid_design = {‘t_ss’: [1, 2, 3], ‘t_ll’: [1, 2, 3]}

# One variable can be fixed to a single value as below:
grid_design = {‘t_ss’: [0], ‘t_ll’: [1, 2, 3]}

# Constrain the grid by using a joint matrix.
t_joint = []
for t_ss in [1, 2, 3]:
    for t_ll in [1, 2, 3]:
        if t_ss <= t_ll: # Use design pairs in which t_ss <= t_ll
            t_joint.append([t_ss, t_ll])
# [[1, 1], [1, 2], [1, 3], [2, 2], [2, 3], [3, 3]]
grid_design = {(‘t_ss’, ‘t_ll’): t_joint}

In much the same way, users can also define a grid for model parameters. For example, a grid for the two parameters of the delay discounting model in Equation (3), k and tau, can be defined as:

grid_param = {
    ‘k’: np.logspace(−5, 0, 20), # 20 points within [10^–5, 10^0] in a log scale
    ‘tau’: np.linspace(0, 5, 20)
}

The reader is directed to Appendix A for more examples for defining grids for the delay discounting task.

Initializing an ADO engine

With the defined Model and Task classes and grids for design and parameter variables, users are now ready to load an Engine for ADO computation. It requires four arguments: (1) the task object (task); (2) the model object (model); (3) a grid for design variables (grid_design); and (4) a grid for model parameters (grid_param):

from adopy import Engine

engine = Engine(model=model, task=task,

                grid_design=grid_design, grid_param=grid_param)

When initializing an instance of Engine, it pre-computes response probabilities and mutual information for a given sets of designs and parameters. This step may take a while, with linearly increasing computing time in proportion to the number and resolution of the grids. For the three examples provided here, compute time is usually less than two seconds on an average Mac or Windows computer.

Once the engine object is in place, users can access its task objects: the exhaustive list of task objects is (engine.task), its model object (engine.model), the number of possible pairs on design variables (engine.num_design), the number of possible pairs on model parameters (engine.num_param), the grid matrix of design variables (engine.grid_design), the grid matrix of model parameters (engine.grid_param), the prior distribution on the grid matrix of model parameters (engine.prior), the posterior distribution on the grid matrix of model parameters (engine.post), the posterior mean (engine.post_mean), the covariance matrix of the posterior (engine.post_cov), and the standard deviations of the posterior (engine.post_sd).

Two functions are available in ADOpy for the engine object: engine.get_design() and engine.update(). The engine.get_design() provides a set of designs on each trial of the experiment given a specified design type. With an argument of design_type, users can indicate the type of design to use. There are two possible values: ‘optimal’ and ‘random’. The value ‘optimal’ refers to the optimal design calculated by the ADO algorithm, and the value ‘random’ to a uniformly sampled design from the given design grid. The output of this function call is a dictionary that contains key-value pairs for each design variable and its optimal or random value.

# Provides the optimal design
design = engine.get_design(‘optimal’)
# Provides a randomly chosen design from the design grid
design = engine.get_design(‘random’)

If no argument is given for design_type, the optimal design is returned by default:

design = engine.get_design ()

The other important use of the engine object is engine.update(). Here, ADOpy first performs the Bayesian updating step described in Figures 1 and 2 based on a participant’s response given the design, and then computes a new optimal design for the next trial using the updated posterior distributions of model parameters. It takes two arguments: the design used on the given trial (design), and the corresponding response on that trial (response). For example, from the observation that a participant selects the SS option (response = 0) or the LL option (response = 1) on the current trial, users can update the posterior as follows:

engine.update(design, response)

Simulating responses

ADOpy can be run in the simulation mode to assess design quality and experiment efficiency (see next section). The design itself, the model chosen, and the grid resolution of the design space. and model parameters all affect how ADO performs. Simulation mode can be useful to fine-tune the aforementioned variables. Using the engine object of the ADOpy package, users can generate simulated responses given true parameters. As a concrete example, let us run the simulation with true parameter values of k = 0.12 and tau = 1.5 of the delay discounting model described in Equation (3). To acquire a simulated response, we use the Bernoulli probability distribution for a binary choice response as described below:

from scipy.stats import bernoulli

def get_simulated_response(model, design):
    '''Simulate a response using tau = 1.5 and k = 0.04.'''
    # Compute the probability of choosing the LL option
    p_obs = model.compute(t_ss=design[‘t_ss’], t_ll=design[‘t_ll’],
                          r_ss=design[‘r_ss’], r_ll=design[‘r_ll’],
                          k=0.12, tau=1.5)

# Compute a random binary choice response using Bernoulli
return bernoulli.rvs(p_obs)

With the functions and objects defined as above, we can now run the simulations with a code block like this:

NUM_TRIALS = 108 # number of trials for the simulation
for trial in range(NUM_TRIALS):
    design = engine.get_design(‘optimal’) # Design optimization
    response = get_simulated_response(model, design) # Experiment
    engine.update(design, response) # Bayesian updating

Note that the above code block contains the by-now familiar trilogy: design optimization, experimentation, and Bayesian updating, in the same way done in an actual ADO-based experiment as described in Figure 1.

3.6. Practical issues

Users should carefully consider several practical issues when using ADOpy. Grid-based ADO, which is what is used here, may demand a lot of memory. While pre-computing a look-up table lessens repeated calculation between trials, it requires more and more memory as the grid size increases. Thus, users are advised to first determine the proper number of grid points on each dimension of the model parameters and design variables and to check if computation time with the settings is suitable (i.e., fast enough to prevent boredom between trials). For example, by varying grid resolution, users can assess the trade-off in estimation accuracy and the computational cost of that resolution. Another option is to use a dynamic gridding algorithm, in which the grid space is dynamically adjusted and grid points near posterior means are more finely spaced. Adaptive mesh refinement (AMR: e.g., Berger, 1984) is one such method. ADOpy does not currently support dynamic-gridding; it may in the future..

A related practical issue is the computation time required to complete Step 0 in Figure 2, in which initial lookup tables need to be created for the likelihood function and the entropy for all possible values of the response, parameter, and design variables. As noted above, it has been our experience that this step usually takes no more than a few seconds on standard laptops and PCs. To be concrete, for the delay discounting task, it takes ~ 0.5 seconds on an iMac and 1 ~ 2 seconds on a Windows PC to execute the pre-computation step. However, this step can become progressively time-inefficient as the dimensionality of the experimental task increases. In such a case, we recommend to use the pickle module of Python for saving the lookup tables and then loading them back at the start of an experiment with each new participant. Other means of ensuring sufficiently fast computation are using linear algebra libraries (e.g., Intel MKL, LAPACK, or BLAS), which are highly efficient and can take advantage of multi-core CPUs, or using a remote server or a cloud computing system, where optimal designs are computed asynchronously.

ADOpy will eventually start to select the same or similar design on consecutive trials. This is a sign that not much more can be learned from the experiment (e.g., parameter estimation is quite good). This will happen toward the end of an experiment if there are sufficient trials. One option to address the issue is to dilute their presence by using filler trials, showing randomly chosen or predetermined designs for a trial when ADO picks the same design twice or more in a sequence. Another option is to run the experiment in a “self-terminating mode”; stop the experiment once a specific criterion (e.g., efficiency) is reached, e.g., the standard deviations of posterior distributions fall below certain predetermined values.

The focus of this tutorial is on using ADOpy for univariate and discrete responses. One might wonder how to extend it to multivariate and continuous responses, e.g., reaction times in a lexical decision task. Implementation is much the same as in the univariate continuous case. That is, given a multivariate continuous response vector y = (y₁,y₂,…,y_m), first discretize each response variable y_i into finite grids, and then pre-compute the likelihood function p(y∣θ,d) for all discretized values of y_i’s, θ, and d in the pre-computation Step 0 in Figure 2. From there, the remaining steps of the ADO algorithm are the same and straightforward.

4. Tasks and Models implemented in ADOpy

Currently, three tasks are implemented in the ADOpy package; they are listed in Table 1: Psychometric function estimation (adopy.tasks.psi), the delay discounting task (adopy.tasks.dd), the choice under risk and ambiguity task (adopy.tasks.cra). At least two models are available for each task.

In this section, we describe these tasks and illustrate how to use each task/model in ADOpy and how ADO performs compared to traditional non-ADO (e.g., staircase, random) methods, along with simulated results for the three tasks. In addition, we provide and discuss a complete and full Python script for simulating psychometric function estimation in ADOpy.

4.1. Psychometric function estimation

Psychometric function estimation is one of the first modeling problems in the psychological sciences in which a Bayesian adaptive framework was applied to improve the efficiency of psychophysical testing and analysis (Watson and Pelli, 1983; King-Smith et al., 1994; Kujala and Lukka, 2006; Lesmes et al., 2006). The problem involves a 2-alternative forced choice (2AFC) task in which the participant decides whether a psychophysical stimulus, visual or auditory, is present or absent while the stimulus intensity is varied from trial to trial to assess perceptual sensitivity.

The psychometric function that defines the probability of correct detection given stimulus intensity x is given as the following general form (Garcia-Perez, 1998; Wichmann and Hill, 2001):

$$\Psi (x\mid \alpha ,\beta ,\gamma ,\delta )=\gamma +(1-\gamma -\delta )F(x;\alpha ,\beta )$$ (4)

The participant’s response in the psychophysical task is recorded in either y = 1 (correct) or y = 0 (incorrect). The two-parameter sigmoid function F (x; α, β) that characterizes the relationship between the response probability and the stimulus intensity is typically assumed to follow the logistic, cumulative normal, or cumulative log Weibull form (see, e.g., Wichmann and Hill, 2001, for further details). The parameter vector θ = (α, β, γ, δ) of the psychometric function consists of α (threshold), β (slope), γ (guess rate) and δ (lapse rate), as depicted in Figure 5. Note that design variable is stimulus intensity, i.e., d = x.

Fig. 5:

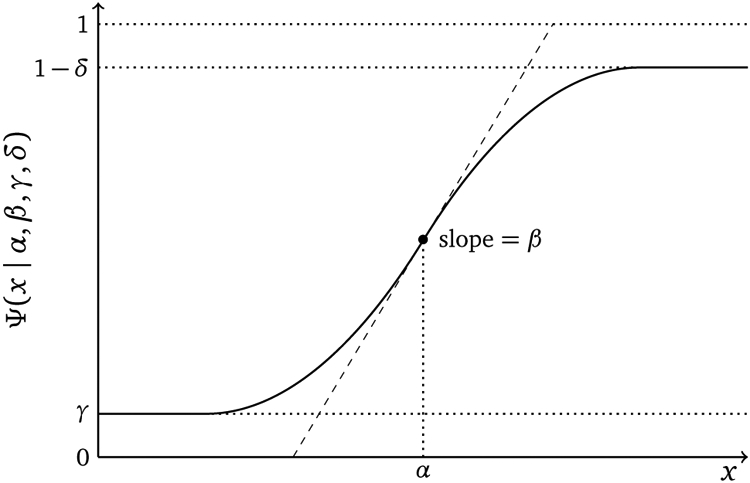
The psychometric function and its parameters defined in Equation (4).

The module ‘adopy.tasks.psi’ included in the ADOpy package provides classes for psychometric function estimation in the 2AFC experimental paradigm (see Table 1). In the module, Task2AFC is pre-defined for 2AFC tasks with a single design variable (stimulus) and binary responses (0 for incorrect or 1 for correct). Without passing any arguments, users can utilize the pre-defined Task2AFC class as below:

from adopy.tasks.psi import Task2AFC
task = Task2AFC()

task.designs # [‘stimulus’]
task.responses # [0, 1]

For the task, users can specify the form of the two parameter sigmoid psychometric function F (x; α, β) as in Equation (4) from three classes: a logistic function (ModelLogistic), a log Weibull CDF (ModelWeibull), and a normal CDF (ModelProbit). Here, assume that the psychometric function has a logistic form which computes correct detection as:

$$\Psi (x\mid \alpha ,\beta ,\gamma ,\delta )=\gamma +(1-\gamma -\delta )\cdot \frac{1}{1+\text{exp}[-\beta (x-\alpha )]}.$$ (5)

Based on Equation (5), the ModelLogistic class in the adopy.tasks.psi provides the equivalent model with four parameters (threshold α, slope β, guess\_rate γ, lapse\_rate δ).

from adopy.tasks.psi import ModelLogistic
model = ModelLogistic()

model.params # [‘threshold’, ‘slope’, ‘guess_rate’, ‘lapse_rate’]

As grid resolutions for the task and model, we provide an example code while fixing guess rate to 0.5 and lapse rate to 0.04 as described below. Especially for stimulus and threshold, users should define them within appropriate ranges for their tasks of interest.

import numpy as np

grid_design = {
    ‘stimulus’: np.linspace(20 * np.log10(.05), 20 * np.log10(400), 100)
}

grid_param = {
    ‘guess rate’: [0.5],
    ‘lapse rate’: [0.04],
    ‘threshold’: np.linspace(20 * np.log10(.1), 20 * np.log10(200), 100),
    ‘slope’: np.linspace(0, 10, 100)
}

Based on the task object, model object, and grids, adopy.tasks.psi provides an Engine class, called EnginePsi, pre-implemented for psychometric function estimation. The EnginePsi class not only provides an optimal design or randomly chosen design, but also computes a design using the staircase method. The staircase method is probably the most commonly used procedure in adaptive estimation of the psychometric function (e.g., Garcia-Perez, 1998) in which stimulus intensity is adjusted by a fixed and pre-determined amount based on a participant’s response on the current stimulus. The following code initializes the engine and computes designs:

from adopy.tasks.psi import EnginePsi
engine = EnginePsi(model, grid_design, grid_param)

engine.get_design(‘optimal’) # Returns the optimal design.
engine.get_design(‘random’) # Returns a randomly chosen design.
engine.get_design(‘staircase’) # Returns a design using the staircase method.

where EnginePsi requires only three arguments (model, designs, and params) since the task is fixed to the psychometric function estimation.

The particular up/down scheme of the staircase method implemented in ‘EnginePsi’ is as follows⁵:

$$x_{t+1}=\{\begin{array}{cc}{x}_t-\Delta \hfill & \text{if}{y}_t=1\hfill \\ x_t+2\Delta \hfill & \text{otherwise}(\text{if}{y}_t=0)\hfill \end{array}\phantom{\}}$$ (6)

where Δ is a certain amount of change for every trial. EnginePsi has a property called d_step to compute Δ, which means the number of steps for an index on the design grid. In other words, the denser the design grid is, the smaller Δ becomes. Initially, d_step is set to 1 by default, but users can use a different value as described below:

engine.d_step # Returns 1.
engine.d_step = 3 # Update d_step to 3.

Having defined and initialized the required task, model, grids, and engine objects, we are now in a position to generate simulated binary responses. This is achieved by using the module scipy.stats.bernoulli. Here, the data-generating parameter values are set to guess_rate = 0.5, lapse_rate = 0.04, threshold = 20, and slope = 1.5:

from scipy.stats import bernoulli

def get_simulated_response(model, design):
    # Compute a probability to respond positively.
    p_obs = model.compute(stimulus=design[‘stimulus’], \
            guess_rate=0.5, lapse_rate=0.04, threshold=20, slope=1.5)

    # Sample a binary response using Bernoulli distribution.
    return bernoulli.rvs(p_obs)

Finally, the following example code runs 60 simulation trials:

num_trials = 60 # number of trials to simulate
design_type = ‘optimal’ # or ‘random’ or ‘staircase’

for i in range(num_trials):
    # Compute a design for the current trial
    design = engine.get_design(design_type)
    # Get a simulated response using the design
    response = get_simulated_response(model, design)
    # Update posterior in the engine
    engine.update(design, response)
    # Print the trial number and posterior means and standard deviations
    print(‘Trial’, i + 1, ‘−’, engine.post_mean, ‘/’, engine.post_sd)

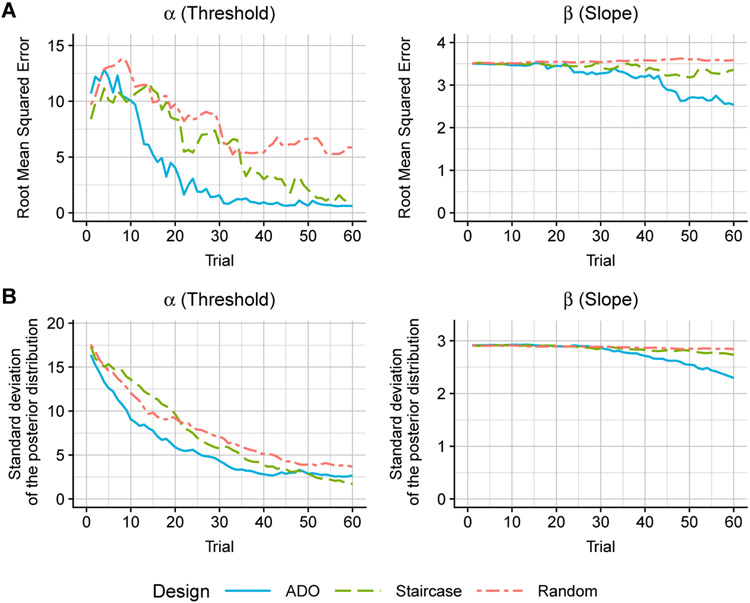
We conclude this section with a brief presentation of simulation results, comparing performance among three design conditions: ADO, staircase, and random (see Appendix B.1 for the details of the simulation setup). The simulation results are summarized in Figure 6. As shown in Figure 6A, for all three conditions, the estimation of the threshold parameter α, as measured by root mean square error (RMSE), converges toward the ground truth, with ADO designs exhibiting clearly superior performance over staircase and random designs. As for the slope parameter β, the convergence is much slower (ADO and staircase) or even virtually zero (random). Essentially the same patterns of results are observed when performance is measured by the posterior standard deviation (Figure 6B). In short, the simulation demonstrates the advantage of using ADO designs in psychometric function estimation.

Fig. 6:

Comparison of ADO, staircase, and random designs in the simulation of psychometric function estimation. Simulations were conducted using the logistic model with parameter values of threshold α = 20, slope β = 1.5, guess rate γ = 0.5, and lapse rate δ = 0.04. The three designed are compared with root mean squared errors (RMSE; Panel A) and standard deviations of the posterior distribution (Panel B). RMSE represents the discrepancy between true and estimated parameters in that the lower RMSE, the better estimation performance. Standard deviations of the posterior distribution indicate the certainty of a belief on the distribution for model parameters, i.e., the lower the standard deviations is, the higher certainty on the model parameters. Each curve represents an average across 1,000 independent simulation runs.

4.2. Delay discounting task

There exists a sizable literature on computational modeling of delay discounting (e.g., Green and Myerson, 2004; Van-DenBos and McClure, 2013; Cavagnaro et al., 2016). As described earlier in Section 3.5, preferential choices between two options, SS (smaller-sooner) and LL (larger-later), are made based on the subjective value of each option, which takes the following form:

$$V=R\cdot D(t)$$ (7)

where V is the value of an option, R and t are the amount of reward and delay of the option respectively, and D(t) is the discounting factor assumed to be a monotonically decreasing function of delay t.

Various models for the specific form of D(t) have been proposed and evaluated, including the ones below:

$$\begin{gathered} \text{Hyperbolic:}D(t)=\frac{1}{1+kt} \\ \text{Exponential:}D(t)=e^{-kt} \\ \text{Hyperboloid:}D(t)=\frac{1}{(1+kt{)}^s} \\ \text{Constant Sensitivity:}D(t)=e^{-(kt{)}^s} \end{gathered}$$ (8)

where the parameter k is a discounting rate and the parameter s reflects the subjective, nonlinear scaling of time (Green and Myerson, 2004). Based on subjective values of options, it is assumed that preferential choices are made stochastically depending on the difference between the subjective values, according to Equation (3). In summary, the models for the delay discounting task assume at most three parameters with θ = (k, s, τ), and there are four design variables that can be optimized, i.e., d = (t_SS,t_LLR_SS,R_LL). The participant’s choice response on each trial is binary in y = 1 (LL option) or 0 (SS option).

The module ‘adopy.tasks.dd’ included in the ADOpy package provides classes for the delay discounting task (see Table 1). TaskDD represents the DD task with four design variables (t_ss, t_ll, r_ss, and r_ll) with a binary choice response.

from adopy.tasks.dd import TaskDD
task = TaskDD()

task.designs # [‘t_ss’, ‘t_ll’, ‘r_ss’, ‘r_ll’]
task.responses # [0, 1]

In addition, the same module ‘adopy.tasks.dd’ includes six models (see Table 1): Exponential model (Samuelson, 1937), Hyperbolic model (Mazur, 1987), Hyperboloid model (Green and Myerson, 2004), Constant Sensitivity model (Ebert and Prelec, 2007), Quasi-Hyperbolic model (Laibson, 1997), and Double Exponential model (McClure et al., 2007). Here, we demonstrate the Hyperbolic model which has two model parameters (k and tau) and computes the discounting factor as in Equation (8):

from adopy.tasks.dd import ModelHyp
model = ModelHyp()

model.params # [‘k’, ‘tau’]

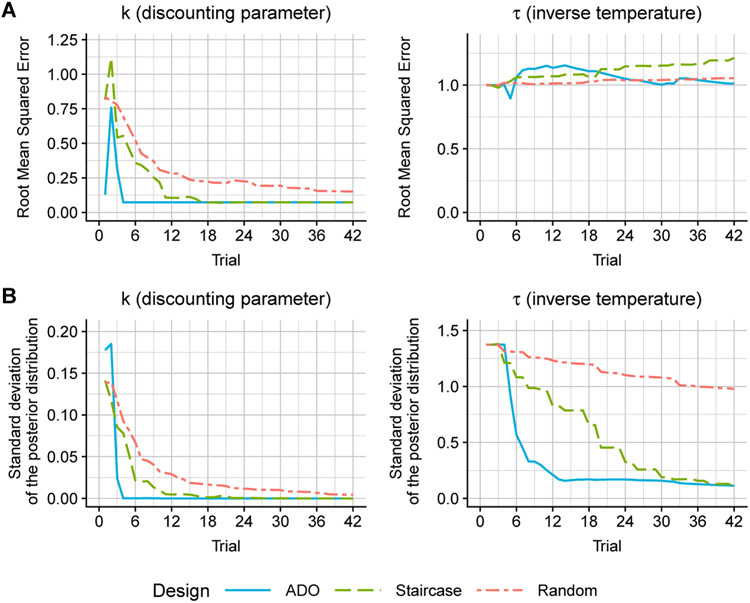
A simulation experiment like that for Psychometric function estimation was carried out with the hyperbolic model, and the results from three designs (ADO, staircase, and random). See Appendix B.2 for the details of the simulation setup and the Python scripts used. The simulation results are presented in Figure 7. As the trial progresses, the discounting rate parameter k converges toward the ground truth for all three design conditions, with the swiftest (almost immediate) convergence with ADO. On the other hand, the inverse temperature parameter τ showed a much slower or even no convergence (staircase), probably due to the relatively small sample size (i.e., 42). In short, the simulation results, taken together, demonstrated the superiority of ADO designs over non-ADO designs.

Fig. 7:

Comparison of ADO, staircase, and random designs in the simulation of the delay discounting task. Simulations were conducted using the hyperbolic model with parameter values of k = 0.12 and τ = 1.5. The three designs are compared with root mean squared errors (RMSE; Panel A) and standard deviations of the posterior distribution (Panel B). Each curve represents an average across 1,000 independent simulation runs.

4.3. Choice under risk and ambiguity task

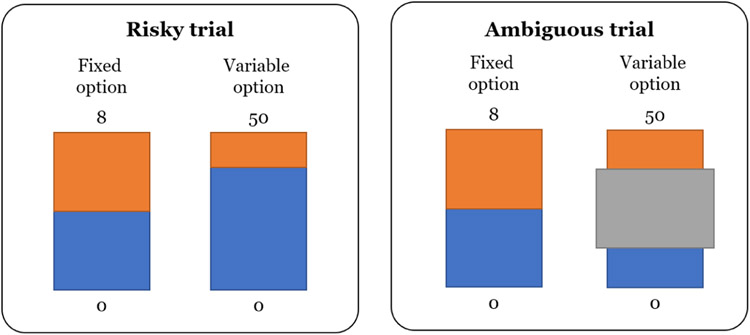
The choice under risk and ambiguity (CRA) task (Levy et al., 2010) is designed to assess how individuals make decisions under two different types of uncertainty: risk and ambiguity. Example stimuli of the CRA task are shown in Figure 8.

Fig. 8:

Illustrated scheme of the choice under risk and ambiguity (CRA) task. The participant chooses one of two options on either a risky trial (left) or an ambiguous trial (right). A risky option has the amount of reward and a probability of winning the reward indicated by the upper, brown proportion of the box. For an ambiguous option, the probability to win is not explicitly shown but partially blocked by a gray box. On each trial, a risk or ambiguous option is always paired with a fixed (reference) option whose probability of winning the reward is set to 0.5. .

The task involves preferential choice decisions in which the participant is asked to indicate a preference between two options: (1) winning either a fixed amount of reward denoted by R_F with a probability of 0.5 or winning none otherwise; and (2) winning a varying amount of reward (R_V) with a varying probability (p_V) or winning none otherwise. Further, the variable option comes in two types: (a) risky type in which the winning probabilities are fully known to the participant; and (b) ambiguous type in which the winning probabilities are only partially known to the participant. The level of ambiguity (A_V) in the latter type is varied between 0 (no ambiguity and thus fully known) and 1 (total ambiguity and thus fully unknown). As a concrete example, the CRA task of Levy et al. (2010) employed the following values: R_F = 5 (reference option); R_V ∈ {5,9.5,18,34,65}, p_V ∈ {0.13,0.25,0.38} and A_V = 0 (variable options on risky trials); and finally, R_V ∈ {5,9.5,18,34,65}, p_V = 0.5 and A_V ∈ {0.25,0.5,0.75} (variable options on ambiguity trials).

The linear model (Levy et al., 2010) for the CRA task assumes that choices are based on subjective values of the two options. The subjective values are computed using the following form:

$$\begin{gathered} U_F=0.5\cdot (R_F{)}^{\alpha } \\ {U}_V=\left[p_V-\beta \left(\frac{A_V}{2}\right)\right]\cdot (R_V{)}^{\alpha } \end{gathered}$$ (9)

where U_F and U_V are subjective values for fixed and variable options respectively, α is the risk attitude parameter, β is the ambiguity attitude parameter. R_F and R_V are the amounts of reward for fixed and variable options, A_V and p_V are the ambiguity level and the probability to win for a variable option. Both choices are made stochastically based on the difference between the subjective values according to the softmax choice rule:

$$P(VoverF)=\frac{1}{1+\text{exp}[-\gamma (U_V-U_F)]}.$$ (10)

where P(V over F) represents the probability of choosing the variable option over the fixed one, and the parameter γ represents the inverse temperature that captures the participant’s response consistency.

To summarize, the CRA model assumes three parameters, θ = (α, β, γ), of α (risk attitude), β (ambiguity attitude), and γ (response consistency). There are four design variables to be optimized: d = (R_F,R_V,A_V,p_V) where R_F > 0, R_V > 0, 0 < A_V < 1, and 0 < p_V < 1 is made up of R_F (reward amount for fixed option), R_V (reward amount for variable option), A_V (ambiguity level) and p_V (winning probability for variable option). The participant’s preferential choice on each trial is recorded in either y = 1 (variable option) or y = 0 (fixed option).

The module ‘adopy.tasks.cra’ in the ADOpy package provides classes for the choice under risk and ambiguity task (see Table 1). TaskCRA represents the CRA task with four design variables denoted by p_var (p_V), a_var (A_V), r_var (R_V), and r_fix (R_F), and a binary choice response.

from adopy.tasks.cra import TaskCRA
task = TaskCRA()

task.designs # [‘p_var’, ‘a_var’, ‘r_var’, ‘r_fix’]
task.responses # [0, 1]

ADOpy currently implements two models of the CRA task: Linear model (Levy et al., 2010) and Exponential model (Hsu et al., 2005). For the linear model in Equation 9, users can define and initialize the model with ModelLinear as:

from adopy.tasks.cra import ModelLinear
model = ModelLinear()

model.params # [‘alpha’, ‘beta’, ‘gamma’]

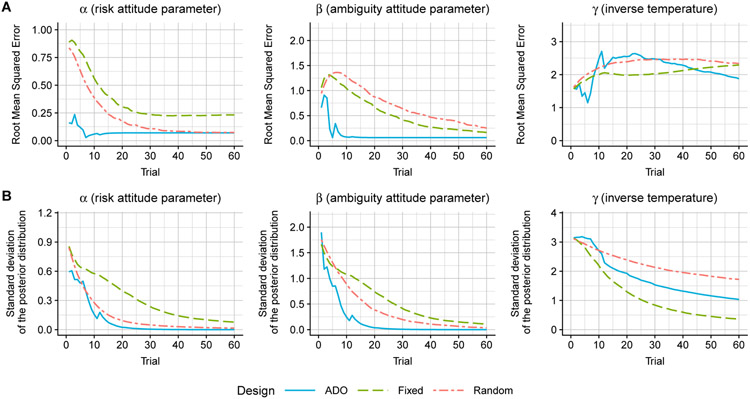
Now, we briefly discuss results of simulated experiments using the linear model with three design conditions: ADO, fixed, and random design. The fixed design refers to those originally used by Levy et al. (2010). See Appendix B.3 for the details of the simulation setup and code. The results summarized in Figure 9 indicate that two parameters, α (risk attitude) and β (ambiguity attitude), converged to their respective ground truth most rapidly under the ADO condition. On the other hand, the inverse temperature parameter (γ) showed little, if any, convergence for any of the designs, probably due to the relatively small sample size (i.e., 60).

Fig. 9:

Comparison of ADO, fixed, and random designs in the simulation of the choice under risk and ambiguity task. The fixed design was pre-determined according to Levy et al. (2010). Simulations were conducted using the linear model with parameter values of α = 0.66, β = 0.67, and γ = 3.5. Three designed are compared with root mean squared errors (RMSE; Panel A) and standard deviations of the posterior distribution (Panel B). Each curve represents an average across 1,000 independent simulation runs.

5. Integrating ADOpy with experiments

In this section we describe how to integrate ADOpy into a third-party Python package for conducting psychological experiments, such as PsychoPy (Peirce, 2007, 2009), OpenSesame (Mathôt et al., 2012), or Expyriment (Krause and Lindemann, 2014). Integration is accomplished following a two-step procedure described below.

First, users should create and initialize an ADOpy Engine object. This corresponds to the initialization step illustrated in Figure 3. Users can create their own task and model as described in Section 3 or use pre-implemented tasks and models in ADOpy (see Section 4). Remember that the number of design variables, model parameters, and the grid sizes affect the computation time, so users should ensure the appropriateness of their choice of grid sizes, for example, by running simulations as described in Section 3.6.

Second, users should integrate this code into the code for a running experiment. The interface between the two requires collecting observations from a participant using a computed optimal design and updating the engine on each trial with the collected response. ‘run_trial(design)’ is an experimenter-created function for data collection. It takes as arguments the given design values on each trial, and then returns the participant’s response:

def run_trial(design):
    … # Collect a response from the participant using the given design
    return response # Return the response from a participant

This function, ‘run_trial(design)’, can be used for both simulated and real data. Users can also run run_trial(design) within a for-loop to conduct an ADO experiment in multiple trials as shown below:

for trial in range(NUM_TRIAL):
    design = engine.get_design() # Design optimization
    response = run_trial(design) # Experiment
    engine.update(design, response) # Bayesian updating

Note that the three lines inside the for-loop correspond to the three steps in Figure 1.

In what follows, we elaborate and illustrate how to run ADOpy in the DD task, using a fully worked-out annotated Python script (Appendix C). Users new to ADO will find the PsychoPy program in the appendix without any modification of the code after installing ADOpy and PsychoPy. The program runs the DD task using optimal designs computed by ADOpy. A short description for the ADO-powered DD task is provided below, while the non-ADO version is available on the Github repository of ADOpy⁶.

To utilize ADO on the program, we first need to load the ADOpy classes (line 58–61), the DD task and the model of our choice (hyperbolic in this case). We could have chosen a different model or defined one by ourselves and used it:

58 # Import the basic Engine class of the ADOpy package and pre-implemented
59 # Task and Model classes for the delay discounting task.
60 from adopy import Engine
61 from adopy.tasks.dd import TaskDD, ModelHyp

To run the DD task, we define a function run_trial(design) (lines 250–288 in Appendix C) that conducts an experiment using a given design on a single trial. Then, for the initialization step, Task, Model and Engine objects should be initialized. As in Section 4.2, users can use the implemented task and models for the DD task (lines 329–357 in Appendix C).

329 # Create Task and Model for the delay discounting task.
330 task = TaskDD()
331 model = ModelHyp()
332
333 # Define a grid for 4 design variables of the delay discounting task:
334 #   ‘t_ss’, ‘t_ll’, ‘r_ss’, and ‘r_ll’.
335 # ‘t_ss’ and ‘r_ll’ are fixed to ‘right now’ (0) and $800.
336 # ‘t_ll’ can vary from 3 days (0.43) to 10 years (520).
337 # ‘r ss’ can vary from $12.5 to $787.5 with an increment of $12.5.
338 # All the delay values are converted in a weekly unit.
339 grid_design = {
340     ‘t_ss’: [0],
341     ‘t_ll’: [0.43, 0.714, 1, 2, 3, 4.3, 6.44, 8.6, 10.8, 12.9,
342                           17.2, 21.5, 26, 52, 104, 156, 260, 520],
343     ‘r_ss’: np.arange(12.5, 800, 12.5), # [12.5, 25, …, 787.5]
344     ‘r_ll’: [800]
345 }
346
347 # Define a grid for 2 model parameters of the hyperbolic model:
348 # ‘k’ and ‘tau’.
349 # ‘k’ is chosen as 50 grid points between 10^–5 and 1 in a log scale.
350 # ‘tau’ is chosen as 50 grid points between 0 and 5 in a linear scale.
351 grid_param = {
352     ‘k’: np.logspace(−5, 0, 50),
353     ‘tau’: np.linspace(0, 5, 50)
354 }
355
356 # Initialize the ADOpy engine with the task, model, and grids defined above.
357 engine = Engine(task, model, grid_design, grid_param)

Once the engine is created, the code to run the ADO-based version is actually simpler than the non-ADO version (lines 420–429 in Appendix C; see lines 435–460 for the non-ADO version on the Github repository). Using the Engine class of the ADOpy package, it finds the optimal design and updates itself from observation with a single line of code for each.

420 # Run the main task
421 for trial in range(n_trial):
422     # Get a design from the ADOpy Engine
423     design = engine.get_design()
424
425     # Run a trial using the design
426     is_ll_on_left, key_left, response, rt = run_trial(design)
427
428     # Update the engine
429     engine.update(design, response)

6. Conclusion

ADOpy is a toolbox for optimizing design selection on each trial in real time so as to maximize the informativeness and efficiency of data collection. The package implements Bayesian adaptive parameter estimation for three behavioral tasks: psychometric function estimation, delay discounting, and choice under risk and ambiguity. Each task can be run in an ADO-based mode or a non-ADO-based mode (random, fixed, staircase depending on the task). Default parameter and design values can be used, or the user can customize these settings, including the number of trials, the parameter ranges, and the grid resolution (i.e., number of grid points on each parameter/design dimension). Furthermore, in addition to conducting an actual experiment with participants, the package can be used to run parameter recovery simulations to assess ADO’s performance. Is it likely to be superior (i.e., more precise and efficient) to random and other (staircase, fixed) designs? By performing a comparison as described in the preceding section, a question like this one can be answered. Causes for unsatisfactory performance can be evaluated, such as altering grid resolution or the number of trials. More advanced users can conduct Bayesian sensitivity analysis on the choice of priors.

The need to tune ADO to a given experimental setup might make readers leery of the methodology. Shouldn’t it be more robust and work flawlessly in any setting without such fussing? Like any machine-learning method, use of ADO requires parameter tuning to maximize performance. ADOpy’s simulation mode is an easy and convenient way to explore how changes in the design and grid resolution alter ADO’s performance. Experimenter-informed decisions about the properties of the design space will result in the greatest gains in an ADO experiment.

Use of ADOpy is not limited to the models that come with the package. Users can define their own model using the Model class. Specification of the model’s probability density (or mass) function is all that is required along with the parameters, including any changes to the design space, as mentioned above. For example, it would be straightforward to create ADO-based experiments for other behavioral tasks, such as the balloon analog risk task (BART: Lejuez et al., 2002; Wallsten et al., 2005) for assessing risk-taking propensity.

The ADOpy package, as currently implemented, has several limitations. ADOpy cannot optimize the selection of design variables that are not expressed in the probability density (or mass) function of the model. For example, if a researcher is interested in learning how degree of distractibility (low or high level of background noise) impacts decision making, unless this construct were factored into the model as a design variable, ADOpy would not optimize on this dimension. This limitation does not prevent ADO from being used by the researcher; it just means that the experiment will not be optimized on that stimulus dimension. Another limitation that users must be sensitive to is the memory demands of the algorithm. As discussed earlier, the algorithm creates a pre-computed look-up table of all possible discretized combinations of the outcome variable, the parameters, and the design variables. For example, for 100 grid points defined on each outcome variable, three parameters, and three design variables, the total memory demand necessary to store the look-up table would be 10¹⁴ bytes (= 100¹⁺³⁺³), i.e., 100 terabytes, assuming one byte allotted for storing each data point. This is clearly well beyond what most desktops or servers can handle. In short, as the dimensionality of the ADO problem increases linearly, the memory demand of the grid-based ADO algorithm grows exponentially, sooner or later hitting a hardware limitation. Grid-based ADO does not scale up well, technically speaking. The good news is that there is a scalable algorithm that does not tax memory. It is known as sequential Monte Carlo (SMC) or particle filter in machine learning (Doucet et al., 2001; Andrieu et al., 2003; Cappe et al., 2007).

In conclusion, the increasing use of computational methods for analyzing and modeling data is improving how science is practiced. ADOPy is a novel and promising tool that has the potential to improve the quality of inference in experiments. This is accomplished by exploiting the predictive precision of computational modeling in conjunction with the power of statistical and machine learning algorithms to perform better inference. It is our hope that ADOpy will empower more researchers to harness this technology, one outcome of which should be more informative and efficient experiments that collectively accelerate advances in psychological science and beyond.

Appendices

A. Defining Grids for Delay Discounting Task

As the first example, suppose that the delay discounting task has two constraints on its designs: the delay of SS option should be smaller than that of LL option (t_ss < t_ll), and the amount of reward of SS option should be smaller than that of LL option (r_ss < r_ll). Considering seven delays (i.e., right now, two weeks, a month, six months, a year, three years, and ten years) and 79 possible rewards (from $12.5 to $787.5 with an increment of $12.5), users can make a grid for design variables by executing the following lines:

 1 # Initialize the possible values of delay and reward variables
 2 
 3 # Delays in a weekly unit
 4 tval = [0, 2, 4.3, 26, 52, 104, 520]
 5
 6 # [12.5, 25, … , 775, 787.5] as reward values
 7 rval = np.arange(12.5, 800, 12.5)
 8
 9 # Make a 2d matrix with rows of [t_ss, t_ll]
10 t_joint = []
11 for t_ss in tval:
12     for t_ll in tval:
13         if t_ss < t_ll:
14             t_joint.append([t_ss, t_ll])
15 t_joint = np.array(t_joint)
16
17 # Make a 2d matrix with rows of [r_ss, r_ll]
18 r_joint = []
19 for r_ss in rval:
20     for r_ll in rval:
21         if r_ss < r_ll:
22             r_joint.append([r_ss, r_ll])
23 r_joint = np.array(r_joint)
24
25 grid_design = {(‘t_ss’, ‘t_ll’): t_joint, (‘r_ss’, ‘r_ll’): r_joint}

As an another example, if users want to use the amount of reward of the SS option (r\_ss) and the delay of the LL option (t\_ll) while fixing t\_ss to 0 and r\_ll to $800, define a grid as shown below:

 1 grid_design = {
 2     # t_ss: [Now]
 3     ‘t_ss’: [0],
 4     # t_ll: [2 weeks, 1 month, 6 months,
 5     # 1 year, 2 years, 10 years] in a weekly unit
 6     ‘t_ll’: [2, 4.3, 26, 52, 104, 520],
 7     # r_ss: [$12.5, $25, … $775, $787.5]
 8     ‘r_ss’: np.arange (12.5, 800, 12.5),
 9     # r_ll: $800
10     ‘r_ll’: [800]
11     }

For model parameters, users should define a grid object containing grid points on a proper range for each parameter. For example, a grid for the hyperbolic model (Mazur, 1987) with two parameters (k and τ) can be defined as follows:

1 grid_param = {
2     # k: 20 points on [10^−5, 1] in a log scale
3     ‘k’: np.logspace(−5, 0, 20),
4     # tau: 20 points on [0, 5] in a linear scale
5     ‘tau’: np.linspace(0, 5, 20)
6 }

B. ADOpy Simulations

B.1. Psychometric function estimation

Simulations for psychometric function estimation were conducted for a simple 2-alternative forced choice (2AFC) task with one design variable. With an assumption that the psychometric function has a logistic function shape, we ran 1,000 simulations for three designs: (a) ADO design, (b) staircase design, and (c) randomly chosen design. For each simulation, responses were simulated for a total of 60 trials, using Task2AFC and ModelLogistic in the module adopy.tasks.psi.

Simulated responses were generated with true parameter values of threshold α = 20, slope β = 1.5, guess rate γ = 0.5, and lapse rate δ = 0.04. The simulation for psychometric function estimation used 100 grid points for the design variable (stimulus) and two model parameters (threshold and slope) each, and the guess and lapse rates were fixed to 0.5 and 0.04, respectively. The grid settings were given as follows:

Design variable

• stimulus: 100 grid points from 20log₁₀0.05 to 20log₁₀400 in a log scale.

Model parameters

• threshold: 100 grid points from 20log₁₀0.1 to 20log₁₀200 in a log scale.

• slope: 100 grid points from 0 to 10 in a linear scale.

• guess_rate: fixed to 0.5.

• lapse_rate: fixed to 0.04.

B.2. Delay discounting task

Assuming the hyperbolic model, simulations for the delay discounting (DD) task were conducted using TaskDD and ModelHyp in the module adopy.tasks.dd. We compared three designs: (a) ADO design, (b) staircase design, and (c) randomly chosen design. The staircase method runs 6 trials for each delay to estimate the discounting rate. While t_SS is fixed to 0, it starts with R_SS of $400 and R_LL of $800. If a participant chooses the SS option, the staircase method increases R_SS by 50%; if the participant chooses the LL option, it decreases R_SS by 50%. After repeating this 5 times, it proceeds to another delay value.

One thousand independent simulations were performed for each design condition, each for a total of 108 trials. Simulated data were generated using the true parameter values of k = 0.12 and τ = 1.5. Grid resolutions used for the simulations were as follows:

Design variables

• t_ss: fixed to 0, which means ‘right now’.

• t_ll: 18 delays (3 days, 5 days, 1 week, 2 weeks, 3 weeks, 1 month, 6 weeks, 2 months, 10 weeks, 3 months, 4 months, 5 months, 6 months, 1 year, 2 years, 3 years, 5 years, 10 years) in a unit of a week.

• r_ss: 63 points from $12.5 to $787.5 with an increment of $12.5.

• r_ll: fixed to $800.

Model parameters

• k (discounting rate): 20 grid points from 10⁻⁵ to 1 in a log scale.

• tau (inverse temperature): 20 grid points from 0 to 5 in a linear scale.

B.3. Choice under risk and ambiguity task

In simulating this CRA task, we assume the linear model and considered three methods for experimental designs in the simulation study: (a) ADO design, (b) ‘fixed’ design of Levy et al. (2010), and (c) random design.

The fixed design was set as follow. The the reward of the fixed option (R_F) to 5 and the rewards of the variable option (R_V) to 5, 9.5, 18, 34, 65. In risky trials, ambiguity (A_V) is set to 0 but the probability of winning for the variable option (P_V) is chosen among 0.13, 0.25, and 0.38. On the other hand, in ambiguous trials, the probability p_V is set to 0.5 but the ambiguity A_V is chosen from 0.25, 0.5, and 0.75. The total number of combinations is 30: 15 of which are for risky trials, and the rest of which are for ambiguous trials.

Grid settings for the four design variables and the three model parameters were set as follows:

Design variables

• p_var and a_var in risky trials: there are 9 probabilities to win for p_var (0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45), and a_var was fixed to 0.

• p_var and a_var in ambiguous trials: there are 6 levels of ambiguity for a_var (0.125, 0.25, 0.375, 0.5, 0.625, 0.75), and p_var was fixed to 0.5.

• r_var and r_fix: based on 10 reward values (10, 15, 21, 31, 45, 66, 97, 141, 206, 300), rewards pairs such that r_var > r_fix were used.

Model parameters

• alpha (risk attitude parameter): 11 grid points from 0 to 3 in a linear scale.

• beta (ambiguity attitude parameter): 11 grid points from −3 to 3 in a linear scale.

• gamma (inverse temperature): 11 grid points from 0 to 5 in a linear scale.

One thousand independent simulations were performed for each design condition, each for a total of 60 trials, with 30 risky and 30 ambiguous trials. Simulated data were generated using the true parameter values of α = 0.66, β = 0.67, and γ = 3.5 based on Levy et al. (2010).

C. Fully Worked-Out Python Script for Delay Discounting Task

  1 #!/usr/bin/env python3
  2 """
  3 Delay discounting task implementation using ADO designs
  4 =======================================================
  5
  6 This is the PsychoPy-based implementation of the delay discounting task using
  7 ADOpy. Delay discounting (DD) task is one of the widely used psychological
  8 tasks that measures individual differences in temporal impulsivity
  9 (e.g., Green & Myerson, 2004; Vincent, 2016). In a typical DD task,
 10 a participant is asked to indicate his/her preference between two options,
 11 a smaller-sooner (SS) option or stimulus (e.g., 8 dollars now) and
 12 a larger-later (LL) option (e.g., 50 dollars in a month).
 13 The DD task contains four design variables: ‘t_ss’ (delay for SS option),
 14 ‘t_ll’ (delay for LL option), ‘r_ss’ (reward for SS option), and ‘r_ll’
 15 (reward for LL option). By the definition, ‘t_ss’ should be sooner than ‘t_ll’,
 16 while ‘r_ss’ should be smaller than ‘r_ll’.
 17 To make the task design simpler, ‘t_ss’ and ‘r_ll’ are fixed to 0 (right now)
 18 and $800, respectively; only two design variables (‘r_ss’ and ‘t_ll’) vary
 19 throughout this implementation.
 20
 21 In each trial, given two options, a participant chooses one;
 22 the response is coded as ‘0’ for choosing SS option and ‘1’ for choosing LL
 23 option. In this implementation, the hyperbolic model is used to estimate the
 24 discounting rate underlying participants’ behaviors. The model contains two
 25 parameters: ‘k’ (discounting rate) and ‘tau’ (choice sensitivity).
 26
 27 Using ADOpy, this code utilizes ADO designs that maximizes information gain
 28 for estimating these model parameters. Also, using grid-based algorithm,
 29 ADOpy provides the mean and standard deviation of the posterior distribution
 30 for each parameter in every trial. Trial-by-trial information throughout
 31 the task is be saved to the subdirectory ‘task’ of the current working
 32 directory.
 33
 34 Prerequisites
 35 -------------
 36 * Python 3.5 or above
 37 * Numpy
 38 * Pandas
 39 * PsychoPy
 40 * Piglet 1.3.2
 41 * ADOpy 0.3.1
 42 """
 43
 44 ###############################################################################
 45 # Load depandancies
 46 ###############################################################################
 47
 48 # To handle paths for files and directories
 49 from pathlib import Path
 50
 51 # Fundamental packages for handling vectors, matrices, and dataframes
 52 import numpy as np
 53 import pandas as pd
 54
 55 # An open-source Python package for experiments in neuroscience & psychology
 56 from psychopy import core, visual, event, data, gui
 57
 58 # Import the basic Engine class of the ADOpy package and pre-implemented
 59 # Task and Model classes for the delay discounting task.
 60 from adopy import Engine
 61 from adopy.tasks.dd import TaskDD, ModelHyp
 62
 63 ###############################################################################
 64 # Global variables
 65 ###############################################################################
 66
 67 # Path to save the output data. Currently set to the subdirectory ‘data’ of the
 68 # current working directory.
 69 PATH_DATA = Path(‘./data’)
 70
 71 # Variables for size and position of an option box in which a reward and a
 72 # delay are shown. BOX_W means the width of a box; BOX_H means the height of
 73 # a box; DIST_BTWN means the distance between two boxes.
 74 BOX_W = 6
 75 BOX_H = 6
 76 DIST_BTWN = 8
 77
 78 # Configurations for text. TEXT_FONT means a font to use on text; TEXT_SIZE
 79 # means the size of text.
 80 TEXT_FONT = ‘Arial’
 81 TEXT_SIZE = 2
 82
 83 # Keys for response. KEYS_LEFT and KEYS_RIGHT contains a list of keys to
 84 # indicate that a participant wants to choose the left or right option.
 85 # KEYS_CONT represents a list of keys to continue to the next screen.
 86 KEYS_LEFT = [‘left’, ‘z’, ‘f’]
 87 KEYS_RIGHT = [‘right’, ‘slash’, ‘j’]
 88 KEYS_CONT = [‘space’]
 89
 90 # Instruction strings. Each group of strings is show on a separate screen.
 91 INSTRUCTION = [
 92     # 0 - intro
 93     """
 94 This task is the delay discounting task.
 95
 96 On every trial, two options will be presented on the screen.
 97
 98 Each option has a possible reward you can earn and
 99
100 a delay to obtain the reward.
101
102
103 Press <space> to proceed.
104 """,
105 # 1 - intro
106 """
107 You should choose what you prefer between two options
108
109 by pressing <f> (left option) or <j> (right option).
110
111
112 Press <space> to proceed.
113 """,
114 # 2 - intro
115 """
116 Let’s do some practices to check if you understand the task.
117
118
119 Press <space> to start practices.
120 """,
121 ’# 3 - intermission
122 """
123 Great job. Now, Let’s get into the main task.
124
125 Press <space> to start a main game.
126 """,
127 ’# 4 - last
128 """
129 You completed all the game.
130
131 Thanks for your participation.
132
133
134 Press <space> to end.
135 """,
136 ]
137
138
139 ###############################################################################
140 # Functions for the delay discounting task
141 ###############################################################################
142
143
144 def convert_delay_to_str(delay):
145     """Convert a delay value in a weekly unit into a human-readable string."""
146     tbl_conv = {
147         0: ‘Now’,
148         0.43: ‘In 3 days’,
149         0.714: ‘In 5 days’,
150         1: ‘In 1 week’,
151         2: ‘In 2 weeks’,
152         3: ‘In 3 weeks’,
153         4.3: ‘In 1 month’,
154         6.44: ‘In 6 weeks’,
155         8.6: ‘In 2 months’,
156         10.8: ’In 10 weeks’,
157         12.9: ‘In 3 months’,
158         17.2: ‘In 4 months’,
159         21.5: ‘In 5 months’,
160         26: ‘In 6 months’,
161         52: ‘In 1 year’,
162         104: ‘In 2 years’,
163         156: ‘In 3 years’,
164         260: ‘In 5 years’,
165         520: ‘In 10 years’
166     }
167     mv, ms = None, None
168     for (v, s) in tbl_conv.items():
169         if mv is None or np.square(delay - mv) > np.square(delay - v):
170             mv, ms = v, s
171     return ms
172
173
174 def show_instruction(inst):
175     """
176     Show a given instruction text to the screen and wait until the
177     participant presses any key in KEYS_CONT.
178     """
179     global window
180
181     text = visual.TextStim(window, inst, font=TEXT_FONT,
182                            pos=(0, 0), bold=True, height=0.7, wrapWidth=30)
183     text.draw()
184     window.flip()
185
186     _ = event.waitKeys(keyList=KEYS_CONT)
187
188
189 def show_countdown():
190     """Count to three before starting the main task."""
191     global window
192
193     text1 = visual.TextStim(window, text=‘1’, pos=(0., 0.), height=2)
194     text2 = visual.TextStim(window, text=‘2’, pos=(0., 0.), height=2)
195     text3 = visual.TextStim(window, text=‘3’, pos=(0., 0.), height=2)
196
197     text3.draw()
198     window.flip()
199     core.wait(1)
200
201     text2.draw()
202     window.flip()
203     core.wait(1)
204
205     text1.draw()
206     window.flip()
207     core.wait(1)
208
209
210 def draw_option(delay, reward, direction, chosen=False):
211     """Draw an option with a given delay and reward value."""
212     global window
213
214     pos_x_center = direction * DIST_BTWN
215     pos_x_left = pos_x_center - BOX_W
216     pos_x_right = pos_x_center + BOX_W
217     pos_y_top = BOX_H / 2
218     pos_y_bottom = -BOX_H / 2
219
220     fill_color = ‘darkgreen’ if chosen else None
221
222     # Show the option box
223     box = visual.ShapeStim(window,
224                            lineWidth=8,
225                            lineColor=‘white’,
226                            fillColor=fill_color,
227                            vertices=((pos_x_left, pos_y_top),
228                                      (pos_x_right, pos_y_top),
229                                      (pos_x_right, pos_y_bottom),
230                                      (pos_x_left, pos_y_bottom)))
231     box.draw()
232
233     # Show the reward
234     text_a = visual.TextStim(window,
235                              ‘${:,.0f}’.format(reward),
236                              font=TEXT_FONT,
237                              pos=(pos_x_center, 1))
238     text_a.size = TEXT_SIZE
239     text_a.draw()
240
241     # Show the delay
242     text_d = visual.TextStim(window,
243                              convert_delay_to_str(delay),
244                              font=TEXT_FONT,
245                              pos=(pos_x_center, −1))
246     text_d.size = TEXT_SIZE
247     text_d.draw()
248
249	
250 def run_trial(design):
251     """ Run one trial for the delay discounting task using PsychoPy."""
252     # Use the PsychoPy window object defined in a global scope.
253     global window
254
255     # Direction: −1 (Left - LL / Right - SS) or
256     #            +1 (Left - SS / Right - LL)
257     direction = np.random.randint(0, 2) * 2 – 1 # Return −1 or 1
258     is_ll_on_left = int(direction == −1)
259
260     # Draw SS and LL options using the predefined function ‘draw_option’.
261     draw_option(design[‘t_ss’], design[‘r_ss’], −1 * direction)
262     draw_option(design[‘t_ll’], design[‘r_ll’], 1 * direction)
263     window.flip()
264
265     # Wait until the participant responds and get the response time.
266     timer = core.Clock()
267     keys = event.waitKeys(keyList=KEYS_LEFT + KEYS_RIGHT)
268     rt = timer.getTime()
269
270     # Check if the pressed key is for the left option.
271     key_left = int(keys[0] in KEYS_LEFT)
272
273     # Check if the obtained response is for SS option (0) or LL option (1).
274     response = int((key_left and is_ll_on_left) or
275                                 (not key_left and not is_ll_on_left)) # LL option
276
277     # Draw two options while highlighting the chosen one.
278     draw_option(design[‘t_ss’], design[‘r_ss’], −1 * direction, response == 0)
279     draw_option (design [‘t_ll’], design [‘ r_ll’], 1 * direction, response == 1)
280     window.flip()
281     core.wait(1)
282
283     # Show an empty screen for one second.
284     window.flip()
285     core.wait(1)
286
287     return is_ll_on_left, key_left, response, rt
288
289
290 ###############################################################################
291 # PsychoPy configurations
292 ###############################################################################
293
294 # Show an information dialog for task settings. You can set default values for
295 # number of practices or trials in the main task in the ‘info’ object.
296 info = {
297     ‘Number of practices’: 5,
298     ‘Number of trials’: 20,
299 }
300 dialog = gui.DlgFromDict(info, title=‘Task settings’)
301 if not dialog.OK:
302     core.quit()
303
304 # Process the given information from the dialog.
305 n_trial = int(info[‘Number of trials’])
306 n_prac = int(info[‘Number of practices’])
307
308 # Timestamp for the current task session, e.g. 202001011200.
309 timestamp = data.getDateStr(‘%Y%m%d%H%M’)
310 
311 # Make a filename for the output data.
312 filename_output = ‘ddt_{}.csv’.format(timestamp)
313
314 # Create the directory to save output data and store the path as path_output
315 PATH_DATA.mkdir(exist_ok=True)
316 path_output = PATH_DATA / filename_output
317
318 # Open a PsychoPy window to show the task.
319 window = visual.Window(size=[1440, 900], units=‘deg’, monitor=‘testMonitor’,
320                        color=‘#333’, screen=0, allowGUI=True, fullscr=False)
321
322 # Assign the escape key for a shutdown of the task
323 event.globalKeys.add(key=‘escape’, func=core.quit, name=‘shutdown’)
324
325 ###############################################################################
326 # ADOpy Initialization
327 ###############################################################################
328
329 # Create Task and Model for the delay discounting task.
330 task = TaskDD()
331 model = ModelHyp()
332
333 # Define a grid for 4 design variables of the delay discounting task:
334 #   ‘t_ss’, ‘t_ll’, ‘r_ss’, and ‘r_ll’.
335 # ‘t_ss’ and ‘r_ll’ are fixed to ‘right now’ (0) and $800.
336 # ‘t_ll’ can vary from 3 days (0.43) to 10 years (520).
337 # ‘r_ss’ can vary from $12.5 to $787.5 with an increment of $12.5.
338 # All the delay values are converted in a weekly unit.
339 grid_design = {
340     ‘t_ss’: [0],
341     ‘t_ll’: [0.43, 0.714, 1, 2, 3, 4.3, 6.44, 8.6, 10.8, 12.9,
342                            17.2, 21.5, 26, 52, 104, 156, 260, 520],
343     ‘r_ss’: np.arange(12.5, 800, 12.5), # [12.5, 25, …, 787.5]
344     ‘r_ll’: [800]
345 }
346
347 # Define a grid for 2 model parameters of the hyperbolic model:
348 # ‘k’ and ‘tau’.
349 # ‘k’ is chosen as 50 grid points between 10^-5 and 1 in a log scale.
350 # ‘tau’ is chosen as 50 grid points between 0 and 5 in a linear scale.
351 grid_param = {
352     ‘k’: np.logspace(−5, 0, 50),
353     ‘tau’: np.linspace (0, 5, 50)
354 }
355
356 # Initialize the ADOpy engine with the task, model, and grids defined above.
357 engine = Engine(task, model, grid_design, grid_param)
358
359 ###############################################################################
360 # Main codes
361 ###############################################################################
362
363 # Make an empty DataFrame ‘df_data’ to store trial-by-trial information,
364 # with given column labels as the ‘columns’ object.
365 columns = [
366     ‘block’, ‘trial’,
367     ‘t_ss’, ‘t_ll’, ‘r_ss’, ‘r_ll’,
368     ‘is_ll_on_left’, ‘key_left’, ‘response’, ‘rt’,
369     ‘mean_k’, ‘mean_tau’
370 ]
371 df_data = pd.DataFrame(None, columns=columns)
372
373 #------------------------------------------------------------------------------
374 # Practice block (using randomly chosen designs)
375 #------------------------------------------------------------------------------
376
377 # Show instruction screens (0 - 2)
378 show_instruction(INSTRUCTION[0])
379 show_instruction(INSTRUCTION[1])
380 show_instruction(INSTRUCTION[2])
381
382 # Show countdowns for the practice block
383 show_countdown()
384
385 # Run practices
386 for trial in range(n_prac):
387     # Get a randomly chosen design for the practice block
388     design = engine.get_design(‘random’)
389
390     # Run a trial using the design
391     is_ll_on_left, key_left, response, rt = run_trial(design)
392
393     # Append the current trial into the DataFrame
394     df_data = df_data.append(pd.Series({
395         ‘block’: ‘prac’,
396         ‘trial’: trial + 1,
397         ‘t_ss’: design[‘t_ss’],
398         ‘t_ll’: design[‘t_ll’],
399         ‘r_ss’: design[‘r_ss’],
400         ‘r_ll’: design[‘r_ll’],
401         ‘is_ll_on_left’: is_ll_on_left,
402         ‘key_left’: key_left,
403         ‘response’: response,
404         ‘rt’: rt,
405     }), ignore_index=True)
406
407     # Save the current data into a file
408     df_data.to_csv(path_output, index=False)
409
410 #------------------------------------------------------------------------------
411 # Main block (using ADO designs)
412 #------------------------------------------------------------------------------
413
414 # Show an instruction screen (3)
415 show_instruction(INSTRUCTION[3])
416
417 # Show countdowns for the main block
418 show_countdown()
419
420 # Run the main task
421 for trial in range(n_trial):
422     # Get a design from the ADOpy Engine
423     design = engine.get_design()
424
425     # Run a trial using the design
426     is_ll_on_left, key_left, response, rt = run_trial(design)
427
428     # Update the engine
429     engine.update(design, response)
430
431     # Append the current trial into the DataFrame
432     df_data = df_data.append(pd.Series({
433         ‘block’: ‘main’,
434         ‘trial’: trial + 1,
435         ‘t_ss’: design[‘t_ss’],
436         ‘t_ll’: design[‘t_ll’],
437         ‘r_ss’: design[‘r_ss’],
438         ‘r_ll’: design[‘r_ll’],
439         ‘is_ll_on_left’: is_ll_on_left,
440         ‘key_left’: key_left,
441         ‘response’: response,
442         ‘rt’: rt,
443         ‘mean_k’: engine.post_mean[0],
444         ‘mean_tau’: engine.post_mean[1],
445         ‘sd_k’: engine.post_sd[0],
446         ‘sd_tau’: engine.post_sd[1],
447     }), ignore_index=True)
448
449     # Save the current data in a file
450     df_data.to_csv(path_output, index=False)
451
452 # Show the last instruction screen (4)
453 show_instruction(INSTRUCTION[4])
454
455 # Close the PsychoPy window
456 window.close ()