Significance
The linear viscoelasticity of soft materials is governed by the microscopic thermal fluctuations of the underlying constituents in the system, which are expected to give rise to mono-exponential stress relaxation processes. However, many soft materials, such as glasses and gels, instead exhibit a broad distribution of stress relaxation times, for which the microscopic origin remains elusive. Here, we investigate the microscopic fluctuations inside an arrested gel and reveal the presence of two distinct microscopic relaxation mechanisms: quiescent relaxations governed by the buildup of internal stresses during arrest, and perturbation-induced avalanche relaxation events governed by mechanical deformations in the system. We show that both nonlinear relaxation mechanisms are essential components of nonexponential stress relaxation in arrested soft materials.
Keywords: soft materials, stress relaxation, avalanches, gels, viscoelasticity
Abstract
Arrested soft materials such as gels and glasses exhibit a slow stress relaxation with a broad distribution of relaxation times in response to linear mechanical perturbations. Although this macroscopic stress relaxation is an essential feature in the application of arrested systems as structural materials, consumer products, foods, and biological materials, the microscopic origins of this relaxation remain poorly understood. Here, we elucidate the microscopic dynamics underlying the stress relaxation of such arrested soft materials under both quiescent and mechanically perturbed conditions through X-ray photon correlation spectroscopy. By studying the dynamics of a model associative gel system that undergoes dynamical arrest in the absence of aging effects, we show that the mean stress relaxation time measured from linear rheometry is directly correlated to the quiescent superdiffusive dynamics of the microscopic clusters, which are governed by a buildup of internal stresses during arrest. We also show that perturbing the system via small mechanical deformations can result in large intermittent fluctuations in the form of avalanches, which give rise to a broad non-Gaussian spectrum of relaxation modes at short times that is observed in stress relaxation measurements. These findings suggest that the linear viscoelastic stress relaxation in arrested soft materials may be governed by nonlinear phenomena involving an interplay of internal stress relaxations and perturbation-induced intermittent avalanches.
A broad distribution of relaxation times in response to linear mechanical perturbations—manifested, for instance, via power-law or stretched-exponential stress relaxation curves—is recognized as a fundamental property of arrested soft materials and occurs ubiquitously in glasses (1), concentrated emulsions (2, 3), gels (4), surfactant solutions (5), granular systems (6), and biological materials (7–11). Despite this universality, the current understanding of this phenomenon is prevalently system-specific; for example, in glasses, nonexponential stress relaxations can be approached from the perspective of dynamic heterogeneity (1), referring to the spatiotemporal heterogeneities of mobilities that manifest within the glass microstructure (12). In associative systems, such as gels, stretched-exponential stress relaxations can be interpreted as a convoluted exponential relaxation process originating from an exponential or logarithmic distribution in the size of different relaxing mechanical components (5, 13, 14). In strongly aging systems such as colloidal glasses and emulsions, relaxations can be analyzed from the viewpoint of activated hops in an exponential potential-energy landscape through a framework known as soft glassy rheology (15, 16). The quest to understand nonexponential stress relaxation in a variety of soft materials has also motivated studies of nonaffine deformations (17), nonlinear internal prestress (8), fractal structures (18), shear-transformation zones (19), aging-induced avalanches (3), interchain locking (20), and phase separation (21). This large variety of system-specific relaxation processes that have been proposed makes extracting the key physics behind broadly distributed stress relaxation dynamics in arrested soft materials a complicated task.
Arrested soft materials also exhibit a common microscopic relaxation behavior, in the form of a compressed exponential decay in the correlation functions arising from the superdiffusive motion of the constituents (22–26). The origins of these dynamics are well understood as being athermal in nature, wherein internal stress heterogeneities generated during arrest are released and cause local strain propagation at a rate exceeding that from thermal rearrangements (22–25, 27, 28). These microscopic dynamics are expected to play an important role in dictating the macroscopic stress relaxation dynamics of arrested systems. Indeed, evidence for this idea lies in past studies on gels (4) and biological networks (11), where correlations between the aging-induced evolution of microscopic relaxation times and macroscopic relaxation times (4) or elastic moduli (11) have been established. However, despite these earlier studies, a connection between the microscopic relaxation dynamics and the statistical features of the broad distribution of relaxation times in macroscopic perturbations (e.g., the mean value and the width of the distribution of relaxation times) has remained elusive.
Here, we aim to address this missing connection through a multiscale investigation of the relaxation dynamics of an arrested model system via rheology, ultra small angle X-ray scattering (USAXS), and X-ray photon correlation spectroscopy (XPCS). To do so, we study a recently developed associative hydrogel platform consisting of water-stabilized iron oxide nanoparticles (NPs) (29), which are bridged by telechelic linkers of four-arm poly(ethylene glycol) (PEG) functionalized with strongly iron-coordinating nitrocatechol ligands (Fig. 1A). Prior work by our group (30), as well as theoretical predictions for such gel systems (31), have shown that polymer-particle configurations facilitate dynamic arrest in the absence of a phase separation (32) through limited-valency interactions. This mechanism of self-assembly results in the dynamic arrest of NPs into a gelled state. The resulting gels are able to reach a structural and mechanical steady state during the experimental time frame—rather than undergo continued aging via an arrested phase separation (30) (SI Appendix, Fig. S2)—while still exhibiting hallmark dynamical characteristics of arrested soft materials such as stretched exponential stress relaxations and compressed exponential correlation decays (30, 33). This makes the polymer-particle gel a useful model system for exploring the microscopic dynamics of arrested systems, as it exhibits quiescent microscopic dynamics associated with the arrested state without the contribution of aging dynamics (2, 4, 34). As a result, this system allows us to isolate and examine the microscopic relaxation dynamics of arrested soft materials that arise in perturbation-free quiescent states as well as in mechanically perturbed states, and analyze their separate contributions to the macroscopic stress relaxation.
Fig. 1.
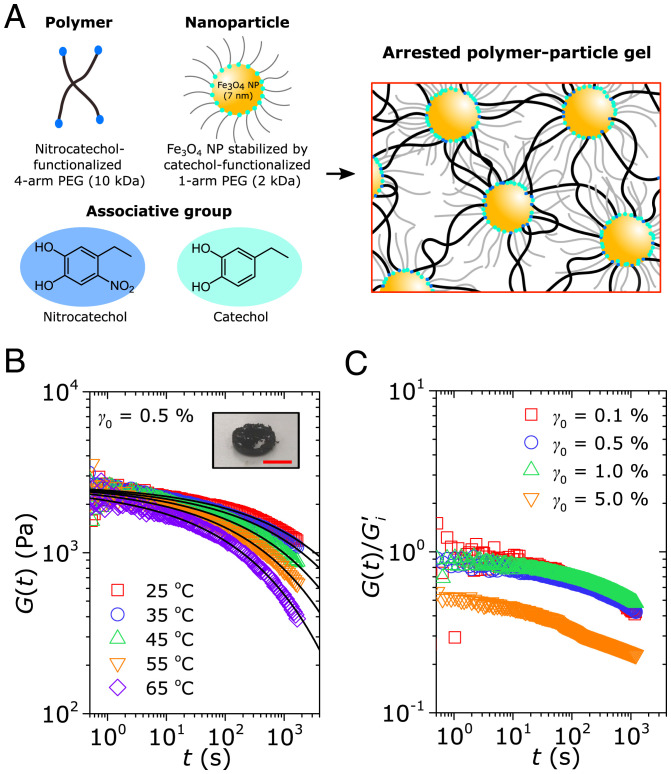
Arrested associative gels exhibit broad nonexponential stress relaxations in response to linear perturbations. (A) Schematic illustration of the model polymer–particle system, consisting of four-arm PEGs (10 kDa) with nitrocatechol groups, and Fe3O4 NPs (7-nm diameter) stabilized by one-arm PEGs (2 kDa) with catechol groups. Upon mixing, the stronger-binding nitrocatechol ligand replaces the catechol ligand on the NP surface and gelation thus occurs via a dynamic ligand exchange from equilibrium. Details on the synthesis and compositions are available in Materials and Methods, and additional characterizations of the quiescent viscoelasticity of the gels are available in ref. 30. (B) Representative of the arrested gel in response to a linear step strain () at . Solid lines indicate fits to the stretched exponential function (Eq. 1) with a constant stretching exponent of . The stretching exponent is consistent at all temperatures, as evidenced by the stretched exponential fit to the time and temperature–superposed data (SI Appendix, Fig. S1). Inset: Representative picture of the model gel material. Scale bar, 1 cm. (C) Step strain measurements of the relaxation modulus of the gelled system measured at varying strain amplitudes (). All values are normalized by the initial storage modulus of the gel measured immediately after gelation (SI Appendix, Fig. S2A). Linear behavior is demonstrated up to a strain of ; this result is also in agreement with amplitude sweep characterizations on the system (SI Appendix, Fig. S2B).
Results
We first begin with macrorheological characterizations of the gel. In response to a step strain in the linear regime, the arrested gel exhibits classic signatures of stretched-exponential stress relaxations of the form:
| [1] |
where is the plateau modulus, is the macroscopic relaxation time, and is the stretching exponent. The gel shows an exponent of across (Fig. 1B and SI Appendix, Fig. S1). Stretched-exponential stress relaxation functions underscore an asymmetric distribution in the relaxation times (with a mean relaxation time and a heavy tail at short times) (35) and are often seen in highly arrested systems such as gels and glasses (1, 4, 5). These relaxation dynamics are distinct from what is commonly seen (and well understood) in associative gels with moderate concentrations of associations, wherein a power-law stress relaxation of emerges due to a “sticky” Rouse relaxation of interconnected components (36, 37). Instead, these relaxation dynamics are observed in associative gels with high concentrations of associations (38) such as our model system, for which the microscopic origins remain unclear.
The microscopic dynamics of our model gel are measured via XPCS, a technique that allows us to directly measure the dynamics of the NPs which serve as cross-linkers in the gel. XPCS bypasses the drawbacks of visible light–based approaches in dealing with material opacity (Fig. 1B, Inset) and capitalizes on the high electron-density contrast between the NPs and the continuous-phase constituents, water and PEG. In XPCS, speckle intensity maps are measured as a function of time (Fig. 2A). The autocorrelation of the wave-vector q-dependent intensities produces a second-order correlation function as a function of delay time , which is related to the intermediate scattering function via the Siegert relation:
| [2] |
Fig. 2.
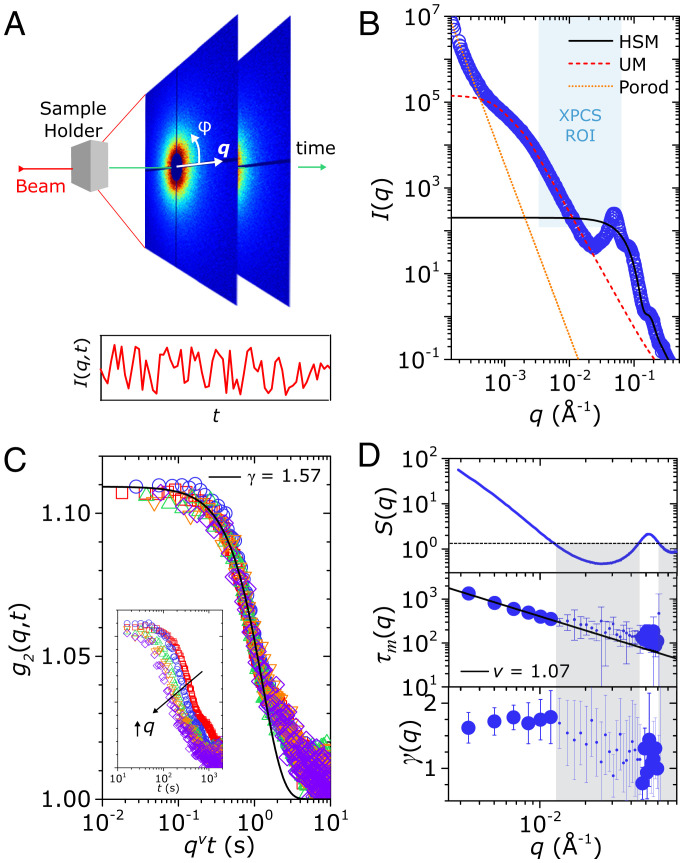
Microscopic dynamics of the arrested gel probed at quiescence via XPCS. (A) Illustration of the XPCS experimental setup. A partially coherent synchrotron X-ray beam strikes the sample, and scattered speckle intensity maps (with coordinates defined by the wave-vector q and azimuth angle ) are measured as a function of time. Correlations of the measured speckle intensity are taken to obtain the second-order correlation function as a function of delay time t. (B) USAXS intensities of the arrested gel. The scattering is captured by a hard sphere model (HSM) at high q, a unified model (UM) at intermediate q, and a Porod scattering response at low q. The region of interest probed by XPCS is shown by the shaded region, which is bound by q = 0.0032 Å−1 and 0.063 Å−1 and a noise floor at low . The UM captures the cluster size of the associative gel and shows that the XPCS region of interest is within the primary cluster size. All fitting parameters are listed in SI Appendix, Table S1. (C) The second-order correlation function as a function of delay time for the arrested system in situ gelled in a capillary (see holder configuration in SI Appendix, Fig. S3). The correlation decay is fitted to the Siegert relation in Eq. 2. The -axis is rescaled by with ; data collapse here indicates that superdiffusive dynamics drive both the fitted decay and the long-time tail. The inset shows the original q-dependent data in the range (increasing in q from right to left). (D) Graphs of the q-dependent structure factor , microscopic relaxation time , and compressing exponent . The and values shown are averages taken from 20 independent experiments conducted in the capillary (see statistics for in SI Appendix, Fig. S5). The structure factor is obtained by dividing by the HSM results (Fig. 2B). The dashed line in the plot indicates the noise threshold dictated by low ; measurements made at corresponding to exhibit larger error bars, as shown. The data points in this noise floor are indicated by smaller symbols, and are shaded in gray. The relaxation times above this noise floor, at , are fitted to the relation to obtain .
where is an instrument-dependent coherence-adjustment factor, is a contrast term, and and measure the microscopic relaxation time and associated stretching () or compressing ( exponent of the decay curve. More details on the technique are provided in (39).
We perform XPCS over a q range of 0.0032 Å−1 to 0.063 Å−1, which covers the intracluster length scale in our gel system. This information is revealed by USAXS measurements on the gels (Fig. 2B), from which contributions from three distinct length scales are identified: a high-q contribution at , an intermediate-q contribution at , and a low-q contribution at . The high-q contribution can be accurately described by a hard-sphere model (HSM)—the dividing of our intensity by the HSM yields the structure factor (Fig. 2D)—and can be attributed to the NPs. The intermediate-q and low-q contributions can be attributed to the existence of clustering at multiple length scales. These features have been commonly observed in other network systems such as polymer gels (40) and nanocomposites (41) through scattering measurements over large length scales beyond the characteristic cluster size. Here, we follow the conventions of these studies and attribute the intermediate-q length scale to the primary cluster size [with a diameter of , obtained via a unified model fit (42)] and the low-q length scale to larger agglomerates (with a characteristic size greater than the largest probed length scale of USAXS, 1 μm, as evidenced by the Porod scaling of ). The XPCS region of interest thus falls within the size of the primary cluster, .
We first probe the microscopic dynamics of the gel system in the quiescent state via XPCS using an in situ capillary-gelled sample (see SI Appendix, Fig. S3 for holder setup). Second-order correlation measurements on the capillary-gelled system reveal a compressed exponential decay, which is paired by superdiffusive dynamical behavior, as evidenced by the collapse of the upon scaling the relaxation times by (Fig. 2C). The scaling exponent is obtained directly through the fitting of the mean value of from 20 independent measurements (Fig. 2D); such ensemble-averaged measurements are only possible due to the negligible aging of the gelled material (SI Appendix, Fig. S2). Within this same q region, the compressing exponent is approximately constant around (Fig. 2D), suggesting that superdiffusive dynamics persists throughout the intracluster length scale. At high q, the relaxation time deviate from this scaling and decrease toward unity, in agreement with previous experiments (22) and simulations (25). These observations are consistent with the aforementioned signatures of elastic stress fluctuations (22–27), in which the relaxation of heterogeneous frozen-in internal stresses modify the elastic strain field and induce superdiffusive local rearrangements in the material.
Though the heavy tail of the correlation decay is not captured by the compressed exponential form of the Siegert relation in Fig. 2C [as also observed in many other measurements that reveal a compressed exponential decay in the correlations (23, 43, 44)], we find a good collapse of the data in this tail region by horizontally shifting the data with , indicating that this heavy tail shares the same superdiffusive origins as the main decay function. We verify this, and directly shed light on the role played by internal stresses on the measured , by performing an azimuthal angle -dependent investigation of in capillary-gelled systems (SI Appendix, Fig. S4 A–C). Capillary environments facilitate anisotropic residual stresses in the gels during dynamic arrest by preventing internal stress relaxations in the direction of boundary conditions such as the capillary walls and the sealant (43). Thus, we can expect arrested systems that are governed by internal stresses to exhibit a -dependence in the correlation decay, such that relaxation is accelerated in directions facing confinement-induced persistence of internal stress. We indeed observe this behavior in our gels, where relaxation is faster along directions that are under confinement by the capillary walls and the Torr seal, and slower in unconfined directions. The heavy tail in (Fig. 2C) can thus be attributed to the distribution of stored internal stresses in the microstructure, arising from the heterogeneous boundary conditions of the capillary (43). Overall, these results show that internal stresses accrued during gelation govern the measured microscopic of the gel system. That such dynamics can dominate the steady-state response of a limited-valency gel system exhibiting negligible aging effects would indicate that these internal stresses are globally trapped in the system during arrest and facilitate spontaneous local relaxations, similar to other arrested systems in which the steady-state responses are also governed by internal stresses (26, 43, 45).
We now seek to establish a connection between the internal stress–dominated microscopic and statistical features of the broad distribution of relaxation times observed in macrorhelogical experiments, namely, the mean relaxation time and the breadth of the distribution. The underlying a stretched exponential function can be obtained by calculating its first moment, which has a simple analytical solution (46):
| [3] |
where is the relaxation time and is the generic scaling exponent in the stretched exponential function, such as the parameters in Eq. 1 and in Eq. 2. As typical values of the exponents obtained through stretched exponential fits to rheology and XPCS data are vastly different (since they are described by stretched and compressed exponential functions, respectively), we thus compare the mean rheological relaxation time , obtained by rescaling with (Eq. 1), with the mean XPCS relaxation time , obtained by rescaling with (Eq. 2). We perform this comparison in a temperature-dependent manner, comparing obtained via rheology at , with obtained via XPCS over the same temperature range. To enable this comparison, we study the microscopic dynamics of our arrested system by gelling the system ex situ and gently loading it into a 1.5 mm–thick aluminum cell which is capable of conducting heat from the Peltier assembly loaded in the XPCS chamber (SI Appendix, Fig. S3). Our ex situ gels are 1.1 mm thick, and thus the cells are underfilled to minimize mechanical perturbations to the sample. These aluminum cell loaded samples exhibit compressed exponential correlation decays which are similar to the capillary-gelled samples discussed thus far (see comparison in SI Appendix, Fig. S7); hence, we also refer to these samples as “quiescent.”
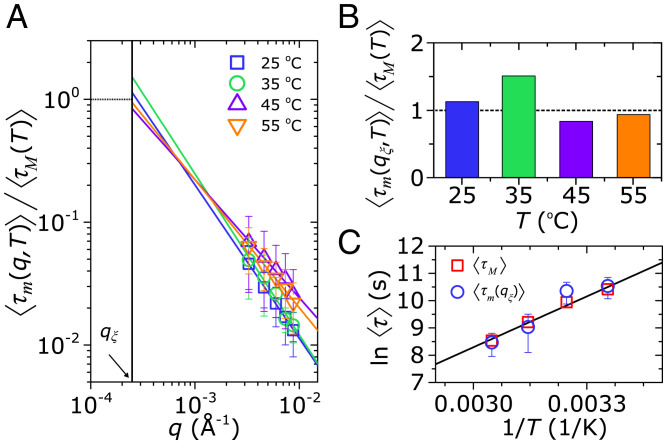
Since is q-dependent (Fig. 2D) and clearly smaller than over the studied q range (Fig. 3A), we select a characteristic microscopic length scale at which reasonable comparisons with macroscopic measurements can be made. For this purpose, we select the primary cluster size as the characteristic length scale, as cluster dynamics are often implicated in the macroscopic viscoelasticity of soft materials (13, 47–49). Various scattering experiments and simulations of arrested systems have shown that reach a plateau at wave-vectors corresponding to the cluster size, (25, 49, 50), as microscopic dynamics can become strongly constrained beyond this length scale. These findings allow us to reliably extrapolate our superdiffusive scalings of (Fig. 2D) towards the cluster-size wave vector to determine the characteristic relaxation times of the primary clusters of the gel, even if the q range of XPCS does not explicitly capture such large length scales.
Fig. 3.
Correlations between quiescent microscopic cluster relaxation times and macroscopic stress relaxation times in the arrested gel. (A) Mean microscopic relaxation times (Eq. 3) over a temperature range of measured in an aluminum cell. All data are normalized to the mean macroscopic stress relaxation time at the corresponding temperatures (Fig. 1B), fitted to the function , and extrapolated to the wave vector corresponding to the cluster size . (B) obtained via extrapolation to the cluster size. (C) Arrhenius plot of the mean relaxation times obtained from rheology, , and from XPCS, . Lines indicate fits of to the Arrhenius relation , which reliably captures as well. Fitting parameters are listed in SI Appendix, Tables S2 and S3.
The comparison between obtained via rheology with obtained via XPCS is shown in Fig. 3A. Excellent agreements are observed between and the extrapolated quantity , with ∼ 1 for all temperatures studied (Fig. 3B). Moreover, we find that both measurements can be captured by a single Arrhenius function of the form , with an activation energy (Fig. 3C). The direct correlation between the mean macroscopic stress relaxation time and mean microscopic relaxation times at the cluster size shown here suggest that internal stress relaxation of clusters at quiescence may govern the mean macroscopic stress relaxation of the gel. This would indicate that stress relaxation in the gel is facilitated by an inherently nonlinear phenomenon, where the energy represents the thermal activation energy of relaxation which is modified by internal stresses in the system (51, 52).
We next seek to understand the connection between microscopic dynamics and the breadth of stress relaxation times observed via linear macrorheology. Though we find that quiescent microscopic fluctuations are directly correlated to the mean macroscopic relaxation time of the system (Fig. 3), the distribution of is Gaussian, with a small variance that can be attributed to the spatial variation of the internal stresses in the microstructure (SI Appendix, Fig. S5). This distribution of is not consistent with the broad distribution of relaxation times underlying a stretched exponential stress relaxation function with a stretching exponent as low as (illustrated analytically in SI Appendix, Fig. S6). Thus, we reasoned that the macroscopic relaxation process may entail nonquiescent or perturbation-induced relaxation processes. Such pertubations, whether they originate from microstructural aging (3, 53–55) or mechanical deformations (56) [even in the linear regime below the yield strain (57)] have been shown to induce avalanche dynamics in arrested systems, and recent simulation studies on emulsions have even hinted at a connection between avalanche dynamics and power-law macroscopic stress relaxation response through a microrheological framework (3). As our quiescent system shows little structural and dynamical aging within experimental time frames (SI Appendix, Fig. S2), we sought to directly induce such perturbations into our system through mechanical compressions. As a simple approach to inducing this perturbation during XPCS, we again load an ex situ gelled material with a controlled thickness into the aluminum cell—the same approach as the one used to study temperature-dependent dynamics in Fig. 3—but in this case, we use a thinner aluminum cell which is 1.0-mm thick. Thus, the polycarbonate windows of the aluminum cell put the sample under a compressive strain of ∼10% in this state, in contrast to the uncompressed quiescent samples (Fig. 4A).
Fig. 4.
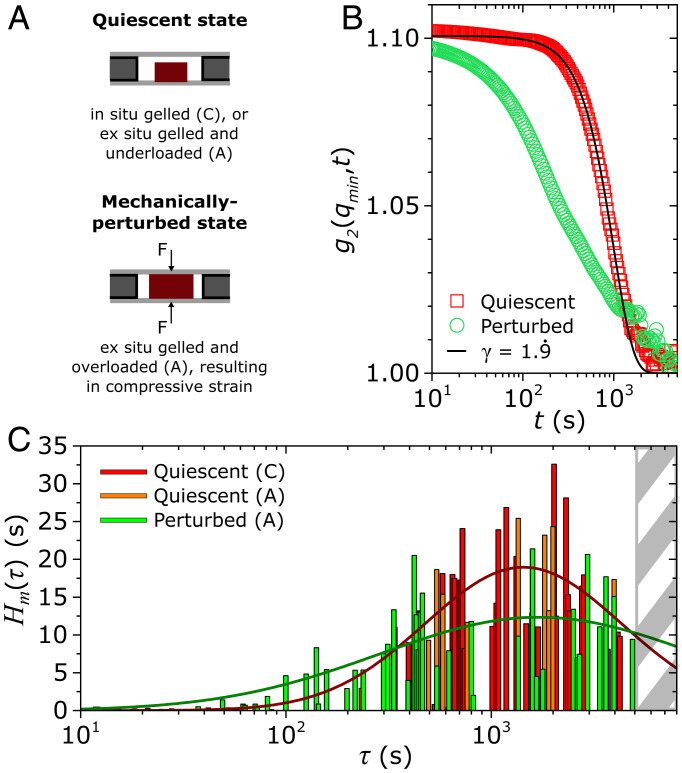
Perturbation-induced broadening of the distribution of microscopic relaxation times in the arrested gel. (A) Configurational descriptions of the gel system in the quiescent state and in the mechanically perturbed state. The quiescent state is probed either through in situ gelation of the system in a capillary (denoted C), or through underloading an aluminum cell (denoted A) with an ex situ gelled material. Detailed illustrations of the C and A configurations are in SI Appendix, Fig. S3. We induce mechanical perturbations to our gels by overloading the aluminum cell with the ex situ gelled material, resulting in a compressive strain of ∼10 %. (B) Representative second-order correlations for the quiescent system (in the capillary) and perturbed system. The data shown here are time-wavevector superposed—in similar vein to the data shifting performed in Fig. 2C—such that data collected over the range are shifted to a reference wave vector of , which allows us to sample longer time scales of up to s. The quiescent system in the aluminum cell shows a similar response to the quiescent system in the capillary (SI Appendix, Fig. S7). The quiescent data show good agreement with Eq. 2, with a ballistic decay exponent of . (C) Discrete spectra of ballistic microscopic relaxation times in the quiescent and perturbed systems at and , obtained via the protocol highlighted in Materials and Methods. The analysis is done on 15 experiments in the capillary configuration, 6 experiments in the aluminum configuration at quiescence, and 11 experiments in the aluminum configuration under perturbations. The vertical shading at denotes the time-scale limitations of the experiments. The data for quiescent (capillary and aluminum-cell data combined) and perturbed conditions are fitted to a Gaussian function of the form (red and green lines, respectively). Note the fits are for visual guidance only to highlight the emergence of short-time dynamics in the perturbed system.
A markedly different response is observed in these mechanically compressed systems compared to the quiescent systems (Fig. 4B). Whereas the quiescent systems exhibit a prototypical , which can almost be completely described by a single ballistic decay curve [with a compressing exponent of (43)], the perturbed systems exhibit a much broader which cannot be described by a single ballistic decay curve. To quantify these differences, we estimate the discrete spectra of ballistic relaxation modes governing the second-order correlation of the quiescent and perturbed systems through an inverse Laplace transform of the relation:
| [4] |
where is the spectrum of ballistic microscopic relaxation modes in the function. The ballistic relaxation mode was modeled here by a compressing exponent of (rather than to circumvent the appearance of a Gaussian and ensure that the function remains monotonic). To perform this inverse Laplace transform, we use a nonlinear regularization estimation (58) that is used commonly in macrorheology to determine ; we find the discrete relaxation modes by identifying the dominant spectral peaks obtained by minimizing the curvature penalty in the regularization protocol (see Materials and Methods). Fig. 4C illustrates the results of this operation performed on the ensemble of correlation data obtained on our arrested gels in quiescent and perturbed states. There is a marked difference in the breadth of the relaxation spectra of our system as shown by the emergence of short-time relaxation modes in the perturbed state, which are absent in the quiescent state but would be expected from the distribution of relaxation times underlying a stretched exponential with (SI Appendix, Fig. S6).
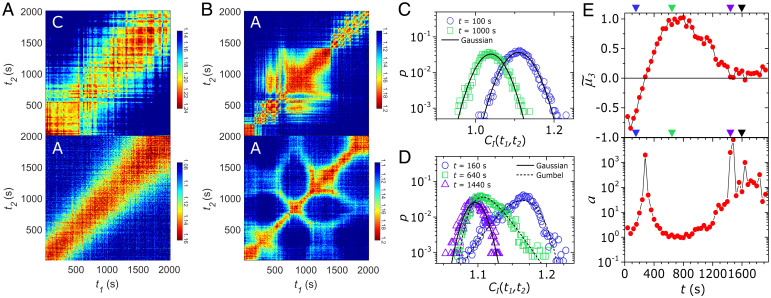
To understand the physics governing these emergent short-time dynamics in the perturbed system, we study the two-time correlations in the system, (39, 44) (Fig. 5 A and B; see SI Appendix, Fig. S9 for larger ensemble of ). The two-time correlation is a matrix representation of the instantaneous correlation of the system at measurement times and , where the delay time is (the correlation decay is thus an average of the instantaneous correlations, obtained by averaging over all pairs of measurement times of an experiment). For the quiescent configurations in the capillary and in the aluminum cell, we observe that the bands are homogeneous across the measurement time (Fig. 5A). These observations indicate that the microscopic relaxation dynamics are temporally homogeneous over experimental time scales and furthermore, show the absence of dynamical processes at short times in the quiescent samples. However, with the introduction of mechanical perturbations, we observe highly intermittent correlation patterns with an abundance of narrowing in the bands, reminiscent of those seen in other disordered solids near the yielding transition (59) (Fig. 5B). These correlation patterns show that perturbation-induced intermittent dynamics give rise to short-time relaxation modes, and thus, a broadening in the observed relaxation spectrum (Fig. 4C).
Fig. 5.
Avalanche statistics of the emergent short-time dynamics in the mechanically perturbed gel. Representative two-time intensity correlation functions of the arrested gel in the (A) quiescent state (Top: capillary; Bottom: aluminum cell) and (B) mechanically perturbed state (aluminum cell) at Å−1 (see SI Appendix, Fig. S9 for a larger ensemble of data). Probability distribution function of the two-time correlation at the indicated delay times at Å−1 for the arrested gel at (C) quiescent states (in capillary) across 15 experiments, and (D) perturbed states across 11 experiments. The instantaneous correlation fluctuations are Gaussian for the quiescent samples at all delay times probed, whereas the perturbed samples exhibit highly non-Gaussian fluctuations at short times, which are captured by a generalized Gumbel distribution (Eq. 5), before reverting to Gaussian statistics near the microscopic relaxation time . The generalized Gumbel distributions shown (dashed lines) are calculated numerically by calculating the skewness parameter directly from the data (by calculating the third moment , where ), rather than fitted. (E) Third moment of the correlation fluctuations and the corresponding skewness parameter as a function of for the perturbed system. Colored triangles indicate delay times corresponding to those shown in D; black triangles indicate the quiescent relaxation time at Å−1 (Fig. 2D).
To quantify the statistical nature of these intermittent dynamics, we compute the ensemble-averaged probability distribution function of the two-time correlation at different delay times. The instantaneous correlations in the quiescent state can be well described by a Gaussian distribution, consistent with the temporally homogeneous nature of the two-time correlation matrices (Fig. 5C). By contrast, the distribution of the instantaneous correlations in the perturbed state are highly non-Gaussian and can be captured by a distribution that is commonly used for scale-free processes, the generalized Gumbel distribution (60, 61):
| [5] |
where and . Here, is the gamma function of ; and are the mean and SD of ; and and in Eq. 5. refer to the direction of the skew (such that − and + produce a heavy tail to the right, and vice versa). The shape parameter in Eq. 5 is given by the skewness or third moment of the distribution . The parameter provides a measure of the distance to criticality in a given system (62, 63), where corresponds to dynamics that follow a Gaussian distribution, and corresponds to scale-free dynamics such as in 1/ noise (64), and in avalanches in foams (53), colloidal gels (54), and glasses (65). The distribution of the instantaneous correlation function in the perturbed system shows a pronounced Gumbel-like behavior at short times (Fig. 5D). This is quantified by evaluating the dependence of the shape parameter on the delay time . At times shorter than of the system (i.e., ), we see that at all times [barring the sudden increase in the skewness at s, which occurs due to a skew direction change about the median timescale of the avalanches (54)]. At long times approaching the mean microscopic relaxation time of the system (i.e., ), increases significantly, indicating that the distribution in the instantaneous correlation function reverts to Gaussian statistics at long times (Fig. 5E). These results indicated that small mechanical perturbations generate avalanche-like fluctuations in the gel that persist at short times, before Gaussian fluctuations emerge at long times approaching the internal stress relaxation time .
Thus, though microscopic internal stress relaxations in quiescent states exhibit strong correlations with the mean timescale of stress relaxation in arrested soft materials, we find that such quiescent dynamics do not explain the breadth of stress relaxation times observed in arrested systems via linear macrorheology. Instead, we find that these broadly distributed stress relaxation events—especially the broadening of the distributions at shorter times (Fig. 4C and SI Appendix, Fig. S6)—are observed at microscopic scales in arrested systems that are perturbed, in our case, through mechanical perturbations. Though these intermittent dynamics arise from a compressive strain that is ostensibly above the yield strain of the system (Fig. 1C), the amount of strain we imposed on the system may not be an important factor in triggering avalanche dynamics in the system. This idea is supported by the fact that the observed stress relaxation responses of the system are self-similar and nonexponential in shape across a wide range of step strains (Fig. 1C), regardless of whether the strain magnitude is above or below the yield strain. At the microscopic level, the broad distribution of relaxation times underlying such stress relaxation behaviors can only be accounted for by non-Gaussian fluctuations arising from intermittent avalanches (Figs. 4 and 5). While avalanche dynamics have been understood to occur in arrested systems strained near or above the yield strain (66, 67), the emergence of such microscopic dynamics in the linear regime can be rationalized by considering that several recent works on dense amorphous materials (e.g., dense glasses) have shown that even small strains well within the linear viscoelastic regime of the material are sufficient for generating intermittent avalanches in the system (56, 57, 68). These findings, therefore, provide qualitative but meaningful insight into the important role played by such intermittent avalanches in the nonexponential macroscopic stress relaxations of arrested soft materials. These insights may have important ramifications for understanding the origins of nonexponential viscoelastic relaxations in a larger variety of soft materials, for instance, biological hydrogels such as cells (10), tissues (9), and mucus (69).
Discussion
Our findings provide a connection between the microscopic relaxation dynamics of arrested systems and the statistical features of the broad distribution of relaxation times in macroscopic mechanical measurements. We find that the quiescent superdiffusive microscopic dynamics of the gel at the cluster scale are governed by internal stress relaxations and show a direct correlation to the mean relaxation time measured via macrorheology. We also find that perturbation-induced intermittent avalanche dynamics are necessary for attaining a broad non-Gaussian distribution of microscopic relaxation times in the system, thus rationalizing the broad distribution of relaxation times observed in macrorheological experiments. A natural extension of the work would be to quantitatively compare the microscopic relaxation modes arising from various rheologically relevant perturbations with macroscopically measured stress relaxation modes. We believe such a feat may be possible through simulations as well as via emerging experimental techniques such as Rheo-XPCS (70), in conjunction with improved temporal resolution in coherent scattering from the planned advancements in synchrotron technology (71). Results from such studies may provide further insight into the quantitative physics connecting dynamic arrest, marginal stability, and linear viscoelasticity in arrested and disordered materials.
Materials and Methods
Materials Synthesis.
Nitrocatechol-functionalized four-arm PEG (10 kDa), catechol-functionalized one-arm PEG (2 kDa), and Fe3O4 NPs (7-nm diameter) (Fig. 1A) are synthesized following the same protocol in ref. 30. The polymer-particle gel is made by mixing 10.0 weight of nitrocatechol-functionalized four-arm PEG and 1.50 volume of NP stabilized by catechol-functionalized one-arm PEG in an aqueous solution with pH adjusted to 2 to induce monofunctional binding between nitrocatechol and iron. All materials for rheological measurements are gelled in situ; the mixture is placed beneath a parallel plate geometry and sealed in mineral oil; the Peltier temperature is raised to ; and the system is left to gel for at least 24 h before rheological measurement. Materials for XPCS measurements are made by placing the reagent mixture either inside a Kapton capillary which is then sealed by Torr, or inside a plastic cap which is then wrapped and sealed with aluminum foil. The reagent mixture is then gelled in an oven at for at least 24 h. The gel sample inside the capillary is used to study in situ conditions, and the gel sample inside the plastic cap is carefully extracted from the plastic cap and placed inside an aluminum cell to study ex situ conditions (see SI Appendix, Fig. S3 for holder details). Detailed characterization of the gel system can be found in ref. 30.
Rheology.
All measurements are conducted using Anton-Paar’s MCR-302 stress-controlled rheometer, with a 10-mm parallel plate geometry and a gap size < 1 mm. All measurements are done on hydrogels which are sealed with mineral oil to minimize dehydration, and conducted with conditions as described in Fig. 1 and SI Appendix, Fig. S2.
X-ray Photon Correlation Spectroscopy.
All measurements are conducted at the XPCS beamline 8-ID-I at the Advanced Photon Source at Argonne National Laboratory. Monochromatic X-rays at an energy of 7.35 keV are used, with a beam size of 15 µm 15 µm, and with a nominal flux of 109 photons/s which is then attenuated to minimize radiation damage. A Large-Area Medipix-Based Detector Array pixel array detector with a pixel size of 55 µm and array size of 516 1,556 is used. The measurements are checked for radiation damage by controlling the dose using filters, and the beam attenuation factor (which attenuates beam strength by a factor of 2n) is increased until no sign of radiation damage was visible (SI Appendix, Fig. S10).
Ultra Small Angle X-ray Scattering.
All measurements are conducted at the USAXS beamline 9-ID at the Advanced Photon Source at Argonne National Laboratory. Samples are mounted in cells with a sample thickness of ∼1 mm and with 3M Scotch tape on either side. Due to variations in the thickness of the actual samples, only relative intensities are reported here. The X-ray energy is 21 keV (wavelength = 0.5905 Å−1), and the beam size is 0.6 0.6 mm for USAXS and 0.1 mm 0.6 mm for small angle X-ray scattering (SAXS). Data collection time for the experiments are set to 90 s for USAXS and 15 s for SAXS; the measured data are then subtracted from those obtained from a blank cell covered with the adhesive tape, reduced, and then merged together using software packages (Indra, Nika, and Irena) provided by the beamline (72, 73). Slit smearing inherent to the USAXS instrument is removed using de-smearing routines in Irena to generate pinhole equivalent data for analysis.
Relaxation Spectrum Analysis.
The continuous relaxation spectra are obtained by making appropriate modifications to the MATLAB implementation (74) of the Tikhonov nonlinear regularization method (58). Briefly, this method aims to minimize the cost function:
| [6] |
where are the experimental decay data, are the predicted decay data based on the continuous relaxation spectrum, and is the regularization parameter. In this expression, the first term denotes the mean-square error and the second term is the regularized smoothing parameter that penalizes curvature and overfitting. In a typical analysis, is optimized for the mean-square error and the smoothness through the L-curve method. For the XPCS data , the best agreement is found by minimizing (and thus minimizing the mean-square error), which results in a continuous relaxation spectrum with strongly peaked relaxation modes (SI Appendix, Fig. S8). These peaks can be well approximated as discrete relaxation spectra and are presented this way in Fig. 4C.
Supplementary Material
Acknowledgments
We acknowledge funding from the NSF (Grants CBET-1605943, CBET-1605699, CBET-1804721, DMR-1419807, and DMR-2026842), the US Army Research Office (through the Institute for Soldier Nanotechnologies under Contract No. W911NF-13-D-0001), and the US Department of Energy (through the Argonne National Laboratory under Contract No. DE-AC02-06CH11357). J.S. thanks H. Le Roy, M. Lenz, T. Divoux, J. F. Douglas, J. H. Cho, I. Bischofberger, and J. Swan for helpful discussions.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2201566119/-/DCSupplemental.
Data Availability
All study data are included in the article and/or supporting information.
References
- 1.Shang B., Rottler J., Guan P., Barrat J.-L., Local versus global stretched mechanical response in a supercooled liquid near the glass transition. Phys. Rev. Lett. 122, 105501 (2019). [DOI] [PubMed] [Google Scholar]
- 2.Gopal A. D., Durian D. J., Relaxing in foam. Phys. Rev. Lett. 91, 188303 (2003). [DOI] [PubMed] [Google Scholar]
- 3.Hwang H. J., Riggleman R. A., Crocker J. C., Understanding soft glassy materials using an energy landscape approach. Nat. Mater. 15, 1031–1036 (2016). [DOI] [PubMed] [Google Scholar]
- 4.Ramos L., Cipelletti L., Ultraslow dynamics and stress relaxation in the aging of a soft glassy system. Phys. Rev. Lett. 87, 245503 (2001). [DOI] [PubMed] [Google Scholar]
- 5.Cates M., Candau S., Statics and dynamics of worm-like surfactant micelles. J. Phys. Condens. Matter 2, 6869 (1990). [Google Scholar]
- 6.Brujić J., et al. , Granular dynamics in compaction and stress relaxation. Phys. Rev. Lett. 95, 128001 (2005). [DOI] [PubMed] [Google Scholar]
- 7.Holland C., Terry A. E., Porter D., Vollrath F., Comparing the rheology of native spider and silkworm spinning dope. Nat. Mater. 5, 870–874 (2006). [DOI] [PubMed] [Google Scholar]
- 8.Mulla Y., MacKintosh F. C., Koenderink G. H., Origin of slow stress relaxation in the cytoskeleton. Phys. Rev. Lett. 122, 218102 (2019). [DOI] [PubMed] [Google Scholar]
- 9.Chaudhuri O., et al. , Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat. Mater. 15, 326–334 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bursac P., et al. , Cytoskeletal remodelling and slow dynamics in the living cell. Nat. Mater. 4, 557–561 (2005). [DOI] [PubMed] [Google Scholar]
- 11.Lieleg O., Kayser J., Brambilla G., Cipelletti L., Bausch A. R., Slow dynamics and internal stress relaxation in bundled cytoskeletal networks. Nat. Mater. 10, 236–242 (2011). [DOI] [PubMed] [Google Scholar]
- 12.Ballesta P., Duri A., Cipelletti L., Unexpected drop of dynamical heterogeneities in colloidal suspensions approaching the jamming transition. Nat. Phys. 4, 550–554 (2008). [Google Scholar]
- 13.Douglas J. F., Hubbard J. B., Semiempirical theory of relaxation: Concentrated polymer solution dynamics. Macromolecules 24, 3163–3177 (1991). [Google Scholar]
- 14.Curro J. G., Pincus P., A theoretical basis for viscoelastic relaxation of elastomers in the long-time limit. Macromolecules 16, 559–562 (1983). [Google Scholar]
- 15.Sollich P., Lequeux F., Hébraud P., Cates M. E., Rheology of soft glassy materials. Phys. Rev. Lett. 78, 2020 (1997). [Google Scholar]
- 16.Fielding S. M., Elastoviscoplastic rheology and aging in a simplified soft glassy constitutive model. J. Rheol. 64, 723–738 (2020). [Google Scholar]
- 17.Liu A. J., Ramaswamy S., Mason T. G., Gang H., Weitz D. A., Anomalous viscous loss in emulsions. Phys. Rev. Lett. 76, 3017–3020 (1996). [DOI] [PubMed] [Google Scholar]
- 18.Muthukumar M., Screening effect on viscoelasticity near the gel point. Macromolecules 22, 4656–4658 (1989). [Google Scholar]
- 19.Bouchbinder E., Langer J. S., Linear response theory for hard and soft glassy materials. Phys. Rev. Lett. 106, 148301 (2011). [DOI] [PubMed] [Google Scholar]
- 20.Semenov A., Charlot A., Auzély-Velty R., Rinaudo M., Rheological properties of binary associating polymers. Rheol. Acta 46, 541–568 (2007). [Google Scholar]
- 21.Witten T., Leibler L., Pincus P., Stress relaxation in the lamellar copolymer mesophase. Macromolecules 23, 824–829 (1990). [Google Scholar]
- 22.Duri A., Cipelletti L., Length scale dependence of dynamical heterogeneity in a colloidal fractal gel. EPL 76, 972 (2006). [Google Scholar]
- 23.Cipelletti L., et al. , Universal non-diffusive slow dynamics in aging soft matter. Faraday Discuss. 123, 237–251 (2003). [DOI] [PubMed] [Google Scholar]
- 24.Ferrero E. E., Martens K., Barrat J.-L., Relaxation in yield stress systems through elastically interacting activated events. Phys. Rev. Lett. 113, 248301 (2014). [DOI] [PubMed] [Google Scholar]
- 25.Bouzid M., Colombo J., Barbosa L. V., Del Gado E., Elastically driven intermittent microscopic dynamics in soft solids. Nat. Commun. 8, 15846 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gnan N., Zaccarelli E., The microscopic role of deformation in the dynamics of soft colloids. Nat. Phys. 15, 683–688 (2019). [Google Scholar]
- 27.Srivastava S., et al. , Hyperdiffusive dynamics in Newtonian nanoparticle fluids. ACS Macro Lett. 4, 1149–1153 (2015). [DOI] [PubMed] [Google Scholar]
- 28.Bouchaud J.-P., Pitard E., Anomalous dynamical light scattering in soft glassy gels. Eur. Phys. J. E 6, 231–236 (2001). [DOI] [PubMed] [Google Scholar]
- 29.Amstad E., Gillich T., Bilecka I., Textor M., Reimhult E., Ultrastable iron oxide nanoparticle colloidal suspensions using dispersants with catechol-derived anchor groups. Nano Lett. 9, 4042–4048 (2009). [DOI] [PubMed] [Google Scholar]
- 30.Song J., et al. , Programmable anisotropy and percolation in supramolecular patchy particle gels. ACS Nano 14, 17018–17027 (2020). [DOI] [PubMed] [Google Scholar]
- 31.Lindquist B. A., Jadrich R. B., Milliron D. J., Truskett T. M., On the formation of equilibrium gels via a macroscopic bond limitation. J. Chem. Phys. 145, 074906 (2016). [DOI] [PubMed] [Google Scholar]
- 32.Zaccarelli E., Colloidal gels: Equilibrium and non-equilibrium routes. J. Phys. Condens. Matter 19, 323101 (2007). [Google Scholar]
- 33.Dudukovic N. A., Zukoski C. F., Nanoscale dynamics and aging of fibrous peptide-based gels. J. Chem. Phys. 141, 164905 (2014). [DOI] [PubMed] [Google Scholar]
- 34.Pastore R., Siviello C., Greco F., Larobina D., Anomalous aging and stress relaxation in macromolecular physical gels: The case of strontium alginate. Macromolecules 53, 649–657 (2020). [Google Scholar]
- 35.Lindsey C., Patterson G., Detailed comparison of the Williams–Watts and Cole–Davidson functions. J. Chem. Phys. 73, 3348–3357 (1980). [Google Scholar]
- 36.Broedersz C. P., et al. , Cross-link-governed dynamics of biopolymer networks. Phys. Rev. Lett. 105, 238101 (2010). [DOI] [PubMed] [Google Scholar]
- 37.Chen Q., Huang C., Weiss R., Colby R. H., Viscoelasticity of reversible gelation for ionomers. Macromolecules 48, 1221–1230 (2015). [Google Scholar]
- 38.Chen Q., Liang S., Shiau H.-S., Colby R. H., Linear viscoelastic and dielectric properties of phosphonium siloxane ionomers. ACS Macro Lett. 2, 970–974 (2013). [DOI] [PubMed] [Google Scholar]
- 39.Leheny R. L., XPCS: Nanoscale motion and rheology. Curr. Opin. Colloid Interface Sci. 17, 3–12 (2012). [Google Scholar]
- 40.Matsunaga T., Sakai T., Akagi Y., Chung U.-i., Shibayama M., SANS and SLS studies on tetra-arm PEG gels in as-prepared and swollen states. Macromolecules 42, 6245–6252 (2009). [Google Scholar]
- 41.Rishi K., et al. , Impact of an emergent hierarchical filler network on nanocomposite dynamics. Macromolecules 51, 7893–7904 (2018). [Google Scholar]
- 42.Beaucage G., Approximations leading to a unified exponential/power-law approach to small-angle scattering. J. Appl. Cryst. 28, 717–728 (1995). [Google Scholar]
- 43.Dallari F., et al. , Microscopic pathways for stress relaxation in repulsive colloidal glasses. Sci. Adv. 6, eaaz2982 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Madsen A., Leheny R. L., Guo H., Sprung M., Czakkel O., Beyond simple exponential correlation functions and equilibrium dynamics in X-ray photon correlation spectroscopy. New J. Phys. 12, 055001 (2010). [Google Scholar]
- 45.Ruta B., et al. , Atomic-scale relaxation dynamics and aging in a metallic glass probed by x-ray photon correlation spectroscopy. Phys. Rev. Lett. 109, 165701 (2012). [DOI] [PubMed] [Google Scholar]
- 46.Guo H., et al. , Entanglement-controlled subdiffusion of nanoparticles within concentrated polymer solutions. Phys. Rev. Lett. 109, 055901 (2012). [DOI] [PubMed] [Google Scholar]
- 47.Whitaker K. A., et al. , Colloidal gel elasticity arises from the packing of locally glassy clusters. Nat. Commun. 10, 2237 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cho J. H., Cerbino R., Bischofberger I., Emergence of multiscale dynamics in colloidal gels. Phys. Rev. Lett. 124, 088005 (2020). [DOI] [PubMed] [Google Scholar]
- 49.Krall A., Weitz D., Internal dynamics and elasticity of fractal colloidal gels. Phys. Rev. Lett. 80, 778 (1998). [Google Scholar]
- 50.Cipelletti L., Manley S., Ball R. C., Weitz D. A., Universal aging features in the restructuring of fractal colloidal gels. Phys. Rev. Lett. 84, 2275–2278 (2000). [DOI] [PubMed] [Google Scholar]
- 51.Nicolas A., Ferrero E. E., Martens K., Barrat J.-L., Deformation and flow of amorphous solids: Insights from elastoplastic models. Rev. Mod. Phys. 90, 045006 (2018). [Google Scholar]
- 52.Schall P., Weitz D. A., Spaepen F., Structural rearrangements that govern flow in colloidal glasses. Science 318, 1895–1899 (2007). [DOI] [PubMed] [Google Scholar]
- 53.Duri A., Bissig H., Trappe V., Cipelletti L., Time-resolved-correlation measurements of temporally heterogeneous dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72, 051401 (2005). [DOI] [PubMed] [Google Scholar]
- 54.Filiberti Z., Piazza R., Buzzaccaro S., Multiscale relaxation in aging colloidal gels: From localized plastic events to system-spanning quakes. Phys. Rev. E 100, 042607 (2019). [DOI] [PubMed] [Google Scholar]
- 55.Evenson Z., et al. , X-ray photon correlation spectroscopy reveals intermittent aging dynamics in a metallic glass. Phys. Rev. Lett. 115, 175701 (2015). [DOI] [PubMed] [Google Scholar]
- 56.Lin J., Wyart M., Mean-field description of plastic flow in amorphous solids. Phys. Rev. X 6, 011005 (2016). [Google Scholar]
- 57.Shang B., Guan P., Barrat J.-L., Elastic avalanches reveal marginal behavior in amorphous solids. Proc. Natl. Acad. Sci. U.S.A. 117, 86–92 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Honerkamp J., Weese J., A nonlinear regularization method for the calculation of relaxation spectra. Rheol. Acta 32, 65–73 (1993). [Google Scholar]
- 59.Das A., Derlet P. M., Liu C., Dufresne E. M., Maaß R., Stress breaks universal aging behavior in a metallic glass. Nat. Commun. 10, 5006 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Planet R., Santucci S., Ortín J., Avalanches and non-Gaussian fluctuations of the global velocity of imbibition fronts. Phys. Rev. Lett. 102, 094502 (2009). [DOI] [PubMed] [Google Scholar]
- 61.Barucci A., et al. , Universal fluctuations in tropospheric radar measurements. EPL 89, 20006 (2010). [Google Scholar]
- 62.Joubaud S., Petrosyan A., Ciliberto S., Garnier N. B., Experimental evidence of non-Gaussian fluctuations near a critical point. Phys. Rev. Lett. 100, 180601 (2008). [DOI] [PubMed] [Google Scholar]
- 63.Bertin E., Global fluctuations and Gumbel statistics. Phys. Rev. Lett. 95, 170601 (2005). [DOI] [PubMed] [Google Scholar]
- 64.Antal T., Droz M., Györgyi G., Rácz Z., 1/f Noise and extreme value statistics. Phys. Rev. Lett. 87, 240601 (2001). [DOI] [PubMed] [Google Scholar]
- 65.Chamon C., Charbonneau P., Cugliandolo L. F., Reichman D. R., Sellitto M., Out-of-equilibrium dynamical fluctuations in glassy systems. J. Chem. Phys. 121, 10120–10137 (2004). [DOI] [PubMed] [Google Scholar]
- 66.Lin J., Lerner E., Rosso A., Wyart M., Scaling description of the yielding transition in soft amorphous solids at zero temperature. Proc. Natl. Acad. Sci. U.S.A. 111, 14382–14387 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Budrikis Z., Castellanos D. F., Sandfeld S., Zaiser M., Zapperi S., Universal features of amorphous plasticity. Nat. Commun. 8, 15928 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Chen Y., Rogers S. A., Narayanan S., Harden J. L., Leheny R. L., Microscopic dynamics of stress relaxation in a nanocolloidal soft glass. Phys. Rev. Mater. 4, 035602 (2020). [Google Scholar]
- 69.Wagner C. E., Turner B. S., Rubinstein M., McKinley G. H., Ribbeck K., A rheological study of the association and dynamics of MUC5AC gels. Biomacromolecules 18, 3654–3664 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Leheny R. L., Rogers M. C., Chen K., Narayanan S., Harden J. L., Rheo-XPCS. Curr. Opin. Colloid Interface Sci. 20, 261–271 (2015). [Google Scholar]
- 71.Borland M., et al., Proceedings of the 9th International Particle Accelerator Conference (2018), pp. 2872–2877.
- 72.Ilavsky J., Nika: Software for two-dimensional data reduction. J. Appl. Cryst. 45, 324–328 (2012). [Google Scholar]
- 73.Ilavsky J., Jemian P. R., Irena: Tool suite for modeling and analysis of small-angle scattering. J. Appl. Cryst. 42, 347–353 (2009). [Google Scholar]
- 74.Takeh A., Shanbhag S., A computer program to extract the continuous and discrete relaxation spectra from dynamic viscoelastic measurements. Appl. Rheol. 23, 24628 (2013). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or supporting information.