Motor learning without movement

Significance

Our brains control aspects of our movements without conscious awareness, allowing many of us to effortlessly pick up a glass of water or wave hello. Here, we demonstrate that this implicit motor system can learn to refine movements that we plan but ultimately decide not to perform. Participants planned to reach to a target but sometimes withheld these reaches while an animation simulated missing the target. Afterward, participants unknowingly reached opposite the direction of the apparent mistake, indicating that the implicit motor system had learned from the animated error. These findings indicate that movement is not strictly necessary for motor adaptation, and we can learn to update our actions without physically performing them.

Abstract

Prediction errors guide many forms of learning, providing teaching signals that help us improve our performance. Implicit motor adaptation, for instance, is thought to be driven by sensory prediction errors (SPEs), which occur when the expected and observed consequences of a movement differ. Traditionally, SPE computation is thought to require movement execution. However, recent work suggesting that the brain can generate sensory predictions based on motor imagery or planning alone calls this assumption into question. Here, by measuring implicit motor adaptation during a visuomotor task, we tested whether motor planning and well-timed sensory feedback are sufficient for adaptation. Human participants were cued to reach to a target and were, on a subset of trials, rapidly cued to withhold these movements. Errors displayed both on trials with and without movements induced single-trial adaptation. Learning following trials without movements persisted even when movement trials had never been paired with errors and when the direction of movement and sensory feedback trajectories were decoupled. These observations indicate that the brain can compute errors that drive implicit adaptation without generating overt movements, leading to the adaptation of motor commands that are not overtly produced.

Prediction errors help to optimize behavior by driving learning processes that correct for our mistakes. Accordingly, their computation is thought to be a fundamental feature of the nervous system (1–4). Specific types of prediction errors are associated with dissociable learning processes, with sensory prediction errors (SPEs) serving as putative teachers of the implicit motor system. SPEs are thought to trigger the adaptation and refinement of movements when the predicted and expected sensory outcomes of a movement differ (5–8). Traditional formulations assume that movement execution is critical for SPE computation (9, 10). However, it has been proposed that the forward model estimates the consequences of movements before the relevant sensory feedback (FB) reaches the brain, thereby overcoming intrinsic physiological delays in sensory signal conduction and allowing for the rapid motor control required by most vertebrates (11). Following this line of thought to one logical extreme, it may be that motor execution is not necessary for the generation of predictions by a forward model.

Recent work offers indirect support for the claim that the brain predicts the sensory consequences of movements before they can be performed, even when the agent does not have a clear intention to move (12–16). Considering that sensorimotor prediction may not in theory require movement, it may be that a prediction can be combined with incoming sense data to support SPE computation without any actual motor execution. In other words, it may be that SPEs can be effectively computed based upon only two events: the generation of a sensory prediction during the commission of a motor command and the observation of subsequent sensory FB (Fig. 1A). On the other hand, it may be that movement execution produces the actionable prediction signal required for SPE computation (e.g., efference copy during movement). In this report, we investigate these possibilities.

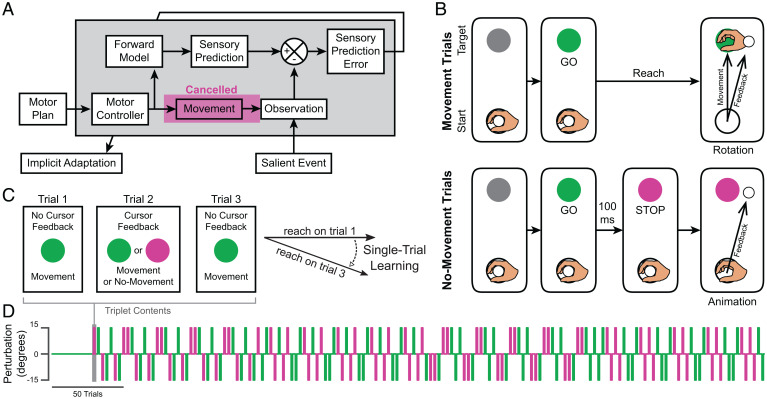
Fig. 1.

Schematics showing the proposed learning framework and task design. (A) Schematic showing how the forward model may support implicit motor adaptation in the presence of sensory FB not causally related to self-generated movement. (B) Events on trials with visual FB. The robotic apparatus brought the participant’s hand to the starting location to initiate a trial. On movement trials (Top), the target turned green (GO), cueing participants to reach through the target. On trials with visual FB, participants observed a white FB cursor move along a rotated trajectory (Rotation). On no-movement trials (Bottom), the target turned magenta 100 ms after turning green, cueing participants to withhold movement (STOP). After a delay, an animation played showing the FB cursor moving 15° off-target (Animation). The hand is shown in the figure for illustrative purposes but was not visible during the experiment. (C) How STL was computed using a triplet paradigm. Triplets were composed of two go trials without visual FB flanking either a movement or a no-movement trial with visual FB. STL was measured as the difference between reach angles on the flanking trials. (D) Pseudorandomized order in which trials were presented for an example participant. Color indicates movement condition (movement, green; no-movement, magenta).

Prior work has illustrated that higher-level cognitive processes support visuomotor learning without movement. For instance, motor adaptation can occur when an observer witnesses another’s motor error (17–19). Motor adaptation in this case might be driven by SPEs, by other types of learning processes and error formats (e.g., reward prediction errors), or perhaps by a combination of multiple sources of error. Here, we isolated implicit motor adaptation to specifically test whether it requires movement execution.

To that end, we measured trial-by-trial implicit adaptation during a visuomotor task in which human participants saw visual FB while performing—or withholding—hand and arm movements, using a modified stop-signal paradigm. To isolate implicit adaptation, we employed a recently developed approach that requires participants to move directly through presented targets and disregard visual FB (20–25). We predicted that single-trial motor adaptation would occur following both typical movement trials that generated sensory error and trials where movements were withheld but simulated sensory errors were observed. If confirmed, this result would imply that the brain can compute SPEs in the absence of movement and can thus drive the adaptation of planned movements that were never performed.

Results

Experiment 1: Simulated and Typical Visuomotor Rotations Cause Motor Adaptation.

In experiment 1, we measured implicit motor adaptation in humans (n = 20) performing or withholding straight reaches during a visuomotor adaptation task (Fig. 1B). Vision of the hand and arm was occluded by a mirror that reflected visual FB from a horizontally mounted monitor. A white cursor provided FB about participants’ hand positions as they reached from a starting location to a displayed target. After a brief acclimation period, trials were organized into triplets, such that each trial with cursor FB was flanked by trials without cursor FB. This allowed for a reliable measurement of single-trial learning (STL) in response to FB, quantified as the difference between the direction of hand movement (hand angle) on the first and third trials of each triplet (Fig. 1C). Trials with cursor FB were either movement trials during which a go signal prompted movement or no-movement trials during which a stop signal immediately followed the go signal to indicate that movements should be withheld. On movement trials, FB involved a visuomotor error (±15° rotation added to the visual cursor path; + = counterclockwise [CCW]; Fig. 1B, Right and Fig. 2A, Left and Center). On no-movement trials, sensory FB involved a simulation of the cursor’s path, using timing variables based on ongoing measurements of participant behavior (see Methods). Both flanking trials of each triplet were go trials and thus required movements. The direction of the error (clockwise [CW] or CCW) was pseudorandomly varied across triplets to maintain overall adaptation near zero throughout the session (Fig. 1D). This straightforward design allowed us to test the hypothesis that motor adaptation does not require movement and sensory FB to be causally linked (Fig. 1A).

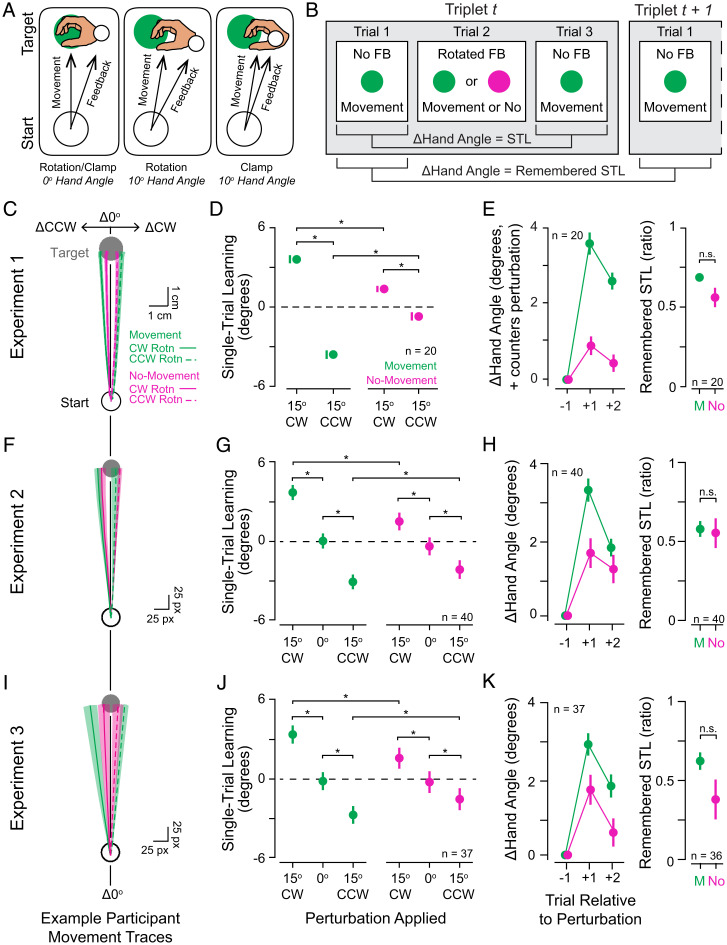
Fig. 2.

Effects of typical and simulated errors during a visuomotor reach adaptation task. (A and B) Schematics illustrating the differences between rotation and error-clamp perturbations (A) and how STL and remembered STL measurements were computed (B). (C) Example subject’s mean ± SEM reach paths across triplets during experiment 1 (green, triplets with rotations on movement trials; magenta, triplets with rotations on no-movement trials; solid lines, perturbation was CW; dashed lines, perturbation was CCW). (D) Mean ± SEM. STL across movement (green) and no-movement (magenta) triplets for all participants (n = 20). Positive changes in hand angle are CCW. (E, Left) Group mean ± SEM Δhand angle values after exposure to movement (green) and no-movement (magenta) trial perturbations. Positive Δ values indicate that the change in hand angle proceeded opposite the direction of the perturbation (i.e., the direction that would counter the error). (E, Right) Group mean of participants’ ratios of remembered STL to initial STL during movement (M) and no-movement (No) trials. (F–H) As in C–E but showing data from experiment 2, where data were collected online (n = 40). See SI Appendix, Table S1 for details on comparisons in G and SI Appendix, Fig. S2A for the participantwise summary statistics of the raw data that was used to build the LMM for this panel. (I–K) As in C–E but showing data from experiment 3, where data were collected online and perturbations were applied in an error-clamp regime instead of a rotational regime (n = 37). See SI Appendix, Table S2 for details on comparisons in J and SI Appendix, Fig. S2B for the participantwise summary statistics of the raw data that was used to build the LMM for this panel. Remembered STL on no-movement trials could not be computed for one participant, so n = 36 in K (Right). Statistical significance (* = P_adj < 0.05; not significant [n.s.] = P_adj ≥ 0.05) is indicated. Δ, change in. When error bars were obscured by the datapoints, they were shown to the left of the corresponding datapoint.

Consistent with our predictions, rotated cursor paths (Fig. 2A, Left and Center) on movement and no-movement trials both caused subsequent hand trajectories to shift opposite the direction of the rotation (Fig. 2B–D), with a two-way repeated-measures ANOVA showing significant main effects of the direction of the rotation applied (CW vs. CCW: F(1, 19) = 98.62, P = 5.89 × 10⁻⁹, ${\eta }_G^2$ = 0.76). While there was no main effect of withholding movement (F(1, 19) = 1.79, P = 0.20), we observed an interaction between rotation and movement conditions (F(1, 19) = 137.32, P = 3.87 × 10⁻¹⁰, ${\eta }_G^2$ = 0.49). Post hoc pairwise comparisons showed that STL was sensitive to rotation direction during both movement triplets (paired t test: t(19) = −12.92, P_adj = 2.96 × 10⁻¹⁰, Cohen’s d = 5.12) and no-movement triplets (t(19) = −4.39, P_adj = 3.14 × 10⁻⁴, Cohen’s d = 1.63) and that STL magnitude was greater across movement than no-movement triplets (paired-samples signed-rank test, CW: V = 210, p_adj = 2.55 × 10⁻⁶, r = 0.88; CCW: t(19) = −9.43, P_adj = 2.70 × 10⁻⁸, Cohen’s d = 2.02). Thus, error-appropriate motor learning occurred during both movement and no-movement triplets, although adaptation was weaker when participants withheld their movements. Notably, however, the overall amplitude of adaptation observed both with and without movement was within the range of implicit learning rates measured in previous studies (SI Appendix, Fig. S1).

To address whether observed STL measured genuine implicit learning, we checked whether adaptation persisted beyond the trial after an error was experienced. We examined participants’ hand angles on the second trial after a perturbation relative to the preperturbation baseline trial (i.e., hand angle on trial 1 of triplet t + 1 relative to hand angle on trial 1 of triplet t, remembered STL; Fig. 2B). As visual FB was withheld on both of these trials, this approach provided a pure measure of persistent memory in the absence of error-driven changes in performance. Hand angle remained adapted in the direction opposite the rotation on trials with nonzero perturbations regardless of movement condition (Fig. 2E, Left), suggesting that genuine implicit learning was observed in response to errors under both movement conditions. Closer examination of the relative ratio of remembered STL to initial STL revealed a marginally significant difference between the relative amount of retention observed between the movement conditions (t(19) = 2.07, P_adj = 0.053; Fig. 2E, Right), leaving it unclear whether or not there was a difference in the amount of retention between the movement conditions. Nonetheless, relative retention ratios differed significantly from zero after both movement triplets (t(19) = 26.20, P_adj = 6.71 × 10⁻¹⁶, Cohen’s d = 5.86) and no-movement triplets (t(19) = 9.20, P_adj = 2.99 × 10⁻⁸, Cohen’s d = 2.06; Fig. 2E, Right), indicating that the adaptation memory was retained regardless of movement condition.

Experiment 2: Implicit Motor Adaptation Proceeds after Simulated Errors in an Online Visuomotor Task.

To address whether the above observations are reproducible and generalize across experimental contexts, we tested whether simulated errors in no-movement trials also induced motor adaptation in an online version of the task. Participants (n = 40) made hand movements using their computer mouse or trackpad to move a cursor toward a target. As in experiment 1, trials were presented in triplets, allowing us to measure STL in response to cursor FB presented during movement and no-movement trials at the center of each triplet (Fig. 1B–D). For this online study, triplets with 0° perturbations/simulated errors were also included to provide an estimate of baseline changes in hand angle in the event that participants exhibited strong movement biases in the online platform.

Because this dataset did not satisfy the assumptions of a two-way repeated-measures ANOVA, we used a linear mixed model (LMM) to assess whether STL occurred during both movement and no-movement triplets. The LMM revealed main effects of rotated cursor FB (F(2, 2,223) = 136.46, P = 1.26 × 10⁻⁵⁶, partial R² = 0.11) and movement condition (F(1, 2,248) = 4.74, P = 0.03, partial R² = 0.002), as well as an interaction (F(2, 2,229) = 12.40, P = 4.41 × 10⁻⁶, partial R² = 0.01). Post hoc pairwise comparisons revealed statistically significant STL on both movement triplets (0° vs. 15° CW: t(2,227) = 9.14, P_adj = 6.39 × 10⁻¹⁹, Cohen’s d = 0.61; 0° vs. 15° CCW: t(2,220) = 7.81, P_adj = 2.61 × 10⁻¹⁴, Cohen’s d = 0.52) and no-movement triplets (0° vs. 15° CW: t(2,225) = 3.92, P_adj = 1.39 × 10⁻⁴, Cohen’s d = 0.31; 0° vs. 15° CCW: t(2,229) = 3.56, P_adj = 4.84 × 10⁻⁴, Cohen’s d = 0.29; Fig. 2F and G). These results indicate that adaptation occurred in both movement and no-movement triplets during this study. Adaptation amplitudes observed both with and without movement were within the range of implicit learning rates measured in previous studies (SI Appendix, Fig. S1), although adaptation was significantly greater in movement than no-movement triplets for CW rotations (t(2,238) = 4.98, P_adj = 1.26 × 10⁻⁶, Cohen’s d = 0.37) and CCW rotations (t(2,239) = −2.06, P_adj = 0.04, Cohen’s d = −0.15).

Further echoing the results of experiment 1, STL on both movement and no-movement trials was retained beyond the triplet in which an error occurred (Fig. 2H). Remembered STL was statistically significantly greater than zero for both movement triplets (one-sample signed-rank test: V = 819, P_adj = 1.09 × 10⁻¹¹, r = 0.87) and no-movement triplets (V = 769, P_adj = 9.69 × 10⁻⁸, r = 0.76), but remembered STL did not significantly differ between movement conditions (paired-samples signed-rank test: V = 441, P_adj = 0.68).

Thus, experiment 2 successfully replicated the findings of experiment 1: visual error FB on no-movement trials was sufficient for STL, although adaptation was of greater amplitude with vs. without movement. These data provide further support for the claim that movements that are not performed can undergo implicit motor adaptation, and they extend our findings to a task with different movement demands (e.g., finger or wrist movements vs. full, center-out arm reaches).

Experiment 3: Motor Adaptation during No-Movement Triplets Does Not Depend on Participants’ Control over Cursor Trajectory during Movement Trials.

We note that rotated visual FB on movement trials was sensitive to people’s actual reaching directions because the rotation was simply added to the measured reach direction, as is typical in visuomotor rotation tasks. It is possible that these directional contingencies affected participants’ responses to error, potentially encouraging them to attempt to deliberately control the cursor’s position via an explicit reaiming process (26). To rule this out, we recruited a new group of participants (n = 37) to perform a variant of the task where the visual cursor moved in a fixed path [error-clamped FB (20); Fig. 2A, Left and Right] in one of three directions (0° or 15° CW/CCW) on the trials with FB.

Replicating and extending the findings reported above, participants assigned to the error-clamp condition exhibited STL after movement and no-movement trials (Fig. 2I and J). An LMM detected statistically significant main effects of error-clamped cursor FB (F(2, 1,829) = 79.46, P = 8.12 × 10⁻³⁴, partial R² = 0.08) and an interaction between error clamp and movement condition (F(2, 1,832) = 8.45, P = 0.0002, partial R² = 0.0003), although there was no main effect of movement condition (F(1, 1,844) = 0.60, P = 0.44). Post hoc comparisons revealed significant STL in response to nonzero error-clamped FB on both movement trials (0° vs. 15° CW: t(1,827) = 7.55, P_adj = 3.08 × 10⁻¹³, Cohen’s d = 0.56; 0° vs. 15° CCW: t(1,828) = 5.57, P_adj = 8.84 × 10⁻⁸, Cohen’s d = 0.41) and no-movement trials (0° vs. 15° CW: t(1,830) = 3.21, P_adj = 0.002, Cohen’s d = 0.29; 0° vs. 15° CCW: t(1,832) = 2.25, P_adj = 0.03, Cohen’s d = 0.22; Fig. 2J). Additionally, adaptation in the presence of a 15° error clamp was significantly greater on movement trials than no-movement trials for CW clamps (t(1,846) = 3.49, P_adj = 0.0009, Cohen’s d = 0.29) and CCW clamps (t(1,846) = 2.29, P_adj = 0.03, Cohen’s d = 0.19)—despite being in the range of previously observed implicit adaptation learning rates under both movement conditions (SI Appendix, Fig. S1)—following the same pattern of results observed in experiments 1 and 2. Remembered STL was significantly greater than zero after both movement triplets (green; one-sample t test: t(36) = 11.31, P_adj = 6.23 × 10⁻¹³, Cohen’s d = 1.86) and no-movement triplets (magenta; one-sample signed-rank test: V = 579, P_adj = 5.96 × 10⁻⁵, r = 0.64) but did not exhibit statistically significant differences between movement conditions (paired t test: t(35) = 1.71, P_adj = 0.09; Fig. 2K). This replication indicates that the learning effect observed on no-movement trials was not dependent on the type of cursor perturbation applied during movement trials, strengthening the claim that motor adaptation does not require movement.

Experiments 4 and 5: Adaptation during No-Movement Triplets Does Not Depend on Within-Session Adaptation during Movement Triplets.

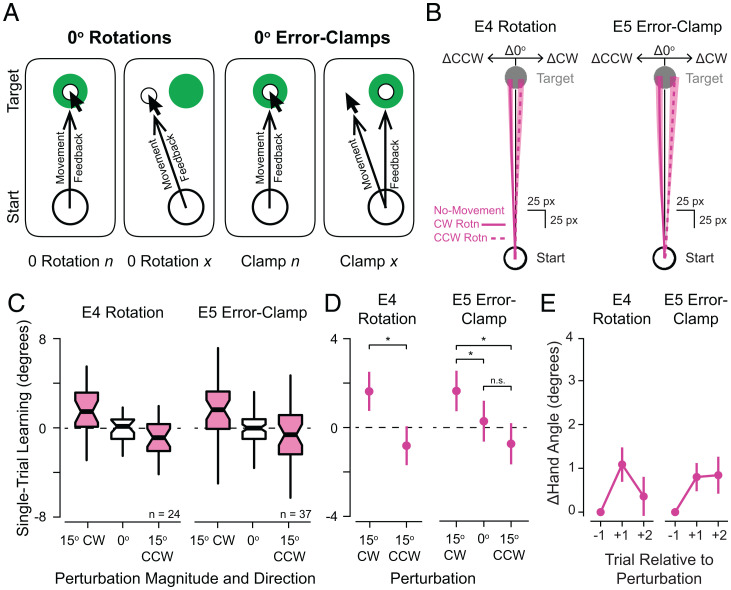
In two further experiments, we asked if adaptation to errors in the no-movement condition was contingent on sharing a context with the movement condition. In other words, if learning in the no-movement condition only occurs when there are neighboring trials in the movement condition producing typical SPEs, it is possible that adaptive responses observed in the no-movement condition reflect a cueing effect, whereby an adapted sensorimotor map might be cued by observation of the visual error and then retrieved on the subsequent trial or trials (27, 28). We opted to directly test this alternative explanation in another pair of experiments conducted online. Here, we only included 0° rotated (Fig. 3A, Left; n = 24 participants, experiment 4) or error-clamped (Fig. 3A, Right; n = 37 participants, experiment 5) FB on movement trials but maintained 0° or 15° CW/CCW errors on the no-movement trials. Thus, visual perturbations were never paired with movement.

Fig. 3.

Effects of simulated errors when perturbations were never applied during movement trials. (A) Schematic illustrating the relationship between movement and visual FB on movement trials during experiments 4 and 5 where nonzero visuomotor rotations (Left) or error clamps (Right) were never applied during movement trials. (B) Example participant’s mean ± SEM changes in reach paths across no-movement triplets from studies in which nonzero rotations (Left, experiment 4) and error clamps (Right, experiment 5) were never applied (solid lines, perturbation was CW; dashed lines, perturbation was CCW). (C) Boxplots showing STL in response to different directions of simulated errors (no-movement triplets indicated in magenta) from rotation (Left, experiment 4, n = 24) and error-clamp (Right, experiment 5, n = 37) studies. (D) Estimated marginal means ± 95% confidence intervals from the LMMs fit to each participant’s STL performance summarized in C. Asterisks indicate statistically significant differences. (E) Mean ± SEM relative hand angles on the two trials after a perturbation was presented on a no-movement trial (Left, experiment 4; Right, experiment 5). Refer to SI Appendix, Table S3 for detailed statistical results. Boxplot centers, median; notches, 95% confidence interval of the median; box edges, first and third quartiles; whiskers, most extreme values within 1.5*inter-quartile range (IQR) of the median. Statistical significance (* = P_adj < 0.05; n.s. = P_adj ≥ 0.05) is indicated for selected comparisons. Δ, change in; E, experiment; n.s., not significant.

The key results were again replicated: learning was preserved in the no-movement condition even when perturbed FB had never been associated with executed movements (Fig. 3C, rotation; LMM: F(557) = 23.01, P = 2.07 × 10⁻⁶, partial R² = 0.04; error clamp: F(802) = 9.41, P = 9.14 × 10⁻⁵, partial R² = 0.02). Post hoc pairwise comparisons showed that adaptation was significantly different between triplets with CW and CCW errors for both the rotation experiments (t(557) = 4.80, P = 2.07 × 10⁻⁶, Cohen’s d = 0.4) and the error-clamp experiments (t(1,453) = 4.32, P = 5.34 × 10⁻⁵, Cohen’s d = 0.37), a hallmark of implicit motor adaptation. Overall levels of STL observed on no-movement trials were comparable during these two experiments to those discussed above and within the range of learning rates previously observed in the literature (SI Appendix, Fig. S1). Furthermore, both groups of participants showed retention of STL that differed significantly from zero (rotation, mean ± SEM: 0.53 ± 0.06 retention ratio, one-sample t test: t(22) = 8.28, P = 3.34 × 10⁻⁸, Cohen’s d = 1.73; error clamp, median: 0.45, interquartile range 0.58, one-sample signed-rank test: V = 507, P = 0.001, r = 0.53). Overall, these experiments support the hypothesis that motor adaptation can proceed without movement execution.

Discussion

Our results demonstrate that movements can be implicitly refined even when they are not performed. Participants who were cued to reach toward a target but suppressed that movement after observation of a stop cue showed consistent, robust STL in response to simulated errors (Figs. 2 and 3). As implicit learning is thought to necessarily proceed subsequent SPEs (20, 26, 29–33), our data may also provide evidence that SPEs are computed even when movements are not performed. These findings support the fundamental assumptions of predictive processing frameworks of motor adaptation, where precise sensory predictions are generated from a movement intent (or plan or goal) and compared against sensory observations to induce error-based learning (11, 14, 16, 34, 35).

We argue that we have measured learning via an implicit process and, by extension, that the STL observed in our study provides evidence that the errors used for implicit adaptation are computed regardless of whether a movement is performed. Although visuomotor learning tasks may sometimes recruit cognitive strategies (e.g., deliberate reaiming of movements), multiple factors indicate that our studies successfully measured implicit learning (26, 36, 37). First, participants were instructed to ignore the displayed cursor and try to contact the target on every trial, a straightforward technique which has been consistently shown to eliminate the explicit reaiming of movements (20–23, 25, 32). Second, randomization of the presence and direction of errors discourages explicit learning, reducing motivation to apply ineffective reaiming strategies (38). Third, data from participants who appeared to not reliably recall the instruction to always aim directly at the target were excluded (see Methods), decreasing the likelihood that strategic reaiming contaminated the analysis (though we note that all key results were replicated without these exclusions; SI Appendix). Fourth, adaptation persisted into subsequent no-FB trials (Figs. 2 E, H, K and 3E), consistent with lingering implicit motor learning; it is unlikely that strategies would be maintained when no FB is expected. Fifth, the magnitude of STL observed was generally consistent with previous studies that measured implicit motor adaptation rates (SI Appendix, Fig. S1) (20, 22, 39). Lastly, the adaptation effects observed in the no-movement conditions were not attributable to the recall of learning that had occurred on movement trials (Fig. 3). Our data thus provide converging evidence that movement is not required for implicit adaptation.

The motor adaptation field has begun to consider the possibility that errors aside from SPE are involved in implicit adaptation. For example, task success/failure as indicated by observation of the cursor hitting or missing the target has been shown to influence the amount of implicit adaptation that occurs, indicating that task errors may contribute to implicit adaptation (31, 40–42). Theoretical approaches have also highlighted a role for task errors in adaptation (43). However, other evidence suggests that inducing task errors in the absence of SPEs does not reliably drive implicit adaptation (31, 44). While we believe that the most parsimonious interpretation of our data in the context of the current literature is that SPEs are responsible for the adaptation that we observed on no-movement trials, future studies will be needed to address a potential role for task errors.

Our data also indicate that participants showed significantly stronger STL over triplets with movement trials vs. no-movement trials. This suggests that movement provides additional training input to the brain. Interestingly, this is consistent with patterns of cerebellar activity during motor behaviors and current thinking about mechanisms for learning in cerebellar-dependent tasks like implicit reach adaptation (20). Purkinje cell complex spikes are powerful teaching signals in the cerebellum, and these complex spikes exhibit firing patterns that may be movement dependent (45–48). During target-directed reaching, complex spikes related to reach goal locations are generated after reach onset (49). If these complex spikes are tied to motor performance and not to motor planning, then the absence of these error signals on no-movement trials may account for reduced levels of STL without movement (50–53). Another non-mutually exclusive possibility is that the precise timing of errors is less effective in our no-movement condition than under normal movement conditions: in the former case, the timing of simulated FB is controlled by the experimenter and not triggered by the subject’s actual movement, potentially injecting noise into the adaptation process (54, 55). Irrespective of the fact that STL was of lesser amplitude across no-movement than movement triplets, our data support significant influence of the brain’s prediction signals on learning: even without the ability to directly attribute sensory FB to an actual movement, prediction of a planned movement’s sensory consequences supports the error computations that drive adaptation of future behavior.

It remains an open question as to precisely how the brain generates sensorimotor predictions and specifies their content. Forward models are thought to learn the relationship between motor plans and their sensory consequences as agents explore the world by generating motor commands and observing their consequences (56–58). At face value, it may seem curious that participants could generate relevant sensory predictions under the highly simplified (and artificial) visual FB conditions employed in this and similar motor learning studies (i.e., a disembodied circular cursor instead of a hand attached to an arm). It may be that the forward model computes sensory predictions in terms of abstract parameters, like the trajectory and position of a specific controlled object, or in terms of relatively simplified parameters of incoming sense data, such as the presence of any change in visual motion in a particular region of space relative to the movement goal. Alternately, it may be that familiarization with the task and its visual cues during the baseline period was sufficient to establish a context for generating sensory predictions about the specific stimuli in our task (i.e., a small white dot that moves in a straight line). Further work will be necessary to clarify the format and content of the sensory predictions that the brain generates based on our motor plans.

We note that our findings add to a body of work indicating that multiple forms of motor learning do not strictly require movement-based practice. For instance, in Mattar and Gribble (59), after human participants observed others adapting to a force field applied during reaching movements, the observers were able to partially compensate for that same force field when they encountered it themselves. Interestingly, this observational learning did not proceed if participants were executing other task-irrelevant movements during the observation period. This finding has been linked to subsequent neuroimaging data showing that observational learning recruits brain areas associated with motor planning, which taken together suggest that engagement in a covert motor planning process may allow for force-field adaptation via observation (59–61). Together, this related prior work and the evidence we have provided here suggest that there may be multiple routes to inducing motor planning and ultimately driving motor adaptation.

Additional reports in the motor learning literature have provided evidence for cognitive compensation for observed motor errors during reaching, improved visual tracking following observation of target movement without engagement in visual pursuit, and improvement in movement speeds as a result of mental imagery training; this work highlights the breadth of motor performance-related processes that can be trained without engagement in physical movements (17, 18, 62, 63). This points to a potential opportunity for the development of motor training or rehabilitation protocols that can be used when people are unable to physically perform target motor behaviors, perhaps improving performance beyond what physical practice can do alone.

Finally, our results echo the fact that other types of learning can occur without overt task execution. As an example, fear associations can be extinguished by instructing participants to imagine a fear-predicting stimulus even when they are not presented with the stimulus, and this imagination protocol generates neural signatures of the negative prediction errors observed during naturalistic fear extinction (64, 65). Considering both this prior work and the findings presented in this study, it may be that the generation of predictions for comparison with sense data are sufficient for error-based learning across motor and nonmotor domains alike. In other words, task execution may not always be required for learning, so long as the predictions and observations needed to compute errors are both present.

Methods

Participants.

Participants (n = 233, aged 18 to 35, 126 female) recruited from the research participation pools at Princeton/Yale University and on Prolific provided informed consent to participate. This study was approved by the Princeton University Institutional Review Board (IRB) and the Yale University IRB.

To limit any potential effects of explicit reaiming, we excluded data from participants who showed evidence of not recalling or understanding the task instructions. All data collected in the laboratory (experiment 1) were included in the final analysis, as an experimenter was present during the study and could address any confusion that arose about the task. Because we did not have this luxury with data collected online (experiments 2 to 5), we queried participants’ understanding of the instructions via a poststudy questionnaire and excluded data from participants who responded incorrectly. The questionnaire asked participants to attest whether or not 1) their goal was to move the real mouse and not the cursor straight through the green targets and whether or not 2) their goal was to move the white cursor (not the real mouse) straight through the green targets. Participants could select the options: true, false, or not sure. The majority of participants answered both questions correctly (1: true, 2: false; 138 of 213 participants [65%]), suggesting that most participants understood the task instructions but that many participants may not have understood the distinction between mouse and cursor movement (an unusual distinction to make in the context of everyday computer use). The 75 participants who did not answer both questions correctly were excluded from our final analyses (experiment 2, 10 exclusions; experiment 3, 13 exclusions; experiment 4, 26 exclusions; and experiment 5: 26 exclusions). We note, however, that all the key results described here held with or without these exclusions, as can be seen in the full dataset (freely available at https://www.github.com/kimoli/LearningFromThePathNotTaken). We further note that the samples used for the online experiments described in the text are around twice the size of similar studies in the literature even after the aforementioned exclusions, providing additional statistical power to compensate for the studies being conducted remotely (66–68).

Task Setup: Experiment 1.

Participants were seated in a chair and made ballistic reaching movements while grasping the handle of a robotic manipulandum with their dominant hand (Kinarm End-Point). The manipulandum restricted movements to the horizontal plane. All visual stimuli were projected to the participant via a horizontal display screen (60 Hz) reflected onto a semisilvered mirror mounted above the robotic handle. The mirror occluded vision of the arm, hand, and robotic handle, preventing direct visual FB of hand position. Tasks were programmed in MATLAB 2019a’s Simulink for deployment in Kinarm’s Dexterit-E software (version 3.9). Movement kinematics were recorded at 1 kHz.

Throughout the study, an experimenter was present in the room. Instructions were shown on the display for participants to read through, and participants indicated that they were ready to begin/resume trials by moving their hand into a circle shown toward the left side of the workspace.

Each participant viewed a single target located at either 45°, 135°, 225°, or 315° (with target position counterbalanced across participants), 8 cm from a central starting location. The target was visible throughout the experiment, except when instructions were being displayed.

Task Setup: Experiments 2 to 5.

Experiments were conducted remotely using a custom JavaScript web application based on Phaser 3.24 (download available at Photon Storm [69]), similar to an approach previously described (70). Each participant viewed a single target located at either 45°, 135°, 225°, or 315° (with target position counterbalanced across participants), 250 pixels from a central starting location. The target was visible throughout the experiment, except when instructions were being displayed.

Participants used an input device of their choice to control their computer cursor during center-out movements. One participant reported using a touchscreen device and was excluded from all analyses. The remaining participants reported using either a trackpad (n = 112), an optical mouse (n = 86), or a trackball (n = 14). An LMM did not show effects of mouse type on STL, although we observed that participants using a trackpad exhibited longer reaction times than others, consistent with a previous report (70).

Mouse position sampling rates depended on the exact hardware that each participant used to complete the task. Sampling rates were likely affected by features of the specific mouse used, along with features of the specific computer used, as browsers may lock the input device report rate to the display refresh rate. In general, sampling rates were around 60 Hz (median ± interquartile range across all 213 online participants recruited: 62.46 ± 2.17 Hz) but ranged from 19.23 to 249.69 Hz. Note that the vast majority of sampling rates were near 60 Hz: Only 5% of sampling rates were <41.79 Hz, and only 5% of sampling rates were >126.65 Hz.

Behavioral Task Protocol: Experiment 1.

Before the onset of the baseline phase, each participant read instructions to hold a hand in the center of the screen to start a trial and slice through the target when it turned green (SI Appendix, Extended Methods, E1 Instructions, Baseline). The robotic manipulandum moved the participant’s hand to a central starting location depicted by a gray circle at the middle of the display while hand and cursor FB were hidden. After a delay (500 ms + random 0 to 500 ms in duration), the target changed color from gray to green, indicating that the participant should slice through the target. The cursor was displayed at the hand position while the participant moved toward the target (online FB). When the participant passed the target, the cursor was displayed at the point where the hand passed the target distance for 50 ms (endpoint FB), after which time the cursor was extinguished. After another 50 ms, the robot moved the hand back to the starting location. Participants completed five trials with this online and endpoint FB before another set of instructions informed them that trials would proceed similarly but they would no longer see the cursor position while they were moving (no-FB; SI Appendix, Extended Methods, E1 Instructions, No-feedback). After five no-FB trials, participants viewed instructions indicating that they should withhold their reach if the target turned magenta after turning green (SI Appendix, Extended Methods, E1 Instructions, No-movement). Participants then completed 10 alternating trials on which the target turned green and stayed green (go trials) and on which the target turned magenta 100 ms after turning green, signaling that they should withhold their movement (stop trials). After this baseline phase, participants were instructed to continue following these instructions for the remainder of the experiment (SI Appendix, Extended Methods, E1 Instructions, Test block).

During the test phase, 480 total trials were divided into three-trial triplets (Fig. 1C). The first and last trials of all triplets were go trials, and participants received neither online nor endpoint FB about cursor location on these trials. The second trial of each triplet was either a movement or a no-movement trial. On movement trials, participants received rotated (15° CW [−] or CCW [+], with sign randomized across trials) or veridical online and endpoint FB of their cursor location. On no-movement (stop) perturbation trials, participants viewed a brief animation of the cursor following a trajectory deflected by ±15° from the target center. Animation onset latency was set as a running median of the participant’s reaction times on the previous five trials, and animation duration was set as a running median of the participant’s movement times on the previous five trials. If a participant took longer than 400 ms to execute a movement, a participant took longer than 800 ms to initiate the movement, their reach trajectory changed by >10° during the movement, or the reach terminated ≥60° away from the target, they received a warning and a 4-s timeout. If a participant moved their hand > 5 mm (radius of the starting location) on a no-movement trial, the trial was immediately aborted, and they received a warning and a 4-s timeout. The stop manipulation was successful: Across the experiments, participants erroneously moved on 34.39 ± 20.63% (mean ± SD) of stop trials, suggesting that, for the most part, they were consistently planning movements on stop trials.

We used four possible triplet perturbation trial types (movement/no-movement: ±15°), each of which occurred 40 times throughout each session. Triplets were pseudorandomly presented within each block, with the constraints that a single rotation (±15°) could not occur on more than two consecutive triplets and that the same movement condition (i.e., movement or no-movement) could not occur on more than three consecutive triplets. Three repetitions of each triplet type occurred in blocks of 18 triplets, and participants received a break after each of these blocks. Text indicating that each break period had arrived was displayed to the participants, along with a reminder about the task instructions (SI Appendix, Extended Methods, E1 Instructions, Break).

Behavioral Task Protocol: Experiment 2.

This experiment was conducted online. The procedure was largely the same as that described above for experiment 1, and any differences are detailed in this section. Instructions differed slightly from those shown in experiment 1 to account for these changes and included animations to help clarify the instructions (SI Appendix, Extended Methods, E2 Instructions and Movies S1–S5). If participants did not follow instructions to aim toward the target (i.e., move within 60° of the target), move quickly (i.e., movement duration < 400 ms or reaction time > 800 ms), or withhold movements on no-movement trials (i.e., move beyond the starting location [4-pixel radius]), they experienced a 4-s timeout during which a reminder about the relevant instruction was played (SI Appendix, Extended Methods, E2 Instructions and Movies S6–S9). Triplets during which one or more warnings occurred were excluded from the analysis, as the resulting timeouts inflated the intertrial interval and may have allowed for greater forgetting than trials without warnings. Additionally, to allow participants to efficiently conduct the task on their personal computers, the cursor automatically reappeared near the starting location 100 ms after a trial ended, rather than requiring that the participant’s hand return to the start.

Further changes were made to the trial structure: the test phase consisted of 270 total trials (90 triplets) to preemptively account for diminishing attentiveness to the task without an experimenter present, and triplets with 0° perturbations were included to verify that no implicit adaptation was observed when zero error occurred in the online experimental context. During movement trials, 0° perturbations involved veridical cursor FB. During no-movement trials, 0° perturbations involved an animation showing the cursor moving directly to the target. Examples of all possible perturbations on no-movement trials are shown in the Movies S10–S12.

Behavioral Task Protocol: Experiment 3.

This experiment was conducted identically to experiment 2, with the exception that cursor FB perturbations followed an error-clamp regime (20) instead of a rotational regime. Error-clamped FB follows a fixed trajectory at a particular angle relative to the target, unlike rotated FB, which appears at a particular angle relative to the participant’s hand location (Fig. 2A). The change to error-clamped FB caused the cursor FB to appear in identical locations on movement and no-movement trials with the same amplitude and sign perturbation, whereas cursor FB locations may have varied between trial types under the rotational regime due to variability in participants’ movements.

Behavioral Task Protocol: Experiment 4.

This experiment was conducted identically to experiment 2 except that we used a reduced set of possible triplet perturbation trial types (no-movement, 15° CW; no-movement, 15° CCW; movement, 0° rotation). We maintained an equal number of movement and no-movement triplets throughout the session to ensure that participants would reliably respond to the go cue presented at the start of each trial. Thus, each no-movement triplet type occurred 22 times, while the movement triplet type occurred 44 times. Triplets were pseudorandomly presented within each block, with the constraints that a single nonzero rotation (15° CW, 15° CCW) could not occur on more than two consecutive triplets.

Behavioral Task Protocol: Experiment 5.

This experiment was conducted identically to experiment 3 except that we used a reduced set of possible triplet perturbation trial types (no-movement, 15° CW; no-movement, 15° CCW; no-movement, 0° perturbation; movement, 0° error clamp). We maintained an equal number of movement and no-movement triplets throughout the session in order to ensure that participants would reliably respond to the go cue presented at the start of each trial. Thus, each no-movement triplet type occurred 15 times, and the movement triplet type occurred 45 times. Triplets were pseudorandomly presented within each block, with the constraints that a single nonzero rotation (15° CW, 15° CCW) could not occur on more than two consecutive triplets.

Data Analysis.

Data were processed in Python 3.8.5 and MATLAB 2018a. Trials with movement were excluded from analysis 1) if any of the reaches in the triplet were not straight (aspect ratio > participantwise mean + 3 × participantwise SD), 2) if the participant received any warning for failure to follow task instructions (see Behavioral Task Protocol: Experiment 1 and Behavioral Task Protocol: Experiment 2, above), or 3) if the triplet included a no-movement, no-go perturbation trial with any detectable mouse movement (>0 pixels online, >5 mm in the laboratory).

Reach endpoint angle was computed as the angular distance between the center of the target and the point at which the mouse passed the target’s radial distance. Because mouse sampling rates did not always allow us to measure mouse position at the exact target radius during the online study, we used the last sample before and the first sample after the mouse passed the target radius to compute an interpolated mouse position at the target radius, as described in a previous report (70). We note that analyses comparing these measures to measurements at the last sample of the reach (even when it was beyond the target) or the hand angle at peak velocity did not result in substantially different hand angle measurements or statistical outcomes.

STL was measured as the difference between reach endpoint angle on the third and first trial of each triplet. For our initial analyses, the sign of STL corresponded to the direction of the relative change in hand angle, with CW changes in hand angle taking a negative sign and CCW changes in hand angle taking a positive sign. When we collapsed STL data across rotation directions, we normalized the sign of STL so that changes in hand angle opposite the direction of the imposed rotation took a positive sign and changes in the direction of the rotation took a negative sign.

Remembered STL was quantified as the difference between reach endpoint angle on the first trial of one triplet and reach endpoint angle on the first trial of the previous triplet. When remembered STL was reported as a ratio, this value was computed by dividing remembered STL by the STL attributable to a given triplet.

Statistics.

Statistical tests were conducted in R (version 4.0.3): packages rstatix (71), coin (72), MuMIn (73), lmerTest (74), lme4 (75), r2glmm (76), emmeans (77), effsize (78), effectsize (79), magrittr (80), ggplot2 (81), ggpubr (82), and ggeffects (83). The reproducible code and data are available at https://www.github.com/kimoli/LearningFromThePathNotTaken. Data from in-laboratory experiments were analyzed using a two-way repeated-measures ANOVA. If an ANOVA showed a significant main effect or interaction, post hoc pairwise tests were performed. When samples failed to satisfy the normality assumption of the pairwise t test (assessed via a Shapiro-Wilk test), we used the more robust paired-samples Wilcoxon signed-rank test. Otherwise, we used the more powerful paired t test. Effect sizes for ANOVA main effects/interactions were quantified via generalized η² (${\eta }_G^2$), we quantified the effect sizes for t tests using Cohen’s d, and we used the Wilcoxon effect size (r) to quantify effect sizes for signed-rank tests. For these and all subsequent analyses, we corrected for multiple comparisons using the false discovery rate approach to maintain family-wise alpha at 0.05.

Data from the experiments conducted online did not satisfy multiple assumptions of the two-way repeated-measures ANOVA (nonexistence of extreme outliers and sphericity), so we employed an LMM (R packages lmerTest and lme4) approach for analysis of these data. LMMs for experiments 2 and 3 included fixed effects of perturbation size and movement condition, as well as random effects of subject. LMMs for experiments 4 and 5 included fixed effects of perturbation size and random effects of subject. Degrees of freedom were estimated using the Kenward-Roger approach, and LMM outcomes were reported using ANOVA-style statistics. Partial R² was computed to report effect sizes for the LMM factors (R package r2glmm). Post hoc pairwise comparisons were performed between estimated marginal means computed from the LMM (R package emmeans).

For one-off comparisons between samples or to distributions with 0 mean, we checked samples for normality. When samples were normally distributed, we ran t tests and computed Cohen’s d to report effect sizes for statistically significant results. Otherwise, we ran Wilcoxon-signed rank tests and measured effect sizes using the Wilcoxon effect size (r).

Data Availability

Anonymized reproducible code and data have been deposited in GitHub (https://www.github.com/kimoli/LearningFromThePathNotTaken) [84]. All other study data are included in the article and/or supporting information.