Abstract
Electrospray ionization mass spectrometry (ESI-MS) is a powerful label-free assay for detecting noncovalent biomolecular complexes in vitro and is increasingly used to quantify binding thermochemistry. A common assumption made in ESI-MS affinity measurements is that the relative ion signals of free and bound species quantitatively reflect their relative concentrations in solution. However, this is valid only when the interacting species and their complexes have similar ESI-MS response factors (RFs). For many biomolecular complexes, such as protein–protein interactions, this condition is not satisfied. Existing strategies to correct for nonuniform RFs are generally incompatible with static nanoflow ESI (nanoESI) sources, which are typically used for biomolecular interaction studies, thereby significantly limiting the utility of ESI-MS. Here, we introduce slow mixing mode (SLOMO) nanoESI-MS, a direct technique that allows both the RF and affinity (Kd) for a biomolecular interaction to be determined from a single measurement using static nanoESI. The approach relies on the continuous monitoring of interacting species and their complexes under nonhomogeneous solution conditions. Changes in ion signals of free and bound species as the system approaches or moves away from a steady-state condition allow the relative RFs of the free and bound species to be determined. Combining the relative RF and the relative abundances measured under equilibrium conditions enables the Kd to be calculated. The reliability of SLOMO and its ease of use is demonstrated through affinity measurements performed on peptide–antibiotic, protease–protein inhibitor, and protein oligomerization systems. Finally, affinities measured for the binding of human and bacterial lectins to a nanobody, a viral glycoprotein, and glycolipids displayed within a model membrane highlight the tremendous power and versatility of SLOMO for accurately quantifying a wide range of biomolecular interactions important to human health and disease.
Short abstract
A novel native mass spectrometry method is described that overcomes the long-standing problem of nonuniform response factors and enables the quantification of biomolecular interactions.
Introduction
Noncovalent interactions underpin all biological processes, from antibody recognition to transcription and translation.1,2 Characterization of these interactions is essential for a complete understanding of normal and pathological processes and is critical to the development of new diagnostics and therapies to treat diseases.3 As a result, considerable research efforts are being directed at the characterization of noncovalent biomolecular interactions, including protein–protein and protein–ligand interactions.4−7 Current surface-based and in-solution techniques available for the quantification of thermodynamic and kinetic parameters include isothermal titration calorimetry (ITC),8,9 surface plasmon resonance (SPR) spectroscopy,10 nuclear magnetic resonance (NMR) spectroscopy,11 enzyme-linked immunosorbent assays (ELISA),12 microscale thermophoresis (MST),13 and mass photometry (MP).14 These techniques require large sample amounts (NMR and ITC), the immobilization of one of the binding partners (SPR and ELISA), or labeling with a fluorophore (labeled MST) or are restricted to high-affinity (≤nM) interactions (MP). Moreover, most assays (e.g., ITC, SPR, ELISA, NMR, and MST) do not directly report on binding stoichiometry; MP, which does measure stochiometry, has a relatively low mass resolution and suffers from a low mass cutoff (∼30 kDa).15
In recent years, electrospray ionization mass spectrometry (ESI-MS) performed under native-like solution conditions (i.e., native MS), has emerged as a powerful method for quantifying the thermodynamic parameters of biomolecular complexes.16−18 In addition to being label- and immobilization-free, ESI-MS analysis is fast (∼1–2 min), consumes small amounts of sample (femtomoles to picomoles), can measure directly the stoichiometry of intact biomolecular complexes, and can monitor multiple equilibria simultaneously. The interaction enthalpy and entropy parameters can also be measured by applying ESI-MS analysis over a range of solution temperatures.19−21 There are numerous reported examples that illustrate the utility of ESI-MS for the qualitative and quantitative analysis of biomolecular complexes.22 However, challenges remain to unlocking the full potential of ESI-MS as a general and accurate method for quantifying protein, and other biomolecular and macromolecular, interactions.23
A common assumption underpinning direct ESI-MS affinity measurements is that the relative ion signal (abundance) of the free and bound proteins (biomolecules) quantitatively reflects their relative concentration in solution.24 However, there are a number of physical and chemical processes during ESI-MS analysis that can cause the apparent relative ion signal to deviate from the actual (in-solution) relative concentrations, leading to errors in the measured Kd and obscuring the true binding stoichiometry.24 These include changes in the temperature and pH of the solution, nonspecific binding, and in-source dissociation.24 Various experimental strategies have been developed to eliminate or minimize these effects.24−28 Additionally, the relative ion signals of free components and their complex(es) may differ from relative concentrations as a result of nonuniform response factors (RF). The RF, which collectively reflects the ionization (ion formation), transmission, and detection efficiency of an analyte, is the proportionality constant that relates the ion signal measured by ESI-MS for a given species to the solution concentration. Comparing the affinities measured by ESI-MS and other assays reveals that unbound and bound species with similar (within ∼5%) molecular weights (MWs) and surface properties have similar RFs.29 Therefore, ESI-MS can be confidently used to quantify interactions of proteins with small-molecule ligands.17,18 However, for the majority of protein complexes, and essentially all multiprotein complexes, the RFs of the free and bound species will differ significantly.29 In such cases, the determination of an accurate Kd requires the measurement of both the relative abundances of the bound and unbound species and their relative RFs.
Several strategies have been developed to address the problem of nonuniform RFs in direct ESI-MS affinity measurements.30−34 Gabelica and co-workers demonstrated the use of a nonreactive internal standard, which resembled the analyte being studied, and equations of mass balance to quantify the ligand affinities for DNA duplexes.33 Measurements performed at different concentrations yield a series of independent linear equations, which can be solved to find the relative (to the standard) RF of each complex formed and the corresponding affinity. This approach was also demonstrated for the quantitative monitoring of the kinetics of DNA duplex formation.33 Gross and co-workers described the application of a mathematical model based on expressions of the abundance of free and bound species, which takes into account both the relative RF and in-source dissociation of the complex(es).34,35 The Kd and relative RF are determined by solving (numerically) the corresponding system of differential equations. This approach has been used to quantify oligomerization and receptor–ligand binding reactions.36−38 Zenobi and co-workers demonstrated that the Kd and relative RF for protein and DNA dimerization reactions can be simultaneously measured by applying a global fitting approach to titration data.36−38 However, it was noted that high-quality binding data (i.e., a low standard deviation) were essential to obtain meaningful parameters.36−38
Common to the aforementioned methods of determining the relative RF in ESI-MS affinity measurements is the need for precise binding data acquired over a range of analyte concentrations and the requirement that the relative RF is independent of the concentration. Satisfying these conditions generally requires the use of a pump-driven ESI source. However, because of limitations in available sample amounts, most biomolecular interaction studies are performed using static nanoflow ESI (nanoESI), which is implemented with pulled glass emitters.39,40 Due to tip-to-tip variability, as well as the physical deterioration of the emitter orifice during normal operation, the condition of a constant relative RF in measurements performed at different analyte concentrations using different nanoESI tips is unlikely to be satisfied. As a result, correcting for the nonuniform RF in binding measurements performed using nanoESI-MS remains an outstanding challenge, one that greatly restricts the utility of the assay.
Here, we introduce slow mixing mode (SLOMO) nanoESI-MS, a direct ESI-MS method implemented with static nanoESI, to quantify biomolecular interactions and other classes of association reactions. Importantly, the method allows the relative RF and Kd to be measured in a single experiment. The SLOMO technique relies on the continuous monitoring of interacting species and their complexes under nonhomogeneous solution conditions. The relative RF values of the free and bound species are determined from the changes in the absolute ion signals of the free and bound forms as the system approaches or moves away from a steady-state condition. Combining the relative RF with relative abundances measured under equilibrium conditions allows the Kd to be measured. We test the reliability of SLOMO and demonstrate the ease of use through affinity measurements performed on peptide–drug, protease–protein inhibitor, and protein oligomerization reactions for which affinity data were measured previously using established assays. We then apply this method to study interactions between a nanobody and human lectins, to examine immune lectin binding to the receptor binding domain of the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) spike glycoprotein, and to look at the interaction of bacterial lectin with glycolipids displayed on a soluble model membrane. The use of SLOMO on these diverse systems highlights the tremendous versatility and power of this new technique for quantifying biomolecular interactions important in human health and disease.
Materials and Methods
Peptides and Proteins
Soybean trypsin inhibitor (STI, molecular weight (MW) 19.99 kDa), trypsin from porcine pancreas (PT, MW 23.46 kDa), vancomycin (Van, MW 1448.4 Da), N-acetyl-d-Ala-d-Ala (AcAA, MW 202.2 Da), and bovine β-lactoglobulin B (BLG, MW 18.3 kDa) were purchased from Sigma-Aldrich Canada (Oakville, Canada). The receptor binding domain (RBD, residues 319–541, MW ∼32 kDa) of the spike protein of SARS-CoV-2 was expressed in HEK293 cells and purified as described elsewhere.41 The C-terminal fragment of the carbohydrate recognition domain of human galectin 3 (GAL-3C, residues 107–250, MW 16.3 kDa) was a gift from Professor C. Cairo (University of Alberta). The N-terminal fragment of the family 51 carbohydrate-binding module (CBM; MW 20.74 kDa) from Streptococcus pneumonia SP3-BS71 GH98 was produced in Escherichia coli and purified as described previously.42 The membrane scaffold protein (MSP) MSP1E1 (MW 27.49 kDa) was produced from the plasmid pMSP1E1 (Addgene, Cambridge, MA) using recombinant technology and purified as reported elsewhere.43,44 The procedures used to produce and purify galectin 1 (GAL-1, monomer MW 14.78 kDa), galectin 3 (GAL-3, MW 26.15 kDa), galectin 7 (GAL-7, monomer MW 14.94 kDa), galectin 13 (GAL-13, MW 16.12 kDa and 15.99 kDa (missing terminal methionine)), and the single-domain antibody (Nanobody, sdAb, MW 19.86 kDa) are given in the Supporting Information. Stock solutions of Van and of AcAA were prepared by dissolving known masses in 200 mM ammonium acetate (pH 6.9). Protein stock solutions were dialyzed into aqueous 200 mM ammonium acetate (at the required pH) using Amicon 0.5 mL microconcentrators (EMD Millipore, Billerica, MA) with a MW cutoff of 10 kDa. Protein concentrations were estimated by UV absorption at 280 nm. All stock solutions were stored at −20 °C prior to use.
Other Reagents
The oligosaccharide β-d-Gal-(1 → 3)-β-d-GlcNAc-(1 → 3)-β-d-Gal-(1 → 4)-d-Glc (LNT, MW 707.63 Da) was purchased from Elicityl SA (Crolles, France), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, MW 677.93 Da) was purchased from Avanti Polar Lipids (Alabaster, AL), and the blood group B trisaccharide neoglycolipid (B-triNGL, MW 1112.47 Da) was a gift from Professor T. Lowary (University of Alberta).45 Both DMPC and B-triNGL were dissolved in HPLC-grade methanol to prepare stock solutions at known concentrations. All the stock solutions were stored at −20 °C prior to use. Other solvents and reagents were purchased from common commercial sources and used without further purification.
Preparation of Nanodiscs
A nanodisc (ND) composed of DMPC and B-triNGL (15%) was prepared according to the protocol described by Sligar and co-workers46 and purified by gel-filtration chromatography using a Superdex 200 10/300 size-exclusion column (GE-Healthcare Life Sciences, Piscataway, NJ). The stock solution was stored at −20 °C prior to use.
Isothermal Titration Calorimetry (ITC)
The ITC measurements of the Van–AcAA complex affinity were carried out using a Microcal PEAQ ITC (Malvern Panalytical, Worcestershire, United Kingdom). Experimental details are given in the Supporting Information.
Mass Spectrometry
ESI-MS measurements were performed in the positive ion mode using a Q Exactive Orbitrap mass spectrometer (Classic) or a Q Exactive Orbitrap with an Ultra High Mass Range (UHMR) (Thermo Fisher Scientific, Bremen, Germany) mass spectrometer, each of which was equipped with a modified nanoflow ESI (nanoESI) device. The nanoESI tips were produced from borosilicate glass capillaries (1.0 mm outside diameter (o.d.), 0.78 mm inner diameter (i.d.), and 10 cm length) using a P-1000 micropipette puller (Sutter Instruments, CA). To perform nanoESI, a voltage of approximately +0.8 kV was applied to a platinum wire that was inserted inside the nanoESI tip and in contact with the solution. For each experiment, two different solutions (solutions 1 and 2) were loaded into the nanoESI tip. For heterocomplex formation, ∼ 2 μL of a solution of both interacting partners at known concentrations (solution 1) was introduced, followed by the injection of 10 μL of solution 2, which contained both interacting partners but with one of them at a high concentration. For protein homo-oligomerization, ∼6 μL of solution 1, the protein solution at a given pH, was loaded, followed by the injection of 10 μL of solution 2, the protein solution at the same concentration but with a different pH. Tip loading was manually performed using 10 μL syringes (Hamilton Microliter syringe, cemented needle, volume 10 μL, needle size of 26s ga (cone tip)). To minimize bubble formation, solution 1 was added slowly (∼20 μL min–1), with the end of the syringe needle placed approximately 2 cm from the end of the nanoESI tip. The tip was then gently shaken to further reduce the presence of bubbles. Solution 2 was then slowly loaded (∼20 μL min–1) with the end of the syringe needle in continuous contact with the meniscus of solution 1.
All experiments were carried out at 25 °C. The capillary temperature was 150 °C, and the key instrumental parameters were as follows: S-lens RF level 40–100 and DC offset from 15 to 100 (for both UHMR and Classic mass spectrometers). A resolution setting of 6250 was used for the UHMR, and that of 17 500 was used for all but one data set (which used 140 000) acquired with the Classic. Raw data were processed using the Thermo Xcalibur 4.2 software. Time-resolved mass spectra were averaged over 1 min intervals, and the sum of the charge-state-normalized abundances of the reactant and the complex ions was calculated automatically using the SWARM software (https://github.com/pkitov/CUPRA-SWARM).47 For mass spectra acquired for the glycoprotein (RBD) sample, which exhibited poorly resolved or unresolved peaks as well as spectral overlap between free and bound species, the analysis was performed using charge-state-normalized peak areas (comprising the combined signal of the free or bound glycoforms), which were determined by fitting the ion signal with Gaussian functions using the IgorPro Multipeak Fitting tool (WaveMetrics Inc., Lake Oswego, OR) and SWARM.
Results and Discussion
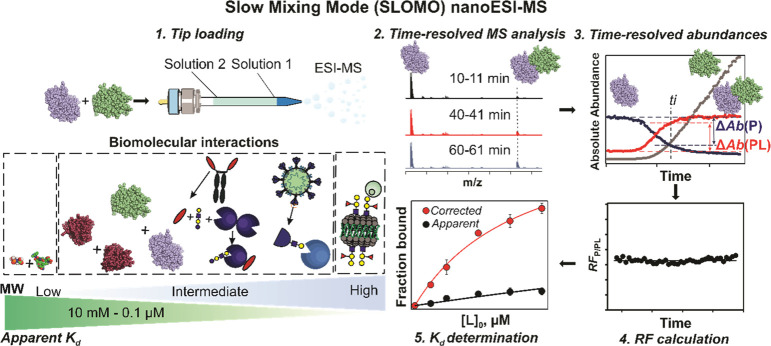
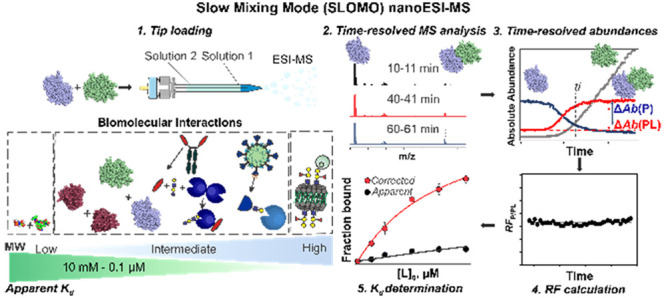
Overview of Slow Mixing Mode (SLOMO) nanoESI MS
One of the principle problems with measuring the Kd of biomolecular complexes using ESI-MS is the variable RF of the unbound (e.g., P) and ligand-bound (e.g., PL) species. We realized that both the RF and Kd can be determined simultaneously by monitoring dynamic changes in the relative abundance of the complex (PL). A pictorial overview of the SLOMO nanoESI MS method we developed is given in Figure 1. The assay relies on the continuous monitoring of interacting species and their complexes under nonhomogeneous solution conditions. Changes in the absolute ion signals of free and bound species as the system approaches or moves away from a steady-state enables their relative RFs to be determined. The critical assumption that underpins the method, that the relative RF is constant (independent of concentration) in a given experiment, was tested in the present work and shown to be generally valid. An overview of the data analysis procedures for homo- and heterocomplexes with relevant examples is given below.
Figure 1.
Overview of the SLOMO workflow for measuring the affinities (Kd) of biomolecular interactions. Step 1. Tip loading (with solution 1 and solution 2). Step 2. Time-resolved ESI-MS analysis. Step 3. Extraction of time-resolved abundances. Step 4. Calculation of the time-dependent relative RF. Step 5. Calculation of Kd from RF and Rapp. The insert summarizes biomolecular interactions used in this work and the range of Kd of interactions that are measurable with SLOMO.
Application of SLOMO to Heterocomplexes
Overview
To apply SLOMO to a monovalent PL complex (eq 1), the nanoESI tip is first loaded with a solution (solution 1) containing both P and L at known concentrations ([P]0 and [L]0,1), followed by a second solution (solution 2) containing the same concentration of P but a different concentration of L (e.g., [P]0 and [L]0,2). Mixing the solutions (as a result of diffusion in addition to electroosmotic and electrophoretic flow) leads to changes in analyte concentrations. However, because mixing is slow, the equilibrium distribution of P, L, and PL (present in the first solution) will initially remain constant, thereby allowing the apparent abundance ratio (Rapp, eq 2) to be measured under known solution conditions (i.e., composition of solution 1). Over time, the equilibrium will shift due to mixing. In the scenario considered here, [P]0 is constant, while the concentration of L ([L]) near the orifice of the nanoESI tip will increase due to mixing, which will in turn shift the equilibrium (eq 1) toward PL and lead to an increase in Rapp.
| 1 |
| 2 |
Here, Ab(PL) and Ab(P) are the total abundances (sum of ion signals) of PL and P, respectively, which are related to the solution concentrations by eqs 3a and 3b.
| 3a |
| 3b |
The relative response factor of P and PL (RFP/PL) is the ratio of RFP to RFPL (eq 3c):
| 3c |
The magnitude of RFP/PL can be found from mass balance considerations in eq 4.
| 4 |
Here, [P]t1 and [PL]t1 are the corresponding concentrations of P and PL measured at time t1 and [P]t2 and [PL]t2 are the corresponding concentrations at t2. The ratio of the absolute change in Ab between the two (acquisition) time points measured for PL and P, under conditions where the concentrations are changing, is shown by eqs 5a and 5b.
| 5a |
| 5b |
Here Abt1(P) and Abt2(P) are the Ab values measured for P at time points t1 and t2, respectively, and Abt1(PL) and Abt2(PL) are the corresponding values for PL.
In principle, RFP/PL can be determined from ΔAb(P) and ΔAb(PL) values calculated using just two time points. In practice, due to variability in the ESI-MS signal, it is advisible to establish RFP/PL using multiple time points. One approach is to use constant values for Abt1(P) and Abt1(PL), which are the average (Abeq(P) and (Abeq(PL), respectively) values measured under equilibrium (or pseudoequilibrium) conditions (i.e., in the absence of appreciable solution mixing). A series of ΔAb(P) and ΔAb(PL) is then calculated from the difference in Abeq(P) or Abeq(PL) and values measured at successive time points, ti (i.e., Abti(P) and Abti(PL)) at which mixing occurs, eqs 6a and 6b.
| 6a |
| 6b |
The individual and average RFP/PL values (RFP/PL,ti and RFP/PL,av, respectively) are calculated from eqs 7a and 7b, respectively.
| 7a |
| 7b |
Here, n is the number of time points considered.
In the present work, the values of Abeq(P) and Abeq(PL) were taken as the average of the 5 min moving average of the time-dependent Rapp (Rapp,i) values prior to mixing. The onset of mixing was identified as the point where the difference between the initial Rapp,i (Rapp,0) and Rapp,i at a given time point (i.e., ΔRapp) exceeded two times the standard deviation (δ) measured for Rapp,0, as shown by eq 8.
| 8 |
The RFP/PL and Rapp values were then used to calculate R (eq 9), and Kd was found from individual time points (eq 10) or by fitting eq 11 to the concentration-dependent fraction of occupied (ligand) binding sites (R/(R+1)).
| 9 |
| 10 |
| 11 |
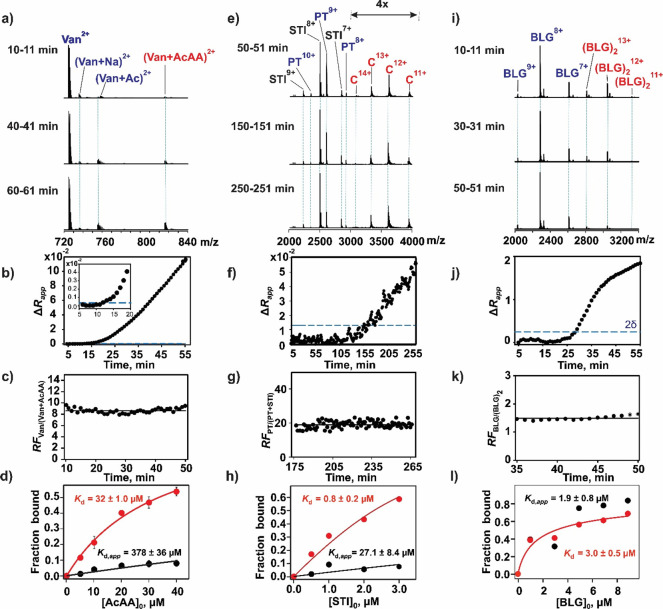
To test the validity of SLOMO for heterocomplexes, we applied it to two complexes, of different sizes and chemical properties for which affinities have been reported: the smaller biomolecular complex of Van and the peptide AcAA and the larger enzyme–protein inhibitor complex of PT and STI detailed below.
Model System for Small Bimolecular Interactions (Van-AcAA Binding)
The affinity of Van (1448.4 Da), a broad-spectrum antibiotic against Gram-positive bacteria, for the dipeptide AcAA (202.2 Da) has been measured to be 63 ± 13 μM (100 mM phosphate buffer, pH 7.0, and 25 °C).48,49 We analyzed this interaction using SLOMO for comparison. We used a fixed concentration of Van (2 μM) and varied concentrations of AcAA (5–40 μM) in solution 1. The concentration of Van in solution 2 was the same as that in solution 1, and that of AcAA was 500 μM. In both cases the antibiotic and peptide were dissolved in 200 mM ammonium acetate (pH 6.9 and 25 °C). All measurements were done in triplicate (n = 3). As can be seen in the representative ESI mass spectra (Figure 2a), the ion signal corresponding to doubly charged Van (doubly protonated and associated sodium and acetate adducts) and the Van–AcAA complex (doubly protonated) was detected; AcAA was detected as singly protonated and sodium adduct ions (Figure S1a). Time-dependent Rapp values measured for a single experiment are plotted in Figure S1b, and the corresponding ΔRapp values are shown in Figure 2b. Notably, Rapp is constant ((2.50 ± 0.17) × 10–2) at incubation times up to 11 min. The RFVan/(Van+AcAA) values calculated at incubation times from 11 to 50 min are plotted in Figure 2c. The Rapp (prior to mixing), RFVan/(Van+AcAA), and R values determined for each AcAA concentration are listed in Table S1. The long incubation times required to detect a significant change in Rapp due to mixing (up to 50 min in some cases, Table S1) are, perhaps, surprising. A series of control experiments (described in the Supporting Information) designed to establish the dominant factors controlling mixing (diffusion, electrophoretic or electroosmotic flow) revealed that analyte mixing inside the nanoESI tip was dominated by diffusion (Figure S2a).
Figure 2.
Validation of SLOMO using model biomolecular interactions with known affinities (a–d) Van–AcAA, (e–h) PT–STI, and (i–l) BLG–BLG. (a) Representative ESI mass spectra acquired in the positive ion mode at three different times for a mixture of ammonium acetate (200 mM, pH 6.9) solutions: solution 1, Van (2 μM) and AcAA (10 μM); solution 2, Van (2 μM) and AcAA (500 μM). (b) Plot of time-dependent ΔRapp values. The inset shows ΔRapp values measured at early times, and the dashed line (blue) indicates two standard deviations (2δ) from the mean. (c) Plot of time-dependent relative response factors (RFVan/(Van+AcAA)) measured for Van and the Van–AcAA complex. (d) Plot of the fraction of Van bound to AcAA versus the initial AcAA concentration determined without (black circles) and with (red circles) consideration of RFVan/(Van+AcAA). Solid curves represent the best fit of eq 11 to the experimental data. (e) Representative ESI mass spectra acquired in the positive ion mode at three different times for a mixture of ammonium acetate (200 mM, pH 4.5) solutions: solution 1, PT (3 μM) and STI (0.5 μM); solution 2, PT (3 μM) and STI (30 μM). (f) Plot of time-dependent ΔRapp values. The inset shows ΔRapp values measured at early mixing times. (g) Plot of time-dependent relative response factors (RFPT/(PT+STI)) measured for PT and the PT–STI complex. (h) Plot of the fraction of PT bound to STI versus the initial STI concentration determined without (black circles) and with (red circles) consideration of RFPT/(PT+STI). Solid curves represent the best fit of eq 11 to the experimental data. (i) Representative ESI mass spectra acquired in the positive ion mode at three different times for a mixture of ammonium acetate (200 mM) solutions of BLG (3 μM): solution 1, pH 6.9; solution 2, pH 10.6. (j) Plot of time-dependent ΔRapp values. (k) Plot of time-dependent relative response factors (RFBLG/(BLG)2) measured for the BLG monomer and dimer. (l) Plot of the fraction of BLG present as the dimer versus the initial BLG (monomer) concentration (1–9 μM) measured without (black circles) and with (red circles) consideration of RFM/D. Solid curves represent the best fit of eq 17 to the experimental data.
The affinity of the Van-AcAA interaction (Table S1) was determined at each concentration tested (eq 2) and by fitting eq 11 to the concentration-dependent fraction of bound Van using both Rapp (i.e., neglecting RFVan/(Van+AcAA)) and R (calculated from Rapp and RFVan/(Van+AcAA)). Both the average Kd,app calculated at each concentration (349 ± 100 μM) and the Kd,app (378 ± 36 μM) obtained by fitting eq 11 to the Rapp data directly (i.e., neglecting RFVan/(Van+AcAA)) from the titration data (Figure 2d) are sixfold larger than the reported value (63 ± 13 μM).48 In contrast, the average RFVan/(Van+AcAA)-corrected Kd (33.5 ± 5.9 μM) and the value obtained from fitting after the RFVan/(Van+AcAA) correction (32 ± 1 μM) (Figure 2d) are within a factor of 2 of the reported value, which was measured in 100 mM phosphate buffer.47 Because the nature of the buffer can, in some cases, lead to measurable differences (typically a factor of 2–3) in affinities of biomolecular complexes, we measured (using ITC) the Kd of the Van–AcAA interaction in 200 mM ammonium acetate at pH 6.9 (Figure S2b). Importantly, the value (50 ± 14 μM) agrees well with value obtained with SLOMO (and the value measured in phosphate buffer).
It is also notable that RFVan/(Van+AcAA) values measured using ESI-MS varied significantly between experiments (from ∼4 to ∼15), even for replicate measurements performed at the same concentrations and instrumental parameters. This finding suggests that applying a global fitting to ESI-MS titration data to establish RFVan/(Van+AcAA) may be not reliable and highlights the value of the SLOMO approach.
Application of SLOMO to Larger Heterocomplex Interactions (PT–STI Binding)
The inhibition of the protease PT (23.46 kDa) by STI (19.99 kDa) is known to have a Kd of 0.67 μM (25 mM potassium acetate and 10 mM calcium chloride buffer, pH 4.25, and 25 °C).9 We measured the binding between these two proteins in 200 mM ammonium acetate solutions (pH 4.5 and 25 °C) using SLOMO. A solution of PT (3 μM) and STI (0.5 μM – 3.0 μM) was injected first (solution 1), followed by a solution (solution 2) of PT (3 μM) and STI (15 μM – 30 μM). Representative mass spectra are shown in Figure 2e. The ion signal corresponding to protonated STI, PT, and PT–STI ions was detected (Figure 2e). The corresponding ΔRapp values are shown in Figure 2f. The time-dependent RFPT/(PT+STI) values determined at one set of concentrations (3 μM PT and 3 μM STI) are shown in Figure 2g. Plotted in Figure 2h are concentration-dependent fractions of bound PT calculated using Rapp and R (corrected using RFPT/(PT+STI)). A Kd (without RFPT/(PT+STI) correction) of 27.1 ± 8.4 μM and the corrected value of 0.8 ± 0.2 μM were obtained by fitting eq 11 to the titration data. To demonstrate the robustness of SLOMO, measurements were performed on the same solutions described above using different instrumental conditions (lower resolution). The resulting titration curves are shown in Figure S3. The Kd values without and with the RF correction are 0.2 ± 0.1 and 0.5 ± 0.1 μM, respectively. Notably, while changing instrumental conditions led to a 140-fold change in Kd,app, the corrected Kd value matched within error between the two conditions. This result highlights both the importance of taking into account RF to obtaining reliable Kd values using native MS and the ease with which this is accomplished with SLOMO.
Application of SLOMO to Homocomplexes
Overview
For homocomplexes, such as a protein homodimer (D) of monomer (M), the Kd of the dissociation reaction (eq 12) can be expressed by eq 13.
| 12 |
| 13 |
Here, [M]0 is the initial concentration of monomer and R is given by eq 14.
| 14 |
Unlike the situation with heterocomplexes, wherein Rapp can be changed by mixing solutions with different concentrations, the implementation of SLOMO for homocomplexes requires a perturbation of solution conditions (e.g., pH or temperature) to alter Rapp at a constant total protein concentration. The resulting change in the Ab of M and D is related to their relative RF (RFM/D), as shown in eq 15.
| 15 |
The equilibrium values Abeq(M) and Abeq(D) can be found using an approach similar to that used for heterocomplexes. The relative RF of the free protein and the homocomplex (RFM/D) for time points after the mixing started was calculated using eqs 16a and 16b.
| 16a |
| 16b |
The Kd can be calculated from a single experiment (eq 13) or by fitting eq 17 to the fraction of bound M (i.e., 2R/(2R+1)):
| 17 |
We tested the validity of using SLOMO to analyze homocomplex formation using the well characterized dimerization of BLG as a model system.
Application of SLOMO to Homocomplex Formation (Dimerization of Bovine β-Lactoglobulin B)
The dimerization of BLG (18.3 kDa) has been studied over a range of pH.50−54 A Kd of 7 μM was obtained at pH 6.9 (phosphate buffer, ionic strength of 0.13),55 while Kd values of 4 and 8.6 μM were obtained at pH 6.5 and 7.5, respectively.51 To quantify BLG dimerization using SLOMO, we used a pH change to affect the equilibrium. As noted above, the Kd of the (BLG)2 dimer increases with the pH.50,51,55 To perform the measurements, the tip was first loaded with 6 μL of a solution (200 mM ammonium acetate, pH 6.9, an 25 °C) of BLG at a concentration of between 1 and 8 μM (solution 1) and then 10 μL of BLG (solution 2) at the same concentration but a different pH (pH 10.6) to induce the dissociation of the dimer. Representative ESI-MS spectra are shown in Figure 2i; the corresponding ΔRapp values are shown in Figure 2j. Protonated ions corresponding to both the BLG monomer and the dimer were detected. RFBLG/(BLG)2 values, calculated as described above, for different concentrations were found to range from 0.4 to 1.5 (Figure 2k). It is reported that the dimerization does not significantly affect the BLG monomer conformation.50 This might explain, at least in part, the similarity in RF values between the monomer and the dimer. The apparent and corrected Kd values (obtained by fitting eq 15 to the uncorrected and corrected fraction bound values of bound BLG, Figure 2l) at pH 6.9 (solution 1) are 1.9 ± 0.8 and 3.0 ± 0.5 μM, respectively. While both values are in reasonable agreement with the reported value (7 μM),55 the fit of eq 15 to the apparent concentration-dependent fraction of bound BLG values is poorer due to scattering caused by variations in RFBLG/(BLG)2 at each experiment.
Applications of SLOMO to Human and Bacterial Lectin Binding
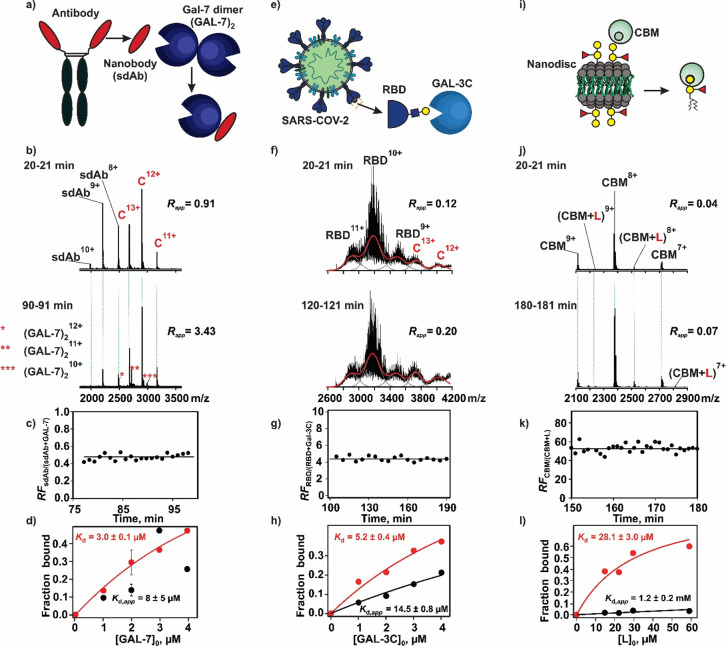
We next demonstrated the versatility of SLOMO by applying the assay to a series of biomolecular interactions involving human and bacterial lectins (glycan-binding proteins, GBPs), which can be challenging to quantify with conventional assays due to limited sample quantities and limitations in detection methods. Considered were the interactions between human galectins and a single-domain antibody (Figures 3a–d) for which the direct measurement of the binding stoichiometry and the quantification of multiple equilibria are needed. The binding of galectins to the receptor binding domain (RBD) of the spike glycoprotein of SARS-CoV-2 (Figures 3e–h), which is a complex mixture of glycoforms that exhibit differential affinities for the lectin, and the binding of a fragment of the family 51 carbohydrate-binding module (CBM) from S. pneumonia with a neoglycolipid (B-triNGL) ligand within a model membrane (Figures 3i-l) are processes for which differential response factors and gas-phase processes have precluded reliable quantification by native MS.
Figure 3.
Applications of SLOMO to the following lectin interactions: (a–d) GAL-7 with sdAb, (e–h) GAL-3C with SARS-CoV-2 RBD glycoprotein, and (i–l) CBM with glycolipid (B-triNGL) presented in a nanodisc (ND) model membrane. (b) Representative ESI mass spectra acquired in the positive ion mode at two different times for a mixture of ammonium acetate (200 mM, pH 7.4) solutions: solution 1, sdAb (3 μM) and GAL-7 (3 μM); solution 2, sdAb (3 μM) and GAL-7 (40 μM). (c) Plot of time-dependent relative response factors (RFsdAb/(sdAb+GAL-7)) measured for sdAb and the sdAb–GAL-7 monomer complex. (d) Fraction of sdAb bound to GAL-7 plotted as a function of the initial GAL-7 (monomer) concentration determined without (black circles) and with (red circles) consideration of RFsdAb/(sdAb+GAL-7). Solid curves represent the best fit of eq 11 to the experimental data. (f) Representative ESI mass spectra acquired in the positive ion mode at two different times for a mixture of ammonium acetate (200 mM, pH 7.4) solutions: solution 1, RBD (4 μM) and GAL-3C (2 μM); solution 2, RBD (4 μM) and GAL-3C (25 μM). (g) Plot of time-dependent relative response factors (RFRBD/(RBD+GAL-3C)) measured for RBD and the RBD–GAL-3C complex. (h) Fraction of RBD bound to GAL-3C RBD plotted as a function of the initial GAL-3C concentration determined without (black circles) and with (red circles) consideration of RFRBD/(RBD+GAL-3C). Solid curves represent the best fit of eq 11 to the experimental data. (j) Representative ESI mass spectra acquired in the positive ion mode at two different times for a mixture of ammonium acetate (200 mM, pH 6.9) solutions: solution 1, CBM (5 μM) and a ND containing B-triNGL (1 μM ND and 30 μM B-triNGL ≡ L); solution 2, CBM (5 μM) and a ND containing B-triNGL (10 μM ND and 300 μM B-triNGL). (k) Plot of time-dependent relative response factors (RFCBM/(CBM+L)) measured for CBM and the CBM–L complex. (l) Fraction of CBM bound to B-triNGL plotted as a function of the initial B-triNGL concentration determined without (black circles) and with (red circles) consideration of RFCBM/(CBM+L). Solid curves represent the best fit of eq 11 to the experimental data.
Immune Lectin–Nanobody Interaction
Human galectins act as key apoptotic regulators and are viewed as potential disease targets in multiple disorders.56 As such, considerable effort has been devoted to the design of galectin-specific modulators, including allosteric modulators.57 To illustrate the ease with which SLOMO can measure the effects of allosteric modulators on galectin dimerization, SLOMO was applied to the interaction between GAL-7 and a single-domain antibody (sdAb) in both the presence and absence of the tetrasaccharide ligand LNT. On its own, GAL-7 exists predominantly in the dimeric form at micromolar concentrations (Figure S4a). According to the SLOMO analysis (with the RF correction), the Kd of the monomer–dimer equilibrium in 200 mM ammonium acetate (pH 7.4 and 25 °C) is 3.1 ± 0.7 μM (Figure S4b), which is in good agreement with the reported value of 1.7 μM.58 Notably, without the RF correction, the apparent Kd (17 ± 22 (average of values measured at individual concentrations (eq 13) or 46 ± 28 nM (eq 17)) is 70- to 180-fold smaller (stronger) than the corrected Kd (Figure S4b). Reports on the effect of glycan binding on GAL-7 dimerization are contradictory, with some studies suggesting ligands, such as lactose, significantly stabilize (>30-fold at 10 mM lactose) the dimer.58 However, the results of SLOMO performed in the presence of the LNT (50 μM), which has a lactose core and exhibits an affinity of 95 ± 3 μM for GAL-7,59 revealed that Kd was essentially unaffected by LNT binding (Figure S5).
When excess sdAb, engineered to bind the dimerization interface of GAL-7, was added to the mixture, only the monomeric form of GAL-7 bound to sdAb was detected (along with excess free sdAb), supporting the hypothesis that sdAb binding prevents GAL-7 dimerization (Figure S6). From SLOMO measurements, the Kd of the 1:1 sdAb interactions with the GAL-7 monomer was found to be 3.0 ± 0.1 μM (Figure 3d), which is comparable in magnitude to the Kd of GAL-7 dimerization. To establish whether glycan binding influences the sdAb recognition of GAL-7, analogous measurements were performed on solutions of GAL-7, sdAb, and LNT. The Kd for the GAL-7 monomer and the sdAb interaction in the presence (4.6 ± 0.4 μM) and absence of LNT are similar, as are the affinities of LNT for GAL-7 and the GAL-7–sdAb complex (143 ± 24 μM) (Figure S7). Together, these results suggest that the binding of sdAb and LNT to GAL-7 are independent processes. Moreover, these results illustrate the power of SLOMO to quantify multiple equilibria simultaneously.
SLOMO was also used to assess the specificity of sdAb for GAL-7 by testing binding to three other available galectins, namely the prototype galectins GAL-1 and GAL-13 and the GAL-3 chimera (Figure S8). Notably, the absence of complex formation detected by direct ESI-MS analysis (Figure S9) was corroborated by the results obtained with SLOMO (i.e., the lack of binding between sdAb and GAL-1, GAL-13, and GAL-3 is not due to the low RF of the sdAb complexes), further confirming that the sdAb is specific to GAL-7. Taken together, these results highlight the tremendous potential of SLOMO for quantitatively assessing the specificities of single-domain antibodies, an emerging therapeutic and imaging tool for many diseases, including cancer.60,61
SARS-CoV-2 RBD–Immune Lectin Interactions
A variety of human immune lectins, including galectins, C-type lectins, and Siglecs, have been reported to recognize the SARS-CoV-2 spike (S) glycoprotein and its RBD.62,63 However, to date, few of these interactions have been quantified.67 To demonstrate the ability of SLOMO for characterizing immune lectin interactions, the assay was used to measure the affinity of a C-terminal fragment of galectin-3 (GAL-3C) for the RBD of SARS-COV-2 (Wuhan strain). Representative ESI mass spectra, acquired for solutions of RBD and for GAL-3C both alone and together, are shown in Figures S10a–c. The RBD, which was produced from HEK293 cells, contains two N-glycosylation sites (N331 and N343) and two O-glycosylation sites (T323 and S325) and according to glycomics studies has predominantly complex-type N-glycans (mostly fucosylated, mono- and disialylated complex type) and core 1 and 2 mucin-type O-glycans.64 From the mass spectrum (Figure S10a), glycan compositions corresponding to 68 distinct MWs were identified (Table S2). Although the mass spectrum is complex, the signal corresponding to the 1:1 RBD–GAL-3C complex is evident for the mixture (Figure S10c). There was no evidence of higher-order complexes at the concentrations tested. Of the 68 MW-unique glycan compositions identified for RBD, 36 were detected in the RBD–GAL-3C complex. Comparison of the distribution of glycan compositions measured for free RBD and the RBD–GAL-3C complex suggests that GAL-3C preferentially binds to the larger glycan structures of RBD (Figures S10d and e). This finding is qualitatively consistent with results obtained via glycan microarray screening, which revealed that GAL-3 had a preference for N-glycans with more LacNAc (Galβ1–4GlcNAc) moieties.65
To implement SLOMO, a solution of 4 μM RBD and 1–4 μM GAL-3C was loaded into the nanoESI tip, followed by a solution of 4 μM RBD and 25 μM GAL-3C. Because of the heterogeneity of RBD (due to glycosylation), the total signal area (of the free and bound RBD glycoforms) was used as opposed to discrete ion abundances (Figure 3f). The relative response factors (RFRBD/(RBD+Gal3C)), found from four concentrations, range from approximately 2 to 4. That RFRBD/(RBD+Gal3C) >1.0 (Figure 3g) suggests that the increase in the MW of RBD (due to binding) more strongly influences the RF than the reduced exposure of glycans to the solvent. From an analysis of the concentration dependence of the fraction of bound RBD (eq 11), the overall (considering all glycoforms) apparent and corrected affinities are 14.5 ± 0.8 (Kd,app) and 5.2 ± 0.4 μM (Kd), respectively (Figure 3h). It is notable that the affinity of GAL-3C for RBD is significantly stronger than that for the simple glycans containing epitopes with terminal galactose (e.g., ∼100 (lactose)66 and ∼50 μM (lactosamine)), emphasizing the importance of the underlying structure on the GAL-3C interaction.67 The binding of GAL-1, GAL-7, and GAL-13 with RBD was also tested. However, none exhibited measurable binding to RBD under the conditions tested (Figure S11). The absence of binding to GAL-7, which is at odds with the results of a recent NMR study,66 is curious but may reflect differences in the glycosylation of the RBD samples used.
Together, these results highlight the unique ability of SLOMO to both quantify protein–glycoprotein interactions and resolve the glycoform specificit in a single experiment. This information will dramatically advance the understanding of how protein glycosylation modulates protein interactions.
Bacterial Lectin Interactions with Glycolipids in Model Membranes
Native MS is a promising tool for detecting GBP interactions with glycolipids in model membranes. Analyzing solutions of GBP and glycolipid-containing membranes allows for the direct detection of ions corresponding to specific GBP–glycolipid complexes, enabling the rapid and facile identification of glycolipid ligands present in mixtures (natural or defined) and, uniquely, establishing binding stoichiometry. However, because the detected intact GBP–glycolipid complex ions arise from the spontaneous detachment of the complexes from the membrane during the ESI process (presumably from Coulombic repulsion between the GBP and the membrane), while the GBP ions originate directly from the solution, the relative abundances of free and ligand-bound GBP will not reflect their relative concentrations due to their nonuniform RF.46
Native MS performed with SLOMO allows not only the detection of GBP interactions with glycolipids in model membranes but also the quantification of these interactions. To demonstrate this capability, we applied the assay to measure the affinity of the interaction between the soluble bacterial lectin CBM and a blood group B trisaccharide neoglycolipid (B-triNGL) presented in a nanodisc (ND). The reported Kd for this system, measured using a competitive assay, was 20.2 ± 2 μM. ESI-MS analysis of a solution of CBM (5 μM) and a B-triNGL-containing ND (4 μM ND; equivalent to 120 μM B-triNGL) reveals ion signal that correspond to free CBM and the 1:1 CBM–B-triNGL complex (Figure S12). The ND appears as a broad peak centered at m/z ∼8000 (Figure S12). To apply SLOMO, a solution of 5 μM CBM and 0.5–2 μM ND (equivalent to 15–60 μM B-triNGL) was added to the nanoESI tip, followed by a solution of 5 μM CBM and 10 μM ND (equivalent to 300 μM B-triNGL). Analysis of the time-resolved mass spectra shows an increase in the relative abundance of the CBM+B-triNGL complex with time (Figure 3j). The RFP/PL was found to vary from 26 to 55 (Figure 3k) at the concentrations tested, indicating that the efficiency by which the CBM–B-triNGL complex is detected is only 2–4% that of free CBM. The large RFP/PL values are, qualitatively, consistent with very different pathways that lead to the free CBM and CBM–B-triNGL complex ions. Specifically, the CBM–B-triNGL complex originates from the ternary CBM–B-triNGL–ND complexes late in the ESI process. The small relative RF of the CBM–B-triNGL–ND complex is likely attributable to the large size and hydrophilicity (low surface activity) of the ND. Analysis of the concentration-dependent fraction of ligand-bound CBM (Figure 3l) yields a Kd,app of 1.2 ± 0.2 mM, while the RF-corrected Kd of 28.1 ± 3.0 μM is in excellent agreement with the reported value.46
The ability to directly detect and quantify the binding of soluble proteins and model-membrane-bound ligands with SLOMO represents a significant methodological advance in the analysis of interactions between soluble proteins and their membrane-bound receptors. It opens up the possibility of applying native MS to quantify cellular receptor interactions in a membrane environment, information that will shed important insights into diverse cellular processes, including bacterial and viral infections, immune system regulation, and various diseases such as cancer and neurodegeneration.
Conclusions
Native MS is a powerful label- and immobilization-free assay for detecting and deducing the stoichiometries of noncovalent biomolecular interactions in vitro and is increasingly being used to quantify binding thermochemistry. However, the widespread adoption of the method for quantitative studies has been hindered by the nonuniform RFs of the interacting species and their complexes. While there exist methods to account for differential ESI-MS RFs, these have been largely limited to conventional pump-driven ESI sources, which tend to consume large, and often prohibitive, amounts of sample. Due to the small sample amount requirements, nanoESI, performed using tips pulled from glass capillaries, is used almost exclusively for native MS studies. In the present work, we show how this longstanding and significant challenge in native MS can be overcome with SLOMO nanoESI-MS. The assay, which is implemented with static nanoESI emitters, relies on the continuous monitoring of interacting species and their complexes under nonhomogeneous solution conditions. Changes in the absolute ion signals of free and bound forms as the system approaches or moves away from a steady-state concentration condition allows the relative RF and Kd of a biomolecular interaction to be determined from a single measurement.
The reliability and ease of use of SLOMO is demonstrated by affinity measurements performed on a series of biomolecular complexes of varying sizes, chemical properties, and affinities. Notably, the affinities measured for the model systems agree, within factor of 2, with reported values. Moreover, the corrected (for RF) Kd values measured by SLOMO were insensitive to the choice of instrumental parameters and exhibited no significant tip-to-tip variability. Applications of SLOMO to interactions between human and bacterial lectins with a single-chain antibody, a glycoprotein antigen, and glycolipids displayed in a model membrane showcase the tremendous power, versatility, and sensitivity of the assay for quantifying the stoichiometry and affinity of biomolecular interactions relevant to human health and disease. Given the growing reliance on native MS for the analysis of biomolecular complexes, the SLOMO technique is expected to be of considerable interest and importance to academic and industrial researchers.
Table 1. Comparison of Affinities (Kd) of Three Biomolecular Interactions (Van–AcAA, PT–STI, and BLG–BLG) Measured by SLOMO nanoESI-MS with Literature Valuesa.
| system | apparent Kd (μM) | corrected Kd (μM) | reported Kd (μM) |
|---|---|---|---|
| Van–AcAAb | 378 ± 36 | 32 ± 1 | 63 ± 13e |
| PT–STIc,d | 0.2 ± 0.1 | 0.5 ± 0.1 | 0.67f |
| 28 ± 9 | 0.8 ± 0.3 | ||
| BLG–BLGb | 1.9 ± 0.8 | 3.0 ± 0.5 | 7.0g |
Included are the apparent Kd (without correction for RF) and the corrected Kd (correction for RF) measured by SLOMO. Errors correspond to one standard deviation.
Measurements were performed in ammonium acetate (200 mM, pH 6.9, and 25 °C) solutions.
Measurements were performed in ammonium acetate (200 mM, pH 4.5, and 25 °C) solutions.
Two sets of data were obtained for the same solutions using different instrumental parameters.
Value taken from ref (48). Measurements were performed in 100 mM phosphate buffer (pH 7.0, 25 °C).
Value taken from ref (9). Measurements were performed in 25 mM potassium acetate and 10 mM calcium chloride buffer (pH 4.5, 25 °C).
Value taken from ref (55). Measurements were performed in phosphate buffer (pH 6.9, ionic strength of 0.13).
Acknowledgments
The authors acknowledge the Natural Sciences and Engineering Research Council of Canada (J.S.K.), the Canada Foundation for Innovation (J.S.K.), the Alberta Innovation and Advanced Education Research Capacity Program (J.S.K.), Canadian Institutes of Health Research (Y.S.P., D.C., N.D.), the Consortium Québécois pour le Recherche sur le Médicament (Y.S.P., D.C., N.D.), and the Canada Excellence Research Chairs (L.K.M.) Program for generous funding. The authors thank Professors T. Lowary (University of Alberta) for the B trisaccharide neoglycolipid and C. Cairo (University of Alberta) for the carbohydrate recognition domain of human galectin 3. Plasmids for expression of SARS-CoV-2 S protein and RBD proteins were generously provided by F. Krammer (Icahn School of Medicine at Mount Sinai, produced under NIAID Centers of Excellence for Influenza Research and Surveillance (CEIRS) contract HHSN272201400008C). This project was funded in part with Federal funds from the National Institute of Allergy and Infectious Diseases, National Institutes of Health, Department of Health and Human Services, under contract no. HHSN272201400004C (S.M.T.).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.2c00215.
Additional details about proteins and reagents, data analysis procedures and related equations, ITC data, summary of Van–AcAA affinities, SLOMO data, table of glycan compositions of free and GAL-3C-bound RBD; and representative ESI mass spectra (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Johnson E. R.; Keinan S.; Mori-Sánchez P.; Contreras-García J.; Cohen A. J.; Yang W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. 10.1021/ja100936w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamauchi O. Noncovalent Interactions in Biocomplexes. Phys. Sci. Rev. 2016, 1 (4), 20160001. 10.1515/psr-2016-0001. [DOI] [Google Scholar]
- Stoney R.; Robertson D. L.; Nenadic G.; Schwartz J.-M. Mapping Biological Process Relationships and Disease Perturbations within a Pathway Network. npj Syst. Biol. Appl. 2018, 4, 22. 10.1038/s41540-018-0055-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stelzl U.; Worm U.; Lalowski M.; Haenig C.; Brembeck F. H.; Goehler H.; Stroedicke M.; Zenkner M.; Schoenherr A.; Koeppen S.; Timm J.; Mintzlaff S.; Abraham C.; Bock N.; Kietzmann S.; Goedde A.; Toksöz E.; Droege A.; Krobitsch S.; Korn B.; Birchmeier W.; Lehrach H.; Wanker E. E. A Human Protein-Protein Interaction Network: A Resource for Annotating the Proteome. Cell 2005, 122, 957–968. 10.1016/j.cell.2005.08.029. [DOI] [PubMed] [Google Scholar]
- Bacon K.; Blain A.; Bowen J.; Burroughs M.; McArthur N.; Menegatti S.; Rao B. M. Quantitative Yeast–Yeast Two Hybrid for the Discovery and Binding Affinity Estimation of Protein–Protein Interactions. ACS Synth. Biol. 2021, 10, 505–514. 10.1021/acssynbio.0c00472. [DOI] [PubMed] [Google Scholar]
- Stynen B.; Tournu H.; Tavernier J.; Van Dijck P. Diversity in Genetic In Vivo Methods for Protein-Protein Interaction Studies: From the Yeast Two-Hybrid System to the Mammalian Split-Luciferase System. Microbiol. Mol. Biol. Rev. 2012, 76, 331–382. 10.1128/MMBR.05021-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanowitz M.; von Zastrow M.. Identification of Protein Interactions by Yeast Two-Hybrid Screening and Coimmunoprecipitation. In Receptor Signal Transduction Protocols; Willars G. B., Challiss R. A. J., Eds.; Methods in Molecular Biology, Vol. 259; Humana Press: Totowa, NJ, 2004; pp 353–369. [DOI] [PubMed] [Google Scholar]
- Su H.; Xu Y. Application of ITC-Based Characterization of Thermodynamic and Kinetic Association of Ligands With Proteins in Drug Design. Front. Pharmacol. 2018, 9, 1133. 10.3389/fphar.2018.01133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velazquez-Campoy A.; Leavitt S. A.; Freire E.. Characterization of Protein-Protein Interactions by Isothermal Titration Calorimetry. In Protein-Protein Interactions: Methods and Applications; Meyerkord C. L., Fu H., Eds.; Methods in Molecular Biology, Vol. 1278; Springer New York: New York, NY, 2015; pp 183–204. [DOI] [PubMed] [Google Scholar]
- Douzi B.Protein–Protein Interactions: Surface Plasmon Resonance. In Bacterial Protein Secretion Systems: Methods and Protocols; Journet L., Cascales E., Eds.; Methods in Molecular Biology, Vol. 1615; Springer New York: New York, NY, 2017; pp 257–275. [DOI] [PubMed] [Google Scholar]
- Becker W.; Bhattiprolu K. C.; Gubensäk N.; Zangger K. Investigating Protein–Ligand Interactions by Solution Nuclear Magnetic Resonance Spectroscopy. Chem. Phys. Chem. 2018, 19, 895–906. 10.1002/cphc.201701253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Larsen K.; Thygesen M. B.; Guillaumie F.; Willats W. G. T.; Jensen K. J. Solid-Phase Chemical Tools for Glycobiology. Carbohydr. Res. 2006, 341, 1209–1234. 10.1016/j.carres.2006.04.045. [DOI] [PubMed] [Google Scholar]
- Wienken C. J.; Baaske P.; Rothbauer U.; Braun D.; Duhr S.; et al. Protein-binding assays in biological liquids using microscale thermophoresis. Nat. Commun. 2010, 1, 100. 10.1038/ncomms1093. [DOI] [PubMed] [Google Scholar]
- Soltermann F.; Foley E. D. B.; Pagnoni V.; Galpin M.; Benesch J. L. P.; Kukura P.; Struwe W. B. Angew. Chem., Int. Ed. 2020, 59, 10774–10779. 10.1002/anie.202001578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sonn-Segev A.; Belacic K.; Bodrug T.; Young G.; VanderLinden R. T.; Schulman B. A.; Schimpf J.; Friedrich T.; Dip P. V.; Schwartz T. U.; Bauer B.; Peters J.-M.; Struwe W. B.; Benesch J. L. P.; Brown N. G.; Haselbach D.; Kukura P. Quantifying the Heterogeneity of Macromolecular Machines by Mass Photometry. Nat. Commun. 2020, 11, 1772. 10.1038/s41467-020-15642-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loo J. A. Studying Noncovalent Protein Complexes by Electrospray Ionization Mass Spectrometry. Mass Spectrom. Rev. 1997, 16, 1–23. . [DOI] [PubMed] [Google Scholar]
- Daniel J. M.; Friess S. D.; Rajagopalan S.; Wendt S.; Zenobi R. Quantitative Determination of Noncovalent Binding Interactions Using Soft Ionization Mass Spectrometry. Int. J. Mass Spectrom. 2002, 216, 1–27. 10.1016/S1387-3806(02)00585-7. [DOI] [Google Scholar]
- Heck A. J. R.; van den Heuvel R. H. H. Investigation of Intact Protein Complexes by Mass Spectrometry. Mass Spectrom. Rev. 2004, 23, 368–389. 10.1002/mas.10081. [DOI] [PubMed] [Google Scholar]
- Daneshfar R.; Kitova E. N.; Klassen J. S. Determination of Protein-Ligand Association Thermochemistry Using Variable-Temperature Nanoelectrospray Mass Spectrometry. J. Am. Chem. Soc. 2004, 126, 4786–4787. 10.1021/ja0316972. [DOI] [PubMed] [Google Scholar]
- Marchand A.; Rosu F.; Zenobi R.; Gabelica V. Thermal Denaturation of DNA G-Quadruplexes and Their Complexes with Ligands: Thermodynamic Analysis of the Multiple States Revealed by Mass Spectrometry. J. Am. Chem. Soc. 2018, 140, 12553–12565. 10.1021/jacs.8b07302. [DOI] [PubMed] [Google Scholar]
- Cong X.; Liu Y.; Liu W.; Liang X.; Russell D. H.; Laganowsky A. Determining Membrane Protein–Lipid Binding Thermodynamics Using Native Mass Spectrometry. J. Am. Chem. Soc. 2016, 138, 4346–4349. 10.1021/jacs.6b01771. [DOI] [PubMed] [Google Scholar]
- Sharon M.; Robinson C. V. The Role of Mass Spectrometry in Structure Elucidation of Dynamic Protein Complexes. Annu. Rev. Biochem. 2007, 76, 167–193. 10.1146/annurev.biochem.76.061005.090816. [DOI] [PubMed] [Google Scholar]
- Laganowsky A.; Reading E.; Hopper J. T. S.; Robinson C. V. Mass Spectrometry of Intact Membrane Protein Complexes. Nat. Protoc. 2013, 8, 639–651. 10.1038/nprot.2013.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitova E. N.; El-Hawiet A.; Schnier P. D.; Klassen J. S. Reliable Determinations of Protein-Ligand Interactions by Direct ESI-MS Measurements. Are We There Yet?. J. Am. Soc. Mass Spectrom. 2012, 23, 431–441. 10.1007/s13361-011-0311-9. [DOI] [PubMed] [Google Scholar]
- Wang W.; Kitova E. N.; Klassen J. S. Influence of Solution and Gas Phase Processes on Protein–Carbohydrate Binding Affinities Determined by Nanoelectrospray Fourier Transform Ion Cyclotron Resonance Mass Spectrometry. Anal. Chem. 2003, 75, 4945–4955. 10.1021/ac034300l. [DOI] [PubMed] [Google Scholar]
- Báez Bolivar E. G.; Bui D. T.; Kitova E. N.; Han L.; Zheng R. B.; Luber E. J.; Sayed S. Y.; Mahal L. K.; Klassen J. S. Submicron Emitters Enable Reliable Quantification of Weak Protein–Glycan Interactions by ESI-MS. Anal. Chem. 2021, 93, 4231–4239. 10.1021/acs.analchem.0c05003. [DOI] [PubMed] [Google Scholar]
- Sun J.; Kitova E. N.; Klassen J. S. Method for Stabilizing Protein-Ligand Complexes in Nanoelectrospray Ionization Mass Spectrometry. Anal. Chem. 2007, 79, 416–425. 10.1021/ac061109d. [DOI] [PubMed] [Google Scholar]
- Mehmood S.; Marcoux J.; Hopper J. T. S.; Allison T. M.; Liko I.; Borysik A. J.; Robinson C. V. Charge Reduction Stabilizes Intact Membrane Protein Complexes for Mass Spectrometry. J. Am. Chem. Soc. 2014, 136, 17010–17012. 10.1021/ja510283g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin H.; Kitova E. N.; Klassen J. S. Quantifying Protein-Ligand Interactions by Direct Electrospray Ionization-Ms Analysis: Evidence of Nonuniform Response Factors Induced by High Molecular Weight Molecules and Complexes. Anal. Chem. 2013, 85, 8919–8922. 10.1021/ac401936x. [DOI] [PubMed] [Google Scholar]
- Young D.-S.; Hung H.-Y.; Liu L. K. An Easy and Rapid Method for Determination of Stability Constants by Electrospray Ionization Mass Spectrometry. Rapid Commun. Mass Spectrom. 1997, 11, 769–773. . [DOI] [Google Scholar]
- Gabelica V.; Galic N.; Rosu F.; Houssier C.; De Pauw E. Influence of Response Factors on Determining Equilibrium Association Constants of Non-Covalent Complexes by Electrospray Ionization Mass Spectrometry. J. Mass Spectrom. 2003, 38, 491–501. 10.1002/jms.459. [DOI] [PubMed] [Google Scholar]
- Pedro L.; Van Voorhis W. C.; Quinn R. J. Optimization of Electrospray Ionization by Statistical Design of Experiments and Response Surface Methodology: Protein–Ligand Equilibrium Dissociation Constant Determinations. J. Am. Soc. Mass Spectrom. 2016, 27, 1520–1530. 10.1007/s13361-016-1417-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gabelica V.; Rosu F.; De Pauw E. A Simple Method to Determine Electrospray Response Factors of Noncovalent Complexes. Anal. Chem. 2009, 81, 6708–6715. 10.1021/ac900785m. [DOI] [PubMed] [Google Scholar]
- Chitta R. K.; Rempel D. L.; Gross M. L. Determination of Affinity Constants and Response Factors of the Noncovalent Dimer of Gramicidin by Electrospray Ionization Mass Spectrometry and Mathematical Modeling. J. Am. Soc. Mass Spectrom. 2005, 16, 1031–1038. 10.1016/j.jasms.2005.04.001. [DOI] [PubMed] [Google Scholar]
- Wilcox J. M.; Rempel D. L.; Gross M. L. Method of Measuring Oligonucleotide–Metal Affinities: Interactions of the Thrombin Binding Aptamer with K+ and Sr2+. Anal. Chem. 2008, 80, 2365–2371. 10.1021/ac701903w. [DOI] [PubMed] [Google Scholar]
- Boeri Erba E.; Barylyuk K.; Yang Y.; Zenobi R. Quantifying Protein-Protein Interactions within Noncovalent Complexes Using Electrospray Ionization Mass Spectrometry. Anal. Chem. 2011, 83, 9251–9259. 10.1021/ac201576e. [DOI] [PubMed] [Google Scholar]
- Barylyuk K.; Gülbakan B.; Xie X.; Zenobi R. DNA Oligonucleotides: A Model System with Tunable Binding Strength to Study Monomer–Dimer Equilibria with Electrospray Ionization-Mass Spectrometry. Anal. Chem. 2013, 85, 11902–11912. 10.1021/ac402669e. [DOI] [PubMed] [Google Scholar]
- Root K.; Wittwer Y.; Barylyuk K.; Anders U.; Zenobi R. Insight into Signal Response of Protein Ions in Native ESI-MS from the Analysis of Model Mixtures of Covalently Linked Protein Oligomers. J. Am. Soc. Mass Spectrom. 2017, 28, 1863–1875. 10.1007/s13361-017-1690-3. [DOI] [PubMed] [Google Scholar]
- Hernández H.; Robinson C. Determining the stoichiometry and interactions of macromolecular assemblies from mass spectrometry. Nat. Protoc. 2007, 2, 715–726. 10.1038/nprot.2007.73. [DOI] [PubMed] [Google Scholar]
- Hilton G. R.; Benesch J. L. P. Two Decades of Studying Non-Covalent Biomolecular Assemblies by Means of Electrospray Ionization Mass Spectrometry. J. R. Soc. Interface 2012, 9, 801–816. 10.1098/rsif.2011.0823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu F.; Zhao S.; Yu B.; Chen Y.-M.; Wang W.; Song Z.-G.; Hu Y.; Tao Z.-W.; Tian J.-H.; Pei Y.-Y.; Yuan M.-L.; Zhang Y.-L.; Dai F.-H.; Liu Y.; Wang Q.-M.; Zheng J.-J.; Xu L.; Holmes E. C.; Zhang Y.-Z. A New Coronavirus Associated with Human Respiratory Disease in China. Nature 2020, 579, 265–269. 10.1038/s41586-020-2008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higgins M. A.; Ficko-Blean E.; Meloncelli P. J.; Lowary T. L.; Boraston A. B. The Overall Architecture and Receptor Binding of Pneumococcal Carbohydrate-Antigen-Hydrolyzing Enzymes. J. Mol. Biol. 2011, 411, 1017–1036. 10.1016/j.jmb.2011.06.035. [DOI] [PubMed] [Google Scholar]
- Denisov I. G.; Grinkova Y. V.; Lazarides A. A.; Sligar S. G. Directed Self-Assembly of Monodisperse Phospholipid Bilayer Nanodiscs with Controlled Size. J. Am. Chem. Soc. 2004, 126, 3477–3487. 10.1021/ja0393574. [DOI] [PubMed] [Google Scholar]
- Ritchie T. K.; Grinkova Y. V; Bayburt T. H.; Denisov I. G.; Zolnerciks J. K.; Atkins W. M.; Sligar S. G.. Reconstitution of Membrane Proteins in Phospholipid Bilayer Nanodiscs. In Methods in Enzymology, Vol. 464; Düzgünes N., Ed.; Academic Press, 2009; pp 211–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Han L.; Xue X.; Roy R.; Kitova E. N.; Zheng R. B.; St-Pierre Y.; Lowary T. L.; Klassen J. S. Neoglycolipids as Glycosphingolipid Surrogates for Protein Binding Studies Using Nanodiscs and Native Mass Spectrometry. Anal. Chem. 2020, 92, 14189–14196. 10.1021/acs.analchem.0c03344. [DOI] [PubMed] [Google Scholar]
- Han L.; Kitova E. N.; Li J.; Nikjah S.; Lin H.; Pluvinage B.; Boraston A. B.; Klassen J. S. Protein–Glycolipid Interactions Studied in Vitro Using ESI-MS and Nanodiscs: Insights into the Mechanisms and Energetics of Binding. Anal. Chem. 2015, 87, 4888–4896. 10.1021/acs.analchem.5b00678. [DOI] [PubMed] [Google Scholar]
- Kitov P. I.; Han L.; Kitova E. N.; Klassen J. S. Sliding Window Adduct Removal Method (SWARM) for Enhanced Electrospray Ionization Mass Spectrometry Binding Data. J. Am. Soc. Mass Spectrom. 2019, 30, 1446–1454. 10.1007/s13361-019-02204-8. [DOI] [PubMed] [Google Scholar]
- Marsot A.; Boulamery A.; Bruguerolle B.; Simon N. Vancomycin. Clin. Pharmacokinet. 2012, 51, 1–13. 10.2165/11596390-000000000-00000. [DOI] [PubMed] [Google Scholar]
- Popieniek P. H.; Pratt R. F. A Fluorescent Ligand for Binding Studies with Glycopeptide Antibiotics of the Vancomycin Class. Anal. Biochem. 1987, 165, 108–113. 10.1016/0003-2697(87)90207-7. [DOI] [PubMed] [Google Scholar]
- MCKenzie H. A.; Sawyer W. H. Effect of pH on β-Lactoglobulins. Nature 1967, 214, 1101–1104. 10.1038/2141101a0. [DOI] [PubMed] [Google Scholar]
- Mercadante D.; Melton L. D.; Norris G. E.; Loo T. S.; Williams M. A. K.; Dobson R. C. J.; Jameson G. B. Bovine β-Lactoglobulin Is Dimeric Under Imitative Physiological Conditions: Dissociation Equilibrium and Rate Constants over the pH Range of 2.5–7.5. Biophys. J. 2012, 103, 303–312. 10.1016/j.bpj.2012.05.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khan S.; Ipsen R.; Almdal K.; Svensson B.; Harris P. Revealing the Dimeric Crystal and Solution Structure of β-Lactoglobulin at pH 4 and its pH and Salt Dependent Monomer–Dimer Equilibrium. Biomacromolecules 2018, 19, 2905–2912. 10.1021/acs.biomac.8b00471. [DOI] [PubMed] [Google Scholar]
- Burgos I.; Dassie S. A.; Villarreal M. A.; Fidelio G. D. Thermodynamic and Structural Analysis of Homodimeric Proteins: Model of β-Lactoglobulin. Biochim. Biophys. Acta - Proteins Proteomics 2012, 1824, 383–391. 10.1016/j.bbapap.2011.11.005. [DOI] [PubMed] [Google Scholar]
- Bello M.; Pérez-Hernández G.; Fernández-Velasco D. A.; Arreguín-Espinosa R.; García-Hernández E. Energetics of Protein Homodimerization: Effects of Water Sequestering on the Formation of β-Lactoglobulin Dimer. Proteins 2008, 70, 1475–1487. 10.1002/prot.21639. [DOI] [PubMed] [Google Scholar]
- Zimmerman J. K.; Barlow G. H.; Klotz I. M. Dissociation of β-Lactoglobulin near Neutral pH. Arch. Biochem. Biophys. 1970, 138, 101–109. 10.1016/0003-9861(70)90289-4. [DOI] [PubMed] [Google Scholar]
- Advedissian T.; Deshayes F.; Viguier M. Galectin-7 in Epithelial Homeostasis and Carcinomas. Int. J. Mol. Sci. 2017, 18, 2760. 10.3390/ijms18122760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dings R. P. M.; Miller M. C.; Griffin R. J.; Mayo K. H. Galectins as Molecular Targets for Therapeutic Intervention. Int. J. Mol. Sci. 2018, 19, 905. 10.3390/ijms19030905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ermakova E.; Miller M. C.; Nesmelova I. V.; López-Merino L.; Berbís M. A.; Nesmelov Y.; Tkachev Y. V.; Lagartera L.; Daragan V. A.; André S.; Cañada F. J.; Jiménez-Barbero J.; Solís D.; Gabius H.-J.; Mayo K. H. Lactose Binding to Human Galectin-7 (P53-Induced Gene 1) Induces Long-Range Effects through the Protein Resulting in Increased Dimer Stability and Evidence for Positive Cooperativity. Glycobiology 2013, 23, 508–523. 10.1093/glycob/cwt005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noll A. J.; Gourdine J.-P.; Yu Y.; Lasanajak Y.; Smith D. F.; Cummings R. D. Galectins Are Human Milk Glycan Receptors. Glycobiology 2016, 26, 655–669. 10.1093/glycob/cww002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Girotti M. R.; Salatino M.; Dalotto-Moreno T.; Rabinovich G. A. Sweetening the Hallmarks of Cancer: Galectins as Multifunctional Mediators of Tumor Progression. J. Exp. Med. 2020, 217, e20182041. 10.1084/jem.20182041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingram J. R.; Schmidt F. I.; Ploegh H. L. Exploiting Nanobodies’ Singular Traits. Annu. Rev. Immunol. 2018, 36, 695–715. 10.1146/annurev-immunol-042617-053327. [DOI] [PubMed] [Google Scholar]
- Lempp F. A.; Soriaga L.; Montiel-Ruiz M.; Benigni F.; Noack J.; Park Y.-J.; Bianchi S.; Walls A. C.; Bowen J. E.; Zhou J.; Kaiser H.; Joshi A.; Agostini M.; Meury M.; Dellota E.; Jaconi S.; Cameroni E.; Martinez-Picado J.; Vergara-Alert J.; Izquierdo-Useros N.; Virgin H. W.; Lanzavecchia A.; Veesler D.; Purcell L.; Telenti A.; Corti D. Lectins Enhance SARS-CoV-2 Infection and Influence Neutralizing Antibodies. Nature 2021, 598, 342–347. 10.1038/s41586-021-03925-1. [DOI] [PubMed] [Google Scholar]
- Gao C.; Zeng J.; Jia N.; Stavenhagen K.; Matsumoto Y.; Zhang H.; Li J.; Hume A. J.; Mühlberger E.; van Die I.; Kwan J.; Tantisira K.; Emili A.; Cummings R. D.. SARS-CoV-2 Spike Protein Interacts with Multiple Innate Immune Receptors. bioRxiv (Biochemistry), July 30, 2020, 227462. 10.1101/2020.07.29.227462. [DOI]
- Zhang Y.; Zhao W.; Mao Y.; Chen Y.; Zheng S.; Cao W.; Zhu J.; Hu L.; Gong M.; Cheng J.; Yang H. O-Glycosylation Landscapes of SARS-CoV-2 Spike Proteins. Front. Chem. 2021, 9, 689521. 10.3389/fchem.2021.689521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao C.; Wei M.; McKitrick T. R.; McQuillan A. M.; Heimburg-Molinaro J.; Cummings R. D. Glycan Microarrays as Chemical Tools for Identifying Glycan Recognition by Immune Proteins. Front. Chem. 2019, 7, 833. 10.3389/fchem.2019.00833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lenza M. P.; Oyenarte I.; Diercks T.; Quintana J. I.; Gimeno A.; Coelho H.; Diniz A.; Peccati F.; Delgado S.; Bosch A.; Valle M.; Millet O.; Abrescia N. G. A.; Palazón A.; Marcelo F.; Jiménez-Osés G.; Jiménez-Barbero J.; Ardá A.; Ereño-Orbea J. Structural Characterization of N-Linked Glycans in the Receptor Binding Domain of the SARS-CoV-2 Spike Protein and Their Interactions with Human Lectins. Angew. Chemie Int. Ed. 2020, 59, 23763–23771. 10.1002/anie.202011015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gimeno A.; Delgado S.; Valverde P.; Bertuzzi S.; Berbís M. A.; Echavarren J.; Lacetera A.; Martín-Santamaría S.; Surolia A.; Cañada F. J.; Jiménez-Barbero J.; Ardá A. Minimizing the Entropy Penalty for Ligand Binding: Lessons from the Molecular Recognition of the Histo Blood-Group Antigens by Human Galectin-3. Angew. Chemie Int. Ed. 2019, 58, 7268–7272. 10.1002/anie.201900723. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Citations
- Gao C.; Zeng J.; Jia N.; Stavenhagen K.; Matsumoto Y.; Zhang H.; Li J.; Hume A. J.; Mühlberger E.; van Die I.; Kwan J.; Tantisira K.; Emili A.; Cummings R. D.. SARS-CoV-2 Spike Protein Interacts with Multiple Innate Immune Receptors. bioRxiv (Biochemistry), July 30, 2020, 227462. 10.1101/2020.07.29.227462. [DOI]