An International Study Evaluating Elemental Analysis

Short abstract

Based on statistical analysis of CHN combustion results of 18 international service providers, it is determined that the ±0.4% deviation most commonly required by chemistry journals is not justified.

Introduction

Fritz Pregl was awarded the 1923 Nobel prize for the “Quantitative Micro-Analysis of Organic Substances” due to his contributions in developing revolutionary methods and balance technology that enabled improvements to where milligram quantities of samples could be analyzed for elemental composition, a monumental step from the macro quantities needed prior. Microanalysis emerged as a leading characterization technique for purity by journals publishing synthetic compounds and is still widely used today. In undergraduate chemistry, percent element composition determination from combustion analysis is one of the first concepts that students learn. Another primary lesson in undergraduate chemistry is understanding what the value obtained in a measurement means. In typical measurements, the digits prior to the last digit are called “certain digits”, and the last digit is called an “uncertain digit” which has an uncertainty associated with it (i.e., ±2). For elemental analysis, the majority of journals require ±0.4% of each value to confirm sufficient purity for publication (representative journal requirements from author guidelines shown in Table 1). For some publishers (e.g., Wiley), there appears to be uniform guidelines among sister journals, while for ACS and RSC publications, the guidelines vary from journal to journal, with some specifying differing acceptable ranges, and others not having an acceptable range specified. Elsevier journals made no comment as to elemental analysis requirements with an exception being the Elsevier-owned Cell branded journals (i.e., Chem), with requirements of ±0.4% specified. The possibility of obtaining acceptable results for pure compounds that show air or temperature sensitivity has been explicitly recognized by some journals (e.g., Organometallics), and appropriate guidance issued that recommends, but does not mandate, acquiring elemental analysis data.¹

Table 1. Selected Author Guidelines Regarding Requirements for Elemental Analysis.

journal	guidelines
Nature Chemistry	Evidence of sample purity is requested for each new compound. Methods for purity analysis depend on the compound class. For most organic and organometallic compounds, purity may be demonstrated by high field 1H NMR or 13C NMR data, although elemental analysis (±0.4%) is encouraged for small molecules.
Journal of Organic Chemistry	Found values for carbon, hydrogen, and nitrogen should be within 0.4% of the Calcd values for the proposed formula. The need to include fractional molecules of solvent or water in the molecular formula to improve the fit of the data usually reflects incomplete purification of the sample.
Inorganic Chemistry	For all new compounds, evidence adequate to establish both identity and degree of purity (homogeneity) must be provided. For known compounds prepared by a new or modified synthetic procedure, the types of physical and spectroscopic data that were found to match cited literature data should be identified, and purity documentation should be provided.
Organometallics	Organometallics strongly encourages the characterization of all new compounds by elemental analysis. For such data, agreement of calculated and found values within 0.4% (e.g., Calcd, 20.14%; Found, 20.54%) is considered acceptable. For deviations slightly outside the accepted range, authors are encouraged to provide an explanation in the relevant paragraph of the Experimental section, and to include a statement such as “although these results are outside the range viewed as establishing analytical purity, they are provided to illustrate the best values obtained to date.”
Organic Letters	To support the molecular formula assignment, either the HRMS data accurate within 5 ppm, or combustion elemental analysis data accurate within 0.4%, must be reported for new compounds.
Journal of the American Chemical Society	Evidence for elemental constitution must be provided by either elemental analysis (e.g., combustion analysis, microprobe analysis) or mass spectrometry. While an X-ray diffraction structure is not considered definitive proof of elemental composition, it is acceptable evidence for composition providing that the results of other physical methods concerning the characterization are conclusive.
Angewandte Chemie	Data should be provided to an accuracy within ±0.4%.
European Journal of Inorganic Chemistry	Data should be provided to an accuracy within ±0.4%.
Chemistry—A European Journal	Data should be provided to an accuracy within ±0.4%.
Chemical Science	For identification purposes for new compounds, an accuracy to within ±0.3% is expected, and in exceptional cases, to within ±0.5% is required. If a molecular weight is to be included, the appropriate form is [Found: C, 63.1; H, 5.4%; M (mass spectrum), 352 (or simply M+, 352). C13H13NO4 requires C, 63.2; H, 5.3%; M, 352].
Chemical Communications	Elemental analysis (within ±0.4% of the calculated value) is required to confirm 95% sample purity and corroborate isomeric purity.
Dalton Transactions	This should include elemental analyses that agree to within ±0.4% of the calculated values.
European Journal of Organic Chemistry	Data should be provided to an accuracy within ±0.4%.
Organic and Biomolecular Chemistry	High-resolution mass spectroscopy (HRMS), with a found value within 0.003 m/z unit of the calculated value of a parent-derived ion. Elemental analysis data may be provided if HRMS is not available.
Chem Catalysis	Evidence of purity is a requirement for all new compounds. The appropriate methods are dependent on the type of compounds reported. For organic and organometallic compounds, high-field 1H and 13C NMR can be used to show purity. Ideally, elemental analysis (±0.4%) should be included for small molecules.
Chem	Evidence of purity is a requirement for all new compounds. The appropriate methods are dependent on the type of compounds reported. For organic and organometallic compounds, high-field 1H and 13C NMR can be used to show purity. Ideally, elemental analysis (±0.4%) should be included for small molecules.

A basis for defining purity is from the book “ACS Reagent Chemicals: Specifications and Procedures for Reagents and Standard-Grade Reference Materials” which defines the accepted standards for purity of reagents and standard-grade reference materials.² Chemical suppliers often list the reagents as “high purity”, and often these cannot feasibly (by labor, financial, or technical methods) be purified further. We believe that, at maximum, the standards for synthetic samples be no greater than the reagents they are derived from as they will likely be of lower purity since some new molecules are multistep syntheses, and some reagents are only available as technical grade. The assay tests to define reagent-grade by the ACS are done by either volumetric or gravimetric analytical procedures and defined as “a substance of sufficient purity to be used in most chemical analyses or reactions” rather than a minimum %. It is noted that these are for “freshly opened containers” which is not the case for the majority of synthetic experiments, and they state that “age, humidity, light, or headspace contamination is recognized” and that the chemist is “cautioned to take appropriate steps to ensure the continued purity of the reagents and standards, especially after opening the container.” The term ACS grade is not universal but rather specific for each chemical as they state that “when a specification is first prepared, it usually will be based on the highest level of purity (of the reagent or to which it applies) that is competitively available” where the term competitively available “is understood to mean that the material is available from two or more suppliers.” This meaning that ACS reagent grade is variable based on the reagent and can be revised as commercial availability and sources change. Most importantly, there is no guideline for the purity of a newly synthesized compound.

Most often, elemental analysis data is obtained externally by a third party where no raw data or error bars are provided for the measurement. Accordingly, journals do not require any evidence for these values, contrary to NMR spectra for example, and there have been controversial incidents over the years.^3,4 Reasons for potential dishonesty may arise from the challenges in obtaining EA data and perceived unrealistic standards, in addition to the lack of requirement for providing any raw analytical data. Most departments do not have on-site facilities, and thus, samples must be shipped causing delays in obtaining the data and potentially delays in publishing urgent results. This issue is further exacerbated for less stable or air-sensitive samples where shipment can result in degradation of the sample over time. Furthermore, operator error or calibration problems, which have been identified as some of the most common sources of error in analytical chemistry, are completely out of the investigating laboratories’ hands when third party laboratories are used.⁵

In considering the term “pure”, 99% seems to be a reasonable bar, although in some cases this may not be nearly pure enough for the required application; conversely, it may be more than pure enough for the intended use of the sample. The ±0.4% guideline for journals would actually require that some samples be 99.6% pure, without factoring in the error associated with measurement and what the trace impurities are. Considering an extreme example, a sample of pure carbon (i.e., C₆₀) should be 100%, but if it was contaminated with 1% NaCl, the data obtained would be 99% which is 1% off the result. Alternatively, any organic sample of 99% purity that would be contaminated by 1% carbon would be 1% higher for carbon than expected. This also does not factor in the error associated with the measurement. Although two extreme scenarios, these suggest that ±0.4% is not reasonable. Examining the literature, we have not been able to determine why ±0.4% was chosen as the standard requirement. Finally, in typical organic compounds, C is of a higher mass percentage than H and N. If carbon is 25% and hydrogen 4%, clearly a 0.4% difference in carbon is less important than a 0.4% difference in hydrogen, but the acceptable percentage difference is the same for both elements. Similarly, the stated accuracy of different instruments varies from element to element, again raising questions about the validity of using a uniform 0.4% criterion for all elements. Finally, some providers perform single analysis and some double analysis or more. There is little to no guidance as to whether authors should use an average or on how to treat the error between the obtained values for replicate analyses. Anecdotally, often the “best” measurement out of the two or more replicates is chosen as the data to present, or worse, the best for each element among the replicates.

While we were undertaking this work, Kowol and co-workers published a study that examined six compounds (3-hydroxy-2-methyl-pyr-4-one, 8-hydroxyquinoline, ferrocene, cobalt(II) acetylacetonate, bis(8-hydroxyquinolato)zinc, and N-acetyl-l-cysteine) by elemental analysis in triplicate by various instruments at four different locations.⁶ One was done in-house at the University of Vienna, and the other three were performed by companies in Europe. They determined that the deviation was quite low among measurements but was still greater than the typical deviation reported in a survey of results from the literature. They suggested that many results in the literature appear to be too precise, thus raising questions about the integrity of elemental analysis data in the literature at large.

Results and Discussion

Samples of the 5 compounds (Table 2 with theoretical mass values for C, H, and N) were sent to 17 laboratories and also analyzed in-house by the Chitnis lab at Dalhousie University. Duplicate analyses were not requested, but 9 laboratories provided them as a matter of course. For selected laboratories, a second batch of selected samples was sent again. For the purpose of this study, each individual analysis obtained for C, H, and N is treated as a single data point. In total, 436 data points were obtained, 146 for C, 146 for H, and 144 for N (on two occasions, data for N was not given).

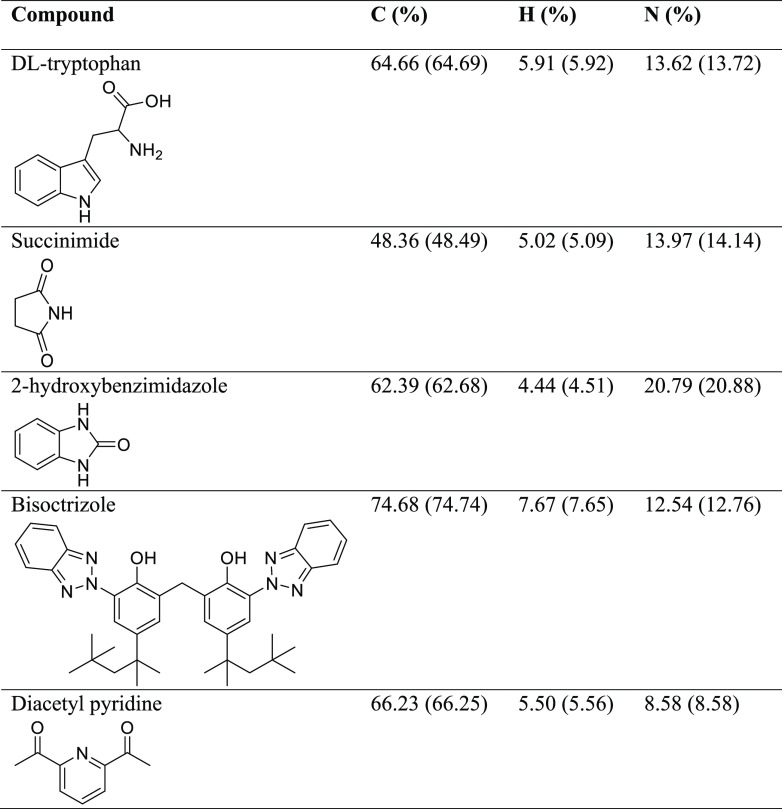
Table 2. Five Compounds Studied Here along with Their Average Measured and Theoretical (in Parentheses) C, H, and N Analysis Values.

A data point was denoted “Fail” if it was not within 0.40% of the theoretical value and “Acceptable” if it was within 0.40% of the theoretical value, as this is the most commonly indicated number in the guidelines for journals. In total, 47 “Fail” results were obtained (10.78% Fail): 24 for C (16.44% Fail), 3 for H (2.05% Fail), and 20 for N (13.89% Fail) (Table 3). Hydrogen clearly returns far fewer “Fail” results, which would be expected as 0.4% is a much greater proportion of the total H content, than the other two elements in most small organic compounds. The bisoctrizole with the highest H content returned only one “Fail” H result across 32 measurements. Carbon returns statistically significantly more “Fail” results, which again would be expected as 0.4% is a lesser proportion of the total C content than the other two elements in most small organic compounds. However, as there is no guidance from journals to treat H or C differently to N, we define 0.4% as the threshold for “Fail” for H and C. A Chi-Square test of homogeneity⁷ found that the proportion of “Fail” results did not vary significantly between the 5 compounds (χ² = 2.5069, df = 4, p-value = 0.6434), suggesting that there is no systematic error with any of the samples.

Table 3. Incidence of Obtaining a “Fail” Result for the Compounds Studied and Each Element Analyzed, with CI Values Expressed as Percentages for Ease of Interpretation.

	sample size	fail results	fail results (%)	95% CI for fail results (%)
all	436	47	10.78	(8.18–14.06)
dl-tryptophan	81	6	7.41	(3.15–15.53)
succinimide	87	10	11.49	(6.18–20.07)
2-hydroxybenzimidazole	90	11	12.22	(6.8–20.74)
bisoctrizole	95	13	13.68	(8.04–22.15)
diacetylpyridine	83	7	8.43	(3.89–16.66)
carbon	146	24	16.44	(11.24–23.35)
hydrogen	146	3	2.05	(0.43–6.14)
nitrogen	144	20	13.89	(9.1–20.56)

Agresti–Coull approximate binomial proportion confidence intervals⁸⁻¹⁰ for the proportion of “Fail” results for the compounds and elements studied are presented in Table 3 below. For ease of interpretation, results are multiplied by 100 in order to be expressed as percentages. Each confidence interval (CI) tells us the range of values within which the true percentage of “Fail” results is likely to lie, for the chemical variable in question. As an example, if we consider the 95% CI for H (0.43–6.14), this tells us that we can be highly confident that the true percentage of H samples that will receive a “Fail” result in an elemental analysis will be between 0.43% and 6.14%. It would be possible, but highly unlikely, to observe a percentage of “Fail” results beyond these bounds when analyzing H samples.

In general, the distributions of the observed C, H, and N analysis values were centered at or close to the corresponding theoretical values, which is to be expected. When considering results for all samples, a one-sample t-test showed that the average difference between an element’s analysis value and theoretical value was nonzero [t = −3.5633, df = 435, p-value <0.01, mean = −0.088, 95% CI (−0.137 to −0.039)]. However, the associated effect size was small (Cohen’s d = −0.1707),¹¹ indicating that in a practical sense all samples may be considered to be as pure as advertised by the manufacturer. The 97% pure 2-hydroxybenzimidazole returned average values furthest from the theoretical value (the other 4 compounds being advertised 99% pure), being 0.29% low in carbon on average.

The difference between the analysis value and theoretical value for each sample in our study was computed, with results summarized in the descriptive box plots presented in Figure 2. Each of these box plots presents key information about the spread and skewness of these observed difference values, for a specific element within a specific compound, and shows the extent to which the difference values are symmetrically or asymmetrically distributed. To aid in the interpretation of the box plots presented within the paper, Figure 1 is included as a visual guide. Here, Q1, the median, and Q3 denote the values below which 25%, 50%, and 75% of the observed values lie, respectively. The box (in blue) spans the range of values from Q1 to Q3, known as the interquartile range (IQR). The lines extending from the box end either at the minimum and maximum values observed or, in the event that extreme values a.k.a. outliers are observed, at the lower fence (Q1–1.5 × IQR) and upper fence (Q3 + 1.5 × IQR) [see, e.g., Plotly (2022)].¹² Any outliers are denoted by points beyond these fences.

Figure 2.

Box plots of differences between analysis and theoretical values for each element, across the five different compounds, with the C outlier from Midwest Micro Analytical Laboratories not shown.

Figure 1.

Box plot visual guide, included for reference purposes.

From the results, it can be observed that diacetyl pyridine exhibited the smallest overall variation from theoretical values, with differences ranging from −0.65% to 0.55%. Larger differences were obtained for the other compounds, most notably a difference of −7.81% for one succinimide carbon measurement.

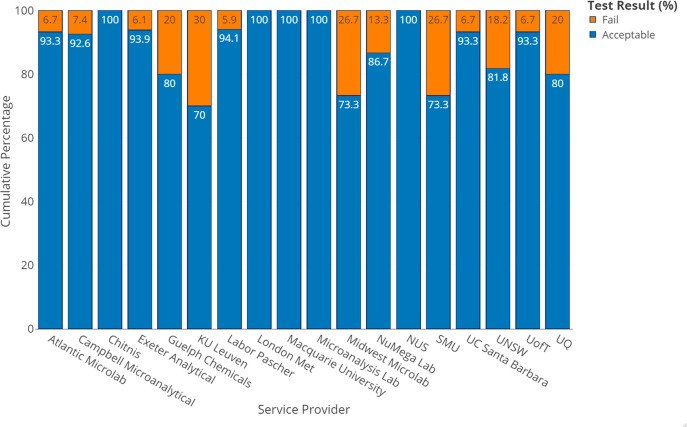
Figure 3 depicts the percentages of “Acceptable” and “Fail” results obtained from each of the service providers used. Four of the service providers and the Chitnis laboratory returned 100% “Acceptable” results, while at the other end of the spectrum, five service providers returned results with a 20% or higher “Fail” rate, with a maximum of 30% “Fail” results received from one provider.

Figure 3.

Percentages of “Acceptable” and “Fail” results for each of the 18 service providers used, across all 5 compounds for C, H, and N.

A Kruskal–Wallis rank sum test¹³ was used to compare the distributions of the differences between the analysis values recorded by each service provider and the corresponding theoretical values. A statistically significant result (χ² = 30.712, df = 17, p-value = 0.02164) was obtained when considering the full data set, but a posthoc Dunn’s test for pairwise multiple comparisons¹⁴ found no significant differences between specific pairs of providers, when controlling the false discovery rate (FDR)¹⁵ at the 5% level. These results indicate that no service provider was systematically prone to returning “Fail” results for any of the compounds.

However, if service providers’ analysis results for individual elements—rather than for all compounds—are compared separately, e.g., if only the service providers’ carbon analysis results are compared, then numerous pairs of providers had statistically significantly different distributions of differences between recorded analysis values and theoretical values, for each of the three elements (see section 3 of the Supporting Information). Box plots comparing the service providers’ results are presented in Figures 4–6 below, for C, H, and N samples, respectively. These results suggest that there is a degree of variability in elemental analysis results between service providers, particularly for nitrogen samples, which may be due to the different instrumental methods used for quantifying each element.

Figure 4.

Box plots of observed differences between analysis and theoretical values for C, for all service providers in this study, with the C outlier from Midwest Micro Analytical Laboratories not shown.

Figure 6.

Box plots of observed differences between analysis and theoretical values for N, for all service providers in this study.

Figure 5.

Box plots of observed differences between analysis and theoretical values for H, for all service providers in this study.

Experimental Section

Five air-stable organic molecules were selected that contain carbon, nitrogen, and hydrogen, the three primary elements required for synthetic verification: dl-tryptophan (C₁₁H₁₂N₂O₂, Aldrich, ≥99%), succinimide (C₄H₅NO₂, BDH, 99%), 2-hydroxybenzimidazole (C₇H₆N₂O, Aldrich, 97%), bisoctrizole (C₄₁H₅₀N₆O₂, Aldrich, 99%), and diacetyl pyridine (C₉H₉NO₂, Aldrich, 99%). The samples all originate from the same sample container as they were purchased by one lab (Dutton, La Trobe), distributed into vials in a N₂ glovebox with polyethylene lined caps, and shipped to the other three collaborators via courier, with a 1–3 week shipping time experienced. Upon receipt, the samples were transferred into vials for shipping to the service providers. While there may be some change in the sample from shipping, this is no different than shipping a sample to a microanalysis lab and thus simulates a real experiment. All laboratories involved regularly send samples packed in this fashion for elemental analysis. The laboratories used were from the USA (Atlantic Microlab, Inc.; Microanalysis, Inc.; UC Santa Barbara Marine Science Institute; Midwest Microlab; NuMega Resonance Laboratories), Australia (Macquarie University; The University of New South Wales; The University of Queensland), New Zealand (Otago University), Singapore (The National University of Singapore), UK (Exeter Analytical, London Metropolitan), Belgium (KU Leuven), Germany (Mikroanalytisches Labor Pascher), Canada (Saint Mary’s University, University of Toronto, Guelph Chemical Laboratory), and the laboratory of author Saurabh Chitnis. In the Chitnis lab, analysis was performed on an Elementar UNICUBE CHNS/O analyzer interfaced with a Radwag MYA 4Y microbalance. Helium was used as the carrier gas. Details of the instruments used in each external laboratory are in the Supporting Information. Additional details on the statistical analyses conducted are also found in the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acscentsci.2c00325.

• NMR spectra of samples as shipped from The Dutton Lab, a spreadsheet of all the data obtained from the service providers, details of all statistical analyses, and additional tables and figures (PDF)

• Transparent Peer Review report available (PDF)

• Raw data file (XLSX)

Author Contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

We are grateful to the Welch Foundation (Grant AA-1846), the National Science Foundation (Award 1753025), the ARC (FT17010007 and DP200100013), the Natural Sciences and Engineering Research Council of Canada (NSERC-RGPIN-05574), and the Engineering and Physical Sciences Research Council (EP/R026912/1) for their generous support of this work.