Unidirectionally excited phonon polaritons in high-symmetry orthorhombic crystals

Abstract

Advanced control over the excitation of ultraconfined polaritons—hybrid light and matter waves—empowers unique opportunities for many nanophotonic functionalities, e.g., on-chip circuits, quantum information processing, and controlling thermal radiation. Recent work has shown that highly asymmetric polaritons are directly governed by asymmetries in crystal structures. Here, we experimentally demonstrate extremely asymmetric and unidirectional phonon polariton (PhP) excitation via directly patterning high-symmetry orthorhombic van der Waals (vdW) crystal α-MoO₃. This phenomenon results from symmetry breaking of momentum matching in polaritonic diffraction in vdW materials. We show that the propagation of PhPs can be versatile and robustly tailored via structural engineering, while PhPs in low-symmetry (e.g., monoclinic and triclinic) crystals are largely restricted by their naturally occurring permittivities. Our work synergizes grating diffraction phenomena with the extreme anisotropy of high-symmetry vdW materials, enabling unexpected control of infrared polaritons along different pathways and opening opportunities for applications ranging from on-chip photonics to directional heat dissipation.

Directly patterning high-symmetry van der Waals crystal enables unidirectionally excited phonon polaritons.

INTRODUCTION

Phonon polaritons (PhPs) in anisotropic polar crystals exhibit exotic optical features (1, 2), which provide unique opportunities to control light at the nanoscale. Inherently, crystalline symmetries play a central role in controlling the excitation and propagation of PhPs. This is because lattice symmetries impose general constraints on the optical properties and thus have important consequences for polaritonic materials, where topology or dispersion of polaritons is closely related to symmetry. Among six crystal systems with anisotropy (except cubic), uniaxial materials supporting a single optical axis crystallize in hexagonal [e.g., SiC (3), hBN (4)], trigonal [e.g., α-quartz (5), calcite (6)], and tetragonal [e.g., SnO₂ (7)] crystal systems, while biaxial materials with two optical axes belong to orthorhombic [Fig. 1A; e.g., α-MoO₃ (8), α-V₂O₅ (9)], monoclinic [e.g., β-Ga₂O₃ (10)], and triclinic ones.

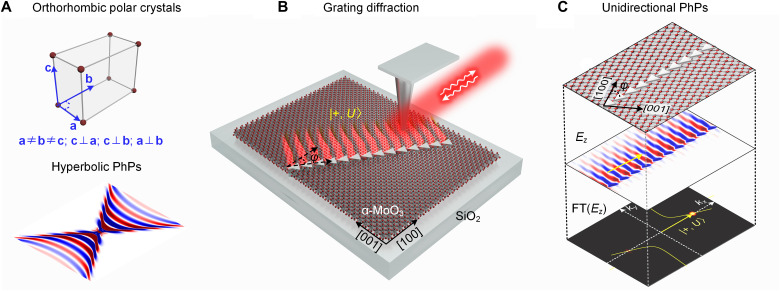
Fig. 1. Schematic of grating diffraction of unidirectional PhPs in high-symmetry orthorhombic crystals.

(A) The crystal structure and dipole launched hyperbolic PhPs (E_z electric field distribution) at the surface of (high symmetry) orthorhombic crystal α-MoO₃. (B) Schematic of unidirectional grating diffraction of PhPs via blazed grating in orthorhombic α-MoO₃. By changing the angle φ between the grating direction and α-MoO₃’s [100] crystal direction, it is possible to break the up-down mirror symmetry in diffraction [see FT(E_z) image in (C)], which enables the unidirectional diffraction of PhPs, as illustrated here for the ∣+ , U⟩ state. (C) Illustration of unidirectional PhPs. Upper layer: Top view of blazed grating and lattice of α-MoO₃; the blazed grating is oriented with an angle φ relative to α-MoO₃’s [100] crystal direction; middle layer: numerically simulated electric field distribution E_z of the grating-excited PhPs; bottom layer: Polaritonic isofrequency contours and Fourier Transform (FT) of the simulated E_z of PhPs (yielding the bright spots). The diffraction state is indicated as ∣+ , U⟩, where + indicates the direction of k (yellow arrow), and U marks the PhP diffraction on the up-side of the grating.

In particular, in-plane hyperbolic PhPs have been found in orthorhombic crystals, such as α-MoO₃ (8, 11) and α-V₂O₅ (9), which can propagate with long lifetime, long-range transport, ray-like collimation, and ultrahigh field confinement. However, because of the high symmetry of orthorhombic crystals, PhPs must propagate symmetrically with four mirror-symmetric beams. In contrast to high-symmetry orthorhombic crystals, monoclinic and triclinic lattices feature lower symmetries, with unequal axis lengths and nonorthogonal axial angles. In these scenarios, asymmetric hyperbolic shear polaritons can emerge in monoclinic β-Ga₂O₃, exhibiting tilted polariton wavefronts breaking mirror symmetry but with preserved rotational symmetry (10). This nontrivial asymmetry in polariton excitation cannot be expected in unpatterned high-symmetry crystals such as orthorhombic lattices with all orthogonal principal crystal axes. Here, we present extremely asymmetric (even unidirectional) excitations and diffraction of PhPs, leveraging linear gratings patterned over orthorhombic crystals (Fig. 1, B and C). We experimentally demonstrate that the interplay between periodic gratings and in-plane anisotropy can break the symmetry in momentum matching for polaritonic grating diffraction (bottom panel in Fig. 1C), hence enabling unidirectional diffraction of PhPs that propagate only on one side of the grating (middle panel in Fig. 1C). This marks a fundamental distinction from previous pioneering studies, which use background surrounding media, such as hybrid plasmonic structures (12, 13), photonic crystals (14, 15), or substrates (16–20), to indirectly drive the flow of polaritons within van der Waals (vdW) materials via weak contacts. Thereby, our work provides a direct recipe for robustly tailoring PhP excitation and propagation, particularly featuring extreme asymmetry, only using vdW materials and within vdW materials alone. So far, unidirectional propagation of surface plasmons and valley exciton polaritons has been realized by controlling optical spin-orbit coupling with a nano-slit (21), metamaterials (22), or plasmonic-transition metal dichalcogenide hybrid systems (12, 13). In these systems, the valley pseudospin couples to the transverse optical spin of metal plasmons, which can unidirectionally propagate along a nanowire or an asymmetrically grooved metasurface. However, plasmons typically suffer from high optical loss, and valley excitons feature short lifetimes at room temperature, both posing limitations on long-range transport for on-chip photonic platforms. On the contrary, our work uses low-loss PhPs and a different mechanism for directionality control, providing a promising and ready-to-adopt approach toward directional and unidirectional polaritonic devices on-chip.

RESULTS

Grating phenomena have been extremely well studied in optics and photonics, yet the diffraction of in-plane anisotropic and spatially dispersive vdW polaritons in the presence of polaritonic gratings is still elusive, although it could offer interesting opportunities for controlling the PhPs’ directionality. For better understanding of polariton diffraction in in-plane anisotropic materials, we recall that in an isotropic medium with circular isofrequency contour (e.g., h-BN; see section S3), the diffraction of polaritons only depends on the grating period Λ and the polariton wavelength λ_p according to Λcosθ = mλ_p, where θ is the diffraction angle and m the diffraction order. To achieve diffraction orders different to m = 0, the grating period needs to be larger than the polariton wavelength (Λ > λ_p) at normal incidence. Compared to circular PhPs in h-BN, biaxial orthorhombic α-MoO₃ supports in-plane hyperbolic PhPs (Fig. 1A) (23, 24), which exhibits hyperbolic isofrequency contours in momentum space. For instance, at a frequency of ω = 920 cm⁻¹ (where ε₁₀₀ < 0 and ε₀₀₁ > 0), the open angle of the hyperbolic isofrequency contour is along the [100] direction (yellow curves in Fig. 2, G to I). Thus, polariton diffraction in α-MoO₃ differs in two aspects: (i) The orientation angle φ of the grating relative to the crystal axis of α-MoO₃ is a critical parameter governing the diffraction of PhPs (Fig. 2, A and B); (ii) the grating’s reciprocal lattice vector (k_G = ±2π/Λ) should have an intersection with the hyperbolic isofrequency contour at a specific orientation angle, regardless of Λ > λ_p or Λ < λ_p.

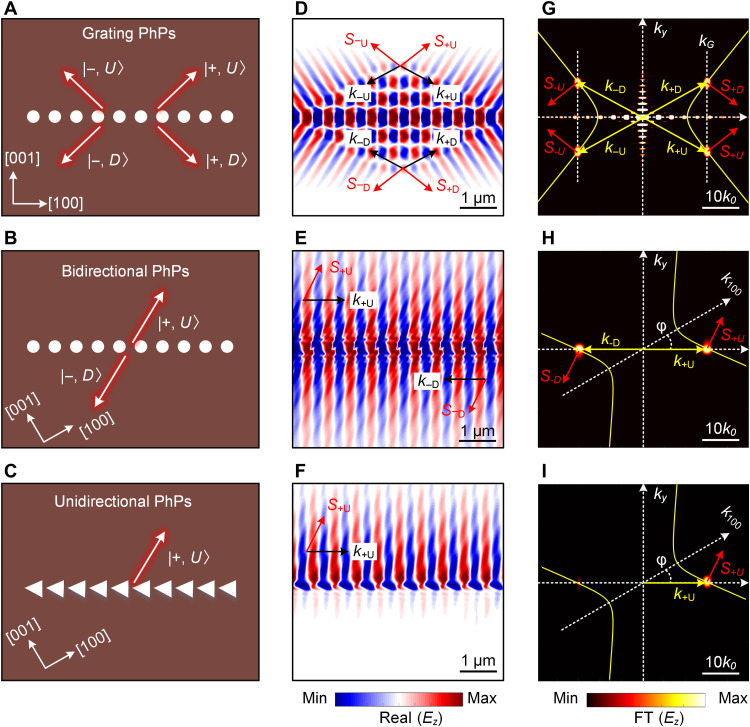
Fig. 2. Theoretical analysis of PhP diffraction and symmetry breaking at grating in α-MoO₃.

(A to C) Schematic of normal grating, bidirectional, and unidirectional diffraction of PhPs at nanogratings. The gratings are oriented φ = 0° and 30° relative to the [100] crystal direction of α-MoO₃. Red arrows indicated the energy flow S for each diffraction state. The grating period is Λ = 600 nm, the hole diameter is 300 nm, the triangle hole size is 600 × 400 nm, and the α-MoO₃ slab thickness is d = 200 nm. (D to F) Numerically simulated electric field distribution E_z of the PhPs excited by gratings in (A) to (C) at frequency 920 cm⁻¹. (G and H) FT of the simulated field distributions shown in (D) and (E). The yellow lines show the analytical hyperbolic isofrequency contours of PhPs in α-MoO₃. The bright spots reveal the wave vectors (momenta) of the grating-excited PhPs, which are located at the intersections of the vertical line of the grating’s reciprocal lattice vector (k_G = ±2π/Λ) and the isofrequency contours of the PhP momenta. (I) The right-half image corresponds to the FT of the up-side PhPs in (F) with a bright +1st-order FT spot, and the left-half image correspond to the FT of the down-side PhPs in (F) with a weak −1st-order FT spot.

Under the above diffraction conditions, we designed a circular-hole grating with Λ = 600 nm at an orientation angle φ = 0° relative to the [100] direction of α-MoO₃ (Fig. 2A). It is shown to support four diffraction states ∣± , U or D⟩, where ± denotes the k direction at the first diffraction order, and U or D stands for the up-side or down-side PhPs relative to the physical edge of the grating. The numerically simulated electric field distribution E_z of the grating-excited PhPs is shown in Fig. 2D (for the simulation details, see Materials and Methods). The diffraction pattern is radically different from the wavefronts launched by a single point source, as the interference of the polaritons launched by the grating elements yields plane wave–like wavefronts that deflect into four directions. The four diffraction states ∣± , U or D⟩ are locked by momentum matching as illustrated in Fig. 2G. The momentum of four diffraction states was obtained by Fourier transform (FT) of E_z. They correspond to four intersection spots between the vertical line along k_G (white dashed line) and the analytical hyperbolic isofrequency contour (yellow solid line) in Fig. 2G. The zero-order diffraction perpendicular to the grating does not exist, because α-MoO₃ does not support PhPs along the [001] direction within the considered Reststrahlen band (RB) (i.e., there is no intersection at k_G = 0 with the hyperbolic isofrequency contour). This forbidden zero-order diffraction allows for a clear observation of the first-order diffracted PhPs. Note that the direction of the energy flow (S, red arrows in Fig. 2G) is perpendicular to the tangent of the hyperbolic isofrequency contour. For causality reasons, it always points away from the grating, even though the wavefronts (determined by k, yellow arrows in Fig. 2G) propagate toward the grating (Fig. 2D), corresponding to backward propagation. The arrows illustrating the U and D diffraction states in Fig. 2A thus indicate the direction of S and not of k.

The PhPs launched by the grating with φ = 0° still show up-down mirror symmetric radiation patterns relative to the grating axis (Fig. 2D). By tuning the grating orientation angle φ with respect to the optical axis of α-MoO₃ (e.g., φ = 30°), the four diffraction channels can be reduced to two (Fig. 2B), with PhPs counterpropagating on the two sides of the grating (Fig. 2E). This indicates that there is no ∣± , D⟩ diffraction channel for the +1st diffraction order. Only the ∣± , U⟩ state is allowed with wave vector parallel to k_G, which hence results in forward (+x) propagation of PhPs at the up-side of the grating (Fig. 2E). Likewise, the backward (−x) propagation of the single ∣− , D⟩ state exists only at the down-side of the grating (Fig. 2E). We define these two oppositely propagating PhPs as bidirectional diffraction. Thus, the orientation angle can be considered as a new degree of freedom to control PhPs. However, the wavefronts of bidirectional diffracted PhPs exist on both sides, hindering the observation of unidirectional PhPs. To solve this issue, we use a blazed grating (Fig. 2C), which is optimized to achieve maximum diffraction efficiency in +1st order while the −1st order is minimized (see section S5). This solution indeed yields unidirectional diffraction of PhPs, which propagate only on the up-side of the grating (Fig. 2F). The FT of the field distribution reveals a bright spot (corresponding to ∣± , U⟩) in +k direction, but only a very faint spot (corresponding to ∣− , D⟩) in −k direction (Fig. 2I). This anisotropic polaritonic diffraction is totally different from the diffractions in isotropic materials (e.g., h-BN; see section S3), where polaritons always exist on both sides of grating, no matter how the grating is oriented and whether it is blazed or not.

We used scattering-type scanning near-field optical microscopy (s-SNOM) (25, 26) to perform real-space imaging of the diffraction of PhPs (see Materials and Methods). Often, PhPs are launched more efficiently by the s-SNON tip than by the sample itself (e.g., at the edges of flakes that support the PhPs). In case of a nanohole grating array, however, polariton diffraction plays a major role, where the diffraction condition requires that the reciprocal lattice vector of the grating (k_G = ±2π/Λ) intersects with the hyperbolic isofrequency contour of the polaritons (regardless of tip or grating-launched PhPs). If the diffraction condition is satisfied, then the resulting diffraction pattern from the grating is composed of the sum of interfering PhPs emanating from each nanohole in the grating. As a result, the sum of the diffracted PhPs from the grating creates a peak or valley in fringe intensity through additive and destructive interference. Because the tip and grating-launched PhPs have different (a factor of two) hyperbolic isofrequency contour, the diffraction condition can be selectively satisfied (for more details, see fig. S9), and thus, we achieve two different case studies of (i) diffraction of tip-launched PhPs in Fig. 3 and (ii) diffraction of grating-excited PhPs in Fig. 4.

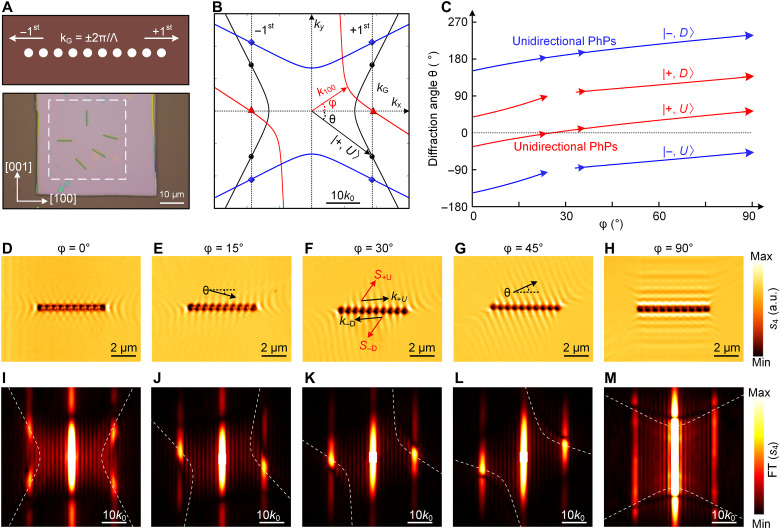
Fig. 3. Experimental observation of directional diffraction of tip-launched PhPs at circular-hole gratings.

(A) Schematic (top) of circular-hole grating and optical image (bottom) of a 220-nm-thick α-MoO₃ sample on an SiO₂/Si substrate with differently oriented gratings (Λ = 600 nm; diameter, 300 nm). (B) Isofrequency contours of the PhP wave vector for different grating orientations relative to the [100] crystal direction of α-MoO₃ (φ = 0°, 30°, and 90°, respectively) at frequency 904 cm⁻¹. The symbols denote the diffraction wave vector of tip-launched PhPs at each rotation angle. All isofrequency contours were multiplied by a factor of two, because of the double optical path of tip-launched PhPs. (C) Diffraction angle θ of the four diffraction states as function of grating orientation φ. (D to H) Experimentally measured near-field amplitude images (s₄) of tip-launched PhPs for different oriented grating. (I to M) FT of the experimental near-field images shown in (D) to (H), respectively. The bright spots reveal the momenta of tip-launched PhPs, which are exactly located at the analytically calculated isofrequency curves of the PhP momenta (dashed lines).

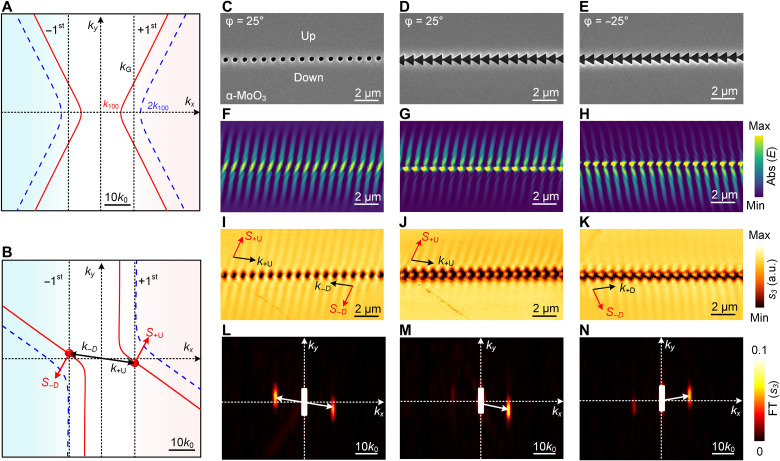
Fig. 4. Experimental observation of grating-excited PhPs and their unidirectional diffraction.

(A) Momentum matching in diffraction for a grating oriented at φ = 0°, illustrated by isofrequency contours. The first-order diffraction of tip-launched PhPs (represented by the blue dashed line) is forbidden because k_G < 2k₁₀₀, whereas the diffraction of grating-excited PhPs is possible because of the intersection of the vertical dashed line at k_G = ±2π/Λ with the isofrequency contour of the grating-excited PhPs. (B) Momentum matching for a grating oriented at φ = 25°; the black (red) arrows indicates the wave vector (energy flow) for bidirectional (circular-hole grating) diffraction. (C to E) Scanning electron microscopy images of the α-MoO₃ samples with circular-hole and blazed gratings. The thickness of the flake is 182 nm, with grating period Λ = 800 nm, circular-hole diameter 400 nm, and triangle size 800 × 1000 nm. (F to H) The simulated wavefronts [abs(E)] of PhPs excited by gratings in (C) to (E) at frequency 904 cm⁻¹. (I to K) Processed near-field images of first-order diffraction of grating-excited PhPs (the processing steps are detailed in fig. S11), showing (I) bidirectional PhP wavefronts at both sides of the circular-hole grating and unidirectional PhPs wavefront at the up-side (J) or bottom-side (K) of the blazed grating by inverting the orientation angle from +25° to −25°. (L to N) Processed FT images of grating-excited PhPs in (I) to (K), where the right-half images correspond to FT of +1st-order diffraction of PhPs, and the left-half images correspond to the FT of −1st-order diffraction of PhPs. The two half images are then spliced together into the final FT result as shown in (L) to (N). The right and left spots off the center correspond to the FT intensity of forward (+1st-order) and backward (−1st-order) diffraction of grating-excited PhPs in (I) to (K).

Diffraction of tip-launched PhPs (2k₁₀₀ < k_G)

As schematically shown in Fig. 3A, the circular-hole gratings (with grating Λ = 600 nm) were fabricated into a large area of a 220-nm-thick α-MoO₃ layer by focused ion beam (FIB) milling (see Materials and Methods). The orientation of the grating relative to α-MoO₃ [100] optical axis was varied from 0° to 90° (bottom panel, Fig. 3A). The metal tip used as near-field probe in our s-SNOM measurements concentrates the infrared illumination below its apex to a nanoscale infrared spot, which launches PhPs scattered back by the grating to the tip. When the tip-scattered field is recorded as a function of tip position, polariton interference fringes with a spacing λ_p/2 are observed. Correspondingly, all isofrequency contours in Fig. 3B are multiplied by a factor of two. Because of the mirror symmetry of circular-hole grating, both the −1st and +1st diffraction orders are generated, which are determined by the grating reciprocal vector k_G = ±2π/Λ (top panel, Fig. 3A). At frequency ω = 904 cm⁻¹, k_G exceeds the wave vector at the hyperbolic vertex along the [100] direction (k_G > 2 k₁₀₀), which has an intersection with all isofrequency contours. Therefore, the near-field distributions show strong diffracted patterns of tip-launched PhPs, as shown in Fig. 3 (D to H). The intersections in Fig. 3B (symbols) reveal the diffraction states. The corresponding diffraction angles between wave vectors and the grating axis for the four diffraction states can be obtained from θ = acos(k_G/k_±), as shown in Fig. 3C (see also section S4). The diffraction angle of each diffraction state can be tuned in a large range. For example, θ for ∣± , U⟩ can be changed from negative to positive when the grating orientation is tuned from φ = 0° to 90° (Fig. 3C), which is confirmed by the experimental near-field images in Fig. 3 (E to G). For grating orientations φ of around 30°, we find that the two diffraction states ∣± , D⟩ and ∣− , U⟩ vanish (shown by the interruptions of the corresponding curves in Fig. 3C), because momentum matching cannot be achieved. This is because one branch of the hyperbolic isofrequency contour is almost parallel to the vertical line at k_G = ±2π/Λ (see red line in Fig. 3B). From the remaining two states, one can be removed by blazing the grating, which yields unidirectional PhPs, as we will demonstrate in Fig. 4.

Figure 3 (D to H) shows the measured near-field amplitude images of tip-launched PhPs with grating orientation angles φ = 0°, 15°, 30°, 60°, and 90°, respectively. The corresponding FTs of the near-field images are shown in Fig. 3 (I to M). They reveal the momenta (bright spots) of the diffracted PhPs, which are exactly located on the analytical isofrequency contours (white dashed lines). When φ = 0°, i.e., the grating is oriented along the [100] direction of α-MoO₃, four diffraction directions are allowed (four bright spots in Fig. 3I), leading to a cross-shaped fringe pattern on both sides of the grating that exhibits a mirror symmetry relative to the grating axis (Fig. 3D). For φ = 30°, the bidirectional diffraction condition is satisfied, that is, on each side of the grating, the tip-launched PhPs are diffracted only in one direction (Fig. 3F). Consequently, only two bright spots are observed in the FT image (Fig. 3K), which correspond to forward (+1st) diffraction on the up-side and backward (−1st) diffraction on the down-side of the grating. The polariton diffraction for φ = 15° and 45° is similar to that of φ = 30°, but the direction of the polariton propagation (i.e., phase velocity) normal to the grating changes from negative to positive (see black arrows in Fig. 3, E and G). At large grating orientation angles (e.g., φ = 90°; Fig. 3H), the zero-order diffraction dominates (as the isofrequency curve crosses k_G = 0; Fig. 3M) and prevents a clear observation of the ±1st-order PhP diffraction. We corroborate our experimental near-field images and our interpretation of them in section S7 (fig. S8), where we show calculated near-field images based on a phenomenological interference model (27, 28) that excellently reproduces the experimental near-field images shown in Fig. 3 (D to H).

Diffraction of grating-excited PhPs (k₁₀₀ < k_G < 2 k₁₀₀)

We found a selection rule to directly observe and map grating-excited PhPs, by deliberately engineering the momentum matching relationships between k_G, k₁₀₀ (describing grating-excited polaritons), and 2k₁₀₀ (describing tip-launched polaritons). We fabricated nanogratings with Λ = 800 nm in a 182-nm-thick α-MoO₃ flake, such that k_G in the range of k₁₀₀ < k_G < 2 k₁₀₀ at frequency ω = 904 cm⁻¹. In this case, the first-order diffraction of tip-launched PhPs (dashed blue isofrequency contour in Fig. 4A) is suppressed, as k_G is smaller than any effective momentum (that is, 2k_p) of the tip-launched polaritons (i.e., the vertical line at k_G does not cross the dashed blue isofrequency contour). However, the diffraction of grating-excited PhPs is allowed, as the vertical line at k_G crosses the isofrequency contour k_p (red) in Fig. 4A (for more details, see fig. S9). Moreover, for a grating orientation angle of φ = 25°, only two diffraction states are allowed (marked by the red circles shown in Fig. 4B), which enables the bidirectional diffraction of grating-excited PhPs. When the grating is additionally blazed, an efficient and selective diffraction into the +1st order can be achieved.

We performed s-SNOM imaging around the circular-hole and blazed gratings. We note that the original near-field images contain both the first-order grating-excited PhPs and second-order tip-launched PhP signals (see figs. S10 and S11). To directly reveal grating-excited PhPs, we filtered out the second-order signal by applying a removing mask on the second-order tip-launched PhPs in the FT image, because the two contributions are well separated in momentum space. The processed near-field images of first-order diffraction of grating-excited PhPs in Fig. 4 (I to K) show excellent agreement with the simulated wavefronts (Fig. 4, F to I), verifying that the processed PhP signals are dominantly excited by the grating. In the case of the circular-hole grating at φ = 25° [scanning electron microscopy (SEM) image in Fig. 4C], the simulated field distribution (Fig. 4F) and corresponding s-SNOM image (Fig. 4I) clearly reveal the wavefronts of the forward and backward bidirectional propagating PhPs as predicted in Fig. 4B. In addition, we also performed FT of the up-side and down-side PhPs, respectively (for full FT images, see fig. S11), e.g., the right-half image in Fig. 4 (L to N) corresponds to FT of +1st-order diffraction of PhPs, and the left-half image corresponds to the FT of −1st-order diffraction of PhPs. Then, we spliced the two half images together into the final FT result as shown in Fig. 4 (L to N). Because of the symmetry of the circular-hole grating, the FT spots for ∣± , U⟩ and ∣− , D⟩ diffraction states have the same intensity, thus revealing two-side propagation of grating-excited PhPs (Fig. 4L).

In the case of the blazed grating (e.g., φ = 25°; Fig. 4D), PhPs are preferentially excited on the up-side (Fig. 4, G and J), because the maximal diffraction efficiency has been blazed into the +1st order, which hence yields the unidirectional diffraction of PhPs. We actually can clearly see a bright FT spot for the up-side PhPs (k_+U spot in Fig. 4M), whereas a weak FT spot for the down-side PhPs is observed (k_−D spot in Fig. 4M). By inverting the orientation angle φ to −25° (Fig. 4E), we observed that the unidirectional wavefronts are flipped to the down-side (Fig. 4, H and K), owing to the fact that the momentum matching has been changed to another branch of the hyperbolic isofrequency contour (k_+D spot in Fig. 4N), and the energy flow S has been changed to the down-side (for more details, see fig. S11F). For symmetry reasons, the field distributions (i.e., the wavefront pattern) excited by these two inversed oriented gratings should be mirror images of each other, which is clearly observed by comparing the results in the experiment (Fig. 4, J and K).

DISCUSSION

By exploiting the selection rule of grating diffraction of hyperbolic polaritons, we can selectively excite, structure, and route PhPs toward the designed direction at the surface of vdW materials. In the future, a dual-layer system could potentially be considered, where the nanograting is fabricated at the bottom substrate and the top α-MoO₃ layer can be rotated to actively control the unidirectional grating-excited PhPs.

In summary, we introduced grating-polaritonics in high-symmetry vdW orthorhombic crystals. The interplay between grating diffraction and material anisotropy enables unprecedented opportunities for directional, bidirectional, and unidirectional excitation and steering of ultraconfined polariton waves. The concept can be readily extended to other frequency ranges and other anisotropic materials (6, 9, 29–31). We foresee that, beyond the grating orientation angle, other parameters (or degrees of freedom), including incident angle (32), polarization, and grating geometric structures, may be used to further control the polariton diffraction. Grating-polaritonics will thus push further the rapidly emerging field of interface nano-optics (33–38) for controlling light on the nanometer scale.

MATERIALS AND METHODS

Sample fabrication

Large-area α-MoO₃ single-crystal flakes were obtained through mechanical exfoliation from high-quality bulk crystals, which were synthesized by the chemical vapor deposition method (11, 39). The as-exfoliated α-MoO₃ flakes on the polydimethylsiloxane sheet were then selected and transferred onto SiO₂ (300 nm)/Si substrates via a deterministic dry transfer microscope system. The circular-nanohole grating and blazed grating on α-MoO₃ were fabricated by high-resolution FIB lithography in an FEI Helios 600 Nanolab dual-beam FIB-SEM system. Ga ions were used as ion sources in our FIB etching process. To minimize the redeposition effect, the patterns were milled in parallel instead of serially with a controllable etching speed. The acceleration voltage and current of Ga ion beams were set as 30 kV and 28 pA, respectively, and the milling depth was controlled until reaching the substrate. Thermal annealing at 300°C for 3 hours was further conducted for these samples to eliminate the Ga ion implantation effect.

Real-space imaging

We used a commercially available s-SNOM from Neaspec to perform infrared nanoimaging experiments. The s-SNOM setup is based on a tapping-mode atomic force microscope (AFM). The tip oscillation frequency and amplitude was set to ~285 kHz and ~70 nm, respectively. A p-polarized frequency-tunable infrared laser beam was focused onto the AFM tip (Arrow-NCPt, NanoWorld) at an angle of about θ = 30° with respect to the grating (or α-MoO₃ surface). The metallic tip acts as an infrared antenna and concentrates the incident field into a nanoscale hotspot a the tip apex, which launches polaritons in α-MoO₃. The tip can also act as a near-field probe for mapping the polariton field launched by nanostructures. The tip-scattered field was recorded by a pseudoheterodyne interferometer, and the subsequent demodulation of the detector signal at the third or fourth harmonic of the tapping frequency yielded near-field amplitude images (s₃ or s₄).

Numerical simulations

We used a finite-difference time-domain (FDTD) method based on commercially available software (Lumerical FDTD, 2020) for full-wave simulations. The gratings are nanoholes within α-MoO₃ slab. Periodic boundary conditions are set along the x direction, and a perfectly matched layer is set along the y direction. To excite PhPs, we use a plane wave source to normally illuminate the grating with polarization parallel to the grating. For the simulations in Figs. 1 and 2, we monitor the real part of E_z at 100 nm above the surface of the sample, which is then Fourier transformed to extract the isofrequency contours. The permittivity of the α-MoO₃ layer is obtained from (23, 24) and is shown in fig. S1.

Supplementary Materials

This PDF file includes:

Sections S1 to S8

Figs. S1 to S14

References