ATP-competitive inhibitors modulate the substrate binding cooperativity of a kinase by altering its conformational entropy

Abstract

ATP-competitive inhibitors are currently the largest class of clinically approved drugs for protein kinases. By targeting the ATP-binding pocket, these compounds block the catalytic activity, preventing substrate phosphorylation. A problem with these drugs, however, is that inhibited kinases may still recognize and bind downstream substrates, acting as scaffolds or binding hubs for signaling partners. Here, using protein kinase A as a model system, we show that chemically different ATP-competitive inhibitors modulate the substrate binding cooperativity by tuning the conformational entropy of the kinase and shifting the populations of its conformationally excited states. Since we found that binding cooperativity and conformational entropy of the enzyme are correlated, we propose a new paradigm for the discovery of ATP-competitive inhibitors, which is based on their ability to modulate the allosteric coupling between nucleotide and substrate-binding sites.

ATP-competitive inhibitors reveal the linkage between a kinase’s conformational entropy and substrate-binding cooperativity.

INTRODUCTION

Eukaryotic protein kinases (EPKs) make up ~2% of the human proteome and control vital processes such as cell development, differentiation, metabolism, and stress response by catalyzing the transfer of the γ-phosphate from adenosine 5′-triphosphate (ATP) to serine, threonine, or tyrosine residues of their substrates (1). Aberrant phosphorylation is linked to a wide range of major human diseases, including cancer, autoimmune disorders, cardiac disease, and diabetes, making these enzymes major drug targets (2, 3). Although some allosteric drugs have been found (4), most of the small molecules targeting kinase active sites are ATP-competitive inhibitors (2, 4). These molecules abolish the catalytic function of kinases by blocking the ATP-binding site, thus preventing phosphorylation of their substrates. However, several ATP-competitive inhibitors display paradoxical activation of kinases in vivo (3), suggesting that they may activate alternative signaling pathways (5).

ATP-competitive inhibitors bind in a pocket situated between the two lobes of the structurally conserved catalytic cores of the kinases. This bilobal fold is preserved among EPKs and was revealed when the first structure of the catalytic subunit of cyclic adenosine 3′,5′-monophosphate (cAMP)–dependent protein kinase A (PKA-C) was determined (Fig. 1A) (6). The small N-lobe comprises a five-stranded β sheet that controls nucleotide binding and a highly conserved αC helix, whose positioning is dynamically regulated and crucial for kinase activation (7). The larger C-lobe is mostly α-helical and includes the substrate-binding site and catalytic residues that are essential for phosphoryl transfer (8). Two stacks of hydrophobic residues, referred to as regulatory (R) and catalytic (C) spines, span the two lobes of the kinase’s hydrophobic core and are docked onto the αF helix in the C-lobe (Fig. 1B) (9). Other conserved structural elements include the linker region and four loops [Gly-rich, Asp-Phe-Gly (DFG), activation and catalytic loops] (8). ATP binding connects all these elements and couples both lobes structurally and dynamically (10). Phosphorylation of the activation loop contributes to the R-spine assembly and orients the αC helix for catalysis. Specifically, the adenine ring of ATP intercalates between A70 and V57 in the N-lobe and L173 in the C-lobe to complete the C-spine, while the α, β, and γ phosphates, which contribute to the coordination of two Mg²⁺ ions, reach over the R-spine, priming the enzyme for efficient catalysis. In this committed state, the conformational fluctuations (i.e., the dynamics) of the spines and other important loops have similar exchange constants k_ex (i.e., they are synchronous) and contribute to the efficiency of the catalytic cycle (11).

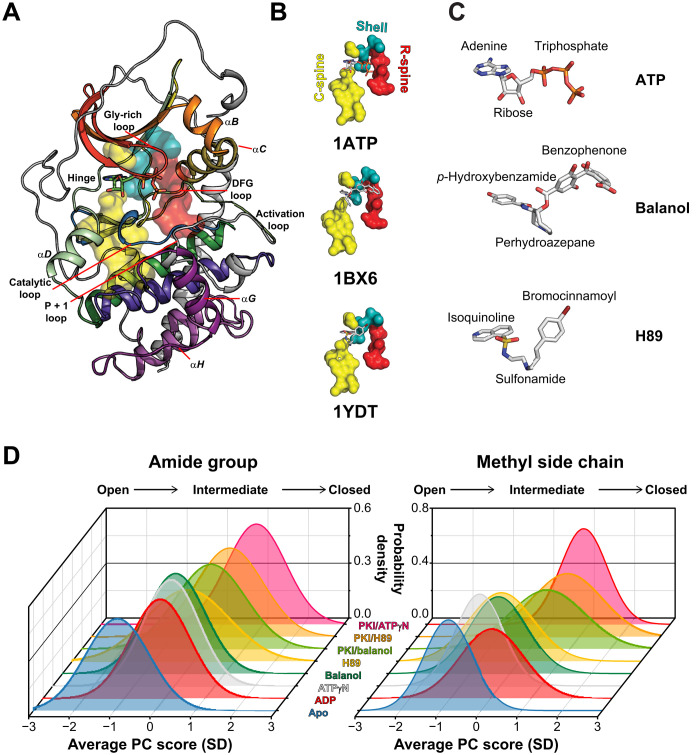
Fig. 1. Structure and conformational transitions of PKA-C upon binding ATP-competitive inhibitors.

(A) X-ray structure of PKA-C [Protein Data Bank (PDB): 1ATP]. The subdomains are colored using Hanks and Hunter convention (1). (B) C-spines, R-spines, and shell residues for the ATP-, balanol-, and H89-bound structures. (C) Chemical structures of ATP, balanol, and H89. The p-hydroxybenzamide group in balanol (or isoquinoline ring in H89) mimics the adenine moiety of ATP, the perhydroazepane ring in balanol (or sulfonamide in H89) occupies the ribose subsite, and the benzophenone group in balanol (or bromocinnamoyl group in H89) mimics the triphosphate of ATP. (D) Coordinate chemical shift behavior plots showing that the ATP-competitive inhibitors shift the distribution of the chemical shifts for the amides and methyl groups of PKA-C toward an intermediate state. PC, principal component. The amide and methyl chemical shift lists used for the analysis are based on Kim et al. (15).

A prominent feature in PKA-C is the binding cooperativity between the nucleotide and substrate (K-type cooperativity). To understand how ATP-competitive inhibitors modulate the substrate binding cooperativity of kinases, we chose PKA-C as a benchmark and analyzed its binding response to a peptide derived from an endogenous protein kinase inhibitor (PKI_5–24) when inhibited by balanol or H89 (N-[2-(p-bromocinnamylamino)ethyl]-5-isoquinoline sulfonamide), two high-affinity ATP-competitive inhibitors widely used for studying PKA and PKC signaling pathways (12). Balanol is a fungal metabolite from Verticillium balanoides (13), while H89 is a synthetic inhibitor used to study PKA signaling in the cardiac and smooth muscle (Fig. 1C) (14). Both balanol and H89 inhibit PKA-C with low nanomolar (nM) affinity, i.e., K_i approximately 4 and 48 nM, respectively. Unexpectedly, however, they display opposite K-type cooperativity with respect to the pseudosubstrate, PKI_5–24; the degree of binding cooperativity ($\mathrm{\sigma }=\frac{K_d(\text{apo})}{K_d(\text{inhibited})}$) is 7 (ΔΔG = 4.8 ± 0.4 kJ mol⁻¹) for balanol and 0.6 (ΔΔG = −1.4 ± 0.3 kJ mol⁻¹) for H89 (table S1) (15). Since the x-ray structures of PKA-C/balanol and PKA-C/H89 are very similar [overall root mean square deviation (rmsd) < 0.7 Å; Protein Data Bank (PDB): 1BX6 and 1YDT] with differences limited to the ATP-binding pocket, we reasoned that their opposite cooperative behaviors might correlate with the different conformational dynamics of the two complexes. To test this hypothesis, we used nuclear magnetic resonance (NMR) chemical shift and relaxation measurements to compare the dynamic response of PKA-C to balanol and H89 binding with that of nucleotides. From the analysis of the chemical shift covariance, we found that these inhibitors alter the structural coupling between the two lobes of the kinase in completely different manners. Notably, they differentially suppress and/or promote the conformationally excited states of the kinase, which are responsible for its allosteric binding cooperativity. We found that the extent of binding cooperativity is correlated with the changes in conformational entropy of methyl-bearing side chains of the kinase. We conclude that the opposite cooperativity observed for these ATP-competitive inhibitors is due to the different ability of these molecules to steer the enzyme toward states with different levels of commitment to substrate binding. Therefore, our studies suggest that it is possible to modulate the allosteric binding cooperativity of this kinase by tuning the chemical nature of the ATP-competitive inhibitor, introducing a new way to fine-tune kinase function.

RESULTS

ATP-competitive inhibitors alter the structural coupling between the kinase lobes

To determine the structural response of the kinase to balanol and H89 binding, we mapped both the amide and methyl group NMR fingerprints (fig. S1), seeking distinct signatures of committed and uncommitted states of PKA-C (16). A hallmark for the committed state (ATP bound) of the kinase is the marked broadening of the amide resonances associated with catalytically important loops such as the Gly-rich, DFG, activation, and P + 1 loops and the αC helix (fig. S2) (17). This phenomenon is correlated with increased conformational dynamics in the intermediate NMR time scale (submillisecond) (17, 18). Neither balanol nor H89 binding causes line broadening in the amide or methyl fingerprint resonances, suggesting that the conformational dynamics are outside this time scale. Instead, these inhibitors induce distinct and global chemical shift perturbations (CSPs; figs. S3 and S4). Both inhibitors cause amide CSPs in the Gly-rich loop, linker region, and C-terminal tail. In addition, balanol binding causes appreciable amide CSPs in specific residues of catalytically important loops: DFG (G186 and A188), activation (T197), and P + 1 loop (E203) (figs. S3A and S4A). The methyl group fingerprints show that balanol binding also perturbs residues in the hydrophobic core (L173, L95, and V104) and the PDK1 Interacting Fragment (PIF)–binding pocket (L116 and V80), the docking site for hydrophobic motif in the C-terminal tail (figs. S3C and S4B). H89, on the other hand, perturbs mostly the methyl side chain resonances of the N-lobe and linker region, which line the adenine-binding site (I46, V104, L106, and V123), with sparse long-range effects involving L132 and I150 (figs. S3B and S4B). The global response of the enzyme to ligand binding is summarized in Fig. 1D, where we report the coordinated behavior of the chemical shifts along the open-to-closed conformational transitions (19). On average, balanol and H89 shift the probability density of the enzyme’s fingerprint resonances toward an intermediate conformational state. This behavior is similar for both amide and methyl side chain resonances, indicating that the enzyme adopts a partially closed conformation in agreement with the corresponding x-ray structures (20, 21). Note that the addition of PKI_5–24 to either PKA-C/balanol or PKA-C/H89 complexes does not shift the conformation of the kinase to a fully closed state. For comparison, we analyzed the behavior of other nucleotides [adenosine 5′-monophosphate (AMP), adenine, adenosine, adenosine 5′-diphosphate (ADP), and adenosine 5′-(β,γ-imido)triphosphate (ATPγN)]. Nucleotide binding shifts the probability density of the kinase toward the intermediate state, showing that the occupancy of the nucleotide-binding pocket causes a similar global response for both inhibitors and nucleotides (Fig. 1D).

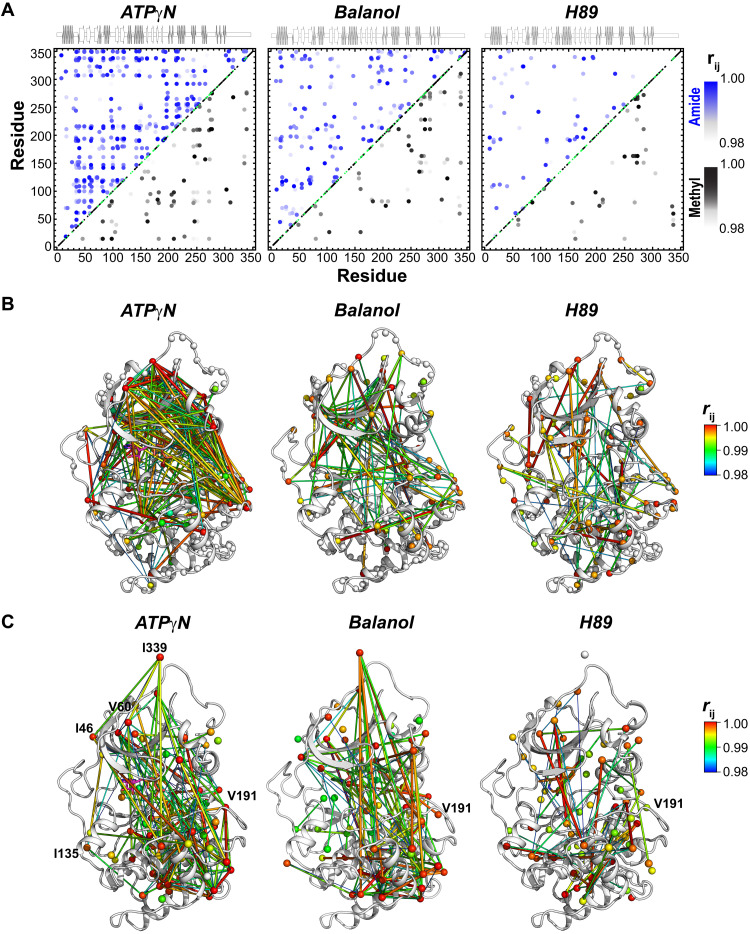
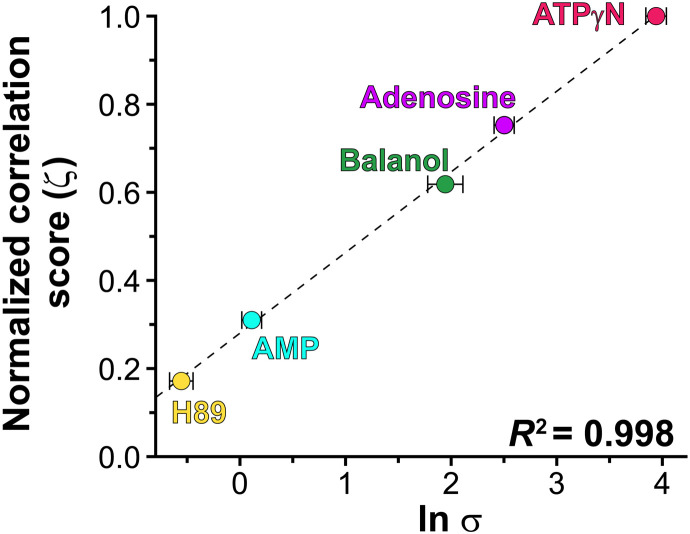
Since the conformations of the inhibited kinases are similar, we then analyzed the possible differences in the internal allosteric network of communication, performing chemical shift covariance analysis (CHESCA) (22) (Fig. 2). Using this analysis, we observed marked differences between nucleotide and inhibitors for both amide and methyl resonances. ATPγN binding causes globally coordinated changes of CSPs, with highly correlated residues across the N- and C-lobes (Fig. 2, A to C, and fig. S5). Specifically, the chemical shifts of the resonances associated with the αA helix (residues 17 to 30), αA-β1 linker (residues 31 to 41), β4 and β5 (residues 107 to 112 and 117 to 119), activation loop (residues 190 to 196), APE motif (residues 206 to 210), αE helix (residues 142 and 147 to 152), and the C-terminal tail (residues 314, 318, 322, 323, 331, 332, 337, and 348 to 350) show highly correlated CSPs (correlation coefficients |r_ij | > 0.98). Furthermore, several correlations are observed between the N-lobe and the substrate-binding cleft (activation loop, P + 1, and APE) with both the αF and αG helices. The correlations found for the αG helix are especially important, as this motif constitutes a docking site for many substrates and the R subunits. The extent of the network of correlated CSPs observed for the ATPγN-bound kinase is potentially underestimated since several residues in the Gly-rich, αC helix, activation loop, etc. are broadened beyond detection and cannot be monitored. A similar scenario is found for the methyl group resonances of the ATPγN-bound state, where extensive chemical shift correlations are found across the core of the enzyme, involving the αC helix; activation loop; P + 1 loop; C-terminal tail; and αE, αF, αG, and αH helices (figs. S2C and S6). The correlations for the αF helix support the structural role of this element that anchors the hydrophobic spines to the C-lobe, constituting a signaling conduit that structurally couples the two lobes (9). Overall, we observe a remarkable number of correlations between the N-lobe and the activation loop in the nucleotide-bound kinase, suggesting a cross-talk between the ATP-binding pocket and the activation loop of the kinase as observed in Src kinase (23). In contrast, the number and the extent of the CSP correlations are much lower in the inhibitor-bound complexes (Fig. 2 and figs. S7 to S10). Although the balanol-bound complex preserves most of the correlations among the activation loop, the αA helix, αA-β1 loop, and αE helix, these are absent in the H89-bound complex (Figures 2A-B). The methyl group resonances display an analogous scenario for balanol, with attenuated chemical shift correlations from the ATP-binding pocket to the peripheral regions of the kinase (Fig. 2C and figs. S7 and S8). Similarly, the PKA-C complex with H89 displays the least number of correlations, showing that the two lobes are essentially uncoupled (Fig. 2C and figs. S9 to S10). Thus, upon nucleotide binding, the CHESCA maps reveal coordinated CSPs between the hydrophobic core of the enzyme and peripheral catalytic motifs, emphasizing the central role of the C- and R-spines and their shell residues in promoting a catalytically committed state with high binding affinity for substrate (11). The density of the internal allosteric network is intimately related to the thermodynamics of binding obtained from isothermal titration calorimetry (ITC) measurements. As shown in Fig. 3, the higher is the density of the allosteric network (ζ score; Eq. 7 in Materials and Methods), the higher is the cooperativity coefficient, with ATPγN showing the highest density of intramolecular correlations and cooperativity coefficient. There is a remarkable linear correlation among the ζ scores of these ATP-binding molecules and their ln σ with a coefficient of determination (R²) value of 0.99. This linearity still holds for the Cushing’s syndrome mutations and the DNAJB1 chimera of PKA-C (24). Overall, our chemical shift analysis reveals that higher binding cooperativity in PKA-C requires coordinated structural changes and extensive communication between the small and large lobes of the enzyme.

Fig. 2. Coordinated chemical shift changes of the kinase in response to ligand binding.

(A) CHESCA maps for the amides (top portion) and methyl groups (bottom portion) upon binding ATPγN, balanol, and H89. The chemical shift covariance was calculated using four states of PKA-C: apo, ADP bound, inhibitor bound, and inhibitor and PKI bound. Only correlation coefficients () > 0.98 are reported. Enlarged CHESCA maps are available in the Supplementary Materials. (B and C) Chemical shift correlation networks for (r_iJ) >0.98 mapped onto the PKA-C structure for amide and methyl groups, respectively. The color-coded spider plots indicate the extent of the correlations, with red being the highest and blue being the lowest. ATPγN shows the highest degree of chemical shift covariance between the two lobes of the enzyme. The number and extent of correlation become gradually lower going from balanol to H89. The amide and methyl chemical shift lists used for the analysis are derived from the spectra published by Kim et al. (15).

Fig. 3. The density of the intramolecular allosteric network is linearly correlated with the degree of binding cooperativity.

The ζ score derived from the CHESCA analysis indicates the density of the chemical shift correlations as defined by Eq. (8), with normalization against ATPγN binding (ζ = 1.0). The cooperativity coefficient (σ) is derived from thermodynamics measurements and represents the ratios of the PKI-binding constants to PKA-C for in the absence and presence of nucleotides or ATP-competitive inhibitors. The σ value is from Kim et al. (15).

Differential suppression and promotion of conformationally excited states of the kinase upon binding the inhibitors

Previously, we emphasized the role of microsecond-millisecond motions in the kinase’s enzymatic cycle (10, 25). To determine whether these motions have a role in the opposite cooperativity of balanol and H89, we quantified the exchange contribution to the transverse relaxation rate (R_ex) of amide groups using Carr-Purcell-Meiboom-Gill (CPMG) relaxation dispersion experiments (26). On this time scale, the backbone of the apo kinase is the most malleable (11), with several residues exhibiting significant R_ex values (fig. S15A and table S2). The most dynamic regions include the linker (residues 124 to 125), the αA-β1 (T37) and the αD-αE loops (residues 138 to 139), β8 (residues 180 to 182), αD (residues 133 to 134), the catalytic loop (residues 165 to 166), and C-terminal tail (residues 314 to 315). With the exception of the αD-αE loop, nucleotide binding further increases the microsecond-millisecond dynamics for Gly loop (L49, M58, L59), activation loop (W196), peptide-positioning loop (L198), portions of αF (residues 216 to 221), and the acidic cluster (residues 331 to 334) (fig. S15A). In contrast, the binding of either balanol or H89 quenches the conformational exchange across the entire enzyme, although to different extents. For the PKA-C/H89 complex, most of the amide resonances show R_ex ≤ 4 s⁻¹, whereas for the PKA-C/balanol complex, we detected notable chemical exchange for resonances in the Gly-rich, DFG, and activation loops, as well as the C-terminal tail (fig. S15A and table S2).

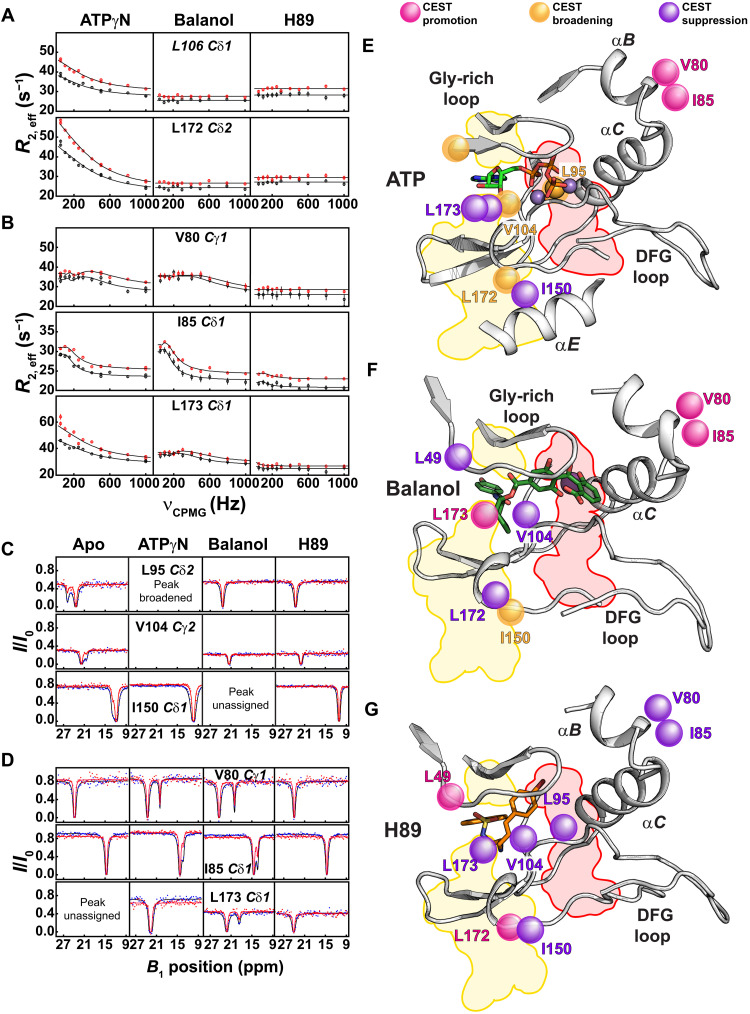
To monitor the conformational exchange for the hydrophobic core, we performed ¹³C CPMG relaxation dispersion experiments on the methyl groups of Ile, Leu, and Val residues (27). As for the amide resonances, the analysis of the methyl group R_ex confirmed that apo PKA-C features a very dynamic hydrophobic core (figs. S16 and S17 and table S3). ATPγN binding increases the conformational dynamics for the methyl group residues lining the binding site, the C- and R-spines, and allosteric hotspots such as I150 (11) (Fig. 4A and fig. S16). Instead, upon binding balanol and H89, the conformational exchange is attenuated (figs. S16 and S18 and tables S4 and S5). While both inhibited complexes show a global reduction in motion, residues located in the hydrophobic core and near the ATP-binding cleft (e.g., L49, V57, L95, L103, V104, and L160) still display significant R_ex, especially the balanol-bound kinase exhibits significant dynamics for residues in the αB helix (V80), αC helix (I85, L89, and I94), and the peptide positioning loop (L198) (fig. S18A). These motions are absent in the PKA-C/H89 complex (Fig. 4B and fig. S16). We modeled the CPMG dispersion curves as a two-state equilibrium, and we obtained the kinetic (k_ex) and thermodynamic (p_A) parameters of the exchange process (tables S6 and S7) (28). For the ATPγN-bound kinase, several residues in the C-spine (L172 and L173), R-spine (L106), and surrounding bridging residues (I150, I180, and V182) fit to a single global exchange process with a rate constant (k_ex) of 2400 ± 200 s⁻¹ and a population (p_A) of 92.8 ± 0.4% for the conformational ground state (Fig. 4E, fig. S16, and table S6). The residues involved in these synchronous motions and the rates of exchange are consistent with the dynamically committed state identified previously for the PKA-C/ATPγN complex (16). Meanwhile, a number of residues of the balanol-bound kinase, positioned in the hydrophobic core and αB and αC helices, fit to a different exchange process with a much slower exchange regime (k_ex = 90 ± 50 s⁻¹ and p_A = 90 ± 4%; fig. S17 and table S6). Because of the limited number of residues showing R_ex > 2 s⁻¹, we were unable to perform group fitting for methyl group resonances in the H89-bound complex (Fig. 4G and fig. S18B). This indicates the existence of heterogeneous conformational dynamics (29). To identify possible conformationally excited states exchanging with k_ex < 200 s⁻¹, we performed ¹³C chemical exchange saturation transfer (CEST) experiments (30). Notably, for residues that show a two-state exchange process, the exchange kinetics (k_ex), population (p_A), and chemical shift difference (Δω) obtained from CEST are in remarkable agreement with those obtained from the CPMG experiments (table S7). For the apo kinase, we found that three residues (L95, V104, and I150) are in equilibrium between a ground state and discrete conformationally excited states (Fig. 4C). Remarkably, we found that the ligand-binding response for the two hydrophobic spines is rather different (Fig. 4D). For the C-spine, ATPγN does not cause any significant perturbation in this exchange regime (Fig. 4E). On the other hand, balanol promotes a new excited state for L173, which is at the end of the C-spine and interacts with the adenine ring of ATP or the hydroxybenzamide moiety in the 1ATP and 1BX6 structures, respectively (Fig. 4, D to F) (20). Instead, H89 promotes new alternate states for L49 and L172, located at the beginning and end of the C-spine, respectively (Fig. 4G and fig. S19A). For the R-spine, both ATPγN and balanol promote new states for V80 and I85 in the αB-αC loop (Fig. 4, D and E). Upon fitting the CEST profiles, we found that residues in the PKA-C/balanol complex interconvert with a k_ex spanning from 40 to 200 s⁻¹, while slower exchange kinetics were found for the PKA-C/H89 complex (k_ex = 40 to 50 s⁻¹) (table S8). In addition, the chemical shifts of these excited states do not follow the open-to-closed conformational equilibrium of the kinase, revealing alternate inactivation pathways. The latter is confirmed by the lack of correlations between the Δω values obtained by CEST and CPMG experiments and Δδ values directly measured from the transverse relaxation-optimized spectroscopy (TROSY)–heteronuclear single-quantum coherence (HSQC) spectra (fig. S19B). Furthermore, the binding of the ATP-competitive inhibitors suppresses the excited states of L95 (broadened in the PKA-C/ATPγN complex), V104, and I150 (resonances overlapped in the PKA-C/balanol complex) that are peripheral to both spines (Fig. 4, C to D). The suppression of these slow-exchanging excited states suggests that these inhibitors shift the motions of the kinase to a faster time scale. In agreement with this experimental observation, [¹H,¹⁵N]-TROSY Hahn echo (TR-HE) experiments, which are sensitive to dynamics closer to the microsecond time scale (31), show that the binding of these inhibitors cause an overall attenuation of$R_{\text{ex}}^{\text{CPMG}}$ across the enzyme but significantly high $R_{\text{ex}}^{\text{TR}-\text{HE}}$ values particularly for the PKA-C/H89 complex (figs. S15B and S20).

Fig. 4. Dynamic response of the spine residues of PKA-C upon binding ATPγN and ATP-competitive inhibitors.

(A and B) Relaxation dispersion curves of the methyl side chain groups measured at 700 MHz (black) and 850 MHz (red). PKA-C shows substantial conformational exchange upon binding ATPγN, a reduced exchange with balanol, and almost no exchange with H89. Duplicate measurements were carried out at ν_CPMGvalues of 50, 500, and 1000 Hz. Errors were propagated and reported as error bars. (C) ¹³C CEST measured on a 900-MHz spectrometer using a B₁ field of 15 Hz (red) and 30 Hz (blue). The methyl groups for L95 (R-spine), V104 (shell), and I150 (allosteric hotspot) show distinct conformationally excited states in the apo form. Binding of ATPγN, balanol, or H89 suppresses the conformationally excited states for these core residues. (D) Formation of new excited states for V80 and I85 (αB helix) for both ATPγN-bound and balanol-bound complexes and L173 (C-spine) for balanol-bound complex. The CEST profiles and the chemical shift difference for V80 and I85 for the ATPγN-bound and balanol-bound complexes are very similar. ppm, parts per million. (E to G) Mapping of the residues showing a change in the excited states (i.e., promotion, suppression, or broadening of the ground state) for PKA-C/ATPγN, PKA-C/balanol, and PKA-C/H89 complexes, respectively. CEST profiles were fit to a two-state exchange process (see Materials and Methods).

Overall, the multitime scale analysis of free and ligand-bound PKA-C shows that ATPγN activates conformational fluctuations of PKA-C that are committed to substrate recognition. In contrast, the binding of two inhibitors steers kinase conformational fluctuations that are less committed to substrate binding, emphasizing that the conformational fluctuations that elicit binding cooperativity arise from coordinated structural and dynamical changes.

Binding cooperativity and conformational entropy are correlated

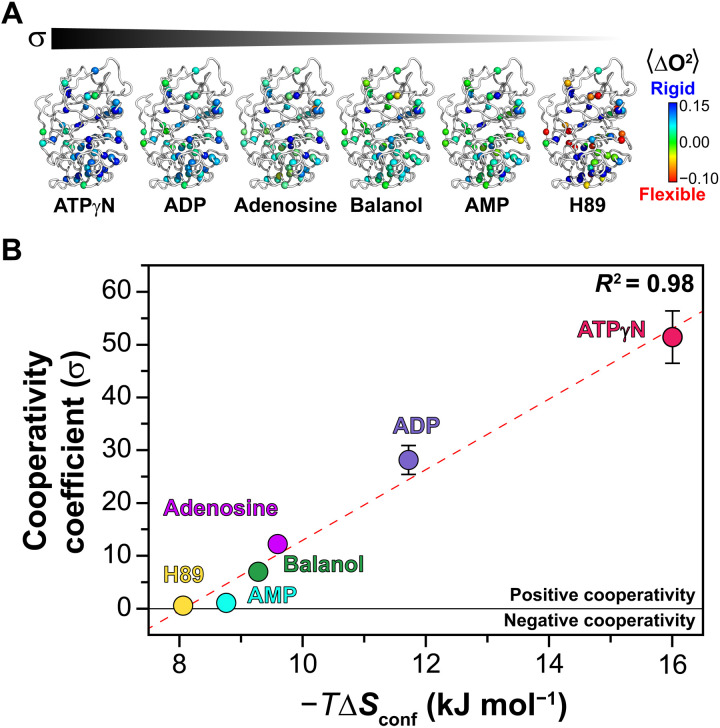
Previous studies have shown that binding affinity at remote sites can be allosterically modulated via conformational entropy probed by NMR relaxation measurements (32–34). To define the role of conformational entropy in the differential binding cooperativity for these inhibitors, we first analyzed the backbone motions of the kinase bound to balanol and H89, measuring the heteronuclear [¹H,¹⁵N] nuclear Overhauser effects (HX-NOEs). Except for a few residues, we did not observe significant differences between the two inhibitor-bound complexes (fig. S21). The average values of HX-NOE changed from 0.84 ± 0.14 to 0.86 ± 0.14 or 0.87 ± 0.13, going from apo to balanol and H89 bound states. The latter suggests that the conformational entropy of the backbone is not implicated in modulating the allosteric cooperativity. We then investigated the involvement of the methyl-bearing side chains of the enzyme in the differential thermodynamic response to ligand binding. To this extent, we calculated the changes in their order parameters (ΔO²) from the apo to the binary complexes. We found that as the binding cooperativity decreases, the protein mobility increases, which is manifested by a decrease in the methyl group order parameters (Fig. 5B and fig. S22). More specifically, the highest degree of binding cooperativity is observed for the PKA-C/ATPγN complex with σ = 52 (ΔΔG = 9.8 ± 0.2 kJ mol⁻¹). This binary complex shows the highest degree of rigidity reflected in the average ΔO² value. For the complexes with ADP (σ = 28, ΔΔG = 8.3 ± 0.2 kJ mol⁻¹), adenosine (σ = 12, ΔΔG = 6.2 ± 0.2 kJ mol⁻¹), balanol (σ = 7.0, ΔΔG = 4.8 ± 0.4 kJ mol⁻¹), AMP (σ = 1.1, ΔΔG = 0.3 ± 0.2 kJ mol⁻¹), and H89 (σ = 0.6, ΔΔG = −1.4 ± 0.3 kJ mol⁻¹) (table S1) (15), the values of ΔO² decrease gradually. These dynamic effects are apparent throughout the hydrophobic core and most prominently at the interface between the N- and C-lobe (Fig. 5A). We then converted ΔO² in ΔS_conf (the change in the conformational entropy of the protein) according to the model-independent formula (35). By plotting the values of σ against −TΔS_conf, we found a linear correlation with R² = 0.98, i.e., the more rigid the side chains are, the higher is the binding cooperativity (positive cooperativity). In contrast, an increase in flexibility corresponds to a higher entropic penalty and lower binding cooperativity. Last, we analyzed the distribution of the methyl order parameters of all forms of PKA-C (fig. S23). For calmodulin and other small proteins, Frederick et al. observed a trimodal distribution of the order parameters that identifies three discrete classes of amplitude of motions (J, α, and ω) (32). While the change in the methyl group order parameter distributions change upon binding different ligands, the overall distribution for the order parameters of the isoleucine-leucine-valine (ILV) methyl groups of PKA-C does not reflect the three different classes. The latter may be due to sparse number of probes we have available in our system or a deviation of PKA-C from the behavior as reported by Best et al. (36) for other proteins.

Fig. 5. Relationship between conformational entropy and binding cooperativity.

(A) Mapping of the methyl group order parameters on the different structures of PKA-C bound to different ligands. For clarity, the ligands are omitted from the figure. (B) Linear relationship between the cooperativity coefficient (σ) and the conformational entropy (ΔS_conf) of methyl side chains for the different ligated species of PKA-C. The ΔS_conf values are calculated using Eq. 4 in Materials and Methods. The σ value is calculated from the isothermal titration calorimetry (ITC) data from Kim et al. (15).

Overall, the multitime scale dynamic analysis of free and ligand-bound PKA-C shows that ATPγN activates conformational fluctuations of PKA-C that are conducive, i.e., committed, to substrate recognition. This phenomenon is reminiscent of the dynamic activation observed for p38 kinase (29). In contrast, the binding of two inhibitors steers the kinase motions toward time scales that are less committed to substrate binding, emphasizing that both coordinated structural changes and dynamics are essential to elicit binding cooperativity. While previous studies suggest the possibility of tuning ligand-binding affinity via conformational entropy (32, 33), our findings reveal that it is also possible to control binding cooperativity at distal sites.

DISCUSSION

Major drug discovery efforts on kinases have been focused on the optimization of both potency and selectivity of ATP-competitive inhibitors (2). To the best of our knowledge, however, there have been no reports on the effects of these inhibitors on the binding cooperativity for substrates when the ATP-binding pocket is occupied. Yet, it is emerging that both canonical and noncanonical functions of kinases are essential to cellular signaling (37, 38). Pseudokinases, for instance, are devoid of catalytic function, but they are still pivotal for the regulation of several cellular events by acting as scaffolds or substrates for binding other kinases. As for pseudokinases, inhibited kinases that are unable to phosphorylate substrates may still act as scaffolds or substrates for other kinases. A notable example is the activation of the RAF kinase in vivo using the ATP-competitive inhibitor PLX4720 (3, 39). In this case, PLX4720 under subsaturating conditions converts B-RAF into a pseudokinase, catalyzing dimerization, and activation of C-RAF (40). More recently, conformation-selective ATP-competitive inhibitors have been shown to control the regulatory interactions and noncanonical function of mitogen-activated protein (MAP) kinases (41). These examples support the phenomenon of paradoxical activation or off-target effects elicited by several kinase inhibitors (3, 42) and, at the same time, generate a growing interest toward manipulating catalytic and noncatalytic kinase functions using small molecules (37).

Our data show that two chemically distinct inhibitors with comparable potency modulate the K-type cooperativity of PKA-C differently. The overall conformation of the inhibited complexes as determined by x-ray crystallography is very similar and does not explain the differential behavior of these compounds. In contrast, NMR measurements reveal a direct correspondence between the extent of coordinated behavior of the chemical shifts and allosteric cooperativity for both nucleotides and inhibitors. Specifically, we found that the gradual loss of cooperativity (σ going from 53 for ATPγN to 7 for balanol and 0.6 for H89) (15) is correlated with the conformational entropy changes and is concomitant with the loss of chemical shift correlation throughout the entire enzyme. These results indicate that small but functionally significant structural rearrangements must occur to allosterically couple the nucleotide pocket with the substrate-binding site to elicit positive cooperativity. The two inhibitors also exemplify the bivalent nature of the ATP-binding site. Both share the hydrophobic adenine binding pocket, as do most kinase inhibitors. However, the way in which these two inhibitors complement the phosphate-binding part of the ATP-binding pocket is completely different, highlighting significant alterations in the dynamic features of the kinase. Moreover, chemical shifts, relaxation dispersion, and CEST measurements show that the opposite binding cooperativity displayed by these ATP-competitive inhibitors is linked to the differential changes in excited states, supporting the hypothesis that these states might be responsible for substrate recognition. Multiple high-energy conformational states are not germane to PKA-C alone. In a recent work, Tzeng and Kalodimos (43) found that Abl kinase interconverts between an active and two inactive conformations, and the structural characterization of them may lead to the development of selective inhibitors.

For PKA-C, the ATPγN-bound or intermediate state is quite dynamic with synchronous motions for catalytically important loops (17) and hydrophobic core (11). The C- and R-spines are highly dynamic and play a key role for generating allostery and rendering the kinase committed to catalysis (11). The PKA-C/balanol complex retains some of the motions in the catalytic loops, the αB helix (I85, V80), R-spine (L95), and C-spine (L173) found in the intermediate state, indicating that dynamics in the hydrophobic core contribute to allosteric control of positive cooperativity. H89 binding, on the other hand, quenches the dynamics in most of these residues, reflecting its negative K-type cooperativity due to the lack of the hydrophilic interactions with the active site eliminating the bivalent nature of the ATP-binding pocket. While both inhibitors attenuate the overall microsecond-millisecond time scale dynamics, balanol engages the two lobes of the kinase as a result of the interactions in the bivalent ATP-binding site. In addition to the hydrophobic interaction between the C-spine residues, when balanol is bound, the benzophenone moiety forms a number of polar interactions with the Gly-rich loop of PKA-C and with D184 of the conserved DFG loop, driving the kinase toward an intermediate-like state, displaying coordinated chemical shift behavior similar to the ATP-bound form. Although balanol does not induce the same degree of cooperativity as ATP, the opening and closing of the enzyme is still synchronous for some of the residues in the hydrophobic core, and the kinase explores high-energy conformations that have enhanced binding affinity for the substrate. The synchronous motions, together with the slow dynamics in αB helix, make it faster for the key elements in the kinase (αB, αC, DFG, activation, and peptide positioning loops) to orient properly for substrate recognition as it has been shown for Erk2 (44). This behavior contrasts that of the H89-bound complex, where the bromocinnamoyl moiety is unable to couple the two lobes structurally, as manifested by the absence of polar interactions between the bromocinnamoyl moiety and the residues lining the phosphate-binding site, thus severing the interactions between the ATP- and substrate-binding sites and abrogating allosteric cooperativity. This is accompanied by an increase in conformational entropy and a shift in the conformational dynamics of the protein backbone to a faster time scale. Motions along αB helix are absent with adenosine 5′-(β,γ-methylene) triphosphate, an ATP-mimic that lacks K-type cooperativity (15), but the hydrophobic spines remain dynamic (11). The disruption of the allosteric network and desynchronization of the motions of the two lobes are also responsible for the negative cooperativity exhibited by the Y204A mutant (17, 18). Kigawa and co-workers (45) reached similar conclusions for phosphoglycerate kinase, proposing that tuning ligand-binding cooperativity may represent a self-regulatory mechanism for enzymes in response to different intracellular cues.

A direct link between cooperativity and conformational fluctuations has also been found for Src kinase (46). In this case, it was found that the reactants (ATP and substrate) display negative cooperativity. On the contrary, for PKA-C, we found that synchronous enzyme dynamics underlie positive binding cooperativity for reactants [ATP and Serine protein kinase substrate (PKS)], while asynchronous dynamics are associated with negative cooperativity for the products (ADP and phosphorylated substrate] (25). Well-tuned conformational dynamics for protein kinases not only are essential for the catalytically important loops (10, 29, 44, 47–53), but it is also a requirement for the hydrophobic C- and R-spines of kinases (33), for which a single mutation leads to complete inactivation of the enzyme (11).

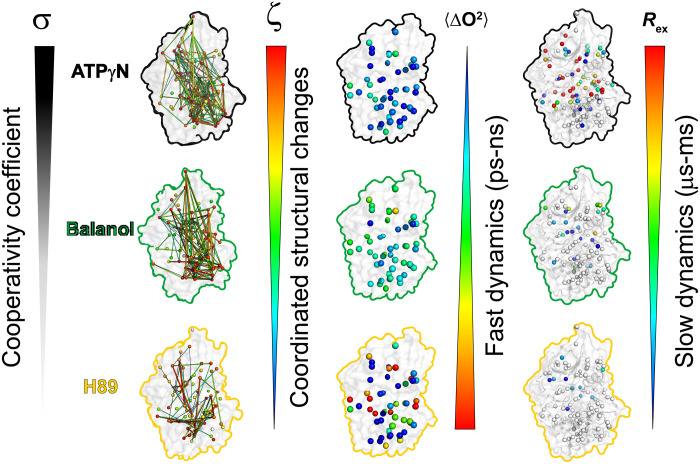
The totality of our observations indicates that the propagation of dynamically driven allostery through hydrophobic motifs is multifarious, with different time scales of motion within distinct regions of the kinase acting to modulate cooperativity and substrate binding. The high cooperativity of ATPγN is reflected in the highly coordinated structural changes, a reduction of side-chain flexibility in the fast time scale dynamics, and an increase of slow time scale motions (i.e., opening and closing of the active site). Low or negative cooperativity are manifested as a low degree of coordinated structural changes, increased side-chain flexibility, and the absence of slow motions (Fig. 6). This model suggests that ATP-competitive inhibitors that engage the two lobes, quench side-chain fast dynamics, and increase the internal allosteric communication are likely to steer the kinase toward a state that is conducive (i.e., committed) to substrate binding. Therefore, by tuning the chemistry of the inhibitors in the phosphate-binding region, it is possible to modulate the binding cooperativity of PKA-C.

Fig. 6. Summary of the ATP-competitive ligands on correlated structural and dynamic changes.

ATPγN binding causes coordinated structural changes as reflected by the high value of σ, which is concomitant to a rigidification of the methyl group fast dynamics (ΔO²_avg) throughout the entire enzyme, and an increase of methyl group slow dynamics (R_ex). Balanol binding shows a decrease of σ value, an increase of ΔO²_avg, and a decrease of R_ex. Last, H89 shows the lowest σ value, the largest ΔO²_avg, and almost no conformational exchange.

Understanding the relationship between excited states and protein function has been a subject of study in recent years (28, 54–56). Dynamic studies on Fyn SH3 domain (57, 58), CAP (43), and dihydrofolate reductase (DHFR) (59) suggest that conformationally excited states are required for protein folding, inhibition, aggregation, and substrate recognition (16). Single-site allosteric mutants that disrupt the transition to excited states ablate binding and catalysis (17, 59). Small molecules also have been shown to suppress excited states in several proteins, including DHFR (60), RAS (61), the R-subunit of PKA (53), and imidazole glycerol phosphate synthase (IGPS) (62). The differential suppression of microsecond-millisecond time scale dynamics, the formation of new alternate conformations, and the difference in exchange kinetics suggest that these ATP-competitive inhibitors exert different dynamic effects on the hydrophobic core of the enzyme and, particularly, the two spines. The changes in the motion of the kinase most likely preclude the enzyme from sampling conformations that have a high binding affinity for the pseudosubstrate.

In conclusion, we have used PKA-C to demonstrate the proof of concept that it is possible to control the binding affinity for substrates using different ATP-competitive inhibitors. While previous studies have shown that changes in protein conformational dynamics in the picosecond-nanosecond time scale directly affect binding affinity (63), we have shown here that allosteric cooperativity is modulated by conformational entropy. Our results suggest a way to modulate downstream signaling of kinases irrespective of the catalytic (canonical) activity, which can be used to control kinase function in vivo. We thus anticipate that future drug discovery programs for kinase inhibitors may benefit from taking into account the bivalent nature of ATP-competitive inhibitors to fine-tune both catalytic and binding functions of other aberrant kinases.

MATERIALS AND METHODS

Materials

All reagents used were analytical grade or higher. AMP, ADP, adenine, adenosine, and H89 were purchased from Sigma-Aldrich (St. Louis, MO, USA). ATPγN was purchased from Roche Diagnostics (Indianapolis, IN, USA). Balanol was purchased from AnalytiCon Discovery LLC (Potsdam, Germany, EU).

Sample preparation

Uniformly, ¹⁵N, ²H, and ¹³CH₃ ILV-labeled murine PKA-C in a pRSET(b) vector was recombinantly expressed in Escherichia coli BL21 (DE3) cells in M9 minimal media in 85% D₂O enriched with ¹⁵NH₄Cl and [²H]-d-glucose at 24°C as described previously (64). Protein expression was induced at OD₆₀₀ (optical density at 600 nm)of 1.2 with 0.4 mM isopropyl ß-d-thiogalactopyranoside (IPTG). PKA-C expression was carried out for 12 hours at 24°C. The ¹³C labeling of the methyl groups of IVL residues was achieved by adding 2-ketobutyric acid-4-¹³C-3,3-d₂ and 2-keto-3-(methyl-d₃)-butyric acid-4-¹³C-3-d sodium salts 1 hour before IPTG induction for a final concentration of 70 and 90 mg/liter, respectively (64). PKA-C was purified by affinity chromatography using the His₆-RIIα(R213K) subunit (65). PKA-C was subsequently dialyzed in a buffer containing 20 mM KH₂PO₄, 25 mM KCl, and 5 mM β-mercaptoethanol at pH 6.5. Since three different phosphorylated isoforms are present (65), we used a cation exchange chromatography using the HiTrap SP (GE Healthcare systems), columned with a linear gradient from buffer A [20 mM KH₂PO₄ (pH 6.5)] to buffer B [20 mM KH₂PO₄ and 1 M KCl (pH 6.5)]. PKA-C was quantified using ultraviolet absorbance at 280 nm (ε = 52060 M⁻¹ cm⁻¹). The NMR samples consisted of 0.20 to 0.42 mM PKA-C solubilized in a buffer containing 20 mM KH₂PO₄, 90 mM KCl, 10 mM MgCl₂, 10 mM dithiothreitol, and 1 mM NaN₃ at pH 6.5. For the CPMG relaxation dispersion and CEST experiments on the PKA-C/ATPγN complex, the MgCl₂ concentration was increased to 60 mM to avoid ATPγN hydrolysis. The nucleotide-bound complex was prepared by saturating the PKA-C with 12 mM ATPγN. The inhibitor-bound complexes were prepared by saturating the enzyme with 1.35 mM balanol and 2 mM H89.

NMR spectroscopy

The assignment of the backbone (66) and side-chain methyl (64) groups has been determined previously. The CSPs were calculated according to the formula

$$\mathrm{\Delta }\mathrm{\delta }=\sqrt{\mathrm{\Delta }{\mathrm{\delta }}_H^2+{(a\mathrm{\Delta }{\mathrm{\delta }}_X)}^2}$$ (1)

where Δδ_H and Δδ_X are the proton and heteronuclear chemical shift changes, respectively and a is a scaling factor for the chemical shift of the heteronuclei, equal to 0.154 and 0.25 for ¹⁵N and ¹³C, respectively (67). The two-dimensional (2D) backbone amide spectrum was acquired using the clean-TROSY (68) version of the original TROSY-HSQC pulse sequence, while the methyl side-chain spectrum was acquired using the methyl TROSY experiment (69) on an 850-MHz spectrometer. The data were acquired using 120 (t₁) × 2048 (t₂) complex points (for backbone amide) and 200 (t₁) × 2048 (t₂) complex points (for methyl side chain) using 16 scans and a recycle delay of 2.0 s.

The measurement of the order parameter was performed using triple quantum (TQ)–based ¹H relaxation–violated coherence transfer cross-correlation experiment (70, 71). The ¹³CH₃ IVL methyl-labeled ²H PKA-C samples had concentrations ranging from 200 to 250 mM, with 800 mM inhibitor/nucleotides. The global rotational correlation time (t_c) was determined using dynamic light scattering. The calculated t_c for the balanol-bound PKA-C resulted in 32.7 ns, while for the H89-bound was 30.3 ns. Single quantum (SQ)– and TQ-filtered spectra were acquired with relaxation delays (T) of 3, 6, 9, 12, 15, 20, 25, 30, and 35 ms using 2048 × 160 complex data points and with a recycle delay of 2 s. A nonlinear fit to the ratio of the intensities was used to extract the cross-correlation rate (η)

$$\frac{I_a}{I_b}=\frac{3}{4}\frac{\mathrm{\eta }\text{tan} \mathrm{h}(\sqrt{{\mathrm{\eta }}^2+{\mathrm{\delta }}^2}T)}{\sqrt{{\mathrm{\eta }}^2+{\mathrm{\delta }}^2}-\mathrm{\delta }\text{tan} \mathrm{h}(\sqrt{{\mathrm{\eta }}^2+{\mathrm{\delta }}^2}T)}$$ (2)

where I_a is the intensity of resonance in the TQ-filtered spectra, I_b is the corresponding intensity for the SQ-filtered spectra, and δ is a constant accounting for the coupling of the methyl group with external protons. Error analysis was performed using Monte-Carlo sampling. From the cross-correlation rate, the order parameter (O²) was estimated using the following formula

$$\mathrm{\eta }\approx \frac{9}{10}{\left(\frac{{\mathrm{\mu }}_0}{4\mathrm{\pi }}\right)}^2{[P_2(\text{cos}{\mathrm{\theta }}_{\mathit{\text{HH}}})]}^2\frac{O^2{\mathrm{\gamma }}_H^4{\mathrm{ћ}}^2{\mathrm{\tau }}_c }{r_{\mathit{\text{HH}}}^6}$$ (3)

where μ₀ is the permittivity of vacuum, P₂ is the second-order Legendre polynomial, θ_HH is the angle between the vector connecting two intramethyl protons and the methyl rotational axis, and r_HH is the distance between two protons within the methyl group.

The contribution of protein motion to the conformational entropy (ΔS_conf) of the nucleotide/inhibitors binding to PKA-C was calculated by measuring the changes in O² as a function of the ligate state, as reported by Wand and coworker (empirical calibration approach) (32, 63, 72). Briefly, the ΔS_conf for each nucleotide/inhibitor was calculated using the following equation

$$∆S_{\text{conf}}=s_d{N}_{\mathrm{\chi }}\mathrm{\Delta }[\langle O_b^2\rangle -\langle O_{\text{apo}}^2\rangle ]$$ (4)

where s_d is a scaling factor equal to −4.8 ± 0.5 (J mol⁻¹ K⁻¹), N_χ is the total number of the torsional angler for methyl-bearing residue tested (N_χ = 90), and $\langle O_b^2\rangle$ and $\langle O_{\text{apo}}^2\rangle$ are the average order parameter calculated for the nucleotide/inhibitor-bound form and for the apo state of PKA, respectively.

The microsecond-millisecond time scale conformational dynamics of backbone amides and methyl groups from the IVL residues of apo PKA-C, PKA-C/ATPγN, PKA-C/balanol, and PKA-C/H89 complexes were measured using CPMG relaxation dispersion experiments (28, 73). The ¹⁵N CPMG relaxation dispersion experiments were performed using the relaxation-compensated version of the CPMG experiment (74), with an improved phase cycle according to Long et al. (75). The ¹³C SQ CPMG pulse sequence by Lundstrom et al. (27) was used for the methyl group relaxation dispersion experiments. Both ¹⁵N and ¹³C relaxation dispersion experiments were performed in an interleaved mode with υ_CPMG values of 0, 50, 100, 150, 200, 250, 300, 400, 500, 600, 800, and 1000 Hz. Effective transverse relaxation rate constant, R_2,eff, were determined at each υ_CPMG value using the peak intensities with and without relaxation period according to the equation (76)

$$R_{2,\text{eff}}=\frac{\text{ln}\left(\frac{I_0}{I}\right)}{T}$$ (5)

where I₀ and I are the peak intensities of the resonances in the 2D spectra acquired in the absence and presence of a relaxation period, respectively, and T is the total CPMG time (40 ms) (76). Duplicate measurements were carried out at υ_CPMG values of 50, 500, and 1000 Hz for error estimation. The errors are indicated as SDs. The backbone ¹⁵N CPMG data were acquired on a Bruker AVANCE III spectrometer operating at 850.3 MHz, while the ¹³C CPMG data were acquired at two different fields using Bruker AVANCE III spectrometers operating at 700.1 and 850.3 MHz, respectively. The ¹⁵N CPMG spectra were acquired with 120 (t₁) × 2048 (t₂) complex points for apo and ATPγN bound, 102 (t₁) × 2048 (t₂) complex points for balanol bound, and 98 (t₁) × 2048 (t₂) complex points for H89 bound using 96 (apo), 64 (ATPγN-bound), and 128 (inhibitor-bound) scans with a recycle delay of 2.50 s. All ¹³C CPMG spectra were acquired as 160 (t₁) × 2048 (t₂) complex points using 48 scans and a recycle delay of 2.50 s.

The TR-HE experiments (31) were performed using a HE period (2/J_NH) of 10.8 ms. The peak intensities of the a, β, and zz spin states were used to calculate the $R_{\text{ex}}^{\text{TR}-\text{HE}}$ according to the following equation (77, 78)

$$R_{\text{ex}}^{\text{TR}-\text{HE}}\approx C_{\text{zz}} \text{ln}({\mathrm{\rho }}_{\mathit{zz}})+C_{\mathrm{\beta }}\text{ln}({\mathrm{\rho }}_{\mathrm{\beta }})$$ (6)

where C_zz = (2 t)⁻¹, C_b = (<k> −1)(4 t)⁻¹, ρ_zz = I_zz/I_a, and ρ_b = I_b/I_a. <κ> is the trimmed mean of the κ (κ =1 to 2 ln ρ_zz/lnρ_b) value for the amide resonances not showing chemical exchange (31, 78). The intensities I_α, I_β, and I_zz were generated from three 2D experiments of TR-HE. All spectra were acquired in an interleaved mode with 120 (t₁) × 2048 (t₂) complex points using 240 (apo) or 256 (inhibitor bound) scans and a recycle delay of 2.0 s. The uncertainties on the $R_{\text{ex}}^{\text{TR}-\text{HE}}$ values were calculated from propagating the errors using the root mean square noise from the spectra. All ¹³C methyl CEST experiments were recorded on a Bruker 900.21-MHz spectrometer equipped with a TCI cryoprobe using the pulse sequence by Bouvignies and Kay (79). The CEST datasets were acquired with an exchange time of 400 ms and at two different B₁ with field strengths of ~15 and ~30 Hz. A series of 79 2D HSQC spectra were acquired with 144 (t₁) × 2048 (t₂) complex points with the ¹³C carrier offsets between 8.73 and 28.71 parts per million (ppm) at 58-Hz (0.256 ppm) intervals. Each 2D spectrum was acquired with 16 scans and 70 increments using a recycle delay of 2.0 s. The ratio of peak intensities with (I) and without (I₀) the exchange delay, T_ex, as a function B₁ offset was used to construct the CEST profiles (79).

The ¹HX-NOE values (77) were calculated from the ratio of signal intensities of the TROSY-select experiments with and without a ¹H saturation of 5 s (80). The datasets were acquired as 120 (t₁) × 2048 (t₂) complex points using 184 to 196 scans and a recycle delay of 5.0 s. The uncertainties on the HX-NOE values were calculated using error propagation of the root mean square noise (81).

Data processing and analysis

All data were processed using NMRPipe (82), and peak intensities were quantified using function and data analysis (FuDA) (http://www.ucl.ac.uk/hansen-lab/fuda/) and national magnetic resonance facility at Madison (NMRFAM)-Sparky (83). Gaussian window function with a line broadening of −12 Hz was applied in the direct dimension, while sine bell window function with an offset of 0.5 was applied in the indirect dimension. The data were zero-filled to the nearest power of 2. The side chains showing significant dispersion (R_ex > 2 s⁻¹) in the balanol-bound and H89-bound complexes were 20 and 9, respectively. The decay of the methyl group resonance intensities was subsequently fitted individually with a two-state exchange model using the graphical user-friendly analysis of relaxation dispersion data (GAURDD) software (84) with k_ex, p_B, Δω, and $R_2^0$ as the fitting parameters. Among the side chains that showed chemical exchange, group fitting into a two-state exchange process was carried out for residues that satisfy: $\frac{{\mathrm{\chi }}_{\text{group}}^2}{{\mathrm{\chi }}_{\text{individual}}^2}<1.20$. For the ATPγN-bound and balanol-bound complexes, group fits of 12 and 7 side chains, respectively, were obtained using a single two-state exchange process, obtaining k_ex and p_B, as well as individual Δω and $R_2^0$. The CEST profiles were analyzed using a two-state exchange model included in the ChemEx software (30), with k_ex, p_B, and Δω as the main fitting parameters. Among the side chains analyzed, a few side chains showed apparent excited states in the CEST profiles for the apo (three residues), ATPγN-bound (two residues), balanol-bound (three residues), and H89-bound (two residues) PKA-C, respectively.

Analysis of chemical shift trajectories

To quantify the global populations of the kinase residues in the transition between open and closed states, the coordinate chemical shift behavior (CONCISE) method (19) was used. For fast exchange residues, CONCISE used the principal component (PC) analysis to identify a set of residues whose chemical shifts respond linearly to the conformational transition. Each residue provides a measure of the equilibrium position for every state in the form of a score along with the first principal component. The chemical shifts of the apo, ADP-bound, and ATPγN/PKI_5–24-bound forms were used as reference states. The equilibrium position for each state is given by the average of the PC scores over all linear residues. A threshold of 1.0 to 3.0 for the ratio of the SDs of PC1 over PC2 was used to identify those residues following a linear pattern. Residues with chemical shifts perturbations below 0.05 ppm were discarded from the analysis.

To determine the allosteric networks of residues that respond in a correlated fashion to ligand binding, a modified version of the CHESCA method (22) was used. A total of four different PKA-C states were used to generate the correlation matrix: apo, ADP-bound, inhibitor or nucleotide-bound, and inhibitor or nucleotide-bound/PKI_5–24 ternary complexes of PKA-C. In addition, the amides and IVL methyl group spectra were referenced as reported by Cembran et al. (19). Briefly, the corrections to the chemical shifts (Dd ¹⁵N^j and Dd ¹H^j) for a specific state j were calculated minimizing a distance function D^j, defined as

$$\begin{array}{c}{D}^j={\displaystyle {\sum }_{i=1}^{N \text{res}}}\mid ({\mathrm{\delta }}^{15}{N}_i^j+∆{\mathrm{\delta }}^{15}{N}_j^j-{\mathrm{\delta }}^{15}{N}_i^{\text{ref}})\mid +\\ \mid ({\mathrm{\delta }}^1{H}_i^j+∆{\mathrm{\delta }}^1{H}_j^j-{\mathrm{\delta }}^{15}{H}_i^{\text{ref}})\mid \end{array}$$ (7)

where the superscript ref indicates the reference state (apo form), the subscript i runs over all of the N residues, and j is the state to be rereferenced. The correlation matrices were constructed from the correlation coefficients (r_ij) greater than 0.98 for both backbone amide and side-chain methyl groups. Only residues with CSPs greater than the average linewidth were considered for the CHESCA analysis. Each correlation matrix was mapped on the 3D structure of PKA-C using a Pymol script generator written in MATLAB with a cutoff value of 0.98. All the programs listed above were written in MATLAB .

To quantify the correlation density of the CHESCA maps, we have used the correlation score (ζ) defined as

$$\text{Corr score},\mathrm{\zeta }=\frac{\text{number of} (r_{\mathit{\text{ij}}}>r_{\text{cutoff}})}{\text{total number of} r_{\mathit{\text{ij}}}}$$ (8)

where r is the CHESCA correlation matrix and i and j are the residue indices. For single-residue correlation score (i^th), j indicates all the remaining assigned residues, whereas for the global correlation score, i and j indicate all the assigned residues. For our analysis, a correlation cutoff (r_cutoff) of 0.9 was used to calculate the global correlation score.

Supplementary Materials

This PDF file includes:

Figs. S1 to S23

Tables S1 to S10

View/request a protocol for this paper from Bio-protocol.