Reconstruction of neocortex: organelles, compartments, cells, circuits, and activity

Summary

We assembled a semi-automated reconstruction of L2/3 mouse primary visual cortex from ~250×140×90 μm³ of electron microscopic images, including pyramidal and non-pyramidal neurons, astrocytes, microglia, oligodendrocytes and precursors, pericytes, vasculature, nuclei, mitochondria, and synapses. Visual responses of a subset of pyramidal cells are included. The data are publicly available, along with tools for programmatic and three-dimensional interactive access. Brief vignettes illustrate the breadth of potential applications relating structure to function in cortical circuits and neuronal cell biology. Mitochondria and synapse organization are characterized as a function of path length from the soma. Pyramidal connectivity motif frequencies are predicted accurately using a configuration model of random graphs. Pyramidal cells receiving more connections from nearby cells exhibit stronger and more reliable visual responses. Sample code shows data access and analysis.

Graphical Abstract

Introduction

Reconstructions of brain tissue from electron microscopy (EM) images of invertebrate and vertebrate species have increased in scale and complexity, aided by automation of image acquisition (Kornfeld and Denk 2018) and analysis (Lee et al. 2019). In vivo calcium imaging has preceded EM reconstruction in a few studies (Briggman, Helmstaedter and Denk, 2011; Vishwanathan et al., 2017; Bae et al., 2018; Wanner and Friedrich, 2020). This combined structure-function approach has been applied to mouse primary visual (V1) cortex (Bock et al., 2011; Lee et al., 2016), but was previously limited to tens of cells. Here we present a reconstruction of mouse V1 including neuronal and non-neuronal cells, mitochondria, cell nuclei, synapses, and calcium imaging from over 100 of the pyramidal cells (PyCs). The data are publicly available (microns-explorer.org), along with tools for programmatic and interactive access. We also provide four vignettes studying on mitochondria, synapses, circuit motifs, and the relationship of connectivity to function, chosen to demonstrate the diversity of quantitative information that can be uncovered with this multifaceted reconstruction.

Results

Reconstruction of mouse visual cortex

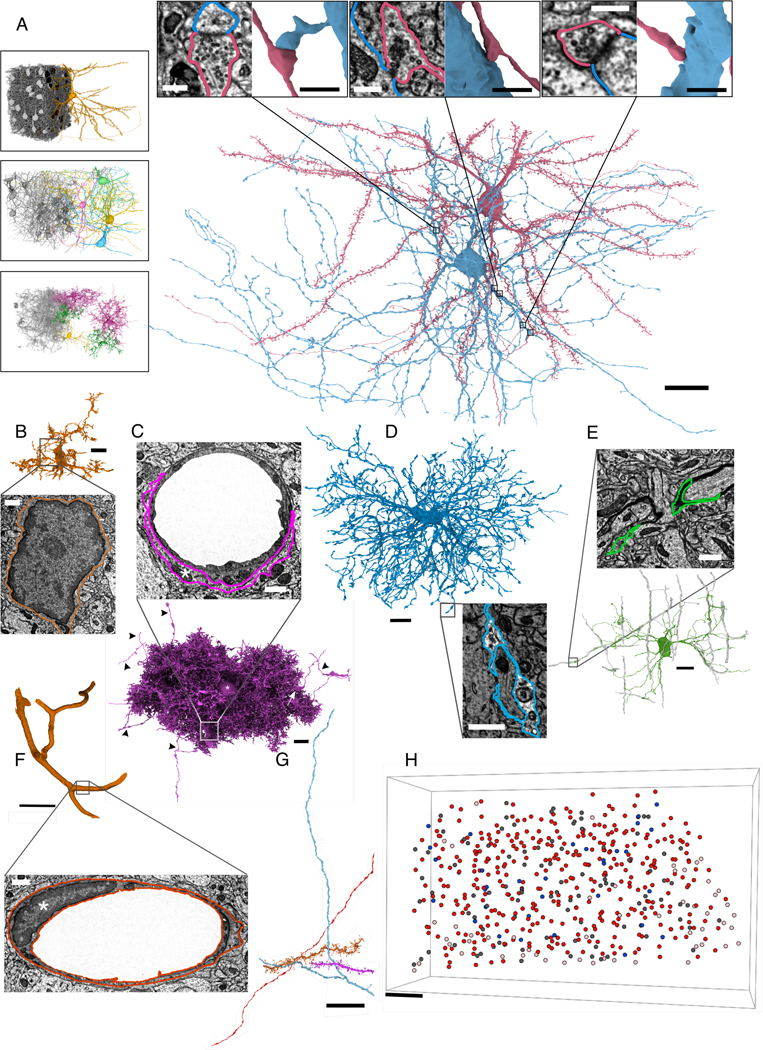
We selected a region in L2/3 of V1 from a male, young-adult (postnatal day 36) mouse in which neural activity had been recorded using calcium imaging (Figures 1A, S1, STAR Methods). Using serial-section EM, we imaged a volume of about 250×140×90 μm³ (mediolateral, radial, and anteroposterior axes). Data S1 compares the volume with other published rodent EM volumes. A nominal resolution of 3.58×3.58×40 nm³/voxel is used throughout (see STAR Methods for in vivo resolution estimates and precise volume dimensions). This resolution is sufficient to visualize and analyze the morphology of cells, their organelles, and chemical synapses in neurons (insets of Figures 1A–1F, S1A–S1C).Alignment and automatic segmentation of the serial-section images yielded roughly 8 million objects describing neurons, non-neuronal cells, and cellular fragments (Figure 1G).

Figure 1. Neuronal and non-neuronal cells.

(A) Rendering of a PyC (red) and basket interneuron (blue) after proofreading. Insets: zoomed-in 2D EM and 3D mesh views for 3 of 5 PyC-to-basket synapses. Left insets: cells with somas in the dataset, by type, with cutouts to show examples. Top to bottom: PyCs, interneurons, non-astrocytic glia (minus 4 cells with merge errors that obscure the view: STAR Methods).

(B) Microglia, without proofreading. Inset: EM view of the soma, showing dark, scarce cytoplasm and dark nucleoplasm.

(C) Astrocyte, without proofreading, showing endfeet (box, inset, white arrow) and merge errors with axon segments (black arrowheads). Asterisks: 3D, soma, 2D, cytoplasm.

(D) Oligodendrocyte precursor cell (OPC). Inset: EM of OPC occupying the small space between neurites. Non-OPC neuropil is artificially dimmed to highlight OPC cytoplasm.

(E) Oligodendrocyte. Wrapped axons shown in gray. Inset: EM of a process transitioning to myelin.

(F) Endothelial cell wrapping a blood vessel, with split errors corrected (merge errors artificially removed for clarity; Figure S1). Inset: EM of soma showing dark cytoplasm and nucleoplasm (STAR Methods). Asterisk: nucleus.

(G) Sample orphan neurites with ≥10 predicted synapses.

(H) Soma centroids in the EM volume. Dark red: PyCs analyzed in this paper (363); light pink: PyCs at edge of volume, not analyzed (53); blue: analyzed inhibitory neurons (34); dark gray: glia (169).

Scale bars: (A): 20 μm, left insets, 25 μm, 3D synapse insets, 1 μm, EM insets, 300 nm; (B-E) 10 μm, insets, 750 nm; (F) 20 μm, inset 100 nm; (G, H) 25 μm.

See also Figure S1.

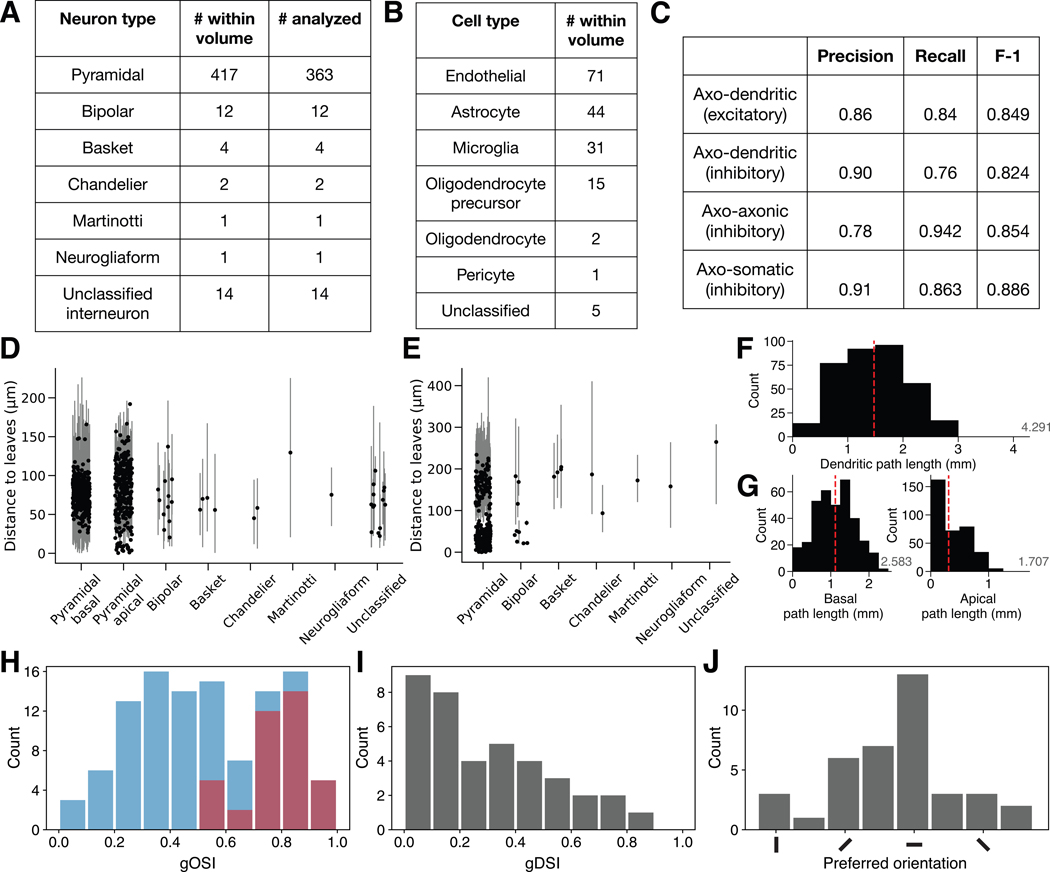
Cells with somas were assigned types using a semi-automated approach based on neurite morphology (Figures 1H, 3A and 3B, STAR Methods). In addition to 416 PyCs, we identified 12 bipolar cells, 4 basket cells, 2 chandelier cells, 1 Martinotti cell, and 1 neurogliaform cell (Figures 5A and S1). There were 14 cells with axons that were severely cut off by the borders of the volume that we could not confidently classify aside from distinguishing them from the excitatory PyCs (Figure 3A, Data S2).

Figure 3. Resource Statistics.

(A-B) Neuron (A) and non-neuronal (B) type classifications.

(C) Estimated synapse detection performance (STAR Methods).

(D-E) Dendrite (D) and axon (E) lengths for proofread cells with accurate compartment labels, measured as path length between each soma and its skeleton leaves (STAR Methods). Points show median branch length for each cell. Lines show the 5th and 95th percentiles (N_pyr=351, N_inh=34).

(F-G) The total dendritic path length (F) or apical & basal path length (G) for each PyC (N=351). Red line shows the median (dendritic=1.475 mm, basal=1.118 mm, apical=0.309 mm). The average length from light microscopy data is shown on the right in gray (Gilman, Medalla and Luebke, 2016).

(H) Global orientation selectivity index (gOSI) of all cells with activity traces (blue, N=112) and significantly tuned orientation selective (OS) cells (red, N=38).

(I) Global direction selectivity index (gDSI) of OS cells (N=38).

(J) Distribution of preferred orientation of OS cells (N=38).

See also Data S1.

Figure 5. Cell type dependent properties of inhibitory neuron inputs.

(A) Classified inhibitory interneurons. 1 truncated basket cell not shown.

(B) Linear synapse density for each cell class.

(C) Surface synapse density for each cell class. 1 basket cell is not included in panel (C) as its soma is highly truncated.

(D) Synapse size distributions (in 3.58×3.58×40 nm³ voxels) for dendrites and somas of each cell class.

(E) Synapse size for inputs from L2/3 pyramidal cells onto dendrites of each cell class.

Error bars and shaded regions in (B) and (C) indicate 95% bootstrap confidence intervals (1000 samples). Scale bars: (A) 50 μm.

See also Figure S3 and Data S2.

We adjusted automated cellular reconstructions to facilitate accurate morphological and connectivity analyses. All nuclei were automatically segmented (STAR Methods) to aid the identification of all somas in the volume. For the 363 of 416 PyCs that had somas and sufficient neurites in the volume, and for the 34 inhibitory cells (Figure 1H), we corrected segmentation errors using an interactive proofreading system for human experts to split and merge objects (Dorkenwald et al., 2019, 2020) that covered ~27% of the volume and took roughly 1,330 person-hours (STAR Methods).

We automatically computed skeletons and meshes for each object in the cellular and mitochondrial segmentations to provide useful representations for visualization and analysis (e.g., for measurements involving length or surface area). In addition, we used a semi-automated approach (STAR Methods) to assign compartment labels to the skeleton nodes of the neurons we proofread. These labels included somatic, axonal, and dendritic for inhibitory cells, as well as apical dendritic and basal dendritic for PyCs. Of the 363 PyCs, 351 possess compartment labels without discernible errors, although the others are still useful for specific analyses.

The 351 PyCs were captured in the volume at varying degrees of completion (Figure 3D–G). Many PyC axons were truncated at lengths <100 μm from the soma (Figures 3E, S4B, S7C), but 111 had axons extending beyond 100 μm (roughly the first branch point). PyC dendrites (both apical and basal) were captured at lengths ranging from ~0 to >200 μm (captured to natural distal endpoint) (Figure 3D). By computing the total path length of the dendritic arbor for each PyC and comparing this measurement to light microscopy data with full arbors (Gilman, Medalla and Luebke, 2016), we estimated that PyC dendritic arbors were between ~0 and 69% complete (median ~34%), with total path lengths of up to 2.98 mm (Figures 3F and 3G). Apical dendrites for PyCs were more cut off than basal dendrites in our volume, as these dendrites largely ramify in L1 (outside the volume).

Non-neuronal cells included 71 endothelial (blood-vessel wrapping) cells, 44 astrocytes, 31 microglia, 15 oligodendrocyte precursor cells (OPCs), 2 oligodendrocytes, and 1 pericyte (Figures 1A bottom left inset, 1B–1F, 3B). Blood vessels totaled 2.03 mm in length (Figure S1F).

Automatic synapse detection yielded over 3.5 million synapses with 93.0% precision (the percentage of correct predictions) and 90.9% recall (the percentage of synapses captured by the predictions) (STAR Methods). Axo-dendritic, axo-axonic, and axo-somatic synapses were all present (Figure 1A insets and Figure S1A–S1C), and detection performance for these synapse types varied (Figure 3C). Synapses onto PyCs with somas were proofread. This yielded a highly accurate map of connectivity between PyCs with somas in the EM volume, consisting of 1981 synapses within 1752 PyC-PyC connections that can be used to analyze properties of cortical circuits (Figure 6; Dorkenwald et al., 2019).

Figure 6. Connectivity motif frequencies can be predicted from degree sequences.

(A) Sampling from the configuration model (Artzy-Randrup and Stone 2005). Swapping connected partners preserves in- and out-degrees.

(B) A generalized Erdős–Rényi (ER) model holding the frequency of bi-directional connections (p_uni≈4.92×10⁻², p_bi≈4.75×10⁻³).

(C) The clustering coefficient expressed with 3-cell motif frequencies.

(D) The observed in- and out-degree distributions and their expected distributions in a standard ER model (edge probability = 0.0540). Red: observed; Black, dashed: ER. Histograms are calculated for 8 bins of equal width on a log scale. Expectations are estimated with 100 samples from the ER model.

(E) 2-cell motif frequencies in the observed network and a configuration model relative to the ER model. Shaded regions show the smoothed distributions of motif counts sampled from the configuration model. White points show medians, solid vertical lines show quartiles, and dashed lines show the 95% confidence interval for 1,000 samples.

(F) Comparison of 2-cell motif counts in the ER model and configuration (CFG) model. Circles indicate mean counts sampled from the configuration model, and triangles indicate mean counts sampled from the ER model.

(G) Same as E for 3-cell motif frequencies in the observed network and the CFG model relative to a generalized ER model (gER).

(H) Same as F for 3-cell motif counts in the gER and CFG model.

(I)The common neighbor rule is significantly more prominent in the pyramidal cell network than in gER random networks. Gray: configuration model; Black, dashed: gER random networks; Red: observed data. (red slope: R² = 0.88, p=6.1×10⁻⁵; gray: R² = 0.99, p=5.2×10⁻⁹; z-test). Error bars show SD of 100 samples.

See also Figures S4–S6, Tables S1–S3.

The reconstruction includes over 2.4 million mitochondria (Figures 4A, 4B, STAR Methods; see Dorkenwald et al., 2017; Haberl et al., 2018; Xiao et al., 2018 for similar methods and Perez et al., 2014; Márquez Neila et al., 2016; Calì et al., 2019; Yuan et al., 2020 for others). Each reconstructed mitochondrion is linked with its host cell’s identifier so they can be analyzed on a per-cell basis. These mitochondria have various morphologies, including a “reticular” type (Figure S2N; see Popov et al., 2005) that extend for longer distances (>100 μm) than previously observed. These reside in orphan dendrites, presumably from deep L2/3, L5, or L6 PyCs.

Figure 4. Spatial organization of mitochondria and synapses in L2/3 PyCs.

(A) Mitochondrial segmentation cutout.

(B) PyC 3D rendering with mitochondria. Insets show the soma (top) and axon (bottom).

(C) Comparison of mitochondrial volume by compartment (N_axonal=11,484, N_somatic=90,193, N_apical=18,608, N_basal=53,318 from 351 PyCs; One-tailed Mann-Whitney U tests; *:p<1×10⁻⁸⁶, **:p≈0). Boxes show the IQR, and whiskers show the 5th and 95th percentiles.

(D-E) Mitochondrial volume per unit length (D) and mitochondrial path length per unit length (E) at different distances to soma.

(F) Median overlap (red) or uncovered (blue) path length within dendritic segments.

(G-I) Median dendrite diameter (G), linear synapse density (H), and areal synapse density (I) at different distances to soma.

(J) Coefficient of variation for linear (red) and areal (blue) synapse density at different distances to soma. Dots and shaded regions in D, E, G, H, and I show mean +/− SD at each distance bin. N=29,591.Scale bars: (A) 1.5 μm (B) 10 μm, top inset 5 μm, bottom inset 2.5 μm.

See also Figure S2.

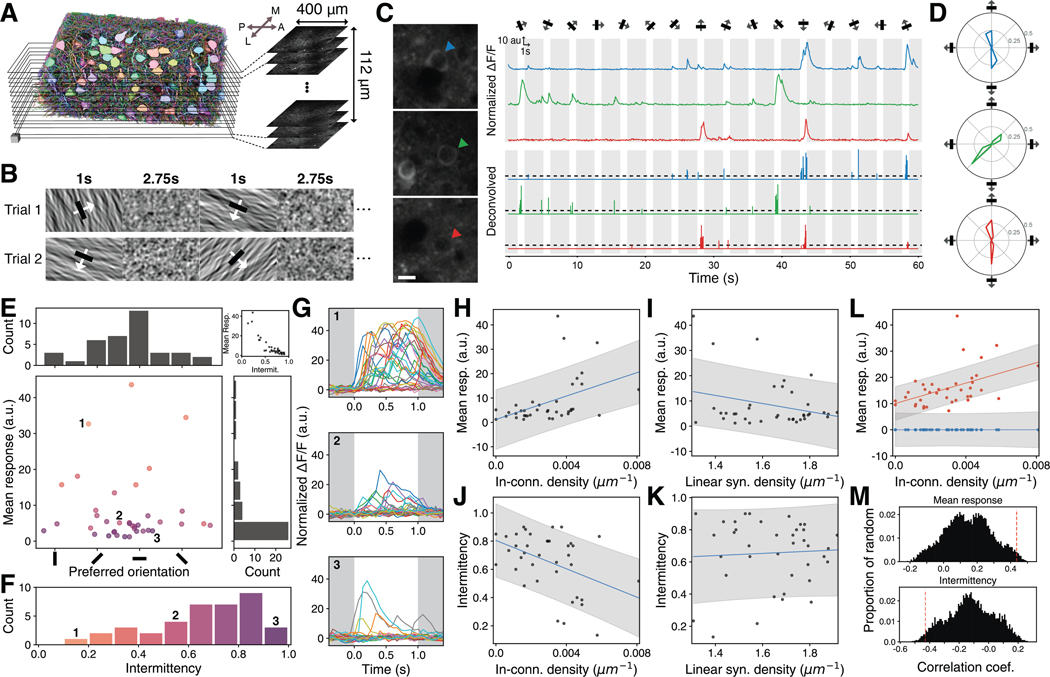
Prior to EM imaging, responses of PyCs to visual stimuli were recorded in an overlapping volume by calcium imaging (Figures 7A–7C, S7A–S7B, STAR Methods). A colored noise stimulus was presented to characterize spatiotemporal receptive fields (Figure 7B), and oriented stimuli moving in any of 16 directions (Figure 7B) were presented to characterize direction and orientation selectivity (Figures 3H–3J). Each direction was shown once for each of 30 trials. Each trial presented the directions in a pseudo-random order, interspersed with the colored noise stimulus (each row of Figure 7B shows part of an individual trial; see STAR Methods). The calcium videos were co-registered to the EM volume (Figures 7A, S7A and S7B) and normalized (STAR Methods). Activity traces were extracted for 112 of the 363 PyCs (Figure 7C) via the EASE algorithm (Zhou et al., 2020). Traces and estimated spike rates were acquired for only a subset of reconstructed PyCs that both overlapped with the calcium imaging volume and were responsive to visual stimuli (STAR Methods).

Figure 7. In-connection density is related to visual function.

(A) 2-photon calcium recording and coregistration. Layered black rectangles (left) represent the 2-photon image planes (right) cropped to roughly match the segmentation. Arrows show cardinal axes (Anterior, Posterior, Medial, Lateral).

(B) Example visual stimuli of oriented patterns (odd columns) interspersed with the pink noise stimulus (even columns).

(C) Examples of 2-photon recordings (left) with noise-normalized ΔF/F traces (top right) and deconvolved traces (bottom right, dashed line: activity threshold for “active” trials) extracted from cells marked with colored arrows during a single trial.

(D) Tuning curves of cells in C. Area under the tuning curve is normalized to be equal to 1.

(E) Preferred orientation and mean response (bottom left) of orientation tuned cells with distribution of preferred orientation (top left) and distribution of mean response (bottom right). Dots are colored by the cell’s intermittency bin in F. Mean response is correlated with intermittency (top right).

(F)Fraction of non-active trials (intermittency) for orientation tuned cells.

(G)Three example cells’ responses to 30 trials of their preferred directional stimulus. Example cells are the numbered dots in E. Different colors show responses in different trials.

(H) Mean response to preferred directions is positively correlated with in-connection density (N=38, Pearson’s r=0.44, p=0.006).

(I) Mean response is not correlated with linear synapse density (N=38, r=–0.28, p=0.095).

(J) In-connection density is negatively correlated with intermittency (N=38, r=–0.43, p=0.007).

(K) Intermittency is not correlated with linear synapse density (N=38, r=0.05, p=0.744).

(L) In-connection density has a greater effect on mean active responses (red, a=1, N=38) than mean inactive responses (blue, a=0, N=38, p=0.002).

(M) Normalized histogram of Pearson correlation coefficients of spatially-restricted randomizations for correlations in H (top, p=0.0161) and J (bottom, p=0.0182) with correlation coefficient of observed data (red dashed line).

(A) Scale cube: 10 μm edge. (C) Scale bar: 10 μm. (C, G) White: directional stimulus shown, Gray: noise stimulus shown. (H, I, J, K, L) Line: linear fit, Shade: 80% prediction interval. (M) All permutation tests used 10,000 iterations.

See also Figure S7.

All our EM data, reconstructed cells, synapses, mitochondria, and visual responses are publicly available at the MICrONS Explorer website, microns-explorer.org (Figure 2, Movie S1). Below, we provide four vignettes that address diverse questions about the cortex on organelles, synapses, circuit structure, and function chosen to illustrate the breadth of science enabled by our resource. Associated Jupyter notebooks are on the MICrONS Explorer website.

Figure 2. Resource Access.

(A) Cell segmentation displayed using Neuroglancer (Maitin-Shepard, 2019), including tabs for multiple data layers (top) and the UI scale bar (bottom-left). Clicking on the red segment under the white arrow selects the cell in panels B-E. Zooming to view the dashed black box shows panel F.

(B) Triangle mesh for the cell selected in panel A. The UI can show the full extent of this cell’s reconstruction within the segmentation bounding box. Zooming to the dashed black box shows panel C.

(C) EM image data rendered along with the mesh from panel B. Changing the view layout shows panel D.

(D) Mitochondria and synapse layers added to the EM slice from panel C. The image has been dimmed using the UI to highlight synapse segments, and all synapse segments were given the same color. Zooming to view the dashed white box shows the view in panel E.

(E) A single synapse in detail. (Left) Raw EM. (Right) Synapse, mitochondria, and cell segmentation layer added (with red cell selected).

(F) Nucleus segmentation added at full opacity. Cell segmentation shown at decreased opacity.

(G) Types of data available in the resource. LM=Light microscopy, vx=voxels. Nominal voxel size is 7.16×7.16×40 nm³ for synapse and mitochondria segmentations, 57.28×57.28×40 nm3 for nucleus segmentation.

Scale bars: (D) 1 μm, (E) 150 nm, (F) 3 μm.

See also Movie S1.

Spatial organization of mitochondria

The compartments of a neuron—axon, dendrites, and soma—have different functions supported by distinct structures, and their intracellular organelles have distinctive properties. Axonal mitochondria are small and punctate, whereas dendritic mitochondria are often much longer (Chang, Honick and Reynolds, 2006; Lewis et al., 2018). The size of axonal mitochondria is functionally important for presynaptic release properties (Sun et al., 2013; Kwon et al., 2016; Cserép et al., 2018; Lewis et al., 2018). The contrast between axonal and dendritic mitochondria is thought to arise from differences in the balance between organelle fusion and fission (Lee et al., 2018; Rossi and Pekkurnaz, 2019).Mitochondrial fusion, fission, and trafficking have been linked with synaptic plasticity (Divakaruni et al., 2018; Rangaraju, Lauterbach and Schuman, 2019) and neurite branching (Li et al., 2004; Bertholet et al., 2013; Courchet et al., 2013; López-Doménech et al., 2016; Lewis et al., 2018). Given these applications, quantifying the spatial organization of mitochondria has biological significance. Our EM reconstruction allows for characterizing how mitochondrial architecture varies between and within compartments of a neuron because it includes large fractions of neuronal arbors, unlike previous EM reconstructions of mitochondria in smaller volumes (Kasthuri et al., 2015; Smith et al., 2016; Bloss et al., 2018; Calì et al., 2018).

We first characterized mitochondrial structure in different PyC compartments. In the 351 PyCs with accurate compartment labels, we automatically labeled each mitochondrion as occupying axon, soma, apical dendrite, or basal dendrite (STAR Methods). We computed the volume of each mitochondrion as well as its mitochondrial complexity index (MCI; Vincent et al., 2019) to measure the shape complexity of individual organelles, and compared these values across compartments (Figures 4C and S2A). Selecting statistical comparisons by ordered median value, axonal mitochondria (N_axonal=11,484, median=0.013 μm³, IQR=[0.008 μm³, 0.021 μm³]) were on average smaller than somatic mitochondria (N_somatic=90,193, median=0.033 μm³, IQR=[0.013 μm³, 0.080 μm³]; one-tailed Mann-Whitney U test: p≈0) and had smaller MCI values (p≈0). Somatic mitochondria were smaller than local apical mitochondria (N_apical=18,608, median=0.062 μm³, IQR=[0.019 μm³, 0.205 μm³], p≈0), and had smaller MCI values (p≈0). Lastly, local apical mitochondria were slightly smaller than basal dendritic mitochondria (N_basal=53,318, median=0.095 μm³, IQR=[0.027 μm³, 0.242 μm³], p<1×10⁻⁸⁵) and had smaller MCI values (p<1×10⁻²⁸). Comparing median values across compartments, we see a roughly 7.5:1 size ratio between basal and axonal mitochondria in agreement with previous work (Lewis et al., 2018), and a 2.5:1 ratio between somatic and axonal mitochondria.

EM resolution is helpful for the analysis of somatic mitochondria, compared to diffraction-limited light microscopy, because they are densely intermingled (Figure 4B). A previous report that mitochondria are smaller in the soma than in the neurites (Calì et al., 2019) is consistent with our finding, as the authors noted that their neurite mitochondria were mostly dendritic.

Size gradients might also exist in the perisomatic neurites to realize these differences. We measured the path length covered by each mitochondrion throughout neurites of the 351 PyCs, divided the neurites into segments (each roughly 10 μm long), and studied the lengths of mitochondria present in any segment at a binned distance from the soma (Figure S2B–S2D). The length distribution for axonal mitochondria (Figure S2B) decreases slightly across the distances we measure. The median mitochondrion length for basal and apical dendrites (Figure S2C) shows a steady increase until roughly 50 μm from the soma and then plateaus until neurites reach the borders of the volume (~125 μm).These dendritic distributions suggest that the largest mitochondria are absent from this proximal region. Still, the dendritic graphs (Figure S2C–S2D) should be interpreted with caution, as large dendritic mitochondria can skew the distribution of many distance bins.

Small-scale variation in the need for ATP production and calcium buffering (Lee et al., 2018; Rossi and Pekkurnaz, 2019) may be visible in covariation of local mitochondria. ATP is produced at the mitochondrial internal membrane and calcium is sequestered by the matrix (Carafoli, 2003), the space enclosed by the internal membrane. As the matrix cannot be consistently resolved in our images, we will use mitochondrial volume contained within a neurite segment as a proxy of mitochondrial matrix measurements.

347 of the 351 PyCs had basal dendrites in the volume. Using the basal dendrite segments from the analysis of Figure S2C, we computed two local measures of mitochondrial density in these segments (Figure S2E, STAR Methods): mitochondrial volume per unit path length (Figures 4D and S2O), and the ratio of mitochondrial length to path length (Figures 4E and S2P; also called mitochondrial index in (Li et al., 2004)). The average mitochondrial index over segments is roughly 70–80% in the perisomatic dendrites and rises to an approximately constant value near 90% for distances more than 60 μm from the soma (Figures S2H and S2P). The average of the mitochondrial volume per path length has similar behavior (Figure S2O).

In distal dendrites, there is little overlap between mitochondria (Figure 4F). Instead, there are clear gaps in mitochondrial coverage. In the perisomatic region, we observe both gaps and overlap, and the variance of the mitochondrial index increases.

We estimated the shaft diameter of basal dendrites from the triangle meshes (STAR Methods). The diameter decreases monotonically with distance from the soma (Figures 4G and S2R), consistent with prior reports (Larkman, 1991a; Benavides-Piccione et al., 2020). Most of this decrease is perisomatic, with less change beyond 60 μm (Figures S2I). Given that mitochondrial volume per unit length is roughly constant along distal dendrites, while dendrite shaft diameter decreases, the volume fraction of the dendrite occupied by mitochondria increases with distance from the soma (Figures S2F and S2Q). The distribution of mitochondria with respect to synapses is described below after characterizing the spatial organization of synapses.

Spatial organization of synapses onto excitatory and inhibitory cells

Dendritic structure is important for understanding dendritic function (Stuart, Spruston and Häusser, 2016). For example, dendritic tapering (e.g., Figure 4G) has been hypothesized to optimize signal transmission from synapse to soma (Bird and Cuntz, 2016). Theoreticians predicted that somatic responses to distal synapses should be attenuated (Rall and Rinzel, 1973), but experiments have found that all synapses “democratically” produce the same response independent of distance from the soma (Magee, 2000). To understand such issues, especially through computational modeling (Cook and Johnston, 1997), it is important to quantify how properties of dendrites and synapses vary with distance from the soma.

Previous work measured the density of synapses received by PyC dendrites and characterized how this density depends on distance from the soma (Larkman, 1991b; Jacobs, 2001; Megías et al., 2001; Elston and DeFelipe, 2002; Ballesteros-Yáñez et al., 2006; Benavides-Piccione et al., 2013; Bloss et al., 2016; Gilman, Medalla and Luebke, 2016). This work often estimated linear synapse density, the number of synapses per unit length of dendrite, by measuring dendritic spine density. Some studies only coarsely divided the arbor into proximal and distal regions. Our volumetric reconstructions of dendrites allow for studying synaptic densities in great detail.

Linear synapse density on basal dendrites of the 351 PyCs with accurate compartment labels is shown in Figures 4H and S2S and are from direct counts that do not distinguish between excitatory and inhibitory synapses. The average density is low in the perisomatic dendrites, rises to a maximum under 2 synapses/μm at roughly 60 μm from the soma, and decreases in the distal dendrites. The location and height of the peak match prior measurements of spine density on basal dendrites of L3 PyCs in mouse neocortex (Ballesteros-Yáñez et al., 2006).

We also computed the areal synapse density by using the triangle meshes to estimate dendritic surface area, including both shaft and spines. The average density rises with distance from the soma in the perisomatic dendrites, and then plateaus at an approximately constant value of roughly 0.33 synapse/μm² in the distal dendrites (Figures 4I and S2T). Areal synapse densities have previously been reported for apical dendrites in mouse cortex (Karimi et al., 2020) and dendrites of hippocampal cells (Bloss et al., 2016). Following this work, we also computed areal synapse density using the area of a cylinder with the same diameter as the dendritic shaft. This “cylinder synapse density” is also roughly invariant with distance from the soma in the distal dendrites (Figures S2G and S2U). Figure S2I is a clear comparison of linear synapse density and the two versions of areal synapse density, which shows their fractional change in the distal dendrites.

Synapse density also fluctuates across dendritic segments at a given distance. A dimensionless measure of the size of these fluctuations is provided by the coefficient of variation, defined as the standard deviation divided by the mean. Areal synapse density has a smaller coefficient of variation than linear synapse density (Figure 4J). To summarize, both systematic and random variations in areal synapse density are small.

Investigating covariance between synapse density and mitochondrial density in dendrites are of interest as mitochondria are relevant to the energetic needs (Harris, Jolivet and Attwell, 2012) and calcium dynamics (Berridge, 1998; Augustine, Santamaria and Tanaka, 2003; Lewis et al., 2018) of synapses. Genetic manipulations show a coupling between mitochondrial and synaptic density for PyC dendrites in vitro (Li et al., 2004; Dickey and Strack, 2011; Bertholet et al., 2013), but in vivo studies have been lacking.

The relation between mitochondrial density and synapse density is weak for systematic variation with distance. In the distal dendrites, the average linear density of synapses decreases with distance from the soma by over 15% (Figure S2I), whereas we saw previously that the average mitochondrial volume per unit length changes by only a few percent (Figure S2H). However, this view ignores fluctuations of synapse and mitochondrial density about their average values, which can be fractionally much larger than the systematic variations. Using the dendritic segment measurements (Figures 4E, 4G, and 4H), we focused on distal dendrites more than 60 μm away from the soma, where the average mitochondrial volume per unit length is roughly invariant. We found that mitochondrial volume per unit length is correlated with linear synapse density within this region (Pearson’s r=0.37, N=9198, p<1×10⁻³⁰⁰; Figure S2J).

We also found a positive correlation between dendritic diameter and linear synapse density (r=0.402, N=9198, p≈0; Figure S2K), similar to a previous report (Larkman, 1991b). Cylinder synapse density is also proportional to the ratio between linear synapse density and dendritic diameter, so the positive correlation between the latter two quantities can explain why areal synapse density is more invariant than linear synapse density. Dendritic diameter is also positively correlated with mitochondrial volume per unit length (r=0.514, N=9198, p≈0, Figure S2L), primarily due to gaps in coverage, as overlap is small (Figure 4F). Analyzing the residuals of predicting linear synapse density from dendritic diameter, mitochondrial volume per unit length explained a small amount of the remaining variance (r=0.181, N=9198, p<1×10⁻⁶⁷, Figure S2M). Together, these results suggest a tight covariance among mitochondrial density, dendritic diameter, and synapse density within the basal dendrites of this cell population.

The density of synapses onto dendrites of inhibitory cells has also been studied in cortex (Kawaguchi, Karube and Kubota, 2006; Kameda et al., 2012; Hioki et al., 2013) and hippocampus (Gulyás et al., 1999; Martina, Vida and Jonas, 2000). This work attempted to characterize input synapse densities in the proximal and distal arbor, but either relied on indirect synapse measurements (Kawaguchi, Karube and Kubota, 2006; Kameda et al., 2012; Hioki et al., 2013), focused on one targeted cell type (Martina, Vida and Jonas, 2000; Kameda et al., 2012; Hioki et al., 2013) or coarsely characterized this proximal/distal boundary (Gulyás et al., 1999; Martina, Vida and Jonas, 2000; Kameda et al., 2012; Hioki et al., 2013). Our reconstruction captured somas and dendrites of 34 inhibitory cells, and we assigned 20 of them to traditional classes (Figure 5A, Data S2, and STAR Methods).

We calculated the linear and areal synapse densities versus distance from the soma for individual cells (Figure S3) and averaged this measure in each inhibitory class (Figures 5B and 5C). For bipolar cells, areal density is roughly constant in distal dendrites, as for PyCs. The data suggest that areal density might turn out to exhibit diverse behaviors for other inhibitory classes, though our sample sizes are small. These panels collapse each cell to a single measurement for each distance bin, and then average over cells. The sample size for each class is the number of cells in that class, whereas the sample size in Figs. 4 and S2 is the number of dendritic segments (STAR Methods).

Synapse sizes reflect their physiological strength and reliability (Bailey and Chen, 1983; Bourne and Harris, 2011; Bailey, Kandel and Harris, 2015; Holler et al., 2021). Synapse size (de Vivo et al., 2017; Santuy et al., 2018) and spine size (Loewenstein, Kuras and Rumpel, 2011) have been measured and modeled using log-normal distributions, though there are also reports of bimodal distributions (Dorkenwald et al., 2019; Spano, Banningh and Marshall, 2019). Little is known about how synapse size distributions vary across cell classes and compartments. We computed these distributions for synapses onto dendrites and somas for inhibitory cell classes (Figure 5D). We also provide the size distributions after restricting the synapses to those from confirmed L2/3 PyCs (Figure 5E). Our sample sizes are limited, but these distributions could suggest hypotheses for future work comparing cell classes and compartments.

Predicting motif frequencies from degree sequence

Synaptic physiology studies in brain slices proposed that bidirectional connections between cortical PyCs are “overrepresented,” or more frequent than expected by chance (Markram et al., 1997; Le Bé and Markram, 2006; Wang et al., 2006). Similar conclusions have been drawn for some three-cell connectivity motifs (Song et al., 2005), and have been interpreted as evidence for cortical circuit theories, such as neuronal group selection (Edelman, 1987; Perin, Berger and Markram, 2011), neuron clustering (Litwin-Kumar and Doiron, 2012; Klinshov et al., 2014), and attractor networks (Brunel, 2016; Zhang, Zhang and Stepanyants, 2019).

These claims were relative to an Erdős-Rényi (ER) model, but a pioneering paper on network motifs (Milo et al., 2002) used a more sophisticated configuration (CFG) model of random graphs (Newman, 2018). Reports of overrepresented motifs in C. elegans (Milo et al., 2002; Reigl, Alon and Chklovskii, 2004; Varshney et al., 2011; Cook et al., 2019) have all been based on a CFG model.

Using our PyC graph, we reexamine claims of motif overrepresentation in the cortex by comparing with a CFG model. The “in-degree” of a cell is defined as the number of its presynaptic partner cells, while the “out-degree” of a cell is the number of its postsynaptic partner cells. Both in-degree and out-degree vary greatly in our large circuit of connected PyCs, more than would be expected from ER random graphs (Figure 6D). We consider a CFG model in which the degree sequence of every random graph is constrained to be the same as that of the observed graph; all in-degrees and out-degrees are matched (Fosdick et al., 2018). We hypothesized that the degree constraint alone would lead to more accurate predictions of motif frequencies, as proposed (Song et al., 2005; Gal et al., 2017; Vegué, Perin and Roxin, 2017).

As mentioned above, ER models treat all cell pairs as having the same probability of connection, an assumption that is presumably violated by cells that are highly truncated by the borders of the volume. We therefore excluded all PyCs with total axonal length less than 100 μm, leaving 111 PyCs in the graph to be analyzed. The criterion was axonal truncation because dendritic arbors are more complete by comparison (Figures 3F and 3G). Below we will discuss the effect of changing the 100 μm threshold that defines “highly truncated” axon.

If a pair of cells is randomly drawn from these 111 PyCs, their connection probability is 5.4% (95% CI=[5.0%, 5.8%]). The number of bidirectionally connected pairs is 1.63× higher than the prediction of the ER model, formed by squaring the connection probability (Figure 6E, 95% CI=[1.11, 3.04]). This result is qualitatively consistent with many brain slice studies (Markram et al., 1997; Song et al., 2005; Le Bé and Markram, 2006; Wang et al., 2006).

For CFG, we sampled from the set of graphs with the same degree sequence as our cortical circuit by applying degree-preserving edge swaps (Figure 6A) with the “hold” technique (Artzy-Randrup and Stone, 2005). We took N Monte Carlo samples and compared their motif counts to the observed data. We found that bidirectional connections were about 1.37× more frequent than the expected CFG count (Figure 6E, 95% CI=[1.04, 2.07], N=1,000), which is less than the ER overrepresentation (Wilcoxon rank-sum test p=6.2×10⁻⁶⁶, N=1,000). The CFG overrepresentation remains statistically significant, though the p-value is larger than its ER analogue (Figure 6F and Table S1; CFG: permutation test p=0.043, N=1,000; ER: permutation test p<0.001, N=1,000).

Most of the highly connected three-cell motifs (#10–16 in Figure 6G) are overrepresented relative to ER (Figure 6G), consistent with previous work (Song et al., 2005; Perin, Berger and Markram, 2011). Here we used a generalization of ER (gER) that preserves frequencies of both unidirectional and bidirectional connections (Figure 6B; Song et al., 2005). The overrepresentations are reduced, however, when compared to CFG (Figure 6G and Table S2). A scatter plot compares model predictions of three-cell motif frequencies, in which CFG is visibly more accurate than gER (Figure 6H). Furthermore, the overrepresentations of motifs 4, 10, 11, 12 are statistically significant relative to gER, but not relative to CFG (Table S2). This better fit is not due to the inflation of confidence intervals. Rather, the standard deviation is much smaller for CFG than for gER for motif 4 (σ_gER=108.81, σ_CFG=66.73; N=1,000), and of similar size for other motifs (Table S2).

In a network with high clustering or transitivity (Holland and Leinhardt, 1971), if α is connected to β, and β is connected to γ, then α and γ are likely connected. This is quantified by the clustering coefficient:

$$C=Pr[\alpha \sim \gamma \mid \alpha \sim \beta \wedge \beta \sim \gamma ]$$ (1)

where α~β means that α is connected to β and the nodes (α,β,γ) are drawn randomly from the network (Figure 6C). We can check the claim that cortical networks are highly clustered (Perin, Berger and Markram, 2011) by rewriting the clustering coefficient as

$$C={\left(1+\frac{1}{3}\frac{\#\text{motifs}4-9}{\#\text{motifs}10-16}\right)}^{-1}$$ (2)

which is a function of the relative frequency of motifs containing two connected pairs (4–9) versus those containing three connected pairs (10–16). The observed clustering coefficient (C_OBS=0.163; Table S3) is much higher than predicted by gER (C_gER=0.103, 95% CI=[0.086, 0.122], N=1,000) but only marginally higher than predicted by CFG (C_CFG=0.150, 95% CI=[0.140, 0.161], N=1,000).

Beyond motif frequencies, the connection probability for a pair of cortical PyCs was reported to increase with the number of common synaptic partners (Perin, Berger and Markram, 2011). This “common neighbor rule” generalizes the idea of high network clustering (Perin, Berger and Markram, 2011) and is inconsistent with the ER model. For our reconstructed circuit, the common neighbor rule was largely predicted by CFG (Figure 6I), as also reported in C. elegans (Azulay, Itskovits and Zaslaver, 2016).

That CFG outperforms ER at predicting motif frequencies was not a foregone conclusion, as it is possible to construct graphs such that CFG falls short of ER in predicting motif frequencies (Figure S6E). CFG can also be compared with ER using criteria designed to handle the tradeoff between goodness of fit and model simplicity. By applying the minimum description length principle (Rissanen, 1978), we found that CFG is superior to ER as a model of the PyC graph, even after accounting for the added complexity of CFG’s extra parameters (STAR Methods).

The above analysis excluded PyCs with axon length less than 100 μm. We found that increasing the axon length threshold improved the fit to observed motif frequencies for both models (note the vertical scale in plots), and reduced differences between the models (Figures S4, S5). When we compared with other model variants (Figure S6B–D, Table S2, and Table S3), generalizing CFG to preserve frequencies of bidirectional connections for each neuron (“bi-degree”; Figure S6A) slightly improved the fit, but preserving the overall frequencies of bidirectional connections (“bi-edge”; Table S2) did not.

In C. elegans, overrepresentation of bidirectional connections can partially be explained by adjacency (Durbin, 1987; Reigl, Alon and Chklovskii, 2004). If a connection from neuron α to β exists, then the neurons must be adjacent, increasing the probability of a reciprocal connection from β to α. The situation is more subtle for cortical neurons, because of the axon-dendrite distinction. Instead, we evaluated a proximity-based model, in which connection probability is a function of soma separation (STAR Methods, Figure S6F). This model’s performance is mixed relative to gER (Figures S6G–S6H). Models of neuron geometry more sophisticated than proximity are also worth exploring (Gal et al., 2017, 2020).

There are some statistically significant deviations from the CFG model (Figures S4, S5, and Table S2; N.B. our permutation tests are effectively “one-tailed,” and we have not corrected for multiple comparisons), but these seem minor relative to deviations from ER. Given that motif frequencies, the clustering coefficient, and the common neighbor rule are predicted quite well from degree sequence by a CFG model, nonrandomness of cortical connectivity seems more subtle than has commonly been supposed.

Relation of in-connection density to visual function

Using our PyC graph, we showed that the frequencies of certain connectivity motifs can be predicted accurately from the degree sequence. For 112 of these same PyCs, calcium imaging data are available (Figures 7A and 7C), allowing us to relate degree to visual function. We define the in-connection density of a node in the PyC graph as the in-degree divided by the total dendritic length of the postsynaptic neuron. In this case, degree counts only connections between PyCs with somas in the EM volume. The in-connection density indicates a cell’s tendency to receive connections from nearby PyCs, relative to a baseline predicted from its total dendritic length in the EM volume (Figures S7D and S7E).

When PyCs are activated by visual stimuli, their responses are thought to be amplified by local recurrent excitation from neighboring PyCs (Douglas et al., 1995; Lien and Scanziani, 2013; Li et al., 2013; Cossell et al., 2015). In-connection density estimates local recurrent excitation, so we hypothesized that L2/3 PyCs with higher in-connection density would exhibit stronger responses to visual stimuli.

For each calcium-imaged cell, we extracted a direction tuning curve (Figure 7D) and computed a global orientation selectivity index (gOSI) and a global direction selectivity index (gDSI) (Ringach, Shapley and Hawken, 2002; Figures 3H and 3I, STAR Methods). To consider only responses to directional stimuli (Figure 7B), we restricted further analysis to cells with statistically significant gOSI values as evaluated by a permutation test (Ecker et al., 2014; Baden et al., 2016). We observed a strong bias toward horizontal orientation preference (Figure 3J) consistent with an age-dependent bias towards cardinal orientations in previous work (Rochefort et al., 2011; Hagihara et al., 2015).

As hypothesized, we found that a cell’s trial-averaged response to its preferred direction or orientation tended to be larger for cells with higher in-connection density (Pearson’s r=0.44, N=38, p=0.006; Figure 7H). In contrast, trial-averaged response was not correlated with the linear synapse density of the cell’s dendrites (from all sources; r=−0.28, N=38, p=0.095; Figure 7I, STAR Methods).

We further hypothesized that L2/3 PyCs with higher in-connection density would exhibit more reliable responses to visual stimuli. Trial-to-trial variability (Stein, Gossen and Jones, 2005) is shown for example cells in Figure 7G. Cells 2 and 3 exhibited little or no response for many trials, yet they responded strongly to their preferred stimuli in several trials, did not respond to non-preferred stimuli, and accordingly their gOSI or gDSI values were statistically significant. These examples show that a cell can be well-tuned for direction or orientation and respond intermittently.

For each trial, we thresholded the response of a neuron to its preferred stimulus (Figure 7C, STAR Methods). A cell’s intermittency index was defined as the fraction of trials for which its response did not exceed the threshold. Most cells have intermittency values exceeding 50% (Figure 7F). These values are likely overestimates, because some spikes may have evaded detection (Huang et al., 2021), so we focused our analysis on relative differences between cells rather than absolute intermittency values.

We found that in-connection density was negatively correlated with intermittency (Pearson’s r=−0.43, N=38, p=0.007; Figure 7J). We also found that intermittency was not correlated with linear synapse density (Pearson’s r=0.05, N=38, p=0.744; Figure 7K).

Other things being equal, more intermittent cells are expected to have lower trial-averaged responses (Figure 7E). To separate the effects of these two variables, we fit a linear model of the form:

$${\overline{r}}_{ia}={\beta }_{1}a+{\beta }_2{d}_i+{\beta }_{3}a{d}_i+c,$$ (3)

where a is a binary variable for whether responses surpassed the intermittency threshold, d_i represents the in-connection density and ${\overline{r}}_{ia}$ is the mean response for cell i given a. We found a significant interaction term. β3 (p=0.002; Figure 7L), suggesting a relationship between in-connection density and responses over the activity threshold.

In-connection density was weakly correlated with cortical depth (Figure S7F). Therefore, we checked whether cortical depth, or 3D location generally, could confound the observed correlations of mean response and intermittency with in-connection density. We computed the same correlations after shuffling cells with similar 3D locations in the volume as a permutation test (Figures S7G and S7H). The observed correlations in our data were still stronger than in the permutations (mean response p=0.0161, intermittency p=0.0182; Figure 7M). Together, these results suggest that cells with higher in-connection density tend to be less intermittent in their responses and exhibit stronger mean responses.

Discussion

The multimodal nature and scale of our EM reconstruction of 250×140×90 μm³ of mouse visual cortex allows it to be used to quantitatively characterize organelles, compartments, cells, circuits, and activity, as well as their interrelations. These vignettes and accompanying Jupyter notebooks illustrate that our resource will be widely useful and accessible for investigating a broad range of questions about cortical structure and function.

We investigated the spatial organization of mitochondria in different compartments of PyCs and evaluated correlations between mitochondrial volume, synapse number, and neurite diameter in distal dendrites. Overall, we found that the size distribution of mitochondria is consistent with previous hypotheses on the limits on their trafficking and dynamics (Lewis et al. 2018). Mitochondrial volumes are positively correlated with synapse number, consistent with the idea that dendritic mitochondria support synaptic function through ATP production and calcium buffering, although the relationship is difficult to disentangle from dendritic diameter.

Our synapse analysis found the average areal synapse density is roughly invariant with distance from the soma in the distal region of basal dendrites and fluctuates less than linear synapse density at any distance from the soma. The observed invariance suggests that 0.33 synapse/μm² is a homeostatic set point for the distal region of basal dendrites. A consequence for dendritic biophysics is that synaptic conductances could scale linearly with dendritic surface area. Intrinsic conductances also scale linearly with surface area, given the common assumption that ion channel densities are constant. Common scaling of synaptic and intrinsic conductances has implications for computational modeling of dendrites.

Computational models of cortical development have assumed that synapses behave as if they are competing for a fixed resource (Miller, 1996), and there is experimental evidence for this idea (Kasthuri and Lichtman, 2003). A pioneering model (von der Malsburg, 1973) proposed that synapses compete for dendritic area, and this could result in approximate invariance of synapse number per unit area. According to a theoretical prediction based on the random geometry of axons and dendrites, the number of synapses received by a dendritic segment should on average be proportional to the surface area of a cylinder that encompasses the spines (Stepanyants, Hof and Chklovskii, 2002). This proportionality is similar to our observed invariance of areal synapse density.

Our connectivity motif examination analyzing our PyC graph using a CFG model of random graphs, as was done in C. elegans (Milo et al., 2002; Reigl, Alon and Chklovskii, 2004; Varshney et al., 2011), was possible due to the scale of the reconstruction. Unlike the C. elegans connectome, our PyC wiring diagram underestimates connectivity because cells are truncated by the borders of the EM volume. For the subset of 111 PyCs with at least 100 μm axon length, the connection probability for somas separated by 50 μm or less is 8.1% (±1.1%, 95% CI, N=2530). This is less than analogous values from brain slice physiology, which range from 14% to 22% in younger mice (Ko et al., 2011, 2013; Cossell et al., 2015). Our underestimation of connectivity did not prevent us from replicating the well-known finding (Markram et al., 1997; Song et al., 2005; Le Bé and Markram, 2006; Wang et al., 2006) that bidirectional connections are overrepresented relative to an ER random graph model. The underestimation reduces the number of bidirectional connections, but it also reduces the ER prediction. Similarly, truncation did not prevent us from finding an overrepresentation of bidirectional connections relative to CFG.

As we are still a long way from an entire mammalian connectome (Abbott et al., 2020), truncation will remain a fact of life for mammalian wiring diagrams. Brain slice experiments are also subject to arbor truncation as recorded neurons are typically only tens of microns from the surface of the slice (Stepanyants et al., 2009; Levy and Reyes, 2012). Reconstructions of larger cortical volumes will tell us how much our findings are affected by truncation. For now, we should be careful about claims that connectivity motifs are highly “nonrandom” in the cortex.

Overrepresentation of motifs could become more dramatic if the analysis is restricted to strong connections (Song et al., 2005). Connection probability is thought to decrease by adulthood (Jiang et al., 2016; Campagnola et al., 2021), consistent with a notion of connectivity refinement. The current study is in a young adult (P36) mouse, and previous studies were in juvenile rats (Song et al., 2005; Le Bé and Markram, 2006; Perin, Berger and Markram, 2011). It would be interesting to look for overrepresented motifs in adult animals.

Finally, in examining the in-connection density to visual function, we found that in-connection density is negatively correlated with intermittency and positively correlated with amplitude of visual response. Our finding is related to previous studies of “chorister” vs. “soloist” PyCs in mouse V1 (Okun et al., 2015). A chorister is more likely than a soloist to receive a connection from a neighboring cell, and also tends to respond more strongly to visual stimuli. Both results are consistent with our analysis showing that in-connection density is correlated with strength of a cell’s response to its preferred stimulus. Our analysis includes cells with a wide range of in-degrees (Figures S7D and S7E), whereas previous work was restricted to small circuits of few cells and extrapolated to larger in-degrees using a random graph model. Prior work also did not consider intermittency of visual responses.

In addition to these vignettes, three articles provide in-depth analyses showing how the resource can be used to study PyC synapse size distributions and multi-synaptic connections (Dorkenwald et al., 2019), chandelier cells (Schneider-Mizell et al., 2021), and oligodendrocyte precursor cells (Buchanan et al., 2021). Two further articles describe our reconstruction of a cubic-millimeter scale volume (MICrONS Consortium et al., 2021; Macrina et al., 2021), which is also publicly available.

Limitations of the study

Each analysis has assumed that PyCs in our sample are a uniform population. Future efforts in cell typing may reveal new dimensions to these results or provide new ways to study the inhibitory cells. Similarly, we have often assumed that branches of the same neurite compartment are uniform, where the placement of organelles and synapses may interact within individual branches to affect cell function. Performing more fine-grained analyses with these reconstructions is likely another valuable avenue for future work. We hope that this work will stimulate our readers to find new applications and realize the full potential of the resource for discovery.

STAR ★ METHODS

RESOURCE AVAILABILITY

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, H. Sebastian Seung (sseung@princeton.edu).

Materials availability

This study did not generate new unique reagents.

Data and code availability

• The EM image data, cellular segmentation, synapse segmentation, mitochondrion segmentation, and nucleus segmentation can be viewed at https://microns-explorer.org/. Raw calcium imaging data are available together with the analysis code at https://github.com/seung-lab/MicronsBinder. Both the MicronsExplorer and MicronsBinder websites demonstrate how to access all intermediate analysis data (deposited as a Zenodo record).

• Along with the analysis code repository (https://github.com/seung-lab/MicronsBinder), the code for generating the cell and organelle reconstructions is available at https://github.com/seung-lab/.

• All original code has been deposited at Zenodo and is publicly available as of the date of publication. DOIs are listed in the key resources table.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Paraformaldehy de, 16% aqueous solution	Electron Microscopy Sciences	cat.#15710, CAS: 30525-89-4
Glutaraldehyde, 25% aqueous solution	Electron Microscopy Sciences	cat.#16220, CAS: 111-30-8
Osmium tetroxide, 4% aqueous solution	Electron Microscopy Sciences	cat.#19190, CAS: 20816-12-0
Potassium ferricyanide	Sigma Aldrich	CAS: 13746-66-2
Thiocarbohydraz ide	Sigma Aldrich	223220, CAS: 2231-57-4
Hard Plus Resin - 812	Electron Microscopy Sciences	cat.#14115
0.2M Sodium cacodylate buffer	Electron Microscopy Sciences	cat.#11652
Uranyl acetate	Polyscienc es	cat.#21447-25
L-aspartic acid	Sigma Aldrich	CAS: 45ZU62
Lead nitrate	Electron Microscopy Sciences	CAS: 10099-74-8
Deposited Data
Electron microscopy image volume	This paper	layer23.microns-explorer.org
Morphological segmentation	This paper	layer23.microns-explorer.org
Synaptic cleft segmentation	This paper	layer23.microns-explorer.org
Mitochondrion segmentation	This paper	layer23.microns-explorer.org
Cellular nucleus segmentation	This paper	layer23.microns-explorer.org
2-Photon calcium traces	This paper	microns-explorer.org/phase1
Deconvolved spike estimates and tuning curves	This paper	github.com/seung-lab/datajoint_seung
Light Microscopy coregistration volume	This paper	github.com/AllenInstitute/MicronsBinder/tree/master/notebooks/vignette_an alysis/function
Synaptic connectivity tables	This paper	https://zenodo.org/record/5579388
PyC-PyC connectivity graph	This paper	https://zenodo.org/record/5579388
Cell classification table	This paper	https://zenodo.org/record/5579388
Mitochondrion information table	This paper	https://zenodo.org/record/5579388
Nucleus information table	This paper	https://zenodo.org/record/5579388
Cell skeletons used for analysis	This paper	https://zenodo.org/record/5579388
Cell triangle meshes used for analysis	This paper	https://zenodo.org/record/5579388
Analysis intermediate data (see MicronsBinder)	This paper	https://zenodo.org/record/5579388
Experimental Models: Organisms/Strains
Mouse line: Cre driver: CamKIIa-Cre	Jax	jax.org/strain/005359
Mouse line: tTA driver: B6;CBA- Tg(Camk2a-tTA)1Mmay/J	Jax	jax.org/strain/003010
GCaMP6f Reporter: Ai93	Allen Institute for Brain Science	jax.org/strain/024103
Software and Algorithms
Python 3	Python.org	python.org
Reconstruction source code	This paper	github.com/seung-lab/microns-L23-reconstruction; doi:10.5281/zenodo.5851066
Data analysis source code	This paper	github.com/AllenInstitute/MicronsBinder; doi:10.5281/zenodo.5856928
Alembic	MICrONS Consortium	github.com/seung-lab/Alembic
TrakEM2	(Cardona et al., 2012)	ini.uzh.ch/~acardona/trakem2.html
Render	(Zheng et al., 2018)	github.com/saalfeldlab/render
VAST	(Berger, Seung and Lichtman, 2018)	lichtman.rc.fas.harvard.edu/vast/
PyTorch	(Paszke et al., 2019)	pytorch.org
ChunkFlow	(Wu et al., 2021)	github.com/seung-lab/chunkflow
zmesh	MICrONS Consortium	github.com/seung-lab/zmesh
PyChunkedGraph	(Dorkenwald et al., 2020)	github.com/seung-lab/PyChunkedGraph
Kimimaro: Densely Labeled Image Skeletonization	MICrONS Consortium	github.com/seung-lab/kimimaro
Igneous	MICrONS Consortium	github.com/seung-lab/igneous
MeshParty	MICrONS Consortium	github.com/sdorkenw/MeshParty
EASE	(Zhou et al., 2020)	github.com/zhoupc/ease
DataJoint	Vathes LLC	datajoint.com
Scipy: Fundamental Algorithms for Scientific Computing in Python	(Virtanen et al., 2020)	scipy.org
Seaborn: statistical data visualization	(Waskom, 2021)	seaborn.pydata.org
Statsmodels: Econometric and statistical modeling with python	(Seabold and Perktold, 2010)	statsmodels.org
Neuroglancer	Google	github.com/google/neuroglancer
ParaView	National Technology & Engineering Solutions of Sandia, LLC (NTESS), Kitware Inc.	paraview.org
MeshLab	Visual Computing Lab, ISTI, Consiglio nazionale delle ricerche (Cnr)	meshlab.net

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Mouse.

Same sex littermates were housed together in individual cages with 1–4 mice per cage. Mice were maintained on a regular diurnal lighting cycle (12:12 light:dark) with ad libitum access to food and water and nesting material for environmental enrichment. Mice were housed in the Taub Mouse Facility of Baylor College of Medicine, accredited by AAALAC (The Association for Assessment and Accreditation of Laboratory Animal Care International).

Functional imaging was performed in a single transgenic mouse, aged P36, expressing fluorescent GCaMP6f, and its tissue was subsequently used for circuit reconstruction using electron microscopy. The animal used for this experiment was a healthy and drug naïve male not involved in any previous procedure or experiment. The mouse was a triple-heterozygote for the following three genes: (1) Cre driver: CamKIIa-Cre (Jax: 005359<https://www.jax.org/strain/005359>), (2) tTA driver: B6;CBA-Tg(Camk2a-tTA)1Mmay/J (Jax: 003010<https://www.jax.org/strain/003010>), (3) GCaMP6f Reporter: Ai93 (Allen Institute). All procedures were done in accordance with the Institutional Animal Care and Use Committees at Baylor College of Medicine and the Allen Institute for Brain Science.

METHOD DETAILS

Cranial window surgery.

Anesthesia was induced with 3% isoflurane and maintained with 1.5% to 2% isoflurane during the surgical procedure. The mouse was injected with 7.5 mg/kg ketoprofen subcutaneously at the start of the surgery. The anesthetized mouse was placed in a stereotaxic head holder (Kopf Instruments), and its body temperature was maintained at 37°C throughout the surgery using a homeothermic blanket system (Harvard Instruments). After the scalp was shaved, bupivicane (0.05 cc, 0.5%, Marcaine) was applied subcutaneously. Then 20 minutes later, an approximately 1 cm² area of skin was removed above the skull, and the underlying fascia was scraped and removed. The wound margins were sealed with a thin layer of surgical glue (VetBond, 3M), and a 13-mm stainless-steel washer clamped in the headbar was attached with dental cement (Dentsply Grip Cement). At this point, the mouse was removed from the stereotaxic holder (while maintaining anesthesia), and the skull was held stationary on a small platform via the newly attached headbar. With a surgical drill and HP 1/2 burr, we made a 3-mm craniotomy centered on the primary visual cortex (V1; 2.7mm lateral of the midline, contacting the lambda suture), and the exposed cortex was washed with ACSF (125 mM NaCl, 5 mM KCl, 10 mM Glucose, 10 mM HEPES, 2 mM CaCl₂, 2 mM MgSO₄). The cortical window was then sealed with a 3 mm coverslip (Warner Instruments), using cyanoacrylate glue (VetBond). The mouse was allowed to recover for 1–2 hours prior to the imaging session. After imaging, the washer was released from the headbar, and the mouse was returned to the home cage.

Widefield imaging.

Prior to two-photon imaging, we acquired a low-magnification image of the 3-mm craniotomy under standard illumination. The location of the subsequent two-photon field of view could then be identified in this image based on surface vasculature. The location of the target two-photon imaging site in V1 was determined by retinotopic mapping using intrinsic signal imaging or GCaMP6 imaging at low magnification.

Two-photon imaging.

Imaging for the mouse was performed in V1, in a 400×400×200 μm³ volume with the superficial surface of the volume at the border of L1 and L2/3, approximately 140 μm below the pia. Laser excitation was at 920 nm at 25–45 mW, depending on depth. We used a 25× Nikon objective with a numerical aperture of 1.1. The imaging point-spread function was measured with 500 nm beads in agarose prior to the experiment and was approximately 0.5×0.5×3 μm³ in x, y, and z. Pixel dimensions of each imaging frame were 256×256 and pixel pitch in x and y were approximately 1.6μm.

Functional imaging scans.

Imaging data was collected with a resonant scanning microscope (ThorLabs) and software (Scanimage 5.1, Vidrio). Nine scans were collected in total, starting superficially and moving deeper into the cortex with each subsequent scan. During each 30-minute scan, a piezo controlled manipulator (PI-726, Physik Instruments) moved the microscope objective between three different z-planes (“focal planes”). These three focal planes were separated by an average of about 8 μm by the piezo, and each focal plane was imaged at 14.8313 frames per second. We refer to each trio of sequential focal planes as one imaging “volume”. We collected 9 volumes with 3 focal planes/volume, producing 27 focal planes in total to span the 200 μm depth of the overall 400×400×200 μm³ imaging volume. Two color channels were recorded: channel one was GCaMP6 calcium imaging, and channel two was blood vessels labeled with red dye (Sulfarhodamine 101).

After the data was collected, we learned that the piezo command functionality of ScanImage 5.1 was not fully optimized, so the movement of the objective between focal planes was slower than expected. As a result, the posterior edge of the field of view of each focal plane was curved in the Z dimension by several microns. This curvature was a deterministic function of the piezo command and can be recovered from the high-resolution (1 μm spacing) structural stack collected with each functional scan, so we have found that it does not greatly affect the alignment with the EM data. All scans were raster-and motion-corrected. Motion correction in X and Y was performed by sub-pixel cross-correlation. Focal plane alignment into the structural stack was performed by 3D image-based cross-correlation.

High-resolution structural stack.

To facilitate alignment with EM, at the beginning of the experiment, we collected a high-resolution structural stack of the imaging volume with the same field of view and (x, y) location as the functional scans. Each plane had resolution of approximately 800×800 nm², higher resolution than the functional scans. This stack began 310 μm deep and ended at the cortical surface, in one micron steps.

Behavioral monitoring.

The mouse was head-restrained but could walk on a treadmill during imaging. During imaging, we collected treadmill speed at 200 Hz and recorded a movie of the mouse’s eye at 20 Hz. Pupil size and (x, y) position were extracted from this movie using custom MATLAB and Python code. Both treadmill traces and pupil traces were subsequently synchronized and interpolated to the imaging clock (27300 samples synchronized to the first focal plane of each imaging volume).

Visual stimulus.

Visual stimuli were presented at 60 fps and synchronized to imaging and behavioral data via a photodiode that recorded the timing of each stimulus frame. For each 30-minute 40-second scan (27300 volumes at 14.8313 volumes per second), we presented 30 one-minute trials of a colored-noise stimulus (Niell and Stryker, 2008) interspersed with periods of coherent motion of oriented noise. Each one-minute trial contained 16 stationary moving stationary blocks, with a different direction presented in each block, pseudo-randomly ordered. The stimulus was interpolated and aligned to the calcium imaging frame times and stored as a 90×160×27300 array. The first 200 frames were blank screen; they were used for extracting calcium traces but not for the analysis.

The visual stimuli were not identical for different experiments at multiple depths, yet they share the same underlying structure.

EM & two-photon co-registration.

Centers of cell bodies were annotated manually for both EM and two-photon, high-resolution stacks. A total of 512 points were labeled in each dataset, and the corresponding cells were determined manually by comparing the relative locations of the cell bodies in both datasets. Based on this list of 512 correspondence points, an affine transformation was estimated. This transformation was applied to the entire EM volume to co-register the volume onto the high-resolution, two-photon structural stack.

Trace extraction and spike inference.

Calcium traces were extracted with the EASE algorithm (Zhou et al., 2020) after normalizing each pixel in the two-photon movies to have the same noise level (Pnevmatikakis et al., 2016). All the traces used in the analysis were signals from the somas. To extract these signals, a corresponding scan for each cell was identified by finding the closest scan from the soma location. The EASE algorithm uses reconstructed cells for initialization, so cells with severely cut-off somas were excluded from the analysis (N=3). For the same reason, calcium traces were extracted only for a subset of reconstructed cells that overlap with the calcium recording volume. Activity traces of cells that had a low signal-to-noise ratio were neglected from the extraction. Spike inference was performed with the modified OASIS algorithm (Friedrich, Zhou and Paninski, 2017), which is implemented within the EASE package.

Tissue preparation and staining.

The protocol of Hua et al. (Hua, Laserstein and Helmstaedter, 2015) was combined with the protocol of Tapia et al. (Tapia et al., 2012) to accommodate a smaller tissue size and to improve transmission EM (TEM) contrast. The mouse was transcardially perfused with 2.5% paraformaldehyde and 1.25% glutaraldehyde in 0.08 M sodium cacodylate buffer, pH 7.4. After dissection, 200 μm-thick coronal slices were cut with a vibratome and post-fixed for 12–48 hours. Following several washes in 0.1 M cacodylate buffer, pH 7.4 (CB), the slices were fixed with 2% osmium tetroxide in CB for 90 minutes, immersed in 2.5% potassium ferricyanide in CB for 90 minutes, washed with deionized (DI) water for 2×30 minutes, and treated with freshly made and filtered 1% aqueous thiocarbohydrazide at 40°C for 10 minutes. The slices were washed 2×30 minutes with DI water and treated again with 2% osmium tetroxide in water for 30 minutes. Double washes in DI water for 30 minutes each were followed by immersion in 1% aqueous uranyl acetate overnight at 4°C. The next morning, the slices in the same solution were placed in a heat block to raise the temperature to 50°C for 2 hours. The slices were washed twice in DI water for 30 minutes each, and then incubated in Walton’s lead aspartate, pH 5.0, for 2 hours at 50°C in the heat block. After another double wash in DI water for 30 minutes each, the slices were dehydrated in an ascending ethanol series (50%, 70%, 90%, 100% × 3) for 10 minutes each and two transition fluid steps of 100% acetonitrile for 20 minutes each. Infiltration with acetonitrile:resin dilutions (2p:1p, 1p:1p and 1p:2p) were performed on a gyratory shaker overnight for 4 days. Slices were placed in 100% resin for 24 hours followed by embedding in Hard Plus resin (EMS, Hatfield, PA). Slices were cured in a 60°C oven for 96 hours. The best slice based on tissue quality and overlap with the two-photon region was selected.

Sectioning and collection.

A Leica EM UC7 ultramicrotome and a Diatome 35-degree diamond ultra-knife were used for sectioning at a speed of 0.3 mm/sec. Eight to ten serial sections were cut at 40-nm thickness to form a ribbon, after which the microtome thickness setting was set to 0 in order to release the ribbon from the knife. Using an eyelash probe, pairs of ribbons were collected onto copper grids covered by 50-nm thick LUXEL film. The grids were then positioned in a stick that could carry up to 16 grids. The stick works as a cartridge, which is then screwed to the VOXA GridStage Sprite (Yin et al., 2020) that handles the samples inside the TEM. As each ribbon has multiple sections, each grid has multiple ribbons, and each stick has multiple grids, each imaging session could include hundreds of sections until vacuum would have to be broken and the stick replaced.

Transmission electron microscopy.

We made several custom modifications to a JEOL-1200EXII 120-kV transmission electron microscope (Yin et al., 2020). A column extension and scintillator magnified the nominal field of view by tenfold with negligible loss of resolution. A high-resolution, large-format camera allowed fields of view as large as (13 μm)² at 3.58-nm resolution. Magnification reduced the electron density at the phosphor, so a high-sensitivity sCMOS camera was selected and the scintillator composition tuned to generate high-quality EM images with exposure times of 90–200 ms. Sections were acquired as a grid of 3840×3840-px² images (“tiles”) with 15% overlap.

Alignment in two blocks.

The dataset was divided by sections into two blocks (1216 and 970 sections), with the first block containing substantially more folds. Initial alignment and reconstruction tests proceeded on the second block of the dataset. After satisfactory results were achieved, the first block was added, and the whole dataset was further aligned to produce the final 3D image. The alignment process included stitching (assembling all tiles into a single image per section), rough alignment (aligning the set of section images with one affine per section), coarse alignment (nonlinear alignment on lower-resolution data), and fine alignment (nonlinear alignment on higher-resolution data).

Alignment, block one.

The tiles of the first block were stitched into one montaged image per section and roughly aligned using a set of customized and automated modules based on the TrakEM2 (Cardona et al., 2012) and Render (Zheng et al., 2018) software packages.

Stitching.

After acquisition, a multiplicative intensity correction based on average pixel intensity was applied to the images, followed by a lens distortion of individual tiles using nonlinear transformations (Kaynig et al., 2010). Once these corrections were applied, correspondences between tiles within a section were computed using SIFT features, and each tile was modeled with a rigid transform.

Rough alignment.

Using 20x downsampled stitched images, neighboring sections were roughly aligned (Saalfeld et al., 2012). Correspondences were again computed using SIFT features, each section was modeled with a regularized affine transform (90% affine + 10% rigid), and all correspondences and constraints were used to generate the final model of one affine transform per tile. These models were used to render the final stitched section image into rough alignment with block two.

Alignment, block two.

The second block was stitched and aligned using the methods of (Saalfeld et al., 2012) as implemented in Alembic (Macrina and Ih, no date).

Stitching.

For each section, tiles containing tissue without clear image defects were contrast normalized by centering the intensities at the same location in each tile, stretching the overall distribution between the 5th and 95th intensity percentiles. During imaging, a 20×-downsampled overview image of the section was also acquired. Each tile was first placed according to stage coordinates, approximately translated based on normalized cross-correlation (NCC) with the overview image, and then finely translated based on NCC with neighboring tiles. Blocks were matched in the regions of overlap between tiles using NCC with 140-px block radius, 400-px search radius, and a spacing of 200 px. Matches were manually inspected with 1x coverage, setting per-tile-pair thresholds for peak of match correlogram, distance between first and second peaks of match correlograms, and correlogram covariance, and less frequently, targeted match removal. A graphical user interface was developed to allow the operator to fine-tune parameters on a section-by-section basis, so that a skilled operator completed inspection in 40 person-hours. Each tile was modeled as a spring mesh, with nodes located at the center of each block-match operation and spring constants 1/100th of the constant for the between-tile springs. The energy of all spring meshes within a section were minimized to a fractional tolerance of 10⁻⁸ using nonlinear conjugate gradient. The final render used a piecewise affine model defined by the mesh before and after relaxation, and maximum-intensity blending.

Rough alignment.

Using 20×-downsampled images, block matching between neighboring sections proceeded using NCC with 50-px block radius, 125-px search radius, and 250-px spacing. Matches were computed between nearest neighbor section pairs, then filtered manually in eight person-hours. Correspondences were used to develop a regularized affine model per section (90% affine + 10% rigid), which was rendered at full image resolution.

Coarse alignment.

Using 4×-downsampled images, NCC-based block matching proceeded with 300-px block radius, 200-px search radius, and 500-px spacing. Matches were computed between nearest and next-nearest section pairs, then manually filtered by a skilled operator in 24 person-hours. Each section was modeled as a spring mesh with spring constants 1/10th of the constant for the between-section springs, and the energy of all spring meshes within the block were minimized to a fractional tolerance of 10⁻⁸ using nonlinear conjugate gradient. The final render used a piecewise affine model defined by the mesh.

Fine alignment.

Using 2×-downsampled images, NCC-based block matching proceeded with 200-px block radius, 113-px search radius, and 100-px spacing. Matches were computed between nearest and next-nearest section pairs, then manually filtered by a skilled operator in 24 hours. Modeling and rendering proceeded as with coarse alignment using spring constants, which were 1/20th of the constant for the between-section springs.

Alignment, whole dataset.

Eleven blank sections were inserted manually between sections where the cutting thickness appeared larger than normal. The alignment of the whole dataset was further refined using the methods of (Saalfeld et al., 2012) as implemented in Alembic (Macrina and Ih, no date).

Coarse alignment.

Using 64×-downsampled images, NCC-based block matching proceeded with 128-px block radius, 512-px search radius, and 128-px spacing. Matches were computed between neighboring and next-nearest neighboring sections, as well as 24 manually identified section pairs with greater separation, then manually inspected in 70 person-hours. Section spring meshes had spring constants 1/20th of the constant for the between-section springs. Mesh relaxation was completed in blocks of 15 sections, 5 of which were overlapping with the previous block (2 sections fixed), and each block relaxing to a fractional tolerance of 10⁻⁸. Rendering proceeded as described above.

Fine alignment.

Using 4×-downsampled images, NCC-based block matching proceeded with 128-px block radius, 512-px search radius, and 128-px spacing. Matches were computed between the same section pairs as in coarse alignment. Matches were excluded only by heuristics. Modeling and rendering proceeded as described above, with spring constants 1/100th the constant for the between-section springs. Rendered image intensities were linearly rescaled in each section based on the 5th and 95th percentile pixel values.

Image volume estimation.

The imaged tissue has a trapezoidal shape in the sectioning plane. To measure this shape, landmark points were placed in the aligned images. We report cuboid dimensions rounded to the nearest multiple of 10 micrometers for both simplicity and comparison using the trapezoid midsegment length. The original trapezoid has a short base length of 216.9 μm, long base length of 286.2 μm, and height of 138.3 μm. The imaged data has 2176 sections, which measure 87.04 μm with a 40-nm slice thickness.

Voxel resolution.

The original size of the EM volume in vivo was estimated by registering the EM image stack with an image stack from two-photon microscopy. We applied polar decomposition to the linear transformation matrix A of the affine transform we used for co-registration,

$$A=UP$$

where U is an orthogonal matrix specifying a rotation, and P is a symmetric matrix.

$$P=\left[\begin{array}{ccc}0.921& -0.016& -0.005\\ -0.016& 1.151& 0.04\\ -0.005& 0.04& 0.923\end{array}\right]$$

It turns out that p is close to the identity matrix, with diagonal elements that are close to unity and off-diagonal elements that are relatively small. We multiplied the nominal voxel resolution (3.58 nm × 3.58 nm × 40 nm) by the diagonal elements of to estimate a voxel size of 3.30 nm × 4.12 nm × 36.9 nm in vivo, corresponding to shrinkage and expansion in different directions. Overall volume was roughly conserved (det p = 0.977). The nominal resolution is used for the analyses in this paper.

Image defect handling.

Cracks, folds, and contaminants were manually annotated as binary masks on 256×-downsampled images, dilated by 2 px, then inverted to form a defect mask. A tissue mask was created using non-zero pixels in the 256×-downsampled image, then eroded by 2 px to exclude misalignments at the edge of the image. The image mask is the union of the tissue and defect masks, and it was upsampled and applied during the final render to set pixels not included in the mask to zero. We created a segmentation mask by excluding voxels that had been excluded by the image mask for three consecutive sections. The segmentation mask was applied after affinity prediction to set affinities not included in the mask to zero.

Affinity prediction.

Human experts used VAST (Berger, Seung and Lichtman, 2018) to manually segment multiple subvolumes from the current dataset and a similar dataset from mouse V1. Annotated voxels totaled 1.29 billion at full image resolution.

We trained a 3D convolutional network to generate three nearest neighbors (Turaga et al., 2010) and 13 long-range affinity maps (Lee et al., 2017). Each long-range affinity map was constructed by comparing an equivalence relation (Jain, Sebastian Seung and Turaga, 2010) of pairs of voxels spanned by an “offset” edge (to preceding voxels at distances of 4, 8, 12, and 16 in x and y, and 2, 3, and 4 in z). Only the nearest-neighbor affinities were used beyond inference time; long-range affinities were used solely for training. The network architecture was modified from the Residual Symmetric U-Net (Lee et al., 2017). We trained on input patches of size 128×128×20 px³ at 7.16×7.16×40 nm³ resolution. The prediction during training was bilinearly upsampled to full image resolution before calculating the loss.

Training used synchronous gradient updates computed by four Nvidia Titan X Pascal GPUs, each with a different input patch. We used the AMSGrad variant (Reddi, Kale and Kumar, 2019) of the Adam optimizer (Kingma and Ba, 2014), with PyTorch’s default settings, except step size parameter α = 0.001. We used the binary cross-entropy loss with “inverse margin” of 0.1 (Huang and Jain, 2013); patch-wise class rebalancing (Lee et al., 2017) to compensate for the lower frequency of boundary voxels; training data augmentation, including flip/rotate by 90°, brightness and contrast perturbations, warping distortions, misalignment/missing section simulation, and out-of-focus simulation (Lee et al., 2017); and several new types of data augmentation, including simulation of lost sections and co-occurrence of misalignment/missing/lost sections.

Distributed computation of affinity maps used chunkflow (Wu et al., 2021). The computation was done with images at 7.16×7.16×40 nm³ resolution. The whole volume was divided into 1280×1280×140 chunks overlapping by 128×128×10, and each chunk was processed as a task. The tasks were injected into a queue (using Amazon Web Service Simple Queue Service). For 2.5 days, 1000 workers (Google Cloud n1-highmem-4 with 4 vCPUs and 26 GB RAM, deployed in Docker image using Kubernetes) fetched and executed tasks from the queue as follows. The worker read the corresponding chunk from Google Cloud Storage using CloudVolume (Silversmith and Tartavull, no date), and applied previously computed masks to black out regions with image defects. The chunk was divided into 256×256×20 patches with 50% overlap. Each patch was processed to yield an affinity map using PZNet, a CPU inference framework (Popovych et al., 2020). The overlapping output patches were multiplied by a bump function, which weights the voxels according to the distance from patch center, for smooth blending and then summed. The result was cropped to 1024×1024×120 vx and then previously computed segmentation masks were applied (see Image defect handling above).

Initial oversegmentation.

The affinity map was divided into 514×514×130 chunks that overlapped by two voxels in each direction. For each chunk, we ran a watershed and clustering algorithm (Zlateski and Seung, 2015), with special handling of chunk boundaries. If the descending flow of watershed terminated prematurely at a chunk boundary, the voxels around the boundary were saved to disk so that domain construction could be completed later on. Decisions about merging boundary domains were delayed, and information was written to disk so decisions could be made later. After the chunks were individually processed, they were stitched together in a hierarchical fashion. Each level of the hierarchy processed the previously delayed domain construction and clustering decisions in chunk interiors. Upon reaching the top of the hierarchy, the chunk encompassed the entire volume, and all previously delayed decisions were completed.

Mean affinity agglomeration.

The watershed supervoxels and affinity map were divided into 513×513×129 chunks that overlapped by one in each direction. Each chunk was processed using mean affinity agglomeration (Lee et al., 2017; Funke et al., 2019). Agglomeration decisions at chunk boundaries were delayed, and information about the decisions was saved to disk. After the chunks were individually processed, they were combined in a hierarchical fashion similar to the watershed process.

Synaptic cleft detection.

Synaptic clefts were annotated by human annotators within a 310.7 μm³ volume, which was split into 203.2 μm³ training, 53.7 μm³ validation, and 53.7 μm³ test sets. We trained a version of the Residual Symmetric U-Net (Lee et al., 2017) with three downsampling levels instead of four, 90 feature maps at the third downsampling instead of 64, and “resize” upsampling rather than strided transposed convolution. Images and labels were downsampled to 7.16×7.16×40-nm³ image resolution. To augment the training data, input patches were transformed by (1) introducing misalignments of up to 17 pixels, (2) blacking out up to 5 sections, (3) blurring up to 5 sections, (4) non-linear warping, (5) varying brightness and contrast, and (6) flipping and rotating by multiples of 90 degrees. Training used PyTorch (Paszke et al., 2019) and the Adam optimizer (Kingma and Ba, 2014). The learning rate started from 10⁻³ and was manually annealed three times (505,000 training updates), before adding 67.2 μm³ of extra training data for another 670,000 updates. The extra training data focused on false-positive examples from the network’s predictions at 505,000 training updates, mostly around blood vessels. The trained network achieved 93.0% precision and 90.9% recall in detecting clefts of the test set, using parameters selected to maximize F1.5 score (biasing toward recall). This network was applied to the entire dataset using the same distributed inference setup as affinity map inference. Connected components of the thresholded network output that were at least 50 voxels at 7.16×7.16×40-nm³ resolution were retained as predicted synaptic clefts.

Synaptic partner assignment.

Presynaptic and postsynaptic partners were annotated for 387 clefts, which were split into 196, 100, and 91 examples for training, validation, and test sets. A network was trained to assign synaptic partners via a voxel association task (Turner et al., 2020). Architecture and augmentations were the same as for the synaptic cleft detector. Test-set accuracy was 98.9% after 710,000 training iterations. Synaptic-cleft detection (above) produced connected components that represent cleft predictions. Subsequently, the volume was separated into non-overlapping chunks of size 7.33×7.33×42.7 μm³ (1024×1024×1068 voxels), and the partner assignment network was applied to each cleft prediction in each chunk. Some cleft predictions crossed chunk boundaries, yet the assignment network yielded a single pair of predicted partners for interior clefts. For a cleft that crossed at least one boundary, we assigned it the synaptic partners inferred by the network within the chunk that contained the most voxels of that cleft.

The cleft predictions from the synaptic-cleft detection step were sometimes split into multiple predictions, often due to voxel anisotropy or imperfect image alignment between slices. To ameliorate this problem, cleft predictions were merged after synaptic partner assignment if they were inferred to connect the same synaptic partners and their centers-of-mass were within 1 μm. This process resulted in 3,556,643 final cleft predictions.

We found a small number of synapses targeting the PyCs whose assignment was incorrect. These synapses were outside of the manually proofread PyC-PyC subgraph, yet we implemented a heuristic to remove these errors before further analysis. We associated each PyC synapse to the closest mesh vertex for both its presynaptic and postsynaptic cells by euclidean distance. We then mapped each PyC skeleton node to its closest mesh vertex in a similar manner. We then associated synapses to skeleton nodes by distance across the mesh. Associating synapses and skeleton nodes by means of the mesh, rather than directly, helped to handle cases where neurites passed near one another. Having associated synapses to skeleton nodes, we found the nine nearest neighbors to each synapse in terms of distance between each synapse’s associated skeleton nodes. Synapses were selected for manual review if a majority of its neighbors were of a different type than the original synapse (presynaptic vs. postsynaptic). This procedure identified 1392 incorrect predictions out of a set of 894,528 (~0.16%).

Mitochondria detection and assignment.

Mitochondria were annotated by human annotators within 1069.8 μm³ of image data, which was split into 462.3 μm³ training, 57.00 μm³ validation, and 550.4 μm³ test sets. The mitochondria labels were eroded by two voxels in-plane in order to prevent merges from organelle contacts. We trained a version of the Residual Symmetric U-Net (Lee et al., 2017) with two downsampling levels instead of four, resize upsampling rather than strided transposed convolution, and [32, 40, 80] feature maps at each downsampling level. Images and labels were downsampled to 7.16×7.16×40-nm³ image resolution. To augment the training data, input patches were transformed by introducing misalignments of up to 30 pixels, (2) blacking out up to three sections, (3) non-linear warping, (4) varying brightness and contrast, and (5) flipping and rotating by multiples of 90 degrees. Training used PyTorch (Paszke et al., 2019) and the Adam optimizer (Kingma and Ba, 2014). The learning rate started from 10−4 and was manually annealed twice (220,000 training updates). The trained network achieved 93.6% precision and 92.7% recall in detecting mitochondria of the test set. These metrics were defined by overlap, and errors for this network were dominated by mergers and splits of true segments rather than fully erroneous objects or missing object predictions. This network was applied to the entire dataset using the same distributed inference setup as for affinity map and synaptic cleft inference. Connected components of the thresholded network output that were at least 300 voxels at 7.16×7.16×40 nm³ resolution were retained as predicted mitochondria. Each predicted mitochondrion was associated with the neuronal segmentation object with which it overlapped most within the final proofread segmentation. We further meshed each mitochondrion segment for visualization and further analysis (see below) using zmesh (Zlateski and Silversmith, no date).

Cell-type assignment.

Cells with somas inside the EM volume were classified as excitatory pyramidal neurons, inhibitory interneurons, or non-neuronal cells based on morphological and synaptic criteria. PyCs (416 in the volume) were identified by the presence of a spiny apical dendrite radiating toward the pia, spiny basal dendrites extending laterally, and a basal axon that extended radially inward toward the white matter. PyCs axons formed asymmetric synapses. Cells that did not fit this description but that were associated with synapses and had dendrites or axons were classified as inhibitory interneurons (34).

Interneurons with identifiable axons inside the volume (20) were also assigned putative subtypes based on a combination of axonal and dendritic morphology, as well as synaptic connectivity properties (Kawaguchi, Karube and Kubota, 2006; Kubota, 2014; Kubota et al., 2016). Interneurons without axons were not assigned types. Basket cells (4) were identified by virtue of their highly branched, local-space-filling axonal arbors. They also had a larger number of primary dendrites, and at least 12% of their postsynaptic targets were pyramidal cell somata. Chandelier cells (2) were identified based on the cartridge-like groups of synapses formed by their axons and their targeting of almost exclusively axon initial segments of pyramidal cells. One Martinotti cell was identified by its apical axon that targeted mostly dendritic shafts and spines of excitatory cells; consistent with (Kawaguchi, Karube and Kubota, 2006), it had four primary dendrites that were spiny. Bipolar cells represented a diverse group of neurons that consistently had two to three primary dendrites. The dendrites were usually spiny and showed a vertical bias. Though it was rare for these cells to have an axon in the volume, in the few cases where this occurred, there was also diversity, with some bipolar cells forming the majority of their synapses with inhibitory dendrites and another targeting mostly excitatory cells. Finally, one neurogliaform cell was identified. This cell had an axon with boutons that rarely formed synapses; consistent with (Kawaguchi, Karube and Kubota, 2006) it also had a large number of primary dendrites and, as described in the results section, possessed a very different pattern of synaptic inputs when compared with other cell types.

Non-neuronal cells were generally not associated with synapses and could be broadly classified by morphology as either vasculature-related or glial cells. Vasculature-related cells (i.e., endothelial cells and pericytes), wrapped tightly around blood vessels in the volume. Endothelial cells formed the walls of blood vessels, and the continuation of their somata into blood vessel walls was readily visible. The one pericyte we identified was wrapped around an endothelial cell, consistent with typical descriptions, as in (Brown et al., 2019). Endothelial cells could also be distinguished from pericytes by their dark, electron-dense cytoplasm.

Glial cells were categorized based on their overall morphology and ultrastructural features. Protoplasmic (cortical) astrocytes had angular-shaped processes with electron lucent cytoplasm that contained numerous glycogen granules. The processes of the cells frequently filled interstices surrounding synapses and bore endfeet that covered the surface of blood vessels (Figure 1B inset). Microglia had electron-dense cytoplasm; dark, irregularly shaped nuclei; and thick branches with spiky endings (Figure 1C inset). Often, there were large lipofuscin granules (residues of lysosomal digestion) in the cell body, whereas lysosomes and scattered phagolysosomes were present in branches. Microglia had long strands of endoplasmic reticulum (ER) in their granular cytoplasm and few microtubules. Microglia are the smallest of neuroglial cells and differ from other types because of their hemopoietic origin (Ginhoux and Prinz, 2015). Most of the microglia in this dataset were also perineuronal satellites and were located adjacent to their host neurons with an astrocytic process between them (Peters, L. and Webster, 1978). Perivascular microglia were in close association with blood vessels, and some of the processes contacted surfaces of the endothelial cells forming the vessel. We grouped both of these microglial types into a single microglia group. OPCs resembled microglia because of their highly ramified branches and perinuclear satellite position with neurons, but OPCs were much larger, with branches extending up to 50 μm from the cell soma (Peters, 2004); Figure 1D inset) Their nuclei were pleomorphic, with dense heterochromatin patterning and undulating nuclear envelopes. The branches were thick near the soma, diving into smaller processes with terminations that bore growth-cone-like structures and filopodia. The cytoskeleton of the cells was composed of numerous microtubules, and there were many organelles throughout. As the OPCs transitioned to oligodendrocytes, morphological changes became evident (Trapp et al., 1997). The nucleus was elongated with a smooth nuclear envelope, and the branches appeared thinner and less ramified. The branch terminations wrapped axons, and there was evidence of myelin formation with uncompacted myelin present as well. Mature oligodendrocytes had a compact elongated soma, containing scant cytoplasm. The branches were thin, smooth, and straight and contained microtubules. These branches terminated in spiral membrane formations of compact myelin, wrapping up to 60 axons (Simons and Nave, 2015); Figure 1E inset).

Each cell with a soma in the volume received at least 2x coverage for identification, and the consensus is reported here.

Tissue quality assessment.

Given the full image volume, segmentation, and cell-type assignment, the tissue was assessed for signs of damage from the entire imaging process. We found no evidence of tissue damage from the two-photon imaging. Both gross and fine morphology of the neurons look healthy. There is no apparent spine loss, beading of excitatory dendrites, or specific shrinkage of neurons or compartments. The cytoplasm of the neurons also looks healthy and without widespread vacuoles. Different glial cell types are seen tiling the cortical space and are not concentrated in any particular location that might require cleaning or support. Moreover, the microglia do not appear to be in the activated state. In some chandelier cell axons, we can find very rare segments with swollen mitochondria, but we think that this appearance is more likely related with some pruning taking place than any damage, given that the surrounding neuropil looks impeccable, and so do other regions of the same axons.

PyC proofreading.

The mean affinity graph of watershed supervoxels was stored in our PyChunkedGraph backend (Dorkenwald et al., 2020), which uses an octree to provide spatial embedding for fast updates of the connected component sets from local edits. We modified the Neuroglancer frontend (Maitin-Shepard, 2019) to interface with this backend, so users could directly edit the agglomerations by adding and removing edges in the supervoxel graph (merge and split agglomerations). Connected components of this graph are meshed in chunks of supervoxels, and chunks affected by edits are updated in real-time, so users can always see a 3D representation of the current segmentation. Using a keypoint for each object (e.g., soma centroid), objects are assigned the unique ID of the connected component for the supervoxel containing that location. This process provides a means to update the object’s ID as edits are made.

Cell bodies in the EM volume were manually identified, and initial proofreading separated segments that merged multiple somas together. PyCs were identified by morphological features, including density of dendritic spines, presence of apical and basal dendrites, direction of main axon trunk, and cell body shape. A team of annotators used the meshes to detect errors in dendritic trunks and axonal arbors, then to correct those errors with 50,000 manual edits in 1,044 person-hours. After these edits, PyCs were skeletonized, and both the branch and end points of these skeletons were identified automatically (with false negative rates of 1.7% and 1.4%, as estimated by annotators). Human annotators reviewed each point to ensure no merge errors and extend split errors where possible (210 person-hours). Putative broken spines targeted by PyCs were identified by selecting objects that received one or two synapses. Annotators reviewed, and attached these with 174 edits in 24 person-hours. Some difficult mergers came from small axonal boutons merged to dendrites. We identified these cases by inspecting any predicted presynaptic site that resided within 7.5 μm of a postsynaptic site of the same cell, and corrected them with 50 person-hours.

PyC-PyC synapse proofreading.

Synapses between PyCs were extracted from the automatically detected and assigned synapses. We reviewed these synapses manually with 2× redundancy (1972 correct synapses out of 2433 putative synapses). Two predicted synapses out of these were merged with other synaptic clefts. These cases were excluded from further analysis. One synapse was split into two predictions, and these predictions were merged for analysis.

Nucleus detection.

Nuclei were segmented by a convolutional neural net predicting the likelihood of being part of a nucleus for each voxel (at the downsampled 57.28×57.28×40 nm³ voxel resolution), followed by a distributed connected components process merging together voxels with a likelihood above the threshold of 0.5.

The convolutional neural net was trained on image data and labels from two other similar EM datasets to be presented elsewhere. The network architecture was a modified version of the Residual Symmetric U-Net (Lee et al., 2017). Specifically, in each residual module, the first convolution used a kernel size of one and was effectively a simple linear layer; a total of three downsampling levels were used instead of four, with [16, 32, 64, 128] feature maps at each downsampling level. An input patch size of 160×160×32 was used in training.

Each nucleus was manually checked to identify all cells with somas in the volume.

Skeletonization.

We generated two separate sets of skeletons for the neuronal segmentation. The first set performed bulk processing of every object in the volume. These skeletons are useful for measuring the lengths of arbitrary objects, their orientations, and topologies. The second set was only produced for specific objects of interest (neurons with somas) and were intended to better handle two failure modes of bulk skeletonization: discontinuous objects generated by proofreading across image defects and “self-contact” sites. This second set of skeletons was used for the analyses within each vignette, though we release both sets for general use.

The bulk set of skeletons were produced using a modified form of TEASAR (Sato et al., 2000; Bitter, Kaufman and Sato, 2001) that operates on 3D labeled images. The dataset was divided into a grid of 513×513×513 cutouts at 28.64×28.64×40 nm³ resolution, with an overlap margin of one voxel in each dimension. Conceptually, each connected component within each cutout was extracted as a binary image using 26-connectivity, and we serially extracted a set of centerlines that form a tree. We selected the foreground root as the farthest foreground voxel from an arbitrarily selected foreground voxel, except at somas, where the root is set as the foreground voxel with maximum distance from the boundary.

We next applied the tree-structure extraction algorithm for accurate and robust skeletons (TEASAR) with the following modifications. (1) In the penalized distance from root voxel field (PDRF), we set M as max(DBF)^1.01 (distance from boundary field), the coefficient to 100,000, and lowered the exponent to four. We normalized the distance from any voxel field (DAF) to one. (3) The invalidated region used cubes instead of spheres. (4) We weighted the PDRF to zero along already traced paths, which results in better branching behavior and faster tracing from target to root. (5) We also assigned priority tracing targets from the centers of the cross sections of the shapes that touch the border.

We then trivially fused all the skeleton fragments for each neuron together at the overlapping voxel, removed detached components smaller than 1 μm, removed loops introduced by the forest fusion, and joined nearby detached components if they were nearer to each other than the DBF radius of the closest two vertices. We make our implementation available through our packages Kimimaro (Silversmith and Bae, no date) and Igneous (Silversmith and Tarvatull, no date). The procedure was set to stop tracing after 50 paths in a given cutout, which tends to exclude glia.

To produce the second set of skeletons, we developed a skeletonization algorithm similar to TEASAR (Sato et al., 2000) that operates on meshes. For each connected component of the mesh graph, we identify a root and find the shortest path to the farthest node. This procedure is repeated after invalidating all mesh nodes within the proximity of the visited nodes until no nodes are left to visit. We make our implementation available through our package MeshParty (https://github.com/sdorkenw/MeshParty). The skeletonization parameters were hand-tuned to largely ignore dendritic spines.

Given the mesh vertices that participate in the skeleton, we estimated the neurite diameter at each location of the skeleton using ray casting. Each ray begins at a location near a skeleton node (moved slightly opposite to its normal), extends in a direction roughly opposite to the skeleton node normal (with some small noise), and travels until it crosses the mesh at another location.

These mesh skeletons were further processed to improve our estimations of path length across cells. Each skeleton was smoothed by iteratively shifting vertices toward a local average computed using a vertex’s neighborhood. Given a vertex v_i, the smoothing neighborhood around v_i consists of the set of vertices less than or equal to two-edges from v_i (excluding v_i itself). After computing the local average from the neighborhood, each vertex is moved to a weighted sum of its original location and its local average $\left({\overline{v}}_i\right)$ with a blending parameter $\left(r\times {\overline{v}}_i+(1-r)\times v_i\right)$.

We used r=0.1, and performed 20 iterations of this smoothing. The soma root node, branch point nodes, and leaf nodes were kept fixed throughout this smoothing procedure.

Neuronal compartment labeling.

Annotators tagged all branches leaving PyC somas and labeled them as one of the following categories: axon, basal dendrite, apical dendrite, ambiguous dendrite, or ambiguous. We mapped these annotations to the closest skeleton nodes in the automatically generated skeletons and moved the label to the closest branch node if one was within 5 μm. Labels were next propagated to all skeleton nodes away from the soma. We then extended the soma label up to the closest of two options: (1) the first branch point labeled as neurite or (2) the first node over 15 μm away from a manually placed soma center coordinate.

Imperfect skeletons introduced errors in the label propagation. We inspected and corrected the resulting compartment labels to acquire a set of 351 cells possessing compartment labels without errors. Out of this set, we manually identified 182 that had their somas fully captured by the EM volume. Some PyCs with mild errors in their compartment labels were still included in specific analyses if their errors had no bearing on their results.

To label compartments for inhibitory neurons, we manually placed labels near the axon initial segment for each cell if it had an axon in the volume. The label was extended to the branch point of the skeleton closest to the cell body. As with pyramidal cells, the soma was defined to include the region within 15 μm of its soma center label. To make neuronal meshes and skeletons continuous, we added links to the meshes where proofreading spanned a gap in the segmentation using the MeshParty function “add_link_edges.”

QUANTIFICATION AND STATISTICAL ANALYSIS

Neurite length calculation.

The skeleton for each PyC and inhibitory neuron was split according to its compartment labels to generate individual sub-skeletons for dendrites and for the axon. For each sub-skeleton, the node closest to the soma centroid was chosen as the source, and all other leaf nodes (nodes with degree 1) were identified as targets. Each leaf node represented either the biological end of a neurite (e.g., the end of a short dendrite in the volume) or the point at which a longer neurite left the volume. The shortest path length was computed from the source to each target node with Dijsktra’s algorithm. We summarized this distribution between its 5th and 95th percentiles to remove a few large outliers.

Synapse detection performance estimation.

To estimate the precision of synapse detection for each class, we defined a “likely subset” of synapses belonging to that class based on a heuristic, and scored synapses that were of the correct type. For example, for axo-axonic synapses, we extracted the set of synapses received by PyC’s within 10 μm of the axon and soma compartment label boundary. In some cases (mostly axo-somatic), a synaptic cleft would be split into two predictions by an image defect or weak prediction. In those cases, we counted that prediction as 50% true positive and 50% false positive.

To estimate the recall for each class, we randomly sampled a set of cells, manually identified a set of synapses for those cells by traversing their neurites or target domains, and compared the manually identified set to the predicted clefts. Each precision and recall value was estimated with roughly 50 synapses each.

PyC dendritic segment analysis.

We computed the path length distance along the computational skeleton to the nearest node with a “soma” label of a given cell. We used a similar computation to measure the distance to the closest leaf node of the skeleton. We then created dendritic segments by separating the skeleton at 10 μm distance intervals from the soma. We also introduced additional separations at boundaries of the compartment labels, such that each segment only contained nodes with one label. Dendritic segments within 5 μm of a leaf node were excluded from analysis to mitigate reconstruction or skeletonization noise near the reconstruction boundaries. The triangle mesh for a given dendritic segment was estimated by grouping the mesh vertices that had the smallest euclidean distance to some skeleton node within the segment.

We computed several features for each dendritic segment. The segment’s surface area and volume were computed from the dendritic segment mesh. The median diameter measurement for each segment used the median diameter value estimated across skeleton nodes within the segment (see Skeletonization above). The synapse count for each segment was computed as the number of predicted postsynaptic terminals that had the smallest euclidean distance to some node in the skeleton of the dendritic segment.

Mitochondrion analysis.

We associated each mitochondrion mesh to the set of skeleton nodes that were closest to any mesh vertex of that object within the 351 PyCs possessing compartment labels without errors. We then assigned a compartment label to each predicted mitochondrion using the skeleton node labels by taking a majority vote over the skeleton nodes associated with that mitochondrion. Each skeleton node’s vote was weighted by the number of mesh vertices associated with that node. Mitochondria with an “ambiguous dendrite” or “ambiguous” label were removed from further analysis. Mitochondria without a soma label that crossed the soma/neurite boundary were also removed, as well as mitochondria within 10 μm of a skeleton leaf node.

The mitochondrial volume for each dendritic segment was computed by dividing the volume of each mitochondrion prediction between the segments to which some mesh vertex was closest. Each segment was assigned volume from a mitochondrion prediction proportional to the number of the mitochondrion’s mesh vertices assigned to skeleton nodes within that segment.

The mitochondrial index within a segment of neurite was computed by first measuring the path length within this segment covered by each present mitochondrion, and then normalizing the sum of these covered lengths by the amount of neurite path length within the section. The mitochondrial volume per unit length was computed by dividing the mitochondrial volume for a dendritic segment by the dendritic path length for that segment.

When measuring mitochondrion length, we took the set of skeleton nodes associated with each individual object, and computed the path length of all edges connecting those nodes together.

When correlating measurements of mitochondrial density, synapse density, and dendritic diameter, we calculated the two-tailed p-value for each Pearson correlation as implemented in Scipy (Virtanen et al., 2020): the null distribution of the r-value is a Beta distribution over [−1, 1] with shape parameters $\alpha =\beta =n/2-1$.

PyC and interneuron cell input analysis.

Separately from the dendritic segment analysis above, synapses were associated with the mesh vertex closest to the location of the synaptic cleft in the synapse detection, and synapses beyond 200 nm from a mesh vertex were omitted. Mesh vertices and their synapses were bidirectionally mapped to the closest skeleton vertex as measured along the surface of the mesh.

Similar dendritic segments were formed to the above analysis, except that they introduced separations into the skeleton in increments of 15 μm instead of 10 μm. For each distance increment (e.g., 15–30 μm), synapses, path lengths and surface areas were pooled across separate segments and averaged to create an estimate of linear and areal synapse density per cell at that distance.

Statistical visualization was performed in Python using Seaborn (Waskom, 2021). Error intervals for line plots were estimated by bootstrap resampling the density values for cells within each distance bin and cell class (1000 bootstrap samples, as implemented in Seaborn). For violin plots, synapses were first log₁₀-transformed and then plotted with a kernel bandwidth of 0.1.

Random network models.

To identify nonrandom connectivity motifs, we compared the simple subgraph of PyCs (removing self-loops and multiple edges) with different random graphs as null models. When studying two-neuron motifs, we first used a directed Erdős-Rényi (ER) model (Gilbert, 1959), G(n,p), as a baseline, where a directed edge between any two distinct vertices is uniformly drawn at random with probability p. The expected number of edges of a directed ER model is m = n(n − 1). To match the data, for example, the subgraph with a 100 μm axon length threshold, we set n=111, m=659, and $p=m/[n(n-1)]\approx 0.0540$. We directly calculated the expected number of different two-neuron motifs in this ER model.

We also used a directed configuration model, $G\left(n,\overrightarrow{d^{+}},\overrightarrow{d^{-}}\right)$, which generates rewired graphs preserving the original degree distribution uniformly at random, where $\overrightarrow{d^{+}}$ and $\overrightarrow{d^{-}}$ are predefined in- and out-degree sequences of the network. We sampled 1,000 random networks uniformly from a set of graphs with the same degree sequences as our PyCs subgraph by applying the switch-and-hold algorithm (Figure 6A; (Artzy-Randrup and Stone, 2005), where we randomly select two edges in each iteration and swap their target endpoints if that does not introduce self-loops or multiple edges (switch), or otherwise keep them unchanged (hold). In the original paper, the switch step is implemented by selecting four vertices at random, while our implementation selects two edges at random, because that is more efficient on a sparse network. In general, the Markov chain for our sampling procedure is reducible, so samples are drawn from only one ergodic component of the set of all simple graphs with the same degree sequence (Carstens and Horadam, 2016). However, all ergodic components share the same motif frequencies, so the lack of ergodicity has no consequence for our analysis (Berger and Müller-Hannemann, 2010). A more complex Markov-chain sampling procedure with true ergodicity is known (Roberts and Coolen, 2012), but as mentioned above would yield the same motif frequencies. To generate one sample, we run the algorithm for 10,000 iterations from the previously sampled network, with an average holding rate of 19.2% for the largest PyC subgraph.

When studying three-neuron motifs, besides the vanilla ER model and configuration model as described above, we also used generalized ER (Figure 6B) and configuration models (Figure S6A) to preserve two-neuron motif statistics. In the generalized ER model, the probability of a unidirectional edge is 4.92×10⁻², and the probability of a bidirectional edge is 4.75×10⁻³. We directly calculated the expected number of different three-neuron motifs in the generalized ER model.

We also modified the switch-and-hold algorithm such that the number of bidirectional edges for each neuron is preserved (gCFG, Figure S6A), or the total number of bidirectional edges is preserved (gCFG (bi-edge), Table S2). Sampling from the first generalized configuration model, we constrain the switch operation to swap two bidirectional connections or two unidirectional connections. Sampling from the second generalized configuration model (bi-edge) involves two phases: mixing and hitting. For each sample, we run the switch-and-hold for 10,000 iterations to ensure the convergence to stationary distribution (mixing), then continue for a few iterations until it reaches a graph with the same number of bidirectional edges as the observed network (hitting). This generalized configuration model efficiently samples graphs with unchanged degree sequences and the statistics of two-neuron motifs without biases. It has the same holding rate and running time as ordinary switch-and-hold, and only increases the required number of iterations by a small constant Θ(log(1/(1-p)), where p is the percentage of graphs with the same frequency of 2-neuron motifs in the entire space. In the experiment, we sampled 1,000 random networks, with an average holding rate of 19.2% for the largest PyC subgraph. The average number of iterations in the hitting phase is 3,736.78, which only increases the total number of iterations by 37.4%.

Because proximity could be a primary predictor of connection probability, we additionally compared a random graph model where the connection probability between a pair of neurons is a function of pairwise soma distance. In such a proximity-based model, the connection probability between two neurons i and j at a distance d_ij is estimated from all pairs of neurons with soma distance in the bin $\mathit{\left[}{d}_{ij}-10\mu \text{m},d_{ij}+10\mu \text{m}\mathit{\right]}$ (Figure S6F). I.e.,

$$p\left(d_{ij}\right)=\frac{\#\text{of}\text{connected}\text{cell}\text{pairs}\text{with}\text{soma}\text{distance}\in \left[d_{ij}-10\mu \text{m},d_{ij}+10\mu \text{m}\right]}{\#\text{of}\text{all}\text{cell}\text{pairs}\text{with}\text{soma}\text{distance}ϵ\left[d_{ij}-10\mu \text{m},d_{ij}+10\mu \text{m}\right]}$$

Edges in the proximity model are drawn independently with probability p(d_ij), where pairwise distance d_ij is given by the data.

Random network model comparison.

We applied the minimum description length principle to determine which random graph model provides the best description of the observed neural network. The description length of a model consists of two parts,

$$\Sigma =L+S$$

where L is the number of nats required to specify the observation when the model is known, and S is the number of nats required to encode the model.

The MDL principle advocates that the model with a smaller Σ is better (Rissanen, 1978). From an information perspective, the description length depicts the trade-off between model accuracy and complexity. One can add more constraints to improve the model’s accuracy, which increases L; in the meantime, it increases the complexity of the model, which penalizes the overall description length by increasing S. The MDL principle prefers the simplest model that can explain the observation.

From a Bayesian perspective,

$$e^{-\Sigma }=e^{-L}·e^{-S}$$

where e^−L can be regarded as the likelihood of the observation given the model, e^−S can be regarded as the prior of the model, and e^−Σ can be regarded as the posterior to be maximized. This yields an equivalence between MDL and Bayesian inference.

Given n nodes and m edges, the description length of the ER model is given by

$${\sum }_{ER}=\text{log}(\#\text{of}\text{graphs}\text{given}n\text{and}m)=\text{log}\left(\begin{array}{c}n(n-1)\\ m\end{array}\right)$$

and the description length of the generalized ER model is given by

$${\sum }_{ER}=\text{log}(\#\text{of}\text{graphs}\text{given}n\text{and}m)=\text{log}\left(\begin{array}{c}n(n-1)\\ m\end{array}\right)$$

$${\sum }_{gER}=\text{log}\left(\#\text{of}\text{graphs}\text{given}n,m\text{and}{m}_{bi}\right)+\text{log}\left(\#\text{of}\text{possible}{m}_{bi}\text{given}n,m\right)$$

$$=\text{log}\left[\left(\begin{array}{c}n(n-1)/2\\ m_{bi}\end{array}\right)\cdot \left(\begin{array}{c}n(n-1)/2-m_{bi}\\ m-2m_{bi}\end{array}\right)\cdot 2^{m-2m_{bi}}\right]+\text{log}(m/2)$$

where m_bi indicates the number of bidirectional edges. The second term assumes a uniform prior of the number of bi-directional edges, which may not be a property of the biological neural network. However, it provides an upper bound for the number of nats of information in the number of bidirectional edges if further compression is possible. The first term alone is a lower bound for ${\Sigma }_{\text{gER}}$. In the subgraph with a 100 μm axon length threshold, n=111, m=659, and m_bi=29. We have ${\Sigma }_{\text{ER}}$ = 2560.56 nats, and 2554.64 nats < ${\Sigma }_{\text{gER}}$ ≤ 2560.44 nats. The above calculation is based on a version of ER model that holds the number of edges exactly. If we use an ER model where the expected number of edges is fixed (Gilbert, 1959), the description length is slightly greater (${\Sigma }_{\text{Gilbert}}$ = 2564.69, and 2561.31 < ${\sum }_{\text{Gilbert}(\text{generalized})}$ ≤ 2567.11).Similarly, the description length of the configuration model is given by

$${\sum }_{CFG}=\text{log}\left(\#\text{of}\text{graphs}\text{given}n,m,\overrightarrow{d^{+}}\text{and}\overrightarrow{d^{-}}\right)+\text{log}(\#\text{of}\text{possible}\text{degree}\text{sequences}\text{given}n,m)$$

The pairings model in (Greenhill, McKay and Wang, 2006) suggests the following upper bound for the total number of directed graphs given degree sequences.

$$\text{log}\left(\#\text{of}\text{graphs}\text{given}n,m,\overrightarrow{d^{+}}\text{and}\overrightarrow{d^{-}}\right)\le \text{log}(m!)-\sum _{i=1}^n\text{log}\left(d_i^{+}!d_i^{-}!\right)$$

Also, we can bound the number of degree sequences by partitioning m into the sum of n non-negative numbers.

$$\text{log}(\#\text{of}\text{possible}\text{degree}\text{sequences}\text{given}n,m)\le 2\text{log}\left(\begin{array}{c}n+m-1\\ n-1\end{array}\right)$$

The log number of possible degree sequences is an upper bound for the number of nats of information in degree sequence if the degree sequence distribution is non-uniform. Combining the above two upper bounds yields ${\Sigma }_{\text{CFG}}$ ≤ 2508.73 nats. Thus, we have ${\Sigma }_{\text{CFG}}<{\Sigma }_{\text{gER}}<{\Sigma }_{\text{ER}}$.

Whole-cell degree and connection density.

Using the 334-node PyC graph, we counted the number of unique presynaptic partners and postsynaptic partners and named them as in-degree and out-degree, respectively. To compensate for the truncated effect due to the limited size of the volume, we normalized these quantities by axon length for out-degree and by dendrite length for in-degree. These normalized quantities are named “connection density.” We also looked at all incoming synapses on dendrites not restricted to the PyC graph (perisomatic synapses within 15 μm from the human-labeled soma centroid are neglected), and named this quantity “linear synapse density.”

Direction and orientation selectivity.

For each calcium-imaged cell, we defined a response matrix R_td as the sum of inferred spike probability, which was thresholded with three standard deviations of spike probabilities of the cells for each scan above zero, triggered by the stimulus in trial t to stimulus direction θ_d. The T×D matrix included response amplitudes in T=30 trials and D=16 directions. The direction tuning function was computed by taking the average of responses over 30 trials for each direction.

$$R_d=\frac{1}{T}\sum _{t=0}^T{R}_{td}$$

From the direction tuning function R_d, we computed a global orientation selectivity index (gOSI) and global direction selectivity index (gDSI) as below (Ringach, Shapley and Hawken, 2002).

$$\text{gOSI}=\left|\frac{{\sum }_{d=1}^D{R}_d\exp \left(i\frac{\pi }{4}d\right)}{{\sum }_{d=1}^D{R}_d}\right|,\text{gDSI}=\left|\frac{{\sum }_{d=1}^D{R}_d\exp \left(i\frac{\pi }{8}d\right)}{{\sum }_{d=1}^D{R}_d}\right|$$

An orientation-tuned cell was defined as one with statistically significant gOSI, evaluated using a permutation test (Ecker et al., 2014; Baden et al., 2016). A direction-tuned cell was defined as one with statistically significant gDSI but not gOSI. Statistical significance was determined by p<0.001, where the p-value indicates the fraction of 10,000 permutations with gDSI/gOSI greater than that of the observed data. The permutation test effectively excludes cells that have a large gDSI or gOSI merely by chance, which can happen due to trial-to-trial variability. Restriction by statistical significance is different from imposing a simple threshold on gDSI or gOSI (Baden et al., 2016).

Preferred orientation.

To compute the preferred orientation of a cell, we first averaged the responses of each direction with its null direction to produce an orientation tuning function from a direction tuning function. The orientation tuning function was modeled with circular Gaussian function. The preferred orientation was determined as an angle from 0° to 180° that has the maximum value of the Gaussian fit.

Mean response.

From the response matrix, a cell’s mean response was computed by taking the average of responses in all 30 trials of the preferred orientation stimuli, preferred direction, and opposite direction (180° from the preferred direction). For significantly direction-tuned cells (p<0.001 for gDSI), the average of responses were computed only for the preferred direction. The Pearson correlation coefficient was calculated to measure the correlation between the intermittency and the in-connection density using the Scipy package (Virtanen et al., 2020). To test for significance, the two-tailed p-value was calculated; a threshold of 0.05 was used to reject the null hypothesis, where the null distribution of the r-value is a Beta distribution over [−1, 1] with shape parameters α=β=n/2–1.

We fit our linear model combining responses that surpass the intermittency threshold and in-connection density using ordinary least squares as implemented in Statsmodels (Seabold and Perktold, 2010).

Intermittency.

We defined a binary-valued function by thresholding the activity after temporal deconvolution (S), where the threshold (λ) was set at three standard deviations of spike greater than the baseline. The standard deviation was determined from the standard deviations of spike probabilities of the cells in each scan. For example, the value of this function for a directional stimulus with direction d and trial t is defined as

$$f_d(t)=\{\begin{array}{cc}1,& max(S(d,t))\ge \lambda \\ 0,& max(S(d,t))<\lambda \end{array}$$

In other words, we define the response of direction d at trial t “active” $\left(f_d(t)=1\right)$ when there exists any activity over the threshold during that period.

A cell’s intermittency is an inverse measure of how consistently a cell responds to preferred stimuli. Here, preferred stimuli are preferred direction and the opposite direction except for significantly direction-tuned cells, where preferred stimulus is only the preferred direction. Therefore, the intermittency value was defined as

$$I=\frac{1}{\left|D_p\right|}\sum _{d\in D_p}\left(1-\frac{1}{T}\sum _{t=1}^T{f}_d(t)\right)$$

where D_p is a set of directions in preferred stimuli, and T is the number of trials for each stimulus. To test for significance, we performed an analogous permutation test for mean response.

Location-restricted permutation test.

To test that significance of correlation is not due to spatial organization, we performed a permutation test with spatial restriction. We divided the volume into small cubes by dividing the x- and z-dimensions into two regions and y-dimension (cortical depth) into four regions. Axis along the cortical depth was divided into finer regions because more distinct spatial organization existed along that axis (Figure S7F), while other axes had less bias. For each cube, we located all the cells that have soma centers within the cube and shuffled the in-connection density values among these cells. Then we computed the correlation coefficient for the randomized distributions. Statistical significance was determined by p<0.05, where the p-value indicates the fraction of 10,000 permutations with correlation coefficient stronger than that of the observed data. We performed this permutation test for mean response and intermittency.

Statistical reporting.

We report p-values greater than 1×10⁻⁴ as a rounded value, those under 1×10⁻⁵⁰ as approximately 0, and those in between 1×10⁻⁵⁰ and 1×10⁻⁴ as less than the value rounded up to two significant figures. We report p-values for permutation tests as the percentage of permutations whose test statistic value is more extreme than the observed value.

Figure rendering information.

The following segment IDs were removed from the insets in Figure 1A to improve their visual clarity: 648518346349526102, 648518346349525545, 648518346349531742, 648518346349508442.

ADDITIONAL RESOURCES

Interactive visualization of the reconstruction, a list of related publications, information about the MICrONS project, and further data releases are made available at the MICrONS Explorer website (microns-explorer.org).

Supplementary Material

1

aData S1. Dataset volumes. Related to Figure 3.

Table comparing connectomic EM volume reconstructions that have been generated to date from rodent central nervous system tissue. For each reconstruction, volume dimensions, the total number of segmented objects, and the total number of segmented objects with somas are provided. Scale bar: 100 μm

Data S2. Inhibitory cell profiles. Related to Figure 5.

2

Table S1. Two-cell motif statistics, Related to Figure 6. Sample size = 1,000. Connection probability for the vanilla Erdős-Rényi model is p_ER=0.0540. “+” indicates over-representation, and “-” indicates under-representation with respect to the configuration model. “*” indicates the significance level 0.01 < p ≤ 0.05. The p-value is computed as the percentile of the observed motif counts in the distribution of motif counts sampled from the configuration model.

3

Table S2 Three-cell motif statistics, Related to Figure 6. Sample size = 1,000. The connection probabilities of the vanilla Erdős-Rényi model is p≈5.40×10⁻². Unidirectional and bidirectional connection probabilities in the generalized Erdős-Rényi model are p_uni≈4.92×10⁻² and p_bi≈4.75×10⁻³. “+” indicates over-representation, and “-” indicates under-representation with respect to the null models. “*”, “**”, and “***” indicate the significance levels 0.01 < p ≤ 0.05, 0.001 < p ≤ 0.01, and p ≤ 0.001 respectively. The p-values are computed as the percentile of the observed motif counts in the distribution of motif counts sampled from the null models. There is no correction for multiple comparisons.

4

Table S3. Clustering coefficients of all versions of PyC subgraph and null models. Related to Figure 6. The expected numbers are computed analytically for ER and generalized ER models, and empirically for the configuration model and generalized configuration model by averaging over 1,000 Monte Carlo samples. Numbers in the square brackets indicate 95% CI based on 1,000 samples. The p-value is computed as the percentile of the observed clustering coefficient in the distribution of clustering coefficients sampled from the configuration model.

6

Movie S1. Public visualization and analysis. Related to Figure 2.

A tutorial demonstrating the use of neuroglancer and access of the online analysis code.

5

Figure S1. Example inhibitory neurons and the reconstructed vasculature, Related to Figure 1. (A) Basket (green) to PyC (blue) axosomatic synapse. Insets: left: 3D view of contact between axonal bouton and PyC soma (box); right: single-section EM view of the synapse.(B) Chandelier (pink) to PyC (blue) axoaxonic synapse cartridge. Insets: left: 2 synapses in series (box); right: EM view.(C) Martinotti (cyan) to spiny dendrite (purple) axodendritic synapse. Insets: left: direct contact between bouton (asterisk) and dendritic shaft; right: EM view.(D) Neurogliaform cell.(E) Bipolar cell with basal axon (arrowhead).(F) Vasculature reconstruction with merge errors.Black dots, (A)-(C): predicted presynaptic terminals of the inhibitory neuron.Scale bars: (A)-(E): 20 μm; shown in (A) only; (A)-(C) insets: left, 2 μm, right, 300 nm. (F): 25 μm.

Figure S2. Additional mitochondria and synapse density analysis for L2/3 PyCs, Related to Figure 4. (A) Comparison of MCI (Vincent et al., 2019) by neuronal compartment (N_axonal=11,484, N_somatic=90,193, N_apical=18,608, N_basal=53,318; One-tailed Mann-Whitney U tests; *:p<1×10⁻²⁸, **:p≈0). Boxes indicate interquartile ranges, and whiskers indicate the 5th and 95th percentiles.(B-D) Single mitochondrion path length vs. distance from soma for axons (B), basal dendrites (C), and the proximal apical dendrites (D). Black dots show the median value, red dots show the mean value, shaded region shows the interquartile range.(E) The number of analyzed basal dendrite segments at each distance from the soma. The number of cells that contain analyzed segments at each distance is indicated in red.(F-G) Mitochondrial volume density (F) and areal synapse density normalized by approximate dendritic cylinder surface area (G) at different distances from the soma. Dots and shaded regions indicate the mean +/− standard deviation values at each distance bin. N=29,591.(H) Percentage change in the mean of basal mitochondria density measurements relative to the value 65 μm away from the soma. Red: mitochondrial volume per unit length. Blue: mitochondrial path length per unit length. Black: mitochondrial volume as a fraction of dendritic volume. Error bars indicate the standard error of the mean.(I) Percentage change in the mean of basal dendrite measurements relative to the value 65 μm away from the soma. Red points: areal synapse density. Blue points: linear synapse density. Black points: cylinder areal synapse density. Magenta diamond: median diameter. Error bars indicate the standard error of the mean.(J) Mitochondrial volume per unit length is correlated with linear synapse density over 60 μm away from the soma (r=0.37, N=9198, p<1×10–300)(K) Median dendritic shaft diameter is correlated with linear synapse density over 60 μm away from the soma (r=0.402, N=9198, p≈0)(L) Mitochondrial volume per unit length is correlated with dendritic diameter over 60 μm away from the soma (r=0.514, N=9198, p≈0)(M) Mitochondrial volume per unit length is only weakly correlated with linear synapse density over 60 μm away from the soma after removing variance explained by dendritic diameter (r=0.181, N=9198, p<1×10−67)(N) Detailed view of a single apical mitochondrion within a pyramidal cell from a deeper cortical layer. Inset shows the morphology of the captured dendrite (grey) and mitochondria (red).(O-U) Proximal vs. distal measurements for each analyzed cell with distal arbor (N=343), displaying mitochondrial volume per unit length (O), mitochondrial path length per unit length (P), volume mitochondrial density (Q), median dendrite diameter (R), linear synapse density (S), areal synapse density (T), and cylinder synapse density (U). Proximal values are averaged across distances <40 μm away from the soma, and distal values are averaged across distances ≥60 μm away.Scale bars: (N) 5 μm, inset 10 μm.

Figure S3. Input synapse density for excitatory and inhibitory cells, Related to Figure 5. (A) Path length captured by the reconstruction volume for each neuron class as a function of distance from the soma.(B) Linear synapse density for each cell grouped in Figure 5.(C) Neurite surface area for each neuron class.(D) Areal synapse density for each cell grouped in Figure 5.(E) Synapse count for each neuron class.(F) Median synapse size for each cell grouped in Figure 5.(G) Median synapse size grouped by neuron class.(H) Areal synapse density for basket and chandelier groups, as well as unclassified cells suspected to be within these classes.(A, C, E, G) Lines: mean value across cells, shaded regions: 95% bootstrap confidence intervals (1,000 samples). (C-H) Dots: value at the soma.

Figure S4. Predicting motif frequencies for PyC subgraphs with different axon length thresholds (0 μm and 300 μm). Related to Figure 6, which is based on a subgraph consisting of PyCs with axon lengths ≥ 100 μm. (A) Spatial location of nodes in PyC subgraphs with axon length threshold = 0 μm. Red: 227 PyCs included in the subgraph. Gray: PyCs excluded due to axon lengths shorter than threshold.(B) Similar to (A) for axon length threshold = 100 μm. The resulting subgraph contains 111 neurons.(C) Similar to (A) for axon length threshold = 300 μm. The resulting subgraph contains 100 neurons.(D) In- and out-degree distributions in an observed network with threshold = 0 μm and the expected distribution of in- and out-degrees in a regular ER model (edge probability = 0.0245). Red: observed data; Black, dashed: ER model. Histograms are calculated with 8 bins of the same widths on a log scale. The expected degree distributions are estimated from 100 samples from the ER model.(E) Similar to (D) for axon length threshold = 300 μm. ER edge probability = 0.0628.(F) 2-cell motif frequencies in the observed network with threshold = 0 μm and a configuration (CFG) model relative to the ER model. The red crosses indicate observed counts. The shaded region shows the smoothed distribution of motif counts sampled from the configuration model. White points indicate medians, solid vertical lines indicate quartiles, and dashed lines indicate the 95% confidence interval for 1,000 samples.(G) Similar to (F) for axon length threshold = 300 μm.(H) 3-cell motif frequencies in an observed network with threshold = 0 μm and the CFG model relative to a generalized ER model. The red crosses indicate observed counts. The violin plot shows the smoothed distribution of the motif counts sampled from the configuration model. White points indicate medians, solid vertical lines indicate quartiles, and dashed lines indicate the 95% confidence interval for 1,000 samples.(I) Similar to (H) for axon length threshold = 300 μm.(J) The common neighbor rule for the graph with threshold = 0 μm. Error bars indicate standard deviation of 100 samples. (red: observed data, R²=0.95, p=1.9×10⁻⁶; gray: configuration model, R²≈1.00, p=1.7×10⁻¹³; z-test, dashed line: generalized ER model).(K) Similar to (J) for axon length threshold = 300 μm. Red: R²=0.88, p=6.3×10⁻⁵; Gray: R²≈1.00, p=5.8×10⁻¹¹; z-test.

Figure S5. Predicting motif frequencies for all 363 PyCs, Related to Figure 6. (A) In- and out-degree distributions of all PyCs and the expected distribution of in- and out-degrees in a regular ER model (edge probability = 0.0113). Red: observed data; Black, dashed: ER model. Histograms are calculated with 8 bins of the same widths on a log scale. The expected degree distributions are estimated from 100 samples from the ER model.(B) 2-cell motif frequencies in the full network and a CFG model relative to the ER model. The shaded region shows the smoothed distribution of motif counts sampled from the configuration model. White points indicate medians, solid vertical lines indicate quartiles, and dashed lines indicate the 95% confidence interval for 1,000 samples.(C) Comparison of 2-cell motif counts in the ER model and CFG model. Circles indicate mean counts sampled from the configuration model, and triangles indicate mean counts sampled from the ER model.(D) 3-cell motif frequencies in the full network and the CFG model relative to a generalized ER model. The violin plot shows the smoothed distribution of the motif counts sampled from the configuration model. White points indicate medians, solid vertical lines indicate quartiles, and dashed lines indicate the 95% confidence interval for 1,000 samples.(E) Comparison of 3-cell motif counts in the generalized ER model (gER) and configuration model. Circles and triangles indicate mean counts sampled from the CFG model and the gER model, respectively.(F) The common neighbor rule is significantly more prominent in the pyramidal cell network than in generalized ER random networks. Gray: CFG model; Black, dashed: generalized ER random networks; Red: observed data. (red slope: R²=0.86, p=9.5×10⁻⁵; gray: R²=0.99, p=2.4×10⁻¹⁰; z-test). Lines indicate standard deviation of 100 samples.

Figure S6. Comparison of the (generalized) Erdős–Rényi model, (generalized) configuration model, and a proximity-based model for predicting three-cell motifs, Related to Figure 6. (A) Illustration of sampling from a generalized configuration model, where the number of bi-directional edges for each neuron in the original network is preserved.(B) Comparison of 3-cell motif counts in the ER model and generalized ER model for the subgraph with the axon length threshold = 100 μm. Circles and stars indicate mean counts sampled from the ER model and the generalized ER model, respectively.(C) Similar to (B), circles and stars indicate mean counts sampled from the configuration model and the generalized configuration model, respectively.(D) Similar to (C), circles and stars indicate mean counts sampled from the generalized ER model and the generalized configuration model, respectively.(E) Illustration of a counter-example where the configuration model fits two-cell motifs worse than the ER model. Networks i-vii share the same degree sequence, and the configuration model underpredicts the number of bi-directionally connected pairs of cells for networks i-iv.(F) Connection probability as a function of soma distance. The red curve indicates connection probability at distance x, which is estimated from pairs of neurons with soma-to-soma distances in the range [x-10μm, x+10μm]. The gray curve indicates cumulative connection probability of all pairs of neurons with soma-to-soma distances ≤ x. The shaded area indicates the 95% confidence interval from a normal distribution approximation to the standard error.(G) 3-cell motif frequencies in the observed network (OBS) and the proximity-based model (PM) relative to a generalized ER model (gER). The violin plot shows the smoothed distribution of the motif counts sampled from the configuration model. White points indicate medians, and lines indicate the 95% confidence interval for 1,000 samples.(H) The common neighbor rule does not hold in the proximity-based model. Gray: proximity-based model; Black, dashed: generalized ER random networks; Red: observed data. (red slope: R2 = 0.88, p=6.1×10−5; gray: R2 = 0.20, p=1.9×10−1; z-test). Error bars indicate standard deviation of 100 samples.

Figure S7. Coregistration and volume truncation in degree-visual response analysis, Related to Figure 7. (A) 2p calcium recording image plane coregistration for all recordings (extension of Figure 7A).(B) Qualitative evaluation of coregistration. Left: segmentation overlaid on top of example 2p slice, right: convex hull of PyCs’ somas in the example slice overlaid on top of 2p slice.(C) Total axon length vs. out-degree of PyCs (N=351).(D) Total dendrite length vs. in-degree of PyCs (N=351).(E) In-connection density distribution (N=351).(F) In-connection density distribution of significantly tuned cells along x, y, and z dimensions (N=38).(G) Spatially restricted randomization cartoon.(H) Number of cells in the cube for spatially restricted randomization (N=38).(B) Scale bar: 50 μm. (C, D, and F) Shade: 80% prediction interval.