Assessment of two statistical approaches for variance genome-wide association studies in plants

Abstract

Genomic loci that control the variance of agronomically important traits are increasingly important due to the profusion of unpredictable environments arising from climate change. The ability to identify such variance-controlling loci in association studies will be critical for future breeding efforts. Two statistical approaches that have already been used in the variance genome-wide association study (vGWAS) paradigm are the Brown–Forsythe test (BFT) and the double generalized linear model (DGLM). To ensure that these approaches are deployed as effectively as possible, it is critical to study the factors that influence their ability to identify variance-controlling loci. We used genome-wide marker data in maize (Zea mays L.) and Arabidopsis thaliana to simulate traits controlled by epistasis, genotype by environment (GxE) interactions, and variance quantitative trait nucleotides (vQTNs). We then quantified true and false positive detection rates of the BFT and DGLM across all simulated traits. We also conducted a vGWAS using both the BFT and DGLM on plant height in a maize diversity panel. The observed true positive detection rates at the maximum sample size considered (N = 2815) suggest that both of these vGWAS approaches are capable of identifying epistasis and GxE for sufficiently large sample sizes. We also noted that the DGLM decisively outperformed the BFT for simulated traits controlled by vQTNs at sample sizes of N = 500. Although we conclude that there are still certain aspects of vGWAS approaches that need further refinement, this study suggests that the BFT and DGLM are capable of identifying variance-controlling loci in current state-of-the-art plant or agronomic data sets.

Introduction

The world’s food baskets face an expanding amount of unpredictable growing seasons due to the ongoing threat of climate change (Ziervogel and Ericksen 2010). If a 4 °C increase in global temperature is not prevented by 2100, there could be a potential loss of $23 quadrillion to agriculture (Schillaci et al. 2019). Unfortunately, most crops are maladapted to highly variable environments, where optimal growing conditions may never be attained (Mulder et al. 2007). An idea that may lend itself to accelerating the development of crops better suited for such variable environments is canalization. Canalization is the hypothesis that natural selection minimizes variation for certain traits in a way that prevents major loci from being influenced significantly by the environment or background genetic variance like epistasis (Waddington 1942; Rönnegård and Valdar 2011). Artificial selection facilitates the decanalization of certain loci, which has allowed domesticated crops to grow in novel environments (Kitano 2004). However, these decanalized loci are disadvantageous if the environment it was adapted to becomes unpredictable (Waddington 1942). Collectively, the combination of decanalized loci and unpredictable environments has resulted in such loci controlling the variance of a targeted trait; that is, as a variance quantitative trait locus (vQTL; Debat and David 2001). A classic example of such vQTLs are genes that encode heat shock proteins, which are involved with various environmental stressors, including heat stress, ultraviolet radiation, cold tolerance, and biotic stressors (Park and Seo 2015). Variance-controlling loci also arise from epistatic gene action, where the marginal effects of one of the epistatically interacting genes appear as a vQTL (see Forsberg and Carlborg 2017 for a review).

The primary purpose of a variance genome-wide association study (vGWAS) is to detect genetic loci that alter the variance of a phenotype between different genotypes (Al Kawam et al. 2018). While vGWASs have been conducted in plants and crops, its utilization is still not widespread. To date, vGWASs have been conducted for ionomic traits, including molybdenum content in Arabidopsis thaliana and cadmium content in bread wheat (Triticum aestivum) (Shen et al. 2012; Forsberg et al. 2015; Hussain et al. 2020), as well as for oil-related traits in maize (Zea mays L.) (Li et al. 2020). Unlike those used in a standard GWAS (denoted as a mean GWAS or mGWAS), the statistical models used for a vGWAS specifically assume unequal phenotypic variance at each genotypic state of a given locus, i.e., in the presence of variance heterogeneity (Rönnegård and Valdar 2011). Variance-controlling loci are connected to many different ideas within quantitative genetics, including epistatic and GxE interactions (Struchalin et al. 2012; Rönnegård and Valdar 2011). One potentially important advantage of using vGWAS for search for the presence of such interactions is it could prioritize genomic regions likely to harbor epistatic interactions, thereby reducing the severity of multiple testing correction (Struchalin et al. 2012; Pettersson and Carlborg 2015). The markers in these regions could then be directly tested for the presence of epistasis or GxE interactions.

Many statistical analyses have been developed to test for variance heterogeneity. From a biological perspective, the choice of test and model can be divided into whether or not one accounts for population structure, relatedness, and other covariates (Rönnegård and Valdar 2012). Of the statistical tests that do not account for such factors, Levene’s test and its median modification, the Brown–Forsythe test (BFT), have been the most popular (Brown and Forsythe 1974; Rönnegård and Valdar 2012). Although they are useful as a quick diagnostic for identifying variance-controlling loci, they cannot explicitly correct for population structure, familial relatedness, or loci that control the mean of a tested trait (called mQTNs or mQTLs) (Hong et al. 2017). In contrast, models that allow for the inclusion of these factors as covariates theoretically offer higher power to detect variance-controlling loci. In particular, the double generalized linear model (DGLM) (Lee and Nelder 1996) adjusts for potential confounding between vQTLs, mQTLs, and population structure through the inclusion of fixed-effect covariates. Excitingly, more sophisticated versions of the DGLM also include random effects to account for confounding due to familial relatedness (Lee and Nelder 2006; Rönnegård and Valdar 2012).

Although statistical approaches seeking to estimate the effects of variance-controlling loci have opened up many opportunities for discovering new sources of quantitative trait variation, detecting variance-controlling loci still poses challenges. For example, the statistical power needed to detect a variance-controlling locus often requires five times as many individuals compared to the precision needed to detect a mean-controlling locus (Lee and Nelder 2006; Rönnegård and Valdar 2012). This suggests that there is a critical need to systematically study the statistical performance of leading vGWAS approaches. Therefore, the purpose of this study was to explore the factors that influence the ability of the BFT and DGLM to detect vQTLs underlying plant traits. We used publicly available whole-genome resequencing data from the 1001 genomes diversity panel in Arabidopsis thaliana (Alonso-Blanco et al. 2016) and the USDA-ARS North Central Region Plant Introduction Station (NCRPIS) Panel in Zea mays L. (Romay et al. 2013) to simulate traits controlled by epistasis, GxE effects, or variance-controlling loci with various effect sizes. We also analyzed explored the ability of these two approaches to find variance-controlling loci associated with the plant height data from Peiffer et al. (2014) that was measured in the Goodman maize diversity panel (Flint‐Garcia et al. 2005).

Materials and methods

Genotypic data and filtering procedures

We conducted simulation studies using genotypic data from two plant species with contrasting levels of linkage disequilibrium (LD) decay. The first genotypic data set was a subset of 1087 accessions from the Arabidopsis thaliana 1001 genomes diversity panel, available at https://1001genomes.org/ (Alonso-Blanco et al. 2016). The 1001 genomes diversity panel consists of germplasm mostly collected from Eurasia, North America, and Northern Africa. These accessions were genotyped using whole-genome resequencing, which produced 10,707,430 biallelic SNPs (Alonso-Blanco et al. 2016). The second set of genotypic data consisted of 2815 lines from the NCRPIS diversity panel in maize (Romay et al. 2013). This diversity panel was genotyped for 681,257 SNPs, as described in Romay et al. (2013). This genotypic data set is publicly available at cbsusrv04.tc.cornell.edu/users/panzea/download.aspx?filegroupid=6.

Both genotypic data sets were filtered with VCFtools (Danecek et al. 2011) to remove SNPs with more than 10% missing data or minor allele frequency (MAF) below 5%. These data sets were then further filtered with LD pruning utilizing PLINK (Purcell et al. 2007). The LD pruning parameters for Arabidopsis were set to r² = 0.10, a window size of 200 SNPs, and a step size of 20 SNPs. The LD pruning parameters for maize were loosely based on the procedure done in Romay et al. (2013), which were r² = 0.20, a window size of 100 SNPs, and a step size of 25 SNPs. This filtering process described above was conducted independently in both species. The resulting number of SNPs was 41,384 for Arabidopsis and 72,359 for maize.

To assess how sample size affects the performance of the tested statistical methodologies, we considered two different sample size scenarios for each species. The first scenario focused on employing all individuals in both panels (i.e., N = 1087 for Arabidopsis and N = 2815 for maize). In the second scenario, we randomly selected N = 500 individuals from each panel using the sample() function in R (R Core Team 2022).

Simulation of traits controlled by variance- and mean-quantitative trait nucleotides

We developed the approach described below to simulate traits controlled by variance quantitative trait nucleotides (vQTNs) and/or mean QTNs (mQTNs). Each of these simulated traits consisted of a unique configuration of vQTNs, mQTNs, their effect sizes, and narrow-sense heritability. These parameters were used in the following formula derived from Hill and Mulder (2010) to obtain simulated trait values for each individual:

$$P_i=A_{m,i}+{\chi }_{i}k\left({\sigma }_E+A_{v,SDi}\right),$$ 1

where P_i is the simulated phenotypic value of the ith individual, A_m,i is the collective genetic value from all simulated mQTNs for the ith individual, χ_i is a standard normal random variable (i.e., N(μ = 0, σ² = 1)) sampled for the ith individual, k is a constant described two paragraphs below that allows for a certain degree of control over the narrow-sense heritability, σ_E is the population standard deviation determined attributed to non-genetic sources, and A_v,SDi is the collective genetic value of all simulated vQTN for the ith individual. The values of A_m,i and A_v,SDi are respectively calculated as the sum of the observed numeric genotype value at each mean and variance QTN, multiplied by the (respective) mean and variance QTN effects for the ith individual. These simulations are conducted assuming that the covariance between A_m,i and A_v,SDi is zero.

One major challenge for simulating traits controlled by vQTNs is the specification of the desired heritability. Because the value of (σ_E + A_v,SDi) changes for every individual, the value of the heritability will also change for every individual. We, therefore, made ad hoc adjustments to Eq. (1) to ensure at least partial control for a desired narrow-sense heritability (h²). First, the value of σ_E was also set to 1, and then A_m,i was centered and scaled, so its sample mean and standard deviation were respectively 0 and 1. These steps were taken to facilitate the estimation of the k in Eq. (1).

We now describe the derivation of the procedure we used to estimate the value of k. Consider the following modified formula for estimating narrow-sense heritability h² for traits controlled by vQTNs:

$${\widehat{h}}^2=\frac{{\widehat{\sigma }}_A^2}{{\widehat{\sigma }}_A^2+k^2{\left({\widehat{\sigma }}_E+Mdn\left\{A_{v,SDi}\right\}\right)}^2}$$ 2

where ${\widehat{\sigma }}_A^2=\mathrm{Var}\left\{A_{mi}\right\}=1$ because A_m,i was scaled, ${\widehat{\sigma }}_E$ was set equal to σ_E = 1 to facilitate calculations, and Mdn {A_v,SDi} is the median value of A_v,SDi across all n individuals (i.e., all individuals in either the Arabidopsis or maize data sets used for the simulations). Thus, solving Eq. (2) for k yields:

$$k=\sqrt{\frac{\frac{{\widehat{\sigma }}_A^2}{{\widehat{h}}^2}-{\widehat{\sigma }}_A^2}{{\left({\widehat{\sigma }}_E+Mdn\left\{A_{v,SDi}\right\}\right)}^2}}$$ 3

where all terms are as previously described. Thus, for each simulation setting, the value of k from Eq. (3) was used in Eq. (1) to obtain simulated trait values for every individual.

Two R functions were used to simulate these traits. Additive mQTNs, which contribute to A_m,i in Eq. (1), were simulated using the create_phenotypes() function in the simplePHENOTYPES R package (Fernandes and Lipka 2020). We then developed our custom R function that was roughly based on the Python code from Dumitrascu et al. (2019) to obtain the remaining necessary values in Eqs. (1)–(3) to simulate the phenotypic values P_i. To facilitate the deployment of our simulation pipeline to future studies, we made it available through simplePHENOTYPES v1.4 (create_phenotypes(…, model = “V”)) (https://github.com/samuelbfernandes/simplePHENOTYPES).

Description of all settings considered in simulation study

We conducted a comprehensive study that simulates traits controlled by either (1) no QTN, (2) epistasis, (3) GxE, or (4) a combination of vQTN and mQTN (using the approach described in the previous section). Consequently, our simulation studies were subdivided into four respective scenarios summarized in Table 1. Across all scenarios, a total of 64 unique settings (i.e., combinations of input parameters) of traits were simulated. At each setting, a total of 100 replicate traits were simulated.

Table 1.

Parameters considered in the simulation study.

dScenario	nQTN	Species	Heritability	Targeted MAF	Sample size	Allelic effect
Null	0	Maize; Arabidopsis	0.00	N/A	500; Maximum	N/A
Epistasisa	3 epistatic QTNsa	Maize; Arabidopsis	0.30; 0.80	0.10	500; Maximum	0.75 for all 3 QTNs;
GxE	2 mQTNs in 2 environments	Maize; Arabidopsis	0.70	0.30	500; Maximum	Env.1: 0.2b, 0.5c Env.2: 0.8b, 0.5c
vQTN	1 mQTN 1 vQTN	Maize; Arabidopsis	0.63; 0.33	0.10; 0.40	500; Maximum	mQTN: 0.25 vQTN: 0.1; 0.5; 0.9

Across all scenarios, a total of 64 unique configurations of these parameters were simulated.

QTN quantitative trait nucleotides, MAF minor allele frequency, GxE genotype by environment, mQTN mean QTNs, vQTN variance QTNs.

^aEach epistatic effect consists of the additive-by-additive effect of two randomly selected single nucleotide polymorphisms.

^bThis environment-specific mQTN was simulated at the SNP in both environments, but the effect sizes differed in each environment.

^cThis environment-specific mQTN was simulated at different SNPs in each environment.

To enable a rigorous assessment of false positive rates of the tested vGWAS approaches, the “Null” scenario (as depicted on Table 1) consisted of traits with broad-sense heritability (H²) set to H² = 0 and zero QTNs. Consistent with the hypothesis that epistasis is responsible for vQTLs (Forsberg and Carlborg 2017), the “Epistasis” scenario simulated traits controlled by three epistatically interacting pairs of loci. For each pair, the epistatic effect was defined as the effect corresponding to the product of additively-encoded explanatory variables at each locus (i.e,. the additive-by-additive effect, i_aa, defined in Cordell 2002). For each individual, the genetic values from each of the epistatically interacting loci were added up, and the resulting simulated trait value was the sum of these genetic values plus a normally distributed random variable with population mean 0 and population variance determined from the broad-sense heritability of the trait. To enable an assessment of the impact of heritability on the results, we kept the effect sizes of each of these epistatic QTN constant at 0.75, and the targeted MAF of all SNPs selected to be QTNs was 0.10. We then simulated traits at two different broad-sense heritabilities, namely H² = 0.3 and H² = 0.8.

For the “GxE” scenario we used the “partial pleiotropy” setting in simplePHENOTYPES (Fernandes and Lipka 2020) to simulate one trait in two environments that was controlled by two environment-specific mQTNs. The first of these mQTNs was at the same randomly selected marker for each environment, but had contrasting additive effect sizes, specifically 0.2 in the first environment (called Environment A) and 0.8 in the second environment (Environment B). The second of these mQTNs were at different randomly selected markers for each environment, and was assigned an additive effect size of 0.5. All simulated QTNs had MAFs of ~0.3. The narrow-sense heritabilities of both traits were set at h² = 0.7. Upon completion of simulating this trait in two environments, each individual had two trait values: one from Environment A (Y_A), and one from Environment B (Y_B). However, a single phenotypic value was needed for each individual for downstream analyses. Thus, for each individual we used the difference between trait values Y_A−Y_B as the response variable in the subsequent statistical analysis.

Finally, we used the findings from previously published vGWAS and vQTL studies conducted in Arabidopsis and maize (Shen et al. 2012; Li et al., 2020; Forsberg et al. 2015) as a basis for the “vQTN” scenario. Collectively, the various parameters we explored in this scenario (summarized in Table 1) enabled us to study the impact of narrow-sense heritability, MAF of vQTNs, and the effect sizes of vQTNs on the performance of the various GWAS approaches we explored. Detailed information about the actual SNPs that were randomly selected to be QTNs across all settings are presented in Supplementary File 1.

Competing GWAS models and tests

We considered two different statistical approaches used in previous plant publications to conduct vGWAS, namely the BFT and the DGLM (Shen et al. 2012; Forsberg et al. 2015; Hussain et al. 2020; Li et al. 2020). In general, the BFT is used in vGWAS to test for variance homogeneity (Brown and Forsythe 1974; Shen et al. 2012). For each locus, the BFT evaluates: H₀: Population variances of traits are equal at all genotypes vs. H_a: Population variances of traits are different for at least one genotype, and uses the corresponding test statistic:

$$F=\frac{\left(N-m\right){\sum }_{j=1}^m{n}_j{\left(y_{.j}^{*}-y_{..}^{*}\right)}^2}{\left(m-1\right){\sum }_{j=1}^m{\sum }_{i=1}^{n_j}{\left(y_{ij}^{*}-y_{.j}^{*}\right)}^2}$$ 4

where N is the total number of accessions, n_j is the number of accessions in the jth genotypic group, m is the number of genotypes at the tested genetic marker, and:

$$y_{ij}^{*}=∣y_{ij}-{\tilde{y}}_j∣$$ 5

In (5), y_ij is the phenotypic value for the ith individual with the jth genotype and ${\tilde{y}}_j$ is the median phenotypic value of individuals with genotype j. Under H₀, the BFT statistic in (4) follows an F distribution with degrees of freedom equal to m − 1, N − m (Shen et al. 2012). The BFT was performed using the brown.forsythe.test() function from the vGWAS R package (Shen et al. 2012). Because the BFT does not allow explicit inclusion of covariates to account for false positives arising from population structure and familial relatedness, it often serves as a quick diagnostic test to see if the trait of interest has any underlying vQTLs. Furthermore, the BFT is robust to phenotypic departures from normality (Dumitrascu et al. 2019; Hussain et al. 2020).

The DGLM belongs to a family of generalized linear models, which relaxes the assumption of normality of phenotypic residuals for more flexible modeling. Specifically, the DGLM consists of two linear predictors that model the relationship between a response variable and (1) explanatory variables controlling its population mean (Eq. (6)), and (2) explanatory variables controlling its population variance (Eq. (7)). The component of the DGLM controlling the population mean is written as follows:

$$Y_{\mathit{i}}={\mu }_m+\sum _{k=1}^q{X}_{ik}{\beta }_k+s_{ij}{a}_{m_j}+{\epsilon }_i$$ 6

where Y_i is the observed phenotypic value of the ith individual, μ_m is the intercept; X_ik the value of the kth principal component from a principal component analysis (PCA) of the markers (Price et al. 2006) observed in the ith individual (the first q = 4 and q = 3 principal components were included in the models used in Arabidopsis and maize, respectively); β_k is the regression coefficient for the kth principal component; s_ij is the value of the jth SNP encoded as 0, 1, 2 for the ith individual; a_mj is the additive effect size of the jth SNP; and ${\epsilon }_i~N\left(0,{\sigma }_{{\epsilon }_i}^2\right)$. In the “vQTN” scenario presented in Table 1, s_j was set equal to the mQTN and a_mj was its effect size; in all other settings, these two terms were omitted from the model because no mQTNs were simulated. The component of the DGLM controlling the population variance of the ith individual ${\sigma }_{{\epsilon }_i}^2$ is written as follows:

$$\log \left({\sigma }_{{\epsilon }_i}^2\right)={\mu }_v+s_{ij}{a}_{v_j}$$ 7

where ${\sigma }_{{\epsilon }_i}^2$ is the residual variance for the ith individual; μ_v is the intercept; s_ij is the value of the observed SNP value encoded 0, 1 and 2 at the jth marker for the ith individual; and a_vj is the effect size of the jth marker.

To test for a significant association between the jth marker and the variance of the tested trait, we used the Wald test (Agresti 2003) to test H₀: a_vj = 0 vs. H_a: a_vj ≠ 0, which follows an asymptotic ${\chi }_1^2$ distribution under H₀. Thus, under H₀, the mean component of the DGLM remains as presented in Eq. (6), while the component presented in Eq. (7) is reduced to:

$$\log \left({\sigma }_{{\epsilon }_i}^2\right)={\mu }_v$$ 8

where all terms are as previously described.

As described in Corty and Valdar (2018), the DGLM framework is flexible in that it allows one to test for either the presence of a vQTN (i.e., test for H₀: a_vj = 0, where a_vj is described in Eq. (7)), presence of an mQTN (i.e., test for H₀: a_mj = 0, where a_mj is described in Eq. (6)), or for the presence of both (i.e., test for H₀: a_vj = 0 and a_mj = 0) at the jth marker. For the sake of a direct comparison between the ability of the DGLM and the BFT to identify vQTNs, we assume that the user has already ran an a priori GWAS scan and that any peak-associated mQTNs were fitted into the mean component of the DGLM, as presented in Eq. (6). Thus, the multiple testing correction, described in detail in the next section, was applied equally to both the BFT and the DGLM. Because our analysis of DGLM is only testing for the presence of vQTNs, the stringency of multiple testing will not be as severe as prior applications of the DGLM (e.g., Corty and Valdar 2018) that tested for the presence of either vQTNs, mQTNs, or both. To perform DGLM, we used the R code from Hussain et al. (2020), which came from the dglm R package (Dunn et al. 2020). The PCAs for population structure were obtained using GAPIT version 4.0 (Lipka et al. 2012).

As a counterpoint to both the BFT and DGLM, we also conducted a GWAS at each replicate using a standard GWAS model. Specifically, we used GAPIT version 4.0 (Lipka et al. 2012) to fit the unified mixed linear model (MLM; Yu et al. 2006) at each SNP and at each replicate trait considered in this study. Within each species, the same PCs that have been previously described were included in the model to account for subpopulation structure, and the method of VanRaden (2008) was used in the filtered marker sets in each species to obtain additive genetic relatedness (i.e., kinship) matrices to account for familial relatedness.

The ensuing analyses using both of these statistical approaches were conducted on a Dell Precision Tower 3240 with 64.0 GB RAM. While the BFT was ran on a single core, DGLM was ran on four cores using the foreach R package.

QTN detection rates for competing models

To assess whether or not the vGWAS methodologies can correctly identify markers as associated with our simulated traits, we evaluated the true and false positive QTN detection rates using the Benjamini and Hochberg (1995) procedure to control the false discovery rate (FDR) at 5%. A statistically significant SNP was labeled as a true positive if it was within a 250 kb window of a simulated vQTN for maize and within 100 kb window of a simulated vQTN in Arabidopsis. Likewise, a statistically significant SNP was labeled as a false positive if it was outside of these windows. We defined the true positive rate as the proportion of times we detected at least one true positive per replication out of 100 replications. Similarly, the false positive rate is defined as the proportion of times we detected at least one false positive per replication out of 100 replications. True and false positive detection rates were further scrutinized by calculating 95% confidence intervals using the method of the Clopper and Pearson (1934) in the PropCIs R package (Scherer and Scherer 2018). For each setting, all SNPs selected to be vQTNs were removed prior to calculating the true and false positive detection rates.

We also developed an approach similar to one presented in Gage et al. (2018) that used receiver operating characteristic (ROC) curves (Metz 1978) to evaluate the ability of the three GWAS approaches to differentiate between true and false positives. For all settings except for those under the “Null” scenario, we randomly selected ten replicate traits. For each replicate trait, we used the genome-wide p values from each of the three GWAS approaches to obtain corresponding ROC curves, where cases were considered to be all SNPs within the aforementioned physical windows of each QTN, and the remaining SNPs outside of these windows were considered to be controls. Thus, for a given replicate trait, a separate ROC curve was obtained for each of the three GWAS approaches. For each resulting ROC curve, we calculated the area under the ROC curve (AUC); values of AUC greater than 0.5 suggest that the corresponding statistical model is capable of discriminating between cases and controls. Finally, for each GWAS approach used in each setting, we reported the median AUC value across the ten replicates.

Analysis of plant height data in a maize diversity panel

We performed a vGWAS using both the BFT and DGLM on plant height best linear unbiased predictors from Peiffer et al. (2014). Briefly, this trait was measured on 279 individuals from the Goodman maize diversity panel (Flint‐Garcia et al. 2005) grown in ten different locations. To implicitly control for population structure and familial relatedness, we performed a two-step approach as described in previous vGWAS publications (Shen et al. 2012; Forsberg et al. 2015; Li et al. 2020; Zhang and Qi 2021). This approach first runs the unified MLM (Yu et al. 2006) with PCs (for this analysis, we used the first five PCs) and the VanRaden (2008) kinship matrix in TASSEL 5.0 (Bradbury et al. 2007) for the first step. The resulting residuals from this step were used as the response variable in our ensuing analyses. The genotypic data for this analysis consisted of a subset of 48,880 SNPs from the Illumina SNP50 chip (Cook et al. 2012). For both the BFT and DGLM, we used the Benjamini and Hochberg (1995) to control for the genome-wide false discovery rate at 5%. To visualize the loci identified for the BFT, DGLM, and MLM, circular Manhattan plot was created using the Cmplots R package (Yin 2018).

Results

False positive detection rates in the “Null” setting suggest BFT and DGLM adequately control for false positives

We ran the “Null” scenario to verify that the observed false positive rates for the BFT and DGLM were similar to what we would expect based on statistical theory (Fig. 1). We also calculated 95% confidence intervals for these false positive rates using the method described by Clopper and Pearson (1934). All of these CIs contained the targeted FDR of 0.05.

Fig. 1. False positive detection rates for the null setting at a false discovery rate of 0.05.

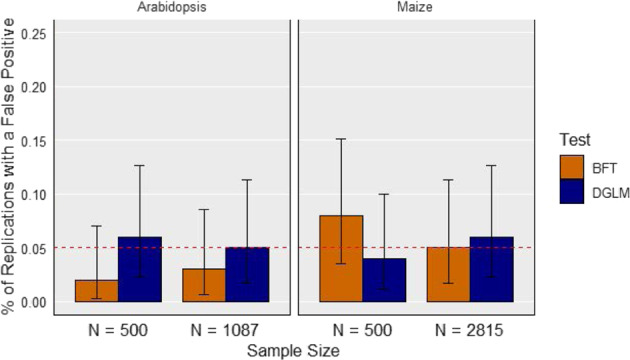
The X-axis represents the sample size of each diversity panel. The Y-axis is the proportion of replications where a false positive is detected at least once. The error bars depict 95% confidence intervals, calculated using the method from Clopper and Pearson (1934). The dotted red horizontal line depicts the targeted false discovery rate of 0.05. Each panel represents the species indicated in the title. BFT Brown–Forsythe test, DGLM double generalized linear model.

High true positive detection rates were obtained for highly heritable epistatic QTNs, especially at larger sample sizes

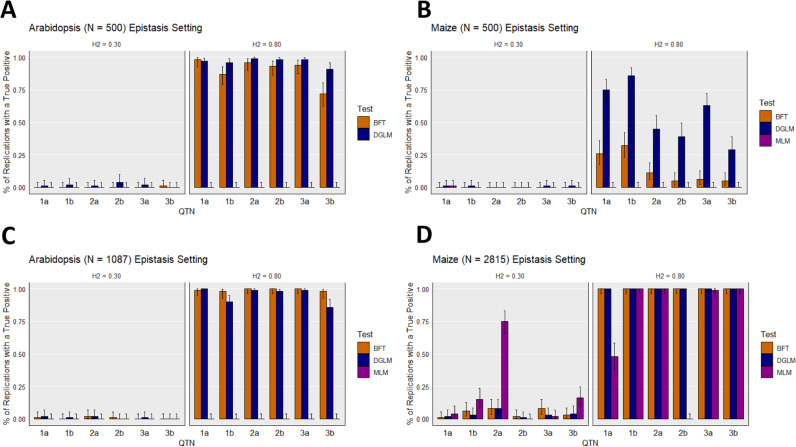
When the heritability of the simulated epistatic QTNs were high (H² = 0.80), both the BFT and DGLM tended to detect SNP pairs contributing to epistatic QTNs for all combinations of species and sample sizes, although these true positive detection rates notably lower for maize at N = 500 (Fig. 2). In contrast, both vGWAS approaches yielded extremely low detection rates of the pairs of SNPs contributing to the epistatic QTNs when the broad-sense heritability of the epistatic QTNs was low (H² = 0.30). In general, both vGWAS approaches tended to detect the epistatic QTNs at similar rates in Arabidopsis, while the DGLM tended to yield either similar (at N = 2815) or higher (at N = 500) true positive detection rates than the BFT in maize. The epistatic QTNs were identified by the MLM at relatively consistent high rates only when they were simulated in maize with sample size N = 2815 and heritability of H² = 0.8. The results from the analysis of the ROC curves and corresponding median AUC values (Supplementary Table 1) support the findings presented in Fig. 2. Thus, these results suggest that the two tested vGWAS approaches are capable of detecting pairwise epistasis, but these epistatic signals need to be highly heritable.

Fig. 2. True positive detection rates under the “Epistasis” scenario.

True positive detection rates for the simulated traits under the “Epistasis” scenario settings at a false discovery rate of 0.05 for A Arabidopsis at a sample size of N = 500, B maize at a sample size of N = 500, C Arabidopsis at a sample size of N = 1087, and D maize at a sample size of N = 2815. In each panel, two sets results are presented: one for the simulated trait with broad-sense heritability of set to H² = 0.30, and one for those with H² = 0.80. On each figure, the X-axis represents the pair of SNPs contributing to the three epistatic quantitative trait nucleotides (QTNs; e.g., “2a” denote the first SNP contributing to the second epistatic QTN). The Y-axis is the proportion of replications where a true positive is detected at least once. The error bars depict 95% confidence intervals, calculated using the method from Clopper and Pearson (1934). BFT Brown–Forsythe test, DGLM double generalized linear model, MLM unified mixed linear model.

vGWAS approaches yielded high true positive detection rates of GxE signals only at the largest evaluated sample size

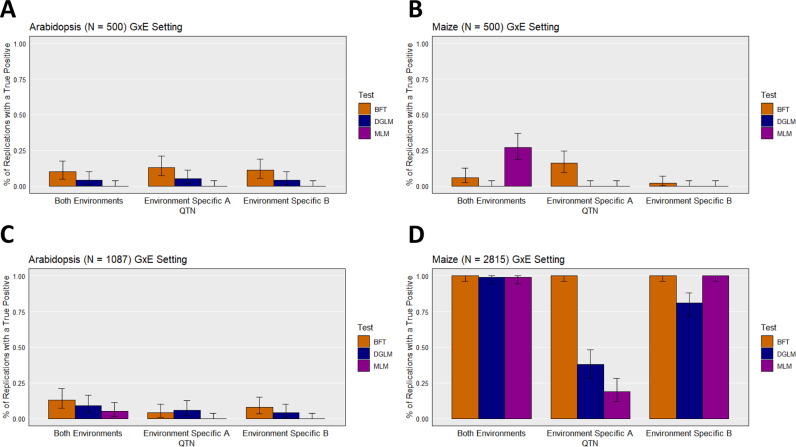
The BFT and DGLM could detect true positive signals from simulated GxE effects at non-negligible rates at only the largest sample size we evaluated, namely at N = 2815 in maize (Fig. 3). At this sample size, both of these approaches yielded similar true positive detection rates at the QTN that was simulated at the same genomic position, but with different effect sizes, in both environments. However, at the two environment-specific QTNs, the BFT yielded higher true positive detection rates than the DGLM (Fig. 3D). At this sample size in maize, we also observed that the BFT detected the QTNs at rates either greater than or similar to those from the MLM. The results from the ROC curves and corresponding median AUC values were consistent with the true positive rates presented in Fig. 3, especially with respect to noticeably higher median AUC values in maize at N = 2815 (Supplementary Table 1). Collectively, these results suggest that the BFT and DGLM are capable of identifying a GxE signal at reasonably high detection rates, but a large sample size (at least N = 2815) is needed.

Fig. 3. True positive detection rates under the “GxE” scenario.

True positive detection rates for the simulated traits under the “GxE” scenario settings at a false discovery rate of 0.05 for A Arabidopsis at a sample size of N = 500, B maize at a sample size of N = 500, C Arabidopsis at a sample size of N = 1087, and D maize at a sample size of N = 2815. On each figure, the X-axis represents the QTN, and a description of the which environment(s) in which they were simulated are detailed in the corresponding X-coordinate label. The Y-axis is the proportion of replications where a true positive is detected at least once. The error bars depict 95% confidence intervals, calculated using the method from Clopper and Pearson (1934). BFT Brown–Forsythe test, DGLM double generalized linear model, MLM unified mixed linear model.

DGLM was capable of identifying vQTNs at smaller sample sizes of N = 500

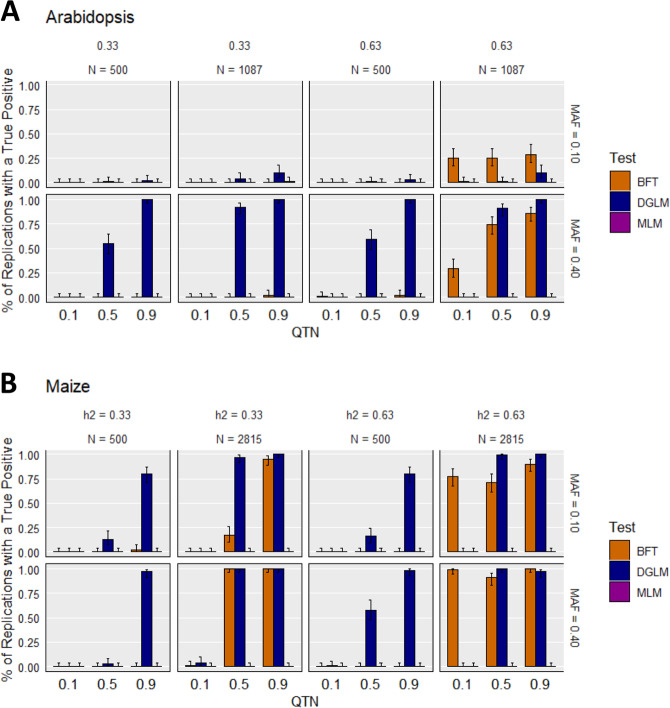
Across both of the evaluated species and narrow-sense heritabilities, we observed that the true positive detection rates of the DGLM tended to monotonically increase with the effect sizes of vQTNs, particularly for those with MAFs of ~0.4 (Fig. 4). This trend was observed for such vQTNs across all of the evaluated sample sizes. In contrast, the BFT consistently yielded low true positive QTN detection rates at N = 500. Although not as pronounced as the DGLM, we also observed that the true positive detection rates of the BFT tended to monotonically increase with vQTN effect sizes at certain settings. While approximately similar trends in true positive detection rates were observed in maize across the two vQTN MAF settings, notably lower true positive detection rates were observed for both vGWAS approaches in Arabidopsis for vQTNs with MAFs of ~0.1. We also observed that the DGLM results were more consistent across the two evaluated narrow-sense heritabilities than the BFT. As expected, the simulated vQTLs were not detected by the MLM, which makes sense considering the MLM assumes that the variances between genotypic groups are equal. Similar trends were noted in the analysis of the ROC curves (Supplementary File 1 and Supplementary Table 1), in particular with median AUCs for the BFT and DGLM tending to monotonically increase with sample size, MAF, and vQTN effect size. Overall, these results suggest that the DGLM is capable of outperforming the BFT at sample sizes of N = 500.

Fig. 4. True positive detection rates under the “vQTN” scenario.

True positive detection rates for the simulated traits under the “vQTN” scenario settings at a false discovery rate of 0.05 for A Arabidopsis and B maize. On each panel, the results are subdivided into heritability (h²), sample size (N), and targeted minor allele frequency of the QTN (MAF). On each figure, the X-axis depicts the effect size of the vQTN, and Y-axis is the proportion of replications where a true positive is detected at least once. The error bars depict 95% confidence intervals, calculated using the method from Clopper and Pearson (1934). BFT Brown–Forsythe test, DGLM double generalized linear model, MLM unified mixed linear model.

BFT and DGLM identified significantly associated markers for plant height

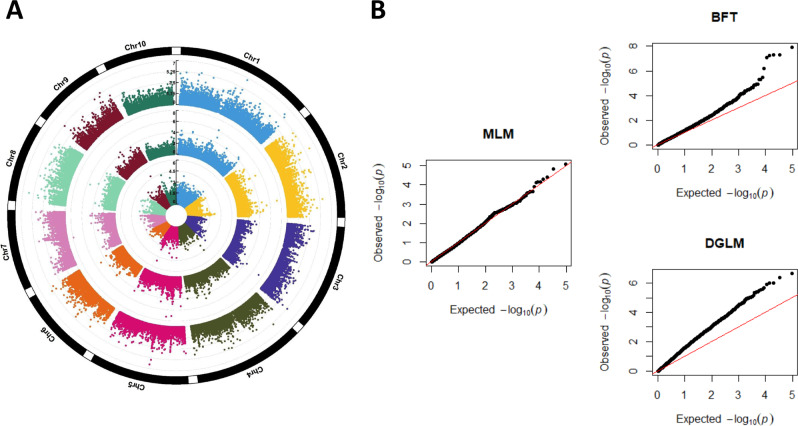
The BFT and DGLM both identified statistically significant associations for plant height in the Goodman diversity panel at a genome-wide FDR of 5% (Fig. 5A), while no statistically significant associations were found using the unified MLM. Interestingly, three statistically significant associations located on chromosomes 1, 2, and 8 were identified by both the BFT and DGLM (Fig. 5A). The quantile-quantile plots presented Fig. 5B suggest that the –log(p values) from the DGLM are more inflated than those from the BFT and MLM.

Fig. 5. Genome-wide association study (GWAS) of plant height in the Goodman maize diversity panel.

A Circular Manhattan plots summarizing the results from the unified mixed linear model (innermost circle), the Brown–Forsythe test (middle circle), and the double generalized linear model (outermost circle). The X-axis is the physical position of the SNPs along the maize genome, and the Y-axis is the −log(p values) from each of the three GWAS models. B Quantile-quantile (Q-Q) plots showing the expected −log(p values) under H₀: No association at tested marker on the X-axis and the observed −log(p values) on the Y-axis. MLM unified mixed linear model (middle column), BFT Brown–Forsythe test (top-right column), DGLM double generalized linear model (bottom-right column).

Discussion

We used both simulated and real traits to evaluate the ability of two vGWAS approaches, namely the BFT and the DGLM, to identify epistasis, GxE, and variance-controlling loci. At the maximum sample size evaluated (N = 2815), both vGWAS approaches frequently identified highly heritable epistatic and GxE signals. For simulated traits that were controlled by vQTNs, we observed that the DGLM yielded substantially higher true positive detection rates than the BFT at sample sizes of N = 500. Collectively, these results provide a potential benchmark for how the BFT and DGLM are expected to perform when deployed to vGWAS in plants. Such an assessment is essential because the more widespread use of vGWAS in plants could substantially facilitate breeding for uniformity of trait values across various environmental conditions.

Prospects on the ability of BFT and DGLM to assist in identifying epistasis and GxE

Because of strong evidence in the literature that both epistasis and GxE could underlie the statistical associations identified in vGWAS (Struchalin et al. 2012; Rönnegård and Valdar 2011), two of our simulation scenarios explicitly simulated these two sources of genomic variability. The results from these two scenarios suggest that the DGLM and BFT are capable of finding highly heritable epistatic and GxE signals at the largest evaluated sample size (N = 2815 in maize). An even more exciting result was that for the highly heritable epistatic QTNs at sample sizes of N = 500, both the vGWAS approaches yielded high detection rates in Arabidopsis, while the DGLM yielded modestly high true positive detection rates in maize.

The fact that we were able to identify these epistatic and GxE loci suggest that vGWAS approaches could assist in the detection of epistasis or GxE effects underlying agronomically important traits. As described in Struchalin et al. (2012), the large number of possible interacting loci to be tested when searching for epistasis or GxE results in a heavy multiple testing correction burden. To overcome this, a preliminary vGWAS scan could be conducted to highlight specific genomic markers likely to harbor these sources of genomic variability. Given our results, we expect vGWAS approaches to be successful in identifying highly heritable epistatic and GxE effects for sample sizes of at least N = 2815. If such loci were to be detected using vGWAS studies, they can then be directly tested for epistasis and/or GxE effects in a follow-up analysis, where the multiple testing correction would be substantially reduced because only the markers identified using vGWAS are analyzed.

Prospects on the ability of the BFT and DGLM to identify vQTN

One consistent result we observed in both species was that the DGLM yielded higher true positive detection rates than the BFT at sample sizes of N = 500 and MAF = 0.4. This suggests that a sample size of 500 could be sufficient for the DGLM to identify non-rare variance-controlling loci. In addition to varying the sample size and species in the “vQTN” scenario, we also evaluated the performance of these two vGWAS approaches across two targeted vQTN MAFs, effect size, and narrow-sense heritabilities. Not surprisingly, we observed that the true positive vQTN detection rates of both models tended to increase monotonically with their simulated effect sizes. We also noted that higher true positive detection rates tended to be observed for vQTNs with the higher targeted MAF = 0.4, which again was consistent with our expectations prior to conducting this study. However, higher than expected true positive detections were observed in maize for vQTNs with targeted MAF = 0.10. Taken together with the less favorable true positive detection rates in Arabidopsis for vQTNs with targeted MAF = 0.10, these results suggest that vGWAS could be used to identify genomic regions likely to harbor rare vQTNs under certain circumstances. Therefore, we recommend that future studies investigate the impact of LD decay and marker technologies on the ability to identify rare vQTNs. Although there were certain settings at h² = 0.63 where the BFT outperformed the DGLM, the latter approach yielded more stable true positive detection rates across the two evaluated narrow-sense heritabilities. This result suggests that the DGLM is more robust than the BFT for controlling the influence of the simulated mQTN on the overall simulated trait variance, and further underscores our recommendation of the DGLM as the preferred vGWAS approach.

Limitations of our simulation studies

Although useful for simulating traits with similar genetic architectures of real traits, the approach we implemented to account for the narrow-sense heritability in the “vQTN” scenario was ad hoc. We recommend that future studies focus on accounting for broad-sense heritabilities, as this would enable more user-control over the total phenotypic variance attributable to genetic effects. Another limitation of our study is that we explored only one configuration of modeling the relationship between vQTNs and a trait. Specifically, the configuration we used in (1) is based on the standard deviation additive model (Hill and Zhang 2004; Hill and Mulder 2010). Other vQTN quantitative genetics models, such as reaction norm model from Hill and Mulder (2010) or the other forms of epistasis discussed in Cordell (2002), could be used to simulate more scenarios where vQTNs could arise.

Areas for future research

While the BFT and DGLM are two commonly used statistical methodologies for vGWAS, the results from our analysis of plant height in maize suggest that they may not adequately control for population structure and familial relatedness (Fig. 5B). Thus, we recommend the consideration of more sophisticated statistical approaches for vGWAS. Two examples are the hierarchical generalized linear model (HGLM) (Lee and Nelder 1996) and double hierarchical generalized linear model (DHGLM) (Lee and Nelder 2006). These models account for familial relatedness by including the individuals as a random effect and setting their variance-covariance to be proportional to an additive genetic relatedness matrix. Although the associated computational complexity of fitting these two models rendered them impractical to evaluate in our simulation studies, they have been previously evaluated in wheat (Hussain et al. 2020) and animal breeding (Rönnegård et al. 2010). Given that the DGLM and HGLM in Hussain et al. (2020) both identified the same loci associated with cadmium content in wheat, we would expect that the HGLM and DHGLM to yield similar true positive detection rates for traits that are not associated with familial relatedness. We recommend that future work focuses on increasing the computational efficiency of the HGLM and DHGLM so that their ability to identify vQTNs could be studied in a manner similar to that which is presented in this work.

One noteworthy aspect of several prior vGWAS investigations is that the search for variance-controlling loci was conducted separately from a mean GWAS scan (e.g. Hussein et al. 2020; Li et al. 2020; Córdova-Palomera et al. 2021). However, Corty and Valdar (2018) demonstrated that models like the DGLM can be used in a single GWAS to test for associations with the mean of a trait, the variance of a trait, or both. Although this results in a 2x- to 3x- increase in the severity of the multiple testing burden (Corty and Valdar 2018), the use of models like the DGLM to search for both mean and/or variance-controlling loci in a single GWAS scan is advantageous because it reduces the possibility of, for example, not identifying a mean-controlling locus because only a vGWAS scan was conducted. We therefore encourage future vGWAS studies to use models like the DGLM to their fullest extent by testing for mean-controlling loci in addition to variance-controlling loci.

The inbreeding species considered in our simulation studies, Arabidopsis, has not been subjected to as much artificial selection compared to what would be expected in crops (Izawa 2007; Woodward and Bartel 2018). Thus, future simulations should consider an inbreeding crop species such as sorghum (Sorghum bicolor L. Moench) or rice (Oryza sativa L). Additionally, our decision to simulate traits similar to those where vQTN have already been identified resulted in our simulated traits resembling metabolic traits with tractable genetic architectures. However, a recent report in maize showed that vQTNs are also present in plant architectural and phenology traits (Zhang and Qi 2021). Thus, the practicality and utility of the BFT and DGLM to identify variance-controlling loci in crops could be more comprehensively explored if a wider range of genetic architectures were studied in future work. In any case, peak-associated markers from a vGWAS could be used for breeding applications. For example, if one wants to constrain the range of possible trait values in a challenging environment, they could potentially select on alleles from peak-associated markers in a vGWAS that reduces the variance of that trait. Finally, recent advances in genome-wide association study (GWAS) approaches, such as that described in Li et al. (2022), can detect and directly quantify the effects of QTN-by-environment and QTN-by-QTN interactions. This may provide another new approach for identifying variance-controlling loci in GWAS.

Conclusion

The ability of vGWAS approaches to identify variance-controlling loci needs to be thoroughly scrutinized before they can become more commonplace in quantitative genetics analysis in plants. We conclude that DGLM is preferred over the BFT for practical use in plant vGWAS because of its observed performance at sample sizes of N = 500. The ability of both vGWAS approaches to identify epistasis and GxE is encouraging, and future simulation studies should focus on other quantitative genetics parameters and additional statistical models in more plant species. To facilitate such future exploration of vGWAS approaches, the computational approaches we used to simulate traits controlled by vQTN are now publicly available free of charge in the simplePHENOTYPES R package (Fernandes and Lipka 2020).

Author contributions

MDM conducted all simulations and analyses, wrote the computer program that will simulate vQTNs, created all figures and tables, and wrote and edited the manuscript. SBF contributed to the design of the simulation settings, made edits to the computer program to make it more computationally efficient, and edited the manuscript. GM contributed to various aspects of the statistical analysis, including how to use the DGLM in a meaningful manner, as well as how to interpret the results of the simulation study. These contributions significantly guided the direction of our study. AEL oversaw the entire analysis, designed the simulation study, designed the procedure for simulating vQTNs, and wrote and edited the manuscript.

Data availability

The genotypic data, simulated trait data, ROC curves, and code to simulate traits are available at https://github.com/mdm10-code/vGWAS_arabidopsis_maize.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41437-022-00541-1.