Abstract
In vivo human diffusion MRI is by default performed using single-shot EPI with greater than 50-ms echo times and associated signal loss from transverse relaxation. The individual benefits of the current trends of increasing B0 to boost SNR and employing more advanced signal preparation schemes to improve the specificity for selected microstructural properties eventually may be cancelled by increased relaxation rates at high B0 and echo times with advanced encoding. Here, initial attempts to translate state-of-the-art diffusion-relaxation correlation methods from 3 T to 21.1 T are made to identify hurdles that need to be overcome to fulfill the promises of both high SNR and readily interpretable microstructural information.
Keywords: Multidimensional diffusion encoding, Diffusion-relaxation correlation, Ultra-high field, 21.1 T, Nonparametric 5D D-R2, In vivo
1. Introduction
NMR diffusion-relaxation correlation methods [1–3] combined with data inversion into nonparametric distributions [4,5] of these MR properties have been applied successfully in low field studies of heterogeneity in materials ranging from porous rocks [6] to dairy products [7] and fruits [8] for decades. The methods more recently have been combined with MRI [9] and demonstrated to have great potential for both ex vivo [10–13] and in vivo [14] clinical applications as summarized in several comprehensive reviews during just the last few years [14–17]. In addition, data challenges aimed to explore sub-sampling strategies has been performed aimed to harness the richness of information in multidimensional data with in feasible clinical scan times [18].
While most previous diffusion-relaxation studies have relied on the simple Stejskal-Tanner sequence [19] for which the effects of multiple aspects of molecular motion including bulk diffusivity, restriction, anisotropy, flow and exchange [20] are merged into apparent diffusion coefficients (ADCs) [21], a few studies [22–26] have incorporated more elaborate encoding strategies deriving from multidimensional solid-state NMR [27] to enable separation and correlation of parameters specific to the various types of motion. These multidimensional diffusion encoding methods build on carefully crafted gradient waveforms to attain selectivity at the expense of requiring higher gradients amplitudes or—when the maximum amplitudes are already reached—longer waveform durations than in conventional diffusion tensor imaging [28,29]. The resulting loss in signal-to-noise ratio (SNR) from transverse relaxation is in practice often compensated by using larger voxel sizes but could in principle be mitigated by ultra-high B0 [30], the general benefits of which has been demonstrated for MRI and MR spectroscopy (MRS) in several papers [31–39].
So far, in vivo preclinical and human studies employing multidimensional or oscillating gradient diffusion encoding have been performed at 3 T [22–24,26,40–62], 4.7 T [63–65], 7 T [57,66–69], 9.4 T [70] and 11.7 T [71–73] while diffusion-relaxation correlation has been limited to 3 T [14,22–24,26]. All of these studies have relied on echo planar imaging (EPI) signal read-out, which allows for acquisition of a complete 2D image plane after a single excitation, but suffers from B0-dependent image distortions due to susceptibility inhomogeneity [31,74] and low SNR for materials with high transverse relaxation rate R2. As ultra-high B0 systems are being developed also for in vivo human studies [30,75,76], we performed pilot measurements with multidimension diffusion-relaxation correlation and EPI readout at the highest field available for in vivo rodent, 21.1 T [77,78] to investigate the feasibility of translating pulse sequences from moderate to ultra-high B0 and identify technical issues that need to be addressed to realize the full potential of combining diffusion-relaxation correlation, multidimensional diffusion encoding and ultra-high B0. Anticipating that transverse relaxation will be one of the main obstacles, we performed measurements yielding nonparametric joint distributions of R2 and diffusion tensors D [22,23].
2. Methods
2.1. MRI equipment
Experiments were performed using the 21.1-T magnet at the National High Magnetic Field Laboratory (NHMFL) in Tallahassee, FL [77,78]. The magnet was designed and built at the NHMFL, and is equipped with a Bruker Avance III console (Bruker-Biospin, MA, USA) using imaging gradients (Resonance Research Inc., MA, USA) capable of producing a gradient strength up to 600 mT/m. An in-house designed and built radio-frequency (RF) coil was used for all in vitro and in vivo experiments. The RF coil used was a double-saddle quadrature surface coil tuned to 900 MHz, the resonance frequency of 1H at 21.1 T. The coil was built to accommodate the head of in vivo rodents weighing up to 350 g [34].
2.2. Phantoms
To validate the implementation of the multidimensional sequence on the 21.1-T magnet and for parameter optimization, a “Hex” liquid crystal phantom that provided high anisotropy was created as described by Nilsson et al [79]. In short, the phantom was placed in a 15-mL conical tube consisting of 41.94 wt% water (Milli-Q quality), 13.94 wt% of the hydrocarbon 2,2,4-trimethylpentane (Sigma-Aldrich, Sweden), and 44.12 wt% of the detergent sodium 1,4-bis(2-ethylhexoxy)-1,4-dioxobutane-2-sulfo nate (trade name AOT from Sigma-Aldrich, Sweden). At room temperature, the liquid crystal is in a reverse 2D hexagonal phase wherein water diffuses along cylindrical channels with ~ 5-nm diameters, which span lengths of hundreds of micrometers and gives rise to highly anisotropic diffusion. Around the 15-mL “Hex” phantom, two NMR tubes with 1-octanol (MilliporeSigma, MA, USA) and n-dodecane (TCI America, OR, USA) were placed. The combined tubes were secured and placed in a 50-mL conical tube filled with water. The phantom was secured into the RF coil and placed in the magnet.
2.3. Animals
Two Sprague Dawley rats weighing between 200 and 250 g were used. The animals were housed in cages with a 12-hour night/12-hour daylight cycle, with water and food available ad libitum. The animals were anesthetized with isoflurane (Baxter, IL, USA) and placed prone inside the coil with fore teeth placed on a bite bar. This bite bar also supplied a continuous flow of oxygen mixed with 1–3% of isoflurane. The concentration of isoflurane was set to maintain a steady respiration rate of 25–30 breaths per minute as monitored by a respiratory pillow (SA Instruments Inc., NY, USA) that was placed in between the rat and probe. Temperature was maintained at 37 °C by means of gradient chiller. The coil was tuned and matched for each individual rat for optimal performance. The same acquisition parameters used for the phantom were acquired for animals with the field-of-view (FOV) set to cover the head of the rat (32 × 11 mm). After confirming accurate placement of the rat, shimming was performed using either Bruker’s automatic B0 shimming sequence or if needed adjusted by localized voxel placed over the parenchyma. All animal procedures were approved by the Florida State University (FSU) Animal Care and Use committee (ACUC).
2.4. MRI measurements
A ParaVision 6.0.1 implementation of a multi-slice 2D spin-echo EPI sequence with pairs of free gradient waveforms bracketing the 180° pulse [80] was kindly provided by Matthew Budde at the Medical College of Wisconsin (https://osf.io/ngu4a). The diffusion encoding tensor b is obtained from the effective gradient g(t) via:
| (1) |
and
| (2) |
where the integration is performed from the center of the excitation 90° pulse to the echo time τE. The sensitivity of the signal to anisotropy is controlled by the “shape” of b, which is conveniently expressed by the normalized anisotropy bΔ given by [81]:
| (3) |
where b is the trace of b and bXX, bYY, and bZZ are the eigenvalues ordered according to (bZZ – b/3) > (bXX – b/3) > (bYY – b/3). Four 10-ms waveforms of the diffusion encoding gradients were used: linear (bΔ = 1), planar (bΔ = −1/2) and spherical (bΔ = 0) as calculated in Ref. [82], as well as linear (bΔ = 1) with a 5-ms half-sine pulse on each side of the 180° pulse. Gradient orientations (Θ, Φ) were obtained by the electrostatic repulsion scheme [83], and the number of directions were varied pseudo-randomly between 11 and 15 for the different values of τE within the range from 14.1 to 60 ms with an approximate logarithmic distribution. A detailed overview of the acquisition scheme can be found in in Fig. 1. Here gradient amplitude was varied between 10, 25, 45 and 80% (depending on diffusion scan) of peak gradient strength (0.6 T/m) The lowest and highest b-values were chosen to suppress spins undergoing flow, to achieve some attenuation of water spins with the lowest diffusivity, and were distributed logarithmically to improve sampling of the exponential signal decay [26,84]. Data was collected using nine slices of 1-mm thickness and FOV to cover the sample. Matrix was 140 × 48 (0.2 × 0.2 mm in-plane resolution) with a bandwidth of 500 kHz, two dummy scans and partial-FT encoding scheme (1.33 coverage). The repetition time (τR) was set to 5 s throughout, and the resultant total acquisition time was 120 min.
Fig. 1.
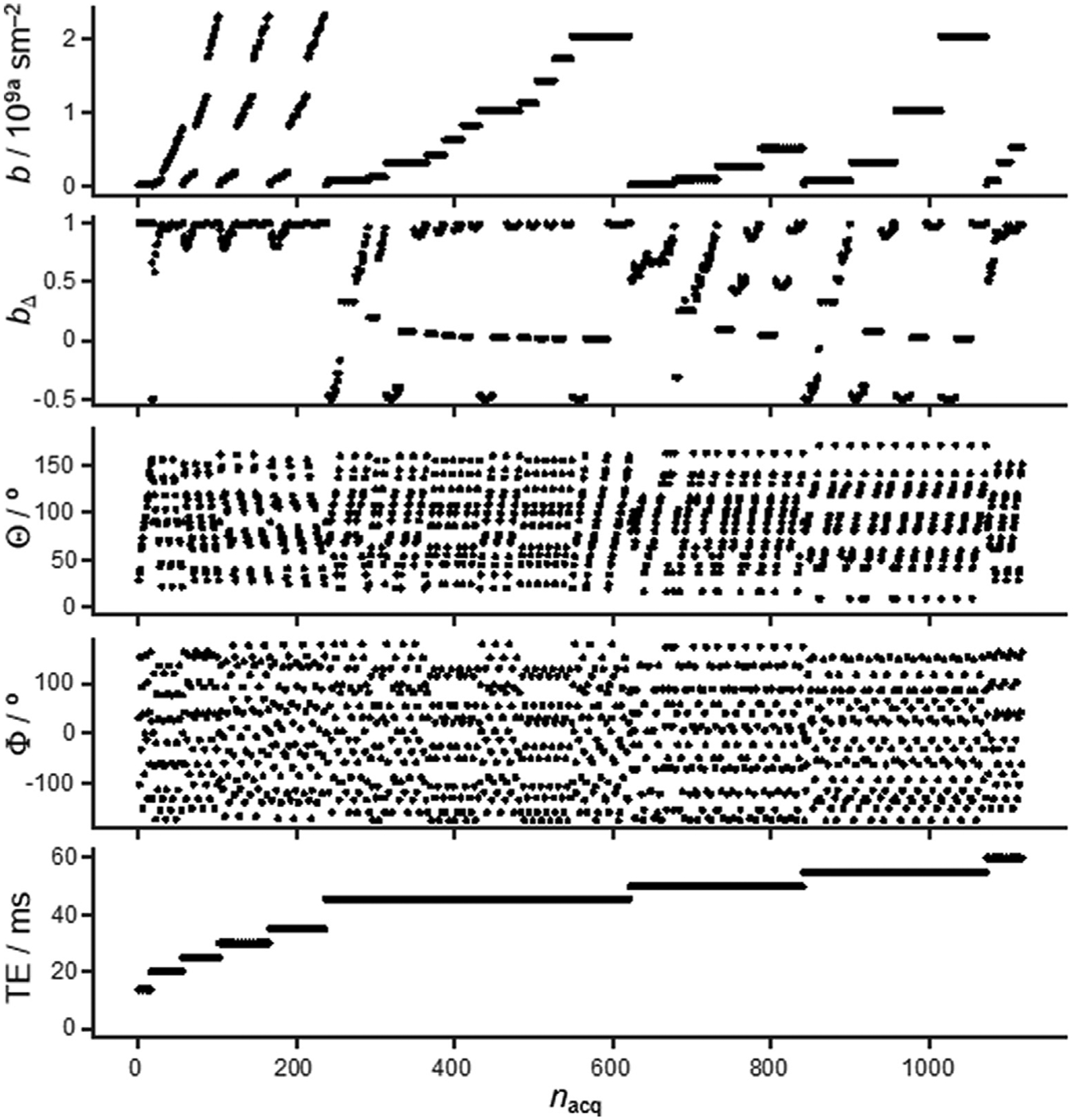
Acquisition scheme for 5D D-R2 distribution MRI. Images are recorded as a function of the magnitude b, normalized anisotropy bΔ (defined in Eq. (3)) and orientation (Θ,Φ) of the b-tensor, as well as the echo time τE at constant repetition time τR of 5 s. All panels share the same abscissa, where nacq is the acquisition number sorted in the order of ascending τE, b, and bΔ.
2.5. Data processing
After image reconstruction in ParaVision, data were exported to MatLab (R2018b MathWorks Inc, MA, USA) for denoising using random matrix theory [85]. In-plane motion and eddy correction with the MatLab routine imregister was used for in-plane affine registration, and Monte Carlo inversion [86] generated nonparametric 5D D-R2 distributions [22] using the dtr2d method in the md-dmri Matlab toolbox [87]. With this method, the signal S(b, τE) acquired as a function of b and τE at constant τR is approximated as originating from multiple sub-populations i, each being characterized by their weight wi, diffusion tensor Di, and transverse relaxation rate R2,i according to:
| (4) |
where the sum of wi gives the non-encoded signal S0 through:
| (5) |
which is nominally proportional to the spin density.
Assuming diffusion with axial symmetry for each sub-population, the diffusion tensors are parameterized in terms of the axial and radial eigenvalues, DA,i and DR,i and orientation (θi,ϕi). In this work, the Monte Carlo algorithm pseudo-randomly explores the parameter space within the ranges 5·10−12 m2s−1 < DA,i, DR,i < 5·10−9 m2s−1 and 1 s−1 < R2,i < 80 s−1 and—independently for each voxel—yields 100 solutions consistent with the input data. Each of these solutions comprises up to 20 components i characterized by the parameter set [DA,i,DR,i,θi,ϕi,R2,i] and the corresponding weights wi. For visualization of the results, the values of DA,i and DR,i are converted to the isotropic diffusivity Diso,i and squared normalized anisotropy by [81,88]:
| (6) |
and
| (7) |
as well as the lab-frame diagonal elements Dxx,i, Dyy,i and Dzz,i according to standard equations. Single-voxel 5D D-R2 distributions are visualized by projecting the components onto the 2D , Diso-R2, and planes, and parameter maps are generated by extracting means E[x], variances V[x], and covariances C[x,y] according to [89]:
| (8) |
| (9) |
and
| (10) |
where x and y are various combinations of Diso, , Dxx, Dyy, Dzz and R2. For comparison with results from conventional diffusion MRI performed at some finite value of τE, the relaxation factor can be included in the calculation of, for instance,
| (11) |
which is closely related to the conventional a ADC [21] and mean diffusivity (MD) [28], and where “τE” serves as a reminder that the mean value includes weighting by R2 relaxation during τE. An even more direct comparison with conventional ADC measured with a single b-value is obtained by:
| (12) |
where S(b,τE) is given by Eq. (4).
The extraction of quantitative metrics according to Eqs. (8–10) are performed for each of the 100 individual solutions per voxel, and the values finally displayed in parameter maps are obtained by taking the medians of the results for the individual solutions.
3. Results
Fig. 2 shows signals and corresponding 5D D-R2 distributions for individual white matter (WM), gray matter (GM) and cerebral spinal fluid (CSF) voxels for a single representative rat brain. The S0 maps are calculated according to Eq. (5), hence corresponding to signal at TE = 0 and b = 0. Consistent with previous in vivo mouse [90], in vivo human [22–24,26] and ex vivo rat results [25], the main distribution components of WM, GM and CSF are located in distinct corners of the 2D projection (WM: low Diso and high , GM: low Diso and low , CSF: high Diso and low ), thereby enabling “binning” for calculation of signal fractions fbin1, fbin2 and fbin3 and associated diffusion-relaxation metrics nominally specific for WM, GM and CSF [22] ss seen in Fig. 3a The challenges of EPI readout at 21.1 T are readily apparent as distortions of the S0 image stemming from susceptibility artifacts and Nyquist ghosting in the phase encoding direction [31,35]. Nevertheless, the bin-resolved fractions map captures the known spatial distributions of WM, GM and CSF. In addition to the binning, Fig. 3 also displays quantitative parameter maps obtained by extracting means E[x], variances V[x], and covariances C[x,y] by applying Eqs. (8)–(10) over selected dimensions and sub-divisions of the per-voxel 5D D-R2 distributions [22–26,61,89,91]. The bin-resolved maps in Fig. 3b reveal E[R2]-values of 70 and 60 s−1 for WM and GM, respectively, which can be contrasted with the values 20 and 15 s−1 observed for in vivo human at 3 T [22]. The per-voxel E[Diso], and E[R2] metrics in Fig. 3c are closely related to the more traditional parameters ADC [21] and MD [28], microscopic fractional anisotropy (μFA) [80,91], and quantitative T2 = 1/R2. Similar to μFA, the metric provides information on diffusion anisotropy independently from the underlying degree of orientational order, which is in contrast to the traditional FA [80,91]. Intravoxel heterogeneity are described with the variance and covariance measures V[x] and C[x,y] for which x and y imply various combinations of Diso, and R2. Out of all these measures, V[Diso] is most familiar from the literature under the names and symbols isotropic 2nd moment [80], size variance VMD [47] and isotropic mean kurtosis MKI [46], and has been shown to be related to intra-voxel variance of cell density in brain tumors [46]. A more detailed discussion about the biological meanings of the remaining heterogeneity metrics can be found in [25,26]. Low GW/WM contrast can be seen in certain structures, in particular the corpus callosum (cc), cerebellum and edges of white matter areas. This decrease is due to partial volume effects from the relatively large slice thickness but also from the chosen human brain-based boundary values for the various bins [90].
Fig. 2.
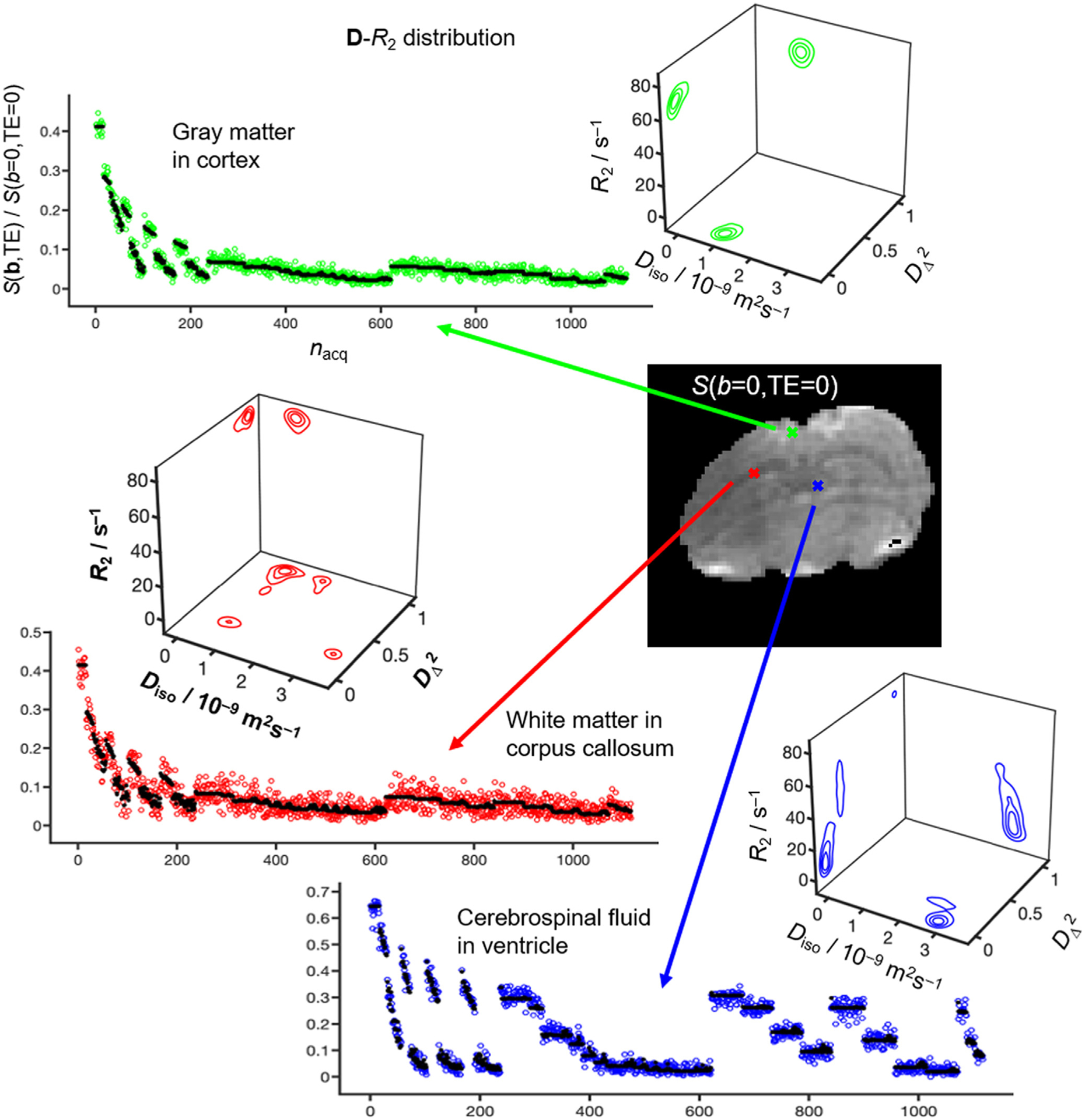
Experimental results for representative WM (red), GM (green) and CSF (blue) voxels of an in vivo rat brain at 21.1 T. The signal S is shown as a function of the acquisition number nacq according to the scheme in Fig. 1 (color-coded circles: experimental, black dots: fit). Nonparametric 5D D-R2 distributions obtained by Monte Carlo data inversion of Eq. (4) are visualized as projections onto the 2D , Diso-R2, and planes, where Diso is the isotropic diffusivity, the squared normalized anisotropy defined in Eqs. (6)–(7), and R2 is the transverse relaxation rate.
Fig. 3.
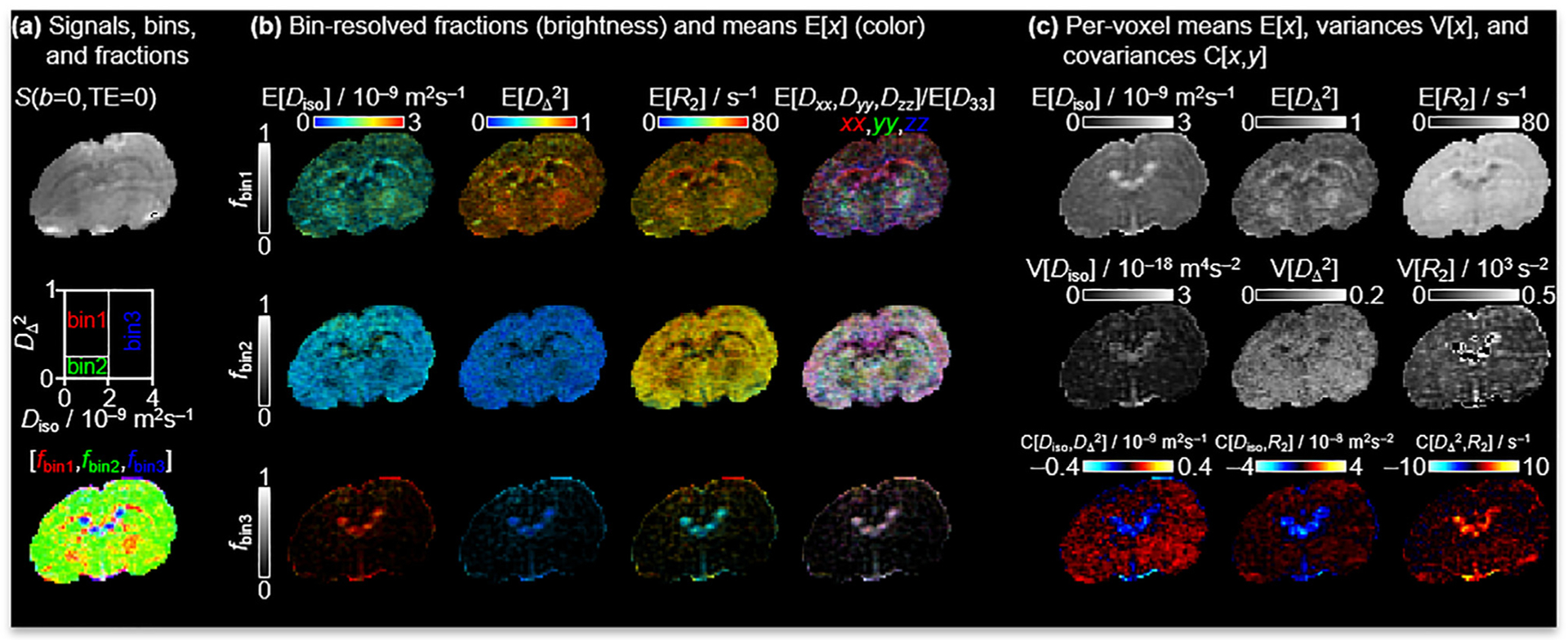
Quantitative parameter maps derived from the per-voxel 5D D-R2 distributions. (a) S0 image obtained by Eq. (5). Image segmentation is performed by dividing the 2D plane into three “bins” and calculating signal fractions [fbin1,fbin2,fbin3] mainly reporting on the spatial distributions of WM, GM and CSF. Here, blue refers to CSF, red to WM and green to GM. (b) Bin-resolved signal fractions and means E[x] over the Diso, , and R2 dimensions according to Eq. (8). The bin fractions and means are coded into brightness intensity, and the properties of interest are represented by the color scales, which are each combined by two orthogonal scales in the image. Direction-encoded colors derive from the lab-frame diagonal values [Dxx,Dyy,Dzz] and maximum eigenvalue D33. (c) Per-voxel means E[x], variances V[x] and covariances C[x,y] of various combinations of Diso, , and R2 are as defined in Eqs. (8–10).
In Fig. 4, data from the phantom are presented. Here, the liquid crystal (red tube in Fig. 4a phantom cartoon), hydrocarbons (yellow and green tubes in Fig. 4a phantom cartoon) and water are used to emulate the diffusion properties of WM, GM and CSF, respectively [79]. Even though the images are heavily distorted from chemical shift artifacts of the hydrocarbons and ghosting in the phase direction, the 21.1-T implementation of the 5D D-R2 method yield parameter maps consistent with the known diffusion and relaxation properties of the constituents of the phantom. Notably, the binning in the plane designed for the calculation of tissue-specific signal fractions in the in vivo data also separates the liquid crystal, hydrocarbons and water fractions in the phantom data cleanly. For the liquid crystal, the directionally color-coded map E[Dxx,Dyy,Dzz] clearly shows the structure of the anisotropic domains [82]. The magnetic susceptibility anisotropy results in an orientational dependence on T2 and as shown in Fig. 4c. These magnetic field dependent distortions are amplified at ultra-high fields as described by ΔB = χmB0, where ΔB is the field imposed by the tissue/material interface and perturbing B0 by the magnetic susceptibility, χm, of the material [92]. Susceptibility differences in the phantom consequently exacerbate the warping artifact of the phantom that is not seen in vivo. Likewise, the low bandwidth in the phase encoding dimension together with the resonance frequency difference between the water and hydrocarbons leads to pronounced chemical shift displacements of the latter from the top to the lower part of the image.
Fig. 4.
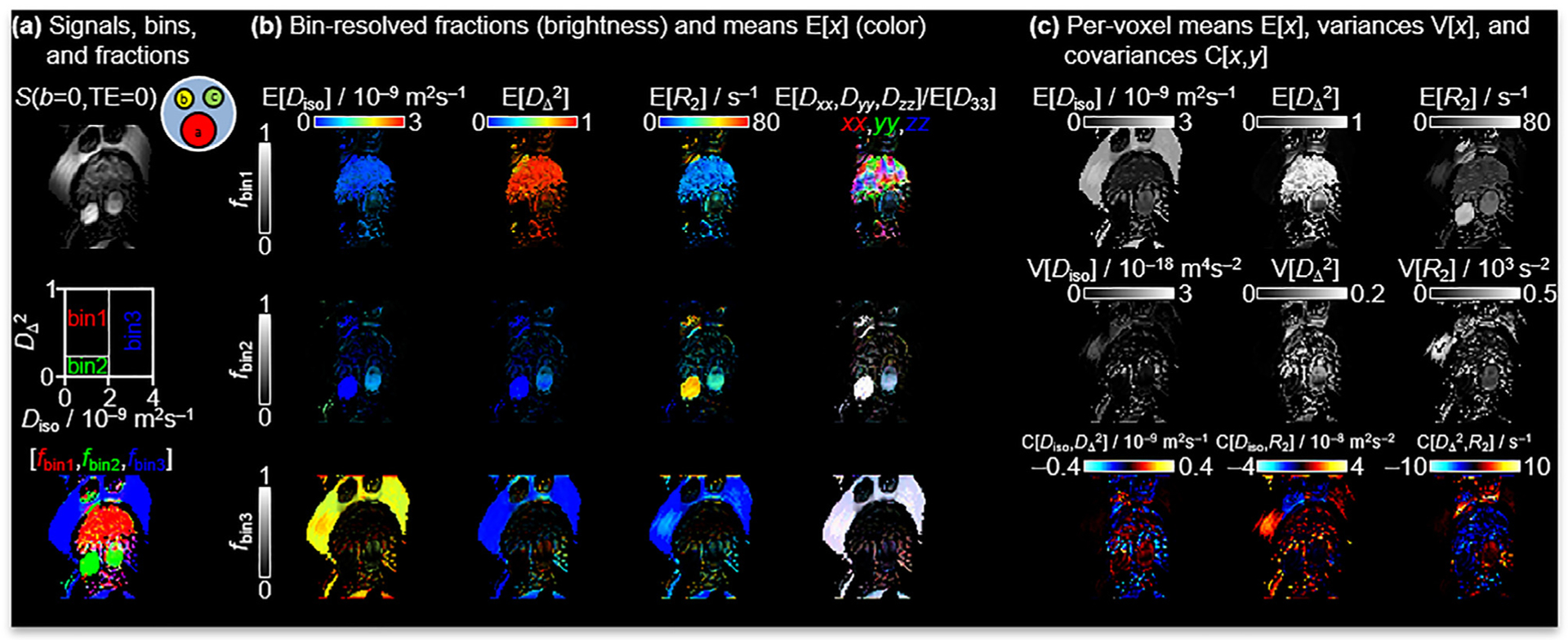
Parameter maps for the composite phantom comprising an assembly of tubes with liquid crystal (red tube in 4a phantom cartoon), hydrocarbons (1-octanol and n-dodecane, shown as yellow and green tubes respectively in 4a phantom cartoon) and water having diffusion properties similar WM, GM and CSF, respectively. See caption of Fig. 3 for detailed explanation of the panels and legends. Image distortions are exacerbated by susceptibility artifacts and chemical shift displacement of the two hydrocarbons not seen in vivo.
4. Discussion
Reassuringly, the straightforward 21.1-T implementation of a standard EPI sequence broadly reproduces previous results from 3 T [22], however with noticeably lower signal on account of the nearly four-fold increase in R2 and field gradients induced by differences in magnetic susceptibility.
The trend towards higher fields is expanding with 7 T becoming more applicable in the clinic [93–95] and now with extension to 11 T for animals as well as humans [30]. Discussions and a feasibility study for a 20-T human magnet further predicts future high field trends [75], showing the importance of translating these sequences to higher fields and identifying needs for improvements to overcome challenges introduced at these field strengths. Increased B0 has many benefits such as SNR, spectral dispersion and higher spatial resolution, but also some impairments such as susceptibility and warping artifacts in EPI-based encoding due to susceptibility gradients and other artifacts that are amplified by low bandwidths [74]. Depending on the application, relaxation can benefit image contrast but also complicate quantitative assessment. Spin-lattice relaxation of tissues is generally increased with some convergence in values for different tissues, leading to a decreased contrast for T1-weighted scans. On the other hand, tissue signals are more readily saturated, benefiting contrast agent and time-of-flight applications. Transverse relaxation (T2) times are generally shortened at increased field strength leading to improved blood oxygen saturation (BOLD) scans and susceptibility imaging, while also increasing the need for short TE scans to compensate for the decreased signal from shortened T2.
Published values of the ADC for the striatum of in vivo rat at 21.1 T cover the range from 0.7 to 0.8·10–9 m2s−1 for image readout using simple spin echo, EPI, and spatio-temporal encoding (SPEN) at b-values up to 1·109 sm−2 and values of τE in the range from 25 to 40 ms [31]. For comparison with literature data, ADC values were calculated from S(b,τE) images synthesized from the 5D D-R2 distributions according to Eq. (12), yielding ADC = (0.78 ± 0.04) 10−9 m2s−1 (mean ± standard deviation) at b = 1·109 sm−2 and τE = 30 ms, which can be contrasted with E[Diso] = (0.99 ± 0.09) 10−9 m2s−1 corresponding to ADC in the limit b = 0 and τE = 0.
To capitalize on the potential SNR gains by ultra-high field, advanced diffusion sequences may require correspondingly ultra-strong gradients [38,39,60,96–98] to minimize the duration of typically lengthy gradient waveforms and, image read-out approaches. SPEN [31,35,90,99] or gradient and spin echo (GRASE) [100] are examples of such approaches that are less susceptible to B0 inhomogeneity and relaxation than single-shot EPI. SPEN has been used at 21.1-T and has shown that B0 artifacts can be overcome despite the minimum τE being longer than that of traditional spin-echo EPI [31,35]. With SPEN, τE increases linearly with the spatial coordinate in the low-bandwidth dimension, producing a gradient in T2-weighting that potentially can produce a bias in diffusion metrics. Yon et al. has expanded on SPEN readout and incorporated the multidimensional diffusion approach at 15.2 T (79, 90). In doing so, Yon et al. employed SPEN in its fully refocusing mode and increased bandwidth to reduce B0 inhomogeneity artifacts without compromising diffusion tensor distribution metrics from the incorporated multidimensional diffusion acquisition scheme [90]. In addition, Yon et al [101] showed that the SPEN technique alleviated artifacts in distortion prone regions of mouse brains for diffusion tensor imaging (DTI). Interleaved multi-segmented EPI acquisitions at 21.1 T also have been shown to reduce echo times and alleviate geometric distortions; however, this approach did not provide reliable ADC values, potentially due to motion or sampling impacts on signal [31]. Notably, the current study, as with other single-shot EPI readouts acquisitions [31,35], did provide expected and reliable diffusion measures. Persistent geometric distortions and artifacts are particularly prevalent in the composite phantom for which susceptibility mismatches together with chemical shift significantly reduce image quality. Nevertheless, as shown not only in this report but also others, in vivo and phantom diffusion data are accurate quantitively [31,35,79]. There are other strategies that can be implemented for future work that are commonly used in clinical settings to correct for EPI or field inhomogeneities, such as acquiring B0 maps or inverted EPI blips. Other corrections such as brain/skull extraction, signal drift correction, denoising, etc [102] to improve data visualization should be considered for future work but may not be relevant in a preclinical setting.
5. Conclusion
In this study, it has been shown that an advanced diffusion scheme such as the multidimensional diffusion can be implemented at 21.1 T to provide results consistent with previous lower field studies. To realize the full potential of ultra-high field, efforts need to be directed to both sequence design and gradient hardware improvements to minimize warping artifacts and reach even shorter values of τE.
Acknowledgement
The authors appreciate the assistance of the staff and scientists of the US National High Magnetic Field Laboratory, as well as the gradient waveforms made available by Matthew Budde at the Medical College of Wisconsin This work was financially supported the Swedish Foundation for Strategic Research, (ITM17-0267) and Swedish Research Council (2018-03697) to DT and the US National Institutes of Health (R01-NS102395) to SCG. DT owns shares in Random Walk Imaging AB (Lund, Sweden, http://www.rwi.se/), holding patents related to the described methods. The US National High Magnetic Field Laboratory is supported by the US National Science Foundation (DMR-1644779) and the State of Florida.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].Galvosas P, Callaghan PT, Multi-dimensional inverse Laplace spectroscopy in the NMR of porous media, Compt. Rendus Phys 11 (2010) 172–180, 10.1016/j.crhy.2010.06.014. [DOI] [Google Scholar]
- [2].Bernin D, Topgaard D, NMR diffusion and relaxation correlation methods: New insights in heterogeneous materials, Curr. Opin. Colloid Interface Sci 18 (2013) 166–172, 10.1016/j.cocis.2013.03.007. [DOI] [Google Scholar]
- [3].Song Y-Q, Venkataramanan L, Kausik R, Heaton N, Chapter 4:Two-dimensional NMR of Diffusion and Relaxation, Diffus. NMR Confin. Syst, 2016, p. 111–55. 10.1039/9781782623779-00111. [DOI] [Google Scholar]
- [4].Benjamini D, Chapter 10:Nonparametric Inversion of Relaxation and Diffusion Correlation Data. Adv. Diffus. Encoding Methods MRI, 2020, p. 278–316. 10.1039/9781788019910-00278. [DOI] [Google Scholar]
- [5].Mitchell J, Chandrasekera TC, Gladden LF, Numerical estimation of relaxation and diffusion distributions in two dimensions, Prog. Nucl. Magn. Reson. Spectrosc 62 (2012) 34–50, 10.1016/j.pnmrs.2011.07.002. [DOI] [PubMed] [Google Scholar]
- [6].Xie R, Xiao L, Advanced fluid-typing methods for NMR logging, Pet. Sci 8 (2011) 163–169, 10.1007/s12182-011-0130-4. [DOI] [Google Scholar]
- [7].Hürlimann MD, Burcaw L, Song Y-Q, Quantitative characterization of food products by two-dimensional D-T2 and T1–T2 distribution functions in a static gradient, J. Colloid Interface Sci 297 (2006) 303–311, 10.1016/j.jcis.2005.10.047. [DOI] [PubMed] [Google Scholar]
- [8].Marigheto N, Venturi L, Hills B, Two-dimensional NMR relaxation studies of apple quality, Postharvest Biol. Technol 48 (2008) 331–340, 10.1016/j.postharvbio.2007.11.002. [DOI] [Google Scholar]
- [9].Zhang Y, Blümich B, Spatially resolved D-T2 correlation NMR of porous media, J. Magn. Reson 242 (2014) 41–48, 10.1016/j.jmr.2014.01.017. [DOI] [PubMed] [Google Scholar]
- [10].Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP, Diffusion-relaxation correlation spectroscopic imaging: A multidimensional approach for probing microstructure, Magn. Reson. Med 78 (2017) 2236–2249, 10.1002/mrm.26629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Benjamini D, Basser PJ, Magnetic resonance microdynamic imaging reveals distinct tissue microenvironments, NeuroImage 163 (2017) 183–196, 10.1016/j.neuroimage.2017.09.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Benjamini D, Iacono D, Komlosh ME, Perl DP, Brody DL, Basser PJ, Diffuse axonal injury has a characteristic multidimensional MRI signature in the human brain, Brain J. Neurol 144 (2021) 800–816, 10.1093/brain/awaa447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Zhang Z, Wu HH, Priester A, Magyar C, Afshari Mirak S, Shakeri S, et al. , Prostate Microstructure in Prostate Cancer Using 3-T MRI with Diffusion-Relaxation Correlation Spectrum Imaging: Validation with Whole-Mount Digital Histopathology, Radiology 296 (2020) 348–355, 10.1148/radiol.2020192330. [DOI] [PubMed] [Google Scholar]
- [14].Slator PJ, Hutter J, Palombo M, Jackson LH, Ho A, Panagiotaki E, et al. , Combined diffusion-relaxometry MRI to identify dysfunction in the human placenta, Magn. Reson. Med 82 (2019) 95–106, 10.1002/mrm.27733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Tax CMW, Estimating chemical and microstructural heterogeneity by correlating relaxation and diffusion, in: Topgaard D, editor. Adv. Diffus. Encoding Methods MRI, Cambridge (UK): Royal Society of Chemistry; 2020. [PubMed] [Google Scholar]
- [16].Kim D, Wisnowski JL, Nguyen CT, Haldar JP, Multidimensional correlation spectroscopic imaging of exponential decays: From theoretical principles to in vivo human applications, NMR Biomed. 33 (2020), 10.1002/nbm.4244 e4244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Benjamini D, Basser PJ, Multidimensional correlation MRI, NMR Biomed. 33 (2020), 10.1002/nbm.4226 e4226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Pizzolato M, Palombo M, Bonet-Carne E, Tax CMW, Grussu F, Ianus A, et al. Acquiring and Predicting Multidimensional Diffusion (MUDI) Data: An Open Challenge. In: Bonet-Carne E, Hutter J, Palombo M, Pizzolato M, Sepehrband F, Zhang F, editors. Comput. Diffus. MRI, Cham: Springer International Publishing; 2020, p. 195–208. [Google Scholar]
- [19].Stejskal EO, Tanner JE, Spin echoes in the presence of a time dependent gradient field, J. Chem. Phys 42 (1965). [Google Scholar]
- [20].Topgaard D, Multiple dimensions for random walks, J. Magn. Reson 306 (2019) 150–154, 10.1016/j.jmr.2019.07.024. [DOI] [PubMed] [Google Scholar]
- [21].Le Bihan D, Breton E, Lallemand D, Grenier P, Cabanis E, Laval-Jeantet M, MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders, Radiology 161 (1986) 401–407, 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
- [22].de Almeida Martins JP, Tax CMW, Szczepankiewicz F, Jones DK, Westin C-F, Topgaard D, Transferring principles of solid-state and Laplace NMR to the field of in vivo brain MRI, Magn. Reson 1 (2020) 27–43, 10.5194/mr-1-27-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Martins JP de A, Tax CMW, Reymbaut A, Szczepankiewicz F, Chamberland M, Jones DK, et al. Computing and visualising intra-voxel orientation-specific relaxation–diffusion features in the human brain. Hum Brain Mapp 2021;42:310–28. 10.1002/hbm.25224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Reymbaut A, Critchley J, Durighel G, Sprenger T, Sughrue M, Bryskhe K, et al. , Toward nonparametric diffusion-T1 characterization of crossing fibers in the human brain, Magn. Reson. Med 85 (2021) 2815–2827, 10.1002/mrm.28604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Narvaez O, Svenningsson L, Yon M, Sierra A, Topgaard D, Massively Multidimensional Diffusion-Relaxation Correlation MRI, Front. Phys 9 (2022). [Google Scholar]
- [26].Martin J, Reymbaut A, Schmidt M, Doerfler A, Uder M, Laun FB, et al. , Nonparametric D-R1-R2 distribution MRI of the living human brain, NeuroImage 245 (2021), 10.1016/j.neuroimage.2021.118753118753. [DOI] [PubMed] [Google Scholar]
- [27].Topgaard D, Multidimensional diffusion MRI, J. Magn. Reson 275 (2017) 98–113, 10.1016/j.jmr.2016.12.007. [DOI] [PubMed] [Google Scholar]
- [28].Basser PJ, Mattiello J, LeBihan D, MR diffusion tensor spectroscopy and imaging, Biophys. J 66 (1994) 259–267, 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Pierpaoli C, Jezzard P, Basser PJ, Barnett A, Di Chiro G, Diffusion tensor MR imaging of the human brain, Radiology 201 (1996) 637–648, 10.1148/radiology.201.3.8939209. [DOI] [PubMed] [Google Scholar]
- [30].Bihan DL, Schild T, Human brain MRI at 500 MHz, scientific perspectives and technological challenges, Supercond. Sci. Technol 30 (2017), 10.1088/1361-6668/30/3/033003 033003. [DOI] [Google Scholar]
- [31].Leftin A, Rosenberg JT, Solomon E, Bejarano FC, Grant SC, Frydman L. Ultrafast in vivo diffusion imaging of stroke at 21.1 T by spatiotemporal encoding. Magn Reson Med Off J Soc Magn Reson Med Soc Magn Reson Med 2015;73:1483. 10.1002/mrm.25271. [DOI] [PubMed] [Google Scholar]
- [32].Shemesh N, Rosenberg JT, Dumez JN, Grant SC, Frydman L, Metabolic T1 dynamics and longitudinal relaxation enhancement in vivo at ultrahigh magnetic fields on ischemia, J Cereb Blood Flow Metab Off J Int Soc Cereb Blood Flow Metab 34 (2014) 1810–1817, 10.1038/jcbfm.2014.149 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Shemesh N, Rosenberg JT, Dumes J-N, Muniz JA, Grant SC, Frydman L, Metabolic properties in stroked rats revealed by relaxation-enhanced magnetic resonance spectroscopy at ultrahigh fields, NatComm 5 (2014) 4958, 10.1038/ncomms5958. [DOI] [PubMed] [Google Scholar]
- [34].Rosenberg JT, Shemesh N, Muniz JA, Dumez JN, Frydman L, Grant SC, Transverse relaxation of selectively excited metabolites in stroke at 21.1 T, Magn. Reson. Med (2016), 10.1002/mrm.26132 [doi]. [DOI] [PubMed] [Google Scholar]
- [35].Leftin A, Rosenberg JT, Yuan X, Ma T, Grant SC, Frydman L. Multiparametric classification of sub-acute ischemic stroke recovery with ultrafast diffusion, 23 Na, and MPIO-labeled stem cell MRI at 21.1 T. NMR Biomed 2020;33: e4186. 10.1002/nbm.4186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Abad N, Rosenberg JT, Roussel T, Grice DC, Harrington MG, Grant SC, Metabolic assessment of a migraine model using relaxation-enhanced (1) H spectroscopy at ultrahigh field, Magn. Reson. Med 79 (2018) 1266–1275, 10.1002/mrm.26811 [doi]. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Bagdasarian FA, Yuan X, Athey J, Bunnell BA, Grant SC, NODDI highlights recovery mechanisms in white and gray matter in ischemic stroke following human stem cell treatment, Magn. Reson. Med 86 (2021) 3211, 10.1002/mrm.28929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Jespersen SN, Olesen JL, Ianusş A, Shemesh N, Effects of nongaussian diffusion on “isotropic diffusion” measurements: An ex-vivo microimaging and simulation study, J. Magn. Reson 300 (2019) 84–94, 10.1016/j.jmr.2019.01.007. [DOI] [PubMed] [Google Scholar]
- [39].Ianusş A, Jespersen SN, Serradas Duarte T, Alexander DC, Drobnjak I, Shemesh N, Accurate estimation of microscopic diffusion anisotropy and its time dependence in the mouse brain, NeuroImage 183 (2018) 934–949, 10.1016/j.neuroimage.2018.08.034. [DOI] [PubMed] [Google Scholar]
- [40].Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasič S, Ståhlberg F, et al. , Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging, Magn. Reson. Med 69 (2013) 1572–1580, 10.1002/mrm.24395. [DOI] [PubMed] [Google Scholar]
- [41].Lampinen B, Szczepankiewicz F, van Westen D, Englund E, Sundgren PC, Lätt J, et al. , Optimal experimental design for filter exchange imaging: Apparent exchange rate measurements in the healthy brain and in intracranial tumors, Magn. Reson. Med 77 (2017) 1104–1114, 10.1002/mrm.26195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Avram AV, Özarslan E, Sarlls JE, Basser PJ, In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient (qPFG) diffusion MRI on a clinical scanner, NeuroImage 64 (2013) 229–239, 10.1016/j.neuroimage.2012.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Lawrenz M, Finsterbusch J, Double-wave-vector diffusion-weighted imaging reveals microscopic diffusion anisotropy in the living human brain, Magn. Reson. Med 69 (2013) 1072–1082, 10.1002/mrm.24347. [DOI] [PubMed] [Google Scholar]
- [44].Szczepankiewicz F, Lasič S, van Westen D, Sundgren PC, Englund E, Westin C-F, et al. , Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors, NeuroImage 104 (2015) 241–252, 10.1016/j.neuroimage.2014.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Lawrenz M, Finsterbusch J, Mapping measures of microscopic diffusion anisotropy in human brain white matter in vivo with double-wave-vector diffusion-weighted imaging, Magn. Reson. Med 73 (2015) 773–783, 10.1002/mrm.25140. [DOI] [PubMed] [Google Scholar]
- [46].Szczepankiewicz F, van Westen D, Englund E, Westin C-F, Ståhlberg F, Lätt J, et al. , The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE), NeuroImage 142 (2016) 522–532, 10.1016/j.neuroimage.2016.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Westin C-F, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, et al. , Q-space trajectory imaging for multidimensional diffusion MRI of the human brain, NeuroImage 135 (2016) 345–362, 10.1016/j.neuroimage.2016.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].L M, B S, F J. Microscopic diffusion anisotropy in the human brain: Age-related changes. Neuroimage 2016;141:313–25. 10.1016/j.neuroimage.2016.07.031. [DOI] [PubMed] [Google Scholar]
- [49].Lampinen B, Szczepankiewicz F, Mårtensson J, van Westen D, Sundgren PC, Nilsson M, Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding, NeuroImage 147 (2017) 517–531, 10.1016/j.neuroimage.2016.11.053. [DOI] [PubMed] [Google Scholar]
- [50].Yang G, Tian Q, Leuze C, Wintermark M, McNab JA, Double diffusion encoding MRI for the clinic, Magn. Reson. Med 80 (2018) 507–520, 10.1002/mrm.27043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Avram AV, Sarlls JE, Basser PJ, Measuring non-parametric distributions of intravoxel mean diffusivities using a clinical MRI scanner, NeuroImage 185 (2019) 255–262, 10.1016/j.neuroimage.2018.10.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Lampinen B, Szczepankiewicz F, Novén M, van Westen D, Hansson O, Englund E, et al. , Searching for the neurite density with diffusion MRI: Challenges for biophysical modeling, Hum. Brain Mapp 40 (2019) 2529–2545, 10.1002/hbm.24542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Lawrenz M, Finsterbusch J, Detection of microscopic diffusion anisotropy in human cortical gray matter in vivo with double diffusion encoding, Magn. Reson. Med 81 (2019) 1296–1306, 10.1002/mrm.27451. [DOI] [PubMed] [Google Scholar]
- [54].Nery F, Szczepankiewicz F, Kerkelä L, Hall MG, Kaden E, Gordon I, et al. , In vivo demonstration of microscopic anisotropy in the human kidney using multidimensional diffusion MRI, Magn. Reson. Med 82 (2019) 2160–2168, 10.1002/mrm.27869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Yang G, McNab JA, Eddy current nulled constrained optimization of isotropic diffusion encoding gradient waveforms, Magn. Reson. Med 81 (2019) 1818–1832, 10.1002/mrm.27539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Lampinen B, Szczepankiewicz F, Mårtensson J, van Westen D, Hansson O, Westin C-F, et al. , Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding, Magn. Reson. Med 84 (2020) 1605–1623, 10.1002/mrm.28216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Lampinen B, Zampeli A, Björkman-Burtscher IM, Szczepankiewicz F, Källén K, Strandberg MC, et al. , Tensor-valued diffusion MRI differentiates cortex and white matter in malformations of cortical development associated with epilepsy, Epilepsia 61 (2020) 1701–1713, 10.1111/epi.16605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Nilsson M, Szczepankiewicz F, Brabec J, Taylor M, Westin C, Golby A, et al. , Tensor-valued diffusion MRI in under 3 minutes: an initial survey of microscopic anisotropy and tissue heterogeneity in intracranial tumors, Magn. Reson. Med 83 (2020) 608–620, 10.1002/mrm.27959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Andersen KW, Lasič S, Lundell H, Nilsson M, Topgaard D, Sellebjerg F, et al. Disentangling white-matter damage from physiological fibre orientation dispersion in multiple sclerosis. Brain Commun 2020;2:fcaa077. 10.1093/braincomms/fcaa077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Tan ET, Shih RY, Mitra J, Sprenger T, Hua Y, Bhushan C, et al. , Oscillating diffusion-encoding with a high gradient-amplitude and high slew-rate head-only gradient for human brain imaging, Magn. Reson. Med 84 (2020) 950–965, 10.1002/mrm.28180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Naranjo ID, Reymbaut A, Brynolfsson P, Lo Gullo R, Bryskhe K, Topgaard D, et al. , Multidimensional Diffusion Magnetic Resonance Imaging for Characterization of Tissue Microstructure in Breast Cancer Patients: A Prospective Pilot Study, Cancers 13 (2021) 1606, 10.3390/cancers13071606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Novello L, Henriques RN, Ianusß A, Feiweier T, Shemesh N, Jovicich J, In vivo Correlation Tensor MRI reveals microscopic kurtosis in the human brain on a clinical 3T scanner, NeuroImage 254 (2022), 10.1016/j.neuroimage.2022.119137 119137. [DOI] [PubMed] [Google Scholar]
- [63].Baron CA, Beaulieu C, Oscillating gradient spin-echo (OGSE) diffusion tensor imaging of the human brain, Magn. Reson. Med 72 (2014) 726–736, 10.1002/mrm.24987. [DOI] [PubMed] [Google Scholar]
- [64].Baron CA, Kate M, Gioia L, Butcher K, Emery D, Budde M, et al. , Reduction of Diffusion-Weighted Imaging Contrast of Acute Ischemic Stroke at Short Diffusion Times, Stroke 46 (2015) 2136–2141, 10.1161/STROKEAHA.115.008815. [DOI] [PubMed] [Google Scholar]
- [65].Does MD, Parsons EC, Gore JC, Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain, Magn. Reson. Med 49 (2003) 206–215, 10.1002/mrm.10385. [DOI] [PubMed] [Google Scholar]
- [66].Maximov II, Vellmer S, Isotropically weighted intravoxel incoherent motion brain imaging at 7T, Magn. Reson. Imag 57 (2019) 124–132, 10.1016/j.mri.2018.11.007. [DOI] [PubMed] [Google Scholar]
- [67].Szczepankiewicz F, Sjölund J, Ståhlberg F, Lätt J, Nilsson M, Tensor-valued diffusion encoding for diffusional variance decomposition (DIVIDE): Technical feasibility in clinical MRI systems, PLoS ONE 14 (2019), 10.1371/journal.pone.0214238 e0214238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Arbabi A, Kai J, Khan AR, Baron CA, Diffusion dispersion imaging: Mapping oscillating gradient spin-echo frequency dependence in the human brain, Magn. Reson. Med 83 (2020) 2197–2208, 10.1002/mrm.28083. [DOI] [PubMed] [Google Scholar]
- [69].Shemesh N, Barazany D, Sadan O, Bar L, Zur Y, Barhum Y, et al. , Mapping apparent eccentricity and residual ensemble anisotropy in the gray matter using angular double-pulsed-field-gradient MRI, Magn. Reson. Med 68 (2012) 794–806, 10.1002/mrm.23300. [DOI] [PubMed] [Google Scholar]
- [70].Alves R, Henriques RN, Kerkelä L, Chavarrías C, Jespersen SN, Shemesh N, Correlation Tensor MRI deciphers underlying kurtosis sources in stroke, NeuroImage 247 (2022), 10.1016/j.neuroimage.2021.118833 118833. [DOI] [PubMed] [Google Scholar]
- [71].Wu D, Martin LJ, Northington FJ, Zhang J, Oscillating gradient diffusion MRI reveals unique microstructural information in normal and hypoxiaischemia injured mouse brains, Magn. Reson. Med 72 (2014) 1366–1374, 10.1002/mrm.25441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Aggarwal M, Jones MV, Calabresi PA, Mori S, Zhang J, Probing mouse brain microstructure using oscillating gradient diffusion MRI, Magn Reson Med 67 (2012) 98–109, 10.1002/mrm.22981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Wu D, Zhang J, The Effect of Microcirculatory Flow on Oscillating Gradient Diffusion MRI and Diffusion Encoding with Dual-Frequency Orthogonal Gradients (DEFOG), Magn Reson Med 77 (2017) 1583–1592, 10.1002/mrm.26242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Jezzard P, Balaban RS, Correction for geometric distortion in echo planar images from B0 field variations, Magn Reson Med 34 (1995) 65–73, 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- [75].Budinger TF, Bird MD, Frydman L, Long JR, Mareci TH, Rooney WD, et al. , Toward 20 T magnetic resonance for human brain studies: opportunities for discovery and neuroscience rationale, Magma 29 (2016) 617–639, 10.1007/s10334-016-0561-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Budinger TF, Bird MD, MRI and MRS of the human brain at magnetic fields of 14T to 20T: Technical feasibility, safety, and neuroscience horizons, NeuroImage 168 (2018) 509–531, 10.1016/j.neuroimage.2017.01.067. [DOI] [PubMed] [Google Scholar]
- [77].Fu R, Brey WW, Shetty K, Gor’kov P, Saha S, Long JR, et al. Ultra-wide bore 900 MHz high-resolution NMR at the National High Magnetic Field Laboratory. J Magn Reson San Diego Calif 1997 2005;177:1–8. 10.1016/j.jmr.2005.07.013. [DOI] [PubMed] [Google Scholar]
- [78].Markiewicz WD, Brey WW, Cross TA, Dixon IR, Gor’kov PL, Grant SC, et al. A Decade of Experience With the UltraWide-Bore 900-MHz NMR Magnet. IEEE Trans Appl Supercond 2015;25. [Google Scholar]
- [79].Nilsson M, Larsson J, Lundberg D, Szczepankiewicz F, Witzel T, Westin C-F, et al. , Liquid crystal phantom for validation of microscopic diffusion anisotropy measurements on clinical MRI systems, Magn Reson Med 79 (2018) 1817–1828, 10.1002/mrm.26814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Lasič S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D, Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector, Front Phys 2 (2014), 10.3389/fphy.2014.00011. [DOI] [Google Scholar]
- [81].Eriksson S, Lasič S, Nilsson M, Westin C-F, Topgaard D, NMR diffusion-encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution, J Chem Phys 142 (2015), 10.1063/1.4913502 104201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Topgaard D, Director orientations in lyotropic liquid crystals: diffusion MRI mapping of the Saupe order tensor, Phys Chem Chem Phys PCCP 18 (2016) 8545–8553, 10.1039/c5cp07251d. [DOI] [PubMed] [Google Scholar]
- [83].null Bak, null Nielsen. REPULSION, A Novel Approach to Efficient Powder Averaging in Solid-State NMR. J Magn Reson San Diego Calif 1997 1997;125:132–9. 10.1006/jmre.1996.1087. [DOI] [PubMed] [Google Scholar]
- [84].Istratov AA, Vyvenko OF, Exponential analysis in physical phenomena, Rev Sci Instrum 70 (1999) 1233–1257, 10.1063/1.1149581. [DOI] [Google Scholar]
- [85].Veraart J, Fieremans E, Novikov DS, Diffusion MRI noise mapping using random matrix theory, Magn Reson Med 76 (2016) 1582–1593, 10.1002/mrm.26059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].M P, Yq S. Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. J Magn Reson San Diego Calif 1997 2008;196:54–60. 10.1016/j.jmr.2008.10.008. [DOI] [PubMed] [Google Scholar]
- [87].Nilsson M, Szczepankiewicz F, Lampinen B, Ahlgren A, de Almeida Martins JP, Lasič S, et al. , An open-source framework for analysis of multidimensional diffusion MRI data implemented in MATLAB, Proceding Int. Soc. Magn. Reson. Med, Paris, France, 2018. [Google Scholar]
- [88].Conturo TE, McKinstry RC, Akbudak E, Robinson BH, Encoding of anisotropic diffusion with tetrahedral gradients: a general mathematical diffusion formalism and experimental results, Magn Reson Med 35 (1996) 399–412, 10.1002/mrm.1910350319. [DOI] [PubMed] [Google Scholar]
- [89].Topgaard D, Diffusion tensor distribution imaging, NMR Biomed 32 (2019), 10.1002/nbm.4066 e4066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Yon M, de Almeida Martins JP, Bao Q, Budde MD, Frydman L, Topgaard D, Diffusion tensor distribution imaging of an in vivo mouse brain at ultrahigh magnetic field by spatiotemporal encoding, Nmr Biomed 33 (2020), 10.1002/nbm.4355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91].Shemesh N, Jespersen SN, Alexander DC, Cohen Y, Drobnjak I, Dyrby TB, et al. , Conventions and nomenclature for double diffusion encoding NMR and MRI, Magn Reson Med 75 (2016) 82–87, 10.1002/mrm.25901. [DOI] [PubMed] [Google Scholar]
- [92].Yang QX, Smith MB, Wang J. Magnetic Susceptibility Effects in High Field MRI. In: Robitaille P-M, Berliner L, editors. Ultra High Field Magn. Reson Imaging, Boston, MA: Springer US; 2006, p. 249–84. 10.1007/978-0-387-49648-1_9. [DOI] [Google Scholar]
- [93].Trattnig S, Springer E, Bogner W, Hangel G, Strasser B, Dymerska B, et al. , Key clinical benefits of neuroimaging at 7T, NeuroImage 168 (2018) 477–489, 10.1016/j.neuroimage.2016.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94].Trattnig S, Bogner W, Gruber S, Szomolanyi P, Juras V, Robinson S, et al. , Clinical applications at ultrahigh field (7 T). Where does it make the difference?, NMR Biomed 29 (2016) 1316–1334, https://doiorg/10.1002/nbm.3272. [DOI] [PubMed] [Google Scholar]
- [95].Isaacs BR, Mulder MJ, Groot JM, van Berendonk N, Lute N, Bazin P-L, et al. , 3 versus 7 Tesla magnetic resonance imaging for parcellations of subcortical brain structures in clinical settings, PLoS ONE 15 (2020), 10.1371/journal.pone.0236208 e0236208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96].Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab JA, et al. , Pushing the limits of in vivo diffusion MRI for the Human Connectome Project, NeuroImage 80 (2013) 220–233, 10.1016/j.neuroimage.2013.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [97].Jones DK, Alexander DC, Bowtell R, Cercignani M, Dell’Acqua F, McHugh DJ, et al. , Microstructural imaging of the human brain with a “super-scanner”: 10 key advantages of ultra-strong gradients for diffusion MRI, NeuroImage 182 (2018) 8–38, 10.1016/j.neuroimage.2018.05.047. [DOI] [PubMed] [Google Scholar]
- [98].Hennel F, Michael ES, Pruessmann KP, Improved gradient waveforms for oscillating gradient spin-echo (OGSE) diffusion tensor imaging, NMR Biomed. 34 (2021), 10.1002/nbm.4434 e4434. [DOI] [PubMed] [Google Scholar]
- [99].Solomon E, Liberman G, Nissan N, Frydman L, Robust diffusion tensor imaging by spatiotemporal encoding: Principles and in vivo demonstrations, Magn. Reson. Med 77 (2017) 1124–1133, 10.1002/mrm.26197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [100].Wu D, Liu D, Hsu YC, Li H, Sun Y, Qin Q, et al. , Diffusion-prepared 3D gradient spin-echo sequence for improved oscillating gradient diffusion MRI, Magn. Reson. Med 85 (2021) 78–88, 10.1002/mrm.28401. [DOI] [PubMed] [Google Scholar]
- [101].Yon M, Bao Q, Chitrit OJ, Henriques RN, Shemesh N, Frydman L, High-Resolution 3D in vivo Brain Diffusion Tensor Imaging at Ultrahigh Fields. Following Maturation on Juvenile and Adult Mice, Front. Neurosci 14 (2020), 10.3389/fnins.2020.590900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [102].Tax CMW, Bastiani M, Veraart J, Garyfallidis E, Okan IM, What’s new and what’s next in diffusion MRI preprocessing, NeuroImage 249 (2022), 10.1016/j.neuroimage.2021.1188301 18830. [DOI] [PMC free article] [PubMed] [Google Scholar]


