Abstract
Deep Learning-based computational pathology algorithms have demonstrated profound ability to excel in a wide array of tasks that range from characterization of well known morphological phenotypes to predicting non human-identifiable features from histology such as molecular alterations. However, the development of robust, adaptable and accurate deep learning-based models often rely on the collection and time-costly curation large high-quality annotated training data that should ideally come from diverse sources and patient populations to cater for the heterogeneity that exists in such datasets. Multi-centric and collaborative integration of medical data across multiple institutions can naturally help overcome this challenge and boost the model performance but is limited by privacy concerns among other difficulties that may arise in the complex data sharing process as models scale towards using hundreds of thousands of gigapixel whole slide images. In this paper, we introduce privacy-preserving federated learning for gigapixel whole slide images in computational pathology using weakly-supervised attention multiple instance learning and differential privacy. We evaluated our approach on two different diagnostic problems using thousands of histology whole slide images with only slide-level labels. Additionally, we present a weakly-supervised learning framework for survival prediction and patient stratification from whole slide images and demonstrate its effectiveness in a federated setting. Our results show that using federated learning, we can effectively develop accurate weakly-supervised deep learning models from distributed data silos without direct data sharing and its associated complexities, while also preserving differential privacy using randomized noise generation. We also make available an easy-to-use federated learning for computational pathology software package: http://github.com/mahmoodlab/HistoFL.
Keywords: Federated learning, Pathology, Computational pathology, Whole slide imaging, Split learning
1. Introduction
The emerging field of computational pathology holds great potential in increasing objectivity and enhancing precision of histopathological examination of tissue. Machine learning – and deep learning in particular – have demonstrated unprecedented performance in various pathology tasks such as characterization of a disease phenotype (Wang et al., 2020; Zhou et al., 2019; Anand et al., 2020; Bulten et al., 2020; Mahmood et al., 2019), quantification of the tumor microenvironment (Javed et al., 2020; Graham et al., 2019; Schapiro et al., 2017), prediction of survival (Muhammad et al., 2019) and treatment response (Niazi et al., 2019; Bera et al., 2019), and integration of genomics with histology for improved patient stratification (Chen et al., 2020; Mobadersany et al., 2018; Lazar et al., 2017). Thanks to the ability of such algorithms to mine sub-visual features – even beyond the scope of known pathological markers – deep learning models have managed to tackle challenging tasks such as estimating primary source for metastatic tumors of unknown origin, identify- ing novel features of prognostic relevance (Yamamoto et al., 2019; Pell et al., 2019; Bera et al., 2019), and predicting genetic mutations from histomorphologic images only, without the use of immunohistochemical staining (Coudray et al., 2018). Among various approaches, weakly-supervised methods such as attention MIL (Lu et al., 2019, 2020a) appear well-suited to potential adoption in clinical practice. Xiao et al. recently presented a censoring-aware deep ordinal regression method for survival prediction in computational pathology Xiao et al. (2020). These models learn from weak annotations in the form of image or patient-level labels which can include labels such as diagnosis or survival associated with the patient. Such information is readily available in clinical records and thus the data annotation does not introduce significant overhead over standard clinical workflow, in contrast to pixel-level annotations of regions of interest required by supervised models.
As in all machine learning affairs, the model’s accuracy and robustness can be significantly increased by incorporating diverse data reflecting variations in underlying patient populations, as well as data collection and preparation protocols. Specifically, in pathology, whole slide images (WSIs) used for computational analysis can exhibit immense heterogeneity. Such diversities arise from not only the patient group corresponding to the histology specimens and variations in the tissue preparation, fixation and staining protocols, but also different scanner hardware that are used for digitization. While it may be possible and desirable to gain increased exposure to such heterogeneity through agglomeration of medical data from multiple institutions into a centralized data repository in order to develop more generalizable models, data centralization poses challenges not only in the form of regulatory and legal concerns (e.g. differing standards for data interoperability may preclude data transfer among institutions Scheibner et al. (2020)) but also technical difficulties such as high cost of transfer and storage of huge quantities of data. The latter is particularly relevant for computational pathology at scale since just 500 gp WSIs can be as large as the entirety of ImageNet (Deng et al., 2009).
Federated learning (Yang et al., 2019; Konecˇny’ et al., 2016; McMahan et al., 2017; Rieke et al., 2020) offers means to mitigate these challenges by enabling algorithms to learn from decentralized data distributed across various institutions. In this way, sensitive patient data are never transferred beyond the safety of institutional firewalls, and instead, the model training and validation occur locally at each institution and only the model specifics (e.g. parameters or gradients) are transferred. In general, federated learning can be achieved through two approaches. 1) Master-server: a master-server is used to transfer the model to each node (i.e. participating institution), where the model trains for several iterations using the local data. The master-server then collects the model parameters from each node, aggregates them in some manner, and updates the parameters of the global model. Updated parameters are then transferred back to the local nodes for the next iteration. 2) Peer-to-peer: each node transfers the locally-trained parameters to some or all of its peers and each node does its own parameter aggregation. The benefit of the master-server approach is that all governing mechanisms are separated from the local nodes which allows for easier protocol updates and inclusion of new institutions. In contrast, the peer-to-peer approach is less flexible – since all the protocols must be agreed-on in advance – however, the absence of a single controlling entity might be preferred in some cases e.g. due to lower costs or greater decentralization.
Although the nodes never transfer data themselves – only the model specifics – if leaked or attacked these can be sufficient to indirectly expose sensitive private information. Data anonymization alone does not provide sufficient protection (Rocher et al., 2019) since parts of the training data can be reconstructed by inversion of model parameters (Carlini et al., 2019; Zhang et al., 2020), gradients (Zhu et al., 2019; Geiping et al., 2020), or through adversarial attacks (Wang et al., 2019; Hitaj et al., 2017). This is particularly worrisome in radiology where the medical scans can be used to reconstruct a patient’s face or body image. Even though histology data do not hold such a direct link with patient identity, it might still allow an indirect patient identification e.g. in the case of rare diseases. The design of countermeasures for increasing differential privacy is thus a very active field of research (Kaissis et al., 2020; Kairouz et al., 2019). A popular strategy in the medical field is a contamination of the input data (Cheu et al., 2019) or the model parameters (Dong et al., 2019) with certain levels of noise. This de- creases the individually recognizable information while preserving the global distribution of the data (Kaissis et al., 2020).
Though federated learning was originally proposed for non-clinical use, since its inception in Konecˇny’ et al. (2016), it has already appeared in some medical applications. These include large-scale multicenter studies of genomics (Mandl et al., 2020; Rehm, 2017; Jagadeesh et al., 2017), electronic health records (Brisimi et al., 2018; Choudhury et al., 2019a, b), or wearable health devices (Chen et al., 2020). In the field of medical imaging, federated learning is particularly popular in the neurosciences. So far it has been applied in tasks such as brain tumor (Li et al., 2019; Sheller et al., 2018) and brain tissue (Roy et al., 2019) segmentation, EEG signal classification (Ju et al., 2020), analysis of fMRI scans of patients with autism (Li et al., 2020b) or MRI scans of neurodegenerative disease (Silva et al., 2019). Further adoption of federated learning in other medical domains is strongly anticipated due to the increasing demand for large and inter-institutional studies.
One of the fields that would strongly benefit from the federated framework is computational pathology (Andreux et al., 2020b, a; Rieke et al., 2020). Since histopathologic diagnosis is the gold standard for many diseases, pathology data is largely available in almost any hospital. Federated learning would in principle enable deep learning models to learn from much larger and more diverse multi-institutional data sources without the challenges associated with data centralization and healthcare interoperability. Furthermore, while fully-supervised approaches are burdened by the need for time-costly pixel-level annotation based on pathologist expertise, weakly-supervised approaches such as MIL simplify collaborative efforts by alleviating the requirement for such human expertise and the burden of creating pixel-level labels under unified annotation protocol in all participating institutions.
Herin, we present the key contributions of our work as follows:
We present a large-scale computational pathology study to demonstrate the feasibility and effectiveness of privacy-preserving federated learning using thousands of gigapixel whole slide images from multiple institutions.
We account for the challenges associated with the lack of de- tailed annotations in most real world whole slide histopathology datasets and demonstrate how federated learning can be coupled with weakly-supervised multiple instance learning to perform both binary and multi- class classification problems (demonstrated on breast cancer and renal cell cancer histological subtyping) using only slide-level labels for supervision.
We extend the usage of attention-based pooling in multiple instance learning-based classification and present an interpretable, weakly-supervised framework for survival prediction (demonstrated on renal cell carcinoma patients) in computational pathology using whole slide images and patient-level prognostic information.
We further validate the effectiveness of weakly-supervised deep survival models in a federated framework, paving the way for the development of prognostic models trained on multi-institutional cohorts with diverse populations.
We also make available an easy-to-use federated learning for computational pathology software package: http://github.com/mahmoodlab/HistoFL
2. Methods
In this section, we will formulate our weakly-supervised federated multiple instance learning framework for performing privacy-preserving federated learning on data from across multiple institutions in the form of digitized gigapixel whole slide images.
2.1. Differential privacy and federated learning
In this problem, we want to develop deep learning models for performing predictive tasks on gigapixel WSIs by using data from different institutions. We denote data owned by institution i as Di, which we assume for simplicity, is simply a data matrix with a finite number of entries. Suppose there are in total B sites and we denote their corresponding data silo as D1, D2, . . ., DB. Since each medical institution will not share data with other parties due to various issues (e.g. institutional policies, incompatible data sharing protocols, technical difficulties associated with sharing large amount of data or fear of privacy loss), we cannot pool together their data and train a single deep learning model fcentralized for solving the desired task. Instead, our objective is to develop a federated learning framework where the data owners collaboratively train a model fglobal, in which each data owner does not need to share its data Di with others but can all benefit from the usefulness of the final model. In this paper, we adapted a master-server architecture, where each client node, representing each medical institution, locally utilizes the same deep learning architecture as one another and the global model, which we assume to be hosted on a central server hub. Each institution trains its respective model using local data and uploads the values of the trainable model parameters to the master server at a consistent frequency (i.e. once every one epoch of local training). We also adopt a randomized mechanism previously utilized on multi-site fMRI analysis (Li et al., 2020a), which allows each data owner to blur the shared weight parameters by a randomly noise vector zi to protect against leak-age of patient-specific information. After the master server receives all the parameters, it averages them in the global model and sends new parameters back to each local model for synchronization. Differential privacy is a popular definition of individual privacy (Dwork et al., 2014; Shokri and Shmatikov, 2015), which informally means that the attacker can learn virtually nothing about an individual sample if it were removed from or added to the dataset (Abadi et al., 2016). In this problem, it means when a data point di is removed from or added to the dataset Di, the attacker can not infer any information about di from the output of weights of model fglobal. Differential privacy provides a bound s to represent the level of privacy preference that each institution can control. Formally, it says (Dwork et al., 2006), given a real-valued function f, and two adjacent datasets Di, Di’ differing by exactly one example, i.e., , fsatisfies (ε, δ)- differential privacy if for any subset of outputs S:
| (1) |
where the introduction of the δ term relaxes the stricter notion of ε-differential privacy and allows the unlikely event of differential privacy being broken to occur with a small probability.
To satisfy (ε, δ)-differential privacy, first, we provide the definition of l2 sensitivity of f, denoted by Δ2(f) as the maximum difference in the outputs of f over all possible adjacent datasets Di, Di ’:
| (2) |
For arbitrary , as stated by Theorem 3.22 (Dwork et al., 2014), adding random noise to f that is generated from a Gaussian distribution with zero mean and standard deviation σ, i.e., , will result in f satisfying -differential privacy if and ln . After rewriting the two inequalities, in other words, for any choice of ε, (ε, δ) -differential privacy can be satisfied for f by using the Gaussian mechanism, where δ is related to the variance of the Gaussian noise distribution via:
| (3) |
In our federated learning setting, f involves a neural network consisting of many layers of trainable parameters making computing intractable. However, without loss of generality, if we assume , we see that for a given level of δ, increasing σ will enable a smaller ε to be satisfied. Following Li et al., (2020b), we let , where η is the standard deviation of the weight parameters of each layer in the neural network, effectively linking α, a parameter adjustable for participating institutions, to the level of differential privacy protection.
2.2. Data preprocessing
We processed and analyzed all of our WSI data at 20 × magnification. Due to the lack of labeled ROIs and the intractable computational expense of deploying a convolutional neural network (CNN) directly to the whole spatial extent of each WSI, we utilize a form of weakly-supervised machine learning known as multiple instance learning (MIL). Under the MIL framework, each WSI is treated as a collection (bag) of smaller regions (instances), enabling the model to learn directly from the bag-level label (diagnosis or survival information) during training. The details of the MIL-inspired weakly-supervised learning algorithms we use are described in Sections 2.3 and 2.4. To construct the MIL bags, we utilize the CLAM (Lu et al., 2020a) WSI processing pipeline to automatically segment the tissue regions in each WSI and divide them into M 256 × 256 image crops (instances), where M varies with the amount of tissue content in each slide. To overcome the computational challenges resulting from the enormous sizes of gigapixel WSI bags, each 256 × 256 RGB instance further undergoes dimensionality-reduction via a pretrained ResNet50 CNN encoder (truncated after the 3rd residual block for spatial average pooling), and is embedded as a 1024-dimensional feature vector for efficient training and inference. Accordingly, each WSI in the dataset is represented by a M × 1024 matrix tensor.
For survival prediction, all WSIs corresponding to each patient case are analyzed collectively, i.e., for a case with N WSIs represented by individual bags of size respectively, the bags are concatenated along the first dimension to form a single patient bag of dimensions .
2.3. Weakly-supervised learning on WSIs
We adopted a multiple instance learning-based framework for weakly-supervised classification and survival prediction and use it as the basis for performing federated learning on gigapixel WSIs. We begin by describing the weakly-supervised learning algorithms in the case of a single local model (no federated learning). Each model consists of a projection module , an attention module , and a prediction layer . The projection module consists of sequential, trainable fully-connected layers that project the fixed feature embeddings obtained using a pretrained feature encoder into a more compact, feature space specific to histopathology images of the chosen disease model. Given the jth incoming WSI/patient bag of Mj patch embeddings in the form of a matrix tensor, for simplicity, we use a single linear layer to project incoming patch-level embeddings into a 512-dimensional latent space, denoted by . The attention module uses attention-based pooling (Ilse et al., 2018) to identify information rich patches/locations from the slides and aggregates their information into a single global representation for making a prediction at the bag level. We use the gated variant of the attention network architecture introduced by Ilse et al. (2018). Accordingly, consists of 3 fully-connected layers with weights Ua, Va and Wa and learns to assign an attention score to each patch embedding (each row entry in Hj), indicating its contribution to the bag-level feature representation , where represents the score for the mth patch and is given by:
| (4) |
Alternatively, the attention score vector for the whole bag is denoted by: . Subsequently, the bag-level representation is calculated by using the predicted attention scores as weights for averaging all the feature embeddings in the bag as:
| (5) |
We used a 256-dimensional representation for the hidden layers in the attention network and apply Dropout with p = 0.25 to these activations for regularization - namely, , and . Lastly, the prediction layer maps the bag representation to predictions logits sj, using a different activation function and loss function for classification and survival prediction: . The methodological details are described below.
Weakly-supervised classification For weakly-supervised classification, we use the prediction layer to predict the unnormalized class-probability logits sj, which are then super-vised using the slide-level label Yj by applying the softmax activation and computing the standard cross-entropy loss.
Weakly-supervised survival prediction For weakly-supervised survival prediction using right-censored survival data, we consider discrete time intervals based on quantiles of event times for uncensored patients. More formally, we first consider the continuous time scale, where each labeled patient entry in the dataset, indexed by j, consists of a follow-up time and a binary censorship status cj where cj = 1 indicates censorship (the event did not occur by the end of the follow-up period) while cj = 0 indicates that the event occurred precisely at time . Next, we partition the continuous time scale into R non-overlapping bins: and discretize accordingly where:
| (6) |
In our study, we investigated R ∈ {2, 4, 6, 8} (results presented in Section 3.5), where for each choice of R (number of bins), are determined based on quantiles of event times of uncensored patients. For simplicity, from now on we refer to a patient’s discrete survival time simply as Tj and to be consistent with the notation we used for classification, we refer to the ground truth label as Yj. Given a patient’s bag-level feature representation as calculated by the model, the prediction layer is responsible for modeling the hazard function defined as:
| (7) |
which relates to the survival function through:
| (8) |
Since we consider the label set to be the support of the hazard function, and R corresponding to number of bins of event times, is a linear layer with weight parameters Finally, given logits , the sigmoid activation is applied to predict hazard distribution since it represents conditional probabilities, which are confined to positive real-values in the range of [0, 1]. For model optimization, we maximize the log likelihood function corresponding to a discrete survival model (Tutz et al., 2016), which is written as:
| (9) |
By rewriting , the loss we minimize based on the log likelihood function (Zadeh and Schmid, 2020) can be expressed as:
| (10) |
During training, we additionally upweight the contribution of uncensored patient cases by minimizing a weighted sum of L and , which is defined by the terms:
| (11) |
Accordingly, the loss we optimize for weakly-supervised sur- vival prediction is:
| (12) |
2.4. Weakly-supervised federated learning with differential privacy
For both classification and survival prediction, we train the models on each client server within a federated learning setup, where each model is trained locally and the weights of the model are collected each epoch and aggregated to update the central model. The central model then sends back the new weights to each client model (Fig. 1). To preserve the differential privacy of the individual data located on each client server, we utilize a randomized mechanism, i.e., the Gaussian mechanism which we introduced in Section 2.1. Hereby, our algorithm for collaboratively training server model and client models is shown in Algorithm 1.
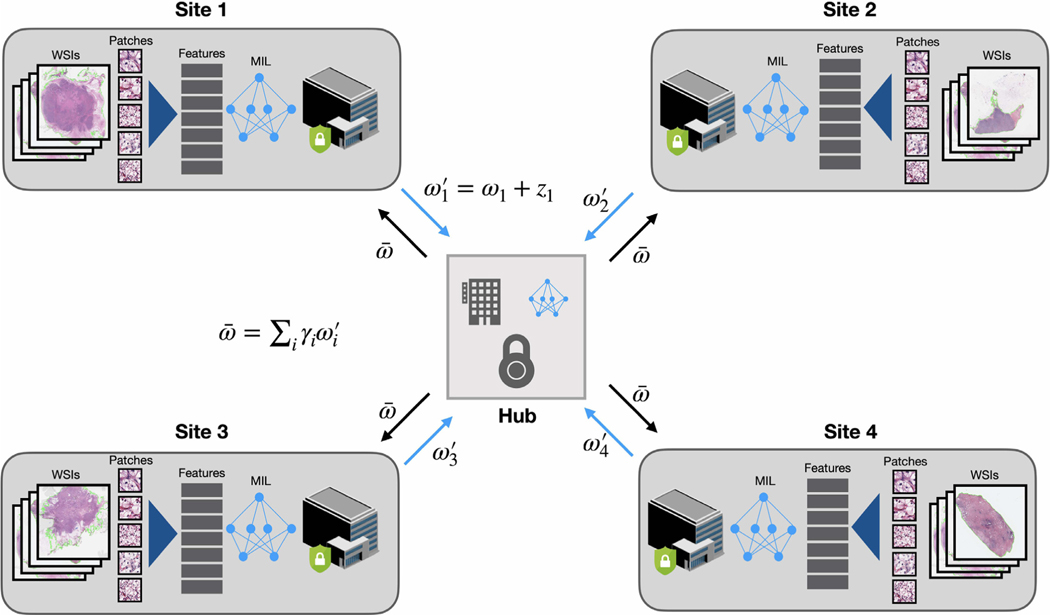
Fig. 1.
Overview of the weakly-supervised multiple instance learning in a federated learning framework. At each client site, for each WSI, the tissue regions are first automatically segmented and image patches are extracted from the segmented foreground regions. Then all patches are embedded into a low-dimension feature representation using a pretrained CNN as the encoder. Each client site trains a model using weakly-supervised learning on local data (requires only the slide-level or patient-level labels) and sends the model weights each epoch to a central server. Random noise can be added to the weight parameters before communicating with the central hub for differential privacy preservation. On the central server, the global model is updated by averaging the model weights retrieved from all client sites. After the federated averaging, the updated weights of the global model is then sent to each client model for synchronization prior to starting the next federated round.
In the proceeding section, we demonstrate the feasibility, adaptability and interpretability of attention-based multiple instance federated learning on three different computational pathology problems: (A) Breast Invasive Carcinoma (BRCA) subtyping (B) Renal Cell Carcinoma (RCC) subtyping (C) Clear Cell Renal Cell Carcinoma (CCRCC) survival prediction.
Algorithm 1.
Privacy-preserving federated learning using attention-based multiple instance learning for multi-site histology-based classification and survival prediction.
| Input: |
| I. WSI Data and weak annotation (e.g. patient diagnosis or prognosis) scattered among B participating institutional sites: |
| , where |
| represents the set of Ni. pairs of WSI data and corresponding label for training stored at site i (in survival prediction, Xi,j. is the set of all diagnostic WSIs for patient j whereas in classification, it is a single WSI). We use |
| to denote WSI data-label pair after pre-processing (patching and feature extraction via a pretrained CNN feature encoder). |
| II. Neural network models on local clients and global model , stored on the central server. Each model , consists of a projection module , an attention module and prediction layer . We denote the weights of the local models as and weights of the global model as . |
| III. Noise generator , which generates Gaussian random noise where a denotes the noise level for and n is the standard deviation of a neural network weight matrix. |
| IV. Number of training epochs or federated rounds, K. |
| V. Optimizers that update the model weights w.r.t a suitable loss metric L using gradient descent. |
| VI. Weight coefficient for each client during federated averaging, e.g. . |
| 1. initialize all model weights |
| 2. for to K do |
| 3. for to B do |
| 4. for to Ni do |
| 5. |
| 6. end for |
| 7. end for |
| 8. |
| 9. for to B do |
| 10. |
| 11. end for |
| 12. end for |
| 13. return global model |
3. Experiments and results
3.1. Dataset description
Weakly-supervised classification.
To evaluate the proposed federated learning framework for weakly-supervised classification in histopathology, we examined two clinical diagnostic tasks for two separate disease models, namely, Renal Cell Carcinoma (RCC) and Breast Invasive Carcinoma (BRCA). For both tasks, we used publicly available WSIs from the TCGA (The Cancer Genome Atlas) in addition to in-house data collected at the Brigham and Women’s Hospital for model development and evaluation. In all cases, each gigapixel WSI is associated with a single ground truth slide-level diagnosis and no pixel or ROI-level annotation available.
Breast cancer dataset.
For the first binary task of classifying primary Breast Invasive Carcinoma as either lobular or ductal morphologial subtypes, 1056 FFPE dianostic WSIs (211 lobular and 845 ductal) were retrieved from the TCGA BRCA (Breast Invasive Carcinoma) study and our in-house dataset consists of 1070 WSIs of primary breast cancer (158 lobular and 912 ductal). Accordingly, in total we used 2126 breast WSIs (369 lobular and 1757 ductal).
Renal cell cancer dataset In the second task of multi-class classification of Renal Cell Carcinoma into clear cell (CCRCC), papillary cell (PRCC) and chromophobe cell (CHRCC) morphological subtypes, we collected 937 WSIs (519 CCRCC, 297 PRCC and 121 CHRCC) from the corresponding studies in TCGA and our in-house dataset consists of 247 WSIs of primary Renal cell carcinoma (184 CCRCC, 40 PRCC and 23 CHRCC). In total we used 1184 kidney WSIs (703 CCRCC, 337 PRCC and 144 CHRCC).
Weakly-supervised survival prediction.
We also examined federated learning for weakly-supervised survival prediction based on histopathology. Specifically, for patients diagnosed with renal clear cell carcinoma, we used right-censored, overall survival data from the TCGA-KIRC available via the cbio- portal. In total, 511 patient cases were retrieved from TCGA-KIRC. All diagnostic WSIs corresponding to each patient case were used for analysis.
3.2. Experiments on multi-institutional WSI data
In each of the two weakly-supervised classification tasks, we considered four distinct “institutional sites”. These sites were identified by first naturally considering all in-house BWH data as one distinct institutional site. Then, for each TCGA cohort, we identified the tissue source site for each patient case. For the purpose of simulating federated learning across multiple institutions, we then randomly partitioned the set of unique tissue source sites into 3 non-overlapping, roughly equal-sized subsets, and grouped together the data corresponding to each subset of tissue source sites to serve as 3 distinct institutional sites. Similarly, for CCRCC survival prediction, we used 3 institutional sites created by randomly partitioning the tissue source sites that contributed to the TCGA-KIRC cohort. The details of these partitions are summarized below for each task (Tables 1–3).
Table 1.
Partition for BRCA subtyping (number of WSIs).
| ILC | IDC | Total | |
|---|---|---|---|
|
| |||
| TCGA Site 1 | 56 | 155 | 211 |
| TCGA Site 2 | 46 | 268 | 314 |
| TCGA Site 3 | 109 | 422 | 531 |
| BWH | 158 | 912 | 1070 |
| Total | 369 | 1757 | 2126 |
Table 3.
Partition for CCRCC survival prediction (number of cases).
| Uncensored | Censored | Total | |
|---|---|---|---|
|
| |||
| TCGA Site 1 | 16 | 88 | 104 |
| TCGA Site 2 | 27 | 49 | 76 |
| TCGA Site 3 | 128 | 203 | 331 |
| Total | 171 | 340 | 511 |
Once the institutional sites were identified, the dataset is then randomly partitioned into a training, validation and test set, respectively consisting of 70, 15 and 15% of patient cases from each site, repeated using 5 different random seeds. For classification, given the class-imbalance nature of the datasets, within each institutional site, stratified sampling is used to ensure sufficient representation of minority classes across the training, validation and test set. Additionally, if a single patient case contains multiple diagnostic slides, all of them were drawn together into the same set when that patient is sampled. Similarly, for survival prediction, sampling is stratified based on both the discretized follow-up time (binned based on quartiles of event times of uncensored patients) and the censorship status.
For each task, we used the model architecture and loss function as described in detail in Section 2.3. To train each local model, we used the Adam optimizer with default hyperparamters, a learning rate of 2e-4 and l2 weight decay of 1e-5 for all experiments. For survival prediction, β, which controls how much the contribution of uncensored patients should be upweighted, was set to 0.15. Additionally, we monitored the validation performance each epoch and performed early stopping on the global model when it does not improve for 20 consecutive epochs (federated rounds), but only after it has been trained for at least 35 epochs. The model check-point with the best validation performance (lowest loss for classification and best c-index for survival prediction) was then used to evaluate on the held-out test set. For each task, we investigated 3 scenarios: (1) training on data from a single institution, (2) training a single model by centralizing or pooling together all data (no federated learning) and (3) training on data from all institutions using federated averaging, as described in Section 2.4 and outlined in details in Algorithm 1.
For scenario 3), while the originally proposed federated aver- aging algorithm (McMahan et al., 2017) weighs the contribution of each local model by its respective number of training samples when updating the weights of the central model, Li et al. (2020a) chose to weigh each local model equally . In our study, we stick to the design of the original algorithm but also investigate the performance between weighted averaging vs. simple averaging in Section 3.6, where results show minimal difference between the two design choices. We also studied changing the strength of Gaussian random noise added to local model weights during federated averaging, and its effect on the performance of the central model. As described in Section 2.1, for each model fi, we generated Gaus- sian noise where η is the standard deviation of the weight parameters in each individual layer of the network and α controls the noise level. In our experiments, we varied . In the next section, we present results demonstrating the effectiveness of weakly-supervised fed- erated learning for both binary and multi- class classification, as well as survival prediction.
3.3. Experimental results
We evaluated our proposed weakly-supervised, federating learning framework on both a multi-class and a binary classification problem (Figs. 2, 3, Tables 4 and 5) as well as survival prediction (Fig. 4 and Table 6) and demonstrated the feasibility of performing privacy-preserving, federated learning on WSI data in all tasks.
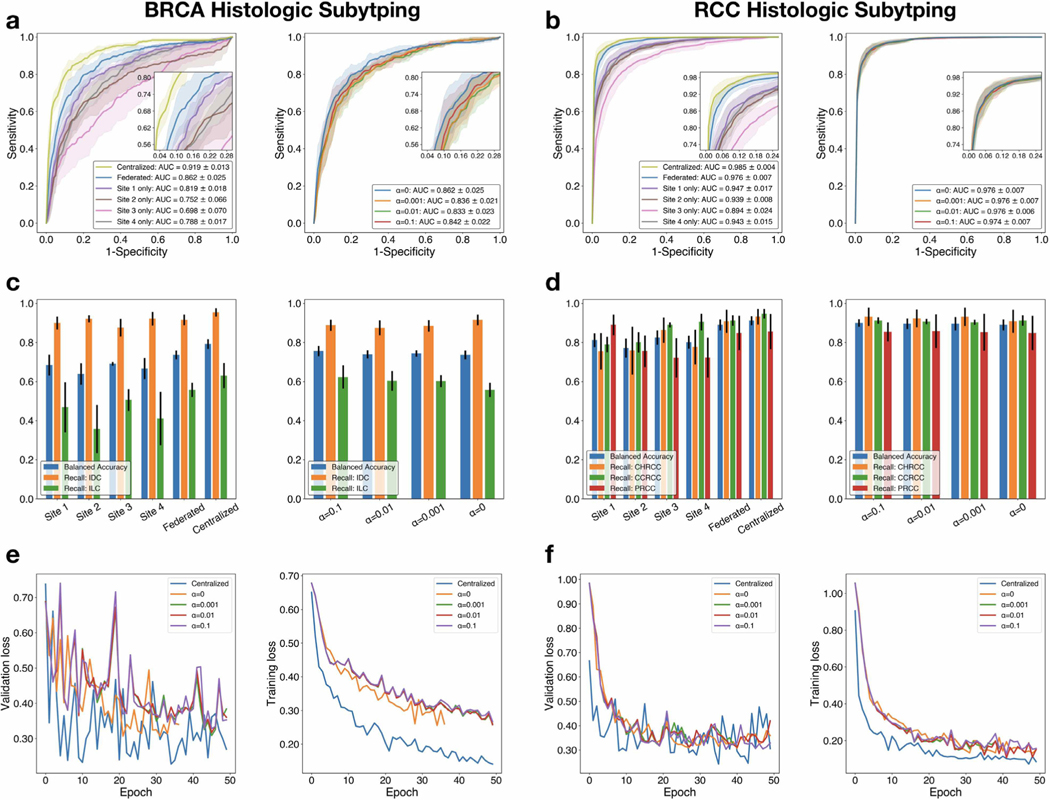
Fig. 2.
Performance, comparative analysis and loss curves. a-c, d-f The classification performance and loss curves of BRCA histologic subtyping and RCC histological subtyping, respectively. Top: ROC curves are generated on the test sets for models trained using a centralized database, federated learning (with different levels of Gaussian random noise added during federated weight averaging) and using training data local to each institution individually. The AUC score (averaged over 5-fold cross-validation, s.d.) is reported for each experiment; macro-averaging is used for the multi-class classification of RCC subytping. Using multiinstitutional data and federated learning, we achieved a mean test AUC between 0.833 and 0.862 on BRCA histologic subtyping and an AUC of between 0.974 and 0.976 on RCC histologic subtyping respectively. Middle: Balanced accuracy score and the sensitivity (recall) for each class (IDC: Invasive Ductal Carcinoma, ILC: Invasive Lobular Carcinoma for BRCA subtyping; CHRCC: Chromophobe Renal Cell Carcinoma, CCRCC: Clear Cell Renal Cell Carcinoma, PRCC: Papillary Renal Cell Carcinoma for RCC subtyping) is plotted for all experiments to assess model performance when accounting for class-imbalance in the respective test set. Error bars show s.d. from 5-fold cross-validation. Bottom: For each experiment, the training loss and validation loss is monitored over each epoch before early stopping is triggered (see Section 3.2). Loss curves are shown for a single cross-validation fold from each task. Federated learning is observed to converge to a higher training and validation loss value in both tasks.
Fig. 3.
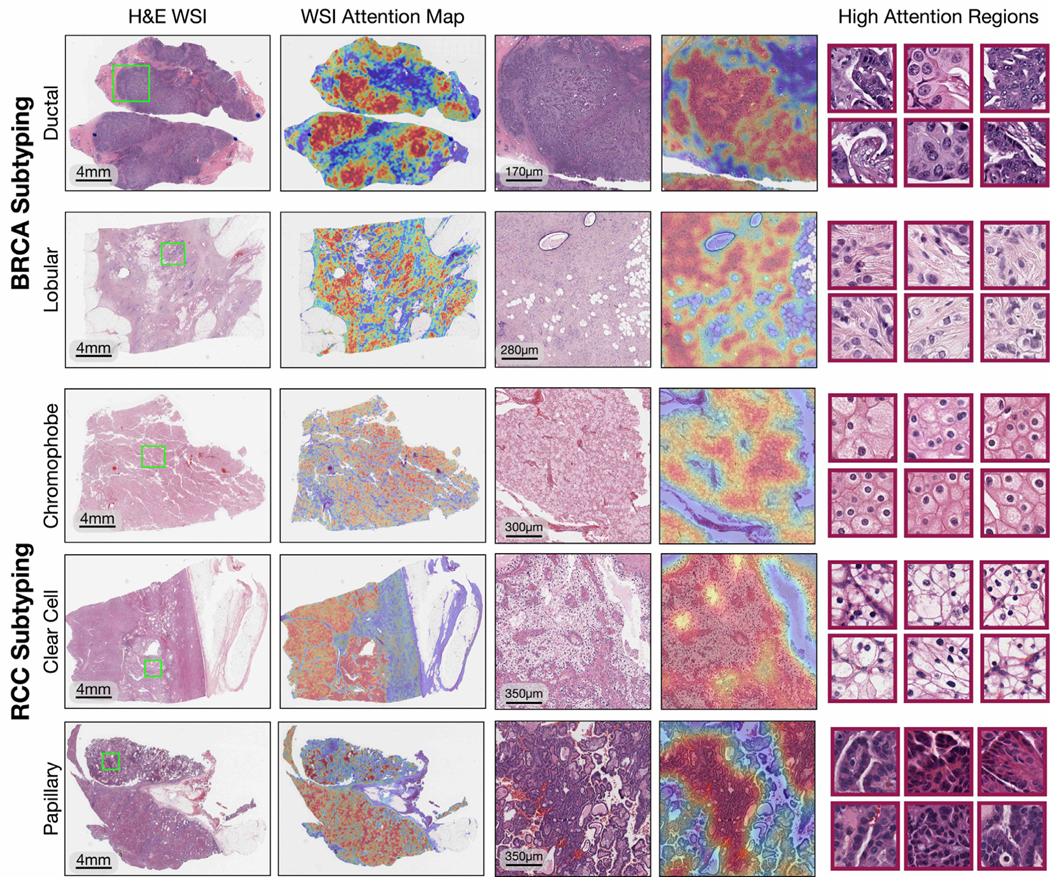
Interpretability and visualization for weakly-supervised federated classification. In order to interpret and validate the morphological features learned by the model for RCC and BRCA histologic subtype classification, for randomly selected WSIs in the respective test set, the model trained with privacy-preserving federated learning (α= 0.01) is used to generate attention heatmaps using 256 × 256 sized tissue patches tiled at the 20 × magnification with a 90% spatial overlap. For each WSI, the attention scores predicted for all patches in the slide are normalized to the range of [0, 1] by converting them to percentiles. For subtype classification, patches with high attention refers to image regions of high diagnostic relevance used for class prediction. The normalized scores are then mapped to their respective spatial location in the slide. Finally, an RGB colormap is applied (red: high attention, blue: low attention), and the heatmap is overlaid on top of the original H&E image for display. For BRCA, patches of the most highly attended regions (red border) exhibited well-known tumor morphology of invasive ductal carcinoma (round cells with varying degrees of polymorphism arranged in tubules, nests, or papillae) and invasive lobular carcinoma (round and signet-ring cells with intracellular lumina and targetoid cytoplasmic mucin arranged in a single-file or trabecular pattern). For RCC, highly attended regions exhibited well-known tumor morphology of chromophobe RCC (large, round to polygonal cells with abundant, finely-reticulated to granular cytoplasm and perinuclear halos), clear cell RCC (large, round to polygonal cells with clear cytoplasm and distinct, but delicate cell borders), and papillary RCC (round to cuboidal cells with prominent papillary or tubulopapillary architecture with fibrovascular cores). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Table 4.
BRCA subtyping test performance reported as five-fold mean (s.d.).
| AUC ↑ | Error ↓ | bACC ↑ | F1 ↑ | mAP ↑ | Cohen’s κ ↑ | |
|---|---|---|---|---|---|---|
|
| ||||||
| Site 1 only | 0.819±0.018 | 0.169±0.015 | 0.667±0.054 | 0.453±0.092 | 0.508±0.026 | 0.359±0.083 |
| Site 2 only | 0.752±0.066 | 0.178±0.018 | 0.684±0.053 | 0.478±0.074 | 0.454±0.075 | 0.373±0.079 |
| Site 3 only | 0.698±0.070 | 0.180±0.015 | 0.639±0.055 | 0.405±0.107 | 0.386±0.065 | 0.305±0.105 |
| Site 4 only | 0.788±0.017 | 0.190±0.029 | 0.691±0.009 | 0.490±0.013 | 0.441±0.050 | 0.375±0.031 |
| Centralized | 0.919±0.013 | 0.104±0.012 | 0.792±0.025 | 0.684±0.032 | 0.761±0.043 | 0.623±0.037 |
| Federated | 0.862±0.025 | 0.149±0.023 | 0.736±0.023 | 0.575±0.043 | 0.610±0.076 | 0.485±0.057 |
| Federated, α = 0.001 | 0.836±0.021 | 0.166±0.023 | 0.744±0.016 | 0.568±0.032 | 0.537±0.049 | 0.467±0.045 |
| Federated, α = 0.01 | 0.833±0.023 | 0.173±0.028 | 0.739±0.021 | 0.557±0.036 | 0.535±0.048 | 0.451±0.052 |
| Federated, α = 0.1 | 0.842±0.022 | 0.159±0.021 | 0.756±0.026 | 0.585±0.036 | 0.550±0.053 | 0.488±0.048 |
| Federated, α = 1 | 0.657±0.033 | 0.426±0.210 | 0.582±0.051 | 0.337±0.046 | 0.294±0.038 | 0.127±0.076 |
Table 5.
RCC subtyping test performance reported as five-fold mean (s.d.).
| AUC ↑ | Error ↓ | bACC ↑ | F1 ↑ | mAP ↑ | Cohen’s κ ↑ | |
|---|---|---|---|---|---|---|
|
| ||||||
| Site 1 only | 0.947±0.017 | 0.165±0.013 | 0.802±0.033 | 0.813±0.021 | 0.903±0.026 | 0.704±0.029 |
| Site 2 only | 0.939±0.008 | 0.185±0.012 | 0.812±0.036 | 0.805±0.023 | 0.898±0.019 | 0.685±0.027 |
| Site 3 only | 0.894±0.024 | 0.219±0.038 | 0.772±0.049 | 0.762±0.050 | 0.817±0.035 | 0.625±0.063 |
| Site 4 only | 0.943±0.015 | 0.163±0.032 | 0.825±0.037 | 0.815±0.039 | 0.899±0.028 | 0.715±0.057 |
| Centralized | 0.985±0.004 | 0.081±0.018 | 0.912±0.023 | 0.910±0.019 | 0.970±0.009 | 0.856±0.033 |
| Federated | 0.976±0.007 | 0.106±0.012 | 0.890±0.028 | 0.881±0.015 | 0.956±0.015 | 0.815±0.025 |
| Federated, α = 0.001 | 0.976±0.007 | 0.107±0.025 | 0.896±0.034 | 0.883±0.030 | 0.956±0.014 | 0.814±0.046 |
| Federated, α = 0.01 | 0.976±0.006 | 0.105±0.017 | 0.896±0.027 | 0.885±0.021 | 0.954±0.015 | 0.818±0.033 |
| Federated, α = 0.1 | 0.974±0.007 | 0.101±0.010 | 0.900±0.020 | 0.891±0.009 | 0.953±0.014 | 0.823±0.020 |
| Federated, α = 1 | 0.789±0.062 | 0.553±0.180 | 0.402±0.090 | 0.266±0.102 | 0.661±0.077 | 0.068±0.071 |
Fig. 4.
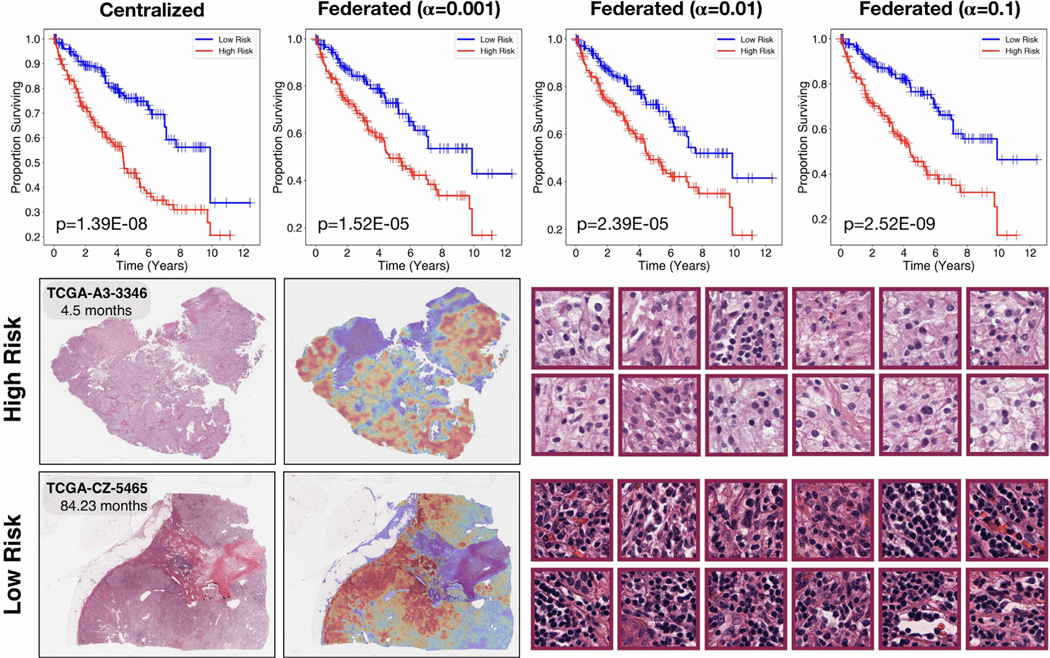
Patient stratification and interpretability for weakly-supervised federated survival prediction. Patients in the test set were stratified into high risk and low risk groups using the median (50% percentile) of the model’s predicted risk score distribution as the cutoff and the log-rank test was used to assess the statistical significance between survival distributions of the resulting risk groups. Top: increasing α by over two orders of magnitude for stronger guarantees on differential privacy did not eliminate the model’s ability to stratify patients into statistically significantly (p -value < 0.05) different risk groups. Bottom: exemplars of Clear Cell Renal Cell Carcinoma patients predicted as high-risk and low-risk respectively by the model, the original H&E (left), attention-based heatmap (center), and highest-attention patches (right). As compared to the subtyping classification problem, since survival analysis is an ordinal regression problem, the high attention patches correspond to regions with high prognostic relevance in stratifying patients into low versus high risk groups. The highest attention patches for the high-risk case focus predominantly on the tumor cells themselves, while the highest attention patches for the low risk case focus predominantly on lymphocytes within the stroma and directly interfacing with tumor cells, which corroborates with the known prognostic relevance of tumor-immune co-localization in pathology.
Table 6.
CCRCC survival prediction test performance reported as five-fold mean (±s.d.).
| c-Index | AUC | P-Value | |
|---|---|---|---|
|
| |||
| Site 1 only | 0.502±0.018 | 0.513±0.032 | 0.937 |
| Site 2 only | 0.506±0.017 | 0.520±0.022 | 0.662 |
| Site 3 only | 0.645±0.064 | 0.674±0.077 | 9.14 × 10−4 |
| Centralized | 0.692±0.043 | 0.729±0.046 | 1.39 × 10−8 |
| Federated, α = 0 | 0.683±0.064 | 0.719±0.070 | 2.86 × 10−8 |
| Federated, α = 0.001 | 0.639±0.090 | 0.664±0.103 | 1.52 × 10−5 |
| Federated, α = 0.01 | 0.648±0.099 | 0.676±0.111 | 2.39 × 10−5 |
| Federated, α = 0.1 | 0.647±0.085 | 0.672±0.098 | 2.52 × 10−9 |
| Federated, α = 1 | 0.508±0.036 | 0.504±0.044 | 0.805 |
In both BRCA subtyping (Table 4) and RCC subtyping (Table 5), the model performance is evaluated using a wide variety of classification metrics including the AUC of the ROC curve, mean average precision (mAP), classification error, F1 score, balanced accuracy (bAcc) and Cohen’s κ (macro-averaging is used to extend binary classification metrics to multi-class classification in the case of RCC subtyping). We found that the model performance benefited significantly from training on multi-institutional data using federated learning, compared to learning from data within a single institution. In fact, we found the models trained using federated learning to be generally competitive in performance even when compared to scenario 2), where model is trained by first centralizing (sharing) all training data from each institution. This is true even when different levels of random noise are applied for privacy preservation. For , for BRCA subtyping, the mean test AUC ranged from 0.833 to 0.862 when using federated learning for different levels of random noise and for RCC subtyping, the macro-averaged test AUC ranged from 0.974 to 0.976. In addition to strong performance, in Fig. 3, we also demonstrated that models trained using privacy-preserving federated learning can saliently localize regions of high diagnostic relevance and identify morphological features characteristic of each underlying tumor subtype. However, consistent with previous studies (Li et al., 2020b), we found that the model performance significantly deteriorated when α was set too high (e.g., α = 1), showing that there is indeed a trade off between model performance and privacy protection.
For survival prediction, we evaluated the model performance using the c-Index, which measures the concordance in ranking patients by their assigned risk w.r.t. their ground truth survival time, as well as the average cumulative/dynamic AUC (Hung and Chiang, 2010) for time dependent ROC curves, which quantifies the ability of a model to distinguish subjects who fail by a given time with subjects who fail after this time, across many time points. Additionally, based on the predicted risk score for each patient in the test set, we performed hypothesis testing using the log-rank test to assess whether each model can stratify patients into distinct high risk and low risk groups (cutoff based on 50th percentile of the model’s predicted risk scores) that resulted in statistically significantly different survival distributions (Table 6). When trained using data from a single institution, only 1 out of 3 institutions was able to yield a model that can stratify patients into distinct survival groups based on predicted risk scores. Notably, we observed that the model trained using data local to site 3 delivered performance comparable to that of centralized training and using federated learning. This can likely be attributed to site 3 having a much larger local dataset (n = 331) compared to the other 2 sites (n = 104 and n = 76 respectively). Similar dataset-size imbalance among different participating institutions frequently occurs in the real-world and is also reflected in the imbalanced distribution of patient cases among the original tissue source sites in the TCGA. In settings where the data at a single institution are insufficient (e.g. site 1 and 2) in either size or diversity to yield a meaningful, generalizable model, soliciting data from collaborating institutions or other external sources may be necessary. On the other hand, we found that federated learning can overcome this challenge as all models trained in the federated framework (with the exception of when using α = 1) resulted in statistical significance (p-value < 0.05) and produced reasonable performance both in terms of c-Index values and average cumulative/dynamic AUC.
Similar to classification, we visualized attention heatmaps over the entire WSI for low risk (long survival) and high risk (short sur-vival) patients in order to interpret the regions and morphological features learned by the weakly-supervised model to be of high prognostic relevance (Fig. 4).
3.4. Intra- and inter-center performance
The ability of a trained AI model to generalize to unseen, heterogeneous data with population and institutional-site specific variations is not only desirable but also crucial to its reliability and usability in real-world settings. As such, for both classification and survival prediction tasks, we examine more closely the intra- versus inter-center performance of different approaches. As expected, federated learning not only enables better generalization on average, as measured in terms of both micro- and macro-averaged scores (ROC AUC for classification and c-indices for survival prediction) across all sites, but is also mostly competitive in performance against models developed using single-site data on their respective intra-center portion of the test data (Tables 7, 8, 9.)
Table 7.
BRCA subtyping performance tested on intra vs. inter-site test data, reported as five-fold mean (±s.d.).
| Site 1 | Site 2 | Site 3 | Site 4 | All (Macro-avg) | All (Micro-avg) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Centralized | 0.929±0.034 | 0.883±0.055 | 0.887±0.060 | 0.938±0.022 | 0.909±0.013 | 0.919±0.013 |
| Site 1 only | 0.841±0.026 | 0.776±0.063 | 0.786±0.074 | 0.853±0.023 | 0.814±0.022 | 0.819±0.018 |
| Site 2 only | 0.703±0.143 | 0.739±0.050 | 0.782±0.045 | 0.847±0.039 | 0.768±0.052 | 0.752±0.066 |
| Site 3 only | 0.620±0.108 | 0.713±0.132 | 0.772±0.084 | 0.798±0.077 | 0.726±0.085 | 0.698±0.070 |
| Site 4 only | 0.806±0.026 | 0.704±0.048 | 0.828±0.045 | 0.853±0.042 | 0.798±0.031 | 0.788±0.017 |
| Federated | 0.859±0.046 | 0.838±0.077 | 0.837±0.041 | 0.919±0.024 | 0.863±0.024 | 0.862±0.025 |
Table 8.
RCC subtyping performance tested on intra vs. inter-site test data, reported as five-fold mean (±s.d.).
| Site 1 | Site 2 | Site 3 | Site 4 | All (Macro-avg) | All (Micro-avg) | |
|---|---|---|---|---|---|---|
|
| ||||||
| Centralized | 0.992±0.007 | 0.978±0.012 | 0.982±0.015 | 0.983±0.005 | 0.984±0.007 | 0.985±0.004 |
| Site 1 only | 0.981±0.019 | 0.928±0.023 | 0.975±0.016 | 0.947±0.018 | 0.958±0.012 | 0.947±0.017 |
| Site 2 only | 0.932±0.032 | 0.976±0.021 | 0.872±0.021 | 0.950±0.015 | 0.933±0.009 | 0.939±0.008 |
| Site 3 only | 0.943±0.020 | 0.846±0.057 | 0.980±0.021 | 0.877±0.050 | 0.911±0.026 | 0.894±0.024 |
| Site 4 only | 0.958±0.021 | 0.914±0.032 | 0.922±0.036 | 0.984±0.006 | 0.945±0.016 | 0.943±0.015 |
| Federated | 0.990±0.008 | 0.967±0.013 | 0.971±0.016 | 0.985±0.004 | 0.978±0.007 | 0.976±0.007 |
Table 9.
CCRCC survival prediction performance tested on intra vs. inter-site test data, reported as five-fold mean (±s.d.).
| Site 1 | Site 2 | Site 3 | All (Micro-avg) | All (Macro-avg) | |
|---|---|---|---|---|---|
|
| |||||
| Centralized | 0.577±0.185 | 0.653±0.148 | 0.709±0.067 | 0.692±0.043 | 0.646±0.068 |
| Site 1 only | 0.463±0.132 | 0.449±0.070 | 0.522±0.039 | 0.502±0.018 | 0.478±0.055 |
| Site 2 only | 0.475±0.076 | 0.566±0.062 | 0.491±0.029 | 0.506±0.017 | 0.511±0.028 |
| Site 3 only | 0.651±0.119 | 0.573±0.119 | 0.685±0.067 | 0.645±0.064 | 0.636±0.061 |
| Federated | 0.594±0.200 | 0.596±0.177 | 0.729±0.062 | 0.683±0.064 | 0.640±0.097 |
3.5. Comparison of weakly-supervised survival prediction and existing strategies
In this section, we investigate the effectiveness of the proposed weakly-supervised survival prediction method for different hyper-parameter choices, and in comparison with existing strategies such as manual grading by pathologists (low vs. high fuhrman nuclear grade) in combination with other covariates such as age and gender on the aforementioned TCGA-KIRC dataset (n = 511). Both the “Grade” only and “Grade + Age + Gender” methods are trained based on the Cox proportional hazard models using the same 5-fold splits as the weakly-supervised survival models are trained in the “centralized” set- ting (without using federated learning). We observed that in general the performance difference between the deep learning model trained using different values of R are under a few percents, with R = 8 performing the best for the particular task (Table 11). Additionally we note that the cox proportional hazard model based on nuclear grade lags behind the weakly- supervised deep learning-based approach, and only matches its performance when combined with additional variables including age and gender, beyond histologic features made available to the deep learning model.
Table 11.
Survival prediction performance for different choices of R and comparison with existing approaches, reported as five-fold mean (±s.d.).
| c-Index | AUC | P-Value | |
|---|---|---|---|
|
| |||
| Grade | 0.648±0.047 | 0.668±0.058 | 0.272 |
| Grade + Age + Gender | 0.693±0.050 | 0.716±0.065 | 0.193 |
| R = 2 | 0.681±0.031 | 0.708±0.044 | 1.28 × 10−8 |
| R = 4 | 0.685±0.020 | 0.723±0.022 | 6.38 × 10−6 |
| R = 6 | 0.678±0.033 | 0.713±0.033 | 7.58 × 10−8 |
| R = 8 | 0.692±0.043 | 0.732±0.048 | 1.39 × 10−8 |
3.6. Ablating hyperparamter choices in federated averaging
Instead of aggregating the weights of local models after each epoch, a less frequent communication pace can be used. We investigated model performance for each task by varying E, the number of epochs each local model is updated before communicating with the central model for aggregation, for E ∈ {1, 2, 4, 8}. As shown in Table 10, for classification tasks, the resulting performance shows minimal difference for larger E (less frequent communication) while survival prediction a decrease in c-indices of around 2 – 3% was observed for E = 4 and E = 8 respectively. This could potentially be explained by the smaller training set sizes available for the task, which makes it easier for client models to overfit on their local training data when a longer communication pace is used.
Table 10.
Federated learning performance for difference communication pace.
| A. BRCA subtyping performance for different communication pace | ||||
|
| ||||
| E=1 | E=2 | E=4 | E=8 | |
|
| ||||
| AUC | 0.862±0.025 | 0.869±0.024 | 0.865±0.027 | 0.867±0.024 |
| B. RCC subtyping performance for different communication pace | ||||
|
| ||||
| E=1 | E=2 | E=4 | E=8 | |
|
| ||||
| AUC | 0.976±0.007 | 0.975±0.006 | 0.975±0.007 | 0.973±0.009 |
| C. CCRCC survival prediction performance for different communication pace | ||||
|
| ||||
| E=1 | E=2 | E=4 | E=8 | |
|
| ||||
| c-index | 0.683±0.064 | 0.686±0.053 | 0.664±0.083 | 0.655±0.074 |
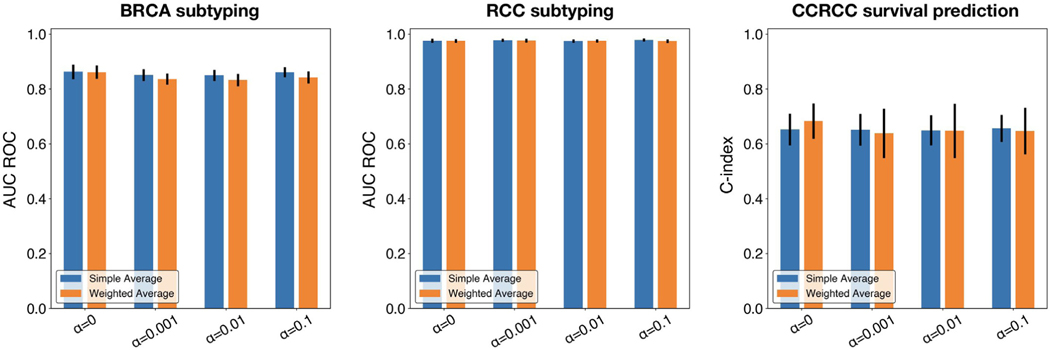
In addition to the weighted averaging aggregation used in the originally proposed federated averaging algorithm, where , and the contribution of each local model is weighted proportionally to the size of its training set, we investigate the alternative choice used by Li et al. (2020a), , where uniform weights are used for averaging the updated weights of different local models in each training round. The results are shown for both classification and survival tasks and for different levels of α (Fig. 5), where minimal differences between the two design choices were observed.
Fig. 5.
Performance comparison between simple averaging vs. weighted aggregation. Performance in terms of AUC ROC for classification and c-index for survival prediction is shown for federated averaging across different levels of α. Error bars show s.d. from 5-fold cross-validation.
4. Conclusion
Over the past several years, computational pathology has seen enormous growth due to deep learning achieving “clinical-grade” performance on many clinically-relevant pathology tasks. As a result, AI algorithms for pathology data have received considerable attention as an support decision system in assisting clinicians in pathology and laboratory medicine services, with recent FDA approval given to weakly-supervised AI algorithms for cancer diagnosis. Despite these breakthroughs, the development and validation in AI algorithms in pathology have been mainly limited to single-institutional datasets, which may not generalize at deployment time due to variations in the underlying patient population, staining protocols, and scanner hardware. Federated learning has been suggested as a path forward in enabling differential privacy and overcoming stagnant healthcare interoperability for sharing sensitive medical data. With increasing demand for multi-institutional studies for validating clinical-grade AI systems in pathology, the robust validation of federated learning systems, in both differential-privacy and model performance, is urgently needed to enable collaboration and validation of all AI systems that would participate in medical decision making.
In this work, we demonstrate the feasibility and effectiveness of applying federated, attention-based weakly-supervised learning for general purpose classification and survival prediction on gigapixel whole slide images from different sites, without the need for institutions to directly share potentially sensitive patient data. Our proposed framework opens the possibility for multiple institutions to integrate their WSI datasets and train a more robust model that tends to generalize better on unseen data than models developed on data from a single institution, while also allowing participating institutions to preserve differential privacy via a randomized mechanism. Backed by a flexible and interpretable attention-based weakly-supervised learning framework, we believe our federated learning framework has the clear potential to be applied to many important computational pathology tasks beyond what we have already shown in this study.
Decreasing barriers to cross-institutional collaborations in this way will be key to the future development of computational pathology tools. This is especially true in two applications: (1) rare diseases, where a single institution may not possess enough cases of a single entity to train an effective model on its own due to a lack of diversity in morphology, and (2) global health, in which AI algorithms are deployed and finetuned in low- and middle-income countries that lack access to pathology and laboratory medicine services (Nabi, 2018; Anglade et al., 2020; Lu et al., 2021). These techniques may also be useful in situations where transferring large quantities of physical or digital slides may be impossible due to institutional or governmental regulations. Models that give institutions greater control over their data while still achieving at or near state-of-the-art perfor- mance will be instrumental in progress towards democratized computational pathology.
Table 2.
Partition for RCC subtyping (number of WSIs).
| CCRCC | PRCC | CHRCC | Total | |
|---|---|---|---|---|
|
| ||||
| TCGA Site 1 | 108 | 120 | 39 | 267 |
| TCGA Site 2 | 78 | 100 | 31 | 209 |
| TCGA Site 3 | 333 | 77 | 51 | 461 |
| BWH | 184 | 40 | 23 | 247 |
| Total | 703 | 337 | 144 | 1184 |
Acknowledgments
The authors would like to thank Alexander Bruce for scanning internal cohorts of patient histology slides at BWH; Jing-wen Wang, Katerina Bronstein, Lia Cirelli and Sharifa Sahai for querying the BWH slide database and retrieving archival slides; Martina Bragg, Sarah Zimmet and Terri Mellen for administrative support. This work was supported in part by internal funds from BWH Pathology, NIH National Institute of General Medical Sciences (NIGMS) R35GM138216 (to F.M.), Google Cloud Research Grant and the Nvidia GPU Grant Program. R.J.C. was additionally supported by the NSF Graduate Research Fellowship. The content is solely the responsibility of the authors and does not reflect the official views of the NIH, NIGMS, NHGRI or the NSF.
Footnotes
Ethics oversight
The study was approved by the Mass General Brigham (MGB) IRB office under protocol 2020P000233.
Declaration of Competing Interest
COI Statement The following applies to all authors included in this study, o All authors have participated in (a) conception and design, or analysis and interpretation of the data; (b) drafting the article or revising it critically for important intellectual content; and (c) approval of the final version. o This manuscript has not been submitted to, nor is under review at, another journal or other publishing venue. o The authors have no affiliation with any organization with a direct or indirect financial interest in the subject matter discussed in the manuscript.
CRediT authorship contribution statement
Ming Y. Lu: Conceptualization, Visualization, Formal analysis, Writing – review & editing. Richard J. Chen: Conceptualization, Visualization, Formal analysis, Writing – review & editing. Dehan Kong: Formal analysis, Writing – review & editing. Jana Lipkova: Visualization, Writing – review & editing. Rajendra Singh: Writing – review & editing. Drew F.K. Williamson: Formal analysis, Writing – review & editing. Tiffany Y. Chen: Formal analysis, Writing – review & editing. Faisal Mahmood: Conceptualization, Visualization, Supervision, Writing – review & editing.
References
- Abadi M, Chu A, Goodfellow I, McMahan HB, Mironov I, Talwar K, Zhang L, 2016. Deep learning with differential privacy. In: Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, pp. 308–318. [Google Scholar]
- Anand D, Gadiya S, Sethi A, 2020. Histographs: graphs in histopathology. Medical Imaging 2020: Digital Pathology. International Society for Optics and Photonics. [Google Scholar]
- Andreux M, Manoel A, Menuet R, Saillard C, Simpson C, 2020a. Federated survival analysis with discrete-time cox models. arXiv preprint arXiv: 2006.08997. [Google Scholar]
- Andreux M, du Terrail JO, Beguier C, Tramel EW, 2020b. Siloed federated learning for multi-centric histopathology datasets. In: Domain Adaptation and Representation Transfer, and Distributed and Collaborative Learning. Springer, pp. 129–139. [Google Scholar]
- Anglade F, Milner DA, Brock JE, 2020. Can pathology diagnostic services for cancer be stratified and serve global health? Cancer 126, 2431–2438. [DOI] [PubMed] [Google Scholar]
- Bera K, Schalper KA, Rimm DL, Velcheti V, Madabhushi A, 2019. Artificial intelligence in digital pathology—new tools for diagnosis and precision oncology. Nat. Rev. Clin. Oncol 16, 703–715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brisimi TS, Chen R, Mela T, Olshevsky A, Paschalidis IC, Shi W, 2018. Federated learning of predictive models from federated electronic health records. Int. J. Med. Inf 112, 59–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bulten W, Pinckaers H, van Boven H, Vink R, de Bel T, van Ginneken B, van der Laak J, Hulsbergen-van de Kaa C, Litjens G, 2020. Automated deep-learning system for gleason grading of prostate cancer using biopsies: a diagnostic study. Lancet Oncol. 21, 233–241. [DOI] [PubMed] [Google Scholar]
- Chen RJ, Lu MY, Wang J, Williamson DFK, Rodig SJ, Lindeman NI, Mahmood F, 2020. Pathomic fusion: an integrated framework for fusing histopathology and genomic features for cancer diagnosis and prognosis. IEEE Trans. Med. Imaging 11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Qin X, Wang J, Yu C, Gao W, 2020. Fedhealth: a federated transfer learning framework for wearable healthcare. IEEE Intell. Syst [Google Scholar]
- Cheu A, Smith A, Ullman J, Zeber D, Zhilyaev M, 2019. Distributed differential privacy via shuffling. In: Proceedings of the Annual International Confer- ence on the Theory and Applications of Cryptographic Techniques. Springer, pp. 375–403. [Google Scholar]
- Carlini N, Liu C, Erlingsson Ú, Kos J.and Song D, 2019. The secret sharer: Evaluating and testing unintended memorization in neural networks. In 28th {USENIX} Security Symposium ({USENIX} Security 19) (pp. 267–284). [Google Scholar]
- Choudhury O, Gkoulalas-Divanis A, Salonidis T, Sylla I, Park Y, Hsu G, Das A, 2019a. Differential privacy-enabled federated learning for sensitive health data. arXiv preprint arXiv: 1910.02578. [Google Scholar]
- Choudhury O, Park Y, Salonidis T, Gkoulalas-Divanis A, Sylla I, et al. , 2019b. Predicting adverse drug reactions on distributed health data using federated learning. In: Proceedings of the AMIA Annual Symposium Proceedings, American Medical Informatics Association, p. 313. [PMC free article] [PubMed] [Google Scholar]
- Coudray N, Ocampo PS, Sakellaropoulos T, Narula N, Snuderl M, Fenyö D, Moreira AL, Razavian N, Tsirigos A, 2018. Classification and mutation prediction from non–small cell lung cancer histopathology im- ages using deep learning. Nat. Med 24, 1559–1567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng J, Dong W, Socher R, Li LJ, Li K, Fei-Fei L, 2009. Imagenet: a large-scale hierarchical image database. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. IEEE, pp. 248–255. [Google Scholar]
- Dong J, Roth A, & Su WJ (2019). Gaussian differential privacy. arXiv preprint arXiv: 1905.02383. [Google Scholar]
- Dwork C, Kenthapadi K, McSherry F, Mironov I, Naor M, 2006. Our data, ourselves: privacy via distributed noise generation. In: Proceedings of the Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer, pp. 486–503. [Google Scholar]
- Dwork C, Roth A, et al. , 2014. The algorithmic foundations of differential privacy. Found. Trends Theor. Comput. Sci 9, 211–407. [Google Scholar]
- Geiping J, Bauermeister H, Dröge H, Moeller M, 2020. Inverting gradients how easy is it to break privacy in federated learning? In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H.(Eds.) Advances in Neural Information Processing Systems. Curran Associates, Inc., pp. 16937–16947. [Google Scholar]
- Graham S, Vu QD, Raza SEA, Azam A, Tsang YW, Kwak JT, Rajpoot N, 2019. Hover-net: simultaneous segmentation and classification of nuclei in multi-tissue histology images. Med. Image Anal 58 101563. [DOI] [PubMed] [Google Scholar]
- Hitaj B, Ateniese G, Perez-Cruz F, 2017. Deep models under the gan: information leakage from collaborative deep learning. In: Proceedings of the ACM SIGSAC Conference on Computer and Communications Security, pp. 603–618. [Google Scholar]
- Hung H, Chiang CT, 2010. Estimation methods for time-dependent auc models with survival data. Can. J. Stat 38, 8–26. [Google Scholar]
- Ilse M, Tomczak J, Welling M, 2018. Attention-based deep multiple instance learning. In: Proceedings of the International Conference on Machine Learning. PMLR, pp. 2132–2141. [Google Scholar]
- Jagadeesh KA, Wu DJ, Birgmeier JA, Boneh D, Bejerano G, 2017. Deriving genomic diagnoses without revealing patient genomes. Science 357, 692–695. [DOI] [PubMed] [Google Scholar]
- Javed S, Mahmood A, Fraz MM, Koohbanani NA, Benes K, Tsang YW, Hewitt K, Epstein D, Snead D, Rajpoot N, 2020. Cellular community detection for tissue phenotyping in colorectal cancer histology images. Med. Image Anal 63 101696. [DOI] [PubMed] [Google Scholar]
- Ju C, Gao D, Mane R, Tan B, Liu Y, Guan C, 2020, July. Federated transfer learning for eeg signal classification. In: Engineering in Medicine & Biology Society (EMBC). IEEE, pp. 3040–3045. [DOI] [PubMed] [Google Scholar]
- Kairouz P, McMahan HB, Avent B, Bellet A, Bennis M, Bhagoji AN, Bonawitz K, Charles Z, Cormode G, Cummings R.and D’Oliveira RG, 2019. Advances and open problems in federated learning. arXiv preprint arXiv: 1912.04977. [Google Scholar]
- Kaissis GA, Makowski MR, Rückert D, Braren RF, 2020. Secure, privacy-preserving and federated machine learning in medical imaging. Nat. Mach. In- tell 2, 305–311. doi: 10.1038/s42256-020-0186-1. [DOI] [Google Scholar]
- Konecˇny’ J, McMahan HB, Yu FX, Richtaŕik P, Suresh AT, Bacon D, 2016. Federated learning: strategies for improving communication efficiency. arXiv preprint arXiv: 1610.05492. [Google Scholar]
- Lazar AJ, McLellan MD, Bailey MH, Miller CA, Appelbaum EL, Cordes MG, Fronick CC, Fulton LA, Fulton RS, Mardis ER, et al. , 2017. Comprehensive and integrated genomic characterization of adult soft tissue sarcomas. Cell 171, 950–965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li T, Sahu AK, Talwalkar A, Smith V, 2020a. Federated learning: challenges, methods, and future directions. IEEE Signal Process. Mag 37, 50–60. [Google Scholar]
- Li W, Milletar’ı F, Xu D, Rieke N, Hancox J, Zhu W, Baust M, Cheng Y, Ourselin S, Cardoso MJ, et al. , 2019. Privacy-preserving federated brain tumour segmentation. In: Proceedings of the International Workshop on Machine Learning in Medical Imaging. Springer, pp. 133–141. [Google Scholar]
- Li X, Gu Y, Dvornek N, Staib LH, Ventola P, Duncan JS, 2020b. Multisite fmri analysis using privacy-preserving federated learning and domain adaptation: abide results. Med. Image Anal 65, 101765. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu MY, Chen RJ, Wang J, Dillon D, Mahmood F, 2019. Semi-supervised histology classification using deep multiple instance learning and contrastive predictive coding. arXiv preprint arXiv: 1910.10825. [Google Scholar]
- Lu MY, Chen TY, Williamson DF, Zhao M, Shady M, Lipkova J, Mahmood F, 2021. Ai-based pathology predicts origins for cancers of unknown primary. Nature 594, 106–110. doi: 10.1038/s41586-021-03512-4. [DOI] [PubMed] [Google Scholar]
- Lu MY, Williamson DF, Chen TY, Chen RJ, Barbieri M, Mahmood F, 2020a. Data efficient and weakly supervised computational pathology on whole slide images. arXiv preprint arXiv: 2004.09666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmood F, Borders D, Chen R, McKay GN, Salimian KJ, Baras A, Durr NJ, 2019. Deep adversarial training for multi-organ nuclei segmentation in histopathology images. IEEE Trans. Med. Imaging [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mandl KD, Glauser T, Krantz ID, Avillach P, Bartels A, Beggs AH, Biswas S, Bourgeois FT, Corsmo J, Dauber A, et al. , 2020. The genomics research and innovation network: creating an interoperable, federated, genomics learning system. Genet. Med 22, 371–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McMahan B, Moore E, Ramage D, Hampson S, Arcas BA, 2017. Communication-efficient learning of deep networks from decentralized data. Artif. Intell. Stat 54, 1273–1282. [Google Scholar]
- Mobadersany P, Yousefi S, Amgad M, Gutman DA, Barnholtz-Sloan JS, Vega JEV, Brat DJ, Cooper LA, 2018. Predicting cancer outcomes from histology and genomics using convolutional networks. Proc. Natl. Acad. Sci 115, E2970–E2979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muhammad H, Sigel CS, Campanella G, Boerner T, Pak LM, Buttner S, IJzermans JN, Koerkamp BG, Doukas M, Jarnagin WR, et al. , 2019. Unsupervised subtyping of cholangiocarcinoma using a deep clustering convolutional autoencoder. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 604–612. [Google Scholar]
- Nabi J, 2018. Artificial intelligence can augment global pathology initiatives. Lancet 392, 2351–2352. [DOI] [PubMed] [Google Scholar]
- Niazi MKK, Parwani AV, Gurcan MN, 2019. Digital pathology and artificial intelligence. Lancet Oncol. 20, e253–e261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pell R, Oien K, Robinson M, Pitman H, Rajpoot N, Rittscher J, Snead D, Verrill C, Driskell OJ, et al. quality assurance working group, U.N.C.R.I.N.C.M.P.C.P., 2019. The use of digital pathology and image analysis in clinical trials. J. Pathol. Clin. Res 5, 81–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rehm HL, 2017. Evolving health care through personal genomics. Nat. Rev. Genet 18, 259–267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieke N, Hancox J, Li W, Milletari F, Roth HR, Albarqouni S, Bakas S, Galtier MN, Landman BA, Maier-Hein K, et al. , 2020. The future of digital health with federated learning. NPJ Digit. Med 3, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocher L, Hendrickx JM, De Montjoye YA, 2019. Estimating the success of re-i- dentifications in incomplete datasets using generative models. Nat. Commun 10, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy AG, Siddiqui S, Po ¨lsterl S, Navab N, Wachinger C, 2019. Braintorrent: a peer-to-peer environment for decentralized federated learning. arXiv preprint arXiv: 1905.06731. [Google Scholar]
- Schapiro D, Jackson HW, Raghuraman S, Fischer JR, Zanotelli VR, Schulz D, Giesen C, Catena R, Varga Z, Bodenmiller B, 2017. Histocat: analysis of cell phenotypes and interactions in multiplex image cytometry data. Nat. Methods 14, 873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheibner J, Ienca M, Kechagia S, Troncoso-Pastoriza JR, Raisaro JL, Hubaux JP, Fellay J, Vayena E, 2020. Data protection and ethics requirements for multisite research with health data: a comparative examination of legislative governance frameworks and the role of data protection technologies. J. Law Biosci 7, 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheller MJ, Reina GA, Edwards B, Martin J, Bakas S, 2018. Multi-institutional deep learning modeling without sharing patient data: a feasibility study on brain tumor segmentation. In: Proceedings of the International MICCAI Brain- Lesion Workshop. Springer, pp. 92–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shokri R, Shmatikov V, 2015. Privacy-preserving deep learning. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, pp. 1310–1321. [Google Scholar]
- Silva S, Gutman BA, Romero E, Thompson PM, Altmann A, Lorenzi M, 2019. Federated learning in distributed medical databases: meta-analysis of large-scale subcortical brain data. In: Proceedings of the IEEE 16th International Symposium on Biomedical Imaging (ISBI). IEEE, pp. 270–274. [Google Scholar]
- Tutz G, Schmid M, et al. , 2016. Modeling Discrete Time-to-Event Data. Springer. [Google Scholar]
- Wang J, Chen RJ, Lu MY, Baras A, Mahmood F, 2020. Weakly supervised prostate tma classification via graph convolutional networks. In: Proceedings of the IEEE 17th International Symposium on Biomedical Imaging (ISBI). IEEE, pp. 239–243. [Google Scholar]
- Wang Z, Song M, Zhang Z, Song Y, Wang Q, Qi H, 2019. Beyond inferring class representatives: user-level privacy leakage from federated learning. In: Proceedings of the IEEE INFOCOM IEEE Conference on Computer Communications, pp. 2512–2520. [Google Scholar]
- Xiao L, Yu JG, Liu Z, Ou J, Deng S, Yang Z, Li Y, 2020. Censoring-aware deep ordinal regression for survival prediction from pathological images. In: Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, pp. 449–458. [Google Scholar]
- Yamamoto Y, Tsuzuki T, Akatsuka J, Ueki M, Morikawa H, Numata Y, Taka- hara T, Tsuyuki T, Tsutsumi K, Nakazawa R, et al. , 2019. Automated acquisition of explainable knowledge from unannotated histopathology images. Nat. Commun 10, 1–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Q, Liu Y, Chen T, Tong Y, 2019. Federated machine learning: concept and applications. ACM Trans. Intell. Syst. Technol. (TIST) 10, 1–19. [Google Scholar]
- Zadeh SG, Schmid M, 2020. Bias in cross-entropy-based training of deep survival networks. IEEE Trans. Pattern Anal. Mach. Intell 43, 3126–3137 9. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Jia R, Pei H, Wang W, Li B, Song D, 2020. The secret revealer: generative model-inversion attacks against deep neural networks. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 253–261. [Google Scholar]
- Zhou Y, Graham S, Alemi Koohbanani N, Shaban M, Heng PA, Rajpoot N, 2019. CGC-Net: cell graph convolutional network for grading of colorectal cancer histology images. In: Proceedings of the IEEE International Conference on Computer Vision Workshops 0–0. [Google Scholar]
- Zhu L, Liu Z, Han S, 2019. Deep leakage from gradients. In: Advances in Neural Information Processing Systems. Curran Associates, Inc., pp. 14774–14784. [Google Scholar]