Arousal impacts distributed hubs modulating the integration of brain functional connectivity

Abstract

Even when subjects are at rest, it is thought that brain activity is organized into distinct brain states during which reproducible patterns are observable. Yet, it is unclear how to define or distinguish different brain states. A potential source of brain state variation is arousal, which may play a role in modulating functional interactions between brain regions. Here, we use simultaneous resting state functional magnetic resonance imaging (fMRI) and pupillometry to study the impact of arousal levels indexed by pupil area on the integration of large-scale brain networks. We employ a novel sparse dictionary learning-based method to identify hub regions participating in between-network integration stratified by arousal, by measuring k-hubness, the number (k) of functionally overlapping networks in each brain region. We show evidence of a brain-wide decrease in between-network integration and inter-subject variability at low relative to high arousal, with differences emerging across regions of the frontoparietal, default mode, motor, limbic, and cerebellum networks. State-dependent changes in k-hubness relate to the actual patterns of network integration within these hubs, suggesting a brain state transition from high to low arousal characterized by global synchronization and reduced network overlaps. We demonstrate that arousal is not limited to specific brain areas known to be directly associated with arousal regulation, but instead has a brain-wide impact that involves high-level between-network communications. Lastly, we show a systematic change in pairwise fMRI signal correlation structures in the arousal state-stratified data, and demonstrate that the choice of global signal regression could result in different conclusions in conventional graph theoretical analysis and in the analysis of k-hubness when studying arousal modulations. Together, our results suggest the presence of global and local effects of pupil-linked arousal modulations on resting state brain functional connectivity.

1. Introduction

Fluctuations of brain and behavioral states during wakefulness are linked with our ability to observe and interact with a changing environment (Gonzalez-Castillo et al., 2021; McGinley et al., 2015; Zagha and McCormick, 2014). In the absence of external tasks, arousal, a behavioral state of being alert, awake, and attentive (Joshi and Gold, 2020; Liu and Falahpour, 2020), is a potential source of brain state variations or time-varying patterns of brain activity during resting state. Recent neuroimaging studies using functional magnetic resonance imaging (fMRI) show that there are neural correlates of arousal in the cerebral cortex (Breeden et al., 2017; DiNuzzo et al., 2019; Schneider et al., 2016; Yellin et al., 2015). In addition to key brain regions of the ascending arousal system, thalamo-cortical and cortico-cortical neural pathways are involved in modulation of arousal (Lee and Dan, 2012; McCormick et al., 2020; Paasonen et al., 2018), suggesting a role of arousal on functional interactions between brain regions. How arousal modulates functional brain organization during resting state remains poorly understood (Barttfeld et al., 2015; Shine et al., 2016; Yeo et al., 2015).

Functional connectivity is widely used to infer a relationship between brain regions by measuring the temporal correlation strength of the blood-oxygen-level-dependent (BOLD) signal. Integration of distinct brain regions can be described by connecting nodes (each representing a brain region) based on the strength of functional connectivity between them (Bullmore and Sporns, 2009). In graph theory, hubs are defined as the nodes with a large number of connections to other nodes using pairwise correlation matrix (Power et al., 2013). Among hubs, connector hubs play a key role in communications between networks, each being a set of inter-connected nodes. Connector hubs are thought to reconfigure their functional connectivity to adapt to changes in brain states such as tasks (Bertolero et al., 2015) or arousal (Boveroux et al., 2010). Brain-wide decreases in network integration were found in patients in the comatose state (Achard et al., 2012), under propofol-induced sedation (Qiu et al., 2017; Schrouff et al., 2011; Vatansever et al., 2020) and sleep (Boly et al., 2012; Cross et al., 2021). Still, the much more subtle question as to whether modulations in arousal during resting state are associated with brain-wide connector hub re-organization remains largely unexplored in healthy non-pharmacologically altered participants (Shine et al., 2016).

In addition, functional connectivity as measured by resting state fMRI involves complex information resulting from a variety of neurobiological, hemodynamic, and physiological components (Cole et al., 2014; Gonzalez-Castillo et al., 2019; Lurie et al., 2020). Components of time-varying functional connectivity at rest have been linked to consciousness (Barttfeld et al., 2015) and ongoing cognition (Gonzalez-Castillo et al., 2015). Other studies have observed time-varying resting state functional connectivity associated with sampling variability, motion artifacts, sleep states (Haimovici et al., 2017; Laumann et al., 2017), physiological noise (Chang et al., 2013), neurovascular coupling (Archila-Meléndez et al., 2020), eyelid closures (Chang et al., 2016; Wang et al., 2016) or eye movements (Koba et al., 2021). Electroencephalography (EEG) markers of arousal, e.g. alpha power, were negatively correlated with fMRI global signal (Wong et al., 2013). Arousal fluctuations indexed by eyelid opening and intracortical EEG had negative correlations with cortical fMRI signals accompanied by thalamocortical anti-correlation (Chang et al., 2016). Decreases in EEG vigilance were associated with increases in thalamocortical anticorrelation in fMRI (Allen et al., 2018) and decreases in anticorrelation between the default mode and task-positive networks (Wong et al., 2013). A similar result was found using the degree of eyelid closure as a proxy of arousal state in sleep deprived individuals (Wang et al., 2016). Arousal-dependent changes in resting state functional connectivity suggest a relation to behavior and cognition. More anticorrelation between the default mode and task-positive networks at peristimulus times at a psychomotor vigilance task was correlated with faster performances (Thompson et al., 2013). Using the analysis of coherence and phase-shift between fMRI and arousal fluctuations, it is suggested that a traveling wave linked to arousal offers a parsimonious account for spatiotemporal features of resting state fMRI signals, including the global organization of functional connectivity gradients (Raut et al., 2021). There were time-locked relationships between the topology of resting state functional connectivity, activity of the ascending arousal system, low dimensional energy landscapes, and spatiotemporal travelling waves (Munn et al., 2021). To this end, how changes in arousal are linked to functional connectivity reconfiguration is a key question in understanding connectivity dynamics and could contribute to the heterogeneity of resting state functional connectivity patterns across subjects (Barttfeld et al., 2015; Laumann et al., 2017; Liu and Falahpour, 2020).

However, level of arousal is not routinely monitored in most resting state fMRI studies, making it challenging to explore its impact on functional connectivity. Pupillometry has an ability to track the level of arousal or behavioral states during wakefulness by measuring changes in pupil size, without a need to place EEG electrodes on the scalp (Joshi and Gold, 2020; Liu and Falahpour, 2020; McCormick et al., 2020). Converging evidence from neuroimaging studies suggests that pupil-linked arousal modulates both the BOLD time-series and patterns of functional connectivity. Fluctuations of pupil diameter were associated with resting state BOLD time-series and the antagonism between regions of the default mode and sensorimotor cortex (Yellin et al., 2015). Pupil dilation was associated with increased BOLD activity of the salience network, frontoparietal regions and the thalamus (Schneider et al., 2016). Using graph theory, spontaneous fluctuations of pupil diameter were correlated with between-network integration during rest, suggesting a link between neural gain and connector hubs (Munn et al., 2021; Shine, 2019; Shine et al., 2016). Yet, it remains unclear how arousal modulates the topology of brain’s functional organizations during resting state and what the role of connector hubs is in arousal level-dependent network reorganization.

To explore this, we identify and quantify changes in between-network integration stratified by arousal and examine its contribution to inter-subject functional connectivity variability. We hypothesize that resting state networks reorganize with arousal fluctuations. Specifically, we expect between-network integration to be lower at low relative to high arousal, based on the previous work showing a positive relationship between the fluctuations of pupil diameter and global between-network integration (Shine et al., 2016). To estimate network integration from resting state fMRI is challenging, due to the multicollinearity of networks when the time-courses of brain networks may be themselves related. In addition, it is unlikely that the brain is organized into several non-overlapping networks, instead, the functional brain organizations may involve overlaps associated with multiple functional processes that a region participates. For example, using a sparsity-based analysis of reliable k-hubness (SPARK)(Lee et al., 2016), the posterior cingulate cortex (PCC) has been shown to participate in two sub-networks of default mode, where one involves the midline components (the PCC and medial prefrontal cortex) and another involves the midline, lateral (inferior parietal lobe), and mesial (hippocampus) components. In this example, network overlap is observed at one of the core regions of the default mode network, rather than at its anatomical boundaries. A similar result was found using an innovative co-activation pattern analysis (Karahanoğlu and Van De Ville, 2015).

To test this hypothesis, we collected resting state fMRI simultaneously with in-scanner pupillometry data from 27 healthy participants, in order to use pupillometry as an index of arousal (Larsen and Waters, 2018; Murphy et al., 2014; Schneider et al., 2016). We stratify high and low arousal states by ranked pupil area and estimate connector hubs in each state, using a recently introduced method; SParse dictionary learning based Analysis of Reliable K-hubness (SPARK)(Lee et al., 2018, 2016). SPARK identifies a set of individually consistent networks and defines connector hubs by measuring “k-hubness”, or the number (k) of functionally overlapping networks for each node (Lee et al., 2018, 2016). We show evidence of a brain-wide decrease in between-network integration and inter-subject variability of connector hubs in low versus high arousal resting states. By studying the hierarchical network organization of connector hubs, we observe that arousal is not localized to specific brain areas known to be directly associated with arousal regulation, but instead has a more extensive, brain-wide impact that involves high-level between-network communications. Lastly, we investigate if global signal regression has an impact on the pairwise fMRI signal correlation structures in the arousal state-stratified data, the analysis of hubs using conventional Graph theory, and the analysis of k-hubness using SPARK. We demonstrate that the choice of global signal regression could result in different conclusions in conventional graph theoretical analysis and in the analysis of k-hubness, and suggest the presence of global and local effects of pupil-linked arousal modulations on resting state brain functional connectivity.

2. Materials and methods

2.1. Participants

This study was approved by the Institutional Review Board at Yale University. We recruited 37 healthy young adults (26.68 ± 4.18 years old; 20/17 females/males; 35/2 right/left-handed. Mean ± standard deviation) from the community of Yale University. Participants had to meet the following inclusion criteria: i) no claustrophobia or ferromagnetic metal in the body, ii) no clinical diagnosis of cognitive or mental disorders, iii) no visual impairments or difficulty in vision without glasses or contact lenses, and iv) no auditory impairments. Subjects were instructed to have a normal sleep before the day of scan and reported 7 ± 1 hours of sleep during the past 24 hours prior to the scan, with a neutral sleep quality scoring 3.4 ± 0.8 out of the five self-rating items: 1 (very bad), 2 (fairly bad), 3 (neutral), 4 (fairly good), 5(very good). Subjects reported a mild level of fatigue scoring 1 ± 0.7 out of the five self-rating items: 4 (worst possible fatigue), 3 (severe fatigue), 2 (moderate fatigue), 1 (mild fatigue), 0 (energetic, no fatigue). After data preprocessing, 10 subjects were excluded based on the following criteria: i) motion, estimated as the mean frame-to-frame displacement (FFD) > 0.15 mm in either of two resting state fMRI runs (Horien et al., 2019), ii) more than 35% of missing datapoints in the pupillometry data, or iii) missing data due to technical problems. Given these criteria, we included 27 subjects (26.52 ± 4.04 years old; 16/11 females/males; 25/2 right/left-handed) in our analyses. The mean FFD was 0.06 ± 0.02 mm for rest 1 and 0.06 ± 0.02 mm for rest 2 across the finally selected 27 subjects. Across the 27 subjects, the percent of discarded time-points was 6.02 ± 9.48 % for rest 1 and 4.33 ± 8.33 % for rest 2. See Table S1 for demographics.

2.2. Data acquisition

Imaging data were acquired using a Siemens 3.0T MAGNETOM Prisma MRI scanner at the Yale Magnetic Resonance Research Center. T1-weighted anatomical images were acquired using a magnetization prepared rapid gradient echo (MPRAGE) pulse sequence with the following parameters: repetition time (TR) = 2,400 ms, echo time (TE) = 1.22 ms, flip angle = 8°, slice thickness = 1 mm, in-plane resolution = 1 × 1 mm, matrix size = 256 × 256, field-of-view(FOV) = 256 mm, 208 contiguous slices acquired in the sagittal plane. Functional T2* -weighted BOLD images were acquired using a multiband gradient echo-planar imaging (EPI) pulse sequence (TR = 1000 ms, TE = 30 ms, flip angle = 55°, multiband acceleration factor = 5, slice thickness = 2 mm, in-plane resolution = 2 × 2 mm², matrix size= 100 × 100, FOV = 220 mm, 75 contiguous slices acquired in the axial-oblique planes parallel to AC-PC line). Two resting state fMRI scans were acquired for each subject. Subjects were instructed to stay still, think of nothing in particular, and maintain fixation on the white cross in the middle of black screen. Total duration of each functional run was 6:50 min (410 frames). The two resting state runs were acquired with an interval of approximately 40-50 minutes between them in the same session, without leaving the scanner, except one subject who needed to use restroom. Between the two rest runs, five task fMRI data were acquired for an independent study that is not part of this work. Eye-tracking data were recorded using a MR-compatible infrared EyeLink 1000 Plus eye-tracking system (SR Research Ltd. Ottawa, ON, Canada) to measure time-varying changes in pupil area with a sampling rate of 1,000 Hz. In the EyeLink 1000 system, a centroid fitting model was used for pupil tracking. We performed a five-point calibration and validation before each functional run to minimize the potential impacts of between-scan difference in measurement environment and subject motion.

2.3. Pupillometry data preprocessing

Eye-tracking data were preprocessed using custom code in MATLAB R2018a. Eye blinks were automatically identified by EyeLink tracker’s online parser. Blink-induced artifacts were corrected using 4-point spline interpolation (Mathôt et al., 2013). Blinks that occurred shortly after each other (< 100 ms) were combined and treated as a single blink (Schneider et al., 2016). The signals were low-pass filtered using a first-order Butterworth filter at cut-off 0.5 Hz, after which the first 10,000 data points (i.e., 10 s) were removed to synch with the fMRI data. The time-course was down-sampled by averaging 1,000 consecutive frames for each 1 s bin, to match the fMRI sampling frequency (1 Hz). Pupil area was z-transformed using the mean and standard deviation over the rest 1 and 2, to control for variability in average pupil area across subjects. To account for the slow response time of the pupil to neuronal activity (Schneider et al., 2016), each time-course was convolved with the canonical HRF generated based on the mixture of two Gamma functions using SPM8 (Friston et al., 1998). Finally, the normalized pupil area time-courses from rest 1 and 2 were temporally concatenated for each subject, to match the concatenated rest fMRI scans. We quantified eye-closure related missing pupillometry data by the proportion of missing (zero-valued) time-points with respect to the total number of time-points.

2.4. fMRI data preprocessing

T1-weighted anatomical images were skull-stripped using FSL opti-BET (Lutkenhoff et al., 2014). All further analyses were performed using BioImage Suite unless otherwise specified (Joshi et al., 2011). Skull-stripped anatomical images were non-linearly registered to the standard Montreal Neurological Institute (MNI) space (Scheinost et al., 2017). Functional images were first motion-corrected and realigned using twenty-four motion parameters (Satterthwaite et al., 2013), including six rigid-body parameters, their temporal derivatives, and their quadratic terms, using SPM8. Subject within scan head motion was quantified by computing the mean FFD across each functional run. The first 10 s volumes were discarded to exclude frames when eye-tracking system was initialized and stabilized. Functional images were linearly registered to skull-stripped anatomical images using the rigid transformation of the mean functional image from the first run (rest 1). 3D spatial smoothing was performed using an isotropic Gaussian kernel with a 4 mm full-width-half-maximum (Scheinost et al., 2014). Nuisance covariates, including 1) 24 motion parameters, 2) slow temporal drifts as modeled by the linear, quadratic, and cubic Legendre polynomials, 3) the mean signals in the cerebrospinal fluid and white matter, and 4) the whole-brain global signal, were regressed. Data were low-pass filtered using a zero-mean unit-variance Gaussian filter with a cut-off frequency of 0.12 Hz. For each run, using a 268-parcel functional atlas that covered the whole brain excluding ventricles and white matter (Finn et al., 2015; Shen et al., 2013), we generated a time-by-node data matrix for each individual by averaging the fMRI signals across voxels within each node. Finally, two data matrices from rest 1 and 2 were temporally concatenated for each subject, after normalizing the time-courses in each run to have zero mean and unit variance.

To evaluate the impact of global signal regression on our hub analyses, we repeated the analyses on a time-by-268 node data matrix after preprocessing data without the whole-brain global signal regression. In addition, to ensure that our results were not specific to this atlas, we repeated our analyses using a 249-parcel atlas, defined by integrating the Schaefer-200 cortex parcellation (Schaefer et al., 2018), subcortical structures from the anatomical Yale Brodmann Atlas (Lacadie et al., 2008), cerebellum from Yeo et al. (2011), and brainstem from the Shen-268 atlas (Finn et al., 2015; Shen et al., 2013).

2.5. Hub analysis

An overview of our analysis pipeline is shown in Fig. 1. We use the pupillometry data, ranked by pupil area, to estimate arousal at each time-point. We stratify high and low arousal states by selecting time-points from the top 20% (large) and bottom 20% (small) pupil areas, resulting in 160 frames of fMRI data for each state. Using data from either the high or low arousal state, we estimated resting state networks and nodal k-hubness using SPARK (Lee et al., 2019, 2016). The choice of 20% was made from our experiment to ensure similar number of sequential frames stratified as a single state to avoid any potential bias in our between-state comparisons (see Supplementary Fig. S1).

Fig. 1.

Analysis pipeline overview. (a) Pupillometry-based fMRI state stratification for arousal level-dependent connector hub analysis. For each subject, pupillometry data were used to stratify the simultaneously acquired fMRI data into two states (high and low arousal). Specifically, time-points where pupil area was within the top or bottom 20% rank were assigned to a high- (orange) or low-arousal state (blue), respectively. A sparsity-based analysis of reliable k-hubness (SPARK) was used to identify connector hubs from state-stratified fMRI data, by measuring k-hubness for each node at the individual level. (b) k-hubness is defined as the number of overlapping networks in each node. (c) Null data generation by randomizing the assignment of pupillometry to fMRI across the 27 subjects. (d) The distribution of Pearson’s correlation coefficients measured between individual pupillometry time-courses.

Let a time(T)-by-node(R) data matrix Y = [y₁ , … , y_R] where y_i represents a BOLD signal in a node i, and E = [ε₁ , … , ε_R] where ε_i represents the corresponding noise. SPARK represents the BOLD signals y_i from each node as a sparse (k), weighted linear combination of atoms in a T-by-N dictionary D = [d₁, … , d_N], where each atom d_i is a T-by-1 temporal feature of each network (Lee et al., 2011).

$${\mathit{y}}_i=\mathit{D}{\mathit{x}}_i+{\epsilon }_i,i=1,\dots ,R$$

SPARK uses a sparse dictionary learning algorithm such as K-SVD (Aharon et al., 2006) to train a subject-specific dictionary D and the corresponding N-by-R sparse coefficient matrix X. For resting state fMRI data Y, a dictionary atom represents a temporal feature (time-course) of a functional network and the corresponding row in X involves a spatial map. Taking advantage of the ability of K-SVD to estimate a sparse code x_i for each node with a small number (k) of non-zero elements, a node involves a node-specific overlap or combination of k (less than N, therefore, sparse) networks among those N networks in D. The two parameters, the total number of atoms in the dictionary or the whole-brain network scale N and node-specific k values, are automatically estimated using a minimum description criterion (Lee et al., 2018). Using this framework, k-hubness is a unique measure of between-network integration and can serve to identify connector hubs, which are obtained by counting the number of functional networks that overlap at each node.

Another objective of SPARK is to achieve a single-subject-level reliability in our estimation of connector hubs and resting state networks from a short duration of fMRI data (e.g. 6-7 minutes). This is useful particularly when a long data acquisition (e.g. >30 minutes) is not appropriate (e.g. scanning patients with epilepsy or pediatric participants). To do this, we assess the reproducibility of sparse dictionary learning using a temporal block bootstrap resampling, using a similar framework to the circular block bootstrap (Efron and Tibshirani, 1994). We generate a large number of surrogate time-series drawn from the same probability distribution of the original data and find network patterns consistently found across surrogate datasets. See Bellec et al. (2010) for details on the theory and validation of using circular block bootstrap in real fMRI network analyses.

In this work, SPARK was applied for an individual fMRI data, a time (T) by node (R) matrix) as follows (Fig. S2 for a summary diagram). Step 1. We generated 300 surrogate datasets (each being a T by R data matrix) from the original data using a block bootstrap approach. The block bootstrap was performed with a block length h. The choice of h, roughly the order of $\sqrt{T}$, is suggested to preserve the temporal dependencies in real fMRI signals during the resampling procedure (Bellec et al., 2010). Instead of using a fixed value of h, we select a random integer h between the square root of T ($\sqrt{T}$) and $2\sqrt{T}$ for each bootstrap sample, to include the variability of SPARK results associated with h in our reproducibility evaluation step (Bellec et al., 2010). The resampled time blocks (a h by R data matrix) are concatenated in time dimension to form a T by R surrogate data matrix. The temporal block falling at the end of time-series is trimmed to fit the desired dimension.

Step 2. For each resampled dataset, a sparse dictionary learning algorithm (Aharon et al., 2006; Lee et al., 2018, 2016) was applied to learn a dictionary involving N time-course atoms (temporal features) and a corresponding sparse coefficient matrix (spatial maps). The algorithm involves an automatic parameter estimation strategy using the minimum description length criteria (Lee et al., 2018). The total number of networks (N) was estimated independently for each resampled dataset by varying N from 1 to the number of principal components that explained 99% of the variance in each resampled dataset. The level of sparsity (k) was determined by varying k from 1 to N/2 for each N. The reproducibility of parameters (N and k) of the sparse model were assessed across bootstraps.

Step 3. After the 300 parallel processes, we collected 300 sparse coefficient matrices (each being a N’ by R matrix) and applied K-means spatial clustering. The number of clusters (N’) was the median of estimated N across 300 resampled datasets. The clustered spatial maps (each generated from a row of sparse coefficient matrices) were averaged within each cluster. Elements of the resultant average matrix $\overline{\mathbf{X}}$ (a N by R matrix) are values representing both the weights (i.e. connectivity strength) and the statistical reproducibility over bootstrap samples. They should exhibit a large value if a node is consistently involved in a network across the 300 bootstrap samples. A small value in $\overline{\mathbf{X}}$ indicates either that a node is not consistently involved in a network or that the involvement of this node in a network is consistently weak across bootstrap samples. Because we are only interested in resting state networks that are consistently found in a single subject, elements with a large value are selected by thresholding the average matrix $\overline{\mathbf{X}}$ at 95% confidence interval, approximating the Gaussian distribution of background noise in $\overline{\mathbf{X}}$. This provided the final sparse matrix, in which each row represented a spatial map of individually reliable resting state networks.

Step 4. Counting the non-zeros for each column of this matrix provided an estimation of k-hubness for each node. This clustering procedure was repeated 100 times to take into account random initializations in K-mean clustering. Finally, nodal k-hubness was determined by the mean of k-hubness values estimated over 100 clustering results. The density of k-hubness was calculated as the % proportion of nodes with non-zero k-hubness to the total number of nodes estimated from data obtained in each arousal.

For comparison purposes, we generate null data by randomizing the assignment of pupillometry to fMRI across the 27 subjects (Fig. 1c). This results in 702 false fMRI-pupillometry pairs, from which we stratify random high/low arousal assignments. Pupillometry time-courses are unique to the individual (Fig. 1d). The distribution of pupil time-course correlations is not skewed (skewness= −.04) and not normal (Lilliefors’ test, p<.003). See Fig. S3 for the individual pupillometry time-courses. We compare our results to those from null data, in order to test the null hypothesis that there is no association between resting state functional connectivity and spontaneous arousal fluctuations defined using pupillometry.

2.6. Hub disruption index

To assess the brain-wide connector hub reorganization with arousal, we defined the hub disruption index (HDI_k) using k-hubness from resting state fMRI at high and low arousal states (Lee et al., 2018). The HDI was first proposed for studying hubs defined using degree centrality in graph theory (Achard et al., 2012) and introduced for k-hubness to study the reorganization of connector hubs in patients with epilepsy (Lee et al., 2015). The HDI_k is a summary measure to quantify overall hub reorganization across the whole brain between a brain state (e.g., high arousal) and another (e.g., low arousal) (Achard et al., 2012). We measured the HDI_k at both the group and single subject levels. At the group level, HDI_<k> is the slope of the linear regression model fit to group average k-hubness across subjects at high arousal (x-axis, <k>_High) and the difference in group average k-hubness between low and high arousal (y-axis, <k>_Low - <k>_High) (Fig. 2). A negative slope means that some of the hubs identified at high arousal lose their hub status at low arousal (i.e., nodes exhibiting a high <k>_High relative to <k>_Low have a negative value of <k>_Low - <k>_High ). HDI_<k> becomes zero when there is no difference in k-hubness between the two states. The same approach is used to define HDI_k at the individual level, by using the individual subject’s nodal k-hubness (k) in a single subject (x-axis, k_High; y-axis, k_Low - k_High).

Fig. 2.

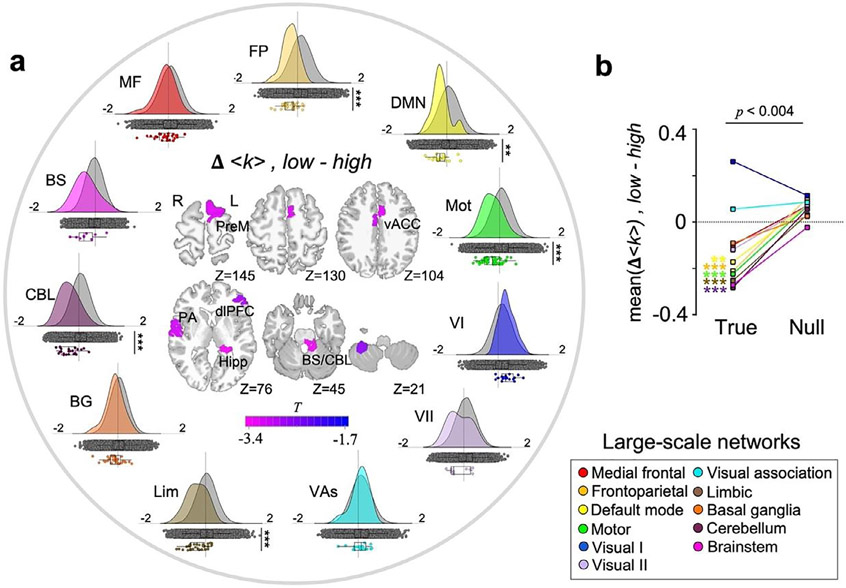
Distributed connector hubs are re-organized with arousal modulations during resting state. (a) The total number of resting state networks (N) detected by SPARK from individuals were preserved between high and low arousal states. (b and c) The group average k-hubness maps at high (b) and low (c) arousal. (d) The map of difference in the group average k-hubness between the low and high arousal states. (e) The estimation of group-level HDI_<k> between high and low arousal. A linear regression model is used to find a linear fit of nodal group-average k-hubness (<k>) estimated from the two states. HDI_<k> is defined as a slope of the linear fit. (f) The estimation of group-level HDI_<k> between two randomized states, by averaging k-hubness across 702 false brain-pupil pairs in each node. (g) An example of individual-level HDI_k from a single subject exhibiting the median of HDI_k within group. Note that nodal k-hubness is an integer, therefore nodes with a same value are superimposed in this scatter plot. (h) The distribution of individual-level HDI_k (top) and those from null data (bottom). p-value estimated using the left-tailed Wilcoxon rank sum test is shown. (i) The bar plot of k-hubness distributions within the eleven pre-defined large-scale networks in each state. Mean ± standard deviation. (j) Data points in figures e, f and j are color-coded using eleven a priori functional networks. Ten networks were defined as described in Noble et al. (2017), and the nodes belonging to the brainstem were assigned to an 11^th network.

2.7. Hub connectivity probability

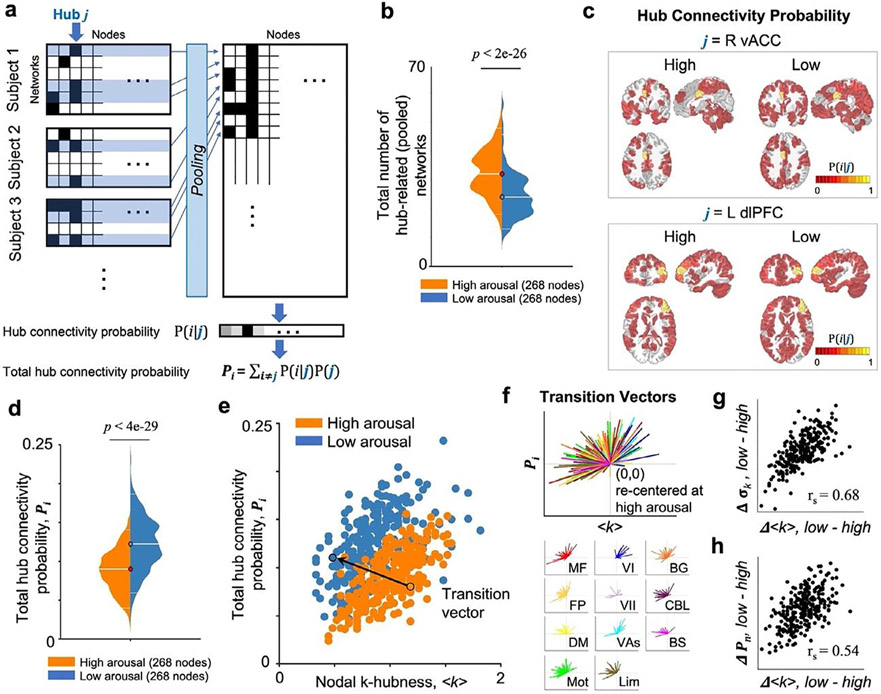
To investigate whether and how state-dependent changes in connector hubs relate to the actual patterns of network integration within these hubs, we computed the conditional probability (p_i) of each node i to be a member of functional networks overlapping in a hub j. To do this, for each arousal state, we first collected all resting state network maps estimated from all individual subjects. Using this collection, p_i was computed by the proportion of the number of functional networks involving both a node i and the hub j over all subjects to the total number of networks that involved the node j over all subjects, such that p_i =1 if i = j.

$${\mathit{p}}_i=P(i\mid j)=\frac{Numberofnetworksinvolvingbothnodesiandj}{Numberofnetworksinvolvinganodej}$$

This provided a probability map of functional connectivity associated with a hub j. A high probability p_i indicates that a node i is more likely to be a part of functional connectivity associated with a specific hub j across subjects, or the extent to which a connector hub contributes to inter-subject consistency of functional connectivity integration across the brain. Next, we calculated for each node i the total functional connectivity across the whole brain as the total hub connectivity probability P_i:

$${\mathit{P}}_i=\sum _{i\ne j}^V\mathit{P}(i\mid j)\mathit{P}(j)$$

where P(j) = 1/(V − 1) and V is the total number of nodes in the brain. The total hub connectivity probability P_i indicates the amount of nodal functional connectivity associated with distributed hubs over the whole brain. Note that the total number of networks involving a hub is state dependent; therefore, it is possible to normalize within state. Then, a transition vector was identified for each node within the scatter plot of the group average k-hubness (<k>, x-axis) and the total hub connectivity probability (P_i, y-axis), as a vector that links a node at high arousal state (<k>_high, P_i(high)) to the same node at low arousal state (<k>_low, P_i(low)). To visualize the magnitude and direction of transition vectors for all nodes, the transition vectors were re-centered to have a link from (0,0) to (<k>_low - <k>_high, P_i(low) - P_i(high)). Note that the total hub connectivity probability P_i is not identical to the conventionally defined mean functional connectivity, i.e. the mean signal correlation in the whole-brain, because it only takes into account hub-related functional connectivity, that is, functional connectivity of the regions that are parts of networks involving connector hubs.

2.8. Networks and parcellations

To compare our hubness measure estimated using the shen-268 parcellation scheme, between two arousal states and between different analysis approaches, we use a priori eleven large-scale functional networks (11Net). The 11Net includes ten a priori large-scale networks defined as described in Noble et al. (2017), whereas the nodes belonging to the brainstem were assigned to an 11^th network (Fig. 2j). Next, when we repeat our analyses using a 249-parcel atlas based on the Schaefer-200 cortex parcellation (Schaefer et al., 2018), we use a priori seven networks defined in Yeo et al. (2011), the subcortical network from the anatomical Yale Brodmann Atlas (Lacadie et al., 2008), cerebellum network from Yeo et al. (2011), and the brainstem network from the Shen-268 atlas (Finn et al., 2015; shen et al., 2013).

2.9. Graph theory

We conducted Graph theory analysis on our state-stratified data to evaluate if we can observe similar patterns of hub reorganization using the hubness metrics derived using Graph theory. It is important to note that k-hubness in SPARK and hubness metrics in Graph theory measure different properties, therefore a direct comparison of these measures is not appropriate. The Brain Connectivity toolbox (https://sites.google.com/site/bctnet/) was used to compute two network measures for each node: within-module degree z-score and participant coefficient (Rubinov and Sporns, 2010). For each time (T=160 time-points)-by-node (R=268) data matrix, a R-by-R individual connectivity matrix was obtained by computing the Pearson’s correlation coefficient between the mean time-series signals in each pair of nodes. We retained only positive correlations after replacing negative correlations by zero and used a resultant weighted individual connectivity matrix to detect modular network structures. We tested both binary and weighted undirected networks. For binary undirected networks, edges with strong weights using a proportional threshold were retained. Three proportional thresholds were tested: 5%, 10% and 30%.

The Louvain modularity algorithm estimated up to 5 non-overlapping networks from individual subjects in our dataset, which were much smaller than the number of overlapping networks estimated using SPARK (up to 50) (see Results). Detection of modular (network) structures is a critical step for hub analysis in both approaches. To reduce this observed discrepancy of the number of modules between two approaches, we used the pre-defined eleven large-scale networks (11Net) as non-overlapping modules for Graph theory to calculate within-module degree z-score (W_i, within-module strength) for each node i (Guimera and Amaral, 2005).

$$W_i=\frac{{\kappa }_i-{\overline{\kappa }}_{s_i}}{{\sigma }_{{\kappa }_{S_i}}}$$

where κ_i is the strength of connections of node i to other node in its module s_i, ${\overline{\kappa }}_{s_i}$ is the average of κ over all the nodes in s_i, and σ_κSi is the standard deviation of κ in s_i. We calculated the participant coefficient (PC_i, between-module strength) for each node to quantify the extent to which a node is connected across between-modules, as follows.

$$P{C}_i=1-\sum _{s=1}^{n_M}{\left(\frac{{\kappa }_{is}}{{\kappa }_i}\right)}^2$$

where κ_is is the strength of all positive connections of node i to nodes in module s, κ_i is the sum of strengths of all positive connections of node i, and n_M is the total number of modules in the graph. The participant coefficient becomes 1 if a node’s connections are uniformly distributed among all the modules and 0 otherwise, when all its connections are within its own module. These two graph measures have continuous values, counting the number of individual edges connected to each node, in contrast to our k-hubness which is a small integer often less than ten, counting the number of overlapping networks involved in each node. Lastly, for group analysis, to evaluate these graph measures using the same processing pipeline as we did for SPARK, we first implemented the graph analysis at the individual level and then averaged each network measures in each node across subjects. This resulted in group average within-module degree z-score (⟨W⟩_i) and group average participant coefficient (⟨PC⟩_i) for each node.

3. Results

We present the results from our connector hub analyses across arousal levels as follows. First, we assessed whether the global scale of functional connectivity is preserved across high and low arousal states (Section 3.1). We then estimated hub disruptions in the whole brain at both the group and single subject levels (Section 3.2). Next, we investigated the impact of arousal on connector hubs in large-scale networks (Section 3.3) and inter-subject variability of the connector hub organizations (Section 3.4). Then, we studied whether and how such connector hub disruptions relate to the actual patterns of functional network integration within these hubs (Section 3.5). The reliability and robustness of our hub estimations are addressed in Section 3.6. Finally, we investigated the impact of global signal regression on pair-wise fMRI signal correlations and the estimation of hubs (Section 3.7). In addition, we evaluated whether traditional hub measures derived using graph theory could detect arousal-level dependent changes in network integration and the impact of global signal regression on these measures.

3.1. Preserved global network scale between high and low arousal states

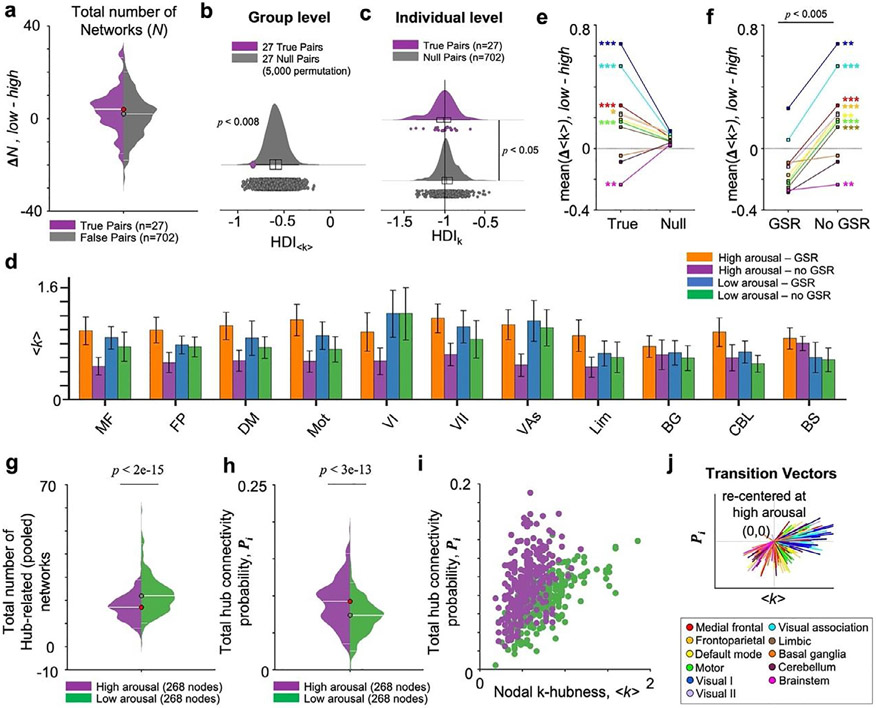
We first assessed whether the total number of functional networks in the whole brain is preserved across high and low arousal states. To avoid any potential confounds introduced by the state stratification strategy in our parameter estimations (e.g., the number and duration of continuous state segments), we did not directly compare the distributions of N between high and low arousal states (Fig. S1). Instead, we compared the between-state differences in N to the difference observed from null data (Wilcoxon rank sum test, p>.05). In-line with previous work (Achard et al., 2012; Vatansever et al., 2020), we found that the total number of networks (N) detected by SPARK from individuals was preserved between states (Fig. 2a). Estimated N was 30 ± 16.3 (median ± interquartile range) at high arousal and 25 ± 8 at low arousal. The goal is to investigate whether the patterns of connector hubs actually change with arousal modulations, while the global network scale is preserved during resting state.

3.2. Brain-wide disruptions of connector hubs from high to low arousal states

We observed differences between the group average k-hubness maps estimated from resting state fMRI at high and low arousal states. At high arousal, connector hubs are widely distributed across the unimodal and transmodal cortices, subcortical structures, cerebellum and brainstem (Fig. 2b). At low arousal, we observe an overall decrease in k-hubness across the brain, relative to the high arousal state, with the exception of some nodes in the visual networks (Fig. 2c, d and i, two-sided Wilcoxon rank sum test, Bonferroni corrected p<.05).

To quantify the overall degree of hub disruptions in the whole brain, we defined the hub disruption index (HDI_k ) using k -hubness (Lee et al., 2018). We found the group-level HDI_<k> to be −0.66, indicating a brain-wide disruption of connector hubs with arousal at resting state (Fig. 2e). From the null data, the estimated HDI_<k> was 0.08, indicating no hub disruption between randomly stratified states (Fig. 2f). We next assessed if our group-level finding was replicated in individual subjects. To do this, using the same approach, we define HDI_k using the individual subject’s nodal k-hubness (k) to quantify the overall connector hub reorganization at the individual level (x-axis, k_High; y-axis, k_Low - k_High) (Fig. 2g). In Fig. 2h, the distribution of individual level HDI_k estimated from 27 subjects (HDI_k = −1.03 ± 0.08) is shown compared to that from 702 randomized pupillometry samples (HDI_k = −0.99 ± 0.12). Consistent with the group results, we observed a negative relationship indicating that connector hubs reorganize from high to low arousal at the individual subject level, when compared to the results from null data (left-tailed Wilcoxon rank sum test, p<.003) (see Fig. S4 for the individual level results from all subjects). The group- and individual-level HDI analyses for k-hubness demonstrate arousal-level-dependent changes in between-network integration in resting state functional connectivity.

Motion can be a difficult confound in fMRI analyses (Power et al., 2015; Satterthwaite et al., 2012). We assessed if individual-level hub disruption was correlated with subject motion in fMRI data and if so, would it account for these findings. We show that inter-subject variability of the estimated HDI_k is not correlated with head motion (Wilcoxon rank sum test, p>.8) (Fig. S5). We also tested if individual-level hub disruption was correlated with the proportion of missing data-points in the pupillometry data. The proportion of missing data-points may affect identification of the arousal state. Potential causes of missing data included technical errors such as a connection issue with the eye-tracking system and inability to quantify pupil size due to blinks and saccades. Across the 27 subjects, we found 6.02 ± 9.48 % discarded time-points for rest 1 and 4.33 ± 8.33 % for rest 2 (Table S1). Inter-subject variability of the estimated HDI_k was not correlated with missing pupillometry data (Wilcoxon rank sum test, p>.2) (Fig. S6).

3.3. Brain-wide decreases in between-network integration at low relative to high arousal

We next investigated the impact of arousal on large-scale networks. In Fig. 3a, we show the distribution of arousal-level-dependent changes in group-average k-hubness (Δ<k>, low - high) within each large-scale network (Noble et al., 2017). For each network, we compare the Δ<k> distribution from the nodes belonging to this network estimated across our 27 subjects (color-coded), to the null Δ<k> distribution from the same nodes estimated from randomized data over 5,000 permutations (in gray color). To do this, the null Δ<k> distribution was obtained by averaging nodal k-hubness across the same 27 subjects with a randomized set of brain-pupillometry pairs. As a result, we found decreases in group-average k-hubness with decreased arousal in the frontoparietal, motor, limbic and cerebellum networks (two-tailed Wilcoxon rank sum test, Bonferroni corrected p<.001) and the default mode network (p<.01).

Fig. 3.

Decreased between-network integration at low relative to high arousal. (a) Around the circle, we show the distributions of between-state changes in group-average k-hubness (Δ<k>, low-high) within each of the pre-defined large-scale networks (color-coded). The null distribution of Δ<k> was generated from the same nodes in each network over 5,000 permutations (shown in grey). Asterisks indicate Bonferroni corrected p-values from the two-tailed Wilcoxon rank sum tests, * : p<.05, **: p<.01, ***: p<.001. At the center of the circle, we show a node-wise two-sample test result (one-tailed bootstrap test, FDR corrected p<.05) with 5,000 bootstraps (Efron and Tibshirani, 1994). (b) A summary of network-level Δ<k> distributions that are shown in (a), using the mean of Δ<k> within each network. p<.004 using the two-tailed Wilcoxon rank sum test. PreM: Premotor cortex. vACC: ventral anterior cingulate cortex. PA: primary auditory cortex. dlPFC: dorsolateral prefrontal cortex. Hipp: hippocampus. BS/CBL: brainstem/cerebellum.

In addition, node-wise statistical tests on individual connector hubs confirmed our observation of a brain-wide decrease in between-network integration, and highlighted nodes that exhibited consistent changes across subjects (Fig. 3a, at the center of circle plot). We used the left-tailed bootstrap-based two-sample tests proposed in Efron and Tibshirani (1994), because individual-level k-hubness is a discrete integer within a small range (e.g. [0, 5]) and the symmetry of distributions are not assumed. We found decreases in k-hubness at low arousal in the premotor/supplementary motor, ventral anterior cingulate, primary auditory and dorsolateral prefrontal cortices, hippocampus, cerebellum, and in the node that spans from the cerebellum to the locus coeruleus in the brainstem (Z= −24 in the MNI coordinates)(Keren et al., 2009) (FDR corrected p<.05, see Table S2). In Fig. 3b, we summarize our findings using the mean of Δ<k> within each network, highlighting arousal-dependent decreases in group-average k-hubness in the five large-scale networks.

3.4. Inter-subject variance in between-network integration decreases from high to low arousal

Next, we quantified the change in inter-subject variance of nodal k-hubness between arousal states. Fig. 4a illustrates the map of between-state differences in the standard deviation of k-hubness (σ_k). At low relative to high arousal, we found a brain-wide decrease in inter-subject variance of k-hubness across the brain in regions belonging to the medial frontal, frontoparietal, default mode, motor, limbic, cerebellum and brainstem networks (Fig. 4b, two-sided Wilcoxon rank sum test, Bonferroni corrected p<.05). To test if such decreases were above chance, we computed the between-state difference in standard deviation of k-hubness (Δσ_k, low − high) across 27 subjects. The null Δσ_k distribution was obtained by averaging nodal k-hubness across the same 27 subjects with a randomized set of brain-pupillometry pairs. Fig. 4c shows that the distribution of Δσ_k from the 268 nodes in the whole brain is lower than the null Δσ_k distribution (two-sided Wilcoxon rank sum test, p<4e-23). In each pre-defined large-scale network, we compared the Δσ_k distribution from the nodes belonging to each network estimated from 27 subjects to the null Δσ_k distribution (in gray color). In Fig. 4d, we summarize our findings using the mean of Δσ_k within each network. We found decreases in inter-subject variance of k-hubness with arousal, again, in the frontoparietal (two-sided Wilcoxon rank sum test, Bonferroni corrected p <.05), default mode (p <.01), motor, limbic and cerebellum networks (p<.001). We did not find state-differences in inter-subject variability at the node level (Levene’s test for equality of variance, 5,000 permutations, FDR corrected p<.05).

Fig. 4.

Inter-subject variability in functional between-network integration decreases from high to low arousal. (A) The map of between-state difference in the standard deviation of k-hubness (Δσ_k) across subjects; between low and high arousal resting states. (B) The bar plot of σ_k distributions within the eleven pre-defined large-scale networks in high and low arousal states. Mean ± standard deviation. (C) The distribution of between-state differences in inter-subject variance of k-hubness (Δσ_k, low − high), estimated across 27 subjects. The null distribution of Δσ_k was generated over 5,000 permutations. (D) A summary of network-level Δσ_k distributions using the mean of Δσ_k within each network (left) compared to the null distribution of Δσ_k (right). (E) Brain-wide changes in σ_k between high and low arousal. The hub disruption index (HDI) for nodal σ_k reveals a brain-wide decrease in inter-subject variability. (F) Whereas there is no difference observed for null data. Asterisk indicates statistical significance from Wilcoxon rank sum tests with Bonferroni corrected p-values, *: p<.05, **: p<.01, ***: p<.001.

To quantify brain-wide changes in inter-subject variability between low and high arousal, we defined a HDI for σ_k, using the method to estimate the HDI for k-hubness. We found a negative slope (−0.67), indicating a brain-wide decrease in inter-subject variability at low relative to high arousal (Fig. 4e). For null data, the slope was 0.02, which is close to zero, indicating no difference in state-dependent HDI for k-hubness (Fig. 4f). Note that the range of σ_k for real and null data in Fig. 4e and f (e.g., less than 2), indicating that there is no sample size bias. Taken together, our results demonstrate an overall decrease in inter-subject variability of k-hubness comparing the low relative to high arousal state.

3.5. Resting state networks at low arousal have reduced network overlaps and increased global connectivity

It is important to investigate how such connector hub disruptions relate to the actual patterns of functional network integration within these hubs. For each arousal state, we generated a probability map of functional connectivity involving each hub, by computing the conditional probability (p_i) of each node i to be a member of any functional network overlapping in a hub j (Fig. 5a). This conditional probability was computed from the pooled collection of all networks estimated from all individual subjects. The total number of hub-related (pooled) overlapping networks was 32 ± 11 (median ± interquartile range across the 268 nodes) at high arousal and 24 ± 11 at low arousal (Fig. 5b; two-sided Wilcoxon rank sum test, p<2e-26). This indicates that there are fewer network overlaps resulting in lower between-network integration at low arousal. In addition, the spatial distribution of p_i varied across hubs. For example (Fig. 5c), for a connector hub in the right ventral anterior cingulate cortex, the spatial distribution of functional connectivity integrated with this hub was broader in the low arousal, suggesting lower inter-subject variance at low relative to high arousal. On the other hand, the probability map for a connector hub in the left dorsolateral prefrontal cortex shows a similar spatial distribution of hub-associated functional connectivity at both high and low arousal, including regions of the frontoparietal and default mode networks, suggesting stable inter-subject variability across arousal levels.

Fig. 5.

Resting state networks at low arousal have reduced network overlaps while exhibiting brain-wide connectivity. (a) A summary diagram to calculate hub connectivity probability (p_i = P(i∣j)) and total hub connectivity probability (P_i). For an arousal state, resting state networks involving a hub j are collected from all subjects. p_i: the conditional probability of each node i to be a member of functional networks overlapping in a hub j. (b) The total number of hub-related networks for each node is lower at low relative to high arousal. (c) Probability maps of functional connectivity integrated in a specific hub (two exemplary nodes in the right vACC and the left dlPFC) across subjects. (d) P_i is higher at low relative to high arousal across the whole brain, indicating an increased global synchronization. (e) Scatter plot of hub measures from 268 nodes at high (orange) and low (blue) arousal data. X-axis denotes the group average k-hubness (<k>). Y-axis denotes P_i calculated for each node i. Left (L)/Right (R) in bold. An exemplary transition vector that links a node at high arousal state (<k>_high, P_i(high)) to the same node at low arousal state (<k>_low, P_i(low)) is shown. (f) Re-centered transition vectors for all nodes, from (0,0) to (<k>_low- <k>_high, P_i(low)- P_i(high)), show a trend pointing toward the quadrant II, indicating a decrease in k-hubness and an increase in P_i from high to low arousal. Transition vectors for nodes in each large-scale network (color-coded as in Figs. 2-4) are shown below. Nodes exhibiting large group-average changes in <k> also exhibit large changes in inter-subject variability (g) and total connectivity probability (h) (r_s: Spearman’s rank correlation, p=0).

Next, we quantified the total amount of functional connectivity of each node i over the whole brain as the total hub connectivity probability P_i (Fig. 5d). The median of P_i distribution was higher at low arousal relative to high arousal (two-sided Wilcoxon rank sum test, p<4e-29), suggesting an increase in global hub connectivity. A scatter plot of the total hub connectivity probability (P_i) and the group average k-hubness (<k>) estimated for 268 nodes shows a clear pattern of connector hub disruption: a decrease in k-hubness and an increase in P_i from high to low arousal (Fig. 5e). In addition, as expected, we found that nodes exhibiting large group-average changes in <k> also exhibit large changes in inter-subject variability (g) and total connectivity probability (h) (r_s: Spearman’s rank correlation, p=0).

Recall that the proposed total hub connectivity probability (P_i) is different from the mean functional connectivity (the mean signal correlation in the whole brain). The mean functional connectivity is usually measured by the mean of Pearson’s correlation coefficients calculated between all pairs of nodes, regardless of their involvement in between-network integration. In contrast, P_i considers functional connectivity of the regions that are actually parts of networks involving connector hubs. Whereas we did not find any difference in the mean functional connectivity between the high and low arousal states (Fig. 6g), there were clear differences in P_i between the high and low arousal states (Fig. 5).

Fig. 6.

Global signal regression (GSR) shifts the distribution of resting state fMRI signal correlations across pupil-linked arousal states. (a and b) GSR introduces negative correlations in resting state functional connectivity. For each pair of nodes defined using the shen268 parcellation scheme, the Pearson’s correlation coefficient (R) was calculated using the average BOLD signals in each node from individual rest 1 (a) and rest 2 (b) data. Signal correlations from all pairs of nodes across 27 subjects are then collected to generate the distribution of R. (c–f) A shift of R distribution by GSR is observed in true pairs of fMRI-pupillometry data (c and d, n=27) and across randomized state datasets (e and f, n=702). In (c), the amount of shift induced by GSR was larger in datasets stratified as high arousal state than in datasets stratified as low arousal state. (g) Without using GSR, there are more positive signal correlations at high relative to low arousal state. (h) In two randomized state datasets, GSR introduces a common shift of the signal correlation distributions toward negative correlations. (i) When GSR is applied, the signal correlation distributions at the two arousal states overlap. (j) The same pattern is found in the randomized state datasets. ***: Uncorrected p=0, two-sample t-test for Fisher’s Z transformed R values.

3.6. Reliability and robustness

The reliability of hub estimations at the single subject level is assessed using SPARK (Lee et al., 2016), to extract the most reproducible patterns of overlapping functional networks. Within this procedure, we select highly reproducible components at 95% confidence interval (CI) by approximating the Gaussian distribution of background noise in network maps estimated from an average across 300 bootstraps. In this study, the density of k-hubness estimated from data obtained in the high arousal state, for instance, decreases with threshold: 0.84 ± 0.38 (median ± interquartile range) at 90% CI, 0.58 ± 0.41 at 95% CI, and 0.35 ± 0.29 at 99% CI (Fig. S7). This means only 35% of nodes are reliably involved in at least one network, when using the most conservative threshold. To validate whether our findings are robust to the choice of CI, we repeated our analyses using 90% and 99% CI. As expected, between-state changes in global network scale (ΔN, low-high) were preserved across arousal states. Furthermore, we observed decreases in the group-average k-hubness (Δ<k>) and their inter-subject variability (Δσ_k) at low relative to high arousal across all CI thresholds, with such changes being most robust in the motor and cerebellum networks (Fig. S7).

To test if our results were replicable using different parcellation schemes, we repeated all analyses using the 249-parcel functional atlas, defined by integrating the Schaefer-200 cortex parcellation (Schaefer et al., 2018) with 49 subcortical regions. Consistent with the results using the Shen-268 atlas, the number of networks (N) were preserved across high and low arousal states (Wilcoxon rank sum test, p>.05). For this 249-parcel atlas, we used ten pre-defined networks: 7 networks defined by Yeo-7 atlas (visual, somatomotor, dorsal attention, salience ventral attention, limbic, control, and default mode), and three anatomically defined subcortical networks (subcortical, cerebellum, and brainstem). Within each of ten pre-defined networks, we compared the distributions of Δ<k>, by averaging k-hubness in each node belonging to this network across 27 subjects, to the null Δ<k> distribution from the same nodes, by averaging k-hubness across 27 randomized data, repeated over 5,000 permutations. The result agreed with what we found using SPARK, particularly the SPARK results with the most conservative threshold (Fig. S8). Group-average k-hubness was associated with decreased arousal in the somatomotor (two-tailed Wilcoxon rank sum test, Bonferroni corrected p<.001), ventral attention (Bonferroni corrected p<.001) and subcortical network (Bonferroni corrected p<.01). We also found increases in the group-average k-hubness in the visual network at low relative to high arousal (Bonferroni corrected p<.001). The total number of hub-related (pooled) overlapping networks was 20 ± 9 (median ± interquartile range across the 249 nodes) at high arousal and 19 ± 8.3 at low arousal (two-sided Wilcoxon rank sum test, p<.03). This indicates that there are fewer network overlaps resulting in lower between-network integration at low arousal. The median of P_i distribution was higher at low arousal relative to high arousal (two-sided Wilcoxon rank sum test, p<.004), suggesting an increase in global connectivity. Again, as expected, we found that nodes exhibiting large group-average changes in <k> also exhibit large changes in inter-subject variability (r_s=0.75, p=0) and total connectivity probability (r_s=0.44, p<e-12).

3.7. Global signals

It is suggested that the global signal in resting state fMRI is associated with arousal fluctuations and the choice of global signal regression may impact observed patterns of functional connectivity, introducing negative correlations (Saad et al., 2012). The global signal is composed of both neuronal and non-neuronal signals (Murphy and Fox, 2017). To assess the impact of GSR on our hub analyses, we repeated all analyses using data preprocessed without GSR and compared with our main results obtained from data preprocessed with GSR. The shen-268 atlas was used for this assessment. The assessment was conducted for (i) the analysis of pair-wise BOLD signal correlations, (ii) the SPARK analysis of k-hubness, and (iii) the analysis of conventional hub measures in Graph theory. As a result, we demonstrate a systematic change in pair-wise fMRI signal correlation structures in the arousal state-stratified data and the presence of global and local effects of arousal on resting state functional connectivity. To this end, we show that the choice of global signal regression could result in different conclusions in conventional graph theoretical analysis and in the analysis of k-hubness.

3.7.1. Impact of GSR on BOLD signal correlations

First, we compared the distribution of pair-wise BOLD signal correlations in the datasets preprocessed with and without GSR. The standard Pearson’s correlation coefficient was calculated between the BOLD signals averaged in each pair of nodes. As expected, GSR introduced negative correlations in both datasets acquired from the rest 1 and 2 runs (p=0, two-sample t-test on Fisher’s Z transformed Pearson’s correlation coefficients R), also from the datasets with temporal concatenation of rest 1 and 2 (p=0). The shift in R distribution to negative, after applying GSR, was observed from both datasets where the arousal states were correctly or randomly identified (Fig. 6c-f). When we did not perform GSR, there were more positive signal correlations at high relative to low arousal (Fig. 6g), suggesting an inhomogeneous association of global signal across arousal levels. The signal correlation distributions in datasets preprocessed using GSR are not different between high and low arousal states (Fig. 6i). This result suggests that there is a global arousal effect involved in the global signals and we may study local effects (e.g. network hubs) of arousal modulations after applying GSR. Note that our main results, the comparison of connector hub organizations across arousal states, were obtained using the datasets preprocessed using GSR (the n=27 datasets used in Fig. 6i), when compared to the null datasets preprocessed using GSR (the n=702 datasets used in Fig. 6j). We did not find evidence to relate motion (Fig-S4) or eye-closure related artifacts (Fig. S5) with our hubness measures (individual level HDI_k and the mean of Δ<k>, low - high) either with or without GSR. Note that GSR resulted in the common impact on the two randomized datasets (false-high arousal and false-low arousal states) introducing a shift toward negative correlations (Fig. 6h and j). Together, we confirmed the well-known impact of GSR on resting state functional connectivity and, in addition, found an inhomogeneous association of global signals with pair-wise signal correlations at high and low arousal.

3.7.2. Impact of GSR on k-hubness

To understand how GSR impacts the estimation of arousal-level dependent changes in the hub structures estimated using SPARK, we repeated our analyses using the same datasets preprocessed without GSR (the same datasets used in Fig. 6g and h). As a result, we observed that GSR had an impact on the hub estimation in resting state fMRI using SPARK (Fig. 7).

Fig. 7.

Global signal regression has an impact on the topology of overlapping functional networks (k-hubness) in across arousal levels. We repeated our SPARK analysis using the datasets preprocessed without GSR. (a) The total number of resting state networks (N) detected by SPARK. (b) The distribution of group-level HDI_<k> compared to those from null data (bottom). p-value estimated using the left-tailed Wilcoxon rank sum test. (c) The distribution of individual-level HDI_k (top) and those from null data (bottom). p-value estimated using the left-tailed Wilcoxon rank sum test is shown. (d) The bar plot of k-hubness within the eleven pre-defined large-scale networks (11Net) in each state. Mean ± standard deviation. The GSR-dependent decreases in <k> at high arousal state is relatively larger than those at low arousal state. (e) A summary of network-level Δ<k> distributions using the mean of Δ<k> within each network. Within each of the 11Net networks, we compared the distributions of between-state changes in group-average k-hubness (Δ<k>, low-high) to the null distribution of Δ<k> that was generated from the same nodes in each network over 5,000 permutations. Asterisks indicate Bonferroni corrected p-values from the two-tailed Wilcoxon rank sum tests, *: p<.05, **: p<.01, ***: p<.001. (f) Comparison of the results obtained using data preprocessed with and without GSR. (g) The total number of hub-related networks for each node is higher at low relative to high arousal, and (h) the total hub connectivity probability (P_i) is lower at low relative to high arousal across the whole brain. (i) Scatter plot of hub measures from 268 nodes at high (purple) and low (green) arousal data. X-axis denotes the group average k-hubness (<k>). Y-axis denotes the total probability P_i calculated for each node i. (j) Re-centered transition vectors for all nodes, from (0,0) to (<k>_low- <k>_high, P_i(low)- P_i(high)), show a trend pointing toward the quadrant IV.

Like the results obtained with GSR (Fig. 2a), the global network scale estimated using SPARK was preserved between high and low arousal (Wilcoxon rank sum test, p>.05, Fig. 7). The estimated total number of resting state networks N was lower at both states when compared to the results obtained with GSR: 21 ± 9.75 (median ± interquartile range) at high arousal and 25 ± 6.25 at low arousal. We found a negative HDI_<k> at the group level (HDI_<k>=−0.84), when compared to the null results by averaging nodal k-hubness across 27 randomized data over 5,000 permutations (left-tailed permutation test, p<.008). When averaged across all 702 data estimated using false fMRI-pupillometry pairs, the HDI_<k> was 0.03. The HDI_k at the individual level was −1.01 ± 0.17 and lower than those estimated from individual null data (−0.97 ± 0.13; left-tailed Wilcoxon rank sum test, p<.05).

Next, given that we previously observed that there were more positive signal correlations at high relative to low arousal when GSR is not applied (Fig. 6g), we expected to observe a difference in the impact of GSR on hubs between high and low arousal states. As a result, when GSR was not applied, there was relatively stronger reduction in <k> at high arousal state compared to <k> values estimated at low arousal state (Fig. 7d), suggesting that the organizations of overlapping networks at high arousal state is more sensitive to the presence of global signals than those at low arousal state. The strong reduction in <k> observed at high arousal state in the data preprocessed without using GSR (Fig. 7d) resulted in changes in our subsequent analyses. We evaluated the distribution of arousal-level-dependent changes in group-average k-hubness (Δ<k>, low - high) within each large-scale network (Noble et al., 2017). As shown in Fig. 7e, we found increases in <k> with decreased arousal in the visual I (two-tailed Wilcoxon rank sum test, Bonferroni corrected p<.001), visual association (p<.001), medial frontal (p<.001), frontoparietal (p<.05), motor (p<.001) networks and decreases in <k> in the brainstem (p<.01). When we directly compare to the distribution of Δ<k>, low − high, estimated from data preprocessed with and without GSR, we observe a shift of Δ<k> from negative to positive values in all cortical networks (Fig. 7f, two-tailed Wilcoxon rank sum test, Bonferroni corrected p<.001). The arousal level-dependent increases in Δ<k>, low − high, at the visual networks and decreases at the brainstem network are observed in both datasets with and without GSR. On the other hand, when GSR was not performed, the arousal level-dependent decreases in Δ<k>, low − high, in the medial frontal, frontoparietal, default mode, motor, and limbic networks were then flipped to increases in Δ<k>, low − high, at low relative to high arousal.

Lastly, we observed that global signals impact the actual patterns of functional between-network integration within these hubs. The total number of hub-related (pooled) overlapping networks was 17 ± 8 (median ± interquartile range across the 268 nodes) at high arousal and 22 ± 9 at low arousal (Fig. 7g; two-sided Wilcoxon rank sum test, p<2e-15). This indicates that there are more network overlaps resulting in more between-network integration at low arousal, and again, it is the opposite of what we found from the data preprocessed using GSR. The median of P_i was lower at low relative to high arousal (two-sided Wilcoxon rank sum test, p<3e-13), suggesting a decrease in global synchronization (Fig. 7h). P_i considers functional connectivity of the regions that are parts of networks involving connector hubs, and different from the mean of all pairwise functional connectivity. In the scatter plot of P_i and <k> estimated for 268 nodes, we found an increase in k-hubness and a decrease in P_i from high to low arousal (Fig. 7i), different from the results obtained using GSR. This was confirmed by the visualization of re-centered transition vectors (from high to low arousal state) for all nodes, showing a trend pointing to the quadrant IV (Fig. 7j).

3.7.3. Impact of GSR on Graph theoretical analysis

Lastly, we evaluated if the observed impact of GSR on the BOLD signal correlation structures could be also observed in conventional hub metrics derived using Graph theory from the same arousal state-stratified datasets. Another goal was to investigate if hub metrics using Graph theory could detect similar changes of network integration as the patterns of network reorganization found using SPARK. To do this, group average participant coefficients ⟨PC⟩ and within-module degree z-score ⟨W⟩ were computed for each node from the weighted undirected networks and the binary undirected networks constructed using three proportional thresholds (30%, 10%, and 5%). Like the results found using SPARK, there were notable differences in nodal participant coefficient between the data preprocessed with and without GSR. On the other hand, we did not find between-state differences in within-module degree z-score from both datasets with and without GSR. In addition, patterns of between-state difference in participant coefficients (low relative to high arousal states) were different between when calculated from the weighted and binary undirected networks, indicating that different analytic choices within Graph theory also result in different conclusions.

Specifically, we first compared the HDI of the graph measures between the high and low arousal states. Using GSR, we did not find any arousal-level dependent changes in the HDI estimated using either within-module degree z-score or participant coefficient. Without using GSR, there were hub disruptions estimated using within-module degree z-score using the binary networks with 5% threshold, when compared to the results from null data (5,000 permutations, left-tailed Wilcoxon rank sum test, p<.05). The HDI using group average participant coefficients showed arousal level dependent hub disruptions from the weighted network and the binary networks using all thresholds (p<.01). Next, we compared the distribution of between-state difference in nodal group average graph measures in the eleven large-scale networks, estimated from the datasets with and without GSR. As a result, we did not find any between-state difference in group average within-module degree z-scores (Δ<W>, low − high.) estimated from the binary undirected networks using all proportional thresholds and from the weighted undirected networks (5,000 permutations, two-tailed Wilcoxon rank sum test). On the other hand, there were between-state differences in group average participant coefficients (Δ<PC>, low − high) within several networks, whereas there was also clear discrepancy in these measures when estimated from datasets with and without GSR (Fig. 8). See Supplementary Fig. S9 for the results using the thresholds 10% (PC_10%) and 5% (PC_5%). The participant coefficients estimated from the weighted and binary networks could result in different patterns of arousal-level dependent changes in network integration. For example, without using GSR, participant coefficients estimated from the weighted network overall decreased at low relative to high arousal (Fig. 8e), however, those estimated from the binary networks overall increased at low relative to high arousal (Fig. 8f).

Fig. 8.

Global signal regression has an impact on hub detection using Graph theory across arousal levels. For each individual subject, participant coefficient (PC) was calculated for each node in the shen-268 functional atlas from the weighted undirected network (PC_W) and the binary undirected networks constructed using the proportional threshold 30% (PC_30%). Group average participant coefficient (⟨PC⟩) was computed by averaging PC across subjects in each node. We compared the distributions of between-state changes in group-average PC (Δ⟨PC⟩, low-high) within each of the 11Net pre-defined large-scale networks (color-coded). The null distribution of Δ⟨PC⟩ was generated from the same nodes in each network over 5,000 permutations. Color-coded asterisks indicate Bonferroni corrected p-values from the two-tailed Wilcoxon rank sum tests, *: p<.05, **: p<.01, ***: p<001. This figure shows the summary of network-level Δ<PC> distributions using the mean of Δ⟨PC⟩ within each network from arousal state-stratified datasets preprocessed (a and b) with GSR and (c and d) without GSR. (e and f) shows the comparisons between the results with and without GSR. p-value is presented on top of each comparison using the two-tailed Wilcoxon rank sum test.

Overall, these results suggest that different choices of GSR can result in different conclusions in the analyses of resting state functional connectivity, and the impact of GSR varies depending on the choice of network analysis methods. We found a systematic shift in pair-wise fMRI signal correlations induced by GSR and reorganization of functional network integration in arousal state-stratified datasets with and without GSR. The observed changes in signal correlation structures in the arousal state-stratified data and patterns of network integration suggest the presence of global and local effects of arousal modulations on resting state functional connectivity. That is, local effect of arousal on the functional organization of the brain exists even after that global signal is removed by GSR.

4. Discussion

Using simultaneous fMRI and pupillometry, we demonstrated changes in functional network integration in the cerebral cortex associated with fluctuations in arousal during the resting-state. In the absence of whole-brain mean global signal, we found decreases in between-network integration from high to low arousal by analyzing k-hubness at both the group- and individual-subject level. K-hubness differences emerged in regions including the frontoparietal, default mode, motor, limbic, and cerebellum networks. These findings establish a relationship between modulations in arousal during resting wakefulness and the dynamics of functional brain organization, including changes in connector hubs or between-network integration. The inter-subject variability of connector hubs decreases at low relative to high arousal, whereas the impact of arousal modulation on connector hub-related functional network integration differed between brain regions. State-dependent changes in connector hubs relate to the actual patterns of network integration within these hubs. While the global network scale, the total number of networks in the brain, was preserved between the high and low arousal states, the number of hub-related networks decreased, and the nodal total connectivity probability increased at low relative to high arousal state. These findings together suggest a brain state transition from high to low arousal characterized by global synchronization or reduced functional network specializations. Control analyses indicated that motion and eye-closure related effects are not driving results. Our results demonstrate that k-hubness is sensitive to arousal levels within resting state and that arousal is not localized to specific brain areas known to be directly associated with arousal regulation, but instead it’s associated with changes involving high-level between-network communications in the cerebral cortex.

Secondly, our results suggest that different choice of GSR can result in different conclusions in the analyses of resting state functional connectivity, and the impact of GSR could vary over different analytic approaches. We first confirmed the well-known shift of the pairwise fMRI signal correlation distribution to negative, after applying GSR, regardless of whether the arousal states were correctly or randomly identified. In addition, surprisingly, we found that when we did not perform GSR, there was more positive signal correlations at high relative to low arousal (Fig. 6), suggesting an inhomogeneous association of global signal across arousal levels. Furthermore, we observed that patterns of network integration estimated using conventional Graph theory and SPARK are different when estimated from data preprocessed with and without GSR. Taken together, our result suggests the presence of global and local effects of arousal modulations on resting state functional connectivity and recommend in future studies on resting state functional connectivity to report results using datasets preprocessed with and without GSR.

These findings demonstrate the utility of simultaneous pupillometry as a proxy for measuring variations in arousal during resting-state fMRI. In the absence of task-related cognitive demands, pupil changes are mainly driven by non-specific factors such as arousal (Joshi and Gold, 2020; Liu and Falahpour, 2020). We observed brain-wide connector hub disruptions between low and high arousal, by measuring the hub disruption index of group-average k-hubness (HDI_<k>) (Fig. 2). This finding indicates the flexibility of functional networks over time even during rest (Barttfeld et al., 2015; Shine et al., 2016; Yeo et al., 2015). The negative HDI_<k> at the group level was replicated using HDI_k values estimated from individual subjects. These results are in agreement with previous work using HDI for degree centrality in graph theory, reporting hub disruptions in patients with coma (Achard et al., 2012), and in healthy subjects with propofol-induced sedation (Vatansever et al., 2020). In this work, we were able to address a more subtle question as to whether modulations in arousal during the resting state are associated with changes in the functional organization of the brain. On the other hand, we found that the HDI_k estimated from the randomized state datasets was higher at the individual level than that estimated at the group level, potentially reflecting the presence of other factors (e.g., ongoing thought, emotion) that could account for a portion of the inter-subject variation. Future work should aim to identify such factors to understand the relationship between these factors and hub configuration in the resting state.

We found decreases in k-hubness at low relative to high arousal in regions of the frontoparietal, default mode, motor, limbic and cerebellar networks (Fig. 3). These regions have been implicated in previous work that assessed co-fluctuations of resting state BOLD activity and simultaneous pupillometry (Breeden et al., 2017; DiNuzzo et al., 2019; Schneider et al., 2016; Yellin et al., 2015). Schneider et al. found a positive coupling of pupil dilation with BOLD activity in the salience and default mode networks, frontal and parietal areas, and a negative relationship between spontaneous pupil constrictions and BOLD activity in the visual and sensorimotor areas (Schneider et al., 2016). Modulations of the default mode network have been observed during sleep deprivation (De Havas et al., 2012; Gujar et al., 2010; Yeo et al., 2015) and light sleep (Boly et al., 2012; Larson-Prior et al., 2011; Spoormaker et al., 2010; Sämann et al., 2011). We found a between-state change in k-hubness in the node that spans from the cerebellum to the locus coeruleus in the brainstem (Z= −24 in the MNI coordinates)(Keren et al., 2009), a core region of the ascending arousal system (Lee and Dan, 2012), in agreement with Murphy et al. who found that pupil diameter covaries with BOLD activity in the locus coeruleus (Murphy et al., 2014). Here, we extend these previous studies by demonstrating that modulations of arousal are not limited to specific brain areas directly associated with the brain’s ascending arousal system, but instead involve brain-wide communication networks.

That we found arousal-level-dependent decreases in between-network integration in regions of the frontoparietal cortex, suggests a role of arousal modulations in baseline activity related to cognition. Decreases in functional connectivity in the frontoparietal network were found during propofol-induced loss of consciousness and sleep (Boly et al., 2012; Boveroux et al., 2010; Schrouff et al., 2011; Schröter et al., 2012). Out finding that arousal modulation is not limited to specific regions of the ascending arousal system, but rather involve brain-wide cortical areas, agrees with other studies using different network analysis approaches (Liu and Falahpour, 2020). Using the analysis of coherence and phase-shift between fMRI and arousal fluctuations, it is suggested that a traveling wave linked to arousal offers a parsimonious account for the global organization of functional connectivity gradients estimated from resting state fMRI (Raut et al., 2021). Others found time-locked relationships between the measurement of participant coefficient using graph theory, BOLD activity of the ascending arousal system, low dimensional energy landscapes, and spatiotemporal travelling waves (Munn et al., 2021). Using in-scanner pupillometry, Shine et al. (2016) proposed that resting state functional connectivity alternates between integrated and segregated network topologies, and demonstrated a positive relationship between pupil diameter and between-network integration within these regions. On the other hand, a set of regions in the visual cortex showed a positive relationship between pupil diameter and within-network integration. Those findings in large part harmonize with our work, particularly the results found using dataset preprocessed using GSR, but there are several key differences. Notably, they identified integrated or segregated “topological” states from data, while we identified high or low “behavioral” arousal states. Our approach did not take into account intermediate levels of arousal and potential transient variations in hubs, but instead focused on detecting the most reproducible and individually consistent hub features characterizing each arousal state. Together, these findings lend support to the theory that state-dependent changes in brain functional connectivity may be driven by ongoing alterations in ascending neuro-modulatory input and global fluctuations in neural gain (Eldar et al., 2013; Shine et al., 2016). Shine et al. (2016) reported consistent group-level results with and without GSR in their task fMRI data, whereas the current work showed discrepancy between the two cases using resting state fMRI data. It might be helpful in future work to study the impact of GSR using an independent, larger dataset acquired from different sites and more diverse population (Marek et al., 2022).

We found decreases in inter-subject variability of k-hubness at low relative to high arousal (Fig. 4). The global network scale, the total number of networks estimated in the whole brain, was preserved between the high and low arousal states (Fig. 2a). The number of networks involving hubs was reduced in the low relative to high arousal state (Fig. 5b). The total functional connectivity increased over the whole brain at low arousal, despite the reduced number of hub-related networks, suggesting a brain state transition from high to low arousal characterized by global synchronization or reduced functional network specializations. In addition, the impact of arousal modulation on connector hubs differed between brain regions (Fig. 5). This suggests that accounting for arousal-dependent changes may help understand individual variability in functional connectivity and its association with behavior. Functional connectivity has been shown to be valuable in identifying individuals using patterns of brain functional connectivity (i.e., fingerprinting)(Finn et al., 2015), and in predictive models relating functional organization to behavior both under rest-(Finn et al., 2015; Shen et al., 2017) and task-conditions (Finn et al., 2017; Greene et al., 2018; Rosenberg et al., 2015, 2016). Task conditions offer a controlled manipulation of brain state, in contrast to the unconstrained nature of resting state; therefore, it is likely that individual differences in task-relevant circuitry can be amplified to help predict related traits (Greene et al., 2018; Lowe et al., 2000). Functional connectivity estimated from higher arousal resting state may play a different role in predicting traits, particularly for some phenotypes associated with high-level functions. It has already been demonstrated that state manipulations can influence trait predictions (Finn et al., 2017) for example. Given this evidence of the cognitive relevance of resting state functional connectivity (Barttfeld et al., 2015; Gonzalez-Castillo et al., 2019) in developing predictive models of behavior, future work should incorporate the role of arousal.

Then, we confirmed the well-known impact of GSR on resting state functional connectivity and observed that GSR had an impact on the estimations of network integration using SPARK and Graph theory. We argue that the impact of GSR on the relationship between arousal and resting state fMRI has been overlooked, and highly recommend reporting results with and without using GSR when analyzing resting state functional MRI data. GSR allows the study of arousal-level dependent changes in brain network topology, removing a global arousal effect associated with the fluctuations of pupil area. In this study, without performing GSR, we observed that there were more positive signal correlations at high relative to low arousal, whereas the signal correlation distributions in datasets preprocessed using GSR were not different between two states (Fig. 6). Although, care is needed for its interpretation, because this result does not indicate complete removal of common, global arousal fluctuations by GSR and unintended effects are possible. As demonstrated in this work, using GSR may allow us to study local effects of pupil-linked arousal modulations that remain after global arousal effects included in the whole-brain mean signal are removed. Using SPARK, we observed that hubs of overlapping networks estimated from high arousal state data were more sensitive to the removal of global signals than hubs estimated from low arousal state. However, this was not the case of the hubs of non-overlapping networks estimated using Graph theory. Consistent with our earlier work (Garrison et al., 2015), the participant coefficients estimated from different network constructions (e.g. weighted or binary) showed different, i.e. reversed, patterns of arousal-level dependent changes from the same datasets. It might be interesting in future studies to investigate why removal of global signals affected hubs in one arousal state more than in another and to explore at meso-scale the mechanisms underlying arousal-level dependent changes in network integration.

On the other hand, for the temporal alignment of pupillometry and fMRI time-courses, our preprocessing strategies included the convolution with canonical HRF, low-pass filtering, and down-sampling by averaging pupillometry data-points within each 1 second bin to match with the fMRI sampling frequency, as suggested in previous work (Schneider et al., 2016; Shine et al., 2016; Yellin et al., 2015). While our results agree with findings in these studies, future study would be necessary to better understand the intra- and inter-subject variability of hemodynamic responses and whether the assumed correspondence between pupillometry and fMRI signal is homogeneous across multiple scales of time and space. In addition, note that there was a long interval between two resting state runs, because we had several task fMRI runs (independent from the purpose of this study) between them in the same session, without leaving the scanner. This study design might have an additional effect on within-subject variability in pupil area fluctuations (Fig. S3; e.g. ID 1560, ID 1913, ID 2106). Future investigation on the involvement of drowsiness, for example, combining pupillometry/fMRI with EEG recordings, should clarify potential other sources of within-subject variability in such pupil area fluctuations.

It should be noted that data were processed identically in both the high and low arousal states and in the null data set. Therefore, our observations cannot be attributed to some methodological artifacts, such as dwell time difference. The fMRI in the high and low arousal states, was balanced in terms of the amount of data included. We did not take into account the potential impact of other potential confounds, such as caffeine and alcohol consumption, anxiety levels and substance use, but since we showed within-subject changes in arousal in the same imaging session these are likely balanced within a run. We focused on comparing the highest (top 20% largest pupil area) and lowest (bottom 20%) arousal states within each subject by using the normalization of pupil area and the ranking of timeframes within each subject. That was because our pre-analysis suggested a potential relationship between the number of sequential time frames stratified as a single state and the number of networks estimated using SPARK (see Supplementary Fig. S1). We wanted to ensure similar number of sequential frames stratified as a single state in our between-state comparisons, therefore limited our analysis to these two states. Future work could consider intermediate levels of arousal, inter-subject variability in baseline arousal level and within-subject variability. Further work is needed to understand fluctuations in arousal over longer periods of time (e.g., days, months) and to relate these measurements to other quantifiable modalities (e.g., salivary cortisol measurement (Page et al., 2009)). It also may be interesting to explore if any specific arousal levels and their associated hub disruptions at specific arousal levels help improve the performance of connectome-based fingerprinting and predictive modeling of individual traits or task performances. To compare arousal level-dependent brain network organizations between resting state and naturalistic paradigms may help to understand why naturalistic paradigms provides a better outcome in predicting behavior in some studies (Finn and Bandettini, 2021).

In conclusion, using the simultaneous measurements of resting state fMRI and pupillometry, we show evidence of a brain-wide decrease in between-network integration and a decrease in inter-subject variability of connector hubs at low relative to high arousal. Our results demonstrate that the estimation of k-hubness using SPARK, which reflects the number of overlapping networks for each node, is sensitive to the level of arousal within the resting state. By studying connector hubs of hierarchical brain network organizations, we suggest that modulations of arousal are not localized to specific brain areas, but rather have a more extensive, brain-wide impact that involves high-level communication between networks. Delineating arousal effects on functional connectivity reconfigurations may help advance future studies on the brain-behavior associations and neurological and psychiatric disorders where arousal may play a role in clinical phenotypes.