Identifying cell state–associated alternative splicing events and their coregulation

Abstract

Alternative splicing shapes the transcriptome and contributes to each cell's unique identity, but single-cell RNA sequencing (scRNA-seq) has struggled to capture the impact of alternative splicing. We previously showed that low recovery of mRNAs from single cells led to erroneous conclusions about the cell-to-cell variability of alternative splicing. Here, we present a method, Psix, to confidently identify splicing that changes across a landscape of single cells, using a probabilistic model that is robust against the data limitations of scRNA-seq. Its autocorrelation-inspired approach finds patterns of alternative splicing that correspond to patterns of cell identity, such as cell type or developmental stage, without the need for explicit cell clustering, labeling, or trajectory inference. Applying Psix to data that follow the trajectory of mouse brain development, we identify exons whose alternative splicing patterns cluster into modules of coregulation. We show that the exons in these modules are enriched for binding by distinct neuronal splicing factors and that their changes in splicing correspond to changes in expression of these splicing factors. Thus, Psix reveals cell type–dependent splicing patterns and the wiring of the splicing regulatory networks that control them. Our new method will enable scRNA-seq analysis to go beyond transcription to understand the roles of post-transcriptional regulation in determining cell identity.

Transcriptome profiling at a single-cell level has revolutionized our understanding of the continuous biological variation in gene expression that determines a cell's unique identity (Wagner et al. 2016; Tanay and Regev 2017). Alternative mRNA splicing is a major source of transcriptome variability that plays an important role in determining the identity of a cell (Wang et al. 2008; Baralle and Giudice 2017), but single-cell analyses have not generally distinguished between different transcript isoforms of a gene. This misses a major source of biological variation; the fine-tuned regulation of splicing contributes to many continuous biological processes such as neurogenesis (Raj and Blencowe 2015; Weyn-Vanhentenryck et al. 2018), whereas its misregulation is associated with complex diseases (Yoshida et al. 2011; Irimia et al. 2014; Parikshak et al. 2016; Climente-González et al. 2017). Thus, a more complete understanding of gene expression variability between cells and its phenotypic consequence require an evaluation of changes in splicing and inference of how these changes are regulated.

Despite the enormous progress in computational modeling of cell identity from single-cell gene expression studies (Lopez et al. 2018; Risso et al. 2018; Eraslan et al. 2019; Stuart et al. 2019; Welch et al. 2019), formidable challenges remain in capturing the impact of alternative splicing (Westoby et al. 2020). A major limitation to this end is the sensitivity with which alternative splicing events can be read from a single cell. Generally, alternative isoforms are distinguished by only a few specific regions of the transcript, which influences accuracy even in bulk-level studies. This limitation becomes more acute in single-cell RNA sequencing (scRNA-seq) data owing to low capture efficiency and extensive PCR amplification, which add technical variation and bias. As a result, the observed rates of an exon's inclusion (described for each cell as the percent of transcripts from its gene in which the exon is present, or Ψ) are greatly distorted, with an inflation of spurious extreme values (Buen Abad Najar et al. 2020; Westoby et al. 2020), especially in exons from moderately or lowly expressed genes.

The high observed variance in an exon's inclusion rate between cells (Shalek et al. 2013; Song et al. 2017), whether owing to biological stochasticity or to the technical artifacts resulting from low mRNA capture efficiency (Buen Abad Najar et al. 2020), can obscure regulated, biologically important splicing changes between different cell types or states. Computational methods have endeavored to reveal these examples amid the noise. One method used spike-in transcripts to measure and model the variance expected from technical noise and looked for splicing with variance beyond this (Welch et al. 2016). Several studies have mitigated the impact of technical variance by looking for differences in the mean inclusion rate of an exon between defined groups of cells, expecting that changes in exon inclusion would be noticeable between cell groups as a whole even when technical noise is high (Welch et al. 2016; Buen Abad Najar et al. 2020; Wen et al. 2020). The problems of low coverage can be further alleviated by incorporating extra information such as gene sequence and cell type as priors in estimating rates of exon inclusion (Huang and Sanguinetti 2017, 2021). However, none of these approaches explicitly model the distortion of splicing observations caused by low capture efficiency. Further, methods that require cells to be clustered by condition or sample cannot take full advantage of the insight that single-cell data provide into continuous biological processes. A method that analyzes splicing across a continuous cell population, while considering the impact of low mRNA capture efficiency, has yet to be developed.

Results

Conceptual overview and method description

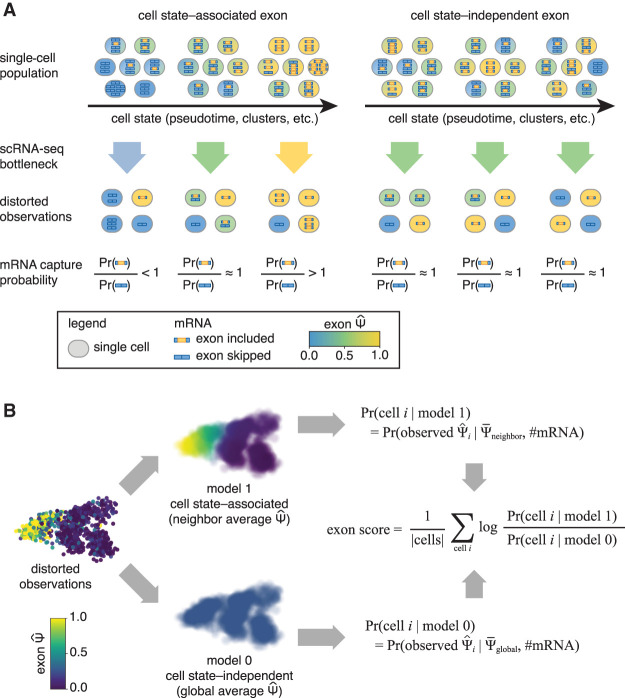
Our goal in this work is to confidently identify alternative splicing events that vary between cells while accounting for limitations in sensitivity and not enforcing any a priori stratification of cells into subpopulations or trajectories. Our approach relies on the notion of increasing sensitivity by using information beyond the observed splicing of the specific exon of interest in the cell of interest. To this end, we frame our objective as the detection of alternative splicing events that reflect changes in cell state, as defined by the entire transcriptome. For instance, an alternative exon of interest might be spliced into mRNAs at low levels in stem cells and at increasingly high levels in differentiating cells (Fig. 1A). Although such an observation may only be supported by a small number of captured mRNA molecules, we posit that its consistency with cell state—as reflected in the similarity of the exon's observed splicing between similar cells—makes it more likely to represent the underlying biology. As we show next, this definition does not require dividing the cells into groups by clustering or by labeling cell types, nor does it require an explicit trajectory of cell progression.

Figure 1.

Conceptual model. (A) Cell state–associated exons change across the phenotypic landscape of a single-cell population. Cell state–independent exons do not change across the phenotypic landscape. Low capture efficiency in scRNA-seq experiments adds additional technical variance depending on the number of captured mRNA molecules. The probability of capturing each alternative isoform depends on the underlying distribution of exons in the single-cell population. (B) Psix compares the likelihood of each single-cell observation given two models: model 1, in which the exon is cell state associated (probability of the cell's $\hat{\mathrm{\Psi }}$ given the average $\hat{\mathrm{\Psi }}$ of its k nearest neighbors), versus model 0, in which the exon is cell state independent (probability of the cell's $\hat{\mathrm{\Psi }}$ given the average Ψ of all cells in the data set). Model 1 is more likely for a cell state–associated exon. For a cell state–independent exon, the expected $\hat{\mathrm{\Psi }}$ of any cell is the same irrespective of its position in the cell state manifold. As a result, the expected value of the average $\overline{\mathrm{\Psi }}$ of a neighborhood of cells is the same as the global average $\overline{\mathrm{\Psi }}$. For this reason, the likelihood of model 1 is similar to the likelihood of model 0 for a cell state–independent exon.

We formulate these ideas as Psix, a probabilistic method inspired by autocorrelation models that identifies splicing events that are associated with cell state. Psix estimates the likelihood of an exon's observation in each cell, $\hat{\mathrm{\Psi }}$, given two models: In the foreground model, we assume that the exon inclusion should be similar to that observed in other, transcriptionally similar cells. In the background model, we assume that the observed exon inclusion reflects sampling noise around a global average (defined separately for each exon) rather than the state of any particular cell. If the exon is associated with cell state, then the first model would be more likely than the second (Fig. 1B). We formalize this as a score for each exon that consists of the likelihood ratio between the two models, and assign it an empirical P-value through randomizing the location of each cell in the low-dimensional manifold. The evaluation of the two likelihood models requires two things: knowledge of which cells are similar (in transcriptome space) and a model of the distribution of observed exon inclusion values, $\hat{\mathrm{\Psi }}$, given an underlying unknown Ψ. For the former, we take the similarity to be the distance between cells in a low-dimensional projection based on gene expression profiles (in this study, we use a PCA projection of the SCONE normalized gene expression [Cole et al. 2019]; other existing methods can also be used [Lopez et al. 2018; Risso et al. 2018; Eraslan et al. 2019]). For the latter, we adopt a binomial model of sampling without replacement, reflecting the observation that if few mRNA molecules are captured, the observed exon inclusion rates $\hat{\mathrm{\Psi }}$ will deviate greatly from the underlying Ψ (Buen Abad Najar et al. 2020).

Assessment of performance on simulated data

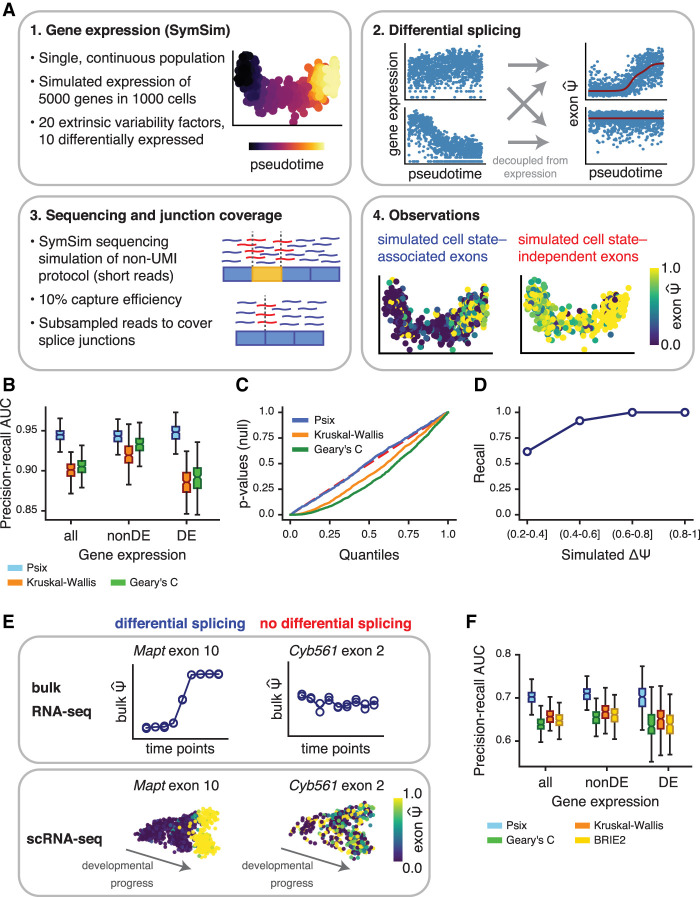
We validated our approach using simulated single-cell splicing data from a model of a continuous trajectory of cell states. The simulation allows us to test Psix's ability to distinguish between two classes of simulated cassette exons: those whose inclusion rates depend on the cell's position in the trajectory and those simulated with no change in splicing across the trajectory (i.e., exons reflecting noise properties of these data) (Buen Abad Najar et al. 2020). First, we simulated gene expression mRNA counts across a continuous trajectory using SymSim (Zhang et al. 2019). For each gene, we then fit a continuous function corresponding to the average underlying Ψ of its cassette exon at a given point of the trajectory: an impulse function for exons with splicing change and a flat line for exons without splicing change. These classes were assigned randomly to each exon, independent of the simulated mRNA counts of each cell. This underlying Ψ was then used to subsample the mRNA counts to simulate the exon inclusion in a subset of mRNA molecules. Finally, we simulated mRNA capture and short-read, full-coverage sequencing and then subsampled reads to reflect the limited number that cover the splice junctions. This resulted in simulated data that show similar increases in extreme values as observed in real data (Fig. 2A; Buen Abad Najar et al. 2020). We tested Psix's performance on correctly classifying exons as simulated with splicing change (cell state associated) or as simulated without splicing change (cell state independent).

Figure 2.

Psix identifies cell state–associated splicing in simulated and real data. (A) Pipeline for simulation of single-cell splicing. Variance in the observations can come from a change in splicing across the cell state (positives) or from other sources, for example, technical noise, or true variance that is not associated with the primary axes of variation in cell state (here, determined by the simulated trajectory; negatives). (B) Area under the precision-recall curve showing success of Psix and other methods at identifying exons simulated to have a |ΔΨ| ≥ 0.2 across a single lineage. Performance was assessed separately on exons in genes simulated as differentially expressed (DE) and not differentially expressed (nonDE). (C) P-value distributions of the negative exons when tested with Psix, Kruskal–Wallis, and Geary's C. The P-values of Psix do not deviate significantly from the uniform distribution. (D) Recall of exons simulated with different magnitudes of ΔΨ. (E) Validation strategy for cell state–associated splicing in single cells based on comparable bulk RNA-seq data. (F) Area under the precision-recall curve representing the overlap of cell state–associated exons in scRNA-seq data and differentially spliced exons in bulk RNA-seq data, both from midbrain neurons. We compared performance on exons in differentially expressed genes (DE) and non-differentially expressed genes (nonDE).

The key distinguishing features of Psix are its usage of information on cell similarity in a continuous phenotype and its explicit model of the distribution of observed $\hat{\mathrm{\Psi }}$ values given an underlying unknown Ψ. We compared Psix's ability to classify simulated exons to that of other methods without these features. First, considering the advantage of a cluster-free approach, we compared Psix's performance on classifying the simulated exons against a Kruskal–Wallis test that detects differences in the median Ψ between cell clusters after clustering the cells from the simulated trajectory (Buen Abad Najar et al. 2020; Wen et al. 2020). Second, we compared the performance of Psix against Geary's C, an autocorrelation (cluster-free) test statistic that does not model the number of mRNAs. We found that Psix outperformed these alternative approaches in detecting splicing changes in simulated data (Fig. 2B). Importantly, the simulations included genes simulated to have differential expression over the trajectory as well as genes with no differential expression, and splicing changes were simulated independently of expression changes. We found that Psix performed equally well at finding splicing changes in genes with and without differential expression, whereas the other methods were more prone to false positives in genes with differential expression (Fig. 2B; Supplemental Fig. 1A,B). Overall, modeling the technical distortion owing to low mRNA recovery enabled Psix to avoid excess false positives, unlike other methods (Fig. 2C). As expected, sensitivity to detect splicing changes increased with the magnitude of the splicing change (Fig. 2D; Supplemental Fig. 1C). Sensitivity was also increased for exons from highly expressed genes (Supplemental Fig. 1D). As discussed in our previous work, capture efficiency can be quite low in scRNA-seq, and Psix performed better than these other methods on data simulated at a range of different capture efficiencies (Supplemental Fig. 1E). The Psix scores were highly correlated regardless of the capture efficiency used in the model to estimate the probability of the observations (Supplemental Fig. 1F), which ensures robust results when the capture efficiency of a data set is not determined. Overall, we show that Psix performs well at recovering cell state–associated splicing, with high sensitivity and precision, and that it is robust against distortions arising from low mRNA counts.

A quintessential use of single-cell data is to explore the differences between groups of cells that would be difficult to distinguish in bulk data (Wagner et al. 2016), for instance, cells along a short developmental trajectory, or a subpopulation of cells with slightly different patterns of gene regulation. We expect that a common task for Psix would be to detect cell state–associated exons whose inclusion differs only in a small subpopulation of cells. To test Psix's performance in such situations, we simulated splicing changes in a three-branched trajectory of single cells, with one branch smaller than the others (Supplemental Fig. 2A,B). Psix outperformed other approaches at recovering cell state–associated exons in this scenario (Supplemental Fig. 2C). Although its sensitivity was higher for splicing changes occurring in the larger branches, Psix was able to recall the majority of splicing changes occurring in the smallest branch of single cells while maintaining a low rate of false positives (Supplemental Fig. 2D). These results highlight the fact that the ability to recover splicing changes in single-cell data may depend on the number of cells that present the change. Given that Psix relies on neighborhood information in order to counteract the loss of data from low capture efficiency in single-cell experiments, we reasoned that the results would potentially be sensitive to the choice of k-nearest neighbors used in modeling. In both the single-lineage and the three-lineage simulation (each with 1000 simulated cells), using a k equivalent to 10% resulted in a strong performance (Supplemental Fig. 3A,B). To further explore the effect of the number of cells, we simulated a single lineage of 10,000 cells, subsampled this set of cells to create sets of varying numbers of cells, and then applied Psix to these sets of different sizes. We found that sensitivity increases along with the number of cells, whereas precision remains consistently high (Supplemental Fig. 3C,D). In these simulations, a k-nearest neighborhood of 100 cells results in a strong performance, independent of the number of subsampled cells (Supplemental Fig. 3E). Based on these results, we propose a k-nearest neighborhood size of 100 cells for Psix in most cases and 10% of the total population as an alternative for data sets with fewer than 1000 cells.

Psix identifies alternative splicing associated with neurogenesis

Next, we sought to test Psix's ability to identify alternatively spliced exons in real single-cell RNA-seq data. We applied Psix to three different published neurogenesis scRNA-seq data sets. We tested Psix's ability to identify exons that were observed as differentially spliced in bulk RNA-seq time series data sets that closely matched the scRNA-seq data sets. For instance, a single-cell data set of embryonic mouse neurons was matched with a bulk RNA-seq time series data set taken from similar time points, and exons discovered as differentially spliced between time points in the bulk data set were considered as positives (Fig. 2E). We used rMATS (Shen et al. 2014) to compare each time point in the bulk time series to the first time point and classified the exons with a significant change (Q-value ≤ 0.05 and $\mid \mathrm{\Delta }\hat{\mathrm{\Psi }}\mid \ge 0.2$) as differentially spliced. We compared Psix against the Kruskal–Wallis and Geary's C tests as described above. We also compared Psix against an existing approach, BRIE2 (Huang and Sanguinetti 2021), which identifies splicing differences between predefined groups of single cells. Psix outperformed all methods in classifying the exons from all three data sets, and in keeping with the results from our simulations, Psix performed well on exons that fell in differentially expressed genes (Fig. 2F; Supplemental Fig. 4A). As expected, sensitivity was higher for exons that showed a higher splicing change in bulk RNA-seq data (Supplemental Fig. 4B). (We did not test BRIE2 on our simulations as it requires the actual sequencing data as input, whereas our SymSim-based simulator generates count matrices directly.)

Psix identifies coregulated groups of exons

Because scRNA-seq reports on the biological state of hundreds or thousands of single cells, it has great potential for uncovering regulatory networks that control changes in individual gene expression. Single-cell data have been used successfully to infer transcription regulatory networks (Aibar et al. 2017), but inference of splicing regulation has been very limited and generally involves pooling predefined clusters of cells (Feng et al. 2021; Huang and Sanguinetti 2021). Alternative splicing is regulated by a network of splicing factors, and we posited that scRNA-seq data could reveal coordinated changes in coregulated exons as well as the corresponding changes in expression of the splicing factors that regulate these exons.

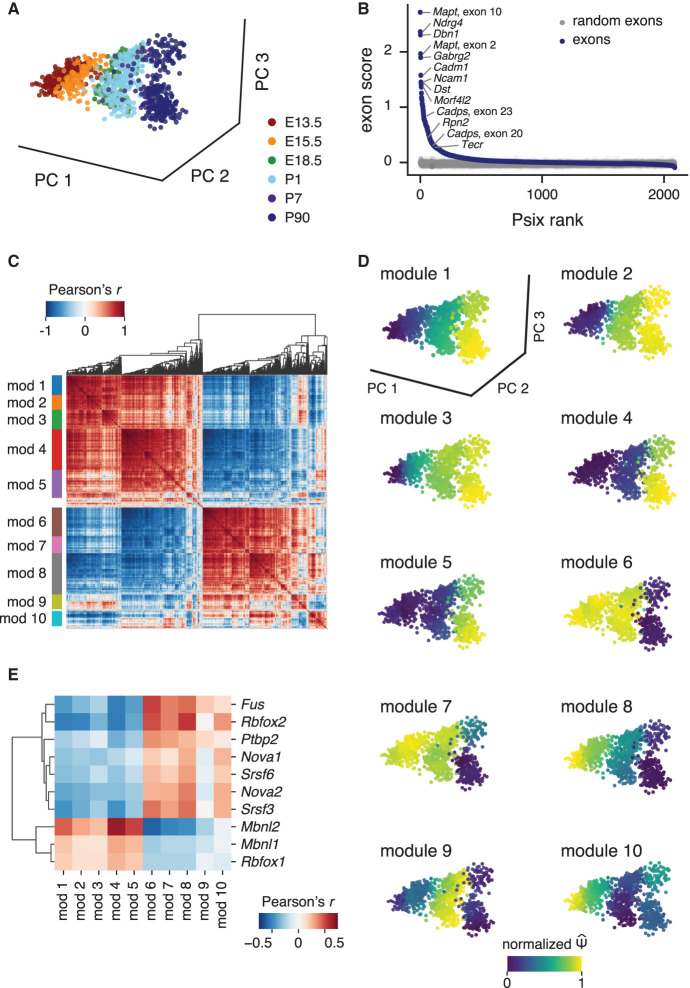
To begin reconstructing splicing regulatory networks, we first applied Psix to a data set of midbrain dopamine neurons across different stages of mouse development (Fig. 3A; Tiklová et al. 2019). Psix identified 798 cell state–associated exons over the brain development landscape, including many exons that have been extensively reported to change in neuronal development (Fig. 3B; Wang and Burt 1991; Speidel et al. 2003; Smith et al. 2011; Weyn-Vanhentenryck et al. 2018). A Gene Ontology enrichment analysis confirmed that the set of genes that harbor the exons identified by Psix was enriched for genes associated with neuronal and synaptic development (Supplemental Fig. 5). To further support the potential functional relevance of these exons, we examined features associated with regulated alternative splicing, including preservation of reading frame and sequence conservation. We found that the cell state–associated cassette exons identified by Psix were more likely to preserve the reading frame (hypergeometric test for enrichment against all the exons tested with Psix, P = 1.1 × 10⁻¹⁵). The cell state–associated cassette exons also had higher sequence conservation near the 5′ and 3′ splice sites; cell state–associated cassette exons had a median phyloP score of 2.27 within 30 nucleotides of each splice site, whereas cell state–independent cassette had a median phyloP score of 1.72 (Wilcoxon rank test P = 4.8 × 10⁻⁴³). These results support the biological importance of the exons identified by Psix as cell state associated.

Figure 3.

Psix identifies alternative splicing patterns in mouse midbrain development. (A) Mouse midbrain dopamine neurons collected at different stages of development (Tiklová et al. 2019), plotted by the first three principal components of normalized gene expression counts. (B) Psix scores of cassette exons, compared with the scores of randomized exons. Some exons known to be regulated in neurogenesis are highlighted. (C) Correlation map of the neighbor average $\overline{\mathrm{\Psi }}$ of the cell state–associated exons. Modules were identified with a modification of the UPGMA algorithm. (D) Neighbor average normalized $\overline{\mathrm{\Psi }}$ of the exons in each module. (E) Correlation of module splicing with gene expression of splicing factors that were enriched for binding in the cell state–associated exons identified by Psix. The 10 splicing factors with significant correlation with at least one module (FDR ≤ 0.05, Pearson's r ≥ 0.25) are shown.

Next, we set out to identify coregulated splicing among the cell state–associated exons. To mitigate the effect that the high variance of individual splicing observations may have on our ability to detect coregulated exons, we used a neighborhood average Ψ (taking the k most similar cells) instead of the individual $\hat{\mathrm{\Psi }}$. We then clustered these smoothed observations into 10 modules of cospliced exons (Fig. 3C). The modules of exons showed distinct patterns of change across midbrain development, suggesting that they may reflect elements of coregulation that take place at different developmental phases (Fig. 3D). The expression patterns of the genes that contain the exons of each module do not reflect the splicing pattern of the modules (Supplemental Fig. 6). In fact, the majority of the cell state–associated exons found by Psix do not fall in differentially expressed genes (Supplemental Fig. 7A), and cell state association occurs in both differentially expressed and nondifferentially expressed genes (Supplemental Fig. 7B–D). This suggests two important points: first, that the groups of seemingly coregulated exons reflect real splicing regulation rather than an artifact of underlying transcription changes, and second, that splicing regulation adds rich biological variation that is not captured solely by transcription-level analysis.

To find potential regulators associated with these modules, we integrated information on splicing factor binding from published CLIP-seq experiments (Supplemental Table 1) and information on splicing factor expression in single cells. We identified 10 splicing factors with enriched binding to the Psix-identified (cell state–associated) exons (hypergeometric test, FDR ≤ 0.05) and whose expression was correlated with the average inclusion rate of exons in at least one of the 10 modules (FDR ≤ 0.05, Pearson's r ≥ 0.25) (Fig. 3E; Supplemental Table 1). These splicing factors included proteins from the NOVA, RBFOX, PTBP, and MBNL families, all of which have known roles in regulation of splicing during neuronal development (Zhang et al. 2010; Charizanis et al. 2012; Licatalosi et al. 2012; Li et al. 2014; Weyn-Vanhentenryck et al. 2014, 2018; Raj and Blencowe 2015). Thus, Psix is able to find exons that are coordinately regulated in midbrain development, as well as their potential regulators.

Single-cell data often represent collections of different mature cells with no developmental trajectory. To see if Psix could capture splicing associated with differences between groups of cells, we applied it to the brain neurons subset of the Tabula Muris Smart-seq2 data set (The Tabula Muris Consortium 2018). This data set is composed of multiple neural and nonneural cell types from the brain of the adult mouse, with a total of 6146 cells after filtering for quality control (Supplemental Fig. 8A). Because of the large number of cells, we performed dimensionality reduction using scVI (Lopez et al. 2018) instead of PCA. Out of 3025 observed alternatively spliced cassette exons, 1278 were cell state associated. Clustering these exons by their neighborhood average Ψ revealed modules reflecting different cassette exon usage across the different cell types (Supplemental Fig. 8B–D). The cell state–associated exons were enriched for multiple Gene Ontology terms related to metabolic processes, as well as terms relevant for the cell types present in this data set such as neuron projection development (Supplemental Fig. 8E). Psix is therefore able to find splicing associated with disjoint cell states, using the same approach based on the similarity of cells in a low-dimensional manifold.

Reconstruction of splicing regulation in late midbrain development

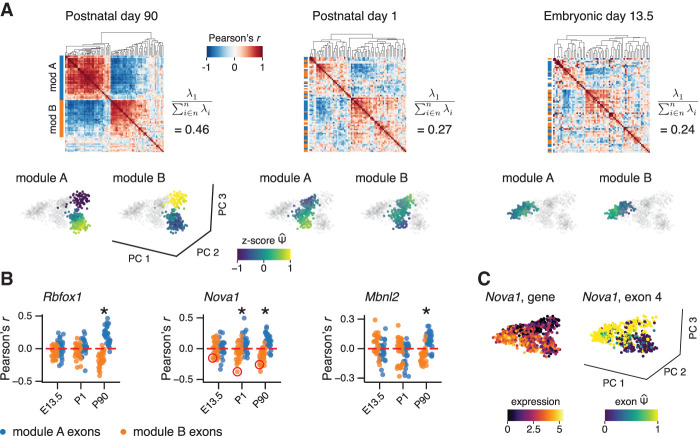
Several splicing modules showed variation within the cells collected at the final time point in the midbrain development time course (Fig. 3D), and we aimed to leverage the high resolution of single-cell data in understanding this hidden heterogeneity. The neurons collected at the final time point, from adult midbrains 90 d postnatal, formed several subpopulations that were separated primarily along the third principal component. The subpopulations express markers of different lineages of midbrain neurons (Supplemental Fig. 9; Tiklová et al. 2019). To identify cell type–specific exon usage among these subpopulations, we performed a separate Psix analysis of just the postnatal day 90 cells (which we refer to as P90 cells). Psix identified 78 exons associated with the variation among neurons in the adult midbrain and grouped them in two modules (Fig. 4A). The two modules showed opposite patterns of exon inclusion: module A exons decreased in inclusion along principal component 3, and module B exons increased in inclusion. To trace the emergence of this coordinated pattern during earlier development, we examined the splicing of the same exons at earlier time points (Fig. 4A). Similar but weaker correlation patterns were visible in postnatal day 1 (P1) cells, and these patterns were almost absent in embryonic day 13.5 (E13.5) cells, suggesting that these exons responded to differences in splicing factor activity that were present at intermediate stages and became more pronounced with time.

Figure 4.

Reconstruction of splicing regulation in late midbrain development. (A) Modules of cell state–associated exons identified in postnatal day 90 (P90) cells, at different stages of development. Heatmaps show the correlation matrix among the P90 module A and B exons at each time point. As a measure of structure, for each correlation matrix, we show its first eigenvalue divided by the sum of all eigenvalues. PCA plots show the splicing patterns of the exons of the module in the cells of each time point. (B) Correlation of splicing factor expression with the observed $\overline{\mathrm{\Psi }}$ of exons from P90 modules A and B at different stages of development. An asterisk indicates significant difference between the exons of module A and B (Wilcoxon rank test, FDR ≤ 0.05) and a mean difference larger than 0.1 between the two modules. Exon 4 of Noval (in module B) is highlighted in red in the correlation plot of Noval gene expression. (C) Gene expression of Noval and splicing of Noval exon 4 in mouse midbrain neurons.

To uncover the regulatory mechanisms that control the emergence of these splicing patterns, we first identified seven splicing factors with enriched binding to the Psix-identified, cell state–associated exons in P90 cells. We then computed the correlation between the expression of each splicing factor and the inclusion rate of each exon in modules A and B. Expression of three splicing factors, Nova1, Rbfox1, and Mbnl2, showed a significant difference in correlation between module A and B (Wilcoxon rank test, FDR ≤ 0.5 and mean difference ≥0.1) (Fig. 4B). Extending the analysis to earlier stages, we found that expression of Nova1 showed a significant difference in correlation with the splicing of the two groups of exons in the P1 cells as well, whereas the other splicing factors did not show this effect at earlier stages of development. This suggests that NOVA1 plays an early role in the emergence of key splicing differences between cell types. We observed that, in keeping with this role, one of the exons most highly correlated to Nova1 expression was exon 4 of the Nova1 gene itself, a cassette exon that encodes a phosphorylation target domain. In an autoregulatory process, NOVA1 protein binding to this exon suppresses its inclusion (Dredge et al. 2005). Consistent with this previous knowledge, we found that expression of Nova1 is strongly anticorrelated with inclusion of exon 4 (Fig. 4B). The strength of this correlation is stronger in later stages of development, as one lineage of neurons maintains high Nova1 expression and low exon 4 inclusion, whereas the other keeps low Nova1 expression and high exon 4 inclusion (Fig. 4C). Our results show that the regulatory dynamics of splicing factors and their target exons change during the process of neuron maturation and consolidate as neurons commit to the distinct midbrain cell lineages. Our analysis exemplifies how single-cell data allow us to study alternative splicing patterns in neurogenesis at high resolution.

Discussion

We have shown that our probabilistic method, Psix, can find cassette exons that vary across cell state, without mistaking gene expression variance for changes in splicing. Low sequencing coverage has previously limited the study of splicing in single cells (Buen Abad Najar et al. 2020) and hindered the potential of single-cell sequencing to define the identity of individual cells. Psix solves this limitation by combining cell identity information from the transcriptome space with probabilistic modeling that accounts for the distortions of low data recovery. Like many single-cell methods, Psix depends on faithful reconstruction of a biologically meaningful low-dimensional manifold. Noise variation within and between groups of cells can impact the selection of nearest neighbors, emphasizing the importance of proper normalization and dimensionality reduction of gene expression data to define the low-dimensional manifold. The method could be generalized to use other similarity metrics for single cells, such as spatial positions (to capture spatially-regulated splicing events) (Valentine et al. 2018; DeTomaso and Yosef 2021) or single-cell lineages (to capture heritable splicing events) (Kester and van Oudenaarden 2018; Jones et al. 2020). We have also shown that Psix can identify groups of exons with similar patterns of biological variation, indicative of potential splicing coregulation. Our methods set the groundwork for further discovery of splicing regulatory networks, taking full advantage of the resolution of single-cell methods.

Methods

Conceptual overview

To determine if a splicing event is associated with cell identity or cell state, we observe how its Ψ varies in a low-dimensional manifold. If a splicing event is informative about a cell's identity, we expect that similar cells will have closer Ψ than cells with different identities across the similarity metric.

For a population of n single cells and for m alternatively spliced exons, Psix uses information from three matrices: one (n, m) matrix of ${\hat{\mathrm{\Psi }}}_{ij}$ observations for each exon i in each cell j (obtained from reads covering splice junctions), another (n, m) matrix of the estimated number of captured mRNA molecules that cover the splice sites of each exon in each cell, and a low dimensional representation of the cells (Fig. 1B). Psix estimates the likelihood of the ${\hat{\mathrm{\Psi }}}_{ij}$ observation of an exon in each cell given the local average Ψ of its closest (k = 100) neighbors (based on the low-dimensional representation) and the number of captured molecules x_ij. It then contrasts this likelihood with the likelihood of the same observations, given the global average $\overline{\mathrm{\Psi }}$ of all cells. If the likelihood of the observations given the local average is significantly higher than the likelihood given the global average, the exon is considered to be informative of the biological state.

Psix obtains ${\hat{\mathrm{\Psi }}}_{ij}$ from splice junction reads of each analyzed cassette exon. Because Smart-seq2 and similar methods do not directly report the number of mRNAs recovered per gene, for Smart-seq2 data, Psix estimates the number of mRNAs, x_ij, from transcripts per million (TPM) counts for each gene, with a modification of the Census normalization (Qiu et al. 2017) as described by Buen Abad Najar et al. (2020). The similarity matrix is estimated from the Euclidean distance in a manifold that summarizes the gene expression space of the single-cell populations. Here, we use the space spanned by the top principal components. Psix could, in principle, use other similarity metrics for single cells not based on gene expression, such as spatial positions.

The Psix model

Psix is built over the likelihood of $\hat{\mathrm{\Psi }}$ observations based on underlying Ψ and r captured mRNA molecules with a capture efficiency, c, that we developed in a previous study (Buen Abad Najar et al. 2020) and reproduced here.

Consider a single cell that has m mRNA copies of a gene that each may skip or include a cassette exon. The exon in the cell has a percentage spliced-in of Ψ (Ψ · m mRNA molecules in the cell contain the exon). In an scRNA-seq experiment, only r out of the original m molecules are reverse transcribed and sequenced. We formalize the probability for observing a splicing ratio $\hat{\mathrm{\Psi }}$ as follows:

$$Pr(\hat{\mathrm{\Psi }}\mid \mathrm{\Psi },r,m)={\displaystyle \frac{\left(\begin{array}{c}m\mathrm{\Psi }\\ r\hat{\mathrm{\Psi }}\end{array}\right)\left(\begin{array}{c}m(1-\mathrm{\Psi })\\ r(1-\hat{\mathrm{\Psi }})\end{array}\right)}{\left(\begin{array}{c}m\\ r\end{array}\right)}.}$$

Notice that in scRNA-seq, we cannot observe how many molecules m of a gene were present in the cell before sequencing. Therefore, with an estimated capture efficiency c, we rewrite this probability as

$$\begin{array}{rl}Pr(\hat{\mathrm{\Psi }}\mid \mathrm{\Psi },r,c)& =\sum _{m=0}^{\mathrm{\infty }}Pr(\hat{\mathrm{\Psi }},m\mid \mathrm{\Psi },r,c)\\ & =\sum _{m=r}^{\mathrm{\infty }}Pr(\hat{\mathrm{\Psi }}\mid \mathrm{\Psi },r,c,m)\cdot Pr(m\mid r,c)\\ & =\sum _{m=r}^{\mathrm{\infty }}Pr(\hat{\mathrm{\Psi }}\mid \mathrm{\Psi },r,m)\cdot Pr(m\mid r,c).\end{array}$$

To estimate $Pr(m\mid r,c)$ we note the following:

$$\begin{array}{rl}Pr(m\mid r,c)& ={\displaystyle \frac{Pr(r\mid c,m)\cdot Pr(m)}{\underset{m^{\mathrm{\prime }}=0}{\sum ^{\mathrm{\infty }}}Pr(r\mid c,m^{\mathrm{\prime }})\cdot Pr(m^{\mathrm{\prime }})}}\\ & ={\displaystyle \frac{Pr(r\mid c,m)}{\underset{m^{\mathrm{\prime }}=0}{\sum ^{\mathrm{\infty }}}Pr(r\mid c,m^{\mathrm{\prime }})}}\\ & ={\displaystyle \frac{\left(\begin{array}{c}m\\ r\end{array}\right)c^r{(1-c)}^{m-r}}{\underset{m^{\mathrm{\prime }}=0}{\sum ^{\mathrm{\infty }}}Pr(r\mid c,m^{\mathrm{\prime }})},}\end{array}$$

where we model the probability of capturing r mRNA molecules as a binomial sample from m with probability c. Note that the third transition is performed under the assumption of a uniform prior on m.

To compute the denominator, we expand

$$\begin{array}{rl}& \sum _{m^{\mathrm{\prime }}=0}^{\mathrm{\infty }}\mathrm{Pr}(r|c,m^{\mathrm{\prime }})=\sum _{m^{\mathrm{\prime }}=r}^{\mathrm{\infty }}\left(\begin{array}{c}{m}^{\mathrm{\prime }}\\ r\end{array}\right)c^r{(1-c)}^{m^{\mathrm{\prime }}-r}\\ & =c^r\sum _{k=0}^{\mathrm{\infty }}\left(\begin{array}{c}r+k\\ r\end{array}\right){(1-c)}^k=c^r\sum _{k=0}^{\mathrm{\infty }}{\displaystyle \frac{(r+k)!}{k!r!}}{(1-c)}^k\\ & =c^r\sum _{k=0}^{\mathrm{\infty }}{\displaystyle \frac{{(-1)}^k}{(k!)}}(r+1)(r+2)\dots (r+1+(k-1)){(c-1)}^k\\ & =c^r\sum _{k=0}^{\mathrm{\infty }}{\displaystyle \frac{1}{k!}(-(r+1))(-r(r+2))}\dots (-r(r+k))1^{r+k+1}{(c-1)}^k\\ & \mathrm{by}\mathrm{Taylor}\mathrm{series}\mathrm{centered}\mathrm{in}1=c^r{\displaystyle \frac{1}{c^{r+1}}={\displaystyle \frac{1}{c}.}}\end{array}$$

Thus,

$$\begin{array}{rl}Pr(\hat{\mathrm{\Psi }}|\mathrm{\Psi },r,c)& =\sum _{m=r}^{\mathrm{\infty }}Pr(\hat{\mathrm{\Psi }}|\mathrm{\Psi },r,c,m)\cdot Pr(m|r,c)\\ & =\sum _{m=r}^{\mathrm{\infty }}{\displaystyle \frac{\left(\begin{array}{c}m\mathrm{\Psi }\\ r\hat{\mathrm{\Psi }}\end{array}\right)\left(\begin{array}{c}m(1-\mathrm{\Psi })\\ r(1-\hat{\mathrm{\Psi }})\end{array}\right)}{\left(\begin{array}{c}m\\ r\end{array}\right)}{\displaystyle \frac{\left(\begin{array}{c}m\\ r\end{array}\right)c^r{(1-c)}^{m-r}}{{\displaystyle \frac{1}{c}}}}}\\ & \approx \sum _{m=r}^{10r/c}\left(\begin{array}{c}m\mathrm{\Psi }\\ r\hat{\mathrm{\Psi }}\end{array}\right)\left(\begin{array}{c}m(1-\mathrm{\Psi })\\ r(1-\hat{\mathrm{\Psi }})\end{array}\right)\cdot c^{r+1}{(1-c)}^{m-r}.\end{array}$$

Using this likelihood equation, we can test the likelihood of an observation given its underlying splicing context. We compare the likelihood of the observations given that the exon is cell state associated versus the likelihood of the observations given that the exon is cell state independent.

Model 1: cell state–associated exons

For an exon j and for every cell i, we estimate the likelihood of the observed exon inclusion ${\hat{\mathrm{\Psi }}}_{ij}$, under model 1: a model in which exon j is cell state associated. First, given a low-dimensional manifold (e.g., the first few principal components of the normalized gene expression), for each cell i we define

$$\mathrm{KNN}\left(i\right)=\{k-\mathrm{nearest}\mathrm{neighbors}\mathrm{of}\mathrm{cell}i,\mathrm{in}\mathrm{Euclidean}\mathrm{distance}\}.$$

By default, we set k = 100 (see “Neighborhood size selection” subsection for details). We also define the sets of cells:

$$X(j)=\{\mathrm{cells}i\mathrm{such}\mathrm{that}{\hat{\mathrm{\Psi }}}_{ij}\mathrm{is}\mathrm{defined}(\mathrm{i}.\mathrm{e}.,\mathrm{not}\mathrm{a}\mathrm{dropout})\}$$

and

$$N\left(i,j\right)=\left\{\mathrm{cells}i\in X\left(j\right)\cap \mathrm{KNN}\left(i\right)\right\}.$$

We calculate the neighbor average Ψ for exon j in cell i as follows:

$$\begin{array}{cc}\begin{array}{c}\overline{\mathrm{\Psi }}(i,j)={\displaystyle \frac{\sum _{k\in N(i,j)}(w_{ik}{\hat{\mathrm{\Psi }}}_{kj})}{\sum _{k\in N(i,j)}{w}_{ik}}},\end{array}& \end{array}$$

where K_i is the set of k-nearest neighbors of cell i (not including itself), and w_ik is a similarity score between cells i and k in a cell-cell metric, defined from the low-dimensional manifold as follows:

$$\mathrm{\forall }k\in \mathrm{KNN}(i):w_{ik}=\exp \left({\displaystyle \frac{-d_{ik}^2}{\underset{k^{\mathrm{\prime }}\in \mathrm{KNN}\left(i\right)}{max}-d_{i{k}^{\mathrm{\prime }}}^2}}\right),$$

where d_ik corresponds to the Euclidean distance between cells i and k in the low-dimensional manifold.

We estimate the probability of the observation ${\hat{\mathrm{\Psi }}}_{ij}$ given model 1 as follows:

$$Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \mathrm{Model}1)=Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \overline{\mathrm{\Psi }}(i,j),r_i,c),$$

where r_i is the number of captured mRNA molecules that are informative for exon j in cell i. In rare instances in which a cell's ${\hat{\mathrm{\Psi }}}_{ij}$ is zero and the neighbor average $\overline{\mathrm{\Psi }}(i,j)$ is one (or vice versa), $Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \overline{\mathrm{\Psi }}(i,j))$ will be equal to zero. To mitigate the impact of these edge cases, we cap this probability to a minimum of 0.01.

Model 0: cell state–independent exons

For an exon j and for every cell i, we estimate the likelihood of the observed exon inclusion ${\hat{\mathrm{\Psi }}}_{ij}$ under model 0, a model in which exon j is cell state independent:

$$Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \mathrm{Model}0)=Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \overline{\mathrm{\Psi }}(j),r_i,c),$$

where $\overline{\mathrm{\Psi }}(j)$ is the unweighted average ${\hat{\mathrm{\Psi }}}_{ij}$ of all cells i in X(j).

The Psix score

To determine if an exon is cell state associated, we compare the likelihood of model 1 versus model 0. We define the Psix score as

$$\begin{array}{cc}\begin{array}{c}\mathrm{score}(j)={\displaystyle \frac{1}{\mid X(j)\mid }\sum _{i\in X(j)}[\log Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \mathrm{Model}1)-\log Pr({\hat{\mathrm{\Psi }}}_{ij}\mid \mathrm{Model}0)]}.\end{array}& \end{array}$$

The probability of deviation of these scores from a null distribution is derived empirically, as described below.

Identifying modules of cospliced exons

We are interested in identifying exons with similar patterns of cell state association because they could potentially share regulatory splicing factors. Because of the high technical noise in single-cell splicing observations, clustering of exons is difficult in the raw data. Instead, for each pair of exons, we obtain the Pearson's correlations of the k-nearest neighbors averages. We cluster the exons in a bottom-up procedure similar to that described by DeTomaso and Yosef (2021): We merge iteratively the two exons or modules that have the highest Pearson's correlation. Then we update the correlation score of the module with all other exons and modules using the UPGMA approach. When a module hits a minimum of 30 exons, we assign a label to it. We stop clustering when the maximal correlation score is lower than 0.3 and return the labeled modules. Exons that do not belong to a labeled module are returned as “unassigned.” The minimum number of exons per module and the minimum correlation score can be defined by the user.

Practical considerations for the application of the Psix model

Estimating captured mRNA molecules in Smart-seq2 data sets

In practical usage, non-UMI based scRNA-seq methods such as Smart-seq2 do not directly quantify the number of captured mRNA molecules of a gene per cell. As a result, it is difficult to estimate the parameter r_i. To approximate r, we use a modification of the Census normalization (Qiu et al. 2017) as reported previously:

$$M_i={\displaystyle \frac{n_i}{F_{X_i}(x_i^{\ast })-F_{X_i}(0.1)},}$$

where $x_i^{\ast }$ is the mode of the distribution of log-transformed gene TPM counts in cell i, $x_i^{\ast }$ is the argmax of a Gaussian kernel density fit to the log TPM distribution, n_i is the number of genes in cell i with a TPM between 0.1 and $x_i^{\ast }$, and $F_{X_i}$ is the cumulative distribution of TPM counts in cell i. As in the work by Qiu et al. (2017), we assume that genes with TPM below 0.1 are not represented by any mRNA molecules.

Low-dimensional manifold

To determine if an exon is informative of a cell's identity, we need a low-dimensional manifold metric that describes the similarity between individual cells. Because of hurdles such as noise, sparsity, and the curse of dimensionality, it is common practice to define this metric as a Euclidean distance in an interpretable low-dimensional manifold representation of the normalized gene expression profiles. In general, the approach to normalization and dimensionality reduction would depend on the size of the data set analyzed. For the Tiklova (Tiklová et al. 2019), Chen (Chen et al. 2016), and Song (Song et al. 2017) data sets, we normalized the TPM counts per gene using SCONE (Cole et al. 2019) owing to the relatively small number of cells and performed dimensionality reduction with PCA over the top 1000 variable (using the fano factor) genes. In the Chen and Song data sets, the first two principal components captured most of the variance, and thus, we used these components as the low-dimensional manifold. For the larger Tiklova data set, we used the first three principal components.

Neighborhood size selection

Our simulation analysis showed that Psix performance was optimal when the size of the neighborhood used for estimating neighbor average $\hat{\mathrm{\Psi }}$ is around 100 cells or ∼10% of the total number of cells in the data set (Supplemental Fig. 3).

Capture efficiency in single-cell data sets

We set a capture efficiency of 0.1, as supported by single-cell studies (Grün et al. 2014; Marinov et al. 2014; Qiu et al. 2017; Ziegenhain et al. 2017).

Empirical P-value estimation

Psix compares the probability of two models. However, the null model (model 0) is not embedded into the alternative model (model 1). For this reason, for each exon j, we obtained an empirical P-value by randomizing the ${\hat{\mathrm{\Psi }}}_{ij}$ observations of all cells i and their respective mRNA counts and obtaining a random distribution of Psix scores. We observed that the mean mRNA counts and the total $\hat{\mathrm{\Psi }}$ variance had a slight effect on the random distribution of the Psix scores. For this reason, we divided the exons into bins according to their ranks in mRNA counts and $\hat{\mathrm{\Psi }}$ variance (by default, five bins for each parameter, totaling 25 bins). For each bin, we randomized the exons of the bin, and for each exon, we estimated an empirical P-value as follows:

$$\begin{array}{cc}\begin{array}{c}p(j)={\displaystyle \frac{x(j)+1}{n+1}},\end{array}& \end{array}$$

where x(j) is the number of random exons in the bin to which the exon j belongs that have a higher Psix score than the nonrandomized exon, and n is the total number of randomized exons in the bin (2000 by default). By default, Psix uses the Benjamini–Hochberg procedure to correct for multiple tests.

Processing of Smart-seq2 data sets

The FASTQ files from the Tiklova (Tiklová et al. 2019) data set were downloaded from the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE116138. We aligned the reads using STAR two-pass mode (Dobin et al. 2013) to the mouse genome (annotation mm10) with added sequences for the Illumina ERCC spike-ins and the enhanced green fluorescent protein (eGFP) gene sequence. TPM was estimated for all data sets using RSEM (Li and Dewey 2011). After quality control and removing a substantial number of outlier cells expressing glial or microglial gene markers, we were left with a total of 1067 cells that we used for downstream analysis. For dimensionality reduction, we first selected genes that are expressed in the data set (average normalized counts ≥ 0.1), and selected the top 1000 genes with high Fano factor. We then applied PCA on the resulting genes, which revealed a clear trajectory of neuron differentiation. This PCA was used as the low-dimensional manifold input for Psix.

The FASTQ files from the brain neurons subset of the Tabula Muris Smart-seq2 data set were downloaded from GEO accession number GSM2967047, whereas metadata were downloaded from https://tabula-muris.ds.czbiohub.org/.

We aligned the reads using STAR two-pass mode (Dobin et al. 2013) to the mouse genome (annotation mm10). TPM was estimated for all data sets using RSEM (Li and Dewey 2011). After quality control, we were left with a total of 6146 cells that were used for downstream analysis. For dimensionality reduction, we applied scVI (Lopez et al. 2018) on the gene read counts and obtained a low-dimensional manifold with 10 dimensions. This low-dimensional manifold was used as input for Psix. For visualization purposes we applied UMAP on the 10 dimensions obtained by scVI.

Cassette exons were identified from the mm10 mouse genomic annotation. We estimated the observed $\hat{\mathrm{\Psi }}$ for each cassette exon j in each cell i as

$${\hat{\mathrm{\Psi }}}_{ij}={\displaystyle \frac{\mathrm{S}{\mathrm{J}}_{A_{ij}}}{\mathrm{S}{\mathrm{J}}_{A_{ij}}+2\mathrm{S}{\mathrm{J}}_{B_{ij}}},}$$

where $\mathrm{S}{\mathrm{J}}_{A_{ij}}$ are the total RNA-seq reads that cover the two splice junctions that support exon inclusion of the exon. In turn, $\mathrm{S}{\mathrm{J}}_{B_{ij}}$ are the total RNA-seq reads that cover the splice junction that support exon exclusion.

For the Tiklova and Tabula Muris data sets, we selected 2087 and 3025 cassette exons, respectively, that had observations (i.e., any splice junction reads, showing either skipping or inclusion) in at least 25% of cells (i.e., a maximum dropout rate of 75%). We applied Psix over these exons using a neighborhood size of 100 cells and a capture efficiency rate of 0.1. We used the previously described PCA and scVI manifold, respectively, as the low-dimensional manifold input. After scoring these exons with Psix, Gene Ontology analysis was performed using the Panther enrichment test (Mi et al. 2012) on the Psix score of the exon. For genes with more than one exon, we used the highest scoring exon's Psix score.

The Chen (Chen et al. 2016) and Song (Song et al. 2017) data sets were downloaded from GEO accession numbers GSE74155 and GSE85908, respectively. We processed these data sets as we described in our previous work (Buen Abad Najar et al. 2020), and we used the first two principal components of the PCA of the normalized expression as the low-dimensional manifold input for Psix. These data sets are smaller than the 1000 cells. A neighborhood of size 30 was used in both cases, which approximates 10% of their total number of cells.

Differentially expressed genes in single-cell trajectories

Differentially expressed genes from both simulated and real scRNA-seq were obtained by fitting a generalized additive model (GAM) with tradeSeq (Van den Berge et al. 2020) over lineage trajectories obtained with Slingshot (Street et al. 2018). Genes with a mean log fold change larger to or equal to 0.25 and a FDR smaller than 0.05 in the GAM were classified as differentially expressed.

Comparison of Psix with other single-cell splicing methods

We compared the performance of Psix against several approaches that have been proposed for addressing single-cell splicing.

Kruskal–Wallis test

The Kruskal–Wallis test is a nonparametric version of ANOVA. It has been previously used to identify if the median $\hat{\mathrm{\Psi }}$ of an exon is different between predefined clusters of cells (Buen Abad Najar et al. 2020; Wen et al. 2020). We applied this test for all the exons we evaluated with Psix in all data sets. We clustered the cells according to the labels provided by the investigators of each data set.

Geary's C

Geary's C is a statistic that measures the spatial autocorrelation of a variable. It has been used for computing the autocorrelation of gene signatures with cell identity (DeTomaso et al. 2019), and we previously used an adaptation of this test for finding autocorrelation of exon observations (Buen Abad Najar et al. 2020).

For each exon, we normalize the observed $\hat{\mathrm{\Psi }}$ as follows:

$${\hat{\mathrm{\Psi }}}_{ij}^{\mathrm{\prime }}={\displaystyle \frac{{\hat{\mathrm{\Psi }}}_{ij}-{\overline{\mathrm{\Psi }}}_i}{\mathrm{Var}({\hat{\mathrm{\Psi }}}_i)},}$$

where ${\hat{\mathrm{\Psi }}}_{ij}$ is the observed splicing of exon j in cell i, ${\overline{\mathrm{\Psi }}}_i$ is the mean $\hat{\mathrm{\Psi }}$ of all the observed exons in cell i, and $\mathrm{Var}({\hat{\mathrm{\Psi }}}_i)$ is the variance of the observed $\hat{\mathrm{\Psi }}$ of all exons in cell i.

We calculate a variant of the Geary's C statistic of each exon j as

$$C(j)={\displaystyle \frac{(N-1)\sum _i\sum _k{w}_{ik}{({\hat{\mathrm{\Psi }}}_{ij}^{\mathrm{\prime }}-{\hat{\mathrm{\Psi }}}_{kj}^{\mathrm{\prime }})}^2}{2W\sum _i{({\hat{\mathrm{\Psi }}}_{ij}^{\mathrm{\prime }}-{\overline{\mathrm{\Psi }}}_j^{\mathrm{\prime }})}^2},}$$

where N is the number of cells in the data set, ${\overline{\mathrm{\Psi }}}_j^{\mathrm{\prime }}$ is the average ${\hat{\mathrm{\Psi }}}_{ij}^{\mathrm{\prime }}$ of exon j across all cells, w_i,k is the weight between cell i and cell k in the cell–cell metric, and W is the sum of all w_i,k. We use the same similarity metric that we used in Psix.

To make the statistic more intuitive, in which a positive score close to one indicates high autocorrelation, we transform our statistic as

$$C^{\mathrm{\prime }}=1-C.$$

BRIE2

BRIE2 is a computational tool that regresses single-cell splicing data against cell-level features and can detect differential splicing between groups of cells.

We applied BRIE2 directly to the STAR-aligned BAM files (Dobin et al. 2013) of the Tiklova, Chen, and Song data sets. We used the investigator-provided labels for each data set.

Alternative splicing in bulk RNA-seq data

We compared each method's ability to detect alternative splicing events identified in bulk RNA-seq data sets using rMATS 3.2.5 (Shen et al. 2014). We compared the Tiklova data set with a bulk mouse brain development data set (Weyn-Vanhentenryck et al. 2018), the Chen data set with a bulk data set of mouse embryonic stem cells induced to neurogenesis (Hubbard et al. 2013), and the Song data set with the bulk RNA-seq data included in the same study (Song et al. 2017).

RNA-binding protein analysis

CLIP-seq data were obtained from multiple public sources (Supplemental Table 1). Some data sets were downloaded from the CLIPdb data set (Yang et al. 2015), whereas others were obtained from their respective studies depending on availability. For the SR protein iCLIP-seq data that were not already preprocessed by CLIPdb, we used Piranha version 1.2.1 (Uren et al. 2012) to call peaks from CLIP-tags. Peaks from different data sets of the same RNA-binding protein (RBP) were combined into a single file per RBP. We next reported the overlap of the RBPs into four regions per cassette exon:

• E1 region—100 nt upstream of and i₁ nt downstream from the splice junction of the upstream flanking exon, where i₁ is the minimum of 100 and half the distance between the upstream flanking exon and the cassette exon;

• S1 region—i₁ nt upstream of and e nt downstream from the 5′ splice junction of the cassette exon, where e is the minimum of 100 and half the distance between the two splice junctions of the cassette exon;

• S2 region—e nt upstream of and i₂ nt downstream from the 3′ splice junction of the cassette exon, where i₂ is the minimum of 100 and half the distance between the cassette exon and the downstream flanking exon; and

• E2 region—i₂ nt upstream of and 100 nt downstream from the splice junction of the downstream flanking exon.

We consider that a splicing factor binds to the exon if it binds to any of the four regions. For the Tiklova data set, we tested the binding enrichment of each RBP independently in the 798 cell state–associated exons identified by Psix, using the hypergeometric test, with the 2087 tested exons as the background. We applied the Benjamini–Hochberg procedure to correct for multiple testing for all the RBPs. We used the same approach to test for enrichment in the 78 cell state–associated exons in the P90 cells versus the background of 2115 tested exons.

Analysis of P90 modules

We implemented Psix on the 290 cells collected from the P90 midbrain cells, using the transcriptomic space in Figure 3A. Because of the smaller sample size (compared with the entire data set), we used a neighborhood of 30 cells ($\sim 10\text{\%}$ of the total number of cells) and a minimum correlation for neighbor joining of 0.1. This resulted in 78 cell state–associated exons and two modules.

To find the potential regulators that control the formation of these patterns during neurogenesis, we identified the RBPs that are significantly enriched in binding to the 78 exons in these modules using CLIP-seq data (hypergeometric test, FDR ≤ 0.05). We tested for enrichment of binding to any of the four regions of the exon previously described.

We ran a Pearson's correlation test between the normalized expression (SCONE normalized TPM counts) of the enriched splicing factors and the observed $\hat{\mathrm{\Psi }}$ of the exons in each module in P90 cells. We tested for significance in the difference in distribution of Pearson's correlation scores using the Wilcoxon rank test and correcting for multiple testing with the Benjamini–Hochberg correction. We repeated these observations with cells from the P1 and E13.5 stages of development.

Simulations of alternative splicing in single cells

We simulate alternative splicing of exons in single cells. This consists of three main steps: First, we simulate gene expression profiles in a population of single-cells sampled from a continuous trajectory; with either a single branch (Fig. 2A) or multiple (Supplemental Fig. 1A,B). Second, we simulate alternative splicing in the exons of this population (accounting for one exon per gene), in which in some exons the inclusion rates are associated with the trajectory and in some the rates are random. These first two parts serve to simulate the true molecular content of the cells. Third, we simulate the measurement process (e.g., mRNA capture, amplification, sequencing), which results in noisy and sparse data, such as limited availability of splice junction reads.

Step 1: simulating gene expression in a single-cell population

We used SymSim (Zhang et al. 2019) to simulate the expression of 5000 genes in a continuous population of 1000 single cells with default parameters. To simulate a single developmental trajectory, we simulated single cells across a phylogenetic tree with two branches with SymSim and then set the endpoint of one branch as the starting point of the lineage and the endpoint of the second branch as the end of the lineage. Each cell's relative position in the tree corresponded to its position in the developmental trajectory, starting from the tip of one branch to the other. We normalized the relative positions of the lineage to span from zero (first cell) to 100 (last cell).

Step 2: simulating splicing in single cells

We simulate splicing in the single cells as three substeps. First, we model the expected Ψ as an impulse function, which was shown by us and others to fit well with empirical time course data (Fischer et al. 2018). For each exon, we simulate a “platonic” Ψ that will be dependent on the cell's position in the lineage:

$$\begin{array}{c}\begin{array}{c}z(t_i)={\displaystyle \frac{1}{h_1}\left(h_0+{\displaystyle \frac{h_1-h_0}{1+e^{-\text{β}\left(t_i-t_1\right)}}}\right)\left(h_2+{\displaystyle \frac{h_1-h_2}{1+e^{\text{β}\left(t_i-t_2\right)}}}\right),}\end{array}\end{array}$$

where z(t_i) = logit(Ψ(t_i)). t_i ∈ [0, 100] is the position of a given cell in the simulated lineage; h₀, h₁, and h₂ are amplitude parameters of the curve (first, second, and third plateau); and t₁ and t₂ are the state transition times; that is, when the inflection points of the impulse happen. β is a slope parameter that determines how steep the impulse is.

We sample the impulse parameters from the following probabilistic distributions:

$$\begin{array}{rl}& t_1\sim \mathrm{Uniform}\left(1,70\right)\\ & t_2\sim \mathrm{Uniform}\left(t_1+20,99\right)\\ & \text{β}\sim \mathrm{Uniform}\left(0.05,0.25\right)\\ & h_x\sim \mathrm{Uniform}\left(-3,\mathrm{logit}\left(0.7\right)\right)\\ & h_y\sim \mathrm{Uniform}\left(\mathrm{logit}\left(\mathrm{expit}\left(h_x\right)+0.2\right),3\right)\\ & h_z\sim \mathrm{Uniform}\left(h_x,h_y\right).\end{array}$$

To simulate different impulse shapes, we set [h₀, h₁, h₂] as a permutation of [h_x, h_y, h_z]. To simulate exons that do not change across the lineage, we randomly select a value c from [h_x, h_y, h_z] and set h₀ = h₁ = h₂ = c to specify a horizontal line.

We add noise to simulate the biological variability that affects the underlying splicing profile of a cell in a manner independent of the lineage:

$$\begin{array}{cc}\begin{array}{c}{z}_i\left(t_i\right)\sim \mathcal{N}\left(z\left(t_i\right),{\sigma }^2\right),\end{array}& \end{array}$$

where z_i(t_i) is the logit transformation of the underlying Ψ of cell i; t_i is the temporal stage of cell i, that is, its position in the continuous trajectory (lineage); and σ² is a variance parameter that is specific of each exon. For each exon, we randomly sample $\sigma \sim \mathrm{Uniform}\left(0.5,1\right)$. Finally, we simulate splicing of the mRNA molecules of each gene as a stochastic process as follows:

$$\begin{array}{rl}& I_i\sim \mathrm{Binomial}\left(X_i,\mathrm{expit}\left(z_i\left(t_i\right)\right)\right)\\ & E_i=X_i-I_i\end{array},$$

where I_i is the number of mRNA molecules of the gene in cell i that include the alternatively spliced exon, E_i is the number of mRNA molecules that exclude the exon, and X_i is the total number of mRNA molecules of the gene in cell i. We merge E and I into a single matrix of mRNA molecules M, in which each isoform corresponds to an independent row.

Step 3: sequencing and splice junction coverage

Once we have simulated the expression and splicing of each gene, we simulate the sequencing of the mRNA molecules. For this, we first assign a transcript length to each molecule as follows: For each gene g with isoforms g_E (excludes the exon) and g_I (includes the exon), we randomly sample without replacement $l_{g_E}$ as the length of g_E from SymSim's transcript length database. We then sample without replacement $l_{g_i}$, the length of the alternative exon of g, from a database of lengths of cassette exons in the human genome. Finally, we set the length of g_I as $l_{g_I}=l_{g_E}+l_{g_i}$.

We use SymSim's True2ObservedCounts function to simulate non-UMI sequencing of the mRNA molecules in M and lengths $l_{g_E}$ and $l_{g_I}$. We used the following parameters: mean capture efficiency, 0.1; capture efficiency standard deviation, 0.05; depth sequencing mean, 1e5; and depth sequencing standard deviation, 1e4. To simulate a data set with bad capture efficiency, we set mean capture efficiency to 0.05 and capture efficiency standard deviation to 0.02, and for a data set with very poor capture efficiency, we set mean capture efficiency to 0.01 and capture efficiency standard deviation to 0.01.

Finally, we simulate the splice junction coverage of isoforms as follows:

$$\begin{array}{rl}& l_r=\mathrm{read}\mathrm{length}\left(\mathrm{constant}\right)\\ & j_{g_I}={\displaystyle \frac{4\left(l_r-1\right)}{l_{g_I}}}\\ & j_{g_E}={\displaystyle \frac{2\left(l_r-1\right)}{l_{g_E}}}\\ & \mathrm{S}{\mathrm{J}}_{g_I}\sim \mathrm{Binomial}\left(R_{g_I},j_{g_I}\right)\\ & \mathrm{S}{\mathrm{J}}_{g_E}\sim \mathrm{Binomial}\left(R_{g_E},j_{g_E}\right),\end{array}$$

where l_r corresponds to the constant read length from the sequencing process (set as default to 50); $\mathrm{S}{\mathrm{J}}_{g_I}$ and $\mathrm{S}{\mathrm{J}}_{g_E}$ are the number of reads that cover informative splice junctions for isoforms g_I and g_E respectively; and $R_{g_I}$ and $R_{g_E}$ are the total number of reads simulated to map to isoforms g_I and g_E respectively.

For each cell, the observed $\hat{\mathrm{\Psi }}$ of each exon is calculated as

$$\begin{array}{cc}\begin{array}{c}\hat{\mathrm{\Psi }}={\displaystyle \frac{\mathrm{S}{\mathrm{J}}_{g_I}}{\mathrm{S}{\mathrm{J}}_{g_I}+2\cdot \mathrm{S}{\mathrm{J}}_{g_E}}}.\end{array}& \end{array}$$

Simulation of a branching lineage of single cells

We simulated a diverging lineage of single cells, using SymSim with the following three-branched phylogenetic tree (Supplemental Fig. 2):

$$\left(\mathrm{A}:1,\left(\mathrm{B}:0.5,\mathrm{C}:0.5\right):0.5\right).$$

We divided the single-cell population into three lineages: lineage 1, root to A; lineage 2, root to B; and lineage 3, B–C splitting point to C.

We simulated the “platonic” Ψ of each lineage as follows:

1. For lineage 1, sample h₀, h₁, t₁, and β as shown for the single-lineage impulse parameters. With a probability of 0.25, simulate differential splicing with a sigmoid function as follows:

   $$z_1(t_i)=\left(h_0+(h_1-h_0){\displaystyle \frac{1}{1+e^{-\text{β}(t_i-t_1)}}}\right).$$

   Elsewhere, we fit a flat line z₁(t_i) = h₀.

2. For Lineage 2, we use the same h₀ as in lineage 1 and randomly sample the other parameters. We simulate differential splicing with a sigmoid z₂ with a probability of 0.25, or fit a flat line z₂(t_i) = h₀ otherwise.

3. For lineage 3, we set h₀ = z₂(t_BC), where z₂ is the function (sigmoid or flat line) used for lineage 2, and t_BC is the timepoint at which lineage 2 and lineage 3 split. We sample the other parameters randomly. We simulate splicing with a sigmoid z₃ with a probability of 0.25, or fit a flat line z₃(t_i) = h₀ otherwise.

Each simulated gene is marked as differentially spliced if the splicing of at least one lineage was simulated with a sigmoid. Otherwise, the gene is marked as nondifferentially spliced. Once we have simulated the “platonic” Ψ of each gene, we repeat the simulation steps for the single lineage simulations.

Software availability

Psix is available as a Python module at GitHub (https://github.com/lareaulab/Psix). The analysis of simulations and publicly available data is documented at GitHub (https://github.com/lareaulab/analysis_psix). Psix source code and analysis are archived as Supplemental Code.

Competing interest statement

The authors declare no competing interests.