Lymphocyte Depletion Rate as a Biomarker of Radiation Dose to Circulating Lymphocytes During Fractionated Partial-Body Radiation Therapy

Abstract

Purpose

Radiation causes exponential depletion of circulating lymphocyte populations; in turn, radiation-induced lymphopenia is associated with worse survival for many solid tumors, possibly owing to attenuated antitumor immune responses. Identifying reliable and reproducible methods of calculating the radiation dose to circulating immune cells may facilitate development of techniques to reduce the risk and severity of radiation-induced toxic effects to circulating lymphocytes.

Methods and Materials

Patient-specific lymphocyte loss rates were derived from a clinical data set including 684 adult patients with solid tumors. Multivariable linear regression was used to model the relationship between the lymphocyte loss rate and physical parameters of the radiation plan that determine circulating blood dose.

Results

During partial-body radiation, lymphocyte loss rates are determined by physical parameters of the radiation plan that reflect radiation exposure to circulating cells, including target volume size, dose per fraction squared, and anatomic site treated. Differences in observed versus predicted lymphocyte loss rates may be partly explained by variations in concurrent chemotherapy regimens.

Conclusions

We describe a novel method of using patient-specific lymphocyte loss kinetics to approximate the effective radiation dose to circulating lymphocytes during focal fractionated photon radiation therapy. Clinical applications of these findings include the early identification of patients at particularly high risk of severe radiation-induced lymphopenia based on physical parameters of the radiation therapy plan.

Introduction

Radiation therapy is a mainstay of cancer treatment, and more than 500,000 patients with cancer are treated with radiation in the US annually.¹ Radiation-induced immunosuppression, which occurs in up to 70% of patients undergoing conventional radiation therapy, primarily manifests as acute lymphopenia² and is increasingly recognized as a clinically significant toxic effect of external beam radiation therapy for cancer. Strong associations between radiation-induced lymphopenia and decreased survival have been reported in common malignancies including lung, pancreatic, and esophageal cancers, as well as malignant glioma and several other solid tumors.³ Mechanistically, a decreased number of circulating lymphocytes reduces the probability that any single cell will respond to stimulation by tumor antigens, thus diminishing the likelihood of antitumor immune responses. Supporting this hypothesis, tumor-specific T cells are diminished in patients with lymphopenia after chemoradiation.⁴ Patients with radiation-induced lymphopenia also have a lower likelihood of response to immune checkpoint blockade.5, 6, 7

Lymphopenia risk is clearly correlated with physical parameters of the radiation plan, including field size, dose per fraction, fraction number, dose rate, type of radiation (proton vs. photon), and organ-specific dosimetric parameters (eg, the volume of the brain receiving ≥5 Gy).8, 9, 10 To date, a robust and clinically validated method of estimating the actual dose received by circulating immune cells has not been described. Calculation of the radiation dose to a dynamic structure such as circulating lymphocytes presents unique challenges. Lymphocytes are heterogeneously distributed throughout the body and are constantly moving through the irradiated field along with the blood and lymphatic circulation. Furthermore, lymphocytes not only have the capacity to at least partially repopulate during a radiation therapy course but also traffic among different compartments of the immune system in relatively short periods of time.^9,11 Prior work has shown that after unintentional single total-body radiation exposures, radiation dose can be approximated as a linear function of the decay constant for an individual lymphocyte loss curve.¹² In the present study, we proposed a similar method that uses individual lymphocyte loss kinetics to estimate radiation dose to circulating lymphocytes in patients undergoing fractionated partial-body radiation therapy for cancer.

Methods

Conceptual foundation

In cases of accidental total-body radiation exposures, when the dose received by patients is often not known, lymphocyte loss kinetics can assist in estimating the dose and triaging patients for intervention. For single total-body exposures, the absolute lymphocyte count (ALC) is considered to be a function of dose and time¹²:

$$AL{C}_t=AL{C}_0\times e^{-kt}$$ (Eq 1)

When k is modeled as a linear function of dose (d = αk), the slope of the regression line (α) allows the total-body dose (d) to be calculated solely based on the lymphocyte decay constant k:

$$d=8.6\times k$$ (Eq 2)

Lymphocyte loss in the setting of fractionated partial-body exposures also exhibits exponential decay kinetics during the initial phase of treatment (fractions 0-15).¹³ Lymphocyte loss rates can therefore be estimated on a patient-specific basis according to the following formula, where ALC₀ is the baseline ALC and ALC_x is the ALC after x fractions:

$$AL{C}_x=AL{C}_0\times e^{-bx}$$ (Eq 3)

Although typical clinical radiation therapy plans only irradiate a portion of the body, the entire blood circulation is expected to receive at least some radiation during each treatment, because blood is continuously circulating through the field (except in instances when exposure duration is less than the heart-to-heart circulation time).¹⁴ In terms of circulating blood dose, then, clinical partial-body radiation therapy can be conceptualized similarly to total-body exposures, and lymphocyte loss kinetics are related to the dose to circulating lymphocytes (d_CL). If the d_CL is calculated correctly, it is expected to have a linear relationship to the decay constant b, similar to total-body dose in the setting of accidental radiation exposure. Based on prior literature correlating the dose per fraction and field size with the risk of clinically apparent lymphopenia, we postulated that d_CL would be a function of the dose per fraction and the volume of blood irradiated relative to the total blood volume, and we attempted to validate this hypothesis among patients undergoing fractionated partial-body radiation therapy.14, 15, 16

Data acquisition and patient population

This was a registry-based study including 684 adult patients who underwent partial-body radiation therapy, with or without concurrent chemotherapy, for the definitive treatment of solid tumors. All patients had provided informed consent for treatment, and the study was approved by the institutional review board of the Indiana University School of Medicine. Please see Table 1 for a summary of baseline patient characteristics and treatment data. To be included in the data set, patients were required to have had a baseline ALC obtained no more than 28 days before commencing radiation and at least 2 additional ALC measurements obtained during the radiation therapy course. All patients underwent external beam photon (x-ray) therapy using modern megavoltage linear accelerators. Data were extracted from clinical medical records and the radiation treatment planning system. All ALC measurements were obtained as part of routine clinical laboratory studies and are expressed as cells/μL, rounded to the nearest 100. The planning target volume (PTV) size in cm³ was obtained from the treatment planning system (Eclipse, version 16, Varian Medical Systems, Palo Alto, California), and the ratio of PTV size (in cm³) to total blood volume was calculated. Total blood volume was estimated as a function of weight using a simplified version of Nadler's formula¹⁷:

$$bloodvolume\left(c{m}^3\right)=weight\left(kg\right)\times 70$$ (Eq 4)

Table 1.

Patient characteristics

Characteristic	Patients, No. (%) (N = 684)
Sex
Female	270 (39.5)
Male	414 (60.5)
Age, median (range), y	61 (19-88)
Site treated
Central nervous system	88 (12.9)
Head and neck	85 (12.4)
Lung	116 (17)
Abdomen	274 (40.1)
Esophagus	83 (12.1)
Liver	73 (10.7)
Pancreas	101 (14.8)
Other abdomen	17 (2.5)
Pelvis	121 (17.7)
Cervix/endometrium	35 (5.1)
Rectum	64 (9.4)
Anus	22 (3.2)
Radiation regimen
Dose per fraction, median (range), Gy	2.0 (1.33-20.0)
Total dose, median (range), Gy	50.0 (30.0-70.0)
Chemotherapy regimen
None	82 (12.0)
Gemcitabine alone	71 (10.4)
5-FU or capecitabine alone	100 (14.6)
5-FU/Mitomycin C	21 (3.1)
Platinum (cis- or carboplatin)	94 (13.7)
Platinum doublet	160 (23.4)
+paclitaxel	85 (12.4)
+5-FU	30 (4.4)
+other	45 (6.6)
Temozolomide	88 (12.9)
Biologic	10 (1.5)
Other/unknown	58 (8.5)

Abbreviation: 5-FU = 5-fluorouracil.

Data are presented as the number (percentage) of patients unless otherwise indicated.

Calculations of lymphocyte loss kinetics

Patient-specific lymphocyte loss kinetics were calculated as previously described; briefly, time-stamped ALC measurements were matched to fraction number (not treatment day) to generate individual lymphocyte loss curves for the first 15 days of treatment. Curves were fitted according to Equation 3 using Matlab, version 18.0 (Mathworks, Natick, Massachusetts), and the value of b (the decay constant) was recorded for all patients.

Statistical analysis

Multivariable linear regression with bivariable screening was used to evaluate the relationship between the decay constant b and physical parameters of the radiation plan, including PTV size, PTV-to-blood-volume ratio, mean body dose, and prescribed dose per fraction, as well as patient clinical characteristics including chemotherapy received and body site treated. Mean body dose, age, weight, sex, and baseline ALC were not significantly correlated with b upon bivariable analysis and were therefore omitted from the multivariable model. An exploratory analysis was conducted to model the relationship between dose per fraction, adjusted for target volume relative to total blood volume, and lymphocyte loss rates. Both linear and nonlinear relationships were tested at this stage using visual inspection of scatterplots and evaluation of correlation coefficients. Finally, a regression equation was derived to express the relationship between lymphocyte loss rate (dependent variable), dose per fraction, PTV-to-blood-volume ratio, and body site treated.

Because the model was designed to evaluate dependence of the lymphocyte loss kinetics on radiation-related parameters only, concurrent chemotherapy regimens were not included in the regression model. Analysis of variance and unpaired-sample t tests were used to evaluate whether lymphocyte loss rates varied by patient age, sex, or use of differing concurrent chemotherapy regimens. All statistical analyses were performed in SPSS, version 25 (IBM Corp, Armonk, New York) with a 2-tailed significance level specified at α =.05.

Results

Curve fitting

Curve fitting was successful for 597 of 684 patients; the most common reason for curve fitting failure was <3 ALC measurements available in the first 15 RT fractions. Decay constant values of b < 0 or > 1 were also considered a curve-fitting failure and were observed in 15 patients (2.2%). The remainder of patients exhibited exponential decay in their initial lymphocyte loss kinetics, as evidenced by generally excellent curve fitting; the median R² after linearization for all individual lymphocyte loss curves fitted to Equation 3 was 0.95.

Relationship between decay constant, PTV size, and dose per fraction

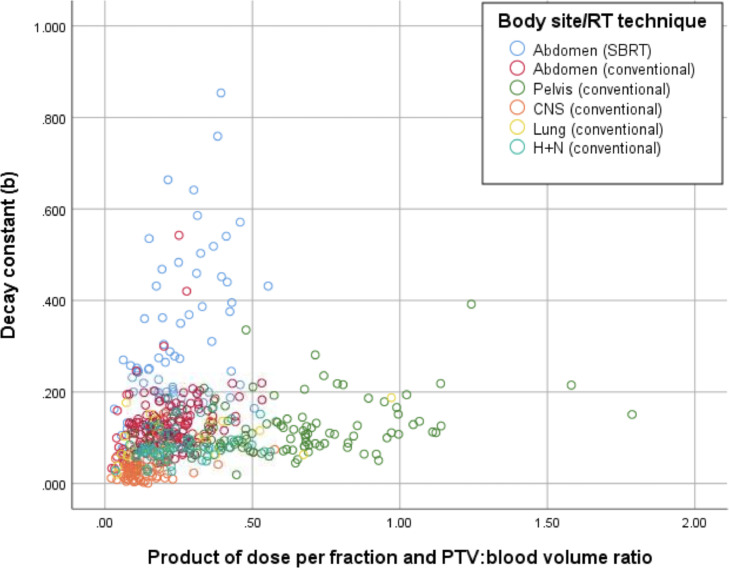
As shown in Figure 1, d_CL is not a linear function of dose × PTV-to-blood-volume ratio.

Figure 1.

Scatterplot of the lymphocyte decay constant versus the product of the dose per fraction and PTV-to-blood-volume ratio. Note abdominal SBRT cases (blue circles), which have a much higher decay constant for similar dose/volume relationships compared with patients receiving conventional fractionation. Abbreviations: PTV = planning target volume; RT = radiation therapy; SBRT = stereotactic body radiation therapy.

However, when d_CL is expressed as

$$d_{CL}=doseperfractio{n}^2\times PTV:bloodvolumeratio$$ (Eq 5)

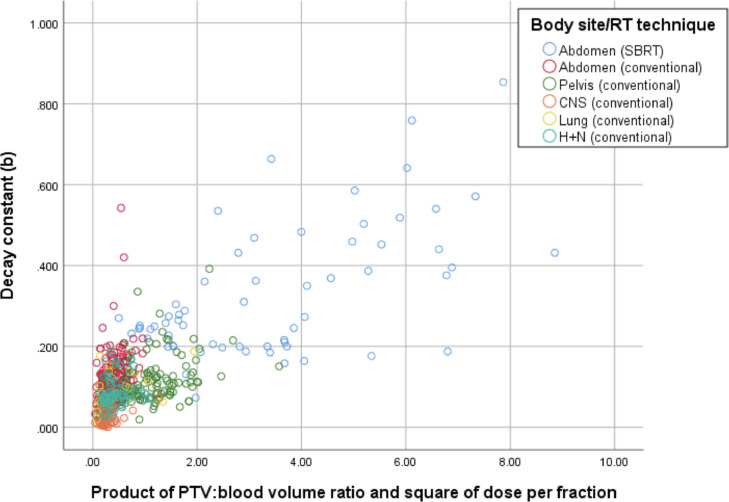
the relationship with the decay constant becomes linear, with r = 0.727 and r² = 0.528 (P < .001), as illustrated in Figure 2.

Figure 2.

Scatterplot showing the linear relationship between the lymphocyte decay constant versus the product of the dose per fraction squared and the PTV-to-blood-volume ratio. Interindividual variability in b for the same combinations of dose/fraction² and PTV:blood volume is observed. Abbreviations: CNS = central nervous system; H+N = head and neck; PTV = planning target volume; RT = radiation therapy; SBRT = stereotactic body radiation therapy.

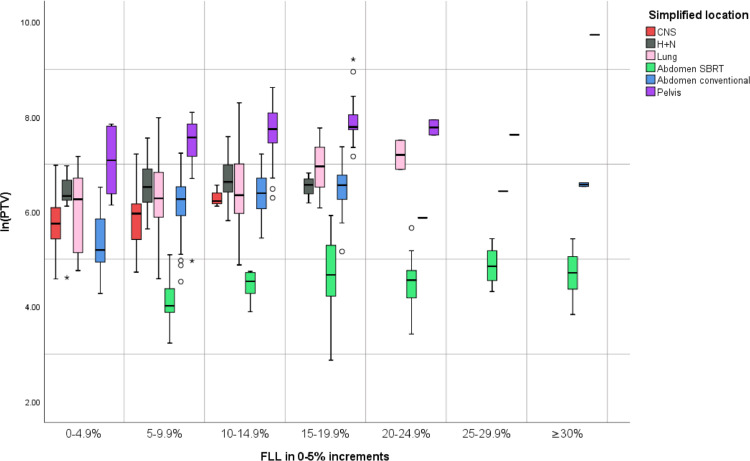
Figure 2 shows that patients undergoing abdominal radiation have a higher-than-expected value of b for the same combination of dose and blood volume in the field, whereas patients with central nervous system tumors have a lower-than-expected b. Similarly, Figure 3 illustrates that lymphocyte loss rates are greater, cm³ for cm³, in certain body areas, presumably those with a larger number of lymphocytes within the field, either owing to the presence of major lymphoid organs such as the spleen or an increased volume of blood traveling through the field in major blood vessels or highly vascular organs. For example, within similar ranges of lymphocyte loss rates, the pelvic target volume size associated with a particular lymphocyte loss rate is approximately one log_e higher than the corresponding abdominal volume. Abdominal stereotactic body radiation therapy is an exception, where the high dose per fraction is associated with a higher ALC loss rate.

Figure 3.

Box plot correlating lnPTV with percent-per-fraction lymphocyte loss rates. The PTV size associated with a particular per-fraction lymphocyte loss rate range (displayed in increments of 5% on the x-axis) varies considerably depending on the body site irradiated and the treatment technique (SBRT vs non-SBRT). The large difference in loss rates seen with SBRT plans likely reflects the higher dose per fraction given during SBRT. Abbreviations: CNS = central nervous system; FLL = per-fraction lymphocyte loss; H+N= head and neck; PTV = planning target volume; SBRT = stereotactic body radiation therapy.

Regression analysis

Multivariable linear regression yielded the following regression equation (r, 0.781; r², 0.61; P = < 0.001):

$$\begin{array}{c}decayconstant=0.058+0.056\times \left(PTV:bloodvolumeratio\times doseperfractio{n}^2\right)\hfill \\ +0.049\left(abdomensite\right)\hfill \\ -0.049\left(CNSsite\right)\hfill \end{array}$$ (Eq 6)

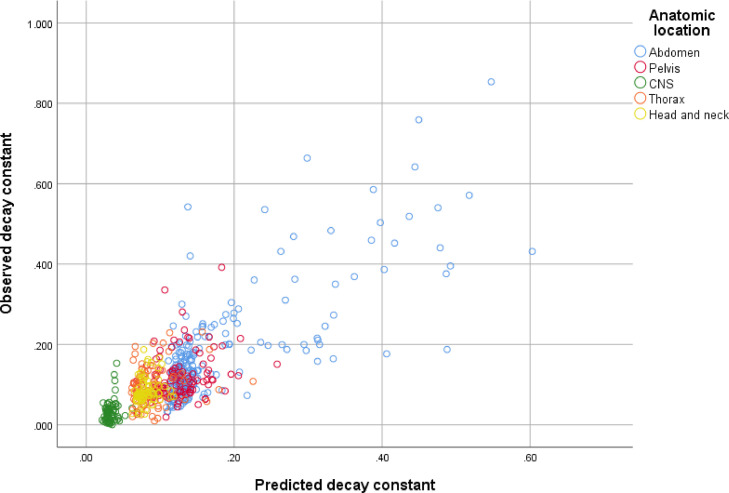
As shown in Figure 4, the output of the regression equation is strongly and linearly correlated with the observed lymphocyte decay constant b, suggesting that the dose to the immune compartment can be estimated using this method. Similar to prior reports of lymphocyte loss kinetics in total-body radiation exposures, our data depict considerable interindividual variability in the decay constant even when physical parameters of the radiation plan, such as dose per fraction, blood volume irradiated, and treated body site, are similar.

Figure 4.

Scatterplot of observed versus predicted decay constants, based on the product of the planning target volume:blood volume ratio and the square of the dose per fraction, adjusted for the site treated and the chemotherapy regimen (Equation 6). Abbreviation: CNS = central nervous system.

The ratio of predicted versus observed lymphocyte loss kinetics, where the predicted decay constant is calculated according to Equation 6, may be used to assess how factors not directly tied to physical parameters of the radiation plan may affect lymphocyte loss rates. For example, this approach could be used to analyze the effects of different clinical factors such as age, sex, or concurrent chemotherapy regimen on lymphocyte loss rates. Analysis of variance demonstrated that patients treated with concurrent 5-fluorouracil chemotherapy had significantly lower than predicted lymphocyte decay constants for the same combination of dose per fraction, PTV:blood volume ratio, and treated site (Table 2). No significant relationships were noted between patient age or sex and the ratio of predicted to observed lymphocyte decay constant.

Table 2.

Comparison of effects of concurrent chemotherapy regimen on radiosensitivity quotient (RSQ) using ANOVA testing with Bonferroni correction

No. of patients	Mean RSQ	No chemotherapy	Gem	5-FU	Plat	Plat/Taxol	Plat/5-FU	Plat/Other	5-FU/MMC	Tem
No chemotherapy (n = 79)	1.07		—	0.0003	—	—	—	—	—	—
Gem (n = 65)	0.97	—		—	—	—	—	—	—	—
5-FU (n = 92)	0.72	0.003	—		0.001	0.00006	0.009	0.027	0.001	0.046
Plat (n = 80)	1.05	—	—	0.001		—	—	—	—	—
Plat/Taxol (n = 80)	1.10	—	—	0.00006	—			—	—	—
Plat/5-FU (n = 20)	1.19	—	—	0.009	—	—		—	—	—
Plat/Other (n = 22)	1.13	—	—	0.027	—	—	—		—	—
5-FU/MMC (n = 16)	1.29	—	—	0.001	—	—	—	—		—
Tem (n = 67)	0.99	—	—	0.046	—	—	—	—	—

Abbreviations: 5-FU = 5-fluorouracil; ANOVA = analysis of variance; Gem = gemcitabine; MMC = mitomycin C; Plat = platinum (cis- or carboplatin); Tem = temozolomide.

Overall ANOVA P = .000001. P values for group-to-group comparisons are indicated in respective intersecting cells; — indicates P > .05.

Discussion

In this study, we demonstrated that partial-body radiation and total-body radiation had similar effects on circulating lymphocytes, resulting in exponential loss of circulating lymphocytes. We describe a novel method of using patient-specific lymphocyte loss kinetics to approximate the effective depletion rate of circulating lymphocytes during focal fractionated photon radiation therapy, which is the most common modern radiation therapy modality. Our analysis shows that lymphocyte loss rate was determined by physical parameters of the radiation plan, including dose per fraction, body site irradiated, and target volume size relative to the total blood volume. We also propose a method of using observed versus predicted lymphocyte loss rates to quantify the influence of differing chemotherapy regimens on lymphocyte loss rates during concurrent chemoradiation.

Our findings are clinically significant because radiation-induced lymphopenia is increasingly recognized as a predictor of worse outcomes in patients with multiple solid tumors. A clear mechanism links lymphocyte depletion with a depressed antitumor immune response, especially in patients treated with immune checkpoint blockade, because lymphocytes are key effector cells in the immune response to cancer as well as the main therapeutic targets of checkpoint inhibitor therapy. The risk of severe lymphopenia at the end of treatment is obviously correlated with both the baseline ALC and the rate of lymphocyte loss during treatment. By providing a method of predicting per-fraction ALC loss rates before treatment begins, the approach described here can be used to identify patients at high risk of radiation-induced lymphopenia as candidates for interventions such as hypofractionation or field size modification, which would be expected to decrease lymphocyte loss rates and ultimately mitigate lymphopenia risk. Our identification of the lymphocyte loss rate as a biomarker of the dose to circulating lymphocytes differentiates the present study from recent reports that have described a correlation between increased estimated dose to circulating blood and worse overall survival in patients with lung cancer but have not directly correlated blood dose with measured changes in absolute lymphocyte count.¹⁸

The present findings validate both prior simulations of radiation dose to circulating lymphocytes and multiple clinical studies correlating field size and organ dosimetry with lymphopenia risk.^9,14 Our results expand on these prior findings by identifying the treated site as a key determinant of lymphocyte loss rates and are consistent with prior clinical studies that have reported a considerably higher risk of severe lymphopenia in patients undergoing abdominal radiation compared with patients with glioma.² In the present analysis, for head and neck, lung, and pelvis sites, lymphocyte loss rate could be estimated solely by dose per fraction and PTV-to-blood-volume ratio without the need to include another weighting factor based on the anatomic site treated, whereas such weighting factors were required to account for lower and higher lymphocyte loss rates among patients undergoing treatment to the brain and abdomen, respectively. Anatomic differences in per-fraction loss rates are likely explained by variations in blood flow distribution, as well as the inhomogeneous distribution of primary and secondary lymphoid organs within the body. For example, the higher lymphocyte loss rate observed in patients undergoing abdominal radiation is likely owed to incidental irradiation of lymphocyte-rich abdominal structures including the spleen and cisterna chyli, as well as highly vascular structures (liver and kidneys) and major blood vessels such as the aorta and inferior vena cava. The lymphocyte decay constant may be influenced not only by the dose to circulating lymphocytes but also by other factors such as concurrent or prior chemotherapy and individual variations in either lymphocyte radiosensitivity or repopulation capacity. The present results demonstrate that the ratio of the observed to predicted lymphocyte loss rate can be used to assess effects of differing chemotherapy regimens on lymphocyte killing during concurrent treatment.

An important advantage of our method is that lymphocyte loss curves can be determined very early in the course of treatment, allowing radiation therapy plans to be adapted with the goal of preserving circulating lymphocyte populations before radiation-induced lymphopenia has the chance to develop. It is additionally possible that in vitro radiosensitivity correlates with clinical lymphocyte loss kinetics, thereby permitting the identification of patients who would benefit from intensified efforts to spare the immune system from radiation therapy–induced toxic effects before treatment even begins. Additional prospective studies would be needed to determine whether such a correlation exists.

Strengths of the present work include the large sample size, which permitted the creation of a robust model that accounts for variations in concurrent chemotherapy regimen as well as differing effects of treatment on multiple body sites. Potential sources of error within the analysis include the fact that clinical ALC measurements at our institution are reported as rounded to the nearest 100 cells/μL, introducing uncertainty into curve fitting and consequent estimations of the decay constant. Uncertainty may also have been introduced by the lack of data on treatment breaks and the fact that the timing of blood sample collection relative to radiation therapy administration varied. Depending on the timing of lymphocyte death after radiation exposure, variations in when ALC was measured may also have affected the shape of the lymphocyte loss curve in individual patients.

Additional refinement of the model could be accomplished by using a more accurate estimate of blood volume than the simplified version of Nadler's formula that was used here. More granular measurements of dose distribution in certain anatomic sites might also help to improve the model. For example, differing spleen¹⁹ or bone marrow²⁰ dose distributions could contribute to variability in lymphocyte loss rates among patients undergoing abdominal radiation. Very large site-specific databases with a range of per-fraction doses would be needed to accurately observe such differences. It is also unclear whether the observed relationship between dose and lymphocyte loss kinetics will hold at either very low (less than approximately 0.5 Gy) or very high (greater than approximately 10 Gy) doses.¹² Further research is needed to evaluate the contribution of doses at the limits of this range to lymphocyte loss rates, particularly at lower doses, which are commonly received in the clinical setting by circulating lymphocytes passing through the penumbra of a radiation field. It is also possible that some other as yet unidentified clinical factor affected lymphocyte loss rates, introducing additional variability in the lymphocyte radiosensitivity index that we were unable to account for. For example, lymphocyte subpopulations vary in radiosensitivity, and interindividual differences in levels of circulating lymphocyte subtypes could affect radiation-induced lymphocyte loss rates in vivo.²¹ Finally, it is important to note that this analysis was based on photon treatments only. Owing to differences in dose distribution and relative biologic effectiveness of charged particle therapies such as proton or carbon ion radiation compared with x-ray therapy, it is possible that the relationship between the dose per fraction and the lymphocyte decay constant for charged particle therapy differs from that described here. Although our analysis has the intrinsic limitations of retrospective data, the findings are quite robust and describe fundamental characteristics of the pathophysiology of radiation-induced lymphopenia. Future applications of the study findings include providing a basis for adaptive radiation planning techniques that incorporate patient-specific lymphocyte loss kinetics, as well as a platform for assessing intrinsic factors that could affect lymphocyte radiosensitivity, such as variations in DNA repair genes or interindividual differences in the distribution of circulating lymphocyte subtypes.