Abstract
In the wake of the COVID-19 pandemic, interest in understanding the turbulent dispersion of airborne pathogen-laden particles has significantly increased. The ability of infectious particles to stay afloat and disperse in indoor environments depends on their size, the environmental conditions and the hydrodynamics of the flow generated by the exhalation. In this work we analyze the impact of three different aspects, namely, the buoyancy force, the upper airways geometry and the head rotation during the exhalation on the short-term dispersion. Large-Eddy Simulations have been used to assess the impact of each separate effect on the thermal puff and particle cloud evolution over the first 2 s after the onset of the exhalation. Results obtained during this short-term period suggest that due to the rapid mixing of the turbulent puff, buoyancy forces play a moderate role on the ability of the particles to disperse. Because of the enhanced mixing, buoyancy reduces the range and increases the vertical size of the small particle clouds. In comparison to the fixed frame case, head rotation has been found to notably affect the size and shape of the cloud by enhancing the vertical transport as the exhalation axial direction sweeps vertically during the exhalation. The impact of the upper airway geometry, in comparison to an idealized mouth consisting in a pipe of circular section, has been found to be the largest when it is considered along with the head rotation.
Keywords: Expiratory event, Unsteady jet, Turbulent puff, Turbulent dispersion, Particle dispersion, Large-Eddy simulation
1. Introduction
Talking, singing, intense breathing and violent expiratory events, as coughs and sneezes, generate expulsion of aerosols. When released by an infected person, these pathogen-laden particles are recognized as vectors of contagion of infectious diseases caused by viruses and bacteria, including the current Severe Acute Respiratory Syndrome CoronaVirus 2 (SARS-CoV-2), the human influenza, the avian influenza, the SARS or the tuberculosis (Bourouiba, 2021). The understanding of the physics of the flow generated and the short-term turbulent dispersion of the aerosol particles expelled during these intense and violent expirations is key to establish preventive measures and guidelines to minimize the risk of airborne disease transmission by expelled pathogen-laden particles. It is now well known that flow injections into quiescent air environments produce particle clouds constituted by small aerosols that remain afloat within the thermal puff. This thermal puff is constituted by the warm turbulent body of fluid that has been ejected into an initially colder undisturbed environment. Larger particles follow ballistic trajectories, leave the thermal puff quickly, reach their terminal vertical velocity and eventually end falling onto the floor (Pourfattah et al., 2021). The typical picture of an isolated violent expiratory event includes a warm, humid, aerosol laden intense flow injection with a short duration (t < 1 s) and maximum velocities ranging from 1 to 30 m/s (Tang et al., 2013) that evolves into a thermal puff and disperses by the effects of turbulent momentum transfer and buoyancy. Continuous expiratory events, such as talking or breathing intensely, generate similar phenomena forming a flow structure in the form of a puff-train (Abkarian et al., 2020). Social distancing and the use of face masks are measures that have been established to minimize the risk of infection taking into account the range of action of these small particle clouds and the range of the large particles expelled in violent expiratory events (WHO, 2021).
Recently, with the outbreak of the pandemic SARS CoV-2, many studies have been performed, using experiments and/or numerical simulations, to determine the characteristics of the flow and the aerosol cloud dispersion generated in coughs and sneezes. The amount of existing literature on the subject is growing fast. However, most of these studies (Abkarian et al., 2020; Diwan et al., 2020; Fabregat, Gisbert, Vernet, Ferré, et al., 2021; Ho, 2021; Lavrinenko et al., 2022; Li et al., 2022; Oh et al., 2022; Trivedi et al., 2021; Wang et al., 2021) consider pipe-like idealized anatomy without head rotation. In this introduction we have selected the most relevant references related to the aspects discussed in this paper concerning the effects of buoyancy, upper respiratory tract geometry and head movement on the flow generated in a violent expiratory episode.
The characteristics of coughs and sneezes have been determined in experiments with human volunteers (Gupta et al., 2009, VanSciver et al., 2011, Tang et al., 2013, Busco et al., 2020, Dudalski et al., 2020, Han et al., 2021, Bahl et al., 2021) and with mannequins (Verma et al., 2020; Bhavsar, 2021; Payri et al., 2021; Xu et al., 2022). The objective of these studies was to quantify and determine the relevant flow and particle dispersion features and to establish realistic boundary conditions at the flow injection for numerical simulations.
The shape and size of the mouth aperture during a cough has been measured by Gupta et al. (2009) and Busco et al. (2021). According to these authors the quasi-elliptical shape and area of the aperture remain essentially constant during a cough with areas of aperture ranging from 1.3 to 6.5 cm2 with averages for men and women around 3.5 cm2. This corresponds to an equivalent circle with a diameter of about 2 cm, which is the shape and diameter usually used in simulations (Fabregat, Gisbert, Vernet, Ferré, et al., 2021; Ho, 2021; Li et al., 2022; Wang et al., 2021). However, Dbouk and Drikakis (2020) measured a more horizontally elongated mouth opening during a cough with a width to height ratio of about 8 and an area of 1.9 cm2.
The experiments with humans have also revealed that the flow injection from an immobile, horizontal mouth is produced downwards with a certain vertical inclination angle because of the bending of the flow as it passes from the larynx to the oral cavity and the curved flow passage between the tongue and the palate in the oral cavity. Measurements (Gupta et al., 2009, Bahl et al., 2021) indicate that this inclination angle ranges from 37° to 16°, with an average value around 25°. The head movement during sneezes has been measured (Bahl et al. 2020, 2021 and Busco et al., 2021). Busco et al. (2021) reported a relatively rapid head rotation during a sneeze with a total duration of about 0.5 s. According to these authors, initially, the mouth is oriented upwards with an angle with respect to the horizontal of about 50°, then, while sneezing, the head is rotated downwards with an angular velocity of about 4 rad/s (230°/s), reaching the horizontal orientation in about 0.22 s. For longer times the head is rotated upwards at a smaller angular velocity (0.6 rad/s, 34°/s), reaching an orientation upwards of about 10° at the end of the sneeze. Bahl et al. (2021) reported more modest head movement in their experiments with maximum displacements of the centroid of the head of about 2 m and linear velocities of 0.28 m/s.
The time evolution of the flow rate during a violent expiratory event also exhibits a relatively large variation of intensity and duration within different individuals and experiments. In addition, in some cases violent expiratory events can be pulsatile, such as the expulsion of a set of two or three sequential coughs (Monroe et al., 2021). However, measurements for a single violent expiratory event show in all the cases a quick ramp up of the flow rate (or spatially averaged injection velocity) and a much slower ramp down. Gupta et al. (2009) reported measurements of the flow rates recorded with a spirometer during coughs for 25 individuals. Peak air flow rates ranged from about 2 l/s to 8 l/s, which correspond, respectively, to maximum velocities of 6 m/s and 25 m/s for a circular mouth diameter of 2 cm. The total duration of the coughs was between 0.3 s and 0.6 s. Similar maximum flow rates but larger durations up to 1 s were determined by Li et al. (2022). Non-intrusive measurements of the velocities of the expelled droplets during a cough carried out with Particle Image Velocimetry are reported by Chao et al. (2009), VanSciver et al. (2011), Kwon et al. (2012) who measured maximum velocities for coughs between 10 m/s and 15 m/s. More recently Oh et al. (2022) suggested values of about 20 m/s.
Considerable research has been carried out to determine the amount and the diameters of the expelled droplets during coughs and sneezes. Duguid (1946) was one of the first to determine the size and the frequency of expelled particles when talking, coughing and sneezing. For coughs this author reported droplets with diameters ranging from 2 μm to 1000 μm, with a more probable value of about 16 μm. The measurements by Xie et al. (2009) determined the peak of the density function of the diameters at about 50 μm.
The number of studies reporting numerical simulations of violent expiratory events and dispersion of pathogen-laden aerosols has also increased significantly since the beginning of the SARS-CoV-2 pandemic. Most of the research has been performed so far using the numerical solution of the unsteady version of the Reynolds-averaged Navier-Stokes equations (URANS) (Dbouk & Drikakis, 2020; Gupta et al., 2011; Ho, 2021; Lavrinenko et al., 2022; Oh et al., 2022; Thatiparti et al., 2017; Yang et al., 2018; Zhang et al., 2021). More computationally expensive Large-Eddy Simulations (LES) (Abkarian et al., 2020; Fontes et al., 2020; Foster & Kinzel, 2021; Liu et al., 2021; Pendar & Páscoa, 2020; Trivedi et al., 2021; Wang et al., 2021) and Direct Numerical Simulations (DNS) (Diwan et al., 2020; Fabregat, Gisbert, Vernet, Ferré, et al., 2021; Li et al., 2022) have also been reported.
The vast majority of these numerical studies model the unsteady flow injection consisting in a relatively fast progressive increase of the flow rate followed by a slower decrease according to the measurements obtained in the experiments with volunteers. Usually, the flow inlet discharges in a cylindrical or parallelepipedal computational domain through immobile circular (Abkarian et al., 2020; Wang et al., 2021) or quasi-elliptical (Busco et al., 2020) areas and the Lagrangian particles released during the exhalation are tracked by solving the pointwise particle force balance. To model the effect of the upper respiratory tract some studies impose a certain vertical angle to the velocity vector at the flow inlet or a certain spread angle (Busco et al., 2020; Li et al., 2022) following the experimental observations. A simplified geometry of the upper respiratory tract consisting in the larynx, pharynx and oral and nasal cavities is considered by Fontes et al. (2020). These authors found that differences in the nasal/buccal passages have a dramatic impact on the spray characteristics that are associated with pathogen transmission rates. To our knowledge the head movement during a sneeze has only been considered in the simulations reported by Busco et al. (2020) who solved numerically the URANS equations and modelled the flow injection with a varying momentum source. The horizontal and vertical components of the momentum source were calculated by considering the time-varying angle of the head movement measured during a sneeze. The comparison of simulations with and without head movement showed that the cloud spread in space and time is about two times larger in the case of the head movement.
In this paper we analyze LES of the flow and the particle dispersion generated in a violent expiratory event. The focus of this study is directed to the short-term flow and particle cloud characteristics, such as their range and dimensions. This information can be important to establish short-range protection measures and to use these flow and cloud characteristics as initial conditions for long-term large scale dispersion models of pathogen laden aerosols, especially in indoor environments. It should be noted that while the flow generated in coughs and sneezes has a time scale of a few seconds (Gupta et al., 2009), with flow injections lasting for less than a second, the background flow, with typical velocities of 0.1–0.2 m/s in indoor ventilated spaces (International Organization for Standardization, 2005) with dimensions of a few or several meters, can have time scales of the order of tens or hundreds of seconds. Therefore the background air currents are expected to dominate the cloud transport soon after the end of the exhalation. We compare the thermal puff trajectory and its dimensions and the particle cloud characteristics for different injection conditions. To our knowledge, this is the first study to analyze, in a combined manner, the flow in the upper airways and the subsequent dispersion, considering both immobile injection and typical head movement during sneezing.
2. Physical models
We consider the evolution of the flow produced by a violent expiratory event and the dispersion of the resulting aerosol cloud in an initially quiescent and isothermal environment using a cylindrical computational domain (Fig. 1 ). The unsteady flow injection into the environment is produced through a circle with diameter D = 0.02 m, which models the typical open of the mouth during a cough (Busco et al., 2020; Gupta et al., 2009). The origin of the system of coordinates is located at the center of this circular flow inlet with z being the streamwise axial direction and gravity is aligned with the negative y-direction (see Fig. 1a).
Fig. 1.
Computational domain for the simulation of the turbulent dispersion of a cough. (a) Full cylindrical domain with a circular flow inlet with diameter D. Note that the origin of the system of coordinates is located at the center of the circular inlet of the large cylindrical domain. (b) Detail of the inlet tube attached to the full cylindrical computational domain for the simulations with a pipe inlet as flow injection. (c) Detail of the circular inlet for the simulations with the flow injection obtained from to the trachea-oral cavity model.
Two different flow injections into the large cylindrical domain have been considered. The first one is the same used in the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) who generated a flow injection through a straight pipe of diameter D and length 2D with a bump to promote turbulence near the pipe exit (see Fig. 1a and b). An unsteady and spatially uniform flow injection typical of a mild cough (Gupta et al., 2009) was imposed at the inlet of the pipe. The flow injection ramps up linearly from zero to a maximum axial velocity of 4.8 m/s at t = 0.15 s and then ramps down linearly from this value to zero velocity at t = 0.4 s. A simulation conducted imposing this velocity profile at a circular inlet gives very similar results in comparison with the simulations reported in this study with the pipe inlet. The second flow injection has been obtained from unsteady flow simulations in a model of the trachea and upper respiratory tract. Several views of the model are shown in Fig. 2 . This model was used by Cheng et al. (1999) to simulate particle deposition and it is described in Lizal et al. (2012). The STL files are available at the ERCOFTAC QNET-CFD Knowledge Base Wiki (ERCOFTAC, 2021). The upper airway corresponds to an adult male and it was not scanned during coughing or sneezing. The computational model used to generate the unsteady flow at the mouth exit shown in Fig. 3 was obtained by attaching the trachea and upper respiratory tract to a cylindrical volume with diameter 12.5D and length 25D. To generate the time evolution of the three velocity components at the mouth exit of this model, an unsteady uniform velocity has been imposed at the bottom of the trachea to obtain the same instantaneous flow rate at the mouth exit as in the pipe inlet of the simulations performed with the computational domain shown in Fig. 1a and b. The unsteady spatially uniform velocity profile imposed at the bottom of the trachea has the same linear ramps as the profile imposed at the pipe inlet but with a different maximum velocity (w max = 8.8 m/s) to obtain the same time evolution of the mass flow rate injected in both conditions. The time evolution of the three velocity components at the mouth exit obtained with the model of Fig. 3 were saved and imposed as inlet boundary conditions at the circular inlet of the cylindrical computational domain shown of Fig. 1a and c for the simulations of the turbulent particle dispersion.
Fig. 2.
Model of the upper airway. The black line corresponds to the plane x = 0 that divides vertically the exit of the circular mouth. The circular mouth exit has a diameter of 2 cm. (a) Frontal view. (b) Lateral view. (c) Cut of the model with the plane x = 0. (d) Bottom view. (e) Top view.
Fig. 3.
Computational domain for the simulations of the flow exit from the oral cavity. The inset shows a detail of the mesh on the oral cavity.
The effect of the head movement during a violent expiratory event on the turbulent particle dispersion has been determined by performing separate simulations with the model of the trachea and upper respiratory tract in non-rotating and rotating non-inertial frames of reference. This non-inertial frame of reference is attached to an axis of rotation aligned with the x-direction located at the back of the oral cavity. As in the simulations with no head movement the time evolution of the three velocity components at the mouth exit were saved and used as initial conditions for simulations of the turbulent particle dispersion carried out with the same non-inertial frame of reference. Fig. 4 shows the time evolution of the ramps of the normalized velocity (w max = 4.8 m/s) and of the angle of inclination of the mouth exit with respect to the horizontal according to the experiments reported by Busco et al. (2020). It can be seen that, initially, the mouth exit has an angle of about 50°. As the head rotates, the angle decreases quasi-linearly to the horizontal position at t ≈ 0.22s and then slightly increases, also linearly, to reach about 5° at t = 0.4 s, when the flow injection ceases. The corresponding time evolution of the normalized exhaled air volume is also indicated in Fig. 3. At t = 0.25 s, after the head has reached the horizontal orientation and the exit velocity has decreased to about a half of the maximum value, about 80% of the air has been exhaled.
Fig. 4.
Time evolutions of the conditions of the flow exit of the simulated mild cough. Green lines correspond to the normalized velocity exit. Red lines, to the angle of inclination of the flow exit with respect to the horizontal. The black line indicates the time evolution of the normalized volume of exhaled air. Continuous lines are taken from Busco et al. (2020) and dashed lines are linear trends of the ramps up and ramps down. The vertical dotted lines indicate the times of the instantaneous velocity distributions shown in Fig. 6. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
As in the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021), the exhaled air in all the cases is considered to be at 34 °C, while the air quiescent environment is at 15 °C. Simulations with buoyancy and without buoyancy (i.e. with temperature as a passive scalar) have been carried out for the different flow injections to determine the effect of the air density variations in the particle dispersion. Table 1 summarizes the total of six simulations performed with the corresponding name coding. Note that the rotation of the head movement has been considered only for simulations with realistic injection conditions obtained from the trachea-oral cavity model.
Table 1.
Summary and codification of the simulations of the turbulent dispersion of a violent expiratory event.
| Buoyancy |
No (B0) |
Yes (B1) |
||
|---|---|---|---|---|
| Rotation | No (R0) | Yes (R1) | No (R0) | Yes (R1) |
| Pipe exit (PE) | PE-B0-R0 | – | PE-B1-R0 | – |
| Mouth exit (ME) | ME-B0-R0 | ME-B0-R1 | ME-B1-R0 | ME-B1-R1 |
For the two types of flow domains (pipe exit and oral cavity-trachea model), idealized spherical particles have been released over the entire duration of the exhalation (0 ≤ t ≤ 0.4s) with an initial velocity equal to that of the local velocity of the fluid at the circular mouth exit. Following the same procedure of Fabregat, Gisbert, Vernet, Ferré, et al. (2021), particles of n = 6 different sizes (n = 1, 2 … 6) with 2n+1 μm in diameter, are released in batches every 2 ms from fixed and uniformly distributed seeding positions across the circular inlet. This assumes that any preferential concentration of particles at the flow injection produced by the lift force or by inertia effects is neglected. The particle size range selected covers the typical sizes of expelled droplets in a violent expiratory event according to Duguid (1946). It should be noted that the breakup of the mucosalivary fluid into droplets continues to occur outside the respiratory tract, as reported by Scharfman et al. (2016), and these phenomena are not considered in the present approach. In addition, given the relatively initial small particle volume fraction (approximately 10−5) expelled in real coughs and sneezes (Duguid, 1946), it is assumed that the particles do not affect the flow and particle-particle interactions are neglected (one-way coupling). When the flow injection ceases a total of 97,200 released particles, corresponding to the 200 batches of 81 particles for each of the 6 diameter sizes are tracked up to t = 2 s. The shapes and characteristics of the particle clouds using 97,200, 48,600 and 24,300 particles are very similar. Considering the relatively low computational cost of the particle tracking, in comparison with the solution of the flow equations, we used approximately the same number of particles (97,200) as the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021). The diameter of the particles is assumed to be constant. Although evaporation effects can be important depending on the ambient conditions (Pal et al., 2021), for the conditions considered in the present simulations, the effect of the progressive reduction of diameter due to evaporation is limited to the moderate size particles (32 μm) (Fabregat, Gisbert, Vernet, Ferré, et al., 2021). Smaller particles, with smaller Stokes numbers, follow well the flow irrespectively of their diameter because of their small inertia. For the larger particles, with a gravity dominated motion, the reduction of the diameter only affects slightly the terminal velocity when the particles are free falling out of the generated thermal puff. For example, for the smallest particles (4 μm) and the largest particles (256 μm) the Galileo number (, with ) are 0.05 and 25, respectively. The corresponding Stokes numbers based on the maximum velocity of the injection (4.8 m/s) and the diameter of the flow exit (0.02 m) are 0.01 and 48. In any case the effect of the ambient humidity on the particle dispersion has been neglected and the results presented here are relevant for situations in which the potential evaporation and condensation effects play a minor role, as in the conditions considered in the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) with an ambient temperature and humidity of 15 °C and 65%, respectively.
The physical properties of the air and the particles, corresponding to water at ambient temperature, are indicated in Table 2 . The Reynolds number based on the maximum velocity is = 6400 and the Rayleigh number, = 1.9·104.
Table 2.
Physical properties of the air and the particles.
| Air | |||
|---|---|---|---|
| ρ0 (kg/m3) | 1.2 | μ (Pa·s) | 1.8·10−5 |
| Cp (J/kg K) | 1006 | β (1/K) | 3.3·10−3 |
|
k (W/m·K) |
2.4·10−2 |
Pr |
0.74 |
| Particles | |||
| ρp (kg/m3) | 998 | dp (μm) | 4, 8, 16, 32, 64, 128, 256 |
3. Mathematical models
The flow is assumed to be incompressible and the fluid physical properties constant, except for the linear variation of density with temperature according to the Boussinesq approximation. The corresponding governing filtered continuity, momentum, and thermal energy equations can be written, respectively, as
| (1) |
| (2) |
and
| (3) |
In Equations (2), (3)), are the components of the velocity vector, is the pressure, is the temperature, is the gravity vector, is the thermal expansion coefficient, is the Levi-Civita symbol, are the components of the rotation rate vector of the rotating frame of reference and and are, respectively, the kinematic viscosity and the thermal diffusivity of the fluid. Correspondingly, and are the subgrid scale kinematic viscosity and thermal diffusivities. The subgrid-scale tensor terms () arising from the application of the spatial filter to the original equations are modelled with the conventional eddy-viscosity assumption.
| (4) |
where is the resolved strain rate tensor. Similarly, in Equation (3) the subgrid-scale heat fluxes () are modelled as
| (5) |
The third and fourth terms in the right-hand side of Equation (2) are, respectively, the buoyancy and the Coriolis term. The centrifugal term is included in the pressure gradient term and the buoyancy centrifugal effect (i.e. variation of density in the centrifugal term) is neglected because of the relatively short time of the head movement (see Fig. 4) and the overall limited effect of buoyancy described in the next section. The angular acceleration produced by the change of the rotation rate at t ∼ 0.22 s (see Fig. 4) has been also neglected and simulations were performed assuming a constant rotation rate of 3.98 rad/s of the rotating frame between 0 < t < 0.22 and a constant rotation rate of = -0.64 rad/s for 0.22 < t < 0.4.
The conditions imposed at the boundaries of the computational domain used for the simulations of the turbulent dispersion of particles are for the momentum equations: non-slip boundary conditions at the circular wall located at z = 0, x 2+y 2>(D/2)2. Constant pressure is set at the cylindrical surface located at x 2+y 2=(20D)2 and at the circular outlet located at z = 50D. For the simulations of the particle dispersion with the pipe inlet non-slip boundary condition is set at the pipe wall and a uniform but unsteady axial (w(t)) velocity distribution at the circular pipe inlet, located at z = −2D. In the case of the simulations with the velocity exit of the mouth the instantaneous three velocity component obtained from the separate simulations with the model of the trachea and oral cavity were imposed at the circular inlet located at z = 0, x 2+y 2<(D/2)2. For the thermal energy equation, a zero-heat flux is imposed at all the boundaries and a constant temperature of 34 °C is set at the inlet of the pipe (Fig. 1b) and at the circular inlet for the simulations with the mouth exit (Fig. 1c).
The simulations to obtain the velocity distributions at the mouth exit were performed in the computational domain shown in Fig. 3 and the flow was assumed isothermal. Considering the origin of coordinates at the center of the circular mouth exit the boundary conditions are non-slip boundary conditions at the walls of the trachea and the oral cavity, a uniform but unsteady y-velocity distribution at the bottom trachea inlet to produce the same time evolution of the flow rate as that used in the simulations with the pipe exit.
All the simulations were initialized with a zero velocity and a constant temperature of 15 °C at z > 0. The temperature at z < 0 for the simulations with the pipe inlet was set initially at 34 °C.
Lagrangian point spherical particles are tracked according to the kinematic relation between their position () and the particle velocity () (Eq. (6)) and the second Newton's law (Eq. (7)) with the following forces per unit mass from left to right: the gravity force, the hydrodynamic drag force and the forces that arise due to rotation of the reference frame, the centrifugal force and the Coriolis force.
| (6) |
| (7) |
In Eq. (7) is the drag coefficient computed following Morsi and Alexander (1972) and and are the particle and fluid reference densities, respectively. The lift force, the pressure gradient force, the virtual mass and Basset forces are neglected according to the relatively small density ratio between the fluid and the particle. The thermophoretic force has been also neglected considering the small temperature gradients within the fluid. The grid-resolved fluid velocity at the position of the particle is used to compute the drag force.
The set of filtered governing equations and the Lagrangian particle tracking have been solved with the commercial code ANSYS Fluent 19.2. (ANSYS 2019). The WALE SGS model with the default values of the model constants has been used to compute the SGS viscosity and thermal diffusivity. The velocity coupling method is solved with the iterative SIMPLE method with a bounded central difference scheme for the spatial discretization of the equations. The bounded second order implicit time marching scheme is used to advance the solution in time with a constant time step of 0.001 s. The same time-step is used to integrate the Lagrangian tracking equations for the particles using a Runge-Kutta method (Cash & Karp, 1990).
Simulations of the turbulent particle dispersion in the computational domain shown in Fig. 1 have been carried out with three different meshes with 1.9, 2.4 and 3.6 million of hexahedral elements. Some details of the medium mesh, as the stretching of the nodes towards the flow inlet, can be seen in Fig. 1. The effect of the grid resolution on the time evolution of the position of the centroid and the dimensions of the thermal puff is shown in Fig. 5 for the same case considered in the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021). The definitions of the position of the centroid of the temperature distribution and its vertical (y) and axial (z) widths ( and ) are defined as
| (8) |
| (9) |
where is the non-dimensional temperature defined as . In Fig. 5, the position of the centroid is shown with continuous lines and the size is represented with dashed lines corresponding to the position plus and minus one standard deviation (i.e. ). It can be seen that the position of the centroid and the sizes of the perturbations of the thermal field predicted by the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) are well reproduced by the present LES with the medium and fine meshes. Consequently, the simulations presented and discussed in the next section have been obtained with the mesh of 2.4 million nodes. Despite the single flow realization for each case presented in this work the mesh independence test shown in Fig. 5 would suggest that the variability of the results due to stochastic effects is modest. A typical run to simulate a total of 2 s took about 48 h of CPU time using 36 nodes.
Fig. 5.
Time evolutions of the position of the centroid and the standard deviation of the temperature field at x = 0 for the case PE-B1-R0 for different grids. The DNS data of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) is included for comparison purposes. (a) axial position and standard deviation. (b) vertical position and standard deviation.
The simulations to obtain the instantaneous velocity distributions at the mouth exit were performed with two different meshes of 0.6 and 0.9 million cells. The meshes combine tetrahedral elements and prisms attached to the model of the trachea and oral cavity. Details of the finer mesh can be seen in Fig. 3. The differences on the instantaneous velocity distributions obtained with these two meshes were small and the mesh with 0.9 million cells was used for the simulations. This grid has 5 layers of prisms attached to the wall with the first grid node at a distance of 0.13 mm from the wall. At the instant corresponding to the maximum velocity (t = 1.5 s) this distance corresponds to y+≈2.
4. Results and discussion
4.1. Characteristics of the flow in the model of the trachea and upper respiratory tract during a violent expiratory event
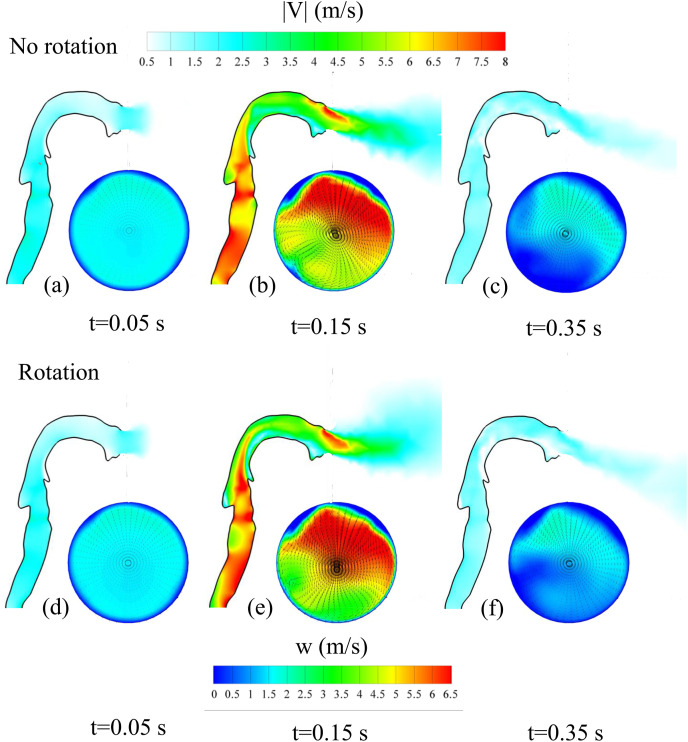
Fig. 6 shows instantaneous velocity contours at three different times of the flow ejection. These times are indicated in Fig. 4 and correspond to the initial stage, the time when the maximum exit velocity is reached and at the final stage of the violent expiratory event. The contours of the instantaneous modulus of the velocity vector are plotted on the plane x = 0, that divides symmetrically the mouth along the vertical direction (see Fig. 2a). Contours of the instantaneous axial (w) velocity component, superimposed to the instantaneous cross stream vector field (u, v), on the circular exit of the mouth are shown at the same time instants. Fig. 6a–c correspond to simulations without rotation (i.e. no head movement) and Fig. 6d–f to simulations with the movement indicated in Fig. 4. Animations of the time evolutions of the velocity distribution at the mouth for the cases with and without rotation of the head are shown in Fig. 7 .
Fig. 6.
Instantaneous distributions of the velocity magnitude, |V|, on the plane x = 0 indicated in Fig. 2 and instantaneous distributions of the axial velocity component, w, on the circular mouth exit at three different times (t = 0.05 s, t = 0.15 s and t = 0.35 s) indicated with vertical dotted lines in Fig. 4. (a), (b) and (c) correspond to a cough with the head immobile and (d), (e) and (f) to a cough with the head movement indicated in Fig. 4.
Fig. 7.
Time evolutions of the velocity distribution at the mouth for the cases with and without rotation of the head. Instantaneous contours of the axial velocity superimposed the cross-stream vector field (Multimedia view). The last frame corresponds to t = 0.4 s.
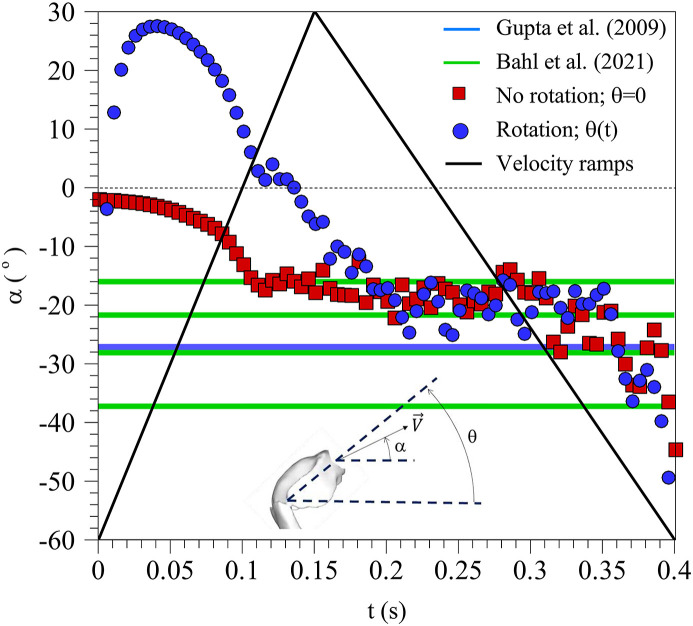
It can be seen that the rotation does not introduce significant differences in the velocity distributions in the respiratory tract and in the mouth exit, specially when the maximum exit velocity is reached. Fig. 6b and e shows that the maximum axial velocities are located at the top part of the mouth exit because of the bend generated by the combined effect of the palate and the tongue. It is also relevant that the velocity distributions are not symmetric with respect the vertical symmetry plane of the circular mouth exit (x = 0). This can be attributed to the slightly inclined position of the trachea to the right, as shown in Fig. 2a that drives the maximum flow exit towards the right of the mouth exit. As shown in Fig. 6b and e, below the region of maximum axial velocity, two weak counter rotating vortexes appear in the cross-stream vector field. This cross-stream vector field at the mouth exit also indicates that the flow is ejected with a certain inclination with respect the horizontal, specially at the upper part of the mouth exit where the axial velocity is maximum. To illustrate this, Fig. 8 shows the time evolution of the spatially averaged inclination angle of the velocity vector at the mouth exit located at z = 0. The averaged inclination angle of the velocity vector has been computed weighting the local value of the angle with the modulus of the local velocity. According to Fig. 8, irrespectively of the movement of the head, the axial flow ejection points downwards with an inclination angle of about −20° with respect to the horizontal. As indicated in Fig. 8, similar time-averaged inclination angles with values ranging between −37° and −16° have been measured experimentally from images of coughs and sneezes of volunteers by Gupta et al. (2009) and Bahl et al. (2021). Note that, as shown in Fig. 4, the head rotation angle starts with an angle of about 50° with respect to the horizontal and ends with an angle close to 5°. However, the averaged inclination of the velocity vector, shown in Fig. 8, reaches about 30° at t = 0.05 s and then ramps down and is kept to about −20° during most of the remaining time of the flow injection.
Fig. 8.
Time evolution of the mean angle of the velocity vector with respect to the horizontal. Squares correspond to a cough with the head immobile (θ = 0) and circles, to a cough with the head movement indicated in Fig. 4. The averaged velocity ramps are indicated with black lines.
4.2. Turbulent dispersion of the thermal field and particles
To illustrate the time evolution of the thermal field, Fig. 9 shows frontal and lateral views of an isosurface of temperature (T* = 0.025) close to the temperature of the environment (T* = 0) at two different times for the different cases considered. The first instant (t = 0.4 s) corresponds to the time when the flow injection stops (see Fig. 4) and the second (t = 1.5 s) is representative of the conditions when the velocity of the decaying jet is of the order of the typical background velocities in indoor ventilated spaces (v 0.1 m/s) (International Organization for Standarization, 2005).
Fig. 9.
Lateral and frontal views of the isosurfaces of temperature () at two different times (t = 0.4s and 1.5 s). (a) PE-B0-R0, (b) PE-B1-R0, (c) ME-B0-R0, (d) ME-B1-R0, (e) ME-B0-R1 and (f) ME-B1-R1.
It can be seen that, in general, the temperature imprints have a quasi-conical shape with different orientations, dimensions and ranges depending on the case considered. The vertexes of the coni are located close to the flow injection and the vertical cross sections of the coni increase along the axial direction, as indicated for example in Fig. 9a–2. The simulations with the pipe inlet (PE-B0-R0 and PE-B1-R0, Fig. 9a and b) generate axially elongated thermal imprints with a leading puff that appears detached from the conical shape of the temperature imprint at t = 1.4 s. In contrast, the mouth exit (ME-B0-R0 and ME-B1-R0, Fig. 9c and d) generates temperature imprints vertically inclined according to the mean angle of inclination of the velocity vector shown in Fig. 8 and larger dispersion of the temperature field as shown, for example, by comparing Fig. 9a–2 and 9c-2. In the lateral views of the isosurfaces of temperature corresponding to the non-buoyant flow injection through an immobile mouth exit (ME-B0-R0, Fig. 9c–1 and 9c-2) we included, in red, the isosurfaces of temperature of the non-buoyant flow through the pipe exit (PE-B0-R0) but rotated −20° in the vertical plane (i.e. θ = −20°, see Fig. 8). These red isosurfaces illustrate the non-buoyant thermal puff produced by a flow expelled through a pipe exit with the constant average orientation of the velocity injection through a mouth exit, as shown in Fig. 8. It can be seen that the thermal puff produced by the inclined pipe exit has a larger axial extension, but smaller radial widths than the corresponding thermal puff released through the mouth exit. This can be attributed to the larger turbulence intensity and flow inhomogeneity of the flow at the mouth exit, produced by the complex geometry of the respiratory tract, in comparison to the spatially more uniform flow at the pipe exit. The movement of the head shown in Fig. 4 (cases ME-B0-R1 and ME-B1-R1, Fig. 9e and f) produces vertically elongated temperature imprints (see for example Fig. 9e–1) and a very effective mixing between the hot exhaled air and the cold environment as deduced from the limited axial extension of the temperature isosurface (T* = 0.025) in Fig. 9e–2 and 9f-2. Note that the movement of the head produces a sweep of the angle of the velocity vector with respect to the horizontal at the exit of the mouth from approximately 30° to −20°, injecting the hot flow within a relatively wide area with a vertical spread angle of 50° (see Fig. 8). This vertical spread of the injected flow is also observed comparing the instantaneous contours of the axial velocity of Fig. 6b and e, corresponding, respectively, to cases without and with rotation of the head.
At t = 0.4 s the shape of the temperature isosurfaces is essentially independent of buoyancy, as suggested by comparison of cases PE-B0-R0 (Figs. 9a–1) and PE-B1-R0 (Figs. 9b–1), the cases ME-B0-R0 (Figs. 9c–1) and ME-B1-R0 (Figs. 9d–1) and the cases ME-B0-R1 (Figs. 9e–1) and ME-B1-R1 (Figs. 9f–1). Differences due to buoyancy are more evident at t = 1.5 s for the cases with the pipe inlet and with the mouth exit without head movement with thermal imprints more elongated along the vertical direction because of the enhanced vertical mixing due to buoyancy.
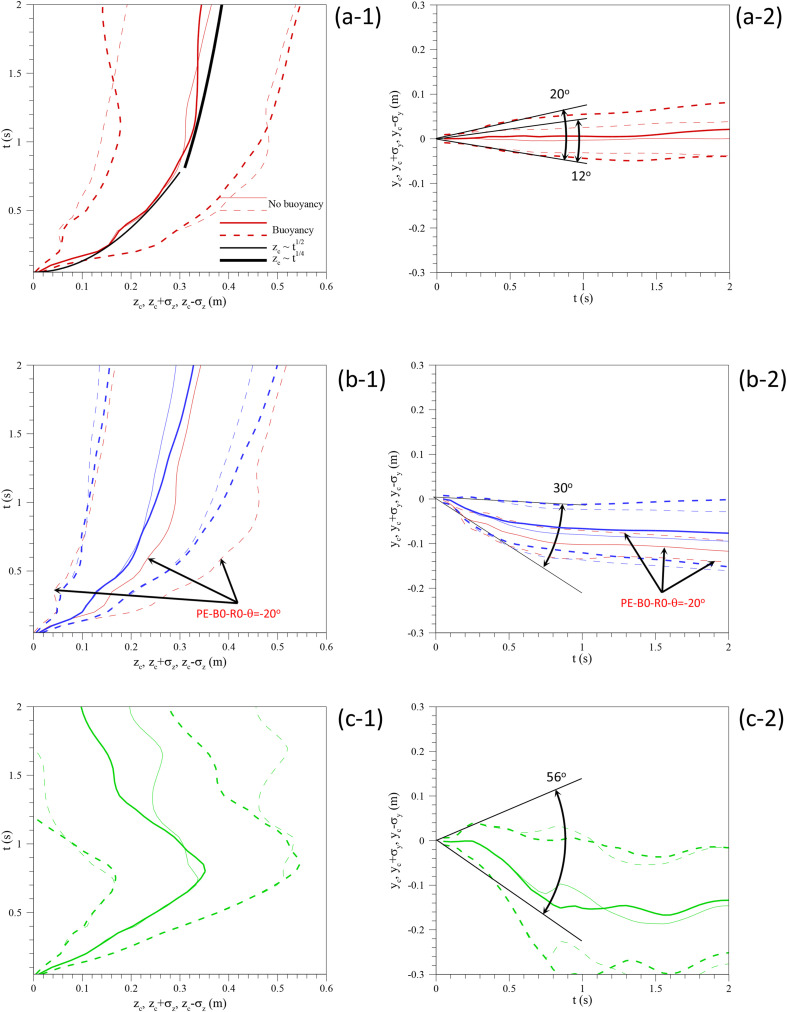
Fig. 10 compares the time-evolutions of the position of the centroid (Eq. (8)) and the sizes (Eq. (9)) of the thermal field for the different cases considered. The axial positions and sizes are plotted in Figs. 10a–1, 10b-1 and 10c-1 while the vertical positions of the centroid and the vertical sizes are in Figs. 10a–2, 10b-2 and 10c-2. As in Fig. 5, the position of the centroid is shown with continuous lines and the size is represented with dashed lines corresponding to the position plus and minus one standard deviation (i.e. ). Cases with buoyancy and without buoyancy are indicated in each graph with different line thickness.
Fig. 10.
Time evolutions of the position of the centroid and the standard deviation of the temperature field at x = 0 for cases (a-1 and a-2) PE-B0-R0 and PE-B1-R0, (b-1 and b-2) ME-B0-R0 and ME-B1-R0 and (c-1 and c-2) ME-B0-R1 and ME-B1-R1.
Comparison of Figs. 10a–1, 10b-1 and 10c-1 suggests, that buoyancy only influences on the axial position of the centroid for t > 0.7 s, well after the flow injection has ceased, at t = 0.4 s. For the cases without head movement (Fig. 10a and b) and at larger times, t ≈ 2 s, the axial extension of the thermal puff is slightly larger for the cases with buoyancy. A similar trend is observed for the vertical position and size of the thermal puff (see Figs. 10a–2 and 10b-2) that appears vertically displaced by the action of buoyancy. For the cases without head movement, the effect of the geometry of the flow exit (Fig. 10a and b) is more evident in the vertical positions and sizes than in the horizontal positions and sizes. It can be seen in Figs. 10b–2 that the flow is expelled from the mouth downwards irrespectively of the buoyancy effect, which tends to move the flow upwards. The vertical spread angles for the different flow injections, which can be deduced from the early time evolution of the vertical width of the thermal puff, are indicated in Figs. 10a–2, 10b-2 and 10c-2. For the pipe exit the vertical spread angle without buoyancy is of about 12 °C and with buoyancy around 20 °C. These values are in agreement with those measured for isothermal jets (11.3°, Scorer, 1997) and buoyant thermal puffs (≈17°, Scorer, 1997 and Pallares & Fabregat, 2022). The mouth geometry without head movement increases the spread angle up to 30°, as measured by Gupta et al. (2009) who reported a value of 25° ± 9° and with head movement to 56°. In fact, Busco et al. (2020) based on their measurements with head movement, performed their numerical simulations with a momentum source with a spread angle of 60°. The positions and sizes of a non-buoyant flow injection through a pipe exit with a vertical inclination of −20 °C are included in red for comparison purposes in Fig. 10b. As previously shown in Figs. 9c–1 and 9c-2, the pipe exit generates more elongated and thinner thermal puffs than the mouth exit.
When the movement of the head is considered (Fig. 10c), the axial position of the centroid decreases for t > 0.7 s. This can be attributed to enhanced turbulent mixing of the hot expelled air with the cold environments produced by the intense change of direction of the flow injection. As a result of this, Figs. 9e–2 and 9f-2, corresponding to the cases with head movement at t = 1.5 s, show that the thermal imprint is concentrated near the mouth (z = 0) and it has vanished for axial positions z > 0.1 m.
The trajectories of the centroid of the thermal puff for the different cases considered are plotted in Fig. 11 . As a reference, the times corresponding to the maximum exit velocity (t = 0.15s) and to the end of the flow injection (t = 0.4s) have been indicated in the trajectories with empty and filled circles, respectively. For comparison purposes, DNS predictions of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) have been included and the average vertical inclination of each type of flow injection is indicated. The horizontal pipe injection generates essentially a horizontal trajectory that slightly moves upwards because of buoyancy. The injections through the mouth geometry produce downward trajectories with an angle of about 20° with respect to the horizontal. This angle increases up to 45° for the cases with head movement which exhibit chaotic trajectories of the centroid of temperature at large times because of the well mixing conditions at these times. As previously, we included the trajectory corresponding to pipe exit inclined −20°.
Fig. 11.
Trajectories of the position of the centroids of the thermal fields for the different cases considered.
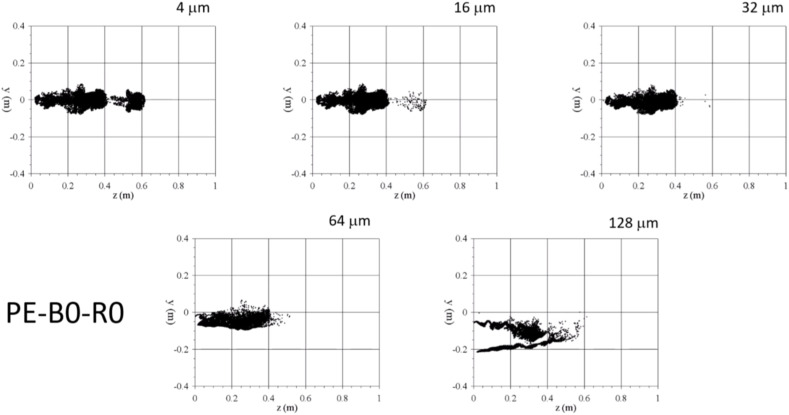
Fig. 12 shows lateral and frontal views of the particle clouds at t = 1.5 s for the six cases simulated. To keep the figure clear only the instantaneous positions of three particle sizes are plotted. Blue corresponds to particles of 64 μm, green to 32 μm and red to 4 μm. Predictions of DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) are included in Fig. 12c for comparison purposes. Time evolutions of the particle positions for the cases, without buoyancy, PE-B0-R0, ME-B0-R1 and ME-B0-R1 are shown in Fig. 12, Fig. 13, Fig. 14 (Multimedia views), respectively. The corresponding time evolutions for the cases with buoyancy are very similar to those corresponding without buoyancy and have been omitted.
Fig. 12.
Lateral and frontal views of the particle positions at 1.5 s. Red: Particle diameter 4 μm, Green: 32 μm and Blue: 64 μm. (a1) and (a2) PE-B0-R0, (b1) and (b2) PE-B1-R0, (c1) and (c2) DNS PE-B1-R0 from Fabregat, Gisbert, Vernet, Ferré, et al. (2021), (d1) and (d2) ME-B0-R0, (e1) and (e2) ME-B1-R0, (f1) and (f2) ME-B0-R1 and (g1) and (g2) ME-B1-R1. (For interpretation of the references to colour in this figure legend, the reader is referred to the Web version of this article.)
Fig. 13.
Time evolutions of the positions of the particles for case PE-B0-R0 (Multimedia view). Video plays back at half the actual speed. The last frame corresponds to t = 2 s.
Fig. 14.
Time evolutions of the particles for case ME-B0-R0 (Multimedia view). Video plays back at half the actual speed. The last frame corresponds to t = 2 s.
It can be seen that, for the horizontal flow injections through the pipe inlet (PE-B0-R0 and PE-B1-R0, Fig. 12a and b), particles with diameters smaller than 32 μm remain within the thermal puff (compare for example Fig. 12a with Figs. 9a–2 or Fig. 12b with Figs. 9b–2) while larger particles tend to free fall outside the puff. Note also that the shapes of the clouds of particles with diameters of 4 μm and to 32 μm resembles the corresponding shapes of the thermal puffs. This is also observable for the cases of the flow injection through the geometry of the mouth without head movement (ME-B0-R0 and ME-B1-R0, Fig. 12d and e) that produce thermal and particle clouds oriented axially and downwards (see Fig. 12d and e and Figs. 9c–2 and 9d-2). The movement of the head during the flow exhalation (ME-B0-R1 and ME-B1-R1, Fig. 12f and g) has an important effect on the spatial distribution of the particle clouds. Figs. 12f and g shows that most of the particles of 64 μm left the computational domain and that the smaller particles are irregularly distributed. Most of these small particles are located at y < 0 and z < 0.6 m but some of them are located at y > 0 and have travelled up to z ∼ 1 m at t = 1.5 s.
The time evolutions, shown in Fig. 15 , (multimedia view) of the particle positions for the case with head movement (PE-B0-R1) reveal that the small particles located close to y ∼ 0.2, z ∼ 0.9 m at t = 1.5 s have been transported by an intense vortex ring detached from the thermal puff. This phenomenon is observed for both cases with or without buoyancy and consequently it can be considered to be associated to a pure inertial effect. Intense vortex rings detached from starting jets can be observed in experiments (Scorer, 1997) and detached from thermal puffs in the DNS of Fabregat, Gisbert, Vernet, Ferré, et al. (2021) and LES of Trivedi et al. (2021).
Fig. 15.
Time evolutions of the particles for case ME-B0-R1 (Multimedia view). Video plays back at half the actual speed. The last frame corresponds to t = 2 s.
5. Conclusions
We simulated unsteady turbulent flows and expelled particle dispersion produced by a prototypical violent expiratory event. Two different geometries are considered for the flow injection, which is released into a quiescent environment. The first consists of a horizontal circular tube, used in previous numerical studies, and the second corresponds to the geometry of a typical human upper respiratory tract from the trachea to the oral cavity. For these two different geometries, flow ejections with temperatures larger and equal to the ambient temperature have been considered to determine the effect of buoyancy on the flow and particle dispersion. Besides these simulations with immobile flow injections, cases with the geometry of the upper respiratory tract with a prototypical movement of the head produced in sneezes have been also carried out.
In the case of no head movement, the flow ejected through the oral cavity during a sneeze has a vertical downward inclination of about 20° with respect to the horizontal. This produces thermal puffs with trajectories with approximately this inclination, while flows ejected from the horizontal pipe exhibit essentially horizontal trajectories of the puff, which tend to slightly ascend in the cases with buoyancy. The inclination of the trajectory of the thermal puff increases up to 45° with respect to the horizontal direction for flow ejections performed with head movement. For the flow and thermal conditions considered and for short times after the flow injection has ceased, buoyancy has a relatively limited effect on the trajectories and sizes of thermal puff and particle clouds, indicating that inertial effects are dominant during the short-term dispersion of the flow and particles expelled during a violent expiratory event. As shown by previous numerical simulations considering immobile flow injections, expelled particles with a diameter smaller than approximately 32 μm remain afloat within the thermal puff while larger particles tend to free fall out of the thermal puff. We observed this, independently of the geometry of the flow outlet. We think this result is important and can be used to stablish general measures to minimize the aerosol exposure during the short-term dispersion. However, the movement of the flow injection following a typical rotation of the head during a sneeze produces a very fast and efficient mixing of the flow and particles, which are expelled within a relatively large spread angle (≈50°) into the quiescent environment. In this situation the dispersion and the range of the particle cloud is significantly increased in comparison with the flow injection from an immobile source. All in all, our results highlight the importance of considering the upper respiratory tract anatomy and the head movement to predict the buoyant flow of airborne pathogen-laden particles generated in a violent expiratory event.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This publication is part of the R&D&I projects (Refs. RTI2018-100907-A-I00 and PID2020-113303 GB-C21), funded by MCIN and FEDER “Una manera de hacer Europa”. The authors gratefully acknowledge the economic support of Generalitat de Catalunya - AGAUR (under project 2017 SGR 01234).
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jaerosci.2022.106052.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- Abkarian M., Mendez S., Xue N., Yang F., Stone H.A. Speech can produce jet-like transport relevant to asymptomatic spreading of virus. Proceedings of the National Academy of Sciences. 2020;117(41):25237–25245. doi: 10.1073/pnas.2012156117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahl P., de Silva C.M., Chughtai A.A., MacIntyre C.R., Doolan C. An experimental framework to capture the flow dynamics of droplets expelled by a sneeze. Experiments in Fluids. 2020;61(8):1–9. doi: 10.1007/s00348-020-03008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bahl P., de Silva C., MacIntyre C.R., Bhattacharjee S., Chughtai A.A., Doolan C. Flow dynamics of droplets expelled during sneezing. Physics of Fluids. 2021;33(11) doi: 10.1063/5.0067609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhavsar A.A. The spread of macroscopic droplets from a simulated cough with and without the use of masks or barriers. PLoS One. 2021;16(5) doi: 10.1371/journal.pone.0250275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bourouiba L. The fluid dynamics of disease transmission. Annual Review of Fluid Mechanics. 2021;53:473–508. [Google Scholar]
- Busco G., Yang S.R., Seo J., Hassan Y.A. Sneezing and asymptomatic virus transmission. Physics of Fluids. 2020;32(7) doi: 10.1063/5.0019090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cash J.R., Karp A.H. A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides. ACM Transactions on Mathematical Software. 1990;16:201–222. [Google Scholar]
- Chao C.Y.H., Wan M.P., Morawska L., Johnson G.R., Ristovski Z.D., Hargreaves M.…Katoshevski D. Characterization of expiration air jets and droplet size distributions immediately at the mouth opening. Journal of Aerosol Science. 2009;40(2):122–133. doi: 10.1016/j.jaerosci.2008.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheng Y.S., Zhou Y., Chen B.T. Particle deposition in a cast of human oral airways. Aerosol Science & Technology. 1999;31(4):286–300. [Google Scholar]
- Dbouk T., Drikakis D. On coughing and airborne droplet transmission to humans. Physics of Fluids. 2020;32(5) doi: 10.1063/5.0011960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diwan S.S., Ravichandran S., Govindarajan R., Narasimha R. Understanding transmission dynamics of COVID-19-type infections by direct numerical simulations of cough/sneeze flows. Transactions of the Indian National Academy of Engineering. 2020;5:255–261. doi: 10.1007/s41403-020-00106-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dudalski N., Mohamed A., Mubareka S., Bi R., Zhang C., Savory E. Experimental investigation of far‐field human cough airflows from healthy and influenza‐infected subjects. Indoor Air. 2020;30(5):966–977. doi: 10.1111/ina.12680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duguid J.P. The size and the duration of air-carriage of respiratory droplets and droplet-nuclei. Epidemiology and Infection. 1946;44(6):471–479. doi: 10.1017/s0022172400019288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ERCOFTAC QNET-CFD knowledge Base Wiki. 2021. https://www.ercoftac.org/products_and_services/wiki/
- Fabregat A., Gisbert F., Vernet A., Dutta S., Mittal K., Pallarès J. Direct numerical simulation of the turbulent flow generated during a violent expiratory event. Physics of Fluids. 2021;33(3) doi: 10.1063/5.0042086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fabregat A., Gisbert F., Vernet A., Ferré J.A., Mittal K., Dutta S., Pallarès J. Direct numerical simulation of turbulent dispersion of evaporative aerosol clouds produced by an intense expiratory event. Physics of Fluids. 2021;33(3) doi: 10.1063/5.0045416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontes D., Reyes J., Ahmed K., Kinzel M. A study of fluid dynamics and human physiology factors driving droplet dispersion from a human sneeze. Physics of Fluids. 2020;32(11) doi: 10.1063/5.0032006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster A., Kinzel M. Estimating COVID-19 exposure in a classroom setting: A comparison between mathematical and numerical models. Physics of Fluids. 2021;33(2) doi: 10.1063/5.0040755. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta J.K., Lin C.H., Chen Q. Flow dynamics and characterization of a cough. Indoor Air. 2009;19(6):517–525. doi: 10.1111/j.1600-0668.2009.00619.x. [DOI] [PubMed] [Google Scholar]
- Gupta J.K., Lin C.H., Chen Q. Transport of expiratory droplets in an aircraft cabin. Indoor Air. 2011;21(1):3–11. doi: 10.1111/j.1600-0668.2010.00676.x. [DOI] [PubMed] [Google Scholar]
- Han M., Ooka R., Kikumoto H., Oh W., Bu Y., Hu S. Experimental measurements of airflow features and velocity distribution exhaled from sneeze and speech using particle image velocimetry. Building and Environment. 2021;205 doi: 10.1016/j.buildenv.2021.108293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho C.K. Modeling airborne pathogen transport and transmission risks of SARS-CoV-2. Applied Mathematical Modelling. 2021;95:297–319. doi: 10.1016/j.apm.2021.02.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Organization for Standardization . ISO; 2005. ISO 7730 2005-11-15 ergonomics of the thermal environment: Analytical determination and interpretation of thermal comfort using calculation of the PMV and PPD indices and local thermal comfort criteria. [Google Scholar]
- Kwon S.B., Park J., Jang J., Cho Y., Park D.S., Kim C.…Jang A. Study on the initial velocity distribution of exhaled air from coughing and speaking. Chemosphere. 2012;87(11):1260–1264. doi: 10.1016/j.chemosphere.2012.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavrinenko A., Fabregat A., Pallares J. Comparison between fully resolved and time-averaged simulations of particle cloud dispersion produced by a violent expiratory event. Acta Mechanica Sinica. 2022;38 doi: 10.1007/s10409-022-09032-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M., Chong K.L., Ng C.S., Bahl P., de Silva C.M., Verzicco R., Doolan C., MacIntyre C.R., Lohse D. Towards realistic simulations of human cough: Effect of droplet emission duration and spread angle. International Journal of Multiphase Flow. 2022;147 [Google Scholar]
- Liu H., He S., Shen L., Hong J. Simulation-based study of COVID-19 outbreak associated with air-conditioning in a restaurant. Physics of Fluids. 2021;33(2) doi: 10.1063/5.0040188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lizal F., Elcner J., Hopke P.K., Jedelsky J., Jicha M. Development of a realistic human airway model. Proceedings of the Institution of Mechanical Engineers - Part H: Journal of Engineering in Medicine. 2012;226(3):197–207. doi: 10.1177/0954411911430188. [DOI] [PubMed] [Google Scholar]
- Monroe K., Yao Y., Lattanzi A., Raghav V., Capecelatro J. Role of pulsatility on particle dispersion in expiratory flows. Physics of Fluids. 2021;33(4) doi: 10.1063/5.0048746. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morsi S.A.J., Alexander A.J. An investigation of particle trajectories in two-phase flow systems. Journal of Fluid Mechanics. 1972;55(2):193–208. [Google Scholar]
- Oh W., Ooka R., Kikumoto H., Han M. Numerical modeling of cough airflow: Establishment of spatial–temporal experimental dataset and CFD simulation method. Building and Environment. 2022;207 [Google Scholar]
- Pallares J., Fabregat A. A model to predict the short-term turbulent indoor dispersion of small droplets and droplet nuclei released from coughs and sneezes. Indoor and Built Environment. 2022;31(5):1393–1404. [Google Scholar]
- Pal R., Sarkar S., Mukhopadhyay A. Influence of ambient conditions on evaporation and transport of respiratory droplets in indoor environment. International Communications in Heat and Mass Transfer. 2021;129 [Google Scholar]
- Payri R., Gimeno J., Martí-Aldaraví P., Marco-Gimeno J. Building and Environment; 2021. Spray characteristics and penetration of the human cough, and the effectiveness of masks to prevent its dispersion. [Google Scholar]
- Pendar M.R., Páscoa J.C. Numerical modeling of the distribution of virus carrying saliva droplets during sneeze and cough. Physics of Fluids. 2020;32(8) doi: 10.1063/5.0018432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pourfattah F., Wang L.P., Deng W., Ma Y.F., Hu L., Yang B. Challenges in simulating and modeling the airborne virus transmission: A state-of-the-art review. Physics of Fluids. 2021;33(10) doi: 10.1063/5.0061469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharfman B.E., Techet A.H., Bush J.W.M., Bourouiba L. Visualization of sneeze ejecta: Steps of fluid fragmentation leading to respiratory droplets. Experiments in Fluids. 2016;57(2):1–9. doi: 10.1007/s00348-015-2078-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scorer R.S. 1st ed. Wiley; New York: 1997. Dynamics of meteorology and climate. [Google Scholar]
- Tang J.W., Nicolle A.D., Klettner C.A., Pantelic J., Wang L., Suhaimi A.B., Tan A.Y.L., Ong G.W., Su R., Sekhar C., Cheong D.D.W., Tham K.W. Airflow dynamics of human jets: Sneezing and breathing-potential sources of infectious aerosols. PLoS One. 2013;8(4) doi: 10.1371/journal.pone.0059970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thatiparti D.S., Ghia U., Mead K.R. Computational fluid dynamics study on the influence of an alternate ventilation configuration on the possible flow path of infectious cough aerosols in a mock airborne infection isolation room. Science and Technology for the Built Environment. 2017;23(2):355–366. doi: 10.1080/23744731.2016.1222212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trivedi S., Gkantonas S., Mesquita L.C., Iavarone S., Oliveira P.M.D., Mastorakos E. Estimates of the stochasticity of droplet dispersion by a cough. Physics of Fluids. 2021;33(11) doi: 10.1063/5.0070528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- VanSciver M., Miller S., Hertzberg J. Particle image velocimetry of human cough. Aerosol Science and Technology. 2011;45(3):415–422. [Google Scholar]
- Verma S., Dhanak M., Frankenfield J. Visualizing the effectiveness of face masks in obstructing respiratory jets. Physics of Fluids. 2020;32(6) doi: 10.1063/5.0016018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Alipour M., Soligo G., Roccon A., De Paoli M., Picano F., Soldati A. Short-range exposure to airborne virus transmission and current guidelines. Proceedings of the National Academy of Sciences. 2021;118(37) doi: 10.1073/pnas.2105279118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- WHO . World Health Organization; 2021. COVID-19 Infection Prevention and Control. Living guideline. Mask use in community settings. [Google Scholar]
- Xie X., Li Y., Sun H., Liu L. Exhaled droplets due to talking and coughing. Journal of The Royal Society Interface. 2009;6(suppl_6):S703–S714. doi: 10.1098/rsif.2009.0388.focus. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J., Wang C., Fu S.C., Chao C.Y. The effect of head orientation and personalized ventilation on bioaerosol deposition from a cough. Indoor Air. 2022;32 doi: 10.1111/ina.12973. [DOI] [PubMed] [Google Scholar]
- Yang L., Li X., Yan Y., Tu J. Effects of cough-jet on airflow and contaminant transport in an airliner cabin section. The Journal of Computational Multiphase Flows. 2018;10(2):72–82. [Google Scholar]
- Zhang Z., Han T., Yoo K.H., Capecelatro J., Boehman A.L., Maki K. Disease transmission through expiratory aerosols on an urban bus. Physics of Fluids. 2021;33(1) doi: 10.1063/5.0037452. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.