Evaluating the impact of X-ray damage on conformational heterogeneity in room-temperature (277 K) and cryo-cooled protein crystals

Analysis of high-resolution data indicated that X-ray damage has little impact on conformational ensemble information from protein crystals at room temperature (277 K). In contrast, X-ray damage can alter conformational distributions obtained from cryo-cooled crystals under common experimental conditions, complicating structural interpretations in some instances. The results presented provide a strong motivation for the expanded use of room-temperature X-ray crystallography.

Abstract

Cryo-cooling has been nearly universally adopted to mitigate X-ray damage and facilitate crystal handling in protein X-ray crystallography. However, cryo X-ray crystallographic data provide an incomplete window into the ensemble of conformations that is at the heart of protein function and energetics. Room-temperature (RT) X-ray crystallography provides accurate ensemble information, and recent developments allow conformational heterogeneity (the experimental manifestation of ensembles) to be extracted from single-crystal data. Nevertheless, high sensitivity to X-ray damage at RT raises concerns about data reliability. To systematically address this critical issue, increasingly X-ray-damaged high-resolution data sets (1.02–1.52 Å resolution) were obtained from single proteinase K, thaumatin and lysozyme crystals at RT (277 K). In each case a modest increase in conformational heterogeneity with X-ray damage was observed. Merging data with different extents of damage (as is typically carried out) had negligible effects on conformational heterogeneity until the overall diffraction intensity decayed to ∼70% of its initial value. These effects were compared with X-ray damage effects in cryo-cooled crystals by carrying out an analogous analysis of increasingly damaged proteinase K cryo data sets (0.9–1.16 Å resolution). X-ray damage-associated heterogeneity changes were found that were not observed at RT. This property renders it difficult to distinguish real from artefactual conformations and to determine the conformational response to changes in temperature. The ability to acquire reliable heterogeneity information from single crystals at RT, together with recent advances in RT data collection at accessible synchrotron beamlines, provides a strong motivation for the widespread adoption of RT X-ray crystallography to obtain conformational ensemble information.

1. Introduction

Structural information from X-ray crystallography has been the cornerstone for interpreting functional studies of proteins and for understanding biological processes and their regulation. It is now routine to visualize the fold, interactions and functional sites of proteins via X-ray crystallography. In addition, the tens of thousands of protein crystal structures in the Protein Data Bank (PDB; Berman et al., 2000 ▸) have been leveraged, together with simplified energetic or empirical rules, to predict protein structures from sequence and to design new proteins (Huang et al., 2016 ▸; Kuhlman & Bradley, 2019 ▸; Senior et al., 2020 ▸).

Function and energetics entail motions and multiple conformational states, such as the states formed through a reaction cycle or in response to regulatory ligands and modifications. However, the advances in predicting structure have not been paralleled by equal progress in connecting structure to function and energetics, and traditional X-ray crystallo­graphy provides limited information about these underlying states (Ringe & Petsko, 1985 ▸; Petsko, 1996 ▸; Furnham et al., 2006 ▸). Formally, the free energy associated with a process such as binding or catalysis is defined by the ensemble of conformational states sampled by the protein and the probability-weighted sum of binding or catalysis over these states. In other words, molecular states and biological function are dictated by conformational landscapes, with each landscape defining a conformational ensemble (Austin et al., 1975 ▸; Boehr et al., 2009 ▸; Frauenfelder et al., 1991 ▸; Ma et al., 2000 ▸; Nussinov et al., 2019 ▸). Thus, ensemble information is required to relate structure to function.

Information about the conformational heterogeneity, the experimental manifestation of ensembles, has sometimes been extracted from crystallographic B factors, but B factors alone are incomplete reporters of conformational heterogeneity (Kuzmanic et al., 2014 ▸; Sun et al., 2019 ▸). Further, the typical practice of cooling crystals to cryogenic temperatures can alter conformational distributions, including at functional sites (Fraser et al., 2009 ▸; Halle, 2004 ▸; Juers & Matthews, 2001 ▸; Keedy et al., 2014 ▸; Sandalova et al., 1999 ▸). In contrast, accurate ensemble information can be obtained at room temperature (RT) from a single protein crystal using novel modeling methods and eliminates potential artifacts from cryo-cooling.

Further enhancing the ability to extract ensemble information from crystallographic data, recent computational methods provide more accurate representations of conformational heterogeneity from X-ray data. The program Ringer systematically samples side-chain dihedral angles and evaluates weak electron-density features to uncover low-population alternative side-chain rotameric states (Lang et al., 2010 ▸), and the program qFit, combined with manual modeling, delivers multi-conformer models with explicit alternative conformations and orientations (van den Bedem et al., 2009 ▸; Keedy, Fraser et al., 2015 ▸). Crystallographic order parameters S ² derived from these models provide a single value to quantify the conformational heterogeneity in multi-conformer models, with these values including contributions from harmonic motions within energy wells encoded by B factors and anharmonic motions across energy wells encoded by alternative states with distinct coordinates. Importantly, comparison of S ² values provides a more direct comparison of conformational heterogeneity and eliminates complicating data manipulation such as B-factor normalization. S ² values from RT X-ray crystallography have been shown to correlate well with the corresponding values from solution NMR (Fenwick et al., 2014 ▸). Thus, RT X-ray crystallography and the accompanying suite of analysis tools allow us to detect and quantify changes in conformational heterogeneity at the atomic level between different protein states (Biel et al., 2017 ▸; Keedy, Kenner et al., 2015 ▸; Yabukarski et al., 2020 ▸).

However, collecting high-quality and complete X-ray diffraction data sets from protein crystals at and near RT is challenging because protein crystals are more sensitive to X-ray damage at RT, so that the overall diffraction intensity decays faster compared with data collection from cryo-cooled crystals (Garman & Weik, 2017 ▸; Garman & Owen, 2006 ▸; Nave & Garman, 2005 ▸; Roedig et al., 2016 ▸; Southworth-Davies et al., 2007 ▸; Warkentin et al., 2011 ▸; Warkentin & Thorne, 2010 ▸). Cryo-crystallography became overwhelmingly popular after the realization that cryo-cooling increased the amount and the quality of diffraction data obtainable from a single crystal (Hope, 1988 ▸, 1990 ▸). Nevertheless, the need for accurate ensemble information and the limitations of cryo-crystallo­graphy in delivering such information reignited interest in RT X-ray crystallography (Dunlop et al., 2005 ▸; Fraser et al., 2011 ▸; Keedy et al., 2014 ▸).

A definitive return to RT X-ray crystallography requires methods to routinely collect high-quality data at widely accessible synchrotron facilities and to minimize X-ray damage to protein crystals that distorts conformational states and heterogeneity (Doukov et al., 2020 ▸; Owen et al., 2012 ▸; Rajendran et al., 2011 ▸; Roedig et al., 2016 ▸; Warkentin et al., 2013 ▸; see Section S1). In previous work, we described a widely applicable approach for collecting high-quality RT X-ray diffraction data sets from single crystals (Doukov et al., 2020 ▸), which now allows us to address the second major challenge: the impact of X-ray damage on the determination of conformational heterogeneity.

X-ray damage inevitably occurs during any synchrotron data collection, but to date only one study that we are aware of has directly addressed the effects of X-ray damage on conformational heterogeneity in protein crystals at RT, concluding that the overall heterogeneity is not damage-dominated (Russi et al., 2017 ▸). Following on from these encouraging findings, there is a clear need for in-depth, quantitative and systematic analysis of the effects of X-ray damage on conformational heterogeneity to determine the capabilities of RT crystallography to deliver atomic-level conformational ensemble information and to learn, if possible, how to minimize or eliminate damage-based artifacts. In addition, studies of X-ray damage under cryo conditions have focused on chemical damage (Burmeister, 2000 ▸; Fioravanti et al., 2007 ▸; Garman & Owen, 2006 ▸; Weik et al., 2000 ▸), but there is little information about, and thus a need for analysis of, damage effects on apparent conformational heterogeneity.

To determine the reliability of conformational heterogeneity information from X-ray diffraction at room temperature, we obtained increasingly damaged data sets from single crystals of thaumatin, proteinase K and lysozyme. Our high-resolution data [RT (277 K) data sets at 1.02–1.52 Å resolution] facilitated the detection and quantification of heterogeneity and the ability to isolate X-ray damage effects. We first determined whether and the extent to which X-ray damage impacts conformational heterogeneity using a data-collection strategy specifically designed to evaluate the effects of X-ray damage. Conformational heterogeneity analyses of individual data sets collected with the same crystal orientation and containing the same amount of data indicated a modest increase in conformational disorder with X-ray damage without the appearance of new side-chain rotameric states. We then evaluated the practical effects of X-ray damage on measurements of conformational heterogeneity in data sets mimicking typical data sets collected for structural studies. In typical data sets, increasingly damaged data are merged. Comparison of such data sets in which we merged increasing amounts of increasingly damaged data indicated an increase in the observed conformational heterogeneity only when the overall diffraction intensity had decayed to about 70% of its initial value. To facilitate future studies, we provide an analysis pipeline to ensure minimal effects from X-ray damage and a simple and generally applicable procedure to extrapolate to zero X-ray dose and obtain damage-free heterogeneity information effects.

Complementary analysis of atomic resolution cryo-temperature X-ray data sets of proteinase K (0.9–1.16 Å resolution) revealed X-ray damage-associated conformational heterogeneity changes that were not observed at room temperature. These observations caution that structures obtained from cryo-cooled crystals without careful evaluation of damage effects may not always represent states from the conformational landscape. Overall, our results, combined with prior findings (Gotthard et al., 2019 ▸; Russi et al., 2017 ▸), suggest that RT X-ray data from single crystals can be used to obtain the accurate conformational heterogeneity information that is needed to connect structure to energetics and to provide a deeper understanding of protein function.

2. Materials and methods

2.1. Protein crystallization and X-ray diffraction data collection

Tritirachium album proteinase K (catalog No. P2308), Thaumatococcus daniellii thaumatin (catalog No. T7638) and hen egg-white lysozyme (catalog No. L4919) were purchased from Sigma. Proteins were crystallized at room temperature using standard literature conditions as described previously [using hanging-drop (proteinase K and lysozyme) and sitting-drop (thaumatin) setups (Doukov et al., 2020 ▸)]. Briefly, lysozyme dissolved in 0.1 M sodium acetate pH 4.6 was crystallized in 0.6 M sodium chloride, thaumatin dissolved in water was crystallized in 24% potassium sodium tartrate, 15%(v/v) ethylene glycol, 0.1 M bis-Tris propane pH 6 and proteinase K dissolved in 0.05 M Tris–HCl pH 7.5 was crystallized in either 1 M ammonium sulfate or 0.5 M sodium nitrate.

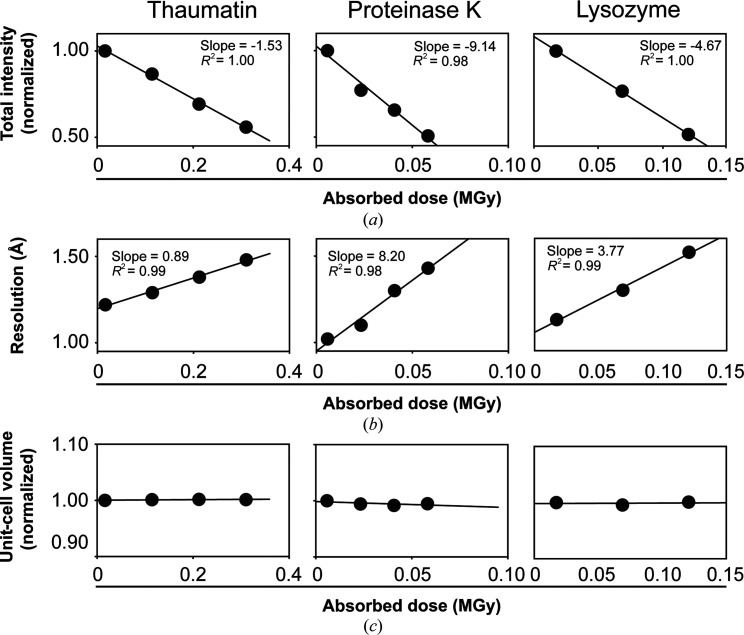
X-ray diffraction data from single crystals were collected at 277 K (referred to as ‘room temperature’ here) using a recently described approach (Doukov et al., 2020 ▸). Briefly, prior to data collection, crystals of size 0.3 × 0.3 × 0.3 mm or larger were transferred from the crystallization solution to Paratone N oil (Hampton Research, Aliso Viejo, California, USA), where excess crystallization solution was stripped, and the crystals were then directly mounted on the goniometer for 277 K data collection. Data were collected at 277 K for the following reasons. Firstly, a large body of work now provides strong evidence that at temperatures above the so-called glass transition (generally in the temperature range 180–220 K) all protein motions are enabled (Ringe & Petsko, 2003 ▸; Tilton et al., 1992 ▸; Keedy, Kenner et al., 2015 ▸). Secondly, there is also evidence that protein crystals become increasingly more sensitive to X-ray damage with increasing data-collection temperature and thus the higher the temperature, the lower the amount of data that can be collected (Warkentin & Thorne, 2010 ▸). The choice of 277 K as the data-collection temperature was a compromise between obtaining data at the physiologically relevant ‘room’ temperature and maximizing the amount of diffraction data (i.e. crystals are expected to be a little less sensitive to X-ray damage at 277 K compared with 298 K). For cryogenic (100 K) data collection a similar procedure was used except that the crystals were cooled in liquid nitrogen for data collection (proteinase K) and then mounted on the gonio­meter; crystals were transferred from their mother liquor to Paratone N oil without cryoprotection additives. The data-collection temperature was controlled using the beamline N₂ cryocooler/heater. Increasingly X-ray-damaged single-crystal diffraction data were collected on beamline BL9-2 at SSRL using a wavelength of 0.88557 Å (14 keV). See Supplementary Tables S1–S4 and S11 for diffraction data-collection statistics. For all crystals diffraction data were collected using the rotation method, collecting consecutive 360° data sets. Only the first 120° of each 360° of rotation were used for subsequent analysis, except for the RT (277 K) thaumatin data sets and 100 K proteinase K data sets, for which the first 120° of every other 360° of rotation were used. For RT and cryogenic temperature data collection, 0.1 s exposure times with 1° oscillation per image and 1.5 s exposure times with 0.5° oscillation per image were used, respectively. Collecting increasingly X-ray-damaged data sets from single crystals allowed potential complications associated with merging partial diffraction data sets from multiple crystals to be circumvented. Because the diffraction resolution inevitably decreases with increasing X-ray damage and high-resolution data are required to reliably detect potential X-ray-induced conformational heterogeneity changes (in particular the appearance or disappearance of alternative rotameric states; Fenwick et al., 2014 ▸; Lang et al., 2010 ▸), we struck a compromise between the extent of damage and the overall resolution of the most damaged data set in each series (Fig. 1 ▸); we collected diffraction data until the total diffraction intensity decreased to about half its initial value (I/I ₁ ≃ 0.5), which represents a significant extent of damage, yet the most damaged data sets were still of high resolution (∼1.4–1.5 Å; resolution was cut at CC_1/2 ≥ 0.30). Any potential benefit of collecting more X-ray-damaged data sets would have been offset by the increasingly lower resolution of the data sets, which in turn would have reduced the accuracy of rotameric state analysis and multi-conformer modeling (for example, making minor side-chain conformations undetectable due to the overall loss of electron-density details with decreasing resolution) and would have made 1 − S ² analyses less reliable. Absorbed X-ray doses were calculated using RADDOSE-3D (Zeldin, Brockhauser et al., 2013 ▸; Zeldin, Gerstel et al., 2013 ▸) and average diffraction-weighted doses (DWDs) are reported. The DWDs for the increasingly damaged RT data sets (Supplementary Tables S1–S4) were comparable to the X-ray doses used in previous studies of the effects of X-ray damage on protein crystals at RT (Gotthard et al., 2019 ▸; Russi et al., 2017 ▸).

Figure 1.

Increasingly X-ray-damaged room-temperature data sets from single crystals of thaumatin, proteinase K and lysozyme. Each point represents a complete data set of 120 images that was collected with the same crystal orientation (referred to here as a sequential X-ray-damaged data set; see Section 2). (a) Normalized data-set intensity, (b) data-set resolution and (c) unit-cell volume as a function of the absorbed X-ray dose [average diffraction-weighted dose (DWD); see Section 2].

2.1.1. Absence of significant dehydration effects

In addition to the increased X-ray damage sensitivity, dehydration, which is not a significant issue under cryo conditions, can occur during RT data collection and alter conformational heterogeneity (Atakisi et al., 2018 ▸). As dehydration often leads to large decreases in unit-cell volume (V _unit cell), we assessed dehydration during our data collection by comparing V _unit cell from the increasingly damaged data sets from each crystal for each protein. Fig. 1 ▸(c) shows that the V _unit cell of increasingly damaged data sets is within ±1% of the initial value, providing evidence against significant dehydration during data collection (see also Supplementary Tables S1–S4 and Doukov et al., 2020 ▸). Our data-collection approach entails coating the crystals with oil, which limits possible dehydration effects and has advantages over other dehydration-protection approaches (Doukov et al., 2020 ▸; Hope, 1988 ▸).

2.2. Crystallographic data processing and model building

Data processing was carried out with the in-house script http://smb.slac.stanford.edu/facilities/software/xds/#autoxds_script. Briefly, data reduction was performed using the XDS package (Kabsch, 2010 ▸), scaling and merging were performed using AIMLESS (Winn et al., 2011 ▸; Evans & Murshudov, 2013 ▸) and structure-factor amplitudes were obtained using TRUNCATE (Winn et al., 2011 ▸; French & Wilson, 1978 ▸). The overall diffraction intensity for a given data set was obtained as reported by XSCALE from the XDS package (Kabsch, 2010 ▸) by integrating the intensity over a consistent oscillation range (120°) and the same crystal orientation. Initial phases were obtained via molecular replacement with Phaser (McCoy et al., 2007 ▸) using PDB entries 1rqw, 1ic6 and 193l as search models for thaumatin, proteinase K and lysozyme, respectively. Model building was carried out with ARP/wARP (Langer et al., 2008 ▸) and manually in Coot (Emsley & Cowtan, 2004 ▸). ARP/wARP was used to rebuild the initial models in the least X-ray-damaged data sets using electron density from the molecular-replacement solution. This procedure was performed to further minimize any bias from the molecular replacement. The commercial thaumatin used in this work (Sigma, catalog No. T7638) is a mixture of thaumatin I and thaumatin II, and the final refined models contained the residues that were the best fitted to the electron density. The thaumatin I and thaumatin II sequences differ at four positions, 68, 85, 89 and 98 (precursor numbering), with the residues in thaumatin I/thaumatin II being Asn/Lys, Ser/Arg, Lys/Arg and Arg/Gln, respectively. The final refined models contain the residues corresponding to thaumatin II, except for position 68, which corresponds to thaumatin I, as these side chains best fit the electron density. The residue at position 207 in the final refined proteinase K models was an aspartate instead of a serine (UniProt code P06373) as the electron density unambiguously supported the modeling of an aspartate, consistent with other high-resolution proteinase K structures from the PDB.

Traditional, single-conformation models, in which only major alternative side-chain and backbone conformations were modeled, were refined manually after visual inspection with Coot using phenix.refine (Afonine et al., 2012 ▸; Liebschner et al., 2019 ▸). Torsion-angle simulated annealing (as implemented in phenix.refine) was used during the initial stages of refinement. Riding H atoms were added in the late stages of refinement and their scattering contribution was accounted for in the refinement. Ligand restraints were generated using eLBOW from phenix.refine. Model quality was assessed using MolProbity (Chen et al., 2010 ▸) as implemented in phenix.refine and via the PDB Validation server (https://validate-rcsb-2.wwpdb.org/). For each protein, a model was built and refined using the least damaged data set (data set 1). The same model was then refined independently against increasingly damaged data sets. Careful visual inspection of models and maps was used to adjust for any damage-related changes and edited models were again refined using phenix.refine. This procedure was used to reduce modeling inconsistencies that could originate if a new model was built and refined independently for each increasingly damaged data set. See Supplementary Tables S1–S3 and S11 for refinement statistics.

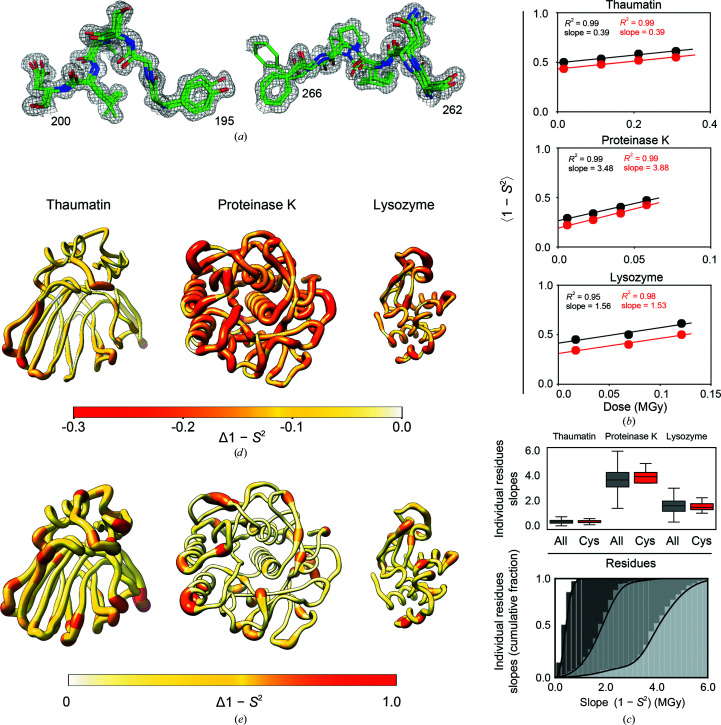
Multi-conformer models were obtained from the 277 K diffraction data sets using previously described methods (van den Bedem et al., 2009 ▸; Fenwick et al., 2014 ▸; Keedy, Fraser et al., 2015 ▸; Keedy, Kenner et al., 2015 ▸; Keedy et al., 2018 ▸). Briefly, the program qFit was used to obtain multi-conformer models (van den Bedem et al., 2009 ▸; Keedy, Fraser et al., 2015 ▸) using as input the traditional single-conformation models obtained above after removal of the riding H atoms. Subsequent to the automated multi-conformer model building, ill-defined water molecules were deleted and alternative protein side-chain and main-chain conformations and orientations were edited manually after visual inspection in Coot based on the fit to the electron density (Emsley et al., 2010 ▸). Both alternative side-chain rotameric states as well as alternative orientations within the same rotameric state were modeled (see Fig. 2 ▸ a for example regions from a typical refined multi-conformer model). Models were subsequently refined with phenix.refine, refining atomic isotropic B factors and occupancies (Afonine et al., 2012 ▸; Liebschner et al., 2019 ▸). Riding H atoms were added in the late stages of refinement and their scattering contribution was accounted for in the refinement. Final multi-conformer model quality was checked by MolProbity (Chen et al., 2010 ▸) and via the PDB Validation server (https://validate-rcsb-2.wwpdb.org/).

Figure 2.

Evaluating the effects of X-ray damage on conformational heterogeneity at room temperature using multi-conformer models and disorder parameters (1 − S ²). (a) Illustration of multi-conformer models; two regions of the proteinase K 277 K multi-conformer model from the least damaged data set (PDB entry 7lpu) are shown. The multi-conformer model is shown as green sticks while the electron density is shown as a gray mesh (contour level of 1σ). (b) Average 1 − S ² for all residues (black circles) and for disulfide bond-forming cysteine residues (red circles) as a function of the absorbed X-ray dose for each protein. (c) Top: boxplot showing the distribution of slopes obtained from a plot of the 1 − S ² value as a function of the absorbed X-ray dose calculated for each residue in each protein. The boxes show the quartiles of the distributions, while the whiskers capture the entire distributions. Bottom: the data for all residues from the top plot now represented as a cumulative fraction. Dark to light gray: thaumatin, lysozyme, proteinase K. (d) Δ(1 − S ²) values between the least and most damaged data sets plotted on the structure of each protein. The diameter of the worm representation and the color both correlate with the magnitude of Δ(1 − S ²). (e) X-ray damage-free (extrapolated zero-dose) 1 − S ² values plotted on the structure of each protein as in (d).

Multi-conformer models from increasingly X-ray-damaged data sets were obtained as follows. For each protein, an initial multi-conformer model was built and refined using the least damaged, highest resolution data set (data set 1). The refined multi-conformer model was then re-refined independently against increasingly damaged data sets. This procedure was used to reduce modeling inconsistencies that could originate when a new multi-conformer model is built and refined for each increasingly damaged data set. In particular, the procedure was essential in eliminating subjectivity in modeling low-population states as the increasingly damaged data sets were of decreasing resolution, which results in electron-density features associated with low-population states becoming visible at different electron-density standard deviation (σ) levels. Using the refined multi-conformer model from the least damaged data set for refinement against increasingly damaged data sets in which the occupancies of alternative states are refined allows the diffraction data and not subjectivity to decide on which alternative states disappear (the occupancy refines to zero, in which case, after inspection, the alternative state is removed and the model is re-refined), which rotameric states persist (nonzero occupancy) and how the distributions of the persisting states change (changes in the occupancies of states). Careful visual inspection of the resulting models and electron-density maps allowed the identification and modeling of any new rotameric states that appeared with increasing damage. Importantly, no evidence for the appearance of new rotameric states with damage was found for the RT data sets (and the lack of X-ray damage-associated changes was supported by independent qFit runs). See Supplementary Tables S4–S10 for the refinement statistics of multi-conformer models. The same set of reflections was used for R _free calculation in the refinement of all models within an increasing damaged data-set series.

All structural models refined in this work have been deposited in the PDB with the following accession codes: 7lfg, 7ljv, 7ljw, 7ljz, 7lk5, 7lk6, 7lnb, 7lnc, 7lnd (thaumatin, 277 K), 7ln7, 7lpt, 7lpu, 7lpv, 7lq8, 7lq9, 7lqa, 7lqb, 7lqc (proteinase K, 277 K), 7ltd, 7lti, 7ltv, 7lu0, 7lu1, 7lqc, 7lu3 (proteinase K, 100 K), 7llp, 7ln8, 7ln9, 7loq, 7lor, 7lp6, 7lpl and 7lpm (lysozyme, 277 K). See Supplementary Tables S1–S7 and S11 for details.

2.3. Crystallographic disorder parameter (1 − S ²) calculation

Crystallographic and solution NMR order parameters (S ²) have been shown to correlate well and range between 1 for a completely rigid residue and 0 for a completely unrestrained residue (Fenwick et al., 2014 ▸). Here, we used the opposite of order parameters and calculated disorder parameters (1 − S ²). High-resolution data (generally better than ∼1.7 Å) are required for crystallographic 1 − S ² analysis, and the high resolution of the data sets obtained in this work (1.02–1.54 Å, Supplementary Tables S1–S4) makes the 1 − S ² analyses reliable. Crystallographic disorder parameters 1 − S ² were obtained from the 277 K multi-conformer models as described previously (Fenwick et al., 2014 ▸; Russi et al., 2017 ▸). These disorder parameters include both harmonic and anharmonic contributions, as captured by the crystallographic atomic displacement parameters (B factors) and by the occupancies of alternative rotameric states. The analysis was applied to the bond most closely associated with the first side-chain dihedral angle (χ₁), using C^β—H for all amino acids other than Gly and C^α—H for Gly. For each residue, the extrapolation to zero-dose 1 − S ² was performed by fitting a linear equation to the plot of 1 − S ² as a function of absorbed X-ray dose and extracting the y intercept. All fits were of good quality, with an average R ² and standard deviation of 0.91 ± 0.09, 0.96 ± 0.06 and 0.93 ± 0.05 for thaumatin, proteinase K and lysozyme, respectively. Raw 1 − S ² values have been deposited in the Zenodo database (https://doi.org/10.5281/zenodo.6408812).

2.4. F _o − F _o difference electron-density maps

Difference electron-density maps were obtained via standard procedures using the Isomorphous difference map script from the Phenix suite (Liebschner et al., 2019 ▸). To obtain the fairest comparisons, the resolution of the two data sets being compared were matched by adjusting the resolution of the less X-ray-damaged data set to match the resolution of the more X-ray-damaged data set. F _o − F _o maps are displayed at a contour level of 3σ unless stated otherwise.

2.5. Ringer analysis

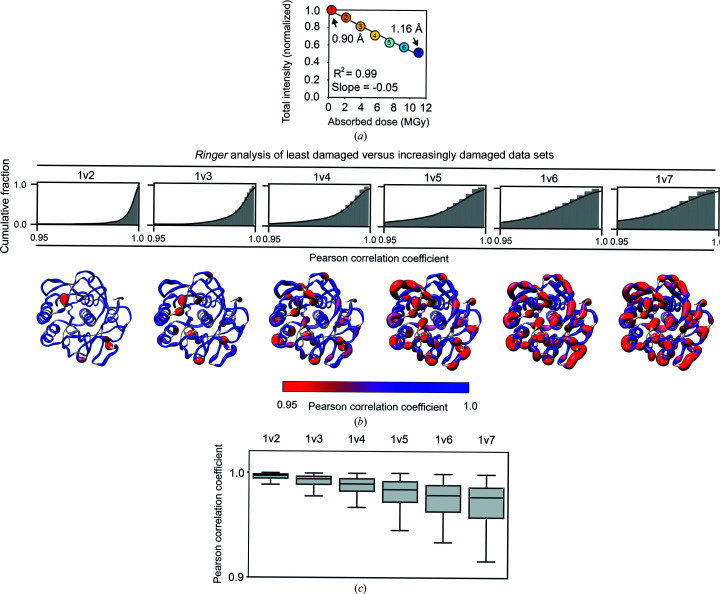
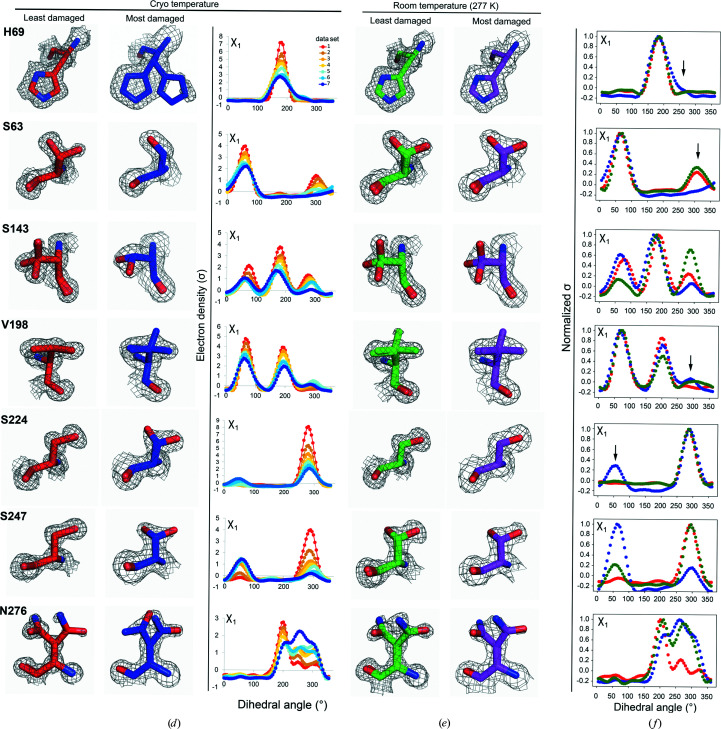
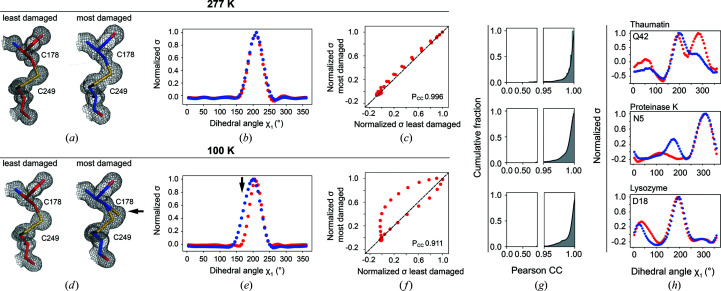
Ringer profiles were obtained for each residue in each protein as follows. The final structural models and diffraction data were used to calculate composite omit maps to reduce potential model bias (Liebschner et al., 2019 ▸). To evaluate the effect of map resolution differences on Pearson correlation coefficients (P _CC), P _CC values were calculated for combinations of Ringer profiles obtained from the proteinase K 100 K data set 1 refined at 0.9 Å (maximum resolution) or 1.16 Å (the resolution of the most damaged data set 7) and composite omit maps calculated from either model at 0.9 Å (maximum resolution) or 1.16 Å (the resolution of the most damaged data set 7). Supplementary Fig. S5 shows that an artefactual decreased P _CC could emerge from differences in the resolution of the electron-density maps, but that when the resolution of the composite omit maps is adjusted ≥99% of the P _CC values are ≥0.99 (Supplementary Fig. S5, far right). Thus, for comparison of Ringer profiles from the least and most damaged data sets, the composite omit maps for both the least and most damaged data sets were calculated at the resolution of the most damaged data set. The resulting map and refined models were then submitted to Ringer as implemented in the Phenix suite using a 5° sampling angle (Lang et al., 2010 ▸; Liebschner et al., 2019 ▸). Because the absolute amount of electron density (σ) can vary between data sets irrespective of changes in rotameric distributions, all Ringer profiles were normalized prior to comparison. The normalized Ringer profiles were then used to calculate the Pearson correlation coefficients (P _CC; see below). Further, the Ringer analysis was predominantly focused on χ₁ angles because (i) most protein side chains have χ₁ and (ii) because most side chains with χ₂ angles are surface-exposed and the electron density required to calculate χ₂ angles is weaker than the average, making accurate quantitative comparisons difficult. Because all analyzed proteinase K 100 K data sets are of atomic resolution (0.9–1.16 Å) and because both the appearance and disappearance of rotameric states were observed (Fig. 5d ▸), the systematic decrease of agreement between Ringer profiles from increasingly damaged data sets observed in Fig. 5(b) and 5(c ▸) is unlikely to be due to poor data resolution that would preclude the detection of rotameric states.

Figure 5.

X-ray damage to cryo-cooled crystals can alter protein side-chain rotameric distributions. (a) Plot of the normalized total intensity versus absorbed dose for sequential X-ray-damaged data sets collected at 100 K from the same orientation of a single proteinase K crystal (Supplementary Table S11). The resolutions of the least and most damaged cryo data sets are indicated and the increasingly X-ray-damaged data sets are labeled with numbers from 1 (least X-ray damaged) to 7 (most X-ray damaged). (b) Cumulative fraction and (c) boxplots of Pearson correlation coefficients between the Ringer profiles for all residues in the least and increasingly damaged sequential cryo data sets. In (b) the lower row shows P _CC values plotted on the proteinase K structure. The diameter of the worm representation is inversely correlated with the magnitude of P _CC. (Supplementary Figs. S13–S18 show the Ringer plots for all residues with P _CC ≤ 0.95.) The numbers above the cumulative plots indicate the data sets compared; for example ‘1v2’ indicates a comparison of data set 1 versus data set 2. (d–f) A subset of residues with a P _CC of ≤0.95. (d) Left and middle columns: the least (data set 1) and most (data set 7) damaged cryo data sets; residues are shown as sticks. Electron density is shown as a gray mesh and is contoured at 1σ for all residues except His69, for which the contour is at 0.4σ. Right: raw Ringer profiles for the residues in (d) from the sequential X-ray-damaged data sets; the colors correspond to those in (a). (e) The same residues as in (d) but from the least (data set 1) and most (data set 4) damaged RT data sets. Electron density is shown as a gray mesh as in (d). (f) Normalized Ringer profiles for the residues in (d) and (e): the least and most damaged 100 K data sets are shown in red and blue, respectively, with the least damaged RT data set shown in green. Arrows show the appearance or disappearance of peaks. The RT Ringer profiles were obtained from electron-density maps with resolution matched to the resolution of the 100 K data sets (i.e. 1.16 Å).

2.6. Calculating Pearson correlation coefficients (P _CC) and mean-square errors (MSE)

The Pearson correlation coefficient (P _CC, also known as Pearson’s r) between normalized Ringer profiles was calculated using the scipy.stats.pearsonr function of the SciPy package in Python 3 (Virtanen et al., 2020 ▸). Mean-square errors were calculated between normalized Ringer profiles using the sklearn.metrics.mean_squared_error function of the scikit-learn package in Python 3, with the non-default parameter squared=False (Pedregosa et al., 2011 ▸). Raw P _CC and MSE values have been deposited in the Zenodo database (https://doi.org/10.5281/zenodo.6408812).

2.7. Hydrogen-bond comparisons

H atoms were added using the Reduce program (Word et al., 1999 ▸). For each comparison, hydrogen bonds were identified in the least X-ray-damaged structure using the MDanalysis Hydrogen Bond Analysis module (Gowers et al., 2016 ▸; Michaud-Agrawal et al., 2011 ▸) with a 3.5 Å heavy-atom distance cutoff and a 120° bond-angle cutoff. Only hydrogen bonds with a nitrogen or oxygen donor/acceptor and those made between protein atoms were included in the analysis; any ‘hydrogen bonds’ identified between backbone atoms of neighboring residues were also excluded. Hydrogen bonds involving atoms with multiple conformations modeled were omitted (Fig. 6 and Supplementary Fig. S23 and S24) and we confirmed our results by including hydrogen bonds involving backbone N or O atoms that have multiple conformations and averaging all possible lengths (Supplementary Fig. S24). Despite the overall high resolution of all data sets, not all hydrogen-bonding groups are similarly well defined in the electron density and more hydrogen-bond length variation is expected for groups with less well defined electron density; these differences are reflected in the relative B factor of a hydrogen-bonding group, and relative B factors were calculated and used as a proxy for positional accuracy. A relative B factor for the hydrogen bond is calculated using the B factors of the least damaged structure,

where B _i,donor is the B factor for the donor heavy atom for hydrogen bond i, B _i,acceptor is the B factor for the acceptor atom for the same hydrogen bond and 〈B〉 is the average B factor of all atoms in the structure.

2.8. Figure generation

PyMOL (Schrödinger) and UCSF Chimera (Pettersen et al., 2004 ▸) were used for figure generation.

3. Results

3.1. Obtaining increasingly X-ray-damaged data from single crystals at room temperature

X-ray damage to protein crystals occurs at all temperatures, but protein crystals are exquisitely sensitive to X-ray damage at RT (the overall diffraction decays more for a given X-ray dose than under cryo conditions; see Section S2). We employed a recent data-collection approach that optimized the RT X-ray diffraction experiment and allowed us to obtain increasingly X-ray-damaged diffraction data from single crystals of thaumatin, proteinase K and lysozyme (Doukov et al., 2020 ▸). The increasingly X-ray-damaged data can be grouped into data sets originating from the same crystal orientation and containing the same amount of diffraction data to ensure that the primary experimental variable is only the extent of X-ray damage (referred to here as ‘sequential’ X-ray-damaged data sets; Supplementary Fig. S1a ). For each crystal, a compromise between the extent of X-ray damage and the resolution of the most X-ray-damaged sequential data set was struck; diffraction data were collected until the total diffraction intensity of the most X-ray-damaged sequential data set decreased to about half of the total intensity of the first X-ray-damaged sequential data set, indicative of significant X-ray damage, while ensuring that the most damaged data sets were still of high resolution (≤1.5 Å; see Section 2; Figs. 1 ▸ a and 1 ▸ b). The collected diffraction data allowed us to obtain four complete, sequential X-ray-damaged data sets from the thaumatin and proteinase K crystals and three from the lysozyme crystal (Fig. 1 ▸; see Supplementary Fig. S1a for diffraction statistics; Section 2). All diffraction data sets were of a sufficiently high resolution to allow accurate and quantitative modeling of conformational heterogeneity using the Ringer and qFit multi-conformer approaches and to quantify conformational heterogeneity via crystallographic order parameters (S ²).

3.2. The effect of X-ray damage on conformational heterogeneity at room temperature

3.2.1. Assessing the conformational heterogeneity within two distinct crystals of the same protein

We carried out the analyses in the following sections on data obtained from a single crystal for each protein. To first assess potential variation from experimental and/or modeling factors, the extent of similarity between the conformational heterogeneity was evaluated, as captured by S ², for two different lysozyme crystals. For a more intuitive representation, S ² parameters were transformed into the complementary disorder parameters 1 − S ² such that larger values indicate greater disorder (Russi et al., 2017 ▸). To eliminate potential 1 − S ² differences due to differences in diffraction resolution, quality or X-ray dose effects, we identified a second crystal that was of similar size, exhibited similar diffraction statistics and absorbed a similar X-ray dose as the lysozyme crystal and data set used above (crystal 1 versus crystal 2; see Supplementary Table S4 for diffraction statistics). The refined multi-conformer models from these two crystals yielded highly similar 1 − S ² values which correlated with an R ² of 0.97 and a slope of 1.01 and an average per-residue Δ(1 − S ²) of 0.01 ± 0.02 (Supplementary Fig. S2). Thus, the conformational heterogeneity information obtained from two different lysozyme crystals was highly similar and these results lead to a general expectation for strong correlation between the conformational heterogeneity from different crystals of the same protein.

3.2.2. Evaluating the effect of X-ray damage on conformational heterogeneity from increasingly damaged data sets

We first assessed whether, to what extent and how X-ray damage impacts conformational heterogeneity by using the sequential X-ray-damaged data sets (Supplementary Fig. S1a ). The experimental electron density from each sequential X-ray-damaged data set for each protein was modeled as a multi-conformer model (Fig. 2 ▸ a). The conformational heterogeneity was then quantified by calculating crystallographic disorder parameters 1 − S ² from each multi-conformer model and quantitative comparisons were carried out. Firstly, the overall impact of X-ray damage on conformational heterogeneity was quantified by comparing the average 1 − S ² values, 〈1 − S ²〉, from the sequential X-ray-damaged data sets. The black symbols in Fig. 2 ▸(b) show that 〈1 − S ²〉 gradually increases with increasing dose for all three proteins. Fig. 2 ▸(b) also compares 1 − S ² values for disulfide bond-forming cysteine residues (red) and for all other residues (black) and suggests similar behavior for cysteine as for other residues. To determine whether heterogeneity increases equally for all residues or whether the effects are heterogeneous, we plotted the 1 − S ² value as a function of X-ray dose for each residue in each protein and the slopes of the corresponding plots were extracted. The gray symbols in Fig. 2 ▸(c) show that there is a wide distribution of positive slopes, indicating that while the conformational heterogeneity increased for all residues, it increased to different extents for different residues. Fig. 2 ▸(d) shows the changes in conformational heterogeneity throughout each protein by plotting the difference 1 − S ² values [Δ(1 − S ²)] for the least and most X-ray-damaged data sets on the protein structure (also see Supplementary Fig. S3). There are regions with greater and lesser X-ray damage effects throughout each protein, with some apparent clustering of regions of higher X-ray damage.

Because 1 − S ² integrates both harmonic and anharmonic heterogeneity, it is not possible to distinguish between an increase in harmonic heterogeneity, such as an increase in vibrational amplitudes, and an increase in anharmonic heterogeneity, such as the appearance, disappearance or redistribution of rotameric states, as being responsible for the observed 1 − S ² increase with X-ray damage. To determine whether changes in side-chain rotameric distributions1 were responsible for the observed increases in 1 − S ² with X-ray damage, the program Ringer was used to systematically sample the electron density around side-chain dihedral angles and identify low-occupancy alternative rotameric states at low electron-density levels (Lang et al., 2010 ▸). Ringer profiles were obtained and compared for each residue in each protein from the sequential X-ray-damaged data sets, and the similarity between profiles was quantified by calculating the Pearson correlation coefficient (P _CC) between the differentially damaged data sets. Each point in a Ringer profile represents the electron density for a specified dihedral angle (see, for example, Fig. 3 ▸ b; see also Section 2). When the least and most sequential X-ray-damaged RT data sets are compared for all residues of thaumatin, proteinase K and lysozyme, 98% of the residues had P _CC ≥ 0.95 (Fig. 3 ▸ g) and the majority of the 2% of outliers exhibited Ringer profiles with little change in their rotameric distributions (Supplementary Fig. S7). No changes in the rotameric distributions for disulfide bond-forming cysteine residues and active-site residues were found (see Supplementary Figs. S8–S10 and Sections S3 and S4).

Figure 3.

Ringer analysis to quantitatively evaluate the effects of X-ray damage on side-chain rotameric distributions. The panels depict examples from the proteinase K data sets obtained in this work. Data from the least (red, left) and most (blue, right) X-ray-damaged sequential data sets collected at (a) RT (277 K) or (d) cryo temperature. Visually, it appears that there is partial X-ray-induced breakage of the disulfide bond in (d) but not in (a). The arrow points to the appearance of a new population for Cys178 that manifests as a broadened distribution. The electron density (1σ, gray mesh) and model (sticks) of the Cys178–Cys249 disulfide bond are shown. (b, e) Normalized Ringer profiles. Plots of electron density (σ) as a function of dihedral angle χ₁ for Cys178 (electron density from the least and most damaged data sets is in red and blue, respectively). Each point in a Ringer profile represents the electron density for a specified dihedral angle (see Section 2). The arrow indicates a difference between the least and most damaged data sets corresponding to the appearance of a new state for Cys178 in the damaged cryo data set (d). (c, f) Correlation plots between electron-density values (σ) from (b) and (e), respectively, of the least (x axis) and most (y axis) damaged data sets. An increasing number of off-diagonal points indicates a decreasing similarity between Ringer plots. The Pearson correlation coefficient (P _CC) represents the agreement between the least and most damaged Ringer profiles, with P _CC = 1 for a perfect correlation (dashed line). (g) Cumulative fraction of P _CC for the dihedral angle χ₁ of each residue in thaumatin (top), proteinase K (middle) and lysozyme (bottom). Similar results were obtained using mean-square error analysis instead of Pearson correlation coefficients (Supplementary Fig. S6). (h) The most significant outliers with P _CC ≤ 0.95 for thaumatin (top), proteinase K (middle) and lysozyme (bottom). Supplementary Fig. S7 shows the Ringer profiles and correlation plots for all residues with P _CC ≤ 0.95 (ten out of 485 residues).

As we were able to collect sequential X-ray-damaged data sets from the same crystal, and as the modest increase in 1 − S ² values was not due to complicating changes in rotameric distributions1, we could obtain 1 − S ² values for each residue that are free of X-ray damage effects by extrapolating to zero dose (zero-dose 1 − S ²). The extrapolation was performed by fitting a linear equation to the plot of 1 − S ² for each residue as a function of the absorbed X-ray dose so that the y intercept represented the zero-dose value of 1 − S ² (see Section 2). Fig. 2 ▸(e) shows the distribution of zero-dose 1 − S ² values for each protein. These extrapolated data provide the highest accuracy conformational heterogeneity information.

In summary, analysis of sequential X-ray-damaged data sets from thaumatin, proteinase K and lysozyme single crystals uncovered a modest but measurable increase in 1 − S ² values with X-ray damage. These increases do not appear to be associated with the appearance, disappearance or redistribution of side-chain rotameric states, suggesting that the observed modest increase in 1 − S ² is due to an increase in local harmonic heterogeneity, and this effect can be corrected via simple extrapolation to zero X-ray dose. Most importantly, modest X-ray damage at room temperature, as introduced here, does not alter the conclusions about local conformational preferences and distributions of disulfide bonds and functional active-site groups.

3.2.3. Evaluating the effect of accumulating X-ray damage on apparent conformational heterogeneity

In the previous section the fundamental question of how X-ray damage impacts conformational heterogeneity in protein crystals at RT (277 K) using increasingly X-ray-damaged data grouped into sequential X-ray-damaged data sets was addressed (Supplementary Fig. S1a ), and it was shown how the modest X-ray damage-associated conformational heterogeneity effects could be eliminated by extrapolating 1 − S ² values to zero X-ray dose (Fig. 2 ▸ e). Nevertheless, it will not be possible, or practical, in all cases to obtain high-resolution and complete sequential X-ray-damaged RT data sets from the same crystal and to extrapolate to zero dose. In most cases, all of the collected X-ray diffraction data will likely be merged into a single data set. Thus, using conformational heterogeneity information from protein crystals at RT with confidence requires an assessment of the extent to which merging increasingly X-ray-damaged data impacts the observed heterogeneity. To emulate a typical data collection and analysis from single crystals, data sets in which an increasing amount of increasingly X-ray-damaged data were merged were analyzed (referred to here as ‘cumulative’ X-ray-damaged data sets; Supplementary Fig. S1b ). We note that while both the ‘sequential’ and the ‘cumulative’ data sets are increasingly X-ray damaged, they contain different amounts of diffraction data X-ray damaged to different extents (compare Supplementary Fig. S1a and Supplementary Fig. S1b ).

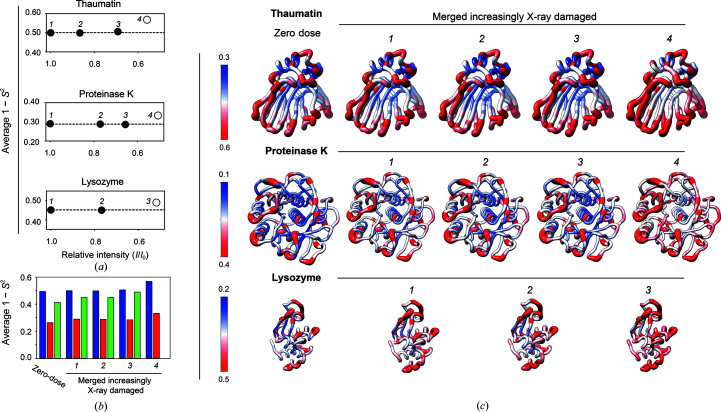
Four cumulative increasingly X-ray-damaged data sets for thaumatin and proteinase K and three such data sets for lysozyme were obtained and multi-conformer models were refined, and 1 − S ² values were calculated for each data set (see Supplementary Tables S8–S10 for diffraction and refinement statistics). The values of 〈1 − S ²〉 as a function of relative overall intensity decay (I/I ₁) for each protein are plotted in Fig. 4 ▸(a). The 〈1 − S ²〉 values are essentially unchanged for cumulative X-ray-damaged data sets for which the diffraction intensity of the merged data has decayed to about 70% of its initial value (I/I ₁ ≃ 0.7, average from all three proteins), whereas merging data decayed to more than I/I ₁ ≃ 0.7 results in an increase in the apparent 〈1 − S ²〉 values (Fig. 4 ▸ a). These results contrast with our observations in the previous section, where a modest but measurable increase in conformational disorder with X-ray dose sequential X-ray-damaged data sets was observed (Fig. 2 ▸ b). These differences must arise from the different data-collection strategies used in these two analyses (Supplementary Fig. S2). The fact that the 〈1 − S ²〉 values are essentially unchanged for data sets for which the diffraction intensity of the merged data has decayed to about 70% of its initial value (Fig. 4 ▸ a) suggests that the relatively less X-ray-damaged but higher resolution data collected early in the diffraction experiment dominate the more X-ray-damaged lower resolution data collected in the later stages with respect to extracting conformational heterogeneity.

Figure 4.

Evaluating the effects of X-ray damage on conformational heterogeneity at RT (277 K) in data sets with increasingly damaged data merged together. (a) Analysis of cumulative X-ray-damaged data sets that have accumulated an increasing amount of damage to emulate typical RT data collection from single crystals. Average 1 − S ² as a function of the relative intensity (I/I ₁) of the most damaged diffraction data merged together. I/I ₁ is the ratio of the total intensity of a diffraction data set from the beginning of data collection (I ₁) and the intensity of a diffraction data set obtained from the same crystal orientation in later stages of data collection (I) (see Section 2). Open symbols are used when (I/I ₁) is less than 0.6. (b) Bar plot of the average values for the zero-dose 1 − S ² from sequential X-ray-damaged data sets and for 1 − S ² from the cumulative X-ray-damaged (merged) thaumatin (blue), proteinase K (red) and lysozyme (green) data sets. (c) Comparison of zero-dose 1 − S ² (far left) and 1 − S ² from the least to most cumulative X-ray-damaged merged data sets (left to right) with 1 − S ² values plotted on the structure of each protein. Note that the scales differ to best visualize each protein. The diameter of the worm representation is correlated with the magnitude of the 1 − S ² values. The zero-dose 1 − S ² and the 1 − S ² from the least damaged data sets are qualitatively and quantitatively similar (see also Supplementary Fig. S11).

Fig. 4 ▸(b) compares the average values for the zero-dose 1 − S ² and 1 − S ² from the cumulative X-ray-damaged data sets, and Fig. 4 ▸(c) shows the per-residue 1 − S ² values for the same data sets plotted on the structure of each protein. This analysis indicates that the average and per-residue values for the zero-dose 1 − S ² from sequential X-ray-damaged data sets and for all 1 − S ² from cumulative X-ray-damaged data sets are of the same magnitude. The values of the zero-dose 1 − S ² and 1 − S ² from the data sets that have decayed by not more than I/I ₁ ≃ 0.7 are highly similar, and the 1 − S ² for the most X-ray-damaged data sets (data set 4 for thaumatin and proteinase K and data set 3 for lysozyme, all of which have decayed to I/I ₁ < 0.6) are the most different when compared with all others (Supplementary Fig. S11). Fig. 4 ▸(c) indicates that the 1 − S ² values increase most strikingly in the central region of the β-sandwich of thaumatin and the solvent-exposed turns, while the most notable increase in 1 − S ² values in proteinase K is predominantly within the core of the protein, in particular in the two central α-helices.

Overall, these results suggest that for data in the 1.0–1.2 Å resolution range diffraction data can be merged when the overall intensity decay is less than ∼70% of its initial value and the extracted conformational heterogeneity information can be used with confidence.

3.3. Evaluating the effects of X-ray damage on conformational heterogeneity at cryo temperature

Much prior work has demonstrated specific X-ray damage to side chains at cryo temperatures, but our current knowledge of the extent and impact of X-ray damage on conformational heterogeneity under these conditions is limited (Fioravanti et al., 2007 ▸; Leiros et al., 2001 ▸; Nave & Garman, 2005 ▸; Ravelli & McSweeney, 2000 ▸; Weik et al., 2000 ▸). Russi and coworkers observed an X-ray-induced increase in average 1 − S ² values under cryo-conditions (Russi et al., 2017 ▸), suggesting a potential impact on rotamer distributions and underscoring the need for further evaluation, which is carried out here for proteinase K.

To assess the effects of X-ray damage on side-chain rotameric distributions at cryo temperature, sequential X-ray-damaged cryo-temperature proteinase K data sets were collected until the total diffraction intensity decreased to about half of its initial value (Fig. 5 ▸ a; see Supplementary Table S11 for diffraction and refinement statistics), paralleling the procedure used in evaluating RT X-ray damage (Fig. 1 ▸). The comparisons were carried out in this way because diffraction intensity decay is often used as a practical measure of damage in X-ray data collection (Owen et al., 2006 ▸) even though the X-ray dose required to decrease the overall diffraction intensity is typically 50–100 times lower at RT than at cryo temperature (see Section S2 for a discussion of X-ray damage sensitivity). Thus, the total X-ray doses absorbed by our proteinase K crystals were substantially higher at cryo temperature.

Potential changes in conformational heterogeneity were not evaluated via multi-conformer modeling and 1 − S ² because at resolutions better than 1 Å (about half of our sequential X-ray-damaged cryo data sets) distinct density begins to appear for H atoms and this can confound analysis of conformational heterogeneity. Instead, the analysis focused on evaluating potential changes in side-chain rotameric distributions using Ringer and visual inspection. To this end, structural models were refined against each of these sequential X-ray-damaged data sets (Supplementary Table S11 gives data-collection and refinement statistics for all models). Diffraction resolution decayed as expected, although the most damaged data set was still of relatively high resolution (1.16 Å; Fig. 5 ▸ a), allowing damage effects on heterogeneity to be readily analyzed.

3.3.1. Evaluating X-ray damage effects on proteinase K side-chain rotameric distributions at cryo temperatures

Proteinase K was used to assess potential changes in side-chain rotameric distributions with X-ray damage to determine whether this could be an issue of concern and to allow the direct comparison of damage profiles for RT and cryo X-ray experiments. To carry out these analyses Ringer profiles were obtained for each side chain in each of the sequential X-ray-damaged proteinase K cryo data sets, and P _CC values between the Ringer profiles of the least damaged data set and each of the increasingly damaged data sets were calculated. The fraction of residues for which P _CC ≥ 0.95 decreased with increasing X-ray damage (Figs. 5 ▸ b and 5 ▸ c), suggesting that X-ray damage alters multiple side-chain rotameric distributions for proteinase K.

Inspection and comparison of the Ringer profiles and electron-density maps for residues with P _CC ≤ 0.95 revealed changes in rotameric state distributions for a number of residues, with the most striking changes shown in Fig. 5 ▸(d). X-ray damage had diverse effects: the disappearance of rotameric states (Ser63), the redistribution of side-chain rotameric distributions (Ser143, Val198, Ser224, Ser247 and Asn276) and the appearance of new rotameric states (His69). Inspection of the electron density for surrounding residues indicated that none of these changes appeared to be directly coupled to the breakage of disulfide bonds. The changes in rotameric distributions appeared incrementally with X-ray exposure (Fig. 5 ▸ d, right) and in some instances were already observable at an I/I ₁ of about 0.9 [for example Ser247 and Asn276 in Fig. 5 ▸ d (right); compare the Ringer profiles in red (data set 1) and tan (data set 2)]. Supplementary Fig. S21 shows that changes of rotameric distributions were observed directly in the electron density at an I/I ₁ of ∼0.7. Thus, even with seemingly high-quality diffraction data, X-ray damage can be present and can affect particular interpretations and conclusions.

3.3.2. Comparing X-ray damage effects on side-chain rotameric distributions at cryo and room temperatures

When the least and most X-ray-damaged sequential cryo data sets are compared (∼50% lower intensity in the most damaged data set), only about 80% of all residues have P _CC ≥ 0.95, whereas 98% of residues maintained P _CC ≥ 0.95 for the analogous comparison at RT [Fig. 5 ▸ b, data set 1 versus data set 7 (‘1v7’); compare with Fig. 3 ▸ g, middle]; even the cryo data set with intermediate damage (70%, data set 4) had more rotameric states affected (∼95% with P _CC ≥ 0.95). These observations suggest that X-ray damage potentially has a more profound impact on rotameric state distributions at cryo temperature than at room temperature.

Fig. 5 ▸(e) shows the electron densities of the least and most X-ray-damaged sequential RT proteinase K data sets for the residues highlighted in Fig. 5 ▸(d) as subject to X-ray damage effects under cryo conditions. The rotameric distributions for these residues do not change with X-ray damage at room temperature, as also determined from the analyses in the previous section (compare the left and middle columns in Fig. 5 ▸ d and the left and right columns in Fig. 5 ▸ e, respectively).

The above results suggest that X-ray damage present in a cryo data set could impact the structural conclusions and also the conclusions made about temperature effects on the conformational landscape. As examples, consider the residues in Fig. 5 ▸(d). Comparing the least damaged cryo data set with the RT data set [Figs. 5 ▸ d (left) and 5 ▸ e (left), respectively] identifies new rotameric states for Val198, Ser247 and Asn276 at room temperature, no changes for Ser63 and His69, and a redistribution of rotameric states for Ser143 and Ser224. However, comparing the most damaged cryo data set with the RT data set [Figs. 5 ▸ d (middle) and 5 ▸ e (left), respectively] would lead to different conclusions: His69 and Ser224 as residues for which rotameric states disappear, Ser63 as a residue for which a new rotameric state appears and Val198 and Ser247 as unchanged. In other words, comparing the RT data set with the most X-ray-damaged cryo data set would identify false-positive changes to residues Ser63 and His69 and false-negative effects at Val198 and Ser247. In addition, comparing the RT data set with either the least or most damaged cryo data set would lead to different estimates of the change of relative rotameric state distributions with temperature for Ser143, Ser224, Ser247 and Asn276 (see also Section S5 and Supplementary Fig. S22).

3.4. Comparison of hydrogen bonds from room-temperature and cryo X-ray data

Hydrogen bonds are ubiquitous and are central to protein folding, molecular recognition and enzyme catalysis, and have been studied broadly using high-resolution protein crystal structures, with the vast majority obtained via cryo X-ray crystallography (Alford et al., 2017 ▸; Bartlett et al., 2013 ▸; Berg et al., 2002 ▸; Fersht, 1985 ▸; Herschlag & Pinney, 2018 ▸; Jeffrey & Saenger, 1991 ▸; Merski et al., 2020 ▸; Morozov et al., 2004 ▸; Morozov & Kortemme, 2005 ▸; Pauling, 1946 ▸). Given the importance of hydrogen bonds, the high-resolution structural data were used to appraise the effects of X-ray damage on hydrogen-bond lengths. All hydrogen-bond pairs involving backbone and side chains within each protein were identified and the hydrogen-bond lengths between the structural models obtained from the least and most sequential X-ray-damaged data sets were compared (see Section 2).

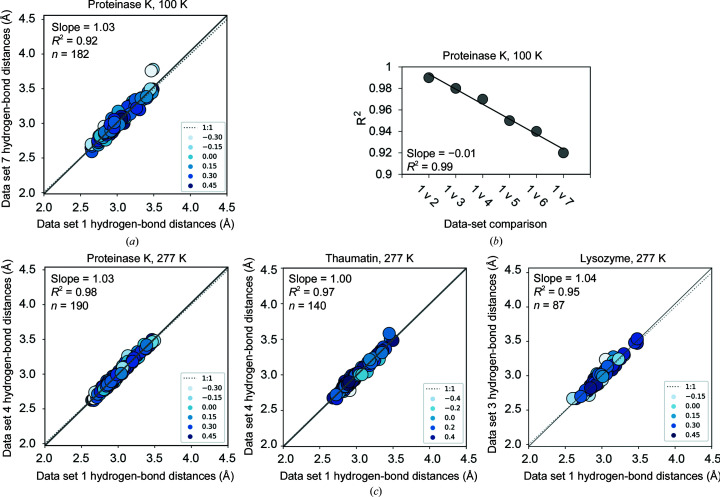
The correlation between hydrogen-bond lengths obtained from the least sequential damaged (data set 1) and most damaged (data set 7) 100 K proteinase K structures has a slope of 1.03 and an R ² value of 0.92 (Fig. 6 ▸ a), with R ² decreasing with increasing X-ray damage (Fig. 6 ▸ b). The same analysis using the least (data set 1) and most (data set 4) sequential damaged RT proteinase K data sets yielded a correlation with a slope of 1.03 and an R ² value of 0.98 (Fig. 6 ▸ c, left), and similar highly consistent correlations for thaumatin and lysozyme least versus most sequential X-ray-damaged RT data sets were found (slope = 1.00 and R ² = 0.97 and slope = 1.04 and R ² = 0.95, respectively; middle and right, respectively, in Fig. 6 ▸ c). Our analyses suggest that X-ray damage is more likely to impact hydrogen-bond lengths obtained from cryo-cooled crystals compared with RT crystals, underscoring the importance of tracing X-ray damage and its impact, especially for in-depth physical analyses.

Figure 6.

X-ray damage impacts the determination of hydrogen-bond lengths more at cryo temperature than at RT (277 K). (a) Correlation plots of hydrogen-bond lengths obtained from the least and most sequential X-ray-damaged data sets at cryo temperature. Correlation points are colored according to the relative B factor of the hydrogen-bonding groups such that higher values (darker blue) and lower values (white) correspond to atoms with low and high B factors relative to the average, respectively (see Section 2). (b) Correlation coefficients (R ²) obtained from correlation plots of hydrogen-bond lengths from the least damaged (‘1’) and increasingly damaged proteinase K 100 K structures (‘2–7’) (see Supplementary Fig. S23 for individual correlation plots). Differences between proteinase K structures are unlikely to result from differences in refinement strategy as all structures were refined using the same refinement parameters and increasingly X-ray-damaged models were refined in a consistent manner (see Section 2). (c) Correlation plots of hydrogen-bond lengths obtained from the least and most sequential X-ray-damaged data sets at room temperature. Colors used are as in (a). The analysis excluded all residues with more than one conformation present in the model (see Section 2). Similar results were obtained with all residues included (Supplementary Fig. S24).

4. Discussion

As we move to a new era of mechanistic understanding in biology, focus has shifted from static protein structures to dynamic ensembles of states that are determined by free-energy landscapes (Austin et al., 1975 ▸; Boehr et al., 2006 ▸, 2009 ▸; Fraser et al., 2011 ▸; Frauenfelder et al., 1991 ▸; Henzler-Wildman & Kern, 2007 ▸; Keedy, Kenner et al., 2015 ▸; Klinman, 2013 ▸). To understand the complex functions carried out by biomolecules and their control, we need to determine how and why these ensembles and their underlying energy landscapes change as biomolecules carry out their function, and how they change in response to interacting with other molecules and to mutation. In principle, molecular-dynamics (MD) simulations can provide conformational ensemble information, but this information is not experimental and outputs can depend on the force field used (Childers & Daggett, 2018 ▸). NMR provides atomic resolution experimental information and has been the approach of choice for studying temporal dynamics, but it is difficult to extract information about how and how much atomic coordinates fluctuate from NMR (Kleckner & Foster, 2011 ▸).

Room-temperature (RT) X-ray crystallography overcomes the limitations of traditional cryo X-ray crystallography and can provide the needed conformational ensemble information (Fraser et al., 2011 ▸; Keedy, Fraser et al., 2015 ▸; Keedy, Kenner et al., 2015 ▸; Lang et al., 2010 ▸; van den Bedem et al., 2009 ▸), but RT X-ray crystallography itself poses challenges: crystals without cryo-cooling generally diffract to lower resolution, are highly sensitive to X-ray damage and present practical challenges for crystal handling and data collection (Doukov et al., 2020 ▸; Roedig et al., 2016 ▸; Southworth-Davies et al., 2007 ▸; Warkentin et al., 2011 ▸; Warkentin & Thorne, 2010 ▸). Serial synchrotron X-ray crystallography (SSX) is an increasingly popular new approach for collecting diffraction data with reduced X-ray damage (Owen et al., 2017 ▸; Martin-Garcia et al., 2016 ▸), but the approach requires specialized equipment that is not available at every synchrotron beamline and a large number of small crystals; it is also difficult to obtain diffraction data at the highest resolution due to the small crystal size, and high resolution greatly enhances the ability to evaluate conformational heterogeneity (Lang et al., 2010 ▸; Fenwick et al., 2014 ▸; van den Bedem et al., 2009 ▸). We previously described approaches to make RT (and variable-temperature) X-ray crystallography more practical and robust at standard beamlines and to collect data from single crystals with reduced X-ray damage (Doukov et al., 2020 ▸). Here, we carried out the next step needed to establish the broad applicability of RT X-ray crystallography in protein biochemistry, building on and extending previous studies to systematically assess the effects of X-ray damage (Gotthard et al., 2019 ▸; Russi et al., 2017 ▸; Warkentin et al., 2012 ▸).

4.1. The impact of X-ray damage at room temperature

In this work, the impact of X-ray damage at RT for single crystals at 1.0–1.5 Å resolution was evaluated and it was found that in this resolution range modest X-ray damage does not cause substantial distortion of the conformations present, including the rotameric distributions of functional active-site residues. Evidence for some X-ray damage occurring to disulfide bonds was found, in agreement with previous work (de la Mora et al., 2020 ▸; Gotthard et al., 2019 ▸; Russi et al., 2017 ▸), but no evidence for X-ray-associated changes in cysteine rotameric distributions and no extreme sensitivity of these bonds was found. The ability to obtain ‘gold standard’ zero-damage conformational heterogeneity information and extract conformational heterogeneity information free of X-ray damage and the lack of X-ray damage effects on hydrogen-bond lengths allow highly accurate information about conformational ensembles and molecular interactions to be obtained.2 The zero-damage extrapolation of 1 − S ² allows overall comparisons of conformational heterogeneity without contributions from X-ray damage to be carried out. Recent work has shown that it is possible to perform such extrapolations on distances between specific atoms (Ebrahim et al., 2019 ▸), and future developments that allow the extension of such extrapolations to atomic features (for example atomic coordinates) will undoubtedly be of great value.

From a practical perspective, in their foundational RT work Blundell and Johnson recommended discarding crystals when the relative diffraction intensity of a given reflection decreased to 0.85 of its original value (I ₀), but suggested that a limiting value of 0.7 could be acceptable if the crystal supply was limited (Blundell & Johnson, 1976 ▸). The analyses in this work allowed us to further evaluate the proposed decay limit for crystals diffracting in the 1.0–1.5 Å resolution range at room temperature. In this work it was found that merging data with overall intensity decreases of up to about 70% of the initial value (I/I ₁ ≃ 0.7) did not impact the calculated heterogeneity. Thus, the lower intensity decay limit from Blundell and Johnson is expected to provide conformational heterogeneity information devoid of major alterations from X-ray damage and can be further tested and refined following the approaches used here.

4.2. The impact of X-ray damage at cryo temperature

The effects of X-ray damage on protein structure at cryo temperatures has been extensively investigated, with a large number of studies revealing X-ray-induced disulfide-bond reduction and side-chain decarboxylation (Burmeister, 2000 ▸; Fioravanti et al., 2007 ▸; Owen et al., 2006 ▸; Weik et al., 2000 ▸), but the effects of X-ray damage on the apparent conformational landscape of a protein have been less studied. Here, it was found that in cryo-cooled proteinase K crystals, X-ray damage caused side-chain rotameric states to appear, disappear and redistribute. The 11 MGy X-ray dose absorbed by the most damaged proteinase K data set is significantly below the Henderson and Garman dose limits of 20 and 30 MGy, respectively, which have been used as a rule of thumb in cryo-crystallographic X-ray data collection (Henderson, 1990 ▸; Owen et al., 2006 ▸), and is consistent with previous estimates of diffraction half-doses for lysozyme (at 1.13 Å resolution) of about 10 MGy at 100 K (Teng & Moffat, 2000 ▸).

The widespread use in recent years of micrometre-sized X-ray beams with increasingly brilliant X-ray sources at many synchrotrons presumably leads to the deposition of large X-ray doses as a general practice. Thus, a significant fraction of high-resolution cryo structures in the PDB may have been obtained from data sets with absorbed X-ray doses of ≥10 MGy. Unfortunately, the X-ray dose and the extent of diffraction decay are not reported for the majority of high-resolution structures in the PDB, and while the extent of X-ray damage present has been difficult to estimate, recent developments enable an estimation of the extent of damage (Shelley & Garman, 2022 ▸). These trends, together with our observations that proteinase K rotameric state changes are already present at I/I ₁ ≃ 0.9, caution that in addition to following the recommended I/I ₁ ≃ 0.7 limit (Owen et al., 2006 ▸) careful in-depth analyses may be required to evaluate and address X-ray damage effects when detailed ensemble comparisons are intended (also see Supplementary Section S6).

When comparing proteinase K cryogenic versus RT data sets of similar resolution and with a similar loss in the overall diffraction intensity due to X-ray damage, fewer effects from X-ray damage at RT were found in this work. Multiple changes and multiple types of changes in rotameric states were also observed for several individual side chains under cryo conditions that were not observed at room temperature. These observations suggest that in contrast to observations from cryo-cooled crystals, at RT the specific X-ray damage that causes changes in side-chain rotameric states occurs at X-ray doses of the same order of magnitude as those at which global X-ray damage causes the disappearance of the overall diffraction intensity, so changes due to specific X-ray damage are not observed. Indeed, the X-ray dose required to halve the diffraction intensity of a protein crystal is typically 50–100 times higher at cryo temperature than at RT and this may contribute to specific X-ray damage effects impacting rotameric states before the global diffraction deteriorates (Roedig et al., 2016 ▸; Southworth-Davies et al., 2007 ▸; Warkentin et al., 2011 ▸; Warkentin & Thorne, 2010 ▸).

These findings have direct implications for the conformational ensemble information extracted from ‘high-sequence similarity PDB’ (HSP) ensembles (Best et al., 2006 ▸). HSP ensembles are obtained from multiple cryogenic X-ray structural models and provide valuable depictions of overall protein ensemble properties (Best et al., 2006 ▸; Yabukarski et al., 2020 ▸). However, these ensembles are typically collections of structural models obtained for other purposes, often from crystals that have absorbed relatively high X-ray doses to obtain structural data to high resolution, so that, correspondingly, the amount of X-ray damage can be high and the effects on rotameric distributions are not known. Thus, analyses of such ensembles require careful controls to ensure that the extracted ensemble information is not biased by, for example, a few highly X-ray-damaged structures (see, for example Figs. S6 and S7 in Yabukarski et al., 2020 ▸). Alternatively, or in addition, it is possible that rotameric states and propagated structural changes that arise in X-ray-damaged structures could correspond to high-energy states of the native conformational landscape that are inaccessible in the un­damaged protein but become stabilized by the X-ray damage.

4.3. X-ray damage and multi-temperature X-ray crystallography

Cryo-cooling can alter conformational heterogeneity, and it has been found that over one-third of residues in protein crystals exhibit a different and generally broader distribution of states at RT (Fraser et al., 2009 ▸, 2011 ▸; Keedy, 2019 ▸; Keedy et al., 2014 ▸; Keedy, Kenner et al., 2015 ▸). In principle, the temperature dependence of a conformational ensemble can provide information about the forces underlying the energy landscape, and particular attention has been paid to changes arising from the so-called glass transition at around 180–220 K (Keedy, Kenner et al., 2015 ▸; Ringe & Petsko, 2003 ▸; Tilton et al., 1992 ▸). More broadly, an exciting new approach termed ‘multitemperature multiconformer X-ray crystallography’ (MMX) has recently been proposed in which a series of data sets obtained at various temperatures can be used to follow changes in rotameric distributions with temperature and could be exploited to uncover energetic coupling between states and provide testable hypothesis about allostery in proteins (Keedy, 2019 ▸; Keedy, Kenner et al., 2015 ▸). Our results show that effects from X-ray damage could alter these conclusions. X-ray damage effects can lead to both false positives and false negatives and to incorrect conclusions that particular changes do or do not happen. More generally, confident interpretation of conformational heterogeneity changes across temperature will require evaluation of the effects of X-ray damage on conformational heterogeneity at each temperature, following the approaches outlined in this work (also see Section S7).

In summary, cryo-cooling protein crystals decreases the X-ray damage sensitivity of the overall crystal diffraction relative to RT, but results from previous work and this work indicate that the higher X-ray damage tolerance comes at a price: X-ray damage causes not only breakage of disulfides but also changes in rotameric distributions. As the dynamic nature of proteins is increasingly being employed for a deeper understanding of function and for drug discovery, the effects of X-ray damage on conformational distributions can impact functional conclusions and practical applications. At RT the overall diffraction intensity decays much faster, but without substantial effects on conformational heterogeneity in data sets with reasonable extents of X-ray damage. The results here and in our previous work (Doukov et al., 2020 ▸) provide a means to readily collect RT X-ray data and to ensure that the data collected and the models obtained are of high integrity. While not every protein will be suitable for RT X-ray crystallo­graphy, due to the need for larger than average crystals to facilitate high-quality data collection (Doukov et al., 2020 ▸) and for relatively high resolutions to robustly model and interpret heterogeneity (generally better than 1.7–2.0 Å, depending on the method; Fenwick et al., 2014 ▸; Keedy, Fraser et al., 2015 ▸; van den Bedem et al., 2009 ▸), many proteins and protein complexes meet these criteria and can be used to obtain generalizable insights into the interplay of dynamics and function and provide ground-truth measurements for testing and developing computational models.

5. Related literature

The following references are cited in the supporting information for this article: Adam et al. (2009 ▸), Carugo & Djinović Carugo (2005 ▸), Chapman et al. (2011 ▸), Coquelle et al. (2015 ▸), Dauter (1999 ▸, 2016 ▸), Doerr (2011 ▸), Garman (2010 ▸), Holton (2009 ▸), Kort et al. (2004 ▸), Lewandowski et al. (2015 ▸), Matsui et al. (2002 ▸), Neutze et al. (2000 ▸), Sjöblom et al. (2009 ▸), Taberman et al. (2019 ▸) and Weik et al. (2002 ▸).

Supplementary Material

PDB reference: thaumatin, 277 K, 7lfg

PDB reference: 7ljv

PDB reference: 7ljw

PDB reference: 7ljz

PDB reference: 7lk5

PDB reference: 7lk6

PDB reference: 7lnb

PDB reference: 7lnc

PDB reference: 7lnd

PDB reference: proteinase K, 277 K, 7ln7

PDB reference: 7lpt

PDB reference: 7lpu

PDB reference: 7lpv

PDB reference: 7lq8

PDB reference: 7lq9

PDB reference: 7lqa

PDB reference: 7lqb

PDB reference: 7lqc

PDB reference: proteinase K, 100 K, 7ltd

PDB reference: 7lti

PDB reference: 7ltv

PDB reference: 7lu0

PDB reference: 7lu1

PDB reference: 7lu2

PDB reference: 7lu3

PDB reference: lysozyme, 277 K, 7llp

PDB reference: 7ln8

PDB reference: 7ln9

PDB reference: 7loq

PDB reference: 7lor

PDB reference: 7lp6

PDB reference: 7lpl

PDB reference: 7lpm

Supplementary tables with raw data.: https://doi.org/10.5281/zenodo.6408812

Funding Statement

This work was funded by a National Science Foundation (NSF) grant (MCB-1714723) to DH. FY was supported in part by a long-term Human Frontier Science Program postdoctoral fellowship. DAM acknowledges support from the Stanford Medical Scientist Training Program and a Stanford Interdisciplinary Graduate Fellowship (Anonymous Donor) affiliated with Stanford ChEM-H.