Mathematical Analysis of COVID-19 Transmission Dynamics Model in Ghana with Double-Dose Vaccination and Quarantine

Abstract

The discovery of vaccines for COVID-19 has been helpful in the fight against the spread of the disease. Even with these vaccines, the virus continues to spread in many countries, with some vaccinated persons even reported to have been infected, calling for administration of booster vaccines. The need for continued use of nonpharmaceutical interventions to complement the administration of vaccines cannot therefore be overemphasized. This study presents a novel mathematical model to study the impact of quarantine and double-dose vaccination on the spread of the disease. The local stability analysis of the COVID-19-free and endemic equilibria is examined using the Lyapunov second technique. The equilibria are found to be locally asymptotically stable if ℛ₀ < 1 and ℛ₀ > 1, respectively. Besides other analytical results, numerical simulations are performed to illustrate the analytical results established in the paper.

1. Introduction

Coronavirus is an infectious disease caused by a novel strain of virus which originated in Wuhan China, in late March 2019. It was diagnosed in three patients with pneumonia connected to a cluster of acute respiratory illness. As of May 21, 2022, Ghana recorded 161,370 confirmed cases, 159,881 recoveries, and 1,445 deaths [1]. The transmission routes of the virus include environment-to-human and human-to-human. The virus is spread by a close contact (susceptible individual) with an infected person who sneezes, or cough, or by an infected environment such as door holdings, curtains, and cutlery. Some common symptoms of COVID-19 infection include dry cough, fever, fatigue, breathing difficulty, and bilateral lung infiltration in severe cases similar to those caused by SARS-CoV and MERS-CoV infections [2]. Mostly, the infected people develop symptoms within an incubation period ranging from 2 to 14 days [3]. Currently, in Ghana, the combination of azithromycin, vitamin C, zinc, and some fever and pain killer medications seems to be working. Several measures have already been put in place which include travel bans, social distancing, use of facemask, and personal hygiene through frequent hand washing and use of appropriate hand sanitizers [4]. Despite efforts being made to curb the spread of the COVID-19 disease, the disease is still endemic in many parts of the world including Ghana. In early 2020, several companies began to develop vaccines against the COVID-19 virus, and a number of vaccines have been successfully developed. These vaccines have proven to be highly efficacious against COVID-19 (estimated at 91.6%,  95%, 82%,  and 94.1% for Sputnik V, Pfizer, AstraZeneca, and Moderna, respectively) [5–8]. Since a large number of people in the world need to be vaccinated to reduce the spread and mortality, vaccines are in limited supply. Developing countries find it difficult to secure large quantities of vaccines, thereby leading to a small portions of the population being vaccinated. As of May 24, 2022, Ghana Health Service administered a total of 15,032,815 vaccine doses (with 9,724,157 persons receiving at least 1 dose and 6,329,702 persons fully vaccinated) [1]. One needs to take double-dose shots of the vaccine to be fully vaccinated.

A lot of research has been conducted employing mathematical modelling to understand dynamics of the disease and to propose strategies of combatting it [9]. Specifically, [10] used a mathematical model combined with an optimization algorithm to determine optimal allocation strategies with one and two doses of vaccine to minimize five metrics of disease burden under various degrees of viral transmission. They suggested that it is crucial to find out the efficacy and durability of single-dose vaccines, as mixed or single-dose vaccination may have the potential to contain the pandemic much more quickly. [11] studied the nature of the virus, in which they developed and presented a review on the study of finding an effective vaccine for this new coronavirus. A new mathematical model formulated by [12] to study the global dynamics of COVID-19 revealed that, in India and Pakistan, the ratio of transmission and death rate is fast as compared to the other two countries (Bangladesh and Sri Lanka) because huge population produces greater chance to more people infected. [13] formulated and qualitatively analyzed a COVID-19 mathematical model, taking into consideration the available therapeutic measures, vaccination of susceptible, and treatment of hospitalized/infected individuals. The results showed that vaccination and treatment are very effective in mitigating the spread of COVID-19 and concurrently applying personal preventive measures (nonpharmaceutical public health interventions) such as face masks, hand washing, and social distancing should continue to be encouraged. [14] research showed that, when self-quarantined is adopted, then the process may go on reverse direction and infection will be decreasing and hence healthy community may be restored. In [15], the results show that the trend of epidemics mainly depends on quarantined and suspected cases. It will reveal that it is important to continue enhancing the quarantine and isolation strategy and improving the detection rate in mainland China. To the best of our knowledge, none of the literature has considered double-dose vaccination and quarantine. Therefore, this study develops a deterministic compartmental COVID-19 model which incorporates double-dose vaccination and quarantine to simulate the prevalence of COVID-19 disease in Ghana. The rest of the paper is organized as follows. The proposed model is formulated in Section 2, and analytical analysis is presented in Section 3. Numerical simulations performed to support the analytical results are presented in Section 4. The conclusion is presented in Section 5.

2. Model Formulation

Annas et al. [16] proposed the following SEIR model to study the impact of isolation and vaccination on the spread of COVID-19 in Indonesia:

$$\begin{array}{c}\left.\begin{array}{c}\frac{\text{d}S}{\text{d}t}=\gamma -\left(\nu +\delta +\beta I\right)S,\hfill \\ \frac{\text{d}E}{\text{d}t}=\beta IS-\left(\delta +\mu \right)E,\hfill \\ \frac{\text{d}I}{\text{d}t}=\mu E-\left(\alpha +\delta +{\delta }_i\right)I,\hfill \\ \frac{\text{d}R}{\text{d}t}=\alpha I+\nu S-\delta R.\hfill \end{array}\right\}\end{array}$$ (1)

In this paper, the work of Annas et al. [16] is extended to study the impact of quarantine and double-dose vaccination for the COVID-19 transmission in Ghana. The total population (N) is divided into the following epidemiological classes: susceptible (individuals who are uninfected but may get infected upon contact with the infectious agent), S(t) (individuals who have received the first dose of vaccine), V₁(t) (individuals who have received the second dose of vaccine), V₂(t) (exposed individuals—individuals who are exposed to the virus), E(t) (individuals who are exposed and have been identified and quarantined), Q(t) (individuals who are infected and infectious), I(t) (individuals who have successfully recovered from infection), and R(t). It has been observed that the rate of infection among those who have been vaccinated is lower than those who have not been vaccinated. The total population size N(t) is thus given by N(t) = S(t) + V₁(t) + V₂(t) + E(t) + Q(t) + I(t) + R(t). Recruitments into the population are assumed to be from only susceptibles at rate γ. The natural death and COVID-19-induced death rates are given as δ and δ_i, respectively. Susceptible individuals are assumed to receive first COVID-19 vaccination and move to the vaccinated compartment (V₁) at rate π. Single-dose-vaccinated persons lose protection from COVID-19 and rejoin the susceptibles at rate ε, while those who receive a second dose move to the V₂ compartment at rate τ. The parameter g is assumed to be the waning rate of immunity following double vaccination. Susceptible individuals may be infected at rate βS(I + E) following effective contact with viral sources. Those who are exposed are quarantined at a rate ω, and it is assumed that a proportion f of the quarantined recovers at rate fκ, while the remainder join the infected class at a rate (1 − f)κ. Those who are exposed become infectious at a rate μ, and those with clinical symptoms recover at rate α. Those who recover may lose immunity at some rate σ and move back to the susceptible compartment. The dynamics described so far are presented in Figure 1. The description of the model variables and parameters are presented in Table 1.

Figure 1.

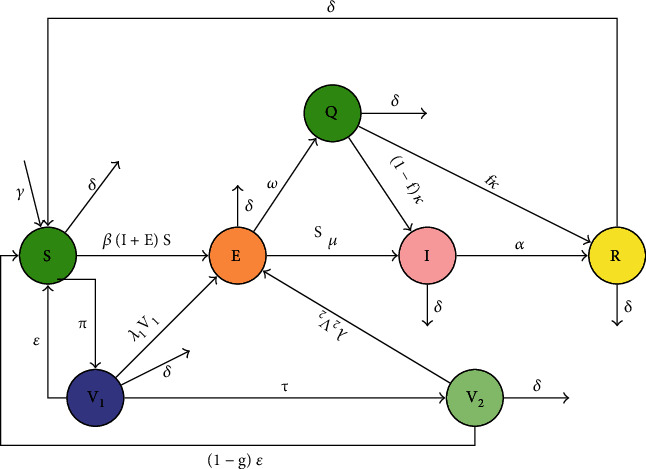
Flowchart for COVID-19 model with double-dose vaccination and quarantine.

Table 1.

Parameters estimates of the model.

Para.	Description	Value (per day)	Source
κ	Rate at which individuals leave the quarantined class	0.1	[20]
μ	Rate of exposed person to infectious	0.3739	Estimated
α	Rate of recovery	0.610	Estimated
β	Transmission rate	0.0369	Estimated
δ	Natural death rate	0.0078	[21]
δ i	COVID-19-induced death rate	0.0045	[1]
σ	Immunity loss rate	0.0167	Estimated
ω	Rate at which exposed persons are quarantined	0.173	Estimated
π	First dose of vaccine rate	0.12	Estimated
γ	Recruitment rate	0.23	Estimated
τ	Second dose of vaccine rate	0.34	Estimated
ε	Rate of waning of immunity after first does	0.6	Estimated
η 1	Efficacy of first dose of vaccine	0.82	[7]
η 2 ≥ η1	Efficacy of second dose of vaccine	0.82	[7]

The dynamics of COVID-19 described thus far is represented by the following system of nonlinear differential equations:

$$\begin{array}{c}\left.\begin{array}{c}\frac{\text{d}S}{\text{d}t}=\gamma +\epsilon \left(V_1+\left(1-g\right)V_2\right)+\sigma R-\beta \left(I+E\right)S-\left(\pi +\delta \right)S,\hfill \\ \frac{\text{d}{V}_1}{\text{d}t}=\pi S-\beta \left(I+E\right)\left(1-{\eta }_1\right)V_1-\left(\epsilon +\delta +\tau \right)V_1,\hfill \\ \frac{\text{d}{V}_2}{\text{d}t}=\tau V_1-\beta \left(I+E\right)\left(1-{\eta }_2\right)V_2-\left(\delta +\left(1-g\right)\epsilon \right)V_2,\hfill \\ \frac{\text{d}E}{\text{d}t}=\beta \left(I+E\right)\left[S+\left(1-{\eta }_1\right)V_1+\left(1-{\eta }_2\right)V_2\right]-\left(\omega +\delta +\mu \right)E,\hfill \\ \frac{\text{d}Q}{\text{d}t}=\omega E-\left(\delta +\kappa \right)Q,\hfill \\ \frac{\text{d}I}{\text{d}t}=\mu E+\kappa \left(1-f\right)Q-\left(\alpha +\delta +{\delta }_i\right)I,\hfill \\ \frac{\text{d}R}{\text{d}t}=\alpha I+f\kappa Q-\left(\sigma +\delta \right)R,\hfill \\ \text{with\hspace{0.17em}nonnegative\hspace{0.17em}initial\hspace{0.17em}conditions}.\hfill \end{array}\right\}\end{array}$$ (2)

In the subsequent discussions, where necessary, the following conventions are used:

$$\begin{array}{c}\begin{array}{c}{k}_1=\left(\pi +\delta \right),\\ k_2=\left(\epsilon +\delta +\tau \right),\\ k_3=\left(\delta +\left(1-g\right)\epsilon \right),\\ k_4=\left(\omega +\delta +\mu \right),\\ k_5=\left(\delta +\kappa \right),\\ k_6=\left(\alpha +\delta +{\delta }_i\right),\\ k_7=\left(\sigma +\delta \right),\\ \mathrm{\Gamma }=k_2{k}_3{k}_1-\pi \epsilon \left(\left(1-g\right)\tau +k_3\right).\end{array}\end{array}$$ (3)

3. Qualitative Properties

3.1. Positivity and Boundedness of Solutions of Model (2)

Lemma 1 . —

The following result concerns the nature of solutions of model (2).

1. If the initial values of state variables of model (2) are nonnegative, then all future values of state variables are also positive

2. The set defined by Ω ⊂ ℝ₊⁷ defined by Ω = {(S, V₁, V₂, E, Q, I, R) ∈ ℝ₊⁷|0 ≤ N(t) ≤ (γ/δ)} is a positively invariant region for model (2)

Proof —

It should be noted that the right-hand side of all components of model (2) is continuous and also locally Lipschitz at t = 0. Therefore, every nonnegative initial conditions of model (2) has a unique nonnegative solution in ℝ₊⁷ for all t > 0, concluding the first part of the lemma.

Furthermore, it is easy to show that if X = (S(t),  V₁(t),  V₂(t), E(t), Q(t), I(t), R(t)) ∈ ℝ₊⁷ and X_i = 0, then (dX_i/dt) ≥ 0. Therefore, from Theorem A.4 of [17], the region ℝ₊⁷ is positively invariant under the flow induced by model (2).

Now, summing all equations in model (2) gives

$$\begin{array}{c}\frac{\text{d}N}{\text{d}t}=\gamma -\delta N-{\delta }_{i}I\le \gamma -\delta N,\end{array}$$ (4)

so that we have $\lim \underset{t⟶\infty }{\sup }N\left(t\right)\le \left(\gamma /\delta \right)$. Since N(t) is bounded, then each component of X is also bounded, and hence, the feasible set of the model is given by Ω.

As for the invariance of Ω, it can be noted that from (dN/dt) ≤ γ − δ N, it is easy to show that (dN/dt) < 0 whenever N > (γ/δ). This shows that Ω is positively invariant under the flow induced by model (2), concluding the proof of the second part of the lemma.

Therefore, model (2) is mathematically and epidemiologically well posed [18] in Ω, and all analyses are therefore considered to be inside of Ω.

3.2. Equilibrium Points of the Model

It is easy to see that model (2) has a COVID-19-free equilibrium point ε₀ = (S⁰, V₁⁰, V₂⁰,0,0,0,0), where S⁰ = γ k₂k₃/Γ, V₁⁰ = π γ k₃/Γ, and V₂⁰ = τ π γ/Γ.

The basic reproduction number (ℛ₀) is defined as the average number of secondary COVID-19 infections caused by a single COVID-19 case throughout his/her entire period of infectiousness. This threshold is determined using the next-generation matrix technique which defines ℱ as transmission matrix and 𝒱 as the transition matrix [19]. The matrices ℱ and 𝒱 are given as

$$\begin{array}{c}\begin{array}{c}\mathcal{F}=\left(\begin{array}{ccc}{\mathcal{B}}_0& 0& {\mathcal{B}}_0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\\ \mathcal{V}=\left(\begin{array}{ccc}{k}_4& 0& 0\\ -\omega & k_5& 0\\ -\mu & -\kappa \left(1-f\right)& k_6\end{array}\right),\end{array}\end{array}$$ (5)

where ℬ₀ = β[S⁰ + (1 − η₁)V₁⁰ + (1 − η₂)V₂⁰].

Therefore,

$$\begin{array}{c}{\mathcal{F}\mathcal{V}}^{-1}={\mathcal{B}}_0\left(\begin{array}{ccc}\frac{1}{k_4}+\frac{\mu k_5+\kappa \omega \left(1-f\right)}{k_5{k}_6{k}_4}& \frac{\kappa \left(1-f\right)}{k_5{k}_6}& \frac{1}{k_6}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\end{array}$$ (6)

and the basic reproduction number is obtained as the largest eigenvalue of ℱ𝒱⁻ and is given by

$$\begin{array}{c}{\mathcal{R}}_0=\frac{{\mathcal{B}}_0}{k_4}\left(1+\frac{\mu k_5+\kappa \omega \left(1-f\right)}{k_5{k}_6}\right).\end{array}$$ (7)

Let ε^∗ = (S^∗, V₁^∗, V₂^∗, E^∗, Q^∗, I^∗, R^∗) be a fixed point of model (2).

Then,

$$\begin{array}{c}\left.\begin{array}{c}{S}^{\ast }=\frac{\gamma k_4{\psi }_1{\psi }_2}{{\psi }_1{\psi }_2\left(k_1{k}_4+\left(k_4-{\psi }_0\right){\lambda }^{\ast }\right)-\pi \left[\left[k_4\epsilon +\left(1-{\eta }_1\right){\psi }_0{\lambda }^{\ast }\right]{\psi }_2+\tau \left[k_4\epsilon \left(1-g\right)+\left(1-{\eta }_2\right){\psi }_0{\lambda }^{\ast }\right]\right]},\hfill \\ V_1^{\ast }=\frac{\pi S^{\ast }}{{\psi }_1},\hfill \\ V_2^{\ast }=\frac{\pi \tau S^{\ast }}{{\psi }_1{\psi }_2},\hfill \\ E^{\ast }=\frac{{\lambda }^{\ast }}{k_4}\left(1+\frac{\pi \left(1-{\eta }_1\right)}{{\psi }_1}+\frac{\pi \tau \left(1-{\eta }_2\right)}{{\psi }_1{\psi }_2}\right)S^{\ast },\hfill \\ Q^{\ast }=\frac{\omega }{k_5}{E}^{\ast },\hfill \\ I^{\ast }=\frac{k_4}{{\mathcal{B}}_0}\left({\mathcal{R}}_0-\frac{{\mathcal{B}}_0}{k_4}\right)E^{\ast },\hfill \\ R^{\ast }=\frac{1}{k_7}\left[\frac{\alpha k_4}{{\mathcal{B}}_0}\left({\mathcal{R}}_0-\frac{{\mathcal{B}}_0}{k_4}\right)+\frac{f\kappa \omega }{k_5}\right]E^{\ast },\hfill \end{array}\right\}\end{array}$$ (8)

where

$$\begin{array}{c}\begin{array}{c}{\psi }_0=\sigma \left(\frac{\alpha k_4}{k_7{\mathcal{B}}_0}\left({\mathcal{R}}_0-\frac{{\mathcal{B}}_0}{k_4}\right)+\frac{f\kappa \omega }{k_5{k}_7}\right),\\ {\psi }_1=\left(1-{\eta }_1\right){\lambda }^{\ast }+k_2,\\ {\psi }_2=\left(1-{\eta }_2\right){\lambda }^{\ast }+k_3,\end{array}\end{array}$$ (9)

and λ^∗ satisfies the following polynomial equation:

$$\begin{array}{c}\left({\mathrm{\Psi }}_3{\left({\lambda }^{\ast }\right)}^3+{\mathrm{\Psi }}_2{\left({\lambda }^{\ast }\right)}^2+{\mathrm{\Psi }}_1{\lambda }^{\ast }+{\mathrm{\Psi }}_0\right){\lambda }^{\ast }=0,\end{array}$$ (10)

where

$$\begin{array}{c}{\mathrm{\Psi }}_3=\left(1-{\eta }_1\right)\left(1-{\eta }_2\right)\left({\psi }_0-k_4\right),\\ {\mathrm{\Psi }}_2=\left(1-{\eta }_1\right)\left(1-{\eta }_2\right)\left(\frac{\beta k_4\gamma {\mathcal{R}}_0}{{\mathcal{B}}_0}+{\pi \psi }_0-k_1{k}_4\right)-\left(k_4-{\psi }_0\right)\left[k_3\left(1-{\eta }_1\right)+k_2\left(1-{\eta }_2\right)\right],\\ {\mathrm{\Psi }}_1=\left(\frac{\beta \gamma k_4{\mathcal{R}}_0}{{\mathcal{B}}_0}-k_1{k}_4\right)\left[k_3\left(1-{\eta }_1\right)+k_2\left(1-{\eta }_2\right)\right]-k_2{k}_3{k}_4+k_2{k}_3{\psi }_0+k_4\pi \epsilon \left(1-{\eta }_2\right)+\pi \left(1-{\eta }_1\right)\left(1-{\eta }_2\right)\frac{\beta \gamma k_4{\mathcal{R}}_0}{{\mathcal{B}}_0}+{\pi \psi }_0\left(k_3\left(1-{\eta }_1\right)+\tau \left(1-{\eta }_2\right)\right),\\ {\mathrm{\Psi }}_0=k_4\pi \epsilon \left(k_3+\tau \left(1-g\right)\right)-k_1{k}_2{k}_3{k}_4+\frac{\beta \gamma k_4{\mathcal{R}}_0}{{\mathcal{B}}_0}\left(k_2{k}_3+k_3\pi \left(1-{\eta }_1\right)+\pi \tau \left(1-{\eta }_2\right)\right).\end{array}$$ (11)

Equation (10) has four roots, namely, λ^∗ = 0 which corresponds with the disease-free equilibrium and the positive real zeros of the following equation:

$$\begin{array}{c}{\mathrm{\Psi }}_3{\left({\lambda }^{\ast }\right)}^3+{\mathrm{\Psi }}_2{\left({\lambda }^{\ast }\right)}^2+{\mathrm{\Psi }}_1{\lambda }^{\ast }+{\mathrm{\Psi }}_0,\end{array}$$ (12)

which correspond to the endemic equilibrium of model (2).

Since all parameter values of the model are positive, Ψ₃ > 0 for ℛ₀ > 1, which implies the existence of at least one positive root for Equation (10). Therefore, the number of positive roots of Equation (10) and the number of endemic equilibrium points of model (2) depend on the signs of Ψ₂, Ψ₁, and Ψ₀.

The following result about the endemic equilibrium of model (2) is thus in the following order.

Theorem 1 . —

1. There is a critical threshold ℛ^∗ = ℬ₀/k₄ such that model (2) has an endemic equilibrium only when ℛ₀ > ℛ^∗

2. Model (2) has three endemic equilibria whenever Ψ_i > 0, ∀i = 0, 1, 2, 3

3. Model (2) has a unique endemic equilibrium for cases 1, 3, and 4 as given in Table 2

Table 2.

Number of possible positive roots of endemic polynomial in (10).

Case	Ψ0	Ψ1	Ψ2	Ψ3	No. of +ve roots of (10)
1	—	+	+	+	1
2	—	+	—	+	0,3
3	—	—	+	+	1
4	—	—	—	+	1
5	+	—	+	+	1,2
6	+	—	—	+	1,2
7	+	+	—	+	1,2

3.3. Local Stability of Equilibria

In this section, we investigate the local asymptotic stability of the equilibria.

Theorem 2 . —

The COVID-19-free fixed point ε₀ of model (2) is locally asymptotically stable whenever ℛ₀ ≤ 1 and unstable otherwise.

Proof —

The Jacobian matrix of (2) at the COVID-19-free equilibrium point is given by

$$\begin{array}{c}\mathcal{J}\left({\epsilon }_0\right)=\left[\begin{array}{ccccccc}-k_1& \epsilon & \left(1-g\right)\epsilon & -\beta S^0& f\kappa & -\beta S^0& \sigma \\ \pi & -k_2& 0& -\beta \left(1-{\eta }_1\right)V_1^0& 0& -\beta \left(1-{\eta }_1\right)V_1^0& 0\\ 0& \tau & -k_3& -\beta \left(1-{\eta }_2\right)V_2^0& 0& -\beta \left(1-{\eta }_2\right)V_2^0& 0\\ 0& 0& 0& {\mathcal{B}}_0-k_4& 0& {\mathcal{B}}_0& 0\\ 0& 0& 0& \omega & -k_5& 0& 0\\ 0& 0& 0& \mu & \kappa \left(1-f\right)& -k_6& 0\\ 0& 0& 0& 0& f\kappa & \alpha & -k_7\end{array}\right].\end{array}$$ (13)

The following is the characteristic polynomial of the Jacobian matrix.

$$\begin{array}{c}\left(\zeta +k_7\right)\left({\zeta }^3+a_1{\zeta }^2+a_2\zeta +a_3\right)\left({\zeta }^3+b_1{\zeta }^2+b_2\zeta +b_3\right)=0,\end{array}$$ (14)

where

$$\begin{array}{c}\begin{array}{c}{a}_1=\frac{\left(\omega \kappa \left(1-f\right)+\mu k_5\right)k_4+\left(1-{\mathcal{R}}_0\right)k_4{k}_5{k}_6}{k_6{k}_5+\omega \kappa \left(1-f\right)+\mu k_5}+k_5+k_6,\\ a_2=\frac{\left(k_6+k_5\right)k_4\omega \kappa \left(1-f\right)+{k_4}^2\mu {k_5}^2{k}_5\left(1-{\mathcal{R}}_0\right)k_6\left(\mu +k_6+k_5\right)}{k_6{k}_5+\omega \kappa \left(1-f\right)+\mu k_5}+k_6{k}_5,\\ a_3=\left(1-{\mathcal{R}}_0\right)k_4{k}_5{k}_6,\\ b_1=k_1+k_2+k_3,\\ b_2=k_3{k}_1-\epsilon \pi +k_3{k}_2+k_2{k}_1,\\ b_3=k_3{k}_2{k}_1-\pi \epsilon \left(\tau \left(1-g\right)+k_3\right).\end{array}\end{array}$$ (15)

It is easy to see that that b₂ > 0 and b₃ > 0, so that all coefficients of the polynomial (14) are positive whenever ℛ₀ ≤ 1. By the Descartes rule of signs, all roots of polynomial (14) are negative. Therefore, ε₀ is locally asymptotically stable whenever ℛ₀ ≤ 1; otherwise, it is unstable, concluding the proof.

3.4. Sensitivity Analysis of ℛ₀

Estimates for some parameters are varied one at a time to investigate the impact on the basic reproduction number (ℛ₀). This is done using the normalized forward sensitivity index (NFSI) defined as follows.

The normalized forward sensitivity index of ℛ₀ with respect to the parameter y is defined as [22]

$$\begin{array}{c}{\mathcal{P}}_y^{{\mathcal{R}}_0}=\frac{\partial {\mathcal{R}}_0}{\partial y}\times \frac{y}{{\mathcal{R}}_0}.\end{array}$$ (16)

Using the parameter values in Table 1, the sensitivity indexes of the model parameters determining ℛ₀ are presented in Table 3. The simulation and analysis made are based on data obtained from literature as displayed in Table 1.

Table 3.

Sensitivity signs of ℛ₀ to the parameters in Equation (7).

Parameter	Sensitivity index
β	+1.000
γ	+1.000
ε	+0.716
μ	+0.324
κ	+0.213
α	-0.980
π	-0.450
τ	-0.176
ω	-0.123
δ i	-0.007

In Table 3, the results show that the parameters β,  γ,  μ,  κ,  and ε have a positive correlation with ℛ₀, which indicates that increasing (decreasing) these parameters will increase the prevalence of COVID-19 disease. On the other hand, the parameters α,  π,  τ,  ω,  and δ_i have a negative correlation with ℛ₀, which indicates that increasing (decreasing) these parameters will decrease the prevalence of COVID-19 disease.

3.5. Bifurcation Analysis

Let v = [v₁ v₂ v₃ v₄ v₅ v₆ v₇] and $\mathbf{w}={\left[\begin{array}{ccccccc}{w}_1& w_2& w_3& w_4& w_5& w_6& w_7\end{array}\right]}^T$ be the left and right eigenvectors, respectively, of the Jacobian matrix 𝒥(ε₀). Then,

$$\begin{array}{c}\left.\begin{array}{r}-k_1{w}_1+\epsilon w_2+\epsilon \left(1-g\right)w_3-\beta S^0\left(w_4+w_6\right)+f\kappa w_5+\sigma w_7=0,\hfill \\ \pi w_1-k_2{w}_2-\beta \left(1-{\eta }_1\right)V_1^0\left(w_4+w_6\right)=0,\hfill \\ \tau w_2-k_3{w}_3-\beta \left(1-{\eta }_2\right)V_2^0\left(w_4+w_6\right)=0,\hfill \\ -k_4{w}_4+{\mathcal{B}}_0\left(w_4+w_6\right)=0,\hfill \\ \omega w_4-k_5{w}_5=0,\hfill \\ \mu w_4+\kappa \left(1-f\right)w_5-k_6{w}_6=0,\hfill \\ f\kappa w_5+\alpha w_6-k_7{w}_7=0.\hfill \end{array}\right\}\end{array}$$ (17)

From the last three equations in (17), we get

$$\begin{array}{c}\begin{array}{c}\begin{array}{c}{w}_5=\frac{\omega }{k_5}{w}_4,\\ w_6=\left(\frac{\mu k_5+\omega \kappa \left(1-f\right)}{k_5{k}_6}\right)w_4,\\ w_7=\left(\frac{\omega f\kappa }{k_5{k}_7}+\frac{\alpha \left(\mu k_5+\omega \kappa \left(1-f\right)\right)}{k_5{k}_6{k}_7}\right)w_4.\end{array}\end{array}\end{array}$$ (18)

Substituting w₅, w₆, and w₇ into the first three equations of (17) gives the following set of equations:

$$\begin{array}{c}\left.\begin{array}{r}-k_1{w}_1+\epsilon w_2+\epsilon \left(1-g\right)w_3=K_1{w}_4,\hfill \\ \pi w_1-k_2{w}_2=K_2{w}_4,\hfill \\ \tau w_2-k_3{w}_3=K_3{w}_4,\hfill \end{array}\right\}\end{array}$$ (19)

where

$$\begin{array}{c}\begin{array}{c}{K}_1=\left[\beta S^0\left(\frac{k_5{k}_6+\mu k_5+\omega \kappa \left(1-f\right)}{k_5{k}_6}\right)-\frac{f\kappa \omega }{k_5}-\frac{\omega \sigma f\kappa }{k_5{k}_7}+\frac{\alpha \sigma \left(\mu k_5+\omega \kappa \left(1-f\right)\right)}{k_5{k}_6{k}_7}\right],\\ K_2=\beta \left(1-{\eta }_1\right)V_1^0\left(\frac{k_5{k}_6+\mu k_5+\omega \kappa \left(1-f\right)}{k_5{k}_6}\right),\\ K_3=\beta \left(1-{\eta }_2\right)V_2^0\left(\frac{k_5{k}_6+\mu k_5+\omega \kappa \left(1-f\right)}{k_5{k}_6}\right).\end{array}\\ \left.\begin{array}{r}\left[\frac{\epsilon k_3}{\tau }+\epsilon \left(1-g\right)-\frac{k_1{k}_2{k}_3}{\pi \tau }\right]w_3=\left(K_1+\frac{k_1{k}_2{K}_3+\tau k_1{K}_2}{\pi \tau }-\frac{\epsilon K_3}{\tau }\right)w_4,\hfill \\ w_1=\left(\frac{k_2{k}_3}{\pi \tau }{w}_3+\frac{k_2{K}_3+\tau K_2}{\pi \tau }{w}_4\right),\hfill \\ w_2=\left(\frac{k_3}{\tau }{w}_3+\frac{K_3}{\tau }{w}_4\right).\hfill \end{array}\right\}\end{array}$$ (20)

The left eigenvectors of 𝒥(ε₀) satisfy the following set of equations:

$$\begin{array}{c}\left.\begin{array}{r}-k_1{v}_1+\pi v_2=0,\hfill \\ \epsilon v_1-k_2{v}_2+\tau v_3=0,\hfill \\ \epsilon \left(1-g\right)v_1-k_3{v}_3=0,\hfill \\ -\beta \left[S^0{v}_1+\left(1-{\eta }_1\right)V_1^0{v}_2+\left(1-{\eta }_2\right)V_2^0{v}_3\right]+\left({\mathcal{B}}_0-k_4\right)v_4+\omega v_5+\mu v_6=0,\hfill \\ f\kappa v_1-k_5{v}_5+\kappa \left(1-f\right)v_6+f\kappa v_7=0,\hfill \\ -\beta S^0{v}_1-\beta \left(1-{\eta }_1\right)V_1^0{v}_2-\beta \left(1-{\eta }_2\right)V_2^0{v}_3+{\mathcal{B}}_0{v}_4-k_6{v}_6+\alpha v_7=0,\hfill \\ \sigma v_1-k_7{v}_7=0.\hfill \end{array}\right\}\end{array}$$ (21)

From (21), we get

$$\begin{array}{c}\begin{array}{c}{v}_1=0,\\ v_2=0,\\ v_3=0,\\ v_7=0,\\ v_6=\frac{{\mathcal{B}}_0}{k_6}{v}_4,\\ v_5=\frac{{\mathcal{B}}_0\kappa \left(1-f\right)}{k_5{k}_6}{v}_4,\end{array}\end{array}$$ (22)

where w₄ and v₄ are chosen such that w•v = 1.

Thus,

$$\begin{array}{c}\left(1+{\mathcal{B}}_0\left(\frac{\omega \kappa \left(1-f\right)}{k_5^2{k}_6}+\frac{\mu k_5+\omega \kappa \left(1-f\right)}{k_5{k}_6^2}\right)\right)v_4{w}_4=1.\end{array}$$ (23)

The bifurcation coefficients are thus obtained as

$$\begin{array}{c}\begin{array}{c}\mathbf{a}=\sum _{i,j,k=1}^n{v}_k{w}_i{w}_j\frac{{\partial }^2{f}_k}{\partial x_i\partial x_j},\\ \mathbf{b}=\sum _{i,k=1}^n{v}_k{w}_i\frac{{\partial }^2{f}_k}{\partial x_i\partial {\beta }^{\ast }},\end{array}\\ \mathbf{a}=v_4\sum _{i,j=1}^7{w}_i{w}_j\frac{{\partial }^2{f}_4}{\partial x_i\partial x_j},\\ f_4=\beta \left(x_4+x_6\right)\left[x_1+\left(1-{\eta }_1\right)x_2+\left(1-{\eta }_2\right)x_3\right]-\left(\omega +\delta +\mu \right)x_4.\end{array}$$ (24)

The nonzero derivatives in a are

$$\begin{array}{c}\frac{{\partial }^2{f}_4}{\partial x_1\partial x_4}=\frac{{\partial }^2{f}_4}{\partial x_1\partial x_6}=\beta ,\\ \frac{{\partial }^2{f}_4}{\partial x_2\partial x_4}=\frac{{\partial }^2{f}_4}{\partial x_2\partial x_6}=\beta \left(1-{\eta }_1\right),\\ \frac{{\partial }^2{f}_4}{\partial x_3\partial x_4}=\frac{{\partial }^2{f}_4}{\partial x_3\partial x_6}=\beta \left(1-{\eta }_2\right),\\ \mathbf{a}=2\beta \left(w_6+w_4\right)\left[w_1+\left(1-{\eta }_1\right)w_2+\left(1-{\eta }_2\right)w_3\right]v_4.\end{array}$$ (25)

Since v₁ = v₂ = v₃ = v₇ = 0 and f₅ and f₆ do not have nonlinear terms, then b can be reduced to

$$\begin{array}{c}\mathbf{b}=v_4\sum _{i=1}^n{w}_i\frac{{\partial }^2{f}_4}{\partial x_i\partial {\beta }^{\ast }}.\end{array}$$ (26)

Also, the nonzero derivatives in b are

$$\begin{array}{c}\frac{{\partial }^2{f}_4}{\partial x_4\partial \beta }=\frac{{\partial }^2{f}_4}{\partial x_6\partial \beta }={\mathcal{B}}_0.\end{array}$$ (27)

Therefore,

$$\begin{array}{c}\mathbf{b}=v_4\left(w_6+w_4\right){\mathcal{B}}_0>0.\end{array}$$ (28)

Therefore, the nature of the bifurcation depends on the sign of a. When a > 0, the bifurcation is subcritical (backward), and when a < 0, there is forward bifurcation.

4. Numerical Simulation and Discussion

In this section, numerical simulations are carried out to support the analytical results and to assess the impact of some model parameters. Numerical simulation for the model of Equation (2) is done using MATLAB R2007b ODE45. The parameter values are given in Table 2, and the initial conditions S(0) = 0.98, V₁(0) = 0.02, V₂(0) = 0.01, E(0) = 0.2, Q(0) = 0, I(0) = 0, and R(0) = 0.01. The trend of β and μ on infected population and π, ω, and τ on infected population are given in Figures 2 and 3.

Figure 2.

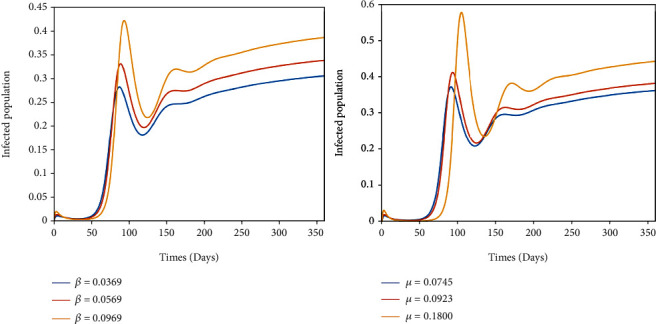
Solution curves depicting the impact of β and μ on infected population of the COVID-19 model.

Figure 3.

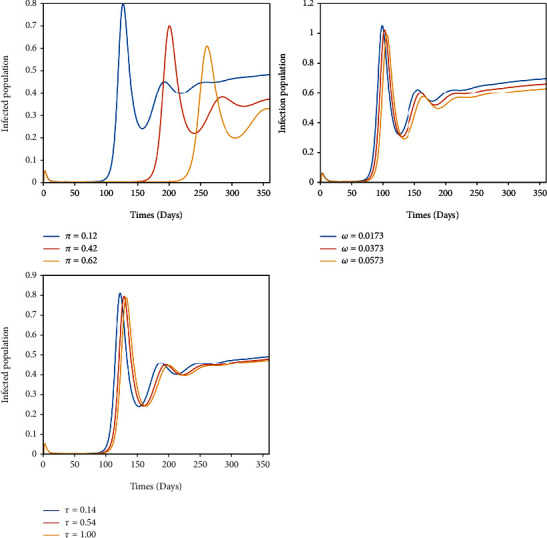
Solution curves depicting the impact of π, ω, and τ on infected population of the COVID-19 model.

In Figure 4, it is observed that β,  γ,  and ε are positively correlated with ℛ₀, thus increasing (decreasing) β,  γ,  or ε by say 5% will lead to an increase (decrease) in ℛ₀. Similarly, when we increase (decrease) τ,  π,  α,  or δ_i by say 5%, ℛ₀ will decrease (increase). This implies that τ,  π,  α,  and δ_i are negatively correlated with ℛ₀.

Figure 4.

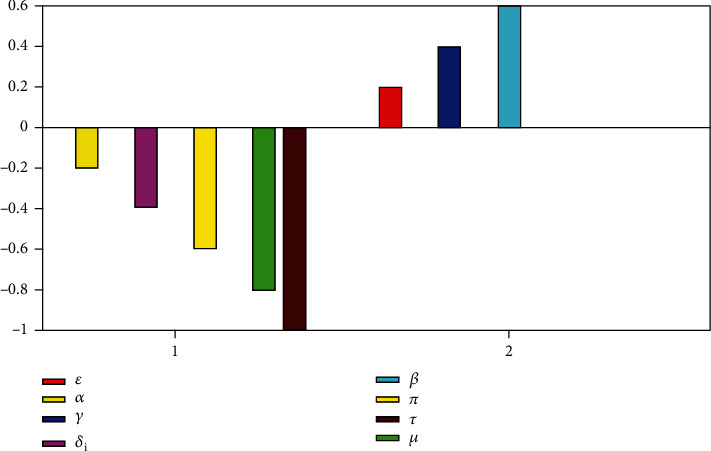
Correlation between the reproduction number (ℛ₀) and the model parameters β,  α,  ε,  π,  γ,  τ,  and δ_i.

Figure 2 shows that the effect of transmission rate (β) and progression rate (μ) on COVID-19 prevalence. It can be seen in these figures that as the transmission (β) and progression rates (μ) increase, then COVID-19 prevalence (infected population) increases, which means that those are directly related with COVID-19 outbreak. Efforts needs to be made to reduce the transmission rate (β) which can be done through mass vaccination.

Figure 3 shows that the increase in first dose vaccination (π), quarantined (ω), and second dose vaccination rates (τ) decrease the COVID-19 prevalence (infected population) and decrease the risk of an outbreak, which means that these measures should be put in place to minimize the spread of the virus.

5. Conclusions

In this paper, a deterministic model is formulated to investigate the spread of COVID-19 in Ghana, taking into account double-dose vaccination and quarantine. Qualitative analysis, bifurcation analysis, and some numerical simulations are conducted on the model. The local stability analysis of the COVID-19-free and endemic equilibria are examined using the Lyapunov second technique. The equilibria are found to be locally asymptotically stable if ℛ₀ < 1 and ℛ₀ > 1, respectively. Figure 3 shows that the disease is expected to become extinct when the basic reproduction number is sufficiently low, which can be achieved by decreasing the parameter β or increasing the parameter τ. The authors in [16] research showed that isolation and vaccination can reduce the spread of the disease. Sensitivity analysis and numerical simulations confirm that the implementation of double-dose vaccination and quarantine will help minimize the spread of COVID-19. This really implies that, when precautionary measures are put in place, the spread of the virus will be minimized as stated by [23]. Therefore, more education should be done for people to avail themselves for vaccination, and mass vaccination should be done to cover most of the population to reduce spread of COVID-19 in Ghana.

Data Availability

The parameter values (data) used to support the findings of this study have been described in subsection 3.4.1.

Conflicts of Interest

The authors declare that they have no conflicts of interest to report regarding the present study.