Abstract
We developed a method to estimate a biomechanically feasible precision grip posture of the human hand for a given object based on a minimization of the muscle effort. The hand musculoskeletal model was constructed as a chain of 21 rigid links with 37 intrinsic and extrinsic muscles. To grasp an object, the static force and moment equilibrium condition of the object, force balance between the muscle and fingertip forces, and static frictional conditions must be satisfied. We calculated the hand posture, fingertip forces, and muscle activation signals for a given object to minimize the square sum of the muscle activations while satisfying the above kinetic constraints using an evolutionary optimization technique. To evaluate the estimated hand posture and fingertip forces, a wireless fingertip force-sensing device with two six-axis load cells was developed. When grasping the object, the fingertip forces and hand posture were experimentally measured to compare with the corresponding estimated values. The estimated hand postures and fingertip forces were in reasonable agreement to the corresponding measured data, indicating that the proposed hand posture estimation method based on the minimization of muscle effort is effective for the virtual ergonomic assessment of a handheld product.
Subject terms: Biomedical engineering, Musculoskeletal system, Motor control
Introduction
Recently, ergonomic assessments of products or workspaces in virtual spaces using digital human models have gained considerable attention. Digital human modeling allows the simulation of mechanical interactions of the human body with products or workspaces, allowing virtual evaluation of the usability and safety of the products or workspaces, thereby reducing the cost and time required for product design and development. Therefore, these virtual techniques have been utilized to evaluate designs of products, such as automobile interiors and aircraft cockpits1,2.
Following this trend, attempts have been made to objectively evaluate the usability of handheld products based on simulated mechanical interactions of the human hand model with models of the products in a virtual space3,4. However, the human hand is a highly complex musculoskeletal system with many joints, muscles, and degrees of freedom; hence, there are a huge number of possible ways to grasp an object by hand. Although hand kinematics are somewhat specified from a huge number of possibilities, there are still a huge number of possible patterns to activate muscles to generate fingertip forces that satisfy the force and moment balance of grasping mechanics. Therefore, the challenge of computationally predicting realistic and anatomically natural grasping postures of the human hand for a given object in a virtual space persists. Subsequently, we address the question of how humans generate appropriate motor commands in muscles that lead to successful object grasping in an anatomically natural way.
Recent neurophysiological studies have suggested that the human central nervous system determines motor commands such that muscle effort, i.e., the sum of the squared muscle activations, is minimized5–8. If such a biologically feasible objective function can be specified, the grasping posture and muscle activation pattern necessary for a given object can be uniquely calculated by searching for the minimum point of the objective function that satisfies the force and moment equilibrium required for stable object grasping. This hand posture estimation method is potentially effective for virtual ergonomic assessment of a hand-held product.
Synthetic simulations of the human hand grasping an object have been conducted in the field of computer graphics for a realistic, natural animation of hand movements9. However, these simulations usually exploit a database of motion-captured hand poses to calculate the humanlike grasp posture for a given object. Moreover, measures to evaluate the quality of grasping, that is, the goodness of the grasping posture evaluated based on the stability or manipulability of the grasped object10, were often introduced to determine a unique solution for the problem11. However, these were not necessarily biologically plausible.
The aim of this study is to develop a method to estimate a geometrically and mechanically feasible grasping posture of the human hand for a given object based on a minimization of the neural effort. In this study, we attempt to incorporate the physiological aspects of human grasps into the synthesis of realistic, natural hand-object interactions in virtual environments. To evaluate whether the proposed methodology can replicate the kinematics and kinetics of the human hand grasping an object, we experimentally measured the fingertip forces and hand posture when grasping an object with the thumb and index finger using a fingertip-force sensing device and a motion-capture system, and compared them with corresponding estimated values.
Materials and methods
Hand model
For a realistic representation of the human hand, a computed tomography (CT) scan of a male hand (height: 1.69 m, weight: 63 kg, age: 50 years) was obtained using a CT scanner (Aquillion One, Canon Medical, Japan). The tube voltage and current were 120 kV and 400 mA, respectively. The pixel size and slice interval were 0.297 mm and 0.25 mm, respectively. Three-dimensional polygonal models of the hand surface and skeleton were then constructed.
The hand musculoskeletal model was modeled as a chain of rigid-body bone segments connected by revolute joints (Fig. 1). The carpal bones were treated as a single rigid body, disregarding inter-carpal mobility. Therefore, the hand was represented as a chain of 21 bone segments: the forearm, carpus, 1–5 metacarpals, and 14 phalanges. For each bone segment, a bone-fixed coordinate system was defined. The x-, y-, and z-axes roughly correspond to the dorso-palmar, medio-lateral, and proximo-distal directions, respectively. Each interphalangeal (IP) joint was represented by a hinge joint with one degree of freedom (DOF). The rotational axis and joint center were determined by approximating the proximal joint surface using a cylindrical surface by the least-squares method, and so was the first metacarpophalangeal (MP) joint. The second to fifth MP joints were each represented by a two-DOF revolute joint (flexion/extension and radial/ulnar rotation), the joint center of which was determined by approximating the proximal joint surface using a spherical surface. Each carpometacarpal (CMC) joint was represented by a gimbal joint. However, the second to fifth CMC joints were assumed to be immobile in this study. The joint center and rotational axes of the first CMC joints were determined by approximating the saddle-shaped joint surface using a hyperbolic paraboloid surface12.
Figure 1.
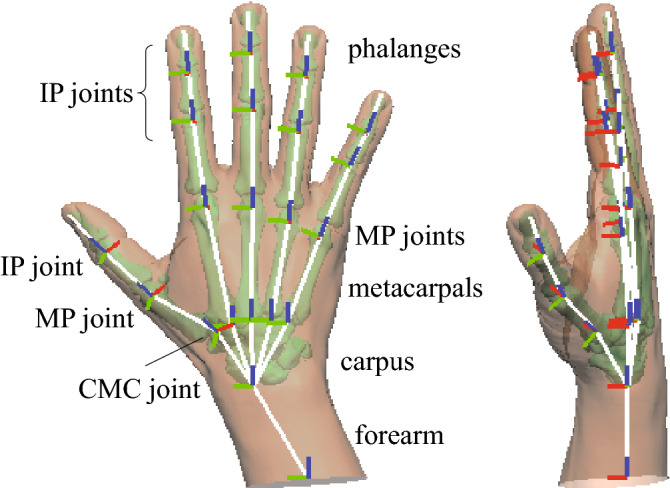
The hand musculoskeletal model.
A skin surface model of the hand was also generated from the CT data as a 3D polygonal mesh model. The surface naturally deforms as the joints move, based on a skin deformation algorithm13. The skin surface is necessary to represent the contact between the hand and grasped object. However, to reduce the computational cost, the surface of the hand was approximated by an aggregate of 65 spheres representing the hand surface, which was used to avoid the penetration of the hand into the object in the search for the grasping posture.
Muscle model
As listed in Table 1, a total of 37 hand muscles were included in the hand model. Each muscle generates a force by receiving a muscle signal from a corresponding motor neuron, as follows:
| 1 |
where is the muscle force, is the maximum muscle force, and ai is the activation of the ith muscle (0 ≤ ai ≤ 1). The maximum force of the muscles was determined as shown in Table 1 by referring to Li et al.11, who reported values based on the physiological cross-sectional areas of the hand muscles in the study by Brand and Hollister14 and specific muscle tension (35 N/cm2 15). The pennation angle was not considered in the calculation because it is typically < 10° for hand muscles; thus, it does not significantly affect the force-generating capacity of the muscles.
Table 1.
Muscle parameters of the hand musculoskeletal model.
| Finger | No | Muscle | Abb | Max Force [N] | Moment arm [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 1CMC | 1MP | 1IP | |||||||
| Flex-Ext | Add-Abd | Flex-Ext | Add-Abd | Flex-Ext | |||||
| Thumb | 1 | Flexor pollicis longus | FPL | 2.7 | 14.3 | 0.2 | 13.6 | − 0.1 | 8.7 |
| 2 | Extensor pollicis longus | EPL | 1.3 | − 8.1 | − 9.5 | − 8.5 | − 4.4 | − 4.1 | |
| 3 | Abductor pollicis longus | ABPL | 3.1 | − 7.1 | 10.5 | 0 | 0 | 0 | |
| 4 | Extensor pollicis brevis | EPB | 0.8 | − 13 | 3.2 | − 8.6 | 3.2 | 0 | |
| 5 | Abductor pollicis brevis | ABPB | 1.1 | − 3.9 | 16.5 | 2.6 | 16.5 | 0 | |
| 6 | Flexor pollicis brevis | FBP | 1.3 | 13.4 | 10.5 | 8.8 | 10.5 | 0 | |
| 7 | Opponens pollicis | OP | 1.9 | 12.9 | 4.8 | 0 | 4.8 | 0 | |
| 8 | Adductor pollicis transverse | APt | 3 | 36.9 | − 20.6 | 9.7 | − 20.6 | 0 | |
| 9 | Adductor pollicis oblique | APo | 3 | 27 | − 17 | 8.2 | − 17 | 0 | |
| Finger | No | Muscle | Abb | Max Force [N] | Moment arm [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 2MP | 2PIP | 2DIP | |||||||
| Flex-Ext | Add-Abd | Flex-Ext | Flex-Ext | ||||||
| Index | 10 | Flexor digitorum superficialis 2 | FDS2 | 2 | 11.9 | 1.7 | 13.6 | 0 | |
| 11 | Flexor digitorum profundus 2 | FDP2 | 2.7 | 10.2 | 0.4 | − 8.5 | 4 | ||
| 12 | Extensor digitorum communis 2 | EDC2 | 1 | − 9.4 | 0.7 | 0 | − 1.6 | ||
| 13 | Extensor indicis | EI | 1 | − 9.4 | 0.7 | − 8.6 | − 1.6 | ||
| 14 | 1st lumbrical | 1LU | 0.2 | 9.6 | − 9.9 | 2.6 | − 2 | ||
| 15 | 1st palmar interossei | 1PI | 1.3 | 6.4 | 8.8 | 8.8 | − 2 | ||
| 16 | 1st dorsal interossei | 1DI | 3.2 | 4.4 | − 9.6 | 0 | 0 | ||
| Finger | No | Muscle | Abb | Max Force [N] | Moment arm [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 3MP | 3PIP | 3DIP | |||||||
| Flex-Ext | Add-Abd | Flex-Ext | Flex-Ext | ||||||
| Middle | 17 | Flexor digitorum superficialis 3 | FDS3 | 3.4 | 11.5 | 0.6 | 5.3 | 0 | |
| 18 | Flexor digitorum profundus 3 | FDS3 | 3.4 | 9.2 | 0.2 | 7.1 | 4.2 | ||
| 19 | Extensor digitorum communis 3 | EDC3 | 1.9 | − 9.3 | − 0.9 | − 3.3 | − 1.5 | ||
| 20 | 2nd lumbrical | 2LU | 0.2 | 10.5 | 8.2 | − 2.8 | − 1.9 | ||
| 21 | 2nd dorsal interossei | 2DI | 2.5 | 8 | 9.4 | − 1.1 | − 0.8 | ||
| 22 | 3rd dorsal interossei | 3DI | 2 | 3.4 | − 7.6 | − 2.6 | − 1.8 | ||
| Finger | No | Muscle | Abb | Max Force [N] | Moment arm [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 4MP | 4PIP | 4DIP | |||||||
| Flex-Ext | Add-Abd | Flex-Ext | Flex-Ext | ||||||
| Ring | 23 | Flexor digitorum superficialis 4 | FDS4 | 2 | 9.9 | − 1.2 | 5 | 0 | |
| 24 | Flexor digitorum profundus 4 | FDP4 | 3 | 8.9 | − 0.8 | 6.2 | 4.1 | ||
| 25 | Extensor digitorum communis 4 | EDC4 | 1.7 | − 8.1 | − 0.5 | − 2.4 | − 1.2 | ||
| 26 | 3rd lumbrical | 3LU | 0.1 | 6.6 | − 7.5 | − 2 | − 1.5 | ||
| 27 | 2nd palmar interossei | 2PI | 1.2 | 3.1 | − 7.6 | − 2 | − 1.5 | ||
| 28 | 4th dorsal interossei | 4DI | 1.7 | 4.7 | 7.1 | − 1.2 | − 0.9 | ||
| Finger | No | Muscle | Abb | Max Force [N] | Moment arm [mm] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 5MP | 5PIP | 5DIP | |||||||
| Flex-Ext | Add-Abd | Flex-Ext | Flex-Ext | ||||||
| Little | 29 | Flexor digitorum superficialis 5 | FDS5 | 0.9 | 8.6 | 3.2 | 4.7 | 0 | |
| 30 | Flexor digitorum profundus 5 | FDP5 | 2.8 | 8.5 | 4 | 5.9 | 3.2 | ||
| 31 | Extensor digitorum communis 5 | EDC5 | 0.9 | − 4.9 | 0.9 | − 2.6 | − 1.3 | ||
| 32 | Extensor digiti minimi | EDM | 1 | − 4.8 | 0.9 | − 2.6 | − 1.3 | ||
| 33 | Abductor digiti minimi | ABDM | 1.4 | 4.7 | − 8 | − 2 | − 1.5 | ||
| 34 | Flexor digiti minimi brevis | FDMB | 0.4 | 7.9 | 0 | 0 | 0 | ||
| 35 | 4th lumbrical | 4LU | 2 | 6.3 | 7.2 | − 2.2 | − 1.7 | ||
| 36 | 3rd palmar interossei | 3PI | 1 | 2.1 | 7.7 | − 2 | − 1.5 | ||
| 37 | Opponens digiti minimi | ODM | 2 | 6 | 0 | 0 | 0 | ||
Abb = abbreviation. CMC = Carpometacarpal joint, MP = Metacarpophalangeal joint, IP = Interphalangeal joint, PIP = Proximal IP joint, DIP = Distal IP joint.
The moment arms of the muscles were assumed to be constant, irrespective of the joint angle, and were determined with reference to An et al.16, Smutz et al.17, and Albrecht et al.18, as shown in Table 1. The joint torques generated by muscle activation a (vector of ai) can be written as
| 2 |
where is the joint torque vector, is the moment-arm matrix, and is the diagonal matrix of .
Grasping mechanics
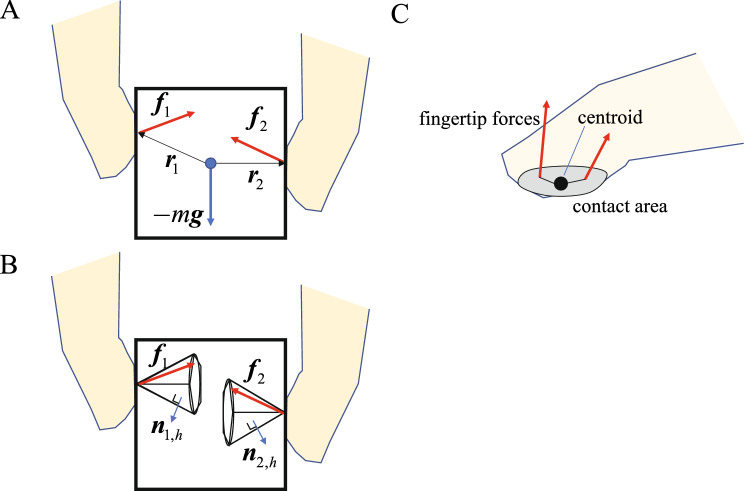
When the hand stably grasps an object, appropriate fingertip forces must be generated by the activation of muscles to achieve static equilibrium of forces and moments applied to the object (Fig. 2A). The force and moment equilibrium conditions of the object can be written as:
| 3 |
where I is a 3 × 3 identity matrix, S is a skew-symmetric matrix representing cross multiplication (), is the position vector connecting the center of mass (COM) of the object to the kth contact point where the kth fingertip force () is applied, m is the mass of the object, and g is the gravitational acceleration. Matrix G is a 6 × 3n matrix referred to as a grasp matrix.
Figure 2.
Grasping mechanics. (A) Forces applied to the object. (B) Friction cone approximated by a polygonal pyramid. The fingertip force vector must be positioned inside the friction cone. (C) Modeling of the contact of the distal phalanx. Two contact points 2 mm away from the centroid of the contact area were introduced to account for generation of a torsional moment during precision grip.
In addition, to achieve stable grasping of an object without slip, Coulomb’s law of static friction must be satisfied, i.e., tangential force must be smaller than the normal force multiplied by the friction coefficient (µ) of the contact surface. For stable contact without slip to occur, the fingertip force vector must be positioned inside the friction cone that determines the set of tangential and normal forces that can be applied to achieve contact without slip (Fig. 2B). Therefore, the apical angle of the frictional cone is given by . If the friction cone is approximated by a polygonal pyramid (Fig. 2B), the condition necessary for contact without slip, i.e., for each fingertip force to always be positioned inside the friction cone, can be expressed as11:
| 4 |
where is the normal vector of the hth side surface of the kth frictional pyramid, corresponding to the kth contact (fingertip) force. In this study, each frictional cone was approximated using a twelve-sided pyramid.
In this study, we assumed that the contact between the object and each segment could be represented by a single contact point, the location of which was determined by the centroid of the contact area. Therefore, a torsional moment with respect to the normal at the contact point was not considered in the present study. However, the contact is actually a so-called soft contact allowing the finger to generate a torsional moment with respect to the normal at the contact point. To account for this, we introduced two contact points for the most distal end of each finger (distal phalanx), 2 mm away from the centroid of the contact area in a precision grip between the thumb and index finger (Fig. 2C).
Mapping between fingertip forces and muscle activations
The muscles must be activated by the central nervous system to generate the fingertip forces necessary for successful grasping. Therefore, the relationship between fingertip forces and muscle activation should be established.
The relationship between the fingertip forces and joint torque is given as
| 5 |
where J is the 3n × 21 Jacobian matrix of the contact points with respect to the joint angles ( where q is the 21 × 1 vector of joint angles and c is the 3n × 1 vector of the contact points represented in the global coordinate system) and f is the contact force vector (). Therefore, the relationship between the muscle activation vector and fingertip force vector is
| 6 |
Estimation of the grasping posture by minimizing muscle effort
The present study explored the kinematic posture of the hand model that minimizes the sum of squared muscle activations while satisfying grasping mechanics. The minimization problem can be formulated as
| 7 |
Equation 7 is subject to the following linear equality and inequality constraints (Eqs. 3, 4, and 6 and range of muscle activation):
| 8 |
This minimization problem can be reformulated as a quadratic programming problem of finding vector x (), which minimizes the following quadratic objective function that is identical to Eq. (7):
| 9 |
subject to
| 10 |
| 11 |
where N is a matrix of the normal vectors of the side surfaces of the frictional pyramids, defined as:
| 12 |
Inverse kinematics of the hand
The fingertips must be in contact with the surface of the grasped object. Therefore, to determine the grasping posture that minimizes muscle effort, we searched for the positions of the fingertips on the surface of the object, and the corresponding hand posture was calculated by solving the inverse kinematics. Specifically, the position and orientation vectors of the carpal segment (p, e) and joint angle vector (q) were calculated for the given target fingertip positions to minimize the objective function (L) using a quasi-Newtonian method.
| 13 |
where is the position of the lth fingertip (), represented as a function of p, e, and q; is the corresponding target position; is the square of the penetration depth of the hand surface represented by the 65 spheres and grasped object; and are the initial position and orientation of the carpal segment, respectively; are the initial (anatomically natural) joint angles of the hand; and are the weighting coefficients. Therefore, the hand posture was calculated such that the fingertips were in contact with the object at the target positions, thereby ensuring that the hand surface did not penetrate the object while minimizing deviations from the neutral joint angles of the hand.
Computational flow
Given the initial guess of the fingertip positions and the carpal segment position and orientation, hand kinematics were calculated based on Eq. (13). Subsequently, the fingertip forces and muscle activations were calculated by minimizing the quadratic function in Eq. (9) under the constraints of Eqs. (10–12), and the value of objective function E was calculated. If no solution satisfied the constraints, a sufficiently large value (sum of square error between the current and initial hand postures) was assigned to E. The fingertip positions were updated, and the above calculations were repeated until objective function E converged to a minimum point. We used the covariance matrix adaptation evolution strategy (CMA-ES) algorithm19 for this optimization process.
However, it must be noted that human fingertip force control includes a safety margin that is higher than the actual fingertip forces necessary to stably grasp an object against unexpected perturbations20,21. In the present study, to account for this, we assumed that the central nervous system estimated the friction coefficient (µ) of the object surface to be half of the actual value (if the value of µ is 0.8, it is estimated to be 0.4 in the central nervous system for grasping).
Experimental validation of the model
To evaluate whether the proposed methodology can replicate the kinematics and kinetics of a human hand grasping an object, it is necessary to experimentally quantify the three-dimensional fingertip forces and hand posture simultaneously when grasping an object. For this purpose, we developed a custom-made wireless fingertip force-sensing device. The device consisted of two six-axis load cells (CFS018CA101AS, Leptrino, Komoro, Japan), amplifiers, A/D converters, and Wi-Fi modules with batteries. The load cells were arranged in opposite directions and an aluminum plate (20 mm × 49 mm) was attached to each load cell (Fig. 3) so that the forces applied by the thumb and index fingers could be measured independently. The amplifiers, A/D converters, and Wi-Fi modules with batteries were attached to the top and bottom of the load cell housing. The device had a weight of 198.4 g. The device is unique in that the electric power is supplied from the batteries in the device, and the data is transmitted to a tablet PC via Wi-Fi communication. Hence, the device has no physical contact with the outside, allowing for precise physiological investigations of how the central nervous system achieves the force and moment balance of the grasped object.
Figure 3.
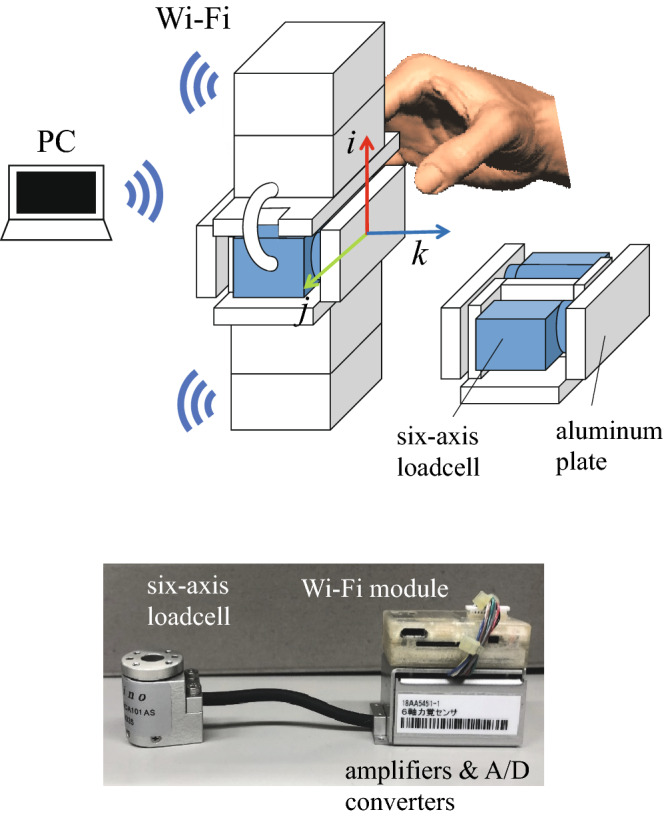
Custom-made wireless fingertip force-sensing device. The device consisted of two six-axis load cells, amplifiers, A/D converters, and Wi-Fi modules with batteries. An aluminum plate (20 mm × 49 mm) was attached to each load cell so that the forces applied by the thumb and index fingers could be measured independently. The amplifiers, A/D converters, and Wi-Fi modules with batteries were attached to the top and bottom of the load cell housing. The vectors i,j,k represent the sensor-fixed local coordinate system.
In the present study, we asked one male participant (178 cm, 63 kg, right-handed), whose hand was approximately equal in size to the hand model, to pinch, lift, and hold the fingertip force-sensing device in the air using the thumb and index finger under different conditions. Specifically, we asked the participant to pinch the center, far side, and near side of the device (Fig. 4) with fingertips (Conditions A, B, and C, respectively) and finger pulps (Conditions D, E, and F, respectively), and the forces applied to the device and the centers of pressure were measured. The participant was instructed to pinch the device as naturally as possible, and no instructions regarding muscle effort and fingertip forces were provided. Two types of precision grip were compared to check if the proposed method can correctly predict that precision grip using fingertips requires larger muscle effort than that using finger pulps. The hand kinematics were recorded using a motion capture system consisting of 17 cameras (OptiTrack; NaturalPoint, Corvallis, OR, USA) (Fig. 5A). A total of 30 reflective markers (4 mm diameter) were attached to the dorsal surfaces of five fingertips; five distal, four intermediate, and five proximal phalangeal joints; five metacarpophalangeal joints; first carpometacarpal joint; four points on the dorsal surface of the carpal bones; radial side of the second metacarpal head; ulnar side of the fifth metacarpal head; ulnar and radial styroid processes; and dorsoradial and dorsoulnar surfaces of the midpoint of the first metacarpal to capture the hand kinematics during the precision grip task (Fig. 5B). We additionally captured the positions of the 12 markers placed on the grasped device (Fig. 5A) to quantify the position and orientation of the grasped object. Measurement was conducted once for each condition confirming that grasping of the device was quite stereotyped at rehearsal. The experiment took about 90 min. Informed consent was obtained from the participant. This study was approved by the Committee on Ergonomic Experiments, AIST (HF2020-618). All methods were performed in accordance with the relevant guidelines and regulations.
Figure 4.
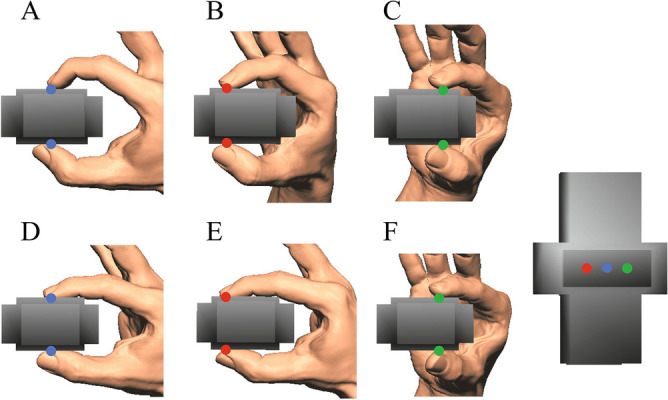
Six measured conditions. We asked the participant to pinch the center, far side, and near side of the device with fingertips (A, B, and C, respectively) and finger pulps (D, E, and F, respectively), and the forces applied to the device and the centers of pressure were measured.
Figure 5.
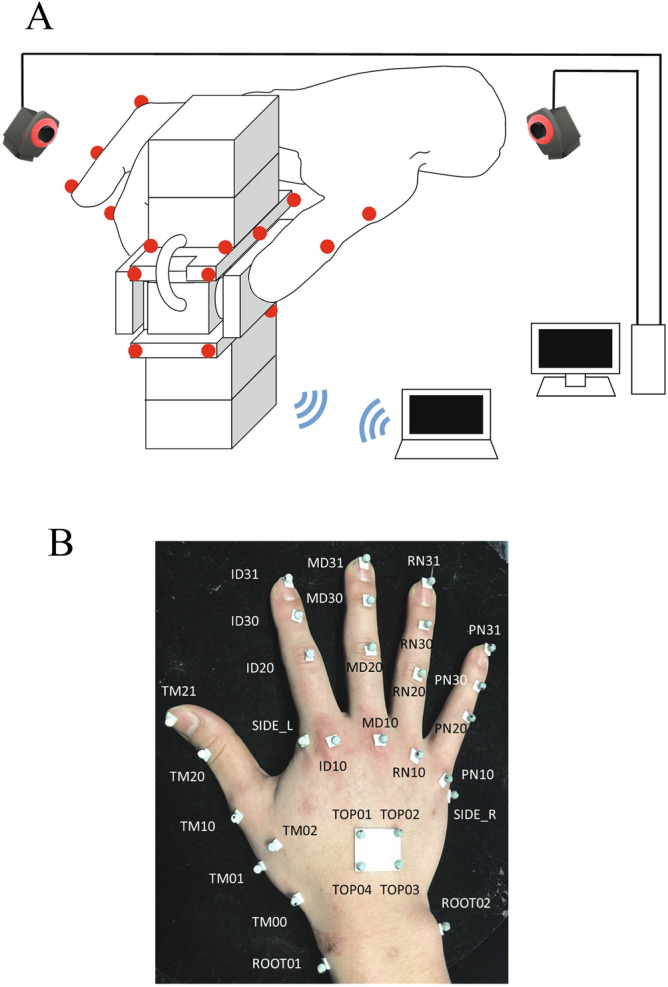
Measurement of hand kinematics using a motion capture system (A) and placement of reflective markers on the dorsal surface of the hand (B).
We replicated the measured hand pose and object in a virtual space using the motion-captured marker positions to minimize the sum of distances between each motion-captured marker and corresponding markers on the hand model. It must be noted, however, that the calculated hand model could penetrate the object or was not in contact with the object because the hand model was not identical to the hand on the actual subject, and there were tiny discrepancies between the position of the markers on the actual hand and those on the model. Therefore, we adjusted the hand posture in the vicinity of the object to minimize the square sum of muscle activations while satisfying the kinematic (i.e., the thumb and index finger were on the aluminum plates of the object) and kinetic constraints (Eqs. (10)–(12)) that must be satisfied for object grasping. By comparing the magnitudes and directions of the measured and estimated fingertip force vectors, we evaluated how well the proposed method could predict grasping kinetics. The accuracy and precision of each force component and moment were evaluated by calculating the mean and standard deviation of the differences between the measured and estimated values.
In addition, we asked the participant to freely pinch the device in a self-selected manner and evaluated whether the proposed method could predict the actual fingertip positions, hand pose, and fingertip forces for a given object based on the present iterative method. In the CMA-ES optimization, the step size was set sufficiently large such that the entire search space (aluminum plate surfaces) was sampled to avoid getting trapped in a local minimum. We solved this optimization problem by using two different sets of initial values (Case I and II, far end and near end of the aluminum plates, respectively) to confirm the convergence of the solution.
Results
Table 2 compares the estimated fingertip forces and moments of the thumb and index finger with the corresponding measured values under the six conditions. The forces and moments are represented by an object-fixed local coordinate system. The estimated fingertip forces generally agreed with the corresponding measured data. The values of the objective function after the optimization are compared in Fig. 6. The value of the objective function tended to be smaller when the object was held at the center of each plate (Conditions A and D). The value was smaller if the object was held with the finger pulps rather than the fingertips.
Table 2.
Comparisons of measured and simulated forces and moments of six grasping conditions.
| Thumb | Index | Thumb | Index | |||||
|---|---|---|---|---|---|---|---|---|
| Fi [N] | Fj [N] | Fk [N] | Fi [N] | Fj [N] | Fk [N] | Mk [Nm] | Mk [Nm] | |
| Fingertip | ||||||||
| A. center | ||||||||
| measured | 0.90 | − 0.32 | − 2.62 | 1.05 | 0.18 | 2.64 | − 0.0001 | − 0.0011 |
| simulated | 0.90 | − 0.63 | − 3.02 | 1.04 | 0.54 | 3.03 | − 0.0019 | − 0.0023 |
| Δ | 0.00 | − 0.32 | − 0.40 | − 0.01 | 0.35 | 0.39 | − 0.0018 | − 0.0013 |
| B. far side | ||||||||
| measured | 0.34 | − 0.26 | − 8.11 | 0.68 | − 1.30 | 8.08 | 0.0034 | − 0.0016 |
| simulated | 0.55 | − 0.93 | − 7.35 | 0.71 | − 0.55 | 7.42 | − 0.0043 | − 0.0028 |
| Δ | 0.21 | − 0.68 | 0.77 | 0.03 | 0.76 | − 0.66 | − 0.0078 | − 0.0012 |
| C. near side | ||||||||
| measured | 0.16 | − 0.46 | − 5.03 | 0.84 | − 1.09 | 4.94 | − 0.0005 | − 0.0066 |
| simulated | 0.34 | − 0.93 | − 4.85 | 0.52 | − 0.81 | 4.78 | − 0.0084 | − 0.0069 |
| Δ | 0.19 | − 0.47 | 0.18 | − 0.32 | 0.28 | − 0.17 | − 0.0079 | − 0.0003 |
| Finger pulp | ||||||||
| D. center | ||||||||
| measured | 0.84 | − 0.37 | − 3.70 | 1.09 | 0.32 | 3.79 | − 0.0033 | − 0.0069 |
| simulated | 1.30 | 0.32 | − 3.60 | 0.95 | − 0.19 | 3.61 | − 0.0015 | − 0.0052 |
| Δ | 0.45 | 0.69 | 0.10 | − 0.13 | − 0.51 | − 0.18 | 0.0018 | 0.0017 |
| E. far side | ||||||||
| measured | 0.66 | − 0.62 | − 4.06 | 1.27 | 0.63 | 4.09 | − 0.0063 | 0.0029 |
| simulated | 1.31 | 0.36 | − 3.49 | 0.64 | − 0.42 | 3.51 | 0.0005 | 0.0037 |
| Δ | 0.65 | 0.98 | 0.58 | − 0.64 | − 1.05 | − 0.58 | 0.0068 | 0.0008 |
| F. near side | ||||||||
| measured | 0.13 | − 0.66 | − 3.31 | 0.78 | − 0.92 | 3.44 | − 0.0021 | − 0.0077 |
| simulated | 0.98 | − 0.94 | − 3.92 | − 0.19 | − 0.84 | 3.90 | 0.0007 | − 0.0110 |
| Δ | 0.84 | − 0.28 | − 0.61 | − 0.97 | 0.09 | 0.45 | 0.0027 | − 0.0033 |
| Accuracy | 0.39 | − 0.01 | 0.10 | − 0.34 | − 0.01 | − 0.12 | − 0.0010 | − 0.0006 |
| Precision | 0.32 | 0.68 | 0.54 | 0.39 | 0.65 | 0.47 | 0.0059 | 0.0018 |
Fi, Fj, and Fk are the load (vertical), transverse and grip (normal) forces, respectively, represented in the object coordinate system.
Mk is the torsional moment at the center of pressure around a normal to the contact surface.
Figure 6.
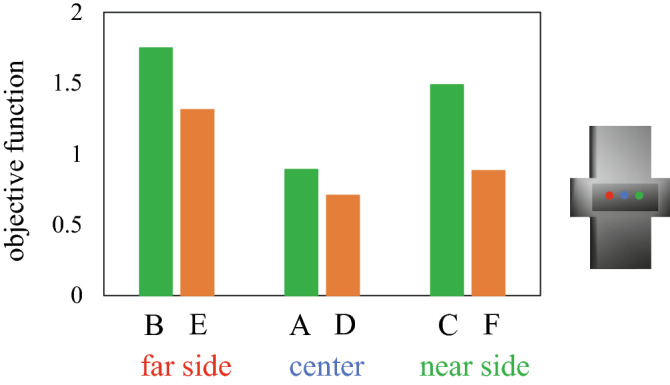
Comparison of the objective functions when the participant pinched the center, far side, and near side of the device with fingertips (A, B, and C, respectively) and finger pulps (D, E, and F, respectively). The value was smaller if the object was held with the finger pulps (orange) rather than the fingertips (green).
The measured fingertip forces and moments of the free pinch were compared with those estimated based on the present method, and the comparison is presented in Table 3 and Fig. 7. The values of the objective function obtained from an optimization that started from the two sets of initial values (I and II) were almost identical (= 0.264), indicating that quasi-global optimal solutions were obtained using the CMA-ES. The estimated fingertip forces were generally comparable to the corresponding measured data; however, the normal components of the estimated fingertip forces (grip forces) in the simulation were substantially smaller than those in the measurement. Furthermore, the value of the objective function for the measured grasping posture was 0.398, indicating that the estimated grasping kinetics in this study were better in minimizing the muscle effort than those that were measured. The differences in the joint angles were − 9.5 ± 20.3 degrees for the case I and − 4.7 ± 14.3 degrees and for case II (corresponding to 12.4% and 8.5% of joint range of motion22, respectively), indicating that the hand kinematics for a given object were predicted with reasonable accuracy considering the fact that the hand model was not identical to the measured hand. The estimated muscle activations are presented in Fig. 7B. The present simulation predicted that FPL, EPL, APL, FPB, FDS2, FDP2, EDC2, EI, and 1DI were activated during the free pinching of the object.
Table 3.
Comparisons of measured and simulated forces and moments of free pinch.
| Thumb | Index | Thumb | Index | |||||
|---|---|---|---|---|---|---|---|---|
| Fi [N] | Fj [N] | Fk [N] | Fi [N] | Fj [N] | Fk [N] | Mk [Nm] | Mk [Nm] | |
| Measured | 0.98 | 0.52 | − 3.03 | 0.97 | − 0.62 | 3.11 | − 0.0052 | − 0.0010 |
| Simulated | ||||||||
| I | 0.93 | 0.32 | − 1.69 | 1.01 | − 0.32 | 1.69 | 0.0000 | − 0.0002 |
| II | 0.78 | 0.02 | − 1.68 | 1.17 | − 0.02 | 1.68 | 0.0001 | − 0.0002 |
Figure 7.
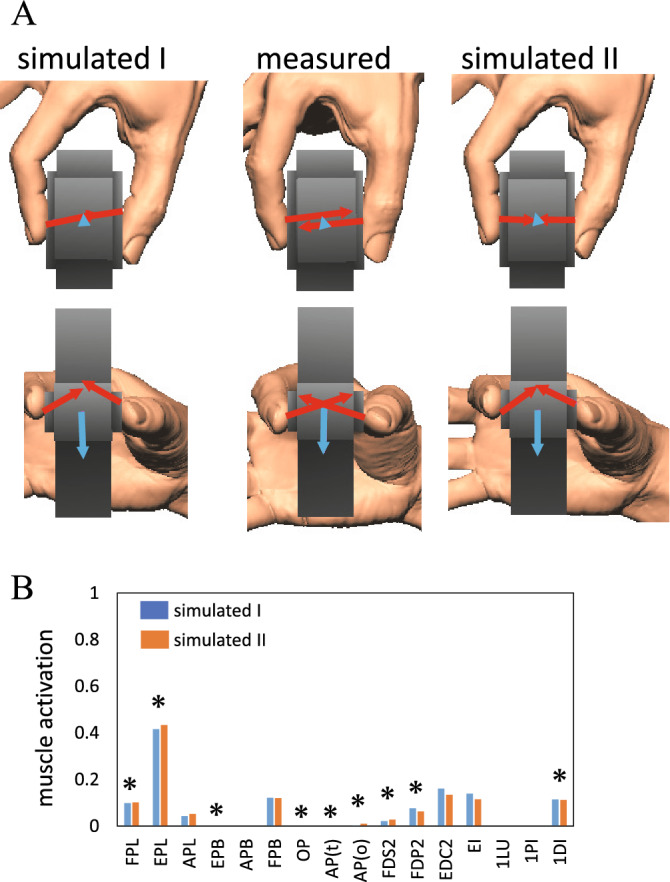
Comparisons of the measured fingertip forces of the free pinch with those estimated based on the present method from the two sets of initial values (I and II) (A). The estimated muscle activations are also presented (B). Asterisks indicated muscles that are reportedly active during precision grip25–27.
Discussion
The present study proposes a physiologically based method to predict the precision grip posture of the human hand. Specifically, the minimization of muscle effort, i.e., the sum of squared muscle activations, was used as an objective function to search for the grip posture. Overall, the proposed method reasonably estimates the kinematics and kinetics of hand grasping for a given object. Therefore, the proposed method can be used to virtually evaluate how a change in the design and dimensions of a product such as a camera alters its usability, without conducting ergonomic sensory evaluation by creating physical mockups of the product with different designs or dimensions, thereby reducing the cost and time required for product design and development.
It should be noted, however, that the predicted fingertip forces and the objective function of the predicted grip posture were slightly lower than that of the measured grip posture. This possibly indicates that the grip kinematics and kinetics for a given object may not be rigorously determined by the exact global optimal solution but are loosely determined within a range of quasi-optimal solutions in the vicinity of the global optimal solution. This is reasonable because a small deviation from the true optimal solution is not significantly different from the optimal solution, and no critical differences exist in of the mechanics and energetics of grasping. This is probably one of the reasons why there is a certain range of variability in the grasping kinematics and kinetics for a certain object. Therefore, the present study indicated that the proposed method for predicting the grasping posture of the human hand based on a minimization of the muscle load may be effective for the virtual ergonomic assessment of a hand-held product.
The present study predicted that the objective function (muscle effort) would be smaller when the object was held at the center than when it was held at the far and near sides (Fig. 6). This is because the COM of the object was located at the center of the object. When the object was pinched at the center by the thumb and index finger, the torsional moments due to gravitational force were only minimally applied to the fingertips because of the small moment arms. Conversely, if the object was pinched away from the COM, relatively large torsional moments that needed to be balanced by larger muscle activations were generated at the fingertips. In addition, the objective function was predicted to be larger when the object was grasped only by the fingertips than when it was grasped by the finger pulp. This was because larger joint torques, hence muscle forces, were necessary to generate a force at the distal end of the finger rather than somewhere relatively proximal. Therefore, the estimated values of the objective function for the six conditions were reasonable for the mechanics of object grasping.
Another unique contribution of the present study is that we attempted to validate the proposed estimation method by measuring the actual forces applied to a grasped object using a custom-made wireless fingertip force-sensing device. To clarify the kinetics of a human precision grip, previous studies have attempted to measure the fingertip forces applied to an object during the precision grip23,24. However, in these previous studies, the grasped object was connected to an electronic wire, making comparisons between the predicted and measured fingertip forces difficult because an unknown external force could be applied to the object in addition to the fingertip forces due to the wire. To the best of our knowledge, this is the first study attempting to construct an experimental setup allowing complete investigation of the kinetics of a precision grip, as well as experimentally validating the simulation of object grasping.
In the present study, we did not record electromyography (EMG) signals of the hand muscles for the evaluation of the predicted muscle activation because of the invasive nature of EMG recordings using wire electrodes, and the inability to separate individual hand muscle signals using surface electrodes. Nevertheless, although direct comparisons were not possible, we compared the muscle activations in Fig. 7B with those in previously published EMG data obtained during a human precision grip25–27. The predicted activations of FPL, EPL, FDS2, FDP2, and 1DI were consistent with those reported previously. However, the present study predicted that APL, FPB, EDC2, and EI were active, although they were reportedly inactive, and OP and AP were inactive, although they were reportedly active during precision grip. Therefore, the predicted muscle activations were not in perfect agreement with those in the previous reports. This discrepancy could be due to the differences between the kinematic and kinetic conditions of the precision grip of the previous and present studies. For a more rigorous validation of the proposed estimation method, in vivo simultaneous recordings of the fingertip forces and EMGs of the hand muscles during object grasping are necessary and should be addressed in future studies.
The discrepancies between the predicted and measured forces, moments, and muscle activation could also be due to errors associated with modeling the human hand. In this study, the moment arms of the muscles were assumed to be constant irrespective of changes in joint angles, but this simplification was not valid and might have affected the estimation results. For more precise modeling, each muscle path should be defined as a series of points connected by line segments (e.g., Mirakhorlo et al.28; Saito et al.29), and the dorsal aponeurosis of the finger should be modeled as a web-like structure30,31. Also, the present model did not incorporate passive elastic elements around the joints and muscle properties, such as force–length and force–velocity relationships (e.g., Zajac15). Further improvements in the musculoskeletal model might also be necessary to improve the accuracy of the predicted kinematics and kinetics of the hand grasping an object. In addition, this study considered grasping an object using only two fingers. We believe that an extension of the proposed method to entire-hand grasping is easy, but this should be confirmed. Furthermore, the present posture estimation method is based on inverse dynamics, but forward dynamics can also be employed to predict the hand posture for a given object32,33. This should be investigated further in future studies. Finally, the present study compared the estimated kinematic and kinetics of the hand model with the corresponding experimental data of the participant whose hand was equal in size to the hand model. However, for more precise validation of the proposed method, it is necessary to make such comparisons with larger numbers of participants with different hand dimensions. However, this will require the development of a representative hand model by warping the present hand model based on a statistical database of hand dimensions, and a method to generate hand models of participants by deforming the representative hand model. These should also be addressed in future research.
Acknowledgements
This study was supported in part by Grants-in-Aid for Scientific Research from JSPS (no. 21H03526).
Author contributions
M.T. and N.O. conceived and designed the study. T.N., Y.A., Y.E., and M.T. constructed the model and conducted calculation, data collection and the analysis. T.N. and N.O. drafted the paper which was reviewed and edited by all authors.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Maurya CM, Karmakar S, Das AK. Digital human modeling (DHM) for improving work environment for specially-abled and elderly. SN Appl. Sci. 2019;1:1326. doi: 10.1007/s42452-019-1399-y. [DOI] [Google Scholar]
- 2.Wolf A, Miehling J, Wartzack S. Challenges in interaction modelling with digital human models—A systematic literature review of interaction modelling approaches. Ergonomics. 2020;63:1442–1458. doi: 10.1080/00140139.2020.1786606. [DOI] [PubMed] [Google Scholar]
- 3.Endo Y, et al. Optimization-based grasp posture generation method of digital hand for virtual ergonomics assessment. SAE Int J. Passeng. Cars Electron. Electr. Syst. 2009;1:590–598. doi: 10.4271/2008-01-1902. [DOI] [Google Scholar]
- 4.Endo, Y., Miyata, N., Kouchi, M., Mochimaru, M., & Kanai, S. Advances in Applied Digital Human Modeling, Chap. Physically-Based Grasp Posture Generation for Virtual Ergonomic Assessment Using Digital Hand 166–175 (CRC Press, Boca Raton 2011).
- 5.Kurtzer I, Pruszynski JA, Herter TM, Scott SH. Primate upper limb muscles exhibit activity patterns that differ from their anatomical action during a postural task. J. Neurophysiol. 2006;95:493–504. doi: 10.1152/jn.00706.2005. [DOI] [PubMed] [Google Scholar]
- 6.Guigon E, Baraduc P, Desmurget M. Computational motor control: redundancy and invariance. J. Neurophysiol. 2007;97:331–347. doi: 10.1152/jn.00290.2006. [DOI] [PubMed] [Google Scholar]
- 7.O’Sullivan I, Burdet E, Diedrichsen J. Dissociating variability and effort as determinants of coordination. PLoS Comput. Biol. 2009;5:1–8. doi: 10.1371/journal.pcbi.1000345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hirashima M, Oya T. How does the brain solve muscle redundancy? Filling the gap between optimization and muscle synergy hypotheses. Neurosci. Res. 2016;104:80–87. doi: 10.1016/j.neures.2015.12.008. [DOI] [PubMed] [Google Scholar]
- 9.Zhang H, Ye Y, Shiratori T, Komura T. ManipNet: Neural manipulation synthesis with a hand-object spatial representation. ACM Trans. Graph. 2021;40:1–14. [Google Scholar]
- 10.Roa MA, Suarez R. Grasp quality measures: review and performance. Auton. Robots. 2015;38:65–88. doi: 10.1007/s10514-014-9402-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Li Y, Fu JL, Pollard NS. Data driven grasp synthesis using shape matching and task-based pruning. IEEE Trans. Vis. Comput. Graph. 2007;13:732–747. doi: 10.1109/TVCG.2007.1033. [DOI] [PubMed] [Google Scholar]
- 12.Ogihara N, et al. Development of an anatomically based whole-body musculoskeletal model of the Japanese Macaque (Macaca fuscata) Am. J. Phys. Anthropol. 2009;139:323–338. doi: 10.1002/ajpa.20986. [DOI] [PubMed] [Google Scholar]
- 13.Lewis, J. P., Cordner, M. & Fong, N. Pose space deformation: a unified approach to shape interpolation and skeleton-driven deformation. Proc. ACM SIGGRAPH00. 165–172 (2000).
- 14.Brand PW, Hollister AM. Clinical mechanics of the hand. 3. Missouri: Mosby; 1999. [Google Scholar]
- 15.Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Crit. Rev. Biomed. Eng. 1989;17:359–411. [PubMed] [Google Scholar]
- 16.An KN, Ueba Y, Chao EY, Cooney WP, Linscheid RL. Tendon excursion and moment arm of index finger muscles. J. Biomech. 1983;16:419–425. doi: 10.1016/0021-9290(83)90074-X. [DOI] [PubMed] [Google Scholar]
- 17.Smutz W, et al. Mechanical advantage of the thumb muscles. J. Biomech. 1998;31:565–570. doi: 10.1016/S0021-9290(98)00043-8. [DOI] [PubMed] [Google Scholar]
- 18.Albrecht, I., Haber, J. & Seidel, H.-P. Construction and animation of anatomically based human hand models. Proc. 2003 ACM SIGGRAPH/ Eurographics SCA. 98–109 (2003).
- 19.Hansen N, Ostermeier A. Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 2001;9:159–195. doi: 10.1162/106365601750190398. [DOI] [PubMed] [Google Scholar]
- 20.Westling G, Johansson RS. Factors influencing the force control during precision grip. Exp. Brain Res. 1984;53:277–284. doi: 10.1007/BF00238156. [DOI] [PubMed] [Google Scholar]
- 21.Kinoshita H, Francis PR. A comparison of prehension force control in young and elderly individuals. Eur. J. Appl. Physiol. Occup. Physiol. 1996;74:450–460. doi: 10.1007/BF02337726. [DOI] [PubMed] [Google Scholar]
- 22.Van Ost L. Cram session in goniometry and manual muscle testing. Thorofare: Slack; 2013. [Google Scholar]
- 23.Johansson RS, Westling G. Role of glabrous skin receptors and sensorimotor memory in automatic control of precision grip when lifting rougher or more slippery objects. Exp. Brain Res. 1984;56:550–564. doi: 10.1007/BF00237997. [DOI] [PubMed] [Google Scholar]
- 24.Hiramatsu Y, Kimura D, Kadota K, Ito T, Kinoshita H. Control of precision grip force in lifting and holding of low-mass objects. PLoS ONE. 2015;10:e0138506. doi: 10.1371/journal.pone.0138506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Cooney WP, III, An KN, Daube JR, Askew LJ. Electromyographic analysis of the thumb: a study of isometric forces in pinch and grasp. J. Hand Surg. Am. 1985;10:202–210. doi: 10.1016/S0363-5023(85)80106-4. [DOI] [PubMed] [Google Scholar]
- 26.Long C, II, Conrad PW, Hall EA, Furler SL. Intrinsic-extrinsic muscle control of the hand in power grip and precision handling. An electromyographic study. J. Bone Joint Surg. Am. 1970;52:853–867. doi: 10.2106/00004623-197052050-00001. [DOI] [PubMed] [Google Scholar]
- 27.Maier MA, Hepp-Reymond MC. EMG activation patterns during force production in precision grip. I. Contribution of 15 finger muscles to isometric force. Exp. Brain Res. 1995;103:108–122. doi: 10.1007/BF00241969. [DOI] [PubMed] [Google Scholar]
- 28.Mirakhorlo M, et al. A musculoskeletal model of the hand and wrist: model definition and evaluation. Comput. Methods Biomech. Biomed. Engin. 2018;21:548–557. doi: 10.1080/10255842.2018.1490952. [DOI] [PubMed] [Google Scholar]
- 29.Saito T, Ogihara N, Takei T, Seki K. Musculoskeletal modeling and inverse dynamic analysis of precision grip in the Japanese macaque. Front. Syst. Neurosci. 2021;15:774596. doi: 10.3389/fnsys.2021.774596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Garcia-Elias M, An KN, Berglund L, Linscheid RL, Cooney WP, Chao EY. Extensor mechanism of the fingers: I. A quantitative geometric study. J. Hand Surg. Am. 1991;16:1130–1140. doi: 10.1016/S0363-5023(10)80079-6. [DOI] [PubMed] [Google Scholar]
- 31.Sancho-Bru JL, Perez-Gonzalez A, Vergara-Monedero M, Giurintano D. A 3-D dynamic model of human finger for studying free movements. J. Biomech. 2001;34:1491–1500. doi: 10.1016/S0021-9290(01)00106-3. [DOI] [PubMed] [Google Scholar]
- 32.Gustus A, Stillfried G, Visser J, Jörntell H, van der Smagt P. Human hand modelling: kinematics, dynamics, applications. Biol. Cybern. 2012;106:741–755. doi: 10.1007/s00422-012-0532-4. [DOI] [PubMed] [Google Scholar]
- 33.Moritani Y, Ogihara N. A hypothetical neural network model for generation of human precision grip. Neural Netw. 2019;110:213–224. doi: 10.1016/j.neunet.2018.12.001. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.