Effect of Shape, Size, and Aspect Ratio on Nanoparticle Penetration and Distribution inside Solid Tissues Using 3D Spheroid Models

Abstract

Efficient penetration and uniform distribution of nanoparticles (NPs) inside solid tissues and tumors is paramount to their therapeutic and diagnostic success. While many studies have reported the effect of NP size and charge on intratissue distribution, role of shape, and aspect ratio on NP transport inside solid tissues remain unclear. Here experimental and theoretical studies are reported on how nanoscale geometry of Jet and Flash Imprint Lithography-fabricated, polyethylene-glycol-based anionic nanohydrogels affect their penetration and distribution inside 3D spheroids, a model representing the intervascular region of solid, tumor-like tissues. Unexpectedly, low aspect ratio cylindrical NPs (H/D ≈0.3; disk-like particles, 100 nm height, and 325 nm diameter) show maximal intratissue delivery (>50% increase in total cargo delivered) and more uniform penetration compared to nanorods or smaller NPs of the same shape. This is in contrast to spherical NPs where smaller NP size resulted in deeper, more uniform penetration. Our results provide fundamental new knowledge on NP transport inside solid tissues and further establish shape and aspect ratio as important design parameters in developing more efficient, better penetrating, nanocarriers for drug, or contrast-agent delivery.

1. Introduction

Nanoparticles (NPs) are being investigated extensively for delivery of therapeutic and diagnostic agents. When encapsulated in, or conjugated to NPs, these agents could be protected from degradation and rapid clearance in the body and thus can be targeted to specific diseased cells and tissues with higher efficacy.^[1] NPs can also be directly used as contrast agents in optical as well as magnetic resonance and X-ray based imaging. NPs allow for efficient intracellular delivery of the cargo, thereby providing means to target specific cellular processes, signal transduction pathways, and organelle-specific molecules for both therapeutic and diagnostic applications.^[1]

Intravenous (IV) injection is the most common route for systemic delivery of NP-based drugs and imaging agents. Under normal physiological conditions, mammalian cells lie within a distance of 50–100 μm from the blood vessels in order to obtain oxygen and nutrients.^[2] However, rapidly growing or diseased tissues, such as solid tumors, are fed by immature, leaky and highly disorganized vasculature which results in abnormal tissue-transport properties and areas of tissue that are farther away from the vasculature where quiescent tumor cells persist under low oxygen and nutrient conditions.^[3] Inflammatory disorders of many organs also results in prolonged and excessive angiogenesis.^[4] Various immune cells such as monocytes, macrophages, granulocytes and other leukocytes release angiogenic growth factors leading to leaky vasculature in inflamed tissues.^[4,5] NPs have been shown to passively accumulate around such leaky vasculatures, through the so-called enhanced permeability and retention effect.^[1,6] However, once at the organ site NPs face a series of barriers which limit their diffusion throughout the dense tissue matrix, tortuous paths, and high interstitial pressure.^[7] The permeability of the neovasculature may also vary throughout a tissue niche, potentially leading to an uneven distribution of therapeutic NPs. For example, in tumors, the regions that are farther away from blood vessels escape lethal doses of drugs delivered through IV injections. These cells in the core tumor can develop drug resistance over time and may also cause relapse even after tumor regression following initial therapies.^[8] Thus, in order to effectively treat solid tumors and similar diseased tissues, NPs must be designed such that they are not only able to extravasate through the vasculature but are also (a) able to penetrate deep inside the dense tissue matrix in high amounts and (b) be evenly distributed throughout the tissue.^[3,9]

Since diffusion plays a major role in NP penetration and distribution inside tissue matrix, various strategies have been investigated to increase NP diffusion in order to overcome interstitial tissue barriers.^[10] While some of these approaches have shown promise in vivo, difficulties arise when comparing NP penetration across various animal models and formulations. This is due to the high spatiotemporal complexity of diseased states (e.g., various types of tumors or tumor stages, site and type of inflamed tissue, etc.) experimental conditions and the number of variables present. Recently, spheroids have been proposed as in vitro tumor models and were shown to closely resemble the architecture, biological properties, and physiological characteristics of human tumor tissues.^[11] Spheroids, due to their 3D architecture and in vivo-like extracellular matrix (ECM) production, provide an opportunity to study NP transport (e.g., penetration and distribution) in solid tissues in a more controlled and high-throughput microenvironment.^[12] Spheroids provide an excellent experimental model to decouple transport barriers from other barriers encountered by NPs in their journey to the tissue (e.g., clearance during circulation, vessel permeability, extravasation, etc.). It is important to note that since spheroids have no blood vessels and they are in the order of several hundred microns in size, they are not representative of entire diseased tissue but represent the intervascular parts between blood vessels as well as more avascular parts at the center, i.e., areas that can be represented as a solid tissue matrix. Once NPs extravasate from the “leaky” blood vessels, they must “diffuse” through this dense ECM to reach the bulk tissue and stromal cells. Goodman et al. used spheroids to show that collagenase coated polystyrene beads can be used to disrupt the ECM and allow deeper penetration compared to uncoated beads.^[13] Liang and colleagues showed that smaller gold NPs (down to 2 nm) penetrate deeper in spheroids and in vivo tumors compared to larger particles.^[14] Albanese et al. used an innovative combination of microfluidic and spheroid system to show that for spherical particles, penetration in the tissue is limited by its diameter.^[15] Although in general, the field has found that spherical particles of diameter <100 nm penetrates the best into tumors,^[13–15] no studies have been performed to understand the effects of NP shape on spheroids. Recently, Kim et al. used cylindroids (a cylindrical version of spheroids) as in vitro tumor models to see the effect of surface charge on 6 nm diameter spherical-particle penetration inside the tissue matrix.^[10c] The group showed that cationic NPs are taken up by proliferating cells at the edges of the cylindroid and do not penetrate deep into the matrix. In contrast, anionic particles diffuse quickly into the deeper tissue matrix. It has also been proposed that hydrophilic stealth particles having neutral to anionic surface charge are ideal carriers for drug delivery applications.^[1,6,16]

Recently, research pertaining to the role of shape in particle transport across biological barriers has gained significant interest^[17] and reports have shown the importance of NP shape on tissue and tumor transport. Fernandes et al. used a skin chamber model and showed that polyethylene-glycol (PEG) coated gold nanorods of aspect ratio 2.8 were able to penetrate in higher in both mouse and human skin compared to nanospheres.^[18] Chauhan et al. used shape specific gold NPs and showed that rod-shaped particles diffuse deeper in solid tumors compared to similar sized spherical particles.^[10b] Park et al. also used gold NPs and showed similar results where nanorods were found further away from blood vessels compared to spheres.^[19] However it is difficult to ascertain whether the enhanced penetration of nanorods was due to higher accumulation of particles near tumor regions or because of ability of nanorods to diffuse rapidly within solid tumors.

Many types of inorganic and polymeric NPs are used for various biomedical applications.^[20] As described above, for tissue penetration applications both organic and inorganic particles have been used and have provided valuable information.^{[10b,13–15,19]} Inorganic NPs are easy to prepare and can be scaled up however only limited shapes can be formed. Synthesis of shape-specific polymeric particles requires complex lithography techniques and has lower throughput. However, polymeric particles can be formed into a wide range of shapes using a variety of materials; their physiochemical properties can be tuned,^[21] and they can be used to deliver both hydrophobic and hydrophilic drugs.

Our group has previously shown that disk-shaped, low aspect ratio (L/D < = 0.5) cylindrical nanohydrogels are internalized at greater efficacy in mammalian epithelial, endothelial, and immune cells compared to cuboidal nanorods and that the mechanism of particle uptake is dependent on NP shape as well as cell types.^[22] We also showed that cell-internalization of anionic, hydrophilic NPs, is a complex manifestation of several shape- and size-dependent biophysical parameters. Based on these observations, we hypothesized that nanoscale particle geometry could also play an important role in NP transport within solid tissues. In the present study we tested equivalent-volume hydrophilic, anionic disk-shaped nanocylinders, and nanorods of two different size sets. We compared their penetration and distribution using a solid tissue-like spheroid model.

2. Results

2.1. Spheroid Synthesis

Spheroids were successfully formed using HEK 293 (human embryonic kidney) cells in both static and rotatory conditions, as shown in Figure 1A,B. HEK 293 cells are transformed embryonic kidney cell line with an epithelial morphology, which shows a similar phenotype to that of fast-growing tumor cells regarding metabolic and physiological characteristics, including high hypoxia inducible factor (HIF)-1α expression^[23] active glycolysis,^[24] and accelerated proliferation.^[25] These cells forms uniform tissue spheroids that are highly reproducible and of a controlled size, thus providing a controlled spheroid volume and shape and allowing us to study the effects of NP geometry^[26] while avoiding spheroid-related variables. To ensure uniform distribution of NPs around the spheroid and minimize the effect of sedimentation in in vitro cultures^[22,27] spheroids under rotatory conditions (on a platform rotating at 240 rpm, Figure 1E) were used in all studies to evaluate NP penetration and distribution. As shown in Figure 1C, these spheroids have uniform cell morphology. It has been previously reported that spheroids larger than 350 μm in diameter could mimic avascularized regions of diseased tissues and tumors.^[11b] At this size, they show characteristic hypoxic areas at the center and proliferating cells at the edges.^[11b] Therefore, all experiments were performed with spheroids of diameters greater than or equal to 400 μm (Figure 1D). Spheroids represented avascular solid tissues (between blood vessels) while the NPs added to the culture medium were analogous to nanocarriers that extravasate out of blood vessels.

Figure 1.

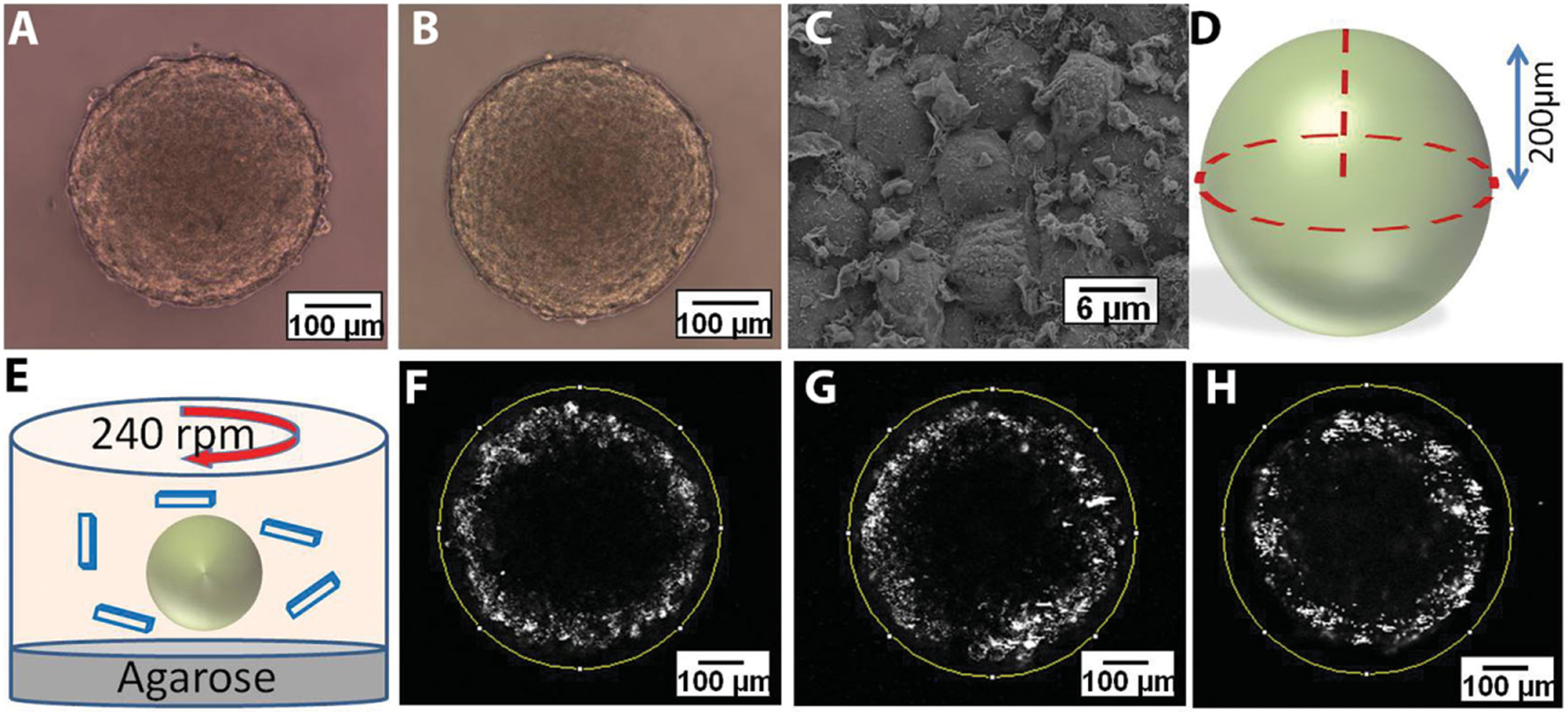
Light microscopy images of HEK spheroids cultured over 2% agarose gel under A) static conditions and B) rotatory shaker at 240 rpm. C) Scanning electron microscopy images of HEK spheroid cultured over 2% agarose gel on rotatory shaker at 240 rpm. D) Illustration of spheroid imaging using two-photon microscope. E) Cartoon showing the configuration of particle incubation with spheroids under rotatory conditions. F–H) Two-photon microscopy images of spheroids at 200 μm deep from the top edge of the spheroids incubated with F) 100 nm polystyrene beads, G) 200 nm polystyrene beads, and H) 500 nm polystyrene beads.

2.2. Spherical Nanoparticle Penetration in Spheroids

For spherical NPs, it is known that penetration in tissues increases with decreasing size.^[14,15] Here we wanted to see how spherical particles of specific sizes, having similar volumes as our shape-specific NPs, penetrate and distribute inside our spheroid model. Commercially available polystyrene NPs were used as model spherical nanocarriers, since the J-FIL process cannot generate truly spherical NPs due to patterning/electron-beam limitations. Thus, although the material and NP surface properties of the spherical NPs are different from the shape-specific NPs used later in our studies, we used these studies to establish our transport model and validate the assessment methods. Polystyrene beads of three different sizes (100, 200, and 500 nm) were incubated with spheroids for 48 h under rotatory conditions (Figure 1E) (keeping the total fluorescence administered for each type of bead constant, thus representing equal drug dosage). Although this results in different number of particles per condition, it allows us to keep the mass of drug delivered constant and hence ask the question: for a given amount of drug, which NP geometry would provide maximum intratissue drug delivery and better drug distribution, i.e., which shape is likely provide the most clinical benefit for a given dose.

Spheroids were washed several times with phosphate buffer saline (PBS) and fixed in 4% paraformaldehyde. To analyze the overall NP distribution and penetration within spheroids, two-photon microscopy was utilized, allowing noninvasive (i.e., without embedding and cutting histological sections) and quantitative imaging throughout the spheroid matrix. Images were collected starting from the surface up to the center of the spheroids (i.e., at a depth of ≈200 μm) (Figure 1D), and results were normalized (see the Experimental Section) before comparison to account for minor differences in size of spheroids (there is a 10% size variation of 20–30 μm in diameter) and allow direct comparison between different particle conditions. Since these experiments were performed under dynamic (shaking) conditions, the distribution of particles was uniform throughout the culture medium. This allowed us to minimize sedimentation and diffusional limitations and assume that the spheroids had isotropic distribution of particles.

Images collected from two-photon microscopy were analyzed for total association of NPs within the spheroids using the software ImageJ (National Institute of Health (NIH) http://imagej.nih.gov/ij/). All three sizes of polystyrene beads used displayed strong association with the spheroids. However, the beads were found localizing only near the surface of each spheroid and did not show penetration beyond the outer 40–50 μm. Figure 1F–H shows characteristic image slices (near the center, i.e., equator; voxel size: 4 μm) of spheroids with polystyrene (PS) beads. Total pixel intensity associated with each spheroid (representing total amount of “drug” delivered) was measured by the average pixel intensity per slice and compared between different particle sizes (as shown in Figure 2A). While, as expected, 500 nm PS beads were least associated with the spheroids, interestingly there were no significant differences between the 200 and 100 nm polystyrene beads.

Figure 2.

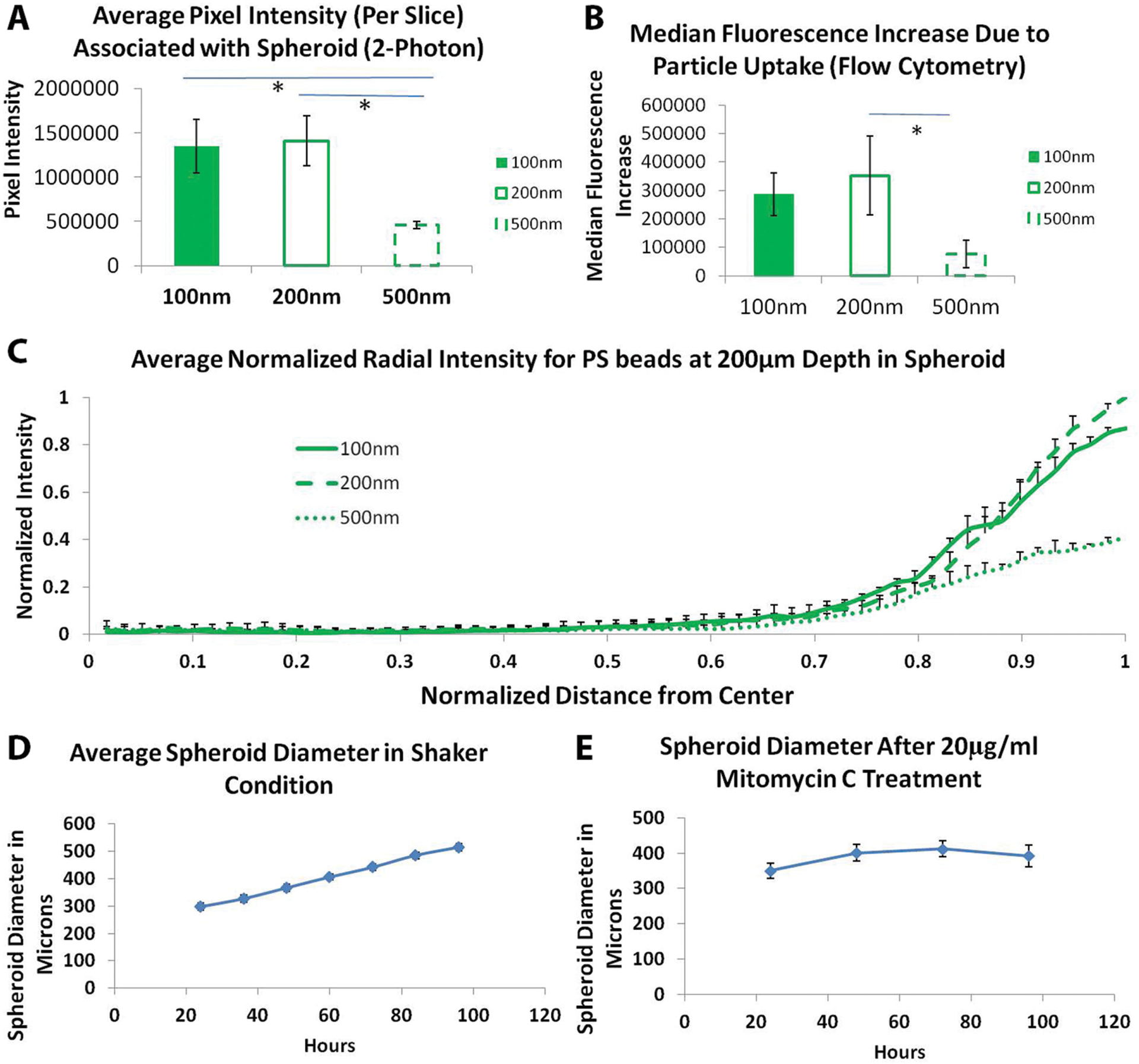
Uptake and penetration of spherical polystyrene particles in untreated spheroid. A) Graph showing comparison of normalized pixel intensity from 2P microscopy associated with spheroid per slice with different diameter polystyrene beads. B) Graph showing comparison of particle association with spheroid after 48 h of incubation with different size polystyrene beads analyzed using flow cytometry. C) Normalized radial intensity distribution of polystyrene nanoparticles as a function of distance from the center of the spheroid. Only positive error bars are shown to allow proper visualization of data. Graphs showing growth of spheroids over time under D) untreated conditions and E) Mitomycin C-treated spheroids. Two-photon microscopy of Mitomycin C-treated spheroids. * denotes p-value <0.05. One-way Anova followed by Tukey’s multiple comparisons test was used to determine statistical significance.

To further confirm these results, we dissociated the spheroids into single cell suspensions using trypsin and collagenase, performed flow-cytometry, and found the same NP-association trend as was seen by two-photon microscopy (Figure 2B). No significant differences between uptake of 200 and 100 nm polystyrene beads was found in 3D spheroid uptake which is in contrast to 2D cultures where 100 nm polystyrene NPs are more efficiently internalized compared to 200 nm NPs.^[17e,22,28]

To quantify the penetration depth and spatial distribution of NPs in the solid-tissue matrix, we created a radial distribution profile of the particles within the spheroid. Specifically, a circle was drawn around the center section (200 μm depth) and a custom ImageJ script was used to find the average pixel intensity as a function of distance from the center of the spheroid. The distance from the center and the pixel intensity were normalized (as detailed in the Experimental Section) to compare results across different particle conditions (Figure 2C). Interestingly, no significant difference in maximum penetration depth was found for the polystyrene NPs. Although smaller particles (100 and 200 nm PS beads) were highly associated with cells at the edges, none of the particle sizes were able to penetrate beyond 50 μm depth. Polystyrene beads, although widely used to model nanocarriers, are hydrophobic and can rapidly get immobilized to hydrophobic cell membranes, thereby limiting their intraspheroidal penetration. Additionally, the size of beads (100 nm or above used in this study) may be too large to allow effective diffusion of such spherical NPs into the tissue matrix. Similar results have also been previously reported by Goodman et al.^[13]

2.3. Spherical Nanoparticle Penetration in Growth Arrested Spheroids

A point of concern during these experiments was the growth of the spheroids following administration of NPs and the effects of this growth on the resulting distribution of particles. Since the spheroids grew over a period of 2 d (Figure 2D), it was not clear whether the penetration results observed were because particles actually traversed the tissue matrix or because new matrix and cells formed around the existing particles. To answer this question we treated the spheroids with a short pulse of Mitomycin C to arrest the cell cycle in S phase.^[29] We optimized the Mitomycin C concentration (pulse treatment with 20 μg mL⁻¹) such that the diameter of spheroid used during association and diffusion studies were maintained constant around 400 μm (Figure 2E). Uptake and penetration experiments were performed with spherical PS beads. All results and trends were found to be similar to that of the non-Mitomycin C-treated studies described above (Figure 3A,B). This indicates that the penetration results were not likely to have been influenced by the growth of cells around the particles in our spheroid model. We further divided the spheroids into four zones based on the distance from the center and evaluated the total pixel intensity associated in each area for all shapes. Pixel intensity associated with 100 and 200 nm diameter PS beads was found to be significantly higher compared to 500 nm PS beads for outer zone, representing 25% depth from the edge (Figure 3C–F). However, for all inner zones no differences were seen.

Figure 3.

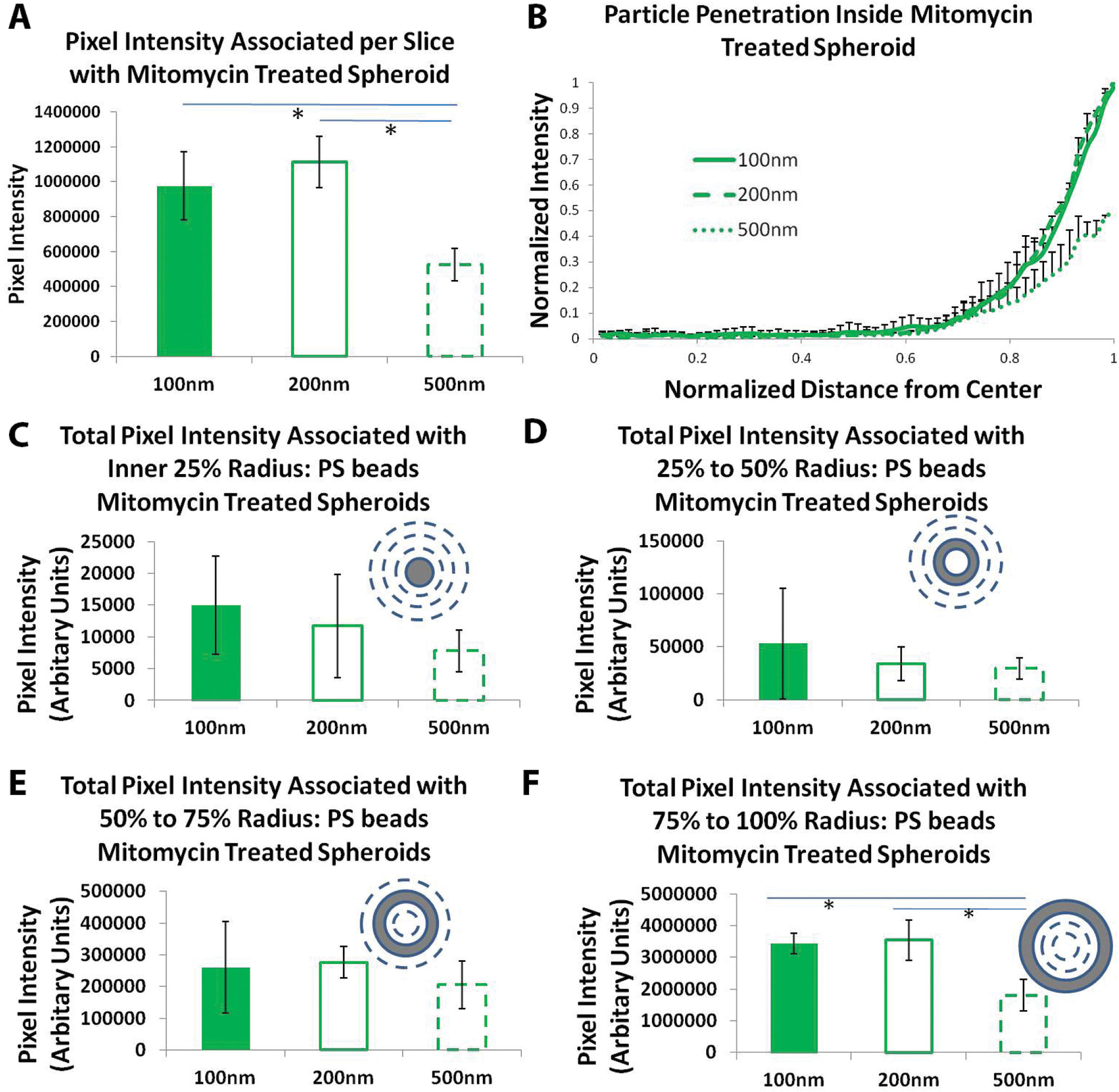
Uptake and penetration of spherical polystyrene particles in Mitomycin C-treated spheroids. A) Graph showing comparison of normalized pixel intensity associated with spheroid per slice with different diameter PS beads. B) Normalized radial intensity distribution of PS beads as a function of distance from the center of the spheroid. Only positive error bars are shown to allow proper visualization of data. Graphs showing total PS beads pixel intensity associated with different zones of mitomycin-treated spheroid corresponding to C) inner 25% radius, D) 25%–50% radius, E) 50%–75% radius, and F) 75%–100% radius. * denotes p-value <0.05. One-way Anova followed by Tukey’s multiple comparisons test was used to determine statistical significance.

2.4. Shape Specific Nanoparticle Penetration in Untreated and Growth Arrested Spheroid

Next, we evaluated the role of shape, size, and aspect ratio in penetration of clinically relevant, PEG-based anionic nanohydrogels inside spheroidal matrix. Experiments similar to those described above for PS beads were performed using two equivalent-volume pairs of PEG-based, mono-dispersed, anionic (zeta potential ≈ −55 mV,^[22] shape-specific NPs fabricated using J-FIL.^[22] One equivalent-volume pair consisted of disk-shaped nanocylinders with an aspect ratio (H/D) of ≈0.45 (220 nm diameter with 100 nm height) and cuboidal nanorods of aspect ratio (H/D) of ≈4 (400 nm length with 100 nm × 100 nm cross section sides). The other equivalent-volume pair consisted of nanocylinders of lower aspect ratio (H/D ≈0.3) 325 nm diameter with 100 nm height) and cuboidal nanorods of aspect ratio ≈8 (800 nm length with 100 nm × 100 nm cross section sides) (Figure 4A–D). The surface area of particles within each equal volume pair was also similar (19% difference between smaller disk and cuboid pair and 21% difference between larger disk and cuboid pair). Since the NP was made of PEG, particle suspension was very stable and we observed no aggregation. For detailed characterization data, refer to our previous publications^[17m,22,30] Particle association and penetration for each NP type was evaluated after 48 h of incubation in both untreated and mitomycin-treated spheroids (Figures 4E–I and 5A–F). Note that we are using anionic PEG-based particles which have low interaction with cell membranes and serum proteins and have been proposed for increasing in vivo circulation times by reducing rapid clearance by the reticulo-endothelial system.^[1,6,16a,c] Thus a longer 48 h time point was chosen to achieve steady state. No uptake or penetration of particles was seen at shorter time points (2–4 h). Use of anionic NPs has also been proposed for deep tissue penetration as such particles reduces interactions with negatively charged cell membrane and allows greater mobility and diffusion inside tissue matrix.^[10C]

Figure 4.

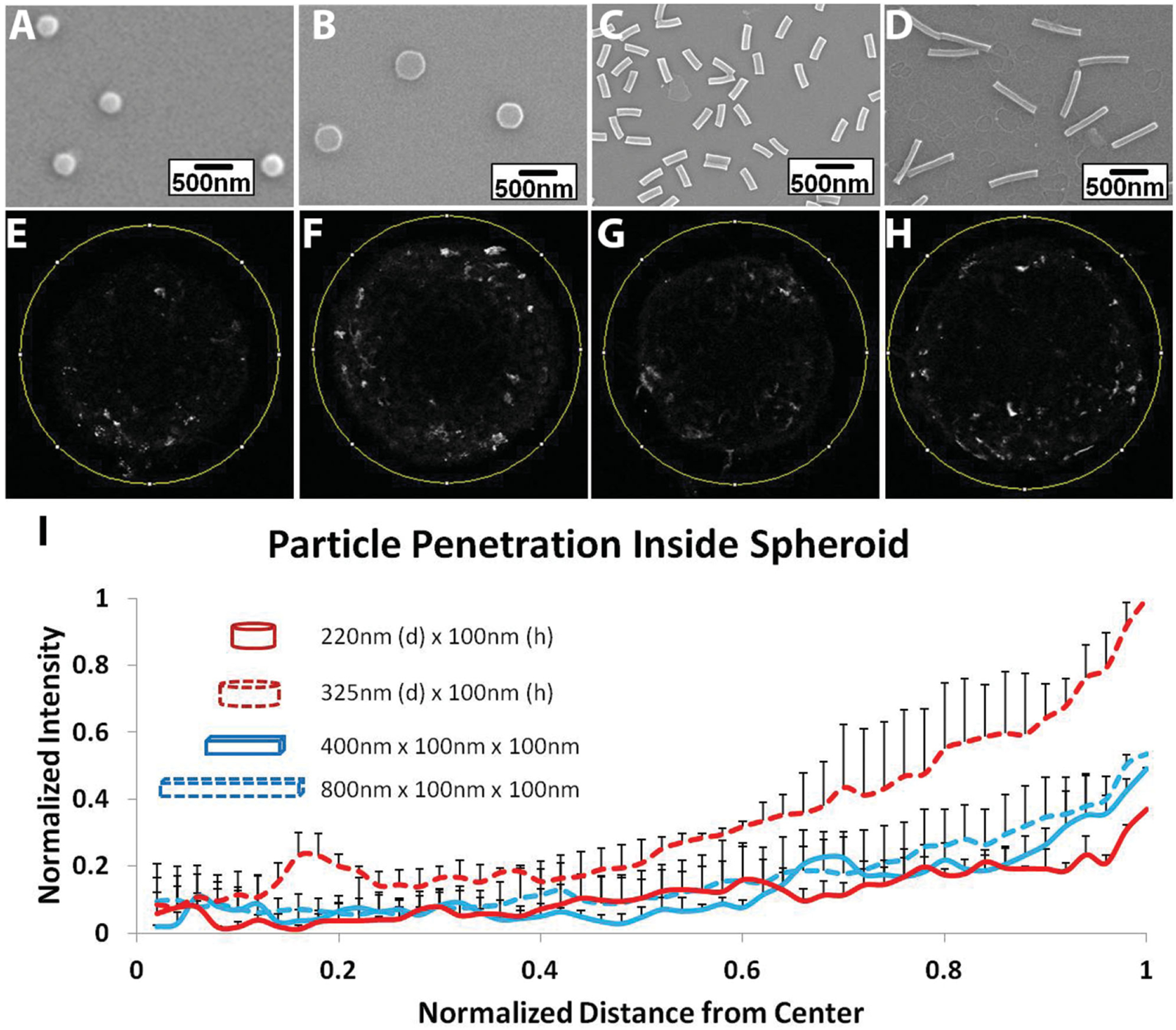
Uptake and penetration of shape specific particles in untreated spheroid. Scanning Electron Microscope (SEM) images of A) 220 nm × 100 nm disks, B) 325 nm × 100 nm disks, C) 400 nm × 100 nm × 100 nm rods, and D) 800 nm × 100 nm × 100 nm rods. Two-photon pictures of spheroids at a depth of 200 μm from the surface incubated with E) 220 nm × 100 nm disks, F) 325 nm × 100 nm disks, G) 400 nm × 100 nm × 100 nm rods, and H) 800 nm × 100 nm × 100 nm rods. I) Normalized radial intensity distribution of shape-specific nanoparticles as a function of distance from the center of the spheroid. Only positive error bars are shown to allow proper visualization of data.

In comparing differences between low aspect ratio cylinders and rods for total particle association with spheroids, we found that the smaller sized NPs (220 nm diameter cylinders and 400 nm rods) were equally associated, while for the larger NP pair (325 nm diameter cylinders and 800 nm rods), the low aspect ratio (≈0.3) disk-like nanocylinders were about two times more associated with spheroids (Figure 5A). We also observed that for nanocylinders, decreasing the aspect ratio and size (H/D, from 0.45 to 0.3) by increasing diameter resulted in a threefold increase in delivery efficiency, while for rods the efficiency was similar irrespective of their aspect ratio. These results suggest that once NPs reach a solid tumor tissue, it is advantageous to have very low, fractional aspect ratio disk-shaped nanocylinders compared to smaller disks or nanorods in order to achieve increased total drug delivery.

Figure 5.

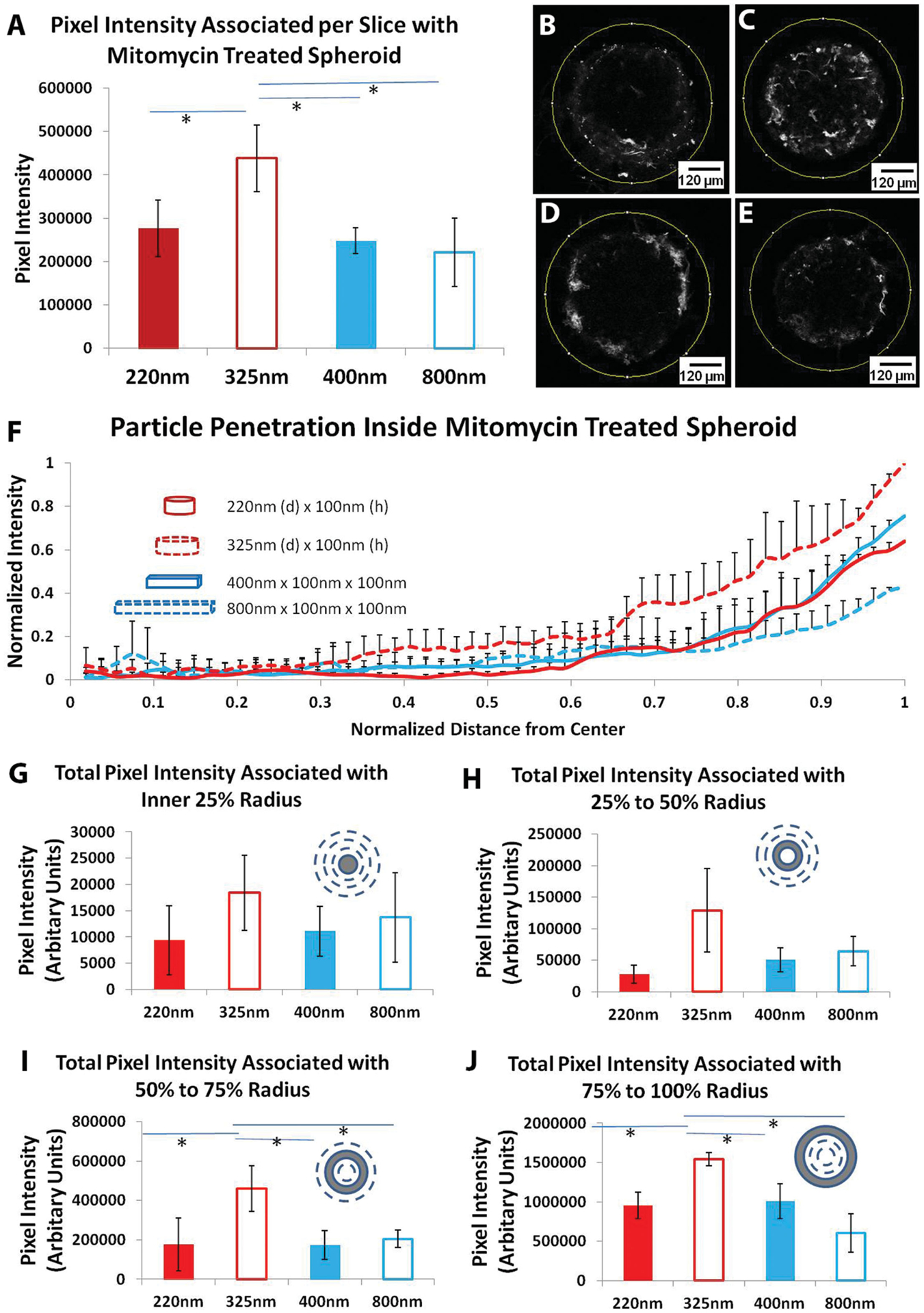
Uptake and penetration of shape specific particles in mitomycin-treated spheroid. A) Graph showing comparison of normalized pixel intensity from 2P microscopy associated with mitomycin-treated spheroid per slice with different shape-specific particles. Two-photon pictures of spheroids at a depth of 200 μm from the surface incubated with B) 220 nm × 100 nm disks (n = 3), C) 325 nm × 100 nm disks (n = 4), D) 400 nm × 100 nm × 100 nm rods (n = 3), and E) 800 nm × 100 nm × 100 nm rods (n = 4). F) Normalized radial intensity distribution of shape-specific nanoparticles as a function of distance from the center of the mitomycin-treated spheroid. Only positive error bars are shown to allow proper visualization of data. Graphs showing total PS beads pixel intensity associated with different zones of mitomycin treated spheroid corresponding to G) inner 25% radius, H) 25%–50% radius, I) 50%–75% radius, and J) 75%–100% radius. * denotes p-value <0.05. One-way Anova followed by Tukey’s multiple comparisons test was used to determine statistical significance.

Further, we analyzed the radial distribution of various shapes of particles similar to the PS bead study within spheroids. All PEG-based shape-specific NPs were able to penetrate deeper inside the tumor matrix compared to PS beads (Figures 4E–I and 5B–F). While PS bead penetration dropped to only about 10% of surface levels at a depth of 40 μm from the surface and no penetration occurred at the center of the spheroid, shape-specific PEG particles were present at around 20%–40% of the surface level at 40 μm depth. Since PEG is a hydrophilic material with low adhesion, PEG-based NPs are expected to adhere and interact less to hydrophobic cell membranes and thus could penetrate deeper into the dense tissue matrix.^[31] It is important to note that although the smallest dimension in all of the shape-specific particles tested was 100 nm, they still penetrated deeper compared to 100 nm spherical PS beads. We also observed that 325 nm, 0.3 aspect ratio, disk-like nanocylinders were able to associate in larger quantities compared to other rods and similar-shaped NPs in outer half of the spheroid (>1.5 times in outer zone and >2 times in the second zone from the edge). Zonal analysis of spheroids showed significant differences in pixel intensity associated with outer two zones representing outer 25% and 50% of radial depth (Figure 5G–J). Particle associations for all shapes dropped to basal level for inner two zones. This enhancement of penetration could be a combination of both shape and material differences between PEG-based rods and disks and PS-based spherical particles.

In addition, these results suggest that higher aspect ratio rods are as effective in delivering drugs and biological agents inside tissue matrix as low aspect ratio rods and do not provide any transport advantage through dense tissue matrices. This is similar to previous reports indicating that increasing aspect ratio of rod shaped PEG particles does not affect their ability to pass through narrow pores.^[32] Collectively, our results indicate that penetration of rod shaped particles through a tissue matrix is governed primarily by their smallest dimension. In contrast, for disk-like cylindrical particles, results show that very low aspect ratio (height: diameter) particles penetrate deeper.

3. Discussion

It is not entirely clear why the larger disk-like nanocylinders with lowest aspect ratio are associated in higher quantities compared to smaller disks and nanorods in the outer 50% radius of the spheroid. Three types of mechanisms: passive (diffusional), convective, and active cell mechanisms could play important roles in the penetration of NPs inside of spheroids. Polymeric particles are capable of bending and undergoing deformations. Softer particles are known to circulate in the body for longer periods compared to rigid metal particles. This phenomenon is attributed to particle deformability that allows soft particles to evade physiological barriers (such as clearance by spleen) encountered during particle voyage through blood vessels. Red Blood cell mimicking deformable particles has been shown to circulate in blood for long periods of time.^[33] Deformability of any particle depends on its shape. High aspect ratio particles are more deformable compared to low aspect ratio particles of same shape. This could further play a part in deep penetration of high aspect ratio disks and rods. However, the particles used in this study are tightly crosslinked nanohydrogels of high modulus and negligible swelling (elastic modulus around 20 MPa).^[17R,30] This is also supported by the data that higher aspect ratio nanorods did not show any difference in maximum penetration or distribution compared to lower aspect ratio rods. Hence we conclude that for the NPs used here, deformability is unlikely to play a significant role.

3.1. Theoretical Analysis

Theoretical analysis of other parameters that can be involved in passive and convective transport such as diffusion, intrinsic viscosity and radius of gyration were also performed but were insufficient to completely explain the experimental data (see the Experimental Section and Figure 6). Nevertheless, the theoretical treatise described here provides a basis for biophysical analysis of NP transport in solid tissues.

Figure 6.

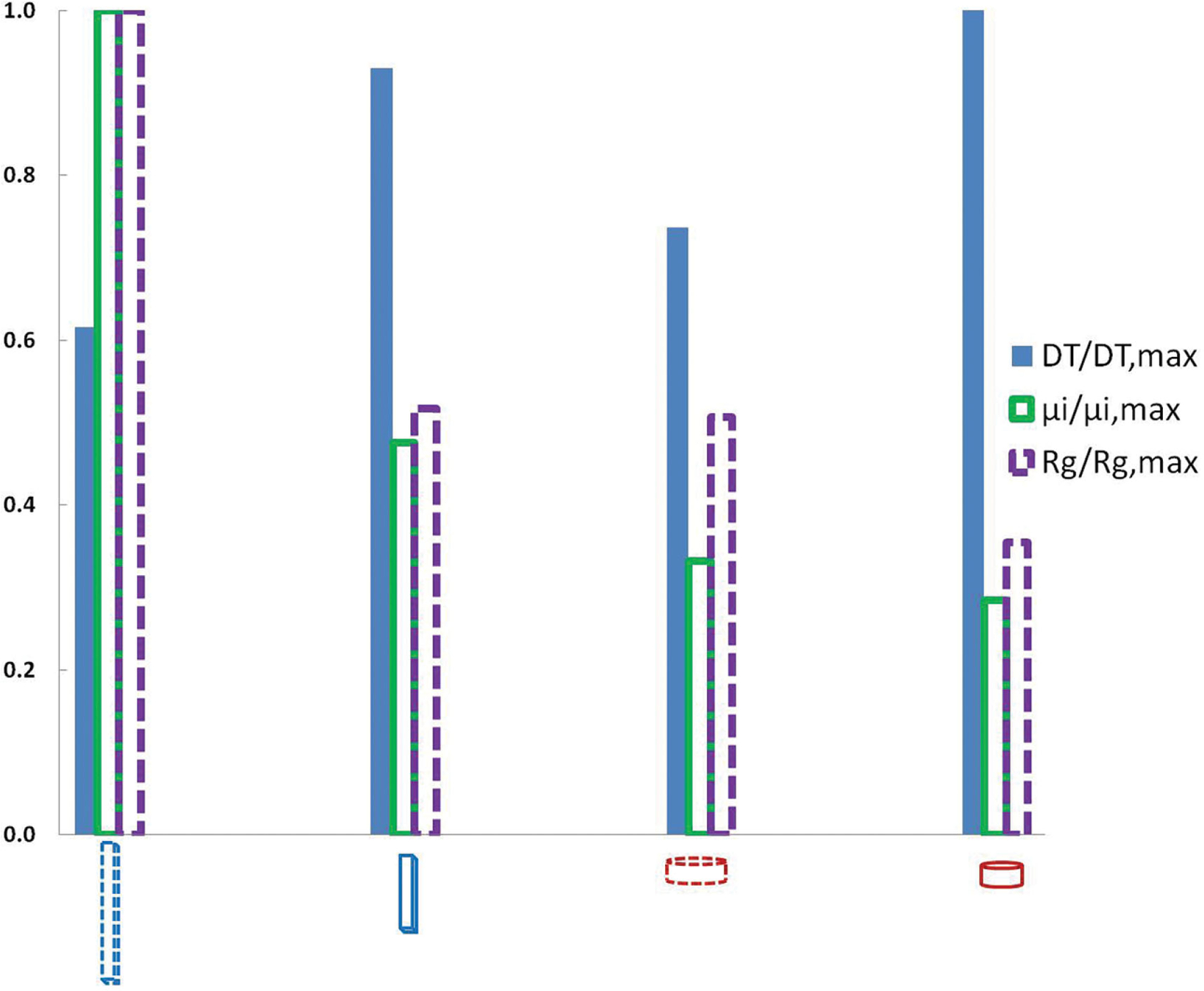
Theoretical analysis of hydrodynamic properties of the four nanoparticle shapes used in uptake and penetration studies.

We see no consistent trends in the three parameters considered here that account for varying diffusional properties of NPs inside spheroids. An increase in intrinsic viscosity due to the presence of NPs would result in a decrease in diffusion while any increase in the diffusional coefficient of a particular particle would increase its diffusion length. However we have not considered the complexities of the solid-tissue microenvironment including tortuosity, porosity, and fluid displacement due to cell movement. Since the 325 nm NPs associate in much higher quantities near the outer half of the spheroid, they have a larger concentration gradient but not necessarily a larger diffusion coefficient. For this reason and the lack of a clear trend in the calculated diffusion parameters, the difference in penetration seen in our experimental results could be associated with active surface interactions on the outermost cells of the spheroid similar to what was described in Agarwal et al.^[22] We have previously shown that epithelial cells preferentially uptake 325 nm disks in much higher quantities compared to other shapes^[22] which could explain higher association of these particles at the surface of spheroid. These indicate that NP penetration may not be purely passive or convective and that active mechanisms might play a dominant role in particle distribution. In our previous publication we had shown that these NPs mainly utilize macropinocytosis for uptake in cells.^[22] Nanodisks were also shown to use caveolae mediated pathway. However, it is unclear how cell uptake mechanisms and other passive and convective mechanisms affect tissue penetration.

We argue that NP penetration and distribution in solid tumors is a balance between several factors: the surface contact area that allows the particle to interact with the tortuous pathways and penetrate (either passively or actively), the largest dimension (large dimension should hinder penetration) of the particle, the cell/tissue to particle adhesion (which is minimal for our particles because of charge and hydrophilicity), etc. From our data it seems that for NPs at <400 nm dimensions, the surface contact area is dominant while at >400 nm, the largest dimension takes over. Thus, at <400 nm the lager disk outperforms, but for larger dimension, the 800 nm particles have a difficult time navigating through the tortuous pores of the tissue, especially given that we have fairly rigid particles (highly crosslinked, low molecular weight PEG particles).

Diseased tissues and tumors can be significantly diverse and dynamic depending on their location, type, and disease stage. Such tissues can be highly variable and can exhibit completely different penetration and accumulation of shape specific NPs for different types of tumors.^[17I] Hence it is important to test different models of solid tumors and diseases for penetration studies. Further, other cells present in the tissue microenvironment, e.g., tumor stromal cells, monocyte-derived suppressor cells, dendritic cells, tumor-associated macrophages and T cells, could also affect the overall transport of NPs within a tissue. Nevertheless, the spheroid-culture model provides a strong basis of identifying critical geometrical parameters for improving drug and contrast agent delivery.

4. Conclusions

In conclusion we demonstrate that shape specific, anionic hydrophilic NPs can penetrate deep inside 3D tumor models. With hydrophobic PS beads, penetration was minimal and particles mainly concentrated near the edge of spheroids. Very low aspect ratio, cylindrical, disk-shaped particles emerged as the ideal particle shape among the four particles used in this study for maximal delivery (>50% of total accumulation compared to all other shapes) and penetration in the outer zones (>1.5 times compared to other shapes) of solid tissues. Increasing the aspect ratio of rod shaped particles did not affect their association and penetration in the spheroids. This study provides fundamental new knowledge on NP transport inside solid, tumor-like tissues and demonstrates the role of NP shape as a design parameter to greatly improve efficacy of drug delivery and diagnostics.

5. Experimental Section

Nanoimprinting:

Fifty percent poly (ethylene glycol) diacrylate (Mw: 200 Da), 0.1% w/v final concentration of 2-hydroxyl-1-[4-(hydroxyl) phenyl]-2-methyl-1propanone (I2959, Ciba) as the photoinitiator, and 5% fluorescein acrylate were first dissolved in Dimethyl Sulphoxide (DMSO). A diluted 2% w/v poly (acrylic acid) (PAA) solution was prepared in water. About 5 mL of this PAA solution was spin coated on an 8” Silicon wafer at 4500 rpm for 40 s. The wafer was then baked on a hot plate at 160 °C for 1 min. Nanoimprinting was carried out using Jet and Flash Imprint Lithography (J-FIL) on an Imprio 100 at Molecular Imprints Inc., Austin, TX. In the J-FIL process, a prepatterned transparent quartz template was pressed onto resist droplets which were ink jetted onto a silicon wafer precoated with a PAA release layer, causing the droplets to spread and fill the features of the quartz mold. The resist was then exposed to UV light (365 nm wavelength at 5 mW cm⁻² intensity), for 25 s to photo polymerize the molded resist. The template was then demolded, revealing the desired nanostructures. The imprints were sputter coated with a 3 nm layer of Platinum and the residual layer was measured using cross-sectional Scanning Electron Micrscope (SEM). A low power (35 W) Argon plasma etch (Oxford Instruments Plasma Lab 80+) was performed at a pressure of 10 mTorr with Ar (20 sccm) and O₂ (4 sccm) yielding an etch rate of 0.6 nm s⁻¹.

Release and Characterization of Nanoparticles:

Imprints were washed twice with DMSO after etching on the wafer to remove any unreacted polymer. Imprints were then submerged in DMSO, incubated for 5 min and blow dried with nitrogen. NPs were harvested by pipetting 50 μL of filtered deionized (DI) water over a 5 mm × 5 mm imprint area. The DI water was used to dissolve the underlying PAA layer and the DI water containing the released NPs was then collected after 1 min. The water containing NPs was dialyzed for 3 d using 300 KDa Float-A-Lyzers (SpectrumLabs Inc.).

Cell Culture:

HEK 293 (American Type Culture Collection (ATCC)) cells were cultured in Dulbecco’s modified Eagle medium (Hyclone) supplemented with 10% fetal bovine serum (characterized FBS, Hyclone) and 1% antibiotics (penicillin and streptomycin, Invitrogen). Media was changed every other day and cells were passaged at 80%–90% confluency.

Spheroid Synthesis:

Spheroids were synthesized via seeding of HEK 293 cells on agarose gel filled 96-well plates. To form the agarose gels, 1.6 g of agarose was first suspended in 100 mL of PBS. The agarose and PBS mixture was then microwaved until complete dissolution of the agarose took place, upon which 80 μL of the solution was added to each well in a tissue culture, flat-bottomed 96-well plate. The solution plate was air dried to form solidified gels at 25 °C under sterile conditions. Each well was then twice washed with 200 μL of PBS, waiting 10 min before removing or adding fresh PBS during washing. To initiate spheroid formation, 1000–4000 HEK 293 cells were seeded in each well of the 96-well plate. The spheroids were then incubated under standard cell culture conditions, at 37 °C, 5% CO₂ in humidified incubators, over a BT4000 IncuShaker rotating at 240 rpm. The media in each spheroid well was changed every 2 d.

Spheroid Treatment and Imaging:

Pipette tips were cut at the end before handling and picking spheroids to avoid shearing the surface. To prepare the spheroids for SEM imaging they were twice washed with PBS then fixed for an hour in 4% paraformaldehyde at room temperature. The spheroids were again twice washed with PBS then dehydrated using a series of graded ethyl alcohols (70%, 90%, and 100%) for 15 min each. Dehydration was followed by chemical drying using hexamethyldisilazane (HMDS). The spheroids were then incubated with a 2:1 ratio of 100% ethyl alcohol and HMDS, followed by a 1:2 ratio, and finally 100% HMDS for 15 min each. All HMDS reagents were handled in glass vials. Following incubation the samples were air dried in a hood for 24 h then mounted and imaged using scanning electron microscopy.

Spheroids were allowed to grow up to 400 μm before any experiments were performed. To inhibit growth of the spheroid, each spheroid well was treated with 20 μg mL⁻¹ Mitomycin C solution for 2 h. The spheroids were then washed with PBS and used for subsequent experiments

Two-photon microscopy was used to image NP association and diffusion in spheroids. Three types of polystyrene beads (100, 200, and 500 nm diameter) were incubated at equal fluorescence, normalized using a fluorescence plate reader, (corresponding to 10⁸, 200 nm diameter PS beads) in separate wells of spheroids for 48 h, with shaking at 240 rpm. Similarly, all four types of shape-specific NPs [disk-shaped nanocylinders: 220 nm diameter with 100 nm height and 325 nm diameter with 100 nm height and cuboidal rod: 400 nm length with 100 nm × 100 nm cross section sides and 800 nm length with 100 nm × 100 nm cross section sides] were incubated at equal fluorescence, normalized using fluorescence plate reader (corresponding to 20 μg of particles) in separate wells of spheroids for 48 h, with shaking at 240 rpm. To avoid significant difference between numbers of particles, in our studies we used two-equal volume pairs of different shapes. One pair with low aspect ratio (disk-shaped nanocylinders: 220 nm diameter with 100 nm height and cuboidal rod: 400 nm length with 100 nm × 100 nm cross section sides) and the other pair with a higher aspect ratio (disk-shaped nanocylinders: 325 nm diameter with 100 nm height and cuboidal rod: 800 nm length with 100 nm × 100 nm cross section sides). Since all particles are made up of same material and composition, the equal volume pair has same mass and fluorescence intensity and hence same numbers of particles for those are administered to each spheroid well.

After 48 h the spheroids were twice washed with PBS to remove any loosely attached particles and then fixated via incubation with 4% paraformaldehyde for 30 min at room temperature. Each spheroid was then washed once with PBS and placed inside a 0.5 mm depth cover-well imaging chamber (Grace Bio-Labs) over a glass slide. Two-photon microscopy images were taken at an excitation wavelength of 965 nm, using a 10× objective and a voxel size of 4 μm up to a depth of 200 μm.

Spheroid Image Analysis:

ImageJ (NIH) was used to analyze captured image stacks. To quantify the total particle association for a given spheroid, the total pixel intensity in all images within an obtained z-stack was first averaged. The average background intensity obtained from untreated spheroids was then subtracted to obtain a final average pixel intensity value. To quantify the radial distribution of particles from the center of the spheroid, a customized script in ImageJ (NIH research services branch) was used. The Radial Profile command was used to generate radial intensity value arrays displaying the average pixel intensity at each radial distance from the center to the edge of the spheroid. Within this function, the average radial intensity distribution for each spheroid was obtained at various points by adding the pixel intensities at a given radius and dividing by the number of pixels at that radius. Lowest intensity in each spheroid was assumed as background and was subtracted from all points to obtain a final average pixel intensity value. Distances were then normalized by the spheroid radius at which greatest pixel intensity was found for each spheroid. To normalize intensity values, the average pixel intensity at all normalized distances from center was divided by the largest overall pixel intensity for each spheroid. This was followed by normalization by maximum average intensity across all the particles to allow comparison. Finally normalized pixel intensity was plotted against normalized distance from center to obtain particle distribution in spheroids.

To obtain the total pixel intensity associated with different zones (area) within the center of the spheroid, radial distribution command was used to generate average pixel intensity at various distances from the center for the middle section of the spheroid (200 μm depth). For each distance x from the center, average pixel intensity was multiplied by 2 × 3.14 × x to get the total pixel intensity at each distance. This was further multiplied by the distance between each subsequent point and added together to get the total pixel intensity associated with respective area.

Flow Cytometry Analysis:

Three types of polystyrene beads (100, 200, and 500 nm diameter) or previously synthesized shape specific NPs were incubated in separate plates of spheroids for 48 h. After 48 h, spheroids that were administered the same size and shape particles were pooled together in pairs of two and twice washed with PBS to remove any loosely attached particles. Each pair of spheroids was then incubated for 10 min with 100 μL of 6 mg mL⁻¹ Collagenase D solution in trypsin, followed by neutralization of the trypsin with 100 μL of media. Each spheroid was then dissociated into single cells by gentle pipetting using a micropipette. The dissociated cells were then washed with PBS and resuspended in 2% FACS (flourescence activated cell sorting) buffer (2% FBS in PBS). Flow cytometry was performed on the cells using an Accuri C6 Cytometer (BD Accuri) and all conditions were tested in triplicates. The change in median fluorescence was calculated and plotted against time for analysis.

Theoretical Calculation:

The translation diffusion coefficient (D_T) is given as the ratio of the thermal energy to the translational friction coefficient

$$D_{\text{T}}=\frac{K_{\text{B}}T}{f}$$ (1)

where K_B is the Boltzmann constant, T is the temperature, and f is the translational friction coefficient. The translational diffusion coefficient can be calculated for spherical particles using the simple Stokes–Einstein relationship

$$D_0=\frac{K_{\text{B}}T}{6\pi \mu R}$$ (2)

where μ is the solvent viscosity and R is the radius of the spherical particle. Determining the translational diffusion coefficient of nonspherical particles has been the study of a number of analytic and numerical models beginning with Burgers’^[34] on the translational friction coefficient of cylinders. In general cylinders can be distinguished geometrically by their aspect ratio, γ, which is the ratio of the cylinder’s length to its diameter (γ = L / d). Most numerical studies consider the case for slender rods (i.e., γ → ∞);^[35] however, in his work, Brenner considered the infinitely thin disk case where γ → 0.^[36] In order to find D_T for rods (1<γ < 20) and disks (γ < 1) we use the following expression put forth by De la Torre and Garcia^[35]

$$\frac{f}{f_0}=1.009+1.395\times {10}^{-2}(\text{ln}(\gamma ))+7.880\times {10}^{-2}{(\text{ln}(\gamma ))}^2+6.040\times {10}^{-3}{(\text{ln}(\gamma ))}^3$$ (3)

where f₀ is the translational friction coefficient of a sphere having the same volume as the rod or disk, or from Equations (2) and (3)

$$f_0=6\pi \mu L{\left(3/16{\gamma }^2\right)}^{1/3}$$ (4)

From Equations (1), (3), and (4) we obtain the values of D_T for each of the four shapes considered. The intrinsic viscosity (μ_i) is a measure of the NPs contribution to the fluid viscosity and is defined as

$${\mu }_i=\underset{\phi \to 0}{\text{lim}}\frac{{\mu }_i-\mu }{\mu \phi }$$ (5)

where φ is the NP mass concentration and μ is the solvent viscosity in the absence of NPs. The intrinsic viscosity can be found using the following expression:

$${\mu }_i=v\frac{\pi N_{\text{A}}{L}^3}{4M{\gamma }^2}$$ (6)

where N_A is Avogadro’s number, M is the molecular mass of the particle, and v is the Einstein factor given by v = μ_iM /VN_A and is interpolated by De la Torre and Garcia with the following equations:^[35]

$$v=2.77-0.2049{(\text{ln}(\gamma ))}^2-0.8287{(\text{ln}(\gamma ))}^3-0.1916{(\text{ln}(\gamma ))}^4$$ (7)

for γ < 1, and

$$v=2.77+1.647{(\text{ln}(\gamma ))}^2-1.211{(\text{ln}(\gamma ))}^3-0.6124{(\text{ln}(\gamma ))}^4$$ (8)

for γ > 1

Finally the radius of gyration (R_g) is calculated as the simple geometric relation

$$R_{\text{g}}=\sqrt{\frac{L^2}{12}+\frac{d^2}{8}}$$ (9)

Normalized values for D_T, μ_i, and R_g are plotted in Figure 6 for the four particle sizes used in this study.