Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2022 Jun 9;7(24):21317–21324. doi: 10.1021/acsomega.2c02531

Atomistic Insights into Structure and Dynamics of Neodymium(III) Complexation with a Bis-lactam Phenanthroline Ligand in the Organic Phase

Th Dhileep N Reddy †, Alexander S Ivanov ‡, Darren M Driscoll ‡, Santa Jansone-Popova ‡, De-en Jiang †,*
PMCID: PMC9348006  PMID: 35935293

Abstract

graphic file with name ao2c02531_0011.jpg

Rare-earth elements (REEs) such as neodymium are critical materials needed in many important technologies, and rigid neutral bis-lactam-1,10-phenanthroline (BLPhen) ligands show one of the highest extraction performance for complexing Nd(III) in REE uptake and separation processes. However, the local structure of the complexes formed between BLPhen and Nd(III) in a typical organic solvent such as dichloroethane (DCE) is unclear. Here, we perform first-principles molecular dynamics (FPMD) simulations to unveil the structure of complexes formed by BLPhen with Nd(NO3)3 in the DCE solvent. BLPhen can bind to Nd(III) in either 1:1 or 2:1 fashion. In the 1:1 complex, three nitrates bind to Nd(III) via the bidentate mode in the first solvation shell, leading to the formation of a neutral complex, [Nd(BLPhen)(NO3)3]0, in the organic phase. In contrast, there are two nitrates in the first solvation shell in the 2:1 complex, creating a charged complex, [Nd(BLPhen)2(NO3)2]+. The third nitrate was found to be far away from the metal center, migrating to the outer solvation shell. Our simulations show that the binding pocket formed by the two rigid BLPhen ligands allows ample space for two nitrates to bind to the Nd(III) center from opposite sides. Our findings of two nitrates in the first solvation shell of the 2:1 complex and the corresponding bond distances agree well with the available crystal structure. This study represents the first accurate FPMD modeling of the BLPhen–Nd(III) complexes in an explicit organic solvent and opens the door to more atomistic understanding of REE separations from first principles.

1. Introduction

Rare-earth elements (REEs) are crucial in many energy technologies and national security applications, including magnets, electronics, solar energy, and catalysis.1,2 Neodymium is a critical REE as it is one of the main elements in permanent magnets.3 Reducing the size of the electric motors and wind turbines requires high-performance NdFeB magnets. Nd also has broad uses in colorant for glass, wielding glasses, and laser crystals.4 US Department of Energy has categorized it as a critical material.5

The ever-increasing demand for REEs makes it necessary to update the current separation processes from the REE-containing ores.6 The similarity in chemical and physical properties of trivalent lanthanides makes the separation processes challenging. A two-phase solvent extraction has been the main method on the industrial scale to separate REEs based on the slight differences of their radii,7 which lead to differences in their binding strengths with organic ligands. Many ligands have been explored for their potentials to separate REEs including Nd. Ligands such as 2-ethylhexyl phosphoric acid-mono-2-ethylhexyl ester, also known as PC88A,8 and N,N,N′,N′-tetraoctyldiglycolamide9−11 (TODGA) are considered the state-of-the-art extractants used to separate light lanthanides.

Recently, rigid structures of ligands have gained attention in the field of REE separations,12−16 with 2,9-bis-lactam-1,10-phenanthroline (BLPhen) exhibiting one of the best selectivity between adjacent light lanthanides.17,18 However, the atomistic details pertaining to the solvation and complexation of REEs with these new organic ligands have been elusive; especially, it is unclear what is the role of extracted nitrate ions and water molecules in the first solvation shell of the metal ion in the organic phase.

Computational studies on REE complexes with organic ligands in solvents or solutions are typically carried out at the quantum chemistry level with an implicit solvation model or with a force field and an explicit solvation model.17,19−22 The former approach can miss important interactions and dynamics between the solute and the solvent, whereas the latter depends on the quality of the force field. First principles molecular dynamics (FPMD) simulations can nicely fill this gap by providing an explicit solvation environment and avoiding the issues of fitting force-field parameters.

The present work aims to resolve the first solvation shell of Nd(III) ions in the organic phase using FPMD for the first time. We focus on the dichloroethane (DCE) solvent for two reasons. First, it is a commonly used organic solvent to investigate REE separations as it easily solubilizes a variety of organic ligands that otherwise show limited solubility in non-polar solvents, such as dodecane and kerosene.18,23−26 For example, Healy et al.18 showed efficient extraction of lanthanides by BLPhen ligands into DCE. Second, being a small molecule, DCE has much faster dynamics than the many larger solvent molecules such as octane and heavier hydrocarbons, which makes it more amenable to FPMD simulations. The aim of this work is to reveal the binding patterns and dynamics of the neutral BLPhen ligands and NO3– ions around Nd(III) in the DCE solvent. Below, we first explain our computational method and approach.

2. Computational Method

FPMD simulations were carried out using spin-polarized density functional theory (DFT) within the Vienna Ab initio Simulation Package (VASP).27,28 Projector augmented wave method was used to represent the ion–electron interaction.29,30 Electron exchange–correlation was described by the generalized gradient approximation of Perdew–Burke–Ernzerhof (PBE) functional.31 It was demonstrated that PBE is a reasonable choice to get the very reasonable structure of the metal complexes in a solvent.32−34 The kinetic energy cutoff for the plane-wave basis set was 400 eV.

Two types of complexes were considered for the simulations: BLPhen–Nd(III) = 1:1 and BLPhen–Nd(III) = 2:1. Figure 1 shows the chemical structures of the BLPhen ligand and the DCE solvent used in the simulations. Cubic boxes of 30 and 25 DCE molecules were simulated for 1:1 and 2:1 complexes, respectively. The complexes were placed in the boxes of DCE molecules. To prepare the systems for FPMD simulations, equilibration was first carried out using classical molecular dynamics (CMD) simulations. The OPLS-AA force-field parameters35 were used for DCE and BLPhen. Nitrate anion parameters were obtained from Canongia Lopes and Pádua;36 Nd3+ parameters were obtained from Migliorati et al.37 GROMACS38−41 was used for the CMD simulations. After reaching the constant density from the NPT simulations for 20 ns, the box was subjected to NVT equilibration for 20 ns. Berendsen barostat42 and v-rescale42 thermostat were used during the simulations. During CMD simulations, the Nd–BLPhen complexes were restrained to their gas-phase DFT-optimized structure, while the nitrate ions were free to move. After equilibration, simulation box sizes were 17.35 and 17.36 Å for 1:1 and 2:1 complexes, respectively. The density of DCE from our simulation boxes is about 1.29 g/mL, which is close to the experimental density of 1.27 g/mL.43

Figure 1.

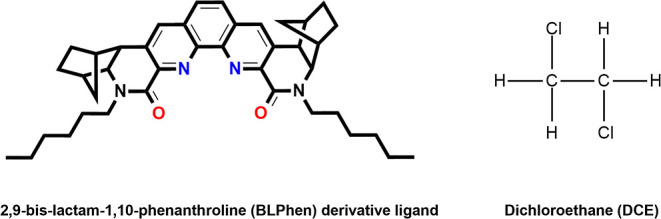
Figure 1

Open in a new tab

Molecular structure of the 2,9-bis-lactam-1,10-phenanthroline (BLPhen) derivative ligand and the DCE solvent.

Final structures of the NVT CMD simulations were used as the initial structures for FPMD simulations, which were carried out at 298 K in an NVT ensemble. A Nose–Hoover thermostat was used to maintain a constant temperature. 1 fs time step was used throughout the simulations. 15 ps simulations were performed, and the last 7.5 ps of the trajectories were used to calculate the equilibrium properties. Visualization of trajectories and some analysis were carried out using the VMD software package.44 TRAVIS software was used to calculate the radial distribution functions (RDFs) and their integrals to obtain coordination numbers.45,46

3. Results and Discussion

3.1. Structure of Nd(III)–BLPhen Complexation

Depending on the relative amount of the ligand to the metal in the organic phase, BLPhen can bind to Nd(III) in either 1:1 or 2:1 stoichiometries. Representative structures of the first solvation shells for the 1:1 and 2:1 complexes from our FPMD simulations are shown in Figure 2. The binding between the BLPhen ligand and Nd(III) is the most important interaction. There are four main interaction sites in the BLPhen ligand: two nitrogen atoms and two oxygen atoms (Figure 1). The space between these interaction sites can be viewed as a pocket. Capturing Nd(III) into this pocket is essential in separation processes.

Figure 2.

Figure 2

Open in a new tab

Snapshots of the first solvation shells of the BLPhen–Nd(NO3)3 complexes in DCE from FPMD: (a) 1:1 complex; (b) 2:1 complex. Nitrate anions are shown in (a) but omitted in (b) for clarity. DCE molecules are not shown. Color code: Nd, pink; O, red; N, blue; C, cyan; and H, white.

Figure 3a shows the RDFs between Nd and the N atom in BLPhen [N(BLPhen)]. One can see the strong coordination bonds between Nd(III) and nitrogen atoms of the ligand. The average Nd(III)–N(BLPhen) distance is 2.69 Å for the two Nd–N bonds in the 1:1 complex and 2.72 Å for the four Nd–N bonds in the 2:1 complex. The 2:1 complex has longer Nd–N distances than does the 1:1 complex. This is likely due to the steric hindrance between two ligands in the 2:1 complex (Figure 2b). Figure 3b displays RDFs between Nd(III) and the O atom of the BLPhen ligand. Nd(III)–O(BLPhen) distances are shorter than Nd(III)–N(BLPhen) distances in both 1:1 and 2:1 complexes. Hard soft acid base theory categorizes the lanthanides as hard electron acceptors, which tend to have a high affinity toward hard O donors.47 Similar to the Nd(III)–N(BLPhen) distances, Nd(III)–O(BLPhen) distances are also longer in the 2:1 complex than that in the 1:1 complex. Integration of RDFs in Figure 3b shows that there are two BLPhen oxygen atoms around Nd(III) in the 1:1 complex and four BLPhen oxygen atoms around Nd(III) in the 2:1 complex, as the snapshots in Figure 2 indicate.

Figure 3.

Figure 3

Open in a new tab

Atom–atom RDFs, g(r), between Nd(III) and the BLPhen ligand for the BLPhen–Nd(NO3)3 complexes in the DCE solvent: (a) Nd–N(BLPhen); (b) Nd–O(BLPhen). Solid lines represent g(r) (left axis); dashed lines (right axis) represent their number integration (NI), that is, coordination number.

3.2. Dynamics of Nd(III)–BLPhen Complexation

FPMD provides not only structure but also dynamics, and we have tracked the dynamics of the first solvation shell in the two Nd(III)–BLPhen complexes by monitoring the evolution of Nd–N(BLPhen) and Nd–O(BLPhen) distances with time. As one can see from Figure 4, the first solvation shell of the 1:1 complex is very stable and tight with much smaller fluctuations in Nd–N and Nd–O distances: Nd–N varies from 2.50 to 2.75 Å (Figure 4a); Nd–O varies from 2.35 to 2.70 Å (Figure 4c). In contrast, the first solvation shell of the 2:1 complex is more dynamic and less stable with much greater fluctuations in Nd–N and Nd–O distances (Figure 4b,d).

Figure 4.

Figure 4

Open in a new tab

Change in Nd–N and Nd–O distances between Nd(III) and the BLPhen ligand with time for the BLPhen–Nd(NO3)3 complexes in the DCE solvent: (a) Nd–N in 1:1 complex; (b) Nd–N in 2:1 complex; (c) Nd–O in 1:1 complex; (d) Nd–O in 2:1 complex. Different line colors represent different O–N atoms in the BLPhen ligands.

3.3. Nd(III)–Nitrate Interactions

When a neutral ligand such as BLPhen extracts Ln(III) into the organic phase, the complex is usually charge neutral. In other words, anions such as the three nitrates will be brought together with Ln(III) into the organic phase. Therefore, nitrate coordination with Nd(III) in DCE is as important as that of BLPhen with Nd(III) in DCE. Figure 5 shows RDFs between Nd and nitrate. One can see that the average distance between Nd(III) and O(NO3) is similar in 1:1 and 2:1 complexes at ∼2.55 Å (Figure 5a). The peak at 4.25 Å is due to the third distant oxygen of the nitrate anion. There are six oxygen atoms in total around Nd(III) in the first solvation shell of the 1:1 complex; in other words, the three nitrates coordinate to Nd(III) all in a bidentate mode (Figure 2a). This is further confirmed in the RDF between Nd(III) and the nitrogen atom of the nitrates (Figure 5b), where one can see that the coordination number of N around Nd is indeed three in the 1:1 complex. In the 2:1 complex, there are ∼2.5 O atoms from nitrates in the first solvation shell of Nd(III) (Figure 5a, with a cutoff of ∼3.0 Å), and they are from two nitrates (Figure 5b); in other words, one nitrate is monodentate with Nd–N distance of ∼3.5 Å, while the other nitrate is switching between monodentate and bidentate (Nd–N distance of ∼3.1 Å).

Figure 5.

Figure 5

Open in a new tab

Atom–atom RDFs, g(r), between Nd(III) and O–N atoms of the nitrate anion for the BLPhen–Nd complexes in the DCE solvent: (a) Nd–O(NO3); (b) Nd–N(NO3). Solid lines represent g(r) (left axis); and dashed lines (right axis) represent their NI, that is, coordination number.

Because nitrate and nitric acid are very commonly used in solvent extraction of Ln(III) ions, the metal–nitrate coordination is important in the organic phase when charge-neutral extractants are used to bring Ln(NO3)3 into the organic phase. To put our findings of Nd(III)–nitrate binding in DCE in a broader perspective, here we compare them with the literature for the popular extractants, such as tri-n-alkyl phosphates, amides, diglycolamides, and malonamides. Diglycolamides tend to form 3:1 ligand-to-metal complexes with Ln(III) ions,48 leading to a total CN of 9, where nitrates are found to be not present in the first coordination sphere; this is supported by both extended X-ray absorption fine structure (EXAFS)49 and single-crystal X-ray diffraction.50 In the case of the bidentate malonamides, classical MD simulations showed that three nitrates are coordinated to Eu(III) in the first coordination shell of the 3:1 complex,51 and EXAFS data suggested that they are about half monodentate and half bidentate.52 This scenario resembles our 2:1 complex case where nitrates can dynamically switch between monodentate or bidentate. The presence of nitrate in the inner coordination of a general amide extractant around Ln(III) will depend strongly on its denticity and the stoichiometry of complexation.53 In the case of tri-n-alkyl phosphates or phosphine oxides, the binding mode of nitrates also depends on the stoichiometry. For example, in a 2:1 complex of tri-tert-butylphosphine oxide, the three nitrates bind to Lu(III) in a bidentate mode, while in a 3:1 complex of tricyclohexylphosphine oxide, two nitrates bind to Yb(III) in a bidentate model and the third nitrate in a monodentate mode.54 From the comparison of the literature cases and our present findings, one can conclude that the total coordination number is the key factor in determining the presence of the nitrate in the first coordination shell or the inner coordination sphere.

3.4. Dynamics of the Nitrate Interaction with Nd(III)

The change in the coordination mode and number of nitrates around Nd(III) from the 1:1 to 2:1 complex begs the question how dynamic the Nd–nitrate interaction is in the two complexes. To this end, we have monitored the evolution of distances from Nd(III) to the closest O atoms in nitrates. Figure 6a shows the evolution for the 1:1 complex: in the beginning, one nitrate coordinates to Nd in a bidentate mode (O1/O2) and two nitrates in a monodentate mode (O4 and O5); then, the second nitrate also becomes bidentate (O3) at ∼1 ps, followed by the third nitrate (O6) at ∼7.5 ps. Completely different behavior of nitrate anions is observed in the case of the 2:1 complex (Figure 6b): the two nitrate anions are mainly in the monodentate state via O1 and O3 in the first 5 ps; then, one nitrate (O3/O4) becomes bidentate at 5 ps and changes to monodentate again at 10 ps, while the other nitrate (O1/O2) is monodentate for most of the time occasionally become bidentate. In other words, nitrate binding to Nd is more dynamic in the 2:1 complex.

Figure 6.

Figure 6

Open in a new tab

Evolution of the Nd–O(NO3) distances around the BLPhen–Nd complexes in the DCE solvent: (a) 1:1 complex; (b) 2:1 complex.

Only two nitrate anions are observed in the first solvation shell of Nd(III) in the 2:1 complex. We have tracked down the third nitrate and found it to be freely moving about in the DCE solvent at a distance about 10 Å away from Nd (Figure 7). To test whether this is indeed a dynamic feature of the third nitrate, we have performed the FPMD simulation of 2:1 Nd–BLPhen complex starting with all three nitrate anions bound to Nd(III). Still, we found that the third nitrate anion comes out of the solvation shell and moves away from the complex. Now a complete picture of the first solvation shell and the nitrate distribution emerges in the 2:1 complex, which is shown as a snapshot in Figure 8. One can see that the two nitrate anions fit quite well into the gap of the binding pocket of Nd(III) with the two rather rigid and planar BLPhen ligands. Figure 8 also shows the positions of the DCE solvent molecules and the third nitrate.

Figure 7.

Figure 7

Open in a new tab

Distance between Nd3+ and N atom of the third nitrate in the BLPhen–Nd 2:1 complex in the DCE solvent.

Figure 8.

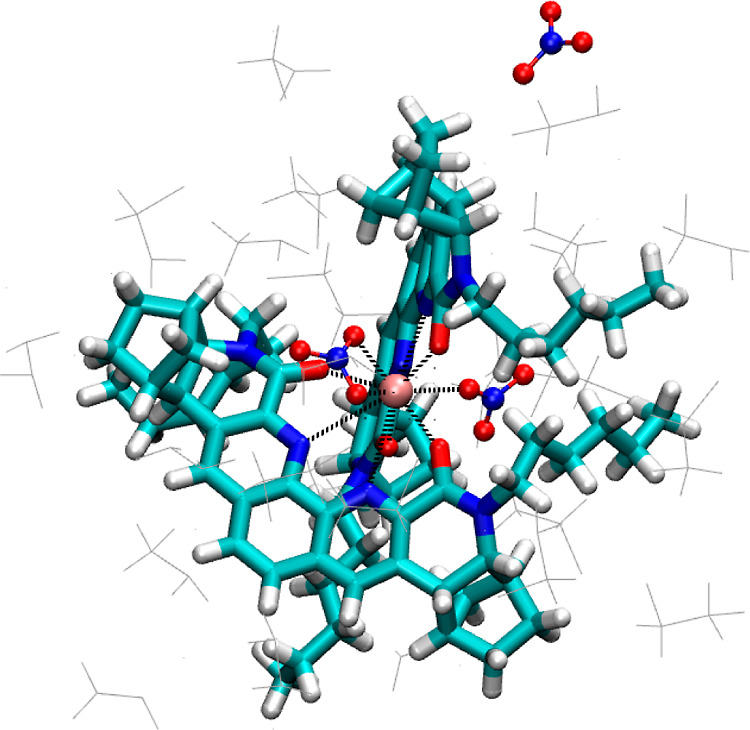
Figure 8

Open in a new tab

Snapshot of the two BLPhen ligands (licorice) and the three nitrate anions (CPK representation) in relation to Nd(III) of the 2:1 complex in the DCE solvent (line).

3.5. Comparison with the Single-Crystal Experimental Data in the Solid Phase Regarding the Key Distances and the First Coordination Shell

An advantage of our FPMD results is that they provide both structure and dynamics of the Nd(III)–BLPhen complexes in the DCE solvent. Although the experimental solution-phase structure is not available for such systems yet, the corresponding single-crystal structures of the metal ion complexes in the solid state are available in many similar cases, which can shed some light on the first coordination shell. Figure 9a shows the available single-crystal structure of a 1:1 Nd(III)–BLPhen complex that is compared with our FPMD simulations (Table 1). One can see that the key average bond distances for the 1:1 Nd(III)–BLPhen complex in DCE agree very well with the experiment in the solid state, suggesting that the DCE solvent here can be considered “non-interacting” as it does not seem to perturb the 1:1 solvation structure of the complex. This observation is in line with the FPMD results that show robustness of the first solvation shell of the 1:1 complex (Figure 4).

Figure 9.

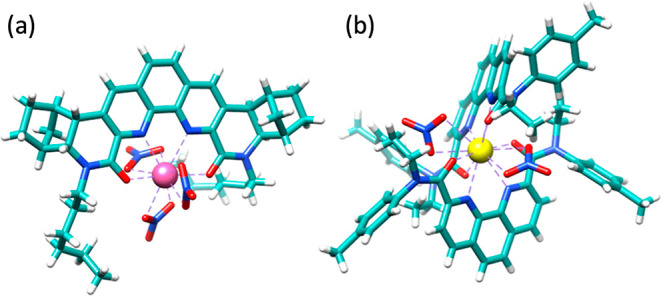
Figure 9

Open in a new tab

Crystal structures of the complexes from the Cambridge Structural Database (CSD): (a) 1:1 Nd(III)–BLPhen;17 (b) 2:1 La(III)–DAPhen.47 Color code: Nd, pink; La, yellow; O, red; N, blue; C, cyan; and H, white.

Table 1. Comparison of Key Distances for the 1:1 Nd(III)–BLPhen Complex between the Experiment (Figure 9a) Based on the Single-Crystal Structure47 and the Present Work from FPMD.

distances (Å) experiment present work
Nd–O(BLPhen) 2.46 2.49
Nd–N(BLPhen) 2.67 2.69
Nd–O(NO3) 2.53 2.56
Nd–N(NO3) 2.96 3.03
Open in a new tab

All attempts to isolate crystals of the 2:1 Nd(III)–BLPhen complex suitable for X-ray diffraction studies were unsuccessful.22 However, our FPMD finding of two nitrates in the first solvation shell of the 2:1 complex is in agreement with the 2:1 crystal structure of the complex (Figure 9b) formed between La(III) and a related ligand, N,N′-diethyl-N,N′-ditolyl-2,9-diamide-1,10-phenanthroline (DAPhen),47 which is a more flexible analogue of rigid BLPhen. Table 2 compares the key distances of 2:1 La(III)–DAPhen from the experiment and 2:1 Nd(III)–BLPhen from the FPMD. One can see that the M–N/O distances between the metal center and the ligands are close, despite the differences in the metal center, the ligands, and the phases (crystal in the experiment vs solution in FPMD). The greater difference lies in the M–O(NO3) distances. As can be seen from Figure 9b, the two nitrates in the first coordination sphere of the 2:1 La(III)–DAPhen complex coordinate to the metal center through a bidentate mode in the absence of solvent molecules (solid phase). From our FPMD, we observed a dynamic switch between bidentate and monodentate nitrate binding in the 2:1 Nd(III)–BLPhen complex simulated in the organic phase. A few factors might explain the difference, including solvation from the DCE solvent, the less flexibility of BLPhen than DAPhen, and the difference in the side chains between BLPhen and DAPhen. Further FPMD simulations of the 2:1 La(III)–DAPhen complex in the DCE solvent could further shed light on this comparison.

Table 2. Comparison of Key Distances between the Experiment for the 2:1 La(III)–DAPhen Complex Based on the Single-Crystal Structure (Figure 9b)47 and the Present Work for the 2:1 Nd(III)–BLPhen from FPMD.

distances (Å) M = La experiment M = Nd present work
M–O(ligand) 2.61 2.58
M–N(ligand) 2.76 2.72
M–O(NO3) 2.71 2.53
M–N(NO3) 3.13 3.13, 3.53
Open in a new tab

3.6. Implications on Solvent Extraction Separations of REE Ions with BLPhen

To be able to directly predict distribution coefficients of REE ions between DCE and the aqueous phase with BLPhen as the extractant is our ultimate goal. The present work is only an initial step to determine the speciation and structure. Our next step is to use the present results from first principles as training and validation data to derive accurate force fields that would allow us to simulate binding free energies and changes in solvation free energies. Only after that are we able to predict distribution ratios and to probe how the local structure and coordination would impact the separation behavior.

The other important question to answer is the role of water in the structure and coordination because the solubility of water in DCE is rather high. We think that nitrate and the BLPhen ligand bind to the metal center more strongly than does water. However, water molecules may form a local hydrogen-bond network in the first coordination shell because both nitrate and the BLPhen have multiple hydrogen bond acceptors. We plan to investigate these important points in a future publication.

4. Conclusions

To shed light on the local structure of the complexes formed between BLPhen and Nd(III) in a typical organic solvent such as DCE, we have performed FPMD simulations to unveil the structure of complexes formed by BLPhen with Nd(NO3)3 in the DCE solvent. We found that three nitrates bind to Nd(III) via the bidentate mode in the first solvation shell of the 1:1 complex, forming a neutral complex, [Nd(BLPhen)(NO3)3]0. In contrast, only two nitrates are found in the first solvation shell in the 2:1 complex, forming [Nd(BLPhen)2(NO3)2]+, with the third nitrate in the outer sphere. The first solvation shell with its key distances from our FPMD agrees well with the single-crystal structure of a 1:1 Nd(BLPhen) complex. Our finding of two nitrates in the first solvation shell of the 2:1 complex is also in line with the available crystal structure for a similar 2:1 complex of DAPhen with La(III); in addition, we found that the two nitrates are quite dynamic in coordinating to Nd(III), switching between monodentate and bidentate. Our FPMD modeling of the BLPhen–Nd(III) complexes in an explicit organic solvent invites more experimental studies of their liquid structure and dynamics that, combined together, would offer more atomistic understanding of REE separations.

Acknowledgments

This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Separation Science program and Materials Chemistry program.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02531.

  • Coordinates of representative snapshots of the simulated systems (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao2c02531_si_001.pdf (207.9KB, pdf)

References

  1. Hurd A. J.; Kelley R. L.; Eggert R. G.; Lee M.-H. Energy-Critical Elements for Sustainable Development. MRS Bull. 2012, 37, 405–410. 10.1557/mrs.2012.54. [DOI] [Google Scholar]
  2. Balaram V. Rare Earth Elements: A Review of Applications, Occurrence, Exploration, Analysis, Recycling, and Environmental Impact. Geosci. Front. 2019, 10, 1285–1303. 10.1016/j.gsf.2018.12.005. [DOI] [Google Scholar]
  3. Gutfleisch O.; Willard M. A.; Brück E.; Chen C. H.; Sankar S. G.; Liu J. P. Magnetic Materials and Devices for the 21st Century: Stronger, Lighter, and More Energy Efficient. Adv. Mater. 2011, 23, 821–842. 10.1002/adma.201002180. [DOI] [PubMed] [Google Scholar]
  4. Zepf V.Rare Earth Elements: A New Approach to the Nexus of Supply, Demand and Use: Exemplified along the Use of Neodymium in Permanent Magnets; Springer Theses; Springer-Verlag: Berlin Heidelberg, 2013. [Google Scholar]
  5. Bauer D.; Diamond D.; Li J.; Sandalow D.; Telleen P.; Wanner B.; U.S. Department of Energy Critical Materials Strategy . https://digital.library.unt.edu/ark:/67531/metadc834802/ (accessed Oct 22, 2021).
  6. Izatt R. M.; Izatt S. R.; Bruening R. L.; Izatt N. E.; Moyer B. A. Challenges to Achievement of Metal Sustainability in Our High-Tech Society. Chem. Soc. Rev. 2014, 43, 2451–2475. 10.1039/c3cs60440c. [DOI] [PubMed] [Google Scholar]
  7. Krishnamurthy N.; Gupta C. K.. Extractive Metallurgy of Rare Earths; CRC Press, 2015. [Google Scholar]
  8. Safarzadeh M. S.; Agarwal V.; Hayes L. New Insights into the Separation of Nd from Pr in Hydrochloric and Sulfuric Acid Solutions. Polyhedron 2018, 153, 82–87. 10.1016/j.poly.2018.06.050. [DOI] [Google Scholar]
  9. Stamberga D.; Healy M. R.; Bryantsev V. S.; Albisser C.; Karslyan Y.; Reinhart B.; Paulenova A.; Foster M.; Popovs I.; Lyon K.; Moyer B. A.; Jansone-Popova S. Inorg. Chem. 2020, 59, 17620–17630. 10.1021/acs.inorgchem.0c02861. [DOI] [PubMed] [Google Scholar]
  10. Ansari S. A.; Pathak P.; Mohapatra P. K.; Manchanda V. K. Chemistry of Diglycolamides: Promising Extractants for Actinide Partitioning. Chem. Rev. 2012, 112, 1751–1772. 10.1021/cr200002f. [DOI] [PubMed] [Google Scholar]
  11. Wilden A.; Kowalski P. M.; Klaß L.; Kraus B.; Kreft F.; Modolo G.; Li Y.; Rothe J.; Dardenne K.; Geist A.; et al. Unprecedented Inversion of Selectivity and Extraordinary Difference in the Complexation of Trivalent f Elements by Diastereomers of a Methylated Diglycolamide. Chem.—Eur. J. 2019, 25, 5507–5513. 10.1002/chem.201806161. [DOI] [PubMed] [Google Scholar]
  12. Lewis F. W.; Harwood L. M.; Hudson M. J.; Drew M. G. B.; Desreux J. F.; Vidick G.; Bouslimani N.; Modolo G.; Wilden A.; Sypula M.; et al. Highly Efficient Separation of Actinides from Lanthanides by a Phenanthroline-Derived Bis-Triazine Ligand. J. Am. Chem. Soc. 2011, 133, 13093–13102. 10.1021/ja203378m. [DOI] [PubMed] [Google Scholar]
  13. Iqbal M.; Mohapatra P. K.; Ansari S. A.; Huskens J.; Verboom W. Preorganization of Diglycolamides on the Calix[4]Arene Platform and Its Effect on the Extraction of Am(III)/Eu(III). Tetrahedron 2012, 68, 7840–7847. 10.1016/j.tet.2012.07.036. [DOI] [Google Scholar]
  14. Lavrov H. V.; Ustynyuk N. A.; Matveev P. I.; Gloriozov I. P.; Zhokhov S. S.; Alyapyshev M. Y.; Tkachenko L. I.; Voronaev I. G.; Babain V. A.; Kalmykov S. N.; et al. A Novel Highly Selective Ligand for Separation of Actinides and Lanthanides in the Nuclear Fuel Cycle. Experimental Verification of the Theoretical Prediction. Dalton Trans. 2017, 46, 10926–10934. 10.1039/c7dt01009e. [DOI] [PubMed] [Google Scholar]
  15. Dam H. H.; Reinhoudt D. N.; Verboom W. Multicoordinate Ligands for Actinide/Lanthanide Separations. Chem. Soc. Rev. 2007, 36, 367–377. 10.1039/b603847f. [DOI] [PubMed] [Google Scholar]
  16. Ellis R. J.; Meridiano Y.; Chiarizia R.; Berthon L.; Muller J.; Couston L.; Antonio M. R. Periodic Behavior of Lanthanide Coordination within Reverse Micelles. Chem.—Eur. J. 2013, 19, 2663–2675. 10.1002/chem.201202880. [DOI] [PubMed] [Google Scholar]
  17. Jansone-Popova S.; Ivanov A. S.; Bryantsev V. S.; Sloop F. V.; Custelcean R.; Popovs I.; Dekarske M. M.; Moyer B. A. Bis-Lactam-1,10-Phenanthroline (BLPhen), a New Type of Preorganized Mixed N,O-Donor Ligand That Separates Am(III) over Eu(III) with Exceptionally High Efficiency. Inorg. Chem. 2017, 56, 5911–5917. 10.1021/acs.inorgchem.7b00555. [DOI] [PubMed] [Google Scholar]
  18. Healy M. R.; Ivanov A. S.; Karslyan Y.; Bryantsev V. S.; Moyer B. A.; Jansone-Popova S. Efficient Separation of Light Lanthanides(III) by Using Bis-Lactam Phenanthroline Ligands. Chem.—Eur. J. 2019, 25, 6326–6331. 10.1002/chem.201806443. [DOI] [PubMed] [Google Scholar]
  19. Manna D.; Ghanty T. K. Complexation Behavior of Trivalent Actinides and Lanthanides with 1,10-Phenanthroline-2,9-Dicarboxylic Acid Based Ligands: Insight from Density Functional Theory. Phys. Chem. Chem. Phys. 2012, 14, 11060–11069. 10.1039/c2cp40083a. [DOI] [PubMed] [Google Scholar]
  20. Manna D.; Mula S.; Bhattacharyya A.; Chattopadhyay S.; Ghanty T. K. Actinide Selectivity of 1,10-Phenanthroline-2,9-Dicarboxamide and Its Derivatives: A Theoretical Prediction Followed by Experimental Validation. Dalton Trans. 2015, 44, 1332–1340. 10.1039/C4DT02402H. [DOI] [PubMed] [Google Scholar]
  21. Singh M. B.; Fu Y.; Popovs I.; Jansone-Popova S.; Dai S.; Jiang D.-e. Molecular Dynamics Simulations of Complexation of Am(III) with a Preorganized Dicationic Ligand in an Ionic Liquid. J. Phys. Chem. B 2021, 125, 8532–8538. 10.1021/acs.jpcb.1c04410. [DOI] [PubMed] [Google Scholar]
  22. Ivanov A. S.; Bryantsev V. S. A Computational Approach to Predicting Ligand Selectivity for the Size-Based Separation of Trivalent Lanthanides. Eur. J. Inorg. Chem. 2016, 2016, 3474–3479. 10.1002/ejic.201600319. [DOI] [Google Scholar]
  23. Kitatsuji Y.; Meguro Y.; Yoshida Z.; Yamamoto T.; Nishizawa K. Synergistic Ion-Pair Extraction of Lanthanide(Iii) with Thenoyltrifluoroacetone and Crown Ether into 1,2-Dichloroethane. Solvent Extr. Ion Exch. 1995, 13, 289–300. 10.1080/07366299508918275. [DOI] [Google Scholar]
  24. Masuda Y.; Zhang Y.; Yan C.; Li B. Studies on the Extraction and Separation of Lanthanide Ions with a Synergistic Extraction System Combined with 1,4,10,13-Tetrathia-7,16-Diazacyclooctadecane and Lauric Acid. Talanta 1998, 46, 203–213. 10.1016/s0039-9140(97)00275-0. [DOI] [PubMed] [Google Scholar]
  25. Atanassova M. Effect of the 18-Crown-6 and Benzo-18-Crown-6 on the Solvent Extraction and Separation of Lanthanide(III) Ions with 8-Hydroxyquinoline. Russ. J. Inorg. Chem. 2007, 52, 1304–1311. 10.1134/s0036023607080244. [DOI] [Google Scholar]
  26. Sasaki Y.; Sugo Y.; Morita K.; Nash K. L. The Effect of Alkyl Substituents on Actinide and Lanthanide Extraction by Diglycolamide Compounds. Solvent Extr. Ion Exch. 2015, 33, 625–641. 10.1080/07366299.2015.1087209. [DOI] [Google Scholar]
  27. Kresse G.; Furthmüller J. Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 1996, 6, 15–50. 10.1016/0927-0256(96)00008-0. [DOI] [PubMed] [Google Scholar]
  28. Kresse G.; Hafner J. Ab Initio Molecular Dynamics for Liquid Metals. Phys. Rev. B: Condens. Matter Mater. Phys. 1993, 47, 558–561. 10.1103/physrevb.47.558. [DOI] [PubMed] [Google Scholar]
  29. Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994, 50, 17953–17979. 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  30. Kresse G.; Joubert D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 1758–1775. 10.1103/physrevb.59.1758. [DOI] [Google Scholar]
  31. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/physrevlett.77.3865. [DOI] [PubMed] [Google Scholar]
  32. Priest C.; Tian Z.; Jiang D.-e. First-Principles Molecular Dynamics Simulation of the Ca2UO2(CO3)3 Complex in Water. Dalton Trans. 2016, 45, 9812–9819. 10.1039/c5dt04576b. [DOI] [PubMed] [Google Scholar]
  33. Priest C.; Li B.; Jiang D.-e. Uranyl-Glutardiamidoxime Binding from First-Principles Molecular Dynamics, Classical Molecular Dynamics, and Free-Energy Simulations. Inorg. Chem. 2017, 56, 9497–9504. 10.1021/acs.inorgchem.7b00711. [DOI] [PubMed] [Google Scholar]
  34. Priest C.; Li B.; Jiang D.-e. Understanding the Binding of a Bifunctional Amidoximate-Carboxylate Ligand with Uranyl in Seawater. J. Phys. Chem. B 2018, 122, 12060–12066. 10.1021/acs.jpcb.8b08345. [DOI] [PubMed] [Google Scholar]
  35. Jorgensen W. L.; Maxwell D. S.; Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. 10.1021/ja9621760. [DOI] [Google Scholar]
  36. Canongia Lopes J. N.; Pádua A. A. H. CL&P: A Generic and Systematic Force Field for Ionic Liquids Modeling. Theor. Chem. Acc. 2012, 131, 1129. 10.1007/s00214-012-1129-7. [DOI] [Google Scholar]
  37. Migliorati V.; Serva A.; Terenzio F. M.; D’Angelo P. Development of Lennard-Jones and Buckingham Potentials for Lanthanoid Ions in Water. Inorg. Chem. 2017, 56, 6214–6224. 10.1021/acs.inorgchem.7b00207. [DOI] [PubMed] [Google Scholar]
  38. Abraham M. J.; Murtola T.; Schulz R.; Páll S.; Smith J. C.; Hess B.; Lindahl E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. 10.1016/j.softx.2015.06.001. [DOI] [Google Scholar]
  39. Berendsen H. J. C.; van der Spoel D.; van Drunen R. GROMACS: A message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 1995, 91, 43–56. 10.1016/0010-4655(95)00042-e. [DOI] [Google Scholar]
  40. Van Der Spoel D.; Lindahl E.; Hess B.; Groenhof G.; Mark A. E.; Berendsen H. J. C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. 10.1002/jcc.20291. [DOI] [PubMed] [Google Scholar]
  41. Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; van der Spoel D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Berendsen H. J. C.; Postma J. P. M.; van Gunsteren W. F.; DiNola A.; Haak J. R. Molecular Dynamics with Coupling to an External Bath. J. Chem. Phys. 1984, 81, 3684–3690. 10.1063/1.448118. [DOI] [Google Scholar]
  43. Chorążewski M.; Postnikov E. B.; Oster K.; Polishuk I. Thermodynamic Properties of 1,2-Dichloroethane and 1,2-Dibromoethane under Elevated Pressures: Experimental Results and Predictions of a Novel DIPPR-Based Version of FT-EoS, PC-SAFT, and CP-PC-SAFT. Ind. Eng. Chem. Res. 2015, 54, 9645–9656. 10.1021/acs.iecr.5b02626. [DOI] [Google Scholar]
  44. Humphrey W.; Dalke A.; Schulten K. VMD: Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
  45. Brehm M.; Kirchner B. TRAVIS - A Free Analyzer and Visualizer for Monte Carlo and Molecular Dynamics Trajectories. J. Chem. Inf. Model. 2011, 51, 2007–2023. 10.1021/ci200217w. [DOI] [PubMed] [Google Scholar]
  46. Brehm M.; Thomas M.; Gehrke S.; Kirchner B. TRAVIS-A free analyzer for trajectories from molecular simulation. J. Chem. Phys. 2020, 152, 164105. 10.1063/5.0005078. [DOI] [PubMed] [Google Scholar]
  47. Yang X.-F.; Ren P.; Yang Q.; Geng J.-S.; Zhang J.-Y.; Yuan L.-Y.; Tang H.-B.; Chai Z.-F.; Shi W.-Q. Strong Periodic Tendency of Trivalent Lanthanides Coordinated with a Phenanthroline-Based Ligand: Cascade Countercurrent Extraction, Spectroscopy, and Crystallography. Inorg. Chem. 2021, 60, 9745–9756. 10.1021/acs.inorgchem.1c01035. [DOI] [PubMed] [Google Scholar]
  48. Antonio M. R.; McAlister D. R.; Horwitz E. P. An Europium(III) Diglycolamide Complex: Insights into the Coordination Chemistry of Lanthanides in Solvent Extraction. Dalton Trans. 2015, 44, 515–521. 10.1039/c4dt01775g. [DOI] [PubMed] [Google Scholar]
  49. Flores R.; Momen M. A.; Healy M. R.; Jansone-Popova S.; Lyon K. L.; Reinhart B.; Cheshire M. C.; Moyer B. A.; Bryantsev V. S. The Coordination Chemistry and Stoichiometry of Extracted Diglycolamide Complexes of Lanthanides in Extraction Chromatography Materials. Solvent Extr. Ion Exch. 2022, 40, 6–27. 10.1080/07366299.2021.1956121. [DOI] [Google Scholar]
  50. Okumura S.; Kawasaki T.; Sasaki Y.; Ikeda Y. Crystal Structures of Lanthanoid(III) (Ln(III), Ln = Tb, Dy, Ho, Er, Tm, Yb, and Lu) Nitrate Complexes with N,N,N′,N′-Tetraethyldiglycolamide. Bull. Chem. Soc. Jpn. 2014, 87, 1133–1139. 10.1246/bcsj.20140139. [DOI] [Google Scholar]
  51. Stemplinger S.; Duvail M.; Dufrêche J.-F. Molecular Dynamics Simulations of Eu(NO3)3 Salt with DMDOHEMA in n-Alkanes: Unravelling Curvature Properties in Liquid-Liquid Extraction. J. Mol. Liq. 2022, 348, 118035. 10.1016/j.molliq.2021.118035. [DOI] [Google Scholar]
  52. Ellis R. J.; Meridiano Y.; Muller J.; Berthon L.; Guilbaud P.; Zorz N.; Antonio M. R.; Demars T.; Zemb T. Complexation-Induced Supramolecular Assembly Drives Metal-Ion Extraction. Chem.—Eur. J. 2014, 20, 12796–12807. 10.1002/chem.201403859. [DOI] [PubMed] [Google Scholar]
  53. Dobler M.; Hirata M. Molecular dynamics simulations of lanthanide(iii) diphenyldimethylpyridinyl-dicarboxyamide complexes in water and in methanol: evidence for both first and second sphere complexes. Phys. Chem. Chem. Phys. 2004, 6, 1672–1678. 10.1039/b314656a. [DOI] [Google Scholar]
  54. Platt A. W. G. Lanthanide Phosphine Oxide Complexes. Coord. Chem. Rev. 2017, 340, 62–78. 10.1016/j.ccr.2016.09.012. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao2c02531_si_001.pdf (207.9KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES