MECHANISTIC AND DATA-DRIVEN MODELS OF CELL SIGNALING: TOOLS FOR FUNDAMENTAL DISCOVERY AND RATIONAL DESIGN OF THERAPY

Abstract

A full understanding of cell signaling processes requires knowledge of protein structure/function relationships, protein-protein interactions, and the abilities of pathways to control phenotypes. Computational models offer a valuable framework for integrating that knowledge to predict the effects of system perturbations and interventions in health and disease. Whereas mechanistic models are well suited for understanding the biophysical basis for signal transduction and principles of therapeutic design, data-driven models are particularly suited to distill complex signaling relationships among samples and between multivariate signaling changes and phenotypes. Both approaches have limitations and provide incomplete representations of signaling biology, but their careful implementation and integration can provide new understanding for how manipulating system variables impacts cellular decisions.

Graphical Abstract

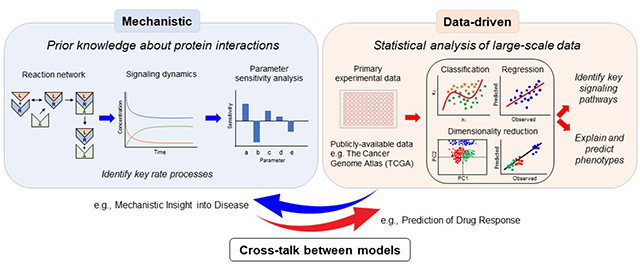
INTRODUCTION

Computational systems biology models have become virtually indispensable tools for integrating our knowledge of complex cell signaling processes. As biochemists characterized elegant protein structure/function relationships and post-translational modifications, the need to synthesize that understanding quantitatively to identify rate-limiting steps in signal transduction became apparent. Mechanistic models are well suited for this because of their ability to capture relevant biophysical processes through kinetic, constitutive, and conservation equations. As omics techniques eventually became common for measuring signaling processes at the network level, a need grew to cluster samples and predict phenotypes based on high-dimensional features. Data-driven models are ideal for these applications because of their ability to reduce system dimensionality while identifying key features and because of a general lack of mechanistic equations connecting phenotypes to multivariate signaling.

The distinction between mechanistic and data-driven modeling approaches can also be illustrated in terms of the useful “cue-signal-response” paradigm [1]. In that conceptual model, extracellular cues (e.g., growth factors) activate receptors, which initiate intracellular signaling processes, and thus elicit cellular responses (Fig. 1). In our view, mechanistic and data-driven models work best at the cue-signal and signal-response levels, respectively.

Figure 1. Modeling intracellular signaling and disease in context of “cue-signal-response” paradigm.

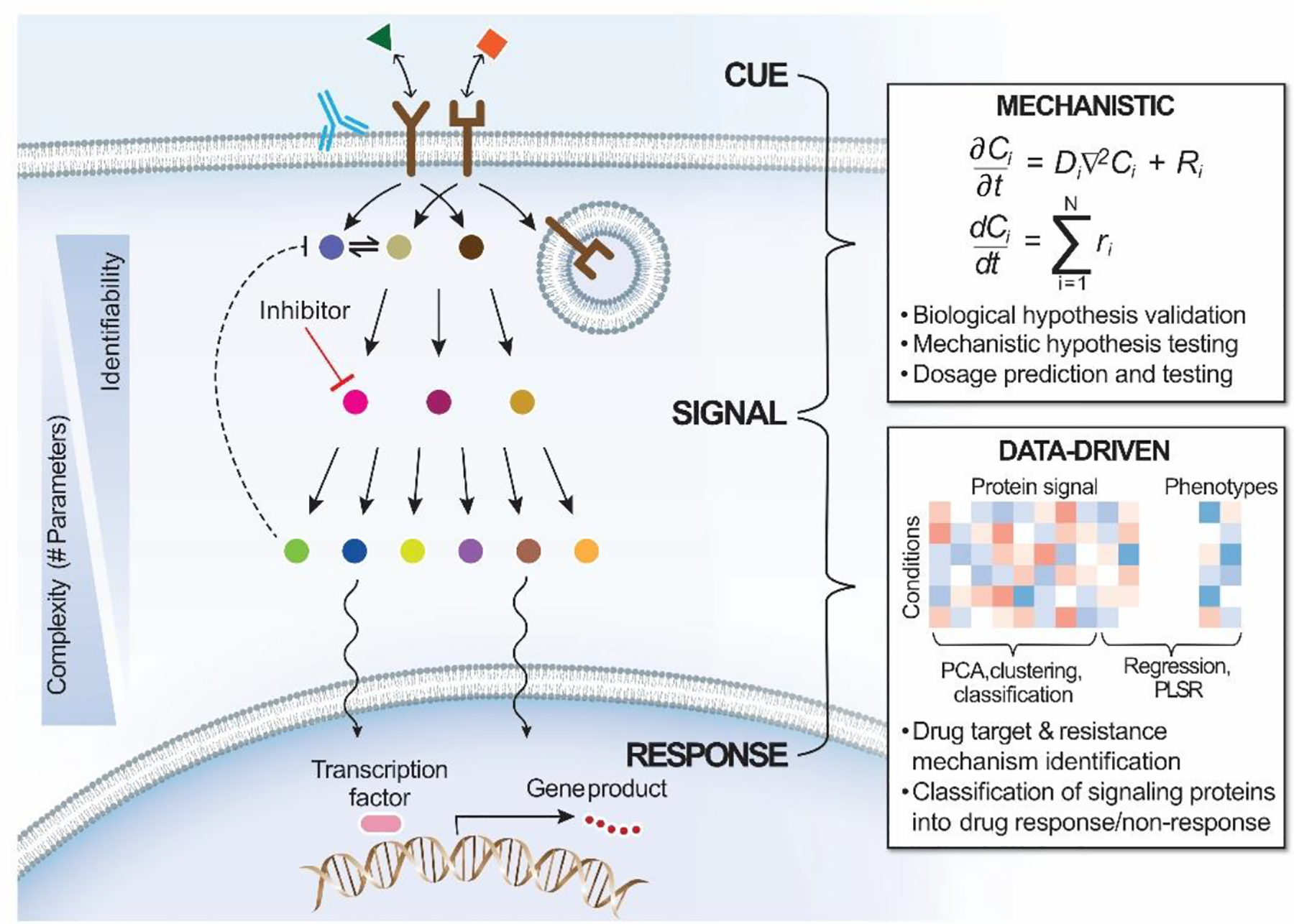
Intracellular signaling generally proceeds with a cue from the extracellular environment in form of ligands. Ligands bind to cognate receptors at the plasma membrane to activate receptors and downstream signaling pathways. Downstream effectors often undergo nucleocytoplasmic shuttling and regulate cell response via regulation of gene transcription. These processes are regulated by a variety of mechanisms, including receptor endocytic trafficking and feedbacks. In mechanistic models of signal transduction, biochemical reactions are typically represented by systems of differential equations, which include numerous parameters reflecting the rates of various binding and catalytic steps. These parameters determine model complexity and identifiability. Signaling dynamics and parameter relations deduced from mechanistic models help to form and validate biological hypotheses and can be applied to predict drug dosing regimens. Insight into signal-to-response relationships is more readily gained by data-driven models, which can reveal relevant structures in large signaling-relevant data sets and predict the importance of groups of signaling pathways in determining complex cell phenotypes. Common applications for data-driven models of signaling include identifying drug targets and resistance mechanisms.

This review highlights recent examples of mechanistic and data-driven signaling models that demonstrate the types of applications described above. Specific methods, model limitations, and implementation issues investigators should consider are described. Use of publicly available data and signaling modeling efforts by the biopharma industry are also discussed.

MECHANISTIC MODELS

Mechanistic signaling models synthesize biophysical understanding of network interactions to predict protein concentrations, post-translational modifications, or localization in response to system perturbations. Within the conceptual framework of Fig. 1, mechanistic models are most appropriate for cue-signal processes because they are governed by conservation and reaction rate laws that can be used to build differential equations. Well-mixed compartmentalized models are common, but mass transfer limitations can exist in signaling and have been incorporated, for example, in modeling signaling at the membrane-cytosol interface and in morphogenic gradients [2,3]. Deterministic solvers are used for abundant species, and stochastic methods can be employed for dilute species (e.g., < 100 molecules per compartment) [4].

While mechanistic models have a powerful ability to adapt to different physical scenarios, they tend to be populated by numerous parameters that are difficult to measure directly and are trained on experimental data with associated error. Thus, even though they are based on physical laws, mechanistic models do not produce output that is free from uncertainty. Moreover, signaling network structures often create scenarios where only a few combinations of rate processes exert meaningful control over system behavior. Dealing with these issues is often the most challenging aspect of mechanistic model design. The tools and methods described below help navigate these issues and should be considered in mechanistic model development.

Parameter Estimation and Inference

In many mechanistic models, protein-protein interactions are encoded based on experimental knowledge, and model tuning focuses primarily on parameters. Often, parameters believed to be well known are fixed, and those that are unknown or whose perturbations produce large changes in model output are estimated through fitting. In other situations, all parameters may be fit simultaneously. In either case, investigators should use caution that fitting results are consistent with magnitudes of established signaling process rates. Investigators should also keep in mind that poor fit may indicate a need to revise model structure and that model selection based on information criteria (e.g., Bayesian) or Bayesian evidence can be used for optimization.

Parameter estimation requires an objective function for minimization. In many cases, that function is defined as the sum of squared errors between model predictions and data [5], a choice used in fitting tools available in MATLAB and COPASI [6]. If errors are normally distributed, maximum likelihood estimation (MLE) provides parameter estimates equivalent to least squares while also providing the joint probability that the estimates explain model fit [7]. When errors are not normally distributed, profile likelihood provides more accurate estimates by finding parameters that minimize the chi-square distribution of the log-likelihood ratio [8]. For signaling models with up to thousands of parameters, the computational cost of estimating the gradient of the objective function can be prohibitive. Adjoint sensitivity analysis can substantially reduce computational costs by efficiently estimating the objective function gradient using backpropagation of the solution in a manner independent of the number of parameters [9].

When parameter distributions rather than point estimates are of interest, inference methods can be used. In Bayesian inference, each parameter is assigned a prior probability distribution representing uncertainty, and this is updated based on available data and optimization to generate a final posterior distribution [7,10–12]. In one recent example, an adaptive metropolis algorithm was used to calculate posterior parameter distributions describing the phosphorylation kinetics of different receptor tyrosine kinases [10]. When both the likelihood function and prior probability distribution are difficult to obtain, as in stochastic models, optimization can proceed via likelihood-free nested sampling, which iteratively simulates the model with parameter combinations sampled from posterior distributions to compute probabilities [13].

The efficiency and accuracy of the methods discussed here and others (e.g., Monte Carlo, Markov Chain Monte Carlo, and iterative filtering inference) are still being explored. Efforts have also recently been made to devise systematic platforms for obtaining probability density functions that work well for differential equation-based models when standard approaches fail [14].

Sensitivity Analysis

Local sensitivity analysis is the simplest technique to identify parameters and rate processes that most impact model output. It involves calculating a change in model output for a perturbation in an individual parameter. Local sensitivity analysis has been used, for example, to identify factors determining the combined effects of two RAF inhibitors on ERK activity [15], signaling protein complex persistence in response to EGFR activation [16], and efficacy of different classes of EGFR-targeted therapies [17]. Global sensitivity analysis is a more sophisticated and computationally demanding method in which all parameters are perturbed simultaneously. This approach more realistically depicts the biological fact that multiple parameters are perturbed at once in signaling systems (e.g., abundances of multiple proteins) [18]. Global sensitivity analysis may identify parameters that do not emerge through local analysis and may suppress the apparent importance of parameters that only exert control near the base model parameters. The discrepancy between local and global analyses tends to grow with more parameters [19], and it is useful to compare the methods to generate biological hypotheses.

One widely used global sensitivity metric is the partial rank correlation coefficient (PRCC), which quantifies the effects of parameter variations on model output using values chosen by random or pseudorandom methods such as Latin Hypercube Sampling (LHS) [20], as in recent immune signaling models [21,22]. PRCC magnitude and significance are assessed to identify important parameters. A more computationally intensive, yet popular, method is extended Fourier Amplitude Sensitivity Test (eFAST), a hybrid local/global sensitivity analysis in which variance in model output, represented by a Fourier series, is decomposed into variance from each parameter sampled from sinusoidal functions. eFAST was recently employed to identify parameters that exert strong influence on ERK activation individually or in groups [23].

Because global sensitivity analysis involves evaluating the model with multiple parameter sets sampled from a defined space, computation time depends on sampling method, with options including random, LHS, and Sobol sequences [20,24]. Although there is no established guideline for choice of sampling method to our knowledge, specific methods have typically been paired with specific sensitivity analysis approaches (i.e., LHS-PRCC or Sobol sequence-Sobol). Pseudorandom sampling such as LHS is generally preferred to random because the former samples parameter space homogenously and efficiently. Kolmogorov-Smirnov statistics is a simpler global method that measures separation between two cumulative trajectory distributions caused by solving the system with nominal parameter and perturbed parameter values [19,25].

Sloppiness, Identifiability, and Uncertainty

Due to lack of prior knowledge of some parameters and the locations of specific parameters within model equations (i.e., model structure), most mechanistic models of cell signaling are “sloppy” [26–28]. In such models, only a small number of parameter combinations control model output. This is characterized mathematically by log-linearly spaced eigenvalues of the Hessian matrix (second derivatives of the chi-squared quality of fit metric with respect to parameters) [12,29]. Uncertainty in model output can be formally quantified and attributed to combinations of “sloppy” or “stiff” parameters. Sloppiness analysis provides a range of fluctuations around the best fit parameters in each eigendirection of the Hessian that produces nearly equivalent model output. Thus, unlike sensitivity analysis, sloppiness directly accounts for error in the data used to fit and identify important parameters.

Many mechanistic models are also structurally non-identifiable or poorly conditioned, meaning that a unique set of parameters that provides a good fit to data cannot be determined, or is practically non-identifiable because parameter confidence intervals cannot be determined due to insufficient amount or quality of data [30]. While it may be tempting to consider model sloppiness and non-identifiability as synonymous, a sloppy model may be structurally identifiable and have unique values of parameter estimates for experimental data [31].

Modeling Cellular Responses using Mechanistic Models

While mechanistic models are typically best-suited to cue-signal problems, their use to understand transcriptional processes can provide a connection to phenotype determination. In one recent example, an ensemble ODE-based model was used to predict prolactin-mediated STAT5 transcriptional regulatory activity and Bcl-XL gene expression to identify strategies to enhance beta cell survival [32]. In another example, delay differential equations were trained on RNA-seq data to demonstrate that the transcription factors EGR1 and FRA-1 filter ERK activity to regulate DNA damage response [33]. In these examples and others (e.g., modeling macrophage phenotypes [34,35] or epithelial-mesenchymal transition [36]), a key element of a successful approach is that phenotypes are controlled by a known and circumscribed set of transcription factors such that a meaningful mechanistic model can be constructed.

DATA-DRIVEN MODELS

Data-driven models use computational algorithms to analyze signaling data without mechanistic knowledge. Datasets must include enough independent observations of the system (e.g., responses to different signaling agonists or drugs) and have sufficiently broad feature measurement (e.g., phosphoprotein measurements) to capture the biochemical processes that distinguish samples and explain how signaling leads to phenotypic changes. A variety of experimental methods can be used to gather these data, depending on the application and sample availability [37]. Within the conceptual framework of Fig. 1, data-driven models are most appropriate for signal-response relationships because of their ability to distill the complexity of high-dimensional features and quantitatively map those features to outcomes despite the lack of physically-based governing equations.

Depending on the approach, data-driven methods are sometimes referred to as machine learning models or statistical models and can be categorized as unsupervised or supervised. Unsupervised approaches analyze unlabeled data (i.e., outcomes are unknown) and focus primarily on sample clustering and dimensionality reduction. Common examples include principal components analysis (PCA) and t-stochastic neighbor embedding (t-SNE). Supervised approaches (i.e., regression and classification) predict outcomes and identify predictive signaling features by building models on labeled training data. Response data can include signals themselves, phenotypes, or group identity (e.g., tumor subtype). Successful data-driven modeling depends on pairing datasets with appropriate computational methods and on model refinement through cross validation.

Clustering and Dimensionality Reduction

For large data sets, dimensionality reduction and clustering has become increasingly common for understanding data structures. These methods identify latent dimensions in the data that best explain sample variance or minimize stress. PCA is a widely known technique based on maximizing variance among samples as they are projected into orthogonal, rank-ordered principal component vectors, defined by linear combinations of all measured features. PCA has become commonplace in signaling research, with recent examples including phosphoprotein analysis to stratify drug-responsive melanoma cell lines [38] and identification of pathways that differentiate primary Sjögren’s syndrome patients from healthy subjects [39].

In recent years, non-linear dimensionality reduction techniques including t-SNE and uniform manifold approximation and projection (UMAP) have also become common. These methods work through nonlinear projections of data into lower dimensional spaces in a way that minimizes the differences between inter-sample distance metrics in the high- and low-dimensional representations of the data. They generally perform better than PCA for separating single-cell measurements (e.g., mass cytometry, single-cell RNA-seq) [40,41] and produce low-dimensional embeddings that are useful as inputs to clustering algorithms (e.g., k-means) or for visualization. One drawback is that quantitative information and interpretations are lost in the non-linear projections. One recent study used t-SNE and decision tree-based classification to identify several clinically relevant epithelial-mesenchymal transition states in lung cancer from mass cytometry data [42]. A similar study used t-SNE and UMAP projections of flow cytometry data as inputs to a self-organizing maps algorithm to identify tumor cell groups with distinct signaling profiles that stratified patients for glioblastoma progression [43]. While the authors concluded that t-SNE and UMAP provided comparable performance, UMAP is generally faster and more accurately represents latent local and global structures within high-dimensional data sets [40]. Dimensionality reduction and cluster analysis can also identify signaling pathways warranting further investigation in mechanistic models [33,44] and supervised regression models [45–47].

Predicting Phenotypic Responses from Multivariate Signaling Data

Data-driven models can also be used to build quantitative relationships between phenotypes and high-dimensional feature data that provide direct or indirect information about signaling. A pervasive approach in the literature is to rely on next-generation sequencing for feature data and some form of pathway analysis for the coarse identification of relevant signaling pathways for different known sample classes (e.g., tumor cell subtypes). While this approach can be useful for a coarse initial survey, it should not be used as the only approach for identifying key signaling pathways for phenotype determination because transcriptomic measurements typically lack temporal resolution and provide only an indirect measure of signaling pathway activity. Phosphoproteomics provide a more direct indication of signaling pathway activity (at least as regulated by kinases) and can be obtained at the network level using various approaches [37]. Phosphoproteomic data can be subjected to differential phosphorylation analyses analogous to gene set enrichment [48–51], but these approaches still lack a connection between signaling measurements and outcomes.

To connect signaling measurements and outcomes, some studies have used partial least squares regression (PLSR), a linear approach that projects signaling and phenotype measurements into a reduced dimensional space by optimizing the alignment of scores vectors for paired matrices of signaling and phenotype measurements. Recent examples include predictions of cell responses to different classes of drugs [47,52,53] or the human immunodeficiency virus [54]. Nonlinear partial least squares regression can also be performed, and the optimal choice of model order can be informed by considering information criteria (e.g., Akaike). Other studies have used elastic net regression [46,55,56], a regularized version of linear regression that allows for correlated predictors without needing to project data onto a separate regression space (as in PLSR). When discrete phenotype or response data are provided (e.g., patient disease or treatment status), classification methods such as logistic regression, partial least squares discriminant analysis (PLS-DA), and support vector machines can be used to identify signaling processes that are predictive of sample class [57–60]. In one recent example, PLS-DA was used to identify novel immune cell-specific phosphoprotein signatures from mass cytometry data that most discriminated between healthy and treatment-naïve juvenile dermatomyositis patients [60].

PUBLICLY AVAILABLE DATASETS

A variety of sources of publicly available data can assist investigators in developing signaling hypotheses. These datasets generally lack dynamic resolution and are typically useful only for data-driven models. For oncology, the Cancer Dependency Map (DepMap) and The Cancer Genome Atlas (TCGA) provide cell line and patient tumor data that have been widely used for bioinformatics approaches. For example, TCGA data sets have been used in approaches similar to pathway analysis to identify activated kinase and oncoprotein networks in KRAS mutant contexts [51,61]. While publicly available snapshot transcriptomic data and cellular drug sensitivity data have been used in both data science and mechanistic models to predict cellular responses to drug perturbations [52,56,62–64], the general lack of dynamic measurements and emphasis on transcript data limits the insight that can be gained. Dynamic data provides richer information for mechanistic model building, but the same is true of data-driven models [56]. Incorporation of dynamic data, especially of phosphoprotein measurements and for complex perturbations (e.g., with combination therapies), in publicly available datasets will facilitate more powerful signaling models.

APPLICATIONS OF SIGNALING MODELS IN INDUSTRY

The biopharma industry has increasingly recognized systems signaling models as useful tools for developing and deploying therapeutics. Recent examples have leveraged mechanistic models to predict the utility of combining DNA damage response inhibitors with doxorubicin or gemcitabine to treat cancer [65], identify cell settings where a bispecific antibody would outperform a monovalent antibody targeting the MET receptor [66], develop design principles for drugs targeting signaling proteins for degradation [67], and design clinical trials for an ErbB3-targeting antibody in ovarian, breast, and lung cancer [68]. Industry practitioners have also used non-mechanistic models such as a decision trees to predict cancer cell line response to targeted inhibitors based on ligand addiction [69].

Industry colleagues have also advocated for advancing computational models, including those for signaling. For example, they have promoted data science as a core discipline in drug discovery and development [70] and urged thinking beyond drug-target binding energetics to build models incorporating the nonidealities of cellular environments from which toxicodynamic effects emerge [71]. They are also leading efforts to develop and disseminate prototype models for refinement by the research community, as in a recent mechanistic model of SARS-CoV-2 based on viral dynamics, immune and inflammatory signaling, and tissue damage [72].

CONCLUDING REMARKS

By necessity, our coverage of signaling modeling approaches was targeted and brief. A lengthier discussion would be needed to survey other relevant topics including multiscale [73,74], logic-based [75,76], Boolean [77], pharmacokinetic/pharmacodynamic [78] and evolutionary models, as well as genetic algorithms and constraint-based approaches [79]. It is also worth noting that distinctions between modeling approaches drawn here are not totally general and that crossover applications are increasingly occurring. For example, data-driven approaches can be used in the development of mechanistic models, as in a recent example using PLSR to interpret global sensitivity analysis for a model of EGF-mediated RAF membrane localization [80]. As another example, some machine learning approaches have modeled signaling dynamics and phenotypes using differential equations, with weighted protein interaction parameters used to fit model outputs to measured phosphoprotein and cell response dynamics [64].

We anticipate that integrated mechanistic and data-driven models will eventually enable quantitative predictions for how changes to the biophysical properties of cellular cues propagate through multivariate signaling processes to drive changes in cell phenotype. The key and challenge to accomplishing that goal is at the signaling effector level, where the output of mechanistic models will become the input of data-driven models. That is, enough pathway nodes will need to be mechanistically modeled to generate meaningful data-driven models of phenotype. Accomplishing that goal will create new and useful modeling frameworks for the development of basic science hypotheses and for the design of targeted therapy approaches for disease.

HIGHLIGHTS.

• Mechanistic models describe the physical basis for signaling network function.

• Parameter sensitivity and uncertainty analyses aid mechanistic model interpretation.

• Data-driven models distill high-dimensional omics into cell phenotype models.

• Data-driven and mechanistic models inform and constrain one another.