Skip to main content
PMC home page
Wiley - PMC COVID-19 Collection logoLink to Wiley - PMC COVID-19 Collection
. 2022 Jul 18:10.1111/tbed.14655. Online ahead of print. doi: 10.1111/tbed.14655

Systematic review and meta‐analyses of superspreading of SARS‐CoV‐2 infections

Zhanwei Du 1,2, Chunyu Wang 1,2, Caifen Liu 1,2, Yuan Bai 1,2, Sen Pei 3, Dillon C Adam 1, Lin Wang 4, Peng Wu 1,2, Eric H Y Lau 1,2, Benjamin J Cowling 1,2,✉
PMCID: PMC9349569  PMID: 35799321

Abstract

Superspreading, or overdispersion in transmission, is a feature of SARS‐CoV‐2 transmission which results in surging epidemics and large clusters of infection. The dispersion parameter is a statistical parameter used to characterize and quantify heterogeneity. In the context of measuring transmissibility, it is analogous to measures of superspreading potential among populations by assuming that collective offspring distribution follows a negative‐binomial distribution. We conducted a systematic review and meta‐analysis on globally reported dispersion parameters of SARS‐CoV‐2 infection. All searches were carried out on 10 September 2021 in PubMed for articles published from 1 January 2020 to 10 September 2021. Multiple estimates of the dispersion parameter have been published for 17 studies, which could be related to where and when the data were obtained, in 8 countries (e.g. China, the United States, India, Indonesia, Israel, Japan, New Zealand and Singapore). High heterogeneity was reported among the included studies. The mean estimates of dispersion parameters range from 0.06 to 2.97 over eight countries, the pooled estimate was 0.55 (95% CI: 0.30, 0.79), with changing means over countries and decreasing slightly with the increasing reproduction number. The expected proportion of cases accounting for 80% of all transmissions is 19% (95% CrI: 7, 34) globally. The study location and method were found to be important drivers for diversity in estimates of dispersion parameters. While under high potential of superspreading, larger outbreaks could still occur with the import of the COVID‐19 virus by traveling even when an epidemic seems to be under control.

Keywords: COVID‐19, dispersion parameter, meta‐analysis, SARS‐CoV‐2, superspreading, systematic review

1. INTRODUCTION

A novel coronavirus (SARS‐CoV‐2) was first identified in Wuhan, China, in early 2020 and rapidly spread throughout the world. The World Health Organization (WHO) declared a pandemic on 11 March 2020 (Wan, 2020). As of 2 July 2022, over 548 million confirmed COVID‐19 cases and 6.34 million deaths have been reported (World Health Organization, 2022a). Worldwide, five variants of concern (VOC, e.g. Alpha, Beta, Gamma, Delta and Omicron) and eight variants of interest (VOI, e.g. Epsilon, Zeta, Eta, Theta, Iota, Kappa, Lambda and Mu) have already been identified by WHO to‐date (World Health Organization, 2022b). Some of these variants have exhibited increased transmissibility and severity compared to wild‐type SARS‐CoV‐2 virus, with some also able to partially evade immunity conferred by prior infection or vaccination (Garcia‐Beltran et al., 2021).

The dispersion parameter (k) is a statistical parameter used to characterize and quantify heterogeneity in certain distributions. In the context of measuring transmissibility, overdispersion in transmission has often been estimated by assuming that the collective offspring distribution follows a negative‐binomial distribution (Lloyd‐Smith et al., 2005; Su et al., 2020). Specifically, the variance of the number of secondary infections from each case is R+R2/k, where R is the mean and k is the dispersion parameter. A small value of k indicates increased heterogeneity in transmission and therefore a high potential of superspreading and describes the phenomenon that a few infectious cases account for most secondary transmissions (Gao et al., 2019). Accurate estimates of k are essential for determining the potential need for, and intensity of, public health and social measures (PHSMs) needed for disease control. When superspreading potential is low, relaxing PHSMs to reopen societies become feasible in low transmission scenarios (R<1). While under high potential of superspreading, larger outbreaks could still occur even when an epidemic seems to be under control (R<1).

For SARS and MERS, most infections are caused by a small proportion of cases, with the dispersion parameter ranging from 0.06 to 2.94 (Wang et al., 2021). However, a comprehensive review and comparison of the superspreading potential of COVID‐19 and its uncertainty over countries is still lacking. We carried out a systematic review and meta‐analysis of published estimates of the dispersion parameter, aiming to estimate the pooled k of SARS‐CoV‐2 infections.

2. MATERIALS AND METHODS

2.1. Search strategy and selection criteria

All searches were carried out on 10 September 2021 in PubMed for articles published from 1 January 2020 to 10 September 2021. We included all relevant articles that were published in peer reviewed journals, coupled with 8 articles recommended by experts. Search terms for superspreading for COVID‐19 variants included (#1) ‘COVID‐19’ OR ‘SARS‐COV‐2’ OR ‘2019‐nCov’ OR ‘Coronavirus 2019’ OR ‘2019 coronavirus’ OR ‘coronavirus Wuhan’ OR ‘pneumonia Wuhan’ and (#2) ‘Superspreader’ OR ‘Spreader’ OR ‘Superspreader event’ OR ‘Super‐spreader’ OR ‘Super‐spreader hosts’ OR ‘Super‐spreading’ OR ‘Superspreading’ OR ‘Overdispersion’ OR ‘Dispersion parameter’ OR ‘20/80 rule’ OR ‘dispersion parameter’ and the final search term was #1 AND #2. After reading the abstract and full text, we included studies in which estimates of the dispersion parameter were reported along with their uncertainty intervals and estimation periods. We excluded other systematic reviews and meta‐analysis from our analyses but included relevant studies mentioned in these reviews. Finally, 144 studies are included with the publish date between 20 March 2020 and 3 September 2021.

2.2. Data extraction

All data were extracted independently and entered in a standardized form by 2 co‐authors (CW and CL). Conflicts over inclusion of the studies and retrieving the estimates of these variables were resolved by another co‐author (ZD). Information was extracted on the estimates of dispersion parameters of COVID‐19 superspreading coupled with the corresponding 95% or 90% confidence interval (CI) or the 95% credible interval (CrI) or 95% range across 500 instances of reconstructed transmission tree (95% Range). This paper converts 90% CI to 95% CI for meta‐analysis. Other information such as study's information (i.e., estimation period and location), model used in estimation measurements of transmissibility and heterogeneity (i.e., dispersion parameter, ‘20/80’ rule and dispersion parameter), and study population and settings (i.e., type of cases) was also extracted for each selected study (see Supplementary Materials for details).

2.3. Estimation of dispersion parameter in studies reporting the ‘20/80’ rule

A framework is proposed to compute the dispersion parameter (k) by reported reproduction number (R) and the transmission distribution profiles in the form of the ‘20/80’ rule (Endo et al., 2020; Lloyd‐Smith et al., 2005). For those articles without k reported, we adopted the framework below to estimate k in Equation (1).

1−P=∫0XNBx;k,kR+kdx, (1)

where X is the upper limit of NB(•), which satisfies,

1−Q=1R∫0XxNBx;k,kR+kdx,

where P is the expected proportion of the most infectious individuals responsible for Q of all transmissions. NB(•) means the negative binomial distribution for secondary cases with mean R and overdispersion parameter k.

2.4. Statistical analysis

We use the I 2 index to assess heterogeneity between studies into the following three categories: I 2< 25% (low heterogeneity), I 2= 25%–75% (average heterogeneity) and I 2> 75% (high heterogeneity). Because of the high I 2 value that was calculated in our results, as well as the significance of the Cochran Q test, a random‐effects model was further used to perform a meta‐analysis in this study. Finally, meta‐regression analysis using a mixed‐effects model was conducted to quantify the association between study's location and the estimate of dispersion parameter. Analyses were conducted in R version 4.1.1.

3. RESULTS

We identified 114 studies published from 1 January 2020 to 10 September 2021 by searching PubMed and additionally included 8 studies from our own reference list. Of these, 59 studies were excluded through title and abstract screening, leaving 55 studies for full‐text assessment. A total of 17 of them were finally included in this study, providing 45 estimates. The detailed selection process is illustrated in Figure 1. The reports are conducted based on data in eight countries (e.g. China, the United States, India, Indonesia, Israel, Japan, New Zealand and Singapore) using three methods (e.g. negative binomial distribution, zero‐truncated negative binomial distribution and phylodynamic analysis) (Table 1).

FIGURE 1.

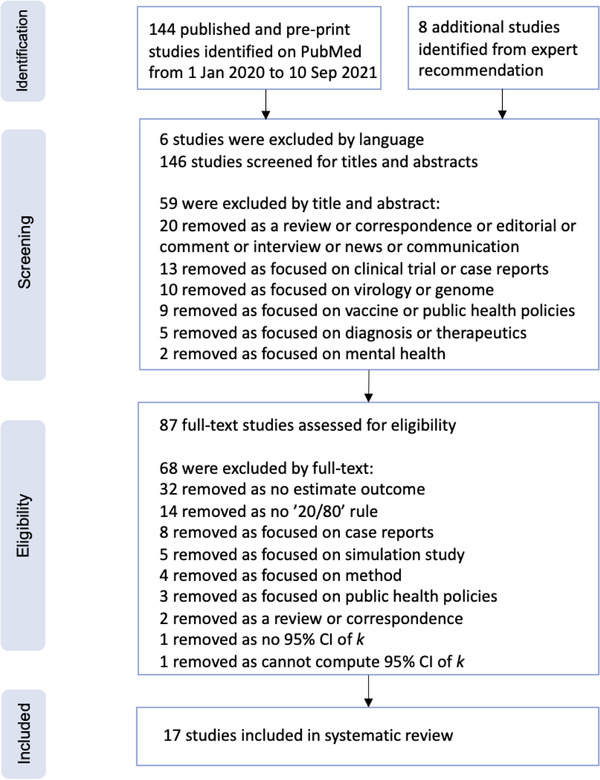
FIGURE 1

Open in a new tab

PRISMA (Preferred Reporting Items for Systematic Reviews and Meta‐Analyses) flow diagram for the studies used to obtain studies that reported measurements of the dispersion parameter. We used PubMed for our primary search

TABLE 1.

Description of studies included in the systematic review and meta‐analysis

Study Method Dispersion parameter (k), (95% CI) Period Region
Sun et al. (2021) Negative binomial distribution 0.30 (0.23, 0.39) 2020‐1‐16 to 2020‐4‐3 Mainland China
Adam et al. (2020) Negative binomial distribution 0.43 (0.29, 0.67) 2020‐1‐23 to 2020‐4‐28 Hong Kong, China
Bi et al. (2020) Negative binomial distribution 0.58 (0.35,1.18) 2020‐1‐14 to 2020‐2‐12 Mainland China
He et al. (2020) Negative binomial distribution 0.70 (0.59, 0.98) 2020‐1‐15 to 2020‐2‐29 Mainland China
Hasan et al. (2020) Negative binomial distribution 0.06 (0.05, 0.07) 2020‐3‐2 to 2020‐3‐31 Indonesia
Hasan et al. (2020) Negative binomial distribution 0.20 (0.09, 0.31) 2020‐3‐19 to 2020‐4‐7 Indonesia
Kwok et al. (2020) Negative binomial distribution 2.30 (0.02, 4.58) By 2020‐3‐3 Hong Kong, China
Kwok et al. (2020) Negative binomial distribution 0.51 (0.21, 1.59) By 2020‐3‐3 Japan
Kwok et al. (2020) Negative binomial distribution 1.78 (0.09, 3.47) By 2020‐3‐3 Singapore
Lau et al. (2020) Negative binomial distribution 0.63 (0.54, 0.85) 2020‐3‐1 to 2020‐4‐3 USA
Lau et al. (2020) Negative binomial distribution 0.66 (0.60, 0.71) 2020‐3‐1 to 2020‐4‐3 USA
Lau et al. (2020) Negative binomial distribution 0.62 (0.54, 0.75) 2020‐3‐1 to 2020‐4‐3 USA
Lau et al. (2020) Negative binomial distribution 0.64 (0.53, 0.75) 2020‐3‐1 to 2020‐4‐3 USA
Lau et al. (2020) Negative binomial distribution 0.39 (0.37, 0.44) 2020‐3‐1 to 2020‐4‐3 USA
Miller et al. (2020) Phylodynamic analysis 2.97 (2.86, 3.08) By 2020‐4‐22 Israel
Tariq et al. (2020) Negative binomial distribution 0.11 (0.05, 0.25) 2020‐1‐23 to 2020‐3‐17 Singapore
Wang et al. (2020) Phylodynamic analysis 0.23 (0.13, 0.38) 2019‐12‐24 to 2020‐2‐14 Mainland China
Zhao et al. (2021) Negative binomial distribution (zero‐truncated framework) 0.37 (0.29, 0.48) 2020‐1‐15 to 2020‐2‐29 Mainland China
Zhao et al. (2021) Negative binomial distribution (zero‐truncated framework) 0.32 (0.15, 0.64) 2020‐1‐23 to 2020‐4‐28 Hong Kong, China
Zhao et al. (2021) Negative binomial distribution (zero‐truncated framework) 0.18 (0.01, 1.79) 2020‐1‐21 to 2020‐2‐26 Mainland China
Zhang et al. (2020) Negative binomial distribution 0.25 (0.13, 0.88) 2020‐1‐21 to 2020‐2‐26 Mainland China
Shi et al. (2021) Negative binomial distribution 0.21 (0.13, 0.33) 2020‐1‐21 to 2020‐4‐10 Mainland China
James et al. (2021) Negative binomial distribution 0.29 (0.10, 2.05) 2020‐3‐25 to 2020‐4‐22 New Zealand
Kremer et al. (2021) Negative binomial distribution 0.43 (0.38, 0.49) 2020‐1‐23 to 2020‐4‐18 Hong Kong, China
Kremer et al. (2021) Negative binomial distribution 0.50 (0.50, 0.51) By 2020‐8‐1 India
Kremer et al. (2021) Negative binomial distribution 0.56 (0.29, 0.83) By 2020‐12‐31 Rwanda
Endo et al. (2020) Negative binomial distribution 0.10 (0.05, 0.20) By 2020‐2‐27 Global
Riou and Althaus (2020) Negative binomial distribution 0.54 (0.01, 8.18) By 2020‐1‐18 Global
Open in a new tab

High heterogeneity was reported among the included studies (I 2= 100% and p < .0001). The mean estimates of dispersion parameter (k) range from 0.06 to 2.97 over eight countries. The pooled estimate of k was 0.55 (95% CI: 0.30, 0.79), with changing means over countries (Figure 2) and decreasing slightly with the increasing reproduction number (Figure 3). The global estimates are 0.54 (95% CI: 0.54, 8.18) in January 2020 (Riou & Althaus, 2020) and 0.10 (95% CI: 0.05, 0.20) in February 2020 (Endo et al., 2020). The expected proportion of cases accounting for 80% infections is 19% (95% CrI: 7, 34) over countries (Table 1).

FIGURE 2.

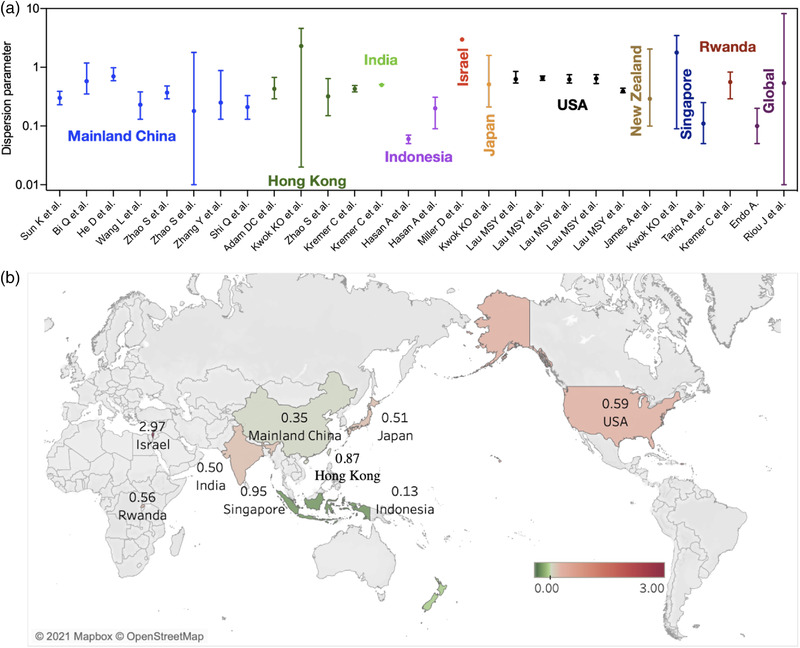
FIGURE 2

Open in a new tab

Dispersion parameter estimates for coronavirus disease 2019 (COVID‐19) reported in 17 unique studies presented by country. (a) Estimates of dispersion parameters over countries. The error bars show the mean values and 95% confidence interval. (b) Mean estimate of dispersion parameters by countries over studies

FIGURE 3.

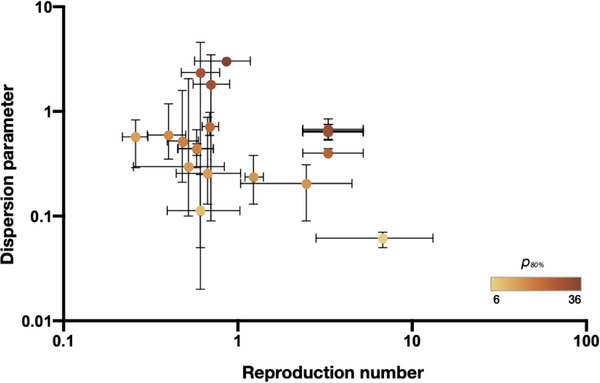
FIGURE 3

Open in a new tab

Dispersion parameter estimates and reproduction numbers for coronavirus disease 2019 (COVID‐19) reported in 17 unique studies presented by country. The error bars show the mean values and 95% confidence interval of the dispersion parameter estimates and reported reproduction numbers in studies (Supplement). The colour denotes the estimated proportion of cases accounting for 80% of all transmissions (p 80%)

The meta‐regression analysis was conducted based on the reported k estimates, which allowed us to explore the potential association between the study attribute (e.g. location, methods, or age groups) and the estimated dispersion parameter (Figure 4). We found that the study location was closely associated with the reported dispersion parameter in the meta‐analysis by including country, age group or method as a categorical variable (p < .0001).

FIGURE 4.

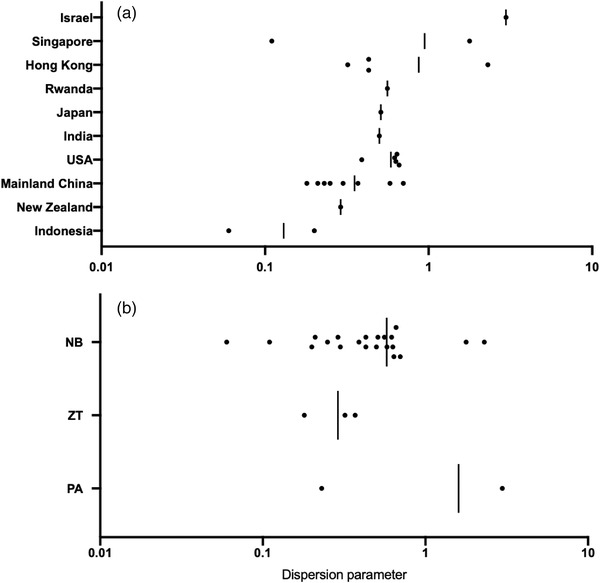
FIGURE 4

Open in a new tab

Distribution of the estimated mean dispersion parameter with respect to (a) countries studied and (b) methods studied. Black circles denote the mean estimates across studies. Vertical lines denote the mean values by averaging that for each country or method. NB: negative binomial distribution; ZT: negative binomial distribution (zero‐truncated framework); PA: phylodynamic analysis

4. DISCUSSION

For SARS‐CoV‐1, SARS‐CoV‐2 and MERS‐CoV, most infections are caused by a small proportion of people. During the 2003 SARS epidemic, 76 infections arose from 1 hospitalized patient in Beijing, China (Shen et al., 2004). And during the 2015 MERS outbreak, 5 patients led to 154 secondary infections in South Korea (Chun, 2016). In this early COVID‐19 outbreak, around 10% of cases in countries outside China accounted for 80% of secondary cases (Endo et al., 2020). But epidemiological population‐level measures (e.g. the basic reproduction number) usually hide immense variation at the individual level (Du, Hong et al., 2022; Du, Javan et al., 2020; Du, Liu et al., 2022; Du, Tian et al., 2022; Du, Xu et al., 2020). We thus carried out a systematic review and meta‐analysis of 17 studies on the dispersion parameter to characterize COVID‐19 superspreading.

Estimation of the dispersion parameter from individual case data requires accurate observation of transmission chains, usually collected through contact‐tracing or phylodynamic analysis, and can be biased, perhaps by reporting bias, estimation methods and transmission scenarios. The negative binomial model with the zero‐truncated framework would reduce the estimation bias of dispersion parameter when the under‐ascertainment of index cases with zero secondary case occurs, for example, in China (Zhao et al., 2021). Estimating and monitoring changes in the dispersion parameter are thus critical for determining the type and stringency of public health and social measures (PHSMs) needed to reduce the occurrence of superspreading events, although we found that the estimate for the variant Delta or even any other variant is not yet available. Japan recognized the importance of superspreading in February 2020, implemented the cluster‐focused backwards contact tracing and promoted awareness of people at risk of infection by closing higher risk locations, followed by the World Health Organization's Western Pacific Region in July 2020 to limit the number of people to gather indoors thus to curb the spread of the virus. And restaurants were estimated to account for 20% of transmissions if all businesses were to reopen in 2020 in the United States (Chang et al., 2021). Such measures can mitigate the impact of superspreading events, which are expected to be major drivers in early epidemics.

In the recent systematic review of COVID‐19 superspreading by 10 February 2021, the estimates of dispersion parameters for COVID‐19 range from 0.01 in the United States to 5 in Israel (Wang et al., 2021). We include most of their studies together with those published by 10 September 2021, and re‐estimate those based on some simple assumptions to conduct the pooled estimates and the meta‐analysis. The major difference is the lower dispersion parameter, which is estimated to be 0.01 in the United States in the published review (Wang et al., 2021). In contrast, we directly extract the estimates from figures in the raw study, which range from 0.39 to 0.66 before the shelter‐in‐place order, resulting in the lower limit changing to 0.06 as that in Indonesia (Table 1). Finally, the pooled estimates from our analysis indicated that the dispersion parameter of COVID‐19 was likely to be 0.55 (95% CI: 0.30, 0.79), approximate to that of India, China and the United States (Figure 2).

The estimate of dispersion parameters in Israel is 2.97 (2.86, 3.08), as the highest among the 8 study countries, which may be attributable to strict PHSMs and border control strategies before the first local case (Wang et al., 2021). These control measures would prevent substantial imported cases, which typically triggered superspreading events (Adam et al., 2020; Wang et al., 2021).

Our study has several limitations. Most articles included in our study used publicly available data. Some studies in our review might have used overlapping data, leading to double counting in the pooled estimates. And with the recent emergence of variants that may be more transmissible and evade immunity acquired through prior infection or vaccination, the future of the pandemic is highly uncertain. Meanwhile, SARS‐CoV‐2 viruses are constantly evolving through mutation; genetic variations have emerged and circulated over the world, which may modify individual infectiousness profiles. We are still not clear about the impact of variants on overdispersion, perhaps by increasing transmissibility. Our pooled estimate is based on the previous transmission of wild‐type in early 2020, which may not be generalizable to the dominant variant Delta and future studies will be needed to conduct the comparison. Our searches were carried out on 10 September 2021 in PubMed. Many studies have been published later. For example, Akhmetzhanov et al. (2021) estimated the dispersion parameter for the variant Epsilon in Taiwan during January and February 2021.

In conclusion, multiple estimates of the dispersion parameter have been published for 17 studies, which could be related to where and when the data were obtained. The study location and method were found to be important drivers for diversity in estimates of dispersion parameters.

CONFLICT OF INTEREST

BJC reports honoraria from AstraZeneca, Sanofi Pasteur, GSK, Moderna and Roche. The authors report no other potential conflict of interest.

AUTHOR CONTRIBUTIONS

ZW, CW, CL and BJC: conceived the study, designed statistical and modelling methods, conducted analyses, interpreted results, wrote and revised the manuscript; YB, SP, DA, LW, PW and EL: interpreted results and revised the manuscript.

CODE AVAILABILITY

Code used for data analysis is freely available upon request.

ETHICS STATEMENT

No ethical approval was required as this is a review study with no original research data.

ACKNOWLEDGEMENTS

We acknowledge the financial support from the AIR@InnoHK Programme from Innovation and Technology Commission of the Government of the Hong Kong Special Administrative Region, the Collaborative Research Fund (Project No. C7123‐20G) of the Research Grants Council of the Hong Kong SAR Government, Seed Fund for Basic Research for New Staff of the University of Hong Kong (grant no. 202009185062), National Natural Science Foundation of China (grant no. 72104208), and Health and Medical Research Fund, Food and Health Bureau, Government of the Hong Kong Special Administrative Region (grant no. 21200632), Natural Science Foundation of Jilin Provincial Science and Technology Department (grant no. 20180101332JC) and the Science and Technology Project of the Jilin Provincial Education Department (grant no. JJKH20210135KJ). The funders of the study had no role in study design, data collection, data analysis, data interpretation or writing of the report.

Du, Z. , Wang, C. , Liu, C. , Bai, Y. , Pei, S. , Adam, D. C. , Wang, L. , Wu, P. , Lau, E. H. Y. , & Cowling, B. J. (2022). Systematic review and meta‐analyses of superspreading of SARS‐CoV‐2 infections. Transboundary and Emerging Diseases, 00, 1–8. 10.1111/tbed.14655

Zhanwei Du, Chunyu Wang and Caifen Liu contributed equally to this manuscript.

DATA AVAILABILITY STATEMENT

All data are collected from open source with detailed description in Supplementary Method.

REFERENCES

  1. Adam, D. C. , Wu, P. , Wong, J. Y. , Lau, E. H. Y. , Tsang, T. K. , Cauchemez, S. , Leung, G. M. , & Cowling, B. J. (2020). Clustering and superspreading potential of SARS‐CoV‐2 infections in Hong Kong. Nature Medicine, 26, 1714–1719. 10.1038/s41591-020-1092-0 [DOI] [PubMed] [Google Scholar]
  2. Akhmetzhanov, A. R. , Jung, S. ‐M. , Cheng, H. ‐Y. , & Thompson, R. N. (2021). A hospital‐related outbreak of SARS‐CoV‐2 associated with variant Epsilon (B.1.429) in Taiwan: Transmission potential and outbreak containment under intensified contact tracing, January‐February 2021. International Journal of Infectious Diseases, 110, 15–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Bi, Q. , Wu, Y. , Mei, S. , Ye, C. , Zou, X. , Zhang, Z. , Liu, X. , Wei, L. , Truelove, S. A. , Zhang, T. , Gao, W. , Cheng, C. , Tang, X. , Wu, X. , Wu, Y. , Sun, B. , Huang, S. , Sun, Y. , Zhang, J. , … Feng, T. (2020). Epidemiology and transmission of COVID‐19 in 391 cases and 1286 of their close contacts in Shenzhen, China: A retrospective cohort study. The Lancet Infectious Diseases, 20, 911–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chang, S. , Pierson, E. , Koh, P. W. , Gerardin, J. , Redbird, B. , Grusky, D. , & Leskovec, J. (2021). Mobility network models of COVID‐19 explain inequities and inform reopening. Nature, 589, 82–87. [DOI] [PubMed] [Google Scholar]
  5. Chun, B. C. (2016). Understanding and modeling the super‐spreading events of the Middle East respiratory syndrome outbreak in Korea. Infection & Chemotherapy, 48, 147–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Du, Z. , Hong, H. , Wang, S. , Ma, L. , Liu, C. , Bai, Y. , Adam, D. C. , Tian, L. , Wang, L. , Lau, E. H. Y. , & Cowling, B. J. (2022). reproduction number of the omicron variant triples that of the delta variant. Viruses, 14, 821. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Du, Z. , Javan, E. , Nugent, C. , Cowling, B. J. , & Meyers, L. A. (2020). Using the COVID‐19 to influenza ratio to estimate early pandemic spread in Wuhan, China and Seattle, US. EClinicalMedicine, 26, 100479. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Du, Z. , Liu, C. , Wang, C. , Xu, L. , Xu, M. , Wang, L. , Bai, Y. , Xu, X. , Lau, E. H. Y. , Wu, P. , & Cowling, B. J. (2022). Reproduction numbers of severe acute respiratory syndrome coronavirus 2 (SARS‐CoV‐2) variants: A systematic review and meta‐analysis. Clinical Infectious Diseases, 73(3), e754–e764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Du, Z. , Tian, L. , & Jin, D. ‐Y. (2022). Understanding the impact of rapid antigen tests on SARS‐CoV‐2 transmission in the fifth wave of COVID‐19 in Hong Kong in early 2022. Emerging Microbes & Infections, 11(1), 1394–1401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Du, Z. , Xu, X. , Wu, Y. , Wang, L. , Cowling, B. J. , & Meyers, L. A. (2020). Serial interval of COVID‐19 among publicly reported confirmed cases. Emerging Infectious Diseases, 26, 1341–1343. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Endo, A. , Abbott, S. , Kucharski, A. J. , Funk, S. , & Centre for the Mathematical Modelling of Infectious Diseases COVID‐19 Working Group . (2020). Estimating the overdispersion in COVID‐19 transmission using outbreak sizes outside China. Wellcome Open Research, 5, 67. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Gao, C. , Su, Z. , Liu, J. , & Kurths, J. (2019). Even central users do not always drive information diffusion. Communications of the Acm, 62, 61–67. [Google Scholar]
  13. Garcia‐Beltran, W. F. , Lam, E. C. , St Denis, K. , Nitido, A. D. , Garcia, Z. H. , Hauser, B. M. , Feldman, J. , Pavlovic, M. N. , Gregory, D. J. , Poznansky, M. C. , Sigal, A. , Schmidt, A. G. , Iafrate, A. J. , Naranbhai, V. , & Balazs, A. B. (2021). Multiple SARS‐CoV‐2 variants escape neutralization by vaccine‐induced humoral immunity. Cell, 184, 2523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hasan, A. , Susanto, H. , Kasim, M. F. , Nuraini, N. , Lestari, B. , Triany, D. , & Widyastuti, W. (2020). Superspreading in early transmissions of COVID‐19 in Indonesia. Science Reports, 10, 22386. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. He, D. , Zhao, S. , Xu, X. , Lin, Q. , Zhuang, Z. , Cao, P. , Wang, M. H. , Lou, Y. , Xiao, L. , Wu, Y. , & Yang, L. (2020). Low dispersion in the infectiousness of COVID‐19 cases implies difficulty in control. Bmc Public Health [Electronic Resource], 20, 1558. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. James, A. , Plank, M. J. , Hendy, S. , Binny, R. N. , Lustig, A. , & Steyn, N. (2021). Model‐free estimation of COVID‐19 transmission dynamics from a complete outbreak. Plos One, 16, e0238800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Kremer, C. , Torneri, A. , Boesmans, S. , Meuwissen, H. , Verdonschot, S. , Vanden Driessche, K. , Althaus, C. L. , Faes, C. , & Hens, N. (2021). Quantifying superspreading for COVID‐19 using Poisson mixture distributions. Science Reports, 11, 14107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Kwok, K. O. , Chan, H. H. H. , Huang, Y. , Hui, D. S. C. , Tambyah, P. A. , Wei, W. I. , Chau, P. Y. K. , Wong, S. Y. S. , & Tang, J. W. T. (2020). Inferring super‐spreading from transmission clusters of COVID‐19 in Hong Kong, Japan, and Singapore. Journal of Hospital Infection, 105, 682–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lau, M. S. Y. , Grenfell, B. , Thomas, M. , Bryan, M. , Nelson, K. , & Lopman, B. (2020). Characterizing superspreading events and age‐specific infectiousness of SARS‐CoV‐2 transmission in Georgia, USA. PNAS, 117, 22430–22435. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lloyd‐Smith, J. O. , Schreiber, S. J. , Kopp, P. E. , & Getz, W. M. (2005). Superspreading and the effect of individual variation on disease emergence. Nature, 438, 355–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Miller, D. , Martin, M. A. , Harel, N. , Tirosh, O. , Kustin, T. , Meir, M. , Sorek, N. , Gefen‐Halevi, S. , Amit, S. , Vorontsov, O. , Shaag, A. , Wolf, D. , Peretz, A. , Shemer‐Avni, Y. , Roif‐Kaminsky, D. , Kopelman, N. M. , Huppert, A. , Koelle, K. , & Stern, A. (2020). Full genome viral sequences inform patterns of SARS‐CoV‐2 spread into and within Israel. Nature Communication, 11, 5518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Riou, J. , & Althaus, C. L. (2020). Pattern of early human‐to‐human transmission of Wuhan 2019 novel coronavirus (2019‐nCoV), December 2019 to January 2020. Euro Surveillance, 25, 10.2807/1560-7917.ES.2020.25.4.2000058 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Shen, Z. , Ning, F. , Zhou, W. , He, X. , Lin, C. , Chin, D. P. , Zhu, Z. , & Schuchat, A. (2004). Superspreading SARS events, Beijing, 2003. Emerging Infectious Diseases, 10, 256–260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Shi, Q. , Hu, Y. , Peng, B. , Tang, X. ‐J. , Wang, W. , Su, K. , Luo, C. , Wu, B. , Zhang, F. , Zhang, Y. , Anderson, B. , Zhong, X. ‐N. , Qiu, J. ‐F. , Yang, C. Y. , & Huang, A. ‐L. (2021). Effective control of SARS‐CoV‐2 transmission in Wanzhou, China. Nature Medicine, 27, 86–93. [DOI] [PubMed] [Google Scholar]
  25. Sun, K. , Wang, W. , Gao, L. , Wang, Y. , Luo, K. , Ren, L. , Zhan, Z. , Chen, X. , Zhao, S. , Huang, Y. , Sun, Q. , Liu, Z. , Litvinova, M. , Vespignani, A. , Ajelli, M. , Viboud, C. , & Yu, H. (2021). Transmission heterogeneities, kinetics, and controllability of SARS‐CoV‐2. Science, 371, 10.1126/science.abe2424 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Su, Z. , Gao, C. , Liu, J. , Jia, T. , Wang, Z. , & Kurths, J. (2020). Emergence of nonlinear crossover under epidemic dynamics in heterogeneous networks. Physical Review E, 102, 052311. [DOI] [PubMed] [Google Scholar]
  27. Tariq, A. , Lee, Y. , Roosa, K. , Blumberg, S. , Yan, P. , Ma, S. , & Chowell, G. (2020). Real‐time monitoring the transmission potential of COVID‐19 in Singapore. Bmc Medicine [Electronic Resource], 18, 166. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Wang, J. , Chen, X. , Guo, Z. , Zhao, S. , Huang, Z. , Zhuang, Z. , Wong, E. L.‐Y. , Zee, B. C.‐Y. , Chong, M. K. C. , Wang, M. H. , & Yeoh, E. K. (2021). Superspreading and heterogeneity in transmission of SARS, MERS, and COVID‐19: A systematic review. Computational and Structural Biotechnology Journal, 19, 5039–5046. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Wang, L. , Didelot, X. , Yang, J. , Wong, G. , Shi, Y. , Liu, W. , Gao, G. F. , & Bi, Y. (2020). Inference of person‐to‐person transmission of COVID‐19 reveals hidden super‐spreading events during the early outbreak phase. Nature Communication, 11, 5006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wan, W. (2020) WHO declares a pandemic of coronavirus disease covid‐19. The Washington Post. [Google Scholar]
  31. World Health Organization (2022a). Novel Coronavirus (2019‐nCoV) situation reports [Online] Available at https://www.who.int/emergencies/diseases/novel‐coronavirus‐2019/situation‐reports (accessed July 2, 2022)
  32. World Health Organization (2022b). Tracking SARS‐CoV‐2 variants [Online] Available at https://www.who.int/en/activities/tracking‐SARS‐CoV‐2‐variants/ (accessed July 2, 2022)
  33. Zhang, Y. , Li, Y. , Wang, L. , Li, M. , & Zhou, X. (2020). Evaluating Transmission heterogeneity and super‐spreading event of COVID‐19 in a metropolis of China. International Journal of Environmental Research and Public Health, 17, 3705. 10.3390/ijerph17103705 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Zhao, S. , Shen, M. , Musa, S. S. , Guo, Z. , Ran, J. , Peng, Z. , Zhao, Y. , Chong, M. K. C. , He, D. , & Wang, M. H. (2021). Inferencing superspreading potential using zero‐truncated negative binomial model: Exemplification with COVID‐19. Bmc Medical Research Methodology [Electronic Resource], 21, 30. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Data Availability Statement

All data are collected from open source with detailed description in Supplementary Method.

Articles from Transboundary and Emerging Diseases are provided here courtesy of Wiley

RESOURCES