Significance
Protein malfunction and misfolding have long been associated with the onset and development of neurodegenerative conditions such as Alzheimer’s and Parkinson’s diseases. Protein misfolding/aggregation proceeds via primary nucleation whereby proteins can convert from their normal physiological forms into pathological amyloid aggregates. The presence of interfaces plays an important role in this aggregation phenomenon and can dramatically modulate nucleation, either by accelerating or inhibiting aggregation. Through coarse-grained computer simulations, kinetic theory, and measurement of the Gibbs free energy of adsorption, we show that systems which have high affinity to adsorb to an interface display delayed kinetics, whereas systems that have low affinities have similar behavior, suggesting a maximum between the two regimes (nonmonotonic behavior) where the aggregation rates are highest.
Keywords: protein aggregation, primary nucleation, adsorption free energy, kinetic analysis, neurodegenerative diseases
Abstract
Primary nucleation is the fundamental event that initiates the conversion of proteins from their normal physiological forms into pathological amyloid aggregates associated with the onset and development of disorders including systemic amyloidosis, as well as the neurodegenerative conditions Alzheimer’s and Parkinson’s diseases. It has become apparent that the presence of surfaces can dramatically modulate nucleation. However, the underlying physicochemical parameters governing this process have been challenging to elucidate, with interfaces in some cases having been found to accelerate aggregation, while in others they can inhibit the kinetics of this process. Here we show through kinetic analysis that for three different fibril-forming proteins, interfaces affect the aggregation reaction mainly through modulating the primary nucleation step. Moreover, we show through direct measurements of the Gibbs free energy of adsorption, combined with theory and coarse-grained computer simulations, that overall nucleation rates are suppressed at high and at low surface interaction strengths but significantly enhanced at intermediate strengths, and we verify these regimes experimentally. Taken together, these results provide a quantitative description of the fundamental process which triggers amyloid formation and shed light on the key factors that control this process.
In order to fulfill their biological roles, proteins typically remain soluble in the cellular environment. Under certain conditions, however, proteins can transition from these physiological forms into pathological amyloid aggregates (1–5). During this aggregation process, small oligomeric species are formed. These intermediates are toxic and have been associated with membrane disruption and synaptic dysfunction (6). Such structures play a crucial role in the development of many neurodegenerative diseases, such as Alzheimer’s and Parkinson’s diseases, which represent a major threat to healthcare systems in an aging society (4, 5). The process of amyloid formation is triggered by primary nucleation events that generate seed aggregates capable of sequestering further protein molecules through rapid growth (7–14). The mechanisms which underpin this fundamental nucleation step and the factors which control its rate have remained challenging to elucidate.
Interfaces and surfaces are ubiquitous in nature and play an important role as a platform for many biological reactions. Hydrophobic–hydrophilic interfaces are essential in biomolecular interactions and can act as catalysts in the self-assembly of micelles and biomembranes (15, 16) or for regulating protein folding (17, 18). Proteins and peptides are among the most common amphiphilic molecules in biological environments, and it has been shown that they can display different behaviors, depending on the interface involved (19–29). More importantly, it has been shown that surfaces can accelerate or retard protein aggregation processes (30–32). To study the effects on protein assembly, introducing well-defined model interfaces into the protein solutions is critical. To date, a mechanistic approach describing the effect of interfaces on protein aggregation has not been well described, and it has remained challenging to determine the molecular mechanisms by which surfaces modulate protein aggregation.
Here we investigate the mechanistic basis by which surfaces can modulate protein aggregation. To this effect, we first explored how different interfaces inhibit or by contrast promote amyloid self-assembly and compare our results with the behavior of a β-sheet rich nonamyloid system, silk (33, 34). We find that increasing the surface-to-volume ratio accelerated protein self-assembly, while the addition of preformed seed aggregates largely negates the influence that interfaces have on the kinetics of amyloid formation, demonstrating that surfaces largely control primary nucleation. Finally, by determining the Gibbs free energy of adsorption for different interface systems we relate the interface affinity to the changes in nucleation rates, providing a quantitative description of how interfaces modulate amyloid formation.
Results and Discussion
Surface-to-Volume Ratio Affects Protein Aggregation by Modulating the Rate of Heterogeneous Primary Nucleation.
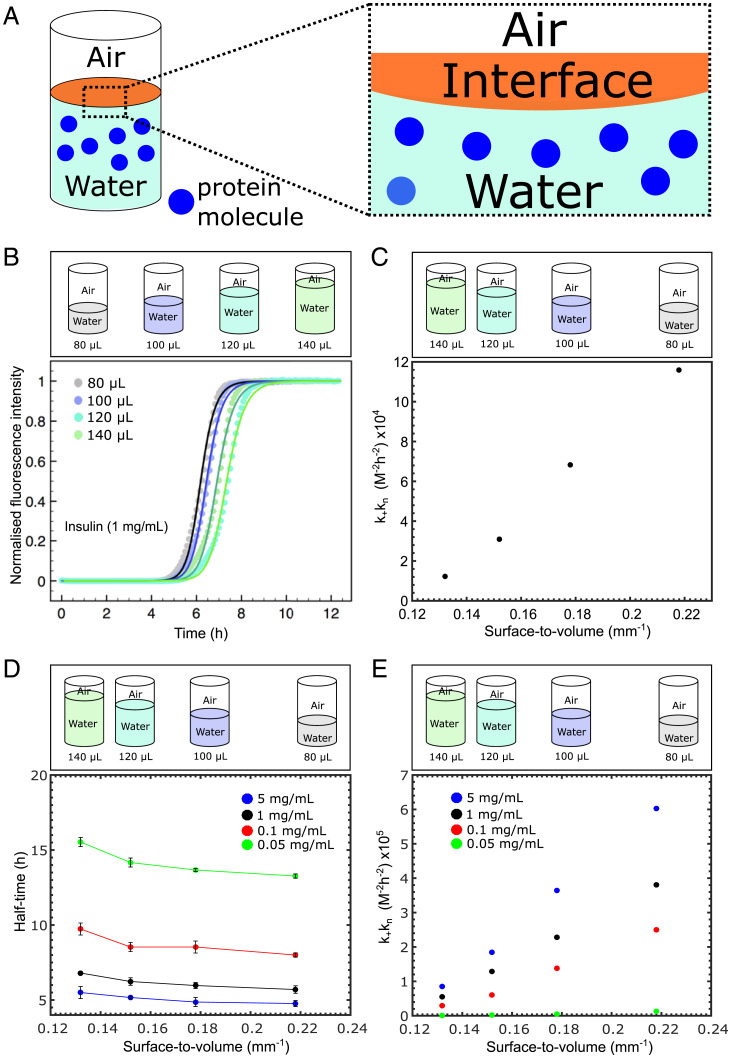
To determine the contribution of interfaces relative to that of bulk solution to the kinetics of amyloid formation, we first investigated the effect of changes in the surface-to-volume (S/V) ratio, as shown in the schematic in Fig. 1A. To this effect, kinetic experiments were conducted in systems with different volumes; by altering the volume of the protein solution in a well from 80 to 140 µL, the S/V ratios in the range from 0.218 to 0.132 mm−1 were explored as shown in Fig. 1B. We first focused on the peptide hormone insulin and monitored the aggregation kinetics through fluorescence spectroscopy. The resulting kinetic curves for the buildup of fibril mass, which display a characteristic sigmoidal shape, show that for the range of interfaces explored a higher S/V results in faster aggregation kinetics (Fig. 1B). To quantify this effect, we employed a chemical kinetics framework (36–38) that allows us to interpret the aggregation profiles in terms of the rate constants of the underlying microscopic steps of aggregation, including primary nucleation, fibril elongation, and secondary processes such as surface catalyzed secondary nucleation and fragmentation. The fitting was done first for one S/V ratio, and all parameters other than were kept constant thereafter. The elongation and secondary nucleation product, , was obtained through this analysis and was found to be 4.04 × 1010 with nc n2 2, where kn, , and k2 are the primary nucleation rate, the elongation rate, and the secondary nucleation rate constant, respectively, while nc is the reaction order of the primary process and n2 is the reaction order of the secondary pathway. In particular, this analysis (Fig. 1C) reveals that the rate constants for elongation and secondary nucleation are independent of the S/V ratio, while the primary nucleation rate constant varies from 1.16 × 105 to 1.23 × 104 M−2 h−2. Thus, changing the surface-to-volume ratio by less than a factor of 2 results in an order of magnitude change in the primary nucleation rate constant. This finding therefore suggests that interfaces can strongly modulate amyloid formation through controlling the rate of primary nucleation.
Fig. 1.
(A) Schematic representation of the interface involved in our experimental approach. (B and C) (Top) Schematic representation of the experimental approach used. Different surface-to-volume ratios were used to investigate the surface dependence on protein self-assembly. (B) Graph of normalized ThT fluorescence intensity as a function of time for a 1 mg/mL solution of insulin for four different volumes. The corresponding kinetic data were then fitted using AmyloFit (35) and are shown as the solid lines. (C) Graph of kkn as a function of the surface-to-volume ratio. (D) Graph of half-time as a function of the surface-to-volume ratio for four different insulin concentrations. (E) Graph of kkn as a function of the surface-to-volume ratio for the four different insulin concentrations in D.
To further establish whether this behavior is concentration dependent, insulin solutions ranging from 0.05 to 5 mg/mL were prepared and monitored (Fig. 1D). These data show that the same trend can be observed across the concentration range tested. The kinetic analysis (Fig. 1E) revealed that the primary rate constants varied across all concentration ranges tested. We next repeated this experiment with the protein lysozyme. The data shown in SI Appendix, Fig. S1A demonstrate that the interfacial effects found for insulin are also characteristic of the kinetics of amyloid formation for lysozyme.
Heterogeneous Nucleation at Interfaces Is Bypassed in the Presence of Preformed Seed Fibrils.
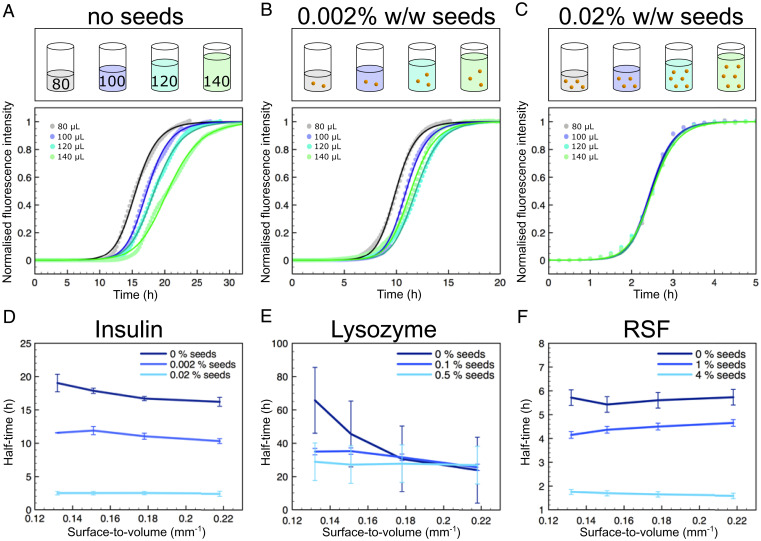
In order to verify the conclusion obtained from kinetic analysis suggesting that interfaces modulate primary nucleation, we sought to bypass this step in the aggregation reaction through addition of preformed protein seeds to the protein solutions in 96-well plates (Fig. 2A–C, Top). If the formation of nuclei predominantly occurs at an interface, the addition of seeds effectively negates any surface dependence on fibrillar growth as the required nuclei would already be in solution, and consequently, there should be minimal differences in kinetics when changing the S/V ratio. This prediction is verified in the aggregation kinetic curves for insulin where independently of the S/V ratio, similar aggregation kinetics are observed upon the addition of seed fibrils, in stark contrast with the behavior observed in the absence of seeds (Figs. 2A–D). Repeating this experiment for the proteins lysozyme and silk fibroin, revealed that also for these systems, the addition of preformed fibril seeds eliminated the dependence of aggregation kinetics on the S/V ratio (Fig. 2E and F). However, as shown in Fig. 2F, reconstituted silk fibroin (RSF) did not perform in a similar manner, and surface-driven aggregation was not observed. This is due to the extraction method in which silk fibroin is obtained, where, during the purification process, small aggregates are formed. These aggregates can consequently act as seeds, thus accelerating self-assembly processes.
Fig. 2.
(A–C) (Top) Schematic representation showing how different concentrations of seeds were added to the protein solutions in order to determine their effect on aggregation. (Bottom) Graphs of normalized ThT fluorescent intensity as a function of time for a 2 mg/mL solution of insulin for four different volumes with increasing seed concentrations. (D–F) Graphs of aggregation half-time against the surface-to-volume ratio of different seed concentrations for insulin (D), lysozyme (E), and RSF (F).
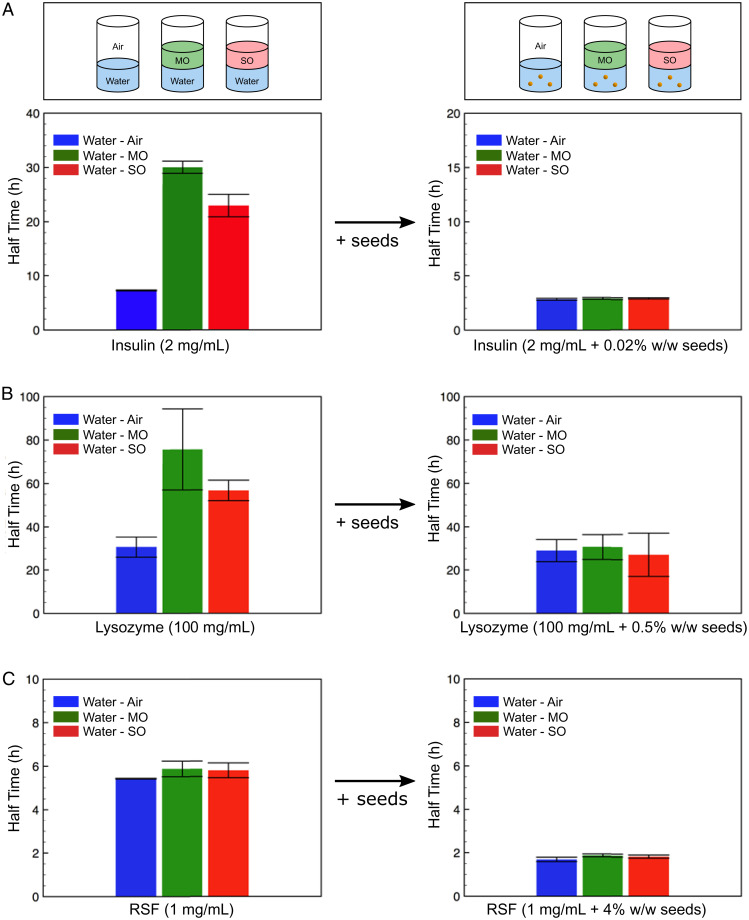
In order to investigate how interfaces affect amyloid formation, we varied the nature of the interface by using immiscible phases such as mineral oil (MO) or silicon oil (SO) on top of each protein solution in the 96-well plate (Fig. 3A, Top). Thus, we had water–MO (W-MO) and water–SO (W-SO). This ensured that the oil fully covered the aqueous phase and thus eliminated the water–air (W-A) interface. Taken together, these data further corroborate the idea that the principal effect of interfaces for amyloid formation is to introduce a heterogeneous nucleation step into the pathway which can substantially modify the effective rate of primary nucleation and that interfaces have a more minor effect on the other processes in the system (Fig. 3). It is remarkable that homogeneous nucleation through secondary processes is not affected by interfaces but rather through primary processes, revealing the much more effective nature of monomer–fibril interactions compared to monomer–monomer interactions. As previously mentioned, due to the formation of nuclei in the purification process for RSF, no significant interface dependence is observed, and the addition of seeds only reduces the overall aggregation time.
Fig. 3.
(A–C) Plots of aggregation half-time for the three different interface systems: water–air (W–A), water–MO (W–MO), and water–SO (W–SO), (Left) without seeds and (Right) with the addition of seeds for insulin (A), lysozyme (B), and RSF (C).
In order to probe whether the oil affects the fibrillization process, Fourier-transform infrared spectroscopy (FTIR) measurements were conducted. We incubated the monomeric protein solution with the oil at room temperature for 10 h and took the FTIR spectra of both that and a monomeric protein solution which was only in contact with an air interface. The spectra of both these samples looked identical and had amide I and II bands at around 1,650 and 1,540 cm−1, respectively, which are characteristic of random coil structure. We then incubated the protein solution that was in contact with the oil at 50 C in order to promote aggregation and took the FTIR spectrum of this sample. The protein seems to have aggregated with the characteristic amide I and II bands shifting to lower wave number, indicating a transition to beta-sheet formation. This shows that the oil interface does not inhibit fibrillization, and it is molecular adsorption which plays a critical role in defining aggregation kinetics (SI Appendix, Fig. S1C).
Morphological Changes due to Varying Interface Chemistry.
The finding that nucleation takes place predominantly at interfaces suggests that the nature of the interface could modulate the morphology of the structures formed. To explore this effect, atomic force microscopy (AFM) micrographs of fibrils nucleated on different interfaces were acquired. As can be seen in SI Appendix, Fig. S3 A–C, the AFM results revealed that the samples where there is a water–air interface formed mature fibrils, whereas the samples where a water–oil interface is present mostly consisted of protofibrils and oligomers. Additionally, AFM micrographs were acquired for protein fibrils grown from preformed seeds. The AFM (SI Appendix, Fig. S3 D–F) images show that under such conditions the surface has a much smaller effect on the morphology of the structures formed and rather that seeded samples give structure to the final fibrils formed.
Molecular Mechanism of Heterogeneous Amyloid Nucleation.
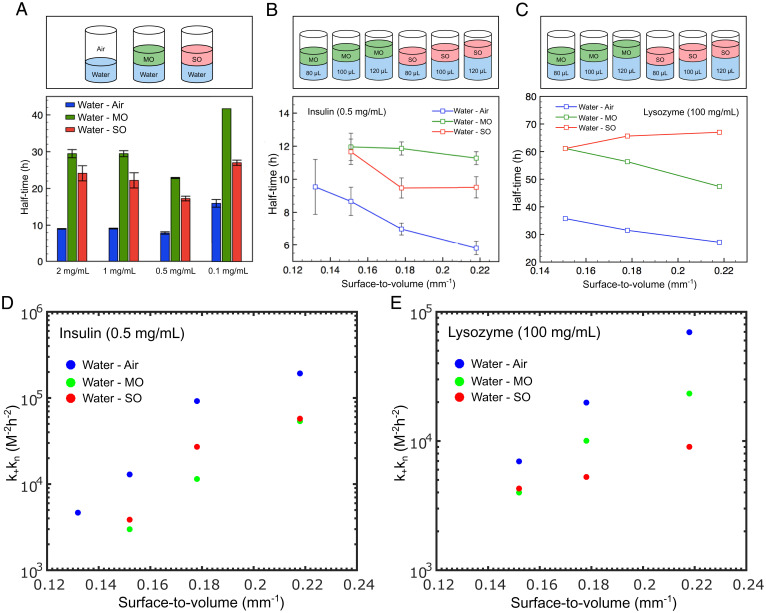
We next explored the origin of the effect of interfaces on amyloid formation by varying the nature of the interface. Again, MO and SO were used. For all concentrations tested in this study, we found that the aggregation reaction was most rapid in the presence of an air–water interface, followed by the water–SO and finally by the water–MO interface (Fig. 4A). This behavior was also observed for lysozyme (SI Appendix, Fig. S1B). We next varied the S/V ratio for the three different interfaces at a fixed insulin concentration. The data shown in Fig. 4B demonstrate that a variation in the aggregation kinetics is observed with changes in the S/V ratio for both water–air and water–SO, and while this trend is also observed for water–MO, the S/V ratio plays a smaller role on the half-time. For lysozyme, a similar trend was observed for both the water–air and water–MO interfaces. Interestingly, however, for the case of water–SO, amyloid formation was independent of the S/V ratio (Fig. 4C). Moreover, was plotted as a function of the S/V ratio for both proteins. Again, the same kinetic analysis approach was employed as in Fig. 1, and was found to be 2.83 × 1010 and 2.08 × 1010 for Fig. 4D and E, respectively, while nc n2 2 for both plots. Moreover, in order to exclude any effects due to evaporation, we conducted a series of experiments with two different protein concentrations and with all three interfacial systems, in order to determine whether the surface to volume ratio is the contributing factor behind the difference in aggregation kinetics. By conducting insulin aggregation kinetics at 40C rather than at 50C, we found that even at lower temperatures, the S/V ratio and not evaporation is the key factor behind the difference in the aggregation kinetics (SI Appendix, Fig. S2 A–E).
Fig. 4.
(A–C) (Top) Schematic showing the investigation into protein aggregation kinetics using different interfaces: air, MO, and SO. (A) Plot of the aggregation half-time for four different insulin concentrations for three interface systems: water–air, water–MO, and water–SO. (B) Graph of half-time as a function of the surface-to-volume ratio for the three different interface systems at a fixed insulin concentration of 0.5 mg/mL. (C) Graph of half-time as a function of the surface-to-volume ratio for the three different interface systems at a fixed lysozyme concentration of 100 mg/mL. (D) Graph of kkn as a function of the surface-to-volume ratio for the three different interface systems at a fixed insulin concentration of 0.5 mg/mL. (E) Graph of kkn as a function of the surface-to-volume ratio for the three different interface systems at a fixed lysozyme concentration of 100 mg/mL.
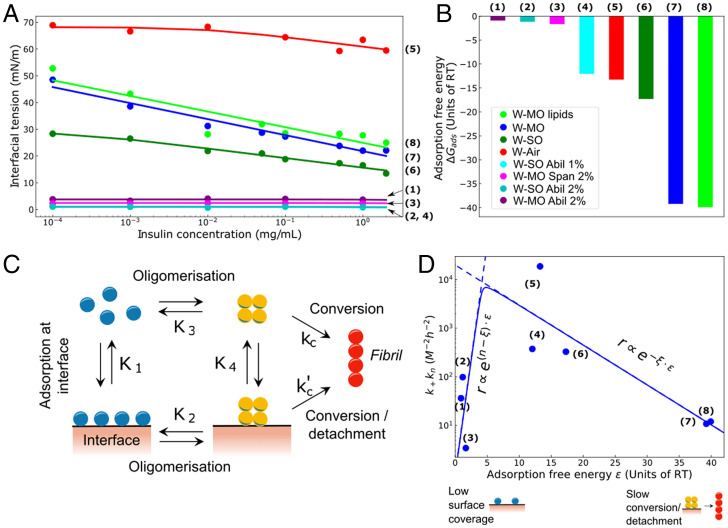
Taken together, the experimental data describing how the S/V ratio affects protein aggregation, coupled with the effect that seeds have on the different systems, show that protein self-assembly has a strong dependence on both the surface area but also on the nature of the interface used. Specifically, when the S/V ratio is increased, the rate of nucleation of protein aggregates is affected (Fig. 1), indicating that nuclei form on the interface, and therefore, increasing the surface-to-volume ratio promotes this effect. These surface effects must, therefore, originate from the interaction of the protein molecules with the interface. To probe these interactions, we next quantified the surface excess concentration, Γ, through measurements of the interfacial tension changes, γ, upon adsorption of proteins. These two quantities are linked by the Gibbs adsorption isotherm where is the total concentration of monomeric protein. Combining the Gibbs adsorption isotherm with the Langmuir adsorption isotherm yields the Langmuir–Szyszkowski equation , where is the maximal surface excess, K1 is the equilibrium adsorption constant of monomers to the interface, and is the maximal surface concentration of adsorbed molecules. Interfacial tension (IFT) measurements for different insulin concentrations were conducted using pendant drop tensiometry for the eight different interface systems (Materials and Methods). The resulting data, shown in Fig. 5A, were fitted to the Langmuir–Szyszkowski equation to yield, for each interface system, the equilibrium adsorption constant K1 and therefore the standard free energy of adsorption . From this analysis (Fig. 5A and B) it can be seen that the W-MO and W-MO(lipids) systems have the largest adsorption free energies, indicating a higher tendency to adhere to the interface, while the W-MO(2%AbilEM90) system has the smallest adsorption energy. The other two systems lie in between these extremes. This observed trend follows that of increasing hydrophobicity of the nonaqueous phase, suggesting a major role for hydrophobic interactions in modulating the surface adsorption process. Strikingly, however, a plot of kkn against adsorption free energy (Fig. 5D) shows that stronger adsorption at the interface does not necessarily yield a faster nucleation rate. Indeed, even though the W-MO and W-MO(lipids) systems promote strongly protein adsorption at the interface, as shown by the surface tension measurements, the acceleration of the nucleation process by these interfaces is less effective than for systems with a lower affinity such as W-SO and W-Air. More generally, the trend between adsorption free energy and nucleation rate is nonmonotonic, displaying a maximum at intermediate values of the strength of adsorption (Fig. 5D).
Fig. 5.
(A) Semilog plot of interfacial tension as a function of monomeric insulin concentration for the five systems. The data were fitted according to the Langmuir–Szyszkowski equation. (B) Plot of the adsorption free energy (.) for the eight different systems investigated. (C) Schematic representation of the mechanism of heterogeneous amyloid nucleation. (D) Volcano plot of as a function of the adsorption free energy ().
To describe quantitatively these effects, we consider a kinetic model of heterogeneous nucleation (Fig. 5C) in order to extend the classical theory of nucleated polymerization to include heterogeneous nucleation (39). It is known that a plot of rate against adsorption energy (volcano plot) displays a nonmonotonic behavior for surface catalyzed reactions. Here we extend these ideas to heterogeneous nucleated polymerization. Monomers in bulk initially adsorb to the interface, where they can form surface-bound nuclei. Adsorption at the interface occurs with adsorption constant , which in turn is determined by the (dimensionless) free energy of adsorption . The oligomerization step at the surface is associated with the equilibrium constant K2. Surface-bound nuclei can undergo structural conversions into growth-competent fibrillar structures, which then detach from the interface, with rate constant , and can elongate into mature fibrils. We note that during this conversion/detachment process, bound proteins lose contact with the surface. Therefore, when the affinity for the surface ε is high, this conversion/detachment step becomes energetically unfavorable at high surface affinities. As such, the conversion/detachment of surface-bound nuclei has a dependence on the adsorption energy of the form (Materials and Methods). In addition to transforming into fibrillar structures, surface-bound nuclei are also in equilibrium with nuclei formed in bulk directly from monomers. The oligomerization step in bulk has equilibrium constant K3, while the adsorption constant for the detachment of surface-bound nuclei is denoted with K4. Fibril formation can also proceed by the direct conversion of bulk nuclei with rate constant kc. The dynamics of this heterogeneous nucleated polymerization process can be obtained in closed form (Materials and Methods) and reveal that the rate of heterogeneous amyloid fibril nucleation is crucially controlled by the parameter K1, which describes the propensity of monomers to adhere to the interface and is related to the Gibbs surface excess Γ. The rate of heterogeneous nucleation increases with ε as in limit of weak adsorption, where n is the reaction order for nucleation, but decreases with increasing ε as for strong adsorption. This nonmonotonic behavior (Sabatier’s principle) of the nucleation rate is the result of two competing factors at play: the adsorption of molecules to the interface can accelerate aggregation through heterogeneous nucleation, but a very strong adsorption prevents effective release of the formed nuclei into solution (31, 40).
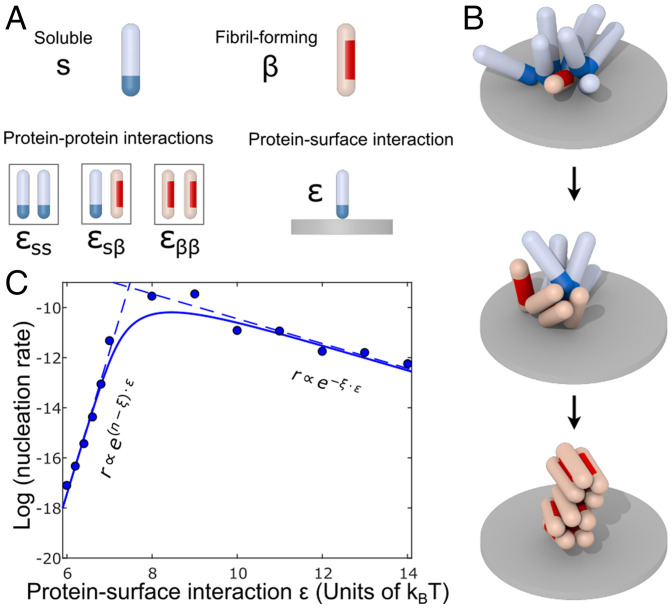
To provide a mechanistic interpretation of the results, we extended a previously developed coarse-grained computer simulation model of heterogeneous nucleation as summarized in Fig. 6. Proteins were modeled as hard spherocylinders, which can exist in two distinct states: a soluble (s) and a fibril-forming β conformation, as in our previous work (41). These states represent the different conformational ensembles of protein molecules in their non–β-sheet states both in solution and bound to the surface and the corresponding β-prone states driving amyloid fibrillation.
Fig. 6.
Computer simulation of heterogeneous nucleation. (A) In the simulation model, proteins can occupy two conformational states: soluble (blue tip) and fibril-forming (red side patch). Both protein states have affinities for the s and β states: and . To facilitate surface-driven nucleations, proteins initially adsorb to the surface through an attractive interaction of strength ε. (B) Representative simulation snapshots: On the surface, proteins first form oligomers through self-affinity. These serve as prenuclei, which are required to overcome the free energy barrier for conversion to the low-entropy fibril-forming conformational state. Finally, after conversion, fibrillar clusters form and detach from the surface and can further grow by addition of soluble proteins. (C) Volcano plot. The rate of nucleation was measured in the computer simulation at different protein–surface attractions ε. At low surface affinity, a low nucleation rate is observed caused by low protein coverage. At high surface affinity, the nucleation rates are observed to be slow as well even though protein coverage is high.
Nonspecific attractive interactions between proteins in the s state of strength are mediated by a patch at the cap of the spherocylinder allowing for the formation of micellar-like oligomers. Additionally, the s state has an affinity for the rigid surface in the simulation, which is set by the parameter ε. Proteins in the β-state interact via an attractive side patch; the strength is set by the parameter , which favors parallel packing required for fibril assembly. The strength of interactions between the s and β-state is set by . Importantly, in the simulations, proteins have a small probability per unit time to transition from the soluble to the fibril-forming state. This is implemented by attempting the conformation switch from s to β-conformation, accompanied by a free energy penalty , for the conformational change. This free energy penalty reflects the loss of conformational entropy associated to the transition to more ordered β-rich conformations. The rigid substrate is modeled as an infinite plane that can bind the attractive caps of the soluble proteins with the interaction strength ε (units of thermal energy ).
We observe that throughout the simulation, proteins deposit on the rigid surface, and oligomer formation can occur. Similarly to what has been previously observed in solution (41), surface-bound oligomers then take the role of prenucleation clusters which facilitate the crossing of the free energy barrier of conversion. Subsequently, a structural transition can occur because the β-sheet–prone state is stabilized sufficiently by interactions within the oligomer, as illustrated in Fig. 6B. Further transitions can take place due to favorable interactions leading to the growth of fibrils, which detach from the surface. To quantify the amyloid formation kinetics, we take the formation rate of a β-state dimer as a proxy for the primary nucleation rate.
As the surface affinity of proteins ε is increased we observe that the nucleation rate is a nonmonotonic function of ε (Sabatier’s principle), as can be seen in Fig. 6C. Since the protein surface affinity increases, more proteins are deposited increasing the probability to form oligomers which are large enough to serve as prenucleation clusters. The reaction order associated to this effect is measured as in our simulations. This value is higher than the reaction order 2 obtained from the experimental data. However, it should be noted that the reaction order in simulations depends on the specific choice of interaction parameters (the conversion free energy barrier and the interactions strengths between proteins) that, however, were not designed to describe a particular experimental system. It is rather our intention to explore the molecular mechanisms behind the general behavior of surface-catalyzed amyloid nucleation processes. Coarse-grained simulations allow us to do so in an orthogonal way to kinetic theory as they assume discrete molecular building blocks and their interactions energies, as opposed to bulk reaction rates.
Interestingly, increasing the protein–surface affinity beyond a threshold value causes the nucleation rate to decay, as also observed in our experimental results shown in Fig. 5D. In this high-affinity regime, the average oligomer size is typically large enough to allow for a fast first conversion within the oligomer and subsequent fibril nucleation. However, instead of the oligomerization in the low-affinity regime, the rate-limiting step now is the detachment of the protein associated to the conformation conversion, in agreement with the analytical theory results shown in Fig. 5D. As the surface–protein affinity is increased the nucleation reaction is gradually inhibited leading to the nonmonotonic behavior shown in Fig. 6B. Analogous behavior has been observed in simulations for the nucleation on lipid membranes and protein fibrils themselves (31, 40). The reaction order of the conversion/detachment step from both simulation and experimental data turns out to be 0.5.
Conclusions
We have revealed the mechanism of nucleation in the presence of a surface and explored the role of interfaces in the context of aggregation kinetics. By designing a robust experimental procedure for monitoring aggregation kinetics of three representative proteins (insulin, lysozyme, and RSF) with different interfaces and surface-to-volume (S/V) ratios, we have found that two regimes exist. Systems that have high affinity to adsorb to an interface display delayed kinetics, whereas systems that have low affinities have similar behavior, suggesting a minimum between the two regimes where the rate of protein aggregation is highest. Moreover, the experimental results are corroborated by combining theory and coarse-grained simulations, which yield that at low and high surface interaction strengths, aggregation rates are suppressed, whereas at intermediate strengths kinetics are augmented.
It was found that by increasing the S/V ratio, protein aggregation is augmented, indicating that nuclei formation initiates at the interface. Moreover, our analysis revealed that the rate constants for elongation and secondary nucleation were independent of the S/V ratio, while the primary nucleation rate varied by an order of magnitude (Fig. 1). Furthermore, the addition of preformed aggregates to the system bypasses the crucial interfacial nuclei formation step and subsequently negates any surface effects. More importantly, when enough seeds are added to the solution, the rate of aggregation is the same regardless of the S/V ratio, which was confirmed for all three proteins tested (Figs. 2 and 3). Finally, we determined that the tendency of monomeric protein molecules to adsorb at an interface varies. This was done through the combination of the Gibbs adsorption isotherm with the Langmuir adsorption isotherm in order to yield the Langmuir–Szyszkowski equation, where it was found that the larger the propensity of a molecule to adsorb, the slower the self-assembly process for that system (Fig. 5). Conversely, if there is poor adsorption to the interface, then the aggregation half-time is also increased, indicating that a minimum between these two regimes exists. This was attributed to the fact that fibrillar formation occurs predominantly through a heterogeneous nucleation pathway, and thus, an interface is necessary; however, too high of an adsorbance does not allow for the final kinetic step, i.e., the conversion of nuclei to their fibrillar state which is in solution (Fig. 5). This effect was also corroborated through coarse-grained simulations (Fig. 6), where a maximum on the nucleation rate as a function of the adsorption free energy was measured. We believe that this systematic and biologically relevant study can help with gaining better mechanistic insights into protein self-assembly at the interface in vivo.
Materials and Methods
Protein Solution Preparation.
To investigate the effect of surface area on protein aggregation, three different protein stock solutions were prepared. Fresh hydrochloric acid solution at pH 1.3 and pH 1.6 was prepared every time to dissolve insulin (from bovine pancreas; Sigma Aldrich) and lysozyme (from chicken hen egg white; Sigma Aldrich), respectively. Lysozyme was dialyzed against Mili-Q water for 2 d at 4C prior to use. Insulin was used without any purification. The acid solution was filtered using 0.22 µm filter paper to remove any impurities which might affect the aggregation kinetics. After that, insulin and lysozyme were dissolved into acid solution at the concentrations of 2 and 200 mg/mL, respectively. For RSF (purification process mentioned below), the purified batch was diluted into 10 mg/mL by using Mili-Q water. Concentrations of these solutions were checked with NanoDrop (Thermo Scientific) and used as stock solutions. Additionally, in order to determine the effect an interface may have on protein self-assembly, MO (BioReagent, light oil; Sigma Aldrich), which is an oil that is composed of a mixture of alkanes, and SO (viscosity 50 cSt [25 C]; Sigma Aldrich) were added to the protein solutions via the experimental procedure mentioned below.
Silk Fibroin Preparation and Purification.
Bombyx mori silk cocoons (Mindsets [United Kingdom] Limited) were used to extract the silk fibroin protein by a well-established protocol (42). Initially, the cocoons were cut into pieces and placed in a beaker containing a solution of 0.02 M sodium carbonate. This was then boiled for 30 min, ensuring that the sericin that is present within the silk fibers dissolved, while the insoluble fibroin remained in the beaker. The fibroin was then removed from the beaker, rinsed with cold water three times, and left overnight to dry out.
A 9.3 M lithium bromide solution was prepared and added to the dried silk fibroin in a 1:4 ratio of silk fibroin to lithium bromide. The mixture was heated to 60 C and left for 4 h, resulting in the silk fibroin dissolving in the lithium bromide. LiBr was removed from the solution by placing the mixture in a 3 kDa dialysis tube. This in turn was placed in a beaker containing ultrapure water, while the use of a large magnetic stir bar with a magnetic stir plate was employed to ensure mixing. The water was changed a total of six times in 48 h.
Finally, the silk fibroin solution was removed from the dialysis tube and placed in Eppendorf tubes. These were then centrifuged at 9,000 rpm at 4 C for 20 min in order to remove small impurities. The process was repeated twice, and the final solution was stored at 4 C. All experiments were conducted within 2 wk of extracting and purifying the silk fibroin to ensure no gelation had occurred.
Aggregation Kinetics at Different Interfaces.
For the experiments involving the investigation of surface-to-volume ratio on protein aggregation kinetics the following procedure was established and followed. As each of the wells in the 96-well plate (Corning 3881, Half-area) used was cylindrical, the cross-sectional surface area remains the same throughout the well. Consequently, by pipetting different volumes of protein solution into the 96-well plate (80, 100, 120, and 140 µL), the surface-to-volume ratio was decreased. This is schematically represented in Fig. 1A, Top. The plates used in all experiments are specifically coated so that proteins do not adsorb to the walls of the wells, and thus, the interactions of the walls are considered to be negligible in this study. Additionally, in order to monitor the self-assembly process (i.e., the transition of protein monomers to β-sheet structures), 40 µM Thioflavin T (ThT), which is a molecule that is known to fluoresce only when in contact with β-sheets, was added to the aqueous solution. ThT fluorescent increase was thus monitored as a function of time using a microplate reader (FLUOstar-BMG labtech), where the intensity directly correlates to the amount of fibrils present in the solution. The temperature during the measurement was kept at 50 C for insulin (except where otherwise stated), 60 C for lysozyme, and 37 C for silk fibroin, and all measurements were performed without agitation.
Furthermore, for the experiments involving the investigation of protein aggregation in the presence of a liquid–liquid interface, the same procedure as described above was employed, with a minor difference: 30 µL of an oil phase, which was either MO or SO, was carefully added on top of the protein solution. Again, different aqueous volumes were used (80, 100, and 120 µL), which resulted in a change of the surface-to-volume ratio. This is schematically represented in Fig. 1D, Top. Also, 40 µM ThT was added to the aqueous phase to monitor protein aggregation by observing the increase of fluorescent intensity as a function of time. Moreover, in order to determine whether the meniscus of the different interfacial systems could affect the surface area, a picture of the three different interface systems was taken (SI Appendix, Fig. S2F). As seen in this image, it is evident that the curvature of the meniscus is quite similar for all three interface systems, and so any effect that this may have on the surface area can be neglected from our current setup. The variation in meniscus area between the water–air and water–MO system is 1.19%, while for the water–air and water–SO systems it was found to be 1.05%.
Finally, different concentration of seeds (obtained from incubating 10% wt/vol protein solutions for 1 month at 65 C) were added to the four volumes of protein solution (80, 100, 120, and 140 µL), as is schematically depicted in Fig. 1A–D, Top. Following the addition of 40 µM ThT, aggregation kinetics were monitored using a microplate reader.
Preparation of Lipid Interface.
A concentration of 1 mg/mL 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) was used in all lipid-based experiments. DOPC was dissolved in MO by means of a variant to the film hydration method. In brief, 1 mg/mL of lipid was initially dissolved in chloroform and was left to evaporate overnight in a fume hood. Following this, 1 mL of MO was added to the dried film and stirred for 2 to 3 min. This lipid–MO solution was now used, rather than plain MO, when added on top of the protein solution in the 96-well plate. A 2 mg/mL solution of insulin was prepared, and the kinetics of the W-MO(lipids) interface was investigated.
Analysis of Kinetic Data.
The kinetic data obtained from the protocol were analyzed using Amylofit (35). All data were normalized with the minimum and maximum fluorescence intensity, and half-time was calculated from the time at which half the protein that is present, initially as monomer, has aggregated, i.e., the time at which the normalized intensity reaches 0.5. Each experiment was repeated four times and then averaged before fitting, while a secondary nucleation dominated model was assumed.
Atomic Force Microscopy.
To characterize the aggregates formed by incubation at different interfaces, protein solutions were collected from the 96-well microplate after incubation and diluted 100 times. Then, 20 µL aliquot of the diluted solution was placed on a freshly cleaved mica and incubated at room temperature for 30 min. The mica was rinsed with Mili-Q water three times and dried with compressed nitrogen gas. AFM images were taken with Park NX10 (Park Systems) using noncontact mode.
Interfacial Tension Measurement.
To measure interfacial tension (IFT) for different interfaces, pendant drop tensiometry (FTA1000B, First Ten Angstroms) was used. Insulin monomer solution with varying concentrations was prepared and filled in a dispensing system consisting of a 100 µL glass syringe and a 27 gauge needle. The drop was generated in either air or an oil bath by carefully pushing the syringe. Twenty pictures of the droplet were taken at 0.5-s intervals, and the images were analyzed with an FTA32 (First Ten Angstroms) software in order to calculate the IFT. The water–air interface was stabilized for 1,000 s before image acquisition. For water–oil interfaces, a quartz cuvette was used to surround the droplet with oil, and droplets were stabilized at the oil interface for at least 1 h before image acquisition.
Simulation Method.
In the coarse-grained simulation model employed here, proteins are represented as hard spherocylinders of diameter and length . The spherocylinders are equipped with interaction patches allowing them to self-assemble into clusters of various morphologies. Two different conformational states are considered: the soluble state (s) and the β-sheet–rich fibril-forming state (β). The s state represents the conformational ensemble of protein molecules in their soluble states, which have a propensity to self-assemble into micellar oligomers. The pairwise interaction potential between tips of two s proteins is given by with cutoff , where in this work . These oligomers play the role of prenucleation clusters in the two-step nucleation pathways explored with this model. The β-state serves as a low-entropy conformational state with a high propensity to assemble into well-defined and thermodynamically fibrillar structures. Fibril-forming proteins are modeled to interact via an anisotropic patch interaction of strength , which drives parallel alignment and fibril formation. The cross-state interaction between soluble and fibril-forming proteins is also anisotropic and has strength in order to modulate the surface coverage.
The simulation box has vertical size (z axis) of . Soluble proteins can adsorb to the top and bottom of the simulation box, which represent homogeneous attractive plates. The affinity of the s state for the plates is set by with a cutoff . The affinity ε is varied between 6 and 14 .
The x and y dimensions of the box are allowed to vary at initial equilibration such that for different protein–surface affinities ε the number of proteins in the system approaches ∼400. Equilibration is achieved by a grand canonical ensemble which can act within the central region of the box which stretches along 60% of the z box size. The chemical potential is set to a fixed value which corresponds to a protein solution concentration of approximately 62 µM.
After equilibration of the adsorption isotherm, rate simulations are carried out where stochastic switching between the soluble and β-forming state are possible. The transition to the low-entropy state fibril-forming state is penalized with a free energy barrier of . The switching between conformations is driven by a Metropolis Monte Carlo algorithm with an attempt frequency of 1/5,000. The nucleation rate is taken to the inverse average Monte Carlo time steps elapsed until the formation of the first β dimer on the plate surface. Statistics of the rates was obtained from five to eight separate simulation runs with different random seeds. In the range of ε explored here, homogeneous nucleation never occurs before heterogeneous nucleation on the plate surface.
Derivation of the Rate of Fibril Formation.
We discuss here in detail the simple kinetic model of heterogeneous nucleation described in the main text and in Fig. 5. Let m be the concentration of free monomers; mb be the concentration of surface-bound monomers; s be the concentration of free surface sites; and N, Nb be the concentrations of free and surface-bound oligomers, respectively. The steps shown in Fig. 5C can be captured by the four equilibria: , and . Using these relations we find , which implies . Consequently, if free monomers absorb at the surface with adsorption constant , where is the free energy of adsorption (in units of thermal energy RT), then detachment of nuclei depends on the adsorption energy ε as . The conversion/detachment constant depends on (dimensionless) free energy of conversion and detachment , where ξ is the absolute ratio between nuclei detachment free energy and monomer adsorption free energy, which implies . Detachment from the surface is therefore hindered at high ε. The rate of nucleation is
| [1] |
We work in a regime when there is an excess of monomers in bulk, such that we can set throughout, where is the total protein concentration. We then impose conservation of the total concentration of surface sites, yielding
| [2] |
Eq. 2 can be solved numerically to yield s in terms of ; here we seek an approximate analytical solution which is obtained by focusing on two limits. In the limit of low surface coverage (), the first term on the right-hand side of Eq. 2 dominates over the nonlinear one, yielding
| [3] |
In the limit when the surface is saturated with monomers (), the dominant term in Eq. 2 is the nonlinear term, yielding
| [4] |
The true solution to Eq. 2 interpolates between these limiting values. We therefore obtain the following expressions for the rate of nucleation
| [5] |
where
| [6] |
is the surface coverage. In the limit (only bulk nuclei convert into fibrils) we recover, as expected, the rate of homogeneous nucleation
| [7] |
In the opposite limit kc = 0 (only surface-bound nuclei convert into fibrils) we obtain
| [8] |
Using and we find
| [9] |
In the limit of weak adsorption (), the rate of nucleation increases with increasing ε. Therefore, increasing the adsorption free energy causes more monomers to adsorb at the interface, resulting in overall faster heterogeneous nucleation. In the case of strong adsorption (), the rate of heterogeneous nucleation r decreases with increasing ε as . Even though the interface is fully covered with monomers, the conversion/detachment step is hindered, resulting in an overall smaller rate of heterogeneous nucleation.
Fitting procedure.
Experimental and simulation data in Figs. 5D and 6C are fitted to the model in Eqs. 1 and 2 with the fitting parameters α, β, and γ defined as
| [10] |
where k0 is defined through . In terms of these parameters, Eqs. 1 and 2 become
| [11] |
| [12] |
where . In the limits and the solution to Eq. 11 is
| [13] |
yielding
| [14] |
In a logarithmic plot, we obtain two straight lines
| [15] |
where , and . The fitting parameters for Figs. 5D and 6C are summarized in Table 1.
Table 1.
Linking surface excess, surface concentration, and surface tension changes.
For completeness and clarity of exposition, we revisit here the link between surface excess and surface concentration. This provides a useful basis for interpreting our surface tension measurements in terms of the free energy of adsorption. As discussed in the main text, the surface excess can be measured by recording how surface tension changes when increasing concentrations of protein are added to the system
| [16] |
While Eq. 16 is a very useful working definition for determining Γ experimentally, to relate Γ to adsorption energy we need another formula for Γ that accounts explicitly for the amount of protein adsorbed at the interface. We consider a binary system consisting of the solvent, denoted as 1, and protein, denoted 2. The bulk concentrations of the species 1 and 2 are (lower bulk phase) and (upper bulk phase). The number of moles of species i at the surface, denoted , is obtained by subtracting from the total number of moles in the system, ni, the amount of moles in the lower () and upper () bulk phases:
| [17] |
| [18] |
where is the volume of the lower bulk phase and is the volume of the upper bulk phase. Using and eliminating we obtain
| [19] |
Dividing by the area of the interface S we obtain the surface excess of species 2 relative to solvent 1:
| [20] |
Assuming the concentrations of solvent and solute to be negligible in the outer phase, , Eq. 20 simplifies to
| [21] |
The second term in the brackets is negligible if the number of moles of solvent adsorbed is negligible relative to total number of moles of the solvent. In this limit, Eq. 21 simplifies to:
| [22] |
We see that the surface excess is the difference between the total protein concentration, c2, and the bulk protein concentration after adsorption has been established. For our experimental system, we have , while can be calculated using the Langmuir adsorption isotherm as:
| [23] |
where is the total concentration of surface sites and is the surface coverage. Therefore,
| [24] |
where is the maximal surface excess and S/V is the surface-to-volume ratio. Combining Eq. 24 with Eq. 16 yields the following formula for the change of surface tension γ with added protein concentration:
| [25] |
which is known as the Langmuir–Szyszkowski equation.
Supplementary Material
Acknowledgments
The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Seventh Framework Programme (FP7/2007-2013) through the ERC grant PhysProt (agreement 337969). We are grateful for financial support from the Biotechnology and Biological Sciences Research Council (BBSRC) (T.P.J.K.), the Newman Foundation (T.P.J.K.), the Wellcome Trust (T.P.J.K. and M.V.), Peterhouse College Cambridge (T.C.T.M.), the ERC Starting Grant (StG) Non-Equilibrium Protein Assembly (NEPA) (A.S.), the Royal Society (A.S.), the Academy of Medical Sciences (A.S. and J.K.), and the Cambridge Centre for Misfolding Diseases (CMD).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission. J.-E.S. is a guest editor invited by the Editorial Board.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2109718119/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Cohen S. I., Vendruscolo M., Dobson C. M., Knowles T. P., From macroscopic measurements to microscopic mechanisms of protein aggregation. J. Mol. Biol. 421, 160–171 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Knowles T. P., Vendruscolo M., Dobson C. M., The amyloid state and its association with protein misfolding diseases. Nat. Rev. Mol. Cell Biol. 15, 384–396 (2014). [DOI] [PubMed] [Google Scholar]
- 3.Wetzel R., Kinetics and thermodynamics of amyloid fibril assembly. Acc. Chem. Res. 39, 671–679 (2006). [DOI] [PubMed] [Google Scholar]
- 4.Chiti F., Dobson C. M., Protein misfolding, functional amyloid, and human disease. Annu. Rev. Biochem. 75, 333–366 (2006). [DOI] [PubMed] [Google Scholar]
- 5.Dobson C. M., Protein folding and misfolding. Nature 426, 884–890 (2003). [DOI] [PubMed] [Google Scholar]
- 6.Haass C., Selkoe D. J., Soluble protein oligomers in neurodegeneration: Lessons from the Alzheimer’s amyloid beta-peptide. Nat. Rev. Mol. Cell Biol. 8, 101–112 (2007). [DOI] [PubMed] [Google Scholar]
- 7.Arnaudov L. N., de Vries R., Thermally induced fibrillar aggregation of hen egg white lysozyme. Biophys. J. 88, 515–526 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Haas J., et al., Primary steps of pH-dependent insulin aggregation kinetics are governed by conformational flexibility. ChemBioChem 10, 1816–1822 (2009). [DOI] [PubMed] [Google Scholar]
- 9.Nielsen L., et al., Effect of environmental factors on the kinetics of insulin fibril formation: Elucidation of the molecular mechanism. Biochemistry 40, 6036–6046 (2001). [DOI] [PubMed] [Google Scholar]
- 10.Campioni S., et al., The presence of an air-water interface affects formation and elongation of α-Synuclein fibrils. J. Am. Chem. Soc. 136, 2866–2875 (2014). [DOI] [PubMed] [Google Scholar]
- 11.Jayamani J., Shanmugam G., Diameter of the vial plays a crucial role in the amyloid fibril formation: Role of interface area between hydrophilic-hydrophobic surfaces. Int. J. Biol. Macromol. 101, 290–298 (2017). [DOI] [PubMed] [Google Scholar]
- 12.Linse S., et al., Nucleation of protein fibrillation by nanoparticles. Proc. Natl. Acad. Sci. U.S.A. 104, 8691–8696 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Toprakcioglu Z., Challa P., Xu C., Knowles T. P. J., Label-free analysis of protein aggregation and phase behavior. ACS Nano 13, 13940–13948 (2019). [DOI] [PubMed] [Google Scholar]
- 14.Toprakcioglu Z., Challa P. K., Morse D. B., Knowles T., Attolitre protein nanogels from droplet nanofluidics for intracellular delivery. Sci. Adv. 6, eaay7952 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Israelachvili J. N., Mitchell D. J., Ninham B. W., Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers. J. Chem. Soc. Faraday Trans. 2. Mol. Chem. Phys 72, 1525–1568 (1976). [Google Scholar]
- 16.Butt H. J., Graf K., Kappl M., Physics and Chemistry of Interfaces (John Wiley & Sons, 2003). [Google Scholar]
- 17.Yano Y. F., et al., Driving force behind adsorption-induced protein unfolding: A time-resolved X-ray reflectivity study on lysozyme adsorbed at an air/water interface. Langmuir 25, 32–35 (2009). [DOI] [PubMed] [Google Scholar]
- 18.Roach P., Farrar D., Perry C. C., Interpretation of protein adsorption: Surface-induced conformational changes. J. Am. Chem. Soc. 127, 8168–8173 (2005). [DOI] [PubMed] [Google Scholar]
- 19.Jiang D., et al., A kinetic model for beta-amyloid adsorption at the air/solution interface and its implication to the beta-amyloid aggregation process. J. Phys. Chem. B 113, 3160–3168 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jordens S., et al., Adsorption at liquid interfaces induces amyloid fibril bending and ring formation. ACS Nano 8, 11071–11079 (2014). [DOI] [PubMed] [Google Scholar]
- 21.LeVine H. III, Thioflavine T interaction with synthetic Alzheimer’s disease beta-amyloid peptides: Detection of amyloid aggregation in solution. Protein Sci. 2, 404–410 (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Li S., Leblanc R. M., Aggregation of insulin at the interface. J. Phys. Chem. B 118, 1181–1188 (2014). [DOI] [PubMed] [Google Scholar]
- 23.Donsmark J., Jorgensen L., Mollmann S., Frokjaer S., Rischel C., Kinetics of insulin adsorption at the oil-water interface and diffusion properties of adsorbed layers monitored using fluorescence correlation spectroscopy. Pharm. Res. 23, 148–155 (2006). [DOI] [PubMed] [Google Scholar]
- 24.Mollmann S. H., et al., Interfacial adsorption of insulin conformational changes and reversibility of adsorption. Eur. J. Pharm. Sci. 27, 194–204 (2006). [DOI] [PubMed] [Google Scholar]
- 25.Sessions K., Sacks S., Li S., Leblanc R. M., epi-Fluorescence imaging at the air-water interface of fibrillization of bovine serum albumin and human insulin. Chem. Commun. (Camb.) 50, 8955–8957 (2014). [DOI] [PubMed] [Google Scholar]
- 26.Baldursdottir S. G., Fullerton M. S., Nielsen S. H., Jorgensen L., Adsorption of proteins at the oil/water interface–Observation of protein adsorption by interfacial shear stress measurements. Colloids Surf. B Biointerfaces 79, 41–46 (2010). [DOI] [PubMed] [Google Scholar]
- 27.Pronchik J., He X., Giurleo J. T., Talaga D. S., In vitro formation of amyloid from alpha-synuclein is dominated by reactions at hydrophobic interfaces. J. Am. Chem. Soc. 132, 9797–9803 (2010). [DOI] [PubMed] [Google Scholar]
- 28.Zhu M., Souillac P. O., Ionescu-Zanetti C., Carter S. A., Fink A. L., Surface-catalyzed amyloid fibril formation. J. Biol. Chem. 277, 50914–50922 (2002). [DOI] [PubMed] [Google Scholar]
- 29.Keller A., et al., Influence of hydrophobicity on the surface-catalyzed assembly of the islet amyloid polypeptide. ACS Nano 5, 2770–2778 (2011). [DOI] [PubMed] [Google Scholar]
- 30.Galvagnion C., et al., Lipid vesicles trigger α-synuclein aggregation by stimulating primary nucleation. Nat. Chem. Biol. 11, 229–234 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Krausser J., Knowles T. P. J., Šarić A., Physical mechanisms of amyloid nucleation on fluid membranes. Proc. Natl. Acad. Sci. U.S.A. 117, 33090–33098 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Campioni S., et al., Interfaces determine the fate of seeded α-synuclein aggregation. Adv. Mater. Interfaces 7, 2000446–2000455 (2020). [Google Scholar]
- 33.Dobson C. M., Swoboda B. E., Joniau M., Weissman C., The structural basis of protein folding and its links with human disease. Philos. Trans. R. Soc. Lond. B Biol. Sci. 356, 133–145 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Shen Y., Johnson M. A., Martin D. C., Microstructural characterization of Bombyx mori silk fibers. Macromolecules 31, 8857–8864 (1998). [Google Scholar]
- 35.Meisl G., et al., Molecular mechanisms of protein aggregation from global fitting of kinetic models. Nat. Protoc. 11, 252–272 (2016). [DOI] [PubMed] [Google Scholar]
- 36.Michaels T. C., et al., Reaction rate theory for supramolecular kinetics: Application to protein aggregation. Mol. Phys. 116, 3055–3065 (2018). [Google Scholar]
- 37.Knowles T. P. J., et al., An analytical solution to the kinetics of breakable filament assembly. Science 326, 1533–1537 (2009). [DOI] [PubMed] [Google Scholar]
- 38.Meisl G., et al., Differences in nucleation behavior underlie the contrasting aggregation kinetics of the Aβ40 and Aβ42 peptides. Proc. Natl. Acad. Sci. U.S.A. 111, 9384–9389 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Oosawa F., Asakura S., Thermodynamics of the Polymerization of Protein (Academic Press, New York, 1975). [Google Scholar]
- 40.Šarić A., et al., Physical determinants of the self-replication of protein fibrils. Nat. Phys. 12, 874–880 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Šarić A., Chebaro Y. C., Knowles T. P., Frenkel D., Crucial role of nonspecific interactions in amyloid nucleation. Proc. Natl. Acad. Sci. U.S.A. 111, 17869–17874 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rockwood D. N., et al., Materials fabrication from Bombyx mori silk fibroin. Nat. Protoc. 6, 1612–1631 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix.