Summary
Objectives
Breast cancer (BC) is the most common cause of cancer death in Iranian women. Sometimes death from other causes precludes the event of interest and makes the analysis complicated. The purpose of this study was to identify important prognostic factors associated with survival duration among patients with BC using random survival forests (RSF) model in presence of competing risks. Also, its performance was compared with cause-specific hazard model.
Methods
This retrospective cohort study assessed 222 patients with BC who were admitted to Ayatollah Khansari hospital in Arak, a major industrial city and the capital of Markazi province in Iran. The cause-specific Cox proportional hazards and RSF models were employed to determine the important risk factors for survival of the patients.
Results
The mean and median survival duration of the patients were 90.71 (95%CI: 83.8-97.6) and 100.73 (95%CI: 89.2-121.5) months, respectively. The cause-specific model indicated that type of surgery and HER2 had statistically significant effects on the risk of death of BC. Moreover, the RSF model identified that HER2 was the most important variable for the event of interest.
Conclusion
According to the results of this study, the performance of the RSF model was better than the cause-specific hazard model. Moreover, HER2 was the most important variable for death of BC in both of the models.
Keywords: Random Survival Forest, Competing risks, Cause-specific hazard model, Breast Cancer
Introduction
Cancer is known as the most leading and the second cause of death in developed and developing countries, respectively. Annually, 7.6 million deaths occur due to cancer, worldwide. Among women, breast cancer (BC) is the most frequent cancer. It is estimated that BC accounts for about 23% of all new cases of cancer [1, 2]. About 27.2% of all new cancer diagnosed cases and about 19% of all deaths due to cancer among Asian women are related to BC. In Iran as a developing country, BC was showed an increasing trend during 1965-2000, and the rank of its prevalence changed from the second most to the first most frequent malignancy [1]. Annually, about 8090 new cases were diagnosed and more than 1300 of them died because of BC. Hence, it is an important public health problem in Iran. Some type of surgery to remove the tumor is the main treatment for women with BC. According to previous studies, the number of involved lymph nodes and tumor size are the most important prognostic factors in BC [3].
Survival analysis is used to analyze the time-to-event data. Cox proportional hazards (PH) regression model is the most common model to analyze survival data. The basic assumption of this model is the proportionality of hazards which is determinative. In practice, the explanatory variables may not satisfy the PH assumption or they may be correlated [4]. Moreover, when data typically has a high rate of censoring, the performance of traditional models such as the Cox PH regression model will not be reliable [5]. In some studies, all covariates are measured at the baseline and none of them are time-varying covariates, but their effects may change over time. So, more flexible models are needed. Moreover, in some situations, a patient only can experience one of the different types of possible events over the follow-up. The probabilities of these events are referred to as competing risks and the competing risks models are the best choice to analyze such data. The random survival forest (RSF) is appropriate to analyze right-censored survival data and also is free of model assumptions. The most important feature of a random forest is its good performance in determining the importance of each variable in predicting the response variable [6]. The aim of this study was to identify important prognostic factors associated with survival among patients with BC using RSF in the presence of competing events and compare its performance with the cause-specific hazard regression model.
Materials and methods
DATA COLLECTION
The data of this study are related to patients with BC who were admitted to Ayatollah Khansari hospital in Arak, a major industrial city and the capital of Markazi province in Iran, during 2012-2015. Due to the lack of electronic medical records, data are extracted from the paper-based medical records into the pre-prepared checklist. The study entrance criteria were female patients with diagnosed BC that had more than 18 years old. Also, patients who had many missing data in their clinical and demographic records were excluded. The gathered data included age at diagnosis, type of surgery (Radical mastectomy, Segmental mastectomy, Simple mastectomy), number of involved lymph nodes (less than 2, 3-6, and more than 7), estrogen receptor (ER), progesterone receptor (PR), and human epidermal growth factor receptor 2 (HER2) status, family history of BC, stage of the tumor, type of tumor (Ductal, Lobular, Medullar), and tumor size (less than 2, 2-5, and greater than 5 cm), based on the American Joint Committee on Cancer classification [7].
Survival time was calculated as the number of months from diagnosis until death due to BC, other causes, or the end of the study. The event of interest was death due to BC and death due to other causes were the competing event. Patients who withdrew, lost-to-follow-up, or did not die up to the end of the study were considered censored.
STATISTICAL ANALYSIS
Describing survival
When there are competing risks, the Kaplan-Meier (KM) may not be very informative to describe survival probability because it is based on an independent assumption about competing risks that cannot be verified. So, the cumulative incidence function that can be used for different causes of failure, was employed for the statistical description of survival [8].
Cause-specific hazard regression model
The cause-specific hazard regression model can be fit with Cox regression by treating failures from the cause of interest as events and failure from other causes as censored observation. The adjusted and unadjusted effects of risk factors on cause-specific hazards were estimated using the Cox PH regression model [4].
Random survival forests model for competing risks
RSF is a survival model based on the tree method for the analysis of right-censored survival data. To develop and validate the RSF, data were divided to learning (63% of data to develop the model) and test (37 of data to check the data validity) parts. Totally, 1000 bootstraps samples were constructed from the learning part. Then a competing risk tree for each bootstrap sample was grown. To split each node of a tree, a subset of p variables was selected randomly, and the node was split using the candidate variable that maximizes a competing risk splitting rule. The tree is grown to full size under the constraint that a terminal node should have no less than unique cases. Then we calculate cumulative incidence functions and cumulative cause-specific hazards for all events (Death of BC, Death of other causes) for each tree. Eventually, take the average of each estimator over all trees to obtain its ensemble [9]. In RSF, variables can be selected by filtering on the basis of their variable importance (VIMP). The VIMP for x, a risk factor, is the prediction error for the original ensemble subtracted from the prediction error for the new ensemble obtained using randomizing x assignments [9, 10]. A large positive VIMP indicates a potentially predictive variable whereas zero or negative values identify non-predictive variables to be filtered [9].
Comparison and computational software
We used the integrated Brier score (IBS) to compare the efficiency of the RSF for competing risks and the cause-specific hazard regression model [11].
Statistical analysis was performed using R packages’ “randomForestSRC” [12], “riskRegression” [13], “cmprsk” [14] and “pec” [11], version 3.3.3 (The R Foundation for Statistical Computing, Vienna, Austria; http://www.r-project.org).
ETHICS STATEMENT
This study was approved by the Research Ethics Committee of Hamadan University (No. IR.UMSHA.REC. 1396.738). We received informed written consentfrom all participants and for illiterate people and participants under the age of 16 from legally authorized parents/representatives.
Results
The study involved 222 patients with BC. Approximately 26% (n = 58) of patients experienced death due to BC, 13% (n = 29) experienced death due to other causes and the remaining were right censored. The mean and median survival time of the patients were 90.71 (95% CI: 83.82-97.60) and 100.73 (95% CI: 89.16-121.46) months, respectively. The mean (SD) age at diagnosis was 46.53 (10.21) years. The baseline characteristics of patients with BC are given in Table I.
Tab. I.
Baseline characteristics of patients with breast cancer.
| Variables | Death of BC N (%) | Death of other causes N (%) | Censored N (%) | Total N (%) |
|---|---|---|---|---|
| Type of surgery | ||||
| Radical Mastectomy | 49 (84.5) | 26 (89.7) | 109 (80.7) | 184 (82.9) |
| Segmental Mastectomy | 5 (8.6) | 1 (3.4) | 9 (6.7) | 15 (6.8) |
| Simple Mastectomy | 4 (6.9) | 2 (6.9) | 17 (12.6) | 23 (10.4) |
| Number of involved lymph nodes | ||||
| ≤ 2 | 34 (58.6) | 13 (44.8) | 80 (59.3) | 127 (57.2) |
| 3-6 | 14 (24.1) | 7 (24.1) | 5 (3.7) | 33 (14.9) |
| ≥ 7 | 10 (17.2) | 9 (31.0) | 28 (20.7) | 47 (21.2) |
| ER | ||||
| Positive | 26 (44.8) | 15 (51.7) | 66 (48.9) | 107 (48.2) |
| Negative | 32 (55.2) | 14 (48.3) | 69 (51.1) | 115 (51.8) |
| PR | ||||
| Positive | 23 (39.7) | 14 (48.3) | 57 (42.2) | 94 (42.3) |
| Negative | 35 (60.3) | 15 (51.7) | 78 (51.1) | 128 (57.7) |
| HER2 | ||||
| Positive | 44 (75.9) | 17 (58.6) | 68 (50.4) | 129 (58.1) |
| Negative | 14 (24.1) | 12 (41.4) | 67 (49.6) | 93 (41.9) |
| Family history of BC | ||||
| No | 6 (10.3) | 2 (6.9) | 8 (5.9) | 16 (7.2) |
| Yes | 52 (89.7) | 27 (93.1) | 127 (94.1) | 206 (92.8) |
| Stage of disease | ||||
| I | 30 (51.7) | 11 (39.7) | 79 (58.5) | 120 (54.1) |
| II | 13 (22.4) | 8 (27.6) | 20 (14.8) | 41 (18.5) |
| III | 15 (25.9) | 10 (34.5) | 36 (26.7) | 61 (27.5) |
| Type of tumor | ||||
| Ductal | 50 (86.2) | 26 (89.7) | 115 (85.2) | 191 (86.0) |
| Lobular | 4 (6.9) | 2 (6.9) | 12 (8.9) | 18 (8.1) |
| Medullar | 4 (6.9) | 1 (3.4) | 8 (5.9) | 13 (5.9) |
| Tumor size (cm) | ||||
| ≤ 2 | 35 (60.3) | 16 (55.2) | 101 (74.8) | 152 (68.5) |
| 2-5 | 21 (36.2) | 12 (41.4) | 33 (24.4) | 66 (29.7) |
| > 5 | 2 (3.4) | 1 (3.4) | 1 (0.7) | 4 (1.8) |
Figure 1 shows that non-parametric estimates of cumulative incidence functions (CIF) for death due to BC and other causes. As can be seen in this figure, cumulative incidence probability for death of BC is higher than the competing event of death.
Fig 1.
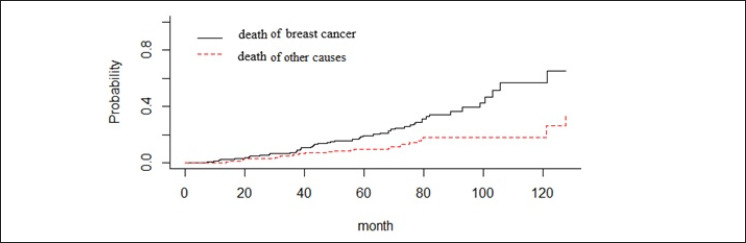
CIF for death due to breast cancer and other causes in patients with breast cancer.
The results of cause-specific model are shown in Table II. According to the results, type of surgery (Segmental Mastectomy) and HER2 were statistically significant for the event of interest (death due to BC) (P < 0.05). So, the risk of death for a patient who has segmental mastectomy was 2.98 times larger compared with a patient with radical mastectomy. Moreover, the risk of death in patients with HER2 positive was higher than patients with HER2 negative.
Tab. II.
Results of cause specific models for BC progression and death competing events.
| Variables | Death of BC | Death of other causes |
|---|---|---|
| HR (95% CI) | HR (95% CI) | |
| Age at diagnosis | 0.99 (0.97, 1.02) | 0.99 (0.96, 1.03) |
| Type of surgery | ||
| Radical Mastectomy | 1.00 | 1.00 |
| Segmental Mastectomy | 2.98 (1.07, 8.28)* | 1.05 (0.12, 8.69) |
| Simple Mastectomy | 1.13 (0.38, 3.35) | 1.20 (0.25, 5.63) |
| Number of involved lymph nodes | ||
| ≤ 2 | 1.00 | 1.00 |
| 3-6 | 1.18 (0.54, 2.58) | 1.39 (0.47, 4.11) |
| ≥ 7 | 0.31 (0.08, 1.23) | 2.31 (0.34, 15.69) |
| ER | ||
| Negative | 1.00 | 1.00 |
| Positive | 0.98 (0.43, 2.27) | 0.87 (0.24, 3.13) |
| PR | ||
| Negative | 1.00 | 1.00 |
| Positive | 0.92 (0.40, 2.14) | 1.57 (0.44, 5.56) |
| HER2 | ||
| Negative | 1.00 | 1.00 |
| Positive | 3.08 (1.58, 6.01)* | 1.28 (0.56, 2.92) |
| Family history of BC | ||
| Yes | 1.00 | 1.00 |
| No | 0.63 (0.26, 1.55) | 1.09 (0.24, 4.83) |
| Stage of disease | ||
| I | 1.00 | 1.00 |
| II | 0.66 (0.21, 2.03) | 1.57 (0.37, 6.50) |
| III | 1.82 (0.50, 6.63) | 0.99 (0.14, 6.71) |
| Type of tumor | ||
| Ductal | 1.00 | 1.00 |
| Lobular | 1.19 (0.41, 3.42) | 0.94 (0.21, 4.17) |
| Medullar | 0.65 (0.21, 2.05) | 0.61 (0.07, 4.85) |
| Tumor size (cm) | ||
| ≤ 2 | 1.00 | 1.00 |
| 2-5 | 1.55 (0.59, 4.08) | 1.12 (0.35, 3.57) |
| > 5 | 0.84 (0.13, 5.35) | 1.03 (0.09, 10.98) |
* Significant (p-value < 0.05); BC: breast cancer.
Results from the event-specific variable importance (VIMP) for all used variables in RSF are given in Table III. The event-specific VIMP were obtained using log-rank splitting. An important variable is known if the value of its VIMP be more than 0.002 [15]. According to Table III, HER2, number of involved lymph nodes and age at diagnosis are the top three variables for death due to BC.
Tab. III.
The event-specific VIMP for risk factors from BC analysis for the two events.
| Variables | VIMP | |||
|---|---|---|---|---|
| Death of BC | Variables’ Rank | Death of other causes | Variables’ Rank | |
| Age at diagnosis | 0.014 | 3 | -0.002 | 5 |
| Type of surgery | 0.010 | 4 | -0.006 | 6 |
| Number of involved lymph nodes | 0.019 | 2 | 0.018 | 4 |
| ER | 0.002 | 7 | -0.015 | 10 |
| PR | -0.003 | 10 | -0.010 | 8 |
| HER2 | 0.079 | 1 | -0.007 | 7 |
| Family history of BC | 0.004 | 6 | 0.024 | 1 |
| Stage of disease | -0.002 | 9 | 0.018 | 3 |
| Type of tumor | 0.005 | 5 | -0.015 | 9 |
| Tumor size (cm) | -0.002 | 8 | 0.020 | 2 |
In order to compare the efficiency of RSF with cause-specific model, the integrated Brier score (IBS) criterion was used. The smaller value of this criterion shows better performance. Values of this criterion for RSF and cause-specific model were reported in Table IV. The IBS score of the RSF was 0.132 for death due to BC, which was smaller than the one for the cause-specific hazard regression model.
Tab. IV.
Overview of the IBS criterion.
| Models | IBS | |
|---|---|---|
| Death due to BC | Death of other causes | |
| RSF* | 0.132 | 0.154 |
| Cause-specific hazard regression model | 0.165 | 0.179 |
* Related to RSFs using generalized log-rank splitting rule.
Discussion
In the analysis of survival data, it is possible that subjects be at risk of more than one event in a way that the occurrence of one, prevents the others. In this situation, there are several methods for analyzing survival data. We focused on modeling with RSF for competing risks. This method is an assumption-free model that is very efficient for the analysis of data with high-correlation predictor variables, nonlinear effects, and high-level interactions [9, 10].
Several studies have been done to determine the importance of risk factors in the survival of BC patients using RSF. In these studies, in which only one death event was considered, factors such as progesterone receptor, number of involved lymph nodes, stage of disease, and so on were recognized as important variables [10, 16, 17].
According to the results of the RSF model in this study, HER2, number of involved lymph nodes, and age at diagnosis as three important prognostic factors of survival in BC patients who died due to BC. This result is similar to the result of the study done by Safe et al. [16]. HER2 was also, statistically significant cause specific of death using traditional competing risks model. As the results of this model showed, the risk of death in patients with HER2 positive was higher than patients with the HER2 negative. However, the other important variables not significant in cause-specific hazards model. This finding was very similar to the results of the study by Poorolajal et al. [18] and Karimi et al. [19].
For the competing event, metastasis status was the most important variable for RSF. For the competing event, the Family history of BC was the most important variable for RSF. However, using classical models, no variable was significant in the cause-specific hazards model.
In order to compare the performance of the cause-specific hazard regression model and RSF were compared were used the integrated Brier score criterion. Based on the results of the IBS criterion, the performance of RSF was better than the cause-specific hazard regression model. This result was consistent with the studies done by Ishwaran et al. [10] and Hamidi et al. [15]. This may be because the nonlinear effects and interactions between variables are considered in the RSF model [10, 15].
The main limitation of this study was the small number of deaths and the high rate of censoring. Despite this limitation, the current study reveals the important prognosis factors for survival in patients with BC.
Conclusion
According to the results of this study, the performance of the RSF model was better than the cause-specific hazard model. Also, HER2 was the most important variable for death of BC in both models.
Acknowledgements
We would like to thank the Vice-Chancellor of Research and Technology, Hamadan University of Medical Sciences for the approval and support of this study (Grant no. 9610266894). We also thank the staff of the Ayatollah Khansari hospital of Arak Province for their collaboration and cooperation with the authors.
Figures and tables
Footnotes
Conflict of interest statement
The authors declare that they have no conflicts of interest.
Funding
This study was funded by Vice-Chancellor of Research and Technology, Hamadan University of Medical Sciences (Grant no. 9610266894).
Author' contributions
RNV and JF contributed to the study design, analysis, and interpretation of data. LT participated in data collection, data analysis. BA, TM and KhNGh participated in the interpretations and drafting of the manuscript. All authors read and approved the final manuscript.
References
- [1].Jafari-Koshki T, Schmid VJ, Mahaki B. Trends of breast cancer incidence in Iran during 2004-2008: A Bayesian space-time model. Asian Pac J Cancer Prev 2014;15:1557-61. http://doi.org/10.7314/APJCP.2014.15.4.1557 10.7314/APJCP.2014.15.4.1557 [DOI] [PubMed] [Google Scholar]
- [2].DeSantis C, Ma J, Bryan L, Jemal A. Breast cancer statistics, 2013. CA: Cancer J Clin 2014;64:52-62. http://doi.org/10.3322/caac.21203 10.3322/caac.21203 [DOI] [PubMed] [Google Scholar]
- [3].Akbari ME, Mozaffar M, Heidari A, Zirakzadeh H, Akbari A, Akbari M, Hosseinizadegan Shirazi F. Recurrence and survival effect in breast conserving surgery: What are the predictive and/or prognostic factors? Iran J Cancer Prev 2011;4:49-54. [Google Scholar]
- [4].Kleinbaum DG, Klein M. Survival analysis. Springer; 2010. [Google Scholar]
- [5].Hsich E, Gorodeski EZ, Blackstone EH, Ishwaran H, Lauer MS. Identifying important risk factors for survival in patient with systolic heart failure using random survival forests. Circ Cardiovasc Qual Outcomes 2011;4:39-45. http://'doi.org/10.1161/CIRCOUTCOMES.110.939371 10.1161/CIRCOUTCOMES.110.939371 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Breiman L. Random Forests. Machine Learning 2001;45:5-32. [Google Scholar]
- [7].Egner JR. AJCC cancer staging manual. JAMA 2010;304:1726-7. http://doi.org/10.1001/jama.2010.1525 10.1001/jama.2010.1525 [DOI] [Google Scholar]
- [8].Pintilie M. Competing risks: a practical perspective. John Wiley & Sons; 2006. [Google Scholar]
- [9].Ishwaran H, Gerds TA, Kogalur UB, Moore RD, Gange SJ, Lau BM. Random survival forests for competing risks. Biostatistics 2014;15:757-73. http://doi.org/10.1093/biostatistics/kxu010 10.1093/biostatistics/kxu010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. Ann Appl Stat 2008;2:841-60. http://doi.org/10.1214/08-AOAS169 10.1214/08-AOAS169 [DOI] [Google Scholar]
- [11].Mogensen UB, Ishwaran H, Gerds TA. Evaluating random forests for survival analysis using prediction error curves. J Stat Softw 2012;50:1. http://doi.org/10.18637/jss.v050.i11 10.18637/jss.v050.i11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ishwaran H, Kogalur UB. Random forests for survival, regression, and classification (RF-SRC), R package version 2.5.1. (2017). [Google Scholar]
- [13].Gerds TA, Scheike TH, Blanche P, Ozenne B. riskRegression: risk regression models and prediction scores for survival analysis with competing risks. R package version 1.3.7. (2017). [Google Scholar]
- [14].Gray B. cmprsk: subdistribution analysis of competing risks. R package version 2.2-7 (2014). [Google Scholar]
- [15].Hamidi O, Tapak M, Poorolajal J, Amini P, Tapak L. Application of random survival forest for competing risks in prediction of cumulative incidence function for progression to AIDS. Epidemiol Biostat Public Health 2017;14. https://doi.org/10.2427/12663 10.2427/12663 [DOI] [Google Scholar]
- [16].Safe M, Mahjub H, Faradmal J. A comparative study for modelling the survival of breast cancer patients in the west of Iran. Glob J Health Sci 2016;9:215. https://doi.org/10.5539/gjhs.v9n2p215 10.5539/gjhs.v9n2p215 [DOI] [Google Scholar]
- [17].Omurlu IK, Ture M, Tokatli F. The comparisons of random survival forests and Cox regression analysis with simulation and an application related to breast cancer. Expert Syst with Appl 2009;36:8582-8. https://doi.org/10.1016/j.eswa.2008.10.023 10.1016/j.eswa.2008.10.023 [DOI] [Google Scholar]
- [18].Jalal Poorolajal NN, Akbari ME, Mahjub H, Esmailnasab N. Breast cancer survival analysis based on immunohistochemistry subtypes (ER/PR/HER2): a retrospective cohort study. Arch Iran Med 2016;19:680-6. [PubMed] [Google Scholar]
- [19].Karimi A, Delpisheh A, Sayehmiri K, Saboori H, Rahimi E. Predictive factors of survival time of breast cancer in kurdistan province of Iran between 2006-2014: a cox regression approach. Asian Pac J Cancer Prev 2014;15:8483-8. http://doi.org/10.7314/APJCP.2014.15.19.8483 10.7314/APJCP.2014.15.19.8483 [DOI] [PubMed] [Google Scholar]


