Sparse Data–Driven Learning for Effective and Efficient Biomedical Image Segmentation

Abstract

Sparsity is a powerful concept to exploit for high-dimensional machine learning and associated representational and computational efficiency. Sparsity is well suited for medical image segmentation. We present a selection of techniques that incorporate sparsity, including strategies based on dictionary learning and deep learning, that are aimed at medical image segmentation and related quantification.

1. INTRODUCTION

Sparsity and sparse representations are an important element of medical image analysis (1), with the overall goal of providing a compact representation of the most important information. In terms of a set of basic elements, the aim is to have as few nonzero weights as are necessary for effective analysis. Sparsity constraints can be exploited to develop more efficient representations and have been used for an array of problems in medical image processing and analysis, including restoration (2, 3), pattern classification (4), image synthesis (5), contour tracking (6), and image segmentation (7). In this review, we present a set of ideas unified around sparsity, with a focus on the challenging task of medical image segmentation. We introduce a taxonomy or hierarchy of representations that covers the use of raw local intensities, local intensities organized around an evolving boundary, local intensity scale space, and more globally organized local intensity arrangements incorporating shape. Sparsity can be embedded in these representations by learning sets of atoms in the form of either dictionaries or other representations, whose entries can then be used for further analysis or implicitly in neural networks through the use of dropout layers or other mechanisms.

We begin by reviewing different types of data representations in medical image segmentation in Section 2. Then, in Section 3, we review how concepts in sparsity and sparse representations can be introduced into a variety of segmentation schemes, while presenting a unified framework for such ideas. In Section 4, we provide more detail by looking at a diverse set of exemplar applications that leverage sparse representation. In Section 5, we present our conclusions.

2. IMAGE-DERIVED INFORMATION FOR APPEARANCE-BASED IMAGE SEGMENTATION

There is a long history of image intensity–derived image segmentation strategies in medical image analysis (e.g., 8, 9), which developed in parallel with research in other areas of pattern recognition and computer vision (e.g., 10, 11). The aim of such strategies is to localize anatomically or biomedically meaningful objects (classes) from medical imaging modalities (12) such as magnetic resonance imaging (MRI), computed tomography (CT), ultrasound, or nuclear medicine. Image segmentation is dependent on the extraction of image features that are either handcrafted or learned, or both.

Some of the most common appearance features used for segmentation can be classified as follows. First, voxel-wise intensity appearance provides the most basic and localized feature information. Segmentation methods using individual voxel intensities perform class assignment by, for example, employing Bayesian decision theory (10), fitting parametric model intensity (13–16), or applying unsupervised strategies such as fuzzy c-means (17). Second, gradient, texture, and higher-order feature appearance capture more spatial complexity than do individual voxel intensities. Here, intensity, gradients, and context can be incorporated into a single feature vector (18); spatial proximity can be included to aid in classification using region clustering or region growing techniques (11); or graph-based representations, with connections based on the similarity of voxel intensity features and spatial proximity, can be constructed, searched, and compared (19). Convolutional neural network (CNN) approaches are designed to be able to learn contextual features from the voxel intensities by optimizing the weights of convolution operations based on training data aimed at a particular segmentation task. Third, image patch appearance incorporates increasing regional appearance influences by using information from neighboring voxels around an image location. Sets of image patches from a spatially local region can be used to form a set of templates or atlases for segmentation (20, 21), or methods using nonlocal patches omit spatial relationships between appearances in favor of a many-to-one matching of appearance that permits many samples to be compared. Finally, shape and geometry appearance can be used to define a more global knowledge of appearance. Shape models can construct efficient representations of segmentation boundaries (22–24), and these shape models can be combined with intensity appearance (25). In general, segmentation methods use one or more of these appearance features in conjunction with classification methods such as support vector machines (26), random forests (27), or neural networks (28) to best determine class boundaries.

A key issue in all of the above appearance categories is the need for efficient representation. Appearance feature spaces can grow too large and suffer from the curse of dimensionality (29) in supervised learning. Principal component analysis (30) is a straightforward technique that enables dimensionality reduction by identifying low-variance dimensions likely associated with noise. It is limited, however, by its linearity and its use of only first- and second-order statistics. Sparsity, as discussed below (see Section 3), enables the development of data-driven adaptive basis sets (e.g., dictionaries) that provide a more flexible and tailored approach to efficient appearance representation.

3. SPARSE REPRESENTATIONS FOR MEDICAL IMAGE SEGMENTATION

Sparse representation is a rigorous mathematical framework for studying high-dimensional data and uncovering the underlying structure of the data (31). Advances in this area have not only caused a small revolution in the community of statistical signal processing (31) but have also led to several state-of-the-art results in computer vision applications, such as face recognition (32), signal classification (33), texture classification, and edge detection (34–36). Sparse image representation exploits the idea that although images are naturally high dimensional, in many applications images belonging to the same class lie on or near a low-dimensional subspace (37). Sparsity has proven to be a powerful constraint for uncovering such degenerate structure. On the basis of sparsity constraints, the subspace of a class can be spanned in the sense of sparse representation by a set of base vectors that can be either predefined, typically in a parametric form such as a Fourier basis (38), or learned from training samples. In the latter case, the subspace of learned base vectors is assembled into a dictionary that encodes the signal patterns of the class. Learned dictionaries typically outperform predefined ones in classification tasks, in particular for distorted data and compact representation (39). Sparse representation has also been applied to medical image analysis settings such as shape prior modeling (40–42), nonrigid registration (43), and functional connectivity modeling (44). We review a general framework for sparsity-based segmentation in Sections 3.1–3.4, below. In addition, we note that a number of recent efforts have aimed to incorporate and interpret sparsity in the context of neural networks (see Section 3.5).

3.1. Representation Framework

The mathematical framework for considering sparse representation in the context of this review can be constructed by first describing the representation of an n-dimensional feature vector derived from a medical image, $y=\left[y_1,y_2,\dots ,y_n\right]\in {ℝ}^n$, as a weighted combination of m sets of similar samples of the same dimension in a representation repository or dictionary, $D=\left[d_1,d_2,\dots ,d_m\right]\in {ℝ}^{n\times m}$. Here, each element d_i is an n-dimensional vector of appearance and is often referred to as a dictionary atom. The data vector y could be one instance of a collection of intensities, features, or even boundary control points, as described above in Section 2. The dictionary D can be either a collection of raw feature data samples themselves or a set of predefined basis functions or of learned feature elements that represent the underlying data distribution (see Section 3.3). A coding vector $X\in {ℝ}^m$ selects the weighted combination of samples from the dictionary that best represents the data vector. Generally, the representation problem aims to find the optimal coding vector x that minimizes the reconstruction error between the data y and the weighted dictionary Dx:

$$\underset{x}{\text{min}}\parallel y-Dx{\parallel }_p,$$ 1.

where ∥·∥_p is the p norm; typically, the ℓ₂ Euclidean norm (p = 2) is used here.

In some applications, sparsity can be imposed not only on the representation x itself but also on regions of abnormality along a boundary. Thus, a position-specific error vector e can be used to capture rare but important discrepancies in a segmentation (see Section 4.4, below).

3.2. Imposing Sparsity

Sparsity is often used in medical image analysis to solve segmentation problems, our focus in this review. We can impose sparsity in its most basic form by simply counting the nonzero entries of any entity and limiting or minimizing that count. The count is denoted by the ℓ₀ norm ∥·∥₀. Sparse solutions can be imposed using the ℓ₀ norm on the representation coding problem defined in Equation 1. One way to impose sparsity is to set a threshold Г on the ℓ₀ norm of the coding vector:

$$\underset{x}{\text{min}}\parallel y-Dx{\parallel }_2^2\text{\hspace{1em} s.t. \hspace{1em}}\parallel x{\parallel }_0\le \Gamma .$$ 2.

The value of Г is chosen specific to the application. Sparsity can also be realized by limiting the overall error with a threshold ϵ instead of a sparsity threshold:

$$\underset{x}{\text{min}}\parallel x{\parallel }_0\text{\hspace{1em} s.t. \hspace{1em}}\parallel y-Dx{\parallel }_2^2\le ϵ.$$ 3.

Again, the threshold ϵ must be chosen according to the application. While in Equation 2 we specify the degree of sparsity, in Equation 3 we specify a limit on the error. As we demonstrate below, this basic idea is developed in different ways. In cases when the exact determination of these sparse solutions has proven to be computationally expensive (45), approximate solutions are considered instead. Several efficient pursuit algorithms have been proposed; these include matching pursuit (46) and orthogonal matching pursuit (OMP) (47–49).

Also, as is well known from the sparsity literature (50), the nonconvexity of the ℓ₀ norm makes the constraints in Equation 2 intractable. Conveniently, the research community has recognized that this problem can be nicely reformulated and made continuous and convex, but nonsmooth, by use of ℓ₁ norm relaxation. In fact, efforts in computer vision (mainly in face recognition) have shown that minimizing with respect to an ℓ₁ norm is equivalent to doing the same for an ℓ₀ norm for sparse-enough solutions (32, 51), and medical image analysis investigators have adopted this approach (52). Thus, replacing the ℓ₀ norm with an ℓ₁ norm in Equation 2, and reformulating using a weighted sum, results in

$$\underset{x}{\text{min}}\parallel y-Dx{\parallel }_2^2+\lambda \parallel x{\parallel }_1.$$ 4.

This basic idea has also been recognized in the statistics literature (53) and termed the least absolute shrinkage and selection operator (LASSO). Alternatively, when the number of data samples m is much greater than the number of selected elements Г, which is often the case in medical imaging problems, robust sparse representation may be achieved by including an ℓ₂ ridge penalty term in the representation functional (54):

$$\underset{x}{\text{min}}\frac{1}{2}\parallel y-Dx{\parallel }_2^2+{\lambda }_1\parallel x{\parallel }_1+\frac{{\lambda }_2}{2}\parallel x{\parallel }_2^2.$$ 5.

This method, termed the Elastic Net, empirically outperforms LASSO while preserving the sparsity of the representation. In particular, the Elastic Net formulation encourages a grouping of highly correlated variables. Elastic Net was successfully used in one of our example applications below (see Section 4.3).

As discussed in Section 4, the basic strategy for sparse representation as represented by Equations 2–4 can be applied and augmented in a number of ways. The methods for actually learning the dictionaries used for representation are discussed in the following section.

3.3. Dictionary Learning

Traditionally, representations of information derived from images have employed standard bases, such as Fourier, Gabor, or wavelet. Instead of using a standard basis, it is possible to learn a dictionary of atoms from the data themselves. Learning a dictionary, $D=\left[d_1,\dots ,d_m\right]\in {ℝ}^{n\times m}$, from a finite training set of image-derived information, $Y=\left[y_1,y_2,\dots ,y_s\right]\in {ℝ}^{n\times s}$, requires solving a joint optimization problem with respect to the dictionary D and the sparse representation coefficients, $X=\left[x_1,x_2,\dots ,x_s\right]\in {ℝ}^{m\times s}$:

$$\underset{D,X}{\text{min}}\parallel Y-DX{\parallel }_2^2\text{\hspace{1em} s.t. }\forall i,{\Vert x_i\Vert }_p\le \Gamma ,$$ 6.

where Г is a predetermined target sparsity constraint and p is the chosen norm. Effective algorithms for solving the dictionary learning problem (Equation 6) using p = 0 or p = 1 include K-SVD (55), the method of optimal directions (56), and a stochastic algorithm (57). K-SVD has been widely used because of its good convergence properties. The main iteration of K-SVD contains two stages: sparse coding and dictionary updating. In the sparse coding stage, D is fixed and the problem stated in Equation 2 or 3 is solved using a matching pursuit algorithm, such as OMP (58), to find the best matching sparse representation X. In the dictionary updating stage, the atoms of the dictionary D are updated. For the application of dictionaries and sparsity to medical image segmentation that is of interest in this review, there are key parameter choices that must be made for each specific problem: the dictionary atom size, the number of atoms included in the dictionary, and the order of sparse regularization. Both the sparse coding and dictionary updating stages of dictionary learning could also be set and solved numerically using a LASSO-style formulation, as shown by Equation 4.

3.4. Classification Using Dictionaries

Given a dictionary, or a set of dictionaries, segmentation of an image may be performed by classifying each individual voxel into a distinct class with label c from a set of application-specific classes $c\in \mathcal{C}$ corresponding to, for example, tissue types. The number of classes corresponds to the set cardinality $\left|\mathcal{C}\right|$. Independently of a particular application’s specific representation of the data, the task of classification using a dictionary D reduces to assigning a class label to all data samples y, which involves solving either Equation 2 or 3 for the sparse coding vector $\widehat{x}$.

For classification, dictionaries can take two forms: (a) intraclass dictionaries, in which a dictionary represents data from a single class c, which we denote as D^c, and (b) interclass dictionaries, in which a dictionary represents data from all possible classes in $\mathcal{C}$. On the basis of these dictionary forms, classification may be performed in one of two ways. First, in the case of intraclass dictionaries, a classification can be made using the data residual reconstruction error:

$$R^c={\Vert y-D^c\widehat{x}\Vert }_2,\forall c\in \mathcal{C},\widehat{c}=\text{arg}\underset{c}{\text{\hspace{0.17em}min}}{R}^c,$$ 7.

where the final class assignment $\widehat{c}$ is made by choosing the class that minimizes these residuals. Here, it is assumed that a data vector will belong to the class best represented by that class’s specific dictionary, that is, the class with minimum residual error. Sections 4.1 and 4.2 demonstrate applications using this method of classification. Additional constraints can be added in order to increase the discriminative power of the dictionaries (59).

Second, in the case of interclass dictionaries, a classification can be made using the sparse coding vector $\widehat{x}$ itself. In its simplest form, a matrix $W\in {ℝ}^{\left|\mathcal{C}\right|\times m}$ can be defined as a set of linear classifier parameters that maps any coding vector $\widehat{x}$ onto a label vector $h\in {ℝ}^{\left|\mathcal{C}\right|}$:

$$\widehat{h}=W\widehat{x},\widehat{c}=\text{arg}\underset{c}{\text{\hspace{0.17em}max\hspace{0.17em}}}{\widehat{h}}_c.$$ 8.

Here, the nonzero values in the label vector h indicate membership in the cth class; for instance, a labeling with a single nonzero value h = [0, 0, … , 1, … , 0, 0] indicates unique class membership in the cth class, and the final class assignment $\widehat{c}$ is given to the class with maximum membership value. The assumption is that the classes will be clustered in the space of the coding vector. Section 4.3 demonstrates an application of this method of classification.

3.5. Sparsity in Deep Learning

For many medical image analysis tasks, deep learning is becoming the dominant approach. An increasing number of large data sets are becoming available for training, and investigators are looking toward learning strategies based on multilayer or deep data-driven neural networks to incorporate this information in effective ways (28). Many approaches to deep learning exist, and there are many ways of incorporating sparsity that aim to reduce the number of nonzero-weighted neurons. Sparsity may lead to more efficient networks and has potential benefits in terms of information disentangling, control of the effective dimensionality of the representation, and easier separability (60). Perhaps the simplest method to incorporate sparsity is to set neuron weights to zero during training if they are below a designated threshold and therefore are inactive (61). In this way, a large network can be pruned, thus reducing the size of the model for greater efficiency, reduced redundancy, and potentially improved performance.

The choice of nonlinear activation function can also influence network sparsity. The use of rectified linear units (ReLUs) tends to create sparse networks with many inactive neurons (60, 62). Unlike other activation functions, such as sigmoids, hyperbolic tangents, or leaky ReLUs, when the input to the ReLU is less than zero, the output is clamped to zero, leading to more inactive neurons and sparser networks.

Sparsity constraints can also be imposed via the cost function. For example, the sparse autoencoder is an unsupervised method of seeking a compressed representation via a hidden layer in a network that attempts to reproduce its input; that is, it seeks an identity function (63). Typically, the size of the hidden layer is small so that a compact structure can be imposed on the hidden representation. However, a sparsity constraint can be imposed by augmenting the cost function with a term that seeks to, for example, have the average activation equal to a target small value, forcing many units to be inactive. Sparsity within the hidden units of autoencoders has been encouraged by penalizing deviation from a target activation ρ (in this case, ρ = 0) measured by the Kullback–Leibler divergence (64). Alternatively, sparsity can be imposed by using an ℓ₁ norm on the network weights (65). The resulting representation can then be used, for example, as input to a classifier for segmentation (66). This LASSO-style approach can also be applied to convolutional networks in a sparse group LASSO objective (67).

Another mechanism that imposes sparsity on a network is by way of dropout. The idea behind dropout is to randomly select a number of the neurons at each stage of training (as many as 80%) and set the corresponding weights to zero (68). The primary goal is to avoid overfitting by making the network less dependent on any particular node and more robust, especially when the training data set is small. Srivastava et al. (68) found that, as a side effect of dropout, the activations of the hidden units became sparse, even when no explicit sparsity-inducing regularizers were present. These authors studied autoencoders and looked at the sparsity of hidden unit activations. In addition, they used ReLU activation functions with and without dropout and found that dropout significantly increased sparsity in the resulting networks.

Papyan et al. (69) developed an interesting connection between sparse modeling via dictionaries and CNNs. They formulated a multilayer convolutional sparse coding (CSC) method by using dictionaries of intensity patches. Both CNNs and the CSC method are based on a convolutional structure, and both use data-driven models. These authors showed how their sparse coding method corresponds to the forward pass evaluation of the CNN.

It is possible to integrate neural network approaches and sparse dictionary learning. Using an encoder–decoder neural network formulation with a sparsity-inducing logistic module in between, Poultney et al. (70) learned effective sparse representations for subsequent processing. For tissue classification in liver images, Ben-Cohen et al. (71) used a fully convolutional network followed by dictionary-based fine-tuning. The sensitivity of the neural network alone was similar to that of the combined approach. However, the combined approach had improved specificity. Thus, the two methods worked synergistically to obtain a more robust solution.

4. KEY APPLICATION EXEMPLARS

We highlight five examples that illustrate the use of sparse representations for a diverse range of applications within biomedical image segmentation. We start in Section 4.1 by describing a dynamical appearance model (DAM) based on sparse representation and dictionary learning for tracking both endocardial and epicardial contours of the left ventricle in echocardiographic sequences (72–74). Here we exploit the inherent spatiotemporal coherence of individual data to constrain cardiac contour estimation. The contour tracker uses multiscale sparse representation of local image appearance and learns online multiscale appearance dictionaries in a boosting framework as the image sequence is segmented frame by frame sequentially. In Section 4.2, we present a method to segment the cortical brain surface in postoperative CT imaging. In this challenging application, image patches are oriented on the basis of the local evolving surface geometry in order to develop an efficient patch dictionary that exploits the consistency of appearance at the surface of the brain (75). This oriented appearance model, built from a clinical training sample, is invariant to rotational changes in the surface. From these patches, a sparse representation of the brain cortical surface appearance is determined in a dictionary-learning framework to model textural appearance near the surface boundary. In Section 4.3, we describe a method for sparse dictionary learning with atlases for brain segmentation (76, 77), an important current topic in neuroimage analysis. Next, in Section 4.4, we examine sparsity in global shape representation for boundary-based modeling. In global models, more complete shapes can be represented, and the sparse data matrix is learned by observing entire shapes of object boundaries in two or three dimensions. Finally, in Section 4.5, we look at the use of data-driven, deep learning of multiscale image patches for tissue classification from multiparameter MRI (mpMRI) data for liver cancer diagnosis and treatment evaluation (78).

For each of these applications, the segmentation performance of sparse representation learning is compared with that of alternative, nonsparse methods. Comparisons are made with conventional algorithms that do not employ sparse coding techniques, and in two cases, the effectiveness of sparse coding (Section 4.3) or sparsity-inducing strategies (Section 4.4) is directly compared with that of representation learning without the sparsity constraint. Throughout this section, segmentation performance is evaluated with respect to expert human-rater manually annotated ground truths. The state-of-the-art quantitative evaluation, and the most popular in the medical image analysis literature, involves computing the Dice overlap measure or various surface point distance metrics, such as the Hausdorff distance. All examples included here make use of one or more of these metrics to provide a clinically meaningful validation with respect to clinically relevant ground truth annotations. The quantitative and qualitative visual results that follow demonstrate the effectiveness of sparsity for data-driven segmentation across a diverse set of biomedical imaging applications.

4.1. Multiple Tissue Class Dictionaries and Sparsity for Left Ventricle Segmentation from Echocardiography

In this section, we discuss a DAM based on sparse representation and dictionary learning for segmenting the endocardial and epicardial surfaces of the left ventricle from echocardiographic sequences (Figure 1) (6), often used as a first step in cardiac motion (e.g., 79, 80) and strain estimation (81). Instead of learning off-line spatiotemporal priors from databases, as might be done in more global appearance-based modeling, this model exploits the inherent spatiotemporal coherence of individual data in order to constrain cardiac surface estimation.

Figure 1.

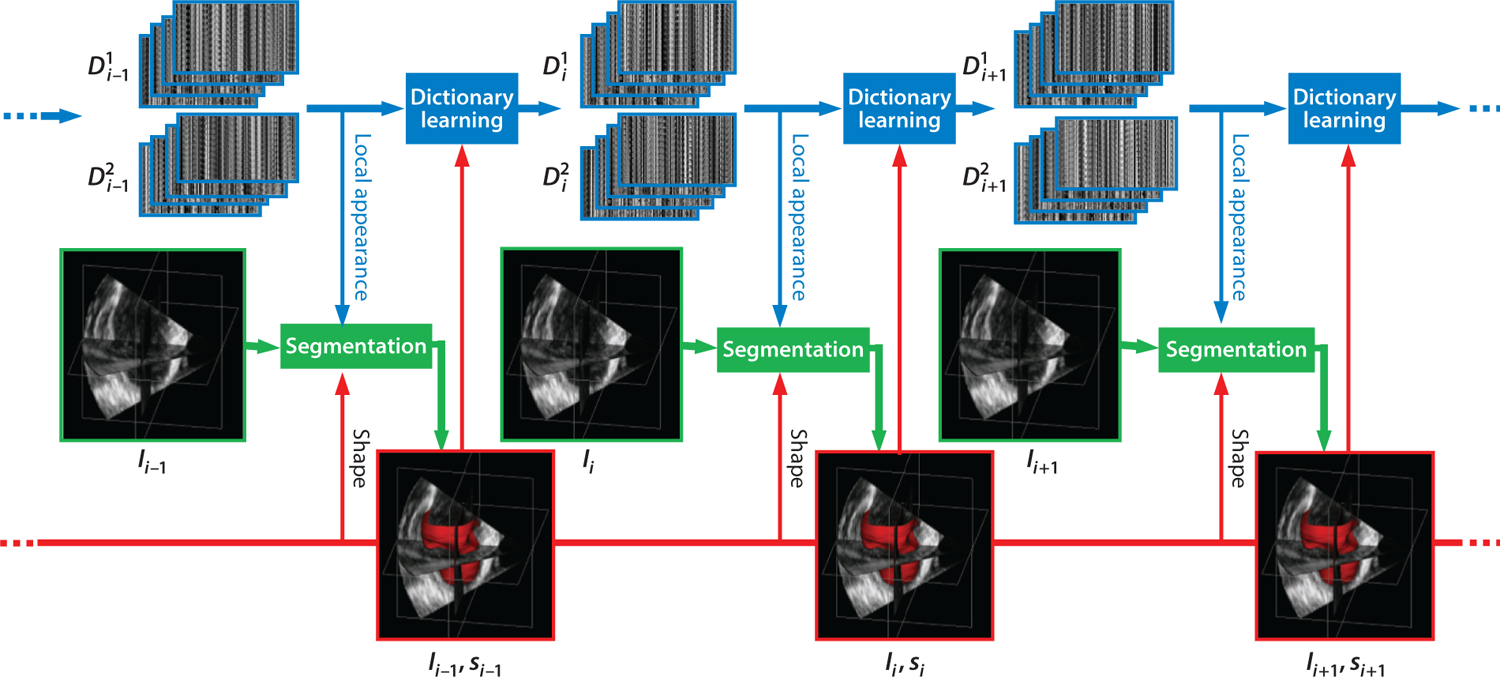
Dynamical dictionary updating interlaced with sequential segmentation. I_i is the image of frame i, s_i is the segmentation of frame i, and $D_i^j$ represents multiscale appearance dictionaries for class j in frame i. Figure adapted from Reference 6 with permission from Elsevier.

For this application, individual class dictionaries are learned and established at sequential time frames for different tissue types for a single subject, given a manual segmentation initialization at the first time frame. The algorithm leverages a variety of complementary information, including intensity, multiscale local appearance, and shape. A multiscale sparse representation of high-dimensional local image appearance is used to encode local appearance patterns with multiscale appearance dictionaries. An online multiscale appearance dictionary learning process is interlaced with sequential segmentation. The local appearance of each frame is predicted by a DAM in the form of multiscale appearance dictionaries based on the appearance observed in the preceding frames. As the frames are segmented sequentially, the appearance dictionaries are dynamically updated to adapt to the latest segmented frame. The multiscale dictionary learning process is supervised in a boosting framework to seek optimal weighting of multiscale information and to generate dictionaries that are both reconstructive and discriminative. Sparse coding with respect to the predictive dictionaries produces a local appearance discriminant that summarizes the multiscale discriminative local appearance information. This method includes both intensity and a dynamical shape prediction to complete the complementary information spectrum that is incorporated into a region-based level-set segmentation formulation in a maximum a posteriori framework.

In this approach, the basic strategy begins with the sparsity equations described above in Section 3. However, the equations are modified to leverage the complementary multiscale local appearance information, which leads to describing the pixel u ∈ Ω as a series of appearance vectors $y_t(u)\in {ℝ}^n$ at different appearance scales at time point t. To obtain this multiscale information, one can extract local images of different physical sizes from images that are smoothed to different degrees. The local images are then subsampled to construct appearance vectors.

Key to this algorithm, and the most relevant point for this review, is sparse learning of separate appearance dictionaries for the blood pool and the myocardium from each frame of the echocardiographic image data. Considering appearance at a single scale as the initial example, suppose that $D_t^1$ and $D_t^2$ are two dictionaries adapted to appearance classes ${\Omega }_t^1$ and ${\Omega }_t^2$, respectively (e.g., blood pool and myocardium). They exclusively span, in terms of sparse representation, the subspaces of the corresponding classes; that is, they can be used to reconstruct typical appearance vectors from the corresponding classes. As introduced in Section 3.4, the reconstruction residuals $R_t^c(u)$ for an appearance vector can be found using Equation 7 for each class, and it is logical to expect that $R_t^1(u)>R_t^2(u)$ when $u\in {\Omega }_t^2$, and $R_t^1(u)<R_t^2(u)$ when $u\in {\Omega }_t^1$ (6). This observation establishes a key basis of sparse representation–based discrimination.

On the basis of this discrimination strategy, Huang et al. (6) developed a local appearance discriminant A_t between two learned dictionaries (blood pool and myocardium), which is used to create a class adherence probability term, p(A_t|Ф_t), where Ф_t is a level-set function. This term is incorporated into a level-set boundary finding optimization functional, which when solved estimates the zero level set that segments the endocardial or epicardial boundary of the left ventricle. In this study, the local appearance discriminant A_t(u) combines complementary multiscale information by learning a series of dictionaries at different scales, and indicates the likelihood that the point u is inside or outside the shape of interest. To obtain this appearance discriminant, Huang et al. (6) leveraged the inherent spatiotemporal coherence of individual data to introduce an online learning process that dynamically adapts multiscale dictionaries to the evolving appearance when the image sequence is segmented sequentially, as illustrated in Figure 1.

Three issues are important in this setting. First, the true distribution underlying the appearance Y is not known. A uniform distribution is usually assumed to place equal emphasis on all the training examples. There are harder and easier parts of the appearance space, and more emphasis should be placed on the harder part so as to enforce the learned dictionaries to include the most discriminative patterns. The relatively easier and harder parts can differ at different appearance scales. Second, the generic dictionary learning formulation in Equation 6 gets trapped in a local minimum and learns only the scale that corresponds to the size of local images (82). Huang et al. (6) decompose the multiscale information into a series of appearance dictionaries, each of which is learned at a single scale. Third, the weighting of different appearance scales needs to be optimized in order to achieve the best joint discriminability of the multiscale dictionaries.

In order to address the above issues and further strengthen the discriminative property of the learned appearance dictionaries, a boosted multiscale appearance dictionary learning process supervised in an AdaBoost (83) framework was proposed (6). The boosting supervision strengthens the discriminative property and optimizes the weighting of multiscale information. In this setting, each pair of learned dictionaries is taken as a weak learning process making a weak hypothesis, wherein each weak learner faces a different distribution of the data that is updated on the basis of the error made by the preceding weak learners. Here, the first weak learner makes the initial guess that the data obey a uniform distribution. The appearance scale varies across the weak learners such that the error made at a certain scale can hopefully be corrected at the other scales. The weighting parameters of the multiscale information are optimized automatically through this boosting process. The coarser-scale dictionaries encode higher-level anatomical patterns, while the finer-scale dictionaries encode lower-level speckle patterns. Finally, all of these weak learners are combined to reach a strong hypothesis.

This approach was validated on 26 four-dimensional (4D) canine echocardiographic images acquired from both healthy and postinfarct canines. The segmentation results agreed well with expert manual tracing (Figure 2) (Table 1). Advantages of this approach are demonstrated by comparisons with conventional, nonsparse methods, such as a pure intensity model using a maximum likelihood estimation and a Rayleigh distribution model (84) or a database-dependent off-line subject-specific dynamical shape model (SSDM) (85). The level-set strategy that incorporates the sparse dictionary learning appearance residuals approach (DAM) outperforms the other approaches in terms of endocardial and epicardial segmentation.

Figure 2.

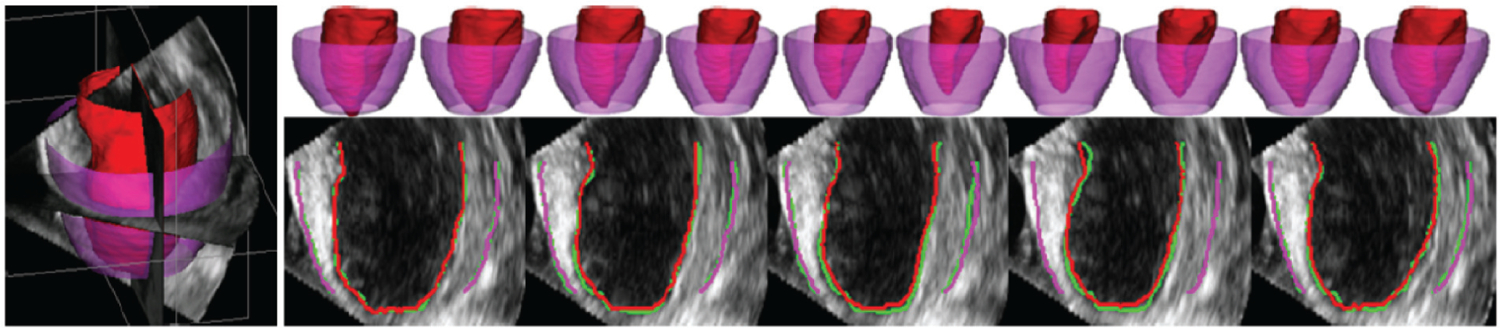
Typical segmentations of endocardium (red) and epicardium (purple) from four-dimensional echocardiography using the dynamical appearance model approach based on sparse dictionary learning. Two-dimensional slices through three-dimensional results show a comparison between expert manual tracing (green) and the algorithm, with excellent concordance. Figure adapted from Reference 6 with permission from Elsevier.

Table 1.

Quantitative comparison of N = 26 canine 4D echocardiographic data sets to expert manual segmentation of Rayleigh, DAM, and SSDM approaches^a

	Approach	Dice (%)	PTP (%)	MAD (mm)	HD (mm)
Endocardial	Rayleigh	74.9 ± 18.8	83.1 ± 16.3	2.01 ± 1.22	9.17 ± 3.37
	DAM	93.6 ± 2.49	94.9 ± 2.34	0.57 ± 0.14	2.95 ± 0.62
	SSDMb		95.9 ± 1.24	1.41 ± 0.40	2.53 ± 0.75
Epicardial	Rayleigh	74.1 ± 17.4	82.5 ± 12.0	2.80 ± 1.55	16.9 ± 9.30
	DAM	97.1 ± 0.93	97.6 ± 0.86	0.60 ± 0.19	3.03 ± 0.76
	SSDMb		94.5 ± 1.74	1.74 ± 0.39	2.79 ± 0.97

^aMean ± standard deviation of voxel overlap (Dice), percentage of true positive voxels (PTP), mean absolute difference (MAD), and Hausdorff distance (HD).

^bMethodology utilizing sparsity.

Abbreviations: DAM, dynamical appearance model; SSDM, subject-specific dynamical shape model; 4D, four-dimensional.

Table adapted from Reference 6 with permission from Elsevier.

4.2. Sparse Orientation-Invariant Tissue Class Dictionaries for Brain Segmentation from Computed Tomography

In segmentation of the cortical brain surface in postoperative CT imaging, specific dictionaries are again learned or established for different tissue classes, but, in contrast to the application described in Section 4.1, these dictionaries are learned from a population of images and are intended to estimate intersubject segmentations for a set of test subjects (not only for a single, intrasubject segmentation). Here, the overall goal is to segment brain surfaces that will be useful for registering presurgical MRI images with postsurgical CT (as in 75), but similar ideas are useful for registering pre- and postimplant MRI (86) and in postsurgical brain shift compensation (e.g., 87–89). During these surgical procedures, neurosurgeons implant electrodes to monitor and localize abnormal electrical activity due to epilepsy, then use this information to plan further surgical procedures, as described in more detail by Onofrey et al. (75). While numerous surface-based, nonrigid registration methods exist (90, 91) to accomplish this task, the main challenge is the extraction of the cortical surface from the images. Methods for segmenting the brain surface from presurgical MRI exist (92); however, segmentation of postoperative CT images is challenging due to (a) large portions of the skull being removed for the craniotomy, (b) imaging artifacts caused by the implanted electrodes, (c) the most likely non-Gaussian appearance of the brain surface, and (d) the variability in the location of the craniotomy across patients, which can confound global models of appearance (25).

To segment the cortical brain surface in postoperative CT imaging, a dictionary learning framework learns a sparse representation of the brain cortical surface appearance (Figure 3). Similar to the dictionary learning approach presented in Section 4.1, this framework models textural appearance of two tissue classes, in this case, the inside and the outside of the cortical surface boundary. Here, dictionaries modeling the locally oriented image appearance based on the geometry of an evolving cortical surface estimate discriminate the appearance around the boundary. The method extracts locally oriented image patches for all points on the segmentation surface estimate, $u\in \widehat{S}$, and transforms these patches into an appearance vector, y(u). As done in Equation 7 (Section 3.4), the appearance model residuals R^c(u) are computed for each class $c\in \mathcal{C}=\left\{\text{ in, out }\right\}$. In contrast to the research described in Section 4.1, the difference between the residual values, D(u) = R^out(u) − Rⁱⁿ(u), drives the evolution of the segmentation surface estimate. Intuitively, if u lies within the true boundary of the cortical surface in the CT image, then D(u) > 0, and if u, in contrast, is outside the true boundary, then D(u) < 0. The cortical surface boundary is thus located at the point where D(u) = 0; in other words, the dictionaries cannot determine to which class the local patch belongs. Finally, to segment the cortical surface in the CT image, the method minimizes the objective function $\widehat{S}={\text{min}}_S{\int }_S\parallel D{\parallel }_2^2\text{d}S$.

Figure 3.

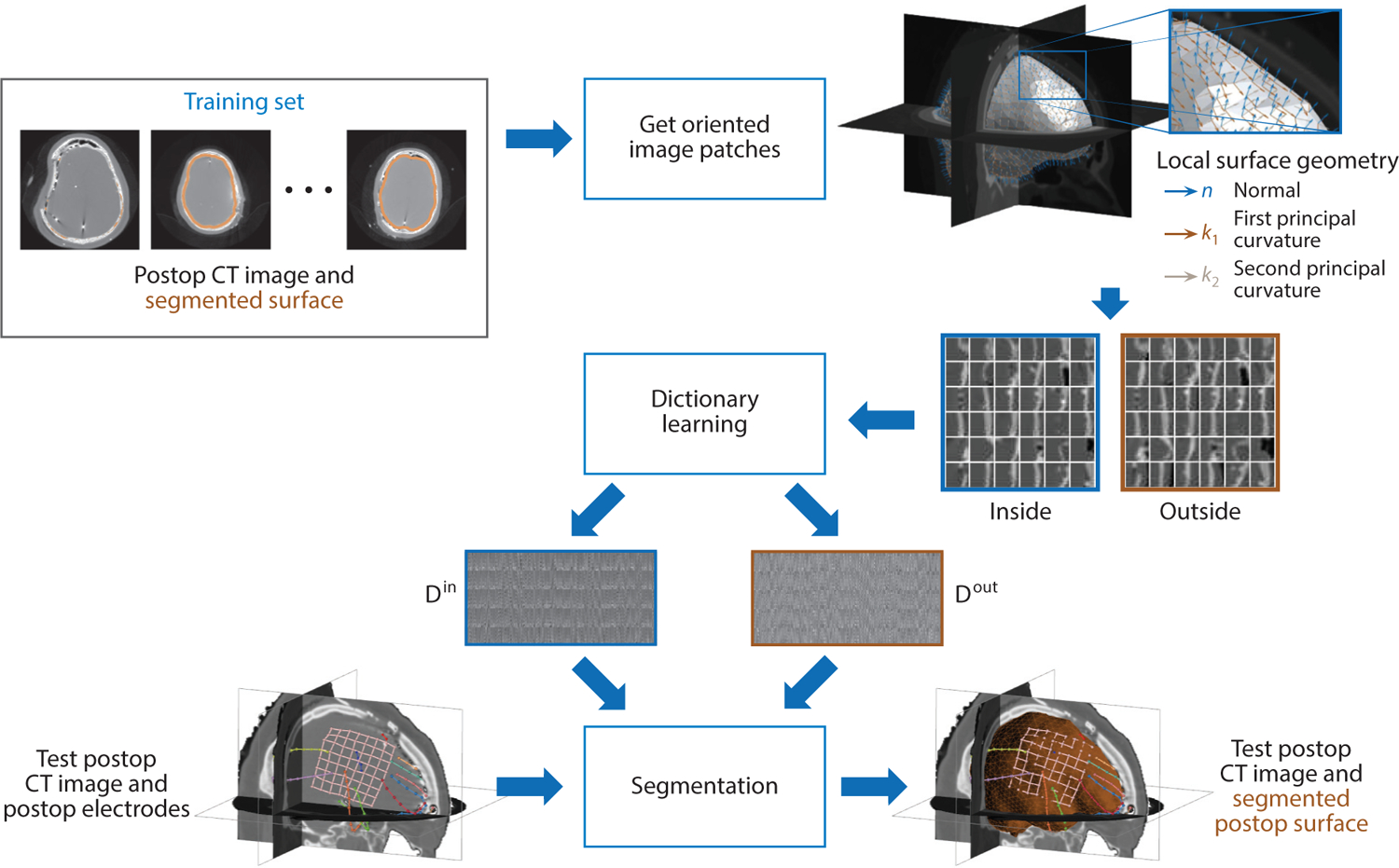
Dictionary learning is used to learn a sparse appearance model in order to segment the cortical brain surface in postsurgical computed tomography (CT) images in epilepsy patients. Image patches are oriented according to the surface’s local differential geometry, and the appearance both inside and outside the brain surface is used to train two dictionaries of appearance from a set of training data. The dictionary models are then used to drive the segmentation process of the cortical surface in test postop CT images.

In contrast to the research described in Section 4.1, which uses image patches canonically aligned with the image axes, this approach uses locally oriented image patches along the evolving segmentation surface. By orienting the image patches with respect to the differential geometry of the surface, the oriented appearance model is invariant to rotational changes in the surface. Furthermore, rather than creating unique intrasubject appearance models for each subject, this approach builds an intersubject appearance dictionary using a population of clinical training data.

Experimental results using clinical images from 18 epilepsy patients who had surgically implanted electrodes demonstrate the accurate segmentation of the cortical surface using dictionary learning of oriented image appearance. The oriented patch dictionary segmentation method is compared with a standard multiatlas registration-based segmentation method as well as a deep CNN approach. Results show accurate cortical surface segmentation in CT images (Figure 4), and quantitative results (Table 2) show significantly more accurate segmentation in the area of the electrodes, which is the region of greatest clinical interest. In comparison to the other tested segmentation methods, the local patch-based sparse dictionary learning approach offers practical advantages for medical imaging data sets that have low sample sizes. In this specific application, the dictionary appearance model can accommodate heterogeneous appearance better than global models of appearance, such as atlas-based segmentation, because surgical site location is specific to each patient and not enough training data exist to span all possible craniotomy locations. The dictionary model is also of much lower dimensionality; for instance, a dictionary with n = 256 atoms and 5³ image patches at three image scales required a total of 96,000 parameters, in contrast to the tested deep CNN, which had more than 22 million parameters. Finally, for applications such as surgery that require a high level of trust in the algorithmic results, the easy interpretability of the learned dictionary atoms contrasts with the difficulty in analyzing the features of a CNN’s hidden layers.

Figure 4.

An example of postsurgical computed tomography cortical surface segmentation results for a single subject using sparse dictionary learning of locally oriented image appearance (blue contour) compared with ground truth segmentation (yellow contour). Arrows indicate accurate cortical surface segmentation at the areas of the implanted surface electrodes near the site of the craniotomy, which is the region of greatest clinical interest. Axial images progress from the bottom of the head (left) to the top (right).

Table 2.

Segmentation evaluation quality measures comparing sparse dictionary learning–based segmentation of the cortical surface to the initial surface estimate, atlas-based segmentation, and a deep CNN^a

Method	Dice (%)	MHD (mm)	MAD (mm)	MESD (mm)
Initial estimate	93.47 ± 1.86	8.09 ± 2.50	3.76 ± 0.68	1.66 ± 0.84
Atlas-based	94.21 ± 1.77	6.81 ± 2.46	3.20 ± 0.70	2.51 ± 1.06
Deep CNN	95.00 ± 1.18	7.00 ± 2.71	2.94 ± 0.44	1.11 ± 0.61
Oriented dictionaryb	94.87 ± 1.05	6.75 ± 2.39	3.23 ± 0.43	0.87 ± 0.24

^aValues are expressed as mean ± standard deviation of voxel overlap (Dice), a modified version of the Hausdorff distance (MHD) that uses the ninety-fifth-percentile distance, mean absolute difference (MAD), and mean electrode to surface distance (MESD), which measures the distance from the surface electrode to the segmentation for the surface electrodes closest to the region of greatest clinical interest (the site of the craniotomy). Bold entries indicate the best-performing method.

^bMethodology utilizing sparsity.

Abbreviation: CNN, convolutional neural network. Table adapted from Reference 75 with permission from IEEE.

4.3. Sparse Dictionary Learning with Atlases for Magnetic Resonance Imaging Brain Segmentation

In sparse dictionary learning with atlases for brain segmentation, and similar to the task discussed in Section 4.2, sparse coding of a collection of labeled images from a population of training data is used to perform segmentation of a test image for a new test subject, in this case segmenting anatomical brain structures in MRI data. This approach is useful in a variety of neuroimaging analysis problems, including those related to both structural and functional biomarker measurement. Here, patch-based sparse appearance learning is used to segment a test subject image by trying to match patch-based features to a set of similar-looking patches found in a set of atlases. The idea is that a patch-based learning problem is posed where weights are sparse and their values are large when the test subject patch matches the correct atlas patch. This method was initially proposed by Tong et al. (76) for two label classes (hippocampus and background) and was then generalized by Roy et al. (77) to include multiple classes (gray matter, white matter, and cerebrospinal fluid). This application contrasts with the previous two (Sections 4.1 and 4.2) in two ways. First, this approach creates separate local appearance dictionaries for each voxel in the test image, as opposed to the other methods, which use global dictionaries of appearance that apply to the whole image domain. Second, the dictionaries in this application contain appearance samples that are representative of all classes of interest (interclass dictionaries), whereas the previous methods utilize separate dictionaries for each class of interest (intraclass dictionaries). In this manner, classification (and the resulting segmentation) is performed on the appearance dictionary’s sparse coefficients instead of on the reconstructed appearance representation. The intuition behind this approach is that, for a given dictionary size, intraclass dictionaries are better suited for global patch-based appearance modeling, wherein appearance is relatively homogeneous within a class throughout the global image domain, whereas interclass dictionaries are better suited for local patch-based appearance modeling because these dictionaries must contain information from a variety of classes that may have an increasingly heterogeneous appearance outside of the local spatial neighborhood.

Inspired by facial recognition research from the computer vision community (32), atlas-based segmentation (Figure 5) is developed in two different ways (76). The first approach, termed sparse representation classification (SRC), uses a dictionary based on a large number of training patches selected from a subset of most similar atlas images. Sparse coding is used to select the most representative patches in the dictionary using Equation 5. Similar to the application in Section 4.1, dictionary reconstruction residual error is used to discriminate class membership, with segmentation performed by selecting the class label with minimal residual (or reconstruction) error (see also Section 3.4). The second strategy, termed discriminative dictionary learning for segmentation (DDLS), attempts to exploit discriminative information in the training patch library by learning a small-sized, (discrimination) task-specific dictionary. This approach adds a linear classifier, f (x, W) = Wx, to the objective function for learning dictionaries that contain the ability to both reconstruct patches and determine to which class a patch belongs (93). The objective function modifies the dictionary learning function in Equation 6 to include two ℓ₂ norms subject to sparsity:

$$\widehat{D},\widehat{W}=\text{arg}\underset{D,\mathbf{W},X}{\text{min}}\parallel Y-DX{\parallel }_2^2+{\beta }_1\parallel H-WX{\parallel }_2^2\text{ s.t. }\forall i,{\Vert x_i\Vert }_0\le \Gamma ,$$ 9.

where $W\in {ℝ}^{\left|\mathcal{C}\right|\times m}$ is the linear classifier parameter and each column of a matrix $H=\left[h_1,\dots ,h_m\right]\in {ℝ}^{\left|\mathcal{C}\right|\times m}$ is a vector h_i corresponding to the central voxel label of the atlas template patch with C different classes. Nonzero entry positions in the vector h_i = [0, 0, … , 1, … , 0, 0] indicate the class label of the data sample y_i surrounding the central pixel or voxel of the patch as belonging to the jth class. In this application, $\mathcal{C}=\left\{\text{ hippocampus, background }\right\}$ with cardinality $\left|\mathcal{C}\right|=2$. Using the set of labeled training atlases, this equation is solved using the method proposed by Mairal et al. (57) to learn a dictionary, $\widehat{D}(u)$, and classifier, $\widehat{W}(u)$, for every possible target voxel u ∈ Ω in the target image. To segment a target voxel, the sparse representation of the target $\widehat{x}(u)$ is found by solving $\widehat{x}(u)=\text{arg}{\text{\hspace{0.17em}min}}_{x(u)}\parallel y(u)-\widehat{D}(u)x(u){\parallel }_2^2+{\beta }_2\parallel x(u){\parallel }_1$ using Equation 5. Finally, the label value of the target voxel $\widehat{c}(u)$ is found from the linear predictive classifier, as in Equation 8.

Figure 5.

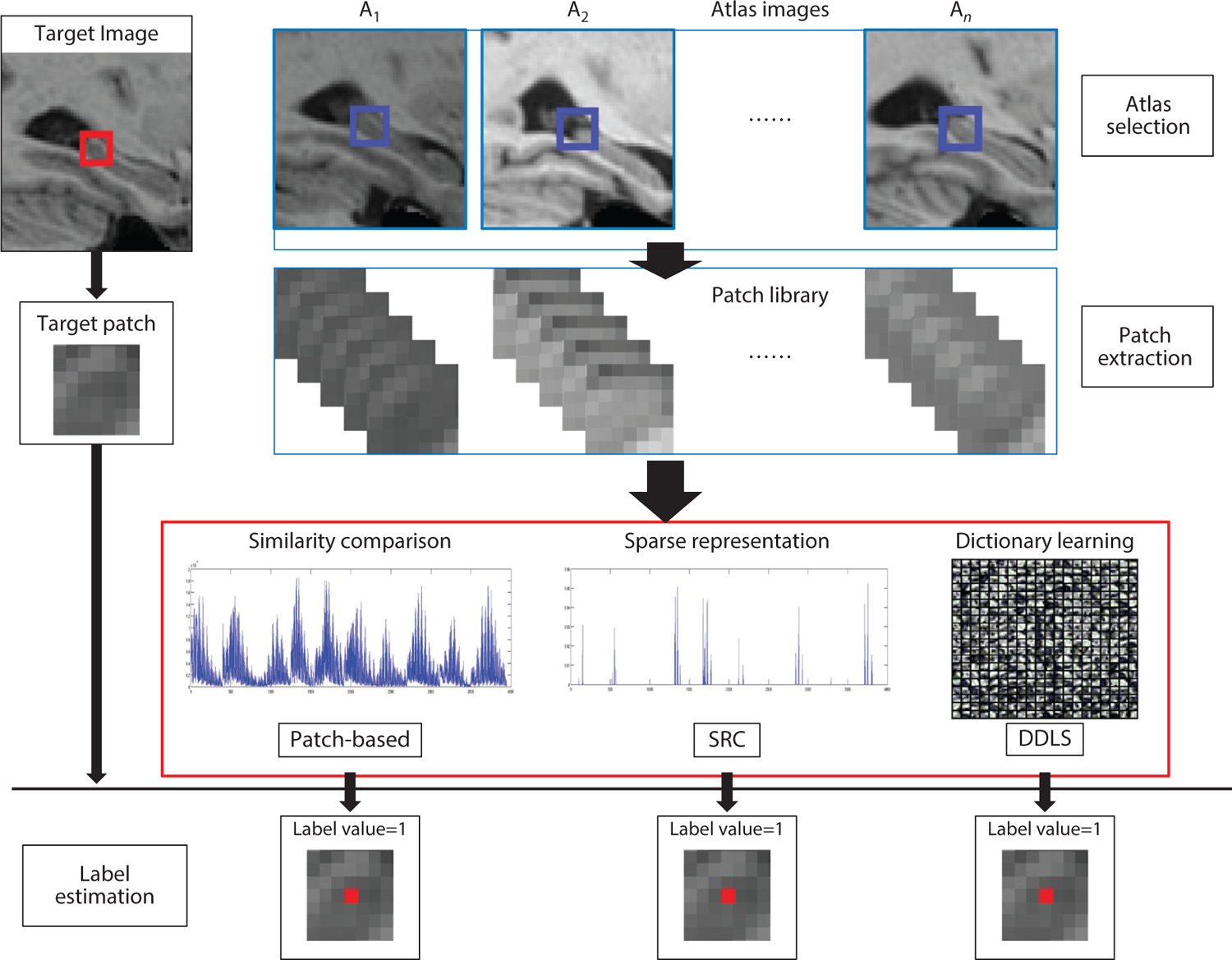
Flow chart of the SRC and DDLS methods (76). One target voxel is labeled by three different methods: patch-based labeling, SRC, and DDLS. The red box in the target image represents the target patch. The blue boxes in the atlas images represent the search volume area for extracting template patches. Abbreviations: DDLS, discriminative dictionary learning for segmentation; SRC, sparse representation classification. Figure adapted from Reference 76 with permission from Elsevier.

The abovementioned sparse segmentation approaches learn subject-specific, voxel-wise dictionaries for multiple classes from a set of labeled atlas images that most closely match the target image in a form of online learning and segmentation. Alternatively, Mairal et al. (57) also propose learning fixed dictionaries off-line to be applied to more efficient online segmentation. In this scenario, fixed DDLS (F-DDLS) forms voxel-wise dictionaries from a subset of subjects in the training set, not only the most similar matching ones, and these dictionaries can be saved and then applied to segment target images.

Testing was performed using 202 T1-weighted MRI data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) data set (94) and 80 images from the International Consortium for Brain Mapping data set (95), with the goal of classifying hippocampus versus background. The sparse coding SRC, DDLS, and F-DDLS methods were compared with a more standard, nonlocal patch-based segmentation method (96) that performs a weighted classification of atlas patches (based on the Euclidean distance). All methods utilized patch sampling within a small, nonlocal 7 × 7 × 7 search window of the target patch. Preprocessing for each data set was performed (94, 96), all images were linearly registered to the MNI (Montreal Neurological Institute) 152 template space, and histogram matching (97) was used to normalize image intensities. For SRC, DDLS, and the patch-based method, the sum of squared differences of intensity values was used to select the 10 atlases most similar to each target image. Visual comparisons based on segmentation results for three of the methods from the ADNI data set are shown in Figure 6, which illustrates the better performance of the sparse coding appearance methods (both SRC and DDLS) compared with the patch-based strategy, indicating the promise of such approaches for atlas-based segmentation. Results in terms of Dice overlap coefficients for finding the right, left, and entire hippocampus using all methods are shown in Table 3, quantifying the potential advantages of the methods on the basis of sparsity. Notably, the atlas selection strategy offered small improvements over F-DDLS. The sparse dictionary learning methods also demonstrated computational efficiency compared with conventional, nonsparse, patch-based segmentation (Table 3). Roy et al. (77) extended all of this research to multiple classes and applied it to whole-brain tissue segmentation in normal subjects as well as to multiple sclerosis lesion segmentation, both from T1-weighted anatomical MRI.

Figure 6.

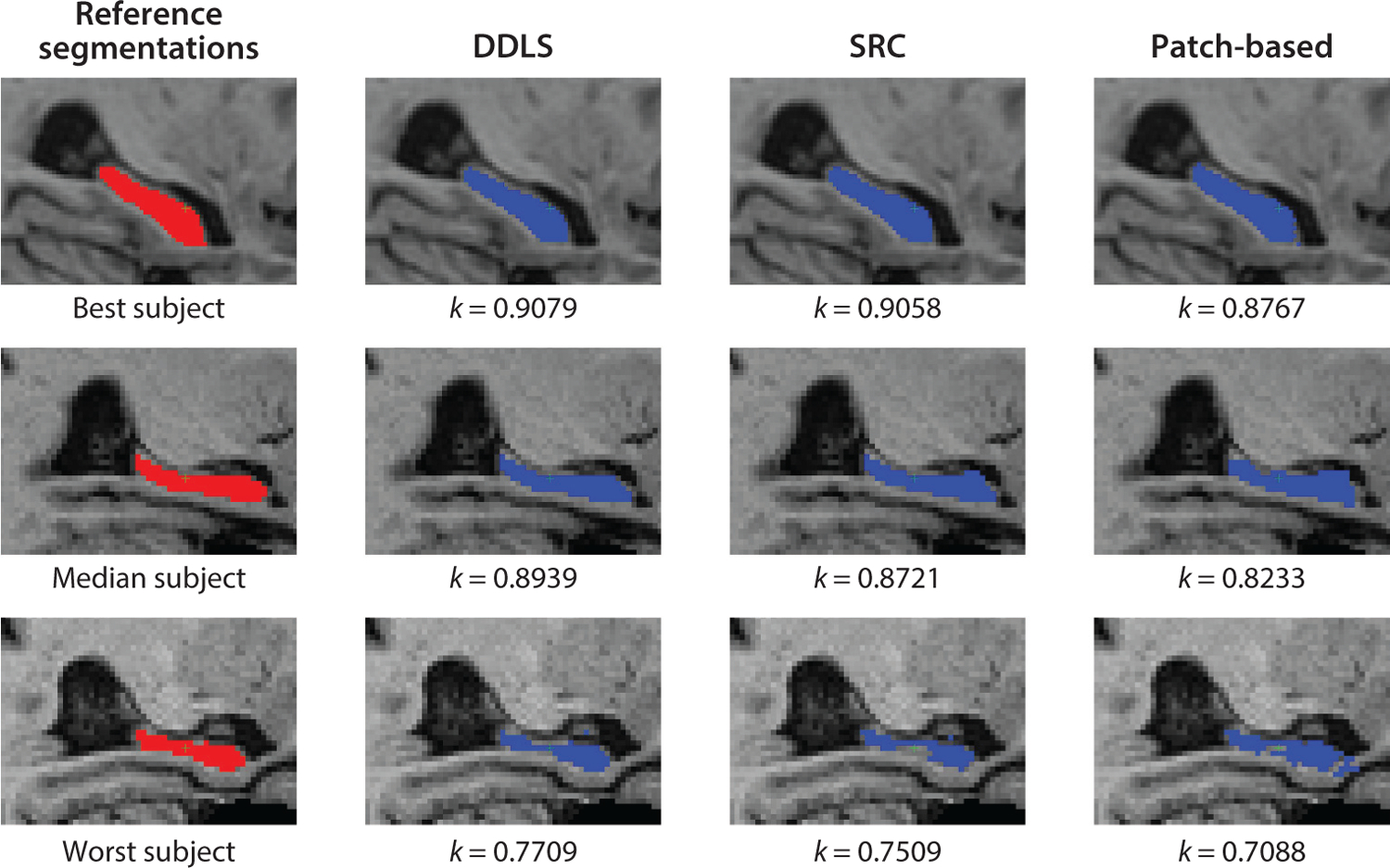
Method comparison. Segmentation results were obtained by DDLS, SRC, and the patch-based method for the subjects from the ADNI data set, with the best-case, median, and worst-case Dice coefficient results depicted. Abbreviations: ADNI, Alzheimer’s Disease Neuroimaging Initiative; DDLS, discriminative dictionary learning for segmentation; SRC, sparse representation classification. Figure adapted from Reference 76 with permission from Elsevier.

Table 3.

Median Dice overlaps for 202 ADNI subjects using different approaches^a

Method	Left hippocampus	Right hippocampus	Whole hippocampus	Time
Patch-based	0.848	0.842	0.844	10 min
SRCb	0.873	0.869	0.871	40 min
DDLSb	0.872	0.872	0.872	3–6 min
F-DDLSb	0.865	0.859	0.864	<1 min

^aThe numbers in bold represent the highest Dice overlaps among different methods. All three sparse coding methods (SRC, DDLS, and F-DDLS) outperform standard nonlocal patch-based classification. The sparse dictionary learning methods are also computationally efficient compared with conventional, nonsparse patch-based segmentation. Bold entries indicate the best-performing method.

^bMethodology utilizing sparsity.

Abbreviations: ADNI, Alzheimer’s Disease Neuroimaging Initiative; DDLS, discriminative dictionary learning for segmentation; F-DDLS, fixed DDLS; SRC, sparse representation classification.

4.4. Sparsity in Global Representations: Representations of Boundary Shape and Boundary-Based Local Appearance Modeling

Many of the applications discussed in this review concern sparse representations of image intensity or image appearance–based information. Sparsity in medical image analysis, especially regarding segmentation, can also be advantageous in object boundary representations. In this section, we describe a primary example of this type of approach, from work by Zhang et al. (98). These authors used a sparse shape composition (SSC) method in which an explicit shape representation [either a two-dimensional (2D) curve or a three-dimensional (3D) triangular mesh] is formed using the coordinates of a set of vertices that define the shape. For each object i, the coordinates are concatenated into a single shape vector, $d_i\in {ℝ}^n$, where n is the product of the number of vertices in a shape multiplied by its spatial dimension. A training depository (or, as above, dictionary) of shapes can be represented as $D=\left[d_1,d_2,\dots ,d_m\right]\in {ℝ}^{n\times m}$. In this framework, any input shape y can be approximately represented as a weighted linear combination of shapes (or shape data) existing in the database d_i, i = 1, 2, … , m, where $x=\left[x_1,x_2,\dots ,x_m\right]\in {ℝ}^m$ are the coefficients or weights and m is the number of shapes. Unique to this approach is the idea that a set of sparse, gross errors in a contour or surface boundary can be incorporated by modeling an error vector, $e\in {ℝ}^n$. Equation 2 can then be modified to model both a sparse linear combination and a sparse error for outliers to find this solution:

$$\text{arg}\underset{x,e,\beta }{\text{\hspace{0.17em}min}}\parallel T(y,\theta )-Dx-e{\parallel }_2^2,\text{\hspace{1em} s.t. }\parallel x{\parallel }_0\le {\Gamma }_1,\parallel e{\parallel }_0\le {\Gamma }_2,$$ 10.

where Г₁ is the predefined sparsity number for x and Г₂ is the sparsity number for e, which captures the sparse but large errors caused by occlusion or missing points at particular locations (vertices) in a model instance. Furthermore, we note that, in this equation, T (y, θ) is the global transformation operator with parameter θ that aligns the input shape y to the mean of the existing data repository D.

Testing was performed on a variety of data sets related to several different clinical problem areas, including 2D lung localization from X-ray images and 3D liver segmentation from low-dose CT, as described by Zhang et al. (98) and in follow-on research by Wang et al. (99). The latter group (99) further developed the sparsity strategy to simplify the solution by stacking the e and x vectors into a single new vector (x′) that could be set up as a one-variable sparsity term. We show an example result for the liver segmentation problem using this sparsity-driven, shape-based approach in Figure 7. In References 98 and 99, the clinical goal was to use the segmented CT surfaces to register to surfaces derived from positron emission tomography data for oncological diagnosis. A total of 67 low-dose CT scans were acquired and annotated by manual segmentation to provide ground truth. Of these, 40 were used for training, both to obtain the landmark data used to do the initial intra-CT shape model registration and to construct the data matrix/dictionary D. The other 27 data sets were used for testing. For training, a reference shape was chosen, and all other data sets were registered to it using a deformable model–based strategy (100). For matching to image gradient data for eventual test case estimation, the fitting of a deformable model based on Reference 101 was incorporated into the sparsity strategy. For both training and testing, each 3D shape had approximately 1,000 vertices, 20 of which were selected as landmarks for initial registration. Also, in this study the weighting parameters in these equations were set to λ₁ = 50 and λ₂ = 0.3 for all results. Table 4 quantitatively compares the SSC method with two other methods to localize liver surfaces. The two approaches whose results are reported in this table are (a) a shape model search approach that is a module within the popular active shape model (24) and (b) a standard thin-plate spline approach (102). Note that the SSC approach had the lowest overall mean voxel distance error (as well as the lowest overall standard deviation over the test cases) between the computed result and the manually segmented, ground truth result, demonstrating the potential power of this approach.

Figure 7.

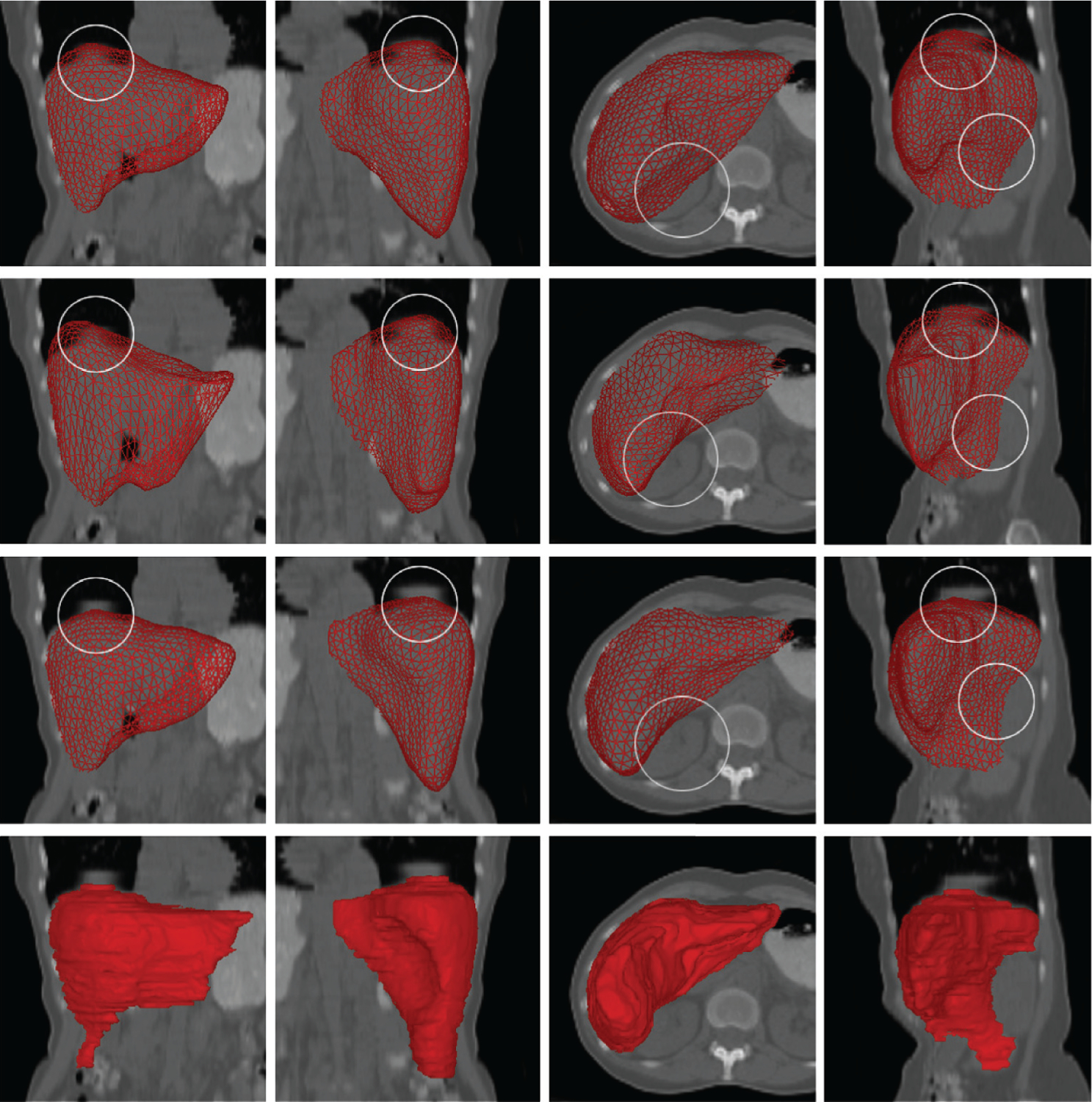
Comparison between SSC liver segmentation from low-dose CT and segmentation approaches based on other shape models (all using the same training data). (First row) Procrustes analysis, rigid + scaling. (Second row) Thin-plate spline model using nonrigid deformation. (Third row) SSC and proposed algorithm. (Fourth row) Manual segmentation (ground truth). Note that the SSC results are closer to the ground truth. Areas marked by circles indicate differences where the other techniques failed, likely due to breathing artifacts. Each result was subsequently further deformed and refined. Abbreviations: CT, computed tomography; SSC, sparse shape composition. Figure adapted from Reference 98 with permission from Elsevier.

Table 4.

Quantitative comparisons of the distances (voxel-based) between algorithm-segmented surfaces and manually segmented ground truth for nonsparse and sparse approaches^a

Method	Mean distance (mm)
Shape model search	2.26 ± 1.72
Thin-late spline	2.92 ± 2.19
Sparse shape compositionb	1.31 ± 0.95

^aResults are reported as mean ± standard deviation. Bold font indicates the best-performing method.

^bMethodology utilizing sparsity.

Table adapted from Reference 98 with permission from Elsevier.

4.5. Tissue Classification via Deep Learning with Dropout Sparsity

The past several years have witnessed a significant trend toward the use of data-driven deep learning approaches to biomedical image segmentation. In this section, we discuss the use of CNNs based on a U-net-style (103) architecture to address tissue classification/segmentation from mpMRI related to liver cancer diagnosis and treatment targeting/evaluation (78). Network sparsity is incorporated through the use of ReLUs as the activation function and dropout layers applied during the training process.

Hepatocellular carcinoma (HCC) is the most common type of primary liver cancer and one of the deadliest cancers worldwide (104). mpMRI data sets contain multiple images from multiple magnetic resonance protocols that reveal different aspects of the tissue. mpMRI is commonly used as a diagnostic tool for suspected HCC cases and is important for defining treatment targets and predicting outcomes for a number of therapeutic strategies, including transarterial chemoembolization (TACE) (105). TACE treatment involves localized injection of embolytic agents that will help destroy the tumor. As a first step, the liver must be segmented from the background using 3D mpMRI and, for example, the strategy described in Section 4.4, above. It is then necessary to classify the liver tissue into its clinically relevant types: normal parenchyma, viable tumor tissue, and necrosis (dead or necrotic tissue).

Recent developments in the design of deep CNNs provide ways to construct powerful models that can learn to extract both low- and high-level features for accurate inference that are usually difficult to formulate with traditional methods (103). However, such models typically need a large quantity of training data with expert-curated labels, which are particularly expensive for this application because training requires 3D segmentation fully annotated by radiologists. To overcome these challenges, Zhang et al. (78) designed a model that classifies each local patch (or region) given a set of patches from the images. These patches are sampled at a fixed size, but with varying resolutions, in order to capture information from different scales efficiently. This model has an autocontext-based (106), multilevel architecture that, when coupled with a multi-phase training procedure, can effectively learn at different levels. The architectural and procedural design proposed by Zhang et al. (78) specifically includes regularization within the CNN using a patch-based learning scheme. This design includes the use of ReLU activation functions and the insertion of dropout layers to implicitly address network sparsity, as discussed above (see Section 3.5).

This study is one of the first to use a neural network approach to segment tissue types on mpMRI in HCC patients without the need to manually design image features, as was done previously (107). While deep CNNs have been developed for liver tumor segmentation from CT images (108, 109), the mpMRI problem faces additional challenges. Also, the coupling of an autocontext-based model and a multiphase training strategy encourages the model to use contextual information from the previous phase. This hierarchical combination of several predictive units outperforms a single U-net model given the available data, without overfitting. This methodology is generalizable to other detection and segmentation tasks in medical images where full image annotation is difficult to acquire.

In order to illustrate the utility of the above approach to tissue classification, experiments were performed on 3D mpMRI data sets from 20 liver cancer TACE patients. Each data set consists of one T2-weighted magnetic resonance image and three T1-weighted dynamic contrast–enhanced (DCE) magnetic resonance images. DCE images reflect the kinetics of injected contrast and are acquired at multiple time points. These images were acquired at three time points during the TACE procedure: precontrast phase (before contrast injection), arterial phase (20 s after injection), and venous phase (70 s after injection). All four images were mutually registered using standard methods (110). In this testing protocol, liver outlines were manually provided, limiting the tissue classification to within the liver in order to achieve a fair comparison with a benchmark method and focus on classification within the liver.

The images used in this study are from HCC patients undergoing TACE as part of a larger clinical study on treatment outcome analysis. In these cases, the number of lesions ranged from one to three, with diameters greater than 20 mm. During TACE, the largest tumors are the most important targets. Therefore, the patch sampling resolutions were selected as 2, 1, and 1 mm with a patch size of 16 × 16 × 16 voxels, in order to focus performance on medium-sized and large tumors. The 20-patient data set generated 1,700 nonoverlapping patches with random sampling and random rotation augmentation. The first two units of the model were designed to differentiate lesions from normal liver tissue, while the last one was designed to identify viable tumor tissue within each detected lesion. For each unit in the model, we implemented a U-net CNN with 10 layers of 3 × 3 × 3 convolution, 10 corresponding layers of dropout, and 2 levels of max pooling/upsampling.

Fivefold cross-validation was used to evaluate the performance of different models. Hyperparameters, such as learning rate and class weights in the loss functions, remained the same across all five folds. Figure 8 and Table 5 show that, with increasing dropout beyond the optimum level (10% in this experiment), the model tends to underfit the data and results in lower accuracy. Figure 8 shows 2D slices through each of three phases of DCE magnetic resonance images, the manually traced ground truth, and the output of the U-net segmentation with a particular level of dropout. Table 5 shows the per-class Dice similarity coefficient when compared with expert radiologist manual segmentations for each of four classes (background, liver parenchyma, tumor, and necrosis) when using three different levels of dropout [no dropout, 10% (optimum), and 30%] for one of the folds during fivefold cross-validation testing. Higher levels of dropout during training tend to lead to a higher percentage of inactive neurons and thus a sparser network.

Figure 8.

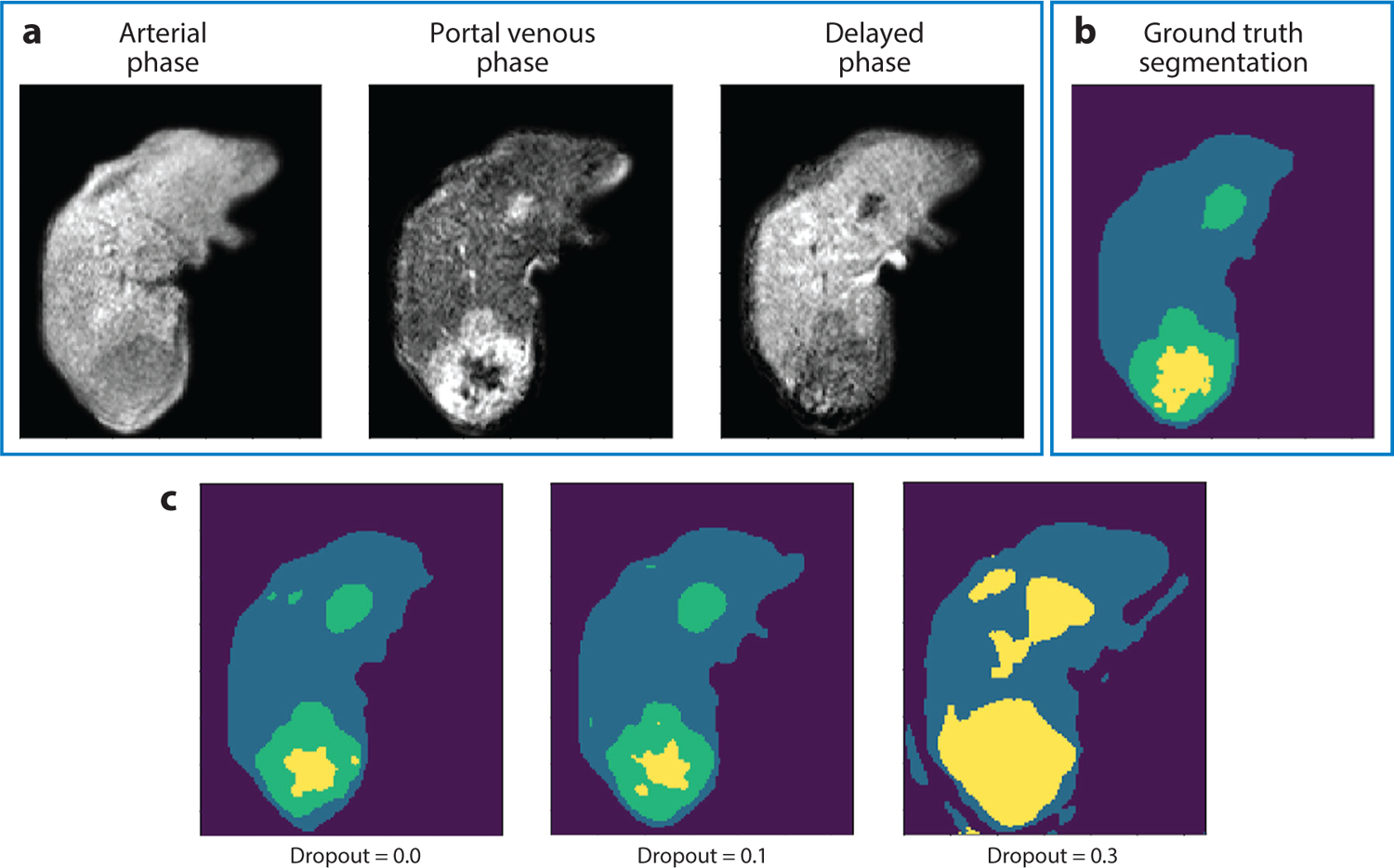
Results with varying levels of dropout. (a) Three dynamic contrast–enhanced magnetic resonance images at one slice level. (b) Manual ground truth tissue class segmentation (dark purple, background; blue, liver parenchyma; green, tumor; yellow, necrosis) and (c) deep neural network segmentation results for different levels of dropout (0.0, 0.1, 0.3), with the best correspondence to ground truth when dropout equals 0.1.

Table 5.

Dice similarity coefficients in comparison to manual expert segmentations for four classes using one fold out of five during cross-training

	Background	Parenchyma	Tumor	Necrosis
No dropout	0.99	0.97	0.73	0.51
P = 0.10a	0.99	0.97	0.77	0.56
P = 0.30a	0.97	0.93	0.40	0.08

^aMethodology utilizing sparsity.

5. CONCLUSIONS AND FUTURE DIRECTIONS

Sparsity is a powerful mechanism for efficient representation and computation in machine learning for medical image segmentation. It has proven to be of great utility in the formulation of data-driven representations suitable for the characterization of appearance and shape suitable for segmentation. We believe that these methods will continue to be relevant in the context of neural networks and will likely continue to be an important strategy in the future.