Informing geometric deep learning with electronic interactions to accelerate quantum chemistry

Significance

The interplay between molecular simulation and artificial intelligence has spurred many insights into chemical discovery, yet the data requirement of machine learning approaches remains a bottleneck. We tackle this challenge by developing a rigorous framework to conserve the symmetries of quantum chemical systems within deep neural networks. Our framework greatly improves the prediction of numerous molecular electronic and energetic properties, even for systems far from the training data. Through tight integration of quantum theory, geometry, and machine learning, our study offers a solution to vastly accelerate the in silico modelling of chemical phenomena in many domains, such as material design and catalysis.

Abstract

Predicting electronic energies, densities, and related chemical properties can facilitate the discovery of novel catalysts, medicines, and battery materials. However, existing machine learning techniques are challenged by the scarcity of training data when exploring unknown chemical spaces. We overcome this barrier by systematically incorporating knowledge of molecular electronic structure into deep learning. By developing a physics-inspired equivariant neural network, we introduce a method to learn molecular representations based on the electronic interactions among atomic orbitals. Our method, OrbNet-Equi, leverages efficient tight-binding simulations and learned mappings to recover high-fidelity physical quantities. OrbNet-Equi accurately models a wide spectrum of target properties while being several orders of magnitude faster than density functional theory. Despite only using training samples collected from readily available small-molecule libraries, OrbNet-Equi outperforms traditional semiempirical and machine learning–based methods on comprehensive downstream benchmarks that encompass diverse main-group chemical processes. Our method also describes interactions in challenging charge-transfer complexes and open-shell systems. We anticipate that the strategy presented here will help to expand opportunities for studies in chemistry and materials science, where the acquisition of experimental or reference training data is costly.

Discovering new molecules and materials is central to tackling contemporary challenges in energy storage and drug discovery (1, 2). As the experimentally uninvestigated chemical space for these applications is immense, large-scale computational design and screening for new molecule candidates have the potential to vastly reduce the burden of laborious experiments and to accelerate discovery (3–5). A crucial task is to model the quantum chemical properties of molecules by solving the many-body Schrödinger equation, which is commonly addressed by ab initio electronic structure methods (6, 7), such as density functional theory (DFT) (Fig. 1A). While very successful, ab initio methods are laden with punitive computational requirements that makes it difficult to achieve a throughput on a scale of the unexplored chemical space.

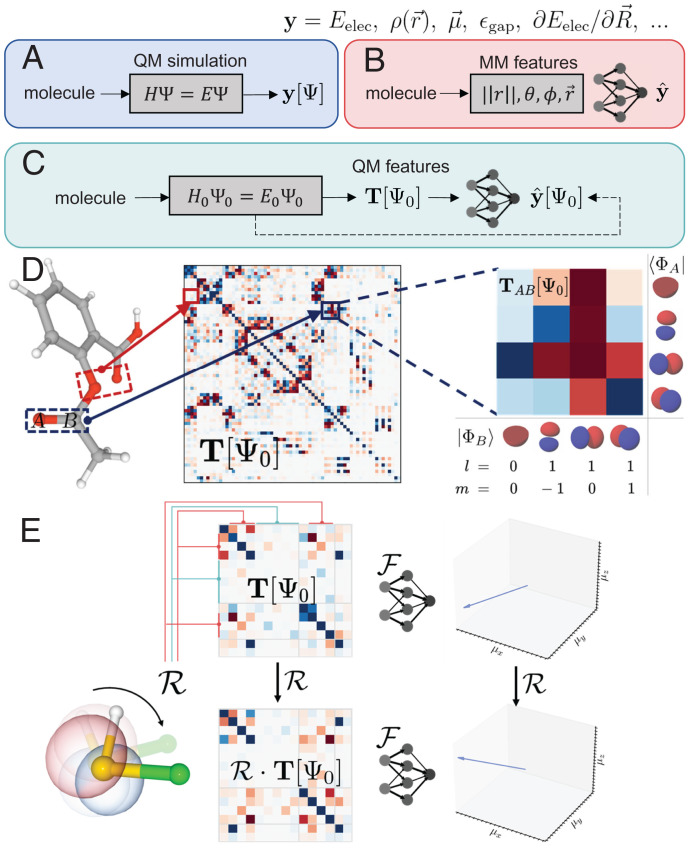
Fig. 1.

QM-informed ML for modeling molecular properties. (A) Conventional ab initio quantum chemistry methods predict molecular properties based on electronic structure theory through computing molecular wave functions and interaction terms, with general applicability but at high computational cost. (B) Atomistic ML approaches use geometric descriptors, such as interatomic distances, angles, and directions, to bypass the procedure of solving the electronic structure problem but often require vast amounts of data to generalize toward new chemical species. (C) In our approach, features are extracted from a highly coarse-grained QM simulation to capture essential physical interactions. An equivariant neural network efficiently learns the mapping, yielding improved transferability at an evaluation speed that is competitive to Atomistic ML methods. (D) Characteristics of the atomic orbital features considered in OrbNet-Equi. The features T are visualized by the density matrix of the molecular system, with red color indicating positive matrix elements and blue color indicating negative matrix elements. Every pair of atoms (A, B) is mapped to a block in the feature matrix, with the row dimension of the block matching the atomic orbitals of the source atom A and the column dimension matching the atomic orbitals of the destination atom B. (E) OrbNet-Equi is equivariant with respect to isometric basis transformations on the atomic orbitals (Eqs. 3 and 4), yielding consistent predictions (illustrated as the dipole moment vector of a thiohypofluorous acid molecule) at different viewpoints. Pink and blue densities overlaying the molecule illustrate an atomic orbital; upon viewpoint rotation $\mathcal{R}$, the original atomic orbital (semitransparent) is reexpressed as a linear combination of atomic orbitals in the rotated frame, leading to a basis transformation that changes the coefficients of feature matrices T.

In contrast, machine learning (ML) approaches are highly flexible as function approximators and thus, are promising for modeling molecular properties at a drastically reduced computational cost. A large class of ML-based molecular property predictors includes methods that use atomic coordinate–based input features, which closely resemble molecular mechanics (MM) descriptors (8–18); these methods will be referred to as Atomistic ML methods in the current work (Fig. 1B). Atomistic ML methods have been employed to solve challenging problems in molecular sciences, such as RNA structure prediction (19) and anomalous phase transitions (20). However, there remains a key discrepancy between Atomistic ML and ab initio approaches regarding the modeling of quantum chemical properties, as Atomistic ML approaches typically neglect the electronic degrees of freedom that are central for the description of important phenomena, such as electronic excitations, charge transfer, and long-range interactions. Moreover, recent work shows that Atomistic ML can struggle with transferability on downstream tasks where the molecules may chemically deviate from the training samples (21, 22) as is expected to be common for underexplored chemical spaces.

Recent efforts to embody quantum mechanics (QM) into molecular representations based on electronic structure theory have made breakthroughs in improving both the chemical and electronic transferability of ML-based molecular modeling (23–29). Leveraging a physical feature space extracted from QM simulations, such QM-informed ML methods have attained data efficiency that significantly surpasses Atomistic ML methods, especially when extrapolated to systems with length scales or chemical compositions unseen during training. Nevertheless, QM-informed ML methods still fall short in terms of the flexibility of modeling diverse molecular properties unlike their atomistic counterparts, as they are typically implemented for a limited set of learning targets, such as the electronic energy or the exchange–correlation potential. A key bottleneck hampering the broader applicability of QM-informed approaches is the presence of unique many-body symmetries necessitated by an explicit treatment on electron–electron interactions. Heuristic schemes have been used to enforce invariance (24, 26, 30–33) at a potential loss of information in their input features or expressivity in their ML models. Two objectives remain elusive for QM-informed ML: 1) incorporate the underlying physical symmetries with maximal data efficiency and model flexibility and 2) accurately infer downstream molecular properties for large chemical spaces at a computational resource requirement on par with existing empirical and Atomistic ML methods.

Herein, we introduce an end-to-end ML method for QM-informed molecular representations, OrbNet-Equi, in fulfillment of these two objectives. OrbNet-Equi featurizes a mean-field electronic structure via the atomic orbital basis and learns molecular representations through an ML model that is equivariant with respect to isometric basis transformations (Fig. 1 C–E). By the virtue of equivariance, OrbNet-Equi respects essential physical constraints of symmetry conservation so that the target quantum chemistry properties are learned independent of a reference frame. Underpinning OrbNet-Equi is a neural network designed with insights from recent advances in geometric deep learning (34–40) but with key architectural innovations to achieve equivariance based on the tensor-space algebraic structures entailed in atomic orbital–based molecular representations.

We demonstrate the data efficiency of OrbNet-Equi on learning molecular properties using input features obtained from tight-binding QM simulations, which are efficient and scalable to systems with thousands of atoms (41). We find that OrbNet-Equi consistently achieves lower prediction errors than existing Atomistic ML methods and our previous QM-informed ML method (26) on diverse target properties, such as electronic energies, dipole moments, electron densities, and frontier orbital energies. Specifically, our study on learning frontier orbital energies illustrates an effective strategy to improve the prediction of electronic properties by incorporating molecular orbital space information.

To showcase its transferability to complex real-world chemical spaces, we trained an OrbNet-Equi model on single-point energies of ∼236,000 molecules curated from readily available small-molecule libraries. The resulting model, OrbNet-Equi/Selected Drug-Like and Biofragment Conformers (SDC21), achieves a performance competitive to state-of-the-art composite DFT methods when tested on a wide variety of main-group quantum chemistry benchmarks while being up to 1,000-fold faster at run time. As a particular case study, we found that OrbNet-Equi/SDC21 substantially improved the prediction accuracy of ionization potentials relative to semiempirical QM methods, even though no radical species were included for training. Thus, our method has the potential to accelerate simulations for challenging problems in organic synthesis (42), battery design (43), and molecular biology (44). Detailed data analysis pinpoints viable future directions to systematically improve its chemical space coverage, opening a plausible pathway toward a generic hybrid physics–ML paradigm for the acceleration of molecular modeling and discovery.

Results

The OrbNet-Equi Methodology.

OrbNet-Equi featurizes a molecular system through mean-field QM simulations. Semiempirical tight-binding models (41) are used through this study since they can be solved rapidly for both small-molecule and extended systems, which enables deploying OrbNet-Equi to large chemical spaces. In particular, we employ the recently reported GFN (geometries [vibrational], frequencies, and noncovalent interactions [NCIs])-xTB (extended tight-binding) (45) QM model in which the mean-field electronic structure ${\mathrm{\Psi }}_0$ is obtained through self-consistently solving a tight-binding model system (Fig. 1C). Built upon ${\mathrm{\Psi }}_0$, the inputs to the neural network comprise a stack of matrices $\mathbf{T}[{\mathrm{\Psi }}_0]$ defined as single-electron operators $\widehat{\mathcal{O}}[{\mathrm{\Psi }}_0]$ represented in the atomic orbitals (Fig. 1D),

$${(\mathbf{T}[{\mathrm{\Psi }}_0])}_{AB}^{n,l,m;n\prime \text{},l\prime \text{},m\prime }=\langle {\mathrm{\Phi }}_A^{n,l,m}\left|\widehat{\mathcal{O}}[{\mathrm{\Psi }}_0]\right|{\mathrm{\Phi }}_B^{n\prime \text{},l\prime \text{},m\prime }\rangle ,$$ [1]

where A and B are both atom indices; $(n,l,m)$ and $(n\prime ,l\prime ,m\prime )$ indicate a basis function in the set of atomic orbitals { Φ } centered at each atom. Motivated by mean-field electronic energy expressions, the input atomic orbital features are selected as $\mathbf{T}=(\mathbf{F},\mathbf{P},\mathbf{H},\mathbf{S})$ using the Fock F, density P, core Hamiltonian H, and overlap S matrices of the tight-binding QM model (Materials and Methods), unless otherwise specified.

OrbNet-Equi learns a map $\mathcal{F}$ to approximate the target molecular property y of high-fidelity electronic structure simulations or experimental measurements,

$$\underset{{}_{\mathcal{F}}}{\min }\hspace{0.17em}\mathcal{L}(\mathbf{y},\mathcal{F}(\mathbf{T}[{\mathrm{\Psi }}_0])),$$ [2]

where $\mathcal{L}$ denotes a cost functional between the reference and predicted targets over training data. The learning problem described by Eq. 2 requires careful treatment on isometric coordinate transformations imposed on the molecular system because the coefficients of $\mathbf{T}[{\mathrm{\Psi }}_0]$ are defined up to a given viewpoint (Fig. 1E). Precisely, the atomic orbitals $\left\{{\mathrm{\Phi }}_A^{n,l,m}\right\}$ undergo a unitary linear recombination subject to three-dimensional (3D) rotations: $\mathcal{R}·|{\mathrm{\Phi }}_A^{n,l,m}\rangle ={\displaystyle {\sum }_{m\prime }{\mathcal{D}}_{m,m\prime }^l}(\mathcal{R})|{\mathrm{\Phi }}_A^{n,l,m\prime }\rangle$, where ${\mathcal{D}}^l(\mathcal{R})$ denotes the Wigner-D matrix of degree l for a rotation operation $\mathcal{R}$. As a consequence of the basis changing induced by $\mathcal{R},\hspace{0.17em}\mathbf{T}[{\mathrm{\Psi }}_0]$ is transformed block wise:

$${(\mathcal{R}·\mathbf{T}[{\mathrm{\Psi }}_0])}_{AB}^{l;l\prime }={\mathcal{D}}^l(\mathcal{R})\hspace{0.17em}{(\mathbf{T}[{\mathrm{\Psi }}_0])}_{AB}^{l;l\prime }\hspace{0.17em}{\mathcal{D}}^{l\prime }{(\mathcal{R})}^{†},$$ [3]

where the dagger symbol denotes an Hermitian conjugate. To account for the rototranslation symmetries, the neural network $\mathcal{F}$ must be made equivariant with respect to all such isometric basis rotations: that is,

$$\mathcal{R}·\mathcal{F}(\mathbf{T}[{\mathrm{\Psi }}_0])\equiv \mathcal{F}(\mathcal{R}·\mathbf{T}[{\mathrm{\Psi }}_0]),$$ [4]

which is fulfilled through our delicate design of the neural network in OrbNet-Equi (Fig. 2). The neural network iteratively updates a set of representations ${\mathbf{h}}^t$ defined at each atom through its neural network modules and reads out predictions using a pooling layer located at the end of the network. During its forward pass, diagonal blocks of the inputs $\mathbf{T}[{\mathrm{\Psi }}_0]$ are first transformed into components that are isomorphic to orbital–angular–momentum eigenstates, which are then cast to the initial representations ${\mathbf{h}}^{t=0}$. Each subsequent module exploits off-diagonal blocks of $\mathbf{T}[{\mathrm{\Psi }}_0]$ to propagate nonlocal information among atomic orbitals and refine the representations ${\mathbf{h}}^t$, which resemble a process of applying time-evolution operators on quantum states. We provide a technical introduction to the neural network architecture in Materials and Methods. We incorporate other constraints on the learning task, such as size consistency solely through programming the pooling layer (Materials and Methods), therefore achieving task-agnostic modeling for diverse chemical properties. Additional details and theoretical results are provided in SI Appendix, sections S1 and S2.

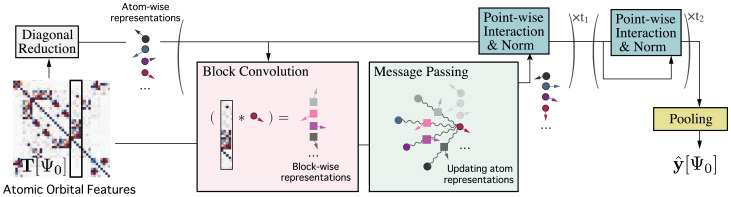
Fig. 2.

Schematic illustration of the OrbNet-Equi method. The input atomic orbital features $\mathbf{T}[{\mathrm{\Psi }}_0]$ are obtained from a low-fidelity QM simulation. A neural network termed UNiTE first initializes atom-wise representations through the diagonal reduction module and then, updates the representations through stacks of block convolution, message-passing, and point-wise interaction modules. A programmed pooling layer reads out high-fidelity property predictions $\widehat{\mathbf{y}}$ based on the final representations. Neural network architecture details are provided in Materials and Methods.

Performance on Benchmark Datasets.

We begin with benchmarking OrbNet-Equi on the QM9 (Quantum Machines 9) dataset (46), which has been widely adopted for assessing ML-based molecular property prediction methods. QM9 contains 133,885 small organic molecules at optimized geometries, with target properties computed by DFT. Following previous works (13, 14, 17, 18, 38, 47), we take 110,000 random samples as the training set and 10,831 samples as the test set. We present results for both the “direct-learning” training strategy, which corresponds to training the model directly on the target property, and whenever applicable, the “delta-learning” strategy (48), which corresponds to training on the residual between output of the tight-binding QM model and the target level of theory.

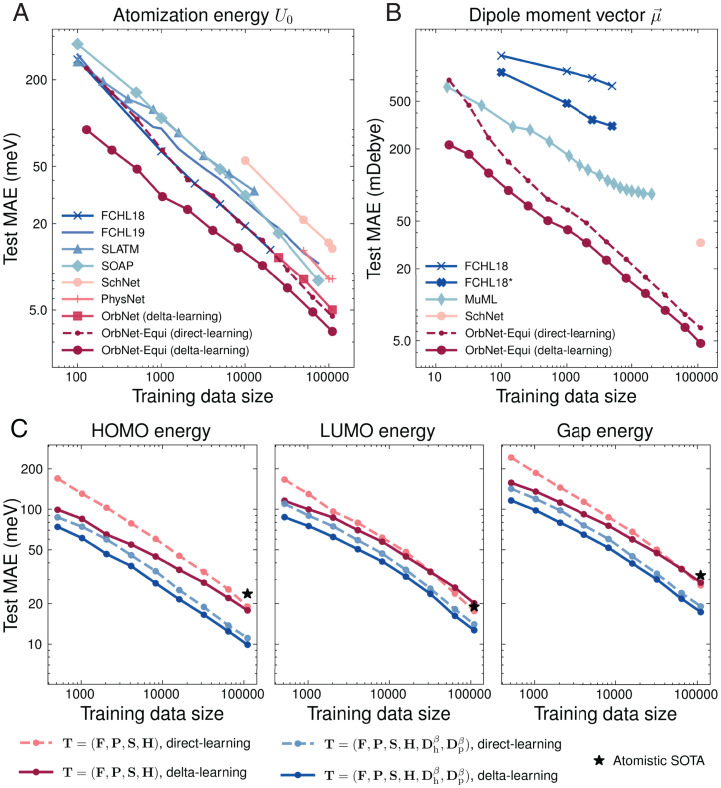
We first trained OrbNet-Equi on two representative targets, the total electronic energy U₀ and the molecular dipole moment vector $\overrightarrow{\mu }$ (Fig. 3 A and B), for which a plethora of task-specific ML models has previously been developed (26, 49–53). The total energy U₀ is predicted through a sum over atom-wise energy contributions, and the dipole moment $\overrightarrow{\mu }$ is predicted through a combination of atomic partial charges and dipoles (SI Appendix, section S1.E). For U₀ (Fig. 3A), the direct-learning results of OrbNet-Equi match the state-of-the-art kernel-based ML method [Faber–Christensen–Huang–Lilienfeld (FCHL)18/GPR (Gaussian Process Regression) (49) in terms of the test mean absolute error (MAE) while being scalable to large data regimes (Fig. 3A, training data size >20,000), where no competitive result has been reported before. With delta learning, OrbNet-Equi outperforms our previous QM-informed ML approach OrbNet (26) by $\sim 45\%$ in the test MAE. Because OrbNet also uses the GFN-xTB QM model for featurization and the delta-learning strategy for training, this improvement underscores the strength of our neural network design, which seamlessly integrates the underlying physical symmetries. Moreover, for dipole moments $\overrightarrow{\mu }$ (Fig. 3B), OrbNet-Equi exhibits steep learning curve slopes regardless of the training strategy, highlighting its capability of learning rotational-covariant quantities at no sacrifice of data efficiency.

Fig. 3.

Model performance on the QM9 dataset. (A and B) Test MAE of OrbNet-Equi is shown as functions of the number of training samples along with previously reported results from task-specific ML methods [FCHL18 (49), FCHL19 (51), Spectrum of London and Axilrod-Teller-Muto (ATM) potential (98), Smooth Overlap of Atomic Positions (50), FCHL18* (51), MuML (52)] and deep learning–based methods [SchNet (13), PhysNet (14), OrbNet (26)] for targets (A) electronic energy U₀ and (B) molecular dipole moment vector $\overrightarrow{\mu }$ on the QM9 dataset. Results for OrbNet-Equi models trained with direct learning and delta learning are shown as dashed and solid lines, respectively. (C) Incorporating energy-weighted density matrices to improve data efficiency on learning frontier orbital properties. The HOMO, LUMO, and HOMO–LUMO gap energy test MAEs of OrbNet-Equi are shown as functions of the number of training samples. For models with the default feature set (red curves), the reduction in test MAE for delta-learning models over direct-learning models gradually diminishes as the training data size grows. The LUMO and gap energy MAE curves exhibit a cross-over around 32,000 to 64,000 training samples; thereafter, direct-learning models outperform delta-learning models. In contrast, when the energy-weighted density matrix features are supplied (blue curves), the test MAE curves between direct-learning and delta-learning models remain gapped when the training data size is varied. The black stars indicate the lowest test MAEs achieved by Atomistic ML methods [SphereNet (17)] trained with 110,000 samples.

We then targeted the learning task of frontier molecular orbital (FMO) properties, in particular energies of the highest occupied molecular orbital (HOMO), the lowest unoccupied molecular orbital (LUMO), and the HOMO–LUMO gaps, which are important in the prediction of chemical reactivity and optical properties (54, 55). Because the FMOs are inherently defined in the electron energy space and are often spatially localized, it is expected to be challenging to predict FMO properties based on molecular representations in which a notion of electronic energy levels is absent. OrbNet-Equi overcame this obstacle by breaking the orbital filling degeneracy of its input features to encode plausible electron excitations near the FMO energy levels: that is, adding energy-weighted density matrices of “hole-excitation” ${\mathbf{D}}_{\text{h}}^{\beta }$ and that of “particle-excitation” ${\mathbf{D}}_{\text{p}}^{\beta }$:

$${(D_{\text{h}}^{\beta })}_{\mu \nu }={\displaystyle \sum _i{C}_{\mu i}^{*}}{C}_{\nu i}·\exp (\text{}-\beta ({ϵ}_{\text{HOMO}}-{ϵ}_i))·n_i$$ [5]

$${(D_{\text{p}}^{\beta })}_{\mu \nu }={\displaystyle \sum _i{C}_{\mu i}^{*}}{C}_{\nu i}·\exp (\beta ({ϵ}_{\text{LUMO}}-{ϵ}_i))\text{}·\text{}(1-n_i),$$ [6]

where ϵ_i and n_i are the orbital energy and occupation number of the ith molecular orbital from tight-binding QM and $C_{\mu i},C_{\nu i}$ denotes the molecular orbital coefficients with μ and ν indexing the atomic orbital basis. Here, the effective temperature parameters β are chosen as $\beta =[4,16,64,256]$ (atomic units), and a global attention-based pooling is used to ensure size-intensive predictions (SI Appendix, section S1.E.4). Fig. 3C shows that the inclusion of energy-weighted density matrices (${\mathbf{D}}_{\text{h}}^{\beta },{\mathbf{D}}_{\text{p}}^{\beta }$) indeed greatly enhanced model generalization on FMO energies, as evident from the drastic test MAE reduction against the model with default ground-state features ($\mathbf{F},\mathbf{P},\mathbf{S},\mathbf{H}$) as well as the best result from Atomistic ML methods. Remarkably, for models using default ground-state features (Fig. 3C, red lines), we noticed a rank reversal behavior between direct-learning and delta-learning models as more training samples became available, mirroring similar observations from a recent Atomistic ML study (56). The absence of this cross-over when (${\mathbf{D}}_{\text{h}}^{\beta },{\mathbf{D}}_{\text{p}}^{\beta }$) are provided (Fig. 3C, blue) suggests that the origin of such a learning slowdown is the incompleteness of spatially degenerate descriptors, and the gap between delta-learning and direct-learning curves can be restored by breaking the energy-space degeneracy. This analysis reaffirms the role of identifying the dominant physical degrees of freedom in the context of the ML-based prediction of quantum chemical properties and is expected to benefit the modeling of relevant electrochemical and optical properties, such as redox potentials.

Furthermore, OrbNet-Equi is benchmarked on 12 targets of QM9 using the 110,000 full training set (SI Appendix, Table S1), for which we programmed its pooling layer to reflect the symmetry constraint of each target property (SI Appendix, section S1.E). We observed top-ranked performance on all targets with average test MAE around twofold lower than atomistic deep learning methods. In addition, we tested OrbNet-Equi on fitting molecular potential energy surfaces by training on multiple configurations of a molecule (SI Appendix, section S3.B). Results (SI Appendix, Tables S2 and S3) showed that OrbNet-Equi obtained energy and force prediction errors that match state-of-the-art ML potential methods (57, 58) on the Molecular Dynamics 17 dataset (57, 59), suggesting that our method also efficiently generalizes over the conformation degrees of freedom apart from being transferable across the chemical space. These extensive benchmarking studies confirm that our strategy is consistently applicable to a wide range of molecular properties.

Accurate Modeling for Electron Densities.

We next focus on the task of predicting the electron density $\rho (\overrightarrow{r}):{\mathbb{R}}^3\to \mathbb{R}$, which plays an essential role in both the formulation of DFT and in the interpretation of molecular interactions. It is also more challenging than predicting the energetic properties from an ML perspective due to the need of preserving its real-space continuity and rotational covariance. OrbNet-Equi learns to output a set of expansion coefficients ${\widehat{d}}_A^{\mathit{nlm}}$ to represent the predicted electron density $\widehat{\rho }(\overrightarrow{r})$ through a density-fitting basis set $\left\{\chi \right\}$ (Materials and Methods and SI Appendix, section S1.E.6),

$$\widehat{\rho }(\overrightarrow{r})={\displaystyle \sum _A^{N_{\text{atom}}}{\displaystyle \sum _l^{l_{\text{max}}(z_A)}{\displaystyle \sum _{m=-l}^l{\displaystyle \sum _n^{n_{\text{max}}(z_A\text{},l)}}}}}{\widehat{d}}_A^{\mathit{nlm}}{\chi }_A^{\mathit{nlm}}(\overrightarrow{r}),$$ [7]

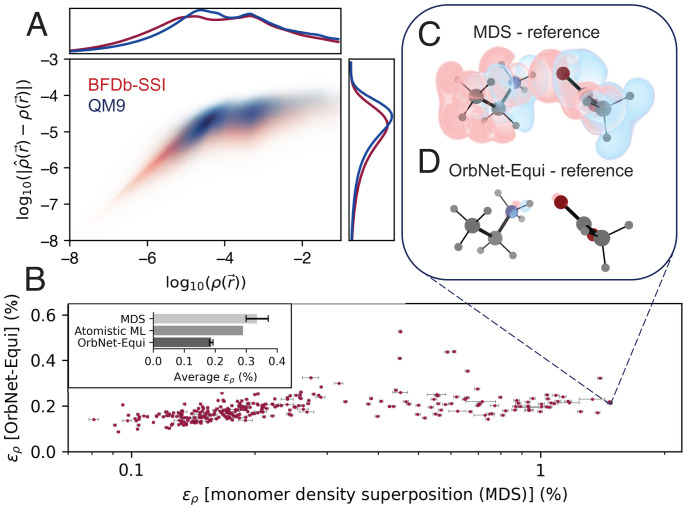
where $l_{\text{max}}(z_A)$ is the maximum angular momentum in the density-fitting basis set for atom type z_A and $n_{\text{max}}(z_A\text{},l)$ denotes the cardinality of basis functions with angular momentum l. We train OrbNet-Equi to learn DFT electron densities on the QM9 dataset of small organic molecules and the BfDB-SSI (Biofragment Database-sidechain-sidechain interactions) (60) dataset of amino acid side-chain dimers (Fig. 4) using the direct-learning strategy. OrbNet-Equi results are substantially better than Atomistic ML baselines in terms of the average L¹ density error ${\epsilon }_{\rho }=\frac{{\displaystyle \int \left|\rho (\overrightarrow{r})-\widehat{\rho }(\overrightarrow{r})\right|}d\overrightarrow{r}}{{\displaystyle \int \left|\rho (\overrightarrow{r})\right|}d\overrightarrow{r}}$ (Materials and Methods); specifically, OrbNet-Equi achieves an average ${\epsilon }_{\rho }$ of 0.191 ± 0.003% on BfDB-SSI using 2,000 training samples compared with 0.29% of Symmetry-Adapted Gaussian Process Regression (61) and an average ${\epsilon }_{\rho }$ of 0.206 ± 0.001% on QM9 using 123,835 training samples as compared with 0.28 to 0.36% of DeepDFT (62). Fig. 4A confirms that OrbNet-Equi predicts densities at consistently low errors across the real space and maintains a robust asymptotic decay behavior within low-density [$\rho (\overrightarrow{r})<{10}^{-4}\hspace{0.17em}{a}_0^{-3}$] regions that are far from the molecular system. Furthermore, analysis of electric multipole moments derived from the predicted charge densities (SI Appendix, S3.C and Figs. S3 and S4) suggests that the OrbNet-Equi–predicted density yields multipole errors comparable with the deviations between different DFT functionals.

Fig. 4.

Learning electron charge densities for organic and biological motif systems. (A) Two-dimensional heat maps of the log-scale reference density $\rho (\overrightarrow{r})$ and the log-scale OrbNet-Equi density prediction error $\left|\widehat{\rho }(\overrightarrow{r})-\rho (\overrightarrow{r})\right|$ (both in $a_0^{-3}$). The heat maps are calculated by sampling real-space query points $\overrightarrow{r}\in {\mathbb{R}}^3$ for all molecules in the (red) BfDB-SSI test set and the (blue) QM9 test set. The nearly linear relationship for ${\log }_{10}(\rho (\overrightarrow{r}))<-4$ low-density regions reveals that OrbNet-Equi–predicted densities possess a physical long-range decay behavior. Distributions of ${\log }_{10}(\rho (\overrightarrow{r}))$ and ${\log }_{10}(\left|\widehat{\rho }(\overrightarrow{r})-\rho (\overrightarrow{r})\right|)$ are plotted within the marginal charts. (B) The L¹ density errors ${\epsilon }_{\rho }$ of OrbNet-Equi are plotted against the ${\epsilon }_{\rho }$ of densities obtained through MDS across the BfDB-SSI test set. Error bars mark the 99% CIs of ${\epsilon }_{\rho }$ for individual samples. Inset shows the average ${\epsilon }_{\rho }$ for MDS, an Atomistic ML method (61), and OrbNet-Equi predictions on the BfDB-SSI test set. OrbNet-Equi yields the lowest average prediction error and consistently, produces accurate electron densities for cases where intermolecular charge transfer is substantial. (C and D) Visualization of density deviation maps for (C) MDS and (D) OrbNet-Equi–predicted densities on the ${\text{Glu}}^{-}/{\text{Lys}}^{+}$ system (SSI-139GLU-144LYS-1), a challenging example from the BfDB-SSI test set. Red isosurfaces correspond to $\mathrm{\Delta }\rho =-0.001\hspace{0.17em}{a}_0^{-3}$, and blue isosurfaces correspond to $\mathrm{\Delta }\rho =+0.001\hspace{0.17em}{a}_0^{-3}$, where $\mathrm{\Delta }\rho$ is the model density subtracted by the DFT reference density.

To understand whether the model generalizes to cases where charge transfer is significant, as in donor–acceptor systems, we introduce a simple baseline predictor termed monomer density superposition (MDS). The MDS electron density of a dimeric system is taken as the sum of independently computed DFT electron densities of the two monomers. OrbNet-Equi yields accurate predictions in the presence of charge redistribution induced by noncovalent effects, as identified by dimeric examples from the BfDB-SSI test set for which the MDS density (Fig. 4B, x axis) largely deviates from the DFT reference density of the dimer due to intermolecular interactions. One representative example is a strongly interacting glutamic acid–lysine system (Fig. 4 C and D) whose salt-bridge formation is known to be essential for the helical stabilization in protein folding (63), for which OrbNet-Equi predicts $\rho (\overrightarrow{r})$ with ${\epsilon }_{\rho }=0.211\pm 0.001\%$ significantly lower than that of MDS (${\epsilon }_{\rho }=1.47\pm 0.02\%$). The accurate modeling of $\rho (\overrightarrow{r})$ offers an opportunity for constructing transferable DFT models for extended systems by learning on both energetics and densities while at a small fraction of expense relative to solving the Kohn–Sham equations from scratch.

Transferability on Downstream Tasks.

Beyond data efficiency on established datasets in train–test split settings, a crucial but highly challenging aspect is whether the model accurately infers downstream properties after being trained on data that are feasible to obtain. To comprehensively evaluate whether OrbNet-Equi can be transferred to unseen chemical spaces without any additional supervision, we have trained an OrbNet-Equi model on a dataset curated from readily available small-molecule databases (Materials and Methods). The training dataset contains 235,834 samples with chemical space coverage for drug-like molecules and biological motifs containing chemical elements C, O, N, F, S, Cl, Br, I, P, Si, B, Na, K, Li, Ca, and Mg and thermalized geometries. The resulting OrbNet-Equi/SDC21 potential energy model is solely trained on DFT single-point energies using the delta-learning strategy. Without any fine-tuning, we directly apply OrbNet-Equi/SDC21 to downstream benchmarks that are recognized for assessing the accuracy of physics-based molecular modeling methods.

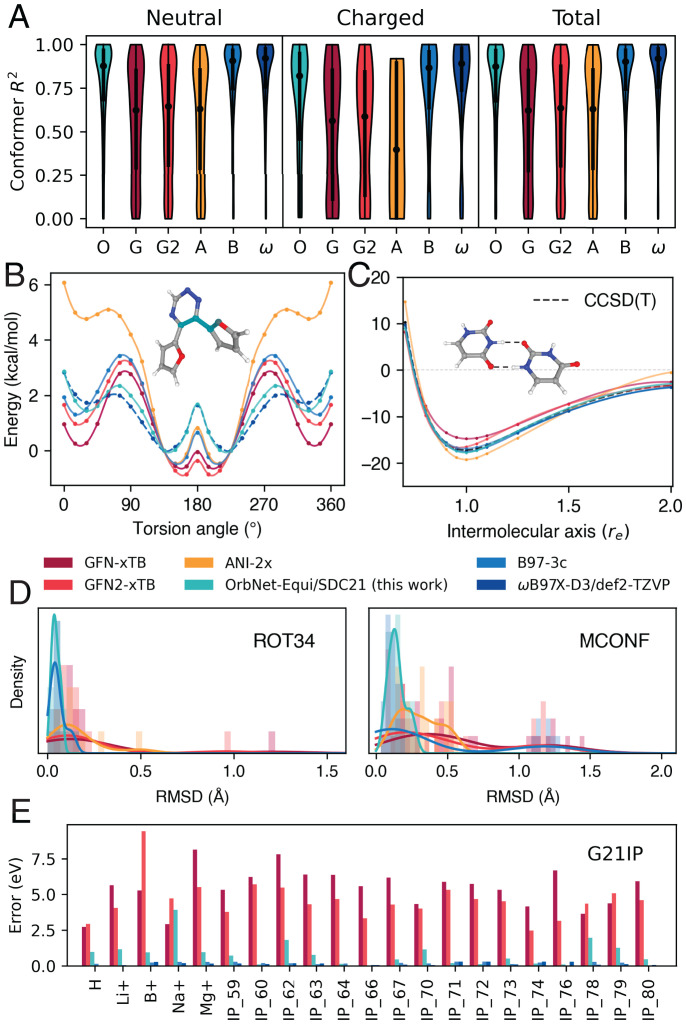
The task of ranking conformer energies of drug-like molecules is benchmarked via the Hutchison dataset of conformers of ∼700 molecules (21) (Fig. 5A and SI Appendix, Table S5, rows 1 and 2). On this task, OrbNet-Equi/SDC21 achieves a median R² score of 0.87 ± 0.02 and R² distributions closely matching the reference DFT theory on both neutral and charged systems. On the other hand, we notice that the median R² of OrbNet-Equi/SDC21 with respect to the reference DFT theory (ωB97X-D3/def2-TZVP) is 0.96 ± 0.01, suggesting that the current performance on this task is saturated by the accuracy of DFT and can be systematically improved by applying fine-tuning techniques on higher-fidelity labels (64, 65). Timing results on the Hutchison dataset (SI Appendix, Table S4) confirm that the neural network inference time of OrbNet-Equi/SDC21 is on par with the GFN-xTB QM featurizer, resulting in an overall computational speed that is 100- to 1000-fold faster relative to existing cost-efficient composite DFT methods (21, 66, 67). To understand the model’s ability to describe dihedral energetics, which are crucial for virtual screening tasks, we benchmark OrbNet-Equi on the prediction of intramolecular torsion energy profiles using the TorsionNet500 (68) dataset, the most diverse benchmark set available for this problem (SI Appendix, Table S5, row 3). Although no explicit torsion angle sampling was performed during training data generation, OrbNet-Equi/SDC21 exhibits a barrier MAE of 0.173 ± 0.003 kcal/mol, much lower than the 1-kcal/mol threshold commonly considered for chemical accuracy. On the other hand, we notice an MAE of 0.7 kcal/mol for the TorsionNet model (68), which was trained on ∼1 million torsion energy samples. As shown in Fig. 5B, OrbNet-Equi/SDC21 robustly captures the torsion sectors of potential energy surface on an example challenging for both semiempirical QM (45, 69) and cost-efficient composite DFT (66) methods, precisely resolving both the suboptimal energy minima location at an $\sim {30}^{°}$ dihedral angle as well as the barrier energy between two local minimas within a 1-kcal/mol chemical accuracy. Next, the ability to characterize noncovalent interactions (NCIs) is assessed on the S66X10 dataset (70) of intermolecular dissociation curves (SI Appendix, Table S6), on which OrbNet-Equi achieves an equilibrium-distance binding energy MAE of 0.35 ±0.09 kcal/mol with respect to the reference DFT theory compared against 1.55 ±0.17 kcal/mol of the GFN-xTB baseline. As shown from a uracil–uracil base pair example (Fig. 5C) for which high-fidelity wave function–based reference calculations have been reported, the binding energy curve along the intermolecular axis predicted by OrbNet-Equi/SDC21 agrees well with both DFT and the high-level CCSD(T) (Coupled Cluster single-double and perturbative triple) results. To further understand the accuracy and smoothness of the energy surfaces and the applicability on dynamics tasks, we perform geometry optimizations on the ROT34 dataset of 12 small organic molecules and the MCONF (Melatonin Conformer Space) dataset of 52 conformers of melatonin (71, 72) (Fig. 5D and SI Appendix, Table S5, rows 4 and 5). Remarkably, OrbNet-Equi/SDC21 consistently exhibits the lowest average rmsd among all physics-based and ML-based approaches (SI Appendix, Table S5), including the popular cost-efficient DFT method B97-3c (66). Further details regarding the numerical experiments and error metrics are provided in Materials and Methods.

Fig. 5.

OrbNet-Equi/SDC21 infers diverse downstream properties at an efficiency of semiempirical tight-binding calculations. (A) Conformer energy ranking on the Hutchison dataset of drug-like molecules. The horizontal axis is labeled with acronyms indicating each method (O, OrbNet-Equi/SDC21 [this work]; G, GFN-xTB; G2, GFN2-xTB; A, ANI(Accurate NeurAl networK engINe for Molecular Energies)-2x; B, B97-3c; ω, ωB97X-D3/def2-TZVP). The y axis corresponds to the molecule-wise R² between predictions and the reference [DLPNO-CCSD(T)] conformer energies. Violin plots display the distribution of R² scores for each method over the (Left) neutral, (Middle) charged, and (Right) all molecules from the Hutchison dataset. Medians and first/third quantiles are shown as black dots and vertical bars, respectively. (B) A torsion profile example from the TorsionNet500 benchmark. All predicted torsion scans surfaces are aligned to the true global minima of the highest level of theory (ω B97X-D3/def2-TZVP) results, with spline interpolations. (C) A uracil–uracil base pair example for NCIs. The dimer binding energy curves are shown as functions of the intermolecular axis (r_e), where $r_e=1.0$ corresponds to the distance of optimal binding energy. (D) Geometry optimization results on the (Left) ROT34 and (Right) MCONF datasets. Histograms and kernel density estimations of the symmetry-corrected rmsd scores (Materials and Methods) with respect to the reference DFT geometries are shown for each test dataset. (E) Evidence of zero-shot model generalization on radical systems. OrbNet-Equi/SDC21 yields prediction errors drastically lower than semiempirical QM methods for adiabatic ionization potential on the G21IP dataset, achieving accuracy comparable with DFT on 7 of 21 test cases.

Remarkably, on the G21IP dataset (73) of adiabatic ionization potentials, we find that the OrbNet-Equi/SDC21 model achieves prediction errors substantially lower than semiempirical QM methods (Fig. 5E and SI Appendix, Table S7), even though samples of open-shell signatures are expected to be rare from the training set (Materials and Methods). Such an improvement cannot be solely attributed to structure-based corrections since there are no or negligible geometrical changes between the neutral and ionized species for both the single-atom systems and several polyatomic systems (e.g., IP_66, a Phosphanide anion) in the G21IP dataset. This reveals that our method has the potential to be transferred to unseen electronic states in a zero-shot manner, which represents early evidence that a hybrid physics–ML strategy may unravel under-investigated chemical processes, such as unknown electron-catalyzed reactions (74).

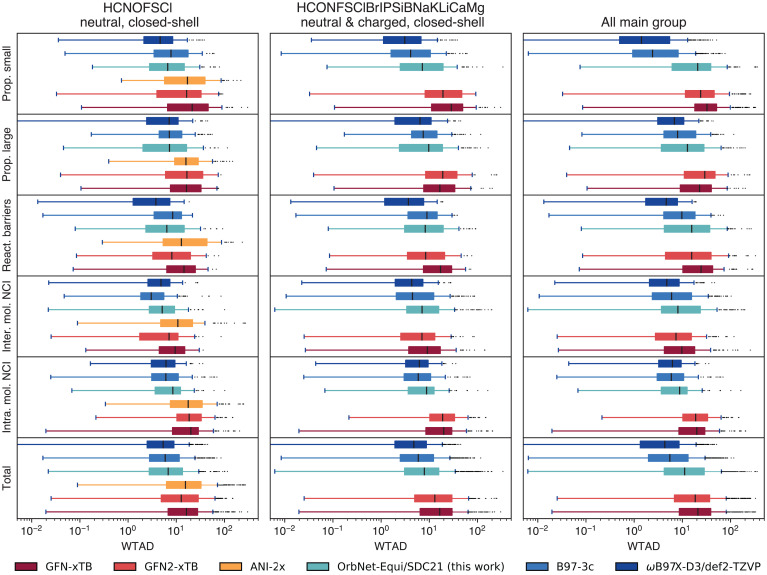
To comprehensively study the transferability of OrbNet-Equi on complex underexplored main-group chemical spaces, we evaluate OrbNet-Equi/SDC21 on the challenging, community-recognized benchmark collection of the General Thermochemistry, Kinetics, and Noncovalent Interactions (GMTKN55) (75) datasets (Fig. 6). Prediction error statistics on the GMTKN55 benchmark are reported with three filtration schemes. First, we evaluate the WTMAD (weighted mean absolute deviation) error metrics (Materials and Methods) on reactions that only consist of neutral and closed-shell molecules with chemical elements CHONFSCl (Fig. 6A), as is supported by an Atomistic ML–based potential method, ANI-2x (76), which is trained on large-scale DFT data. OrbNet-Equi/SDC21 predictions are found to be highly accurate on this subset, as seen from the WTMAD with respect to CCSD(T) being on par with the DFT methods on all five reaction classes and significantly outperforming ANI-2x and the GFN family of semiempirical QM methods (45, 69). It is worth noting that OrbNet-Equi/SDC21 uses a much smaller number of training samples than the ANI-2x training set, which signifies the effectiveness of combining physics-based and ML-based modeling.

Fig. 6.

Assessing model performance on tasks from the GMTKN55 challenge. Box plots depict the distributions of task difficulty WTADs (Materials and Methods) filtered by chemical elements and electronic states (A) supported by the ANI-2x model, (B) those that appeared in the dataset used for training OrbNet-Equi/SDC21, and (C) all reactions. Statistics are categorized by each class of tasks in the GMTKN55 benchmark as shown in y-axis labels. Inter. mol. NCI, intermolecular noncovalent interactions; Intra. mol. NCI, intramolecular noncovalent interactions; Prop. large, reaction energies for large systems and isomerization reactions; Prop. small, basic properties and reaction energies for small systems; React. barriers, reaction barrier heights; Total, total statistics of all tasks.

The second filtration scheme includes reactions that consist of closed-shell (but can be charged) molecules with chemical elements that have appeared in the SDC21 training dataset (Fig. 6B). Although all chemical elements and electronic configurations in this subset are contained in the training dataset, we note that unseen types of physical interactions or bonding types are included, such as in alkali metal clusters from the ALK8 subset (75) and short strong hydrogen bonds in the AHB21 subset (77). Therefore, assessments of OrbNet-Equi with this filtration strategy reflect its performance on cases where examples of atom-level physics are provided, but the chemical compositions are largely unknown. Despite this fact, the median WTMADs of OrbNet-Equi/SDC21 are still competitive with DFT methods on the tasks of small-system properties, large-system properties, and intramolecular interactions. On reaction barriers and intermolecular NCIs, OrbNet-Equi/SDC21 results fall behind DFT, but they still show improvements against the GFN-xTB baseline and match the accuracy of GFN2-xTB, which is developed with physic-based schemes to improve the descriptions on NCI properties against its predecessor GFN-xTB.

The last scheme includes all reactions in the GMTKN55 benchmarks containing chemical elements and spin states never seen during training (Fig. 6C), which represents on the most stringent test and reflects the performance of OrbNet-Equi/SDC21 when being indiscriminately deployed as a quantum chemistry method. When evaluated on the collection of all GMTKN55 tasks (Fig. 6, total panel), OrbNet-Equi/SDC21 maintains the lowest median WTMAD among methods considered here that can be executed at the computational cost of semiempirical QM calculations. Moreover, we note that failure modes on a few highly extrapolative subsets can be identified to diagnose cases that are challenging for the QM model used for featurization (SI Appendix, Table S7). For example, the fact that predictions are inaccurate on the W4 (Weizmann-4)-11 subset of atomization energies (78) and the G21EA subset of electron affinities (73) parallels the absence of an explicit treatment of triplet or higher-spin species within the formulation of the GFN family of tight-binding models. On the population level, the distribution of prediction WTMADs across GMTKN55 tasks also differs from that of GFN2-xTB, which implies that further incorporating physics-based approximations into the QM featurizer can complement the ML model, and thus, the accuracy boundary of semiempirical methods can be pushed to a regime where no known physical approximation is feasible.

Discussion

We have introduced OrbNet-Equi, a QM-informed geometric deep learning framework for learning molecular or material properties using representations in the atomic orbital basis. OrbNet-Equi shows excellent data efficiency for learning related to both energy-space and real-space properties, expanding the diversity of molecular properties that can be modeled by QM-informed ML. Despite only using readily available small-molecule libraries as training data, OrbNet-Equi offers an accuracy alternative to DFT methods on comprehensive main-group quantum chemistry benchmarks at a computation speed on par with semiempirical methods, thus offering a possible replacement for conventional ab initio simulations for general-purpose downstream applications. For example, OrbNet-Equi could immediately facilitate applications, such as screening electrochemical properties of electrolytes for the design of flow batteries (43) and performing accurate direct or hybrid QM/MM simulations for reactions in transition-metal catalysis (42, 79). The method can also improve the modeling for complex reactive biochemical processes (80) using multiscale strategies that have been demonstrated in our previous study (44), while conventional ab initio reference calculations can be prohibitively expensive even on a minimal subsystem.

The demonstrated transferability of OrbNet-Equi to seemingly dissimilar chemical species identifies a promising future direction of improving the accuracy and chemical space coverage through adding simple model systems of the absent types of physical interactions to the training data, a strategy that is consistent with using synthetic data to improve ML models (81), which has been demonstrated for improving the accuracy of DFT functionals (29). Additionally, OrbNet-Equi may provide valuable perspectives for the development of physics-based QM models by relieving the burden of parameterizing Hamiltonian parameters against specific target systems, potentially expanding their design space to higher-energy scales without sacrificing model accuracy. Because the framework presented here can be readily extended to alternative quantum chemistry models for either molecular or material systems, we expect OrbNet-Equi to broadly benefit studies in chemistry, materials science, and biotechnology.

Materials and Methods

The Unitary N-Body Tensor Equivariant Network Neural Network.

This section introduces Unitary N-Body Tensor Equivariant Network (UNiTE), the neural network model developed for the OrbNet-Equi method to enable learning equivariant maps between the input atomic orbital features $\mathbf{T}[{\mathrm{\Psi }}_0]$ and the property predictions $\widehat{\mathbf{y}}[{\mathrm{\Psi }}_0]$. Given the inputs T, UNiTE first generates initial representations ${\mathbf{h}}^{t=0}$ through its diagonal reduction module (Materials and Methods). Then, UNiTE updates the representations ${\mathbf{h}}^{t=0}\mapsto {\mathbf{h}}^{t=1}\mapsto \cdots \mapsto {\mathbf{h}}^{t=t_f}$ with t₁ stacks of block convolution (Materials and Methods), message-passing (Materials and Methods), and point-wise interaction (Materials and Methods) modules, followed by t₂ stacks of point-wise interaction modules. A pooling layer (Materials and Methods) outputs predictions $\widehat{\mathbf{y}}$ using the final representations ${\mathbf{h}}^{t=t_f}$ at $t_f=t_1+t_2$ as inputs.

${\mathbf{h}}^t$ is a stack of atom-wise representations (i.e., for a molecular system containing d atoms, ${\mathbf{h}}^t≔[{\mathbf{h}}_1^t,{\mathbf{h}}_2^t,\cdots ,{\mathbf{h}}_d^t]$). The representation for the Ath atom, ${\mathbf{h}}_A^t$, is a concatenation of neurons that are associated with irreducible representations of group $\text{O}(3)$. Each neuron in ${\mathbf{h}}_A^t$ is identified by a channel index $n\in \{1,2,\cdots ,n_{\text{max}}\}$, a “degree” index $l\in \{0,1,2,\cdots ,l_{\text{max}}\}$, and a “parity” index $p\in \{+1,-1\}$. The neuron ${\mathbf{h}}_{A,\mathit{nlp}}^t$ is a vector of length $2l+1$ and transforms as the lth irreducible representation of group $\text{SO}(3)$ (i.e., ${\mathbf{h}}_{A,\mathit{nlp}}^t={{\displaystyle \oplus }}_m{h}_{A,\mathit{nlpm}}^t$, where ⊕ denotes a vector concatenation operation and $m\in \{-l,-l+1,\cdots ,l-1,l\}$). We use N_lp to denote the number of neurons with degree l and parity p in ${\mathbf{h}}^t$ and $N≔{\displaystyle {\sum }_{l,p}{N}_{lp}}$ to denote the total number of neurons in ${\mathbf{h}}^t$.

For a molecular/material system with atomic coordinates $\mathbf{x}\in {\mathbb{R}}^{d\times 3}$, the following equivariance properties with respect to isometric Euclidean transformations are fulfilled for any input gauge-invariant and Hermitian operator $\mathcal{O}[{\mathrm{\Psi }}_0]$; for all allowed indices $A,n,l,p,m$,

●translation invariance:

$${\mathbf{h}}_{A,\mathit{nlpm}}^t\mapsto {\mathbf{h}}_{A,\mathit{nlpm}}^t\hspace{1em}\text{for}\hspace{1em}\mathbf{x}\mapsto \mathbf{x}+{\mathbf{x}}_0,$$ [8]

where ${\mathbf{x}}_0\in {\mathbb{R}}^3$ is an arbitrary global shift vector;

●rotation equivariance:

$${\mathbf{h}}_{A,\mathit{nlpm}}^t\mapsto {\displaystyle \sum _{m\prime }{\mathbf{h}}_{A,\mathit{nlpm}\prime }^t}{\mathcal{D}}_{m,m\prime }^l(\alpha ,\beta ,\gamma )$$ [9]

for $\mathbf{x}\mapsto \mathbf{x}·\mathcal{R}(\alpha ,\beta ,\gamma )$, where $\mathcal{R}(\alpha ,\beta ,\gamma )$ denotes a rotation matrix corresponding to standard Euler angles α, β, γ; and

●parity inversion equivariance:

$${\mathbf{h}}_{A,\mathit{nlpm}}^t\mapsto {(-1)}^l·p·{\mathbf{h}}_{A,\mathit{nlpm}}^t\hspace{1em}\text{for}\hspace{1em}\mathbf{x}\mapsto -\mathbf{x}.$$ [10]

The initial vector representations ${\mathbf{h}}^{t=0}$ are generated by decomposing diagonal subtensors of the input T into a spherical-tensor representation without explicitly solving tensor factorization based on the tensor product property of group $\text{SO}(3)$. The intuition behind this operation is that the diagonal subtensors of T can be viewed as isolated systems interacting with an effective external field whose rotational symmetries are described by the Wigner–Eckart Theorem (82), which links tensor operators to their spherical counterparts and applies here within a natural generalization. Each update step ${\mathbf{h}}^t\mapsto {\mathbf{h}}^{t+1}$ is composed of 1) block convolution, 2) message passing, and 3) point-wise interaction modules, which are all equivariant with respect to index permutations and basis transformations. In an update step ${\mathbf{h}}^t\mapsto {\mathbf{h}}^{t+1}$, each off-diagonal block of T corresponding to a pair of atoms is contracted with ${\mathbf{h}}^t$. This block-wise contraction operation can be interpreted as performing local convolutions using the blocks of T as convolution kernels and therefore, is called the block convolution module. The output block-wise representations are then passed into a message-passing module, which is analogous to a message-passing operation on edges in graph neural networks (83). The message-passing outputs are then fed into a point-wise interaction module with the previous step representation ${\mathbf{h}}^t$ to finish the update ${\mathbf{h}}^t\mapsto {\mathbf{h}}^{t+1}$. The point-wise interaction modules are constructed as a stack of multilayer perceptrons (MLPs), Clebsch–Gordan product operations, and skip connections. Within those modules, a matching layer assigns the channel indices of ${\mathbf{h}}^t$ to indices of the atomic orbital basis.

We also introduce a normalization layer termed equivariant normalization (EvNorm) (Materials and Methods) to improve training and generalization of the neural network. EvNorm normalizes scales of the representations h while recording the direction-like information to be recovered afterward. EvNorm is fused with a point-wise interaction module through first applying EvNorm to the module inputs, then using an MLP to transform the normalized frame-invariant scale information, and finally, multiplying the recorded direction vector to the MLP’s output. Using EvNorm within the point-wise interaction modules is found to stabilize training and eliminate the need for tuning weight initializations and learning rates across different tasks.

The explicit expressions for the neural network modules are provided for quantum operators $\mathcal{O}$ being one-electron operators, and therefore, the input tensors T are a stack of matrices (i.e., order 2 tensors). Without loss of generality, we also assume that T contains only one feature matrix. Additional technical aspects regarding the case of multiple input features, the inclusion of geometric descriptors, and implementation details are discussed in SI Appendix, section S1. The proofs regarding equivariance and theoretical generalizations to order N tensors are provided in SI Appendix, section S2.

The diagonal reduction module.

We define the shorthand notations $\mu ≔(n_1,l_1,m_1)$ and $\nu ≔(n_2,l_2,m_2)$ to index atomic orbitals. The initialization scheme for ${\mathbf{h}}^{t=0}$ is based on the following proposition; for each diagonal block of T, ${\mathbf{T}}_{AA}$, defined for an on-site atom pair $(A,A)$,

$$T_{AA}^{\mu ,\nu }≔\langle {\mathrm{\Phi }}_A^{\mu }\left|\widehat{\mathcal{O}}\right|{\mathrm{\Phi }}_A^{\nu }\rangle ,$$ [11]

there exists a set of T-independent coefficients $Q_{\mathit{nlpm}}^{\mu ,\nu }$ such that the following linear transformation ψ,

$$\psi {({\mathbf{T}}_{AA})}_{\mathit{nlpm}}≔{\displaystyle \sum _{\mu ,\nu }{T}_{AA}^{\mu ,\nu }}\hspace{0.17em}{Q}_{\mathit{nlpm}}^{\mu ,\nu },$$ [12]

is injective and yields ${\mathbf{h}}_A≔\psi ({\mathbf{T}}_{AA})$ that satisfies equivariance (Eqs. 8–10).

The existence of Q is discussed in SI Appendix, Corollary S3. For the sake of computational feasibility, a physically motivated scheme is employed to tabulate Q and produce order 1 equivariant embeddings ${\mathbf{h}}_A$ using on-site three-index overlap integrals $\tilde{\mathbf{Q}}$:

$$\begin{array}{l}{\tilde{Q}}_{\mathit{nlm}}^{\mu ,\nu }≔{\tilde{Q}}_{\mathit{nlm}}^{n_1,l_1,m_1;n_2,l_2,m_2}\\ ={\displaystyle {\int }_{\mathbf{r}\in {\mathbb{R}}^3}{({\mathrm{\Phi }}_A^{n_1,l_1,m_1}(\mathbf{r}))}^{*}}{\mathrm{\Phi }}_A^{n_2,l_2,m_2}(\mathbf{r}){\tilde{\mathrm{\Phi }}}_A^{n,l,m}(\mathbf{r})d\mathbf{r},\end{array}$$ [13]

where ${\mathrm{\Phi }}_A$ are the atomic orbital basis and ${\tilde{\mathrm{\Phi }}}_A$ are auxiliary Gaussian-type basis functions defined as (for conciseness, at ${\mathbf{x}}_A=0$)

$${\tilde{\mathrm{\Phi }}}^{n,l,m}(\mathbf{r})≔c_{n,l}·\exp (-{\gamma }_{n,l}·r^2)\hspace{0.17em}{r}^l\hspace{0.17em}{Y}_{lm}\left(\frac{\mathbf{r}}{r}\right)\text{},$$ [14]

where $c_{n,l}$ is a normalization constant such that ${\displaystyle {\int }_{\mathbf{r}}}\left|\right|{\tilde{\mathrm{\Phi }}}_A^{n,l,m}(\mathbf{r}))|{|}^{2}d\mathbf{r}=1$ following standard conventions (84). For numerical experiments considered in this work, the scale parameters γ are chosen as (in atomic units)

$$\begin{array}{l}{\gamma }_{n,l=0}≔128·{(0.5)}^{n-1}\hspace{1em}\text{where}\hspace{1em}n\in \{1,2,\cdots ,16\}\\ {\gamma }_{n,l=1}≔32·{(0.25)}^{n-1}\hspace{1em}\text{where}\hspace{1em}n\in \{1,2,\cdots ,8\}\\ {\gamma }_{n,l=2}≔4.0·{(0.25)}^{n-1}\hspace{1em}\text{where}\hspace{1em}n\in \{1,2,3,4\}.\end{array}$$

$\tilde{\mathbf{Q}}$ adheres to equivariance constraints due to its relation to $\text{SO}(3)$ Clebsch–Gordan coefficients $C_{l_1{m}_1;l_2{m}_2}^{lm}\propto {\displaystyle {\int }_{\mathbf{r}\in {\mathbb{S}}^2}{Y}_{l_1{m}_1}}(\mathbf{r})Y_{l_2{m}_2}(\mathbf{r}){(Y_{lm}(\mathbf{r}))}^{*}d\mathbf{r}$ (82). Note that the auxiliary basis ${\tilde{\mathrm{\Phi }}}_A$ is independent of the atomic numbers; thus, the resulting ${\mathbf{h}}_A$ are of equal length for all chemical elements. $\tilde{\mathbf{Q}}$ can be efficiently generated using electronic structure programs, here done with ref. 85. The resulting ${\mathbf{h}}_A$ in explicit form are

$$\begin{array}{l}{\mathbf{h}}_A≔\underset{n,l,p,m}{{\displaystyle \oplus }}{h}_{A,\mathit{nlpm}}\hspace{1em}\text{where}\\ h_{A,nl(p=+1)m}={\displaystyle \sum _{\mu ,\nu }{T}_{AA}^{\mu ,\nu }}\hspace{0.17em}{\tilde{Q}}_{\mathit{nlm}}^{\mu ,\nu }\\ h_{A,nl(p=-1)m}=0.\end{array}$$

${\mathbf{h}}_A$ are then projected by learnable linear weight matrices such that the number of channels for each (l, p) matches the model specifications. The outputs are regarded as the initial representations ${\mathbf{h}}^{t=0}$ to be passed into other modules.

The block convolution module.

In an update step ${\mathbf{h}}^t\mapsto {\mathbf{h}}^{t+1}$, subblocks of T are first contracted with a stack of linearly transformed order 1 representations ${\mathbf{h}}^t$:

$${\mathbf{m}}_{AB,\nu }^{t,i}={\displaystyle \sum _{\mu }(}{\rho }_i({\mathbf{h}}_A^t){)}_{\mu }\hspace{0.17em}{T}_{AB}^{\mu ,\nu },$$ [15]

which can be viewed as a one-dimensional convolution between each block ${\mathbf{T}}_{AB}$ (as convolution kernels) and the $\rho ({\mathbf{h}}_A^t)$ (as the signal) in the ith channel where $i\in \{1,2,\cdots ,I\}$ is the convolution channel index. The block convolution produces block-wise representations ${\mathbf{m}}_{AB}^t$ for each block index $(A,B)$. ρ_i is called a matching layer at atom A and channel i, defined as

$${({\rho }_i({\mathbf{h}}_A^t))}_{\mu }=\text{Gather}({\mathbf{W}}_l^i·{({\mathbf{h}}_A^t)}_{l(p=+1)m},n[\mu ,z_A]).$$ [16]

${\mathbf{W}}_l^i\in {\mathbb{R}}^{M_l\times N_{l,+1}}$ are learnable linear weight matrices specific to each degree index l, where M_l is the maximum principle quantum number for shells of angular momentum l within the atomic orbital basis used for featurization. The $\text{Gather}$ operation maps the feature dimension to valid atomic orbitals by indexing ${\mathbf{W}}_l^i·{({\mathbf{h}}_A^t)}_{l(p=+1)m}$ using $n[\mu ,z_A]$, the principle quantum numbers of atomic orbitals μ for atom type z_A.

The message-passing module.

Block-wise representations ${\mathbf{m}}_{AB}^t$ are then aggregated into each atom index A by summing over the indices B, analogous to a “message passing” between nodes and edges in common realizations of graph neural networks (83),

$${\tilde{\mathbf{m}}}_A^t={\displaystyle \sum _B\underset{i,j}{{\displaystyle \oplus }}}{\mathbf{m}}_{BA}^{t,i}·{\alpha }_{AB}^{t,j},$$ [17]

up to a nonessential symmetrization and inclusion of point-cloud geometrical terms (SI Appendix, Eq. S5). ${\alpha }_{AB}^{t,j}$ in Eq. 17 are scalar-valued weights parameterized as SE(3) (the Special Euclidean Group in 3 dimensions)-invariant multihead attentions:

$${\mathit{\alpha }}_{AB}^t=\text{MLP}(({\mathbf{z}}_{AB}^t·{\mathbf{W}}_{\text{α}}^t)\odot \mathit{\kappa }(\left|\right|{\mathbf{T}}_{AB}\left|\right|)/\sqrt{N}),$$ [18]

where $\odot$ denotes an element-wise (Hadamard) product, and

$${\mathbf{z}}_{AB}^t=\underset{n,l,p}{{\displaystyle \oplus }}{\displaystyle \sum _{m=-l}^l{h}_{A,\mathit{nlpm}}^t}·h_{B,\mathit{nlpm}}^t,$$ [19]

where $\text{MLP}$ denotes a two-layer MLP, ${\mathbf{W}}_{\text{α}}^t$ are learnable linear functions, and $j\in \{1,2,\cdots ,J\}$ denotes an attention head (one value in ${\mathit{\alpha }}_{AB}^t$). $\mathit{\kappa }(·)$ is chosen as Morlet wavelet basis functions:

$$\mathit{\kappa }(|\left|{\mathbf{T}}_{AB}\right||)≔{\mathbf{W}}_{\text{κ}}(\underset{k}{{\displaystyle \oplus }}{\displaystyle \sum _{n,l}{\displaystyle \sum _{n\prime \text{},l\prime }{\xi }_k}}(\log (|\left|{\mathbf{T}}_{AB}^{n,l;n\prime \text{},l\prime }\right||)))$$ [20]

$${\xi }_k(x)≔\exp (-{\gamma }_k·x^2)·\cos (\pi {\gamma }_k·x),$$ [21]

where ${\mathbf{W}}_{\text{κ}}^t$ are learnable linear functions and γ_k are learnable frequency coefficients initialized as ${\gamma }_k=0.3·{(1.08)}^k$, where $k\in \{0,1,\cdots ,15\}$. Similar to the scheme proposed in $\text{SE}(3)$ transformers (40), the attention mechanism Eq. 18 improves the network capacity without increasing memory costs as opposed to explicitly expanding T.

The aggregated message ${\tilde{\mathbf{m}}}_A^t$ is combined with the representation of current step ${\mathbf{h}}_A^t$ through a point-wise interaction module $\varphi$ (Materials and Methods) to complete the update ${\mathbf{h}}_A^t\mapsto {\mathbf{h}}_A^{t+1}$.

EvNorm.

We define $\text{EvNorm}:\mathbf{h}\mapsto (\overline{\mathbf{h}},\widehat{\mathbf{h}})$, where $\overline{\mathbf{h}}$ and $\widehat{\mathbf{h}}$ are given by

$${\overline{\mathbf{h}}}_{\mathit{nlp}}≔\frac{\Vert {\mathbf{h}}_{\mathit{nlp}}\Vert -{\mu }_{\mathit{nlp}}^h}{{\sigma }_{\mathit{nlp}}^h}\hspace{1em}\text{and}\hspace{1em}{\widehat{\mathbf{h}}}_{\mathit{nlpm}}≔\frac{{\mathbf{h}}_{\mathit{nlpm}}}{\Vert {\mathbf{h}}_{\mathit{nlp}}\Vert +1/{\beta }_{\mathit{nlp}}+ϵ},$$ [22]

where $\Vert ·\Vert$ denotes taking a neuron-wise regularized L² norm:

$$\Vert {\mathbf{h}}_{\mathit{nlp}}\Vert ≔\sqrt{{\displaystyle \sum _m{\mathbf{h}}_{\mathit{nlpm}}^2}+{ϵ}^2}-ϵ.$$ [23]

${\mu }_{\mathit{klp}}^h$ and ${\sigma }_{\mathit{klp}}^h$ are mean and variance estimates of the invariant content $\Vert \mathbf{h}\Vert$ that can be obtained from either batch or layer statistics as in normalization schemes developed for scalar neural networks (86, 87); β_klp are positive, learnable scalars controlling the fraction of vector scale information from h to be retained in $\widehat{\mathbf{h}}$, and ϵ is a numerical stability factor. The EvNorm operation Eq. 22 decouples h to the normalized frame-invariant representation $\overline{\mathbf{h}}$ suitable for being transformed by an MLP and a “pure-direction” $\widehat{\mathbf{h}}$ that is later multiplied to the MLP-transformed normalized invariant content to finish updating h. Note that in Eq. 22, $\mathbf{h}=\mathbf{0}$ is always a fixed point of the map $\mathbf{h}\mapsto \widehat{\mathbf{h}}$, and the vector directions information h is always preserved.

The point-wise interaction module and representation updates.

A point-wise interaction module $\varphi$ (Eqs. 24–26) nonlinearly updates the atom-wise representations through ${\mathbf{h}}^{t+1}=\varphi ({\mathbf{h}}^t,\mathbf{g})$, which consist of coupling another $\text{O}(3)$-equivariant representation g with ${\mathbf{h}}^t$ and performing normalizations. In Eqs. 24–26, $C_{l_1{m}_1;l_2{m}_2}^{lm}$ are Clebsch–Gordan coefficients of group $\text{SO}(3),\hspace{0.17em}{\delta }_i^j$ is a Kronecker delta function, and ${\text{MLP}}_1$ and ${\text{MLP}}_2$ denote MLPs acting on the feature (nlp) dimension. ${\mathbf{W}}_{l,p}^{\text{in},t}\in {\mathbb{R}}^{N_{l,p}\times N_{l,p}}$ and ${\mathbf{W}}_{l,p}^{\text{out},t}\in {\mathbb{R}}^{N_{l,p}\times N_{l,p}}$ correspond to learnable linear weight matrices specific to the update step t and each (l, p).

$${\mathbf{f}}_{\mathit{lpm}}^t={({\text{MLP}}_1({\overline{\mathbf{h}}}^t))}_{lp}\odot ({\widehat{\mathbf{h}}}_{\mathit{lpm}}^t·{\mathbf{W}}_{l,p}^{\text{in},t})\hspace{1em}\text{where}\hspace{1em}({\overline{\mathbf{h}}}^t,{\widehat{\mathbf{h}}}^t)=\text{EvNorm}({\mathbf{h}}^t)$$ [24]

$${\mathbf{q}}_{\mathit{lpm}}={\mathbf{g}}_{\mathit{lpm}}+{\displaystyle \sum _{l_1,l_2}{\displaystyle \sum _{m_1,m_2}{\displaystyle \sum _{p_1,p_2}({\mathbf{f}}_{l_1{p}_1{m}_1}^t\odot {\mathbf{g}}_{l_2{p}_2{m}_2})}}}\hspace{0.17em}{C}_{l_1{m}_1;l_2{m}_2}^{lm}\hspace{0.17em}{\delta }_{p_1·p_2·p}^{{(-1)}^{l_1+l_2+l}}$$ [25]

$${\mathbf{h}}_{\mathit{lpm}}^{t+1}={\mathbf{h}}_{\mathit{lpm}}^t\text{}+\text{}{({\text{MLP}}_2(\overline{\mathbf{q}}))}_{lp}\text{}\odot \text{}({\widehat{\mathbf{q}}}_{\mathit{lpm}}·{\mathbf{W}}_{l,p}^{\text{out},t})\text{}\hspace{1em}\text{where}\hspace{1em}(\overline{\mathbf{q}},\widehat{\mathbf{q}})=\text{EvNorm}(\mathbf{q}).$$ [26]

For $t<t_1$, the updates are performed by combining ${\mathbf{h}}^t$ with the aggregated messages ${\tilde{\mathbf{m}}}^t$ from step t:

$${\mathbf{h}}_A^{t+1}=\varphi ({\mathbf{h}}_A^t,{\rho }^{†}({\tilde{\mathbf{m}}}_A^t)),$$ [27]

where ${\rho }^{†}$ is called a reverse matching layer defined as

$${({\rho }^{†}({\tilde{\mathbf{m}}}_A^t))}_{l(p=+1)m}={\mathbf{W}}_l^{†}·{\displaystyle \sum _{\mu }\text{Scatter}}({\tilde{\mathbf{m}}}_{A,\mu }^t,n[\mu ,z_A])$$ [28]

$${({\rho }^{†}({\tilde{\mathbf{m}}}_A^t))}_{l(p=-1)m}=\mathbf{0}.$$ [29]

The $\text{Scatter}$ operation maps the atomic orbital dimension in ${\tilde{\mathbf{m}}}^t$ to a feature dimension with fixed length M_l using $n[\mu ,z_A]$ as the indices and flattens the outputs into shape $(N_{\text{atoms}},M_{l}IJ)$. ${\mathbf{W}}_l^{†}\in {\mathbb{R}}^{N_{l,+1}\times M_{l}IJ}$ are learnable linear weight matrices to project the outputs into the shape of ${\mathbf{h}}^t$.

For $t_1\le t<t_2$, the updates are based on local information:

$${\mathbf{h}}_A^{t+1}=\varphi ({\mathbf{h}}_A^t,{\mathbf{h}}_A^t).$$ [30]

Pooling layers and training.

A programmed pooling layer reads out the target prediction $\widehat{\mathbf{y}}$ after the representations ${\mathbf{h}}^t$ are updated to the last step ${\mathbf{h}}^{t_f}$. Pooling operations employed for obtaining main numerical results are detailed in SI Appendix, section S1.E; hyperparameter, training, and loss function details are provided in SI Appendix, section S4. As a concrete example, the dipole moment vector is predicted as $\overrightarrow{\mu }={\displaystyle {\sum }_A({\overrightarrow{x}}_A·q_A+{\overrightarrow{\mu }}_A)}$, where ${\overrightarrow{x}}_A$ is the 3D coordinate of atom A and atomic charges q_A and atomic dipoles ${\overrightarrow{\mu }}_A$ are predicted using scalar (l = 0) and Cartesian-coordinate vector (l = 1) components of ${\mathbf{h}}_A^{t_f}$, respectively.

QM-Informed Featurization Details and Gradient Calculations.

The QM-informed representation employed in this work is motivated by a pair of our previous works (26, 88), but in this study, the features are directly evaluated in the atomic orbital basis without the need of heuristic postprocessing algorithms to enforce rotational invariance.

In particular, this work (as well as refs. 26 and 88) constructs features based on the GFN-xTB semiempirical QM method (45). As a member of the class of mean-field quantum chemical methods, GFN-xTB centers around the self-consistent solution of the Roothaan–Hall equations:

$$\mathbf{F}\mathbf{C}=\mathbf{S}\mathbf{C}\mathit{ϵ}.$$ [31]

All boldface symbols are matrices represented in the atomic orbital basis. For the particular case of GFN-xTB, the atomic orbital basis is similar to STO-6G and comprises a set of hydrogen-like orbitals. C is the molecular orbital coefficient, which defines ${\mathrm{\Psi }}_0$, and $\mathit{ϵ}$ is a diagonal eigenvalue matrix of the molecular orbital energies. S is the overlap matrix and is given by

$$S_{\mu \nu }=\langle {\mathrm{\Phi }}^{\mu }\text{|}{\mathrm{\Phi }}^{\nu }\rangle ,$$ [32]

where μ and ν index the atomic orbital basis $\left\{\mathrm{\Phi }\right\}$. F is the Fock matrix and is given by

$$\mathbf{F}=\mathbf{H}+\mathbf{G}\left[\mathbf{P}\right].$$ [33]

H is the one-electron integral including electron–nuclear attraction and electron kinetic energy. G is the two-electron integrals comprising the electron–electron repulsion. Approximation of G is the key task for self-consistent field methods, and GFN-xTB provides an accurate and efficient tight-binding approximation for G. Finally, P is the (one electron–reduced) density matrix and is given by

$$P_{\mu \nu }={\displaystyle \sum _{i=1}^{n_{\text{elec}}/2}{C}_{\mu i}^{*}}{C}_{\nu i}.$$ [34]

$n_{\text{elec}}$ is the number of electrons, and a closed-shell singlet ground state is assumed for simplicity. Eqs. 31 and 33 are solved for P. The electronic energy E is related to the Fock matrix by

$$\mathbf{F}=\frac{\delta E}{\delta \mathbf{P}}.$$ [35]

The particular form of the GFN-xTB electronic energy can be found in ref. 45.

UNiTE is trained to predict the quantum chemistry properties of interest based on the inputs $\mathbf{T}=(\mathbf{F}$, P, S, $\mathbf{H})$ with possible extensions (e.g., the energy-weighted density matrices). For the example of learning the DFT electronic energy with the delta-learning training strategy,

$$E_{\text{DFT}}\approx E_{\text{TB}}+\mathcal{F}(\mathbf{T}).$$ [36]

Note that F, P, S, and H all implicitly depend on the atomic coordinates x and charge/spin-state specifications.

In addition to predicting E, it is also common to compute its gradient with respect to atomic nuclear coordinates x to predict the forces used for geometry optimization and molecular dynamics simulations. We directly differentiate the energy Eq. 36 to obtain energy-conserving forces. The partial derivatives of the UNiTE energy with respect to F, P, S, and H are determined through automatic differentiation. The resulting forces are computed through an adjoint approach developed in appendix D of our previous work (88), with the simplification that the Symmetry-Adapted Atomic Orbital transformation matrix X is replaced by the identity.

Dataset and Computational Details.

Training datasets.

The molecule datasets used in Performance on Benchmark Datasets and Accurate Modeling for Electron Densities were all previously published. Following section 2.1 of ref. 61, the 2,291 BFDb-SSI samples for training and testing are selected as the side-chain–side-chain dimers in the original BFDb-SSI dataset that contain $\le$ 25 atoms and no sulfur element to allow for comparisons among methods.

The SDC21 dataset used for training the OrbNet-Equi/SDC21 model described in Transferability on Downstream Tasks is collected from several publicly accessible sources. First, 11,827 neutral SMILES (simplified molecular-input line-entry system) strings were extracted from the ChEMBL database (89). For each SMILES string, up to four conformers were generated and optimized at the GFN-xTB level. Nonequilibrium geometries of the conformers were generated using either normal mode sampling (90) at 300 K or ab initio molecular dynamics for 200 fs at 500 K in a ratio of 50/50%, resulting in a total of 178,836 structures. An additional 2,549 SMILES strings were extracted from ChEMBL, and random protonation states for these were selected using Dimorphite-DL (91) as well as another 2,211 SMILES strings, which were augmented by adding randomly selected salts from the list of common salts in the ChEMBL Structure Pipeline (92). For these two collections of modified ChEMBL SMILES strings, nonequilibrium geometries were created using the same protocol described earlier, resulting in 21,141 and 27,005 additional structures for the two sets, respectively. To compensate for the bias toward large drug-like molecules, ∼45,000 SMILES strings were enumerated using common bonding patterns, from which 9,830 conformers were generated from a randomly sampled subset. Lastly, molecules in the BFDb-SSI and JSCH-2005 datasets were added to the training dataset (60, 93). In total, the dataset consists of 237,298 geometries spanning the elements C, O, N, F, S, Cl, Br, I, P, Si, B, Na, K, Li, Ca, and Mg. For each geometry, DFT single-point energies were calculated on the dataset at the ωB97X-D3/def2-TZVP level of theory in Entos Qcore version 0.8.17 (85, 94, 95). We additionally filtered the geometries for which DFT calculation failed to converge or broken bonds between the equilibirum and nonequilibrium geometries are detected, resulting in 235,834 geometries used for training the OrbNet-Equi/SDC21 model.

Electronic structure computational details.

The dipole moment labels $\overrightarrow{\mu }$ for the QM9 dataset used in Performance on Benchmark Datasets were calculated at the B3LYP level of DFT theory with def2-TZVP AO basis set to match the level of theory used for published QM9 labels using Entos Qcore version 1.1.0 (85, 95, 96). The electron density labels $\rho (\overrightarrow{r})$ for QM9 and BFDb-SSI were computed at the ωB97X-D3/def2-TZVP level of DFT theory using def2-TZVP-JKFIT (97) for Coulomb and Exchange fitting, also as the electron charge density expansion basis $\left\{\chi \right\}$. The density expansion coefficients d are calculated as

$$d_{\gamma }={\displaystyle \sum _{\xi }{\displaystyle \sum _{\mu ,\nu }(}}{({\mathbf{S}}^{\rho })}^{-1}{)}_{\gamma \xi }{S}_{\mu \nu ;\xi }{P}_{\mu \nu },$$ [37]

where $\mu ,\nu$ are AO basis indices and $\xi ,\gamma$ are density-fitting basis indices. Note that γ stands for the combined index $(A,n,l,m)$ in Eq. 7. P is the DFT AO density matrix, ${\mathbf{S}}^{\rho }$ is the density-fitting basis overlap matrix, and $S_{\mu \nu ;\xi }$ are three-index overlap integrals between the AO basis and the density-fitting basis $\left\{\chi \right\}$.

Benchmarking details and summary statistics.

For the mean L¹ electronic density error over the test sets reported in Accurate Modeling for Electron Densities, we used 291 dimers as the test set for the BFDb-SSI dataset and 10,000 molecules as the test set for the QM9 dataset following the literature (61, 62). ${\epsilon }_{\rho }$ for each molecule in the test sets is computed using a 3D cubic grid of voxel spacing $(0.2,0.2,0.2)$ Bohr for the BFDb-SSI test set and voxel spacing $(1.0,1.0,1.0)$ Bohr for the QM9 test set, both with cutoffs at $\rho (\overrightarrow{r})={10}^{-5}\hspace{0.17em}{a}_0^{-3}$. We note that two baseline methods used slightly different normalization conventions when computing the dataset-averaged L¹ density errors ${\epsilon }_{\rho }$: 1) computing ${\epsilon }_{\rho }$ for each molecule and normalizing over the number of molecules in the test set (62) or 2) normalizing over the total number of electrons in the test set (61). We found that the average ${\epsilon }_{\rho }$ computed using normalization 2 is higher than normalization 1 by around 5% for our results. We follow their individual definitions for average ${\epsilon }_{\rho }$ for the quantitative comparisons described in the text: that is, using scheme 1 for QM9 but scheme 2 for BfDB-SSI.

For downstream task statistics reported in Fig. 5 and SI Appendix, Table S5, the results on the Hutchison dataset in Fig. 5A are calculated as the R² correlation coefficients comparing the conformer energies of multiple conformers from a given model with the energies from DLPNO-CCSD(T). The median R² vales in SI Appendix, Table S5 with respect to both DLPNO (domain-based local pair natural orbital)-CCSD(T) and ωB97X-D3/def2-TZVP are calculated over the R² values for every molecule, and error bars are estimated by bootstrapping the pool of molecules. The error bars for TorsionNet500 and s66 × 10 are computed as 95% CIs. Geometry optimization experiments are performed through relaxing the reference geometries until convergence. Geometry optimization accuracies in Fig. 5D and SI Appendix, Table S5 are reported as the symmetry-corrected rmsd of the minimized geometry vs. the reference level of theory (ω B97X-D3/def2-TZVP) calculated over molecules in the benchmark set. Additional computational details for this task are provided in SI Appendix, section S3.E.

For the GMTKN55 (general main group thermochemistry, kinetics and noncovalent interactions) benchmark dataset collection, the reported CCSD(T)/complete basis set results are used as reference values. The weighted absolute deviation (WTAD) scores for producing Fig. 6 are defined similar to the updated weighted mean absolute deviation (WTMAD-2) in ref. 75 but computed for each reaction in GMTKN55:

$${\text{WTAD}}_{i,j}=\frac{56.84}{\frac{1}{N_i}{\displaystyle \sum _j|}\mathrm{\Delta }E{|}_{i,j}}·|\mathrm{\Delta }E{|}_{i,j}$$ [38]

for the jth reaction in the ith task subset. Note that the subset-wise WTMAD-2 metric in SI Appendix, Table S7 is given by

$${\text{WTMAD-}2}_i=\frac{1}{N_i}{\displaystyle \sum _j{\text{WTAD}}_{i,j}}.$$ [39]

The overall WTMAD-2 is reproduced by

$$\text{WTMAD-}2=\frac{1}{{\displaystyle \sum _i^{55}{N}_i}}{\displaystyle \sum _{i,j}{\text{WTAD}}_{i,j}}.$$ [40]

Data Availability

Source data for results described in the text and SI Appendix, the training dataset, code, and evaluation examples have been deposited in Zenodo (https://zenodo.org/record/6568518#.YrtTKHbMK38) (99).