Deep neural networks constrained by neural mass models improve electrophysiological source imaging of spatiotemporal brain dynamics

Significance

Electrophysiological source imaging (ESI) is an indispensable tool for noninvasively studying brain function and dysfunction. The moderate to low spatial resolution of electroencephalography/magnetoencephalography recordings has been a major hindrance to their wide utility in the field. Although this challenge is mitigated significantly by ESI techniques, it is difficult for individuals without relevant training to select and optimize hyperparameters for these ESI solvers. We propose a deep learning–based source imaging methodology that incorporates current advances in biophysical computational models and neural networks into the ESI framework, and it requires minimal user intervention after the model is trained. Our work promises to enable precise and robust high-resolution spatiotemporal functional brain imaging for a variety of neuroscience research studies and clinical applications.

Abstract

Many efforts have been made to image the spatiotemporal electrical activity of the brain with the purpose of mapping its function and dysfunction as well as aiding the management of brain disorders. Here, we propose a non-conventional deep learning–based source imaging framework (DeepSIF) that provides robust and precise spatiotemporal estimates of underlying brain dynamics from noninvasive high-density electroencephalography (EEG) recordings. DeepSIF employs synthetic training data generated by biophysical models capable of modeling mesoscale brain dynamics. The rich characteristics of underlying brain sources are embedded in the realistic training data and implicitly learned by DeepSIF networks, avoiding complications associated with explicitly formulating and tuning priors in an optimization problem, as often is the case in conventional source imaging approaches. The performance of DeepSIF is evaluated by 1) a series of numerical experiments, 2) imaging sensory and cognitive brain responses in a total of 20 healthy subjects from three public datasets, and 3) rigorously validating DeepSIF’s capability in identifying epileptogenic regions in a cohort of 20 drug-resistant epilepsy patients by comparing DeepSIF results with invasive measurements and surgical resection outcomes. DeepSIF demonstrates robust and excellent performance, producing results that are concordant with common neuroscience knowledge about sensory and cognitive information processing as well as clinical findings about the location and extent of the epileptogenic tissue and outperforming conventional source imaging methods. The DeepSIF method, as a data-driven imaging framework, enables efficient and effective high-resolution functional imaging of spatiotemporal brain dynamics, suggesting its wide applicability and value to neuroscience research and clinical applications.

Imaging complex and distributed brain activity is crucial for advancing our understanding of brain function and dysfunction and for clinical management of a variety of brain disorders. Developing noninvasive brain imaging techniques that provide high spatial resolution, high temporal resolution, and whole-brain coverage is of utmost importance. Hemodynamic imaging modalities, such as functional MRI (fMRI), can map brain activities within millimeter spatial resolution but have poor temporal resolution due to the hemodynamic response (1). Electromagnetic recording modalities, such as electroencephalography (EEG) and magnetoencephalography (MEG), have been widely used for a broad range of applications, such as studying cognitive function (2), diagnosis of psychiatric disorders (3), peri- or intraoperative monitoring of patients’ level of consciousness (4), or delineation and mapping of the epileptogenic zone in epilepsy patients (5) to name a few. EEG and MEG are the only noninvasive techniques that offer millisecond-scale temporal resolution and whole-brain coverage, making them suitable for studying brain dynamics from transient or oscillatory activities (6, 7). For instance, EEG and MEG are commonly used to analyze the oscillatory activity and functional connectivity of the brain during interictal and ictal periods (5, 8) for assisting in the diagnosis and treatment planning of intractable epilepsy, which affects about a third of the more than 65 million people suffering from epilepsy worldwide (9). However, compared with other imaging modalities, such as fMRI, the scalp EEG/MEG measurements are limited in their spatial resolution due to the volume conduction effect (10, 11) and low signal-to-noise ratio (SNR), especially for deeper sources (12, 13).

Many efforts have been made toward boosting the spatial resolution of EEG/MEG by means of electrophysiological source imaging (ESI) (10, 14). ESI is the process of estimating the underlying brain electrical activity by solving an optimization problem aimed at finding the brain sources that best fit the measured EEG/MEG. It has been used in basic neuroscience research and clinical applications, such as mapping brain functions and networks (15–17), brain–computer interfacing (18), and aiding with the diagnosis and surgical planning in epilepsy (19–22). However, due to the ill-posed nature of the problem, current ESI methods require a priori assumptions to limit the solution space either to model brain activity using equivalent current dipole models with only a few dipoles (23, 24) or to determine regularization terms in the distributed source models based on a priori knowledge about brain activities (25–29). Considering the complexity of brain sources and networks, it is challenging to choose, formulate, and customize the correct regularization priors that fully represent the properties of underlying sources. The complications associated with selecting and tunning regularization terms limit the positive impact of conventional ESI methods on neuroscience research and clinical applications from the following aspects. First, the ESI performance would suffer if improper regularizations were chosen due to inaccurate or incomplete modeling of the underlying sources (30). Second, the accessibility of ESI is reduced since hyperparameters in the priors need to be tuned manually or via data-driven approaches for almost every given optimization problem (for any new instance of data), which could prove difficult for end users of such ESI systems (31). Lastly, reproducibility is not guaranteed, as different choices of the hyperparameters will lead to varying source imaging results on the same data (32).

A limitation of conventional ESI methods also manifests itself in that such methods mainly utilize physical modeling of electrical sources, such as regional equivalent current dipoles, without leveraging advanced computational brain dynamics models. Computational methods, such as neural mass models (NMMs) (33, 34), have been shown to model brain dynamics using biophysical characteristics of neural excitation and inhibition. NMMs are capable of modeling various kinds of neuronal activities, such as the human alpha rhythm (35), evoked potentials (36), or epileptiform activities (37), through nonlinear systems of differential equations. It is not straightforward to explicitly formulate the knowledge arising from these mesoscale dynamic models into regularization terms within the conventional ESI framework, even though such neuronal models provide an important mathematical and biophysical tool to summarize our understanding of the brain dynamics and could potentially alleviate the ill posedness of the ESI problem by providing a more realistic source model to constrain the space of possible imaging solutions.

In light of the current challenges and opportunities in the ESI field, we propose a deep learning–based source imaging framework (DeepSIF), incorporating biophysically inspired computational neuronal models into the source imaging pipeline to provide an accurate, easily accessible, and objective ESI solver. Ideally, adequate real data from underlying brain sources with simultaneous scalp recordings are needed to train a neural network for the ESI problem. However, real scalp data in which the location, extent, and dynamics of the underlying brain sources are known and labeled correctly, are extremely difficult to come by due to technical difficulties of simultaneously recording invasive intracranial and noninvasive scalp signals. Large-scale computational brain models (33, 34), could fill this gap by generating synthetic brain-like data in both spatial and temporal domains to be used as the training data for the DeepSIF model.

Compared with conventional ESI methods, our framework circumvents the challenges caused by explicitly defining regularization terms, providing a new perspective to formulate the ESI problem. The advantages of using the DeepSIF method are threefold. First, complex brain dynamics can be embedded in the training data and will be implicitly manifested as the weights and nonlinear connections in the trained neural networks without explicitly defining a regularization term. Second, after the time-consuming training process, the evaluation of the neural network is efficient when applied to new instances of data, sparing the need to search for the hyperparameters for each new instance of EEG/MEG measurement. This will also increase the reproducibility of the ESI results without the ambiguity of choosing hyperparameters. Third, computational models provide access to a large amount of data covering brain sources with different characteristics (different noise levels, depth from scalp electrodes, etc.). The trained DeepSIF model is expected to have robust performance for sources with various signal properties and under different conditions.

In this work, a deep neural network (DNN) was trained using synthetic training data generated by a large-scale brain dynamics model consisting of interconnected NMMs, resembling realistic mesoscale neuronal activity, which via biophysical volume conduction modeling, was transformed to macroscale scalp electromagnetic signals (Fig. 1). Once trained, the DeepSIF algorithm can provide estimates of spatiotemporally distributed brain activities given noninvasive scalp electrophysiological measurements. We demonstrated in a series of numerical experiments that the trained DNN is capable of accurately and reliably reconstructing the location, extent, and temporal dynamics of the sources. Additionally, we empirically demonstrated the generalizability of DeepSIF by imaging the epileptogenic brain tissue in a cohort of 20 drug-resistant focal epilepsy patients. The sources of the epileptiform discharges recorded from the preoperative scalp EEG were imaged and validated against clinical findings derived from the intracranial electroencephalography (iEEG) recordings and resection volumes in these patients. We further showed the applicability of the DeepSIF algorithm in imaging cortical sensory and cognitive processing evoked by visual and somatosensory stimuli in a total of 20 healthy human subjects. Through rigorous validations, we successfully demonstrated that DeepSIF can return robust and accurate imaging results concordant with the “ground truth” in human subjects.

Fig. 1.

The concept of the proposed DeepSIF. Brain activities are modeled by the spatiotemporal source model consisting of interconnected NMMs. Realistic synthetic EEG and the corresponding brain activities are generated and used to train a DNN for spatiotemporal source imaging. The trained model can be directly used to estimate physiological and pathological brain activities. In this study, using high-density interictal EEG data recorded from drug-resistant epilepsy patients and evoked EEG data recorded in healthy human subjects, we validated the accuracy and robustness of the DeepSIF approach in estimating underlying brain sources from scalp electrophysiological measurements.

Results

Model Training and Evaluation.

In the proposed DeepSIF model, the source space was segmented into 994 regions, and brain sources with various locations, sizes, and shapes were generated by randomly selecting a seed region and subsequently grouping neighboring regions to form patches of activity on the cortex. The time course of activity within all these 994 regions, whether that region was designated as either an active region (i.e., nonzero activation, such as spikes or evoked potentials) or a noisy background region, was generated by interconnected NMMs. The 76-channel EEG signals were generated by solving the EEG forward problem, with additive noise added to the scalp signal. The input of the DeepSIF model is the normalized noisy EEG signal, and the network is trained with the synthetic scalp–source pairs to provide the corresponding source activity for each spatiotemporal scalp pattern. The DeepSIF model contains a spatial module consisting of multilayer perceptrons to process and partially delineate the spatial information in the scalp data distorted by the volume conduction and a temporal module consisting of recurrent layers to process the spatiotemporal activities projected to the source space to ultimately provide the time course of activity of every brain region as the final source estimation (Fig. 2). Detailed data generation and network training procedures are described in Methods and SI Appendix, Supplementary Notes 1 and 2.

Fig. 2.

The proposed neural network structure. The spatial module consists of fully connected layers to process the spatial information at each time step, and the temporal module consists of recurrent layers to model the temporal dynamics of the brain sources. W, the weights of fully connected layers; LSTM, long short term memory.

Following the aforementioned procedure, a realistic training dataset containing two simultaneously active brain sources was generated and used to train a DeepSIF model. Three testing datasets containing one to three extended sources from random locations were generated separately, with different levels of white Gaussian noise added to the scalp signals to simulate noise-contaminated data (SNRs of 5, 10, 15, and 20 dB). The trained DeepSIF model is evaluated using metrics (Fig. 3A) quantifying its performance in localizing activity (Fig. 3D), estimating the extent (Fig. 3C), and delineating the temporal evolution (Fig. 3B) of underlying sources, with examples shown in Fig. 3E. The DeepSIF approach demonstrated excellent performance across all three datasets, with little performance degradation for the three-source dataset in all evaluation metrics, even though it was only trained on the two-source dataset, indicating its robustness and generalizability.

Fig. 3.

Model performance evaluation on the synthetic test datasets. (A) Metric definitions. Precision examines the false positives in the reconstruction, and it is defined as the ratio between the overlap and the reconstruction, where the overlap refers to the common area of the reconstruction and the ground truth. Recall, which can also be called true-positive rate or sensitivity, evaluates the model’s ability to detect all the true sources and is defined as the ratio between the overlap and the ground truth. High precision and recall values mean there are few spurious sources in the reconstruction, and the model can recover most true sources. For each region in the reconstructed source, the LE is defined as the minimum distance to the ground truth regions. One test sample consists of multiple cortical regions, and the LE for one test sample is the mean LE for all regions in the reconstructed source. Linear correlation is the correlation between the solution’s reconstructed waveform and the simulated waveform. (B) Temporal estimation. (Left) The linear correlation between ground truth and reconstruction for all three datasets (n = 47,712; one source: 0.99 ± 0.02; two sources: 0.91 ± 0.16; three sources: 0.85 ± 0.19). (Right) The mean correlation for all source locations displayed on a cortex. (C) Extent estimation. (Left) The precision (n = 47,712; one source: 0.88 ± 0.15; two sources: 0.79 ± 0.18; three sources: 0.76 ± 0.17) and recall (n = 47,712; one source: 0.95 ± 0.07; two sources: 0.83 ± 0.18; three sources: 0.75 ± 0.19) of three test datasets with one, two, and three sources. The distributions are demarcated within the 10th to 90th percentiles. The gray bars span the 25th to 75th percentiles, the white circles are the medians, and the colored horizontal bars are the means of the distribution. (Center) Simulated source area vs. estimated source area for three datasets combined. Data points show 5% of all the test samples in the datasets (n = 13,424 samples). The black line is the identity line provided for reference. (Right) The mean precision/recall for all source locations displayed on a cortex. (D) LE analysis. The LE distributions for all three datasets (n = 47,712; one source: 1.12 ± 2.14 mm; two sources: 1.55 ± 1.74 mm; three sources: 1.56 ± 1.66 mm). LE vs. SNR (n = 35,784; SNR = 5dB: 1.65 ± 2.12 mm; SNR = 10dB: 1.43 ± 1.95 mm; SNR = 15dB: 1.29 ± 1.67 mm; SNR = 20dB: 1.26 ± 1.67 mm). The error bar shows the standard deviation (Std). LE vs. depth. The plot shows the average LE for all sources within a particular depth. The error bar shows the standard error of mean (SEM). The mean LE for all source locations displayed on a cortex. (E) Imaging examples. Source locations and waveforms of ground truth and reconstructed activities for three sources (Left) and a single source (Right).

To investigate the efficacy of the trained DeepSIF model in estimating underlying source extents, the estimated sources’ area as a function of the simulated area is shown in Fig. 3C. High precision (0.81 $\pm$ 0.17) and recall (0.85 $\pm$ 0.18) are achieved across the one-, two-, and three-source scenarios for all SNR levels. A significant Pearson’s correlation of 0.83 is achieved (P < 0.001) between the simulated source areas and estimated source areas. The DeepSIF model also provides a low average localization error (LE; 1.41 $\pm$ 1.87 mm) for all source configurations across different SNR levels and source depth (defined as the distance of the source location to the closest EEG electrode). As shown in the LE cortical maps (Fig. 3D), the DeepSIF maintains a consistently low LE in almost all brain areas, including deep sources, where an average LE of 6 mm is reached. It can also provide robust estimates when a combination of deep and superficial sources is simultaneously coactivated (SI Appendix, Fig. S6). The DeepSIF estimates the temporal evolution of the source activities and the relative amplitudes among multiple sources with high accuracy (Fig. 3B, Movie S1, and SI Appendix, Fig. S11). Source magnitudes in their physical unit (nanoampere.meter, $nA.m$) can also be reconstructed from the DeepSIF output post hoc within a reasonable scale of what is expected and reported on current dipole magnitudes in the literature (SI Appendix, Supplementary Note 3). The consistent and robust performance of the DeepSIF approach gives it an advantage over conventional methods (SI Appendix, Fig. S12) in noninvasively imaging distributed brain sources. DeepSIF was further examined in two-source configuration tests where DeepSIF’s performance is depicted as the intersource distance (SI Appendix, Fig. S4) or the temporal correlation between sources (SI Appendix, Fig. S5) varies. Our results indicate robust performance regardless of distances or correlations among simultaneously active sources, indicating DeepSIF’s capability in distinguishing multiple closely located or correlated sources. These results show that DeepSIF can precisely estimate the location, extent, and temporal dynamics of brain sources under challenging conditions, such as low SNR, and deeply or closely located sources, which are highly desirable features for ESI applications (30, 38).

The impact of discrepancies between the training data and testing data was also evaluated to further investigate the generalizability of the trained DeepSIF model. Different noise types, source modeling protocols, head–brain boundary element models (BEMs), electrode locations, and temporal profiles for source activities (signal with different morphology) as well as various spectral profiles were used to generate various test conditions. Detailed information is described in SI Appendix, Supplementary Note 4 and Figs. S7–S10. The overall performance for all these test conditions is on par with the original test data, showing a superior imaging performance with at most a 1-mm increase in median LE, even though these test datasets were generated following different protocols. This demonstrates that the trained DeepSIF model is not overfitted to certain design choices in the training data and can provide excellent imaging results dealing with variations in the test data, which is of the utmost importance for deep learning (DL)–based ESI since the real data will not necessarily be identical to the synthetic training data.

Validation of DeepSIF in Epilepsy Patients.

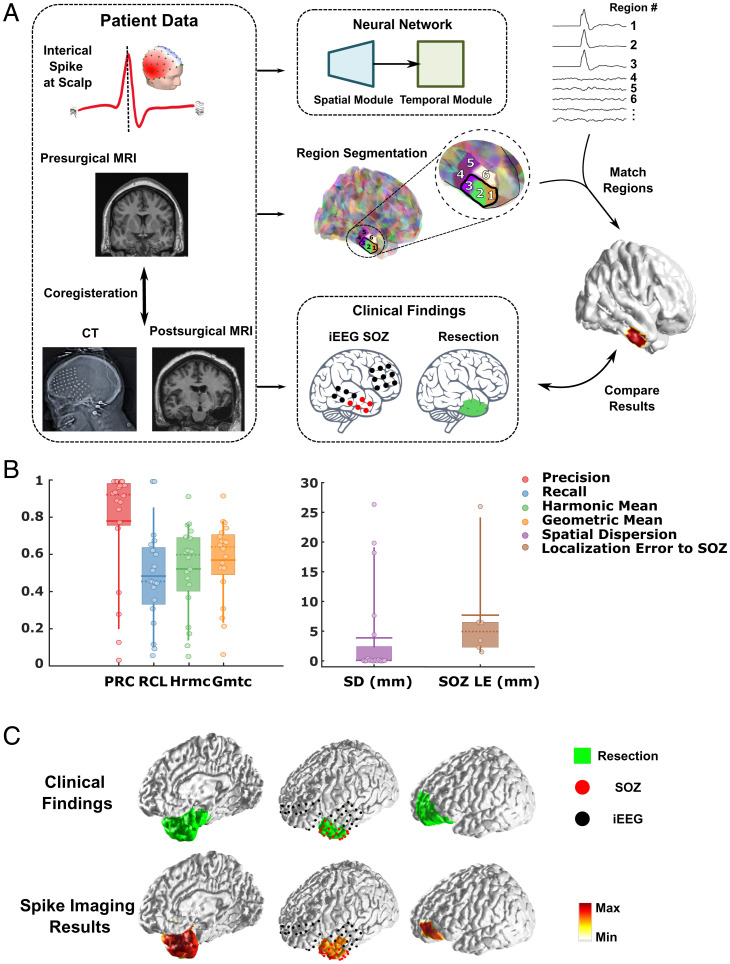
The trained DeepSIF model was rigorously validated in a cohort of 20 patients suffering from drug-resistant focal epilepsy who underwent resective surgery with seizure-free outcomes for at least a year following the surgery. Fourteen patients underwent iEEG study, and the intraoperative computer tomography (CT) images from which electrode locations were quantitatively determined were only available in six of these patients. High-density 76-channel preoperative scalp EEG recordings were acquired, and 18 $\pm$ 20 interictal spikes were identified for each patient. Averaged spikes in each patient were used as the input to the DeepSIF model, and the reconstructed activity from the segmented brain regions was mapped onto the patients’ cortical surface by matching the output of each region to its corresponding segmented region on an individual patient’s cortex using the individual subject’s MRI (Fig. 4A).

Fig. 4.

Clinical validation in drug-resistant epilepsy patients in comparison with surgical resection and iEEG-defined SOZ. (A) The study design. The interictal spikes were exacted and used as the input for the trained DeepSIF model. Each output waveform corresponds to one segmented region in the source space. The reconstructed waveform was compared with the clinical findings (resection region and iEEG SOZ electrodes) extracted from postoperational MRI and CT images. (B) Quantitative spike imaging results. The horizontal solid lines show the means, the dashed lines show the medians, the boxes span the 25th to 75th percentiles of the data, the vertical bars span the 10th to 90th percentiles of the data, and circles represents individual patients. The overlap area between the reconstructed sources and the resection area was calculated. The precision or recall is defined as the ratio between the overlap and the reconstruction or the resection region. The harmonic and geometric means of the precision and recall are also included. The spatial dispersion is defined as the mean distance of each reconstructed region to the resection area weighted by the reconstructed source map. Extent estimation and spatial dispersion with respect to resection regions are calculated for all 20 patients (precision: n = 20, 0.79 ± 0.31; recall: n = 20, 0.49 ± 0.25; harmonic mean: n = 20, 0.53 ± 0.23; geometric mean: n = 20, 0.58 ± 0.21; SD: n = 20, 3.87 ± 7.92 mm); the SOZ LE is calculated as the average distance between every SOZ electrode and the solution boundary for six patients with CT images of the iEEG electrode available (LE: n = 6, 7.45 $\pm$ 8.91 mm). Equations to calculate the metrics are described in SI Appendix, Supplementary Note 6. Gmtc, geometric; Hrmc, harmonic; PRC, precision; RCL, recall. (C) Examples of spike imaging results along with the surgical resection outcome and iEEG-defined SOZ.

We compared the interictal spike imaging results with the resection area to calculate the precision, recall (as well as the harmonic and geometric means of the precision and recall), and spatial dispersion (Fig. 4B). A high precision value with a median of 0.93 is achieved, which means that the noninvasive DeepSIF source imaging results from epileptiform spikes are in good concordance with the clinical ground truth defined by the resection region without having nuisance spurious activities extended outside the epileptogenic region. The spatial dispersion of the imaging results compared with the resection is 3.87 $\pm$ 7.92 mm. Examples of spike imaging are shown in Fig. 4C, indicating the excellent performance of the DeepSIF as compared with the surgical resection outcome and iEEG-defined seizure onset zone (SOZ). The interictal spikes from iEEG recordings and the spike waveform estimated by DeepSIF are compared for two patients in Fig. 5, and a high correlation of ∼0.95 between the two waveforms was achieved for both patients. Examples of the estimated source distributions over time are presented in Movies S2 and S3 and SI Appendix, Fig. S13, where the evolution of source activities as reconstructed by the DeepSIF model are also depicted. Note that even though the iEEG spikes are not recorded simultaneously with scalp spikes, they still serve as empirical evidence to indicate the efficacy of DeepSIF in estimating the temporal dynamics of the signal given that epileptic biomarkers have major similarities over time due to the same underlying pathology giving rise to these signals at different times.

Fig. 5.

Comparing estimated source time courses from EEG with iEEG recordings. (A) DeepSIF spike imaging results and iEEG electrodes (in red) from which the interictal spike activities were selected are plotted in two patients. (B) DeepSIF output waveform in the source regions (orange) and the averaged iEEG spikes (blue) for the two patients in A. Procedures for generating the iEEG waveform are described in Methods. Patient numbers correspond to the numbers in SI Appendix, Table S1.

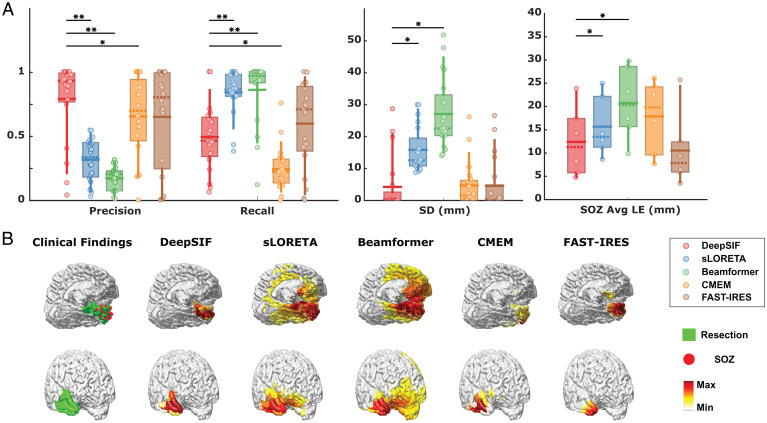
Fig. 6 shows the comparison of DeepSIF with other benchmark ESI methods: standardized low-resolution brain electromagnetic tomography (sLORETA) (26), unit–noise–gain minimum variance Beamformer (39), coherent maximum entropy on the mean (CMEM) (40), and fast spatiotemporal iteratively reweighted edge sparsity (FAST-IRES) (5). DeepSIF performs better compared with sLORETA and Beamformer in terms of localization (statistically significant). As to extent estimation, DeepSIF has larger precision and recall values compared with CMEM (statistically significant) and is on par with FAST-IRES. However, DeepSIF has the advantage of fast inference time over the two methods, providing a speedup factor of several thousands (SI Appendix, Supplementary Note 5). These validation results demonstrated the validity and excellent performance of the proposed DeepSIF approach to reliably image and localize the epileptogenic tissue.

Fig. 6.

Interictal spike imaging results in 20 drug-resistant focal epilepsy patients using DeepSIF, sLORETA, Beamformer, CMEM, and FAST-IRES. (A) Quantitative results. The horizontal solid lines show the means, the dashed lines show the medians, the boxes span the 25th to 75th percentiles of the data, the vertical bars span the 10th to 90th percentiles of the data, and circles represent individual patients. Extent estimation and spatial dispersion with respect to resection regions are calculated for all 20 patients (n = 20; [precision] DeepSIF: 0.79 ± 0.31; sLORETA: 0.31 ± 0.16; Beamformer: 0.17 ± 0.09; CMEM: 0.65 ± 0.32; FAST-IRES: 0.65 ± 0.40; [recall] DeepSIF: 0.49 ± 0.26; sLORETA: 0.84 ± 0.17; Beamformer: 0.86 ± 0.25; CMEM: 0.24 ± 0.17; FAST-IRES: 0.60 ± 0.33; [spatial dispersion] DeepSIF: 3.87 ± 7.72 mm; sLORETA: 14.50 ± 6.28 mm; Beamformer: 24.76 ± 9.90 mm; CMEM: 4.30 ± 6.39 mm; FAST-IRES: 4.16 ± 7.51 mm). The SOZ LE is defined as the average distance between every SOZ electrode and the solution boundary. On the other hand, we also calculated the averaged distance of every reconstructed source region to the closest SOZ. The averaged value of these two (which we call SOZ avg LE) is calculated for the six patients with CT images of the iEEG implantations (n = 6; DeepSIF: 12.33 ± 7.44 mm; sLORETA: 15.58 ± 6.41 mm; Beamformer: 20.66 ± 7.78 mm; CMEM: 17.78 ± 7.75 mm; FAST-IRES: 10.48 ± 8.01 mm). The paired one-sided Wilcoxon signed rank test was used with statistical significance cutoffs. SD, spatial dispersion. *P < 0.05; **P < 0.005. (B) Examples of interictal spike imaging results along with the clinical findings. The color bar refers to reconstructed sources. The green color depicts resective areas, and the red dots illustrate iEEG-defined SOZ.

Source Imaging of Cortical Sensory and Cognitive Processing in Healthy Humans.

To further test the applicability of the proposed DeepSIF to image brain activation in healthy human subjects, we evaluated a trained DeepSIF model on three publicly available datasets: 1) a visual evoked potential dataset available from the MNE-Python toolbox (59-channel EEG) (41), 2) a somatosensory evoked potential dataset (60-channel EEG) (42), and 3) a visual two-stimulus oddball dataset (64-channel EEG) (43). A DeepSIF model was trained with the same synthetic source activity (as in the clinical validation study), but the lead-field matrix was derived from a 64-channel Biosemi EEG configuration with the same template MRI used throughout the study. The evoked potential data were mapped to the 64-channel montage through spherical spline interpolation (44), and these interpolated data were provided as the input to the trained DeepSIF model.

In the visual evoked potential experiment, checkerboard patterns were presented into the right visual field (41); 56 events were averaged, and the P100 component was identified at 93 ms after the stimulus. The source location provided by the DeepSIF model shows that the source of P100 lies in Brodmann area 17 (BA17) and BA18, the primary and secondary visual areas, as indicated by the green shading in Fig. 7. The source of the early P100 component is usually believed to be generated by the lateral extrastriate cortex (45), which is consistent with our DeepSIF result.

Fig. 7.

DeepSIF imaging results for cortical sensory and cognitive processing in 20 healthy human subjects. The figure shows the topographical maps at the peak of the events, the EEG channels of interest, the relevant source regions, and the source reconstruction of the DeepSIF model. (A) Visual evoked potential for one subject. (B) Somatosensory evoked potential for one subject. Green areas show BA17 and 18 in A and BA1 to 3 in B. (C) Event-related potential evoked by visual oddball stimuli for 18 subjects. The averaged waveform for all subjects is shown in black, the gray shade shows the SEM, and the orange dots indicate the P300 peak latency for each subject. Expected P300-related source regions are labeled as PPC, IT, and SMA.

In the somatosensory evoked potential experiment, electric stimuli were delivered to the little finger. Five hundred events were averaged, and a P30 component was identified at 29 ms (42). The postcentral gyrus (primary somatosensory cortex; BA1-3) is generally believed to be the region that responds to the electric finger stimulation with a latency in the 20- to 35-ms range (46). The DeepSIF localizes the source to the primary somatosensory cortex, indicating its ability to correctly identify physiological signals involved with cortical sensory processing.

In the visual two-stimulus oddball experiment, around 270 images were presented to 18 subjects. Around one of seven of the images was an oddball image, and subjects were instructed to identify the oddball images with a button press (43). The largest positive peak between 250 and 600 ms, in channel Cz, was identified for each subject. The source imaging results at the peak were averaged and plotted in Fig. 7C. The most prominent activity identified by the DeepSIF model lies in the posterior parietal cortex (PPC), which has been shown to participate in behaviors like decision-making, movement planning, and higher-order cognitive processing (47). Activities in other regions, including inferior temporal (IT) cortex and supplementary motor area (SMA), were also identified, which is consistent with fMRI and intracranial studies of the P300 components (48, 49). Note that the training dataset for the clinical data in epilepsy patients and the evoked potential data in healthy subjects is the same, indicating the generalizability of the proposed DeepSIF model in processing different types of signals even when trained on a different type of synthetic training data from the testing dataset.

Discussion

We have proposed DeepSIF, which combines mesoscale neurophysiology knowledge, captured by the synthetic training data generated by interconnected NMMs, with highly effective computational structures, DNNs with recurrent layers, to enable spatiotemporal imaging of brain dynamics from noninvasive electromagnetic scalp measurements. The trained DeepSIF model demonstrates superior performance for estimating the location, extent, and temporal activities of the brain sources and can reliably and robustly localize and image physiological or pathophysiological signals across different subjects, outperforming the conventional benchmark methods. The generalizability of the model on real data is a crucial advancement for DL-based ESI methods, demonstrating its potential in being applied to various applications, including presurgical planning for epilepsy patients (19–21) or real-time ESI studies (18, 50).

Due to the ill-posed nature of the ESI problem, a wide majority of the ESI methods explicitly define regularization terms as part of the optimization objective, including imposing constraints on solutions’ energy (26, 51), covariance (27), or sparsity levels (52). While these methods have demonstrated success in many applications, formulating and optimizing the proper priors are challenging (30). For instance, Euclidean norm based methods, such as sLORETA, are widely employed due to their effectiveness and simple closed-form solutions, but their estimates tend to be overly diffused. On the other hand, sparsity-inducing methods provide accurately localized but extremely focal solutions, losing information about the extent of the underlying brain activity. Formulating the proper and easy to use priors that reflect all characteristics of underlying sources is not a trivial task. Improper priors hugely affect the solutions’ quality and what can be subsequently inferred from such estimates. On the other hand, many state-of-the-art biophysical models incorporate recent advances in our understanding of the brain dynamics and brain functions, but it is challenging to formulate these into explicit mathematical terms as a more detailed prior in current ESI frameworks. Deep learning approaches can provide an alternative for solving ill-posed source imaging problems by incorporating biophysical models into ESI solutions.

The proposed DeepSIF method is a fully data-driven approach, in which by training a DNN with a large amount of sensor-source mapping examples, the essence and implicit characteristics of the brain activity distributions are learned to circumvent the need for explicitly defining priors for the ESI optimization problem. The distribution of the training dataset must reflect that of the real signals the network will encounter at its intended application. As such, it can be said that while the researchers do not explicitly design priors in predefined mathematical formulas, they implicitly provide them to the algorithm by ensuring a diverse training dataset. Once the DeepSIF model is trained, it can be directly applied to real test data with minimal user intervention as the prior information is “remembered” in the weights of the trained network. This increases the reproducibility and accessibility of the ESI technology since expert knowledge in parameter selection or model tunning represents a bottleneck for the wide adoption of ESI imaging, making it easier to translate source imaging assessment as a standard tool in various clinical settings (8, 31). Furthermore, the trained neural network is efficient and fast to execute (SI Appendix, Supplementary Note 5) (i.e., to solve the ESI problem), making the proposed approach appropriate for real-time applications, such as brain–computer interface applications (18).

There have been few attempts to solve the dipole fitting problem using artificial neural network approaches (53, 54), where a few dipoles were modeled and localized, not fully representing the spatiotemporal distribution of brain activation. To properly model the complex brain activities using neural networks, it is critically important to have big-enough labeled datasets, with enough variations of the source and scalp data. Due to practical limitations in acquiring simultaneous brain and scalp measurements from all possible source locations in the brain (55), a synthetic dataset is a natural alternative. A recent study (56) that attempted to solve the distributed ESI problem using neural networks focused on imaging the source variations in the spatial domain with biophysical patch–source models and merely tested the model on real recordings from a single subject. Since the neural network learns to perform the ESI task based on the properties of the training data, simplified source models, because of limited or incomplete modeling of the underlying brain sources, could be one of the reasons that hinder the performance of DL-based ESI methods when applied to real data recorded from different subjects.

Recent advances in biophysical modeling of brain dynamics provide us the opportunity to incorporate neuroscience knowledge about the brain into the ESI problem as well as realistic training data for the DL-based ESI. The source model for DeepSIF is a large-scale brain network model consisting of biophysically inspired interconnected mesoscale NMMs. Compared with the physical source models that most source imaging approaches utilize, an NMM models neuronal activation by describing the local interactions among neuronal subpopulations within an ensemble (i.e., primary neurons and neuron subpopulations for excitatory or inhibitory feedbacks) through a set of nonlinear differential equations based on physiologically meaningful parameters. Once the equation parameters are set, NMMs will dynamically generate signal dynamics with no further user input (SI Appendix, Supplementary Note 1 and Fig. S1 have more details). They are capable of providing various dynamics that manifest different temporal, spectral, and higher-order statistical features (33), which are expected to better resemble spatiotemporal brain activities, such as interictal epileptiform discharges, ictal activities, and alpha oscillations to name a few (35, 37, 57). It has even been suggested that such models are useful in determining stimulation or intervention sites (58). The large-scale modeling capability and realistic neuronal temporal dynamics make such models a suitable simulator to generate synthetic labeled training data for ESI tasks (34). While various studies showed the strength and capability of such models to capture realistic brain dynamics, no prior work has employed these models to develop a noninvasive imaging and modeling framework and rigorously validated the results using ground truth, such as intracranial recordings and surgical resection outcomes in epilepsy patients. Our proposed deep learning framework (59) represents an effort at integrating biophysically inspired mesoscale models of neuronal activation, as embodied by NMMs, into DL-based ESI for distributed source imaging. The use of biophysically inspired brain network models for generating big training data represents an important undertaking as the performance, usability, and robustness of a neural network are based upon and bounded by the quality and nature of its training examples.

With this newly proposed training framework and training in a big synthetic dataset consisting of ∼300 million scalp topographies, we demonstrated that the DeepSIF model has a superior performance by producing smaller LEs and higher precision and recall. The DeepSIF model also shows robustness for challenging conditions, such as localizing noisy signals, deep sources, and closely located or correlated sources. It is worth noting that DeepSIF takes normalized EEG signals as input and outputs normalized estimates of source activity during the training; therefore, DeepSIF cannot directly provide the physical magnitude of the estimated sources. However, DeepSIF can provide reasonable estimates consistent with empirical values reported in the literature after a simple postprocessing step (SI Appendix, Supplementary Note 3). In many applications, an accurate estimate of the location, extent, relative amplitudes of different sources, and time course of sources’ activity should be what is needed without necessarily having to estimate actual source magnitudes in physical units.

Although advanced source modeling provided ample variations of sources compared with physical patch models, the real testing scenario will not share the exact same distribution as the synthetic training data. Some discrepancies are expected, and we substantially modified the forward modeling protocol to simulate testing conditions that one might encounter in real applications that are not included in the training data (details are in SI Appendix, Supplementary Note 4), such as different head geometries, temporal waveforms for the signal, tissue conductivity ratios, sensor locations, noise types, etc. The trained DeepSIF model demonstrates a high level of robustness dealing with these mismatches. Although a limited amount of performance decrease is expected and observed, the overall performance remains at a superior level across all test conditions. This is because the realistic training datasets have provided enough spatial and temporal features about the key features of underlying sources to the neural network during the training phase that the network’s performance is consistently satisfactory for conditions that might be challenging for conventional methods.

This generalizability and robustness are also reflected in the real data evaluation. DeepSIF trained on a generic head/brain model can be successfully applied to real data from a cohort of focal epilepsy patients with certain spatiotemporal robustness. The solution can then be warped to the individual anatomical space to coregister with other anatomical or functional information, including the resection region or the SOZ electrodes. Note that most of the patients included in the current study are temporal lobe epilepsy (TLE) cases. TLE surgery often follows standard procedures, where selected regions of the temporal lobe are removed, and up to 70% of TLE surgeries can achieve seizure freedom outcome (60). However, there is always a trade-off between an aggressive resection to guarantee the removal of all epileptogenic tissue and a conservative resection to preserve more cognitive functions with the risk of residual epileptogenic tissue (61). The final resection region is not solely dependent upon electrophysiological signals recorded or inferred at the brain level. Multiple factors, including the patient’s preferences, are taken into consideration; thus, the resection region is not the ground truth for the epileptogenic areas. However, since our patient cohort achieves seizure-free outcome, it is reasonable to assume that the resection region is a valid benchmark to validate our imaging results, with the possibility of it being larger than the actual epileptogenic areas. We have demonstrated quantitatively that the DeepSIF spike imaging coincides well with the resection region, with a high precision value of 0.79 (which translates to low false positives). DeepSIF also shows significantly superior performance compared with most of the benchmark methods. Although no statistically significant differences were observed between DeepSIF and FAST-IRES (Wilcoxon rank sum test), DeepSIF can provide the spike imaging results in tens of milliseconds without the need to tune its parameters for every new instance of data it encounters. On the other hand, FAST-IRES is formulated within the optimization framework, which requires hyperparameter selection and tuning for instances of new data and component selection for the purpose of identifying the time basis function for each patient individually, and it takes minutes to generate one solution. DeepSIF as a fast and effective source imaging pipeline could make a significant impact on the presurgical planning in drug-resistant epilepsy patients by providing a high-resolution map of the epileptic activities from noninvasive scalp EEG.

Moreover, we cross-validated DeepSIF on three types of evoked potentials in a total of 20 healthy human subjects from three public datasets. Even though it is not trained with evoked potential data, the DeepSIF provides concordant results with neuroscience understandings, demonstrating the generalizability of the framework on different subjects as well as different signal types. The consistent performance on various real datasets is a cornerstone for DL-based ESI imaging based on realistic NMM training datasets, indicating its potential in various ESI applications. Special attention, however, has to be paid to interpreting the visual oddball results. Note that frontal regions and the cingulate cortex are also believed to be associated with the generation of P300, while DeepSIF only identified a limited involvement of the cingulate cortex. Studies have shown that the frontal lobe signal is weaker in the two-stimulus paradigm compared with the three-stimulus paradigm (49), and it is more easily evoked by auditory stimuli (62). Studies also found that parietal areas and the IT cortex generated the scalp visual P300 component, whereas the prefrontal cortex and cingulate gyrus sources make little to no contribution to the scalp potential (48, 63). Nevertheless, it is possible that DeepSIF might have missed a weak frontal source in the two-stimulus visual oddball experiment or underestimated the involvement of the cingulate cortex. Future investigation with different event related potential (ERP) datasets or training a network specifically for ERP responses could potentially help explain the current DeepSIF results, providing better insight into the problem.

Although a high level of generalizability and robustness was shown in our test results, there are cases in real applications that call for more careful consideration before using the current approach. For instance, patients with prior resections or large brain lesions or neonatal patients with possibly significantly different head shapes will introduce significant anatomical differences in the forward modeling, in which case, DeepSIF imaging results from general head models might have a larger deviation, needing further tuning or retraining. Note that the proposed framework does not limit the source model and the network architecture to NMMs and recurrent neural networks. The framework can implicitly incorporate arbitrary prior knowledge into the solution through complex source models, providing the potential to include the most advanced forward models in the field as they are developed and validated. We have demonstrated one feasible implementation of the framework using NMM networks and tested it on scalp EEG data. The DeepSIF is a versatile framework that can incorporate various source models and network designs and be applied to both EEG and MEG data with careful modifications.

To conclude, we have proposed a non-conventional data-driven dynamic functional source imaging framework by means of DNNs constrained with biophysically inspired brain network modeling. The present results demonstrate the superior performance of DeepSIF over conventional methods in a series of numerical experiments and real data analysis in a sizeable cohort of human subjects, including healthy subjects and patients with drug-resistant epilepsy, with robustness and generalizability. The DeepSIF promises to establish ESI as a widely adopted approach for spatiotemporal dynamic human brain imaging, aiding clinical diagnosis and treatment of a variety of neurological and mental diseases.

Methods

DeepSIF Outline.

The distributed source imaging problem can be formulated mathematically as an optimization problem. For this underdetermined optimization problem to be solvable, regularization terms or prior assumptions are necessary. Typically, assumptions about the spatial distribution or characteristics of underlying sources as well as their temporal dynamics need to be made. Naturally, this translates to solving optimization problems of the following form:

$$\widehat{\mathbf{j}}={\text{argmin}}_{\mathit{j}}\parallel \mathbf{\varphi }-\mathcal{K}\mathbf{j}{\parallel }_2^2+{\mathcal{ℛ}}_s\left(\mathbf{j}\right)+{\mathcal{ℛ}}_{\mathcal{T}}\left(\mathbf{j}\right).$$ [1]

In Eq. 1, $\varphi$ is a matrix of EEG (or MEG) recordings over a certain time interval; $\mathcal{K}$ is the lead-field matrix that models how current densities, $\mathbf{j}$, are related to scalp recordings; ${\mathcal{R}}_s$ is a regularization term that captures spatial priors; and ${\mathcal{R}}_{\mathcal{T}}$ is a regularization term that expresses temporal priors. Implementing Eq. 1 using a DNN has the advantage that we do not have to explicitly express the regularization terms, ${\mathbf{ℛ}}_{\mathit{s}}$ and ${\mathbf{ℛ}}_{\mathcal{T}}$, and we can let DNN structures learn these priors from training examples. Our proposed structure, as depicted in Fig. 2, consists of a spatial module to process and prefilter the spatial distribution of the scalp data and a temporal module to model the temporal relationship of the sources to ultimately provide the time course of activity of every brain region as the final source estimation. To train a neural network, a large amount of training data must be available. An aspect of the proposed approach is to use a biophysically inspired spatiotemporal brain network model for generating the training data that describes both the spatial and temporal features of the brain activity.

Simulating Synthetic Dataset.

The template T1-weighted MRI (fsaverage5) was used to get the segmentation of the cortical surface, the skull, and the scalp. The cortical surface was segmented into 994 similarly sized regions in Freesurfer (64). To simulate sources with enough spatial variations, a region-based growing procedure was used for each source. One of the parcellated brain regions was randomly chosen as the seed, and its neighboring regions were randomly selected and grouped with the seed region, forming patches of activation in the source space (details are in SI Appendix, Supplementary Note 1 and Fig. S2).

The time course of activity within all 994 regions was generated by coupled Jansen–Rit models. The model can simulate brain signals similar to resting-state brain activity with default parameters (36); when the average excitatory synaptic gain (defined as $A$) is increased, it can generate spike-like activities (37). We assigned the seed region to have an increased excitatory synaptic gain ($A$) value (from the default 3.25 to 3.5, 3.55, or 3.6) and kept the NMM parameters of the other regions as the default. Example outputs of the NMM models from the active source region (increased $A$ value) and nonactive source region (default NMM parameters) are shown in SI Appendix, Fig. S1C. The brain network modeling was conducted in The Virtual Brain simulator (34). The details of the Jansen–Rit model and brain network simulation are described in SI Appendix, Supplementary Note 1.

The 76-channel electrode layout (5, 51) based on a 10-10 montage was used for the EEG electrode configuration. The lead-field matrix was calculated using the three-shell BEM model with openMEEG (65, 66) in Brainstorm with default settings (67). To enable imaging multiple activated sources, a two-source training dataset was generated, and scalp signals were simulated based on the superposition principle. The NMM signal from each region was scaled so that the ratio between the activity signal and the background signal (from other regions) was scaled to a random number between 10 and 20 dB. There are two reasons behind this step. First, the NMM models the temporal dynamics of the cortical regions by generating the mean postsynaptic potentials of the pyramidal cells in the unit of $V$. Assuming current dipole strength to be roughly proportional to the average membrane potential of the excitatory population (68), a scaling process is needed to transform the NMM output to the correct unit for the forward calculation (SI Appendix, Supplementary Note 3). Second, by following such a procedure, we can be certain that sources with different magnitudes and levels of SNR will be present in scalp recordings to cover various source distributions in the training and testing datasets. Afterward, different levels of Gaussian white noise were added to the scalp potential to simulate noise-contaminated EEG measurements, so that the SNR level of 5, 10, 15, or 20 dB was obtained. Both the source and sensor space signals were scaled by their maximum absolute value to have a maximum or minimum of 1 or −1 (depending on the polarity of the signal). In total, the training dataset contained 620,256 spatiotemporal samples consisting of over 300 million spatial topographical distributions. The test data were separately generated following the same protocol. Datasets containing one to three sources were generated with 47,712 samples in each dataset. Examples of the waveform and the topological maps of the synthetic EEG data are shown in SI Appendix, Fig. S3.

Training the DNN.

The spatial module was composed of residual network (ResNet) architecture (69) composed of fully connected layers, which process the spatial information at each time point separately. One ResNet block (ResBlock) was composed of two fully connected layers with a skip connection, and exponential linear unit (ELU) activation function (70) was used. For the ResBlock with different input and output dimensions (ResBlock as shown in Fig. 2) (dimension increased from 64 to 500), the skip connection was another fully connected layer to account for the dimension change. Another fully connected layer with ELU activation function and output dimension 500 followed ResBlock. The temporal module aggregated the output from the spatial module over time and finally, provided the spatiotemporal activity of the source. It had three hidden layers and employs long short-term memory (LSTM) (71) with hyperbolic tangent activation units. The first LSTM layer had an input size of 500 and output size of 994, and the other two layers had the same input and output dimension of 994 (SI Appendix, Supplementary Note 2).

During training, the loss function is the mean square error loss between the model output and the ground truth source activity. The Adam optimizer (72) was used for the training with a weight decay of 1e-6. The initial learning rate was 3e-4 and decreased by a factor of 10 for every 10 epochs. The batch size was 64. The whole network was implemented in PyTorch and trained on one NVIDIA Telsa V100 graphics processing unit (73).

Ethics Statement.

Our clinical study, including data collection and data analysis, was approved by and performed in accordance with the regulations of the institutional review boards of Carnegie Mellon University and the Mayo Clinic, Rochester. Patients gave their informed consent to participate in this study. The evoked EEG data were obtained from anonymous open-source datasets freely available online that complied with institutional ethical standards.

Patient Information.

A total of 20 patients (14 females; ages 34 $\pm$14 y) were included in this study. All patients suffered from drug-resistant focal epilepsy and underwent surgical treatment at Mayo Clinic, Rochester. The resection region was determined by coregistering the pre- and postsurgical MRI images in Curry (Compumedics). Fourteen patients underwent iEEG study, and six of them had CT images to quantitatively determine the electrode locations. The outcome of the surgical intervention was scored based on the International League Against Epilepsy (ILAE) system by the physicians during the follow-up period (20 $\pm$ 9 mo). Eighteen patients were scored as ILAE 1, and two were scored as ILAE 2 (SI Appendix, Table S1).

High-density EEG electrodes (76 in total) were glued individually based on a 10-10 montage with the reference electrode at CP_z. The EEG signals were recorded with a sampling rate of 500 Hz using the Xltek EEG amplifier (Natus Medical Incorporated). Interictal spikes were extracted from the EEG recordings and band-pass filtered between 0.5 and 40 Hz.

Patient Analysis.

The interictal spikes were averaged for each patient and scaled by the maximum of the absolute value. The output source reconstruction was averaged for a 100-ms window around the peak of the spike, and a threshold was determined using Otsu’s (74) thresholding technique. Note that from the reconstruction examples (Figs.4 and 6), the activities in the identified source regions had a much larger magnitude compared with other regions, such that the threshold value has a relatively small impact on the evaluation metrics. The obtained results were then warped to each subject’s brain by segmenting the brain following the same segmentation atlas as used in the generic brain model in Freesurfer, mapping the network output for each region on the generic cortex to the regions in the patient’s individualized cortical space. A similar approach, warping a spherical general model to a patient’s individual geometry (75), has been shown to be robust and consistent in the conventional source imaging literature (76).

The data analysis results for sLORETA and unit–noise–gain minimum variance Beamformer were calculated using MNE-Python (version 0.22.0) (41); CMEM was calculated using the BrainEntropy plug-in (version 2.7.3) in Brainstorm, and FAST-IRES was calculated using the published code.* Otsu’s (74) method was used to find the extent of the imaging solution when calculating the precision and recall for all methods except FAST-IRES, which does not need thresholding to identify the source.

In two TLE patients, iEEG interictal spikes were extracted by the researcher and clustered using the k-means algorithm into spike clusters. The scalp EEG channel with the maximum magnitude was extracted, and the linear correlation between the time course extracted from this channel with the centers of the iEEG interictal spike clusters was calculated. Since iEEG spikes may contain different spike types from the spikes observed in EEG, this correlation was used to select the iEEG cluster spike type that is most similar to the morphological features of the scalp EEG spikes. The iEEG spikes in the selected cluster were averaged and compared with the DeepSIF imaging result in Fig. 5.

Sensory and Cognitive Data Analyses.

In the visual evoked potential analysis, the EEG data were initially filtered between 0 and 40 Hz for the subsequent analysis. In the somatosensory evoked potential analysis, data were filtered between 1 and 250 Hz in Brainstorm. In the visual oddball dataset analysis, the cleaned EEG data (line noise removal, interpolate bad channels, and independent component analysis-based artifact removal) provided by ref. 43 were used for the analysis with band-pass filtering at 0.5 to 30 Hz. Only the epochs with the correct button-press responses were selected and averaged for each subject. There are 27 $\pm$ 3 epochs in the target (oddball) group. Difference waveforms between the target and nontarget groups were calculated and used for imaging analysis (48).

Data Availability

Custom codes and EEG data on 20 epilepsy patients have been deposited in GitHub (https://github.com/bfinl/DeepSIF) (77) and Figshare (https://doi.org/10.6084/m9.figshare.19688043) (78). All other study data are included in the article and/or SI Appendix.