Incorporating family history of disease improves polygenic risk scores in diverse populations

Summary

Polygenic risk scores (PRSs) derived from genotype data and family history (FH) of disease provide valuable information for predicting disease risk, but PRSs perform poorly when applied to diverse populations. Here, we explore methods for combining both types of information (PRS-FH) in UK Biobank data. PRSs were trained using all British individuals (n = 409,000), and target samples consisted of unrelated non-British Europeans (n = 42,000), South Asians (n = 7,000), or Africans (n = 7,000). We evaluated PRS, FH, and PRS-FH using liability-scale R², primarily focusing on 3 well-powered diseases (type 2 diabetes, hypertension, and depression). PRS attained average prediction R²s of 5.8%, 4.0%, and 0.53% in non-British Europeans, South Asians, and Africans, confirming poor cross-population transferability. In contrast, PRS-FH attained average prediction R²s of 13%, 12%, and 10%, respectively, representing a large improvement in Europeans and an extremely large improvement in Africans. In conclusion, including family history improves the accuracy of polygenic risk scores, particularly in diverse populations.

Graphical abstract

Highlights

• •Polygenic risk scores perform poorly when applied to diverse populations
• •Including family history improves prediction accuracy
• •The improvement is particularly large in diverse populations

Polygenic risk scores (PRSs) and family history (FH) of disease provide valuable information for predicting disease risk, but PRSs perform poorly when applied to diverse populations. Hujoel et al. explore methods for combining PRSs and FH and find that including FH improves prediction accuracy, particularly in diverse populations.

Introduction

Polygenic risk scores (PRSs) derived from genetic data can provide information for predicting disease risk, enhancing prospects for clinical utility.^1,2 However, a limitation of PRS methods is their poor cross-population transferability.3, 4, 5, 6, 7 Family history (FH) of disease can provide complementary information about disease risk,8, 9, 10, 11 consistent with the rich history of leveraging data from ungenotyped but phenotyped relatives in analyses of quantitative traits in livestock.11, 12, 13, 14 In particular, FH has the potential to alleviate the poor cross-population transferability suffered by PRS. Combining PRS and FH information is an appealing paradigm for predicting disease risk, but it is currently unclear how to optimally combine these two sources of information. Previous studies that combined PRS and FH information restricted the PRS component to genome-wide significant loci,^9,15,16 instead of leveraging genome-wide polygenic signals; did not differentially incorporate FH for each type of relative,^9,15, 16, 17, 18, 19 to allow for differential environmental effects²⁰ (in particular, So et al.⁹ relies on external narrow-sense heritability estimates); and did not model contributions of PRS and FH that vary as a function of the target population,^9,15, 16, 17 to optimize cross-population transferability. In addition, So et al.⁹ did not incorporate covariates; the study is not applicable to UK Biobank data, in which sibling history is reported as a binary variable (at least one sibling has the disease), rather than the number of affected siblings; and relies on external data to estimate model parameters. Other studies only considered PRS and FH information separately.^10,21

Here, we develop a framework for predicting individuals’ risk of disease conditional on both their PRS and their FH (PRS-FH), using either a logistic model²² or a liability threshold model.²³ We show via simulations and application to complex diseases from the UK Biobank²⁴ that incorporating FH using PRS-FH improves the accuracy of polygenic risk scores, with a particularly large improvement in diverse populations. The logistic model outperforms the liability threshold model in analyses with covariates, and we thus recommend the use of the logistic model.

Results

Overview of methods

We considered two PRS-FH methods based on a logistic model (PRS-FH_log) and a liability threshold model (PRS-FH_liab), respectively (see STAR Methods). Both methods require a large training sample to estimate SNP effect sizes for the PRS (in this study, we use European training data), and a small additional training sample (e.g., N_eff ≥ 500; see STAR Methods) from the target population to fit PRS-FH model parameters, which are specific to the target population. Both PRS-FH_log and PRS-FH_liab allow for sibling history to be reported as the presence or absence of at least one affected sibling (together with the total number of siblings), as in the UK Biobank. Both PRS-FH methods can be extended to incorporate covariates. We have publicly released open-source software implementing both methods as well as model parameters (specific to each target population) for both methods (see data and code availability).

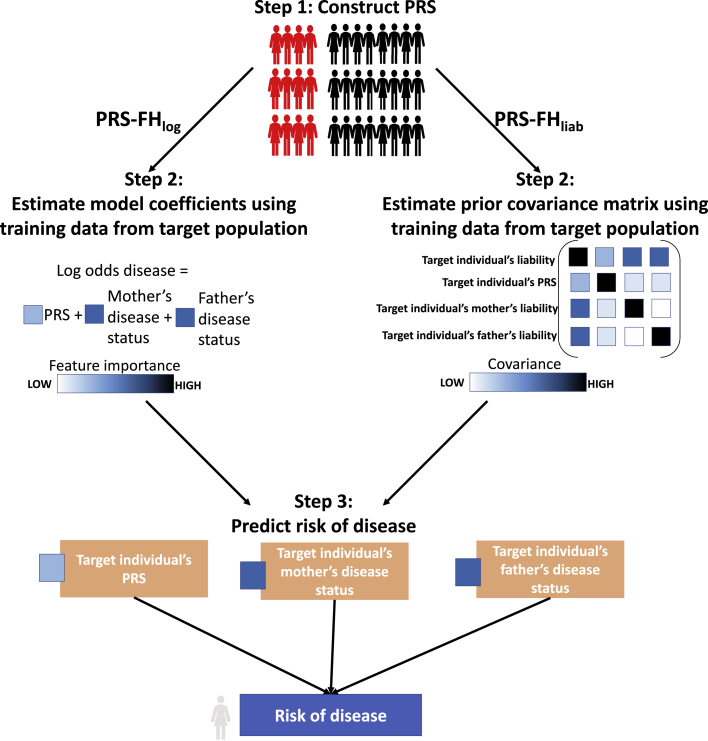
The PRS-FH_log method relies on a logistic model and consists of 3 main steps (Figure 1): (1) compute PRS in all target population individuals by applying standard methods to training data, (2) use the training individuals from the target population to estimate logistic model coefficients, and (3) for each target individual, compute their predicted risk of disease, conditional on their PRS and the disease status of their first-degree relatives. In step 1, we apply BOLT-LMM^25,26 to training data to jointly fit SNP effect sizes under a non-infinitesimal model, and compute PRS in target population individuals using these SNP effect sizes. In step 2, we estimate the contributions of the PRS and the disease status of first-degree relatives (mother, father, siblings; we allow different coefficients for each type of relative, to allow for differential environmental effects²⁰) to the log-odds of disease, making a strong assumption that the log-odds of disease depends linearly on the PRS and disease status of first-degree relatives (see Discussion). These parameters are specific to the target population, requiring an extra layer of training data from the target population; in this study, we use 10-fold cross-validation in the target population. In step 3, we predict the risk of disease for each target individual as the log-odds of disease based on the PRS and disease status of first-degree relatives.

Figure 1.

Overview of PRS-FH methods

We list the 3 steps of PRS-FH_log and PRS-FH_liab. Although the PRS-FH_log model coefficients and PRS-FH_liab prior covariance shown here are the same for each parent, they may differ between mother and father. In addition, both methods can incorporate sibling history.

The PRS-FH_liab method relies on a liability threshold model²³ and consists of 3 main steps (Figure 1): (1) compute PRS in all target population individuals by applying standard methods to training data; (2) use the training individuals from the target population to estimate liability threshold model parameters, and (3) for each target individual, compute their predicted risk of disease, conditional on their PRS and the disease status of their first-degree relatives. In step 1, we use BOLT-LMM^25,26 (see above). In step 2, we estimate the variance/covariance matrix for a target individual’s total liability, their PRS, and the total liabilities of their first-degree relatives (we allow different covariances for each type of relative, analogous to above). As above, these target population-specific parameters require an extra layer of training data from the target population. In step 3, we predict the risk of disease for each target individual as the posterior probability of disease based on the PRS and disease status of first-degree relatives. The prevalence of disease (determined by the liability threshold) among target individuals may vary as a function of number of siblings, consistent with empirical data. The PRS-FH_liab method is conceptually related to the method of So et al.,⁹ but key differences include the incorporation of genome-wide polygenic risk scores, the incorporation of different covariances for each type of relative, the way in which model parameters are estimated, the incorporation of target population-specific model parameters, and the way in which covariates are incorporated.

We compare PRS-FH_log and PRS-FH_liab to PRS alone as well as a predictor based on FH alone. The PRS method (and the PRS used within both PRS-FH methods) can use any PRS algorithm; in this study, we use BOLT-LMM, which has been shown to attain high polygenic prediction accuracy in the UK Biobank.^25,26 The FH predictor can be constructed using FH_log or FH_liab. Under a logistic model, the disease status of relatives linearly affects the log-odds of disease for an individual. Under a liability threshold model, the posterior risk of disease is computed conditional on FH alone. We evaluate all of the methods using liability-scale R² (Lee et al.²⁷). We compute the standard error of liability-scale R², and associated p values, via a jackknife across individuals. Further details of all of the methods are provided in the STAR Methods section.

Simulations

We simulated genotypes at 100,000 unlinked SNPs for 400,000 unrelated PRS training samples and 40,000 unrelated target samples from the same population. We simulated case-control status for the PRS training samples and case-control status plus FH (parental history for both parents) for the target samples (we did not include sibling history in these simulations); we simulated genotypes for both parents, used these to simulate genotypes for target samples (offspring), and simulated case-control status for both parents and target samples using a liability threshold model. PRS training samples and target samples were not ascertained for case-control status. Our default parameter settings involved 10,000 causal SNPs, total liability-scale heritability ($h^2$) equal to 50%, liability-scale SNP heritability ($h_g^2$) equal to 25%, and disease prevalence (K) equal to 1% (very low prevalence), 5% (low prevalence), or 25% (high prevalence) (implying liability threshold [T] equal to 2.33, 1.64, or 0.67 and total observed-scale heritability equal to 4%, 11%, or 27%, respectively), with the same prevalence for parents and target samples; other parameter settings were also explored. Further details of the simulation framework are provided in the STAR Methods section and Table S1. We note that simulations using real linkage disequilibrium (LD) patterns are essential for methods affected by LD between SNPs, and that LD can affect the performance of PRS methods;¹ however, PRS-FH_log and PRS-FH_liab are not otherwise affected by LD between SNPs, as no genotype data are used except for computing the PRS. We further note that simulations with LD using a subset of individuals from UK Biobank would not be feasible, as simulations of FH require genotypes of both target samples and relatives (to simulate the case-control status of both target samples and relatives), but genotypes of relatives are not available for (nearly all) UK Biobank samples.

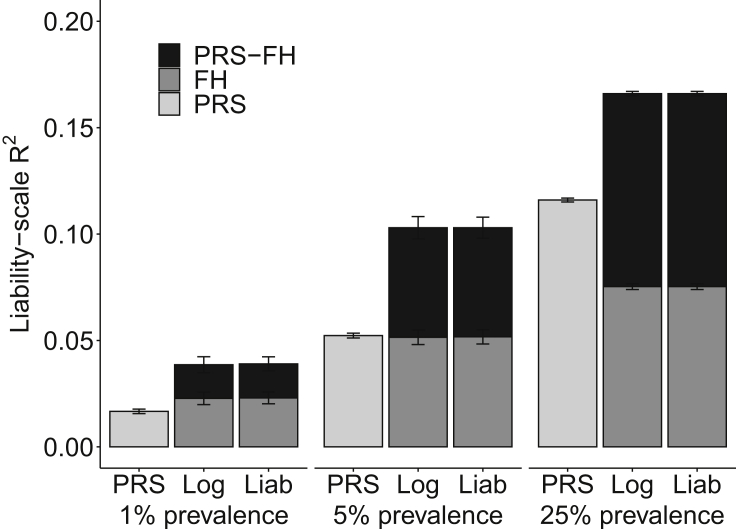
We assessed the prediction accuracy of PRS, FH_log, FH_liab, PRS-FH_log, and PRS-FH_liab by computing liability-scale R² (Lee et al.²⁷). Results are reported in Figure 2 and Table S2. PRS attained higher accuracy at higher prevalence, as expected due to higher observed-scale SNP-heritability (as PRS training samples were not ascertained for case-control status). FH_log and FH_liab performed similarly, and also attained higher accuracy at higher prevalence; at lower prevalence, most individuals have no affected parents, allowing little discrimination of risk based on FH. PRS and FH methods (FH_log and FH_liab) performed similarly at low (5%) prevalence, but PRS outperformed FH at high (25%) prevalence, which was the opposite of the results reported in Do et al.;¹⁰ this difference can be explained by the fact that we analyzed unascertained case-control data.

Figure 2.

PRS-FH_log and PRS-FH_liab increase prediction accuracy in simulations

We report mean liability-scale R² across 10 simulations for PRS alone, FH alone (FH_log and FH_liab), and PRS-FH methods (PRS-FH_log and PRS-FH_liab) for different values of disease prevalence. Error bars denote standard errors. Numerical results are reported in Table S2.

PRS-FH_log and PRS-FH_liab performed similarly, and outperformed both PRS and FH methods at all prevalence values. Given that PRS-FH_liab makes assumptions that match the generative model used in these simulations, the strong performance of PRS-FH_log is supportive of the flexibility of the logistic model, even though it imposes a strong linearity assumption (on the log-odds scale). Differences in prediction R² between PRS-FH_log (respectively PRS-FH_liab) versus PRS were smaller than the prediction R² achieved by FH_log (respectively FH_liab), due to positive correlations between PRS and FH predictions (average correlation = 0.03, 0.08, and 0.18 at very low, low, and high prevalence, respectively). Due to the poor performance (liability-scale R² < 0.05) of all methods at very low prevalence, we restricted all further analyses to low or high prevalence.

We performed five secondary analyses. First, we assessed the calibration of each method (PRS, FH_log, FH_liab, PRS-FH_log, and PRS-FH_liab) by regressing observed disease status on the predictor (a slope of 1 implies correct calibration²⁸). All of the methods were well calibrated in both the low and high prevalence scenarios (Table S3). Second, we increased the parental prevalence to twice the offspring prevalence. In these simulations, the predictive accuracy for all of the methods that incorporate FH (FH_log, FH_liab, PRS-FH_log, and PRS-FH_liab) increased (Table S4). Third, we introduced environmental correlation, considering two scenarios in which the offspring had either the same or different environmental correlations with the mother and father. In both scenarios, the predictive accuracy for methods that incorporate FH (FH_log, FH_liab, PRS-FH_log, and PRS-FH_liab) increased (Table S5). Fourth, we decreased or increased the heritability. Prediction accuracies increased with increasing heritability, but PRS-FH attained similar improvements (Table S6). Fifth, we decreased or increased the polygenicity (number of causal SNPs) while keeping heritability constant. Prediction accuracies decreased with increasing polygenicity for methods incorporating a PRS predictor, but again, PRS-FH attained similar improvements (Table S7).

We conclude that, in these simulations, incorporating FH (PRS-FH_log and PRS-FH_liab) increases the prediction accuracy as compared to PRS alone. We further conclude that PRS-FH_log and PRS-FH_liab generally perform similarly in these simulations. We note that the generative model in all of our simulations was the same as the liability threshold model that FH_liab and PRS-FH_liab use for prediction, and thus these simulations should be viewed as a best-case scenario for FH_liab and PRS-FH_liab.

Analysis of complex diseases from the UK Biobank

We analyzed data for 10 complex diseases from the UK Biobank,²⁴ consisting of genotype data, case-control status, and FH information for parents and siblings (Table 1). PRS were trained using all British individuals (N = 409,000), applying BOLT-LMM to autosomal genotyped SNPs with missingness <10% and minor allele frequency (MAF) >0.1% (672,288 SNPs). Target samples consisted of unrelated non-British Europeans (N = 42,000), South Asians (N = 7,000), or Africans (N = 7,000); target samples were unrelated to training samples and to one another (see STAR Methods). Our primary focus was on three well-powered diseases (type 2 diabetes [T2D], depression, and hypertension [HTN]). These 3 diseases were the only diseases of the 10 considered with (liability-scale) prediction R² > 0.05 for PRS and/or FH methods in each target population (no additional criteria were applied); 2 of these diseases (T2D, HTN) have higher prevalence in South Asians and Africans (Table 1). We report averages across the three well-powered diseases. We also report results for each of the 10 diseases, defined as the set of diseases in the UK Biobank for which (1) FH (parental and sibling history) was available for most target samples and (2) prediction R² was statistically significant (after Bonferroni correction) for PRS and/or FH methods in the largest target population (non-British Europeans; Table S8).

Table 1.

List of 10 UK Biobank diseases analyzed

Diseases	British ${\mathit{h}}_{\mathit{g}}^2$	British N	British K	Non-B. Eur. N	Non-B. Eur. K	S.A. N	S.A. K	Afr. N	Afr. K
Lung cancer	0.096	408,903	0.006	41,842	0.006	7,048	0.002	7,087	0.003
Bowel cancer	0.160	408,903	0.013	41,842	0.011	7,048	0.005	7,087	0.009
Stroke	0.090	408,903	0.024	41,842	0.020	7,048	0.025	7,087	0.025
COPD	0.172	408,903	0.035	41,842	0.035	7,048	0.022	7,087	0.013
Prostate cancer	0.296	187,889	0.038	18,192	0.032	3,811	0.014	3,096	0.050
T2D	0.372	407,565	0.042	41,642	0.040	6,881	0.155	6,961	0.098
Breast cancer	0.204	221,014	0.061	23,650	0.061	3,237	0.036	3,991	0.028
Depression	0.116	408,903	0.073	41,842	0.075	7,048	0.054	7,087	0.044
CAD	0.206	408,903	0.085	41,842	0.077	7,048	0.140	7,087	0.063
HTN	0.311	408,903	0.323	41,842	0.293	7,048	0.377	7,087	0.425

For each disease, we report the SNP-heritability ($h_g^2$) in UK Biobank British training data and the number of samples (N) and disease prevalence (K) in each UK Biobank training (British) and target (Non-British European, South Asian, or African) population. We note that the sample size and prevalence in British training data includes information from related individuals, but SNP-heritability was estimated using unrelated British individuals. Diseases are listed in order of disease prevalence in British training data. Our primary focus was on 3 well-powered diseases (type 2 diabetes, depression, and hypertension; denoted in bold) with (liability-scale) prediction R² > 0.05 for PRS and/or FH in each target population (no additional criteria were applied).

Non-B. Eur., Non-British European; S.A., South Asian; Afr., African; COPD, chronic obstructive pulmonary disease, defined as chronic bronchitis/emphysema; T2D, type 2 diabetes; CAD, coronary artery disease; HTN, hypertension.

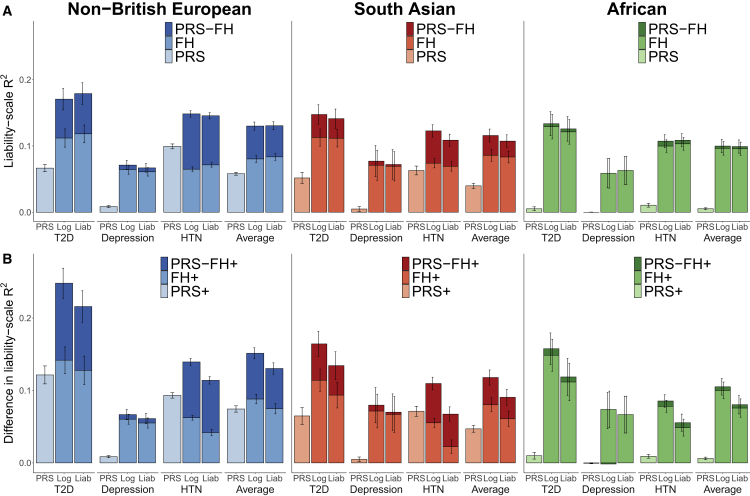
We assessed the prediction accuracy of PRS, FH_log, FH_liab, PRS-FH_log, and PRS-FH_liab. Results are reported in Figure 3A and Table S9. Across the three well-powered diseases, PRS attained average prediction R² of 5.8%, 4.0%, and 0.53% in non-British Europeans, South Asians, and Africans, respectively, confirming poor cross-population transferability.3, 4, 5, 6, 7 In contrast, FH_log attained similar prediction R² across populations: 8.0%, 8.6%, and 9.6%, with similar results for FH_liab. Notably, PRS-FH_log attained average prediction R² of 13%, 12%, and 10%, with similar results for PRS-FH_liab. Thus, PRS-FH_log and PRS-FH_liab attained a large relative improvement versus PRS in Europeans (consistent with simulations) and an extremely large relative improvement versus PRS in Africans. For each disease and each target population, the difference between PRS-FH_log (or PRS-FH_liab) and PRS was statistically significant (p < 2 × 10⁻⁶). Differences in prediction R² between PRS-FH_log (or PRS-FH_liab) and PRS were generally slightly smaller than the prediction R² attained by FH, due to slight correlations between PRS and FH predictions (average = 0.07 across the 3 well-powered diseases and 0.05 across all 10 diseases; the correlations varied across the 3 populations and was lowest in Africans, likely due to the less accurate PRS; Figure S1; Table S10). Parameters estimated by PRS-FH_log and PRS-FH_liab are reported in Table S11. Across the three well-powered diseases, sibling history was assigned a higher weight than parental history regardless of target population (likely due to differential shared environmental effects²⁰), whereas the weight assigned to PRS depended on the target population.

Figure 3.

PRS-FH increases prediction accuracy in analyses of UK Biobank diseases

(A) Analyses without covariates. We report liability-scale R² for PRS alone, FH alone (FH_log and FH_liab), and PRS-FH methods (PRS-FH_log and PRS-FH_liab) for different diseases and target populations.

(B) Analyses with covariates. We report difference in liability-scale R² (see text) for the corresponding methods incorporating covariates (PRS⁺, FH⁺, PRS-FH⁺), for different diseases and target populations. Error bars denote standard errors; error bars are jittered for PRS-FH (left) and FH (right) for visualization purposes. We focus on three well-powered diseases with R² > 0.05 for PRS and/or FH in each target population (no additional criteria were applied). For depression in Africans, PRS-FH_log performs slightly worse than FH_log (difference in R² of −0.001 [p = 0.003 for difference] in analyses without covariates and difference in R² of −0.002 [p = 0.13 for difference] in analyses with covariates). Numerical results are reported in Tables S9 and S20.

More broadly, PRS-FH_log (and PRS-FH_liab) consistently attained higher prediction R² than PRS across all 10 diseases (Table S9). The prediction accuracy of PRS increased as a function of observed-scale SNP-heritability (which is partly determined by prevalence) (Figure S2), and the prediction accuracy of FH increased as a function of both the covariance between liabilities of target samples and first-degree relatives (which is largely determined by total narrow-sense heritability) and the prevalence in first-degree relatives (Figure S2; Tables S4–S6). The correlations between PRS and FH predictions were low for all of the diseases (−0.02 to 0.13), but increased as a function of prevalence and SNP-heritability (Figure S1; Table S10).

We performed eight secondary analyses. First, we assessed the calibration of each method (by regressing observed disease status on the predictor; a slope of 1 implies correct calibration²⁸). We determined that PRS-FH_log attained better calibration than PRS-FH_liab (average regression slope of 0.93 versus 0.60 across 3 well-powered diseases; Table S12). Second, we assessed the performance of a simplified logistic regression-based method that used a single binary independent variable for overall (parental and sibling) FH. We determined that PRS-FH_log attained significantly higher prediction accuracy than this method (average absolute change in prediction R²: 2.0%, 3.0%, and 3.7% in non-British Europeans, South Asians, and Africans, respectively, across 3 well-powered diseases; Table S13). This result demonstrates the advantage of incorporating each type of relative separately (mother, father, or sibling, as well as the number of siblings); we specifically note the difference in PRS-FH model parameters for maternal, paternal, and sibling history (e.g., the PRS-FH_log coefficient for sibling history is roughly double that of parental history for T2D for all three target populations; Table S11). Third, we compared the performance of both PRS-FH methods when incorporating parental history only versus both parental and sibling history. Incorporating both parental and sibling history attained moderately higher predictive accuracy (Table S14). Fourth, we decreased the number of training samples from the target population used to fit PRS-FH model parameters below its default level (which is based on 10-fold cross-validation; see overview of methods in Figure 1). For both PRS-FH_log and PRS-FH_liab, the number of training samples from the target population had little impact on predictive accuracy for values of N_eff ≥ 500 (Figure S3). Fifth, we assessed the potential benefit to FH_log and PRS-FH_log of including in the logistic model an interaction term between number of siblings and sibling history. We determined that there was no significant benefit (Table S15). Sixth, we assessed whether FH_log and PRS-FH_log would benefit from incorporating the total number of siblings of each target individual using indicator variables in addition to a continuous variable. We determined that disease prevalence empirically varied non-linearly as a function of the number of siblings (which is known to correlate with socioeconomic factors) (Table S16), and that accounting for this generally produced non-significant improvements (Table S17). Seventh, we assessed whether FH_liab and PRS-FH_liab benefit from allowing the prevalence of disease (determined by the liability threshold) among target individuals to vary as a function of the number of siblings. We determined that FH_liab and PRS-FH_liab attained slightly higher prediction accuracy than corresponding methods that do not allow the prevalence of disease to vary as a function of the number of siblings (Table S18); we elected to allow the primary FH_liab and PRS-FH_liab methods to benefit from this information as a conservative choice, as they were not ultimately the methods of choice (see below). Eighth, for each of the 5 methods, we evaluated the prevalence of disease in each percentile of predicted disease risk.² We confirmed that PRS-FH_log and PRS-FH_liab also performed best under this metric (Figures S4–S6).

We conclude that incorporating FH (PRS-FH_log and PRS-FH_liab) increases prediction accuracy as compared to PRS alone, particularly in Africans. We further conclude that PRS-FH_log and PRS-FH_liab generally perform similarly in analyses without covariates.

Incorporation of covariates in UK Biobank analyses

We repeated the analyses of 10 complex diseases from the UK Biobank by incorporating covariates into each method: PRS⁺, FH⁺_log, FH⁺_liab, PRS-FH⁺_log, and PRS-FH⁺_liab; the covariates included age, sex, BMI and 20 principal components (see STAR Methods). PRS⁺ incorporates covariates by training a logistic model with PRS and all of the covariates. FH⁺_log and PRS-FH⁺_log incorporate covariates by including them as independent variables in the logistic model. FH⁺_liab and PRS-FH⁺_liab incorporate covariates by estimating a disease threshold for the liability (exclusive of covariates) that varies based on the covariates (see STAR Methods). We evaluated the predictive accuracy of each method using difference in liability-scale R² (defined as liability-scale R² minus the liability-scale R² attained using covariates alone). As above, our primary focus was on the three well-powered diseases (T2D, depression, and HTN); the impact of covariates on these diseases was substantial, as covariates alone attained average prediction R² of 20%, 17%, and 15% in non-British Europeans, South Asians, and Africans, respectively, with most of the prediction R² contributed by age and BMI (Table S19). For example, for T2D, there was a large contribution of BMI (prediction R² ranging from 4.5% in South Asians and Africans to 17% in non-British Europeans, with large differences across populations analogous to PRS); for HTN, there was a large contribution of age (prediction R² ranging from 13% to 21% in the 3 populations, with relatively small differences across populations in contrast to PRS); and for depression, the overall contribution of covariates was limited (prediction R² ranging from 2.0% to 3.3% in the 3 populations).

We assessed the prediction accuracy of PRS⁺, FH⁺_log, FH⁺_liab, PRS-FH⁺_log, and PRS-FH⁺_liab. Results are reported in Figure 3B and Table S20. Across the 3 well-powered diseases, PRS⁺ attained average prediction accuracy (difference in liability-scale R²) of 7.4%, 4.7%, and 0.62% in non-British Europeans, South Asians, and Africans, respectively, again reflecting poor cross-population transferability.3, 4, 5, 6, 7 In contrast, FH⁺_log attained similar prediction accuracy across populations: 8.8%, 8.0%, and 10% in the 3 populations; results were also similar across populations for FH⁺_liab. Notably, PRS-FH⁺_log outperformed PRS-FH⁺_liab, with prediction accuracies of 15%, 12%, and 11% for PRS-FH⁺_log in the 3 populations versus 13%, 9.1%, and 8.0% for PRS-FH⁺_liab in the 3 populations (most differences were statistically significant: p = 0.0001–0.0007 for T2D, p = 0.05–0.6 for depression, p = 6 × 10⁻²⁸–5×10⁻⁹ for HTN); similarly, FH⁺_log outperformed FH⁺_liab. We note that PRS-FH⁺_log and FH⁺_log model the effects of FH and covariates jointly, whereas PRS-FH⁺_liab and FH⁺_liab model the effects of covariates marginally (see STAR Methods); as both FN and PRS are correlated with covariates (Table S21), this may explain the better performance of PRS-FH⁺_log and FH⁺_log. The differences in prediction R² attained by PRS⁺, FH⁺_log, FH⁺_liab, PRS-FH⁺_log, and PRS-FH⁺_liab versus a prediction model based on covariates alone were generally similar to the absolute predictive R² attained by PRS, FH_log, FH_liab, PRS-FH_log, and PRS-FH_liab, with limited exceptions (Tables S9–S20). Surprisingly, the relative prediction accuracy of PRS⁺ was sometimes larger than the prediction accuracy of PRS alone, which is mathematically possible under a logistic model. The pairwise correlations between PRS, FH_log, FH_liab, and a prediction based on covariates alone ranged from −0.06 to 0.16 (Table S21).

We performed three secondary analyses. First, we assessed the calibration of each method (by regressing observed disease status on the predictor; a slope of 1 implies correct calibration²⁸). We determined that PRS-FH⁺_log attained better calibration than PRS-FH⁺_liab (average regression slope of 0.92 versus 0.68 across 3 well-powered diseases; Table S22). Second, we assessed the performance of a simplified logistic regression-based method (incorporating covariates) that used a single binary independent variable for overall (parental and sibling) FH. We determined that PRS-FH⁺_log attained significantly higher prediction accuracy than this method (average absolute change in prediction R²: 1.6%, 1.3%, and 3.2% in non-British Europeans, South Asians, and Africans, respectively, across 3 well-powered diseases; Table S23, analogous to Table S13); again, this result demonstrates the advantage of incorporating each type of relative separately. Third, we compared the performance of both PRS-FH⁺ methods when incorporating parental history only versus both parental and sibling history. Incorporating both parental and sibling disease history attained moderately higher predictive accuracy for PRS-FH⁺_log, but results were mixed for PRS-FH⁺_liab (Table S24).

We conclude that when covariates are included in the predictions, incorporating FH (PRS-FH⁺_log and PRS-FH⁺_liab) continues to increase prediction accuracy as compared to PRS⁺ alone, particularly in Africans. We further conclude that PRS-FH⁺_log outperforms PRS-FH⁺_liab in analyses with covariates.

Discussion

Summary of findings

We have explored methods for combining PRS-FH to predict the risk of disease in diverse populations, using a logistic model or a liability threshold model. We determined that PRS-FH increases prediction accuracy as compared to PRS alone across a broad set of simulations and empirical analyses, including analyses incorporating covariates. Although PRS and FH in principle contain overlapping information (PRS reflects genetic risk, and FH reflects both genetic and environmental factors), correlations between PRS and FH predictors were low (averaging approximately 0.05), implying that they provide orthogonal information; in particular, FH includes an environmental component. (We note that the correlations between PRS and FH varied across the three populations; the environmental component of FH may vary across populations, but in practice FH attained similar prediction accuracy across the three populations.) We recommend the use of the logistic model, which outperformed the liability threshold model in analyses with covariates (however, we note that the liability threshold model has proven valuable in other settings^23,29, 30, 31, 32, 33). The logistic model, unlike the liability threshold model, models the effects of PRS, FH, and covariates jointly; as both FH and PRS are correlated with covariates, this joint modeling may explain the better performance of the logistic model in analyses with covariates. The increase in prediction accuracy attained by PRS-FH was particularly large in non-European populations (e.g., Africans), suggesting that PRS-FH will be a method of choice for closing the well-documented gap in disease risk prediction accuracy in diverse populations.3, 4, 5, 6, 7 More broadly, PRS-FH increases prediction accuracy in all of the populations analyzed, enhancing prospects for clinical utility.^2,34 Our findings emphasize the value of collecting and incorporating FH data, as well as data on clinical covariates, whenever it is practical to do so.

PRS-FH incorporates each type of relative separately

The main methodological advance of PRS-FH over previous approaches for combining PRS and FH information^9,15, 16, 17, 18, 19 is how it incorporates different types of relatives. Previous methods incorporate each type of relative equally, but PRS-FH incorporates each type of relative separately to allow for differential environmental effects.²⁰ We have shown that PRS-FH outperforms an analogous method that uses a single binary independent variable for overall (parental and sibling) FH, both in analyses without covariates (Table S13) and in analyses with covariates (Table S23); these results demonstrate the advantage of incorporating each type of relative separately. In particular, a recent study that used a single binary independent variable for overall (parental and sibling) FH reported no significant improvement from incorporating FH in prostate cancer analyses of UK Biobank Europeans³⁵ (area under the curve [AUC] = 0.836 versus 0.833; analogous to Table S13), whereas PRS-FH⁺_log attained a significant improvement from incorporating FH in prostate cancer analyses of UK Biobank Europeans (R² = 0.100 versus 0.069, p = 0.029 in analyses without covariates, Table S9; p = 0.0035 in analyses with covariates, Table S20). We specifically note the difference in PRS-FH model parameters for maternal, paternal, and sibling history (e.g., the PRS-FH_log coefficient for sibling history is roughly double that of parental history for T2D for all three target populations; Table S11).

Comparison to previous studies

Distinct from methodological advances, our study differs from previous studies in several ways. First, our application of PRS-FH leverages genome-wide polygenic signals in the PRS component (increasing predictive value¹), whereas some previous studies^9,15,16 restricted the PRS component to genome-wide significant loci. Second, PRS-FH optimizes the contributions of PRS and FH as a function of the target population (increasing prediction accuracy in diverse populations), whereas previous studies did not allow these contributions to vary as a function of the target population⁹ or did not consider separate training and target samples;15, 16, 17, 18, 19 in particular, PRS-FH differs from So et al.⁹ in that model parameters are estimated within the target population of interest, rather than relying on external data sources. Third, PRS-FH models the effects of FH and covariates jointly, in which some previous studies either did not incorporate covariates⁹ or included covariates but did not model FH and covariates jointly¹⁶ (likewise, the approach for incorporating covariates discussed as a future direction in So et al.⁹ did not model FH and covariates jointly). Fourth, PRS-FH leverages the information available in UK Biobank data, in which sibling history is reported as a binary variable (at least one sibling has the disease), whereas some previous studies⁹ cannot be extended to this type of data as the disease status of each sibling is required. We further note that many studies15, 16, 17, 18, 19 analyzed only one disease as the primary outcome (and did not incorporate each type of relative separately; see above).

Limitations of the study

Although PRS-FH increases prediction accuracy, it has several limitations. First, PRS-FH requires an additional layer of training data from the target population to optimize the contributions of PRS and FH to the target population. However, this requires only a small number of training samples from the target population (e.g. N_eff ≥ 500; see Figure S3), and the additional training step can be omitted for the diseases and target populations that we have analyzed here (for which these model parameters are reported in Table S11). Second, the logistic model makes a strong assumption that the log-odds of disease depend linearly on the PRS and disease status of first-degree relatives—an assumption that lacks a strong theoretical justification. However, simulations and empirical results are strongly supportive of the practical ramifications of this assumption. Third, FH may reflect a different underlying genetic architecture than case-control status, for example, due to differences in the etiology of early-onset versus late-onset disease or differences in diagnostic criteria over time; however, we previously reported very high genetic correlations between case-control and FH phenotypes in the UK Biobank.³³ Fourth, self-reported FH information may be missing or inaccurate (e.g., due to recall bias). However, the rate of missing data is fairly low (88% of individuals in the UK Biobank report complete parental history, and 93% of individuals in the UK Biobank report complete sibling history), and we previously determined that self-reported family history is reasonably accurate in the UK Biobank (∼80% correlation between true and self-reported FH, based on sibling concordance³³); we caution that certain diseases may be more susceptible to inaccuracy—for example, depression (67% correlation between true and self-reported FH) and hypertension (70% correlation between true and self-reported FH). The imperfect accuracy is explicitly accounted for by PRS-FH model parameters, and incorporating self-reported FH clearly improves the prediction accuracy in our study. Fifth, we did not perform analyses in which we trained and validated in different cohorts. We anticipate that this will become possible in the future with the emergence of large biobanks collecting a rich set of phenotypes, including FH.^36,37 Sixth, the current implementation of PRS-FH is not designed to include all types of FH information (e.g., all siblings affected); however, the PRS-FH framework can easily be extended to include other FH information. Seventh, PRS-FH_liab does not account for shared environment between parents, which can induce correlations between parents. However, PRS-FH_log models parental disease statuses jointly, allowing for correlations between parents. Eighth, incorporating FH into genome-wide association studies (GWASs) increases association power,^33,38 implying that training the PRS using association statistics informed by the FH of training samples has the potential to increase the accuracy of the PRS component of PRS-FH; exploration of this approach remains as a future research direction, distinct from incorporating the FH of target samples via the FH component. Ninth, we have focused here on autosomal-PRS, but incorporating sex-chromosomal-PRS remains as a future research direction. Finally, incorporating training data from auxiliary traits has substantial potential to improve polygenic prediction accuracy,^39,40 but this was not implemented in our study; incorporating auxiliary traits into PRS-FH is straightforward under the PRS-FH framework, and remains a future research direction. Despite these limitations, we anticipate that PRS-FH will attain large increases in prediction accuracy in future studies, particularly in diverse populations.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
UK Biobank	Bycroft et al., 2018	https://www.ukbiobank.ac.uk
SNP weights to construct PRS scores for 12 diseases with family history in UK Biobank	This paper	https://alkesgroup.broadinstitute.org/UKBB/PRSFH/UKBB_PRS_weights/ https://zenodo.org/record/6598868
PRS and family history weights for prediction models for 10 diseases in UK Biobank	This paper	https://alkesgroup.broadinstitute.org/UKBB/PRSFH/UKBB_model_fits/ https://zenodo.org/record/6598868
Software and algorithms
BOLT-LMM	Loh et al., 2015 Loh et al., 2018	https://alkesgroup.broadinstitute.org/BOLT-LMM/
PRS-FH	This paper	https://alkesgroup.broadinstitute.org/UKBB/PRSFH/ https://zenodo.org/record/6598868

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Margaux L.A. Hujoel (mhujoel@broadinstitute.org).

Materials availability

This study did not generate new unique reagents.

Method details

PRS-FH_log method

The PRS-FH_log method models the PRS and the disease status of relatives as linearly impacting the log-odds of disease for an individual, as detailed below.

$$\begin{array}{l}\log \frac{p}{1-p}={\alpha }_0+{\alpha }_1{D}_{p1}+{\alpha }_2{D}_{p2}+{\alpha }_3{D}_{sib}+{\alpha }_4{N}_{rel.sib}+{\alpha }_{5}PRS\end{array}$$ (Equation 1)

where $D_{p1},D_{p2},$ and $D_{sib}$ are the binary disease status variables for an individual’s parents and siblings, respectively, $N_{rel.sib}$ is the number of relevant siblings of an individual (number of total siblings for non-sex-specific diseases, number of sisters for breast cancer, and number of brothers for prostate cancer), and $PRS$ is the individual’s PRS. An individual’s PRS is constructed as a weighted sum of their genotypes:

$$\begin{array}{l}PRS=\sum _i{\hat{\beta }}_i{g}_i\end{array}$$ (Equation 2)

where $g_i$ are an individual’s genotypes at SNP $i$ (0,1,2) and ${\hat{\beta }}_i$ are the per-allele effect sizes of SNP $i$ estimated using training data. We note that there are multiple algorithms for constructing PRS, however the construction of PRS is not the primary focus of this work.

We considered a logistic model incorporating the PRS (as a continuous covariate), the three binary indicators for the disease status of mother, father, and siblings, and a continuous covariate for the number of relevant siblings (see Equation 1). We elected not to use indicator variables for the number of total siblings an individual has (e.g. $\mathbb{I}\left(N_{sib}=1\right),\mathbb{I}\left(N_{sib}=2\right),\dots ,\mathbb{I}\left(N_{sib}\ge 5\right)$) in the primary method as this generally produced non-significant improvements (Table S17) and increased model complexity.

PRS-FH_liab

The PRS-FH_liab method models the family history of disease and PRS using a liability threshold model.²³ The liability threshold model assumes an individual has an underlying liability, $ϵ$, which is normally distribution with a mean of 0 and variance of 1. An individual is a case ($z=1$) if and only if $ϵ\ge T$ otherwise the individual is a control ($z=0$). $T$ determines the disease prevalence $K$; $K=1-\text{Φ}\left(T\right)$ where $\text{Φ}\left(T\right)$ is the normal cumulative distribution function, i.e. $\text{Φ}\left(T\right)=\text{Pr}\left(N\left(0,1\right)\le T\right)$.

We assume a multivariate normal distribution for the individual’s liability, the individual’s PRS, and the target individual’s relatives’ liabilities. For example, to incorporate the individual’s PRS as well as the parental and a sibling’s disease history we assume,

$$\begin{array}{l}\left(\begin{array}{l}\begin{array}{l}{ϵ}_o\\ PR{S}_o\\ {ϵ}_{p1}\\ {ϵ}_{p2}\end{array}\\ {ϵ}_s\end{array}\right)\sim MV{N}_5(\left(\begin{array}{l}0\\ 0\\ 0\\ 0\\ 0\end{array}\right),\left(\begin{array}{lllll}1& V& \frac{{\tilde{h}}_{p1}^2}{2}& \frac{{\tilde{h}}_{p2}^2}{2}& \frac{{\tilde{h}}_s^2}{2}\\ V& V& \frac{V}{2}& \frac{V}{2}& \frac{V}{2}\\ \frac{{\tilde{h}}_{p1}^2}{2}& \frac{V}{2}& 1& 0& \frac{{\tilde{h}}_{p1}^2}{2}\\ \frac{{\tilde{h}}_{p2}^2}{2}& \frac{V}{2}& 0& 1& \frac{{\tilde{h}}_{p2}^2}{2}\\ \frac{{\tilde{h}}_s^2}{2}& \frac{V}{2}& \frac{{\tilde{h}}_{p1}^2}{2}& \frac{{\tilde{h}}_{p2}^2}{2}& 1\end{array}\right)),\end{array}$$ (Equation 3)

where ${ϵ}_o$ is the total liability of the target individual, $PR{S}_o$ is the PRS of the target individual, and ${ϵ}_{p1},{ϵ}_{p2}$, and ${ϵ}_s$ are the liabilities of the parents and the sibling, respectively, ${\tilde{h}}_{p1}^2,{\tilde{h}}_{p2}^2,$ and ${\tilde{h}}_s^2$ are the pseudo-heritabilities of the disease on the liability scale of the parents and the sibling, respectively, and $V$ is the amount of variance the PRS can explain on the liability scale. The pseudo-heritabilities of the disease reflect a combination of heritability and shared environmental effects (which may vary across classes of relatives), and can be estimated using maximum-likelihood methods (see Methods S1 and Table S25 for justification of pseudo-heritability and details on its estimation). We can estimate the variance explained by the PRS on the liability scale as

$$\begin{array}{l}V=corr{\left(PRS,Z\right)}^2\frac{K\left(1-K\right)}{\phi {\left(T\right)}^2},\end{array}$$ (Equation 4)

where $K$ is the disease prevalence, Z is the disease status, $\text{T}={\text{Φ}}^{-1}\left(K\right)$, and $\phi$ is the normal probability density function. This estimate of $V$ is similar to previous derivations converting between the observed-scale and the liability-scale (see Methods S1).²⁹ After estimating the liability-scale variance explained by the PRS (V), the raw PRS is scaled to have mean zero and the desired variance prior to being utilized by PRS-FH_liab. Setting ${\tilde{h}}_{p1}^2={\tilde{h}}_{p2}^2={\tilde{h}}_s^2=h^2$ models PRS and family history of disease assuming no environmental correlation.

Using the distribution shown in Equation (1), we can compute the posterior mean and variance of ${ϵ}_o$, conditional on the individual’s PRS and the disease status of family members (e.g. if parent 1 is a case we can condition on ${ϵ}_{p1}\ge T_{p1}$). Given the mean and variance of the posterior distribution, denoted ${\mu }_{{ϵ}_o|\cdot }$ and ${\sigma }_{{ϵ}_o|\cdot }^2$ respectively, we assume normality and compute the posterior risk of disease for an individual to be:

$$\begin{array}{l}r=1-\Phi \left[\frac{T_{offspring}-{\mu }_{{ϵ}_o|\cdot }}{{\sigma }_{{ϵ}_o|\cdot }}\right],\end{array}$$ (Equation 5)

where $T_{offspring}$ is either ${\text{Φ}}^{-1}\left(K_{offspring}\right)$ or a function of covariates, depending on the model being implemented (see below). We note that the posterior risk of disease is distinct from the posterior mean (and variance) of liability. We elected to use the posterior risk of disease, rather than simply the posterior mean or variance, as this appropriately weights the mean and variance of the liability for disease. Conditioning on family history will result in a non-normal distribution, however, this deviation from normality is generally small.^9,23 We elected to have $T_{offspring}$ depend on the number of total siblings an individual has through the use of indicator variables (e.g. $\mathbb{I}\left(N_{sib}=1\right),\mathbb{I}\left(N_{sib}=2\right),\dots ,\mathbb{I}\left(N_{sib}\ge 5\right)$) as a conservative choice as it optimized the performance of PRS-FH_liab (Table S18), which ultimately was not the recommended method.

We use the Pearson-Aitken formula, as well as properties about truncated normal distributions, to compute posterior distributions.^9,41 Sibling history is reported as a binary condition in UK Biobank; individuals report whether at least one or none of their siblings are affected. For individuals who report at least one of their siblings is affected, the posterior mean and variance is estimated analytically (see Methods S1).

Missing family history for some relatives is not an issue as the posterior distribution is computed conditional on known information, and therefore the number of relatives being modeled is reduced when missing family history exists. We use estimates of disease prevalence which differ for mother, father, and offspring as well as estimates of pseudo-heritability which differ for mother and father.

Simulations

We simulated genotypes at 100,000 unlinked SNPs and case-control status for 400,000 unrelated training samples. For computational simplicity we generated 10 genotype matrices for the training data and given these genotype matrices, can then generate 10 different case-control vectors represent different scenarios of ranging prevalence, $h_l^2$, $h_g^2$, and polygenicity (number of causal SNPs). To obtain PRS, we computed prediction $\beta$ for all 100,000 unlinked SNPs using BOLT-LMM.^25,26

We simulated genotypes at 100,000 unlinked SNPs and case-control status plus family history (parental history for both parents) for 40,000 unrelated target samples. We simulated genotypes for both parents using the same minor allele frequency (MAF) values as the training data, used these to simulate genotypes for target samples (offspring), and simulated case-control status for both parents and target samples using a liability threshold model; target samples were not ascertained for case-control status. Again, for computational simplicity we generated 10 genotype matrices for the testing data and given these genotype matrices, then generated case-control and family history information under 16 different scenarios; the same 10 scenarios as the training data as well as 4 additional scenarios in which family members shared environmental correlation and 2 additional scenarios in which the parental disease prevalence was double that of the offspring (Table S1). We note that environmental correlation and differing parental prevalence does not impact our training data as we are using case-control data only (not family history data) to train.

Within the target samples we use 10-fold cross-validation: for each fold we use the remaining 9 folds to estimate relevant model parameters. Given these parameters, the predicted risk of disease can be estimated for each individual within the held-out fold. For each simulation scenario, we computed the mean $R_l^2$ and standard error (see Quantification and Statistical Analysis; Tables S2 and S4–S7); calibration of the main simulations was assessed by regressing observed disease status on the predictor (a slope of 1 implies correct calibration;²⁸ Table S3).

UK Biobank data set

We analyzed 10 complex diseases from the UK Biobank.²⁴ To construct PRS, we computed prediction $\beta$ for genotyped SNPs using all British individuals using BOLT-LMM.^25,26 These individuals were individuals of European ancestry (based on self-reported white-ethnicity) and British-ancestry individuals passing principal component analysis filters.²⁴ Our PRS consisted of 672,288 SNPs with missingness <10% and minor allele frequency (MAF) > 0.1%; we mean normalized PRS based on the allele frequency within the training population.

We considered three distinct testing sets; these consisted of non-British European, South Asian (Indian, Pakistani, Bangladeshi), and African individuals (Black or Black British, Caribbean, African, Any other Black background). These testing sets were constructed through self-reported ethnicity; non-British European were individuals of European ancestry (based on self-reported white-ethnicity; White, British, Irish, Any other white background) who did not pass British-ancestry principal component analysis filters. We restricted to unrelated individuals (both unrelated to other individuals within the testing sets as well as unrelated to the training set). We use 10-fold cross-validation within the three testing sets to estimate relevant model parameters for both PRS-FH_log and PRS-FH_liab. In detail, for individuals in a given fold we estimate the relevant parameters using the remaining 9-folds and use these parameters to predict risk.

UK Biobank collects family history of disease information for 12 diseases. The rate of missing data is fairly low: 88% of individuals in UK Biobank report complete parental history, and 93% of individuals in UK Biobank report complete sibling history.³³ In this work we focused on the 10 diseases for which PRS or FH produces a positive liability-scale R² with a p-value less than the nominal 0.05/36 within non-British Europeans (Table 1; Table S8). We primarily focused on three well-powered diseases (type 2 diabetes, depression, and hypertension) with (liability-scale) prediction R² > 0.05 for PRS and/or FH in each target population (no additional criteria were applied; Table S9). We note that depression was included as a well-powered disease despite its low SNP-heritability, because the contribution of sibling disease history (Table S11) led to prediction R² > 0.05 for FH in each target population. On the other hand, CAD was not included as a well-powered disease, due to poor performance of both PRS and FH in the African target population. For any individuals who reported 0 relevant siblings, disease status of siblings was set to 0.

Application of PRS-FH_log to UK Biobank data

We applied PRS-FH_log to 10 complex diseases from the UK Biobank. Prior to model training and fitting, individuals with missing parental disease status for a given parental class (mother or father) were assigned the mean parental disease status for the respective parental class across the 9 training folds. Individuals with missing sibling disease status (for whom the number of siblings must be at least one or unknown) were assigned the mean sibling disease status across all individuals in the 9 training folds if the number of siblings was unknown, or the mean sibling disease status across individuals in the 9 training folds with at least one sibling if the number of siblings was known. Individuals with missing number of siblings were assigned the mean number of siblings across the 9 training folds if the sibling disease status was unknown, or the mean number of siblings subject to the same sibling disease status if known.

Model parameters for PRS-FH_log, both averaged across the 10 folds as well as estimated using all training data, are available in Table S11.

Application of PRS-FH_liab to UK Biobank data

We applied PRS-FH_liab to 10 complex diseases from the UK Biobank. We used different estimates of disease prevalence for mother, father, siblings, and offspring; in any fold, when the prevalence of disease was 0 (for mother, father, sibling, or offspring) we set it equal to 1/(number of individuals within that fold). For all analyses that included sibling history, except when otherwise specified, the liability threshold for disease used to predict disease risk accounted for number of siblings (indicator variables for 0, 1, 2, 3, 4, ≥5 siblings), as we generally observed a U-shaped relationship between disease prevalence and number of siblings (Table S16).

We used estimates of pseudo-heritability that differ for mother, father, and siblings; pseudo-heritability was estimated using maximum-likelihood (see Methods S1). If there were pairs of individuals with concordant disease status (e.g. both offspring and relative have disease), pseudo-heritability was set to 0 and the liability was not conditioned on this relative. UK Biobank collects sibling disease history as a binary “at least one” affected indicator, and as such we could estimate pseudo-heritability either using individuals with exactly one sibling or using all individuals with at least one sibling (see Methods S1). We elected to estimate pseudo-heritability using all individuals with at least one sibling, as the number of individuals with exactly one sibling can be prohibitively low (and may include no concordant disease pairs for diseases of low prevalence). In some of our early experiments in this project, we observed computational problems when estimated pseudo-heritability > 1.8 (i.e. pseudo-heritability/2 ≥ 0.9). Our software thus caps estimates of pseudo-heritability at 1.8. However, this did not impact any of the analyses reported in the current manuscript.

We estimated the amount of variance explained by the PRS on the liability scale, V, that varied based on the target population (Equation 4). For each fold, we ran a permutation test (1,000 permutations) of $H_0:V=0$, if we failed to reject the null hypothesis with $p>0.05$ we set $V=0$ (i.e. we did not use PRS to inform posterior disease risk).

Model parameters for PRS-FH_liab, both averaged across the 10 folds as well as estimated using all training data, are available in Table S11.

Additional details regarding analysis of complex diseases from the UK Biobank

The correlations between PRS and the two FH prediction methods were computed across the 10 diseases in UK Biobank (Table S10 and Figure S1). The relationship between observed-scale SNP-heritability on accuracy of PRS as well as the impact of pseudo-heritability and disease prevalence in first-degree relatives on accuracy of FH was investigated (Figure S2). Calibration of the 5 considered prediction methods was assessed by regressing observed disease status on the predictor (a slope of 1 implies correct calibration;²⁸ Table S12). For each of the 5 methods, the prevalence of disease in each percentile of predicted disease risk was computed for three well-powered diseases (Figures S4–S6). For all secondary analyses, we analyzed mean $R_l^2$, or the difference in $R_l^2$ between methods (see Quantification and Statistical Analysis; Tables S13–S15 and S17–S18).

Decreasing the number of training samples from the target population

We decreased the number of training samples from the target population to different values of expected effective training sample size (N_eff, which can vary with the number of cases sampled; see Equation (6)). For a given value of expected N_eff, we constructed multiple independent training sample sets of that size by down-sampling individuals from each of the 10 folds, and averaged the resulting prediction accuracies across the training sample sets of that size (Table S26 and Figure S3).

The effective sample size (N_eff) is computed for a training sample as:

$$\begin{array}{l}{N}_{eff}=\frac{4}{\frac{1}{N_{cases}}+\frac{1}{N_{ctrls}}}.\end{array}$$ (Equation 6)

Incorporation of covariates in UK Biobank analyses

We repeated the analyses of 10 complex diseases from the UK Biobank by incorporating covariates into each method. We included 23 covariates: age, sex, BMI, and 20 principal components. Prior to model training and fitting, individuals with missing BMI, age, or sex were assigned the mean age, sex, and BMI across the 9 training folds. The prediction method based solely on covariates modeled the 23 covariates linearly impacting the log-odds of disease for an individual; PRS+ (the prediction method based on covariates and PRS) models PRS and the 23 covariates (age, sex, BMI, and 20 principal components) linearly impacting the log-odds of disease for an individual (Table S19). The correlation between PRS and FH predictions and covariate predictions was computed across all 10 diseases (Table S21).

PRS-FH_log simply adds the 23 covariates into the logistic model incorporating family history of disease (FH_log) or PRS and family history of disease (PRS-FH_log). For FH_liab and PRS-FH_liab, covariates were modeled as impacting the threshold for disease; a logistic model for disease as a function of covariates (23 covariates as well as indicators for number of siblings) was used to predict the risk of disease for an individual, thereby estimating the threshold for disease conditional on covariates.

Calibration of all considered prediction methods was assessed by regressing observed disease status on the predictor (a slope of 1 implies correct calibration;²⁸ Table S22). For all secondary analyses, we analyzed mean $R_l^2$, or the difference in $R_l^2$ between methods (see Quantification and Statistical Analysis; Tables S23 and S24).

Quantification and Statistical Analysis

Jackknife standard errors of prediction accuracy and differences in prediction accuracy

We report estimates of liability-scale R² ($R_l^2)$ or the difference in $R_l^2$ between two methods ($\text{Δ}{R}_l^2$). Given predicted disease risks ($r)$ and observed phenotypes (Z), $R_o$ is estimated as ${\hat{R}}_o=corr\left(r,Z\right)$ and $R_l^2$ is estimated as ${\hat{R}}_l^2=corr{\left(r,Z\right)}^2\frac{K\left(1-K\right)}{\phi {\left(T\right)}^2}$ (Lee et al.²⁷) for which $corr\left(r,Z\right)=\text{max}\left(corr\left(r,Z\right),0\right)$. (When using 10-fold cross-validation within a testing set to estimate relevant model parameters, ${\hat{R}}_l^2$ for a method is computed by concatenating across the 10 folds and computing a single ${\hat{R}}_l^2$, rather than computing the average of ${\hat{R}}_l^2$ across the 10 folds.)

To test for significantly non-zero prediction accuracy or differences between methods we assess whether $R_o$ or $\text{Δ}{R}_o$ (where $\text{Δ}$ denotes either the difference between 2 prediction methods, or the difference versus a covariates-only predictor in the setting with covariates) is significantly different from zero. We compute both jackknife standard errors as well as jackknife p-values (for $H_0:R_o>0$ or $H_0:\text{Δ}{R}_o=0)$, employing a jackknife across individuals (we note that the alternative of employing a genomic block-jackknife is of interest for evaluation of PRS methods, but is not applicable to evaluation of FH and PRS-FH methods). We let all individuals in fold $i$ be represented by $D_i$ and we construct n jackknife samples (n = 100 in this study) by deleting each of the n folds as follows, $D_{\left[i\right]}=\left\{D_1,D_2,\dots ,D_{i-1},D_{i+1},\dots ,D_n\right\}.$ Each of these $D_{\left[i\right]}$ are denoted blocks. We then compute ${\hat{R}}_o$ on each $D_{\left[i\right]}$, denoting each such value as ${\hat{R}}_{o,i}$. We then define the jackknife variance as $\begin{array}{l}var\left({\hat{R}}_o\right)=\frac{n-1}{n}\sum _{i=1}^n{\left({\hat{R}}_{o,i}-{\hat{R}}_{o,\cdot }\right)}^2\end{array}$ where ${\hat{R}}_{o,\cdot }=\frac{1}{n}\sum _{i=1}^n{\hat{R}}_{o,i}.$ The jackknife variance for the difference in $R_o$ (or for $R_l^2$ ) between two methods is computed in a similar manner. We computed a jackknife p-value by constructing pseudovalues as ${\hat{R}}_{o,pseudovaluei}=n{\hat{R}}_o-(n-1){\hat{R}}_{o,i}$ and test the hypothesis $H_0:R_o=0$ by using the fact that

$$\frac{\sqrt{n}\left({\hat{R}}_{o,pseudovalue\cdot }-R_o\right)}{\sqrt{\frac{1}{n-1}(\sum {\left({\hat{R}}_{o,pseudovaluei}-{\hat{R}}_{o,pseudovalue\cdot }\right)}^2)}}\to N\left(\mathrm{0,1}\right),$$

where ${\hat{R}}_{o,pseudovalue\cdot }=\frac{1}{n}\sum {\hat{R}}_{o,pseudovaluei}$. The jackknife p-value for $H_0:\text{Δ}{R}_o=0$ between two methods is computed in a similar manner. (We note the n folds used when computing jackknife standard errors and p-values are unrelated to the 10-folds used during cross-validation: individuals are concatenated across the 10 cross-validation-folds and then randomly assigned to the n jackknife folds.)

Jackknife assumes independence between blocks, while individuals are independent (by construction), individual predictions within a fold could use information from other folds, thus potentially inducing a correlation. To determine the potential effect of this we assessed the calibration of jackknife standard errors in simulations. For every simulation scenario, we computed an estimated variance of $R_o$ across the 10 simulation replicates (denoted empirical variance), as well as the average jackknife variance across the 10 simulation replicates (denoted mean jackknife variance). Across all simulation scenarios, the sum of the empirical variance was 0.00063 and 0.00059 while the sum of the mean jackknife variance was 0.00060 and 0.00057 for PRS-FH_log and PRS-FH_liab, respectively. This suggests the standard errors are well-calibrated.

Published: July 13, 2022

Supplemental information

Table S11: Model parameters estimated by PRS-FHlog and PRS-FHliab, related to STAR Methods

We report (a) model parameters estimated by PRS-FH_log (using 10-fold cross-validation training data; average across 10 folds), (b) model parameters estimated by PRS-FH_liab (using 10-fold cross-validation training data; average across 10 folds), (c) model parameters estimated by PRS-FH_log (using all training data), (d) model parameters estimated by PRS-FH_liab (using all training data).

Data and code availability

• This work used genotype and phenotype data from the UK Biobank (http://www.ukbiobank.ac.uk/). The SNP weights to construct the PRS, and the relevant weights for prediction using PRS and family history are available at https://data.broadinstitute.org/alkesgroup/UKBB/PRSFH/ or Zenodo: https://zenodo.org/record/6598868#.YqD9Mi-B2Ru.

• PRS-FH software (and relevant code) is available at https://data.broadinstitute.org/alkesgroup/UKBB/PRSFH/ or Zenodo: https://zenodo.org/record/6598868#.YqD9Mi-B2Ru.

• Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.