Abstract
Studying the brain circuits that control behavior is challenging, since in addition to their structural complexity there are continuous feedback interactions between actions and sensed inputs from the environment. It is therefore important to identify mathematical principles that can be used to develop testable hypotheses. In this study, we use ideas and concepts from systems biology to study the dopamine system, which controls learning, motivation, and movement. Using data from neuronal recordings in behavioral experiments, we developed a mathematical model for dopamine responses and the effect of dopamine on movement. We show that the dopamine system shares core functional analogies with bacterial chemotaxis. Just as chemotaxis robustly climbs chemical attractant gradients, the dopamine circuit performs ‘reward-taxis’ where the attractant is the expected value of reward. The reward-taxis mechanism provides a simple explanation for scale-invariant dopaminergic responses and for matching in free operant settings, and makes testable quantitative predictions. We propose that reward-taxis is a simple and robust navigation strategy that complements other, more goal-directed navigation mechanisms.
Author summary
Research on certain circuits in simple organisms, such as bacterial chemotaxis, has enabled the formulation of mathematical design principles, leading to ever more precise experimental tests, catalyzing quantitative understanding. It would be important to map these principles to the far more complex case of a vertebrate behavioral circuit. Here, we provide such a mapping for the midbrain dopamine system, a key regulator of learning, motivation, and movement. We demonstrate a mathematical analogy between the regulation of dopamine and movement by rewards and the well-characterized bacterial chemotaxis system. We use the analogy to quantitively explain previously puzzling observations on the dopamine circuit, as well as classic empirical observations on operant behavior.
Introduction
Dopamine transmission in the midbrain has several major biological functions for the regulation of behavior and learning. Dopamine signals encode reward prediction errors (RPEs) [1–6] (Fig 1A). Reward prediction errors are the difference between the experienced and predicted rewards. They play a key role in a method of reinforcement learning called temporal difference learning (TD learning) [5–8], and theory from reinforcement learning has been pivotal for explaining dopamine function.
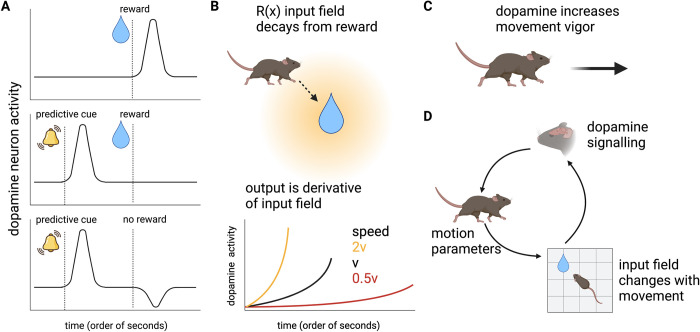
Fig 1. Experimental observations on dopamine imply feedback between motion and sensing.
(A) Dopamine responses represent predictions errors over expected rewards, as observed in the classical experiments of Schultz [28]. Dopaminergic neurons fire at a constant rate of ~4-5Hz, and the delivery of a reward causes them to fire over this baseline rate (upper panel); however, when reward delivery is preceded by a predictive cue, the increase in firing occurs following the cue, and there is no increase following reward delivery (middle panel). Dopaminergic neurons fire below their baseline following the omission of an expected reward (lower panel). (B) As the animal approaches a reward, dopamine activity may increase, a phenomenon known as dopamine ramps. In elegant experiments based on virtual reality manipulations of animal movement (including change of movement velocity and teleportation), Kim et al. [12] demonstrated that dopamine ramps correspond to a temporal derivative calculation over a spatial input field that decays away from the reward. Thus, for example, movement at higher velocity leads to higher dopamine levels. (C) Finally, higher dopamine levels increase movement vigor. (D) There is thus feedback between dopamine sensing and movement–the movement of the animal (including movement velocity) changes the temporal derivative of the sensed input field, which affects dopamine levels, which then feed back on movement parameters. Figures were created with BioRender.com.
In addition to rapid sub-second responses encoding reward prediction errors, dopamine may also slowly ramp up when approaching a reward [9–11]. A recent experiment by Kim et al. showed that even on this slower timescale (seconds), dopamine levels track a derivative of the input signal [12]. Kim et al. used virtual reality to manipulate the rate of change of the movement of a mouse as it moved towards a target. Dopamine changed in a way that is consistent with computing a temporal derivative of an input field that decays away from the reward (Fig 1B, such an input field is referred to as the spatially-discounted expected reward).
Finally, another well-established function of dopamine is the invigoration of movement and motivation [13–18]. Dopamine increases movement vigor [17] (Fig 1C) and defects in dopamine transmission underlie movement difficulties in Parkinson’s disease [19]. While the relation between RPEs and learning is well understood, it is unclear why an RPE signal should invigorate movement [18,20]. Theoretical studies have analyzed this question from the perspectives of learning [21,22] and cost-benefit theories [13,18,23,24], while early work on TD learning anticipated a connection with biological navigation [2].
Considering both the signal processing and movement-invigorating properties of dopamine reveals an intriguing feedback that is inherent to the system (Fig 1D). Since dopamine computes a temporal derivative on a spatial input field, the modulation of movement speed by dopamine should by itself affect dopaminergic output (as directly observed by Kim et al. [12], Fig 1C). Thus, in the context of a moving animal, the different roles of dopamine become tightly coupled. Analyzing such feedback interactions is challenging for current theoretical frameworks for dopamine, which typically model behavior using discrete choice processes occurring in discrete steps (see for example [25]).
Our study aims to use concepts from systems biology to analyze functional properties of the interaction between sensing and movement in the dopamine system. We first develop a minimal mechanistic model of dopamine responses. The model is similar to a continuous version of the classic TD-RPE model, with an important modification based on dopaminergic response curves–the circuit is activated by the logarithm of expected reward. Our model provides a new and simple explanation for the puzzling rescaling of dopaminergic responses [26]. Notably, the model establishes a connection between the dopamine circuit and the concepts of exact adaptation and fold-change detection, which have fundamental importance in the systems biology of signaling circuits [27].
We then use the model to study the interaction between dopamine signaling and movement. We considered one of the best-established empirical behavioral laws–the matching law of operant behavior, where the ratio of responses to concurrent rewarding alternatives is proportional to the ratio of obtained rewards raised to a power β (where β~1). Matching is typically observed in experiments where the animal is allowed to move freely, presenting a challenge to modelling approaches based on discrete choices and time steps. By considering a simple movement model, which we call reward-taxis, we show that the dopamine model predicts matching and provides a quantitative value for β as the ratio of dopamine gain to baseline activity. Matching results from the mathematical analogy between stochastic movement guided by reward-taxis and algorithms for the sampling of probability distributions. We conclude by proposing that reward-taxis is a simple and robust navigation strategy that complements other, more goal-directed navigation strategies employed by animals.
Results
Dopamine release as fold-change detection of expected reward
We begin by developing a minimal model for continuous dopamine dynamics (Fig 2A). Consider a behaving animal exploring an open field for a reward of magnitude u, such as a food or drink. For simplicity, we assume a uniform response amongst all dopaminergic neurons. In reality, there are heterogeneities between and within midbrain structures, and some dopaminergic neurons may be specialized to specific cues [29–31,17,32–35]. As the animal approaches the reward, there is an increase in expected reward R, which decays with distance from the target [9,12,36].
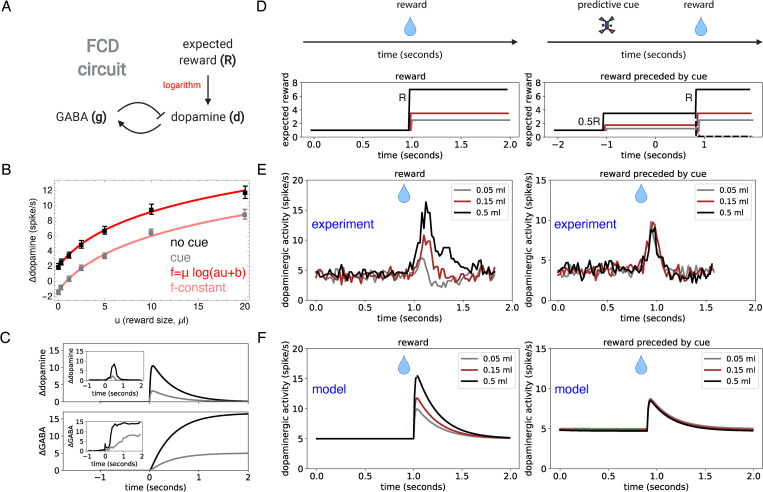
Fig 2. Logarithmic activation of dopamine dynamics explains scale invariant responses.
(A) Minimal circuit for dopamine responses. Dopamine (d) is activated by the logarithm of expected reward (log R) and is inhibited by negative feedback from GABAergic input (g). See Methods for equations and parameters. (B) The response of VTA dopaminergic neurons in mice (n = 5) to a water reward of variable volume (black squares, mean ± SEM, taken from Fig 1C in [38]) is well-described by the logarithmic relation Δd = μ log(au+b) (red line r2 = 0.999, best-fit parameters a = 0.5±0.1, b = 1.5±0.05, μ = 4.9±0.45, N = 7 reward magnitudes). When the reward is preceded by an odor cue (gray squares) the response is well-described by subtracting a constant from the uncued response (pink line, r2 = 0.99, best-fit subtraction constant is −3.2±0.1). (C) Simulation of dopamine and GABA responses to a step increase in expected reward input which corresponds to the presentation of a reward-predicting cue. The step is given by R(t) = R0+λθ(t−t0) where θ(t−t0) is a unit step function, R0 = 1 and λ = 7 for the black line (large reward) and λ = 1.8 for the gray line (small reward). Insets. Average change in firing rates from dopaminergic (type I) and GABAergic (type II) VTA neurons, in response to reward-predicting cues for a small reward (gray) or a large reward (black). Data from Fig 2D of [49]. (DE) Population responses of dopaminergic neurons of two Macaque monkeys to variable size liquid reward, either without a preceding cue (left panels, n = 55 neurons), or with a preceding visual cue that predicts reward delivery with 50% probability (right panels, n = 57 neurons). (D) The expected-reward input following the reward-predicting cue is R = 0.5(b+λu) (where λ is proportional to reward magnitude), which is doubled following reward delivery, R = b+λu, where u is the reward magnitude (we use b = 2 and λ = 10ml−1). Dashed lines correspond to reward omission. (E) Experimentally measured average dopaminergic responses, using data from Fig 2A and Fig 4B of [26]. When the reward is delivered without a cue, dopaminergic responses increase with reward magnitude (left panel). When it is given after a cue that predicts reward delivery with 50% probability, dopaminergic responses to reward delivery are identical (right panel), as predicted by the FCD property. This is despite the 10-fold difference in reward magnitude. (F) Simulations of the dopamine model capture the experimentally observed dynamics. All simulation parameters are provided in Table 1.
Table 1. Parameter values.
| Parameter | Value (mouse experiments) | Value (primate experiments) |
|---|---|---|
| ω d | 50 s-1 | 100 s-1 |
| ω | 15 s-1 | 30 s-1 |
| C | 15 spike s-1 | 15 spike s-1 |
| μ | 6 spike s-1 | 6 spike s-1 |
| α | 0.7 | 0.7 |
| d 0 | 5 spike s-1 | 5 spike s-1 |
Here expected reward is defined based on TD learning: the expected temporally discounted sum of present and future rewards (see Methods). According to the TD-RPE theory of dopamine function, the difference between dopamine and its baseline Δd encodes a prediction error signal about expected rewards [4,5]. The prediction error signal allows the agent to learn about the spatial input field R with recursive learning rules [7,37].
What is the quantitative relationship between reward magnitude and the dopaminergic response? Recordings from VTA dopaminergic neurons in mice reveal a sublinear relationship between the magnitude of received rewards u and Δd(u) [30,38] (Fig 2B). The sublinear relationship indicates that dopamine neurons may (at least in some magnitude range) be responding to the logarithm of reward, namely Δd(u) = μ log(R(u)), with R(u) = au+b, where a is a scaling factor and b is a magnitude-independent component of the reward activation. The parameter μ is the gain of the dopaminergic response. Logarithmic responses are consistent with widespread logarithmic coding in the brain [39–44] as well as with economic notions of utility [45,46].
To test this, we fit the function μ log(au+b) to the average dopaminergic response to a variable water reward in mice [30], finding an excellent fit (r2 = 0.999), with a gain of μ = 4.94±0.45.
In addition to activation by expected reward, dopaminergic neurons in the VTA are inhibited following the presentation of a predicting cue in a subtractive manner ([30,38], Fig 2B, the presented cue is the same for all reward magnitudes). The subtractive inhibition is thought to be due to the increase in the activity of adjacent GABAergic neurons [30,38]. We therefore propose the following minimal description of dopamine release dynamics:
| (1) |
Where C is the baseline activity of the dopaminergic neurons when log R = g = 0, μ is the gain, R is perceived expected reward, and α is the effectiveness of inhibition by the GABAergic output g. Note that both the expected reward R(t) and the GABAergic output g(t) are dynamical, time-dependent variables. Since our model focuses on the regulation of behavior, rather than on learning or representation, we will assume that the log-transformed expected reward log R is an input signal that is provided to the circuit. Additionally, while subtractive inhibition was established for VTA dopaminergic neurons, we assume that similar regulation is shared among all midbrain dopaminergic neurons.
To complete the model requires a minimal description of the dynamics of GABAergic output g. The mechanisms of interaction between GABAergic and dopaminergic neurons are complex and there are many local and remote interactions [47,48]. However, there are experimental observations that impose constraints on these interactions. Upon presentation of a reward-predicting cue—equivalent to a step increase in R(t)—dopamine d(t) rapidly increases and then drops and adapts precisely to its baseline on a sub-second timescale [5,26,49] (Fig 2C), a phenomenon called exact adaptation, while GABAergic activity g(t) increases to a new steady-state that tracks R(t) [49] (Fig 2C).
Exact adaptation is a well-studied property of biological circuits, which can be implemented by a handful of specific feed-forward and feedback mechanisms [50,51]. Since we do not know the mechanistic implementation of the adaptation property in the dopamine circuit, we make the simple assumption of a negative feedback loop. In this design, inhibitory neuron activity g is given by an integral-feedback equation with respect to dopamine release d:
| (2) |
Or, more generally, where F(d) increases with d and has a single zero at d = d0. This feedback loop generates exact adaptation of d: the only steady state solution is d = d0, which is the homeostatic activity level of dopaminergic neurons. This is about ~5 spikes/s in mice [30,52]. The parameter ω determines the adaptation time of the dopaminergic neurons after a change in R(t). This timescale is on the order of hundreds of milliseconds. For the GABAergic neurons, after a step change in R(t), the steady-state firing rate in the model increases proportionally to the logarithm of R(t), such that (this is because GABAergic output integrates dopaminergic activity). Finally, dopamine release represents a temporal-derivative-like computation of R(t) as observed by Kim et al. [12] (S1 Fig).
Taken together, Eqs 1 and 2 provide a minimal model for dopamine responses to expected reward inputs R(t). The model is similar to the classic TD-RPE model of dopamine function and can explain the classic observations of prediction error signals that occur during learning. However, there is an important difference: in the TD-RPE model dopamine is activated by expected reward, whereas in our model it is activated by the logarithm of expected reward. For learning R, this difference requires a slight modification of the recursive learning rules (Methods). In the following sections we will show that logarithmic sensing has crucial implications for the dynamics of learning and behavioral regulation.
Model predicts scale-invariant dopamine responses
We now show that the model given by Eqs 1 and 2 can explain one of the most puzzling observations on dopaminergic responses–the scale invariant dopamine responses observed by Tobler et al. [26] (Fig 2D and 2E). In their experiment, Tobler et al. recorded midbrain dopamine neurons of primates presented with a visual cue that predicted liquid rewards with 50% probability. Three cues were presented in pseudorandom order, and each of the cues predicted a reward of a different magnitude over a 10-fold range (0.05ml, 0.15ml, 0.5ml, note that this is in contrast to the case presented in Fig 2B where the same cue was used for all reward magnitudes). Both predictive stimuli and reward reception elicited a positive dopaminergic response, as expected from the TD-RPE theory. However, while the response to the predictive stimuli increased with expected reward magnitude (S2 Fig), the response to the reward itself was invariant despite large differences in reward magnitude. This scale invariance is not consistent with the classical TD-RPE model which predicts that responses to rewards should also increase with reward magnitude [53]. In order to explain this puzzling observation, it has been suggested that there is a normalization process that scales dopamine responses, e.g. according to the standard deviation of the reward distributions [26,53].
Here we show that the observations of Tobler et al. [26] can be explained by our model without invoking any additional normalization process (Fig 2F). The reason for this is that the model has a circuit feature known in systems biology as fold-change detection (FCD) [54,55]. FCD is a property where after adaptation the circuit output depends only on relative changes in the input, rather than absolute changes. FCD circuits output the temporal (logarithmic) derivative of low-frequency input signals [56–58]. We therefore call the dopamine model presented here the dopamine-FCD model (see Methods for a proof that the model has the FCD property).
To see why the FCD property can explain the observations of Tobler et al., [26] consider the input function for each of the cue-reward sequences. When a reward-predicting stimulus appears, the expected reward changes from its previous baseline value in a step-like manner to some value 0.5R that depends on predicted reward magnitude, causing a dopamine response that increases with R. At the time point when the reward itself is received, the input function increases by ~2-fold (from 0.5R to R, which again for simplicity is modeled as a step increase). Since the dopaminergic response depends only on the fold-change in input, the model predicts identical responses, as observed by Tobler et al. [26]
The FCD property causes the learning and behavior-regulating functions of dopamine to be invariant (i.e., not affected by) multiplying the input field by a scalar [54]–in other words, by multiplying all expected rewards by a constant factor λ. The model thus predicts scale-invariance of the dopamine system. This property may be crucial for the dopamine circuit, since rewards can vary widely in magnitude.
A reward-taxis model for dopamine regulation of behavior
In the following section we will consider whether we can use Eqs 1 and 2 to gain insight into the regulation of behavior by dopamine. To link the dopamine circuit to animal behavior, we first provide an additional equation as a minimal model for dopamine control of motion. The equation is motivated by the well-established role of dopamine as a regulator of action vigor and locomotor activity [13,17,59–61]. The equation posits that dopamine d increases movement speed v:
| (3) |
Where v0 is movement speed at the homeostatic level d = d0. Dopamine d in Eq 3 corresponds to the (normalized) dopaminergic activity in the brain, so that loss of dopaminergic neurons (as occurs in Parkinson’s disease) reduces d proportionally, which effectively reduces homeostatic movement speed v0. We assume a proportional relation between movement speed and d, which is consistent with the gradual increase in movement vigor with dopaminergic activity (see Fig 1J and 1K in da Silva et al. [17]).
When the animal is moving towards higher expected rewards, that is, the input field R(x) increases as the animal moves, d rises above its baseline and movement speed increases; conversely, when the animal moves down R(x), movement speed decreases. The change in d may be transient if the change in the input is step-like or gradual (linear); veering away from the reward, however, will result in an undershoot in d, and such movements will be inhibited. More generally, since d tracks the temporal logarithmic derivative of the input, then as the animal moves its speed will be continuously modulated according the spatial gradients of log R(x), with movements up the gradient invigorated and movements down the gradient inhibited. This movement regulation, defined by Eq 1–3, results in spending longer times near the peaks of the reward field R(x). We thus call this model reward-taxis.
Reward-taxis quantitatively provides the matching law of operant behavior
In the following section we will argue that the reward-taxis model provides a distinct and quantitative explanation for the general matching law of operant behavior, one of the best-established behavioral phenomena [62–66,66–70]. Matching is typically observed in concurrent reward schedules where a freely behaving animal harvests rewards that appear stochastically in two separate locations x1, x2. The rewards are depleted after harvesting and renew after a random time-interval drawn from a memoryless distribution. In the simplest setting, the same reward is provided in both locations but the average renewal time differs between the locations. In more general settings other parameters (e.g. amount or quality of reinforcement) can vary [71]. There is also usually a cost to switching between options. The matching law, in its time-allocation form [72], posits that the long-term average of the relative amount of time the animal chooses each reward location P(x1), P(x2) goes as a power β of the ratio of rewards harvested from the locations R1, R2 (Fig 3A and 3B):
| (4) |
where R1, R2 correspond to the expected reward at each location (the product of rate and amount of reinforcement [72]). The parameter k is a bias term which corresponds to the tendency of the animal to prefer one reward over another even when reinforcement is equal (R1 = R2). The bias term typically varies between experiments. The matching law was originally proposed with perfect matching β = 1 [73]. A large number of studies in various vertebrate species under different experimental conditions observed that β can be somewhat variable, showing slight undermatching (β<1) and overmatching (β>1), with the former more commonly observed [63–65,68,69,74,75]. Matching has also been observed in wild animal foraging [76,77]. Matching is a robust property which holds over orders of magnitude of reward ratios (up to ~1:500 in pigeons [65]). The overall robustness of the matching law has led authors to suggest that it reflects intrinsic properties of the vertebrate nervous system [69].
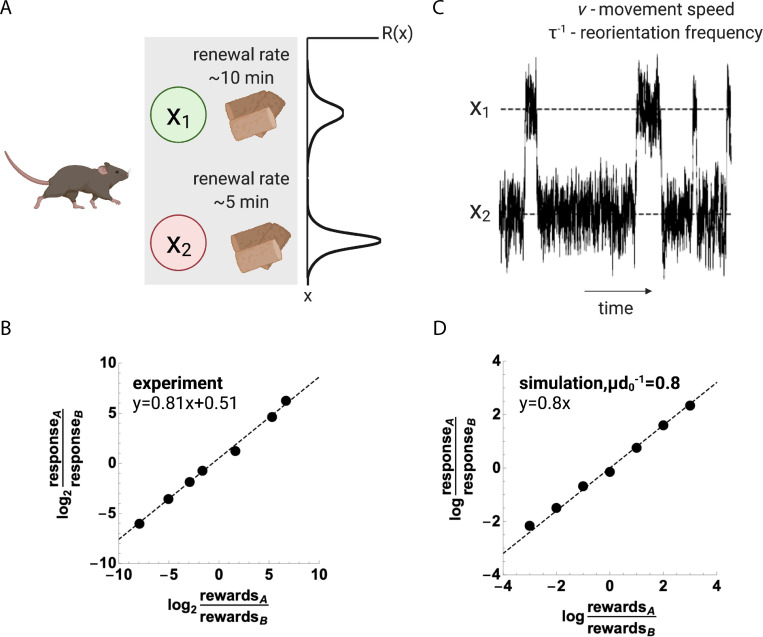
Fig 3. Reward-taxis model provides the generalized matching law.
(A) Matching is observed in experiments where the animal can harvest rewards from two locations, which may be baited or empty. Following the consumption of the reward, the location becomes re-baited after some random amount of time, which may be different between the locations. The generalized matching law, amply supported experimentally, is a power-law relation between the reward harvested and the frequency of responses , R1, R2 are rewards harvested at locations A = x1, B = x2. Perfect matching occurs for β = 1, while undermatching/overmatching are due to variations in β. Undermatching, with β<1, is often observed, as in (B) (data from Fig 1 of [65]). (C,D) To model stochastic choice behavior of a freely behaving animal, we use a random walk model where the animal moves at speed v and reorients at frequency τ−1, with v modulated by dopamine. Random walk model simulation for choice between two expected rewards R1, R2. Expected reward input field is the sum of two Gaussians: (the exact distribution is not important for matching) with τ = 100ms, μ = 4, d0 = 5, v = 10cm s−1, x1 = +30cm, x2 = −30cm, b = 10cm (, Methods). An example of a simulation is presented in panel C. The model was simulated for different ratios of R1/R2, and the response ratio was estimated by the ratio of the time spent ±2.5cm from A = x1, B = x2. Figures were created with BioRender.com.
Matching is an emergent property of the free behavior of the animal, but its underlying origins are unclear. The continuous, free behavior of the animal contrasts with the discrete choice trials processes that are typical for reinforcement learning models. Matching is not optimal–the optimal policy would be for the animal to regularly switch between the alternatives [78], whereas behavior in experiments is characterized by a memoryless switching process (that is, fixed switching probabilities) [79]. Previous explanations for the general matching law assumed an underlying choice process, such as competition between the groups of neurons representing each reward location [80–83].
Here we provide a novel and distinct explanation for the matching law based on the reward-taxis mechanism (Eqs 1–3). We show that matching is a robust emergent property of the dopamine system, and, moreover, we provide an estimate for β in terms of parameters of the dopamine system that can be directly inferred from neuronal recordings (Fig 3C and 3D).
To test whether the model provides the matching law, we model the dynamics of the location of a behaving animal as a stochastic process. Let R(x) be the input field, which is the expected reward R as a function of location x. We assume that R(x) is fixed at x1, x2 by the harvested rewards R1, R2. To account for the stochastic behavior of the animal in the matching experiments, we model its movement as a biased random walk process, where the animal moves in straight lines at speed v (modulated by dopamine) and reorients at random with some fixed probability τ−1. Allowing the new direction to be correlated with the previous direction does not affect the conclusions, and a model where τ (rather than v) is modulated by dopamine leads to the same conclusions.
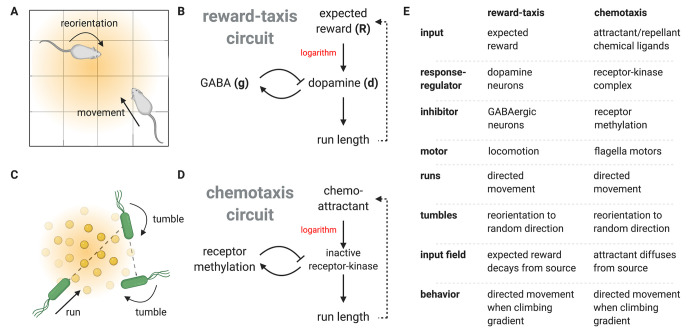
This biased random walk model is analogous to bacterial chemotaxis: bacteria such as E. coli use a run-and-tumble navigation strategy to climb gradients of chemical attractants (Fig 4A–4E) [54,56,84,85]. The bacterial chemotaxis signaling network is based on an FCD circuit that controls run duration [54,86]. It therefore maps onto dopamine release dynamics, where expected-reward inputs play the role of chemoattractant concentration in chemotaxis. The key difference is that in chemotaxis the input field results from the diffusion of attractant molecules, whereas in the dopamine system the input field (expected reward) is learned by the animal.
Fig 4. Dopamine regulation of behavior in the model is analogous to bacterial chemotaxis.
(A) The behavior of an animal in an open field is modelled as a series of directed movements (runs). The direction of each run is chosen at random (or, more generally, stops between runs decorrelate motion direction), and the duration of each run increases with dopamine level. (B) Dopamine is controlled by an FCD circuit activated by expected reward. (CD) The reward-dopamine-behavior circuit is analogous to the chemotaxis circuit that underlies bacterial navigation towards chemo-attractants. Bacterial motion is composed of a series of runs. The direction of each run is randomized by tumbling events, and run duration increases with the inactivation of a receptor-kinase complex, which is controlled by an FCD circuit activated by chemoattractant concentration. (E) Table detailing the mapping between the dopamine system and the chemotaxis system. Figures were created with BioRender.com.
At long time- and length-scales, run-and-tumble motion resembles Brownian motion [87], with a diffusion coefficient D≈m−1v2τ, where m is the dimension (we assume that d is close to the adapted level d0). Brownian motion in the model is biased by longer runs when the agent is moving up the gradient. To account for this, one can add to the diffusion process an advection term that is proportional to the logarithmic gradient: χ∇ log R(x) [88–90]. The advection term corresponds to the average flow at location x. Taken together, the stochastic dynamics of the agent are approximated by a Langevin equation similar to the classic Keller-Segel equation used to model chemotaxis [91]:
| (5) |
where W is an m-dimensional Wiener process (see S1 Text for the derivation of Eq 5). For relatively short runs compared with the adaptation time (sub-second timescale), the advection parameter χ, also called chemotactic drift, is given by: [88], and thus rises with velocity v, gain μ and mean run duration τ. It is important to note that Eq 5 holds also for the model variant in which dopamine modulates τ (see S1 Text).
Eq 5 captures how animal movement depends on the parameters of the dopamine circuit, as well as on movement parameters τ, v. Decreasing the average run duration τ or average movement speed v (as in Parkinson’s disease) decreases both diffusivity D and advection χ, resulting in slower effective motion and gradient climbing. Gradient climbing efficiency (chemotactic drift) increases with , which is the gain of dopamine neurons normalized by their baseline activity. Other circuit parameters do not affect movement dynamics.
Eq 5 is equivalent to the Langevin Monte Carlo algorithm, a widely-used algorithm from statistical physics for sampling probability distributions and for global optimization [92–95]. The steady-state distribution can be readily solved, using standard methods of statistical physics, similar to a Boltzmann distribution in a potential field. The motion samples a probability distribution P(x) proportional to a power β of the expected-reward distribution:
| (6) |
where the power-law β equals the normalized gain of the dopaminergic neurons: . From Eq 6 we infer that for any two expected rewards R1, R2 the response rates P(x1), P(x2) obey the general matching law of Eq 4. We note that this results in matching with k = 1, but any biases in reward preference, which are multiplicative in R1 or R2, will result in a fixed bias term k≠1.
The reward-taxis model therefore predicts operant matching with a power law of . Thus, β is equal to the average ratio of gain to baseline activity in dopaminergic neurons. As mentioned above, these values can be estimated from the neuronal measurements of Eshel et al. [30], μ≈5 spikes/s and d0≈5 spikes/s. These values yield β≈1, in agreement with the matching law. Similar parameters are found also in primates (S2 Fig). The agreement is striking since there is no a-priori reason for the gain and baseline to be similar; normalized gain could in principle have a wide range of values including or .
The matching exponent β only depends on parameters that are intrinsic to the dopaminergic neurons; β is independent of movement speed v or run duration τ, which may vary depending on animal physiology and the environmental context, as well as on the number of dopaminergic neurons. This may explain the robustness of the matching phenomena across species and experimental conditions. The logarithmic derivative property is crucial for obtaining the matching law. A non-logarithmic derivative, or absolute responses, do not provide matching (S1 Text). Taken together, the reward-taxis model can provide a physiological mechanism underpinning operant matching.
Variation in intrinsic neuronal parameters can affect gain μ and baseline firing rate d0. The model predicts that manipulating the relative gain of dopamine neurons will change the reward sensitivity parameter β in the matching law. This prediction can be tested by measuring in genetically modified animals where matching behavior is different from wild-type. One such case is mice that are deficient in the cannabinoid type-1 receptor (CB-/-), which have β that is lower by ~30% compared with wild-type mice [96]. In agreement with the model prediction, CB-/- mice also have deficient dopaminergic responses relative to baseline [97].
Other disorders can be due to reduction in the number of functional dopaminergic neurons, as in Parkinson’s disease, where SNc dopaminergic neurons are lost. Such damage is predicted to change v0. If the damage does not sizably affect the intrinsic properties of surviving neurons, such as gain and baseline, they are not expected to change β in matching experiments.
Discussion
In this study we showed that concepts from systems biology, including exact adaptation, fold-change detection and stochastic navigation, can be mapped to the dopamine system in the brain. We showed that the dopamine circuit may implement a ‘reward-taxis’ mechanism that shares core analogies with bacterial chemotaxis. To show this we developed a mechanistic model of dopamine dynamics based on experimental measurements. The model has similar behavior to the classic TD-RPE model, with a key difference–the circuit is activated by the logarithm of expected reward. The model predicts that dopamine output is invariant to the scale of the distribution of rewards, as observed by Tobler et al. [26], and explains matching in free-operant behavior. Reward-taxis results from the interaction between sensing and movement and implements a simple strategy for climbing gradients of expected reward.
Scale invariance is a recurring motif in biological sensory systems [55]. The model of dopamine transmission as fold-change detection (FCD) of expected reward is thus in line with the conceptualization of dopamine neurons as sensory neurons for reward [98]. FCD includes the classic Weber’s law of sensory systems, which posits that the maximal response to a change in input is normalized by the background level of the signal [99]. FCD is more general than Weber’s law in that the entire dynamics of the output, including amplitude and duration, is normalized by the background input level. FCD allows the system to function in a scale-invariant manner across several decades of background input [54]. It also provides a common scale to compare different types of sensory inputs, by referring to their relative (rather than absolute) changes [100].
While the model focused on the average activity of dopaminergic neurons, the proposed mechanism for FCD (inhibition from neighboring GABAergic neurons) may apply at the level of individual dopaminergic neurons or groups of neurons. This raises the possibility that different dopaminergic neurons could become adapted to different expected-reward levels at the same time, consistent with a recent study that demonstrated that a single reward can simultaneously elicit positive and negative prediction errors in different neurons [101].
The FCD model proposes that RPEs become normalized by the scale of the rewards, but does not account for possible effects of the reward distribution. Such distribution-based effects are evident in the dopamine system. In a recent study, Rothenhoefer et al. showed that rare rewards appear to amplify RPEs more than commonly observed rewards [102]. To further disentangle effects of reward distribution vs. reward scale, we propose the following set of experiments. The FCD model predicts that for a reward schedule with a fixed distribution and a shifted mean X, the dopaminergic responses should decay as X is increased. To test this we may consider a reward schedule where the animal is randomly rewarded with rewards of magnitudes r1 = X+Y, r2 = X−Y, preceded by a cue that predicts that some reward will be delivered. The FCD model predicts that dopaminergic responses should decay as X increases. For example, when the reward schedule alternates between rewards of magnitude r1 = 1.5, r2 = 0.5 (X = 1, Y = 0.5), the dopaminergic response to the reward of magnitude 1.5 should be larger than the dopaminergic response to a reward of magnitude 11.5 under an alternating schedule with rewards of magnitude r1 = 11.5, r2 = 10.5 (X = 11, Y = 0.5). This contrasts with models based on std. normalization which predict identical responses in both scenarios. Similarly, the FCD model predicts that dopaminergic responses should increase with Y, while models based on std. normalization predict identical dopaminergic responses in this scenario as well.
The present study unifies two main effects of dopamine, encoding reward-derivative and increasing movement vigor, by mapping them to a reward-taxis navigational circuit. The circuit is analogous to the bacterial chemotaxis circuit, where in the dopamine case navigation is along gradients of expected reward. The mapping is based on mathematical analogies at both the physiological and behavioral levels. At the physiological level both circuits have the FCD property. At the behavioral level, dopamine increases the probability and vigor of movements, thus increasing the duration of correlated motion (“runs”) compared with reorientations (“tumbles”). Both aspects map to the well-characterized chemotaxis navigation circuit in bacteria.
The stochastic model is sufficient for explaining matching behavior, and provides an accurate mechanistic estimate for the matching constant β. The estimate is derived under mild mechanistic assumptions–that movement speed (or run length) is controlled proportionally by dopamine levels, and that run times are relatively short compared with adaptation time. Improved experimental characterization of movement control by dopamine will allow us to relax these assumptions to obtain better estimates for β. For example, a nonlinear gain for movement speed regulation by dopamine v∝dh would result in multiplication by a constant prefactor β = hμ/d0, and longer run times would result in a proportional decrease in β [103]. As long as these effects are mild, we expect our estimate β≈1 to hold. Importantly, we still expect the matching constant β to be proportional to μ and inversely proportional to d0.
Our study connects between vertebrate motion regulation and the wider family of run-and-tumble stochastic navigation circuits, which includes motion regulation in bacteria, algae, and simple animals [104–107]. Reward-taxis was anticipated in the early work on TD learning, where Montague et al. showed that run-and-tumble dynamics driven by reward prediction errors can explain observations on bee foraging [2].
There are also differences between bacterial chemotaxis and the reward-taxis model for dopamine. The value of β in bacterial chemotaxis is much larger than in the dopamine reward-taxis model, with β>10 in E. coli [108,109] and β~1 estimated for the dopamine system. The high β value in bacteria indicates a strong preference for higher rewards, akin to an optimization for accumulation near attractant peaks. It also allows for collective migration [91]. A value of β~1 (which results in the matching law) allows a greater range for exploration of submaximal rewards.
The reward-taxis model was presented for whole-body spatial movement, but its assumptions are general and may potentially extend to other aspects of behavior. One such aspect is hippocampal replay, the activation of hippocampal place cells during sharp-wave ripples [110–112]. Hippocampal replay consists of a firing sequence of neurons that represents temporally compressed motion trajectories [111,113,114]. It can occur either during sleep or rest (“offline”) or when the animal is awake and engaged in a task (“online”). Online replay plays an important role in planning and navigation [114]. The activation of the place neurons corresponds to stochastic movement trajectories with a characteristic speed [115] that are biased towards the location of rewards [114]; when foraging is random, the trajectories are diffusive, resembling Brownian motion [112]. Hippocampal activity during online replay is tightly coordinated with reward-associated dopamine transmission [110]. To map reward taxis to hippocampal replay requires that dopamine transmission modulate the stochastic trajectories of hippocampal replay, for example through the modulation of velocity or reorientation frequency.
Another potentially relevant system is eye movements. Eye movements are modulated by dopamine and impaired in Parkinson’s disease [34,116,117], and their vigor is modulated by reward prediction errors [118]. Additionally, random walk models capture gaze dynamics during tasks such as visual search [119–121]. Since eye movements are commonly studied in behavioral experiments such as reward matching, they may be a good candidate to test the reward-taxis model.
While taxis navigation systems in organisms such as E. coli are based on gradients that are created due to diffusion, for the dopamine system the input field is generated by learning—TD learning is sufficient for generating gradients of expected reward. From the point of view of signal processing, TD learning smooths away the high-frequency (or “phasic”) input components [122], leaving a low-frequency input signal that is used for navigation. In this way the dopamine system can allow for gradient-based navigation over fields that are derived from arbitrary sensory inputs.
The reward-taxis model does not assume any explicit choice process–in the model, navigation towards regions of higher expected reward is only due to the modulation of movement statistics by dopamine. This may at first sight appear more primitive than standard reinforcement strategies, where the agent compares the expected reward of different alternatives before acting. However, reward-taxis may be advantageous in certain settings. The first advantage is that reward-taxis is computationally cheap–it only requires activation by a single local scalar–which allows for efficient continuous modulation of movements, rather than discrete movement adjustments. The second advantage is that it provides effective sampling of the rewards distributed in the environment by implementing a search algorithm (Eq 5) mathematically analogous to the Langevin Monte Carlo (LMC) algorithm for sampling probability distributions [92–95] and for global optimization [123–128]. Sampling allows the animal to incorporate uncertainty on reward magnitude, probability, or location into its navigation. It also allows the animal to efficiently navigate in complex input fields that include many local minima and maxima [109]. Finally, run-and-tumble navigation provides benefits beyond the Langevin Monte Carlo algorithm by boosting gradient climbing only on sufficiently steep reward gradients due to the positive feedback between behavior and sensing. The positive feedback occurs since running along the gradient provides an increasing input that further enhances the run duration [129]. These advantages suggest that reward-taxis may be a useful strategy when the expected reward input field is complex or uncertain.
The relation between the dopaminergic system and sampling, and in particular the relation between dopaminergic parameters and the matching law parameter β, may be relevant to recent findings on dopamine and exploration [130,131]. In mice and humans, dopaminergic antagonists appear to specifically increase random exploration, rather than affect learning [130,131]. Under our modelling framework, this effect may correspond to a decrease in β by the treatment, for example, due to a reduction in the effective dopaminergic gain. This would result in altered behavioral output, without necessarily affecting learning. More generally, the sampling framework can provide a quantitative theoretical framework to model the relation between dopamine and various aspects of stochastic exploration, such as novelty-driven exploration [132,133].
A more realistic and complete model would include other aspects of decision making such as goal-directed behavior and planning. It is important to note that since the FCD model does not hinder learning, it is compatible with these aspects and they are likely to complement reward-taxis with more directed movement. Such a combination of navigation mechanisms is evident also in simple organisms that employ run-and-tumble navigation. For example, in C. elegans thermotaxis, run-and-tumble navigation is combined with biased reorientations in order to navigate towards an optimal temperature range [106]. Formally, while run-and-tumble navigation resembles Langevin-based sampling, directed reorientations are more closely related to gradient descent, which is efficient for local optimization but poor for global optimization [127,134,135]. We thus propose that the reward-taxis mechanism we describe can complement other navigation and decision making-mechanisms to allow for efficient navigation in complex environments.
Methods
Model equations and fold-change detection
The equations for dopamine (d) and GABAergic inhibition (g) are provided by:
| (7) |
| (8) |
For the dopamine equation, ωd determines the dopamine degradation rate, μ is dopamine gain, R is expected reward (defined in the next Methods section), and α is GABAergic inhibition strength. For the GABAergic inhibition equation, ω determines the adaptation rate and d0 is the adapted steady-state of dopamine. For simplicity, we assume that dopamine dynamics are faster than the dynamics of adaptation due to g (i.e., ωd is large compared with ω, this assumption is not important for our conclusions) so we take:
| (9) |
Eqs 7, 8 and 9 can represent the average activity of individual neurons, or the total activity of many neurons. We therefore used the same equations both to model average individual neuron recordings (as in Fig 2), and to model the effect of dopamine on movement, which is likely to be the sum of the activity of many neurons.
Consider now a constant input R = R0, so that after some time the system reaches steady-state. To find the steady state, we solve Eqs 7 and 8, taking , which yields the steady-state solutions dst = d0 and gst = α−1(C−d0+μ log R0). The observation that dst = d0 regardless of R0 and other circuit parameters is an important circuit feature from systems biology known as exact adaptation [27,50,136–138]. This feature is essential for explaining why dopamine activity returns precisely to baseline after a step increase in expected reward, while GABAergic activity increases in a way that tracks expected reward.
Beyond exact adaptation, the system has an even stronger property of fold-change detection (FCD). FCD is defined as dynamics of dopamine (d) in response to an input λR(t) that are independent of λ, starting from initial conditions at steady-state for λR(0). To show this we relabel g = g′+α−1 μ log λ:
| (10) |
| (11) |
Note that the rate equation for is the same as for since . Eqs 10 and 11 are completely independent of λ, and their steady-state and dst = d0 is also independent of λ. This means that the dynamics of the system have the FCD property. The FCD property is essential for explaining the scale invariance of the dopaminergic responses to rewards in Fig 2 –the response only depends on the fold-change of expected reward (two-fold change upon reception of reward at p = 0.5) but not on reward magnitude.
While Eqs 7, 8 and 9 provide FCD, they are not the only possible model that provides FCD for this system. In particular, a feed-forward model where expected reward activates g is also possible, i.e.:
| (12) |
| (13) |
For this circuit, the steady state for a constant input R = R0 is and dst = d0. FCD can also be analogously shown. Given an input λr(t), we can take g = g′+α−1 μ log λ, which again provides equations and steady-state that are independent of λ:
| (14) |
| (15) |
While this simple log-linear model captures various important experimental observations, it is important to note that it has some clear limitations. One limitation is that both d and g can in principle reach negative values when R is small. Measurements of dopamine responses in monkeys indeed show deviations from sub-linearity for small rewards [139]. The model can be adjusted to prevent negative undershoots (S3 Fig). Future studies may build on improved measurements and better mechanistic characterization of the dopamine circuit to refine this model. Finally, the original studies quantifying the input/output relation between reward magnitude and dopaminergic output, presented in Fig 2, considered fits by strongly sublinear power- and hill-functions [30,38]. It is not possible to discriminate between these functions and the logarithmic relation with the available data, and such a fit would require more accurate measurements over large magnitude ranges.
Definition of expected reward and relation between the circuit and TD learning
Here we will define the input to the circuit, which is the logarithmic expected reward log R, and present it in the context of the temporal difference (TD) learning theory of dopamine function [5,7]. We first define the expected temporally discounted sum of future rewards V (also known as the value function in TD learning):
| (16) |
Where γ<1 is a “future discounting” factor and r(t) is the reward received at time t into the future (here for simplicity we take discrete time; for equivalent formulation for continuous time, see Doya [140]). It is possible to think of V as a function of the current state s of the agent, which may include for example its location in space x. This is known as the Markovian setting, where we denote the value function as V(s). The value function plays an important role in decision making—learning the value function is a principal focus of reinforcement learning algorithms [5,7].
In our model, the input to the circuit for an agent moving into a state s at time t is defined using the expected reward R:
| (17) |
As an example, consider the setting of Fig 2D–2F, where a reward of size r = y is delivered with probability p at Δt time-units into future: the expected reward would in this case be R(0)≈pγΔty. An actual delivery of the reward would then increase R to R(Δt)≈y, so the ratio is independent of reward magnitude.
Note that due to discounting and uncertainty, R decays with the distance from a location where a reward is delivered, as in Fig 1D [36].
We will now show that our model is consistent with the TD learning theory of dopamine function with a slight modification to the TD learning rule. We will first briefly present the TD learning algorithm. In reinforcement learning, the agent usually does not know V and needs to learn it from experience. This presents a computational problem, since V is an infinite sum over unknown future events. A way to get around this is to update the learned V using dynamic programming [141]. The key insight is that Eq 16 can be rewritten as:
| (18) |
The above equation implies that V can be estimated iteratively with a simple update rule, which is at the heart of TD learning. If the agent is at state s at time t, and at state s’ at time t+1, the update rule is:
| (19) |
Where V(t, s) is the computed estimate of the expected reward at state s at time t, α is the learning rate, r(t) is the reward delivered at time t and γ is the discounting factor. There is extensive literature demonstrating correspondence between TD learning and midbrain dopamine function (reviewed by [8]); specifically, experiments show a correspondence between phasic dopamine secretion and the prediction error term of Eq 19 [5,8], in the sense that positive or negative firing of dopamine neurons relative to baseline corresponds positive and negative predictions errors in TD models of learning.
We will now show that our model is capable of learning the logarithm of V (that is, the logarithm of the entire discounted sum over future rewards), in a manner similar to the learning of V by classic TD learning. Since both are equivalent, our model is sufficient for explaining TD learning by dopaminergic responses. For this we will develop a plausible temporal difference learning rule based on logarithmic prediction errors: . The learning rule is an extension of the learning rule presented in Eqs 15–17 in Coulthard et al. [142]. To devise the learning rule, consider the Taylor expansion of the logarithm of the update rule given in Eq 19 around r(t)+γV(t, s′) = V(t, s):
| (20) |
The above equation represents an update rule that only needs the modified prediction error term δlog in order to learn the value function. In the continuous limit, and in the absence of reward, the error term is approximately proportional the logarithmic derivative of the value function. This corresponds to the output of our proposed FCD model for low frequency signals.
The output of the circuit to a delivered reward in a transition from a state s to a state s’ is also approximately proportional to the above error term:
| (21) |
The final equality is due to the fact that prior to reward delivery, GABAergic output adapts to α−1(C−d0+μ log V(s)). The FCD model is therefore compatible with the TD learning theory of dopamine function. In S4 Fig we provide simulations for learning with the modified learning rule, where we show that it indeed learns log V.
Analysis
The fit of the dopaminergic responses in Fig 2 (including confidence intervals) was performed using the NonlinearModelFit function of Mathematica (version 12.1.1). All other figures and simulations were produced using Python (version 3.8.5). The source code and data to produce all the figures is available at https://github.com/omerka-weizmann/reward_taxis.
Supporting information
(DOCX)
Dopamine output to movement in a reward gradient given by , with h = 1.5, x0 = 1, v0 = 1 and γ = 0.04, and perturbations as described in Fig 2 of [12]. Insets. Corresponding dopaminergic outputs from mice (left to right: n = 11, n = 11, n = 15, n = 5) VTA neurons measured by calcium imaging, from Fig 2C, 2G, 2K and 2O in [12], smoothed using a Savitzky–Golay filter. All simulations were performed with the parameters provided in Table 1.
(DOCX)
Dopamine responses in Macaque monkeys to cues predicting variable size liquid rewards (dashed lines) correspond to model simulations, given by a step R(t) = R0+λuθ(t−t0) where θ(t−t0) is a unit step function, R0 = 1 and λ = 20 ml−1, and u is the expected value of the liquid volume that the cue predicts. Data is from the population neuron recordings of Fig 1B in Tobler et al. [26], corresponding to, from left to right: 0.0 ml with probability p = 1, 0.05 ml with probability p = 0.5, 0.15 ml with probability p = 0.5, 0.15 ml with probability p = 1, and 0.5 ml with probability p = 0.5. The probabilistic responses correspond to the responses where scale invariance is observed in Fig 2.
(DOCX)
(A) Reward reception and omission was simulated according to Eqs 1,2 in the manuscript in a manner similar to the simulations in Fig 1. The input is given by R(t) = R0+λθ(t−t0) where θ(t−t0) is a unit step function, R0 = 1 and λ = 7 for the reward reception and R0 = 7, λ = −6 for reward omission. Note that Eq 1 reaches negative values upon reward omission. (B) Dynamics for model where Eq 1 is adjusted as (here taking kd = 1). This model does not reach negative values of d, and behaves similarly to the FCD model if kd≪d0.
(DOCX)
(A) Simulation setup. The agent progresses through a series of N states S1,…,SN, where in the final stage SN a reward is drawn according to a distribution with a fixed mean reward value. In the simulations we use three distributions (deterministic reward, normal distribution with CV = 0.3, and Bernoulli trials). A logarithmic value function log V is learned recursively according to the rule . (B,C) Learning simulations with reward magnitude 50 (B) and 200 (C). Thick line denotes a log Vt+1(S1) in a single simulation, while thin dashed line denotes expected . Simulation parameters are N = 5, α = 0.02. Figures were created with BioRender.com.
(DOCX)
Acknowledgments
We are grateful to Peter Dayan for providing feedback on the manuscript, and for members of the Alon lab for useful discussions. U.A. is the incumbent of the Abisch-Frenkel Professorial Chair.
Data Availability
The source code and data to produce all the figures is available at https://github.com/omerka-weizmann/reward_taxis.
Funding Statement
O.K. acknowledges support from the James S. McDonnell Foundation 21st Century Science Initiative Understanding Dynamic and Multi-scale Systems - Postdoctoral Fellowship Award. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Barto AG. Adaptive critics and the basal ganglia. 1995. [Google Scholar]
- 2.Montague PR, Dayan P, Person C, Sejnowski TJ. Bee foraging in uncertain environments using predictive hebbian learning. Nature. 1995;377: 725–728. doi: 10.1038/377725a0 [DOI] [PubMed] [Google Scholar]
- 3.Houk JC, Davis JL, Beiser DG. Models of information processing in the basal ganglia. MIT press; 1995. [Google Scholar]
- 4.Montague PR, Dayan P, Sejnowski TJ. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. J Neurosci. 1996;16: 1936–1947. doi: 10.1523/JNEUROSCI.16-05-01936.1996 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275: 1593–1599. doi: 10.1126/science.275.5306.1593 [DOI] [PubMed] [Google Scholar]
- 6.Steinberg EE, Keiflin R, Boivin JR, Witten IB, Deisseroth K, Janak PH. A Causal Link Between Prediction Errors, Dopamine Neurons and Learning. Nat Neurosci. 2013;16: 966–973. doi: 10.1038/nn.3413 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sutton RS, Barto AG. Introduction to reinforcement learning. MIT press; Cambridge; 1998. [Google Scholar]
- 8.Glimcher PW. Understanding dopamine and reinforcement learning: the dopamine reward prediction error hypothesis. Proc Natl Acad Sci. 2011;108: 15647–15654. doi: 10.1073/pnas.1014269108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Howe MW, Tierney PL, Sandberg SG, Phillips PE, Graybiel AM. Prolonged dopamine signalling in striatum signals proximity and value of distant rewards. nature. 2013;500: 575–579. doi: 10.1038/nature12475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hamid AA, Pettibone JR, Mabrouk OS, Hetrick VL, Schmidt R, Vander Weele CM, et al. Mesolimbic dopamine signals the value of work. Nat Neurosci. 2016;19: 117–126. doi: 10.1038/nn.4173 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mohebi A, Pettibone JR, Hamid AA, Wong J-MT, Vinson LT, Patriarchi T, et al. Dissociable dopamine dynamics for learning and motivation. Nature. 2019;570: 65–70. doi: 10.1038/s41586-019-1235-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim HR, Malik AN, Mikhael JG, Bech P, Tsutsui-Kimura I, Sun F, et al. A Unified Framework for Dopamine Signals across Timescales. Cell. 2020. [cited 28 Nov 2020]. doi: 10.1016/j.cell.2020.11.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Niv Y, Daw ND, Joel D, Dayan P. Tonic dopamine: opportunity costs and the control of response vigor. Psychopharmacology (Berl). 2007;191: 507–520. doi: 10.1007/s00213-006-0502-4 [DOI] [PubMed] [Google Scholar]
- 14.Mazzoni P, Hristova A, Krakauer JW. Why don’t we move faster? Parkinson’s disease, movement vigor, and implicit motivation. J Neurosci. 2007;27: 7105–7116. doi: 10.1523/JNEUROSCI.0264-07.2007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Berridge KC. The debate over dopamine’s role in reward: the case for incentive salience. Psychopharmacology (Berl). 2007;191: 391–431. doi: 10.1007/s00213-006-0578-x [DOI] [PubMed] [Google Scholar]
- 16.Dudman JT, Krakauer JW. The basal ganglia: from motor commands to the control of vigor. Curr Opin Neurobiol. 2016;37: 158–166. doi: 10.1016/j.conb.2016.02.005 [DOI] [PubMed] [Google Scholar]
- 17.da Silva JA, Tecuapetla F, Paixão V, Costa RM. Dopamine neuron activity before action initiation gates and invigorates future movements. Nature. 2018;554: 244–248. doi: 10.1038/nature25457 [DOI] [PubMed] [Google Scholar]
- 18.Shadmehr R, Ahmed AA. Vigor: neuroeconomics of movement control. MIT Press; 2020. [DOI] [PubMed] [Google Scholar]
- 19.Meder D, Herz DM, Rowe JB, Lehéricy S, Siebner HR. The role of dopamine in the brain-lessons learned from Parkinson’s disease. Neuroimage. 2019;190: 79–93. doi: 10.1016/j.neuroimage.2018.11.021 [DOI] [PubMed] [Google Scholar]
- 20.Berke JD. What does dopamine mean? Nat Neurosci. 2018;21: 787–793. doi: 10.1038/s41593-018-0152-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Friston K. The free-energy principle: a unified brain theory? Nat Rev Neurosci. 2010;11: 127–138. doi: 10.1038/nrn2787 [DOI] [PubMed] [Google Scholar]
- 22.Bogacz R. Dopamine role in learning and action inference. Elife. 2020;9: e53262. doi: 10.7554/eLife.53262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Niv Y, Daw N, Dayan P. How fast to work: Response vigor, motivation and tonic dopamine. Adv Neural Inf Process Syst. 2005;18: 1019–1026. [Google Scholar]
- 24.Yoon T, Geary RB, Ahmed AA, Shadmehr R. Control of movement vigor and decision making during foraging. Proc Natl Acad Sci. 2018;115: E10476–E10485. doi: 10.1073/pnas.1812979115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Daw ND, O’doherty JP, Dayan P, Seymour B, Dolan RJ. Cortical substrates for exploratory decisions in humans. Nature. 2006;441: 876–879. doi: 10.1038/nature04766 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tobler PN, Fiorillo CD, Schultz W. Adaptive Coding of Reward Value by Dopamine Neurons. Science. 2005;307: 1642–1645. doi: 10.1126/science.1105370 [DOI] [PubMed] [Google Scholar]
- 27.Alon U. An introduction to systems biology: design principles of biological circuits. CRC press; 2019. [Google Scholar]
- 28.Schultz W. Predictive reward signal of dopamine neurons. J Neurophysiol. 1998;80: 1–27. doi: 10.1152/jn.1998.80.1.1 [DOI] [PubMed] [Google Scholar]
- 29.Brischoux F, Chakraborty S, Brierley DI, Ungless MA. Phasic excitation of dopamine neurons in ventral VTA by noxious stimuli. Proc Natl Acad Sci. 2009;106: 4894–4899. doi: 10.1073/pnas.0811507106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Eshel N, Tian J, Bukwich M, Uchida N. Dopamine neurons share common response function for reward prediction error. Nat Neurosci. 2016;19: 479–486. doi: 10.1038/nn.4239 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Parker NF, Cameron CM, Taliaferro JP, Lee J, Choi JY, Davidson TJ, et al. Reward and choice encoding in terminals of midbrain dopamine neurons depends on striatal target. Nat Neurosci. 2016;19: 845–854. doi: 10.1038/nn.4287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lee RS, Mattar MG, Parker NF, Witten IB, Daw ND. Reward prediction error does not explain movement selectivity in DMS-projecting dopamine neurons. Behrens TE, Schoenbaum G, Schoenbaum G, Willuhn I, editors. eLife. 2019;8: e42992. doi: 10.7554/eLife.42992 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Engelhard B, Finkelstein J, Cox J, Fleming W, Jang HJ, Ornelas S, et al. Specialized coding of sensory, motor and cognitive variables in VTA dopamine neurons. Nature. 2019;570: 509–513. doi: 10.1038/s41586-019-1261-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kori A, Miyashita N, Kato M, Hikosaka O, Usui S, Matsumura M. Eye movements in monkeys with local dopamine depletion in the caudate nucleus. II. Deficits in voluntary saccades. J Neurosci. 1995;15: 928–941. doi: 10.1523/JNEUROSCI.15-01-00928.1995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Matsumoto M, Hikosaka O. Two types of dopamine neuron distinctly convey positive and negative motivational signals. Nature. 2009;459: 837–841. doi: 10.1038/nature08028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gershman SJ. Dopamine ramps are a consequence of reward prediction errors. Neural Comput. 2014;26: 467–471. doi: 10.1162/NECO_a_00559 [DOI] [PubMed] [Google Scholar]
- 37.Daw ND, Tobler PN. Chapter 15—Value Learning through Reinforcement: The Basics of Dopamine and Reinforcement Learning. In: Glimcher PW, Fehr E, editors. Neuroeconomics (Second Edition). San Diego: Academic Press; 2014. pp. 283–298. doi: [DOI] [Google Scholar]
- 38.Eshel N, Bukwich M, Rao V, Hemmelder V, Tian J, Uchida N. Arithmetic and local circuitry underlying dopamine prediction errors. Nature. 2015;525: 243–246. doi: 10.1038/nature14855 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Dehaene S. The neural basis of the Weber–Fechner law: a logarithmic mental number line. Trends Cogn Sci. 2003;7: 145–147. doi: 10.1016/s1364-6613(03)00055-x [DOI] [PubMed] [Google Scholar]
- 40.Nieder A, Miller EK. Coding of cognitive magnitude: Compressed scaling of numerical information in the primate prefrontal cortex. Neuron. 2003;37: 149–157. doi: 10.1016/s0896-6273(02)01144-3 [DOI] [PubMed] [Google Scholar]
- 41.Shen J. On the foundations of vision modeling: I. Weber’s law and Weberized TV restoration. Phys Nonlinear Phenom. 2003;175: 241–251. [Google Scholar]
- 42.Dehaene S, Izard V, Spelke E, Pica P. Log or linear? Distinct intuitions of the number scale in Western and Amazonian indigene cultures. Science. 2008;320: 1217–1220. doi: 10.1126/science.1156540 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Nieder A, Dehaene S. Representation of number in the brain. Annu Rev Neurosci. 2009;32: 185–208. doi: 10.1146/annurev.neuro.051508.135550 [DOI] [PubMed] [Google Scholar]
- 44.Laughlin SB. The role of sensory adaptation in the retina. J Exp Biol. 1989;146: 39–62. doi: 10.1242/jeb.146.1.39 [DOI] [PubMed] [Google Scholar]
- 45.Bernoulli D. Specimen theoriae novae de mensura sortis. Gregg; 1968. [Google Scholar]
- 46.Rubinstein M. The strong case for the generalized logarithmic utility model as the premier model of financial markets. Financial Dec Making Under Uncertainty. Elsevier; 1977. pp. 11–62. [Google Scholar]
- 47.Morales M, Margolis EB. Ventral tegmental area: cellular heterogeneity, connectivity and behaviour. Nat Rev Neurosci. 2017;18: 73–85. doi: 10.1038/nrn.2016.165 [DOI] [PubMed] [Google Scholar]
- 48.Cox J, Witten IB. Striatal circuits for reward learning and decision-making. Nat Rev Neurosci. 2019;20: 482–494. doi: 10.1038/s41583-019-0189-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Cohen JY, Haesler S, Vong L, Lowell BB, Uchida N. Neuron-type-specific signals for reward and punishment in the ventral tegmental area. nature. 2012;482: 85–88. doi: 10.1038/nature10754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ma W, Trusina A, El-Samad H, Lim WA, Tang C. Defining network topologies that can achieve biochemical adaptation. Cell. 2009;138: 760–773. doi: 10.1016/j.cell.2009.06.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Adler M, Szekely P, Mayo A, Alon U. Optimal regulatory circuit topologies for fold-change detection. Cell Syst. 2017;4: 171–181. doi: 10.1016/j.cels.2016.12.009 [DOI] [PubMed] [Google Scholar]
- 52.Robinson S, Smith DM, Mizumori SJY, Palmiter RD. Firing properties of dopamine neurons in freely moving dopamine-deficient mice: Effects of dopamine receptor activation and anesthesia. Proc Natl Acad Sci. 2004;101: 13329–13334. doi: 10.1073/pnas.0405084101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Gershman SJ. Dopamine, inference, and uncertainty. Neural Comput. 2017;29: 3311–3326. doi: 10.1162/neco_a_01023 [DOI] [PubMed] [Google Scholar]
- 54.Shoval O, Goentoro L, Hart Y, Mayo A, Sontag E, Alon U. Fold-change detection and scalar symmetry of sensory input fields. Proc Natl Acad Sci. 2010;107: 15995–16000. doi: 10.1073/pnas.1002352107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Adler M, Alon U. Fold-change detection in biological systems. Curr Opin Syst Biol. 2018;8: 81–89. [Google Scholar]
- 56.Tu Y, Shimizu TS, Berg HC. Modeling the chemotactic response of Escherichia coli to time-varying stimuli. Proc Natl Acad Sci. 2008;105: 14855–14860. doi: 10.1073/pnas.0807569105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Adler M, Mayo A, Alon U. Logarithmic and power law input-output relations in sensory systems with fold-change detection. PLoS Comput Biol. 2014;10: e1003781. doi: 10.1371/journal.pcbi.1003781 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lang M, Sontag E. Scale-invariant systems realize nonlinear differential operators. 2016 American Control Conference (ACC). IEEE; 2016. pp. 6676–6682. [Google Scholar]
- 59.Beierholm U, Guitart-Masip M, Economides M, Chowdhury R, Düzel E, Dolan R, et al. Dopamine modulates reward-related vigor. Neuropsychopharmacology. 2013;38: 1495–1503. doi: 10.1038/npp.2013.48 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Panigrahi B, Martin KA, Li Y, Graves AR, Vollmer A, Olson L, et al. Dopamine is required for the neural representation and control of movement vigor. Cell. 2015;162: 1418–1430. doi: 10.1016/j.cell.2015.08.014 [DOI] [PubMed] [Google Scholar]
- 61.Ek F, Malo M, Åberg Andersson M, Wedding C, Kronborg J, Svensson P, et al. Behavioral Analysis of Dopaminergic Activation in Zebrafish and Rats Reveals Similar Phenotypes. ACS Chem Neurosci. 2016;7: 633–646. doi: 10.1021/acschemneuro.6b00014 [DOI] [PubMed] [Google Scholar]
- 62.Herrnstein RJ. On the law of effect 1. J Exp Anal Behav. 1970;13: 243–266. doi: 10.1901/jeab.1970.13-243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Baum WM. On two types of deviation from the matching law: bias and undermatching 1. J Exp Anal Behav. 1974;22: 231–242. doi: 10.1901/jeab.1974.22-231 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Baum WM. Optimization and the matching law as accounts of instrumental behavior. J Exp Anal Behav. 1981;36: 387–403. doi: 10.1901/jeab.1981.36-387 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Baum WM, Schwendiman JW, Bell KE. Choice, contingency discrimination, and foraging theory. J Exp Anal Behav. 1999;71: 355–373. doi: 10.1901/jeab.1999.71-355 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Sugrue LP, Corrado GS, Newsome WT. Matching behavior and the representation of value in the parietal cortex. science. 2004;304: 1782–1787. doi: 10.1126/science.1094765 [DOI] [PubMed] [Google Scholar]
- 67.Dallery J, Soto PL. Herrnstein’s hyperbolic matching equation and behavioral pharmacology: Review and critique. Behav Pharmacol. 2004;15: 443–459. doi: 10.1097/00008877-200411000-00001 [DOI] [PubMed] [Google Scholar]
- 68.Lau B, Glimcher PW. Dynamic response-by-response models of matching behavior in rhesus monkeys. J Exp Anal Behav. 2005;84: 555–579. doi: 10.1901/jeab.2005.110-04 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.McDowell JJ. On the theoretical and empirical status of the matching law and matching theory. Psychol Bull. 2013;139: 1000. doi: 10.1037/a0029924 [DOI] [PubMed] [Google Scholar]
- 70.Houston AI, Trimmer PC, McNamara JM. Matching Behaviours and Rewards. Trends Cogn Sci. 2021. doi: 10.1016/j.tics.2021.01.011 [DOI] [PubMed] [Google Scholar]
- 71.Davison M, McCarthy D. The matching law: a research review. Hillsdale, N.J: L. Erlbaum; 1988. [Google Scholar]
- 72.Baum WM, Rachlin HC. Choice as time allocation 1. J Exp Anal Behav. 1969;12: 861–874. doi: 10.1901/jeab.1969.12-861 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Herrnstein RJ. Relative and absolute strength of response as a function of frequency of reinforcement. J Exp Anal Behav. 1961;4: 267. doi: 10.1901/jeab.1961.4-267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.William BM. Matching, undermatching, and overmatching in studies of choice. J Exp Anal Behav. 1979;32: 269–281. doi: 10.1901/jeab.1979.32-269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Davison M. Choice, changeover, and travel: A quantitative model. J Exp Anal Behav. 1991;55: 47–61. doi: 10.1901/jeab.1991.55-47 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Baum WM. Choice in free-ranging wild pigeons. Science. 1974;185: 78–79. doi: 10.1126/science.185.4145.78 [DOI] [PubMed] [Google Scholar]
- 77.Houston A. THE MATCHING LAW APPLIES TO WAGTAILS’FORAGING IN THE WILD. J Exp Anal Behav. 1986;45: 15–18. doi: 10.1901/jeab.1986.45-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Houston AI, McNamara J. How to maximize reward rate on two variable-interval paradigms. J Exp Anal Behav. 1981;35: 367–396. doi: 10.1901/jeab.1981.35-367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Heyman GM. A MARKOV MODEL DESCRIPTION OF CHANGEOVER PROBABILITIES ON CONCURRENT VARIABLE-INTERVAL SCHEDULES 1. J Exp Anal Behav. 1979;31: 41–51. doi: 10.1901/jeab.1979.31-41 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Herrnstein RJ, Prelec D. Melioration: A theory of distributed choice. J Econ Perspect. 1991;5: 137–156. [Google Scholar]
- 81.Soltani A, Wang X-J. A biophysically based neural model of matching law behavior: melioration by stochastic synapses. J Neurosci. 2006;26: 3731–3744. doi: 10.1523/JNEUROSCI.5159-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Loewenstein Y, Seung HS. Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity. Proc Natl Acad Sci. 2006;103: 15224–15229. doi: 10.1073/pnas.0505220103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Simen P, Cohen JD. Explicit melioration by a neural diffusion model. Brain Res. 2009;1299: 95–117. doi: 10.1016/j.brainres.2009.07.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Berg HC, Brown DA. Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature. 1972;239: 500–504. doi: 10.1038/239500a0 [DOI] [PubMed] [Google Scholar]
- 85.Sourjik V, Wingreen NS. Responding to chemical gradients: bacterial chemotaxis. Curr Opin Cell Biol. 2012;24: 262–268. doi: 10.1016/j.ceb.2011.11.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Lazova MD, Ahmed T, Bellomo D, Stocker R, Shimizu TS. Response rescaling in bacterial chemotaxis. Proc Natl Acad Sci. 2011;108: 13870–13875. doi: 10.1073/pnas.1108608108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Berg HC. Random walks in biology. Expanded ed. Princeton, N.J: Princeton University Press; 1993. [Google Scholar]
- 88.Si G, Wu T, Ouyang Q, Tu Y. Pathway-Based Mean-Field Model for Escherichia coli Chemotaxis. Phys Rev Lett. 2012;109: 048101. doi: 10.1103/PhysRevLett.109.048101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Dufour YS, Fu X, Hernandez-Nunez L, Emonet T. Limits of Feedback Control in Bacterial Chemotaxis. PLOS Comput Biol. 2014;10: e1003694. doi: 10.1371/journal.pcbi.1003694 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Menolascina F, Rusconi R, Fernandez VI, Smriga S, Aminzare Z, Sontag ED, et al. Logarithmic sensing in Bacillus subtilis aerotaxis. NPJ Syst Biol Appl. 2017;3: 16036. doi: 10.1038/npjsba.2016.36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Keller EF, Segel LA. Model for chemotaxis. J Theor Biol. 1971;30: 225–234. doi: 10.1016/0022-5193(71)90050-6 [DOI] [PubMed] [Google Scholar]
- 92.Roberts GO, Tweedie RL. Exponential convergence of Langevin distributions and their discrete approximations. Bernoulli. 1996;2: 341–363. [Google Scholar]
- 93.Neal RM. MCMC using Hamiltonian dynamics. Handb Markov Chain Monte Carlo. 2011;2: 2. [Google Scholar]
- 94.Girolami M, Calderhead B. Riemann manifold langevin and hamiltonian monte carlo methods. J R Stat Soc Ser B Stat Methodol. 2011;73: 123–214. [Google Scholar]
- 95.Dalalyan AS. Theoretical guarantees for approximate sampling from smooth and log-concave densities. ArXiv Prepr ArXiv14127392. 2014. [Google Scholar]
- 96.Sanchis-Segura C, Cline BH, Marsicano G, Lutz B, Spanagel R. Reduced sensitivity to reward in CB1 knockout mice. Psychopharmacology (Berl). 2004;176: 223–232. doi: 10.1007/s00213-004-1877-8 [DOI] [PubMed] [Google Scholar]
- 97.Li X, Hoffman AF, Peng X-Q, Lupica CR, Gardner EL, Xi Z-X. Attenuation of basal and cocaine-enhanced locomotion and nucleus accumbens dopamine in cannabinoid CB1-receptor-knockout mice. Psychopharmacology (Berl). 2009;204: 1–11. doi: 10.1007/s00213-008-1432-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Watabe-Uchida M, Eshel N, Uchida N. Neural circuitry of reward prediction error. Annu Rev Neurosci. 2017;40: 373–394. doi: 10.1146/annurev-neuro-072116-031109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Gös Ekman. Weber’s law and related functions. J Psychol. 1959;47: 343–352. [Google Scholar]
- 100.Hart Y, Mayo AE, Shoval O, Alon U. Comparing apples and oranges: fold-change detection of multiple simultaneous inputs. PloS One. 2013;8: e57455. doi: 10.1371/journal.pone.0057455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Dabney W, Kurth-Nelson Z, Uchida N, Starkweather CK, Hassabis D, Munos R, et al. A distributional code for value in dopamine-based reinforcement learning. Nature. 2020;577: 671–675. doi: 10.1038/s41586-019-1924-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Rothenhoefer KM, Hong T, Alikaya A, Stauffer WR. Rare rewards amplify dopamine responses. Nat Neurosci. 2021;24: 465–469. doi: 10.1038/s41593-021-00807-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Salek MM, Carrara F, Fernandez V, Guasto JS, Stocker R. Bacterial chemotaxis in a microfluidic T-maze reveals strong phenotypic heterogeneity in chemotactic sensitivity. Nat Commun. 2019;10: 1877. doi: 10.1038/s41467-019-09521-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Pierce-Shimomura JT, Morse TM, Lockery SR. The Fundamental Role of Pirouettes in Caenorhabditis elegans Chemotaxis. J Neurosci. 1999;19: 9557–9569. doi: 10.1523/JNEUROSCI.19-21-09557.1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Polin M, Tuval I, Drescher K, Gollub JP, Goldstein RE. Chlamydomonas Swims with Two “Gears” in a Eukaryotic Version of Run-and-Tumble Locomotion. Science. 2009;325: 487–490. doi: 10.1126/science.1172667 [DOI] [PubMed] [Google Scholar]
- 106.Luo L, Cook N, Venkatachalam V, Martinez-Velazquez LA, Zhang X, Calvo AC, et al. Bidirectional thermotaxis in Caenorhabditis elegans is mediated by distinct sensorimotor strategies driven by the AFD thermosensory neurons. Proc Natl Acad Sci U S A. 2014;111: 2776–2781. doi: 10.1073/pnas.1315205111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Kirkegaard JB, Bouillant A, Marron AO, Leptos KC, Goldstein RE. Aerotaxis in the closest relatives of animals. Elife. 2016;5: e18109. doi: 10.7554/eLife.18109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Hu B, Tu Y. Behaviors and strategies of bacterial navigation in chemical and nonchemical gradients. PLoS Comput Biol. 2014;10: e1003672. doi: 10.1371/journal.pcbi.1003672 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Karin O, Alon U. Temporal fluctuations in chemotaxis gain implement a simulated-tempering strategy for efficient navigation in complex environments. Iscience. 2021;24: 102796. doi: 10.1016/j.isci.2021.102796 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Gomperts SN, Kloosterman F, Wilson MA. VTA neurons coordinate with the hippocampal reactivation of spatial experience. Eichenbaum H, editor. eLife. 2015;4: e05360. doi: 10.7554/eLife.05360 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Ólafsdóttir HF, Bush D, Barry C. The role of hippocampal replay in memory and planning. Curr Biol. 2018;28: R37–R50. doi: 10.1016/j.cub.2017.10.073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Stella F, Baracskay P, O’Neill J, Csicsvari J. Hippocampal reactivation of random trajectories resembling Brownian diffusion. Neuron. 2019;102: 450–461. doi: 10.1016/j.neuron.2019.01.052 [DOI] [PubMed] [Google Scholar]
- 113.Lee AK, Wilson MA. Memory of sequential experience in the hippocampus during slow wave sleep. Neuron. 2002;36: 1183–1194. doi: 10.1016/s0896-6273(02)01096-6 [DOI] [PubMed] [Google Scholar]
- 114.Pfeiffer BE, Foster DJ. Hippocampal place-cell sequences depict future paths to remembered goals. Nature. 2013;497: 74–79. doi: 10.1038/nature12112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Davidson TJ, Kloosterman F, Wilson MA. Hippocampal replay of extended experience. Neuron. 2009;63: 497–507. doi: 10.1016/j.neuron.2009.07.027 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Chan F, Armstrong IT, Pari G, Riopelle RJ, Munoz DP. Deficits in saccadic eye-movement control in Parkinson’s disease. Neuropsychologia. 2005;43: 784–796. doi: 10.1016/j.neuropsychologia.2004.06.026 [DOI] [PubMed] [Google Scholar]
- 117.Pretegiani E, Optican LM. Eye movements in Parkinson’s disease and inherited parkinsonian syndromes. Front Neurol. 2017;8: 592. doi: 10.3389/fneur.2017.00592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Sedaghat-Nejad E, Herzfeld DJ, Shadmehr R. Reward prediction error modulates saccade vigor. J Neurosci. 2019;39: 5010–5017. doi: 10.1523/JNEUROSCI.0432-19.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Stephen DG, Mirman D, Magnuson JS, Dixon JA. Lévy-like diffusion in eye movements during spoken-language comprehension. Phys Rev E. 2009;79: 056114. doi: 10.1103/PhysRevE.79.056114 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Roberts JA, Wallis G, Breakspear M. Fixational eye movements during viewing of dynamic natural scenes. Front Psychol. 2013;4: 797. doi: 10.3389/fpsyg.2013.00797 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Marlow CA, Viskontas IV, Matlin A, Boydston C, Boxer A, Taylor RP. Temporal structure of human gaze dynamics is invariant during free viewing. PloS One. 2015;10: e0139379. doi: 10.1371/journal.pone.0139379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Tsai H-C, Zhang F, Adamantidis A, Stuber GD, Bonci A, De Lecea L, et al. Phasic firing in dopaminergic neurons is sufficient for behavioral conditioning. Science. 2009;324: 1080–1084. doi: 10.1126/science.1168878 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Chiang T-S, Hwang C-R, Sheu SJ. Diffusion for Global Optimization in $\mathbb{R}^n $. SIAM J Control Optim. 1987;25: 737–753. doi: 10.1137/0325042 [DOI] [Google Scholar]
- 124.Gelfand SB, Mitter SK. Recursive Stochastic Algorithms for Global Optimization in $\mathbb{R}^d $. SIAM J Control Optim. 1991;29: 999–1018. doi: 10.1137/0329055 [DOI] [Google Scholar]
- 125.Lee H, Risteski A, Ge R. Beyond Log-concavity: Provable Guarantees for Sampling Multi-modal Distributions using Simulated Tempering Langevin Monte Carlo. In: Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, Garnett R, editors. Advances in Neural Information Processing Systems 31. Curran Associates, Inc.; 2018. pp. 7847–7856. Available: http://papers.nips.cc/paper/8010-beyond-log-concavity-provable-guarantees-for-sampling-multi-modal-distributions-using-simulated-tempering-langevin-monte-carlo.pdf [Google Scholar]
- 126.Erdogdu MA, Mackey L, Shamir O. Global Non-convex Optimization with Discretized Diffusions. In: Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, Garnett R, editors. Advances in Neural Information Processing Systems 31. Curran Associates, Inc.; 2018. pp. 9671–9680. Available: http://papers.nips.cc/paper/8175-global-non-convex-optimization-with-discretized-diffusions.pdf [Google Scholar]
- 127.Ma Y-A, Chen Y, Jin C, Flammarion N, Jordan MI. Sampling can be faster than optimization. Proc Natl Acad Sci. 2019;116: 20881–20885. doi: 10.1073/pnas.1820003116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Chen Y, Chen J, Dong J, Peng J, Wang Z. Accelerating Nonconvex Learning via Replica Exchange Langevin Diffusion. ArXiv200701990 Cs Math Stat. 2020. [cited 13 Oct 2020]. Available: http://arxiv.org/abs/2007.01990 [Google Scholar]
- 129.Long J, Zucker SW, Emonet T. Feedback between motion and sensation provides nonlinear boost in run-and-tumble navigation. PLoS Comput Biol. 2017;13: e1005429. doi: 10.1371/journal.pcbi.1005429 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 130.Eisenegger C, Naef M, Linssen A, Clark L, Gandamaneni PK, Müller U, et al. Role of dopamine D2 receptors in human reinforcement learning. Neuropsychopharmacology. 2014;39: 2366–2375. doi: 10.1038/npp.2014.84 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Cinotti F, Fresno V, Aklil N, Coutureau E, Girard B, Marchand AR, et al. Dopamine blockade impairs the exploration-exploitation trade-off in rats. Sci Rep. 2019;9: 1–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Frank MJ, Doll BB, Oas-Terpstra J, Moreno F. The neurogenetics of exploration and exploitation: Prefrontal and striatal dopaminergic components. Nat Neurosci. 2009;12: 1062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Costa VD, Tran VL, Turchi J, Averbeck BB. Dopamine modulates novelty seeking behavior during decision making. Behav Neurosci. 2014;128: 556. doi: 10.1037/a0037128 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 134.Raginsky M, Rakhlin A, Telgarsky M. Non-convex learning via Stochastic Gradient Langevin Dynamics: a nonasymptotic analysis. ArXiv170203849 Cs Math Stat. 2017. [cited 2 Aug 2020]. Available: http://arxiv.org/abs/1702.03849 [Google Scholar]
- 135.Xu P, Chen J, Zou D, Gu Q. Global Convergence of Langevin Dynamics Based Algorithms for Nonconvex Optimization. In: Bengio S, Wallach H, Larochelle H, Grauman K, Cesa-Bianchi N, Garnett R, editors. Advances in Neural Information Processing Systems 31. Curran Associates, Inc.; 2018. pp. 3122–3133. Available: http://papers.nips.cc/paper/7575-global-convergence-of-langevin-dynamics-based-algorithms-for-nonconvex-optimization.pdf [Google Scholar]
- 136.Barkai N, Leibler S. Robustness in simple biochemical networks. Nature. 1997;387: 913–917. doi: 10.1038/43199 [DOI] [PubMed] [Google Scholar]
- 137.Alon U, Surette MG, Barkai N, Leibler S. Robustness in bacterial chemotaxis. Nature. 1999;397: 168–171. doi: 10.1038/16483 [DOI] [PubMed] [Google Scholar]
- 138.Ferrell JE Jr. Perfect and near-perfect adaptation in cell signaling. Cell Syst. 2016;2: 62–67. doi: 10.1016/j.cels.2016.02.006 [DOI] [PubMed] [Google Scholar]
- 139.Stauffer WR, Lak A, Schultz W. Dopamine reward prediction error responses reflect marginal utility. Curr Biol. 2014;24: 2491–2500. doi: 10.1016/j.cub.2014.08.064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Doya K. Reinforcement learning in continuous time and space. Neural Comput. 2000;12: 219–245. doi: 10.1162/089976600300015961 [DOI] [PubMed] [Google Scholar]
- 141.Barto AG, Sutton RS, Watkins C. Learning and sequential decision making. University of Massachusetts Amherst, MA; 1989. [Google Scholar]
- 142.Coulthard EJ, Bogacz R, Javed S, Mooney LK, Murphy G, Keeley S, et al. Distinct roles of dopamine and subthalamic nucleus in learning and probabilistic decision making. Brain. 2012;135: 3721–3734. doi: 10.1093/brain/aws273 [DOI] [PMC free article] [PubMed] [Google Scholar]