General Equation to Express Changes in the Physicochemical Properties of Organic Homologues

Abstract

Changes in various physicochemical properties (P_(n)) of organic compounds with the number of carbon atoms (n) can be roughly divided into linear and nonlinear changes. To date, there has been no general equation to express nonlinear changes in the properties of organic homologues. This study proposes a general equation expressing nonlinear changes in the physicochemical properties of organic homologues, including boiling point, viscosity, ionization potential, and vapor pressure, named the “NPOH equation”, as follows: P_(n) = P₍₁₎α^n – 1e^{∑_i=2n(β/(i – 1))} where α and β are adjustable parameters, and P₍₁₎ represents the property of the starting compound (pseudo-value at n = 1) of each homologue. The results show that various nonlinear changes in the properties of homologues can be expressed by the NPOH equation. Linear and nonlinear changes in the properties of homologues can all be correlated with n and the “sum of carbon number effects”, ∑_i=2ⁿ(1/i – 1). Using these two parameters, a quantitative correlation equation can be established between any two properties of each homologue, providing convenient mutual estimation of the properties of a homologue series. The NPOH equation can also be used in property correlation for structures with functionality located elsewhere along a linear alkyl chain as well as for branched organic compounds. This work can provide new perspectives for studying quantitative structure–property relationships.

1. Introduction

In 2021, Kontogeorgis et al.¹ investigated the industrial requirements for thermodynamic and transport properties, reporting that: “In terms of models, companies ideally wish for a single universal model for all/many applications, but there is understanding that this is possibly utopian. The second major wish is the need for predictive models validated on extensive experimental databases and not only on just a few available experimental data points.” This shows the importance of molecular modeling. The quantitative structure–property relationship (QSPR) method is important for understanding and predicting compound properties and it has seen rapid development.^2,3 Recently, molecular dynamics and machine learning have also been used in drug design.⁴

The two key steps for developing successful QSPR models are molecular descriptor calculations and equation selection. Generally, the development of validated QSPR models first involves calculating the molecular descriptors and then, based on experimental data, selecting an appropriate number of descriptors from a large number of calculated molecular descriptors to establish the QSPR equation.^2,5−9 In this method, descriptor screening and equation optimization are time-consuming, and the physical meaning of the resulting equations is unclear and difficult to interpret. Other methods are also available for predicting the physicochemical properties of compounds. In these methods, theoretical equations are first proposed and molecular characteristic parameters are extracted for specific compounds. Data fitting is then used to form specific application equations, such as in state equation 1(2)

1

where u and w are characteristics of the equation (u = 1 and w = 0 or u = 2 and w = −1 for Redlich-Kwong¹⁰ or Peng–Robinson (PR),¹¹ respectively), and a and b are parameters computed using critical pressure (P_c) and temperature (T_c), as shown in eqs 2 and 3

2

3

where Ω_a and Ω_b have specific values depending on the selected equation, and the temperature function, α(T), is equal to 1 for T = T_c. Similar to eq 1, these theoretical equations have clear physical meanings, allowing molecular descriptors to be calculated in a targeted manner. However, this type of equation is not easy to propose.

The aforementioned methods show that a QSPR equation can be established more easily if the general regularity of changes in compound properties is known in advance and then molecular descriptors are selected. Therefore, we have considered classifying chain organic compounds and discussing the regularity of changes in their properties, which is more conducive to establishing QSPR equations. Accordingly, organic compounds with different functional groups were first divided into homologues and then into isomers. Following the concept of homologue–isomer property correlation, we can establish a structure–property correlation equation for chain organic compounds with different functional groups. Changes in the properties (P) of organic homologues are known to be related to the number of carbon atoms (n), allowing a theoretical equation between P and n, P = f(n), to be established. On this basis, the characteristic parameter of the molecular structure of an isomer (s) can be extracted using the molecular descriptor calculation in the QSPR method, and then the property-change equation of the chain organic compound (P = f(n, s)) can be established. This accounts for the advantages of the two aforementioned methods and reduces the difficulty of establishing structure–property correlation equations. This study aimed to explore a general equation for expressing changes in the physicochemical properties of organic homologues.

Much research has focused on expressing the regularity of property changes in organic homologues, with four types of empirical expression having been proposed. As early as 1961, Kreglewsky¹² proposed eq 4 to evaluate the boiling points of n-paraffin compounds in the range of C₁–C₁₀₀. This work pioneered the quantitative correlation of homologue properties

4

where Y is the boiling point value at carbon number n and Y₀ is the boiling point pseudo-value at n = 0, Y_∞ = 1078, and β = 4.999 × 10^–3.

In 1985, Gasem and Robinson et al.^13,14 proposed eq 5 for evaluating the critical properties of n-paraffins, known as the ABC equation

5

where variables Y, Y_∞, and Y₀ are property values at carbon number n, the limiting property value as n becomes very large, and the property pseudo-value at n = 1, respectively, and β and α are adjustable parameters.

In 1997, Marano and Holder¹⁵ proposed eq 6 to correlate the thermodynamic and transport properties of n-paraffins and other homologous series, which can be used for a wide range of different thermophysical properties

6

where five adjustable parameters, n₀, Y₀, Y_∞, β, and γ, are employed.

In 2009, Zenkevich¹⁶ employed a recurrent function to correlate the properties of homologous series, as shown in eq 7

7

where A(n + 1) is the physicochemical property value for homologues with (n + 1) carbon atoms, A(n) is the property value for homologues with n carbon atoms, and coefficients a and b are calculated by the least squares method. Equation 7 is different from eqs 4–6 because the parameter Y_∞ is not required.

Notably, eq 4 was proposed more than 60 years ago, and the inherent change regularity of homologue properties with carbon number n remains unknown. The equations proposed previously provide great insight, but two problems remain: (i) Their physical meaning is unclear, making them difficult to explain; and (ii) they cannot correlate one property to another property for a series of homologues. Therefore, this study investigated the change regularity of homologue properties with carbon atom number n to explore the relationship between the properties of homologues.

2. Results and Discussion

2.1. Theoretical Analysis

Changes in the physicochemical properties (P) of organic homologues with carbon atom number n can be roughly divided into linear and nonlinear changes. The linear change of a property is relatively simple and will not be discussed in detail here. This study focuses on the complex nonlinear change of a property. Using n-paraffins (H–(CH₂)_n–H) as an example, some P values increase with an increasing n value, while some P values decrease with an increasing n value, The P changes show significant differences, as shown in Figure 1. We investigated how these different changes are dominantly affected by n, and whether all of these changes follow a common rule, through theoretical analysis. Usually, organic homologues can be represented as X–(A)_n–Y, where A is a repeating structural unit, n is the number of repeating structural units, and X and Y are end groups. For n-paraffins, A is CH₂, and both X and Y are H atoms, represented by H–(CH₂)_n–H. In a series of organic homologues, the property of compound X–(A)_n–Y containing n repeating structural units is represented by P_(n), and the property of another compound containing n – 1 repeating structural units X–(A)_n−1–Y is represented by P_(n–1). The molecular structure of X–(A)_n–Y is known to be formed by adding repeating structural unit A to molecule X–(A)_n−1–Y, namely, X–(A)_n−1–Y becomes X–(A)_n−1–A–Y. The addition of unit A causes a change of property P_(n–1) of X–(A)_n−1–Y to property P_(n) of X–(A)_n–Y. Therefore, property P_(n) of X–(A)_n–Y can be considered a perturbation based on property P_(n–1) of X–(A)_n−1–Y. This perturbation effect must be related to the original molecular chain length (A)_n−1. Assuming that the perturbation effect acts in the form of an exponential, exp(β/(n – 1)), then, the relationship between P_(n) and P_(n–1) can be expressed by eq 8

8

where α is the proportional coefficient of the property change and β is an adjustable parameter of the perturbation effect. Based on eq 8, expressions for P₍₂₎, P₍₃₎, P₍₄₎, ..., can be deduced as follows

9

10

11

From eqs 9–11, eq 8 can also be expressed as eq 12

12

Equation 12 expresses the relationship between the property of organic homologues X–(A)_n–Y and the number of repeating structural units, n. If the logarithm is taken, eq 12 can be expressed as eq 13

13

where a = ln(P₍₁₎), b = ln(α), and c = β. These are characteristic coefficients related to the properties of each homologue and can be obtained by regression analysis. For convenience, term 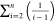in eqs 12 and 13 is subsequently denoted as S_CNE (abbreviation of “sum of carbon number effects”). Accordingly, eqs 12 and 13 can be written in compact forms of eqs 14 and 15, respectively, named the “NPOH equation” (that is, the abbreviation of “Nonlinear Properties of Organic Homologues equation”)

14

15

In contrast to eqs 4–7, eqs 12 and 14 show that property P_(n) of homologue X–(A)_n–Y is related to the starting compound property P₍₁₎ (property pseudo-value at n = 1) of each homologue, as well as the number of repeating structural units, n, and the cumulative perturbation effect, S_CNE, of repeating structural units.

Figure 1.

(a) Relationship of boiling point (T_b), (b) viscosity (μ), and (c) ionization potential (I_p) with the carbon atom number (n) of n-paraffins.

2.2. Applicability of NPOH Equation

2.2.1. Correlation with the Properties of n-Paraffins

To test the applicability of NPOH equations 14 or 15, quantitative correlation analysis was conducted using various physicochemical properties (nonlinear changes) of n-paraffins. First, the S_CNE value was calculated, as listed in Table 1, and then eq 15 was employed as a model to perform regression analysis of properties P_(n) of n-paraffins. The results are listed in Table 2.

Table 1. Number of Repeating Structural Units, n, and S_CNE Values.

n	n – 1	SCNE	n	n – 1	SCNE	n	n – 1	SCNE	n	n – 1	SCNE
1	0		26	25	3.8160	51	50	4.4992	76	75	4.9014
2	1	1.0000	27	26	3.8544	52	51	4.5188	77	76	4.9145
3	2	1.5000	28	27	3.8915	53	52	4.5380	78	77	4.9275
4	3	1.8333	29	28	3.9272	54	53	4.5569	79	78	4.9403
5	4	2.0833	30	29	3.9617	55	54	4.5754	80	79	4.9530
6	5	2.2833	31	30	3.9950	56	55	4.5936	81	80	4.9655
7	6	2.4500	32	31	4.0272	57	56	4.6115	82	81	4.9778
8	7	2.5929	33	32	4.0585	58	57	4.6290	83	82	4.9900
9	8	2.7179	34	33	4.0888	59	58	4.6463	84	83	5.0021
10	9	2.8290	35	34	4.1182	60	59	4.6632	85	84	5.0140
11	10	2.9290	36	35	4.1468	61	60	4.6799	86	85	5.0257
12	11	3.0199	37	36	4.1746	62	61	4.6963	87	86	5.0374
13	12	3.1032	38	37	4.2016	63	62	4.7124	88	87	5.0489
14	13	3.1801	39	38	4.2279	64	63	4.7283	89	88	5.0602
15	14	3.2516	40	39	4.2535	65	64	4.7439	90	89	5.0715
16	15	3.3182	41	40	4.2785	66	65	4.7593	91	90	5.0826
17	16	3.3807	42	41	4.3029	67	66	4.7744	92	91	5.0936
18	17	3.4396	43	42	4.3267	68	67	4.7894	93	92	5.1044
19	18	3.4951	44	43	4.3500	69	68	4.8041	94	93	5.1152
20	19	3.5477	45	44	4.3727	70	69	4.8186	95	94	5.1258
21	20	3.5977	46	45	4.3949	71	70	4.8328	96	95	5.1363
22	21	3.6454	47	46	4.4167	72	71	4.8469	97	96	5.1468
23	22	3.6908	48	47	4.4380	73	72	4.8608	98	97	5.1571
24	23	3.7343	49	48	4.4588	74	73	4.8745	99	98	5.1673
25	24	3.7760	50	49	4.4792	75	74	4.8880	100	99	5.1774

Table 2. Correlation Equations of Properties for n-Paraffins H–(CH₂)_n–H (Model Equation: ln(P_(n)) = a + b(n – 1) + cS_CNE).

no.	propertya	range of nb	ref	a	b	c	R	S	Nc	F
1	Tb	2–100	(17)	4.6973	–0.004569	0.51040	0.9999	0.0057	34	73 691.18
2	Tc	2–20	(20)	5.2972	–0.008981	0.42758	0.9999	0.0030	19	65 747.43
3	Pc	2–20	(20)	1.9097	–0.050147	–0.24698	0.9992	0.0191	19	5084.85
4	Cp	4–16	(21)	3.6382	0.025666	0.66368	0.9997	0.0099	11	7888.46
5	λ	5–16	(22)	–2.7579	–0.014647	0.30762	0.9944	0.0101	7	177.44
6	ST	5–16	(22)	1.1369	–0.048077	0.86717	0.9990	0.0108	7	978.56
7	μ	5–35	(18)	–5.6286	0.043485	1.79992	0.9996	0.0448	28	14 301.74
8	nD	4–20	(21)	0.15997	–0.003447	0.076226	0.9987	0.0012	16	2534.24
9	Pv	2–16	(21)	7.4528	–0.461790	–0.36834	1.0000	0.0103	15	347 794.19
10	ω	2–20	(23)	–3.2314	–0.005694	0.90514	0.9997	0.0158	19	13 904.65
11	Ip	2–11	(19)	2.5643	0.004981	–0.12156	0.9996	0.0020	10	4094.40
12	D	5–16	(19)	–1.0445	–0.016174	0.30966	0.9994	0.0025	12	3850.05
13	TF	3–16	(24) and (25)	4.4783	0.000031	0.45456	0.9970	0.0213	14	915.62
14	Pw	2–8	(26)	1.1261	0.536478	0.12495	0.9990	0.0716	6	736.35

^aT_b, boiling point (K); T_c, critical temperature (K); P_c, critical pressure (MPa); C_p, heat capacity (J·mol^–1·K^–1); λ, thermal conductivity (W·m^–1 K^–1); S_T, surface tension (mN·m^–1); μ, liquid viscosity [μm Pa·s(300 K)]; n_D, refractive Index; P_v, vapor pressure (regression in the form of log P_v); ω, acentric factor; I_p, ionization potential (eV); D, liquid density (g·cm³); T_F, flash point (K); and P_w, partition coefficient (regression in the form of log P_w). These properties data are listed in the Supporting Information.

^bCarbon atom number range.

^cNumber of data points.

The results listed in Table 2 show that the correlation coefficients (R) were all above 0.99 for the correlation equations of 14 properties of n-paraffins, indicating that eq 15 can be used to express the regularity of property changes among homologues using the carbon atom number n. That properties with different change regularities can have the same expression is surprising and has not been reported previously.

We noted that a value of boiling point T_b equation in Table 2 (no. 1) is 4.6973, indicating that ln(P₍₁₎) is 4.6973, and the starting compound boiling point (pseudo-value at n = 1), P₍₁₎, is 109.65 K for n-paraffins. The experimental boiling point of methane is known to be 109.15 K, which is very close to 109.65 K.

Interestingly, for the linear change property, P_LC(n), of homologues, it was only necessary to directly replace term ln(P_(n)) in eq 15 with term P_LC(n), as shown in eq 16

16

For example, for the critical volume²¹ (V_c) of n-paraffins (n = 2–18), n was used directly to perform regression against V_c, giving eq 17, while eq 16 was used as the model equation to perform regression against V_c to obtain eq 18. Equation 18 showed better correlation compared with eq 17, and the standard error (S) was greatly reduced

17

18

As another example, the vaporization enthalpy²¹ (H_v) of n-paraffins (n = 2–20) was regressed with the methods used in eqs 17 and 18, giving eqs 19 and 20. The correlation of eq 20 was better than that of eq 19, and the standard error (S) of eq 20 was greatly reduced

19

20

The above regression analysis results show that eq 16 is more suitable for expressing the linear change properties of homologues compared with directly using n. However, for some linear change properties of homologues, such as molar mass (M_mol), coefficient c in eq 16 was equal to zero, meaning that the term S_CNE did not need to be used in such cases.

2.2.2. Correlation with the Properties of Other Homologues

Regarding whether eq 15 was applicable to other homologues, cycloalkanes, terminal alkenes, terminal alkynes, linear alcohols, 2-methylparaffins, 2,2-dimethylparaffins, 2,3-dimethylparaffins, and 1-cyclopentylparaffins were selected as model compounds for testing. Using the boiling points T_b of cycloalkanes, terminal alkenes, terminal alkynes, linear alcohols, 2-methylparaffins, 2,2-dimethylparaffins, 2,3-dimethylparaffins, and 1-cyclopentylparaffins and the partition coefficient P_w of alcohols as verification examples, quantitative correlation analysis was conducted using model equation15. The results are listed in Table 3, showing that the property correlation was very good for each homologue, and that the correlation coefficients (R) of the nine equations were all greater than 0.999. These results showed that eq 15 is a general equation that can be used to express the change regularity of properties P of various homologues using carbon atom number n.

Table 3. Correlation Equations of Properties for Cycloalkanes, Alkenes, Alkynes, Alcohols, 2-Methylparaffins, 2,2-dimethylparaffins, 2,3-Dimethylparaffins, and 1-Cyclopentylparaffins (Model Equation: ln(P_(n)) = a + b(n – 1) + cS_CNE).

^a)P_w, partition coefficient (regression in the form of logP_w); other symbols are defined in Table 1. These properties data are listed in the Supporting Information.

^b)Carbon atom number range.

^c)Number of data points.

The results obtained in Sections 2.2.1 and 2.2.2 show that, regardless of whether the properties of homologues vary linearly or nonlinearly with carbon atom number n, they can be related using variables (n – 1) and S_CNE.

2.2.3. Relationship between Nonlinear Properties of Homologues

Equation 15 not only expresses the change regularity of the properties of homologues with the carbon atom number n but can also link the change regularities of different properties of homologues. If one property of homologue is P_(n) and the other property is P′_(n), basing on eq 15, we can theoretically deduce eqs 21 and 22

21

22

In eq 21, a_r = ln(P₍₁₎) – ln(P′₍₁₎), b_r = ln(α) – ln(α′), and c_r = β – β′, while in eq 22, a_s = ln(P₍₁₎) + ln(P′₍₁₎), b_s = ln(α) + ln(α′), and c_s = β + β′. For the two specific physicochemical properties, P_(n) and P′_(n), of the same series of compounds, parameters a_r, b_r, c_r, a_s, b_s, and c_s can be obtained using the regression method.

When the logarithms of eqs 21 and 22 are removed, they return to eqs 23 and 24

23

24

Equations 23 and 24 express the relationship between two properties of a homologues series, where k, l, c_r, m, q, and c_s are all coefficients. Therefore, one property of homologues can be correlated with another using eqs 23 and 24, providing convenient correlation of the homologue properties.

For example, the relationship between the critical temperature (T_c) and boiling point (T_b) of n-paraffins is shown in eq 25

25

Equation 25 expresses the quantitative relationship between T_b and T_c for n-paraffins. Using eq 25, the critical temperatures of n-paraffins can be calculated from their boiling points. Table 4 shows the results of critical temperature calculations for n-paraffins with n = 2–32, where the average absolute error between the experimental value (T_c,exp.) and the calculated value (T_c,cal.) was 1.84 K for the 19 compounds (n = 2–20). Figure 2 shows a plot of the calculated and experimental values of critical temperature versus the boiling point of n-paraffins.

Table 4. Experimental and Calculated Critical Temperature, T_c (K), for n-Paraffins H–(CH₂)_n–H.

na	Tb,exp.b	Tc,exp.c	Tc,cal.d	na	Tb,exp.b	Tc,exp.c	Tc,cal.d	na	Tb,exp.b	Tc,exp.c	Tc,cal.d
2	184.55	305.6	307.84	13	508.29	676.1	678.36	24	664.29		793.90
3	231.05	369.2	368.85	14	526.69	693.1	694.86	25	674.29		798.76
4	272.65	425.2	421.91	15	543.59	708.1	709.23	26	685.19		804.63
5	309.25	469.9	466.84	16	559.99	722.1	722.82	27	695.09		809.28
6	342.15	507.7	505.80	17	574.79	734.1	734.23	28	704.59		813.41
7	371.55	540.7	539.25	18	589.09	747.1	744.90	29	713.79		817.16
8	398.85	568.9	569.35	19	601.99	755.4	753.71	30	722.69		820.52
9	423.92	594.6	596.00	20	615.99	767.6	763.81	31	731.69		823.96
10	447.27	617.8	620.00	21	629.49		773.20	32	740.09		826.68
11	468.79	639.1	641.24	22	641.59		780.77
12	489.29	658.2	660.90	23	653.19		787.67

^aNumber of carbon atoms.

^bExperimental boiling point (K), from ref (17).

^cExperimental critical temperature (K), from ref (20).

^dCritical temperature calculated using eq 25.

Figure 2.

Plot of calculated (solid line) and experimental (open circle) critical temperature (T_c) values versus experimental boiling point (T_b) of n-paraffins (n = 2–32).

As further examples, eqs 23 and 24 were used as model equations to quantitatively correlate the boiling point of n-paraffins with other properties in Table 2. The results are listed in Table 5, showing that any nonlinear change property of n-paraffins could be correlated with the boiling point. As another example, the liquid viscosity (μ) equation in Table 5 (no. 6) was used to calculate the μ values (at 300 K) of n-paraffins using boiling points (T_b), with the results shown in Figure 3. The calculated values were in good agreement with the experimental values.

Table 5. Correlation Equations between the Boiling Point, T_b, and Other Properties of n-Paraffins (Model Equations 23 and 24).

no.	propertya	range of n	ar(as)	br(bs)	cr(cs)	R	S	N	F
1	Tc	2–20	0.593807	–0.0056465	–0.07651	0.9989	0.0042	19	3715.10
2	Pc	2–20	–2.79364	–0.0468120	–0.75107	0.9996	0.0235	19	10 289.86
3	Cp	4–16	–1.01102	0.0314657	0.13146	0.9988	0.0095	11	1670.97
4	λ	5–16	–7.39959	–0.0084513	–0.22859	0.9979	0.0104	7	476.21
5	STb	5–16	(5.77866)	(−0.0542733)	(1.40338)	0.9998	0.0106	7	4300.28
6	μ	5–32	–10.2984	0.0487215	1.27732	0.9992	0.0475	25	6681.44
7	nD	4–20	–4.48113	0.0030487	–0.46118	1.0000	0.0019	16	98 646.53
8	Pv	2–16	2.737019	–0.4605237	–0.86135	1.0000	0.0119	15	339 306.10
9	ω	2–10	–7.934717	–0.0023596	0.401052	0.9991	0.0126	19	4279.41
10	Ip	2–11	–2.172143	0.0013372	–0.593327	0.9999	0.0056	10	19 231.41
11	D	5–16	–5.686163	–0.0099647	–0.226592	0.9998	0.0026	12	12752.15
12	TFb	3–16	(9.143340)	(−0.0048236)	(0.977959)	0.9993	0.0206	14	4213.98
13	Pw	2–8	–3.631401	0.5256402	–0.321655	0.9985	0.0686	6	487.63

^aSymbols are defined in Table 1, obtained using model equation 23 except when noted otherwise.

^bObtained using model equation 24.

Figure 3.

Plot of calculated (−) and experimental (△) liquid viscosity, μ, values versus experimental boiling point, T_b, of n-paraffins (n = 5–32).

2.2.4. Relationship between Nonlinear and Linear Properties of Homologues

Equation 16 expresses the change regularity of the linear properties of homologues, while eq 15 expresses the change regularity of the nonlinear properties of homologues. Comparing eq 16 with eq 15 showed that they had the same variables (n – 1) and S_CNE. Therefore, a correlation between the nonlinear and linear properties of the homologues can be established by combining eqs 16 and 15, as shown in eq 26

26

where, for the two specific physicochemical properties, P_(n) and P_LC(n), of the same series of homologues, parameters a′, b′, and c′ can be obtained by the regression method

Using the boiling point (T_b) and critical volume (V_c) of n-paraffins as an example

27

Therefore

28

Here, taking V_c, (n – 1), and S_CNE as variables, regression equation 29 can be obtained for ln(T_b)

29

Equation 29 can be rewritten as eq 30

30

Using eq 30 and employing parameters V_c, (n – 1), and S_CNE of n-paraffins, the T_b values of n-paraffins can be calculated. The average absolute error between the experimental and calculated T_b values was 0.94 K for the 17 n-paraffins with n = 2–18.

2.2.5. Simplification of Equation

Equations 12 and 13 contain the term , which is inconvenient to use. This section discusses the simplification of this term. According to mathematical principles, for the infinite series SS{1, 1/2, 1/3, ..., 1/n}, the sum of the first n terms is shown in eq 31

31

Equation 31 can also be approximately expressed as eq 32

32

Therefore, the term 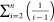can be expressed as follows

33

Therefore, eqs 12 and 13 can be simplified to eqs 34 and 35

34

35

For example, using eq 35 as a model equation to perform regression analysis of T_b and T_c values of n-paraffins, respectively, afforded eqs 36 and 37

For the boiling point (T_b)

36

For the critical temperature (T_c)

37

Equations 36 and 37 still show good correlation, which is only slightly worse than that of the corresponding equations (nos. 1 and 2 of Table 2). However, eqs 36 and 37 are more convenient to use than eqs 12 and 13.

2.2.6. Relationship between S_CNE and the Parameter c(G)

Recently, Mukwembi et al.²⁷ proposed a new graph parameter c(G), called the conduction of a graph, and exploited the conduction of a graph to develop a single parameter model for predicting the boiling point of any given alkane. This work is very meaningful, which simplifies the parameters for estimating the boiling point of alkanes. It is interesting to compare and contrast the S_CNE parameter with the parameter c(G). Here, we made a plot of exp(S_CNE) of this work versus the parameter c(G)²⁷ of n-paraffins (n = 4–14), and obtained Figure 4. From Figure 4, we can see that there is a good linear correlation of exp(S_CNE) with the parameter c(G). It means that the parameter exp(S_CNE) is intrinsically related to the parameter c(G) for n-paraffins. Whether there is a relationship of exp(S_CNE) to other graph theoretical parameters or not is worth studying, and the interested readers can pursue this area.

Figure 4.

Plot of exp(S_CNE) versus the parameter c(G) of ref (27) for n-paraffins (n = 4–14).

2.2.7. Application of NPOH Equation in Branched Alkanes and Alcohols

For the branched alkanes and organic compounds with functionality located elsewhere along a linear alkyl chain, their physical properties are first affected by the number of carbon atoms in the structure, and second by their molecular structure differences. Therefore, we can establish an estimation model of their properties by adding structural parameters that characterize the molecular carbon atomic skeleton to the NPOH equation. We take the boiling points of alkanes and alcohols for example.

2.2.7.1. Example 1, Boiling Point of Alkanes

Alkane molecules are almost nonpolar, and their boiling points are affected by both the number of carbon atoms and the molecular carbon atomic skeleton in the molecule. The effect of the number of carbon atoms on the boiling point can be expressed with the parameters (n – 1) and S_CNE, while that of the molecular carbon atomic skeleton can be expressed using the Odd–Even Index (OEI) difference, ΔOEI.²¹ That is, for the alkane molecule with n carbon atoms, ΔOEI = OEI (branched alkane) – OEI (normal alkane). Based on Yuan’s method,²¹ the OEI values of 2-methylpropane and butane are 4.5000 and 5.2222, respectively. Thus, ΔOEI(2-methylpropane) = 4.5000 – 5.2222 = −0.7222; ΔOEI (butane) = 4.5000 – 4.5000 = 0. It means that ΔOEI = 0 for any normal alkane. Then, we employed (n – 1), S_CNE, and (ΔOEI/n) as variables to perform the regression analysis of boiling points, T_b(n), of alkanes and obtained eq 38 in which the boiling points for all alkanes were taken from a listing by Cao et al.²⁸ These data are listed in the Supporting Information

38

In eq 38, the 210 alkanes involve all isomers of C₂–C₁₀, and the carbon atoms are in the range of C₁–C₁₀₀. The average absolute error between the experimental value (T_b,exp.) and the calculated value (T_b,cal.) was 3.07 K, and the average percentage error was 0.69%.

2.2.7.2. Example 2, Boiling Point of Alcohols

The molecular structure of alcohol is different from that of alkane in which there is a polar functional group OH. Thus, the boiling points of alcohols are affected by the number of carbon atoms, molecular carbon atomic skeleton, and position of group OH located at the alkyl chain in a molecule. The effect of the latter two factors on the boiling point can be expressed by the polarization effect index PEI_OH difference, ΔPEI_OH, because the PEI_OH of the alcohol is related to the alkyl skeleton and the position of the OH group in the molecule. That is, for the alcohol molecule with n carbon atoms, ΔPEI_OH = PEI_OH (branched alcohol) – PEI_OH (normal alcohol). Taking 2-propanol (CH₃)₂CHOH (i-PrOH) and 1-propanol CH₃CH₂CH₂OH (PrOH), for example, the PEI_OH values of i-Pr and Pr are 1.2811 and 1.1887, respectively. Hence, the difference in PEI_OH of i-PrOH is ΔPEI_OH(i-PrOH) = 1.2811 – 1.1887 = 0.0924, and the difference in PEI_OH of PrOH is ΔPEI_OH(PrOH) = 1.1887 – 1.1887 = 0. It means that ΔPEI_OH = 0 for any normal alcohol. For the detailed calculation method of PEI_OH, one can refer to Cao’s report.²⁸ Thus, we employed (n – 1), S_CNE, and (ΔPEI_OH/n) as variables to perform regression analysis of boiling points T_b(n) of alcohols and obtained eq 39 in which the boiling points for all alcohols were taken from a listing by Cao et al.²⁸ These data are listed in the Supporting Information

39

In eq 39, the 105 alcohols involving the carbon atoms are in the range of C₂–C₁₁. The average absolute error between the experimental value (T_b,exp.) and the calculated value (T_b,cal.) was 4.40 K, and the average percentage error was 1.01%.

The results indicate that eqs 38 and 39 provide very satisfactory results. We noted that it is difficult to compare the results of this work with those of other works because different data sets and different number of variables were employed in various works. In particular, many of the other works only include alkanes with below 11 carbon atoms. Nevertheless, it is instructive that Allison et al.,²⁹ in 2022, used a graph convolutional neural network to predict the normal boiling point and obtained an average absolute error of 6 K (corresponding to an average percentage error of 1.32%). Cordes and Rarey³⁰ compared some group contribution methods for predicting the boiling points of acyclic alkanes and found that these methods produced average absolute errors ranging from 6.5 to 26.7 K. Palatinus et al.³¹ proposed eq 40 to calculate the Y_R parameter and then used the calculated Y_R values and eq 41 to predict the boiling point for linear and branched alkanes in which the average absolute deviation between experimental and predicted boiling points was 1.45 K, and the average percentage error was 0.32%. Liu et al.³² used the QSPR method to predict the boiling points of alcohols and obtained the standard error of 5.69 K

40

41

The above two examples show that the NPOH equation can also be used in property correlation for structures with functionality located elsewhere along a linear alkyl chain as well as for branched organic compounds.

3. Conclusions

This research shows that various nonlinear change properties of homologues can be expressed using a general equation, named the NPOH equation (eqs 14 or 15), while various linear change properties of homologues can be expressed by general equation16. Therefore, both linear and nonlinear change properties of homologues can be correlated with the number of carbon atoms (n) and the “sum of carbon number effects” (S_CNE). Furthermore, using the two parameters n and S_CNE, a quantitative correlation equation can be established between any two properties of each homologue, providing convenient mutual estimation of properties of a series of homologues. Finally, for nonstraight-chain isomers, using the NPOH equation, we can add structural parameters that characterize the molecular carbon atomic skeleton to establish an estimation model for their properties. The study on the properties of branched chain organic compounds will be reported in a subsequent paper.

This work can provide a new perspective for studying quantitative structure–property relationships (QSPRs).

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.2c02828.

• Physicochemical properties of n-alkanes (Table S1); physicochemical properties of cycloalkanes, alkenes, alkynes, alcohols, 2-methylparaffins, 2,2-dimethylparaffins, 2,3-dimethylparaffins, and 1-cyclopentylparaffins (Table S2); boiling points of 210 alkanes (Table S3); and boiling points of 105 alcohols (Table S4) (PDF)

The authors declare no competing financial interest.